Stress Analysis and Operational Limits of an SLA-Printed Soft Antagonistic Actuator Using a Yeoh-Calibrated Finite Element Model

Abstract

Soft robotics has emerged as a promising approach for safe human–machine interaction, adaptive manipulation, and bioinspired motion, yet its progress relies on accurate material characterization and structural analysis of actuators. This study presents the mechanical behavior and stress analysis of a stereolithography-printed pneumatic actuator with antagonistic architecture, fabricated using Elastic 50A resin V2. Uniaxial tensile tests were performed according to ASTM D412 to derive material parameters, which were fitted to hyperelastic constitutive models. The Yeoh model was identified as the most accurate and implemented in finite element simulations to predict actuator deformation under multiple pressurization modes. Results revealed critical stress zones and established operational pressure limits of 110–130 kPa, beyond which the material approaches its tensile strength. Experimental testing with a controlled pneumatic system validated the numerical predictions, confirming both bending and multidirectional actuation as well as structural failure thresholds. The integration of material characterization, numerical modeling, and experimental validation provides a robust workflow for the design of SLA-fabricated antagonistic actuators. These findings highlight the advantages of combining digital fabrication with antagonistic actuation and material modeling to expand the understanding of soft robots’ behavior.

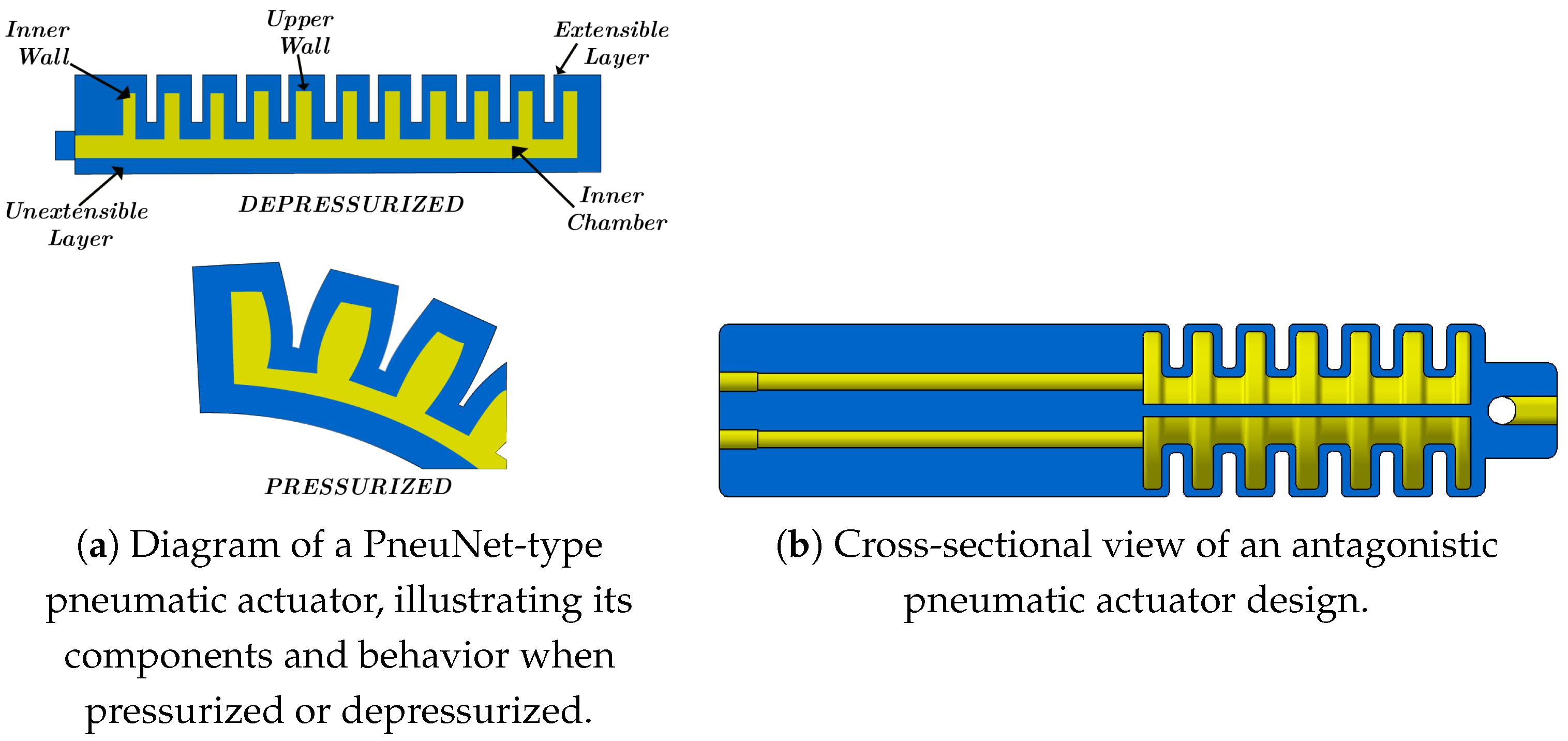
1. Introduction

Soft robotics is an emerging field that aims to replicate the movements and mechanical properties of living organisms through bioinspired systems [1,2]. These robots are fabricated using highly deformable elastomeric materials, including silicones, resins, hydrogels, and polymers [3,4]. Their motion arises from structural deformation, which provides flexibility and adaptability, making them particularly suitable for operation in uncertain or dynamic environments [5], for delicate object manipulation [6], and for ensuring safe human interaction in fields such as medicine, agriculture, and exploration [7,8,9].

Unlike conventional rigid robots powered by electric motors, soft robots rely on alternative actuation mechanisms such as tendons, pressurized fluids, magnetic or electric fields, and chemical reactions [10,11,12,13,14]. Among these, pneumatic actuators are the most extensively studied. They operate by inflating or deflating internal chambers to generate motions such as bending, stretching, compression, and twisting [15]. These actuators, known as PneuNets (Pneumatic Networks), are shown in Figure 1. By arranging multiple PneuNet actuators antagonistically, it is possible to reproduce muscle-like coordinated movement.

Traditionally, soft pneumatic actuators are manufactured by casting silicone elastomers. Although effective, this process is slow, costly, and limited in geometric complexity [16,17]. Additive manufacturing (AM), particularly stereolithography (SLA), has emerged as a promising alternative, enabling the mold-free fabrication of complex actuators with high resolution and geometric precision [18,19,20,21,22,23].

Several studies have demonstrated the potential of SLA in soft actuator fabrication. Peele et al. [20] pioneered the stereolithographic printing of an antagonistic four-chamber actuator capable of 3D deformation. However, the relatively stiff resin used (Shore 65A, Elastomeric Precursor (EP); Spot-E resin, Spot-A Materials Inc., Askeby, Denmark, elongation ≈40%) limited its strain capacity, and no constitutive modeling or finite element analysis (FEA) was performed. Subsequent works, notably by Xavier et al., advanced the integration of analytical modeling, FEA, and experimental validation for 3D-printed actuators. In [24], they emphasized the need for accurate hyperelastic characterization to capture nonlinear deformation and pressure–geometry coupling. In a related study [25], the authors reviewed computational modeling techniques, identifying the limitations of simplified analytical methods and stressing the importance of constitutive calibration for predictive reliability, principles that guided the present study.

Recent advances have extended toward functional materials and smart actuation strategies. Tawk et al. [26] presented a modular SLA-printed gripper integrating mechanical metamaterials for conformal grasping, validated through FEA and experimental testing. Gunawardane et al. [27] introduced deep learning algorithms to identify variable-stiffness configurations in zig-zag pneumatic actuators. These works illustrate a trend toward adaptive and intelligent soft systems. However, they primarily focus on motion control and stiffness tuning rather than on an experimental–numerical correlation of material properties, stress distribution, and failure behavior, critical aspects for reliability and scalability.

Parallel advances in material characterization have also underscored the need for rigorous constitutive modeling. The nonlinear and nearly incompressible behavior of elastomers requires robust hyperelastic formulations such as Neo-Hookean, Mooney–Rivlin, Yeoh, or Ogden models [28,29]. Shahzad et al. [30] demonstrated how fitting procedures based on uniaxial data can accurately reproduce material response under multiple loading modes when properly optimized. However, many SLA-based actuator studies still rely on nominal manufacturer data rather than experimentally fitted parameters, introducing uncertainty into FEA simulations. Recent works by Zamora-García et al. [22] and Zhuang et al. [23] characterized the mechanical response of photopolymer resins but did not link these data to actuator-level stress prediction or performance analysis.

In this work, we present the stress analysis of an SLA-printed soft antagonistic pneumatic actuator designed with four independent PneuNet chambers, inspired by Peele’s architecture.The actuator is fabricated using Elastic 50A Resin V2 (Formlabs Inc., Somerville, MA, USA), a softer material with improved elongation properties. The material is experimentally characterized through uniaxial tensile tests following the ASTM D412 standard [31]. Subsequently, the parameters of several hyperelastic models are calibrated in the Abaqus environment to identify the model that best reproduces the experimental behavior. The actuator’s response is then simulated using the Yeoh hyperelastic model under various operating modes, and the simulation results are validated experimentally, confirming the predictive capability of the numerical model.

Unlike previous studies that only demonstrated the printability of soft structures or performed basic material characterization, the present study integrates material testing, hyperelastic modeling, finite element simulation, and experimental validation. The main contributions of this work are as follows: (1) the direct fabrication of a four-chamber antagonistic actuator in a single SLA printing step, without molds, bonding, or assembly, capable of producing multidirectional bending, elongation, and compression; (2) the experimental characterization of Elastic 50A Resin V2 and calibration of the Yeoh hyperelastic model for accurate numerical prediction; (3) the finite element modeling of pressure thresholds, structural failure, and stress localization to define safe operational limits and (4) the experimental quantification of rupture pressures and their comparison with simulation results, confirming the conservative accuracy of the FEA-based predictions. Together, these contributions provide a complete digital–experimental workflow that supports the development of structurally reliable, reproducible and scalable soft actuators for bioinspired and biomedical robotic applications.

The remainder of this paper is organized as follows: Section 2 presents the material characterization process and the selection of appropriate hyperelastic models for the elastomer. Section 3 describes the design and fabrication of the actuator using stereolithography and the finite element analysis setup. Section 4 reports the finite element simulation results performed in Abaqus/CAE 6.14-1 (Dassault Systèmes, (Simulia Corp, Vélizy-Villacoublay, France), together with the corresponding experimental validation. Finally, Section 5 discusses the findings and outlines the main conclusions.

2. Materials and Methods

2.1. Elastic Materials

Elastomers, such as silicone rubbers used in soft robotics and pneumatic actuators, are highly deformable polymers capable of sustaining large reversible strains exceeding 500% without fracture. At small strains, their response can be approximated by linear stress–strain relationships using properties such as Young’s modulus and Poisson’s ratio. However, for large deformations, nonlinear elasticity frameworks based on continuum mechanics are required [32,33].

The deformation of a solid is described by the relationship between the material reference frame $\mathbf{R}$ and its deformed configuration $\mathbf{r}$, expressed as:

$$\mathbf{r}=\mathbf{r}(\mathbf{R},t)=\mathbf{R}+\mathbf{d}$$

(1)

where $\mathbf{d}$ is the displacement vector.

From this formulation, the deformation gradient $\mathbf{F}$ is defined as: $\mathbf{F}={\displaystyle \frac{\partial \mathbf{r}}{\partial \mathbf{R}}}$. The scalar quantity $J=det\left(\mathbf{F}\right)$ represents the local volume change. For nearly incompressible materials, it is typically assumed that $J\approx 1$. To objectively characterize deformation independently of orientation, the invariants of the Cauchy–Green deformation tensor are employed. These invariants, expressed in terms of the principal stretches ${\lambda }_1$, ${\lambda }_2$, and ${\lambda }_3$, are:

$$\begin{array}{cc}\hfill I_1=& {\lambda }_1^2+{\lambda }_2^2+{\lambda }_3^2\hfill \\ \hfill I_2=& {\lambda }_1^2{\lambda }_2^2+{\lambda }_2^2{\lambda }_3^2+{\lambda }_1^2{\lambda }_3^2\hfill \\ \hfill I_3=& {\lambda }_1^2{\lambda }_2^2{\lambda }_3^2\hfill \end{array}$$

(2)

These invariants provide the foundation for defining the strain energy functions used in hyperelastic models.

2.2. Hyperelastic Models

Hyperelastic models employ a strain energy density function W that depends on the invariants $I_1$, $I_2$, and, in general, $I_3$. For incompressible materials, $I_3=1$, so W is primarily expressed as a function of $I_1$ and $I_2$ [34,35].

The simplest model is the Neo-Hookean model, in which the strain energy depends only on the first invariant:

$$W=C_1(I_1-3)$$

(3)

where $C_1$ is a material constant directly related to the initial shear modulus.

For moderate deformations, the Mooney–Rivlin model incorporates a dependence on the second invariant:

$$W=C_{10}(I_1-3)+C_{01}(I_2-3)$$

(4)

where $C_{10}$ and $C_{01}$ are experimentally determined material constants.

For large deformations (exceeding 400%), the Yeoh model is widely employed [25,30]. It uses a polynomial expansion in terms of the first invariant:

$$W=C_{10}(I_1-3)+C_{20}{(I_1-3)}^2+C_{30}{(I_1-3)}^3$$

(5)

where $C_{10}$, $C_{20}$, and $C_{30}$ capture the material response across different strain levels.

These models allow prediction of the stress–strain relationship under different loading modes based on relatively simple energy functions, making them well suited for implementation in finite element simulations.

2.3. Material Characterization and Hyperelastic Model Fitting

The material used was Elastic 50A Resin V2, which, after curing, exhibits a Shore hardness of 55A, a tensile strength of 3.4 MPa, an elongation at break of 160%, and a density of 1.01 g/cm³ [36]. These properties make it well suited for pneumatic soft actuators due to its elasticity, resilience, and durability under repeated loading cycles. Moreover, its fabrication via stereolithography (SLA) 3D printing eliminates the need for traditional molding, bonding and post-assembly techniques, streamlining the production process.

To accurately characterize the mechanical and nonlinear behavior of this elastomer, a series of mechanical tests should ideally be conducted, including uniaxial, biaxial, planar tensile, and compression tests. The nonlinear response obtained enables the determination of the coefficients for hyperelastic models. Several studies have shown that these coefficients can be reliably estimated from uniaxial tensile tests alone [29,30].

Following ASTM (American Society for Testing and Materials) D412 standards, uniaxial tensile tests were performed using a SHIMADZU Autograph AGS-X testing machine, (SHIMADZU Corp, Kyoto, Japan) equipped with a 50 kN load cell. Five dumbbell-shaped specimens (Type C) [31] were fabricated using the Elastic 50A Resin V2 (see Figure 2) printed on a Form 3+ SLA printer (Formlabs Inc., Somerville, MA, USA). Nominal stress–strain data were calculated as:

$${\epsilon }_{\mathrm{nominal}}=\lambda -1,{\sigma }_{\mathrm{nominal}}={\displaystyle \frac{F}{A_0}},$$

(6)

where $\lambda$ is the stretch ratio, defined as: $\lambda ={\displaystyle \frac{L_0+\delta L}{L_0}}$, with $L_0$ as the initial specimen length and $\delta L$ the elongation during the test. F is the applied force, and $A_0$ is the initial cross-sectional area.

To assess data repeatability, the coefficient of variation (CV) was calculated for the five tensile specimens. The CV values for tensile strength and elongation at break were 16.3% and 10.7%, respectively, indicating acceptable repeatability and consistency across the SLA-fabricated samples.

For the analysis of the material’s mechanical response, only three hyperelastic models were considered: the Neo-Hookean model, known for its accuracy at small strains; the Mooney–Rivlin model, commonly applied at moderate strains; and the Yeoh model, which has demonstrated reliable performance when fitted exclusively to uniaxial data [25,37].

Figure 3 shows the experimental stress–strain curves obtained from the five uniaxial tests. The data were used to identify the hyperelastic parameters through the material calibration module in Abaqus [38].

In this tool, the constitutive coefficients can either be entered manually, when known from prior studies, or automatically computed from experimental data by selecting the desired hyperelastic formulations. In this study, the latter approach was employed to evaluate the Neo-Hookean, Mooney–Rivlin, and Yeoh models using the uniaxial test data.

The fitting procedure in Abaqus is based on a nonlinear least-squares optimization that minimizes the residual error between experimental and modeled stresses, following the criterion:

$$E=\sum _{i=1}^n{[{\sigma }_{\exp ,i}-{\sigma }_{\mathrm{model},i}]}^2,$$

(7)

where n is the number of experimental data points and ${\sigma }_{\mathrm{model}}$ represents the nominal stress predicted by the constitutive equations listed in

Table 1. Constitutive equations used to compute nominal stress for each hyperelastic model.

Model	Equation	Parameters
Neo-Hookean	${\sigma }_{\mathrm{model}}=2C_1({\lambda }^2-{\lambda }^{-1})$	$C_1$: material constant
Mooney–Rivlin	${\sigma }_{\mathrm{model}}=2({\lambda }^2-{\lambda }^{-1})(C_1+C_2{\lambda }^{-1})$	$C_1$, $C_2$: material constants
Yeoh	${\sigma }_{\mathrm{model}}=2({\lambda }^2-{\lambda }^{-1}){\sum }_{i=1}^{n}i{C}_i{({\lambda }^2+2{\lambda }^{-1}-3)}^{i-1}$	$C_i$: material constants,
		n: model order

. For each selected model, Abaqus automatically predicts the material response under multiple deformation modes (uniaxial, biaxial, planar, and volumetric compression) to verify the numerical stability of the fitted parameters and to detect potential nonphysical behaviors such as negative stiffness or divergence at high stretch ratios.

Convergence was achieved when successive updates in the fitted parameters were below ${10}^{-5}$, and all evaluated models demonstrated stable behavior across the deformation modes. Despite relying solely on uniaxial tensile data, as recommended for elastomers with near-incompressible behavior [29,30], the fitting procedure provided accurate parameter identification for all three models.

Figure 4 compares the experimental stress–strain data with the model predictions, while

Table 2. Hyperelastic material coefficients (MPa) for Elastic 50A Resin V2.

Mooney–Rivlin, $\mathit{n}=1$	Neo-Hookean, $\mathit{n}=1$	Yeoh, $\mathit{n}=3$
$C_{10}$ = $1.1987$	$C_{10}$ = $0.7807$	$C_{10}$ = $0.7546$
$C_{01}$ = $-0.6287$		$C_{20}$ = $-4.1645\times {10}^{-2}$
		$C_{30}$ = $3.0304\times {10}^{-2}$

lists the obtained coefficients for Elastic 50A Resin V2. The comparison confirmed that the Yeoh formulation offered the best agreement with the experimental curve throughout the entire deformation range, accurately reproducing the characteristic S-shaped behavior of the resin. This observation is consistent with the reliability criteria proposed by Chagnon et al. [39], which emphasize both stability, minimal parameterization, and predictive robustness across deformation modes. Therefore, the Yeoh model was selected for the finite element simulations presented in this study.

3. Actuator Design

The actuator consists of two antagonistic pneumatic systems [20], comprising a total of four independently actuated cavities. The upper half incorporates a pair of opposing PneuNet chambers (first antagonistic system) that enable bending in one direction. The lower half includes a second pair of opposing PneuNet chambers, oriented at 90° with respect to the upper set (second antagonistic system), complementing the deformation produced by the upper cavities.

CATIA V5R21 (Dassault Systèmes, Simulia Corp., Vélizy-Villacoublay, France) was used to design an actuator suitable for additive manufacturing via stereolithography (SLA). The design considered three key parameters: the thickness of the top wall ($t_w$), the thickness of the side walls ($s_w$) of the internal chambers, and the radius of the inner air chamber ($r_c$). A proper balance of wall thicknesses was essential: excessive thickness increases the actuator’s stiffness, hindering deformation, whereas overly thin walls may cause over-inflation of the chambers, reducing the deflection capacity and increasing the risk of mechanical failure.

The optimal parameter selection for the actuator was determined through finite element simulations in Abaqus. This approach minimized costs, reduced production time, and avoided material waste during prototyping. Multiple simulations were conducted, varying the main design parameters while analyzing the relationship between input pressure and chamber expansion, as well as actuator deformation and stress concentration at critical points. Based on this analysis, the final parameter values were established, as illustrated in Figure 5.

Since the actuator’s total length was a secondary parameter, it was defined according to the maximum build dimension of the 3D printer, resulting in a length of 170 mm. The actuator diameter was set to 36 mm, with each of the four PneuNets containing six chambers. In addition, the central wall dividing the two upper cavities was designed with two longitudinal perforations of $3.5$ mm in diameter, allowing airflow into the lower cavities. This configuration enables bending and elongation when all four cavities are pressurized, as well as compression when air is simultaneously extracted from them.

3.1. Additive Manufacturing Parameters and Post-Processing

The actuator was fabricated using a Formlabs Form 3+ stereolithography (SLA) printer and Elastic 50A V2 resin. The printing workflow was managed through the PreForm 3.53.0 software (Formlabs Inc., Somervile, MA, USA), which was used to define the part orientation, layer resolution, and support configuration. A layer thickness of 100 μm was selected, consistent with the manufacturer’s recommended settings for this material, providing an adequate balance between surface quality and printing time.

The actuator was oriented diagonally across the build platform to maximize the printable length, resulting in a ${45}^{\circ }$ orientation of the printing layers relative to the XY-plane. The printing parameters were adjusted to prevent the addition of internal supports within the cavities, ensuring that the actuator could be fabricated as a single piece. The printing process required approximately $8.5\mathrm{h}$ and consumed a total of $97.65\mathrm{mL}$ of resin, generating 420 layers.

Following fabrication, the actuator was washed for $20\min$ in a Form Wash (Formlabs Inc., Somervile, MA, USA) unit containing isopropyl alcohol (IPA) to remove surface and partially trapped resin. Additional manual cleaning was performed using a pipette to ensure complete removal of residual resin from the internal cavities. The final post-curing stage was conducted in a Form Cure (Formlabs Inc., Somervile, MA, USA) chamber at 70 °C for $30\min$, following the same protocol applied to the test specimens to ensure material consistency across all samples.

The selected printing parameters and post-processing protocol ensured high dimensional fidelity and consistent mechanical behavior, which are critical for accurate experimental validation of the actuator’s performance.

3.2. Soft Pneumatic Behavior Analysis

A finite element analysis (FEA) was conducted to predict the behavior and performance of the soft pneumatic actuator, to optimize its design parameters, and to address the system’s inherent nonlinearities. These nonlinearities include the hyperelastic behavior of elastomers, contact interactions between the external lateral walls of the chambers, and large geometric deformations of the actuator, all of which make the modeling of soft robotic systems particularly challenging. Moreover, FEA enables the visualization of stress concentrations and strain distributions, providing valuable insights for design refinement.

The simulations were performed in Abaqus within the Standard/Explicit framework on a workstation equipped with an Intel Core i9-14900HX processor (Intel Corp., Santa Clara, CA, USA) (24 cores, 32 threads), 32 GB of RAM, and an NVIDIA GeForce RTX 4060 graphics card (NVIDIA Corp., Santa Clara, CA, USA) with 8 GB of memory. The actuator geometry, designed in CATIA V5R21, was imported into Abaqus, where the mechanical properties of the elastic resin were assigned based on experimental uniaxial tensile test data. The Yeoh hyperelastic model was selected due to its superior accuracy in capturing the material’s nonlinear behavior.

In the experimental setup, the actuator is anchored at its upper end to a rigid support that secures it to the test platform. Accordingly, in the simulation, the upper surface of the model was constrained in all six degrees of freedom to represent that fixation (see Figure 6a). The actuator’s lower, free end was left unconstrained to allow deformation under the action of internal pressure and the actuator geometry. Self-contact interactions were defined between the actuator’s external walls (Figure 6b), since upon pressurization, opposing (antagonistic) cavities tend to compress and come into contact. In the simulation, these contact definitions prevent nonphysical penetration between nodes or elements, faithfully reproducing the real material behavior and ensuring numerical stability during large deformations. The effect of friction between contacting surfaces was also included because a high friction coefficient can restrict sliding and alter the actuator’s mechanical response.

A mesh convergence analysis was performed to determine the optimal element size. This iterative procedure involved defining an initial mesh size, running the simulation, recording the stress and strain results, and refining the mesh until convergence. The convergence criterion—or refinement stopping point—was defined as the stage at which the percentage variation in the relative error of the maximum principal stress and strain was below $5\%$, a threshold adopted to ensure numerical stability of the results. Comparative analysis across different mesh sizes showed that for element sizes smaller than $1.5\mathrm{mm}$, the relative error variation remained below $5\%$. Consequently, a global element size of $1.3\mathrm{mm}$ was selected, complemented by local mesh refinement to $1.0\mathrm{mm}$ in critical regions, particularly along the inner walls of the actuator where pressure is applied, following the recommendations of [25,40,41]. The final mesh consisted of 432,140 quadratic tetrahedral C3D10H elements, ensuring independence of the results from mesh discretization. These elements, specifically formulated for hyperelastic materials, enhance accuracy under nonlinear deformations and mitigate volumetric locking, making them particularly suitable for modeling nearly incompressible elastomers.

Pressure loads were applied exclusively to the internal chambers (Figure 6c), activating one or more cavities depending on the desired deformation mode. The applied pressure ranged from 20 kPa to 130 kPa, consistent with the capacity of the available pneumatic system. To avoid convergence issues, the time increment was set to $0.1\mathrm{s}$ for the gravity application step and $0.01\mathrm{s}$ for the pressure application step. Pressure was applied gradually to minimize numerical instabilities and to improve the accuracy of the predicted deformations. Additionally, the NLgeom option was activated to account for geometric nonlinearities and large displacements, both of which are critical in simulations of hyperelastic materials and highly deformable structures.

4. Numerical and Experimental Validation

4.1. Numerical Simulations: Bending Behavior Results

In the first stage of the simulations, the bending behavior of the soft pneumatic actuator was evaluated by pressurizing a single upper cavity. Since the posterior cavity undergoes compression as a consequence of the pressure applied to the opposite cavity, simulating the activation of only one upper cavity was deemed sufficient. Figure 7 illustrates the actuator’s bending response, showing how the distribution of principal stresses evolves with increasing pressure. Different internal pressure levels were applied to assess the structural integrity of the hyperelastic material, with particular attention to the point at which the resin’s rupture limit is exceeded. The results show that the critical pressure is approximately 130 kPa, beyond which the maximum principal stresses exceed 3.4 MPa and the maximum principal strains reach 111.7%, thereby compromising the material’s integrity (Figure 7).

In the second stage, the same procedure was repeated to evaluate the actuator’s response when pressurizing one of the lower cavities. Simulations at different internal pressures revealed a similar overall response to that of the upper cavities. However, failure occurs earlier: at pressures above 110 kPa, stresses exceed 3.4 MPa and the maximum strain reaches 68.7% (Figure 8).

This behavior indicates that the lower cavities generate higher stress concentrations at lower pressures compared to the upper cavities, likely due to the geometric constraints imposed by the actuator’s structure. Increased stress and strain concentrations were also observed in the central region, where the upper and lower cavities diverge.

In the third stage, simultaneous pressurization of one upper and one lower cavity was simulated. This configuration enabled deformations in multiple directions, depending on the activated cavities and applied pressures. Figure 9a,b demonstrate that the combined pressurization enhances motion versatility. As long as the applied pressures remained below 150 kPa, the actuator preserved its structural integrity without exceeding stress or strain limits. This configuration therefore facilitates more complex directional movements, which may be advantageous in applications requiring multidirectional actuation.

Finally, in the fourth stage, the actuator’s response was assessed when all four cavities were simultaneously pressurized. This configuration enabled not only bending but also elongation and compression, thereby providing three of the four fundamental PneuNet motion modes. Elongation occurred when all cavities were uniformly pressurized, leading to axial extension (Figure 10a). Conversely, applying negative pressure simultaneously to all cavities resulted in compression. As shown in Figure 10b, the lower cavities, located farther from the air inlet, were the first to contract and exhibited the highest strain concentrations.

4.2. Experimental Validation

This section presents the experimental results obtained with the pneumatic actuator manufactured using stereolithography (SLA) 3D printing with Elastic 50A Resin V2. Pressurization of the chambers was performed using a portable pneumatic system capable of generating controlled pressures up to 280 kPa. The pressures were measured with an XGZP6847A500KPG sensor, (CFSensor, Wuhu, China) ( operating within a 0–500 kPa range, and the signals were acquired using an Arduino Mega (Arduino S.r.l., Somerville, MA, USA). The sensor was directly connected to the actuator’s air inlet. Additionally, a RealSense camera (RealSense Inc, Cupertino, CA, USA) operating at 60 frames per second was used to capture the actuator’s motion and maximum deformation at the pressure levels evaluated in the simulations.

A visual comparison was carried out between the experimentally observed deformations and those predicted by finite element simulations. These comparisons were performed in three stages: (i) pressurizing one upper chamber individually, (ii) pressurizing one lower chamber, and (iii) simultaneously pressurizing two chambers, as illustrated in Figure 11.

The experimental results show a strong correlation between simulation and experiment for the upper cavities, with both exhibiting similar displacement ranges. However, for the lower cavities, the experimental deformations were greater than those predicted, resulting in a larger bending angle.

Destructive tests were conducted to determine the elastic limits of both the material and the structure, and to compare them with the predictions from numerical simulations. The upper cavities exhibited a maximum operating pressure of approximately 190 kPa (see Video S1 in the Supplementary Materials), while the lower cavities showed a lower threshold of around 160 kPa (see Video S2). These results establish the operational limits of the proposed actuator design.

The observed discrepancies between simulation and experimental results may be attributed to geometric deviations introduced during the printing or post-curing process, which are not fully captured in the simulation model. Additionally, uncertainties in material characterization or parameter fitting of the hyperelastic model may also contribute to the differences.

To facilitate a direct comparison between simulations and experimental observations, the critical pressure thresholds obtained for each actuation mode are summarized in

Table 3. Comparison between finite element predictions and experimental thresholds for different actuation modes.

Actuation Mode	FEA Critical Pressure (kPa)	Experimental Threshold (kPa)	Failure Indicator
Upper cavities	∼130	∼190	Stress > UTS (3.4 MPa)
Lower cavities	∼110	∼160	Stress > UTS (3.4 MPa)
Combined (two cavities)	Stable ≤ 150	Stable ≤ 150	No failure observed
All four cavities	Stable ≤ 100	Stable ≤ 100	Deformation only

. The table highlights the differences between numerical predictions and destructive tests, showing that the experimental limits were consistently higher than those predicted by the finite element simulations. This outcome suggests that while the FEA model is conservative in estimating failure, it provides a reliable safety margin for the design of SLA-printed antagonistic actuators.

5. Discussion

This study demonstrates that SLA-printed antagonistic actuators can be effectively modeled using the Yeoh hyperelastic formulation, yielding reliable predictions of stress distribution and operational pressure limits. These results extend previous work on cast soft actuators [20] by validating SLA as a reproducible method for rapid prototyping. In contrast to [42], which optimized design parameters across different geometries, our work focuses on identifying structural failure thresholds and experimentally validating safe operating pressures.

Geometric deviations and internal resin residues, as reported in [43], were also observed in our samples and likely contributed to discrepancies between experimental and simulated results. Such deviations led to higher rupture pressures in experiments than in FEA predictions assuming ideal geometries. Our antagonistic architecture achieves multidirectional motion without fiber reinforcement, simplifying fabrication while preserving flexibility, though this simplicity comes with trade-offs in mechanical precision.

Several limitations must be acknowledged regarding both fabrication and modeling. First, fabrication tolerances inherent to the SLA process introduce slight geometric deviations between the CAD model and the printed parts. For example, tensile test specimens designed with a width of $6.0\mathrm{mm}$ and a thickness of $3.0\mathrm{mm}$ showed average printed dimensions of $6.03\pm 0.02\mathrm{mm}$ and $2.90\pm 0.09\mathrm{mm}$, respectively. Similarly, the actuator’s external diameter exhibited a variation of less than $1.17\%$ from the nominal $36\mathrm{mm}$. While these deviations are minimal, they may influence localized stress distribution and, consequently, the failure pressure thresholds observed experimentally.

Two fabrication-related defects were particularly relevant. First, residual uncured resin within internal cavities could not be entirely removed, even after sequential external and internal washing cycles. Once post-cured, these residues locally increased stiffness, potentially altering deformation profiles. Second, tensile stresses generated during the UV post-curing process caused slight warping after support removal. Although minor, these deformations suggest that stress relaxation during curing can influence the final geometry and, consequently, the actuator’s performance. Despite these imperfections, the reproducibility across actuators remained high, indicating that fabrication tolerances had a greater impact on accuracy than on repeatability.

Another source of uncertainty arises from potential material anisotropy. The Elastic 50A V2 resin is designed to exhibit near-isotropic behavior; however, the photopolymerization process may lead to directional differences in stiffness and elongation depending on layer orientation, laser exposure uniformity, and post-curing depth [36]. In this study, all actuators were printed with the same orientation and curing protocol, and no significant directional variation was observed. Nevertheless, future work should quantitatively evaluate anisotropy through mechanical testing of specimens printed along different axes (X, Y, Z) and include corresponding anisotropic material models in FEA simulations. Such analysis would help determine whether layer orientation or local curing gradients introduce measurable mechanical heterogeneity.

Regarding post-curing variability, all actuators underwent identical UV exposure conditions, minimizing operator-induced inconsistencies. However, excessive immersion in isopropyl alcohol during cleaning could alter surface chemistry and lead to minor changes in elasticity. Systematic evaluation of these effects could improve long-term reproducibility of material properties.

Finally, this study focused on quasi-static pressurization and did not account for dynamic loading or fatigue effects. While rupture tests identified the maximum safe operating pressure, the cyclic durability and Mullins effect of the printed actuators remain unexplored. Assessing the fatigue life under repeated actuation cycles would provide valuable insights into long-term reliability and structural degradation mechanisms. Similarly, the finite element simulations assumed static internal pressure and did not incorporate time-dependent viscoelasticity or cyclic stress accumulation, which could partially explain the discrepancy between numerical and experimental deformation magnitudes.

Future work should incorporate biaxial and shear material characterization, anisotropic constitutive modeling, and topology or shape optimization frameworks to identify geometries that maximize deformation range while minimizing stress concentration. Integration of quantitative tracking systems, such as optical or depth-based sensors, will also enhance experimental validation by enabling precise deformation mapping across multiple actuation modes. Moreover, cyclic actuation tests will be essential to establish fatigue thresholds and further validate the durability of SLA-printed soft actuators for real-world applications.

6. Conclusions

This work presented the design, material characterization, and structural analysis of an SLA-printed antagonistic soft pneumatic actuator fabricated from Elastic 50A Resin V2. Material calibration from uniaxial tensile tests identified the Yeoh hyperelastic formulation as the best fit for the tested deformation range and was successfully implemented in Abaqus to predict actuator behavior. Finite element simulations reproduced the principal deformation modes observed experimentally (multidirectional bending and axial elongation) and identified critical stress zones. The simulations predicted conservative failure thresholds of approximately $130\mathrm{kPa}$ for the upper cavities and $110\mathrm{kPa}$ for the lower cavities, while destructive tests yielded experimental rupture pressures near $190\mathrm{kPa}$ (upper) and $160\mathrm{kPa}$ (lower). The material ultimate tensile strength, according to the manufacturer, was measured at $3.4\mathrm{MPa}$, and the maximum principal stresses from FEA approaching this value were used to define safety margins for operation.

Beyond summarizing results, several practical conclusions and limitations emerge. Manufacturing reproducibility is high: dimensional deviations measured in tensile specimens were small and actuator diameters deviated by less than $1.17\%$ from the CAD nominal value. Nonetheless, two fabrication issues materially affect mechanical accuracy: (i) residual uncured resin trapped in internal cavities locally increases stiffness after curing and can raise the experimental rupture pressure relative to idealized simulations; and (ii) minor warping induced by UV post-curing and support removal alters the final geometry. These factors explain part of the conservative bias of the FEA results and indicate that tight control of cleaning and curing protocols is essential for predictive accuracy.

Concerning the scalability and integration of this prototype, the present actuator length (170 mm) was constrained by the printer’s build volume and by the chosen diagonal orientation that maximized printable length but introduced 45° layer directions. Scaling to larger devices will require either segmentation combined with reliable bonding strategies or alternative print orientations and support management. For practical deployment, for instance, in adaptive grippers or biomedical manipulators, designs should account for geometric tolerances and incorporate safety factors consistent with the observed conservative FEA predictions (e.g., limiting operational pressures to approximately 70–$80\%$ of the experimentally observed rupture pressures for continuous use).

Long-term performance and repeatability under cyclic loading remain open issues. This study did not perform systematic fatigue testing or quantify Mullins-type stress softening or viscoelastic relaxation. Preliminary repeated-pressurization trials showed no immediate failure but are insufficient to establish service life. We recommend that future testing aims to (a) quantify fatigue life under representative duty cycles (for example, target benchmarks of ${10}^3$–${10}^5$ cycles for components intended for repeated actuation), (b) measure Mullins and hysteresis effects under cyclic loading, and (c) incorporate time-dependent viscoelastic material models into FEA to improve dynamic prediction.

Finally, practical recommendations and research directions derived from our findings include: (1) performing biaxial and shear tests to complement uniaxial characterization and enable anisotropic modeling if required and (2) applying topology or shape optimization constrained by the identified stress hotspots to enhance performance while maintaining manufacturability. By following these guidelines and adopting conservative operational limits informed by both FEA and destructive testing, SLA-printed antagonistic actuators can advance toward reliable, repeatable applications in fields such as adaptive grippers and bioinspired manipulators, while addressing the additional steps required to ensure long-term durability and scalability.