Analytical Modeling and Simulation of Machinery Containing Hydraulic Lines with Fluid Transients
Abstract
1. Introduction
2. Materials and Methods
3. Results
3.1. Example 1—Water Hammer
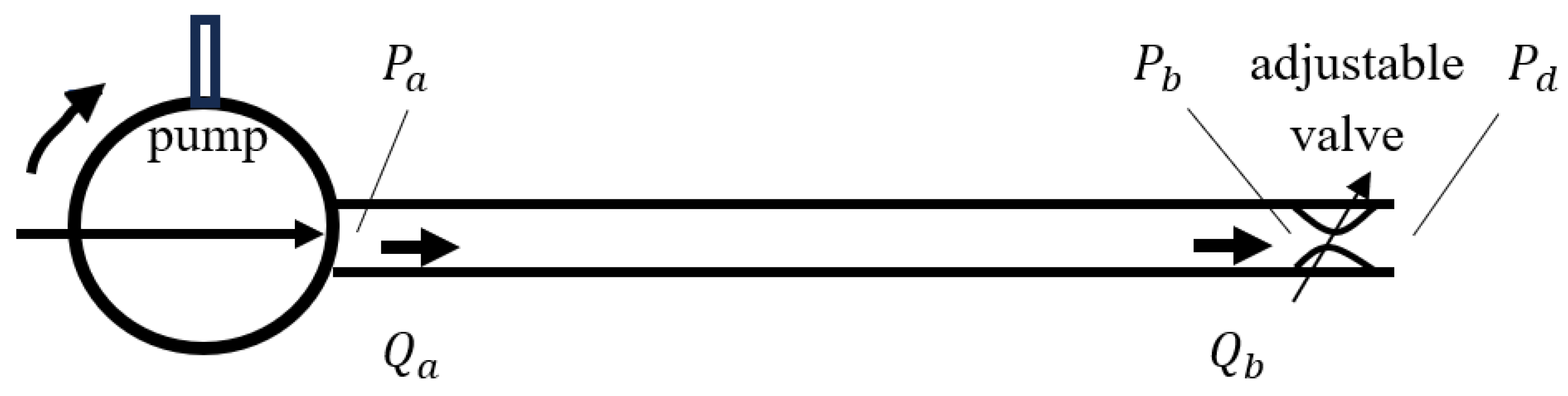
3.2. Example 2—Lines with Pumps and Valves
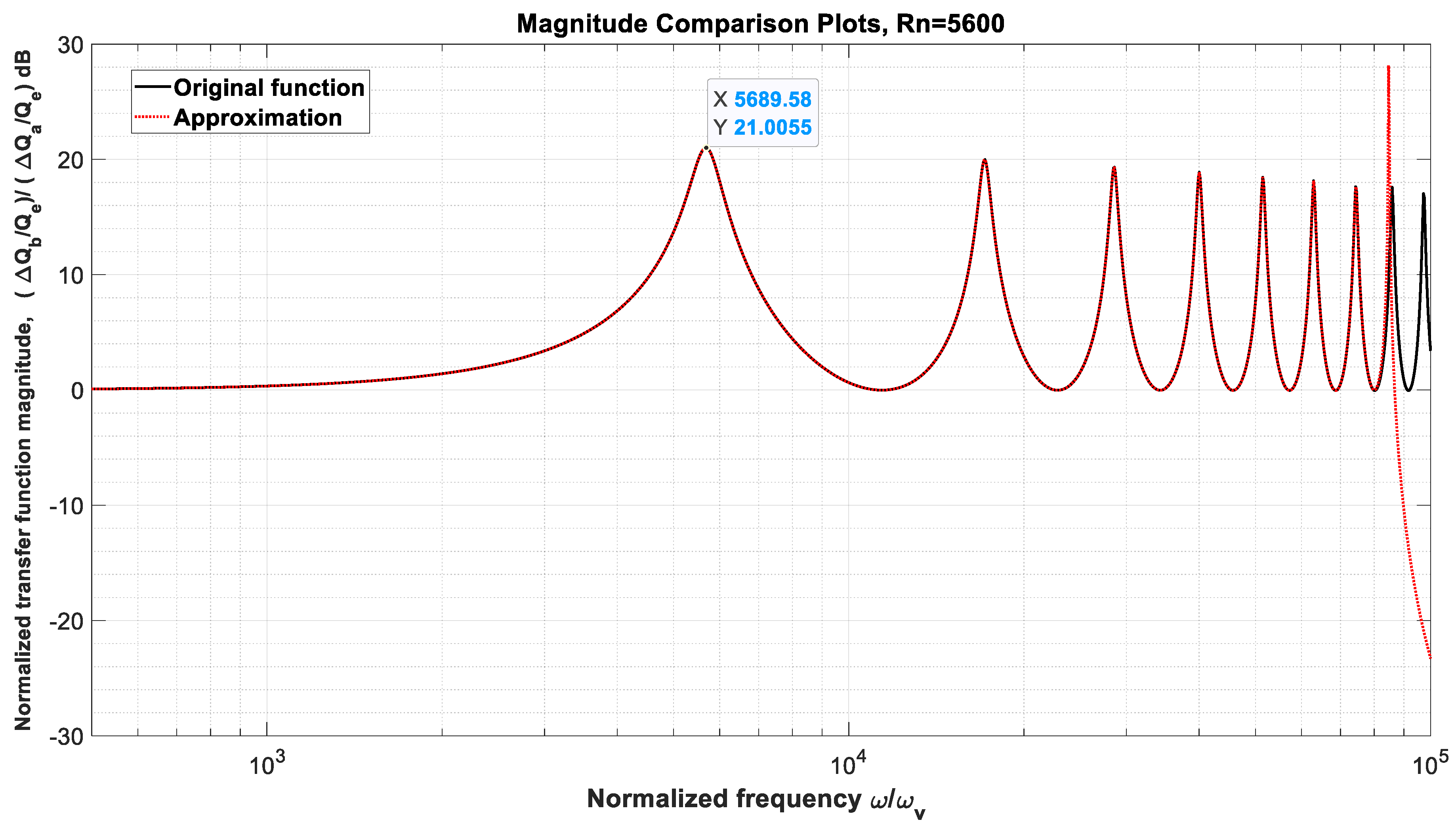
3.2.1. Case 1—Constant Flow from Pump with Changing Valve Area
3.2.2. Case 2—Constant Valve Area with Changing Flow from a Variable Displacement Pump
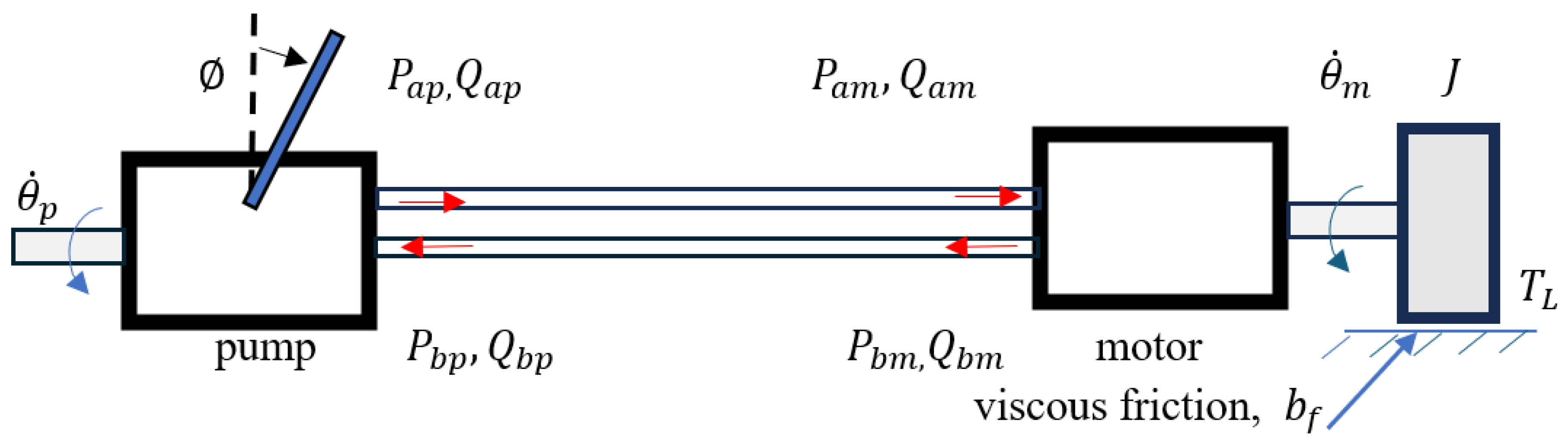
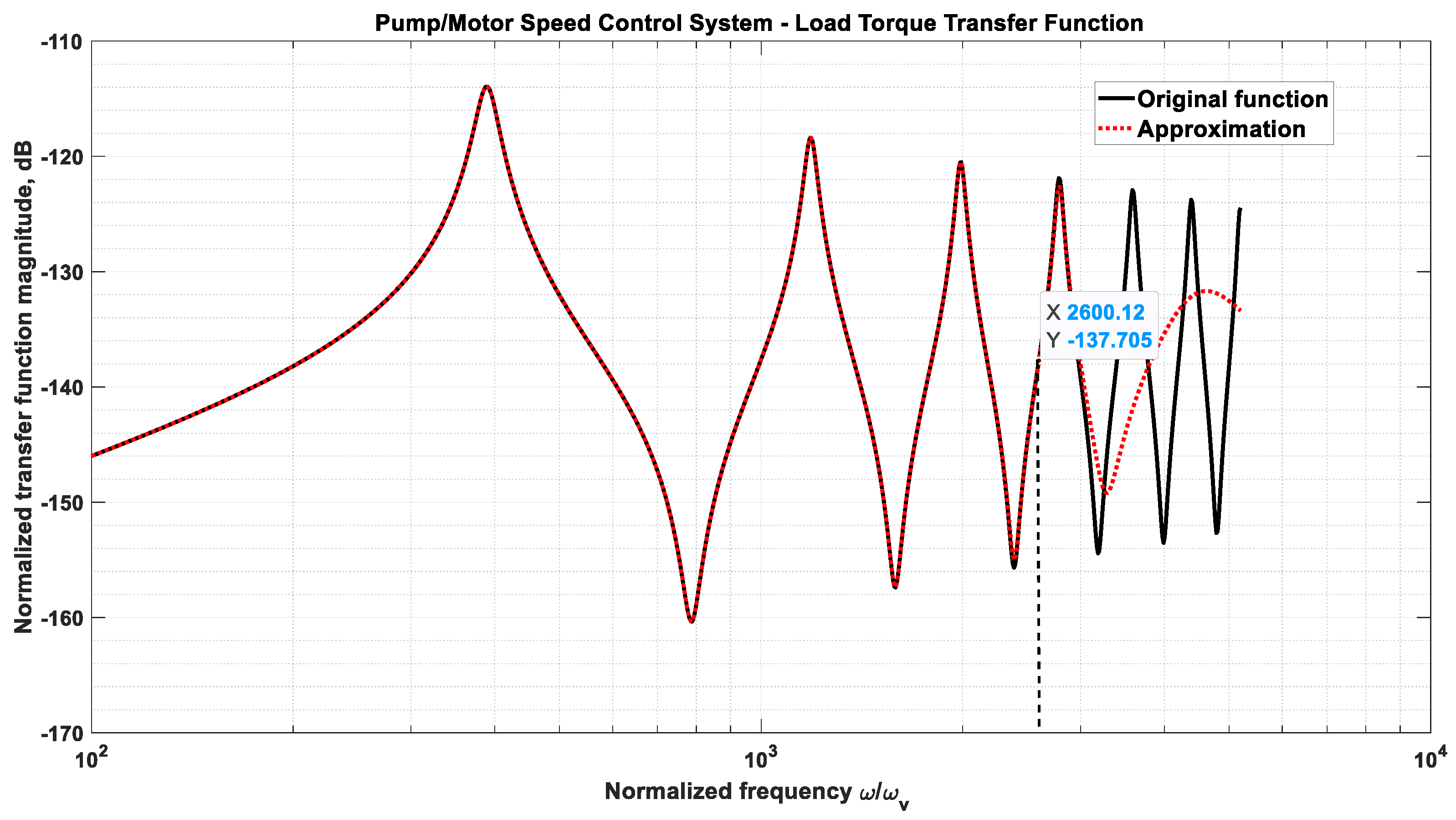
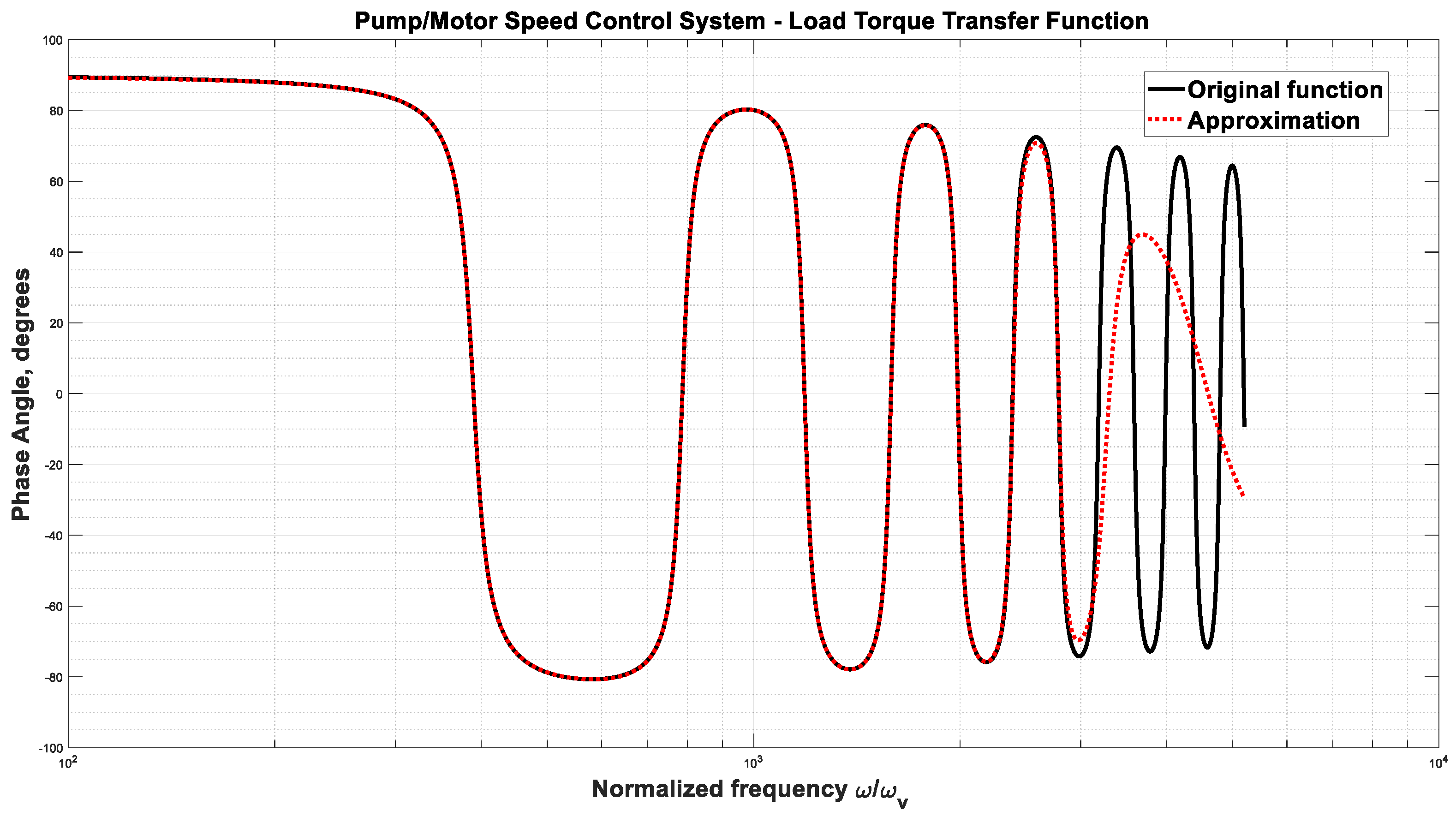
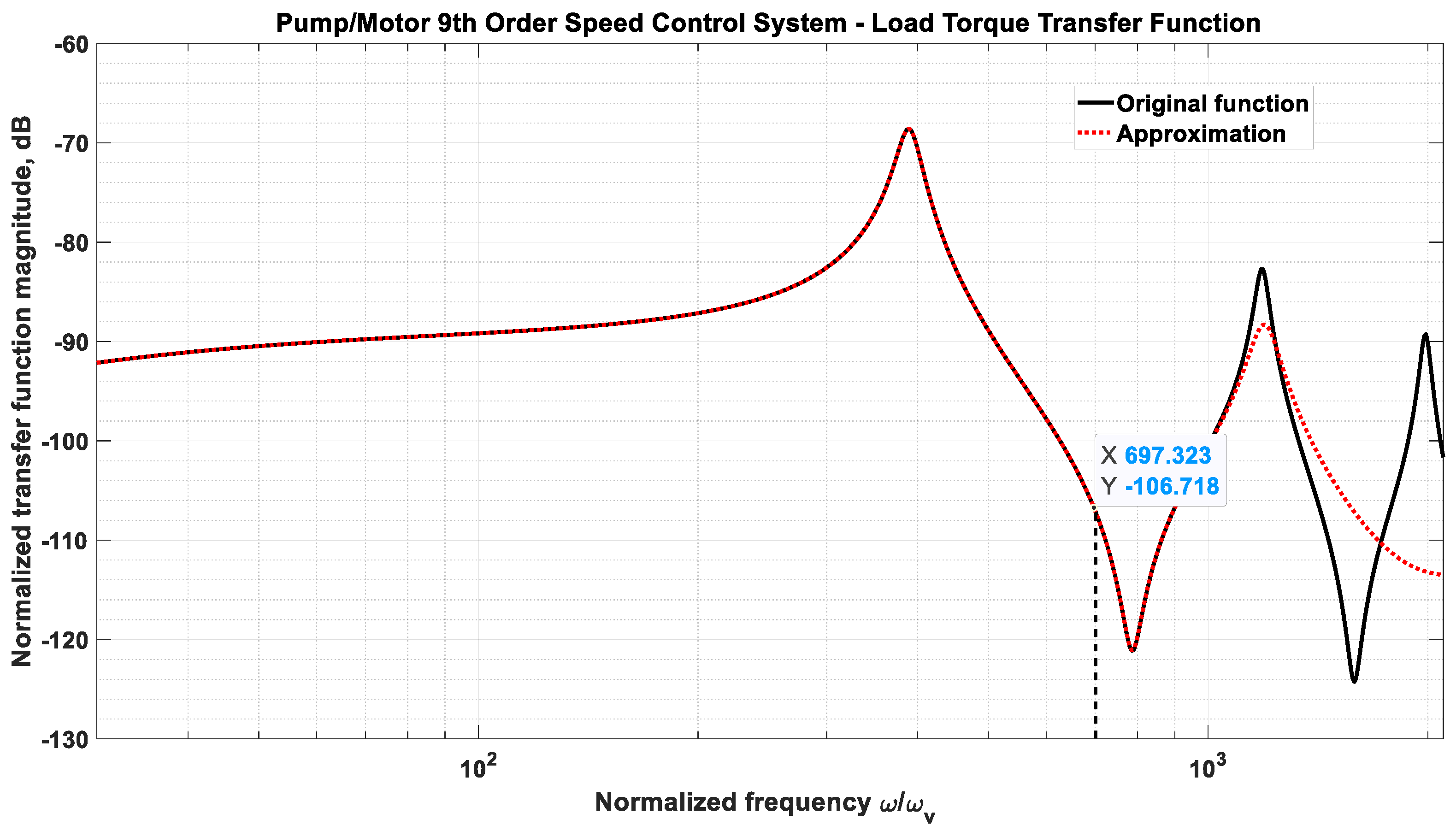
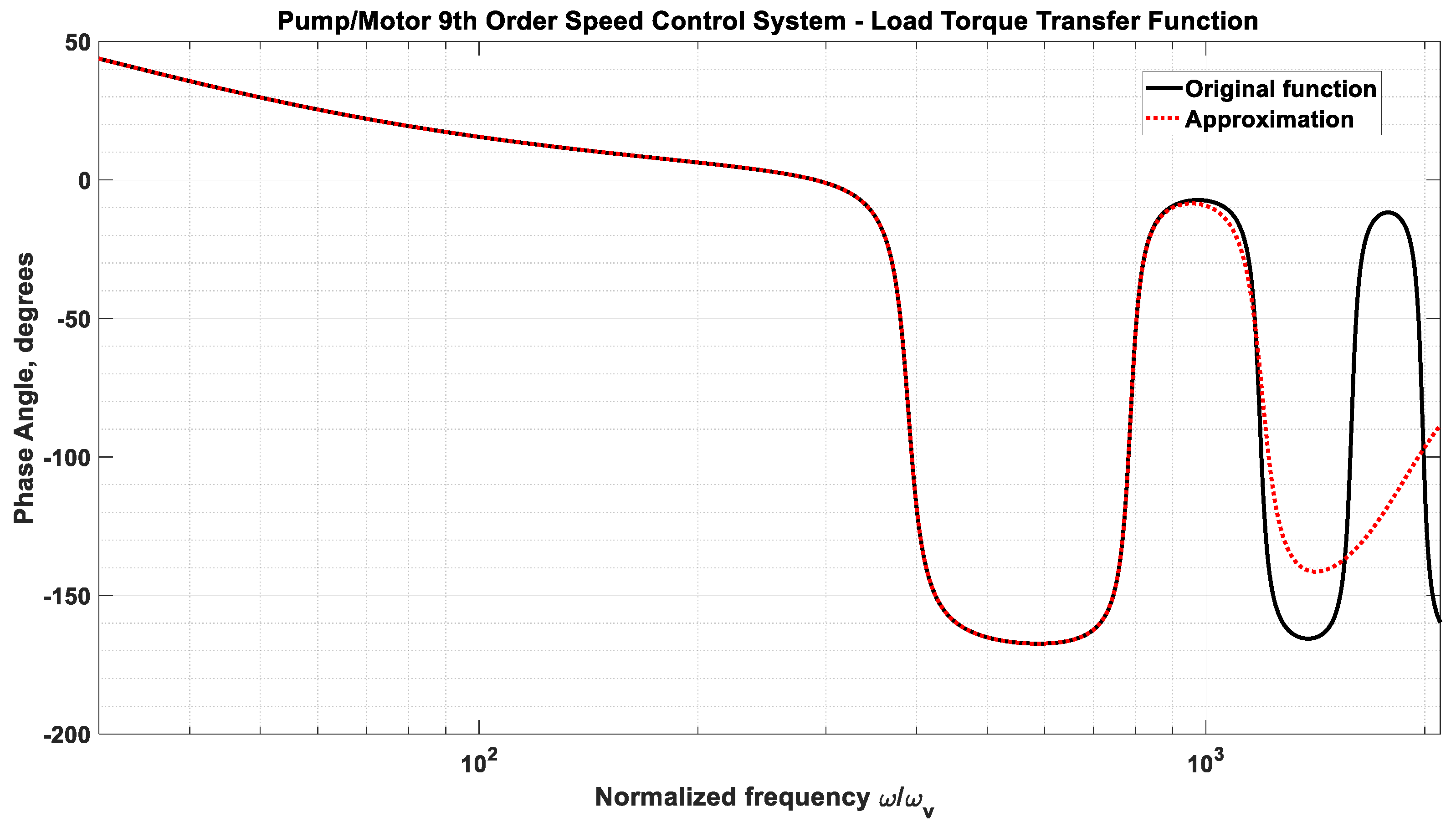
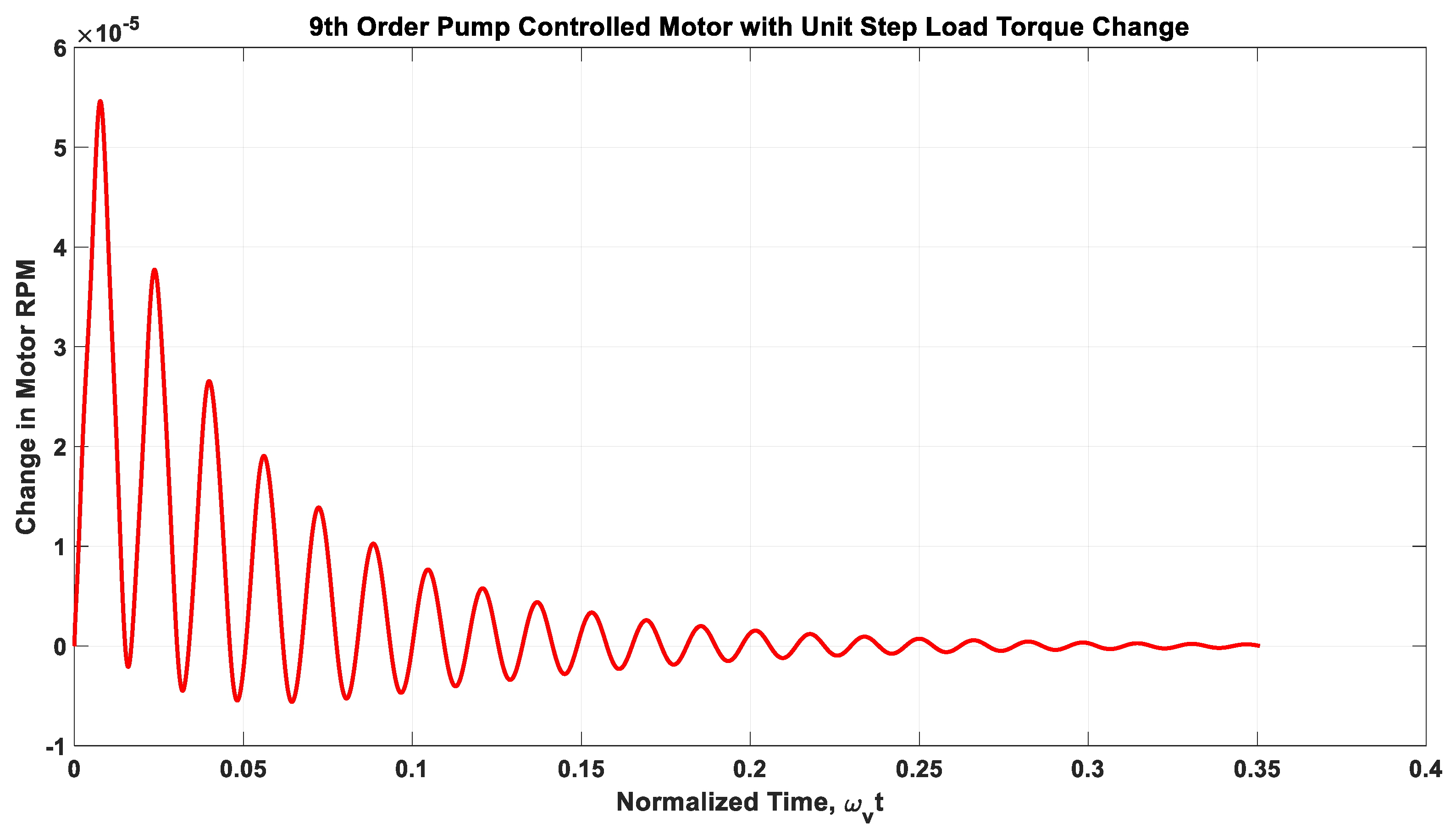
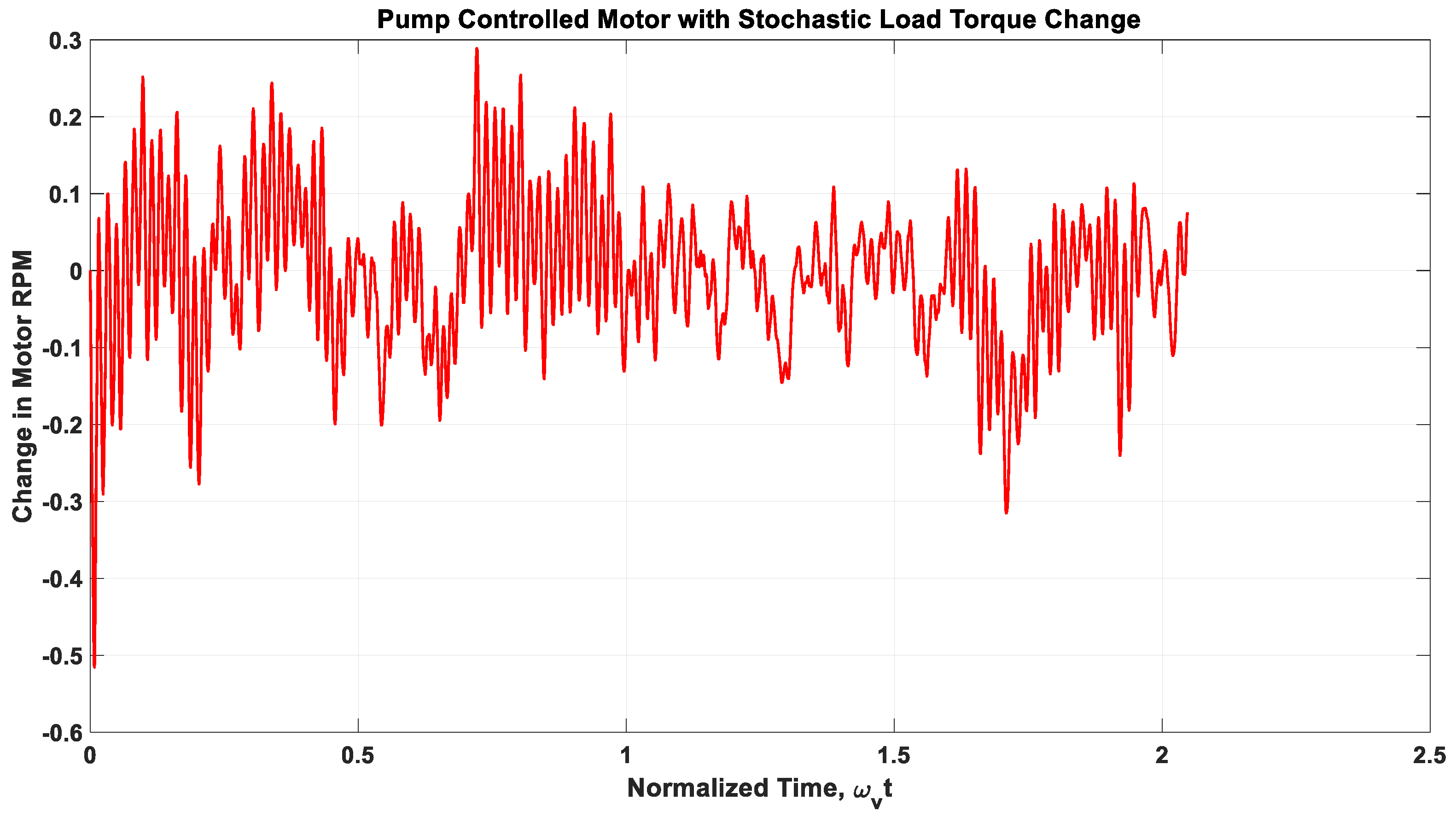
3.3. Example 3—Rotary Actuator Controlled by a Variable Displacement Pump
- Required peak motor torque: 5000 Nm
- Desired pre-transient motor speed: 10 RPM
- Pump peak pressure: 250 bar
- Pump speed: 1600 RPM
- Mass moment of inertia:
- Viscous damping coefficient:
4. Discussion
5. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Wave velocity, (m/s) | |
| Element in transfer function matrix in Equation (4) | |
| A | Short notation for terms defined in Equation (A33) |
| Pre-transient steady-flow valve area, m2 | |
| Change in valve area, m2 | |
| Normalized valve area change, | |
| Constant in the Blasius friction factor equation, | |
| Viscous friction coefficient, (Nms/rad) | |
| Ratio of Bessel functions, | |
| C | Orifice discharge coefficient divided by |
| Motor torque coefficient, (rad) | |
| Coefficient defined by terms in Equation (A42) associated with boundary conditions | |
| Coefficient defined by terms in Equation (A43) associated with boundary conditions | |
| Pump swash angle volume coefficient, (m3/rad2) | |
| Motor displacement, (m3/rad) | |
| Pump displacement, (m3/rad) | |
| Dimensionless dissipation number, | |
| Modulus of elasticity of pipe material, (N/m2) | |
| Function used in solving the partial differential equations | |
| Symbol used for a transfer function | |
| Dimensionless parameter in Equation (14) | |
| J | Notation for |
| Motor and load mass moment of inertia, (Nms2/rad) | |
| Bessel function of order 0 | |
| Bessel function of order 1 | |
| Length of fluid line, | |
| Short notation for terms in Equation (A26) | |
| Number of line sections in the turbulence model | |
| Dimensionless parameter | |
| Pressure at the upstream end of the line, (N/m2) | |
| Change in the pressure , (N/m2) | |
| Pressure at the upstream end of the ith line segment, (N/m2) | |
| Pressure at the downstream end of the line, (N/m2) | |
| Change in the pressure , (N/m2) | |
| Pressure at the downstream end of the line segment, (N/m2) | |
| Short notation for pre-transient pressure differential , (N/m2) | |
| Valve downstream pressure | |
| Q | Pre-transient dimensionless flow resistance ratio, |
| Volumetric flow rate at upstream end of line, (m3/s) | |
| Change in the flow rate , (m3/s) | |
| Flow at the upstream of the line segment, (m3/s) | |
| Volumetric flow rate at downstream end of line, (m3/s) | |
| Change in the flow rate , (m3/s) | |
| Flow at the downstream of the line segment, (m3/s) | |
| Pre-transient steady state flow rate in line, (m3/s) | |
| Radial position from the center of the fluid line, (m) | |
| Internal radius of fluid line, (m) | |
| Laminar steady flow resistance in line, (Ns/m5) | |
| Reynolds number, | |
| Additional steady flow resistance in line associated with turbulence, (Ns/m5) | |
| Laplace variable | |
| Normalized Laplace variable, | |
| Time, (s) | |
| Normalized time, | |
| Thickness of pipe wall, (m) | |
| Motor load torque, (Nm) | |
| Change in Motor load torque, (Nm) | |
| Fluid velocity, function of and , (m/s) | |
| Pre-transient steady flow velocity, function of , (m/s) | |
| Laplace transform of , (m/s) | |
| Normalized Laplace transform of , | |
| Perturbation of | |
| Short notation for terms in defined Equation (A69) | |
| Axial position along the fluid line, (m) | |
| Transfer function matrix () element | |
| Dimensionless parameter defined by the terms in Equation (A19) | |
| Characteristic impedance of the line defined in, (Ns/m5) | |
| Impedance constant, , (Ns/m5) | |
| Equivalent bulk modulus, (N/m2) | |
| Motor speed, (rad/s) | |
| Pump speed, (rad/s) | |
| Axial position ratio, | |
| Propagation operator of line, | |
| Oldroyd-B retardation time constant, (s) | |
| Oldroyd-B relaxation time constant, (s) | |
| Normalized time constant | |
| Normalized time constant | |
| Dynamic viscosity for pre-transient steady flow, , (Ns/m2) | |
| Kinematic viscosity for pre-transient steady flow, (m2/s) | |
| Density for pre-transient steady flow, (kg/m3) | |
| Shear stress, function of and , (N/m2) | |
| Shear stress at wall for pre-transient steady flow, (N/m2) | |
| Normalized shear stress at wall, function of | |
| Perturbation of | |
| Frequency, (rad/s) | |
| First mode frequency obtained from eigenvalues, (rad/s) | |
| Viscous frequency, , (rad/s) | |
| Normalized frequency, | |
| Pump swash plate angle, (rad) |
Appendix A. Analytical Solution to the Partial Differential Equations Considering Potentially Non-Newtonian Turbulent Flow Conditions
Appendix A.1. Newtonian Fluids
Appendix A.2. Extension of the Newtonian Analytical Model to Non-Newtonian Fluids
Appendix A.3. Extension to Pre-Transient Turbulent Flow
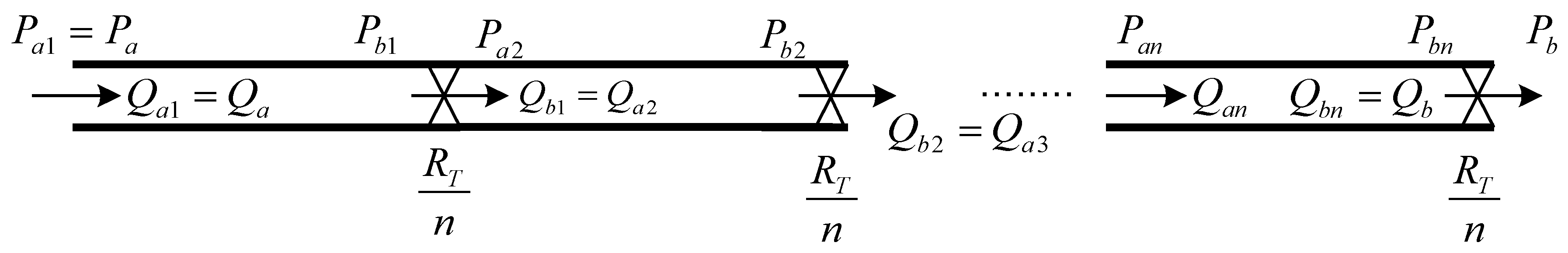
References
- Goodson, R.E.; Leonard, R.G. A Survey of Modeling Techniques for Fluid Line Transients. ASME J. Basic Eng. 1971, 94, 474–482. [Google Scholar] [CrossRef]
- Manhartsgruber, B. Transmission Line Models for Fluid Power Hoses Identified from Measurement Data. Fluid Power Syst. Technology. 2024, 88193, V001T01A026. [Google Scholar] [CrossRef]
- Catania, G.; Sorrentino, S. Dynamical analysis of fluid lines coupled to mechanical systems taking into account fluid frequency-dependent damping and non-conventional constitutive models: Part 2—Coupling with mechanical systems. Signal Process. 2015, 50, 281–295. [Google Scholar] [CrossRef]
- Bordbar, M. Analytical Solution of Quasi-Two-Dimensional Method for Unsteady Transient Pressurized Pipe Flows in the Time Domain. J. Hyd. Eng. 2025, 151, 04025035. [Google Scholar] [CrossRef]
- Manhartsgruber, B. A Set of Benchmark Problems for Fluid Power System Simulation. Fluid Power Syst. Technol. 2022, 86335, V001T01A044. [Google Scholar] [CrossRef]
- Kogler, H.; Scheidl, R.; Schmidt, B.H. Analysis of Wave Propagation Effects in Transmission Lines due to Digital Valve Switching. Fluid Power Syst. Technol. 2015, 57236, V001T01A057. [Google Scholar] [CrossRef]
- Brunone, B.; Meniconi, S.; Capponi, C. The Damping of Pressure Peaks during Transients for Fault Detection in Pressurized Pipelines: An Expeditious and Manager-Oriented Diagnosis Procedure. J. Hydraul. Eng. 2023, 149, 02523002. [Google Scholar] [CrossRef]
- Hullender, D.A.; Healey, A.J. Rational Polynomial Approximations for Fluid Transmission Line Models. In Fluid Transmission Line Dynamics, Proceedings of the Winter Annual Meeting, Washington, DC, USA, 15–20 November 1981; American Society of Mechanical Engineers: New York, NY, USA, 1981; pp. 33–55. [Google Scholar]
- Urbanowicz, K.; Jing, H.; Bergant, A.; Stosiak, M.; Lubecki, M. Progress in Analytical Modeling of Water Hammer. J. Fluids Eng. 2023, 145, 081203. [Google Scholar] [CrossRef]
- Braun, R.; Nordin, P.; Ericson, L.; Viktor, L.; Krus, P.; Pettersson, M. Hopsan: An Open-Source Tool for Rapid Modelling and Simulation of Fluid and Mechatronic Systems. Fluid Power Syst. Technol. 2020, 83754, V001T01A047. [Google Scholar] [CrossRef]
- Bruhl, M. Analytical Solution for Laminar Water Hammer with Frequency-Dependent Friction. J. Fluids Eng. 2020, 144, 111302. [Google Scholar] [CrossRef]
- Hullender, D. Alternative Approach to Modeling Transients in Smooth Pipe with Low Turbulent Flow. ASME J. Fluids Eng. 2016, 138, 121202. [Google Scholar] [CrossRef]
- Hullender, D. Water Hammer Peak Pressures and Decay Rates of Transients in Smooth Lines with Turbulent Flow. ASME J. Fluids Eng. 2018, 140, 061204. [Google Scholar] [CrossRef]
- Wongopotorn, P.; Hullender, D.A.; Woods, R.L. Rational Polynomial Transfer Function Approximations for Fluid Transients in Lines. Fluids Eng. Div. Summer Meet. 2003, 36967, 2797–2804. [Google Scholar] [CrossRef]
- Urbanowicz, K.; Bergant, A.; Grzejda, R.; Stosizk, M. About Inverse Laplace Transform of a Dynamic Viscosity Function. Materials 2022, 15, 4364. [Google Scholar] [CrossRef] [PubMed]
- Bergant, A.; Zlatko, R.; Urbanowicz, K. Analytical, Numerical 1D and 3D Water Hammer Investigations in a Simple Pipeline Apparatus. Stroj. Vestn.-J. Mech. Eng. 2025, 71, 149–156. [Google Scholar] [CrossRef]
- Bergant, A.; Simpson, A.R.; Vitkovsk, J. Developments in Unsteady Pipe Flow Friction Modelling, ASCE. J. Hydraul. Res. 2001, 39, 249–257. [Google Scholar] [CrossRef]
- Hullender, D.A.; Woods, R.L.; Hsu, C.H. Time Domain Simulation of fluid Transmission Lines Using Minimum Order State Variable Models. In N: Fluid Transmission Line Dynamics 1983, Proceedings of the Winter Annual Meeting, Boston, MA, USA, 13–18 November 1983; American Society of Mechanical Engineers: New York, NY, USA, 1983; pp. 51–78. [Google Scholar]
- Regetz, J.D., Jr. An Experimental Determination of the Dynamic Response of a Long Hydraulic Line; National Aeronautics and Space Administration: Washington, DC, USA, 1960; Technical Note D-576.
- Hullender, D. Analytical non-Newtonian Oldroyd-B transient model for pre-transient turbulent flow in smooth circular lines. J. Fluids Eng. 2019, 141, 021303. [Google Scholar] [CrossRef]
- Bird, R.B.; Armstrong, R.C.; Hassager, O. Dynamics of Polymeric Liquids, 2nd ed.; Wiley: New York, NY, USA, 1987; Chapter 2; Volume 1. [Google Scholar]
- Oldroyd, J.G. Non-Newtonian effects in steady motion of some idealized elastic-viscous liquids. Proc. R. Soc. 1958, A 245, 278–297. [Google Scholar]
- Oldroyd, J.G. On the formulation of rheological equations of state. Proc. R. Soc. 1950, A 200, 523–541. [Google Scholar]
- McGinty, S.; McKee, S.; McDermott, R. Analytic Solutions of Newtonian and Non-Newtonian Pipe Flows Subject to a General Time-Dependent Pressure Gradient. J. Non-Newton. Fluid Mech 2009, 162, 54–77. [Google Scholar] [CrossRef]
- Garcia, F.J.G.; Alvarino, P.F. On the analytic explanation of experiments where turbulence vanishes in pipe flow. J. Fluid Mech. 2022, 951, A4. [Google Scholar] [CrossRef]
- Urbanowicz, K.; Di Nucci, C.; Sharma, B.K.; Ashok, K.; Kawiak, M.; Krajewski, S. Revisiting Yamaguchi-Ichikawa water hammer model. Chin. J. Phys. 2025, 94, 487–503. [Google Scholar] [CrossRef]
- Guse, F.; Pasquini, E.; Schmitz, K. Consideration of Air Bubble Dynamics in 1D Hydraulic Pipeline Simulation—Source Term Development and Verification Utilizing Transmission Line Theory. Fluid Power Syst. Technol. 2021, 85239, V001T01A002. [Google Scholar] [CrossRef]
- Vıtkovsky, J.P.; Lee, P.J.; Zecchin, A.C.; Simpson, A.R.; Lambert, M.F. Head-and Flow-Based Formulations for Frequency Domain Analysis of Fluid Transients in Arbitrary Pipe Networks. ASCE J. Hydraul. Eng. 2011, 137, 556–568. [Google Scholar] [CrossRef]
- Danes, L. The influence of line and fluid parameters on pressure ripple in hydraulic transmissions. SN Appl. Sci. 2020, 2, 1281. [Google Scholar] [CrossRef]
- Bayle, A.; Rein, F.; Plouraboue, F. Frequency varying rheology-based fluid-structure-interactions wave in liquid-filled visco-elastic pipes. J. Sound Vib. 2023, 562, 117824. [Google Scholar] [CrossRef]
- Adamkowski, A.; Lewandowski, M. Experimental Examination of Unsteady Friction Models for Transient Pipe Flow Simulation. ASME J. Fluids Eng. 2006, 128, 1351–1363. [Google Scholar] [CrossRef]
- Blackburn, J.F.; Reethof, G.; Shearer, J.L. Fluid Power Control; The M.I.T. Press: Cambridge, MA, USA, 1960; Lib. of Congress Catalog No. 59-6759; pp. 499–508. [Google Scholar]

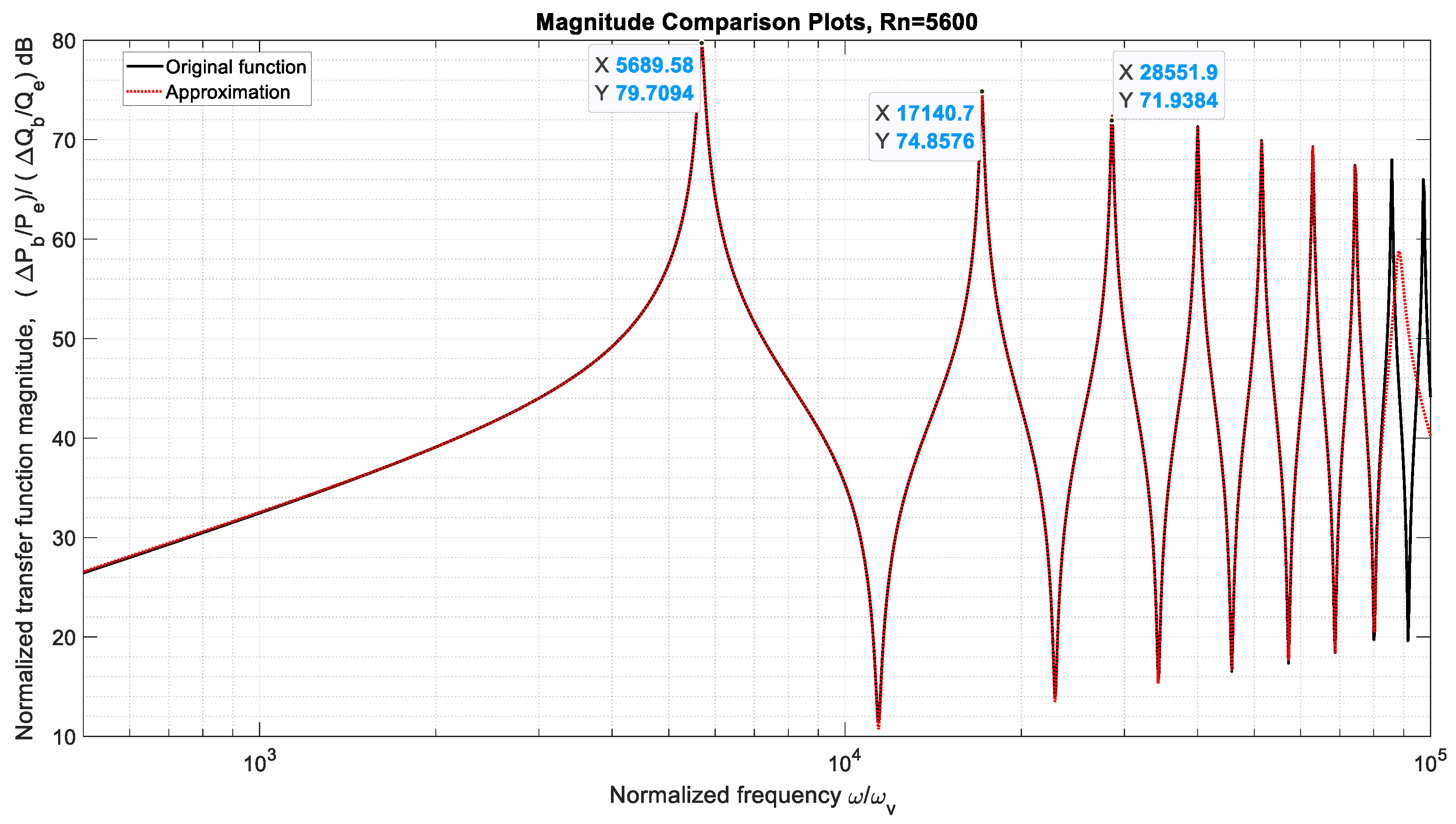
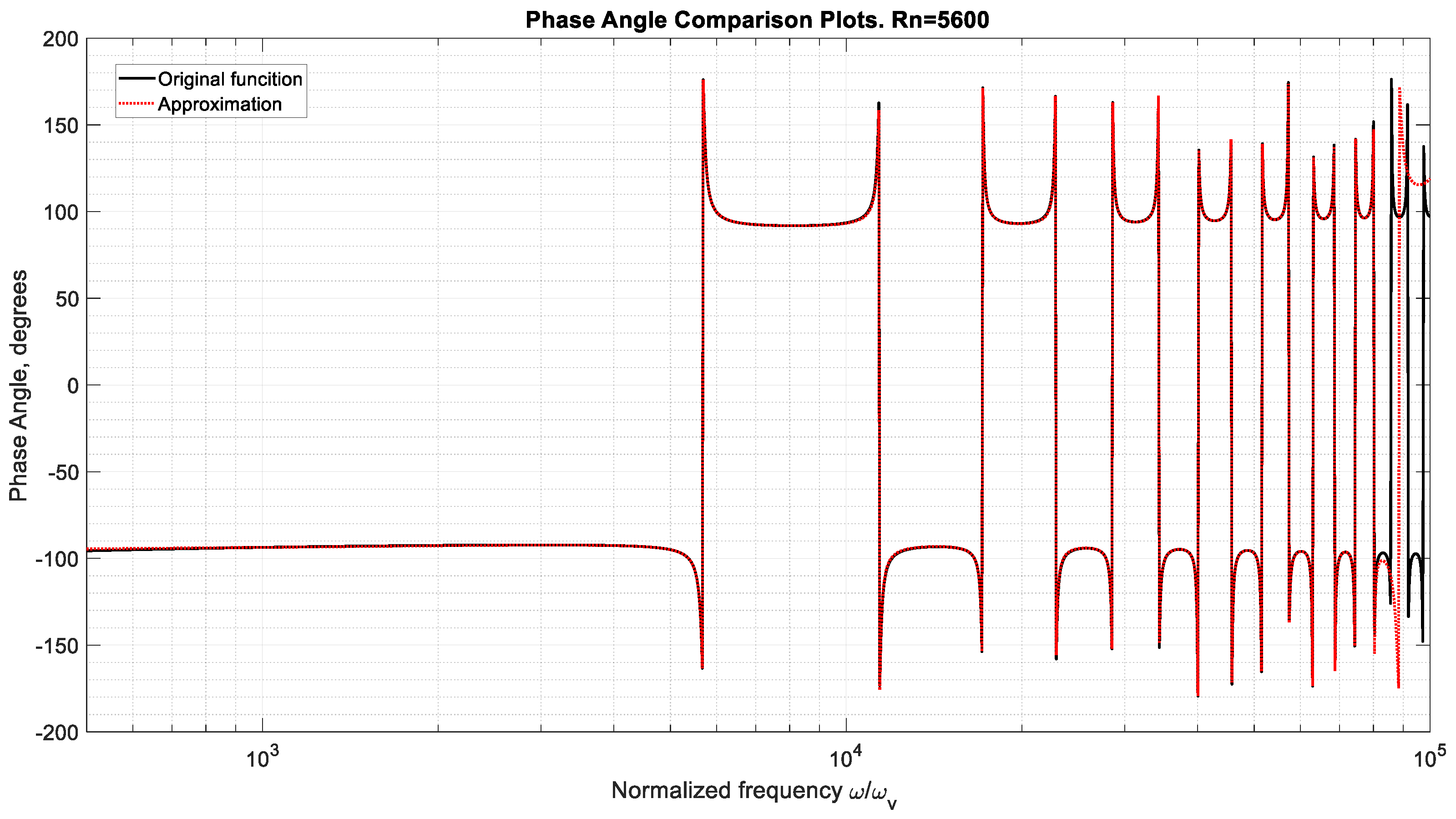
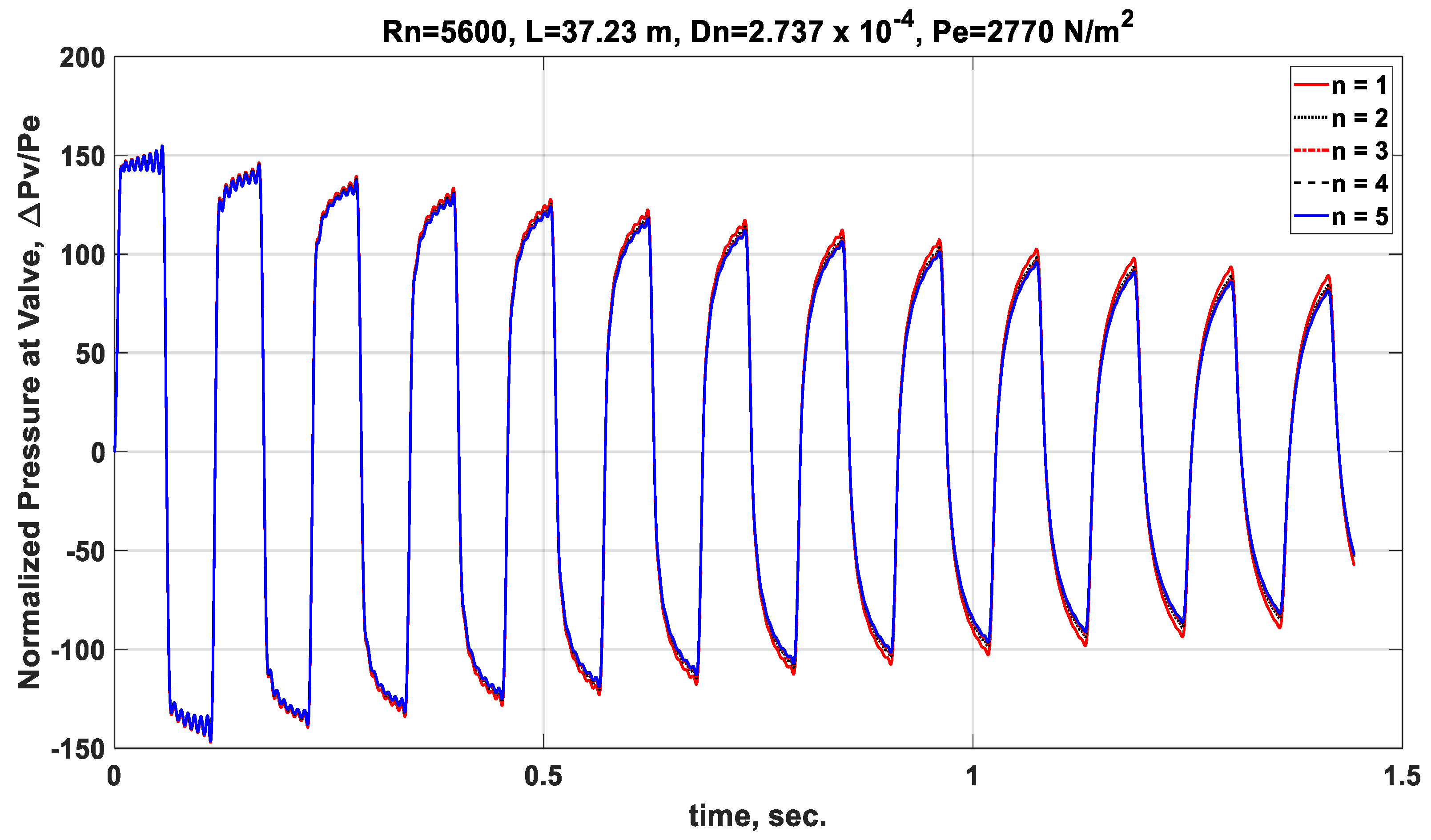

| Normalized Eigenvalues |
|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hullender, D. Analytical Modeling and Simulation of Machinery Containing Hydraulic Lines with Fluid Transients. Actuators 2025, 14, 489. https://doi.org/10.3390/act14100489
Hullender D. Analytical Modeling and Simulation of Machinery Containing Hydraulic Lines with Fluid Transients. Actuators. 2025; 14(10):489. https://doi.org/10.3390/act14100489
Chicago/Turabian StyleHullender, David. 2025. "Analytical Modeling and Simulation of Machinery Containing Hydraulic Lines with Fluid Transients" Actuators 14, no. 10: 489. https://doi.org/10.3390/act14100489
APA StyleHullender, D. (2025). Analytical Modeling and Simulation of Machinery Containing Hydraulic Lines with Fluid Transients. Actuators, 14(10), 489. https://doi.org/10.3390/act14100489







