Incremental Sliding Mode Control for Predefined-Time Stability of a Fixed-Wing Electric Vertical Takeoff and Landing Vehicle Attitude Control System
Abstract
1. Introduction
2. Materials and Modeling
2.1. The Target eVTOL Vehicle
2.2. The Mathematical Model of the eVTOL
2.3. The Attitude Control System of the eVTOL
2.4. Incremental Model of the Attitude Control System
3. Incremental Sliding Mode Controller Design of the Attitude Control System
3.1. Predefined-Time Sliding Mode Surface Design
3.2. Incremental Sliding Mode Controller Design
4. Simulation Results
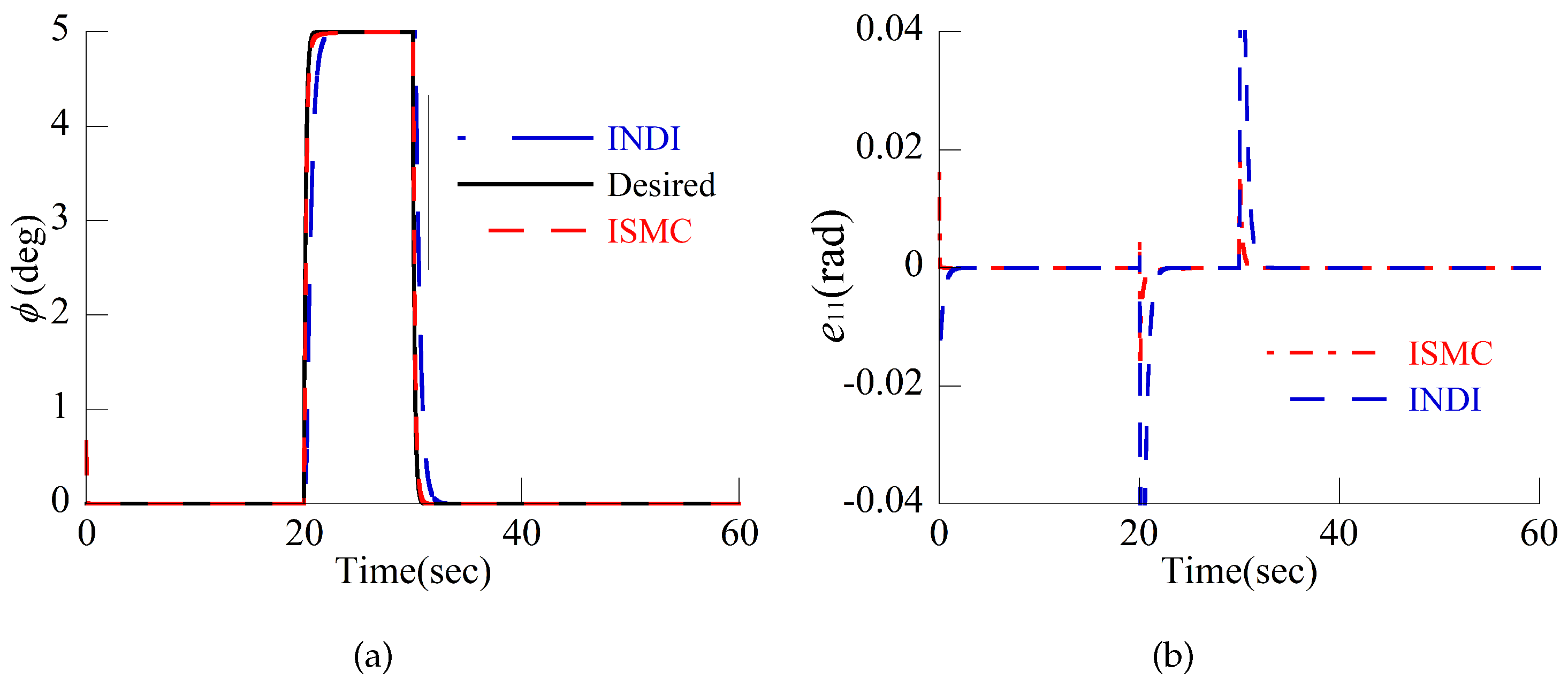
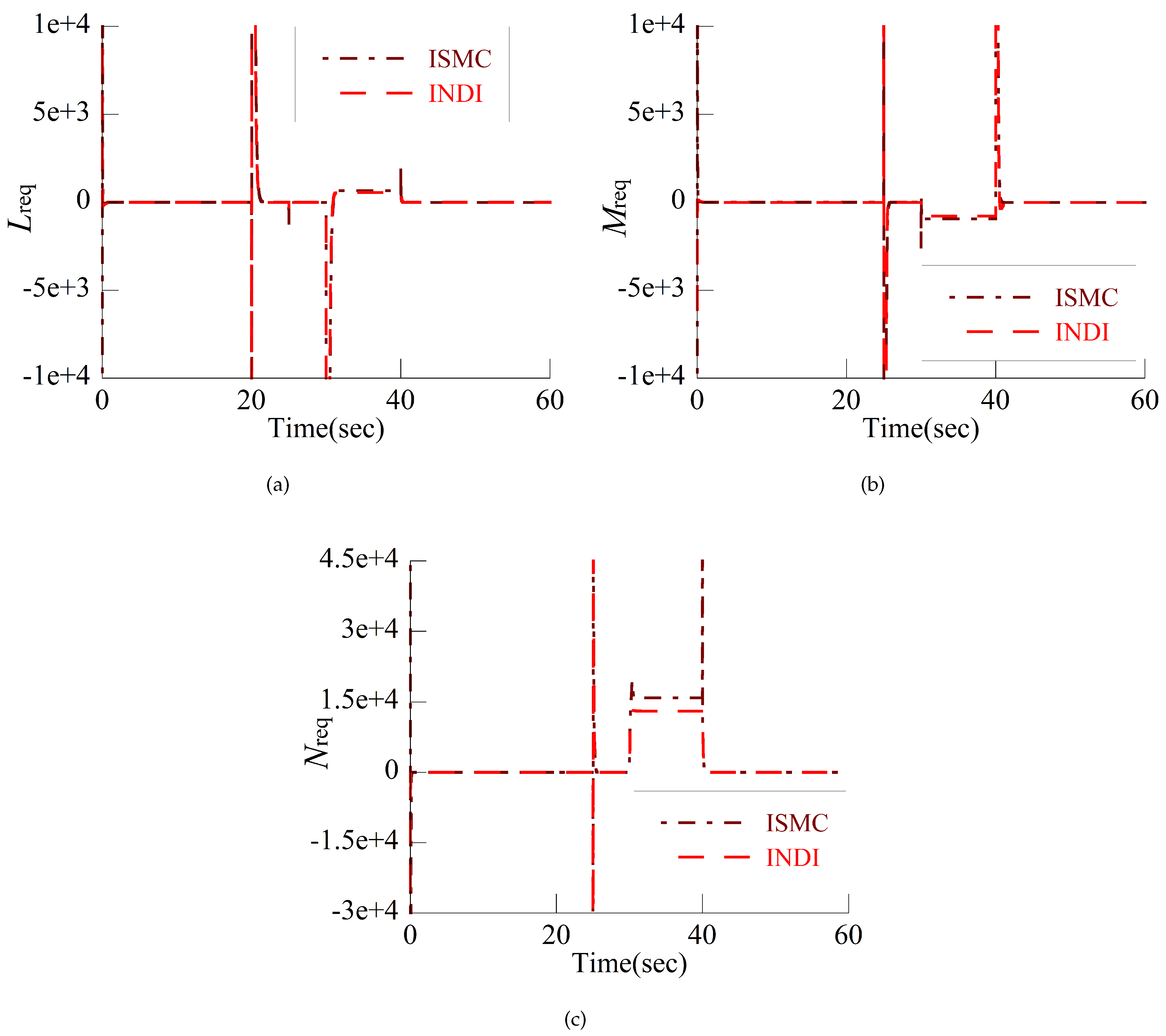
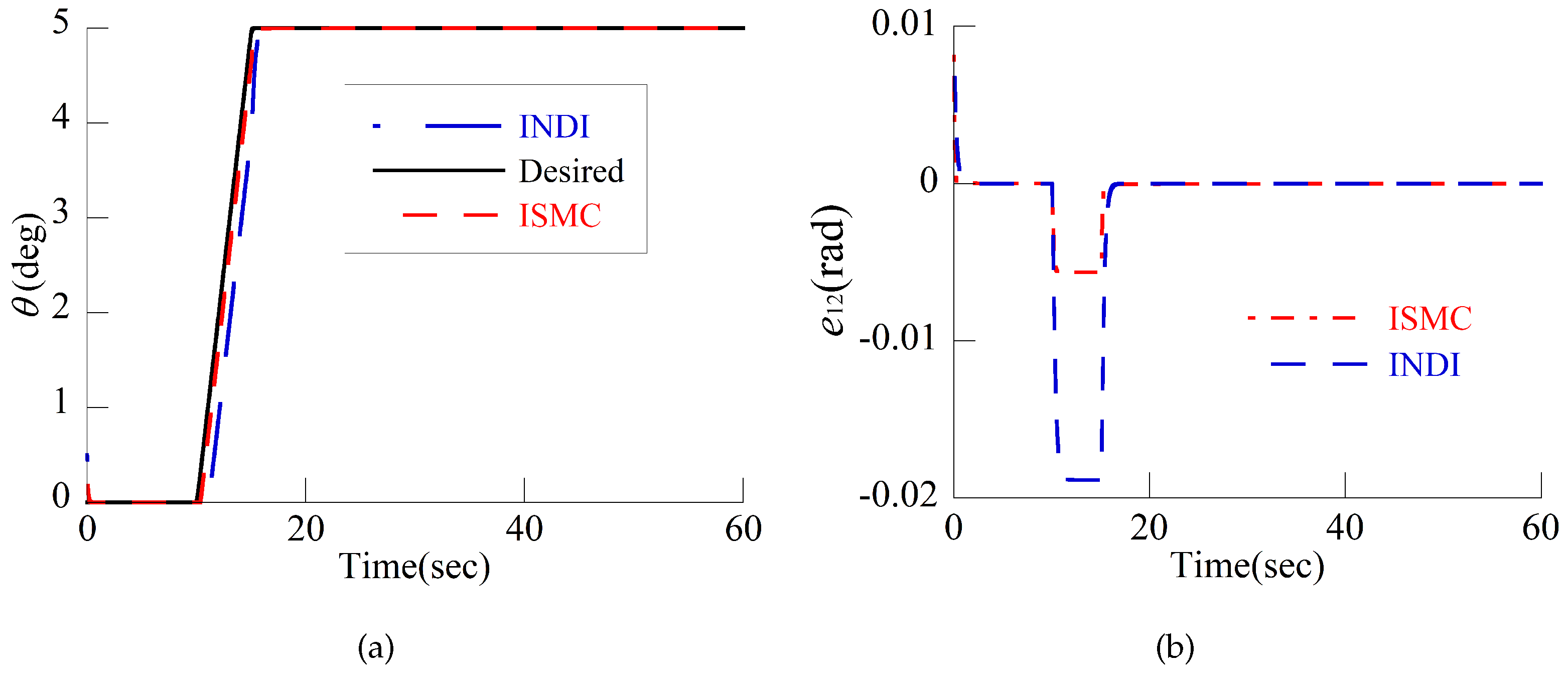
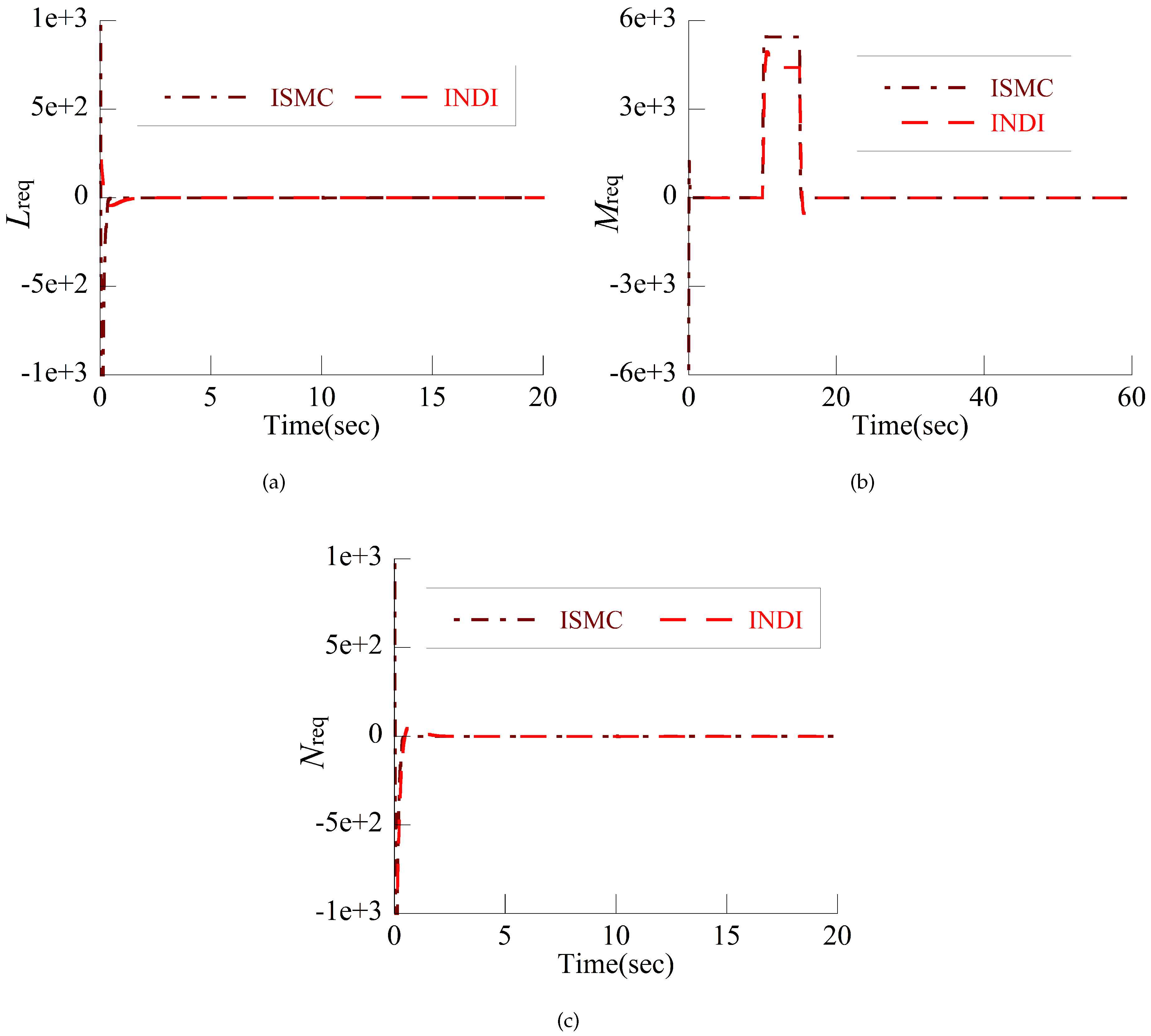
4.1. Attitude Tracking Control in Helicopter Mode
4.2. Attitude Tracking Control in Airplane Mode
4.3. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xiang, S.; Xie, A.; Ye, M.; Yan, X.; Han, X.; Niu, H.; Li, Q.; Huang, H. Autonomous eVTOL: A summary of researches and challenges. Green Energy Intell. Transp. 2024, 3, 100140. [Google Scholar] [CrossRef]
- Ye, Z.; Chen, Y.; Cai, P.; Lyu, H.; Gong, Z.; Wu, J. Control design for soft transition for landing preparation of light compound-wing unmanned aerial vehicles based on incremental nonlinear dynamic inversion. Appl. Sci. 2023, 13, 12225. [Google Scholar] [CrossRef]
- Liu, Z.; He, Y.; Yang, L.; Han, J. Control techniques of tilt rotor unmanned aerial vehicle systems: A review. Chin. J. Aeronaut. 2017, 30, 135–148. [Google Scholar] [CrossRef]
- Wang, M.; Chu, N.; Bhardwaj, P.; Zhang, S.; Holzapfel, F. Minimum-time trajectory generation of eVTOL in low-speed phase: Application in control law design. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 1260–1275. [Google Scholar] [CrossRef]
- Qiao, Z.; Wang, D.; Xu, J.; Pei, X.; Su, W.; Wang, D.; Bai, Y. A comprehensive design and experiment of a biplane quadrotor tail-sitter UAV. Drones 2023, 7, 292. [Google Scholar] [CrossRef]
- Rohr, D.; Stastny, T.; Verling, S.; Siegwart, R. Attitude and cruise control of a VTOL tiltwing UAV. IEEE Robot. Autom. Lett. 2019, 4, 2683–2690. [Google Scholar] [CrossRef]
- Mao, S.; Gong, Z.; Ye, Z.; Wang, Z.; Guo, T.; Zhang, C. A linear-active-disturbance-rejection-based vertical takeoff and acceleration strategy with simplified vehicle operations for electric vertical takeoff and landing vehicles. Mathematics 2022, 10, 3333. [Google Scholar] [CrossRef]
- Deng, Z.; Wu, L.; You, Y. Modeling and design of an aircraft-mode controller for a fixed-wing VTOL UAV. Math. Probl. Eng. 2021, 2021, 7902134. [Google Scholar] [CrossRef]
- Allenspach, M.; Ducard, G.J.J. Nonlinear model predictive control and guidance for a propeller-tilting hybrid unmanned air vehicle. Automatica 2021, 132, 109790. [Google Scholar] [CrossRef]
- Xili, Y.; Yong, F.; Jihong, Z. Transition flight control of two vertical/short takeoff and landing aircraft. J. Guid. Control Dyn. 2008, 31, 371–385. [Google Scholar] [CrossRef]
- Ajel, A.R.; Humaidi, A.J.; Ibraheem, I.K.; Azar, A.T. Robust model reference adaptive control for tail-sitter VTOL aircraft. Actuators 2021, 10, 162. [Google Scholar] [CrossRef]
- Liu, N.; Cai, Z.; Wang, Y.; Zhao, J. Fast level-flight to hover mode transition and altitude control in tiltrotor’s landing operation. Chin. J. Aeronaut. 2021, 34, 181–193. [Google Scholar] [CrossRef]
- Liang, Z.; Fan, L.; Wen, G.; Xu, Z. Design, modeling, and control of a composite tilt-rotor unmanned aerial vehicle. Drones 2024, 8, 102. [Google Scholar] [CrossRef]
- Dalwadi, N.; Deb, D.; Kothari, M.; Ozana, S. Disturbance Observer-Based Backstepping Control of Tail-Sitter UAVs. Actuators 2021, 10, 119. [Google Scholar] [CrossRef]
- Yang, H.; Morales, R. Robust full-envelope flight control design for an evtol vehicle. In Proceedings of the AIAA Scitech 2021 Forum, Online, 19–21 January 2021; p. 0254. [Google Scholar]
- Yun, W.J.; Jung, S.; Kim, J.; Kim, J.H. Distributed deep reinforcement learning for autonomous aerial eVTOL mobility in drone taxi applications. ICT Express 2021, 7, 1–4. [Google Scholar] [CrossRef]
- Lane, S.; Stengel, R. Flight control design using non-linear inverse dynamics. Automatica 1988, 24, 471–483. [Google Scholar] [CrossRef]
- Georgie, J.; Valasek, J. Evaluation of longitudinal desired dynamics for dynamic-inversion controlled generic reentry vehicles. J. Guid. Control Dyn. 2003, 26, 811–819. [Google Scholar] [CrossRef]
- Enenakpogbe, E.; Whidborne, J.F.; Lu, L. Control of an eVTOL using non-linear dynamic inversion. In Proceedings of the 2022 UKACC 13th International Conference on Control, Plymouth, UK, 20–22 April 2022; pp. 158–164. [Google Scholar]
- Lombaerts, T.; Kaneshige, J.; Schuet, S.; Hardy, G.; Aponso, B.; Shish, K. Dynamic inversion based full envelope flight control for an eVTOL vehicle using a unified framework. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020; p. 1619. [Google Scholar]
- Sieberling, S.; Chu, Q.P.; Mulder, J.A. Robust flight control using incremental nonlinear dynamic inversion and angular acceleration prediction. J. Guid. Control Dyn. 2010, 33, 1732–1742. [Google Scholar] [CrossRef]
- Wang, X.; van Kampen, E.J.; Chu, Q.; Lu, P. Stability analysis for incremental nonlinear dynamic inversion control. J. Guid. Control Dyn. 2019, 42, 1116–1129. [Google Scholar] [CrossRef]
- Sun, S.; Wang, X.; Chu, Q.; de Visser, C. Incremental nonlinear fault-tolerant control of a quadrotor with complete loss of two opposing rotors. IEEE Trans. Robot. 2021, 37, 116–130. [Google Scholar] [CrossRef]
- Di Francesco, G.; Mattei, M. Modeling and incremental nonlinear dynamic inversion control of a novel unmanned tiltrotor. J. Aircr. 2016, 53, 73–86. [Google Scholar] [CrossRef]
- Lombaerts, T.; Kaneshige, J.; Schuet, S.; Hardy, G.; Aponso, B.; Shish, K. Nonlinear dynamic inversion based attitude control for a hovering quad tiltrotor evtol vehicle. In Proceedings of the AIAA Scitech 2019 Forum, San Diego, CA, USA, 7–11 January 2019; p. 0134. [Google Scholar]
- Suiçmez, E.; Kutay, A. Full envelope nonlinear flight controller design for a novel electric VTOL (eVTOL) air taxi. Aeronaut. J. 2024, 128, 966–993. [Google Scholar] [CrossRef]
- Matamoros, I.; de Vissery, C. Incremental nonlinear control allocation for a tailless aircraft with innovative control effectors. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Honolulu, HI, USA, 18–21 August 2018; p. 1116. [Google Scholar]
- Wang, X.; Sun, S. Incremental fault-tolerant control for a hybrid quad-plane UAV subjected to a complete rotor loss. Aerosp. Sci. Technol. 2022, 125, 107105. [Google Scholar] [CrossRef]
- Zhang, S.; Han, W.; Zhang, Y. Finite time convergence incremental nonlinear dynamic inversion-based attitude control for flying-wing aircraft with actuator faults. Actuators 2020, 9, 70. [Google Scholar] [CrossRef]
- Liu, J.; Sun, L.; Tan, W.; Liu, X.; Li, G. Finite time observer based incremental nonlinear fault-tolerant flight control. Aerosp. Sci. Technol. 2020, 104, 105986. [Google Scholar] [CrossRef]
- Tal, E.; Karaman, S. Accurate tracking of aggressive quadrotor trajectories using incremental nonlinear dynamic inversion and differential flatness. IEEE Trans. Control Syst. Technol. 2021, 29, 1203–1218. [Google Scholar] [CrossRef]
- Zhou, Y.; Van Kampen, E.J.; Chu, Q. Incremental approximate dynamic programming for nonlinear adaptive tracking control with partial observability. J. Guid. Control Dyn. 2018, 41, 2554–2567. [Google Scholar] [CrossRef]
- Zhou, Y.; van Kampen, E.J.; Chu, Q.P. Incremental model based online dual heuristic programming for nonlinear adaptive control. Control Eng. Pract. 2018, 73, 13–25. [Google Scholar] [CrossRef]
- Acquatella, B.P.; Chu, Q.P. Agile spacecraft attitude control: An incremental nonlinear dynamic inversion approach. IFAC-PapersOnLine 2020, 53, 5709–5716. [Google Scholar] [CrossRef]
- Meng, Q.; Yang, H.; Jiang, B. Fault-tolerant optimal spacecraft attitude maneuver: An incremental model approach. J. Guid. Control Dyn. 2022, 45, 1676–1691. [Google Scholar] [CrossRef]
- Bacon, B.; Ostroff, A.; Joshi, S. Reconfigurable NDI controller using inertial sensor failure detection & isolation. IEEE Trans. Aerosp. Electron. Syst. 2001, 37, 1373–1383. [Google Scholar]
- Xiao, B.; Zhang, H.; Chen, Z.; Cao, L. Fixed-time fault-tolerant optimal attitude control of spacecraft with performance constraint via reinforcement learning. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 7715–7724. [Google Scholar] [CrossRef]
- Moulay, E.; Léchappé, V.; Bernuau, E.; Defoort, M.; Plestan, F. Fixed-time sliding mode control with mismatched disturbances. Automatica 2022, 136, 110009. [Google Scholar] [CrossRef]
- Xiao, B.; Zhang, H.; Zhao, S.; Chen, Z.; Cao, L. Unified sufficient conditions for predefined-time stability of non-linear systems and its standard controller design. Actuators 2024, 13, 173. [Google Scholar] [CrossRef]
- Feng, Y.; Yu, X.; Han, F. On nonsingular terminal sliding-mode control of nonlinear systems. Automatica 2013, 49, 1715–1722. [Google Scholar] [CrossRef]
- Wu, C.; Yan, J.; Shen, J.; Wu, X.; Xiao, B. Predefined-time attitude stabilization of receiver aircraft in aerial refueling. IEEE Trans. Circuits Syst. II Express Briefs 2021, 68, 3321–3325. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, Z.; Xiao, B.; Li, B. Fast fixed-time attitude tracking control of spacecraft with prescribed performance. Int. J. Robust Nonlinear Control 2023, 33, 5229–5245. [Google Scholar] [CrossRef]




| Variable | Explanation | Value |
|---|---|---|
| S | Reference area | 0.460 m2 |
| b | Wingspan | 2.286 m |
| c | Mean aerodynamic chord | 0.2 m |
| m | Mass | 6.2 Kg |
| Moment of inertia around the x-axis | 0.5614 Kg·m2 | |
| Moment of inertia around the y-axis | 0.4479 Kg·m2 | |
| Moment of inertia around the z-axis | 0.8700 Kg·m2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Tan, Y. Incremental Sliding Mode Control for Predefined-Time Stability of a Fixed-Wing Electric Vertical Takeoff and Landing Vehicle Attitude Control System. Actuators 2024, 13, 371. https://doi.org/10.3390/act13090371
Liu J, Tan Y. Incremental Sliding Mode Control for Predefined-Time Stability of a Fixed-Wing Electric Vertical Takeoff and Landing Vehicle Attitude Control System. Actuators. 2024; 13(9):371. https://doi.org/10.3390/act13090371
Chicago/Turabian StyleLiu, Jujiang, and Yusong Tan. 2024. "Incremental Sliding Mode Control for Predefined-Time Stability of a Fixed-Wing Electric Vertical Takeoff and Landing Vehicle Attitude Control System" Actuators 13, no. 9: 371. https://doi.org/10.3390/act13090371
APA StyleLiu, J., & Tan, Y. (2024). Incremental Sliding Mode Control for Predefined-Time Stability of a Fixed-Wing Electric Vertical Takeoff and Landing Vehicle Attitude Control System. Actuators, 13(9), 371. https://doi.org/10.3390/act13090371





