A Double-Rotating Ferrofluid Vane Micropump with an Embedded Fixed Magnet
Abstract
1. Introduction
2. Ferrofluid and Driving Principle
2.1. Properties and Basic Theory of Ferrofluid
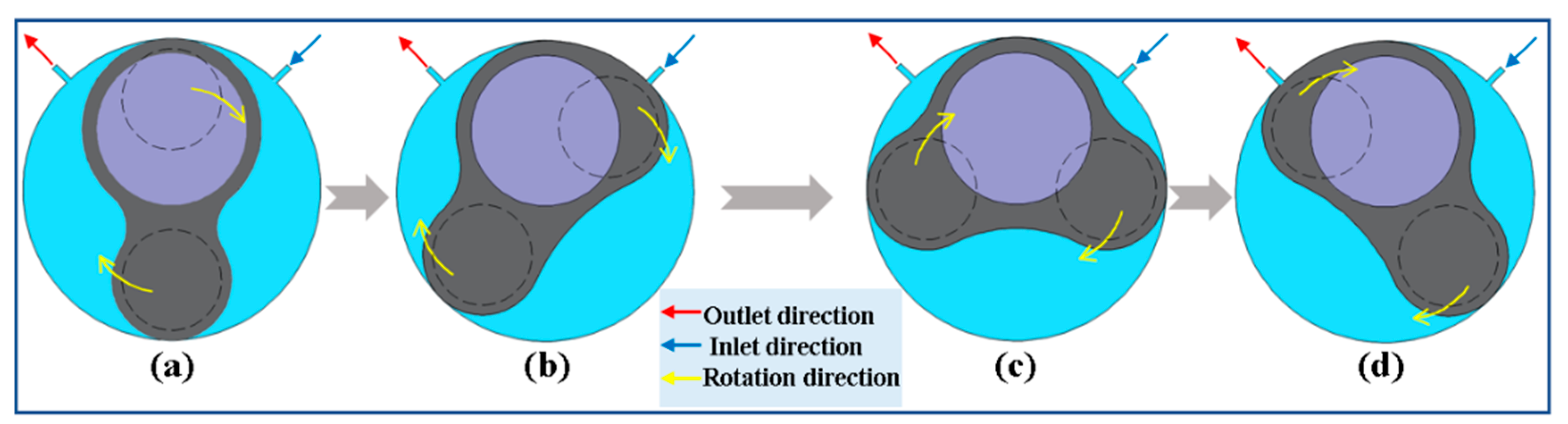
2.2. Design and Driving Principle of Micropump
3. Magnetic Field Numerical Analysis and Design Parameter Optimization
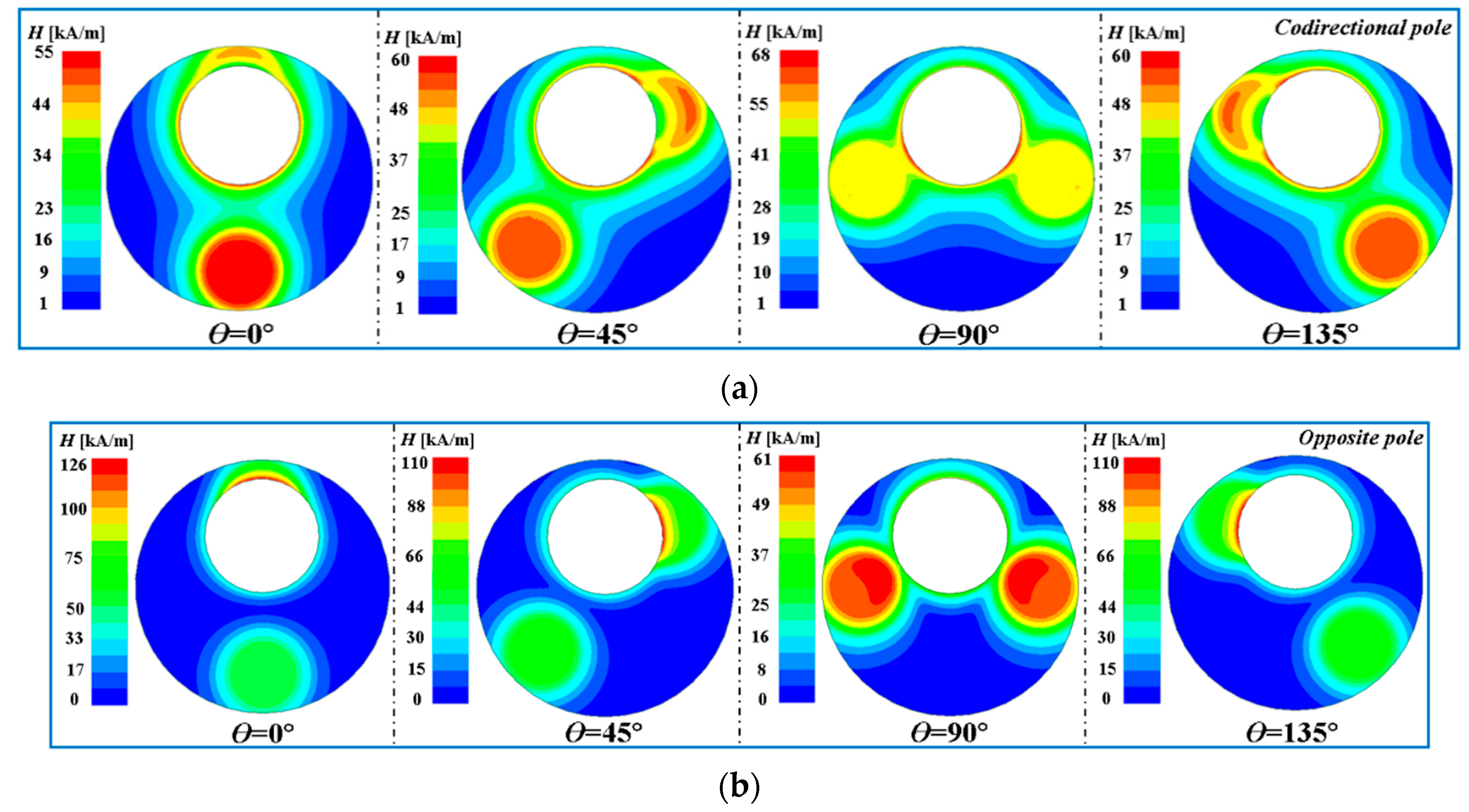
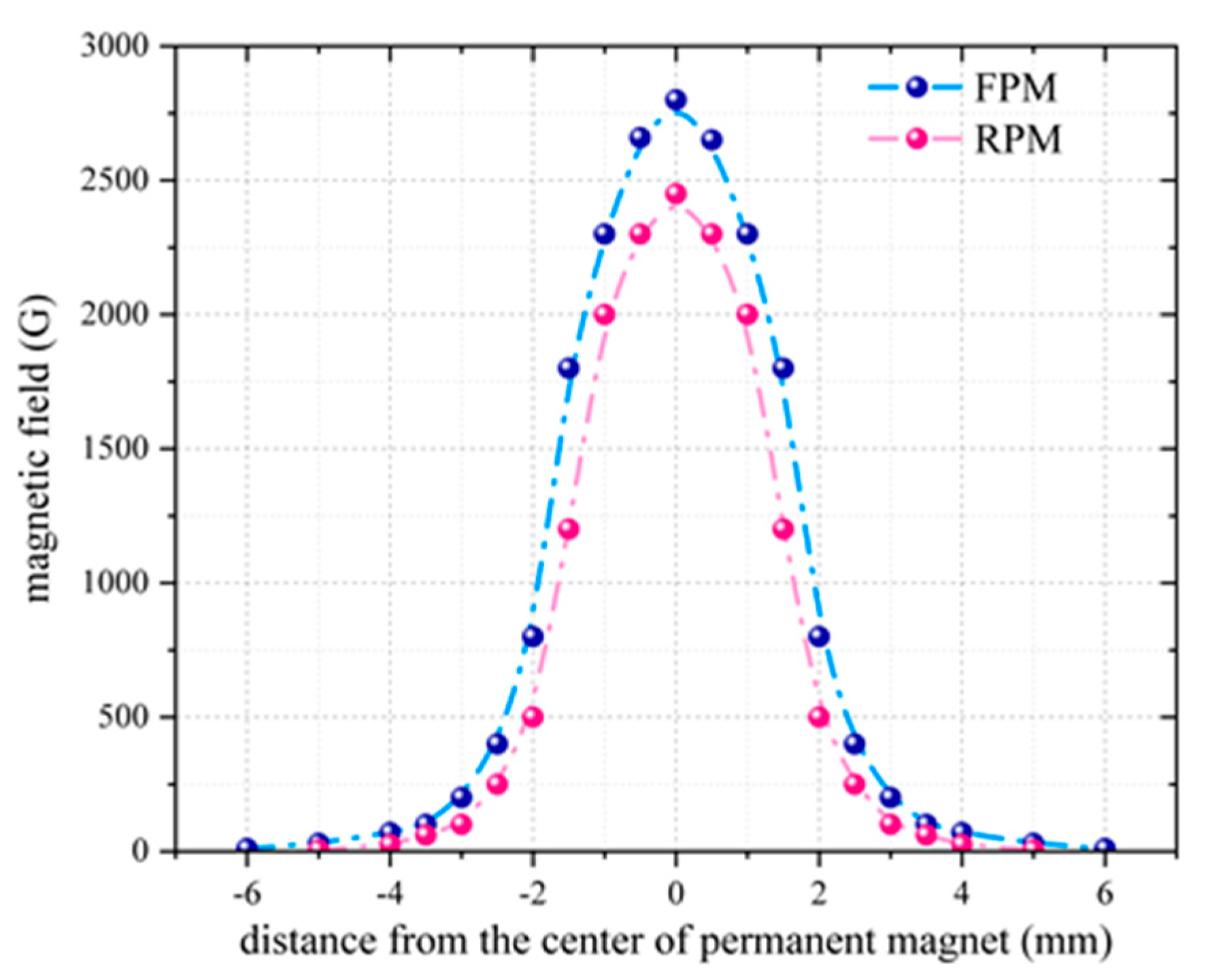
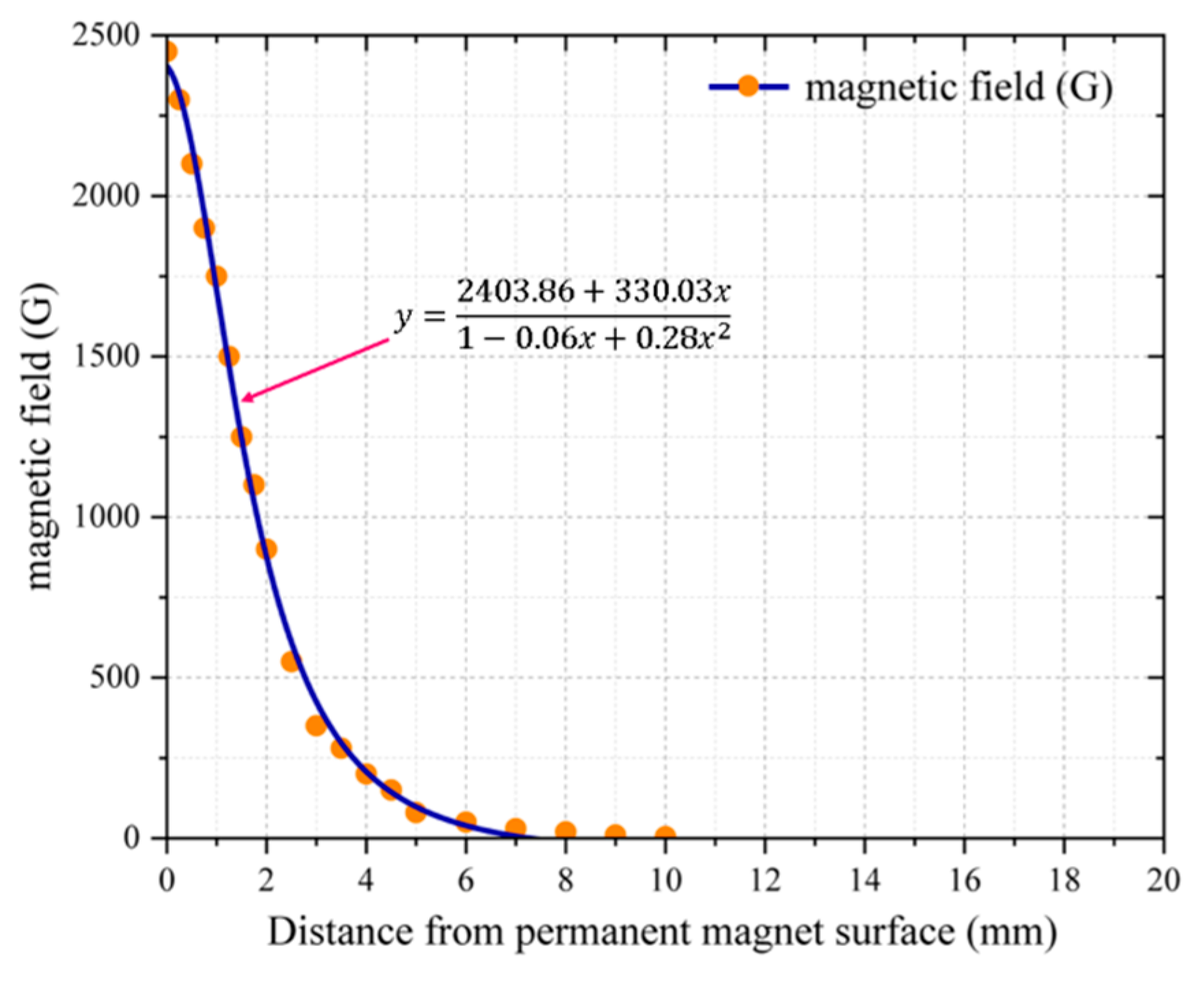
3.1. Numerical Analysis of Magnetic Field
3.2. Validation and Parameter Optimization
4. Experimental Tests
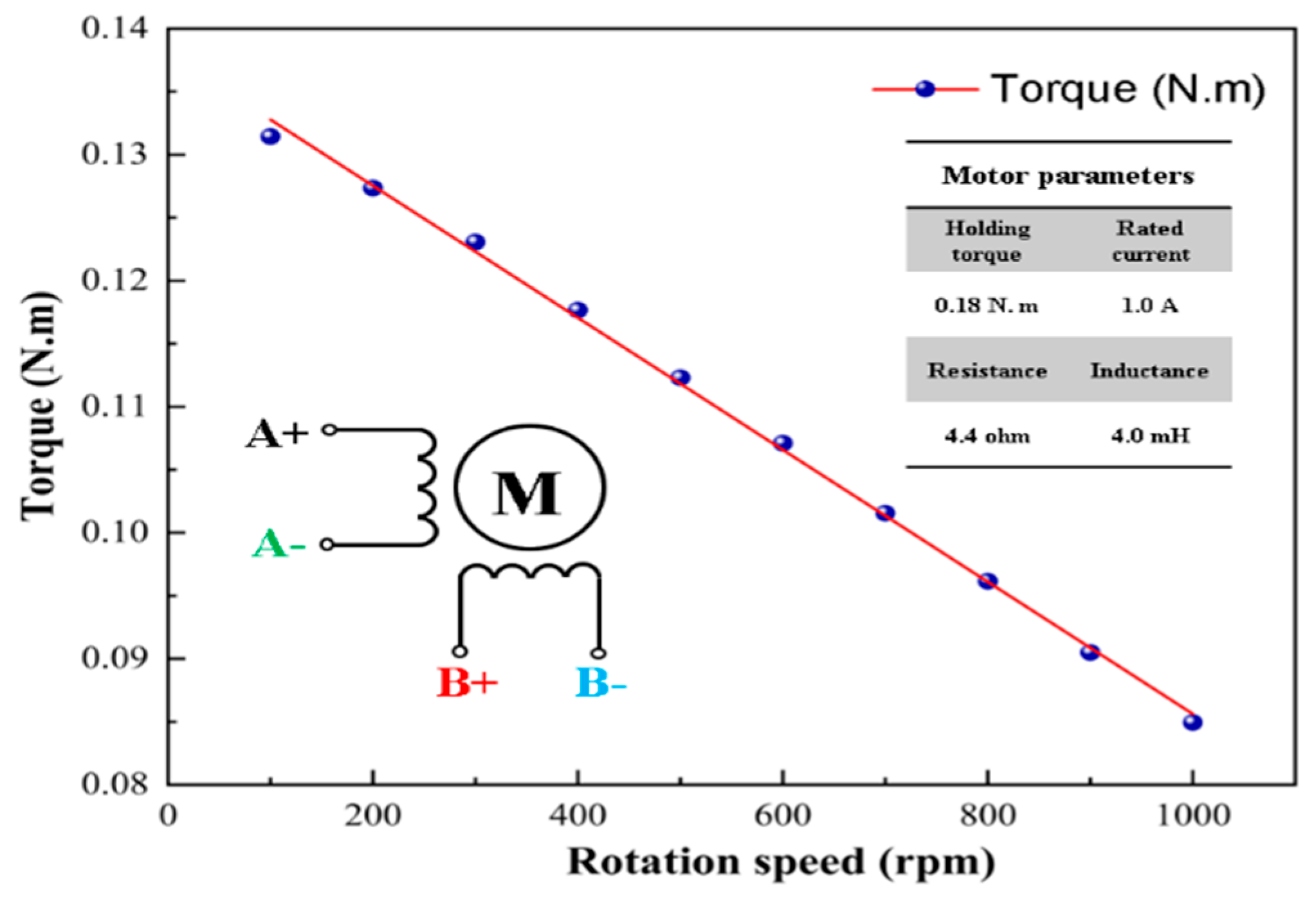
4.1. The Ferrofluid Micropump Test System
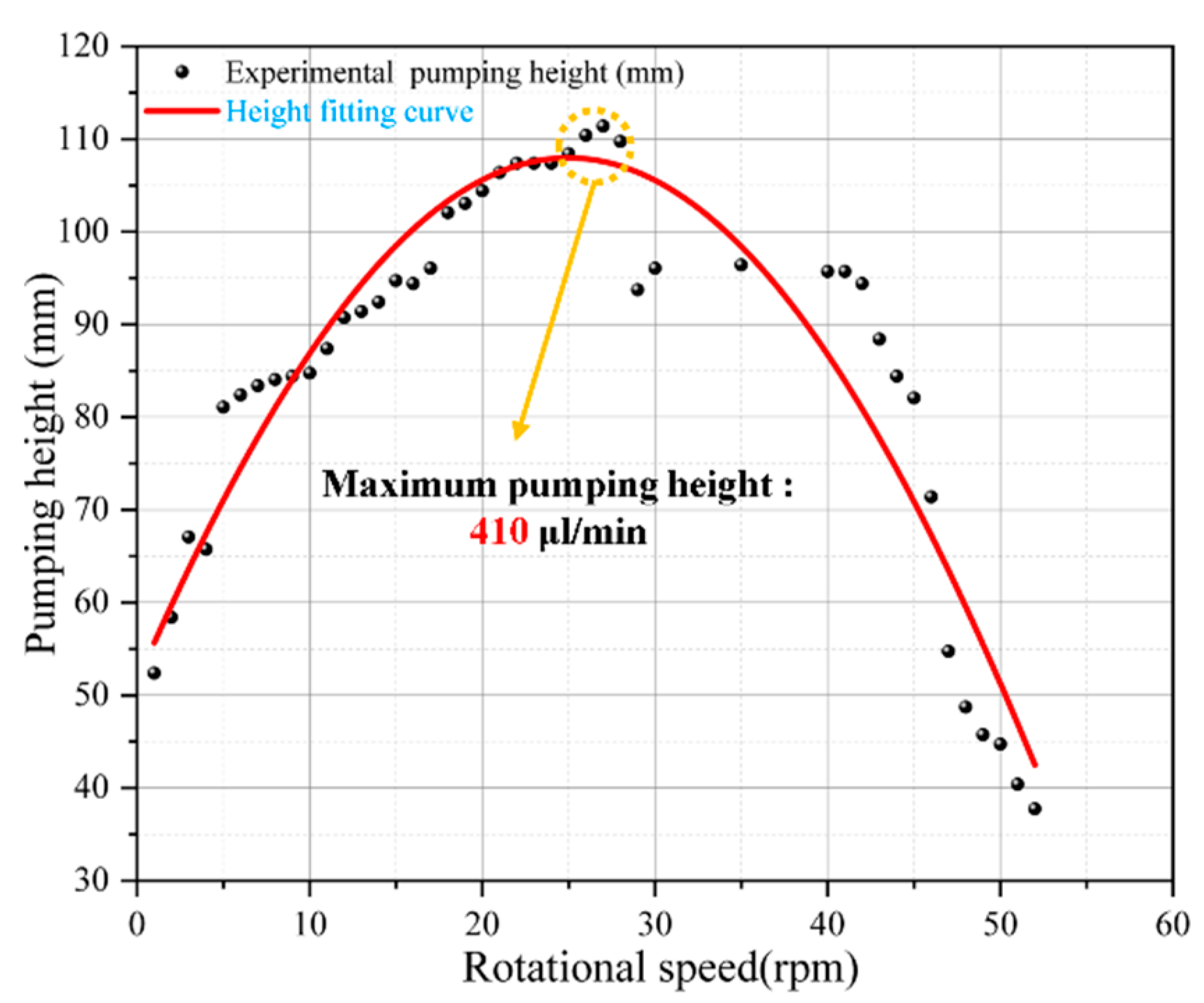
4.2. The Micropump Pumping Experiment Test
5. Results and Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, Z. Microsystem Design and Fabrication, 2nd ed.; Tsinghua University Press: Beijing, China, 2015. [Google Scholar]
- Mohith, S.; Karanth, P.N.; Kulkarni, S.M. Recent trends in mechanical micropumps and their applications: A review. Mechatronics 2019, 60, 34–55. [Google Scholar] [CrossRef]
- Chaimayo, C.; Kaewnaphan, B.; Tanlieng, N.; Athipanyasilp, N.; Sirijatuphat, R.; Chayakulkeeree, M.; Angkasekwinai, N.; Sutthent, R.; Puangpunngam, N.; Tharmviboonsri, T.; et al. Rapid SARS-CoV-2 antigen detection assay in comparison with real-time RT-PCR assay for laboratory diagnosis of COVID-19 in Thailand. Virol. J. 2020, 17, 177. [Google Scholar] [CrossRef]
- Adampourezare, M.; Dehghan, G.; Hasanzadeh, M.; Feizi, M.A. Application of lateral flow and microfluidic bio-assay and biosensing towards identification of DNA-methylation and cancer detection: Recent progress and challenges in biomedicine. Biomed. Pharmacother. 2021, 141, 111845. [Google Scholar] [CrossRef]
- Koh, A.; Kang, D.; Xue, Y.; Lee, S.; Pielak, R.M.; Kim, J.; Hwang, T.; Min, S.; Banks, A.; Bastien, P.; et al. A soft, wearable microfluidic device for the capture, storage, and colorimetric sensing of sweat. Sci. Transl. Med. 2016, 8, ra165–ra366. [Google Scholar] [CrossRef] [PubMed]
- Sultana, N.; Gunning, S.; Furst, S.J.; Garrard, K.P.; Dow, T.A.; Vinueza, N.R. Direct analysis of textile dyes from trace fibers by automated microfluidics extraction system coupled with Q-TOF mass spectrometer for forensic applications. Forensic Sci. Int. 2018, 289, 67–74. [Google Scholar] [CrossRef] [PubMed]
- Golozar, M.; Chu, W.K.; Casto, L.D.; McCauley, J.; Butterworth, A.L.; Mathies, R.A. Fabrication of high-quality glass microfluidic devices for bioanalytical and space flight applications. MethodsX 2020, 7, 101043. [Google Scholar] [CrossRef] [PubMed]
- Pothuri, C.; Azharudeen, M.; Subramani, K. Rapid mixing in microchannel using standing bulk acoustic waves. Phys. Fluids 2019, 31, 122001. [Google Scholar] [CrossRef]
- Laser, D.J.; Santiago, J.G. A review of micropumps. J. Micromech. Microeng. 2004, 14, R35–R64. [Google Scholar] [CrossRef]
- Doganay, S.; Cetin, L.; Ezan, M.A.; Turgut, A. A rotating permanent magnetic actuator for micropumping devices with magnetic nanofluids. J. Micromech. Microeng. 2020, 30, 075012. [Google Scholar] [CrossRef]
- Spencer, W.J.; Corbett, W.T.; Dominguez, L.R.; Shafer, B.D. An electronically controlled piezoelectric insulin pump and valves. IEEE T. Son. Ultrason. 1978, 25, 153–156. [Google Scholar] [CrossRef]
- Das, P.K.; Hasan, A.B.M.T. Mechanical micropumps and their applications: A review. In Proceedings of the 7th BSME International Conference on Thermal Engineering, Dhaka, Bangladesh, 22–24 December 2016; AIP Publishing LLC: New York, NY, USA, 2017; pp. 917–942. [Google Scholar]
- Forouzandeh, F.; Arevalo, A.; Alfadhel, A.; Borkholder, D.A. A review of peristaltic micropumps. Sens. Actuators 2021, 326, 112602. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.H.; Wang, Y.; Huang, J. Advances in valveless piezoelectric pump with cone-shape. Chin. J. Mech. Eng. 2017, 30, 766–781. [Google Scholar] [CrossRef]
- Okamoto, Y.; Ryoson, H.; Fujimoto, K.; Ohba, T.; Mita, Y. On-chip CMOS-MEMS-based electroosmotic flow micropump integrated with high-voltage generator. J. Microelectromech. Syst. 2019, 29, 86–94. [Google Scholar] [CrossRef]
- Pollack, M.G.; Paik, P.Y.; Shenderov, A.D.; Pamula, V.K.; Dietrich, F.S.; Fair, R.B. Investigation of electrowetting-based microfluidics for real-time PCR applications. In Proceedings of the Seventh International Conference on Miniaturized Chemical and Biochemical Analysis Systems (MicroTAS’03), Squaw Valley, CA, USA, 5–9 October 2003; pp. 611–619. [Google Scholar]
- Qu, Y.; Zhou, J. Lumped parameter model and numerical model of vapor bubble–driven valve-less micro-pump. Adv. Mech. Eng. 2017, 9, 1687814017695958. [Google Scholar] [CrossRef]
- Gusenbauer, M.; Mazza, G.; Posnicek, T.; Brandl, M.; Schrefl, T. Magnetically actuated circular displacement micropump. Int. J. Adv. Manuf. Technol. 2018, 95, 3575–3588. [Google Scholar] [CrossRef]
- Chen, F.; Zhang, J.; Li, Z.; Yan, S.; Li, W. Effect of the surface coating of carbonyl iron particles on the dispersion stability of magnetorheological fluid. Sci. Rep. 2024, 14, 11358. [Google Scholar] [CrossRef] [PubMed]
- Fan, X.; Jiang, Y.; Li, M.; Zhang, Y.; Tian, C.; Mao, L.; Xie, H.; Sun, L.; Yang, Z.; Sitti, M. Scale-reconfigurable miniature ferrofluidic robots for negotiating sharply variable spaces. Sci. Adv. 2022, 8, eabq1677. [Google Scholar] [CrossRef]
- Miller, C.W.; Resler, E.L., Jr. Magnetic forces and the surface instability in ferromagnetic fluids. Phys. Fluids 1975, 18, 1112–1118. [Google Scholar] [CrossRef]
- Hatch, A.; Kamholz, A.E.; Holman, G.; Yager, P.; Bohringer, K.F. A ferrofluidic magnetic micropump. J. Microelectromech. Syst. 2001, 10, 215–221. [Google Scholar] [CrossRef]
- Chang, Y.J.; Hu, C.Y.; Lin, C.H. A microchannel immunoassay chip with ferrofluid actuation to enhance the biochemical reaction. Sens. Actuators B Chem. 2013, 182, 584–591. [Google Scholar] [CrossRef]
- Ashouri, M.; Behshad Shafii, M.; Moosavi, A. Theoretical and experimental studies of a magnetically actuated valveless micropump. J. Micromech. Microeng. 2017, 27, 015016. [Google Scholar] [CrossRef]
- Liu, B.; Zhang, Z.; Yang, J.; Yang, J.; Li, D. A rotary ferrofluidic vane micropump with C shape baffle. Sens. Actuators B Chem. 2018, 263, 452–458. [Google Scholar] [CrossRef]
- Li, W.; Li, Z.; Han, W.; Li, Y.; Yan, S.; Zhao, Q.; Gu, Z. Pumping-velocity variation mechanisms of a ferrofluid micropump and structural optimization for reflow inhibition. Phys. Fluids 2023, 35, 052005. [Google Scholar]
- Shaker, S.; Hajjawi, M.; Khan, A. Effect of inlet and outlet angles on the flow performance of the ferrofluidic magnetic micropump. Cogent Eng. 2023, 10, 2158611. [Google Scholar] [CrossRef]
- Chi, C. Physical Basis and Application of Ferromagnetic Fluids; Beijing University of Aeronautics and Astronautics Press: Beijing, China, 2011. [Google Scholar]
- Li, W.; Li, Z.; Han, W.; Tan, S.; Yan, S.; Wang, D.; Yang, S. Time-mean equation and multi-field coupling numerical method for low-Reynolds-number turbulent flow in ferrofluid. Phys. Fluids 2023, 35, 125145. [Google Scholar] [CrossRef]
- Li, D.C. Theory and Application of Magnetic Liquid Seal; Science Press: Beijing, China, 2010; pp. 43–46. [Google Scholar]
- Stefania, F.; Musenich, R. Biot–Savart approach to analytical computation of magnetic fields and forces of CCT magnets. IEEE Trans. Appl. Supercond. 2021, 31, 4900308. [Google Scholar]
- Yamahata, C.; Chastellain, M.; Parashar, V.K.; Petri, A.; Hofmann, H.; Gijs, M.A. Plastic micropump with ferrofluidic actuation. J. Microelectromech. Syst. 2005, 14, 96–102. [Google Scholar] [CrossRef]
- Lee, C.Y.; Leong, J.C.; Wang, Y.N.; Fu, L.M. A ferrofluidic magnetic micropump for variable-flow-rate applications. Jpn. J. Appl. Phys. 2012, 51, 047201. [Google Scholar] [CrossRef]
- Shen, C. Design and Experimental Study of Valveless Magnetic Fluid Driver Micropump; Beijing University of Technology: Beijing, China, 2021. [Google Scholar]
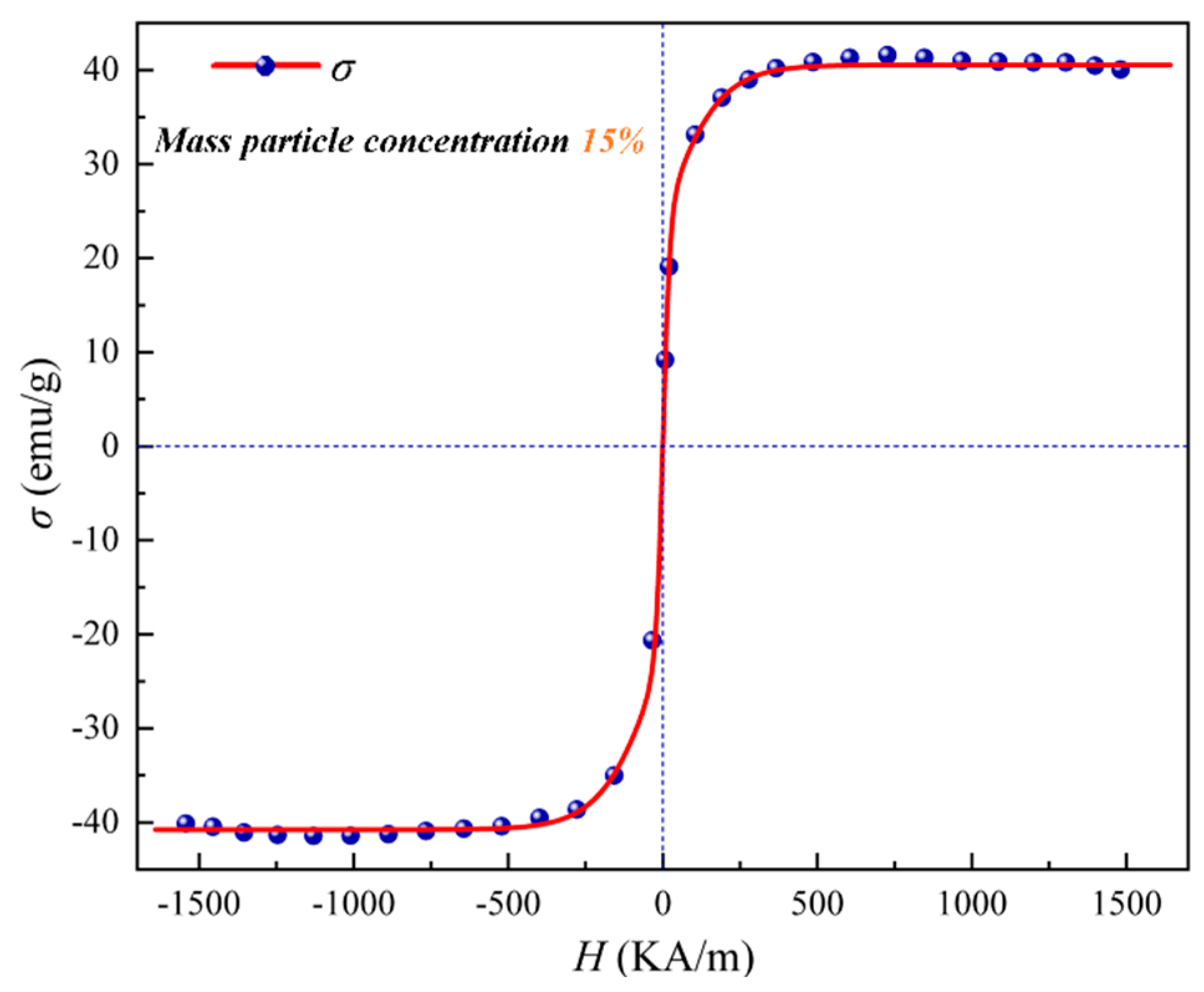






| Carrier Fluid | Magnetic Particles | Average Particle Size | Mass% Particle Concentration | Saturation of Magnetization |
|---|---|---|---|---|
| Kerosene | Magnetite particle | 8 nm | 40 | 350 Gs |
| Name | Symbol | Value |
|---|---|---|
| Inlet width (mm) | Win | 1 |
| Outlet width (mm) | Wout | 1 |
| Pump chamber diameter (mm) | D | 20 |
| Pump chamber depth (mm) | H | 0.5 |
| Air gap width (mm) | Wgap | 0.5 |
| FPM diameter (mm) | Df | 8 |
| FPM diameter (mm) | Hf | 1 |
| RPM diameter (mm) | Dr | 6 |
| RPM diameter (mm) | Hr | 1 |
| Center distance (mm) | dc | 4 |
| Reference | Layers of Structure | Dimensions of Micropump (mm) | Numbers of Magnets | Maximum Pumping Flow (μL/min) | Backpressure (Pa) |
|---|---|---|---|---|---|
| Yamahata [32] | 7 | 36 × 22 × 6 | 1 | 30 | 2500 |
| Hatch [22] | 2 | D12 × 0.75 | 2 | 45.8 | 1200 |
| Bendong Liu [25] | 2 | 25 × 25 × 3.5 | 1 | 49.32 | 1125.9 |
| Chia-Yen Lee [33] | 2 | D21 × 0.46 | 1 | 93 | 660 |
| C. Shen [34] | 2 | D15 × 3 | 1 | 256.83 | 4195.04 |
| Majid Ashouri [24] | 3 | 54 × 15 × 4 | 1 | 700 | 750 |
| This work | 2 | D18.5 × 1.5 | 3 | 410 | 1092 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Li, Z.; Li, D.; Chen, F.; Zhao, Q.; Qing, J.; Li, X.; Yang, C.; He, X.; Zhao, Y. A Double-Rotating Ferrofluid Vane Micropump with an Embedded Fixed Magnet. Actuators 2024, 13, 308. https://doi.org/10.3390/act13080308
Wang Y, Li Z, Li D, Chen F, Zhao Q, Qing J, Li X, Yang C, He X, Zhao Y. A Double-Rotating Ferrofluid Vane Micropump with an Embedded Fixed Magnet. Actuators. 2024; 13(8):308. https://doi.org/10.3390/act13080308
Chicago/Turabian StyleWang, Ye, Zhenggui Li, Decai Li, Fang Chen, Qin Zhao, Jie Qing, Xin Li, Chao Yang, Xinyue He, and Yi Zhao. 2024. "A Double-Rotating Ferrofluid Vane Micropump with an Embedded Fixed Magnet" Actuators 13, no. 8: 308. https://doi.org/10.3390/act13080308
APA StyleWang, Y., Li, Z., Li, D., Chen, F., Zhao, Q., Qing, J., Li, X., Yang, C., He, X., & Zhao, Y. (2024). A Double-Rotating Ferrofluid Vane Micropump with an Embedded Fixed Magnet. Actuators, 13(8), 308. https://doi.org/10.3390/act13080308





