Trajectory Synthesis and Linkage Design of Single-Degree-of-Freedom Finger Rehabilitation Device

Abstract

For injured and after-stroke patients who temporarily lose their hand’s grasping abilities, assisting them in regaining their index finger mobility is very important in the rehabilitation process. In this paper, a finger rehabilitation device based on one degree-of-freedom (DOF) linkage mechanism is designed, aiming to lead the index finger through the flexion–extension trajectory during grasping tasks. Two types of one-DOF mechanisms, a four-bar linkage and a Watt-I six-bar linkage, are synthesized for the task trajectory. Various algorithms such as PSO, GA, and GA–BFGS are adopted and compared for the synthesis of these two types of mechanisms, among which the Watt-I six-bar linkage obtained with GA–BFGS shows the optimal performance in accuracy. Clinical biomechanical data are utilized to perform static analyses of the mechanisms, and the feasibility of the Watt-I six-bar linkage models is tested, compared, and demonstrated. Finally, the prototype of the six-bar linkage as well as a wearable exoskeleton finger rehabilitation device are designed to show how they are applied in the finger rehabilitation scenario.

1. Introduction

Population aging is a common challenge currently faced globally [1], with stroke being one of the major diseases threatening the health of the elderly, characterized by high incidence, disability, and recurrence rates. Stroke can result in varying degrees of functional impairment, with the most common being contralateral upper limb paralysis, with a high incidence of upper limb movement disorders reaching up to 75% [2]. Among the upper limb movement disorders caused by stroke, hand function impairment has a higher incidence rate, necessitating the early selection of appropriate rehabilitation strategies for treatment [3]. Repeatedly completing grasping movements with the fingers to rebuild hand nerves and effectively exercising affected muscles is an effective method for restoring hand motor function in patients [4]. Debaditya et al. [5] recorded the flexion and extension movements of the index finger by grasping a specific object 30 times, obtained finger trajectory data after image processing, and applied these data as the target trajectory in the trajectory synthesis of the single-degree-of-freedom Stevenson III six-bar mechanism for the index finger exoskeleton. Single-degree-of-freedom mechanisms, due to their simple structure and convenient control, have been widely used in the field of rehabilitation [6,7,8,9].

Watt-I six-bar mechanisms are a major category of single-degree-of-freedom six-bar mechanisms with significant engineering applications [10], but domestic research on six-bar mechanisms mainly focuses on Stevenson-type six-bar mechanisms, with relatively less research on Watt-I six-bar mechanisms [11]. J. Lee et al. [12] compared the fitting of four-bar, six-bar, and eight-bar mechanisms to lower limb gait trajectories and found that all three types of link mechanisms can achieve good fitting of gait trajectories. Therefore, this study compares the tracking errors of single-degree-of-freedom four-bar mechanisms and single-degree-of-freedom Watt-I six-bar mechanisms, selecting the optimal link mechanism as the finger rehabilitation device.

The kinematic synthesis of single-degree-of-freedom mechanisms involves synthesizing paths based on required movements and satisfying the functional relationship between input and output links. There are three types of path synthesis methods for single-degree-of-freedom mechanisms: mathematical analytical methods, graphical methods, and optimization algorithms. Optimization algorithms are divided into traditional numerical methods and modern heuristic methods. Traditional numerical methods are generally deterministic algorithms. Unlike heuristic methods, they have faster computational speeds but are prone to converge with local optimal solutions, and the convergence effect highly depends on the selection of initial values [13]. Common ones include gradient descent, conjugate gradient method, and quasi-Newton algorithms; heuristic algorithms generally have strong global convergence capabilities, but their qualitative analysis is difficult to quantify, and most algorithms are based on random characteristics, often resulting in slow convergence speeds and high computational complexity. Common ones include particle swarm optimization, simulated annealing, and genetic algorithms (GA). For heuristic algorithms, M. Mandal et al. [14] compared the optimization performance of differential evolution (DE), particle swarm optimization (PSO), and genetic algorithms (GA); simulated annealing [15] and other search algorithms have also been applied to link optimization problems. The genetic-quasi-Newton (GA–BFGS) algorithm is a hybrid algorithm that combines the global search capability of the GA algorithm with the local fine-tuning capability of the quasi-Newton algorithm, combining strengths to achieve faster convergence speeds and stronger global and local convergence capabilities. The GA–BFGS algorithm has been applied in engineering-related fields, such as Fan et al. [16] applying it to the recognition of fuzzy neural networks and proving its excellent optimization effect and faster convergence speed and Wang [17] applying it to solving the dynamic balance points of vehicles. The GA–BFGS algorithm has been applied in the field of rehabilitation and has proven its rationality and effectiveness, achieving excellent optimization performance for lower limb rehabilitation robots [18]. It enables the accurate fitting of gait trajectories during the rehabilitation process with higher precision.

In addition to the application of optimization algorithms, another focus is the selection of cost functions. In the application of link synthesis, trajectory point/trajectory distance errors are commonly set as cost functions in the optimization process [19,20]. In this study, we use the Euclidean distance between generated trajectory points and desired trajectory points to replace the contour error between generated and desired trajectories and use it as the cost function in the optimization process. To make the optimization effect universal, we introduce the average Euclidean distance to characterize its optimization effect.

In the process of finger rehabilitation, the use of pneumatic, controlled rehabilitation gloves may not be easy to control and easily produces secondary injuries. In this paper, a finger rehabilitation device based on a one-degree-of-freedom (DOF) linkage mechanism is designed, aiming to lead the index finger through the flexion–extension trajectory during grasping tasks. The designed institution structure is simple, easy to control, and can make a rehabilitation plan according to the actual situation of patients, which does not easily produce secondary injuries.

The main contributions of this paper are as follows:

(1)

Kinematic modeling was conducted for four-bar and six-bar linkages, with known finger-grasping trajectories defined as task trajectories. Several commonly used single-objective optimization algorithms were employed to analyze and optimize both the four-bar and six-bar linkages. Trajectory distance errors were compared among different optimization algorithms for trajectory synthesis. Ultimately, the GA–BFGS hybrid algorithm, which yielded smaller trajectory errors, was employed to optimize the design of a Watt-I six-bar linkage.

(2)

After using the optimization algorithm and static analysis, the optimal optimization parameters for the Watt-I six-bar mechanism were determined and modeled.

(3)

The prototype of the six-bar linkage as well as a wearable exoskeleton finger rehabilitation device are designed to show how they are applied in the finger rehabilitation scenario. The effectiveness of the design is demonstrated through physical experiments.

The rest of this paper is structured as follows: Section 2 compares the four-bar mechanism and the Watt-I six-bar mechanism, introducing the optimized design process of finger rehabilitation institution. Section 3 introduces the single-objective optimization algorithm GA–BFGS used in the text, and using known finger rehabilitation tracks for the task trajectory, the mean error of PSO, GA and GA–BFGS is compared. The Watt-I six-bar mechanism is selected as the source mechanism of the finger rehabilitation device. Then, Section 4 is the topology optimization design for its fixed end. Section 5 uses the SolidWorks2022 software to complete the final design of the overall exoskeleton finger rehabilitation device and build a six-bar mechanism for trajectory experiments; it proves the feasibility of designing finger rehabilitation devices through the Watt-I six-bar mechanism. Finally, the paper is concluded in Section 6.

2. Optimized Design of Finger Rehabilitation Mechanism

In the field of rehabilitation, four-bar and six-bar mechanisms are widely used. Among six-bar mechanisms, common configurations include the Watt and Stephenson types. The Watt-I six-bar mechanism is one of the simplest configurations of the six-bar mechanism. Therefore, in the section of this study concerning the selection of six-bar mechanism configurations, the Watt-I six-bar mechanism is used as a substitute.

This study focuses on two different mechanisms: the four-bar mechanism and the Watt-I six-bar mechanism. The plane four-bar linkage and the plane six-bar linkage are widely used in the field of rehabilitation robotics, which proves the rationality and effectiveness of the bar group mechanism in solving the path synthesis problem. However, we hope to design institutions that are more suitable to the task trajectory, so we need to compare and analyze the fitting of the task trajectory between the two types of institutions and choose a more suitable mechanism to pull the finger flexion and extension posture.

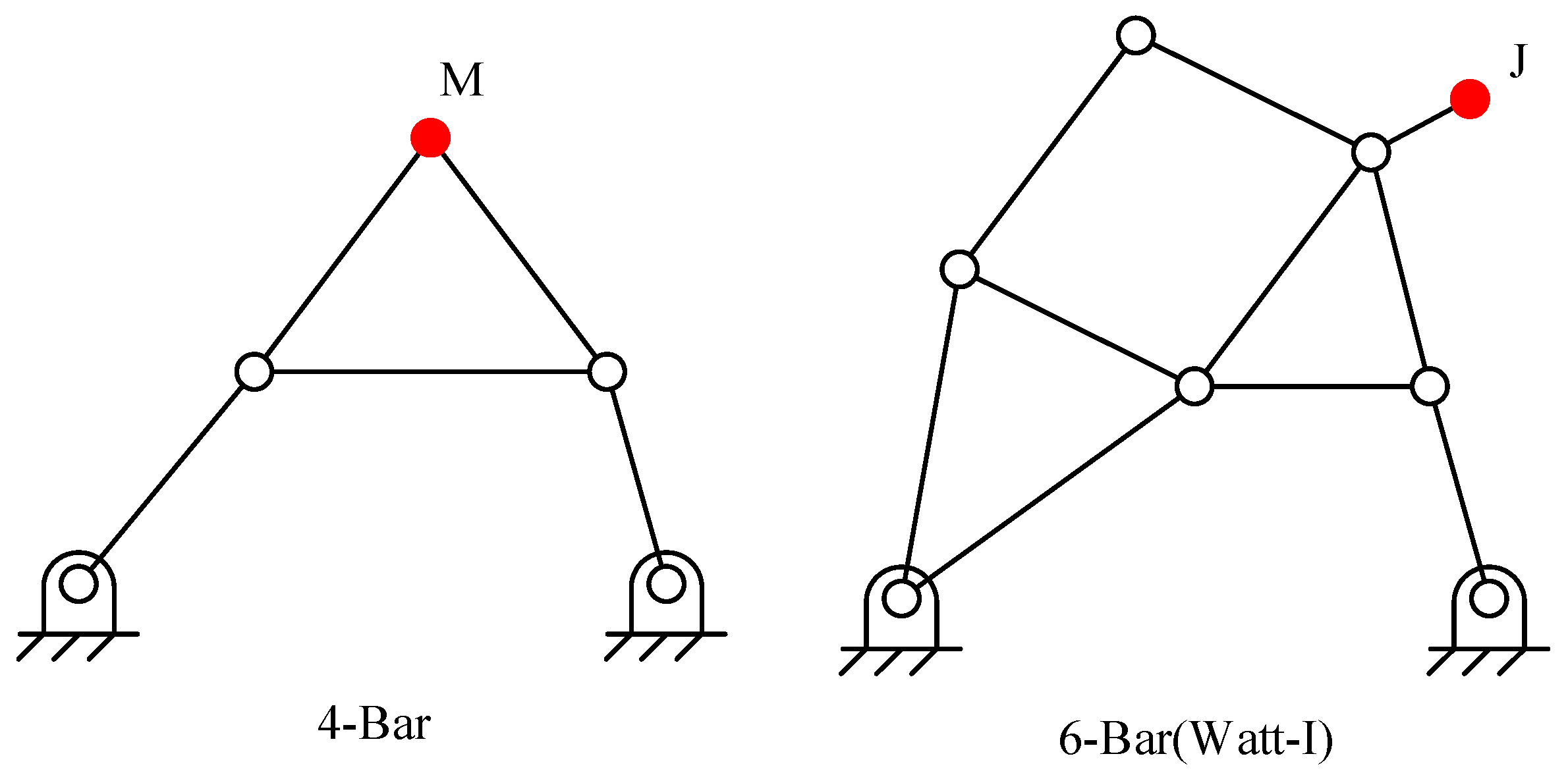
The typical topological structures of these two types of mechanisms are illustrated in Figure 1, where the positions of the end effector task points are denoted by the red solid points M and J, respectively. A single-degree-of-freedom finger rehabilitation mechanism should possess the ability to mimic finger-grasping actions effectively and should be easily customizable for personalized rehabilitation. This chapter provides a detailed discussion on the dimensional synthesis of each mechanism for finger-grasping and compares the distance errors of their data points to obtain the optimal mechanism configuration.

2.1. The Equation for the Position of the End Trajectory Point

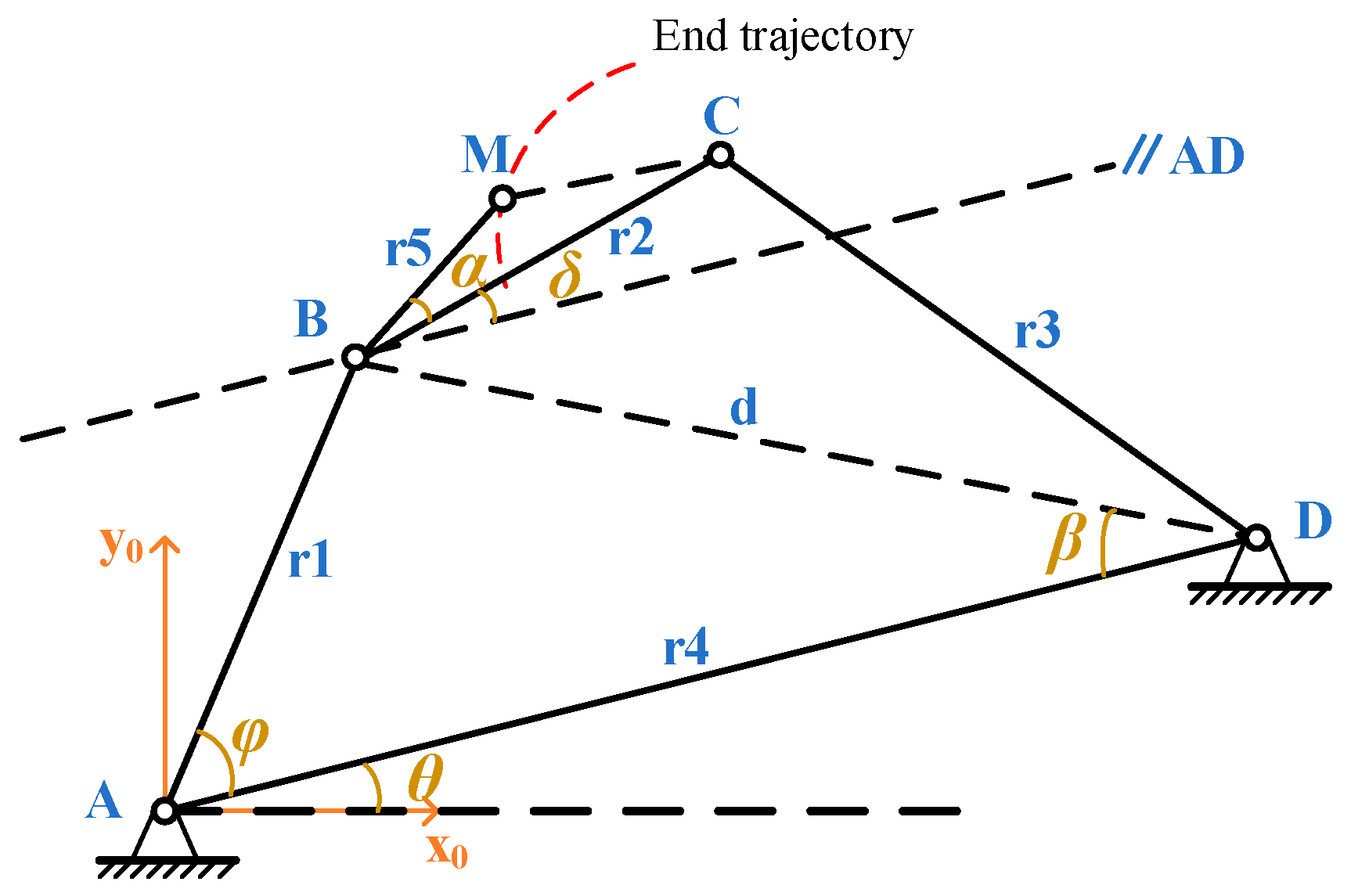
The schematic diagram of the four-bar mechanism is depicted in Figure 2, where AB represents the crank. Point M is located on the connecting link, and the dimensions of the various links are denoted as $r_1$, $r_2$, $r_3$, $r_4,$ and $r_5$. The angle between AD and the x-axis is denoted as θ, between AD and AB as φ, and between BM and BC as α, the angle between the auxiliary line AB parallel to AD passing through point B is δ. The generated end trajectory is defined by the motion of point M, and the design variable is denoted as $x=\left[r_1,r_2,r_3,r_4,r_5,x_A,y_A,\alpha ,\theta \right]$

It is evident that the position of the target point M in the reference frame XOY is represented as follows:

$$\left[\begin{array}{c}{x}_M\\ y_M\end{array}\right]=\left[\begin{array}{c}{x}_B\\ y_B\end{array}\right]+r_5\left[\begin{array}{c}\cos \left(\theta +\delta +\alpha \right)\\ \sin \left(\theta +\delta +\alpha \right)\end{array}\right]$$

(1)

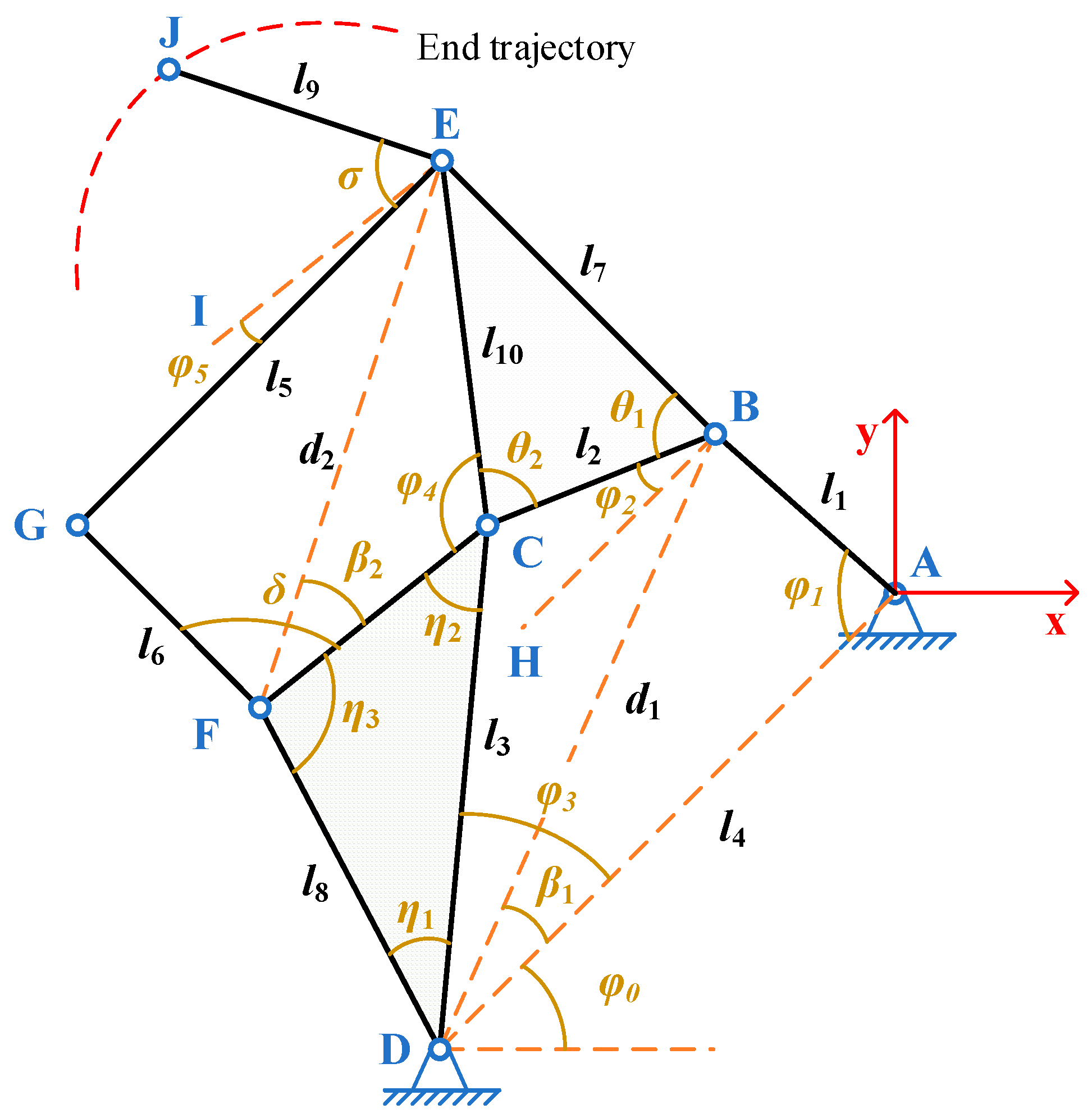
In Figure 3, the Watt-I six-bar mechanism is depicted, with point A as the origin of the coordinate system XOY. The length parameters of the Watt-I six-bar mechanism are denoted as follows: $l_1-l_{10}$. Point AD is fixed, forming an angle ${\phi }_0$ with the x-axis. The angle between the links AB and AD is ${\phi }_1$. Passing through point B, a line parallel to AD is drawn, denoted as BH. The angle between BC and BH is ${\phi }_2$. Angle ${\phi }_3$ is formed between CD and AD, and angle ${\phi }_4$ is formed between CF and CE. Point E is used to draw a line parallel to CF, denoted as EI, and the angle between EG and EI is ${\phi }_5$. Angle ${\eta }_1$ is formed between CD and DF, angle ${\eta }_2$ between CD and CF, and angle ${\eta }_3$ between CF and FD. Angles ${\theta }_1$ and ${\theta }_2$ are formed between BC and BE, and BC and CE, respectively. Angle ${\beta }_1$ represents the angle between AD and BD, while ${\beta }_2$ is the angle between CF and FE, and $\delta$ is the angle between FG and CF. The angle between EG and the extension of the link EJ is denoted as $\sigma$. The lengths of BD and EF are represented by $d_1$ and $d_2$, respectively. Point J serves as the generation point of the end trajectory. The optimization parameter is selected as $x^{\prime }=\left[l_1,l_2,l_3,l_4,l_5,l_6,l_7,l_8,l_9,x_A,y_A,{\theta }_1,{\eta }_1,{\phi }_0,\sigma ,{\phi }_1\right]$.

From Figure 3, ABCD forms a four-bar mechanism. Therefore, we can obtain the coordinates of points B and D as shown in Equations (2) and (3):

$$\left[\begin{array}{c}{x}_B\\ y_B\end{array}\right]=\left[\begin{array}{c}{x}_A\\ y_A\end{array}\right]+l_1\left[\begin{array}{c}\cos ({\varphi }_1-{\varphi }_0)\\ \sin ({\varphi }_1-{\varphi }_0)\end{array}\right]$$

(2)

$$\left[\begin{array}{c}{x}_C\\ y_C\end{array}\right]=\left[\begin{array}{c}{x}_B\\ y_B\end{array}\right]+l_2\left[\begin{array}{c}\cos ({\varphi }_0-{\varphi }_2)\\ \sin ({\varphi }_0-{\varphi }_2)\end{array}\right].$$

(3)

Therefore, based on the classical holonomic constraints, the theoretical coordinates of endpoint J can be obtained, as shown in Equation (4):

$$\left[\begin{array}{c}{x}_J\\ y_J\end{array}\right]=\left[\begin{array}{cc}\cos (\delta +{\varphi }_0)& -\sin (\delta +{\varphi }_0)\\ \sin (\delta +{\varphi }_0)& \cos (\delta +{\varphi }_0)\end{array}\right]\left[\begin{array}{c}{l}_{10}\cos ({\varphi }_4)+l_9\cos ({\varphi }_5-\sigma )\\ -l_{10}\sin ({\varphi }_4)+l_9\sin ({\varphi }_5-\sigma )\end{array}\right]+\left[\begin{array}{c}{x}_C\\ y_C\end{array}\right]$$

(4)

2.2. Kinematic Constraints

The four-bar mechanism must comply with Grashof’s law and the constraint of the extreme transmission angle, with the minimum transmission angle ${\tau }_{min}=40°$ being selected.

$$2\left[\min (r_1,r_2,r_3,r_4)+\max (r_1,r_2,r_3,r_4)\right]<(r_1+r_2+r_3+r_4)$$

(5)

$$\{\begin{array}{l}40°-\arccos \frac{{r_3}^2+{r_4}^2-{(r_1-r_2)}^2}{2r_3{r}_4}\le 0\\ -140°+\arccos \frac{{r_3}^2+{r_4}^2-{(r_1+r_2)}^2}{2r_3{r}_4}\le 0\end{array}$$

(6)

In the Watt-I six-bar mechanism, ABCD needs to satisfy all the requirements of the four-bar mechanism. Additionally, since GF and GE form a rotational pair, in order to meet their assembly conditions, the sum of the two sides of triangle GFE must be greater than the third side, and the difference between the two sides must be less than the third side, that is:

$$\max \left|EF\right|\le \left|GF\right|+\left|GE\right|$$

(7)

$$\min \left|EF\right|\ge \left|GF\right|-\left|GE\right|.$$

(8)

This can be expressed as:

$$\begin{array}{c}max\left|d_2\right| \le \left|l_5\right|+\left|l_6\right|\\ min\left|d_2\right| \ge \left|l_5\right|-\left|l_6\right|\end{array}.$$

(9)

During the optimization process, it is necessary to define the upper and lower bounds for each optimization variable, as shown in

Table 1. The upper and lower bounds for the optimization parameters of the four-bar mechanism.

Parameter	r1	r2	r3	r4	r5	xA	yA	α	θ
Lower limit	0	0	0	0	0	−50	−50	0	0
Upper limit	50	50	50	50	50	50	50	2π	2π

and

Table 2. The upper and lower bounds for the optimization parameters of the Watt-I six-bar mechanism.

Parameter	l1	l2	l3	l4	l5	l6	l7	l8	l9
Lower limit	0	0	0	0	0	0	0	0	0
Upper limit	50	50	50	50	50	50	50	50	50
parameter	xA	yA	θ1	η1	φ0	σ	φ1
Lower limit	−50	−50	0	0	0	0	0
Upper limit	50	50	2π	2π	2π	2π	2π

. Table 1 illustrates the upper and lower bounds for optimization parameters of the four-bar mechanism, while Table 2 presents the upper and lower bounds for the optimization parameters of the Watt-I six-bar mechanism.

2.3. Objective Functions

The crank rotates counterclockwise at a constant speed. During one complete rotation cycle of the crankshaft, the crank angle relevant to the desired trajectory is represented as ${\phi }_{\mathrm{i}}=\mathsf{\theta }+\frac{2\pi }{n}\left(i-1\right)\in$ [0, 2π], where $i=1,\cdots ,200$. This indicates that within one complete cycle, the crank undergoes 200 uniform increments. Subsequently, points along the target trajectory are sequentially sampled at equal time intervals. Utilizing a classical strategy of path synthesis, the generated trajectory is optimized against the desired trajectory to minimize contour errors. 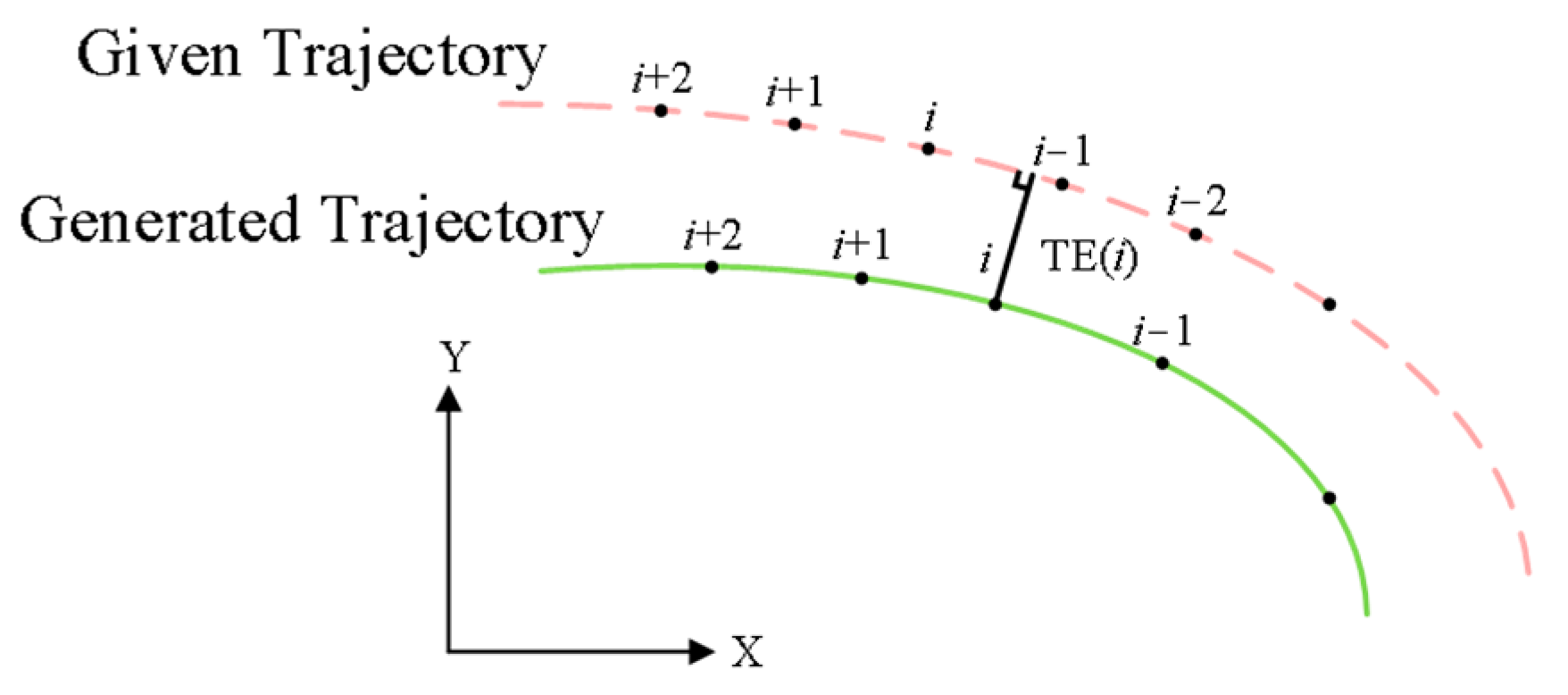Employing contour error as the objective function is highly reasonable [21]. Contour error, as depicted in Figure 4, represents the shortest orthogonal distance at each point between the generated trajectory and the desired trajectory (not necessarily occurring simultaneously).

The commonly used contour error function can be represented by the Euclidean distance between the given trajectory point and the generated trajectory point. It is based on the temporal correspondence and its formula is as follows:

$$TE(i)=\sqrt{{\displaystyle \sum _{i=1}^n{\Vert E(i)-E^{\ast }(i)\Vert }^2}}$$

(10)

Among them, $\mathrm{E}\left(\mathrm{i}\right)$ represents a given trajectory point, ${\mathrm{E}}^{*}\left(\mathrm{i}\right)$ represents the actual operating trajectory point at the end of the mechanism, ${\mathrm{E}}^{*}\left(\mathrm{i}\right)=\left[{\mathrm{x}}^{*}\left(\mathrm{i}\right),{\mathrm{y}}^{*}\left(\mathrm{i}\right)\right]$, $\mathrm{i}=1,\cdots ,$ n. To ensure the generality of the optimization results, we can use the average Euclidean distance $\overline{TE(i)}$ to characterize the optimization effectiveness of contour errors, where the expected coordinates of each point are given by the formula, with n representing the number of trajectory points:

$$\overline{TE(i)}=\frac{1}{n}TE(i)$$

(11)

3. Single-Objective Optimization Algorithm

A genetic algorithm (GA) is a stochastic algorithm developed by borrowing the ideas of biological evolution. It uses simple coding techniques to simulate complex structures into gene fragments for genetic operations similar to biological evolution and adopts the law of survival of the fittest to guide learning and determine search directions, with good global search ability. Due to the complex optimization problems involved in the parameter optimization process of members, traditional gradient-based algorithms often converge prematurely to local optima for optimization problems with multiple variables and complex functional relationships. Genetic algorithms suitable for global search have weak local fine search capabilities. Therefore, combining a genetic algorithm (GA) with a BFGS algorithm with good numerical stability and fast convergence speed can achieve fast and accurate comprehensive road problems as both algorithms learn from each other’s strengths and weaknesses. Wang et al. [22] have demonstrated that the hybrid algorithm of the GA–BFGS is superior to the GA in the process of bar optimization for four-bar mechanisms. The PSO, DE, SA, and ICA algorithms are used in this article for an optimization comparison to verify their application in the trajectory planning of four-bar and Watt-Ⅰ six-bar mechanisms.

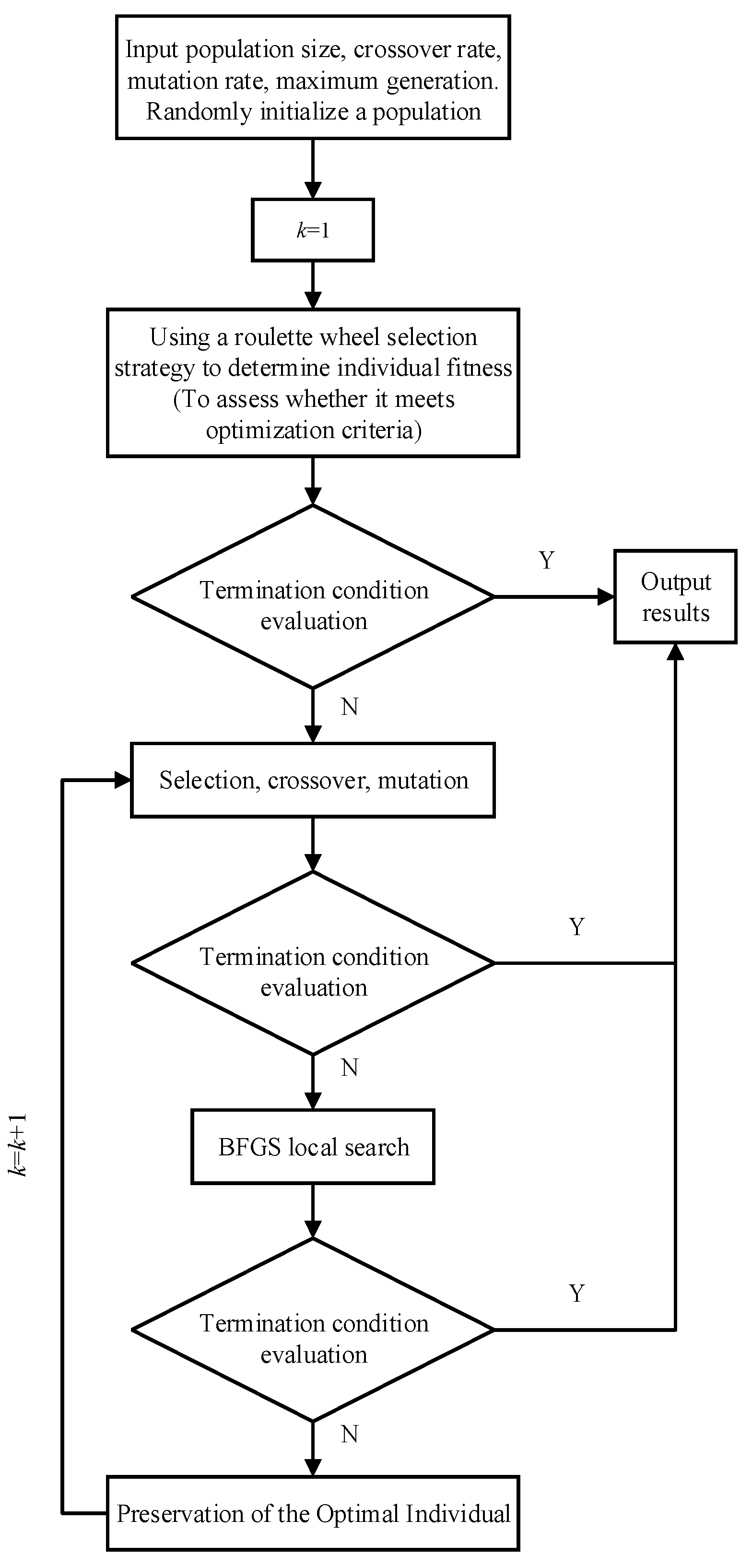
The flowchart of the GA–BFGS algorithm is shown in Figure 5. The specific steps are as follows: first, use the GA algorithm to globally search and optimize the cost function, use the obtained satisfactory solution vector as the initial value, and continue to use the BFGS algorithm for local iterative optimization. This overcomes the low search efficiency of the GA algorithm in the later stage and the sensitivity of the BFGS algorithm to initial values, and it has a high degree of global convergence ability. We set the genetic algebra of the GA to 40 generations and then perform local optimization using the BFGS algorithm. The optimal result is output upon meeting the termination condition of the iterations. This ensures the stability, convergence, and robustness of the results.

In the optimization process, we first use the genetic algorithm (GA) to achieve global search and then use the BFGS algorithm to achieve fast local optimization. Among them, the steps of the quasi-Newton algorithm (BFGS) are as follows:

(1)

Given the initial point x₀, with an accuracy of ξ, take H₀ = I, k = 0.

(2)

Given gradient $g_{k-1}=\nabla f\left(x_{k-1}\right)$, if $g_{k-1}<$ ξ, then $x^{*}=x_{k-1}$, stop the step, or use the BFGS formula, as shown in Equation (12), solve for $H_{k-1}$, let $p_{k-1}=-H_{k-1}{g}_{k-1}$, and use one-dimensional search to find the step size $t_{k-1}$.

$$H_k=\left[I-\frac{\Delta x_{k-1}{(\Delta g_{k-1})}^T}{{(\Delta x_{k-1})}^T\Delta g_{k-1}}\right]H_{k-1}{\left[I-\frac{\Delta x_{k-1}{(\Delta g_{k-1})}^T}{{(\Delta x_{k-1})}^T\Delta g_{k-1}}\right]}^T+\frac{\Delta x_{k-1}{(\Delta x_{k-1})}^T}{{(\Delta x_{k-1})}^T\Delta g_{k-1}}$$

(12)

(3)

x_k = x_k−1 + t_k−1p_k−1, k = k+1, return to (2).

During the process of optimizing the mechanism parameters using MATLAB, the fmincon function used in the article is as follows:

$$[x,fval,exitflag]=f\min con(fun,x_0,A,b,Aeq,beq,1b,ub)$$

(13)

where fun is the objective function; As the initial values, A,b satisfies linear inequality constraints, Aeq and beq satisfy linear equality constraints, and lb and ub satisfy boundary constraints.

Algorithm Example

Debaditya et al. [5] used a finger rehabilitation mechanism synthesized by a Stephenson-III six-bar mechanism, which used Kinovea 0.9.5 software to track the movement trajectory of the fingers. After setting the tracking environment, the subjects grasped a cylindrical object and recorded the bending and extension of the fingers multiple times, obtaining multiple precision points. Six of these precision points were selected as the ideal trajectory points. The trajectory points of the points collected at the distal phalangeal tip are shown in

Table 3. The grasping trajectory points of the index finger collected in [5].

Trajectory Points	1	2	3	4	5	6
X	−9.61	−9.52	−8.52	−7.34	−5.21	−3.55
Y	1.04	2.07	3.97	5.02	5.47	5.34

.

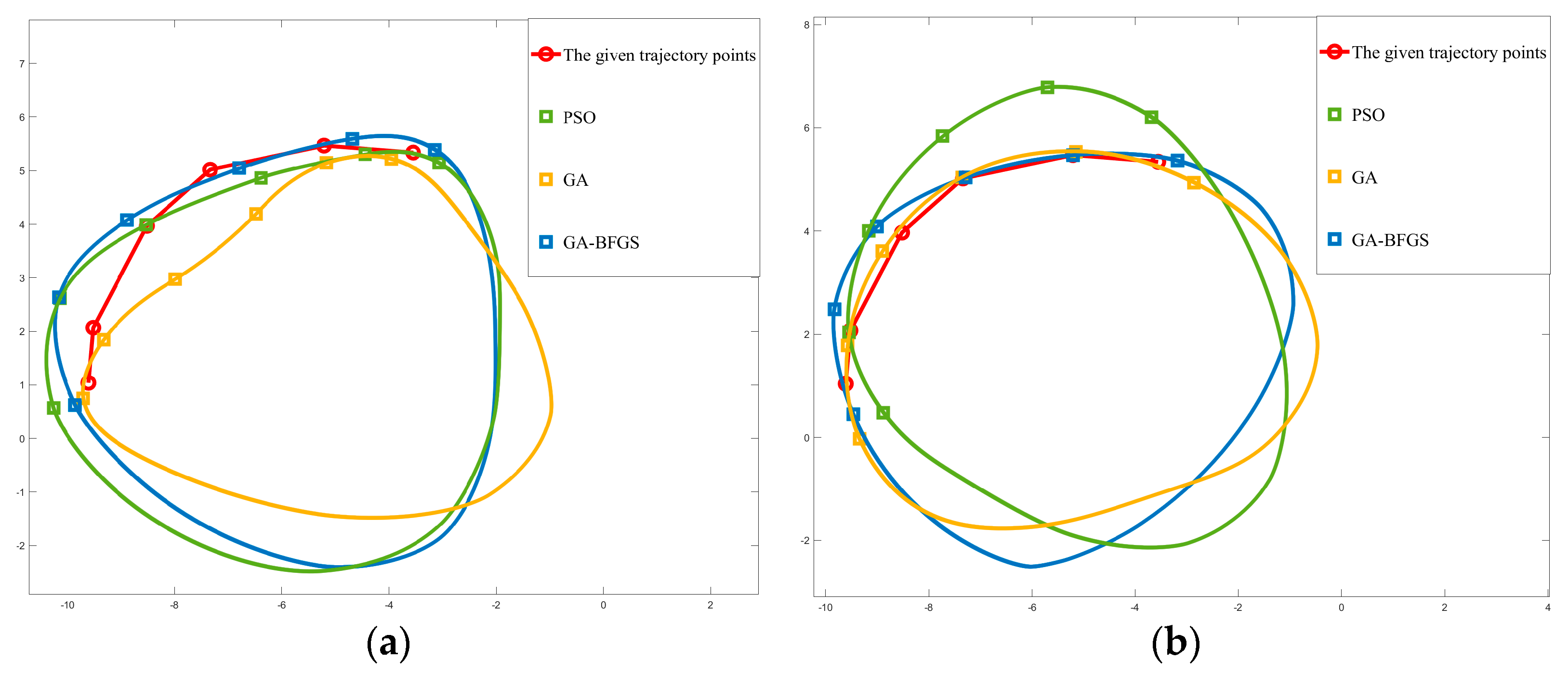
The mechanism synthesis of the four-bar mechanism and the Watt-Ⅰ six-bar mechanism was carried out, and the particle swarm optimization algorithm (PSO) was compared with the traditional genetic algorithm (GA), and the hybrid optimization algorithm, GA–BFGS, mentioned in this article, as shown in Figure 6a, is the optimization result of the four-bar mechanism, and Figure 6b is the optimization result of the Watt-Ⅰ six-bar mechanism. The optimal parameters and average trajectory point errors generated by each optimization algorithm are shown in

Table 4. The optimal parameters of the four-bar mechanism.

Optimization Algorithm	PSO	GA	GA–BFGS
l1	4.38	3.76	4.13
l2	17.42	19.02	14.18
l3	16.67	7.30	14.56
l4	18.43	19.45	20.06
l5	29.44	36.64	27.76
xA	20.76	19.42	21.20
yA	14.06	28.58	7.01
α	5.86	6.79	6.28
θ	3.05	3.61	2.54
$\overline{TE}$	0.6541	0.6102	0.5268

and

Table 5. The optimal parameters of the Watt-I Six-bar Mechanism.

Optimization Algorithm	PSO	GA	GA–BFGS	[5]
l1	5.02	5.12	8.89	/
l2	12.59	9.31	24.09	/
l3	11.31	8.93	16.47	/
l4	17.33	11.44	26.02	/
l5	8.92	13.49	23.74	/
l6	23.36	12.49	14.45	/
l7	6.34	8.89	21.93	/
l8	8.38	17.54	19.84	/
l9	10.53	6.86	20.56	/
xA	−1.31	4.43	10.82	/
yA	−1.80	0.72	11.48	/
θ1	0.42	0.90	0.89	/
η1	2.32	0.72	0.72	/
φ0	1.31	4.03	4.14	/
σ	3.56	4.85	5.23	/
φ1	3.13	0.83	0.70	/
$\overline{TE}$	0.7999	0.471	0.191867	0.2210

, where Table 4 is the optimal parameters of the four-bar mechanism using each optimization algorithm, and Table 5 is the optimal parameters of the Watt-I six-bar mechanism using each optimization algorithm. In the optimization of four-bar mechanisms, the GA–BFGS algorithm reduced the average trajectory error by 13.7% compared to the GA algorithm, and by 19.5% compared to the PSO algorithm. In the optimization of six-bar mechanisms, the GA–BFGS algorithm reduced the average trajectory error by 59.3% compared to the GA algorithm, by 76% compared to the PSO algorithm, and by 13.2% compared to the average trajectory error reported in reference [5].The average trajectory point error is indicated in both tables; according to the data in the table, the fitting effect of the six-bar mechanism is good. Moreover, in the six-bar parameter optimization with the same time step, the genetic algorithm performs better, and the genetic algorithm (GA) can also achieve a small contour error. However, it uses target data points and generated data points to calculate the trajectory error, so the optimization effect of the GA–BFGS algorithm is better and the trajectory error is lower.

Figure 7 shows the fitting of the given task trajectory using the GA–BFGS hybrid optimization algorithm for the Watt-I six-bar mechanism and the four-bar mechanism. Among them, the Watt-I six-bar mechanism has better fitting results for finger trajectories than the four-bar mechanism. As shown in the table, the fitting results of the GA–BFGS hybrid algorithm selected in this paper are significantly better than the GA and PSO algorithms, and the average fitting error is 0.192, which is smaller than the average fitting error of the finger trajectory using the Stephenson-III six bar mechanism in [5]. It can be proved that our proposed optimization algorithm and the feasibility of member selection are feasible.

4. Topology Optimization Design for the Fixed End

This chapter will conduct structural optimization design on the key components of the six-bar mechanism as needed, mainly including the analysis and shape optimization of the fixed end (main supporting component) of the six-bar mechanism, in order to reduce overall weight and improve work efficiency. Using the base bracket as the main supporting component, we imported it into the Workbench module of ANSYS 2021 software for finite element analysis. Considering the mass and additional force of the member, as well as the average maximum gripping force of the human hand based on biomechanical characteristics, we applied a force of 1000 N to the supporting component, and the two holes were subjected to a force of 500 N, respectively. Considering the actual gripping force a human hand can exert, we should apply a force at the end effector that is not less than this value. In fact, the applied force should often significantly exceed this value for the overall design and modeling, thereby preventing situations where unexpected gripping forces could damage the mechanism beyond control.

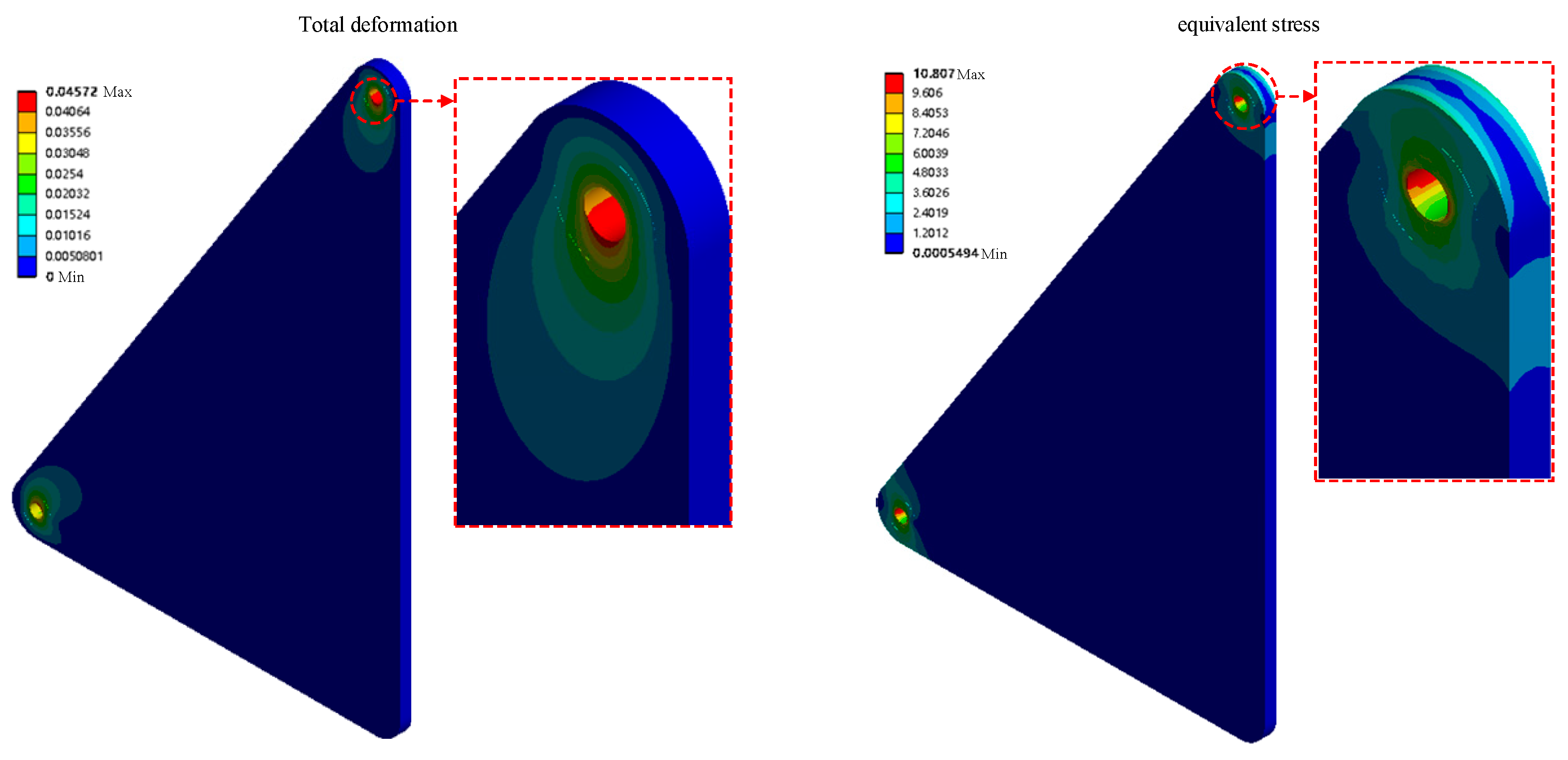
As shown in Figure 8, the maximum stress of the base is only 10.807 MPa, and the maximum total deformation is 0.04572 mm, with a large design margin. Therefore, lightweight design can be carried out by optimizing its relevant size parameters.

We used the finite element analysis method for topology optimization of the fixed end of the bar, and the optimization design steps are as follows: When using the shape optimization module of ANSYS2021 software to perform shape optimization analysis on the base, we first set a response target. Subsequently, we limit the proportion of retained materials to between 20% and 30%. After the optimization analysis, the results are shown in Figure 9a, where the red area indicates the excess material that can be removed.

It can be clearly observed from Figure 9a that there is redundant material in the middle of the base, while the two sides have been optimized into a circular arc structure. Considering the processing cost and efficiency, the optimization of the base is planned as shown in Figure 9b. There are a total of four input parameters: (P1) right width L1, (P2) bottom width L2, (P3) diagonal width L3, and (P4) filet radius R1. There are three output parameters in total: (P5) total mass, (P6) maximum total deformation, and (P7) maximum equivalent stress.

Using the MOGA algorithm for optimization, after setting optimization objectives and constraints, the optimal parameters and original set parameters are shown in

Table 6. Comparison of Parameter Optimization Results.

Design Variable	Before Optimization	After Optimization	Change Rate/%
P1/mm	15	16	+6.7
P2/mm	15	14.5	−3.3
P3/mm	15	13	−13.3
P4/mm	10	11	+10
P5/kg	0.111	0.0456	−58.9
P6/mm	0.0457	0.0458	+0.2
P7/MPa	10.807	11.448	+5.9

.

The total mass of the part has decreased by 58.9%. Although the maximum total deformation and maximum equivalent stress of the parts have increased, they are all within the allowable range.

5. Structural Design of Finger Rehabilitation Mechanism

5.1. Modeling of the Testing Machine

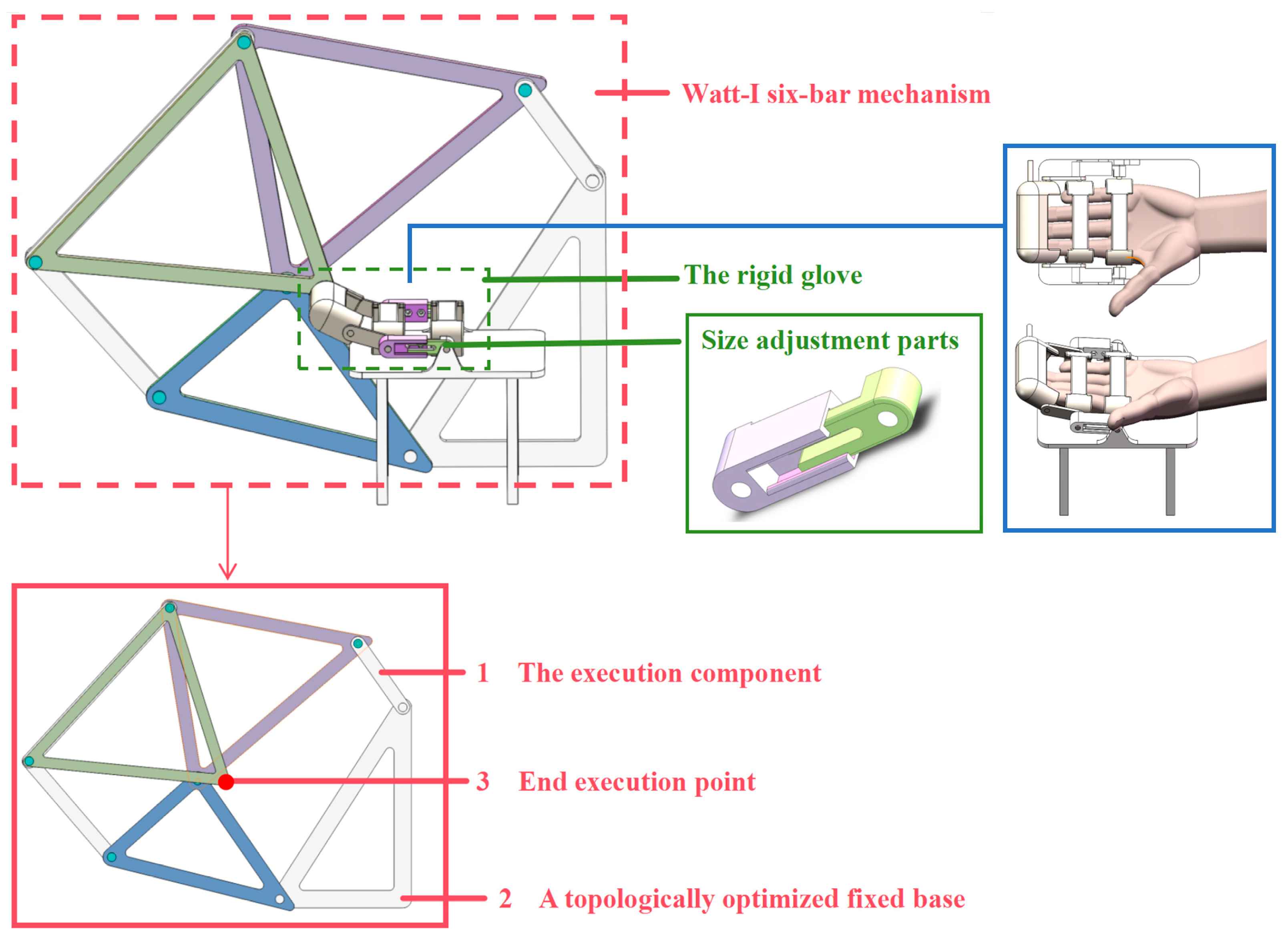
According to the optimal parameters optimized by the GA–BFGS algorithm and the final results obtained from topology optimization, The overall structure of the testing machine is shown in Figure 10, where link 1 is the execution end:

The overall structure of the six-bar testing machine consists of a Watt-I six-bar mechanism and a rigid glove connected to the end of the mechanism. The red frame indicates the Watt-I six-bar mechanism; 1 is the execution component of the overall mechanism. Rotation 1 can drive the distal phalanx of the glove to rotate and simulate a handheld posture for finger rehabilitation, while 2 is a topologically optimized fixed base, and 3 represents the end-execution point of the overall mechanism. The green frame indicates the component of the rigid glove. It contains the specific description of the adjustable part of the glove. The rigid glove can be fixed to the table by attaching the point to the tabletop, and when the finger is placed in the glove, the input lever rotates, and the end of the six-bar mechanism will drive the fingers in the glove to simulate the gripping action. The blue frame represents the connection between the human hand and the rigid glove. This rehabilitation glove can accommodate all four fingers except the thumb. Since the grip of the thumb cannot be in the same plane as the other four fingers, we designed the mechanism to accommodate the thumb. However, we found that for the hand-grasping rehabilitation, the grasping trajectory of the thumb is also approximately in a plane, so we will subsequently measure the grasping trajectory of the thumb, try to use a four-bar or six-bar mechanism for fitting, and control the two devices as a whole, so the thumb and other fingers can achieve a grasping posture at the same time. Since not only the thumb but the other fingers play a major role in grasping objects, this article uses the movements of the other four fingers to synthesize a six-bar mechanism.

We set in the model that the position of the end point (distal knuckles of the hand) will not change regardless of the size parameter of the adjustable glove part. This leaves only a fixed trajectory. The adjustable glove sides are only designed to place the finger conveniently and allow it to move within a range to prevent secondary injuries caused by the rigid exoskeleton glove during rehabilitation. However, this rehabilitation device cannot be carried around because it must be fixed to the desktop, and the device requires a certain amount of working space. In the field of upper limb rehabilitation, there are numerous applications of wearable exoskeleton devices for the upper limbs [23,24,25]. In our subsequent research, we will also explore the integration of the overall mechanism control of this rehabilitation glove to enhance our study.

Therefore, our main work in the future will integrate the mechanism that drives the thumb and the mechanism that drives the other four fingers to complete the overall rehabilitation of the fingers. We will use a reasonable control strategy to achieve accurate synchronization of the multi-faceted integration of the organization, making it more integrated, convenient, and safe [26,27]. We can see that the overall glove part can be infinitely adjusted within a certain range according to the size of the human hand, which can meet personalized customization for different parameter groups while ensuring safety and stability requirements during use and avoiding secondary injuries during the rehabilitation process.

5.2. Watt-I Six-Bar Mechanism Trajectory Experiment

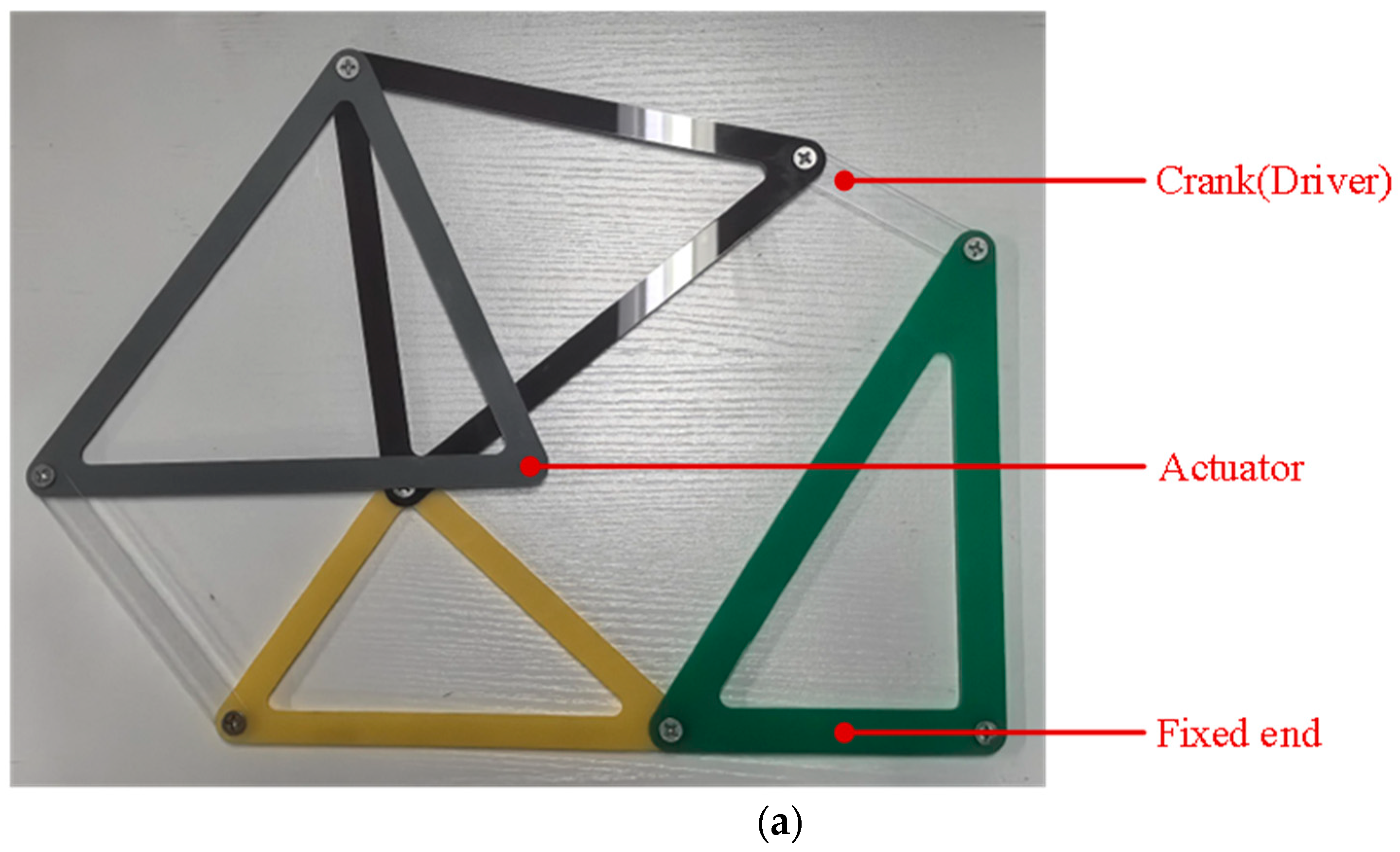
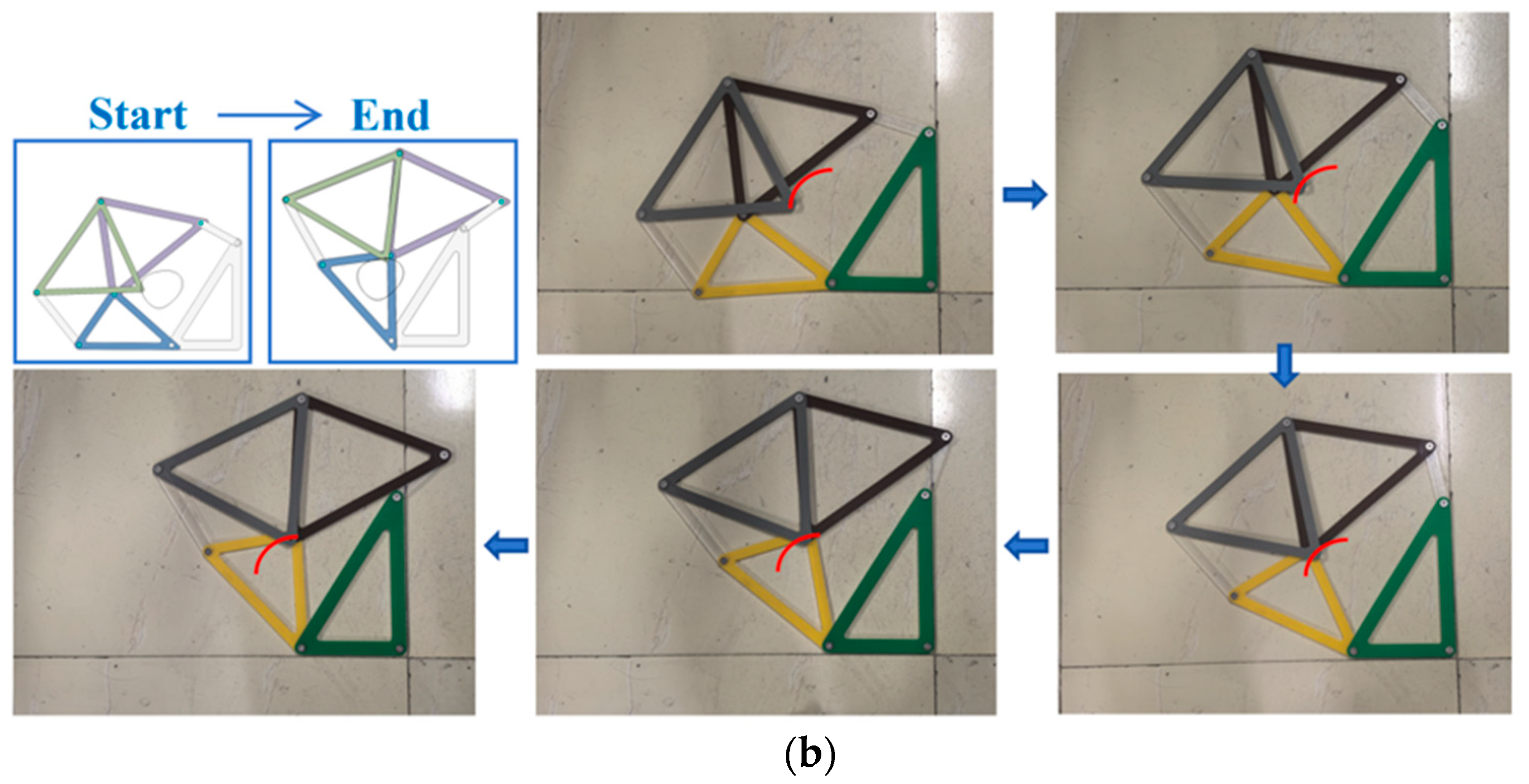
To prove that the designed finger rehabilitation institution can pull the finger to complete the flexion and extension movement, we built the Watt-I six-bar mechanism part of the institution to conduct the trajectory experiment on its ends. In the process of building the test machine, we chose the optimal parameters generated by the GA–BFGS hybrid optimization algorithm and the topology optimization results of the fixed end. Because the parameters of the bar are relatively small, the overall mechanism is very small, and only the running attitude of the end trajectory can be taken through the depth camera. In the follow-up work, we will load the finger rehabilitation institution with the actuator and controller to obtain more comprehensive experimental results.

Figure 11 shows a testing machine built based on the optimal parameters of the Watt-I six-bar mechanism. The bar group is made of acrylic material, installed with sliding friction bearings in its joint part; the upper right corner is the execution end Link 1, and the gray triangle bar is the extension bar.

The input Link 1 is made to rotate in the same time step, and the depth camera is used to track the movement track of the end point. When the Link 1 is rotated around a certain angle, the generating trajectory of the end position of the six-bar mechanism is consistent with its running trajectory in SolidWorks2022 software, both approximately a quarter arc trajectory, which proves the feasibility of our design. The six-bar mechanism can fit the finger grasp posture by changing the angle of the execution bar. Considering that the physical generated trajectory is smooth, the physical experiment of the six-bar testing machine can prove its effectiveness.

6. Conclusions

In this paper, a finger rehabilitation device based on the single-degree-of-freedom (DOF) linkage mechanism is designed, aiming to lead the index finger through the flexion–extension trajectory during grasping tasks. Taking the finger-grasping posture as an example, various optimization algorithms such as PSO are used, the GA and GA–BFGS hybrid optimization algorithms are used to optimize and compare the mechanism synthesis of a four-bar mechanism and a Watt-I six-bar mechanism, achieving the flexion extension grasping posture of the fingers. Using the GA–BFGS hybrid optimization algorithm, we compared the distance errors between the four-bar linkage and the Watt-I six-bar linkage. We selected the Watt-I six-bar linkage with smaller distance errors as the source mechanism to construct the overall model of the finger rehabilitation device. Subsequently, topology optimization was performed to design and refine this mechanism. The final design of the overall exoskeleton finger rehabilitation device can be completed, and physical experiments can be conducted. The trajectory generated by the mechanism can be tracked through the deep camera device, ultimately proving the feasibility of the finger rehabilitation device designed through the six-bar mechanism. This device can help patients with stroke and those who have lost their index finger activity due to other diseases recover their finger-grasping ability and improve their quality of life.

Future work: The rehabilitation glove mentioned in the text does not target the functionality of the thumb in grasping actions. During a complete grasping process, the movement trajectory of the thumb is not in the same plane as the trajectories of the other four fingers’ distal fingertips. Therefore, to accomplish a complete grasping action, it would be necessary to track the movement trajectory of the thumb in subsequent iterations. This could involve adding a four-bar or six-bar mechanism, or incorporating a soft pneumatic thumb sleeve in another measurement, and integrating its control to allow for grasping actions at different angles based on the graded hand mobility. Additionally, designing a user interface to provide an intuitive understanding of the grasping process would be beneficial. Moreover, we intend to increase the rehabilitation trajectory of fingers to accommodate multiple types of people, change the parameters of a four-bar or six-bar mechanism, and use a multi-objective optimization algorithm to perform trajectory synthesis to improve our work.