Optimization Comparison of Torque Performance of Axial-Flux Permanent-Magnet Motor Using Differential Evolution and Cuckoo Search
Abstract
1. Introduction
- (1)
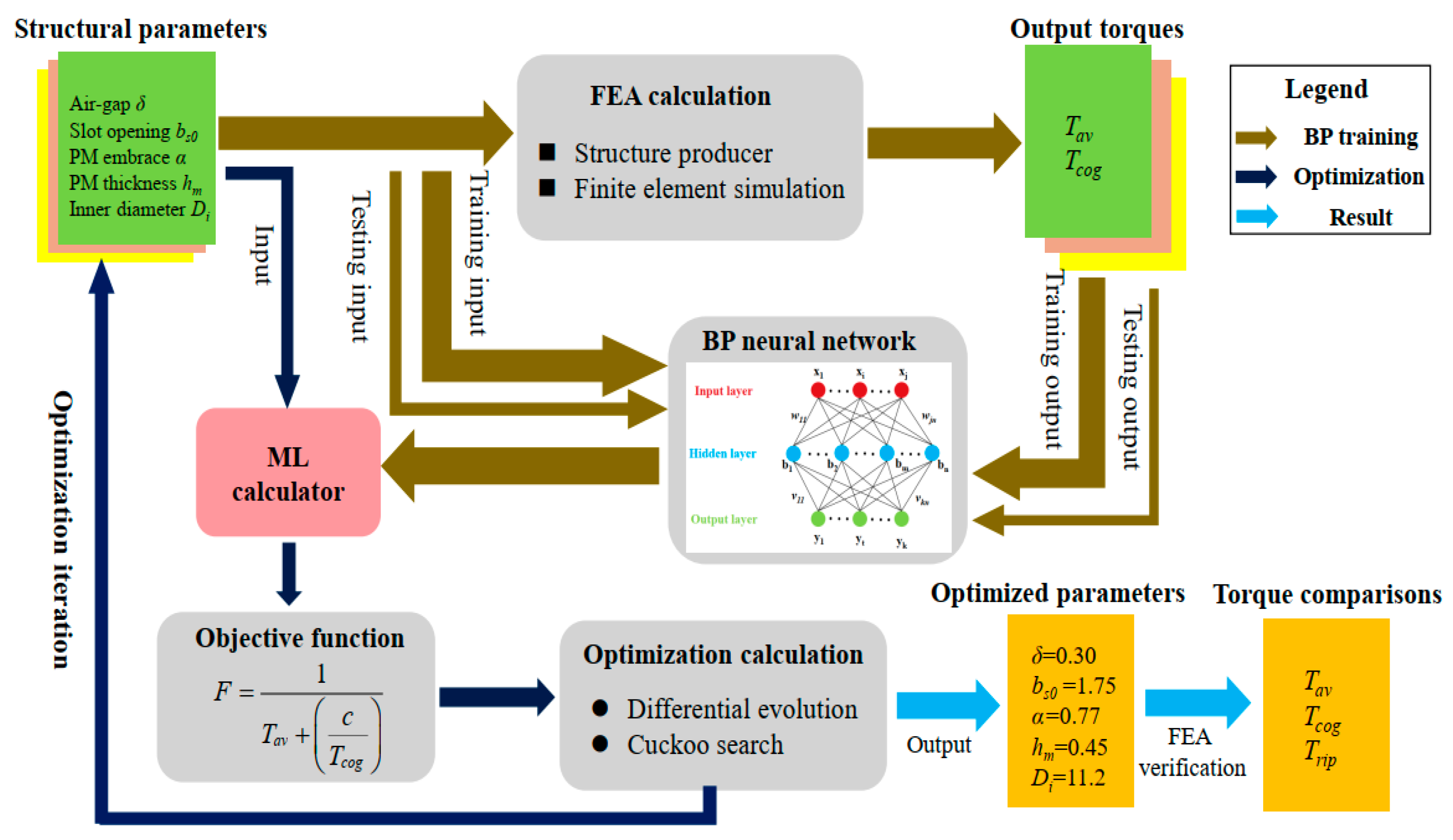
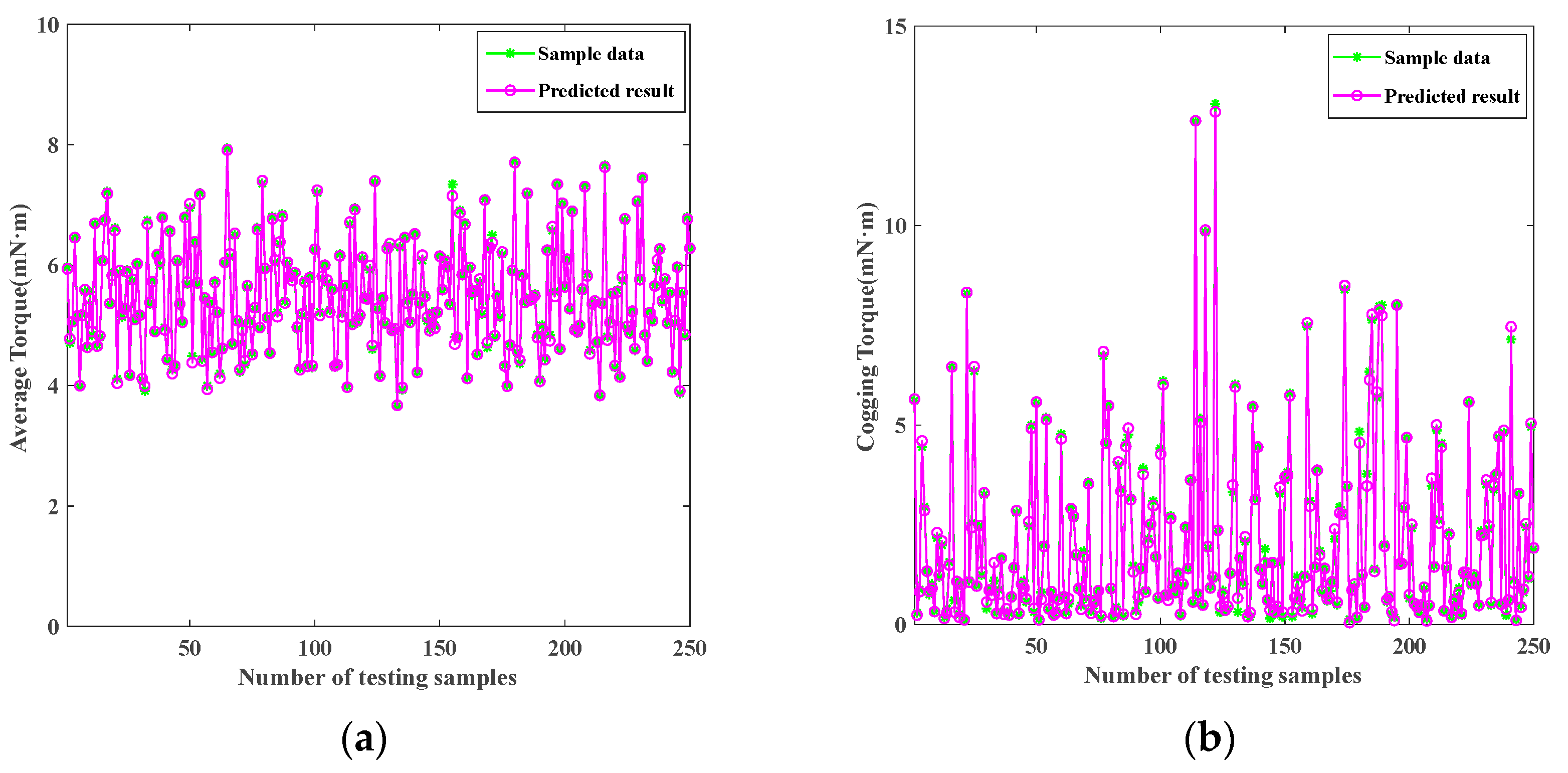
- To obtain an ML calculator, a method combining the 3D FEA and BP neural network is proposed to train the accurate relationships between the five input structural parameters and two output torque parameters (i.e., the Tav and Tcog) using 1024 sets of input–output simulation sample data. The 3D FEA is suitable for solving the complex AFPMM structure with high calculation accuracy, and the input–output parameter relationships can be accurately fitted when combined with BP ML.
- (2)
- Based on the obtained ML calculator, an optimization objective function is designed as the inverse function of the sum of the Tav and the inverse values of Tcog of the AFPMM, thereby reducing the multi-objective function to a single-objective function.
- (3)
- The objective function is iteratively optimized using the DE and CS, respectively. The iteration speed, optimization time, and computational resources occupied by the two algorithms are compared and analyzed.
- (4)
- For the initial model before optimization and the optimized models obtained by the two algorithms, the 3D FEA is performed for the comparative analysis to verify the quality of the motor torque optimization results. The results show that both algorithms achieved almost the same optimized structural parameters, but the DE is more advantageous compared to the CS due to faster iteration speed and less resource consumption.
2. Structure of the AFPMM and Its Output Torque ML Calculator Based on FEA and BP Neural Network Training
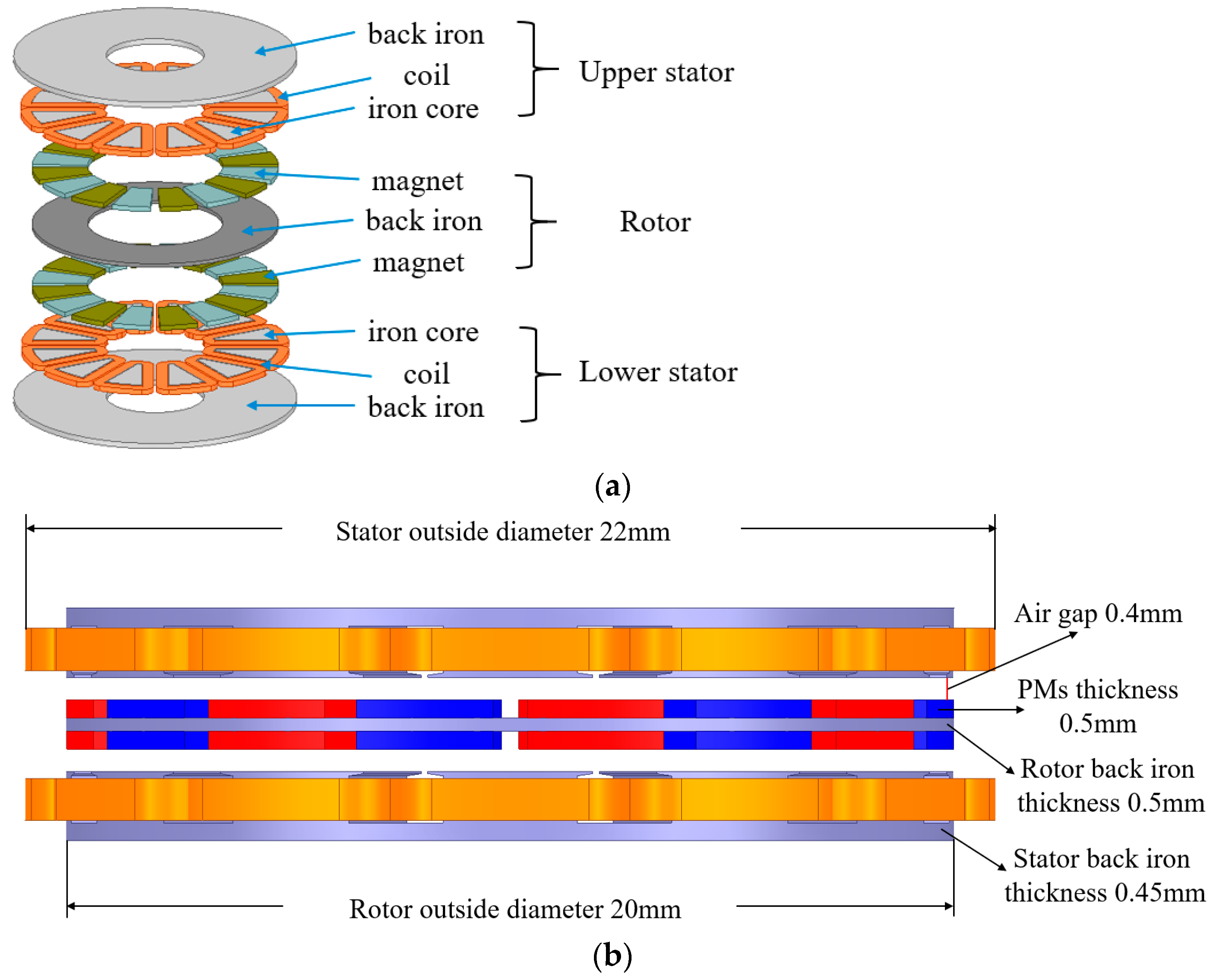
2.1. Structure of the AFPMM
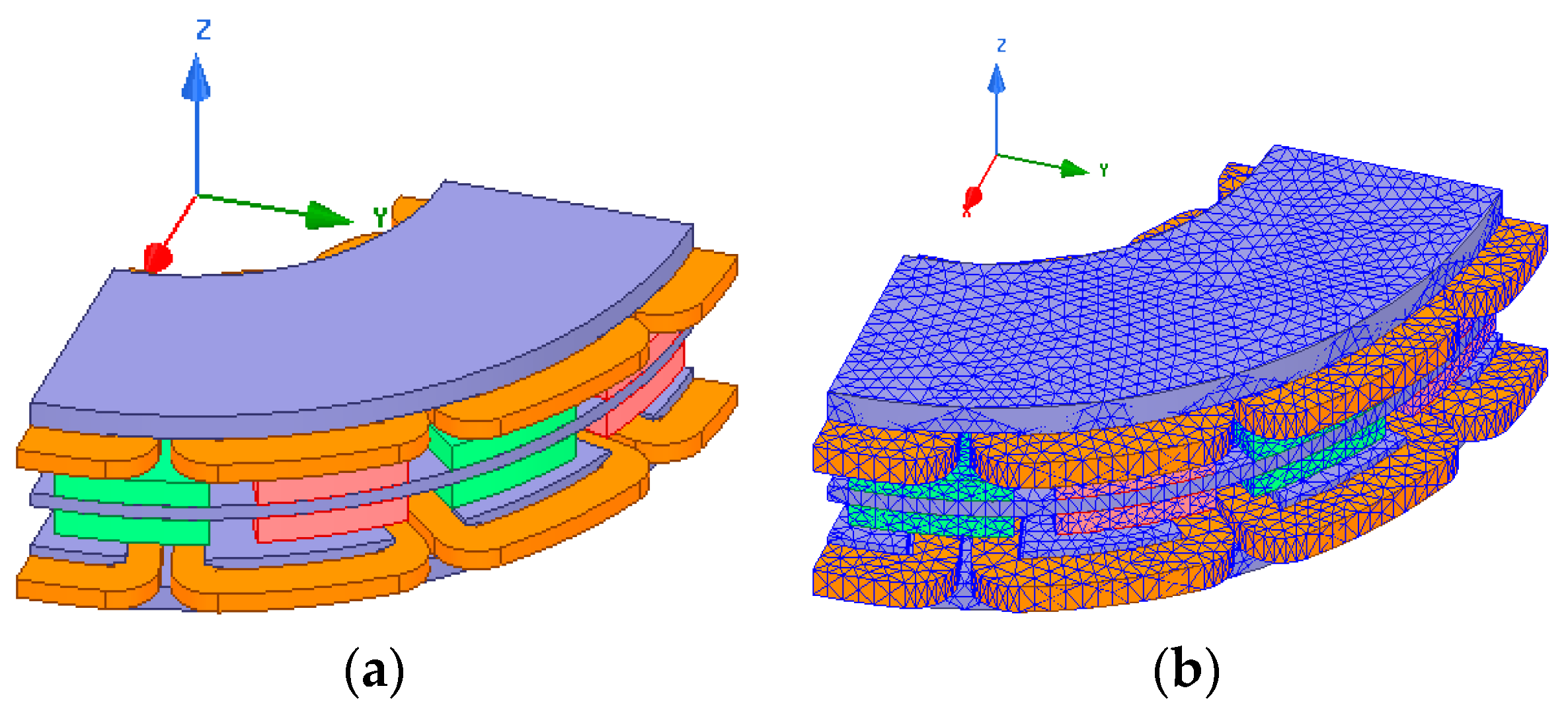
2.2. Output Torque of the AFPMM and Its FEA Simulation
2.3. ML Calculator for AFPMM Output Torque Based on FEA and BP Neural Network Training
3. Design and Optimization of Objective Function for the AFPMM Torque Using the DE and CS
3.1. Design of Objective Function for Motor Torque Optimization
- (1)
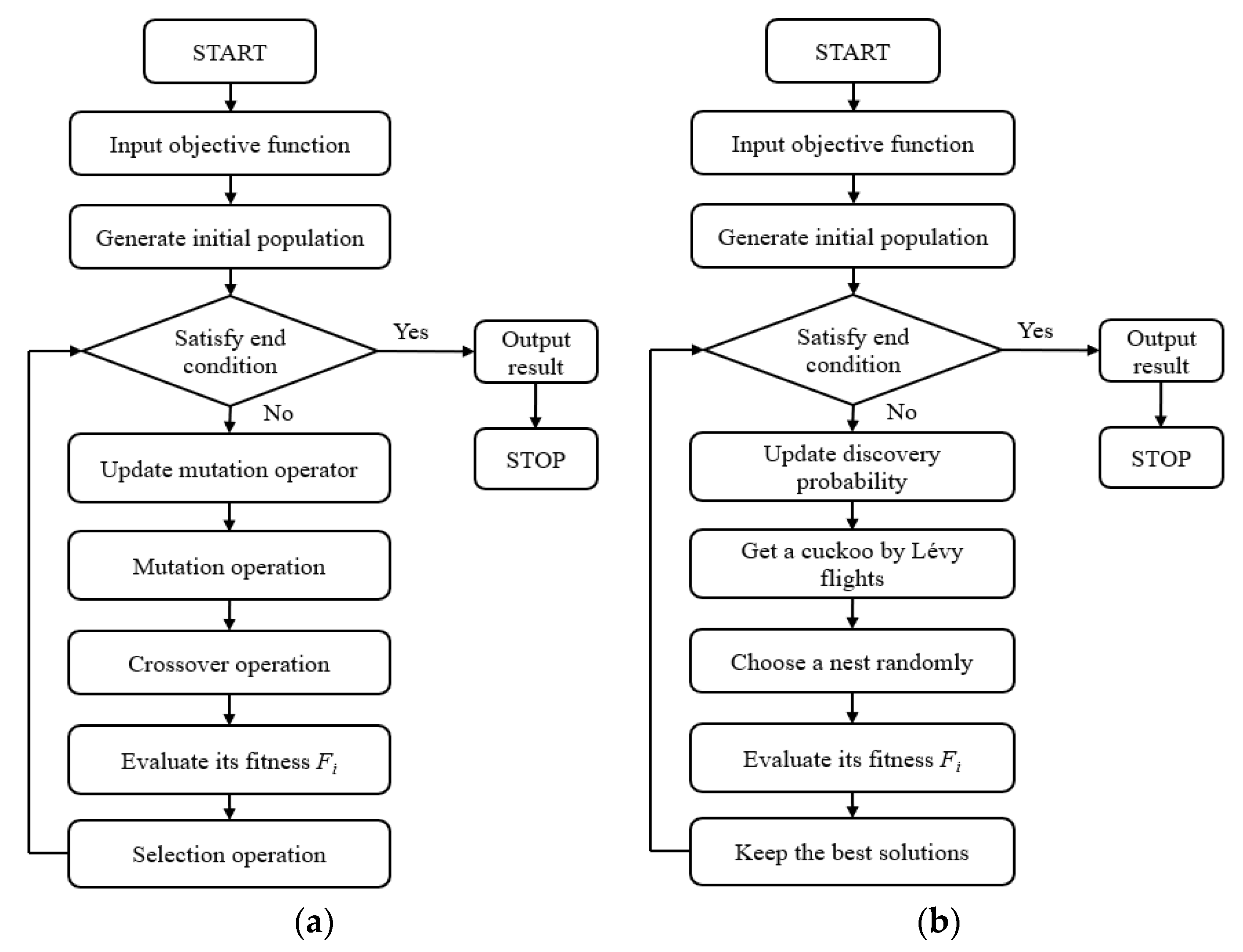
- DE: number of populations: 100; number of variables: 5; number of generations: 100; initial assignment of mutation operator: 0.6; and crossover operator: 0.4. The mutation operator is dynamically adjusted through annealing factors during optimization iterations [36].
- (2)
- CS: number of nests: 100; number of variables: 5; number of generations: 100; and initial assignment of the probability of establishing a new bird nest: 0.25. The discovery probability is dynamically adjusted during optimization iterations [37].
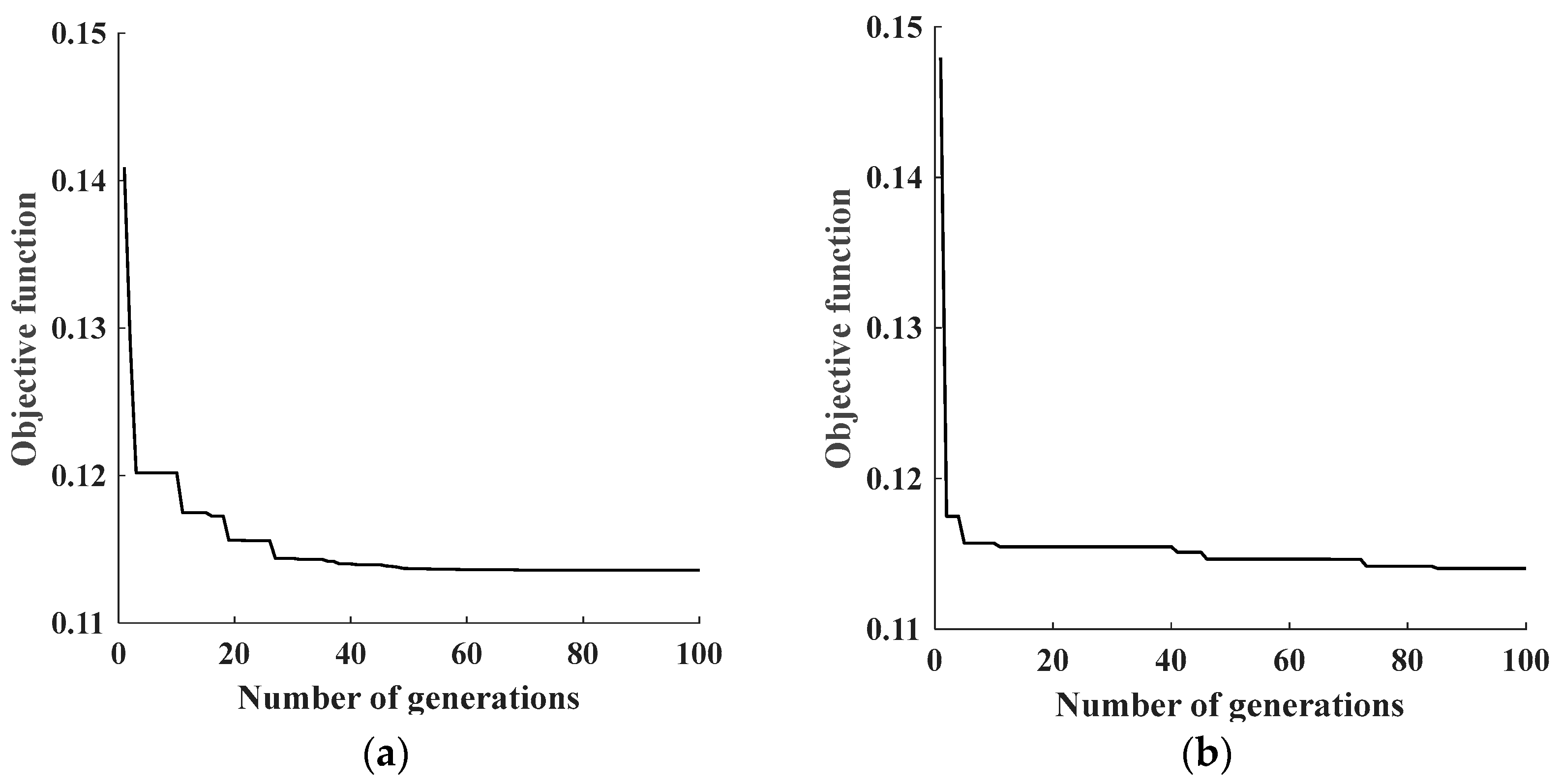
3.2. Comparison of the DE and CS for Finding Optimization Solution
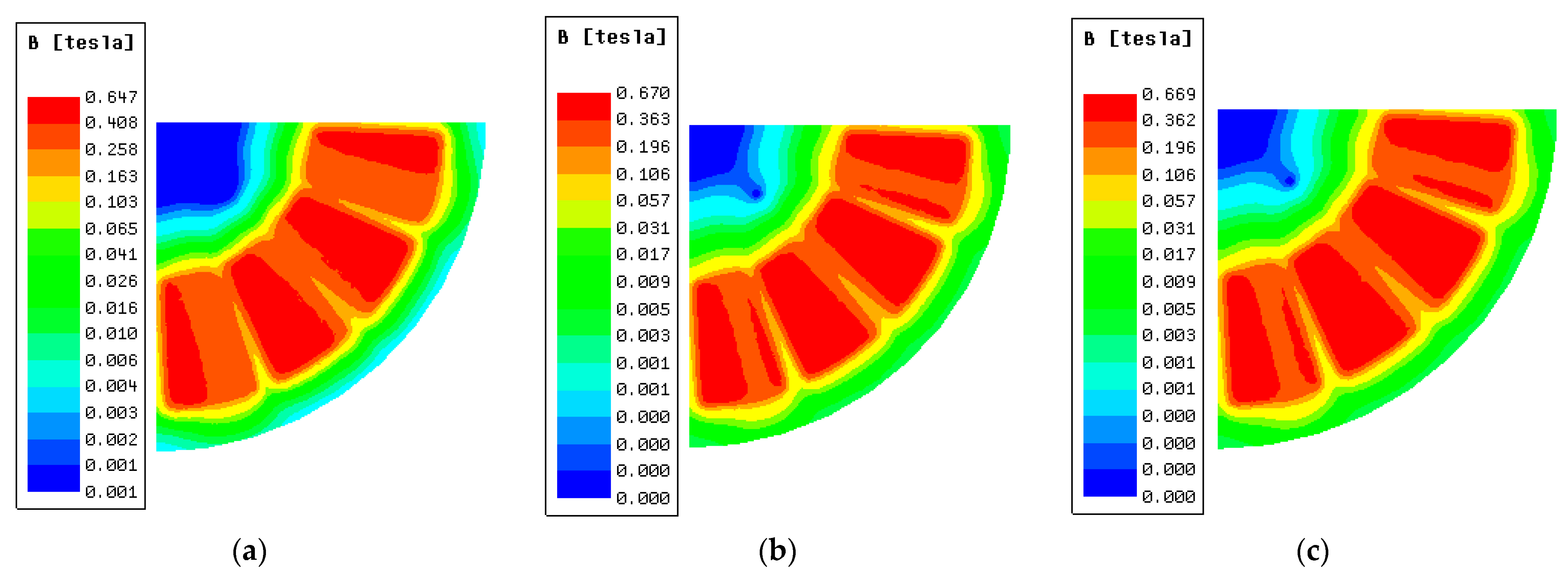
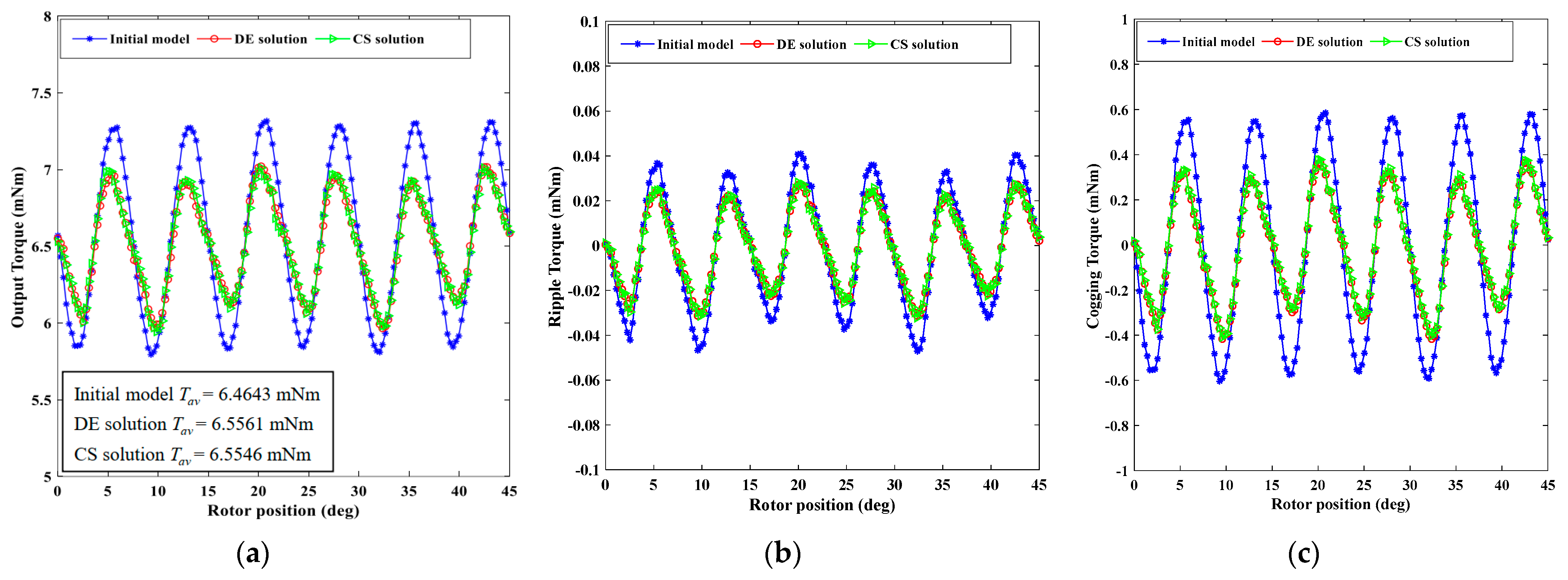
4. Verification of Optimization Results by the FEA
5. Conclusions
- (1)
- To obtain an ML calculator, a method combining the 3D FEA and BP algorithm is proposed to fit the relationships between five structural parameters and two output torque parameters (i.e., Tav and Tcog) using 1024 sets of input–output simulation sample data.
- (2)
- The inverse function of the sum of the Tav and the inverse values of the Tcog of the motor are designed as the optimization objective function. For this objective function, the selected motor parameters are optimized using the DE and CS algorithms, respectively. The iteration speed and optimization time of the two algorithms in the motor optimization process are specifically analyzed. The DE and CS achieve optimal solutions in 52 and 87 iterations, respectively, with optimization times of 26.537 s and 67.044 s. During optimization, the LinkedBlockingQueue class in Java was called 1873 times by the DE and 4169 times by the CS, accounting for 60.23% and 72.76% of the total optimization time, respectively.
- (3)
- The validity of the optimized AFPMM structural models is verified using the 3D FEA. The air-gap flux density, average torque, cogging torque, and ripple torque before and after optimization are compared. The results indicate that both DE and CS can improve the air-gap flux density and the motor output torque performance. Compared with the initial model, the two optimized models have a smaller Tcog, an increased Tav, and a reduced Trip. Specifically, after the DE or CS optimization, the Tav of the motor is increased by about 1.4%, the Tcog is decreased by about 32.1%, and the Trip is decreased by about 31.7%, achieving a better optimization effect.
- (4)
- In summary, under the premise of achieving similar optimization results, the DE is more advantageous compared to the CS due to its faster iteration speed and lower resource consumption.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pranjić, F.; Virtič, P. Cogging torque reduction techniques in axial flux permanent magnet machines: A review. Energies. 2024, 17, 1089. [Google Scholar] [CrossRef]
- Larbi, B.; Hatti, M.; Kouzi, K.; Ghadbane, A. Axial flux machine with non-slotted TORUS-NS rotor type. Design and investigate for electric traction. Electr. Eng. Electromechanics 2023, 6, 10–15. [Google Scholar] [CrossRef]
- Shin, D.Y.; Jung, M.J.; Lee, K.B.; Lee, K.D.; Kim, W.H. A study on the improvement of torque density of an axial slot-less flux permanent magnet synchronous motor for collaborative robot. Energies. 2022, 15, 3464. [Google Scholar] [CrossRef]
- Zhang, Z.; Geng, W.; Liu, Y.; Wang, C. Feasibility of a new ironless-stator axial flux permanent magnet machine for aircraft electric propulsion application. CES Trans. Electr. Mach. Syst. 2019, 3, 30–38. [Google Scholar] [CrossRef]
- Aydin, M.; Huang, S.; Lipo, T.A. Torque quality and comparison of internal and external rotor axial flux surface-magnet disc machines. IEEE Trans. Ind. Electron. 2006, 53, 822–830. [Google Scholar] [CrossRef]
- Islam, M.S.; Islam, R.; Sebastian, T. Experimental verification of design techniques of permanent-magnet synchronous motors for low-torque-ripple applications. IEEE Trans. Ind. Appl. 2011, 47, 88–95. [Google Scholar] [CrossRef]
- Xiao, L.; Li, J.; Qu, R.; Li, D. Cogging torque analysis and minimization of axial flux PM machines. IEEE Trans. Ind. Appl. 2016, 53, 1018–1027. [Google Scholar] [CrossRef]
- Yu, Y.; Pan, Y.; Chen, Q.; Zeng, D.; Hu, Y.; Goh, H.H.; Niu, S.; Zhao, Z. Cogging torque minimization of surface-mounted permanent magnet synchronous motor based on RSM and NSGA-II. Actuators 2022, 11, 379. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, G.; Du, G. An investigation into the pole–slot ratio and optimization of a low-speed and high-torque permanent magnet motor. Appl. Sci. 2024, 14, 3983. [Google Scholar] [CrossRef]
- Wu, S.; Wang, B.; Zhang, T.; Gu, Q. Design optimization and electromagnetic performance analysis of an axial-flux permanent magnet brushless DC motor with unequal-thickness magnets. Appl. Sci. 2022, 12, 7863. [Google Scholar] [CrossRef]
- Qiao, Z.; Zhang, Y.; Luo, J.; Fu, W.; Shao, D.; Cao, H. A non-permanent magnet DC-biased vernier reluctance linear machine with non-uniform air gap structure for ripple reduction. Actuators 2022, 12, 7. [Google Scholar] [CrossRef]
- Lee, S.; Kim, C.; Choo, Y.; Yun, G.; Lee, C. Torque analysis of a permanent magnet synchronous motor using flux densities in air gap. AIP Advances 2023, 13, 025313. [Google Scholar] [CrossRef]
- Fazil, M.; Rajagopal, K.R. A novel air-gap profile of single-phase permanent-magnet brushless DC motor for starting torque improvement and cogging torque reduction. IEEE Trans. Magn. 2010, 46, 3928–3932. [Google Scholar] [CrossRef]
- Ilka, R.; Alinejad-Beromi, Y.; Yaghobi, H. Cogging torque reduction of permanent magnet synchronous motor using multi-objective optimization. Math. Comput. Simul. 2018, 153, 83–95. [Google Scholar] [CrossRef]
- Belkhadir, A.; Belkhayat, D.; Zidani, Y.; Pusca, R.; Romary, R. Torque ripple minimization control of permanent magnet synchronous motor using adaptive ant colony optimization. In Proceedings of the 2022 8th International Conference on Control, Decision and Information Technologies (CoDIT), Istanbul, Turkey, 17–20 May 2022; pp. 629–635. [Google Scholar]
- Zaaraoui, L.; Mansouri, A.; Smairi, N. NMOPSO: An improved multiobjective PSO algorithm for permanent magnet motor design. UPB Sci. Bull. Series C. 2022, 84, 201–214. [Google Scholar]
- Malagoli, J.A.; Camacho, J.R.; da Luz, M.V.F. Optimal electromagnetic torque of the induction motor generated automatically with Gmsh/GetDP software. Int. Trans. Electr. Energy Syst. 2021, 31, e12773. [Google Scholar] [CrossRef]
- Park, J.W.; Koo, M.M.; Seo, H.U.; Lim, D.K. Optimizing the design of an interior permanent magnet synchronous motor for electric vehicles with a hybrid ABC-SVM algorithm. Energies 2023, 16, 5087. [Google Scholar] [CrossRef]
- Knypiński, Ł.; Kuroczycki, S.; Márquez, F.P.G. Minimization of torque ripple in the brushless DC motor using constrained cuckoo search algorithm. Electronics 2021, 10, 2299. [Google Scholar] [CrossRef]
- Cvetkovski, G.; Petkovska, L. Nature inspired optimal design of axial flux permanent magnet motor for electric vehicle. In Proceedings of the 2018 IEEE 18th International Power Electronics and Motion Control Conference (PEMC), Budapest, Hungary, 26–30 August 2018; pp. 580–585. [Google Scholar]
- Chakkarapani, K.; Thangavelu, T.; Dharmalingam, K.; Thandavarayan, P. Multiobjective design optimization and analysis of magnetic flux distribution for slotless permanent magnet brushless DC motor using evolutionary algorithms. J. Magn. Magn. Mater. 2019, 476, 524–537. [Google Scholar] [CrossRef]
- Zhu, Z.; Zhu, J.; Zhu, H.; Zhu, X.; Yu, Y. Optimization design of an axial split-phase bearingless flywheel machine with magnetic sleeve and pole-shoe tooth by RSM and DE algorithm. Energies 2020, 13, 1256. [Google Scholar] [CrossRef]
- Mutluer, M.; Bilgin, O. Comparison of stochastic optimization methods for design optimization of permanent magnet synchronous motor. Neural Comput. Appl. 2012, 21, 2049–2056. [Google Scholar] [CrossRef]
- Fard, J.R.; Arand, S.J.; Hemmati, S. Optimal design of a yoke-less axial flux switching PM motor based on multi-objective PSO. COMPEL-Int. J. Comput. Math. Electr. Electron. Eng. 2023, 42, 1248–1262. [Google Scholar] [CrossRef]
- Radmanesh, H.; Sharifi, R. Design and simulation of axial flux permanent magnet electrical machine for electric vehicles application. In Proceedings of the 2021 29th Iranian Conference on Electrical Engineering (ICEE), Tehran, Iran, 18–20 May 2021; pp. 340–345. [Google Scholar]
- Ouldhamrane, H.; Charpentier, J.F.; Khoucha, F.; Zaoui, A.; Achour, Y.; Benbouzid, M. Optimal design of axial flux permanent magnet motors for ship RIM-driven thruster. Machines 2022, 10, 932. [Google Scholar] [CrossRef]
- Ruiz-Ponce, G.; Arjona, M.A.; Hernandez, C.; Escarela-Perez, R. Design optimization of an axial flux magnetic gear by using reluctance network modeling and genetic algorithm. Energies 2023, 16, 1852. [Google Scholar] [CrossRef]
- Wu, H.; Zhou, Y.; Yang, X. An improved two-dimensional simplification calculation method for axial flux permanent magnet synchronous motor. Appl. Sci. 2023, 13, 11748. [Google Scholar] [CrossRef]
- Ge, W.; Xiao, Y.; Cui, F.; Liu, W.; Wu, X. Rapid design of structural parameters of axial-flux micro-motor based on deep learning. J. Electr. Eng. Technol. 2024. [Google Scholar] [CrossRef]
- Wang, X.; Liu, C.; Zhou, S.; Wan, N.; Liu, Y. Cogging Torque Reduction in Axial Flux PMSM with Different Permanent Magnet Combination. Trans. Nanjing Univ. Aeronaut. Astronaut. 2021, 38, 726–736. [Google Scholar]
- Chen, H.; Zhao, J.; Wang, H.; Zhang, Q.; Luo, X.; Xu, H.; Xiong, Y. Multi-objective optimum design of five-phase squirrel cage induction motor by differential evolution algorithm. Energy Rep. 2022, 8, 51–62. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, Y.; Li, X.; Qu, R. Design of an IE5 5.5 kW synchronous reluctance machine with low torque ripple. In Proceedings of the 2023 26th International Conference on Electrical Machines and Systems (ICEMS), Zhuhai, China, 5–8 November 2023; pp. 4879–4884. [Google Scholar]
- Knypiński, Ł. A novel hybrid cuckoo search algorithm for optimization of a line-start PM synchronous motor. Bull. Pol. Acad. Sci. Tech. Sci. 2023, 71, e144586. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential evolution-a simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Yang, X.-S.; Deb, S. Cuckoo search via lévy flights. In Proceedings of the 2009 World Congress on Nature & Biologically Inspired Computing (NaBIC), Coimbatore, India, 9–11 December 2009; pp. 210–214. [Google Scholar]
- Zeng, Z.; Zhang, M.; Chen, T.; Hong, Z. A new selection operator for differential evolution algorithm. Knowl.-Based Syst. 2021, 226, 107150. [Google Scholar] [CrossRef]
- Valian, E.; Tavakoli, S.; Mohanna, S.; Haghi, A. Improved cuckoo search for reliability optimization problems. Comput. Ind. Eng. 2013, 64, 459–468. [Google Scholar] [CrossRef]
- Cvetkovski, G.; Petkovska, L. Multi-objective approach of design optimisation of axial flux permanent magnet motor. Int. J. Appl. Electromagn. Mech. 2016, 51, S115–S123. [Google Scholar] [CrossRef]

| Description | Unit | Value |
|---|---|---|
| Rated power | W | 4.0 |
| Rated speed | rpm | 6000 |
| Pole number | / | 16 |
| Slot number | / | 12 |
| Stator’s outside diameter | mm | 22 |
| Rotor’s outside diameter | mm | 20 |
| Stator’s back iron thickness | mm | 0.45 |
| Rotor’s back iron thickness | mm | 0.3 |
| Parameters | Lower Boundary | Upper Boundary | Value 1 | Value 2 | Value 3 | Value 4 |
|---|---|---|---|---|---|---|
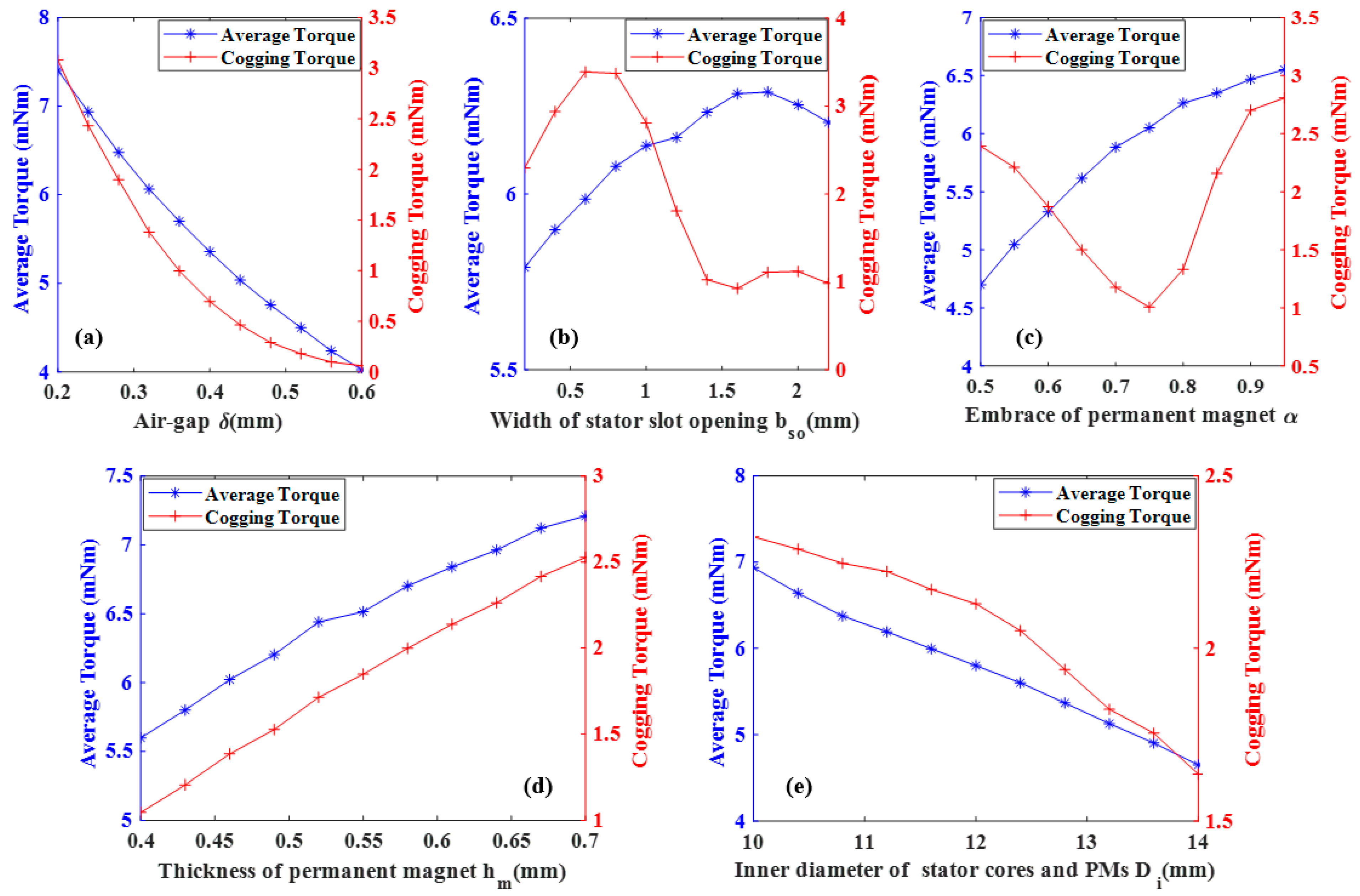
| Air gap, δ/mm | 0.25 | 0.55 | 0.25 | 0.35 | 0.45 | 0.55 |
| Slot opening, bs0/mm | 0.5 | 2.0 | 0.5 | 1.0 | 1.5 | 2.0 |
| PM embrace, α | 0.6 | 0.9 | 0.6 | 0.7 | 0.8 | 0.9 |
| PM thickness, hm/mm | 0.4 | 0.7 | 0.4 | 0.5 | 0.6 | 0.7 |
| Inner diameter, Di/mm | 10.0 | 13.0 | 10.0 | 11.0 | 12.0 | 13.0 |
| Function Name | Calls | Total Time | Self Time | Function Name | Calls | Total Time | Self Time |
|---|---|---|---|---|---|---|---|
| DE_1 | 1 | 26.537 s | 3.559 s | CS_1 | 1 | 67.044 s | 4.799 s |
| Parallel_function | 100 | 21.139 s | 0.093 s | Parallel_function | 200 | 58.933 s | 0.143 s |
| Parallel_function > distributed_execution | 100 | 20.294 s | 0.156 s | Parallel_function > distributed_execution | 200 | 57.720 s | 0.290 s |
| Remoteparfor.getCompletelntervals | 1001 | 19.252 s | 1.111 s | Remoteparfor.getCompletelntervals | 2395 | 55.713 s | 2.371 s |
| LinkedBlockingQueue | 1873 | 15.982 s | 15.982 s | LinkedBlockingQueue | 4169 | 48.781 s | 48.781 s |
| DE_1 > func | 50 | 1.141 s | 0.008 s | CS_1 > func | 100 | 1.619 s | 0.009 s |
| network.sim | 50 | 1.133 s | 0.039 s | network.sim | 100 | 1.610 s | 0.055 s |
| Parameters | Initial Model | DE Solution | CS Solution |
|---|---|---|---|
| δ/mm | 0.35 | 0.3004 | 0.3012 |
| bs0/mm | 2.0 | 1.7525 | 1.7532 |
| α | 0.8 | 0.7675 | 0.7665 |
| hm/mm | 0.5 | 0.4508 | 0.4513 |
| Di/mm | 11.0 | 11.2106 | 11.2083 |
| Tav/mNm | 6.4643 | 6.5561 | 6.5546 |
| Tcog/mNm | 0.6041 | 0.4106 | 0.4097 |
| Objective function | 0.12625 | 0.11493 | 0.11491 |
| Parameters | DE Solution | FEA-DE | Error | CS Solution | FEA-CS | Error |
|---|---|---|---|---|---|---|
| Tav/mNm | 6.5561 | 6.5187 | −0.57% | 6.5546 | 6.5128 | −0.64% |
| Tcog/mNm | 0.4103 | 0.4169 | 1.61% | 0.4097 | 0.4156 | 1.44% |
| Objective function | 0.11493 | 0.11588 | 0.84% | 0.11491 | 0.11587 | 0.84% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ge, W.; Xiao, Y.; Cui, F.; Wu, X.; Liu, W. Optimization Comparison of Torque Performance of Axial-Flux Permanent-Magnet Motor Using Differential Evolution and Cuckoo Search. Actuators 2024, 13, 255. https://doi.org/10.3390/act13070255
Ge W, Xiao Y, Cui F, Wu X, Liu W. Optimization Comparison of Torque Performance of Axial-Flux Permanent-Magnet Motor Using Differential Evolution and Cuckoo Search. Actuators. 2024; 13(7):255. https://doi.org/10.3390/act13070255
Chicago/Turabian StyleGe, Wei, Yiming Xiao, Feng Cui, Xiaosheng Wu, and Wu Liu. 2024. "Optimization Comparison of Torque Performance of Axial-Flux Permanent-Magnet Motor Using Differential Evolution and Cuckoo Search" Actuators 13, no. 7: 255. https://doi.org/10.3390/act13070255
APA StyleGe, W., Xiao, Y., Cui, F., Wu, X., & Liu, W. (2024). Optimization Comparison of Torque Performance of Axial-Flux Permanent-Magnet Motor Using Differential Evolution and Cuckoo Search. Actuators, 13(7), 255. https://doi.org/10.3390/act13070255






