Abstract
To achieve cost-effective micro-/nano-displacement adjustment, this paper integrates the advantages of flexible hinge micro-/nano-displacement transmission. A linear stepper motor is utilized as the driving component to design and develop a high-precision, low-cost micro-/nano-positioning system. The structure, design, and working principles of the micro-/nano-positioning platform are introduced. The scaling factor model between micro-positioning platforms and nano-positioning platforms is analyzed. Static and dynamic models of flexible mechanisms have been established. The dimensions of the mechanical structure and the selection of motors are determined. The mechanical characteristics of the micro-/nano-positioning platform are validated through finite element analysis. To address the characteristic of increasing loads during the transmission process, an intelligent control system based on current feedback is designed and developed. The integration of drive and control provides a high level of system integration. Finally, experimental calibration was conducted to test the motion characteristics of the linear stepper motor-driven micro-/nano-positioning platform. It achieved a minimum displacement control resolution of 100 nm and demonstrated a certain level of stability.
1. Introduction
Micro-/nano-positioning technology represents a sophisticated discipline in displacement measurement and control, targeting precise manipulation and localization at the micron and nanoscale levels [1]. Synthesizing expertise from microelectronics, precision engineering, materials science, control theories, and systems, it stands as a cornerstone in contemporary high-tech applications [2]. Its prevalence spans across avant-garde sectors such as semiconductor fabrication, biomedical diagnostics, precision metrology, material characterization, and advanced manufacturing processes [3,4,5,6]. Fundamental to its efficacy are advancements in precision actuation, high-resolution sensing, control algorithms, environmental isolation, and vibration mitigation technologies [7], rendering the design and development of innovative micro-/nano-positioning systems crucial for technological progress and catering to diverse sectoral needs, with cost-effectiveness being a paramount consideration for users of micro-/nano-positioning platforms.
A prevalent strategy in micro-positioning involves piezoelectric ceramic actuators combined with compliant mechanisms for guidance. Flexible hinges leverage elastic deformation for guidance, offering a non-contact, frictionless, lubrication-free, and assembly free transmission and steering mechanism. Piezoceramic-driven systems can thereby attain nanoscale positioning resolution [8]. Nonetheless, their restricted stroke confines their utility in millimeter-scale operations, and the supplementary high-cost sensor systems necessary for enhancing motion precision pose adoption barriers.
Voice Coil Motors (VCMs), capitalizing on their unique performance attributes such as rapid response times, high-precision positioning capabilities, and the capacity to deliver substantial thrust within confined spaces, occupy a pivotal role in micro-/nano-positioning systems. VCM positioning systems can employ guidance mechanisms including sliding guides, hydrostatic guides, or flexible hinge architectures, with their positioning accuracy being utterly contingent upon feedback and control systems, exemplified by optical encoders, laser displacement sensors, and strain gauges [9,10,11]. Kihyun Kim introduced a novel, precision-grade 3 Degrees of Freedom (X-Y-θ) configuration utilizing an array of four coplanar VCMs [12]. Xu has designed a series of large-stroke micro-positioning platforms integrating VCMs with flexible hinges [13,14,15]. Building upon VCM technology, Hashizume developed a hybrid linear motor and validated a high-speed nano-positioning platform under hydrostatic rail guidance [16]. Liang proposed a novel moving-coil VCM designed for actuating nano-positioning devices, which, supported by compliant mechanisms, achieves both large strokes and nanoscale positioning precision [17]. Nevertheless, VCM systems, with their inherently low damping, are prone to mechanical vibrations, thereby limiting the operational speed of precision positioning systems [18]. Research has illuminated that through ingeniously designed flexible hinge structures, millimeter-scale extensive travels can be attained. Moreover, the synergy of VCM actuation and sensor feedback mechanisms permits millimeter-scale strokes with nanoscale resolution positioning. However, the necessity for VCMs to operate in tandem with high-accuracy sensors significantly escalates the overall cost of positioning systems.
Linear stepping motors are an excellent solution for positioning applications that require rapid acceleration and high-speed moves with low mass payloads. Mechanical simplicity and precise open-loop operation are additional features of the micro stepping linear motor systems. However, there is a scarcity of literature investigating micro-/nano-positioning systems employing linear stepper motors.
In summary, of the aforementioned analysis, this study endeavors to realize low-cost micro-/nano-scale displacement orientation. Leveraging the advantages of flexible hinge transmission, we employ linear stepper motors as driving components to engineer a high-precision, cost-effective micro-/nano-positioning system. Additionally, we devise a stepper motor drive and control system tailored for nano-positioning. Moreover, we introduce a PID-based current loop closed-loop control mechanism. This enables fine-tuning of the stepper motor’s operational current via upper-computer software, thereby modulating motor thrust and mitigating input errors on the micrometer stage.
2. Micro-/Nano-Positioning Platform: Structural Design and Modeling
2.1. Micro-/Nano-Positioning Platform Design
The overall composition of the micro-/nano-positioning platform is illustrated in Figure 1, consisting of the main structure based on a flexible hinges, a linear stepper motor, couplings, and a motor mounting plate. The micro stage utilizes long-stroke flexible beams for translational guidance, achieving micrometer-level positioning accuracy through direct coupling with a linear stepper motor. Conversely, the nano stage employs short flexible beams for guidance. By exploiting the stiffness difference between the large-stroke and short-stroke flexible beams, the micro-motion stage’s micrometer resolution is effectively downscaled to nanometer resolution, consequently attaining nanometer-level positional precision. The overall dimensions of the motion platform are 110 × 90 × 42 mm, with the linear stepper motor installed inside the structure. There are two motion platforms, including the micro-positioning stage and the nano-positioning stage. The linear stepper motor is connected to the micro-positioning platform via a coupling, as shown in Figure 1c. The coupling utilizes flexible hinge transmission technology, providing certain flexibility in the axial direction to mitigate the impact of installation errors.
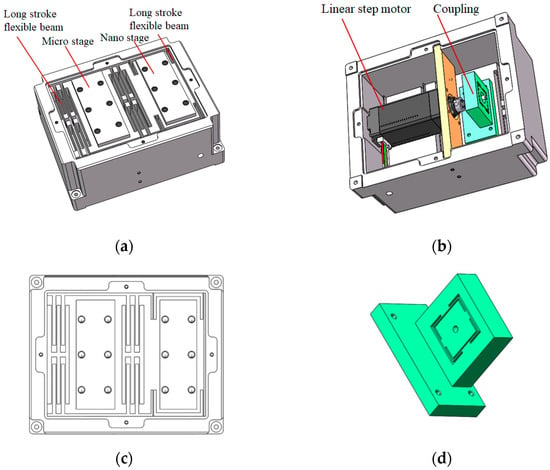
Figure 1.
Micro-/nano-positioning system based on a stepper motor. (a) Overall view of the micro-/nano-positioning platform; (b) interior view of the micro-/nano-positioning platform; (c) top view of the micro-/nano-positioning platform based on a flexible hinge; (d) coupling based on a flexible hinge.
2.2. Design of the Flexible Hinge-Based Transmission Mechanism
A flexible mechanism utilizes material deformation to transmit or convert motion, force, or energy. Flexible mechanisms implement motion through flexible hinge joints, commonly referred to as flexible hinge mechanisms. Compared to rigid mechanisms, flexible hinge mechanisms offer several advantages: (1) they can be integrated into the overall design and manufacturing process, enabling miniaturization, assembly free construction, cost reduction, and increased reliability; (2) they exhibit no backlash or friction, allowing for high-precision motion; (3) they are free from friction wear and do not require lubrication.
Based on the principles of materials mechanics, it is known that utilizing symmetrically distributed flexible beams as guiding structures can yield significant displacement output. Typically, by adjusting the length of the flexible beams, various stiffness levels can be achieved, enabling both micron- and nanometer-level displacement ranges. Based on the difference in guiding stiffness, the transition from micron-level displacement to nanometer-level displacement can be achieved. The transmission principle of the micro-motion platform, as shown in Figure 2, consists of a micrometer platform, a nanometer platform, and two different types of straight-beam flexible hinges. The micrometer platform is guided by symmetrically distributed long flexible beams, resulting in lower stiffness, while the guiding flexible beams of the nanometer platform are shorter, resulting in higher stiffness.
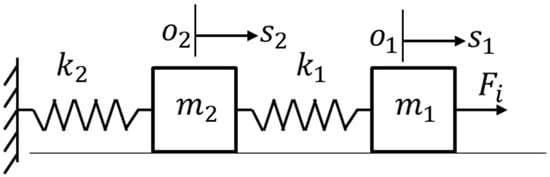
Figure 2.
Design principle of the micro-/nano-positioning platform.
As shown in Figure 2, under the action of driving force , the displacement of the micro stage is , which represents the input displacement of the system. According to Hooke’s Law, s1 can be expressed as:
represents the stiffness of the micrometer platform along the driving direction, while represents the stiffness of the nanometer platform along the driving direction.
The output displacement s2 of the nanometer platform can be expressed as:
The proportional relationship between the driving input and the platform output can be expressed as:
In the equation, λ represents the displacement scaling factor.
When λ is larger, the output displacement of the platform is smaller under the same driving input, resulting in higher platform resolution. This means that through the flexible beam guiding mechanism, lower-precision actuators can achieve high-resolution and high-precision output displacements. As a result, the cost of precision positioning platforms is significantly reduced.
2.3. Stiffness Modeling Analysis of the Flexible Mechanism of the Micro-Positioning Platform
The basic elastic elements in the structure are mainly long, straight flexible beams, and the flexibility modeling model of a single cantilever beam is shown in Figure 3. First, a generalized force is applied to the reference point at the end of the flexible beam on the moving platform. Then, the deformation of the end of the flexible beam on the moving platform under the action of each component force and is calculated, and the deformation is and respectively.
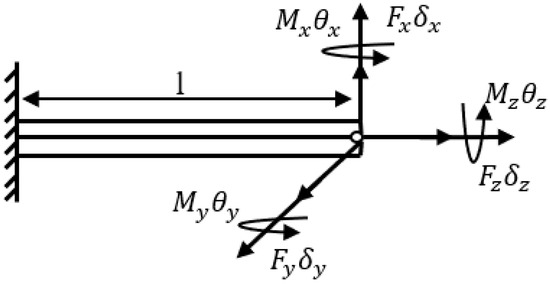
Figure 3.
Model for the flexibility of a single cantilever beam.
According to the knowledge of material mechanics, it is easy to obtain the deformation at the reference point of the flexible beam end when and are acted on the end of the flexible beam on a moving platform.
When acting alone, , the deformation is given by:
When acting alone, , the deformation is given by:
When acting alone, , the deformation is given by:
In the equation, and are the moments of inertia about the x-axis and y-axis, respectively; is the polar moment of inertia; E is the Young’s elastic modulus; and A is the cross-sectional area of the homogeneous flexible beam.
The total deformation at the reference point E of the flexible beam on the moving platform is given by:
For a flexible beam guide platform consisting of two pairs of symmetrical long straight flexible beams, as shown in Figure 4, for a symmetrical arrangement, the platform is translational under the action of thrust.
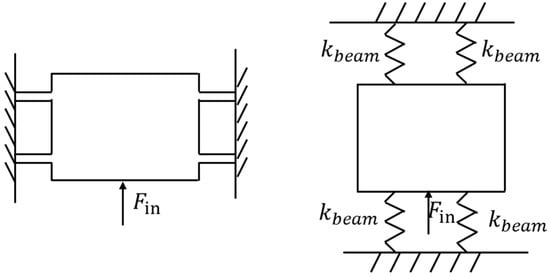
Figure 4.
Parallel four-bar guide flexible beam mechanism and equivalent diagram.
Due to the symmetric flexible hinge joint, the moving platform undergoes translational motion under thrust, resulting in zero rotation at the end of the flexible beam. Therefore, the rotation angle of the flexible beam under the action of and is zero.
Thus, we have:
Therefore, the displacement at the end of the flexible beam is:
Hence, the stiffness of a single-guided flexible beam is:
The equivalent stiffness of the platform is illustrated in Figure 3. The input stiffness of the dynamic platform, with four guided beams, is denoted as . Through force analysis, it is known that:
Thus, the stiffness of the platform in the micro-feeding direction is:
The elastic deformation of the flexible beam can serve as the micro-feeding stroke, but typically, the stroke is limited. To increase the stroke of the flexible beam, the length of the flexible beam can be increased. To maintain compact dimensions, a series-connected flexible beam guiding mechanism is designed, as shown in Figure 5. Due to the symmetry of the overall system, the moving platform achieves feed motion in the thrust direction. Its serial-parallel compound equivalent model is depicted in Figure 5.
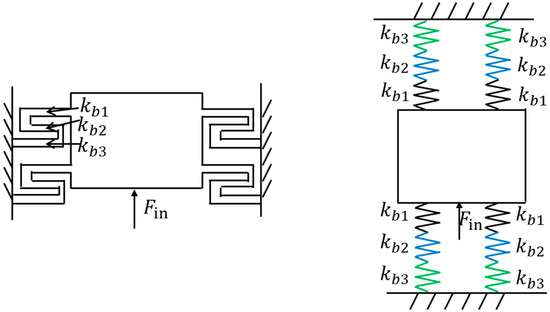
Figure 5.
Long-stroke parallel-guided flexible beam mechanism and its equivalent diagram.
Based on the above analysis, it can be deduced that the stiffness of multiple serially connected flexible beams in their micro-displacement direction is:
Therefore, the stiffness of a platform guided by four symmetrically arranged serial flexible beams in its micro-displacement direction is:
2.4. Dynamic Modeling of Flexible Mechanisms in the Micro-Positioning Platform
To analyze the system’s dynamic performance, as shown in Figure 2, generalized coordinates and are chosen. The system’s kinetic energy is expressed as:
The potential energy of the system is:
By applying the Lagrange equations, the system’s equations of motion can be directly obtained:
Thus, the natural frequency expression of the platform is:
3. Finite Element Simulation Verification
3.1. Scaling Analysis of the Micro-/Nano-Positioning Platform
Finite element simulation is a mature and effective method for analyzing the static and dynamic characteristics of mechanical systems. The structural material of the mechanical system is chosen as aluminum alloy 7075, with a density of 2810 , Poisson’s ratio of 0.3, and elastic modulus of 71 GPa. The simulation is conducted using the finite element simulation software ANSYS.
When a driving displacement of 5 mm is applied in the translational direction of the micro-positioning platform, the simulated displacement variation results, as shown in Figure 6a, indicate an output displacement of 0.18 mm for the nano-positioning platform. The displacement scaling ratio is 27.8, meaning that when the range of motion for the micro-positioning platform is (−5 mm, 5 mm), the output range for the nano-positioning platform is (−180 μm, 180 μm).
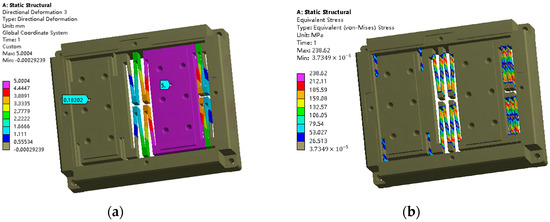
Figure 6.
Simulation analysis of the micro-/nano-positioning platform. (a) Micro-/nano-positioning platform displacement analysis; (b) micro-/nano-positioning platform stress analysis.
Similarly, when a driving displacement of 5 mm is applied in the translational direction of the micro-positioning platform, the simulated stress results, as shown in Figure 6b, indicate a maximum stress of 238.6 MPa. This value is significantly lower than the allowable stress of the material, satisfying the material’s usage requirements. The maximum stress occurs at the root of the flexible guiding beam of the micro-positioning platform.
3.2. Stiffness Analysis
When a driving force of 50 N is applied to the micro-positioning platform, it can be observed from Figure 7 that the output displacement of the micro-positioning platform is 5.75 mm and the output displacement of the nano-positioning platform is 0.208 mm. Thus, the input stiffness and output stiffness of the platform are determined to be 8.7 N/mm and 240.4 N/mm, respectively. Due to the limitations imposed by the motor thrust and stroke, there are maximum requirements for the platform’s stiffness. Therefore, the design stiffness of the flexible hinge joints is relatively small.
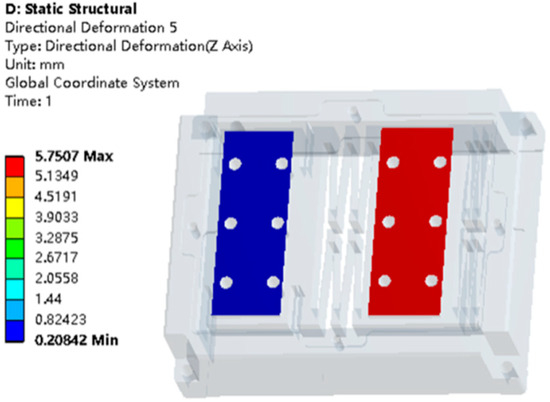
Figure 7.
Displacement analysis of the micro-/nano-positioning platform under a 50 N driving force.
3.3. Modal Analysis
Modal analysis of the micro-/nano-positioning platform was conducted using the finite element software ANSYS. The first two modal frequencies are 57.4 Hz and 114.3 Hz, respectively. Their mode shapes are depicted in Figure 8, corresponding to the translational and rotational modes of the micro-positioning platform. Due to the requirement for a compact structure, combined with the dimensions and thrust of the selected motor, the designed hinge structure has relatively low stiffness, thereby limiting the operating frequency of the platform to around 20 Hz. By reducing the mass of the working platform, the natural frequency of the positioning platform can be increased, thereby achieving higher natural frequencies.
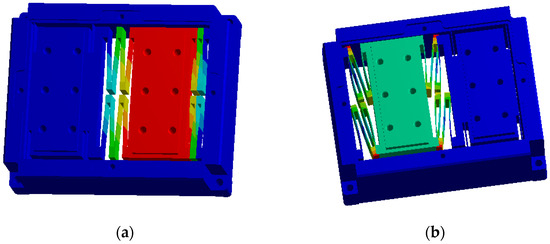
Figure 8.
Modal analysis of the micro-positioning platform. (a) Translational modal analysis; (b) rotational modal analysis.
4. Integrated Design of Stepper Motor Drive and Control
In the proposed micro-/nano-positioning platform driven by a stepper motor, the driving force of the motor increases with the stroke, necessitating dynamic adjustment of the motor’s driving force during operation. To address this, an integrated control system based on current feedback is designed and developed, as illustrated in Figure 9. The control board consists of communication, control, drive, power supply, encoder, and current feedback modules. The host computer sends control commands to the control module via the communication module, prompting it to send pulse commands to the drive module, which then sends pulses to the stepper motor. The motor provides speed, angle signals, and current feedback to the host computer through the encoder and current feedback modules, forming a closed-loop control system.
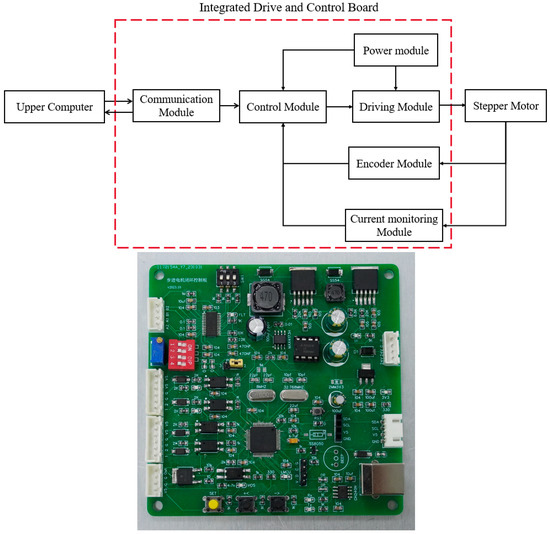
Figure 9.
Schematic diagram and physical diagram.
5. Experimental Testing
The micro-/nano-positioning platform designed in this paper is made of aluminum alloy and processed using advanced wire electrical discharge machining technology. Figure 10 shows the overall experimental setup, consisting primarily of the micro-/nano-positioning platform, stepper motor, integrated drive and control board, 24 V switch power supply, capacitive displacement sensor, host computer, dSPACE, and calibration block.

Figure 10.
Overall experimental setup.
5.1. Micro-Positioning Platform Input Displacement Calibration Analysis
Due to the selected motor’s step angle of 1.8° and the lead screw pitch of 0.609 mm, the displacement per pulse sent to the stepper motor should be 3.04 μm, resulting in a resolution of 3.04 μm. After setting up the platform, 22 pulses were sent via the host computer software for both unloaded testing and testing while driving the micro-positioning platform. The data were processed using MATLAB R2017 to obtain the curve depicting the unloaded displacement of the stepper motor versus the input displacement of the micro-positioning platform, as shown in Figure 11.
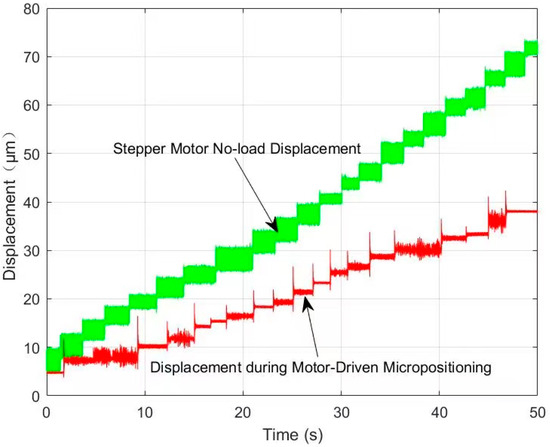
Figure 11.
Stepper motor unloaded—micro stage input displacement curve.
In Figure 11, it can be observed that as the number of pulses increases, the actual input displacement curve of the micro-positioning platform driven by the stepper motor gradually deviates from the unloaded curve, and the deviation becomes larger over time. This discrepancy arises from the resistance of the micro-/nano-positioning platform. When the motor drives the micro-positioning platform to generate nanometer-level output along with the nano-positioning platform, the resistance increases as the motor stroke increases, resulting in a deviation between the input displacement of the micro-positioning platform and the theoretical value.
5.2. Nano-Positioning Platform Output Displacement and Scaling Ratio Calibration Analysis
The capacitive displacement sensor probe is placed against the surface of the calibration block on the nano-positioning platform of the micro-/nano-positioning platform. After the stepper motor drives the micro-positioning platform to generate micrometer-level displacement, the actual output displacement of the nano-positioning platform is obtained via dSPACE. The displacement curve is depicted in Figure 12.
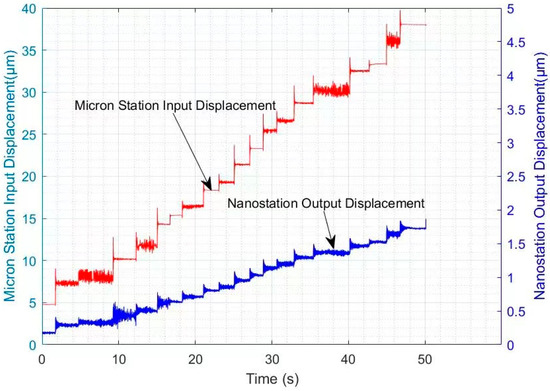
Figure 12.
Displacement curve.
It can be observed that both the displacement curves of the micro-positioning platform driven by the stepper motor and the displacement curves of the nano-positioning platform exhibit a linear trend, indicating that as the stroke of the stepper motor increases, the output displacement of the nano-positioning platform also increases. From the graph, it is evident that both the micro-positioning platform and the nano-positioning platform’s displacement curves show a step-like increase.
Figure 13 illustrates the relationship between the displacement generated by driving the micro-positioning platform with the stepper motor and the output displacement of the nano-positioning platform. Based on the stiffness of the micro-positioning platform (8.4 N/mm) and the nano-positioning platform (236.8 N/mm), the estimated scaling ratio between the micro-positioning platform and the nano-positioning platform is 29.19. Through simulation, the displacement scaling ratio of the micro-/nano-positioning platform was found to be 27.8. However, the calibration experiment reveals that the actual scaling ratio of the platform displacement is 20.76.
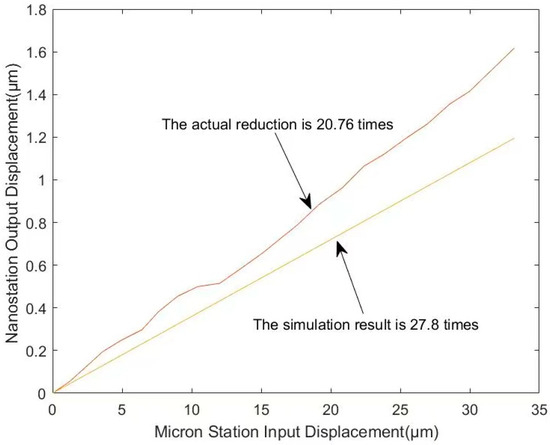
Figure 13.
Curve depicting the relationship between the input displacement of the micrometer stage and the output displacement of the nanometer stage.
5.3. Stability and Round-Trip Testing of the Micro-/Nano-Positioning Platform
- (1)
- Stability Testing
The stability of the micro-/nano-positioning platform is a crucial indicator of the micro-/nano-positioning system and requires testing experiments. Using the host computer software, a pulse is sent to the stepper motor every 2 s, totaling 32 pulses. The platform is paused for approximately one minute at the 2nd, 12th, 22nd, and 32nd pulses, and the stability of the input displacement and output displacement is observed. Figure 14 illustrates the stability testing of the micro-positioning platform and the nano-positioning platform.
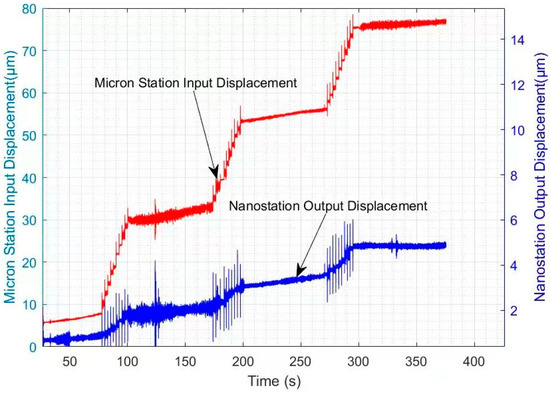
Figure 14.
Stability testing of the micro and nano stage displacements.
From Figure 14, it can be observed that both the input displacement of the micro-positioning platform and the output displacement of the nano-positioning platform stabilize after pausing for approximately one minute at the 2nd, 12th, 22nd, and 32nd pulses. It is evident from the graph that after pausing for about one minute at the 12th and 22nd pulses, both the micro-positioning platform and the nano-positioning platform exhibit relatively stable and step-like increasing curves. This indicates that the stability of the micro-/nano-positioning system is good.
- (2)
- Round-Trip Testing
Using the host computer software, control the stepper motor to drive the micro-/nano-positioning platform forward in the positive direction and then reverse to return. During the round-trip motion, send 22 pulses to the stepper motor for each direction, totaling 44 pulses. Measure the displacement using the capacitive displacement sensor, send the data to dSPACE, and obtain the round-trip curve as shown in Figure 15. From Figure 15, it can be observed that the displacement curve generated by driving the micro-positioning platform with the stepper motor is essentially symmetrical with the round-trip operation curve of the nano-positioning platform. The resolution of the nano-positioning platform is 100 nm, indicating good operation of the micro-/nano-positioning system.
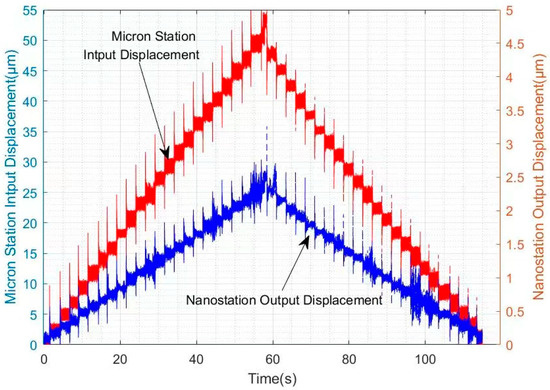
Figure 15.
Micro-/Nano-positioning Platform Round-trip Test.
The aforementioned experiments illustrate that the micrometer-nanometer positioning platform, driven by a linear stepping motor and guided by a flexible hinge mechanism, successfully achieves the anticipated nanoscale positioning functionality. The deformation range of the serially connected flexible hinges and the thrust generated by the stepping motor influence the effective stroke of the platform. The guidance stiffness ratio between the micrometer and nanometer stages, along with the micro-stepping displacement of the stepping motor, constitute the primary factors affecting the platform’s resolution. An increase in travel range leads to a larger system structure and a decrease in system stiffness, which in turn impacts stability. Consequently, stepping motors with greater thrust capacities and more sophisticated, stable control strategies become imperative.
6. Conclusions
In this study, a micronano-positioning system with micron-level travel and nanometer-level resolution was designed based on the principles of open-loop driving of linear stepper motors and flexible hinge guiding. A stiffness model of the flexible mechanism was established, and the scaling ratio model between the micro-positioning platform and the nano-positioning platform was analyzed. Based on the operational requirements, the dimensions of the mechanical structure and the selection of motors were determined. The mechanical properties of the micronano-positioning platform were verified using finite element analysis software. Additionally, an integrated design of stepper motor drive and control was implemented, with a closed-loop current control system designed based on PID control theory. An experimental platform was constructed to test and analyze the system. The results demonstrate that the micronano-positioning platform designed in this study achieves a single-pulse resolution of 100 nm, with a compact overall structure and simple control method, enabling precise adjustment of micro-/nano-scale displacements.
Author Contributions
Conceptualization, M.L. and L.C.; methodology, Y.Y.; validation, N.J. and X.D.; writing—M.L., Y.Y., L.C., and N.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Tianjin Natural Science Foundation, NO. 23JCQNJC00990 and Tianjin Education Committee Scientific Research Project, grant number 2023KJ189.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Wu, Z.; Xu, Q. Survey on Recent Designs of Compliant Micro-/Nano-Positioning Stages. Actuators 2018, 7, 5. [Google Scholar] [CrossRef]
- Ukraintsev, V.; Banke, B. Review of reference metrology for nanotechnology: Significance, challenges, and solutions. J. Micro/Nanolithography MEMS MOEMS 2012, 11, 011010. [Google Scholar] [CrossRef][Green Version]
- Istriţeanu, S.; Gheorghe, I.G. Research Work and Study on Ultraprecise High-Tech Robotic Micro-Nano- Systems for Measurement, Positioning and Alignment Used in the Fields of Mechatronics and Integronics; The Scientific Bulletin of VALAHIA University: Waltham, MA, USA, 28 May 2024. [Google Scholar]
- Lin, H.B.; Yang, G.Z. Design and Analysis for a Nano-Positioning Micro-Motion Platform Driven by Piezoelectric Ceramic Linear Motors. Adv. Mater. Res. 2010, 102, 402–406. [Google Scholar] [CrossRef]
- Jha, N.; Singh Naruka, G.; Dutt Sharma, H. Design of Embedded Control System Using Super-Scalar ARM Cortex-A8 for Nano-Positioning Stages in Micro-Manufacturing. Signal Image Process. Int. J. 2013, 4, 71–82. [Google Scholar] [CrossRef]
- Hyde, H.C.; Sandtner, W.; Vargas, E.; Dagcan, A.T.; Robertson, J.L.; Roux, B.; Correa, A.M.; Bezanilla, F. Nano-Positioning System for Structural Analysis of Functional Homomeric Proteins in Multiple Conformations. Structure 2012, 20, 1629–1640. [Google Scholar] [CrossRef] [PubMed]
- Ru, C.; Liu, X.; Sun, Y. Nanopositioning Technologies. In Piezoelectric Motor Technology: A Review; Springer: Cham, Switzerland, 2016; Chapter 2; pp. 33–59. [Google Scholar] [CrossRef]
- Javed, A.; Rout, B.K.; Mittal, R.K. A Review on Design and Synthesis of Compliant Mechanism for Micro Actuation. In Proceedings of the 2nd ISSS National Conference on MEMS, Microsensors, Smart Materials, Structures and Systems, Pilani, India, 16–17 November 2007. [Google Scholar]
- Jeong, J.H.; Kim, M.H.; Woo, S.W.; Gweon, D.G.; Hong, D.P. Optimal Design of Voice Coil Motor for Micro Stage. Appl. Mech. Mater. 2014, 607, 507–510. [Google Scholar] [CrossRef]
- Lin, S.; Jia, Y.; Lei, I.P.; Xu, Q. Design and Optimization of a Long-Stroke Compliant Micropositioning Stage Driven by Voice Coil Motor. In Proceedings of the 2012 12th International Conference on Control Automation Robotics & Vision (ICARCV), Guangzhou, China, 5–7 December 2012; IEEE: Piscataway, NJ, USA, 2012. [Google Scholar]
- Shan, G.; Li, Y.; Zhang, L.; Wang, Z.; Zhang, Y.; Qian, J. Contributed Review: Application of voice coil motors in high-precision positioning stages with large travel ranges. Rev. Sci. Instrum. 2015, 86, 101501. [Google Scholar] [CrossRef] [PubMed]
- Kim, K.H.; Gweon, D.G.; Jung, H.S.; Lee, S.H.; Hong, M.S.; Lee, M.G. A Stage Based on Voice Coil Motor with High Speed and Long Range for Laser Micro/Nano Fabrication. Key Eng. Mater. 2007, 345–346 Pt 1, 757–760. [Google Scholar] [CrossRef]
- Xu, Q. Design and implementation of a novel rotary micropositioning system driven by linear voice coil motor. Rev. Sci. Instrum. 2013, 84, 063701. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Xu, Q. Design of a flexure-based auto-focusing device for a microscope. Int. J. Precis. Eng. Manuf. 2015, 16, 2271–2279. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, Q. Design, fabrication and testing of a novel symmetrical 3-dof large-stroke parallel micro/nano-positioning stage. Robot. Comput. Integr. Manuf. 2017, 54, 162–172. [Google Scholar] [CrossRef]
- Shinno, H.; Hashizume, H. High Speed Nanometer Positioning Using a Hybrid Linear Motor. CIRP Ann. 2001, 50, 243–246. [Google Scholar] [CrossRef]
- Dong, L.; Chen, J.; Zhang, C.; Wu, D.; Yu, G. A Novel Voice Coil Motor Used in Nano-Positioning Device. In Proceedings of the 2015 18th International Conference on Electrical Machines and Systems (ICEMS), Pattaya, Thailand, 25–28 October 2015; IEEE: Piscataway, NJ, USA, 2016. [Google Scholar]
- Youm, W.; Jung, J.; Lee, S.; Park, K. Control of voice coil motor nanoscanners for an atomic force microscopy system using a loop shaping technique. Rev. Sci. Instrum. 2008, 79, 013707. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).