Abstract
In this paper, a novel three-degree-of-freedom piezoelectric-driven micro-positioning platform based on a lever combination compound bridge-type displacement amplification mechanism is proposed. The micro-positioning platform proposed in this paper aims to solve the current problem of the large size and small travel of the three-degree-of-freedom piezoelectric-driven micro-positioning platform. In this paper, a lever combination compound bridge-type displacement amplification mechanism combined with a new biaxial flexible hinge is proposed, the structural dimensions of the lever mechanism and the compound bridge mechanism are optimized, and the amplification multiplier is determined. The maximum output simulation analysis of the micro-positioning platform is carried out by using ANSYS, and the experimental test system is built for verification. The validation results show that the maximum errors between simulation and experiment in the z-direction, rotation direction around x, and rotation direction around y are 64 μm, 0.016°, and 0.038°, respectively, and the corresponding maximum relative errors are 5.6%, 2.4%, and 6.6%, respectively, which proves the feasibility of the theoretical design.
1. Introduction
In recent years, the research scale of cutting-edge science and technology has gradually reached the micro–nano level, such as the production of micro–nano CPU, the processing and manufacturing of MEMS micro–nano electromechanical systems, cell injection, etc. []. In the above fields, precision positioning technology is an essential technology, and its core component is the micro-positioning platform. The driving components of the traditional micro-positioning platform generally use a ‘servo motor and ball screw’, which has the advantage of a large stroke. However, this driving mechanism has a large volume, low driving accuracy, and slow response speed. It has gradually been unable to meet the needs of industrial production and scientific research []. Piezoelectric driving technology is a new type of driving technology that converts electrical energy into mechanical energy by using the inverse piezoelectric effect of piezoelectric ceramic materials. Piezoelectric ceramic actuators made of piezoelectric ceramic materials have the advantages of a fast response speed [], a high displacement resolution [], a strong anti-magnetic field interference ability [], no noise [], a large driving force [], a small size [], a high energy conversion efficiency [], and no daily maintenance []. At present, they are widely used in micro–nano positioning platforms [], micro–miniature robots [], space mechanisms [], vibration suppression [], precision machining [,], optical instrument posture adjustment [], and life science research [].
At present, there are four main drive modes for piezoelectric ceramic actuators: ultrasonic drive, inertial drive, walking drive, and direct drive [,]. The ultrasonic-driven piezoelectric ceramic actuator is also known as the ultrasonic motor. The source of driving force is dynamic friction, and the form of motion output is rotation or linear displacement []. Li [] proposed a linear standing wave ultrasonic motor with a hollow symmetrical stator. The maximum no-load speed of the motor in forward motion is 30.86 mm/s, and the maximum no-load speed in reverse motion is 32.31 mm/s. Wang [] proposed a novel single-mode linear piezoelectric ultrasonic motor based on an asymmetric structure. The maximum no-load speed of the motor is about 127.31 mm/s under 150 V voltage and 30 N preload. Yan [] proposed a novel type of linear ultrasonic motor using a combination of two orthogonal bending vibration modes. The maximum speed of the motor is 735 mm/s. Liu [] proposed an ordered stacking structure with a piezoelectric strain unit (OSSPSU), and designed a micro ultrasonic linear motor (5 mm × 1.3 mm × 1.06 mm) based on the OSSPSU stator. The unit volume speed of the motor reaches 4.66 s−1mm−2. Under open-loop control, the moving resolution is about 3 nm, which is two orders of magnitude higher than other piezoelectric motors. The working principle of the inertial-driven piezoelectric ceramic actuator is the principle of inertia []. By utilizing the fast response speed and the inertia of the piezoelectric ceramic material, the actuation is achieved through the rapid change in the voltage []. Zeng [] proposed an inertial impact linear micromotor with an asymmetric structure, which is driven by inertial impact force and outputs linear motion through the cumulative output of small displacement difference. The maximum speed of the micromotor is 16.87 mm/s at 35 Hz frequency and 100 V voltage. Sun [] proposed a new type of impact inertial piezoelectric actuator with an asymmetric compliant mechanism. The impact inertial piezoelectric actuator can achieve two-way motion, and the forward and backward speeds are basically the same, and the maximum speed is 7.311 mm/s. Zhang [] proposed a new two-degree-of-freedom inertial rotary motor with a stick–slip mechanism. Under the condition of 210 V voltage and 630 Hz frequency, the maximum speed of the x-axis and y-axis is 263.26 mrad/s and 268.48 mrad/s, respectively. Burhanettin Koc and Bülent Delibas [] proposed a new two-phase inertia-driven piezoelectric rotary motor without any bending and leverage. The rotary motor can operate at frequencies up to 30 kHz, output no-load speeds greater than 16.0 mm/s, and output forces higher than 3.0 N. The walking-driven piezoelectric ceramic actuator is also known as the inchworm piezoelectric actuator. It imitates the way of multi-legged animal movement in nature, and completes the accumulation of small displacement by clamping the piezoelectric actuator unit and driving the coordination of the piezoelectric actuator unit, and then realizes the large stroke displacement output []. Ma [] proposed a new inchworm piezoelectric actuator with two multi-functional driving feet and only two piezoelectric stacks, which has a more compact structure and a stable stepping process. The maximum output speed of the piezoelectric actuator is 2081.16 μm/s, the effective load is more than 6.442 kg, and the output force is 14 N at 150 V voltage and 50 Hz frequency. Bai [] proposed a new inchworm piezoelectric actuator with a diamond-shaped amplification mechanism (magnification of 7.5) and a compact structure. The maximum output displacement of the piezoelectric actuator is 72.3 μm, the maximum output speed is 1260 μm/s, and the output force is 3.5 N. Yu [] proposed an inchworm piezoelectric linear actuator with a two-stage amplification mechanism. The driving efficiency of the stator is improved by alternating three piezoelectric stacks. The driving speed is 5.53 mm/s at 135 V voltage and 70 Hz frequency. The stacked piezoelectric actuator is the most widely used in the direct-drive piezoelectric ceramic actuator. It consists of multiple layers of piezoelectric ceramic sheets stacked so as to be structurally connected in series. In the meantime, electrodes are built in between neighboring piezoelectric ceramic sheets, thereby connected in parallel on a circuit []. The stacking of the displacements of the piezoelectric ceramic sheets is realized in the above manner. However, the displacement output of the stacked piezoelectric ceramic actuator is small [], which limits the further expansion of its application field. Therefore, it is usually combined with the displacement amplification mechanism to form a micro-positioning platform to achieve micro–nano positioning. Scholars in various countries have conducted more research on single- and double-degree-of-freedom micro-positioning platforms with stacked piezoelectric ceramic actuators as the driving elements, and less research on three-degree-of-freedom micro-positioning platforms for machining complex parts. Existing test benches are complex and often contain only one degree of rotational freedom. Huang [] realized bidirectional active drive through a series bridge displacement amplification mechanism, and designed a two-dimensional piezoelectric drive micro-positioning platform with a symmetrical displacement curve. The theoretical magnification is 7.36, and the maximum driving stroke is 129.41 μm. Zhang [] proposed a novel two-dimensional decoupled XY-compatible micro-positioning platform. The platform combines a bridge amplification mechanism and a triangular amplification mechanism. The maximum motion output of the stage is 346.1 μm and 357.2 μm in the x-axis and y-axis, respectively, with displacement amplification ratios of 5.39 and 5.51, respectively. Sun [] proposed a two-dimensional piezoelectric-driven micro-positioning platform with a nested structure, equal stiffness, equal travel, and low coupling. The displacement magnification of the x-axis and y-axis is 9.96 and 9.94, respectively; the maximum output displacement is 489 µm and 493 µm, respectively. Na [] proposed a three-degree-of-freedom piezoelectric-driven tripod manipulator with a stacked three-layer reverse bridge displacement amplifier. The height of the tripod manipulator is 56 mm, the diameter is 48.6 mm, the maximum output displacement is 880 μm, and the maximum rotation angle is 2.0 °. However, the size of the tripod is large and the structure is complex. In order to overcome the shortcomings of the large size and complex structure of the three-degree-of-freedom micro-positioning platform, this paper proposes a three-degree-of-freedom piezoelectric-driven micro-positioning platform with a simple and compact structure and a large stroke.
The three-degree-of-freedom piezoelectric-driven micro-positioning platform proposed in this paper can realize rotation around the x-axis and y-axis and translation along the z-axis, and it has the advantages of a small size and large stroke. In this paper, the combination mechanism of the lever mechanism and the compound bridge mechanism is used as the amplification mechanism, and the new two-axis flexible rotation hinge and the straight beam flexible hinge are used to replace the traditional rotating pair and the moving pair as the guiding mechanism. The size of the amplification structure is optimized by MATLAB, and then the platform is simulated and analyzed by ANSYS/workbench. Finally, the experimental system is built for experimental verification. The experimental results show that the three-degree-of-freedom piezoelectric drive micro-positioning platform can be applied to the field of micro-positioning technology.
2. The Overall Structure and Working Principle of the Platform
2.1. Overall Structure of the Platform
In this paper, a three-degree-of-freedom piezoelectric drive micro-positioning platform is designed by combining the compound bridge combined lever-type displacement amplification mechanism and the flexible hinge guidance mechanism. The structure of the three-degree-of-freedom piezoelectric drive micro-positioning platform is shown in Figure 1, and its overall size is 200 mm × 200 mm × 77 mm.
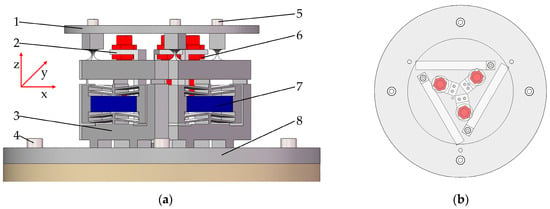
Figure 1.
The overall structure of the three-degree-of-freedom piezoelectric drive micro-positioning platform. (a) Front view. Micro-positioning platform components: Moving platform (1). Scaffold (2). Displacement amplifier (3). Hexagon socket screw (4). Hexagon socket screw (5). Displacement sensor (6). Piezoelectric ceramic actuator (7). Fixed platform (8). (b) Vertical view.
The micro-positioning platform mainly includes a moving platform, a fixed platform, and three combined displacement amplification mechanisms symmetrically arranged at 120° along the center of the moving platform. The flexible hinge is used to replace the traditional moving pair and revolute pair on each branch, which avoids the influence of the hinge assembly gap and friction.
As shown in Figure 2, the displacement amplification mechanism is mainly composed of a lever mechanism [] and a compound bridge mechanism []. The new two-axis flexure hinge only plays the role of connecting the moving platform. Eight long straight beam flexure hinges and connecting blocks together form four symmetrically distributed parallelogram guiding mechanisms, which can reduce the coupling motion of the micro-positioning platform and improve its positioning accuracy.
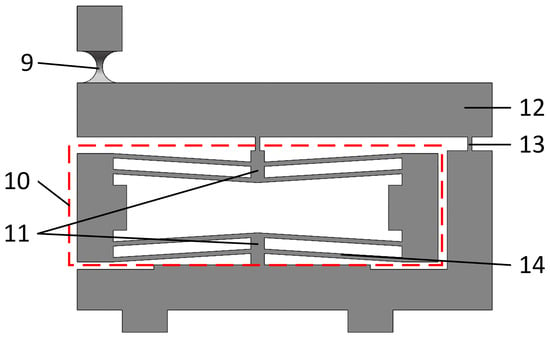
Figure 2.
The structure of the displacement amplification mechanism. Displacement amplification mechanism components: A new type of biaxial flexible hinge (9). Compound bridge-type displacement amplification mechanism (10). Connecting member (11). Lever-type displacement amplification mechanism (12). Corner-filleted flexure hinge (13). Long straight beam flexible hinge (14).
2.2. Working Principle of the Platform
The displacement amplification mechanism of the three-degree-of-freedom piezoelectric-driven micro-positioning platform is composed of three identical compound bridge combined lever-type displacement amplification mechanisms. The piezoelectric ceramic actuator is fixed on the inner convex block of the compound bridge part. The compound bridge displacement amplification mechanism itself can provide a certain preload for the piezoelectric ceramic to meet the requirements of use, and avoid the phenomenon of empty distance caused by the assembly gap of the piezoelectric ceramic.
Figure 3 shows the working principle of the compound bridge combined lever-type displacement amplification mechanism. When a specific voltage is applied to the piezoelectric ceramic actuator, the piezoelectric ceramic actuator outputs a displacement of . Under the action of the piezoelectric ceramic actuator, the long-arm flexible hinge of the compound bridge displacement amplification mechanism produces a small deformation and turns over the angle, which effectively amplifies the input displacement of the piezoelectric ceramic actuator and outputs at point 2. The output of point 2 is used as the input displacement of the lever part, which makes the straight-arm flexible hinge of point 2 compress and rotate, and the straight-arm flexible hinge of point 3 produces tensile and rotational deformation, and then makes the lever produce angle rotation, so that the input displacement is output to the moving platform after secondary amplification. The three eddy current sensors placed in the hollow part of the piezoelectric-driven micro-positioning platform are used to monitor the position of the moving platform in real time and feedback. By controlling the output displacement of the three branches, the three-degree-of-freedom positioning output is finally realized by the moving platform.
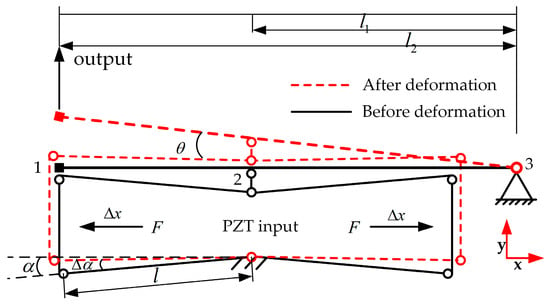
Figure 3.
Working principle of the compound bridge combined lever-type displacement amplification mechanism.
3. Design of the Displacement Amplification Mechanism
3.1. Structural Design of the Lever Displacement Amplification Mechanism
One of the important indicators of the performance of the micro-positioning platform is the magnification, which is the ratio of the output displacement to the input displacement. The core component of the piezoelectric drive positioning platform is the displacement amplification mechanism, so the magnification analysis of the lever mechanism is first performed.
Figure 4 shows the force analysis of the lever structure. In Figure 4, the black solid line is the initial position before the force deformation of the lever mechanism, and the red dotted line is the position after the force deformation. is the input force to the lever section, is the total length of the lever, and is the length of the lever between point 1 and point 2. The size of the straight beam flexible hinge at point 1 and point 2 is exactly the same. It is assumed that and are the force and moment of the straight-arm flexure hinge at two points, respectively, and are the deformation and rotation angle of the flexure hinge, respectively, and the rotational stiffness and tensile stiffness of the straight-arm flexure hinge are and , respectively. Then, the torque and force of the flexure hinge have the following relationship with the deformation:
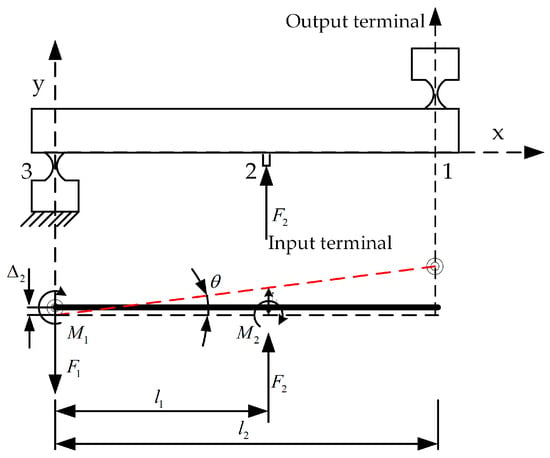
Figure 4.
Force of the lever mechanism.
In Equation (3), is the Young’s modulus of the material, is the width of the hinge, is the length of the hinge, and is the thickness of the hinge. When the lever rotates the angle, it has the following relationship with the hinge rotation angle:
When the flexible hinges at point 1 and point 2 have equal rotational stiffness, then the equilibrium equation for point 3 can be listed.
When the displacement is applied in the vertical direction at point 2, the hinge 2 is compressed to produce the shape variable , and the hinge 3 rotates to produce the offset , where and are the effective input displacement and the actual output displacement, respectively, with the following relationship:
The collation gives the amplification of the lever mechanism as
According to Equation (11), it can be seen that the amplification of the lever mechanism is mainly affected by the tensile stiffness of the hinge, the rotational stiffness , and the lever length. Therefore, reasonable optimization of the structural parameters of the lever mechanism can make the lever mechanism have a better amplification effect.
In the case of a constant hinge size, the relationship between the leverage length of the lever mechanism and the magnification is shown in Figure 5. When the leverage length gradually increases, the magnification gradually decreases. When the leverage length gradually increases, the magnification gradually increases. The piezoelectric-driven micro-positioning platform should have a structural size that is not too large to avoid increasing its mass and volume. The length of the final lever and lever is 47 mm and 82 mm, respectively, and then the size parameters of the hinges , , , and are brought into Equation (11) to obtain the magnification of the lever mechanism.
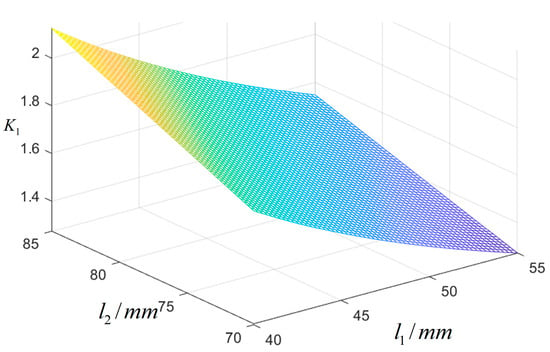
Figure 5.
The relationship between the leverage amplification ratio and leverage length.
3.2. Structure Design of the Compound Bridge Displacement Amplification Mechanism
The combined displacement amplification mechanism is composed of a lever mechanism and a compound bridge mechanism in series. Therefore, it is necessary to analyze the magnification of the compound bridge mechanism. The structural diagram and the force diagram are shown in Figure 6 and Figure 7, respectively.
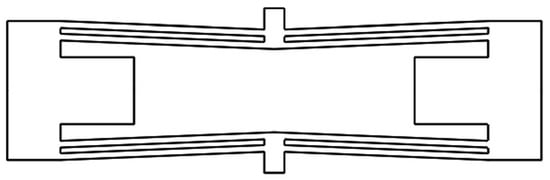
Figure 6.
Structure of the compound bridge displacement amplification mechanism.
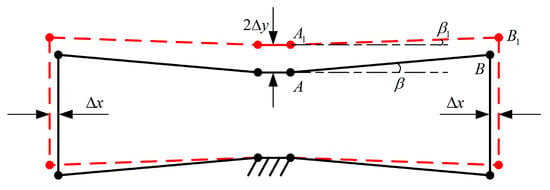
Figure 7.
Force of the compound bridge displacement amplification mechanism.
In Figure 7, the black solid line is the initial position before the force deformation of the composite bridge mechanism, and the red dotted line is the position after the force deformation. and are the two endpoints of the compound bridge displacement amplification mechanism. The angle between the long straight beam flexible hinge and the horizontal direction before the movement is . When the two ends of the piezoelectric ceramic actuator output displacement , respectively, the compound bridge mechanism outputs the amplified input displacement at , and the output displacement is . The angle between the long straight beam flexure hinge that reaches the new equilibrium position and the horizontal direction is , and the angle of rotation at points and is
Figure 8 shows the force analysis results of one-eighth of the compound bridge mechanism. From the moment and moment act on the flexible hinges and , respectively, it can be obtained that
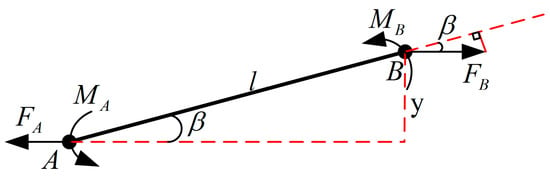
Figure 8.
The force of one-eighth of the compound bridge mechanism.
The A point of the flexible hinge is constrained. According to the force balance, the force is decomposed into the force perpendicular to the rod and the force along the rod direction, and the tensile stiffness of the hinge can be obtained:
Force balance equation of one-eighth of the compound bridge mechanism:
In the above formula, is the moment of inertia, E is the Young’s modulus of the material, is the rotational stiffness, is the tensile length of the flexible hinge, and is the length of the flexible hinge. According to the principle of virtual work, it can be obtained:
According to Figure 8, we can see that
Both sides of the equation are differentiated and replaced by small increments,
Substituting Equations (14) and (15) yields
And the magnification of the compound bridge mechanism is
According to Equation (24), it can be seen that the magnification of the bridge displacement amplification mechanism is mainly affected by the thickness , length , and tilt angle of the hinge. As shown in Figure 9, when the tilt angle of the flexure hinge gradually increases, the magnification first increases rapidly and then decreases slowly. When the length of the flexible hinge increases gradually, the magnification also increases gradually. When the tilt angle
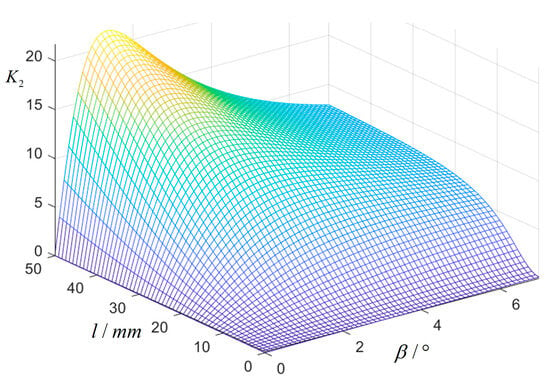
Figure 9.
Relationship between the magnification ratio of the compound bridge mechanism and hinge parameters.
Its magnification is the largest. Combined with the engineering practice, the inclination angle of the flexible hinge
And the length of the flexible hinge,
Is finally selected. Finally, the theoretical magnification of the compound bridge mechanism:
According to the Formulas (12) and (28), the overall magnification factor of the double-bridge combined lever-type displacement amplification mechanism is
3.3. Design of the Flexible Hinge
The flexible hinge has the advantages of a compact structure, no lubrication, no transmission gap, and no friction []. It can also provide the appropriate preload to avoid the gap caused by the tensile stress of the piezoelectric ceramic actuator. The elastic deformation of its relatively weak part is used to realize the transmission of motion, which is widely used in ultra-high precision positioning platforms []. Flexure hinges can be divided into uniaxial flexure hinges, universal flexure hinges, and biaxial flexure hinges according to their functions (see Figure 10a, Figure 10b, and Figure 10c, respectively). The hinge connected to the moving platform needs to use multi-axis hinges. In order to effectively use space to reduce the overall size, the traditional two-axis hinge is improved to a new two-axis flexible hinge (see Figure 10d).
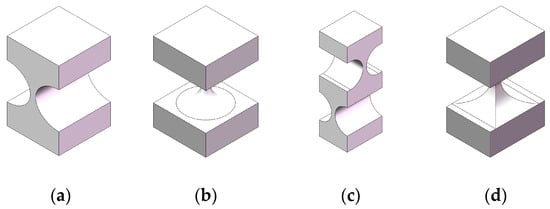
Figure 10.
The types of flexible hinges are: (a) single-axis flexure hinge; (b) universal flexure hinge; (c) double-axis flexure hinges; and (d) a new type of biaxial flexible hinge, proposed in this paper.
The notch shape of the flexure hinge has an important influence on the accuracy, life, and output displacement of the flexure hinge. According to the characteristics of its cross-section shape, the uniaxial flexible hinge unit can be mainly divided into four different hinge types []: straight beam type, semi-circular type, elliptical type, and hyperbolic type (see Figure 11a, Figure 11b, Figure 11c, and Figure 11d, respectively).
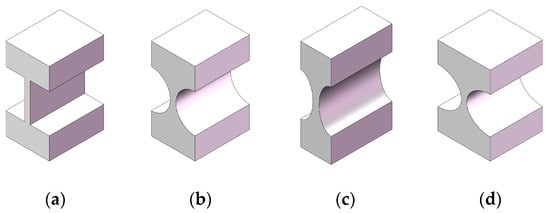
Figure 11.
The types of flexible hinges are: (a) straight beam type; (b) semi-circular type; (c) elliptic type; and (d) hyperbolic type.
One end of the flexible hinges with four different notch contour shapes is constrained, and the other end has applied to it a force of 0 to 70 N and a step of 10 N, respectively. Taking the output displacement of different flexure hinges as the research target, a three-dimensional model of flexure hinges is established. In the case of each parameter being unchanged, only the shape of the flexible hinge incision is changed, and the three-dimensional model of the flexible hinge is imported into ANSYS/workbench for analysis. The material library of ANSYS/workbench does not have 7075 aluminum alloy. Firstly, the material properties of 7075 aluminum alloy are customized. The material properties are shown in Table 1.

Table 1.
Performance parameters of different materials.
The analysis results are shown in Figure 12.

Figure 12.
Stress analysis of (a) straight beam-type flexible hinges; (b) semi-circular-type flexible hinges; (c) elliptic-type flexible hinges; and (d) hyperbolic-type flexible hinges.
The analysis results are shown in Figure 12. It can be seen from Figure 12 that under the same force, the maximum stress concentration is the straight beam flexure hinge, but it is far less than the yield strength of 7075-T651 aviation aluminum.
It can be seen from Figure 13 that there is a linear relationship between the elastic deformation and the input force of the four different flexible hinges. In the case of the same input force, the deformation of the straight beam flexure hinge is the largest, followed by the elliptical flexure hinge, while the hyperbolic and semi-circular flexure hinges are relatively small. Therefore, the straight beam flexible hinge is used as the flexible hinge in the displacement amplification mechanism.
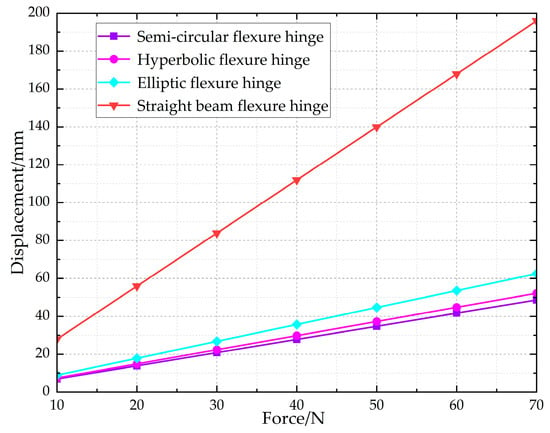
Figure 13.
The relationship between the output displacement and input force of different types of flexure hinges.
4. Simulation Analysis and Experimental Verification of the Piezoelectric Drive Platform
4.1. Simulation Analysis of the Output Performance of the Piezoelectric Drive Platform
The three-dimensional model of the piezoelectric drive micro-positioning platform is imported into ANSYS for simulation analysis. The material is 7075-T651 aviation aluminum. Firstly, the bottom of the fixed platform is fixed, and the connecting blocks at the upper end of the three displacement amplification mechanisms are connected to the moving platform through M4 screws. The preload of each screw is 800 N. The connecting block at the lower end is connected to the fixed platform through M4 screws, and the preload of each screw is 1200 N.
When the two ends of the installation end face of the three displacement amplification mechanisms are input 25 μm, the piezoelectric-driven micro-positioning platform will move and output in the z-direction. The simulation results are shown in Figure 14a,b. The maximum output displacement of the moving platform of the piezoelectric drive micro-positioning platform in the z-direction is about 804 μm, and the displacement magnification is 16.08, which has a large stroke.
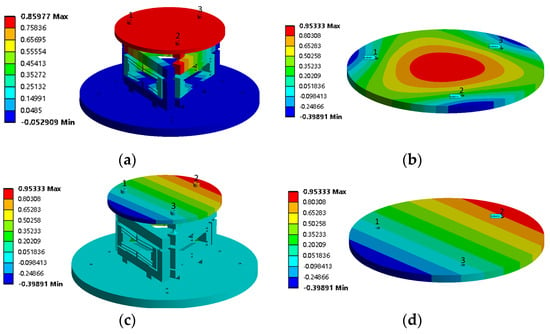
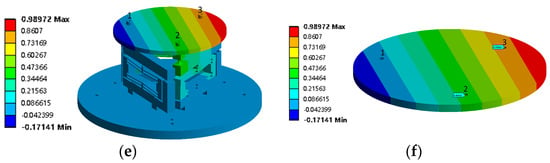
Figure 14.
Platform simulation output. Points 1, 2 and 3 are the displacement output points of the displacement amplification mechanism 1, 2 and 3 respectively. (a) Overall output in the z−direction; (b) z−direction moving platform output; (c) rotating the whole output around x; (d) rotating the platform output around x; (e) rotating the whole output around y; and (f) rotating the platform output around y.
When 25 μm is input at both ends of the mounting end face of the No.2 piezoelectric ceramic actuator, the piezoelectric drive micro-positioning platform will rotate around the x-axis. The simulation results are shown in Figure 14c,d. The maximum output displacement of the moving platform at point 2 connected to the No.2 displacement amplification mechanism is 804 μm, which is converted into a rotation angle of 0.665°. At the same time, there are slight coupling phenomena at point 1 and point 3.
When 12.5 μm and 25 μm are input at both ends of the mounting end faces of No.2 and No.3 piezoelectric ceramic actuators, the piezoelectric drive micro-positioning platform will rotate around the y-axis. The simulation results are shown in Figure 14e,f. The maximum output displacement of the moving platform at point 3 is 799 μm, and the output displacement at point 2 is 404 μm. According to the formula, it is converted into a rotation angle, which is 0.572°. At the same time, it can be seen that there is also a slight coupling at point 1.
4.2. Piezoelectric Drive Platform Output Experiment
In order to test the output of the piezoelectric-driven micro-positioning platform, an experimental test system consisting of a computer, a drive power supply, a micro-positioning platform, a displacement transducer, a piezoelectric ceramic driver, and a dspace1104 controller is constructed, as shown in Figure 15.
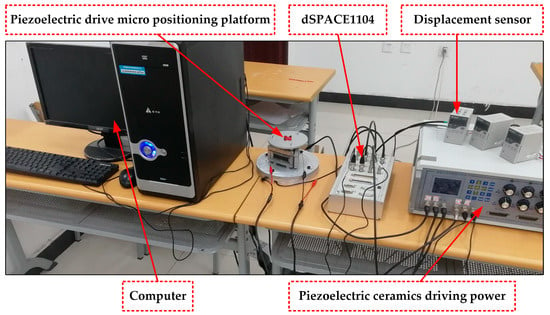
Figure 15.
Composition of the experimental system.
The material of the micro-positioning platform is 7075-T651 aluminum alloy. The processing method is slow-speed wire cutting processing. The piezoelectric stack actuator type-RP150/10×10/58 supply from Harbin Rongzhi Naxin Technology Co., Ltd. (Harbin, China) was used. The driving voltage of the actuator is 0–150 V. The maximum load displacement of the actuator is 50 μm. The response frequency of the actuator is 3000 Hz. The piezoelectric constant is
Realization of control schemes on the computer used MATLAB/Simulink(R2018a) and controldesk 6.4 software. The computer generates input signals and transmits them to the controller. The controller is dSPACE1104, produced by the dSPACE Ltd. in Paderborn, Germany. The dSPACE1104 controller is responsible for sending drive signals and receiving acquisition signals. The drive power supply is RH13, produced by the Harbin Rongzhi Nanxin Technology Co., Ltd. in Harbin, China. The analog signal is amplified and output to the piezoelectric stack actuator through the voltage and power amplifier circuit inside the power supply. The sensor adopts the Keanes EX-110 V eddy current displacement sensor, the amplification unit is EX-V02, the range is 0–2 mm, the resolution is 1 μm, and the maximum sampling frequency is 40,000 times per second. The sensor collects the signal and processes it before feeding it to the dSPACE1104 controller. The controller feeds the signal into the computer, which displays the signal in the controldesk software.
According to the experimental test system shown in Figure 15, the verification analysis is carried out. The maximum displacement output result is shown in Figure 16.
Figure 16.
Maximum displacement output experiment of (a) the z-direction; (b) around the x-axis; and (c) around the y-axis.
The maximum output experimental test is carried out in the z-direction. From 0 to 150 V and 150 to 0 V, respectively, the increment of 15 V is applied to the piezoelectric actuator. The sensor is used to detect the output of the moving platform. The relationship between the output displacement and the corresponding voltage is shown in Figure 16a. In the figure, the step-up curve does not coincide with the step-down curve, and there is an obvious hysteresis phenomenon. The maximum output displacement in the z-direction is 759 μm. The maximum hysteresis occurs at 30 V voltage, and the maximum hysteresis displacement is 64 μm.
Similarly, the maximum output experimental test is performed on the rotation around the x/y axis. The relationship between the rotation angle of the x/y axis and the corresponding voltage is shown in Figure 16b and Figure 16c, respectively. It can be seen from Figure 16b,c that the step-up curve does not coincide with the step-down curve, and has obvious hysteresis. The maximum output angle around the x-axis is 0.649°, and the maximum output angle around the y-axis is 0.534°. When the loading voltage is 30 V, the hysteresis angle around the x-direction is the largest, which is 0.064°. When the loading voltage is 15 V, the hysteresis angle around the y-direction is the largest, which is 0.065°.
Table 2 shows the comparison of the maximum output results of the simulation and experiment in three directions of the piezoelectric drive micro-positioning platform. It can be seen from the table that the maximum error between the simulation analysis results and the experimental test results in the z-direction is 64 μm, and the maximum relative error is 5.6%. The maximum error in the rotation direction around the x-axis is 0.016°, and the maximum relative error is 2.4%. The maximum error in the rotation direction around the y-axis is 0.038°, and the maximum relative error is 6.6%.

Table 2.
Comparative analysis of platform output simulation and experiment.
The dynamic output performance of the platform is experimentally verified according to the experimental test system shown in Figure 15. The experimental results are shown in Figure 17.
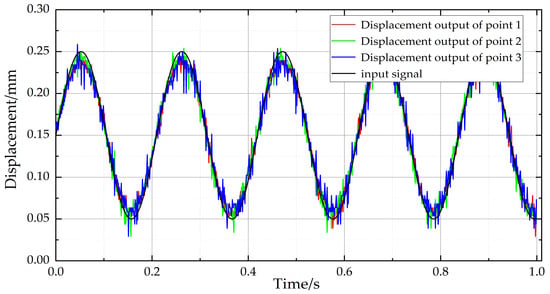
Figure 17.
4.75 Hz sinusoidal closed-loop experiment in the z-direction.
The micro-positioning platform achieves output in different directions by controlling the output displacements of the three displacement amplification mechanisms. Therefore, experiments are conducted in the z-direction to verify the dynamic output performance of the micro-positioning platform. The closed-loop control scheme is built in MATLAB/simulink and controldesk software. The input signal is set to be the sinusoidal signal with an amplitude of 50 μm, a frequency of 4.75 Hz, and a bias of 150 μm. From the experimental results, it can be seen that the output displacement of the platform is basically the same as the input signal.
5. Discussion
Multi-degree-of-freedom micro-positioning stages are indispensable key components for the machining of micro-complex parts. In this paper, a novel three-degree-of-freedom piezoelectric-driven micro-positioning platform is proposed, its structure is designed and optimized, the output simulation is carried out by using ANSYS/workbench, and an experimental system is built to verify its maximum output. Compared with the current existence of the same level of the three-degree-of-freedom piezoelectric-driven micro-positioning platform, the three-degree-of-freedom piezoelectric-driven micro-positioning platform designed in this paper has the advantages of a compact structure, a large output stroke, multiple rotational degrees of freedom, and a simple structure of the displacement amplification mechanism.
Due to the above advantages of the platform and the advantages of piezoelectric ceramics itself such as fast response speed, the platform is suitable for micro-fine EDM machining of shaped holes, which provides a new way of thinking about the driving device of electrodes for EDM machine tools. Meanwhile, the new biaxial flexible hinge designed in this paper provides a new idea for the miniaturization of micro-positioning platforms containing biaxial flexible hinges. Despite the contributions of the research in this text, there are limitations.
First, in this paper only the maximum output and dynamic output of the test bed is experimentally verified. Other properties of the test stand are subject to further experimental verification. Second, this paper does not conduct controlled experiments on the test bed to be verified subsequently. Last, the compensation of the inherent hysteresis characteristics of piezoelectric ceramics is not addressed in this paper and is to be investigated in subsequent work. Overall, the three-degree-of-freedom piezoelectric-driven micro-positioning platform designed in this paper is still a long way from practical application.
6. Conclusions
In this paper, a new type of three-degree-of-freedom piezoelectric drive micro-positioning platform is designed. The driving element adopts piezoelectric ceramics, the transmission mechanism adopts flexible hinges, and the displacement amplification mechanism adopts a two-stage amplification mechanism composed of a lever mechanism and a compound bridge mechanism. The actual magnification can reach 15.18-times. Through the theoretical analysis of the combined displacement amplification mechanism and the optimization of the structure size, the magnification is determined. The maximum output simulation analysis of the three degrees of freedom of the micro-positioning platform is carried out by using ANSYS/workbench (2022 R1), and the experimental test system is built for experimental verification.
The comparison between simulation results and experimental results shows that the maximum output displacement in the z-direction of the micro-positioning platform designed in this paper is 759 μm, the maximum rotation angle around the x-axis is 0.649°, and the maximum rotation angle around the y-axis is 0.534°; the maximum errors in the three degrees of freedom are 64 μm, 0.016°, and 0.038°, respectively. The corresponding maximum relative errors are 5.6%, 2.4%, and 6.6%, respectively. The reliability of the theoretical design is proved, and the design goal of a small size and large stroke is realized. The results of following experiments prove that the platform has a good dynamic output performance and fast response speed, which theoretically can meet the requirements of EDM.
The focus of future work is mainly concentrated on both the validation of the other properties of the test rig and the compensation methods for the inherent hysteresis characteristics of piezoelectric ceramics. Therefore, the next plan is to verify the other properties of the test stand and to use composite control to solve the accuracy problem caused by the inherent hysteresis characteristics of piezoelectric ceramics.
Author Contributions
Conceptualization, methodology, validation, formal analysis, C.Z.; writing—original draft preparation, data processing, Z.L.; funding acquisition, project administration, J.J.; supervision, F.S. and H.Z.; visualization, writing—review and editing, F.X. and X.Z. resources, L.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research is supported by the National Natural Science Fund of China, grant number 52375258, 52005345, and 52005344; the National Key Research and Development Project, grant number, 2020YFC2006701; the Scientific Research Fund Project of Liaoning Provincial Department of Education, grant number LJKMZ20220506, LJKMZ20220460, and JYTMS20231191; the Major Project of the Ministry of Science and Technology of Liaoning Province, grant number 2022JH1/10400027; and the Key Project of the Ministry of Science and Technology of Liaoning Province, grant number 2022JH1/10800081).
Data Availability Statement
Data are contained within this article.
Acknowledgments
We thank S.W. (Shuo Wang) and Y.H. (Yansong Hao) for their suggestions and recommendations.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Mohith, S.; Upadhya, A.R.; Navin, K.P.; Kulkarni, S.M.; Rao, M. Recent trends in piezoelectric actuators for precision motion and their applications: A review. Smart Mater. Struct. 2021, 30, 013002. [Google Scholar] [CrossRef]
- Duan, Q.R.; Zheng, Y.J.; Jin, J.; Hu, N.D.; Zhang, Z.L.; Hu, H.P. Design and Experimental Study of a Stepping Piezoelectric Actuator with Large Stroke and High Speed. Micromachines 2023, 14, 267. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.X.; Deng, J.; Su, Q. Review on Multi-Degree-of-Freedom Piezoelectric Motion Stage. IEEE Access 2018, 6, 59986–60004. [Google Scholar] [CrossRef]
- Shi, Y.L.; Zhao, C.S. Simple new ultrasonic piezoelectric actuator for precision linear positioning. J. Electroceram. 2012, 28, 233–239. [Google Scholar] [CrossRef]
- Tian, X.Q.; Zhang, B.R.; Liu, Y.X.; Chen, S.; Yu, H.P. A novel U-shaped stepping linear piezoelectric actuator with two driving feet and low motion coupling: Design, modeling and experiments. Mech. Syst. Signal Process. 2019, 124, 679–695. [Google Scholar] [CrossRef]
- Berry, D.; Vo, T.V.K.; Li, K.H.H.; Lubecki, T.M.; Gupta, A. Progressing towards high performance non-resonant piezoelectric stepping actuators. Sens. Actuators A Phys. 2023, 358, 114439. [Google Scholar] [CrossRef]
- Chang, S.J.; Chen, J. Design and Fabrication of the Large Thrust Force Piezoelectric Actuator. Adv. Mater. Sci. Eng. 2013, 2013, 912587. [Google Scholar] [CrossRef]
- Delibas, B.; Koc, B. A Method to Realize Low Velocity Movability and Eliminate Friction Induced Noise in Piezoelectric Ultrasonic Motors. IEEE/ASME Trans. Mechatron. 2020, 25, 2677–2687. [Google Scholar] [CrossRef]
- Yu, Y.; Gao, Q.; Qiao, G.D.; Zhang, X.S.; Lu, X.H.; Cheng, T.H. A direction-guidance hybrid excitation method for inertial flexible hinge piezoelectric actuator with high speed performance. Sens. Actuators A Phys. 2020, 314, 112229. [Google Scholar] [CrossRef]
- Jin, H.N.; Gao, X.Y.; Ren, K.L.; Liu, J.F.; Qiao, L.; Liu, M.Z.; Chen, W.; He, Y.H.; Dong, S.X.; Xu, Z.; et al. Review on Piezoelectric Actuators Based on High-Performance Piezoelectric Materials. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2022, 69, 3057–3069. [Google Scholar] [CrossRef]
- Wu, Z.Y.; Xu, Q.S. Design, Fabrication, and Testing of a New Compact Piezo-Driven Flexure Stage for Vertical Micro/Nanopositioning. IEEE Trans. Autom. Sci. Eng. 2019, 16, 908–918. [Google Scholar] [CrossRef]
- Hussein, H.; Damdam, A.; Ren, L.J.; Charrouf, Y.O.; Challita, J.; Zwain, M.; Fariborzi, H. Actuation of Mobile Microbots: A Review. Adv. Intell. Syst. 2023, 5, 2300168. [Google Scholar] [CrossRef]
- Jia, B.T.; Wang, L.; Wang, R.F.; Jin, J.M.; Wu, D.W. Theoretical modeling and experimental investigation on a novel screwed-type piezoelectric focusing mechanism for space cameras. Mech. Syst. Signal Process. 2022, 171, 108844. [Google Scholar] [CrossRef]
- Shivashankar, P.; Gopalakrishnan, S. Review on the use of piezoelectric materials for active vibration, noise, and flow control. Smart Mater. Struct. 2020, 29, 053001. [Google Scholar] [CrossRef]
- Shao, Y.; Xu, M.L.; Song, S.Y.; Tian, Z.; Shao, S.B. Modeling and experiment of an inertial piezoelectric rotary actuator. Int. J. Appl. Electromagn. Mech. 2019, 59, 309–316. [Google Scholar] [CrossRef]
- Liu, Y.T. Recent Development of Piezoelectric Fast Tool Servo (FTS) for Precision Machining. Int. J. Precis. Eng. Manuf. 2024, 25, 851–874. [Google Scholar] [CrossRef]
- Lu, Y.; Chen, C.Z.; Zhu, J.Q. Design of a Focusing Mechanism Actuated by Piezoelectric Ceramics for TMA Telescope. Sensors 2023, 23, 4610. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.L.; Wei, Y.D.; Lou, J.Q.; Fu, L.; Fang, S. Design and control of a multi-DOF micromanipulator dedicated to multiscale micromanipulation. Smart Mater. Struct. 2017, 26, 115016. [Google Scholar] [CrossRef]
- Gao, X.Y.; Yang, J.K.; Wu, J.G.; Xin, X.D.; Li, Z.M.; Yuan, X.T.; Shen, X.Y.; Dong, S.X. Piezoelectric Actuators and Motors: Materials, Designs, and Applications. Adv. Mater. Technol. 2020, 5, 1900716. [Google Scholar] [CrossRef]
- Li, J.P.; Huang, H.; Morita, T. Stepping piezoelectric actuators with large working stroke for nano-positioning systems: A review. Sens. Actuators A Phys. 2019, 292, 39–51. [Google Scholar] [CrossRef]
- Wang, S.P.; Rong, W.B.; Wang, L.F.; Xie, H.; Sun, L.N.; Mills, J.K. A survey of piezoelectric actuators with long working stroke in recent years: Classifications, principles, connections and distinctions. Mech. Syst. Signal Process. 2019, 123, 591–605. [Google Scholar] [CrossRef]
- Li, J.; Che, F.; Deng, J.; Chen, W.S.; Liu, J.K.; Liu, Y.X. A linear ultrasonic motor with a hollowed and symmetrical stator. Int. J. Mech. Sci. 2024, 262, 108718. [Google Scholar] [CrossRef]
- Wang, L.; Liu, J.K.; Liu, Y.X.; Tian, X.Q.; Yan, J.P. A novel single-mode linear piezoelectric ultrasonic motor based on asymmetric structure. Ultrasonics 2018, 89, 137–142. [Google Scholar] [CrossRef] [PubMed]
- Yan, J.P.; Liu, Y.X.; Liu, J.K.; Xu, D.M.; Chen, W.S. The design and experiment of a novel ultrasonic motor based on the combination of bending modes. Ultrasonics 2016, 71, 205–210. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.F.; Gao, X.Y.; Jin, H.N.; Ren, K.L.; Guo, J.Y.; Qiao, L.; Qiu, C.R.; Chen, W.; He, Y.H.; Dong, S.X.; et al. Miniaturized electromechanical devices with multi-vibration modes achieved by orderly stacked structure with piezoelectric strain units. Nat. Commun. 2022, 13, 6567. [Google Scholar] [CrossRef] [PubMed]
- Hunstig, M. Piezoelectric Inertia MotorsA Critical Review of History, Concepts, Design, Applications, and Perspectives. Actuators 2017, 6, 7. [Google Scholar] [CrossRef]
- Huang, H.H.; Wang, L.F.; Wu, Y. Design and Experimental Research of a Rotary Micro-Actuator Based on a Shearing Piezoelectric Stack. Micromachines 2019, 10, 96. [Google Scholar] [CrossRef]
- Zeng, P.; Sun, S.J.; Li, L.; Xu, F.; Cheng, G.M. Design and testing of a novel piezoelectric micro-motor actuated by asymmetrical inertial impact driving principle. Rev. Sci. Instrum. 2014, 85, 035002. [Google Scholar] [CrossRef] [PubMed]
- Sun, W.X.; Xu, Z.; Wang, K.F.; Li, X.; Tang, J.Y.; Yang, Z.J.; Huang, H. An Impact Inertial Piezoelectric Actuator Designed by Means of the Asymmetric Friction. IEEE Trans. Ind. Electron. 2023, 70, 699–708. [Google Scholar] [CrossRef]
- Zhang, S.J.; Liu, Y.X.; Deng, J.; Tian, X.Q.; Gao, X. Development of a two-DOF inertial rotary motor using a piezoelectric actuator constructed on four bimorphs. Mech. Syst. Signal Process. 2021, 149, 107213. [Google Scholar] [CrossRef]
- Koc, B.; Delibas, B. Impact Force Analysis in Inertia-Type Piezoelectric Motors. Actuators 2023, 12, 52. [Google Scholar] [CrossRef]
- Wang, L.; Chen, W.S.; Liu, J.K.; Deng, J.; Liu, Y.X. A review of recent studies on non-resonant piezoelectric actuators. Mech. Syst. Signal Process. 2019, 133, 106254. [Google Scholar] [CrossRef]
- Ma, X.F.; Liu, Y.X.; Deng, J.; Gao, X.; Cheng, J.F. A compact inchworm piezoelectric actuator with high speed: Design, modeling, and experimental evaluation. Mech. Syst. Signal Process. 2023, 184, 109704. [Google Scholar] [CrossRef]
- Bai, D.; Deng, S.L.; Li, Y.T.; Li, H. A novel inchworm piezoelectric actuator with rhombic amplification mechanism. Sens. Actuators A Phys. 2023, 360, 114515. [Google Scholar] [CrossRef]
- Yu, S.M.; Liang, J.Y.; Yang, F.; Wang, H.T.; Liu, X.L.; Xu, C.; Wang, Z.; Xu, D.M. A novel inchworm piezoelectric actuator using two-stage amplification mechanism with high speed: Design, modeling, and experimental evaluation. Smart Mater. Struct. 2023, 32, 055020. [Google Scholar] [CrossRef]
- Schlinquer, T.; Homayouni-Amlashi, A.; Rakotondrabe, M.; Mohand-Ousaid, A. Design of Piezoelectric Actuators By Optimizing the Electrodes Topology. IEEE Rob. Autom. Lett. 2021, 6, 72–79. [Google Scholar] [CrossRef]
- Li, Z.; Su, Z.R.; Zhao, L.; Han, H.T.; Guo, Z.Y.; Zhao, Y.Y.; Sun, H.X. Design and Locomotion Study of Stick-Slip Piezoelectric Actuator Using Two-Stage Flexible Hinge Structure. Micromachines 2021, 12, 154. [Google Scholar] [CrossRef] [PubMed]
- Huang, W.Q.; Lian, J.K.; Chen, M.Y.; An, D.W. Bidirectional Active Piezoelectric Actuator Based on Optimized Bridge-Type Amplifier. Micromachines 2021, 12, 1013. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.; Zhao, J.G.; Shen, X.; Xiao, Q.; Huang, J.; Wang, Y. Design, Modeling, and Testing of a Novel XY Piezo-Actuated Compliant Micro-Positioning Stage. Micromachines 2019, 10, 581. [Google Scholar] [CrossRef]
- Sun, F.; Hao, Y.S.; Xu, F.C.; Jin, J.J.; Li, Q.; Tong, L.; Zhang, M.; Zhang, X.Y. Proposal of an Equal-Stiffness and Equal-Stroke 2D Micro-Positioning Platform Driven by Piezoelectric Actuators. Actuators 2020, 9, 47. [Google Scholar] [CrossRef]
- Na, T.W.; Choi, J.H.; Jung, J.Y.; Kim, H.G.; Han, J.H.; Park, K.C.; Oh, I.K. Compact piezoelectric tripod manipulator based on a reverse bridge-type amplification mechanism. Smart Mater. Struct. 2016, 25, 095028. [Google Scholar] [CrossRef]
- Cui, F.N.; Li, Y.M.; Qian, J.N. Development of a 3-DOF Flexible Micro-Motion Platform Based on a New Compound Lever Amplification Mechanism. Micromachines 2021, 12, 686. [Google Scholar] [CrossRef]
- Iqbal, S.; Malik, A. A review on MEMS based micro displacement amplification mechanisms. Sens. Actuators A Phys. 2019, 300, 111666. [Google Scholar] [CrossRef]
- Wei, H.X.; Tian, Y.L.; Zhao, Y.J.; Ling, M.X.; Shirinzadeh, B. Two-axis flexure hinges with variable elliptical transverse cross-sections. Mech. Mach. Theory 2023, 181, 105183. [Google Scholar] [CrossRef]
- Yan, L.; Jiang, A.N.; Jiang, F.; Liu, G.D.; Wang, F.Z.; Wu, X. Design and Performance Analysis of a Micro-Displacement Worktable Based on Flexure Hinges. Micromachines 2022, 13, 518. [Google Scholar] [CrossRef] [PubMed]
- Qiu, L.F.; Liu, Y.S.; Yu, Y.; Bai, Y.T.B. Design and stiffness analysis of a pitch-varying folded flexure hinge (PFFH). Mech. Mach. Theory 2021, 157, 104187. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).