Abstract
This paper addresses the active target protection problem in a three-player (Target–Attacker–Defender, TAD) conflict by proposing a cooperative integrated guidance and control (IGC) strategy. Unlike previous studies that have designed guidance and control loops separately, this work establishes an IGC model by linearizing both the translational motion and the rotational motion of the vehicles, thereby generating actuator commands directly. This model integrates the kinematics and short-period dynamics, providing a more comprehensive and accurate representation of the vehicles’ characteristics. Based on the linearization and order reduction, differential game theory and the sweep method are employed to derive and analytically solve the Riccati differential equation, yielding an optimal control strategy with an explicit expression. The theoretical rigor of the proposed approach is ensured through a proof of optimality sufficiency. Furthermore, factors influencing the computational accuracy of the Riccati equation solution, including the singular values of the control matrix and condition numbers of the solution matrix, are analyzed. Taking into account the dynamic response and limitations of the actuators, numerical simulations demonstrate the effectiveness and superiority of the proposed IGC strategy in intercepting the attacker and protecting the target compared to traditional separated guidance and control designs.
1. Introduction
Differential game theory, a branch of mathematical control theory, explores the strategic interactions in dynamic settings where players’ decisions influence the outcome over time [1]. One of the pivotal applications of differential games is in pursuit–evasion scenarios, which involve multiple agents with conflicting objectives. These scenarios are not only academically intriguing but have substantial practical implications in areas such as military tactics, security systems, and autonomous vehicle navigation [2,3,4].
Among the various configurations of pursuit–evasion games, three-player conflicts involving a Target, Attacker, and Defender (TAD) present a particularly complex and rich problem space [5,6,7]. In the classic two-player pursuit–evasion game, the scenario typically involves an attacker pursuing a target whose primary strategy is passive evasion. Instead, in TAD configurations the target benefits from the active protection provided by the defender, whose role is to intercept or obstruct the attacker’s efforts.
As a multi-agent system, with the inherent dynamics and interdependencies, the TAD conflict has garnered increasing attention due to its relevance to real-world scenarios in which valuable assets are actively defended [8]. Garcia et al. analyzed the game’s dynamics, focusing on the regions where the attacker prevails and the defender’s optimal interception strategies [9]. Their subsequent work in [10] developed optimal strategies for the attacker while ensuring that solutions were aligned with the Hamilton–Jacobi–Isaacs equation. A barrier analysis was introduced in [11] to delineate winning regions for both the attacker and the target–defender team, facilitating strategic decision-making through explicit policy and geometric analysis. Subsequent research explored stage-based strategies for a fast nonsuicidal attacker while adjusting tactics based on capture radii [12]. In [13], the authors presented a geometric interception strategy using the Apollonius circle, offering a practical approach for a slower defender to intercept a faster attacker.
The insights gained from TAD scenarios significantly enhance active protection systems for aerial vehicles, improving their effectiveness and survivability in hostile environments. The work in [14] optimized control inputs for the target and the defender, allowing effective interception even with slower defenders. The guidance law for defense missiles of nonmaneuverable aircraft was developed in [15], demonstrating superiority in non-coplanar engagements through high-fidelity simulations. Similar work was presented in [16], focusing on an air combat scenarios in which a defending missile aims to maximize the separation between a target aircraft and an attacking missile at the point of interception.
However, the aforementioned modeling approach in aerial pursuit–evasion games often simplifies the dynamics by directly using heading angles as control inputs, overlooking critical factors such as turning radii and the dynamic response of the system to commands, such as oscillations or delays. Additionally, these models tend to ignore the physical limitations of the maneuverability and actuators, which play a crucial role in the realistic implementation of control strategies. The oversimplified approach does not adequately leverage the general principles and knowledge of dynamics, and neglects the characteristics of aerial vehicles. As a result, the obtained strategies usually lack realistic feasibility. In fact, although there are nonlinear factors such as actuator saturation, aerial vehicles typically still exhibit pronounced linear characteristics, which form the classical foundation for the design of guidance and control systems [17,18]. It is essential for the design of guidance and control systems to include considerations of these linear characteristics along with the vehicle’s dynamic response processes.
This need for realistic modeling and design has led to the development of research that focuses on model linearization and order reduction. The prevailing research trend gravitates towards one-sided optimal control or differential games. The distinction lies in that optimal control theory-based guidance laws necessitate prior knowledge of the adversary’s control tactics. Although the reliance on prior information for one-sided optimization can be reduced through information sharing between the target and the defender [19], there are still challenges, such as the impracticality of deploying numerical optimization algorithms onboard [20,21]. Conversely, the differential game has attracted broader interest for its independence from presumptions regarding the opponent’s strategy [22]. The differential game can obtain the game strategy of the two opponents by finding the saddle point solution; under the condition of accurate modeling, this can guarantee the optimality of the strategy against the opponent’s arbitrary maneuver [23,24]. Considering the drawback that the control of linear quadratic differential game guidance law may exceed operational bounds, the bounded differential game was proposed and verified in a two-dimensional plane and three-dimensional space [25,26]. In addition, in order to be closer to the real combat scenarios, recent studies have accounted for constraints such as limited operational capabilities [27], state estimation under imperfect information through Kalman filtering [28], relative intercept angle limitations on attack protocols [24,29,30], cooperative multi-vehicle strategy against an active defense target [24,31], and weapon–target allocation strategies [32].
However, traditional active protection research has focused on designing guidance laws that generate acceleration commands without considering how these commands are effectively tracked by the autopilot. Such approaches overlook the control loop required to generate actuator commands. With the introduction of advanced guidance laws and increased confrontation, oversimplification can lead to significant distortion [33]. Moreover, in the endgame phase of engagements, where the relative motion between vehicles changes rapidly, the assumption of spectral separation between the guidance and control loops becomes untenable [34,35]. Therefore, integrated guidance and control (IGC) was proposed to address these issues by merging the guidance and control loops, thereby mitigating the negative impacts of their coupling [36,37]. IGC ensures that the commands sent to actuators are both feasible and effective within the physical constraints of the system. In the view of engineering designers, IGC is expected to significantly improve missile performance, resulting in lower weight and enhanced lethality [18]. In recent years, the development of IGC has progressed rapidly, with research increasingly focusing on a variety of advanced methods, including sliding mode control [38,39], back-stepping [40], robust control [41], and small-gain theorem [42], among others.
Building on the previously discussed challenges and advancements in three-player conflicts and IGC, this article aims to delve deeper into an IGC design specifically tailored for aerial vehicle active protection scenarios. We present an IGC model for active protection distinguished by the linearization of both the center of mass motion and rotation around the center of mass. Our approach leverages differential game theory and the sweep method to derive and solve the Riccati differential equation analytically. The main contributions of this paper are summarized as follows:
- Advanced IGC Modeling for Active Protection: An advanced modeling approach for active protection is introduced that uniquely combines linearization of both translational and rotational dynamics around the center of mass. Although the linearization technique is a well-established practice in aerial vehicle design, our contribution lies in applying this approach to the IGC design in a three-player conflict scenario. This modeling framework allows for a more comprehensive and accurate representation of the characteristics of aerial vehicles compared to previous studies.
- Analytical Derivation and Solution of Riccati Equation: Through the application of differential game theory and the sweep method, this study derives and solves the Riccati differential equation, providing an analytical expression for the optimal control strategy and in turn presenting possibilities for real-time onboard calculation.
- Theoretical Rigor in Solution Analysis: The theoretical rigor of the proposed approach is provided through a proof of optimality sufficiency. Additionally, we examine factors that influence the computational accuracy of the Riccati equation solution using singular values of the control matrix and condition numbers of the solution matrix.
The rest of the paper is organized as follows. In Section 2, we describe the three-player conflict in the IGC framework, focusing on model linearization and order reduction. Section 3 is dedicated to the derivation of the IGC active protection strategy. In Section 4, we conduct a theoretical analysis of the IGC strategy. Following this, Section 5 presents simulations to demonstrate the practical applicability and effectiveness of the strategy. Finally, Section 6 concludes the paper by summarizing the findings.
2. Problem Formulation
2.1. Nonlinear Engagement Model
In the TAD three-player conflict, the adversarial attacker aims at the target, which is protected by a defender aiming to intercept the incoming threat mid-course. In general, the target is weak in maneuvering and has difficulty avoiding being hit by the attacker through simple maneuvering strategies; thus, the target adopts an active defense strategy in order to survive.
As shown in Figure 1, the engagement is refined into a geometric representation within an inertial coordinate system . In the aerial conflict, each entity’s flight state is characterized by its flight path angle (), flight velocity (V), and actual acceleration (a), denoted by the respective subscripts A, T, and D for attacker, target, and defender. The engagement is divided into two distinct but interrelated processes: the attacker’s pursuit of the target () and the defender’s interception of the attacker to protect the target (). In these engagements, r stands for the distance between the respective vehicles, denotes the line-of-sight, and represents the line-of-sight angle. Specifically, , , and denote the respective derivatives of , , and r. Initial conditions at the start of the engagement are indicated by the subscript 0.
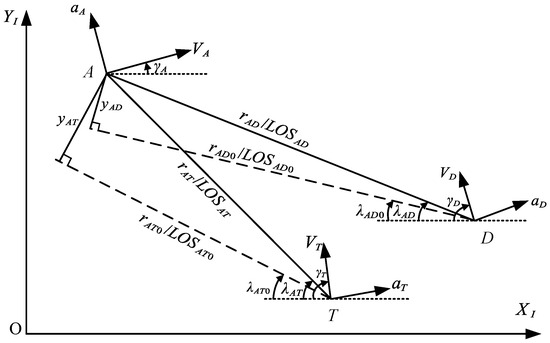
Figure 1.
Three-body confrontation engagement geometry.
As shown in Figure 1, the nonlinear engagement model of attacker–target and attacker–defender can be represented as
where A stands for the attacker and i represents the target or defender, i.e., .
The rate of change of the flight path angle for each vehicle can be expressed as
where represents the mass of the vehicle j and is the normal aerodynamic force acting on the airframe, which is a function of the angle of attack and the fin deflection from the actuator.
Unlike previous studies focusing solely on translational motion in active protection, the IGC design incorporates rotational kinematics and dynamics around the center of mass involving the pitch angle and pitch rate q. The angular acceleration is generated by the torque applied to the airframe divided by the moment of inertia . Thus, it is possible to obtain
Although the nonlinear differential Equations (1)–(3) can be solved numerically, adopting an analytical approach provides clearer insights and understanding of the engagement dynamics. To facilitate this, we linearize the equations around an operating condition, which allows for analysis and design based on linear systems theory.
2.2. Linearization and Order Reduction
To facilitate analysis of the engagement dynamics in the terminal phase, the model is simplified based on the following set of assumptions:
- Constant Velocity: The velocities of the entities are assumed to be constant.
- Co-planar Movement: The three entities are considered to move within the same plane; the defender is launched by the target, meaning that and coincide.
- Linear Plant Models: The dynamics of each entity are approximated as linear systems.
- Linearization of Collision Triangles: It is assumed that the two collision triangles can be linearized along their respective initial lines of sight (LOS).
The dynamics model of each vehicle can be represented by a linear equation of arbitrary order:
where represents the internal state variables of each vehicle, is the acceleration perpendicular to the initial line-of-sight direction, and is the corresponding control input.
In previous studies, vehicles described by Equation (4) have generally been simplified to ideal dynamics or first-order delay dynamics. Ideal dynamics implies that and . First-order delay dynamics implies that , , , and with the time constant of . In both cases, represents the command acceleration. We further extend the scope of Equation (4) to cover the short-period dynamics described by Equation (3) for the target and the defender [43], which means that
where the numerical coefficients are defined by
The target and defender are modeled as IGC configurations and the attacker is modeled with first-order lag dynamics. Choosing the state variables as , the equations of motion for the attacker to engage the target or defender can be expressed as
where
The symbols ∓ in Equation (8) correspond to and , respectively. For the target and the defender, the control input is defined as the fin deflection of the actuator . For the attacker, the control input is the commanded acceleration .
The time-to-go between the attacker–target pair and the defender–attacker pair is denoted by and , respectively. The time-to-go can be calculated by and , where the interception time is defined as
We assume that the engagement of the attacker with the defender precedes the engagement of the attacker with the target, i.e., and satisfy in the timeline. This is because once the attacker hits or misses the target, it means that the game is over and the defender is no longer needs to continue the engagement.
Therefore, unlike previous studies that only considered guidance loops, the linearization encompasses two aspects: linearization of the airframe and linearization of engagement geometry.
- Linearization of the airframe: Linearization of the airframe dynamics is typically performed around a trim condition, which represents a steady-state flight condition; in our case, this corresponds to flight at a constant velocity and a small angle of attack. This approach is widely accepted in aerospace control systems design, especially for short-period dynamics, as deviations from this trim condition during maneuvers are usually small enough to maintain the validity of the linear model.
- Linearization of engagement geometry: For the engagement geometry, we employ linearization around a nominal collision course. This approach is commonly used and justified in terminal guidance problems, particularly in the endgame phase, where the relative geometry changes are relatively small and can be approximated linearly.
This situation can be formulated as a three-player differential game between two opposing sides with different objectives. The cost function that we utilize incorporates both miss distance and energy consumption through a linear–quadratic (LQ) form, striking a balance between the two factors. This also means that it is a soft constraint, ensuring that the control effort does not exceed the maneuverability. The specific formulation of the cost function is as follows:
where and are non-negative weight coefficients related to miss distance and the coefficients and reflect the maneuverability of the target and defender relative to the attacker. When the target has weaker maneuverability compared to the attacker, takes a larger value; indicates that the target has no maneuverability. When the defender has stronger maneuverability compared to the attacker, takes a smaller value, with signifying strong maneuverability of the defender.
It is still difficult to obtain the analytical solution of the above linear optimal control problem, so reducing the model’s order is essential. In the context of guidance analysis, the zero-effort miss (ZEM) is a commonly used concept, which physically represents the miss distance of the interceptor if no maneuver is performed, i.e., the control command is zero from the current moment. From the perspective of signal processing, this is equivalent to the zero-input response of the linear system. Using the terminal projection transformation of the linear system, the ZEM and can be expressed as
where is a coefficient matrix and is the state transition matrix.
The derivatives of and with respect to time in compact matrix form are
where
Correspondingly, the cost function of the reduced-order differential game problem is provided by
where
3. Derivation of IGC Active Protection Strategy
The differential game approach is applied to solve for the optimal control of each vehicle. The Hamiltonian of the linearized system is
where stands for the introduced costates. According to the calculus of variations, by equating the derivatives of the Hamiltonian with respect to the players’ controllers to zero we obtain
It follows that in order to solve for the expression of the optimal control we need to obtain an expression for the costate . From the adjoint equation and the transversality condition, we have
As shown in Equation (20), the expression for includes and . However, unlike previous studies such as [22] which tackled more idealized dynamic models, the complexity inherent to the IGC problem precludes a straightforward analytical solution. Therefore, to address these challenges we adopt the sweep method to solve for the costates. We assume that can be written in the form of linear feedback of reduced-order states as
i.e.,
with the transversality condition
Taking the derivative of , as shown in Equation (21), yields
Next, incorporating the reduced-order dynamics of the system, represented by Equation (15), results in
Upon rearranging and simplifying the terms, we obtain the Riccati differential equation
Equation (26) characterizes the evolution of the matrix over time. The terms within the brackets represent the combined influence of the system dynamics and the control effort costs on the evolution of . However, the matrix in Equation (26) has four elements and the variables are coupled, which makes it impossible to solve it directly. In order to find the analytical expression for , the matrix is introduced to satisfy
where I is the identity matrix. Therefore, the derivative of can be expressed in terms of :
This leads to the fully decoupled matrix differential equation for :
This decoupled differential equation for is more tractable and its terms purely depend on the matrices , , , and , which are typically known from the system dynamics and cost function. The terminal condition for the matrix can be determined from the costate’s terminal condition stated in (23):
Correspondingly, the terminal condition for is provided by
This setup allows for backward integration from to the initial time while using to calculate , providing a method for determining across the engagement timeline.
In light of the computational challenges posed by backward integration and the specific representation of the state transition matrix in terms of time-to-go, it is useful to reverse the time in the differential equation for the matrix . Moreover, reversing the time allows for dynamic adjustment of control inputs based on changes in the engagement through state feedback, rather than relying on a precomputed offline . This adjustment leads to
Simultaneously, the terminal conditions in (31) are converted into initial conditions for the integration process in terms of . Thus, the problem is transformed into an initial value problem for system ordinary differential equations in a decoupled form. The decoupling facilitates solving for directly through indefinite integration, which in turn allows for determining the solution of the Riccati differential Equation (26).
Furthermore, in order to obtain the analytical expression of the optimal control it is necessary to solve for the relevant elements in Equation (16). Because in (7) is time-invariant, the state transition matrix can be solved by . To find the inverse of , we can augment the given matrix with the identity matrix and perform Gaussian elimination. By performing elementary row and column operations on the augmented matrix, we obtain
Thus, and in and can be given by
In order to solve the inverse Laplace transform of the above equation, the following transformation is provided:
where , . It should be noted that Equations (35)–(37) are not a partial fraction decomposition of the original fraction, as we have not found the roots of the denominator. The rational fractions in Equations (35)–(37) allow us to utilize the following inverse Laplace transform:
Let , and , ; then, the first row of the state transition matrix used to compute the ZEM and can be derived from the inverse Laplace transform lookup table, which can be represented as
and
Substituting and into and in (32), it can be found that the elements of share the following form and that the indefinite integral can be expressed in terms of elementary functions:
This indefinite integral can be obtained by expanding the square and employing general integration techniques.
At this point, we can obtain the expression of directly through an indefinite integral, thereby obtaining the solution of the Riccati equation.
4. Theoretical Analysis of IGC Active Protection Strategy
4.1. Saddle Point Sufficiency Proof
In the development of IGC strategies, establishing the optimality of a control solution is crucial. This not only ensures the effectiveness of the control in achieving its goals, thereby minimizing miss distance and control effort, it provides theoretical validation that the proposed solution indeed performs better than any other strategy under the given model assumptions. To this end, proving that a solution to the Riccati equation serves as a sufficient condition for the existence of an optimal saddle point solution is essential. Such a proof confirms that the derived control law is not just a feasible solution but the best possible strategy within the framework of the IGC problem [44].
Theorem 1.
The existence of a solution to the Riccati equation (Equation (26)) is a sufficient condition for the existence of a saddle point solution, and the control derived from the Riccati equation is optimal.
Proof.
Consider the reduced-order active protection problem defined by
subject to the dynamics
To analyze this, we construct the identity
Using the chain rule for differentiation, we obtain
Substituting and expanding within S, we obtain
From this, we can deduce that the performance index satisfies
The expression clearly shows that , indicating that the performance index is minimized for the optimal controls and , confirming the saddle point nature of the solution. This completes the proof. □
4.2. Analysis of the Invertibility of Matrix
The invertibility of the matrix is critical in solving the Riccati equation and ensuring the computation accuracy of the proposed strategy. The ill-conditioning of significantly impacts the numerical stability, especially during matrix inversion operations. Ill-conditioning refers to scenarios where small variations in inputs cause large changes in outputs, leading to significant numerical errors in calculations such as matrix inversion. An ill-conditioned can undermine the reliability of computing its inverse.
It can be seen through Equation (32) that are influenced by the matrices and , which incorporate control inputs from , , and . Significant differences in the control matrices can be amplified through quadratic operations in Equation (32), leading to wide disparities in the magnitudes of the elements in and exacerbating its ill-conditioning.
In practical terms, control inputs such as fin deflection and commanded accelerations differ fundamentally in scale and system impact. For example, a single-degree change in fin deflection might equate to a 20 change in acceleration. The difference in control efficiency affects how sensitive the system state is to increments in and .
In multiple-input–multiple-output (MIMO) systems, the disparity in control effectiveness across different actuators can be quantitatively expressed through the singular values of their control matrices. The largest singular value of control matrices offers a measure of the “control efficiency”, reflecting the sensitivity of the system’s state to changes in respective control inputs. This is because the largest singular value in a control matrix provides critical insight into the maximum stretch factor that the matrix imparts to any vector it multiplies.
To illustrate the relationship between matrix scaling and the largest singular values, we consider a scenario where the short-period dynamics parameters for the target and defender are taken from [45] and [17], respectively. We define the scaled control matrices as follows:
where is a scaling factor. The sensitivity of the system’s state to different control inputs is demonstrated by comparing the largest singular values of the control matrices under various scaling factors.
Figure 2 presents the variation of the largest singular value for each control matrix under different scaling factors. Given that the defender’s control input typically exhibits the highest control efficiency, we use the largest singular value of as the benchmark. The graph shows that the largest singular values approximate a linear relationship on a logarithmic scale. For the flight characteristics considered here, when the scaling factor for is about 10 and for about 250 the relationships satisfy
This finding suggests that the magnitude differences in control matrices must be considered when applying the IGC active protection strategy, as they directly affect the ill-conditioning of and potentially the robustness of the control solution.
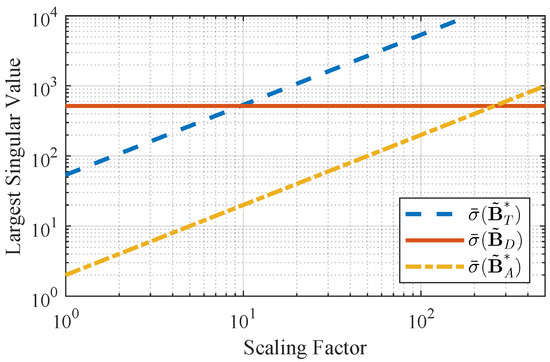
Figure 2.
Comparison of largest singular values of different control matrices.
Furthermore, in order to check the accuracy of the calculation for during the simulation, we introduce the condition number as a real-time monitor. The condition number of a matrix K is defined as
where is a norm of K. The condition number quantifies the sensitivity of the solution of a system of linear equations to changes in the input or errors in the data. A low condition number indicates that the matrix is well-conditioned, meaning that it is stable and reliable for numerical calculations. Conversely, a high condition number suggests that the matrix is ill-conditioned, which can lead to significant numerical errors in computations, especially inverses. Matrices with very high condition numbers may result in large errors in computed solutions, indicating that even small errors in data can lead to unreliable or incorrect results.
In Section 5, we demonstrate through specific examples how the methodologies proposed in this paper effectively reduce the condition number of matrix . By improving the conditioning of , we enhance the reliability and accuracy of the matrix inversion operations critical to the IGC active protection strategies.
4.3. Simplified IGC Active Protection Strategy
In the development of the IGC active protection strategy, while modeling both the target and the defender within the IGC framework is feasible, it tends to increase computational complexity and numerical instability. A more streamlined approach can be adopted by focusing the IGC model primarily on the defender.
In general, the defender exhibits more significant agility and dynamic response than the target in active protection scenarios. By concentrating the IGC model on the defender, we can effectively capture and manage these dynamics while reducing the model’s overall complexity. This simplified strategy simplifies calculations while addressing the more pronounced coupling effects between guidance and control loops in high-speed and highly maneuverable defenders.
The state vector for this simplified model is chosen as
This state vector includes the relative positions, velocities, and accelerations of the attacker and target as well as the angle of attack and pitch rate relevant to the defender.
The linearized dynamics model representing the three-player conflict can be expressed as
where
This model simplifies the integration of guidance and control for the defender by isolating and directly addressing the most dynamically significant elements of the system. The derivation follows procedures similar to those previously discussed; for the sake of brevity, it is not repeated here.
5. Simulation Results and Analysis
This section describes the simulation setup and presents the results of two specific simulation examples to validate the proposed IGC approach within the context of aerial vehicle active protection scenarios. The results are compared to traditional methods where guidance and control loops are designed separately.
5.1. Simulation Setup
The simulation is designed to evaluate the effectiveness of the IGC strategy proposed in this paper. The defender model is based on the one described in [17]. The fin deflection commands generated by the autopilot (AP) or IGC are transmitted to the actuator. In aerial vehicle systems, the actuator is a critical component that converts the autopilot’s commands into physical movements, such as the deflection of tail fins, to achieve the desired motion. Considering the need for rapid response, actuators in aerial vehicles are typically high-bandwidth devices which exceed the bandwidth of the flight control loop itself. Although most modern actuators are electromechanical, hydraulic options are used in specific applications.
For the initial design and analysis phases, it is common to model the actuator dynamics using a simplified second-order transfer function. While this model does not capture the full complexity of the actuator hardware, it provides a reasonable approximation for understanding how the actuator’s response characteristics can influence the performance of the guidance and control loops. The second-order modeling is expressed by the transfer function
where is the actuator output, is the command from the autopilot, is the natural frequency, and is the damping ratio of the actuator. Reasonably designing the parameters of actuators is also crucial for the stability of a control system. A series of curves comparing different settings of the second-order response and the characteristics of these responses are shown in Figure 3.
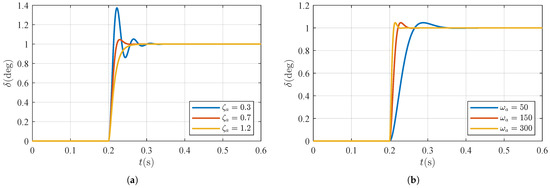
Figure 3.
Step response of a second-order actuator model: (a) setting and (b) setting .
For subsequent simulations, the parameters chosen for the actuator model are rad/s and . These parameters are selected to balance responsiveness and stability, ensuring that the actuator can adequately follow the control commands without inducing undue oscillations or delays in the vehicle’s response.
5.2. Simulation Scenario I
In this simulation example, the attacker directly employs the Proportional Navigation (PN) guidance law to engage the target. The defender’s performance is evaluated under two different configurations: an IGC design, and a traditional approach in which guidance and control loops are designed separately, i.e., PN+AP. In the traditional setup, the defender uses a PN guidance law coupled with a classic three-loop autopilot to track acceleration commands. The initial conditions for this simulation are detailed in Table 1:

Table 1.
Initial parameters for simulation scenario I.
The engagement trajectories of the vehicles are depicted in Figure 4. Under the IGC design, the defender successfully intercepts the attacker at 2.55 s with a miss distance of only 0.16 m. This high-precision interception effectively neutralizes the threat, preventing any damage to the target. In stark contrast, the defender utilizing the traditional AP+PN design results in a significantly larger miss distance of 28.67 m. This considerable deviation results in the attacker successfully hitting the target, demonstrating the limitations of the traditional approach in high-stakes scenarios requiring precise interception.
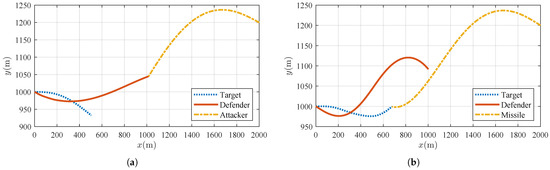
Figure 4.
Trajectory when the attacker adopts the PN guidance law: (a) trajectory when the defender employs IGC and (b) trajectory when the defender employs PN+AP.
In addition, the defender employing the IGC design follows a more direct and efficient flight path. This path not only demonstrates the system’s enhanced responsiveness to dynamic threats, it indicates a lower demand for the defender’s maneuvering capabilities; conversely, the trajectory of the defender using the traditional PN+AP design exhibits more curvature and requires greater maneuvering effort, which can lead to higher fuel consumption and greater stress on the defender.
The ZEM is a critical metric in three-player aerial engagements, providing insight into the effectiveness of the active protection strategy by measuring the predicted miss distance (assuming that no further maneuvers are performed). An analysis of the ZEM for both the IGC strategy and the PN+AP reveals significant differences in performance and stability.
For the defender utilizing the IGC design, the ZEM exhibits a stable and smooth convergence towards zero, as shown in Figure 5. This stable convergence indicates that the defender effectively locks the attacker within the interception triangle, maintaining a consistent trajectory that ensures successful interception. Conversely, the ZEM values for the defender employing the traditional PN+AP display considerable fluctuations, highlighting instability and a lack of control precision. The erratic nature of the ZEM curve when using PN+AP suggests that the defender frequently adjusts their path, reacting to the attacker’s maneuvers rather than anticipating, which leads to a failure to intercept.
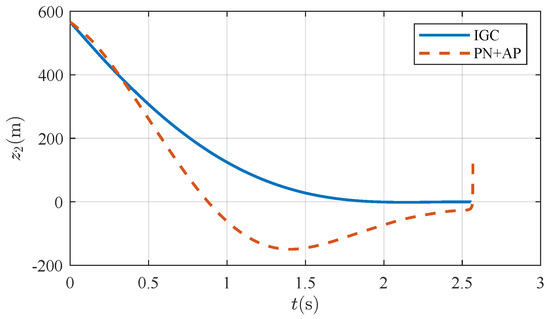
Figure 5.
ZEM .
In the proposed IGC design, computing the inverse of matrix is crucial for solving the Riccati differential equation in order to derive the solution matrix . The condition number of matrix serves as a critical indicator of its invertibility and the potential for numerical instability. A low condition number suggests that the matrix is not sensitive to small perturbations or numerical errors, ensuring the reliability of the matrix inversion operation.
Throughout the engagement process, the condition number of matrix maintained values typically below 10, as depicted in Figure 6. This indicates that matrix remained non-singular and well-conditioned, ensuring the accuracy and reliability of the inversion computations required for solving . This stability in the condition number affirms the method’s robustness against potential numerical issues, particularly when real-time onboard calculations are required for dynamic aerial engagements.
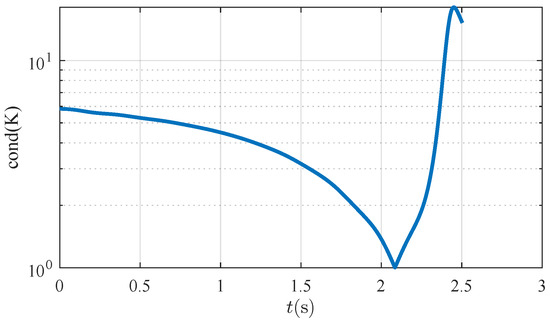
Figure 6.
Condition number of .
Our approach based on the differential game framework does not necessitate prior knowledge of the adversary’s exact strategies or their functional form; however, it does demand specific battlefield information, such as the attacker’s time constant and acceleration . Although can be inferred from open-source information or engineering experience, and can be estimated in real-time using filtering algorithms, these methods introduce inevitable errors. In order to assess potential disadvantages, we conducted Monte Carlo simulations considering deviation in estimates of and . In addition, we introduced varying levels of noise interference in the measurement of the Line-of-Sight (LOS) rotation rate. The defender’s kill radius was set to 5 m, meaning that an interception is successful if the miss distance is less than 5 m. The attacker’s initial position was varied between 1500–3000 m laterally and 200–1800 m longitudinally.
We compiled the defender’s interception success rates under different noise levels, as shown in Table 2. The results indicate that when the measurement noise and model deviation are below 25% the proposed IGC strategy’s performance remains largely unaffected, demonstrating the method’s robustness to noise interference.

Table 2.
Success rate under noise and deviation.
These findings address concerns about sensor noise while providing a more comprehensive evaluation of our IGC strategy’s performance under realistic conditions. In addition, they demonstrate the practical applicability of our approach in scenarios where sensor imperfections and countermeasures are present.
5.3. Simulation Scenario II
The vehicles’ simulation parameters are detailed in Table 3. Faced with the threat of interception, the attacker employs weave maneuvers to evade the defender. If the attacker succeeds in evading the defender, it then switches to the proportional navigation (PN) guidance law to strike the target.

Table 3.
Initial parameters of the vehicles.
With the implementation of the IGC design, the trajectories of the three vehicles are illustrated in Figure 7a. The defender successfully intercepts the attacker with a miss distance of 0.33 m, demonstrating the effectiveness of the IGC approach in protecting the target.
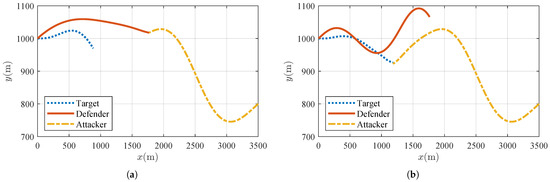
Figure 7.
Trajectory when attacker performs weave maneuver: (a) trajectory when the defender employs IGC and (b) trajectory when the defender employs PN+AP.
To highlight the superiority of the proposed IGC approach, we compare it against a traditional scheme where the guidance and control loops are designed separately. In this traditional configuration, the defender employs a PN guidance law coupled with a three-loop autopilot to follow the acceleration commands. The trajectory for this separation design scheme is depicted in Figure 7b. In contrast to the IGC approach, the defender using the PN+AP scheme fails to intercept the attacker, resulting in a significant miss distance of 49.64 m. Consequently, this failure allows the attacker to successfully hit the target.
The ZEM comparison is illustrated in Figure 8. The defender utilizing IGC shows markedly less influence from the attacker’s evasive maneuvers, successfully locking the attacker within the interception triangle. In contrast, the defender using the separate PN+AP approach experiences significant fluctuations in , ultimately failing to intercept the attacker.
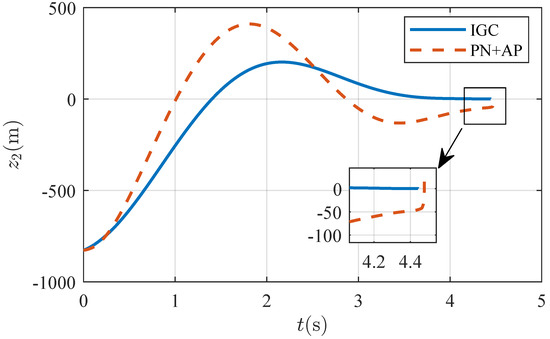
Figure 8.
ZEM .
The acceleration curves of the flight vehicles under both the integrated and separated guidance and control schemes are presented in Figure 9a,b. The simulation with the IGC design ends at 4.44 s, whereas the simulation with the PN+AP approach extends to 5.94 s. Notably, the attacker’s acceleration profile before evading the defender remains consistent in both figures until it switches to a PN guidance law heading to the target.
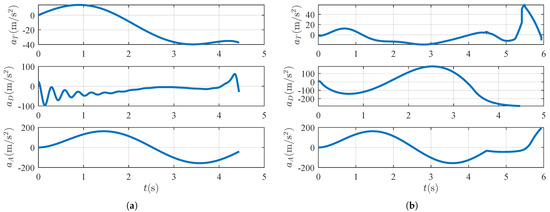
Figure 9.
Acceleration when attacker performs weave maneuver: (a) acceleration when the defender employs IGC and (b) trajectory when the defender employs PN+AP.
The acceleration of the defender under these two scenarios is particularly noteworthy. With the IGC approach, the defender experiences brief initial oscillations before quickly stabilizing. Throughout the engagement, the defender maintains relatively low overload levels generally not exceeding 5 g, with a maximum peak below 10 g. In contrast, under the traditional separated design the defender’s demand for maneuverability significantly increases, with peak overloads reaching up to 30 g.
The comparison in acceleration clearly illustrates the advantages of integrating guidance and control loops in the IGC design. By considering the dynamic characteristics of the vehicle comprehensively, the IGC approach effectively reduces the demand for maneuverability in high-dynamic environments, leading to more stable and efficient flight performance. Such an integrated design enhances interception efficacy while minimizing the stress on the vehicle’s structural and operational limits.
The fin deflection of the defender is depicted in Figure 10, showing a smooth variation that accounts for actuator response delays. This controlled adjustment ensures compatibility with realistic hardware capabilities, demonstrating the practical applicability of the IGC approach.
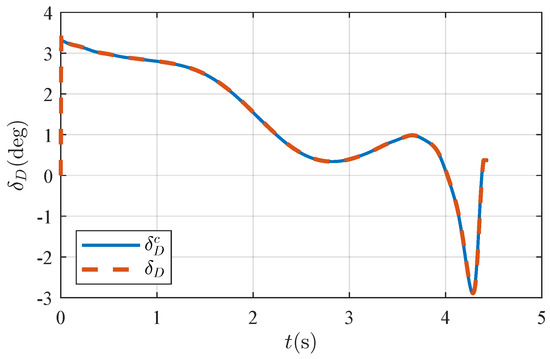
Figure 10.
Fin deflection.
To ensure the numerical accuracy during the inversion operation of matrix , we analyzed the changes in the elements of matrix and its condition number. As displayed in Figure 11, the variation curves of each element confirm that the matrix does not exhibit any singularity, validating the feasibility of obtaining matrix through inversion. In addition, we compared the theoretical solution obtained from the linearized model with the actual values observed in the nonlinear model simulations. The close agreement between the two sets of results shown in Figure 11 serves as empirical evidence supporting the validity and feasibility of the linearization method employed in this work.
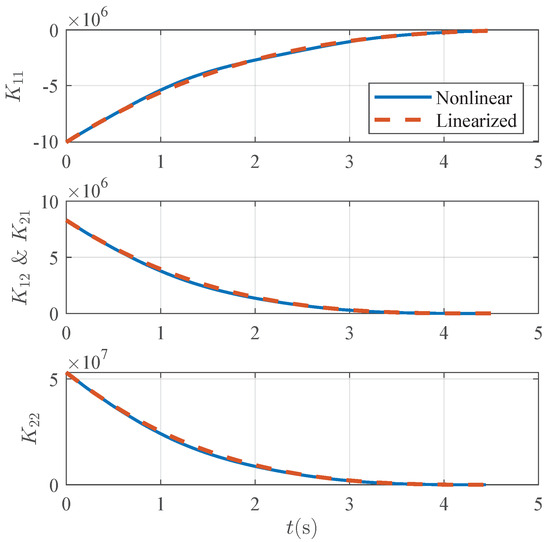
Figure 11.
Matrix .
Further, as shown in Figure 12, the condition number of matrix generally remains below 10 and does not exceed 100. This indicates that matrix is not ill-conditioned, ensuring that the precision of the inversion operation is safeguarded.
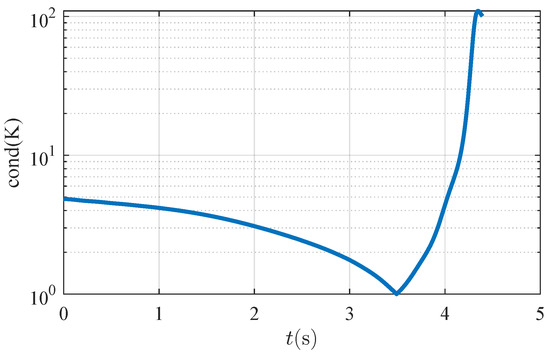
Figure 12.
Condition number of .
6. Conclusions
This paper has proposed a cooperative IGC strategy for active target protection in a three-player conflict scenario. The IGC model was established by linearizing both the translational and rotational dynamics of the target and defender vehicles. Differential game theory and the sweep method were applied to derive and solve the Riccati differential equation analytically, providing an optimal control solution. The theoretical optimality of the derived strategy was proven and the computational accuracy of the solution was analyzed in terms of the control matrix singular values and solution matrix condition numbers. Compared to traditional separated guidance and control designs, the IGC strategy demonstrates superior performance, smoother control trajectories, and reduced maneuverability demands on the defender, leading to enhanced interception efficacy and minimized stress on the vehicle’s structural and operational limits. The proposed IGC strategy provides a promising framework for active target protection in aerial vehicle engagements. Future work could explore extending the model to incorporate more complex vehicle dynamics, multi-vehicle cooperation, and robustness against uncertainties in system parameters.
Author Contributions
Conceptualization, X.G. and W.C.; methodology, X.G.; software, Z.C.; validation, X.G.; formal analysis, X.G.; investigation, X.G.; resources, Z.C.; data curation, W.C.; writing—original draft preparation, X.G.; writing—review and editing, Z.C.; visualization, X.G.; supervision, Z.C.; project administration, Z.C. and W.C.; funding acquisition, Z.C. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the China Postdoctoral Science Foundation (Grant No. 2021M700321) and the Fundamental Research Funds for the Central Universities (Grant No. YWF-23-Q-1041).
Data Availability Statement
All data used during the study appear in the submitted article.
Acknowledgments
The study described in this paper was supported by the China Postdoctoral Science Foundation (Grant No. 2021M700321) and the Fundamental Research Funds for the Central Universities (Grant No. YWF-23-Q-1041). The authors fully appreciate the financial support.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Isaacs, R. Differential Games: A Mathematical Theory with Applications to Warfare and Pursuit, Control and Optimization; Dover Publications: Mineola, NY, USA, 1999. [Google Scholar]
- Wei, X.; Yang, J. Optimal Strategies for Multiple Unmanned Aerial Vehicles in a Pursuit/Evasion Differential Game. J. Guid. Control Dyn. 2018, 41, 1799–1806. [Google Scholar] [CrossRef]
- Hayoun, S.Y.; Shima, T. On guaranteeing point capture in linear n -on-1 endgame interception engagements with bounded controls. Automatica 2017, 85, 122–128. [Google Scholar] [CrossRef]
- Buzikov, M.; Galyaev, A. The Game of Two Identical Cars: An Analytical Description of the Barrier. J. Optim. Theory Appl. 2023, 198, 988–1018. [Google Scholar] [CrossRef]
- Singh, S.K.; Reddy, P.V. Dynamic Network Analysis of a Target Defense Differential Game with Limited Observations. IEEE Trans. Control Netw. Syst. 2023, 10, 308–320. [Google Scholar] [CrossRef]
- Wang, K.; Zhou, S.; Yao, Y.; Sun, Q.; Wang, Y. A target defence–intrusion game with considering the obstructive effect of target. IET Control Theory Appl. 2024. [Google Scholar] [CrossRef]
- Liang, L.; Deng, F.; Wang, J.; Lu, M.; Chen, J. A Reconnaissance Penetration Game With Territorial-Constrained Defender. IEEE Trans. Autom. Control 2022, 67, 6295–6302. [Google Scholar] [CrossRef]
- Weintraub, I.E.; Pachter, M.; Garcia, E. An Introduction to Pursuit-evasion Differential Games. In Proceedings of the 2020 American Control Conference (ACC), Denver, CO, USA, 1–3 July 2020; pp. 1049–1066. [Google Scholar] [CrossRef]
- Garcia, E.; Casbeer, D.W.; Pachter, M. Pursuit in the Presence of a Defender. Dyn. Games Appl. 2019, 9, 652–670. [Google Scholar] [CrossRef]
- Garcia, E.; Casbeer, D.W.; Pachter, M. The Complete Differential Game of Active Target Defense. J. Optim. Theory Appl. 2021, 191, 675–699. [Google Scholar] [CrossRef]
- Liang, L.; Deng, F.; Peng, Z.; Li, X.; Zha, W. A differential game for cooperative target defense. Automatica 2019, 102, 58–71. [Google Scholar] [CrossRef]
- Liang, L.; Deng, F.; Lu, M.; Chen, J. Analysis of Role Switch for Cooperative Target Defense Differential Game. IEEE Trans. Autom. Control 2021, 66, 902–909. [Google Scholar] [CrossRef]
- Nayak, S.P.; Rajawat, A.P.; Kothari, M. Inverse Geometric Guidance Strategy for a Three-Body Differential Game. In Proceedings of the AIAA Scitech 2021 Forum, Reston, VA, USA, 11–15 & 19–21 January 2021; AIAA SciTech Forum. pp. 1–17. [Google Scholar] [CrossRef]
- Garcia, E.; Casbeer, D.W.; Pachter, M. Cooperative Strategies for Optimal Aircraft Defense from an Attacking Missile. J. Guid. Control Dyn. 2015, 38, 1510–1520. [Google Scholar] [CrossRef]
- Harini Venkatesan, R.; Sinha, N.K. A New Guidance Law for the Defense Missile of Nonmaneuverable Aircraft. IEEE Trans. Control Syst. Technol. 2015, 23, 2424–2431. [Google Scholar] [CrossRef]
- Garcia, E.; Casbeer, D.W.; Fuchs, Z.E.; Pachter, M. Cooperative Missile Guidance for Active Defense of Air Vehicles. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 706–721. [Google Scholar] [CrossRef]
- Zarchan, P. Tactical and Strategic Missile Guidance, 6th ed.; Progress in Astronautics and Aeronautics; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2012; Volume 239. [Google Scholar] [CrossRef]
- Yanushevsky, R. Modern Missile Guidance, 2nd ed.; Taylor et Francis/CRC Press: Boca Raton, FL, USA; London, UK; New York, NY, USA, 2019. [Google Scholar]
- Shaferman, V.; Oshman, Y. Stochastic Cooperative Interception Using Information Sharing Based on Engagement Staggering. J. Guid. Control Dyn. 2016, 39, 2127–2141. [Google Scholar] [CrossRef]
- Prokopov, O.; Shima, T. Linear Quadratic Optimal Cooperative Strategies for Active Aircraft Protection. J. Guid. Control Dyn. 2013, 36, 753–764. [Google Scholar] [CrossRef]
- Shima, T. Optimal Cooperative Pursuit and Evasion Strategies Against a Homing Missile. J. Guid. Control Dyn. 2011, 34, 414–425. [Google Scholar] [CrossRef]
- Perelman, A.; Shima, T.; Rusnak, I. Cooperative Differential Games Strategies for Active Aircraft Protection from a Homing Missile. J. Guid. Control Dyn. 2011, 34, 761–773. [Google Scholar] [CrossRef]
- Alkaher, D.; Moshaiov, A. Game-Based Safe Aircraft Navigation in the Presence of Energy-Bleeding Coasting Missile. J. Guid. Control Dyn. 2016, 39, 1539–1550. [Google Scholar] [CrossRef]
- Liu, F.; Dong, X.; Li, Q.; Ren, Z. Cooperative differential games guidance laws for multiple attackers against an active defense target. Chin. J. Aeronaut. 2022, 35, 374–389. [Google Scholar] [CrossRef]
- Rubinsky, S.; Gutman, S. Three-Player Pursuit and Evasion Conflict. J. Guid. Control Dyn. 2014, 37, 98–110. [Google Scholar] [CrossRef]
- Rubinsky, S.; Gutman, S. Vector Guidance Approach to Three-Player Conflict in Exoatmospheric Interception. J. Guid. Control Dyn. 2015, 38, 2270–2286. [Google Scholar] [CrossRef]
- Qi, N.; Sun, Q.; Zhao, J. Evasion and pursuit guidance law against defended target. Chin. J. Aeronaut. 2017, 30, 1958–1973. [Google Scholar] [CrossRef]
- Shaferman, V.; Shima, T. Cooperative Multiple-Model Adaptive Guidance for an Aircraft Defending Missile. J. Guid. Control Dyn. 2010, 33, 1801–1813. [Google Scholar] [CrossRef]
- Shaferman, V.; Shima, T. Cooperative Differential Games Guidance Laws for Imposing a Relative Intercept Angle. J. Guid. Control Dyn. 2017, 40, 2465–2480. [Google Scholar] [CrossRef]
- Saurav, A.; Kumar, S.R.; Maity, A. Cooperative Guidance Strategies for Aircraft Defense with Impact Angle Constraints. In Proceedings of the AIAA Scitech 2019 Forum, Reston, VA, USA, 7–11 January 2019. [Google Scholar] [CrossRef]
- Liang, H.; Wang, J.; Liu, J.; Liu, P. Guidance strategies for interceptor against active defense spacecraft in two-on-two engagement. Aerosp. Sci. Technol. 2020, 96, 105529. [Google Scholar] [CrossRef]
- Shalumov, V.; Shima, T. Weapon–Target-Allocation Strategies in Multiagent Target–Missile–Defender Engagement. J. Guid. Control Dyn. 2017, 40, 2452–2464. [Google Scholar] [CrossRef]
- Chen, Z.; Chen, W.; Liu, X.; Cheng, J. Three-dimensional fixed-time robust cooperative guidance law for simultaneous attack with impact angle constraint. Aerosp. Sci. Technol. 2021, 110, 106523. [Google Scholar] [CrossRef]
- Li, G.; Liu, L.; Liu, J.; Wu, Y.; Zhao, J. Three-dimensional low-order fixed-time integrated guidance and control for STT missile with strap-down seeker. J. Frankl. Inst. 2023, 360, 9788–9811. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, X.; Zhang, H.; Zhang, F. Three-dimensional approximate cooperative integrated guidance and control with fixed-impact time and azimuth constraints. Aerosp. Sci. Technol. 2023, 142, 108617. [Google Scholar] [CrossRef]
- Williams, D.; Richman, J.; Friedland, B. Design of an integrated strapdown guidance and control system for a tactical missile. In Proceedings of the Guidance and Control Conference, Reston, VA, USA, 15–August 1983. [Google Scholar] [CrossRef]
- Santoso, F.; Garratt, M.A.; Anavatti, S.G. State-of-the-Art Integrated Guidance and Control Systems in Unmanned Vehicles: A Review. IEEE Syst. J. 2021, 15, 3312–3323. [Google Scholar] [CrossRef]
- Yao, C.; Liu, Z.; Zhou, H.; Gao, C.; Li, J.; Zhang, Z. Integrated guidance and control for underactuated fixed-trim moving mass flight vehicles. Aerosp. Sci. Technol. 2023, 142, 108680. [Google Scholar] [CrossRef]
- Shima, T.; Idan, M.; Golan, O.M. Sliding-Mode Control for Integrated Missile Autopilot Guidance. J. Guid. Control Dyn. 2006, 29, 250–260. [Google Scholar] [CrossRef]
- Xingling, S.; Honglun, W. Back-stepping active disturbance rejection control design for integrated missile guidance and control system via reduced-order ESO. ISA Trans. 2015, 57, 10–22. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Jiang, B.; Zhang, K. Adaptive Fault-Tolerant H-Infinity Output Feedback Control for Lead-Wing Close Formation Flight. IEEE Trans. Syst. Man, Cybern. Syst. 2019, 50, 2804–2814. [Google Scholar] [CrossRef]
- Yan, H.; Hou, M. A Small-Gain Approach for Three-Dimensional Integrated Guidance and Control in Pursuit-Evasion Games. In Proceedings of the 2020 Chinese Control And Decision Conference (CCDC), Hefei, China, 22–24 August 2020; pp. 4069–4076. [Google Scholar] [CrossRef]
- Stevens, B.L.; Lewis, F.L.; Johnson, E.N. Aircraft Control and Simulation: Dynamics, Controls Design, and Autonomous Systems, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Green, M.; Limebeer, D.J.N. Linear Robust Control, dover ed.; Dover Publications Inc.: Mineola, NY, USA, 2012. [Google Scholar]
- Yechout, T.R.; Morris, S.L.; Bossert, D.E.; Hallgren, W.F.; Hall, J.K. Introduction to Aircraft Flight Mechanics: Performance, Static Stability, Dynamic Stability, Classical Feedback Control, and State-Space Foundations, 2nd ed.; AIAA Education Series; American Institute of Aeronautics and Astronautics Inc.: Reston, VA, USA, 2014. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).