Ramp Start and Speed Control of Self-Driving Commercial Vehicles under Ramp and Vehicle Load Uncertainty

Abstract

In order to improve the performance of self-driving commercial vehicles for half-hill starting, a ramp control strategy based on the back-slip speed corresponding to the parking moment is proposed. Firstly, the longitudinal dynamics model of the vehicle is established, the force of the vehicle on the ramp is analyzed, and the rear slip speed of the vehicle is matched with the parking moment, and finally the target speed is tracked based on the sliding-mode controller, and in order to validate the validity of the method, two comparative algorithms of the pure PI controller and the proportional gain controller based on the back-sliding speed corresponding to the resting moment are designed for comparative experiments, and the data results show that the control strategy based on the resting moment corresponding to the backsliding speed of the sliding mode ramp start control strategy can stably complete the ramp start under different weights and different slopes, and greatly reduce the backsliding distance of the vehicle.

1. Introduction

Among the many working conditions of vehicle driving, hill start belongs to one of the working conditions with higher requirements on driver’s maneuvering [1,2,3], especially for commercial vehicles, with larger loads, it requires that the driver have superior driving skills in order to make the vehicle start smoothly on the ramp [4,5]. If the driver presses the gas pedal hard during hill start, it may lead to a dangerous situation of stalling, and if the gas pedal and brake pedal are not well coordinated during hill start, it may lead to a dangerous situation of vehicle rear skidding [6]. Due to the high requirements of the hill start algorithm, the vehicle drive response is required to be faster during hill start, while the distributed drive electric vehicle is installed near the drive wheels due to the electric motor, which makes the vehicle chassis structure more compact and the power transmission efficiency high, and the electric motor directly controls the driving and braking of each wheel with flexible torque distribution and rapid response, which makes it easier to satisfy the quickness of the vehicle control, and thus better realizes the hill assist function [7,8,9,10].

In order to solve the safety problem of hill starting, researchers and developers have conducted in-depth studies in this field and developed different hill assist systems. Hill assist is a very practical function, and the main principle is that when starting on a hill, the driver still has braking force within 3 s after releasing the brake, so that the driver has enough time to switch from the brake pedal to the gas pedal to complete the hill start [11,12,13,14]. With only minimal changes to the mechatronic system, the mechanical system consists of a gearbox-integrated hill-holding system, which can realize the hill-holding and automatic parking brake functions by purely mechanical or mechatronic means [15]. For heavy commercial vehicles, Song [16] et al. realized the hill-hold function by changing the brake system structure to maintain a certain amount of oil pressure in the brake system at the moment when the driver releases the brake pedal. Peng [17] et al. proposed a two-layer, large-scale adaptive control framework for commercial vehicles equipped with an electronic parking brake, using online estimation of the vehicle mass using the tractive force, braking force, road gradient, and longitudinal acceleration. The vehicle mass is estimated, and the feasibility and robustness of the two-layer mass-adaptive hill-climb start assist framework are further verified in vehicle experiments. Zhao [18] et al. proposed a ramp assist control method that cooperatively controls the clutch and hydraulic brake control unit and ensures the stability and robustness of the automatic hill-start algorithm by using the H infinity control theory. However, the above method for commercial vehicles requires precise coordinated control of driving and braking forces, which will cause greater wear on the braking system during startup.

In order to solve the problem of large wear and tear on the braking system for commercial vehicle ramp start, and considering that the sliding mode control has the advantages of fast response, no need for online identification of the system, and insensitivity to parameter changes and perturbations, etc., this paper proposes a ramp assist function, a sliding mode ramp start control method based on the rear skidding speed corresponding to the parking torque, by analyzing the change rule of the parking torque in different gradients and different weights, the parking torque based on the change of the rear skidding speed is derived, and finally, the vehicle is controlled to follow the target speed using a sliding mode variable structure controller. The proposed method is compared with the pure PI controller and the proportional gain ramp start control method based on rear slip speed corresponding to the standstill moment by using MATLAB and TruckSim for simulation verification, which takes into account the evaluation indexes such as the distance of the rear slip, the rise time of the vehicle following the speed, and the slip rate and verifies the validity of the proposed method in the case of different weights and different slopes, and it can stably and accurately carry out the ramp start and speed control.

2. Vehicle Model

As this paper involves the longitudinal speed control of the vehicle, it is necessary to establish the longitudinal dynamics model of the vehicle. When the vehicle arrives from a stationary state to maintain the state of motion, there must be an external force, by the vehicle traveling process, the driving force and a variety of resistances between the formation of the vehicle’s driving equations [19]. The vehicle force situation is shown in Figure 1.

As the vehicle is traveling on a ramp:

$$\left\{\begin{array}{l}{F}_t=F_f+F_w+F_j+F_i\\ F_f=mgf\cos \theta \\ F_w=\frac{C_{D}A{v}^2}{21.15}\\ F_j={\delta }_{m}m\frac{dv}{dt}\\ F_i=mg\sin \theta \end{array}\right.$$

(1)

where $F_t$ for the driving force; $F_f$ for the rolling resistance; $F_w$ for the air resistance; $F_j$ for the acceleration resistance; $F_i$ for the slope resistance; $g$ for the gravity coefficient; $f$ for the rolling resistance coefficient; $C_D$ for the air resistance coefficient; A for the windward area of the vehicle; ${\delta }_m$ for the vehicle rotating mass conversion coefficient; θ for the slope of the road.

3. Materials and Methods

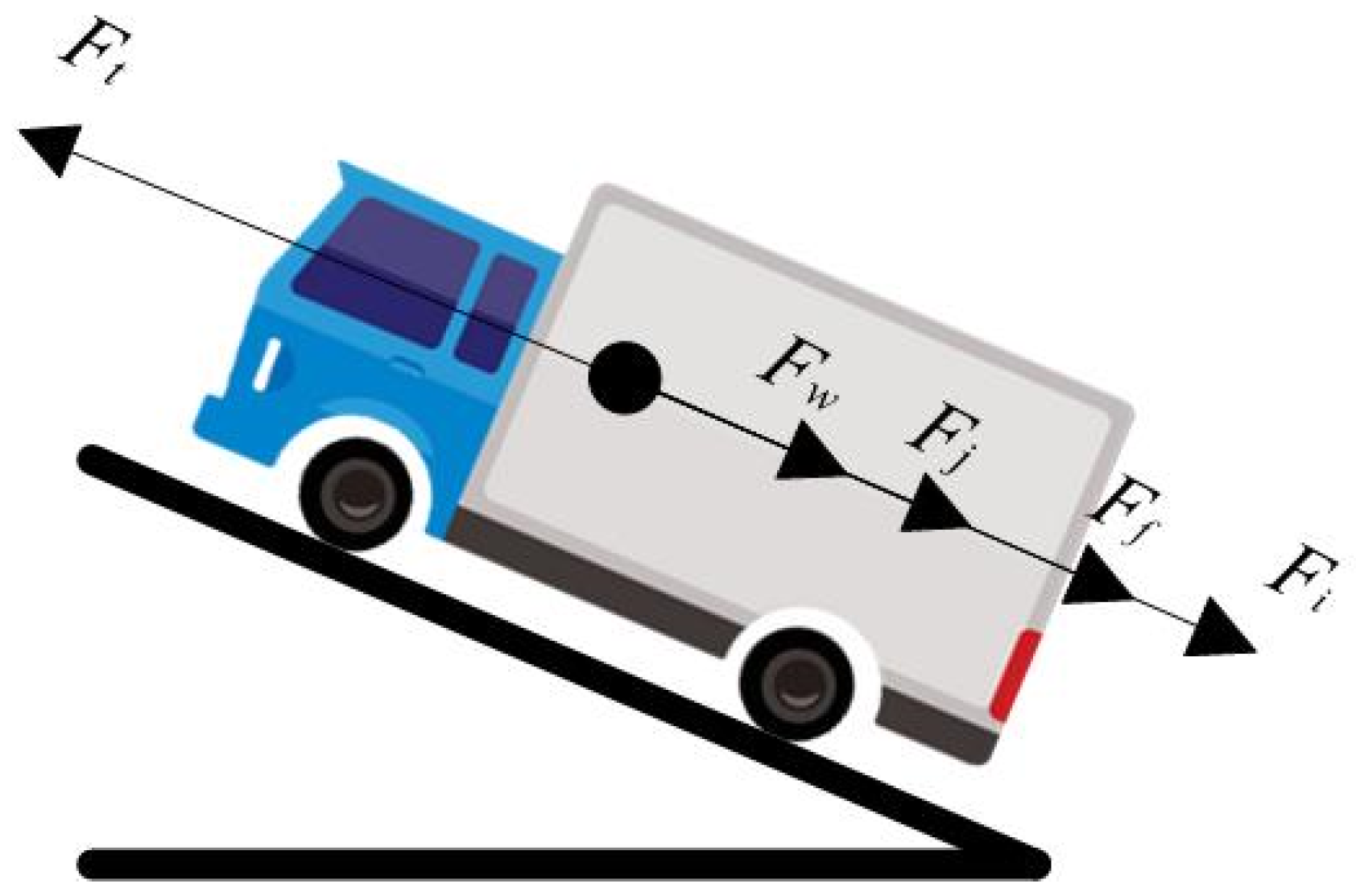
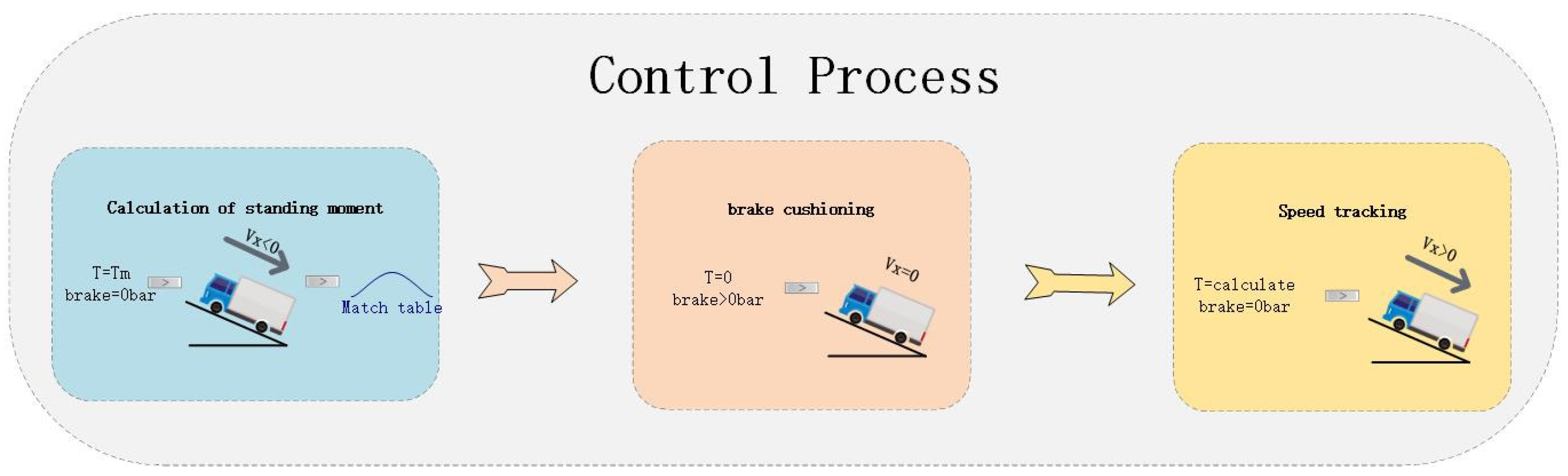
3.1. Ramp Start Process Analysis

The ramp start process in the starting process is slow and visible as a quasi-static process. In order to simplify the problem study, the vehicle will be subjected to air resistance, which is ignored; the vehicle is subjected to the force for the driving force, gravity, as shown in Figure 1. When the vehicle starts on the ramp, the gravity component is converted into ramp resistance, so that the vehicle has a tendency to skid back along the ramp [20]. The traditional driver’s operation will be conducted by stepping on the brakes and, at the same time, stepping on the gas pedal. The driving force is greater than the braking and braking forces. Increase the driving force so that the driving force is greater than the ramp resistance and braking force, and when the driving force is at the critical point of breaking through greater than the ramp resistance and braking force, the vehicle will shake violently, and the driver releases the brake pedal, and the vehicle accelerates uphill to complete the ramp start. The self-driving car cannot accurately feel the shaking of the vehicle and measure the weight of the vehicle and cannot have strong self-regulation ability, so we propose a ramp start control method based on the parking moment corresponding to the backward glide speed, the vehicle matching the parking moment during the ramp start, and the use of the sliding mode controller to complete the tracking of the specific speed.

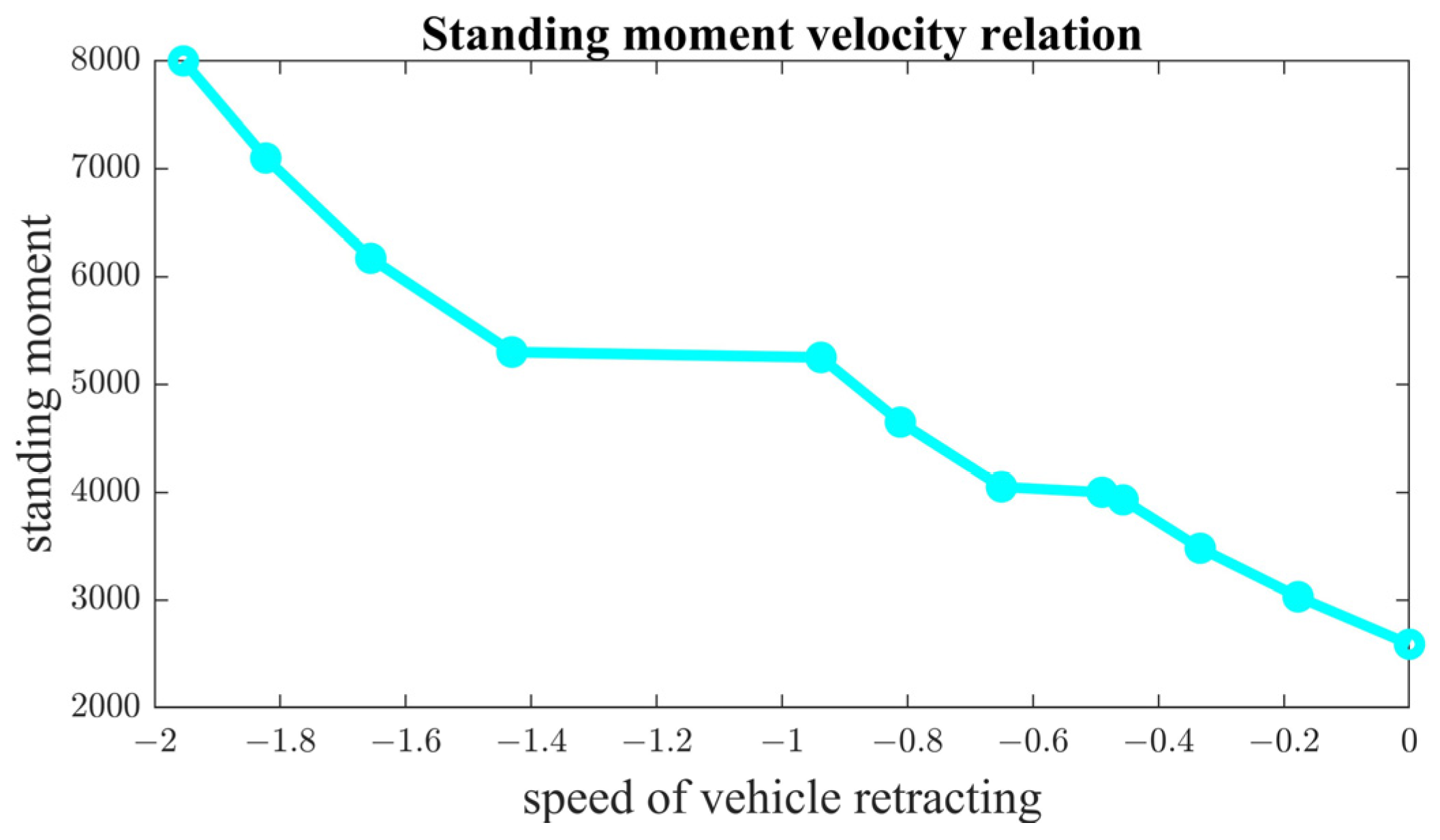
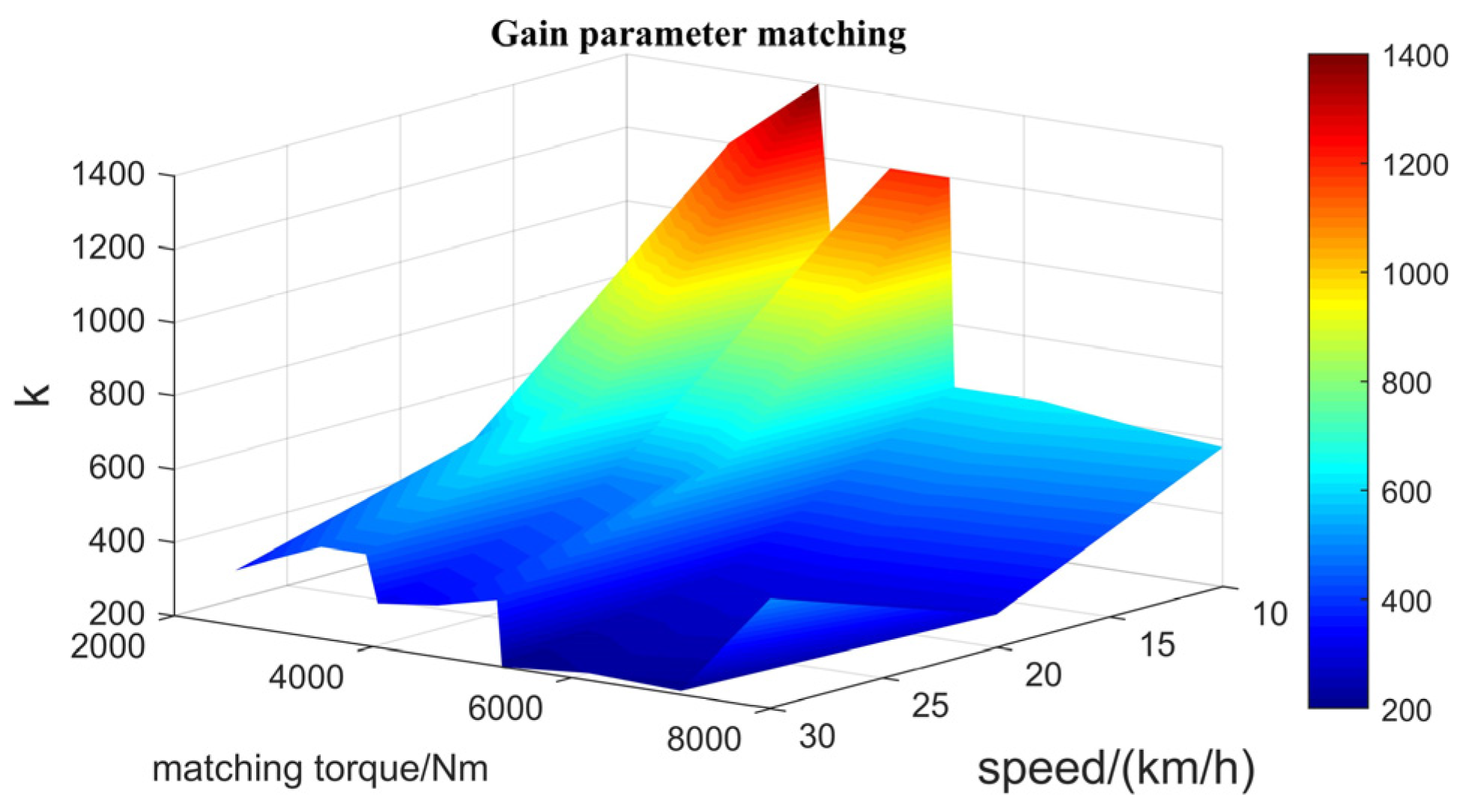
3.2. Matching of Hill-Starting Moments during Hill Starts

In order to get the standing slope moment of the vehicle on the ramp, the force analysis of the vehicle ramp starting conditions, which affects the vehicle rear skidding larger factors for the ramp resistance, and the main factors affecting the ramp resistance are the vehicle load and road gradient, thus, the standing slope moment will be established with the relationship between the vehicle load and road gradient, and at the same time, the establishment of the road gradient-vehicle load-standing slope moment three-dimensional diagram, which indicates that in the different road gradient, different vehicle loads, the change rule of the standing slope moment, as shown in Figure 2.

As can be seen from the above figure, with the increase in road gradient and vehicle load, the parking moment also increases, the parking moment and these two variables are linearly related, so consider the 0.5 s within the vehicle rear skidding speed and the parking moment to match, through the vehicle itself on the ramp 0.5 s within the rear skidding speed and the parking moment to establish a one-to-one correspondence between the relationship, to obtain a vehicle ramp parking torque, the torque–speed relationship. The torque–velocity relationship is shown in Figure 3.

Set the simulation parameters for matching the standing moment based on the rear slip speed as (7000 kg, 7°), (6455 kg, 7°), (5000 kg, 10°), (4700 kg, 10°), and (4455 kg, 5°), and the simulation results are shown in Figure 4.

From the above figure, it can be seen that the use of rear slip speed matching of the parking moment can be adapted to different weights, different gradients of the vehicle parking slope, and the above method of matching based on the rear slip speed after 0.5 s and the rapidity of the vehicle to carry out the ramp start, so the simulation effect of the rear slip speed—parking moment curves of 0.1 s and 0.5 s are compared, as shown in Figure 5.

From the Figure 5, it can be seen that the longer the rear slip speed counting time, the larger its rear slip distance, in order to obtain a better ramp starting effect, this paper adopts the rear slip speed counting time of 0.1 s, when the vehicle 0.1 s after the acquisition of the speed, give the vehicle braking pressure to bring the vehicle to a standstill, and then according to the 0.1 s acquisition of the rear slip speed to match the ramp parking moment, withdraw the braking pressure, give the vehicle to apply the parking moment, at this time, the vehicle’s ramp parking moment is exactly equal to the sum of the vehicle’s ramp resistance and rolling resistance, and the vehicle is at a standstill.

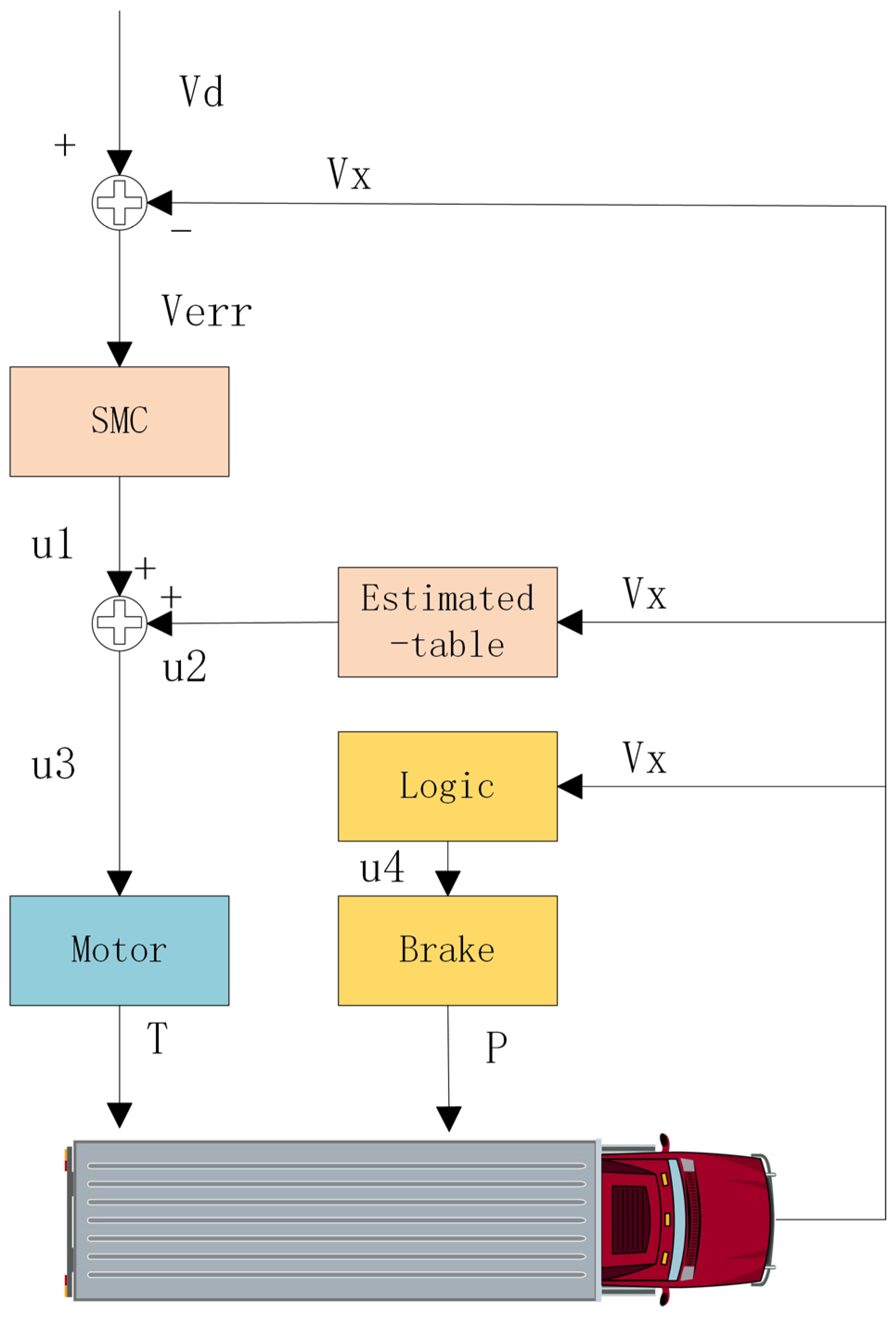
3.3. Sliding Mode Variable Structure Controller

There are three main parts to designing the sliding mode variable structure controller: the simplification of the dynamic part of the vehicle, the determination of the sliding mode surface, and the derivation of the sliding mode variable structure control law.

The power part of the vehicle is driven by a distributed motor, and the motor torque is related to the rotational speed, as can be seen from the previous section, the ramp start is a quasi-static process, the motor rotational speed is approximated to be zero, and the motor can output the maximum torque, and the mass of the vehicle does not change in the transportation process from the origin to the destination, and the loading and unloading of the goods only in the origin or the destination, which results in a change in the mass of the loaded goods, i.e., within a certain time span, the mass of the vehicle and the slope of the roadway can be regarded as constant, so the rolling resistance and ramp resistance of the vehicle are fixed, i.e., the longitudinal dynamics equation of the vehicle is Equation (2):

$$F_t-(F_f+F_w+F_i)=F_j=m\dot{V}$$

(2)

Based on the above conditions, air resistance is neglected and rolling resistance and ramp resistance are fixed values, i.e., the above equation can be transformed into Equation (3):

$$T-r(F_f+F_i)=rm\dot{V}$$

(3)

where T is the motor torque and r is the wheel radius, i.e., the motor torque can be reduced to a linear function of the speed derivative as in Equation (4).

$$T=h\dot{V}$$

(4)

In order to make the vehicle speed follow the ideal value, the switching function is designed as in Equation (5):

$$s=V_d-V_x$$

(5)

Derivation of the switching function gives:

$$\dot{s}={\dot{V}}_d-{\dot{V}}_x$$

(6)

The convergence law for designing the sliding mode variable structure controller is:

$$\dot{s}=-\epsilon \mathrm{sgn}(s)-ks$$

(7)

where ε < 0, k < 0.

Define the Lyapunov function as $V=\frac{1}{2}{s}^2$. Using the exponential convergence law above yields:

$$\dot{V}=s·\dot{s}=s·(-\epsilon \mathrm{sgn}(s)-ks)=-\left|s\right|\epsilon -k{s}^2\le 0$$

(8)

Can be obtained from Equation (8):

$$\dot{V}\le 0$$

(9)

Therefore, the system can be stabilized in the end, and the control law can be obtained by substituting (4) into Equation (6) and associating (7):

$$T=h({\dot{V}}_d+\epsilon \mathrm{sgn}(s)+ks)$$

(10)

where g, k, and ε are sliding mode control parameters.

3.4. Sliding Mode Control Based on Rear Slip Speed Matching the Standing Hill Moment

Using the sliding mode speed controller from Section 3.3, as shown in (10), the vehicle control process is as shown in Figure 6.

The sliding mode ramp start control method based on the backward skidding speed corresponding to the parking moment is shown in the figure above. Firstly, a constant torque is given to the vehicle to obtain the vehicle’s backward skidding speed of 0.1 s on the ramp, which is correspondingly inputted into the parking moment table to derive the estimated parking moment of the vehicle at this slope and the vehicle mass. Then the vehicle torque is withdrawn, and a sufficiently large brake pressure is applied to make the vehicle static on the ramp. Finally, the sliding mode controller calculates the torque required for the vehicle to follow the target speed, which is combined with the estimated parking torque to become the vehicle control torque to complete the ramp start and speed tracking; The vehicle control block diagram is shown in Figure 7.

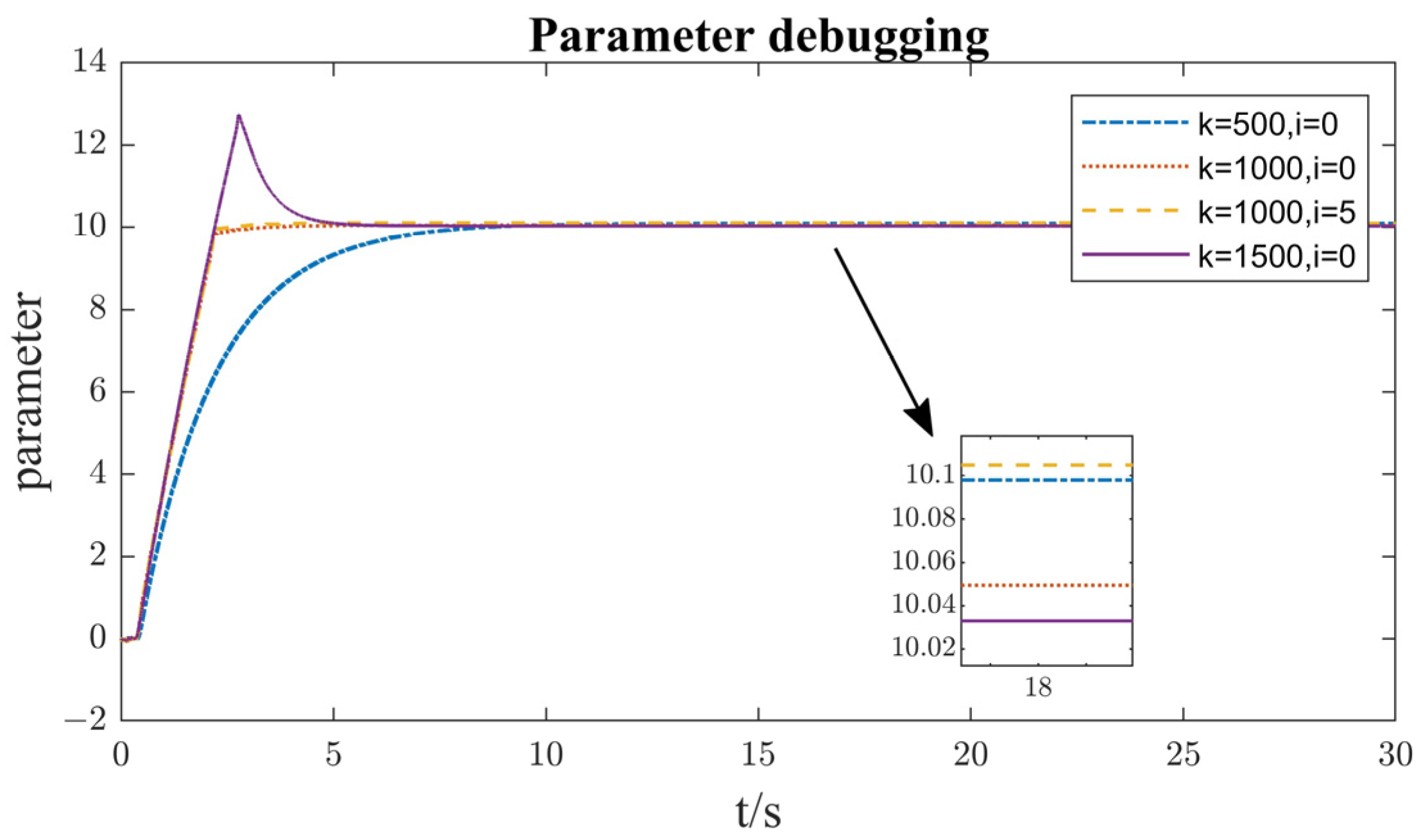
3.5. Proportional Gain Control Based on Rear Slippage Velocity-Matched Standing Moment

As commercial vehicles are in the process of transporting materials, the vehicle load will change, the vehicle does not have additional sensors to sense the vehicle load, the traditional PID regulation cannot meet the vehicle performance requirements, the PID controller cannot regulate the vehicle speed based on the existing information, there will be a speed error, and the vehicle load is too large in the case of the vehicle, which even causes back skidding. Based on the above problems, the standing hill moment calculated by the sliding mode controller in the previous section will be Based on the above-mentioned problems, the feed-forward proportional controller is introduced into the feed-forward proportional controller to solve the problem of the large distance of the car skidding. In order to obtain more accurate speed control, the gain parameters are matched, and different gain parameters are matched for the calculated hill moments to obtain the optimal control effect. The vehicle loading is changed within a certain range, and the gain parameters are matched for the four vehicle masses. The vehicle mass is divided into 4455 kg, 5455 kg, 6455 kg, and 7455 kg, and the gain parameters are matched for the four vehicle masses, and the time-domain characteristics such as rise time and overshoot are taken into account when choosing the gain, as shown in Figure 8.

As can be seen from Figure 8, for the weight of 4455 kg and following speed of 10 km/h, different PI parameters are tested to analyze the influence law of PI parameters, when k = 500, i = 0, the vehicle can track the target speed stably, try to increase k to shorten the rise time, adjust the parameter to k = 1000, i = 0, the vehicle can track the target speed stably, and the rise time becomes shorter, try to adjust i to reduce the steady state error, adjust the parameter to k = 1000, i = 5, the vehicle can track the target speed stably, but the steady state error increases, i.e., try to continue to increase k to shorten the rise time, keep i = 0, adjust the parameter to k = 1500, i = 0, the vehicle follows the speed rise time is shortened but the overshooting quantity is increased, so the group of k = 1000, i = 0 is the optimal PI parameter, namely Select the PI controller parameters as k = 400, i = 0. After many experiments, the four weights corresponding to the torque–gain coefficient matching curve are obtained, as shown in Figure 9.

It can be seen from Figure 9 that the gain coefficient in matching against a single torque increases as the matching torque increases.

When the vehicle is following the speed, the speed demand will be constantly changing because of the environment; therefore, on a certain ramp, this paper will accurately follow the vehicle speed of 10 km/h, 20 km/h, and 30 km/h, and in this way, form the gain matching coefficient according to the vehicle torque, the speed of the joint change, as shown in Figure 10.

From the figure, it can be seen that the mapping relationship between the gain matching coefficient and the matching torque and following speed is not linearly varying, and the gain matching coefficient tends to be saturated when the vehicle is in the case of large matching torque and medium-high speed, due to the limitation of the ground adhesion coefficient and the motor torque, and the vehicle torque is not possible to be infinitely large.

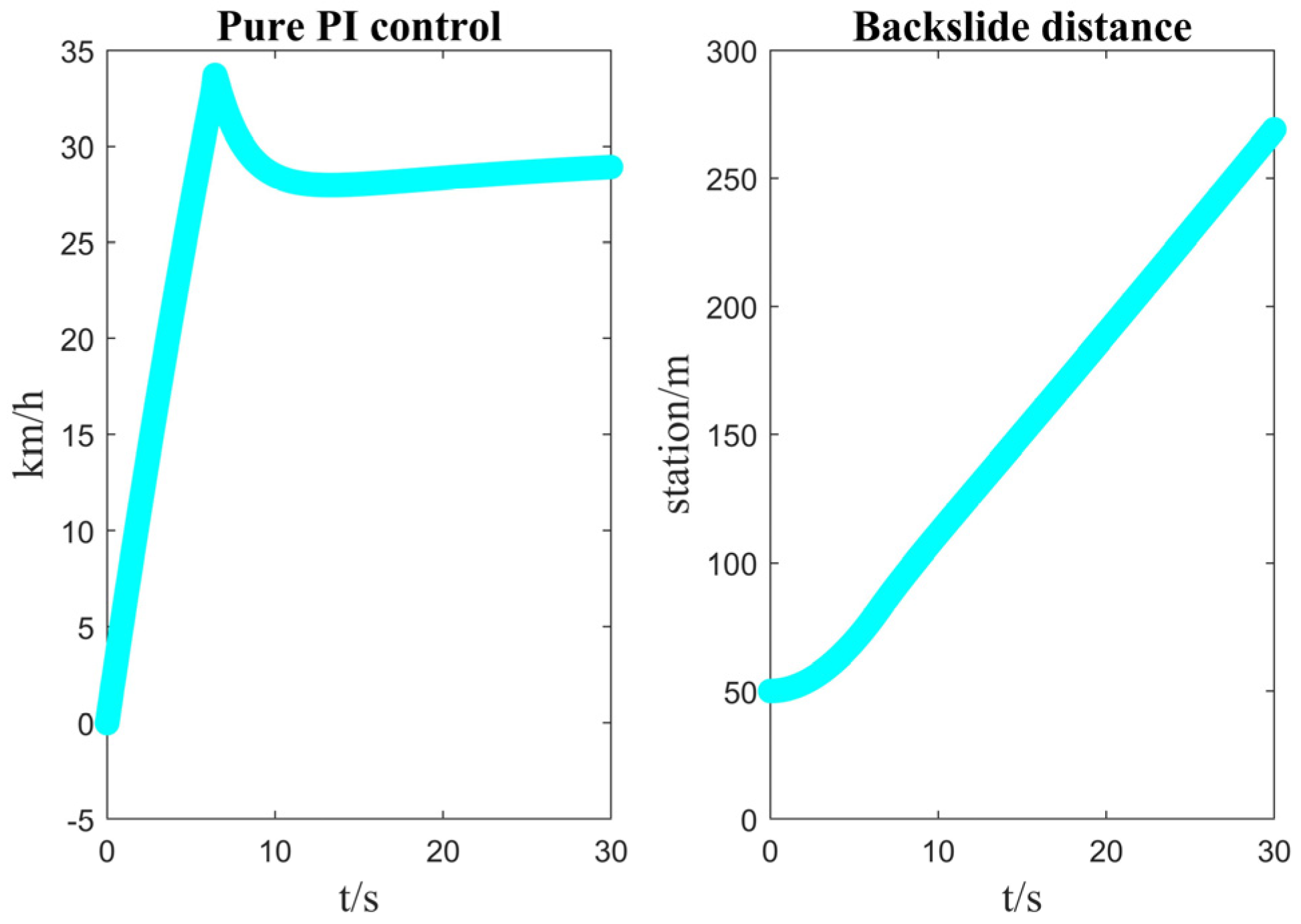
3.6. Pure PI Controller

In the debugging process, it is found that the PI parameters debugged with the maximum load cannot be used for the minimum load vehicle, the torque will be too large, therefore, the minimum load debugging pure PI controller parameters. In the 5° gradient road section, the initial position of the vehicle is set to 50 m, debugging the PI parameters. After many times of debugging the parameters of the pure PI controller, to obtain k = 500, i = 20, that is, the overall mass of the vehicle is 4455 kg, the speed of 30 km/h under 5° gradient, the tracking results of the pure PI controller are shown in the figure below. The tracking effect of the pure PI controller is shown in Figure 11.

From the above figure, it can be seen that the pure PI controller is able to go uphill normally and stably under the current working conditions, tracking the target speed better, and the vehicle does not have the phenomenon of back-sliding. In order to judge the effect of ramp starting and speed tracking of the self-driving vehicle, three evaluation indexes are proposed: rise time, vehicle back-slip distance, and slip rate.

4. Discussion

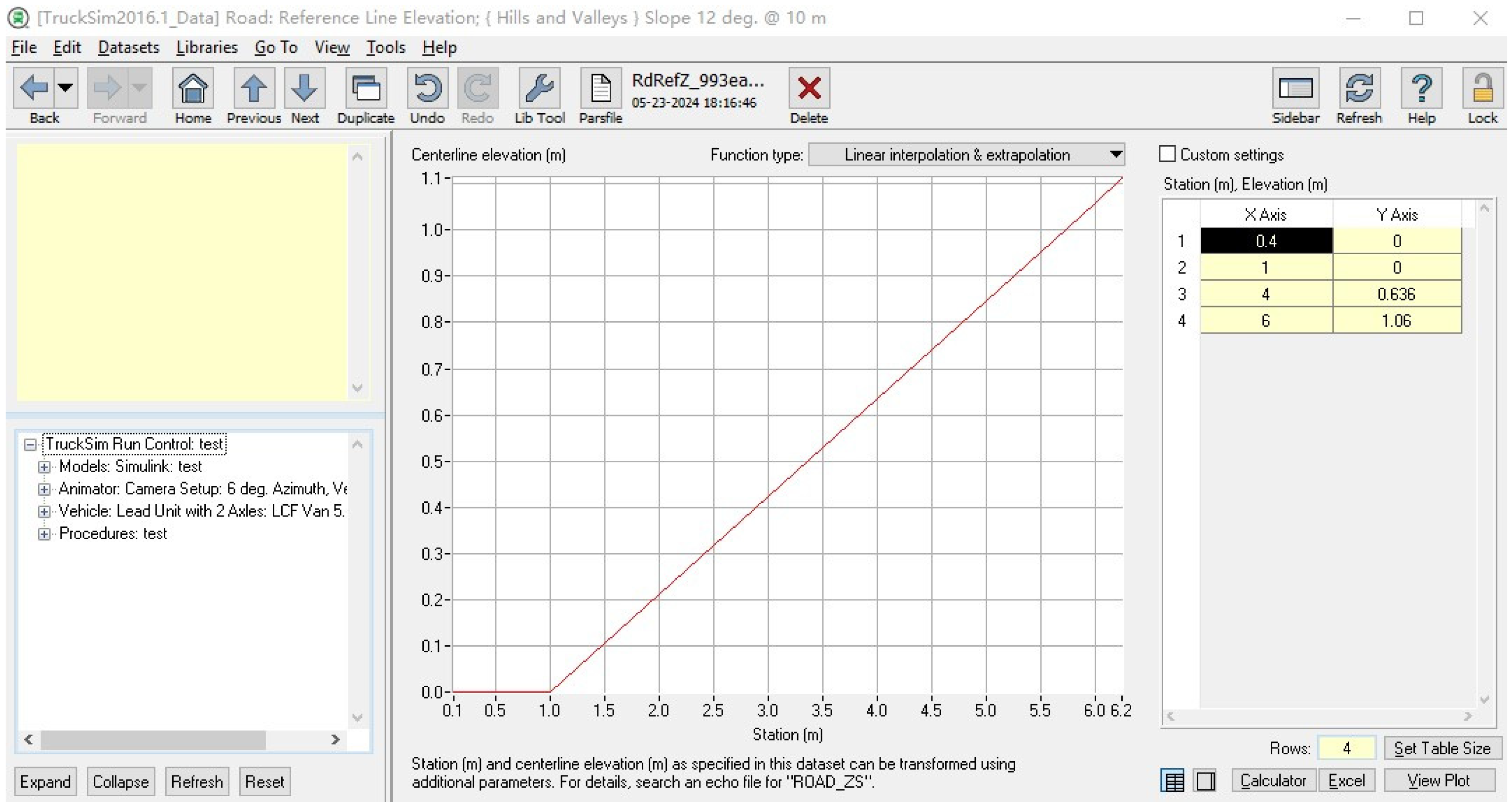
4.1. Simulation Environment Setup

As shown in Figure 12, 5 degree, 7 degree, and 10 degree ramps were built, the driving vehicle was changed to external torque input, and the mass of the vehicle was set to 4455 kg, 5455 kg, 6455 kg, and 7455 kg, respectively.

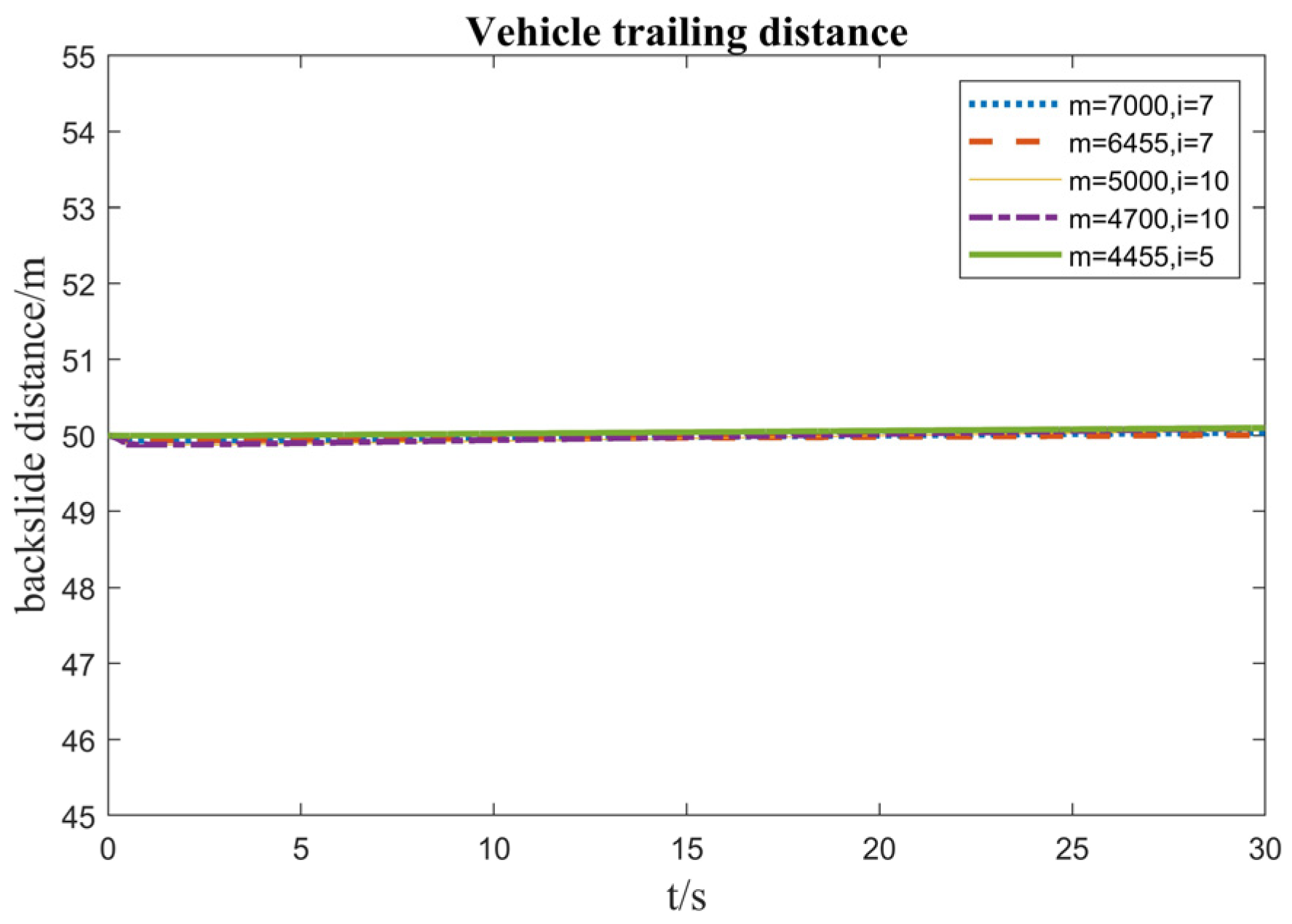
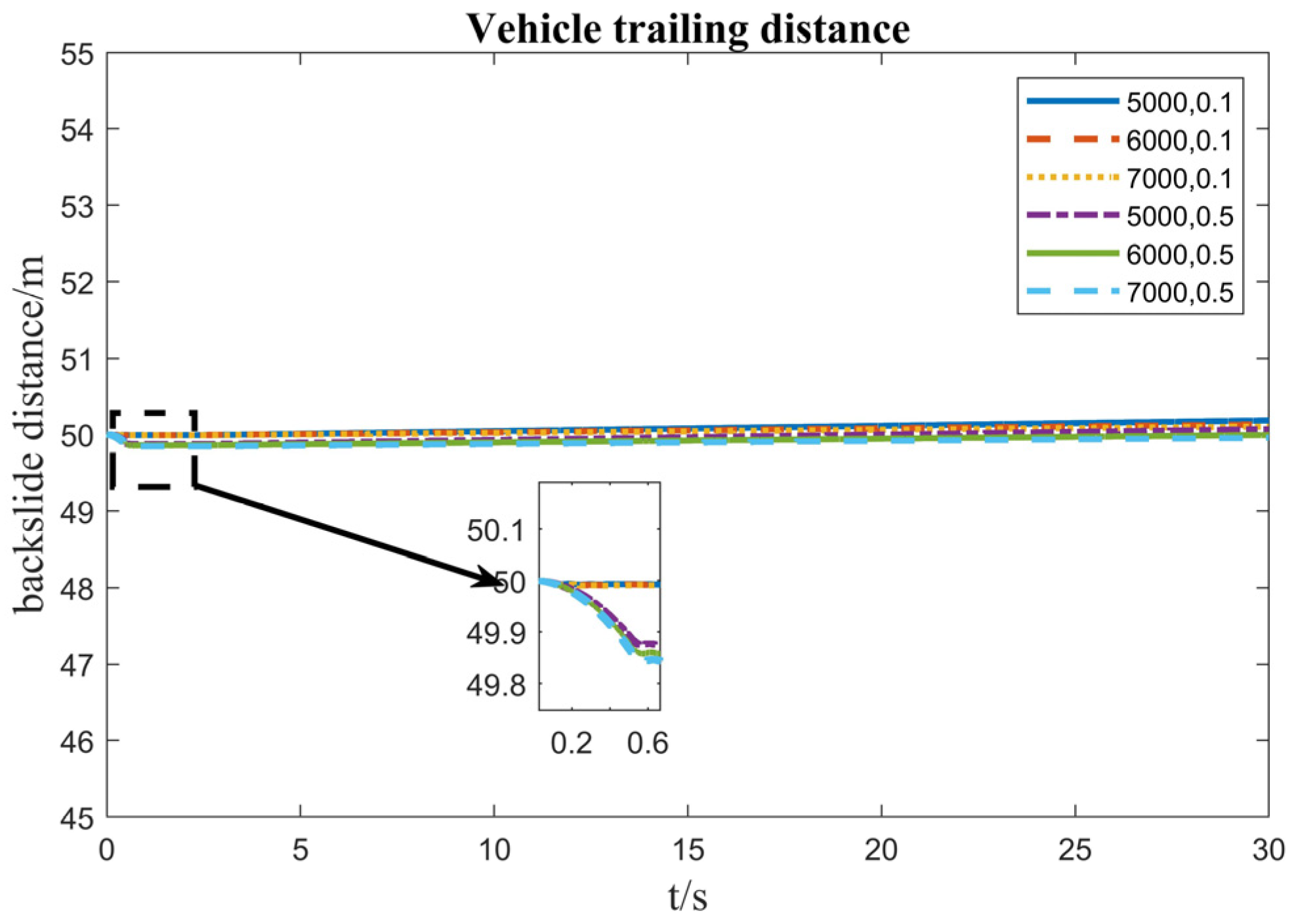
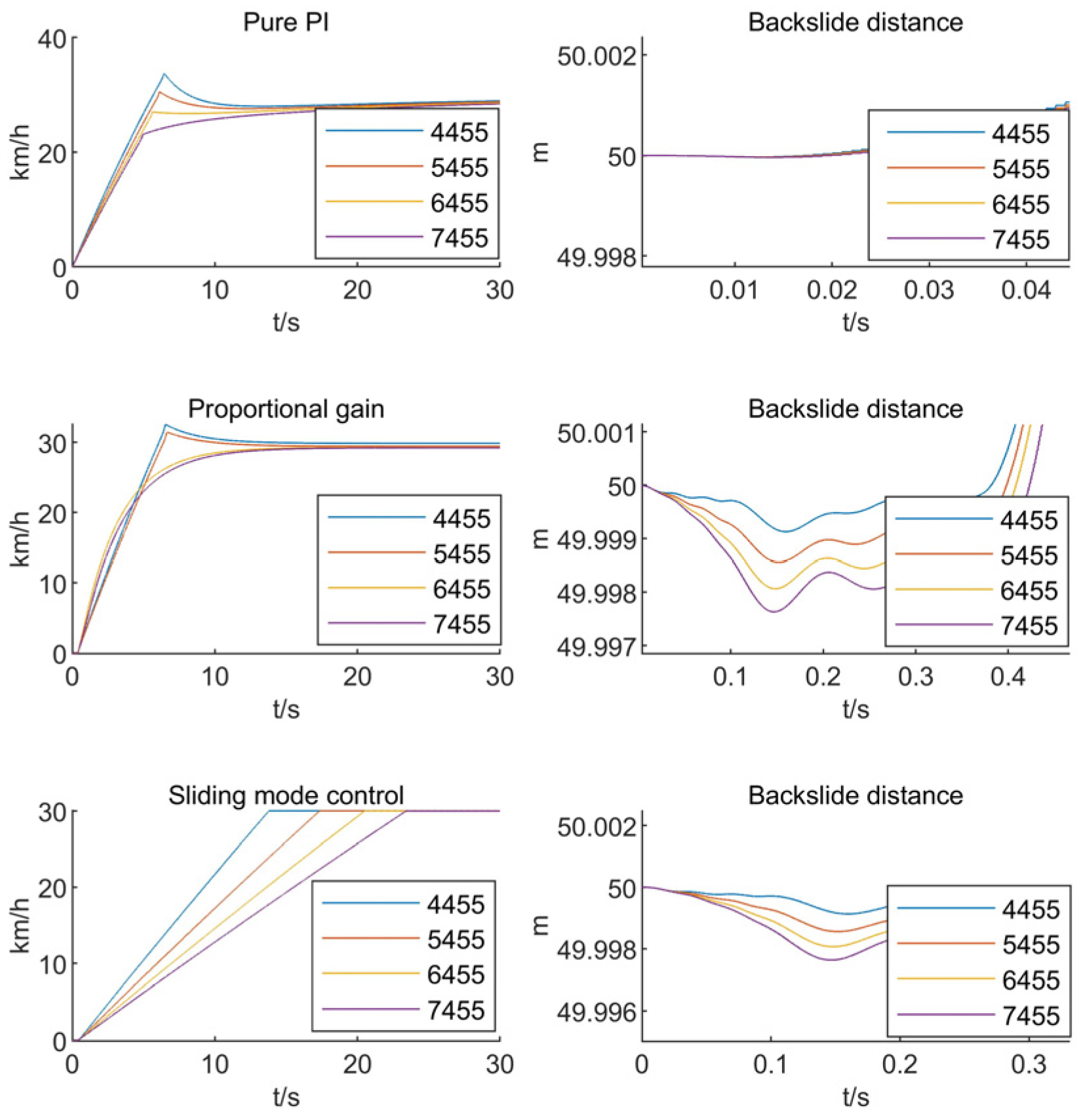
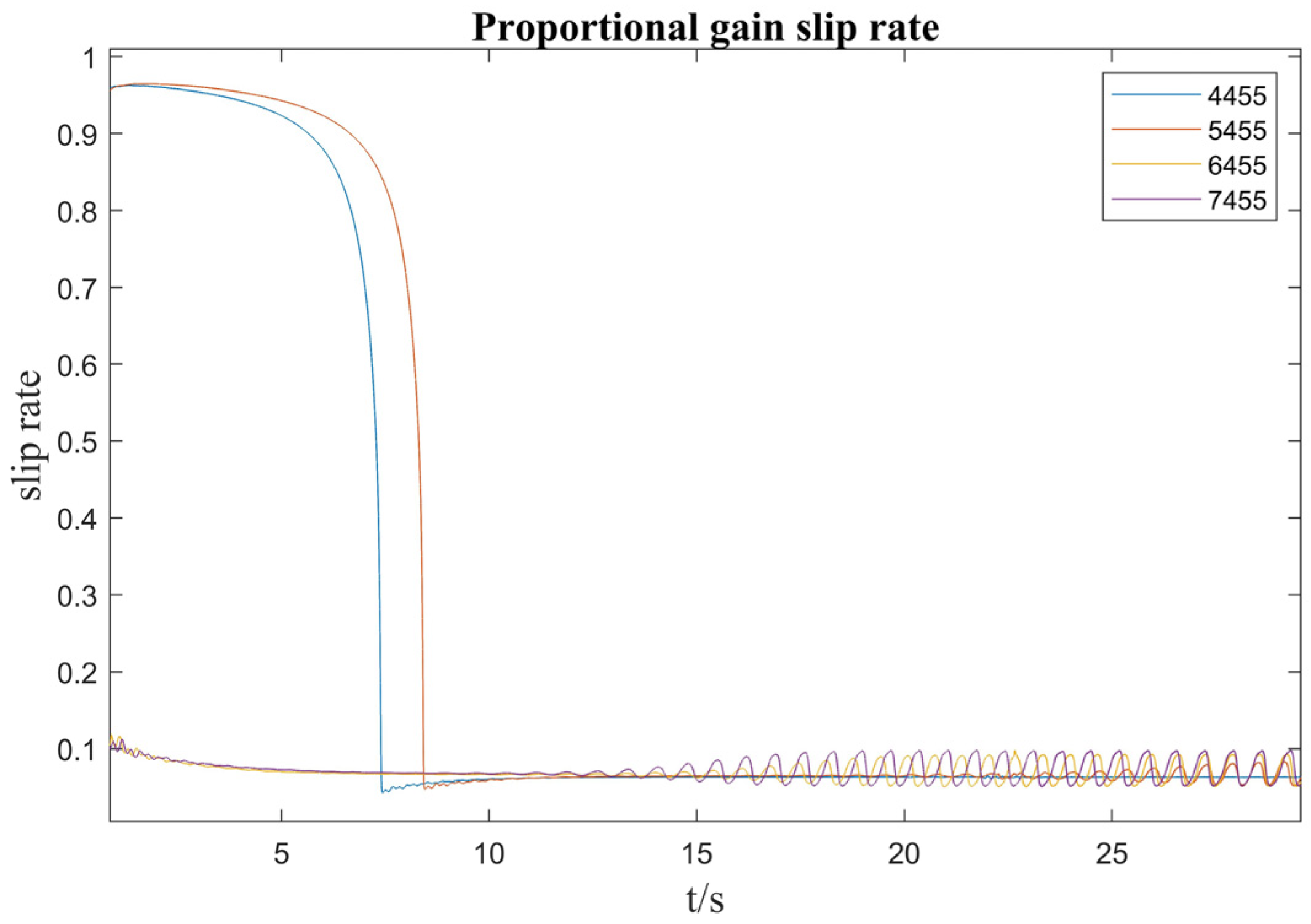
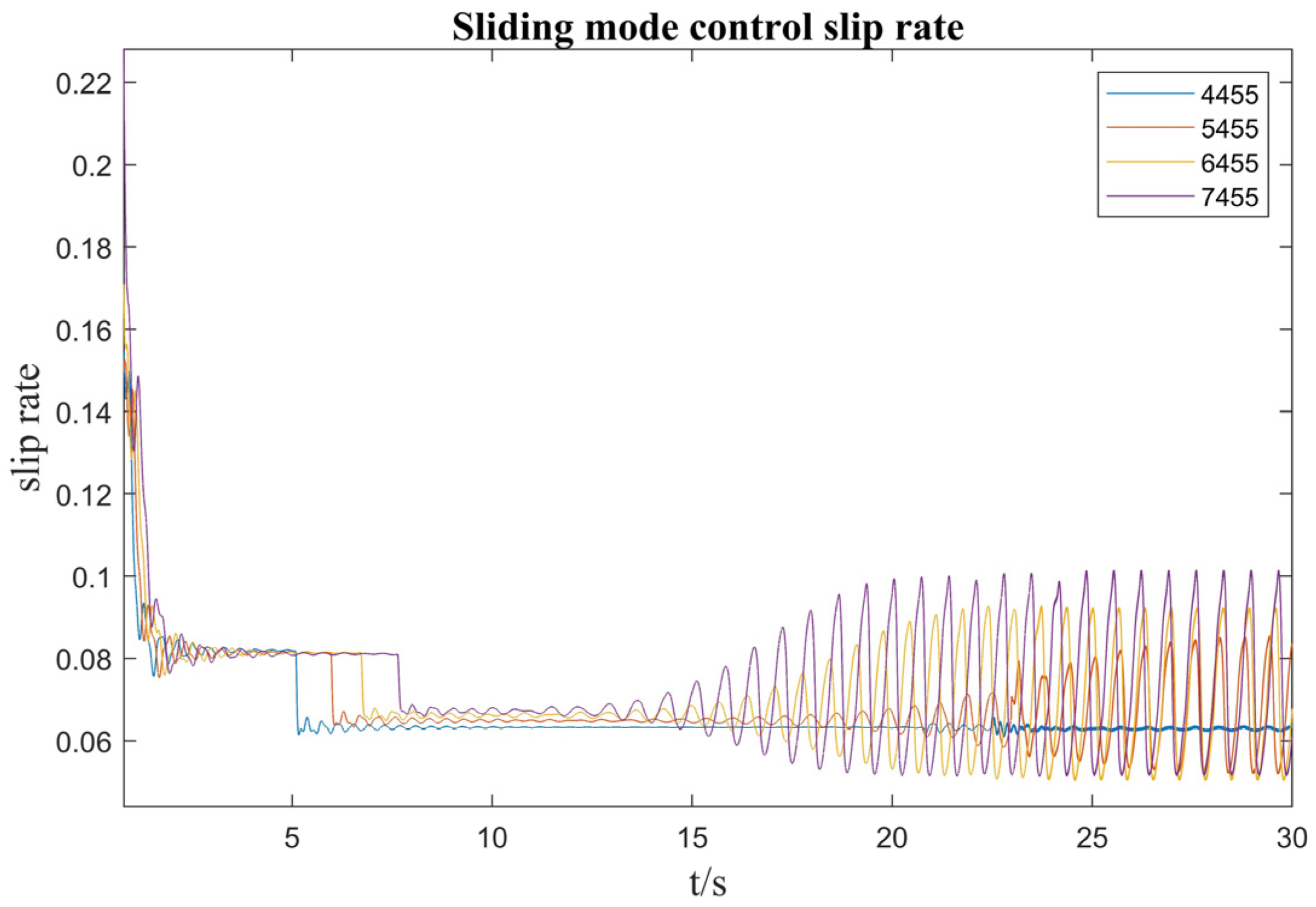
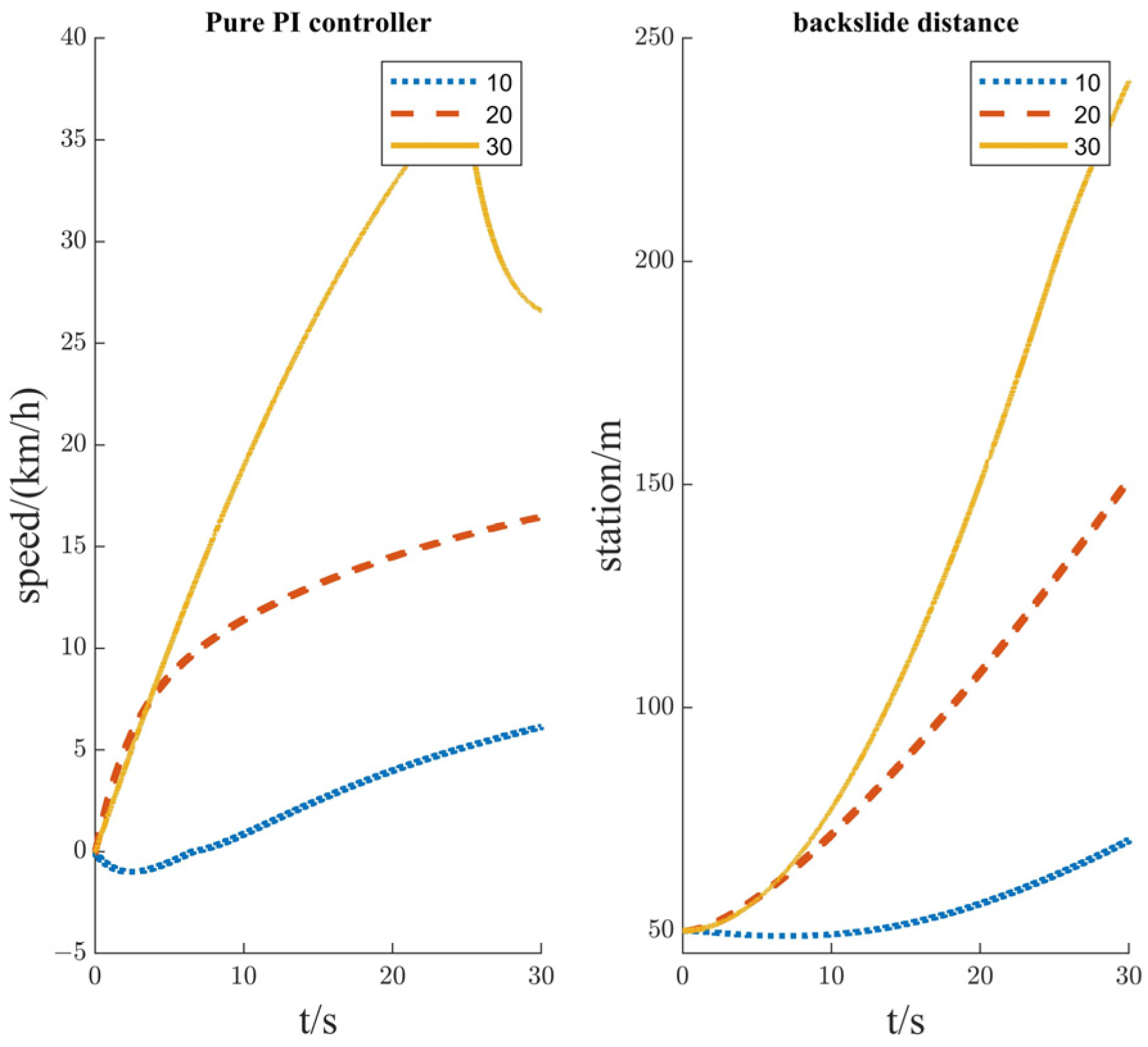
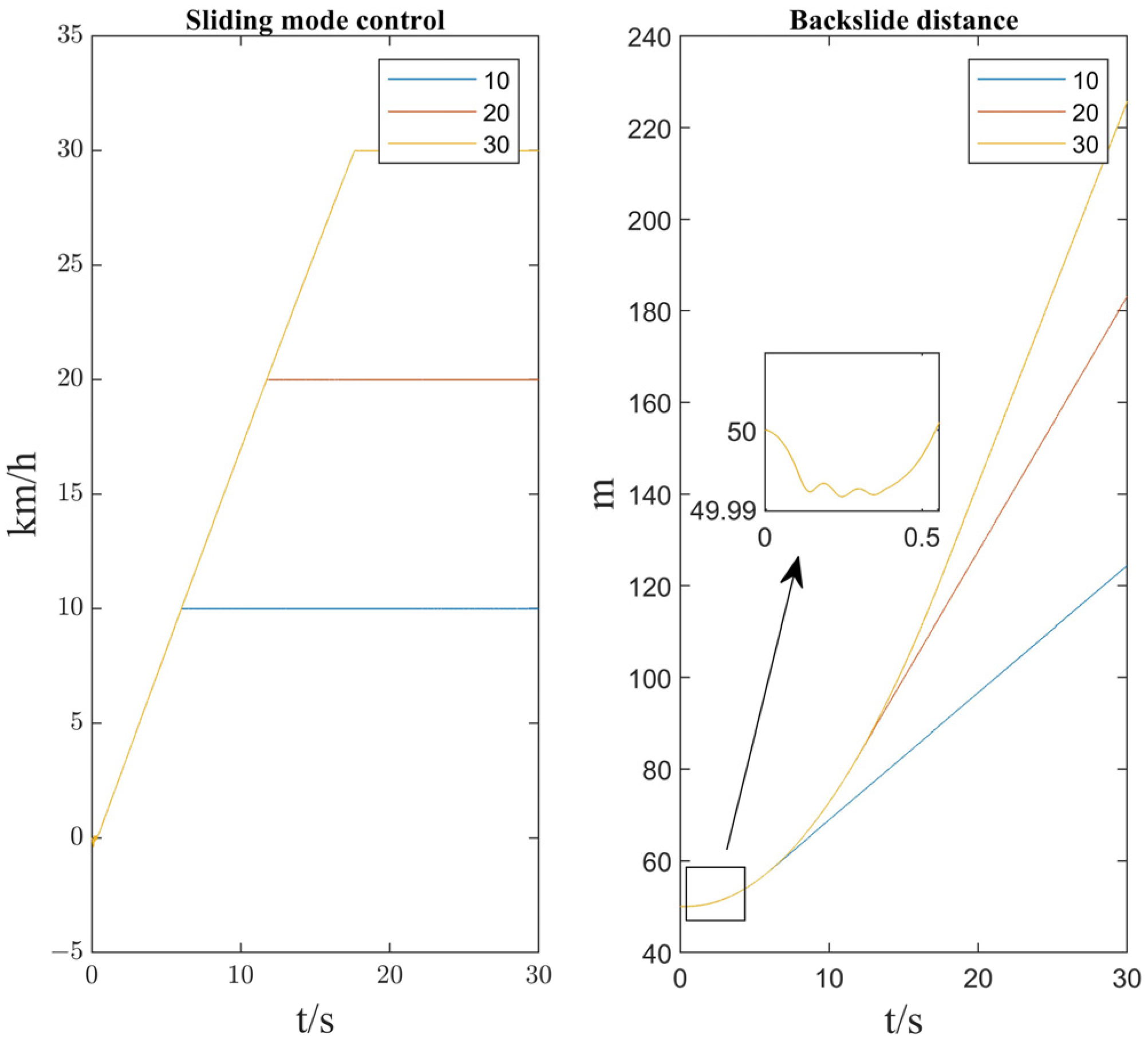
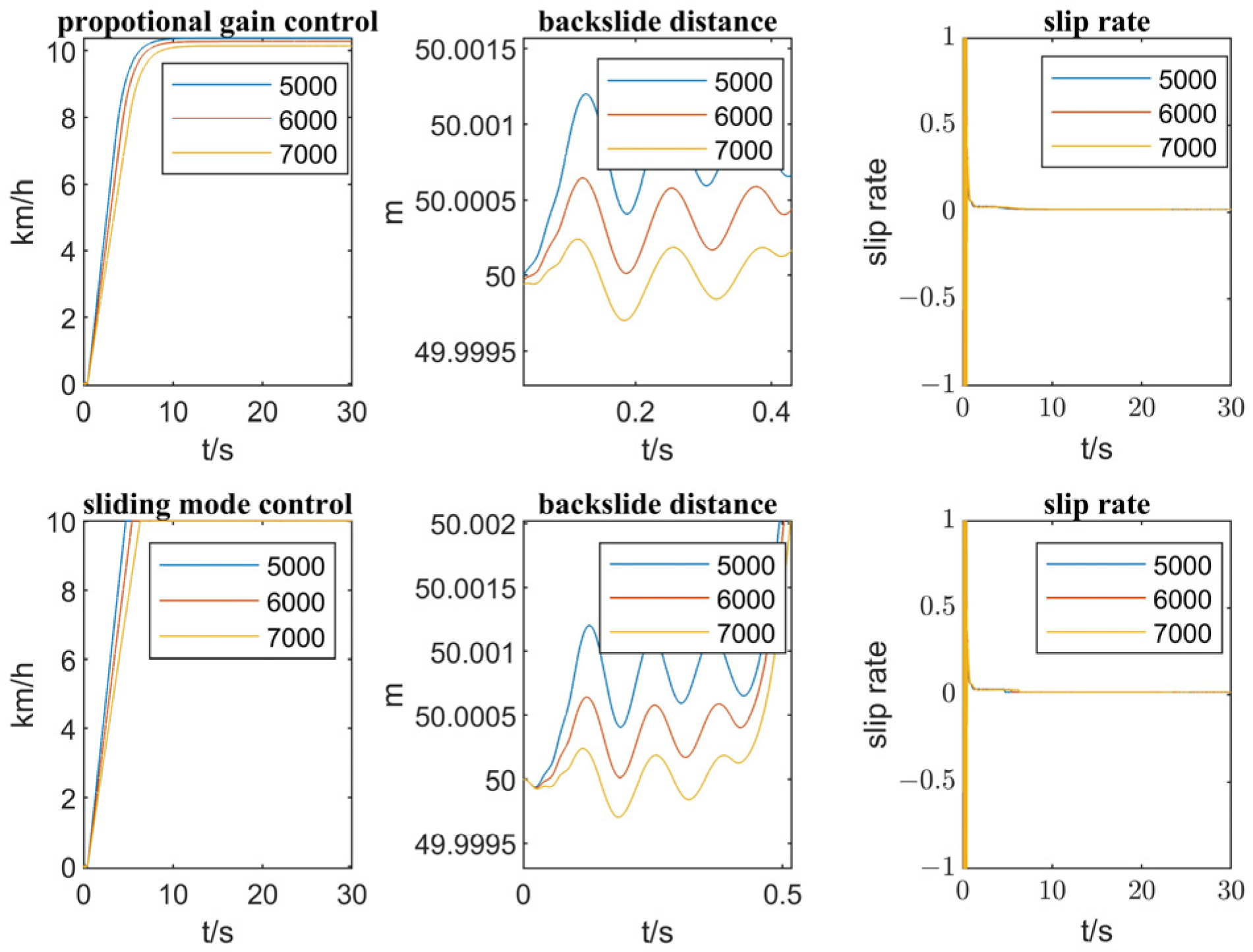
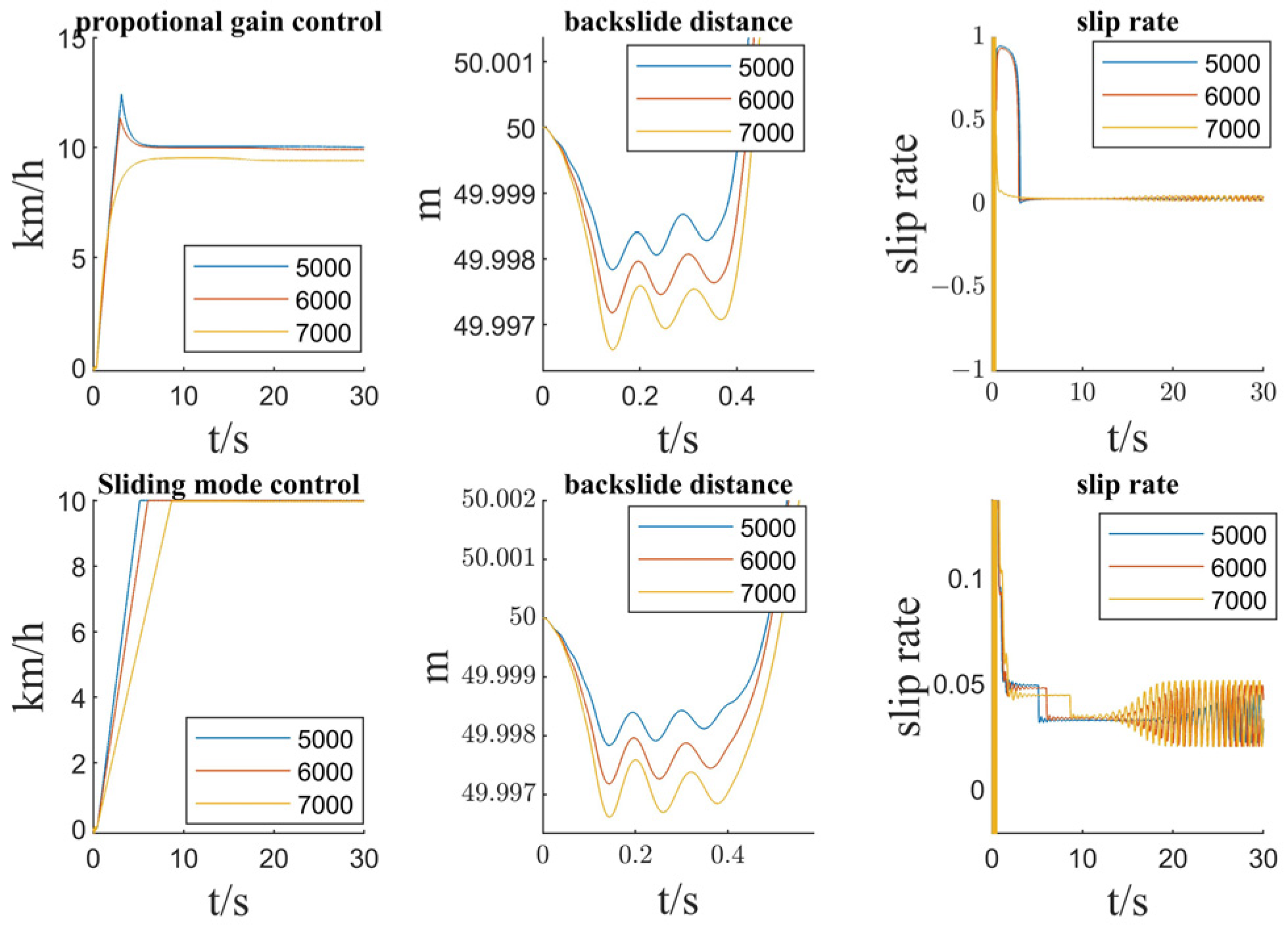
4.2. Comparison of Calibration Slope Quality Algorithms

In order to make the speed tracking effect better, the proportional gain coefficient is the parameter derived from the pre-calibration of the gradient of 5°, 7°, and 10°, and the mass of 4455 kg, 5455 kg, 6455 kg, and 7455 kg. In this section, the pure PI controller, the ramp start variable proportional control, is used for comparison with the sliding mode ramp start control. Setting the different vehicle masses as 4455 kg, 5455 kg, 6455 kg, and 7455 kg, a simulation test is carried out, and the effects of pure PI control, proportional gain control, and sliding mode control are shown in Figure 13.

From the above figure, it can be seen that the pure PI control can quickly reach within the steady-state error after the increase in vehicle mass, with a shorter rise time, and can reach 27 km/h within 15 s, and the rear skid distance is less than 0.0001 m. The proportional gain hill start control method based on the rear skid speed, which corresponds to the hill stopping torque, can quickly reach within the steady-state error after the increase in vehicle mass, with a shorter rise time, and can also reach 27 km/h within 15 s, compared with the pure PI controller, which can rapidly increase the vehicle speed and track the vehicle speed more accurately. That is, the proportional gain hill start control method based on backward skidding speed compared with the pure PI controller, the proportional gain controller can increase the speed quickly, with shorter rise time and more accurate tracking of the speed. From the point of view of the back-slip distance, the back-slip distance is less than 0.003 m. Based on the back-slip speed corresponding to the resident slope torque of the sliding mode ramp start control method in the vehicle mass increase, it can also accurately track the target speed, but the rise time is longer compared to the two methods of the comparison, and the back-slip distance is less than 0.003 m. The control method can also be used to track the target speed accurately, but the rise time is shorter than that of the two methods.

The above simulations were done on 5° slopes only with vehicles of different masses; now the tests are done on 10° slopes with vehicles of different masses. This is shown in Figure 14.

As can be seen from the above figure, in the 10° ramp, the pure PI controller has been unable to follow the 10 km/h speed of stability, and with the increase in vehicle mass, the vehicle rear skidding distance also increased. The ramp start function cannot be normal to meet. The other two control methods can track the target speed better, the rise time is shorter, the vehicle mass is the largest, the maximum rear slip distance is less than 0.01 m, and they can meet the normal ramp start function.

The slip rates for both the medium proportional gain and sliding mode control methods for ramp start tracking speed are shown in Figure 15 and Figure 16.

As shown in Figure 15 and Figure 16, it can be seen that when using the proportional gain control method based on the back-slip speed matching torque for the 4455 kg and 5455 kg vehicles, the driving force exceeds the adhesion force, the wheels slip, and the slip rate is more than 90% in the first 5 s, which makes the vehicle driving unstable, whereas when using the sliding-mode control method based on the back-slip speed matching torque for the 4455 kg, 5455 kg, 6455 kg, and 7455 kg vehicles, the driving force of the vehicle is less than the adhesion force and the slip rate is less than 20%, which ensures stable driving of the vehicle.

Above, only the self-driving commercial vehicles with different vehicle masses on a 10° slope tracking the same speed have been simulated for comparison, now the self-driving commercial vehicles with a vehicle mass of 5455 kg on a 10° slope tracking different speeds have been tested, and the tracking effect of the pure PI controller is shown in Figure 17.

As shown in Figure 17, it can be seen that the pure PI controller is not able to respond well to the vehicle speed demand due to the change in gradient and mass and has a large backward skidding distance.

The control effect of the proportional gain hill start control and the sliding mode control method based on the rear slip speed corresponding to the dwell moment is shown in Figure 18.

As shown in Figure 19, it can be seen that the proportional gain method based on the rear slip speed matching torque can respond to the vehicle’s demand for different speeds in a shorter period of time, and in the case of 5455 kg vehicle mass, the rear slip distance is less than 0.01 m, and the effect of hill start is better compared to the pure PI controller.

Comparison of the three control methods from the dimension of different masses and different speeds shows that, in the proportional gain coefficient calibrated to the slope mass, the proportional gain ramp start control based on the back-slip speed corresponding to the parking moment can have a smaller back-slip distance, can track the target speed stably, and has less wear and tear on the braking system; similarly, the sliding-mode ramp start control based on the back-slip speed corresponding to the parking moment is also more effective, but the wheel skidding will occur with the larger gradient for ramp start control. Similarly, the sliding mode hill start control method based on the back-slip speed corresponding to the standing moment is also more effective, but the proportional gain hill start control based on the back-slip speed corresponding to the standing moment will have a wheel slip situation for a larger gradient, and the stability is poor. The pure PI controller cannot adaptively adjust the motor torque with the change of gradient and mass, and the hill start control effect is poor. The parameters in the above proportional gain control are pre-calibrated parameters, which have a better tracking effect on the target speed and will be discussed in the next section from the uncalibrated condition.

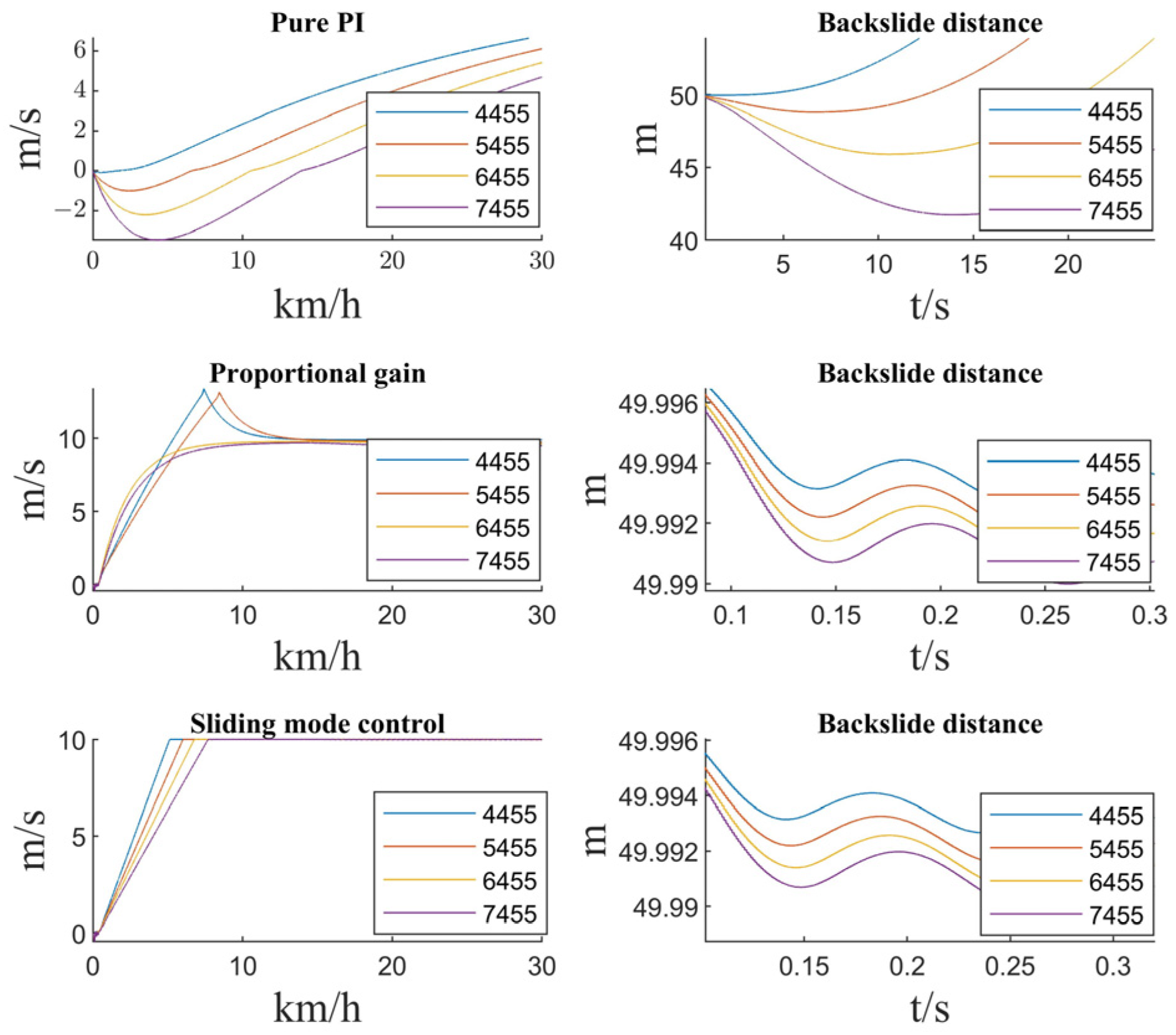
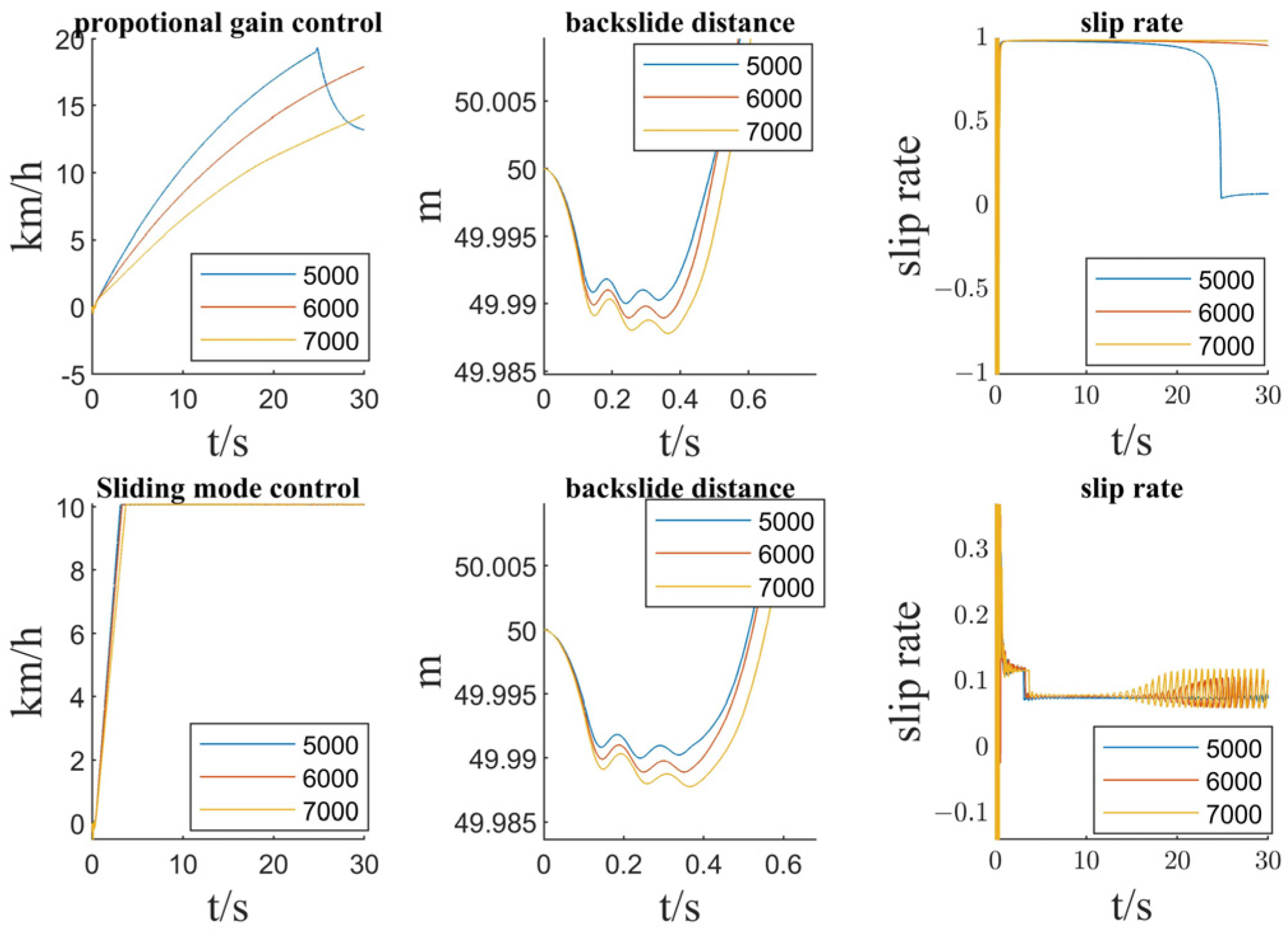
4.3. Comparison of Uncalibrated Slope Quality Algorithms

From the previous section, the proportional gain control method based on the back-slip speed matching torque is calibrated to follow the target speed when the gradient is 5° and 10° and the mass is 4455 kg, 5455 kg, 6455 kg, and 7455 kg to ensure the control performance of the vehicle, but the control effect of the control method for the un-calibrated gradient and mass needs to be further explored, and for this reason, the gradient is set to be 3°, 6°, and 12°, and the mass to be 5000 kg, 6000 kg, and 7000 kg in this section. For this reason, in this section, the slope is set to be 3°, 6°, and 12°, and the mass to be 5000 kg, 6000 kg, and 7000 kg, respectively. Since the pure PI cannot adaptively adjust the motor torque with the change of slope and mass, this section will not discuss this method and will only conduct a comparative study on the proportional gain control based on the back-slip speed matching torque and the sliding mode control based on the back-slip speed matching torque. The initial position of the vehicle is set to 50 m, and now the two methods are used for a 3° ramp with 5000 kg, 6000 kg, and 7000 kg.

Simulation experiments are carried out for different masses of self-driving commercial vehicles tracking the target speed (10 km/h) and the simulation results are shown in Figure 20.

From Figure 20, it can be seen that in the small angle ramp for the uncalibrated slope and mass, the proportional gain control method based on the back-slip speed matching torque and the sliding mode control method based on the back-slip speed matching torque are able to complete the tracking of the target speed, and the back-slip distance is less than 0.0005 m, and the slip rate is less than 20%. At this time, the vehicle can obtain a larger longitudinal force and lateral force.

The two methods are simulated for a 6° ramp, 5000 kg, 6000 kg, and 7000 kg different mass tracking target speed 10 km/h. The simulation results are shown in Figure 21.

As can be seen from Figure 21, in the medium angle ramp for the uncalibrated slope and mass, although the proportional gain control method based on the rear slip speed matching moment can complete a better tracking of the target speed, and the slip distance is less than 0.004 m, but for the vehicle mass of 5000 kg and 6000 kg, it will have a starting wheel slip situation, which is more unstable, and the sliding mode control method based on the rear slip speed matching moment can complete the tracking of the target speed, and can make the slip distance less than 0.004 m, and the vehicle driving the whole process slip rate is less than 20%, to keep can provide the vehicle with a greater speed. The sliding mode control method based on the torque can not only complete the tracking of the target speed but also make the rear skid distance less than 0.004 m and the vehicle driving the whole process of the slippage rate less than 20% to maintain the ability to provide the vehicle with a large longitudinal force and lateral force.

The two methods are simulated for 12° ramp, 5000 kg, 6000 kg, and 7000 kg different mass tracking target speed 10 km/h. The simulation results are shown in Figure 22.

As can be seen from Figure 22, in the larger gradient ramp for the uncalibrated gradient and mass, the proportional gain control method based on the back-slip speed matching torque can no longer achieve better tracking of the target speed, and 5000 kg, 6000 kg, and 7000 kg three kinds of mass have appeared in the case of wheel slip, which is more unstable, and the sliding mode control method based on the back-slip speed matching torque still is. The sliding mode control method based on the back-slip speed matching torque can complete the tracking of the target speed, the back-slip distance is less than 0.004 m, and the vehicle traveling the whole process of the slip rate is less than 20%, to maintain the ability to provide the vehicle with a large longitudinal force and lateral force.

5. Conclusions

Aiming at the skidding problem caused by the uncertainty of the vehicle driving moment on the slope triggered by the change in the vehicle mass and the change in the gradient of the self-driving commercial vehicle, a new ramp start control strategy is proposed, and a sliding-mode variable structure controller is designed to calculate the standing moment. The standing moment obtained is introduced as the start moment to obtain the standing moment required by the vehicle at different weights and different gradients, and then the sliding-mode variable structure controller is used to calculate the moment required to follow the target speed. Then, a sliding mode variable structure controller is used to calculate the torque required to follow the target speed and is compared with the slope mass-calibrated and un-calibrated proportional gain control controller and the pure PI controller. The simulation results show that the proposed sliding mode ramp start control method based on the backward sliding speed corresponding to the standstill torque can not only complete the ramp start function under different slopes and vehicle masses but also stably follow the speed of the vehicle.