Abstract
As important auxiliary equipment, rehabilitation robots are widely used in rehabilitation treatment and daily life assistance. The rehabilitation robot proposed in this paper is mainly composed of an omnidirectional mobile platform module, a lower limb exoskeleton module, and a support module. According to the characteristics of the robot’s omnidirectional mobility and good stiffness, the overall kinematic model of the robot is established using the analytical method. Passive and active training control strategies for an omnidirectional mobile lower limb exoskeleton robot are proposed. The passive training mode facilitates the realization of the goal of walking guidance and assistance to the human lower limb. The active training mode can realize the cooperative movement between the robot and the human through the admittance controller and the tension sensor and enhance the active participation of the patient. In the simulation experiment, a set of optimal admittance parameters was obtained, and the parameters were substituted into the controller for the prototype experiment. The experimental results show that the admittance-controlled rehabilitation robot can perceive the patient’s motion intention and realize the two walking training modes. In summary, the passive and active training control strategies based on admittance control proposed in this paper achieve the expected purpose and effectively improve the patient’s active rehabilitation willingness and rehabilitation effect.
1. Introduction
As typical rehabilitation equipment with human–robot interaction ability, rehabilitation training robots can help patients with lower limb movement disorders according to the preset scientific training trajectory. Lower limb paralysis, as one of the movement disorders, is common in the elderly with stroke, and hemiplegia is more common [1]. Clinical medicine shows that accurate and timely repeated rehabilitation training can promote the compensation or reorganization of nerve tissue function so that patients can improve their motor control ability and finally restore walking function [2,3]. Compared with the time-consuming and low efficiency of artificially assisted rehabilitation, the introduction of lower limb rehabilitation robots can not only reduce the manpower and material resources but also standardize the treatment method to accelerate the recovery of patients’ independent walking ability.
At present, extensive research has been carried out on robot technology and applied to the field of rehabilitation, and various lower limb rehabilitation robots have been developed. Examples include standing lower limb rehabilitation robots Lokomat [4], ReWalk [5], and Ailegs [6], as well as sitting lower limb rehabilitation robots Motion Maker [7,8], LR2 [9], and LRR-Ro [10]. These rehabilitation robots can provide passive training, active training, and auxiliary training [11]. The sitting and lying lower limb rehabilitation robot can reduce the unnecessary weight load on the body and improve the comfort of the person, as well as facilitate exercise and increase the range of motion of the lower limb joints. The standing lower limb rehabilitation robot can provide the most real walking experience for patients with exoskeletons. The rehabilitation robot presented in this paper [12] is mainly composed of an omnidirectional mobile platform module, a lower limb exoskeleton module, and a support module, which can provide patients with body support and exoskeleton-assisted walking. The reason for the development of this specific rehabilitation robot is that compared with the existing types of rehabilitation robots, few studies combine the advantages of an omnidirectional mobile platform and lower limb exoskeleton for application in actual rehabilitation scenarios. This advantage includes omnidirectional movement, good stability, good repetition and consistency of movements, rich training modes, and good training feedback.
The rehabilitation robot-assisted training mode is divided into passive training and active training according to the rehabilitation stage. Patients need to receive passive and active training in different recovery stages [13]. Passive training is generally used in the early rehabilitation of patients. At this stage, the muscle strength of the patient’s leg is small, and the coordination between nerves and muscles is not enough. The purpose of the passive training method is that when the patient is connected to the rehabilitation robot by wearing, the device can drive the patient’s lower limbs to train according to the prescribed rehabilitation gait, thereby improving athletic ability and reducing muscle atrophy [14]. Wang et al. [15] developed a bedside rehabilitation robot to cope with the sports rehabilitation challenges of patients with lower limb paralysis. The equipment adopts a freely rotating leg support mechanism, which can reduce the load on the ankle caused by gravity, and it involves a two-stage series elastic mechanism under the foot support to provide passive compliance output of the robot power, allowing for more natural movement and reducing the risk of injury. Liaoyuan Li et al. [16] used sliding mode adaptive and speed feedforward plus a PID control strategy based on the RBF neural network to realize terminal trajectory tracking. On this basis, admittance control was added to realize multimode active and passive compliant tracking control of force threshold control, which also ensured the safety of patients during human–computer interaction.
For patients who have restored part of the lower limb muscle strength, the active training control mode pays more attention to the patient’s movement intention than the passive training control. Only by fully mobilizing the patient’s willingness to recover can the patient achieve better results in rehabilitation training. Active training control usually uses force–position hybrid control and impedance control [17]. Force–position hybrid control refers to the simultaneous control of the contact force and position of the lower extremity exoskeleton to achieve the tracking and control of the desired position and the desired contact force. However, there is an instability problem resulting from switching between position control and force control in the control process. For example, the American ALEX lower limb exoskeleton adopts a force–position hybrid control strategy in the active training mode [18] to track the desired gait trajectory and reduce the human–computer interaction force. Mirzaei et al. adopted an adaptive impedance control method in the lower limb rehabilitation exoskeleton [19], which reduced the interaction force between the lower limb exoskeleton and the ground and improved the stability of active training walking. Japan’s HAL [20] robot and the BLEEX [21] robot, developed in the United States, also use impedance control as the main method of active training mode. At the same time, based on impedance control, the University of Electronic Science and Technology of China and Shanghai University have proposed a variable impedance control method based on PI2 and an impedance control strategy in multi-sensor mode, respectively, which further improves the application of this technology in passive and active training modes [22,23]. Amiri and Ramli developed a robust adaptive controller integrated with an admittance model and initialized the parameters of the ASIA controller using the swarm antenna search method, which can enhance the functionality and usability of exoskeletons in helping humans walk [24]. The limitation of this rehabilitation robot is that the exoskeleton structure does not have adjustable links, which does not allow for testing the controller with a more diverse patient population. The results demonstrate the effectiveness of the proposed method in terms of control performance, steady-state error reduction, and robustness. Jyotindra Narayan et al. proposed a novel human-to-human cooperation framework based on admittance and trajectory control schemes, in which the admittance model was designed in the outer ring to recast the desired human trajectory into a reference trajectory, and the robust adaptive controller was designed in the inner loop to track the reference gait trajectory under parameter uncertainty and external perturbation [25]. The limitation of this rehabilitation robot is that the control of low admittance is more likely to allow the subject to participate in the training process more easily, with a relatively single training control mode. Experimental results show that the human cooperative control based on a robust adaptive thrust reverser is more promising than the human cooperative controller based on variable structure adaptive robustness.
To meet the different rehabilitation training needs of patients, this study proposes a control strategy with passive and active training modes based on admittance control. Compared with the two abovementioned rehabilitation robots based on admittance control [24,25], the new rehabilitation robot proposed in this study has an adjustable length of link in its structure and therefore can adapt to more subjects and provide precise cam trajectory to achieve an accurate gait mechanism; it can also accurately recognize people’s movement intentions when in control so that passive and active modes can be directly switched during rehabilitation training. The passive mode rehabilitation robot can assist or guide the patient’s legs to walk, while the active mode rehabilitation robot can detect the person’s movement intention and follow the person’s leg movement. The two training modes of the rehabilitation robot not only ensure the stability of the system when switching between active and passive training modes but also improve the rehabilitation effect of patients.
2. Mechanical Structure
This paper introduces a new omnidirectional lower limb rehabilitation robot that has both good center-of-gravity control and the stiffness and hardness of an exoskeleton. During patient training, rehabilitation robots can provide support and boost for patients. In addition, the proposed rehabilitation robot can move in any direction along the plane and at the same time realize exoskeleton assistance and guide the patient to ideally complete the gait rehabilitation training. The rehabilitation robot is mainly composed of three parts: (1) an omnidirectional mobile platform module, (2) a lower limb exoskeleton module, and (3) a body support module. The overall structure is shown in Figure 1.
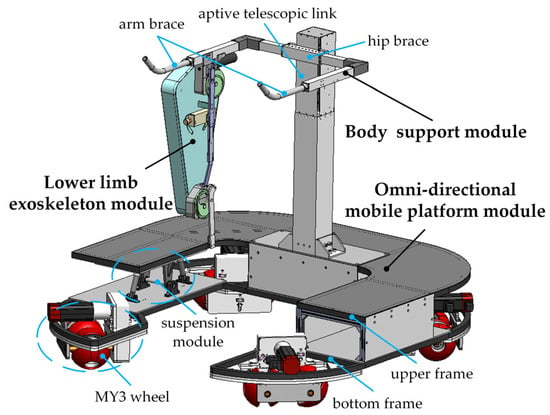
Figure 1.
Omnidirectional mobile lower limb exoskeleton robot.
2.1. Body Support Module
The body support module is mainly composed of an adaptive telescopic link, a hip brace, an arm brace, and a belt, as shown in Figure 1. The adaptive telescopic link can automatically adjust the height of the body support module according to the different heights of patients. The hip brace and the arm brace can provide partial support in the vertical direction. The belt is used to connect the person to the rehabilitation robot and prevent the body from leaning forward.
2.2. Lower Limb Exoskeleton Module
Considering the gait of the human body during normal walking and the movement posture of the hip and knee joints, it can be seen that the thighs and calves reciprocate within a certain range. Therefore, the movement of the lower limb exoskeleton module can be simplified to a continuous rotation from a grooved cam (active member) to a reciprocating movement or oscillation converted into a follower. The structure of the lower limb exoskeleton module can be divided into the following two parts, namely a leg adjustment mechanism and a hip and knee mechanism, as shown in Figure 2.
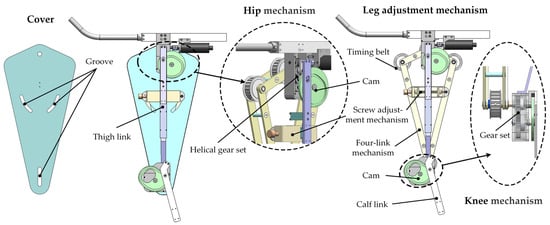
Figure 2.
Lower limb exoskeleton module.
2.2.1. Leg Adjustment Mechanism
The purpose of designing a leg adjustment mechanism is to meet the physiological characteristics of human beings and the needs of different patients so that it can be adjusted according to the height and body shape of the user. The structure is mainly composed of a four-link mechanism, a screw adjustment mechanism, a timing belt, and a cover. The adjusting mechanism involves a two-way lead screw, which is connected to the four-link mechanism through the lead screw nut. When the nuts are twisted in different directions, the rotating pairs act at the junction of the three grooves on the slideway trajectory on the cover. At this time, the four-link mechanism will deform, thus changing the center distance of the synchronous pulley, to achieve the purpose of adjusting to the leg length of different people.
2.2.2. Hip and Knee Mechanism
According to the posture analysis of normal gait, it is found that the movement with the largest rotation angle amplitude at the hip and knee is flexion and extension movement. Therefore, we referred to the relevant data required for the design of exoskeletons, and the data on the human range of motion in medical treatment/rehabilitation were derived from the literature [26,27]. The rotation movement and extension movement of the thigh and calf have a smaller defense range, and the two degrees of freedom can be ignored. Therefore, the exoskeleton mechanism can be simplified into a two-link structure, in which the hip mechanism includes a 45° helical gear set, a cam, and a thigh link. The knee is designed as a follow-up mechanism, which mainly includes a timing belt, a gear set, a cam, and a calf link. The outer curve of the cam was obtained by fitting the Fourier function to the gait trajectory of a person walking normally. The movement of the exoskeleton drives the motor located at the hip, which transmits power to the helical gear set to drive the cam mechanism and the timing belt, which in turn transmits the power to the calf. Then, the thigh and calve are driven by a link to the cam. Finally, the cam movement is converted into the flexion and extension angle of the thigh and the flexion movement of the calf.
2.3. Omnidirectional Mobile Platform Module
The goal of the omnidirectional mobile platform module is to solve the problem of low physical stability due to the reduced performance of the patient’s torso and lower limb support to ensure the patient’s walking balance. As shown in Figure 1, the mobile platform is mainly composed of four MY3 wheels [28], a bottom frame, a suspension module, and an upper frame. The MY3 wheel used in this study is a new type of omnidirectional wheel, which retains the crown part of the wheel while taking advantage of the complementarity between the crowns to achieve movement. The bottom frame is divided into two parts: The left side is connected to the upper frame by profile, and the right side is connected to the upper frame by a suspension module. When either omnidirectional wheel is driving into an obstacle, the MY3 wheelset on the same side still maintains good contact with the wheels on the ground.
3. Kinematics
3.1. Omnidirectional Mobile Platform Kinematics
The kinematic model of the platform adopts the velocity equation method, which is simplified to reduce the complexity of the equation and establish the equation under ideal conditions. It is assumed that the wheels of the platform do not slip during movement, and the center of mass of the robot coincides with the geometric center. As shown in Figure 3, the world coordinate system fixed on the ground and the kinematic coordinate system fixed at the geometric center of the robot are established. The coordinate system represents the position of the contact point between each MY3 wheelset on the platform and the ground.
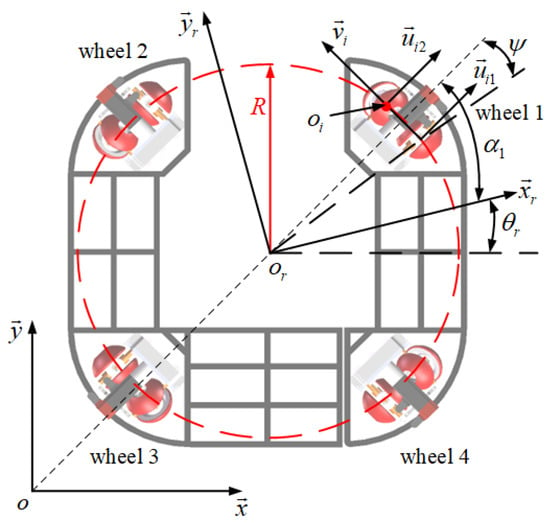
Figure 3.
Omnidirectional mobile platform kinematic model.
The pose of the platform in the world coordinate system can be expressed as , and the movement speed of the platform can be expressed as follows:
where represents the attitude angular velocity of the platform in the world coordinate system. represents the radius of the platform. indicates the deflection angle of the wheel unit. indicates the active driving direction of the wheel. indicates the passive direction of rotation of the wheel. In a counterclockwise direction, represents the number of wheelsets, and represents the number of wheels in the wheelset.
Assuming that there is no relative sliding between the wheels and the ground, the contact points between each wheel and the ground can be expressed as follows:
where indicates the speed of the wheel contact point.
The kinematic equations of the mobile platform can be obtained by combining Equations (1) and (2) as follows:
Equation (3) can be simplified to a complete kinematic equation as follows:
where represents the positive angle between the centerline of the wheel and the x-axis. represents the radius of the wheel, and represents the Jacobian matrix of the platform. The inverse kinematic equation is as follows:
where represents the pose coordinates of the four-wheeled moving platform, and represents the rotation angle of four groups of MY wheels.
3.2. Lower Limb Exoskeleton Kinematics
The lower limb exoskeleton module is designed with a hip and knee mechanism. By establishing the kinematic model of the lower limb exoskeleton module, the correspondence between the hip drive motor and the lower limb posture can be obtained. The kinematics of the lower limb exoskeleton module are solved by using the modified Denavit–Hartenberg (MD-H) [29] method to construct the base coordinate system {e} and the joint coordinate system {4}, {5}, as shown in Figure 4. P indicates the end of the joint. The hip brace and lower limb exoskeleton module are simplified into a three-link mechanism. The corresponding coordinate system is shown in Figure 4.
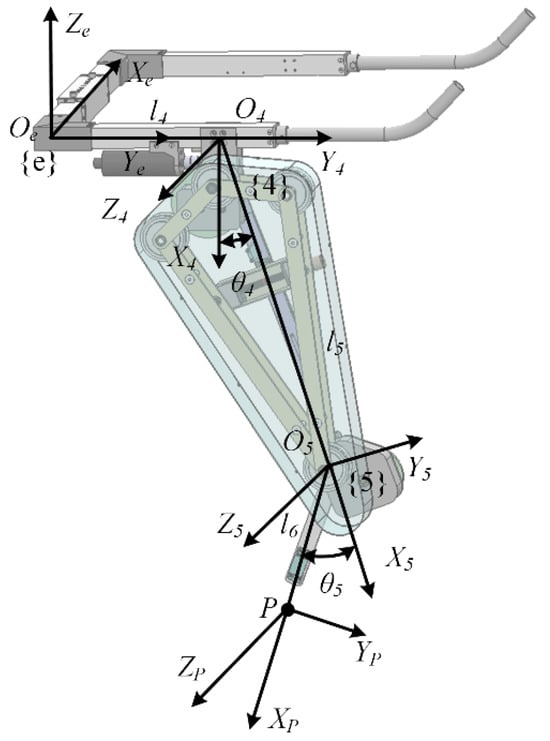
Figure 4.
Lower limb exoskeleton kinematic model.
From the coordinate system of the exoskeleton module, the parameters are determined and listed in Table 1.

Table 1.
Lower limb exoskeleton coordinate system parameters.
The formula of the transformation matrix between the lower limb links is as follows:
Bringing the MD-H parameter into the kinematic equation of the endpoint of the lower limb, link 2 relative to the base coordinate system is obtained as follows:
where , ; , , and represent the length of the hip support module and the length of the thigh and calf link; and represent the angle of the flexion and extension of the hip and knee.
When the end position is known, the joint angle of the lower limb exoskeleton can be solved by inverse kinematics with and as follows:
where , .
3.3. Overall Kinematics
During rehabilitation training, the patient and the robot system should maintain a unified and coordinated movement at all times. Therefore, it is necessary to establish an overall kinematics for the rehabilitation robot to ensure that the patient and the robot have a synchronized movement rhythm.
In the process of establishing the overall kinematics, the platform and the lower limb exoskeleton module can be considered as a whole. The world coordinate system is established on the ground, and the moving coordinate system , is set at the center of the trolley. The rotational coordinate system {3} is set on the support column. Thus, four coordinate systems , , and are defined. In Figure 5, there are a total of six coordinate systems, which have different names.
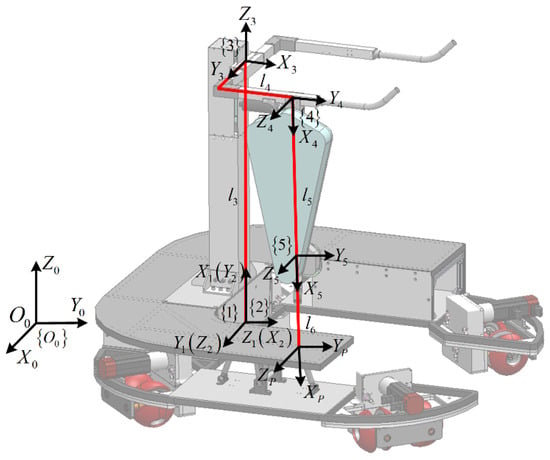
Figure 5.
Overall kinematic model.
According to the established coordinate system, the homogeneous transformation matrix of the corresponding joint is written, and then the positive kinematic equation of the end of the lower limb link relative to the base coordinate system is obtained as follows:
where , , and .
The overall inverse kinematics is derived as follows: When the last matrix is a known matrix, the matrix does not contain unknowns, so the transformation is as follows:
By transforming Equation (9), we can obtain the angular changes , , , , and . The joint angle is solved as follows:
where , .
The differential transformation method can be used to solve the robot’s Jacobian matrix. For the rotating joint, the differential rotation of the robot is . For moving joints, the differential movement is . The differential motion equation of the origin of the terminal coordinate system can be obtained according to the relationship between and as follows:
Therefore, the Jacobian matrix of the robot as a whole is as follows:
When the joint is a rotational joint, the Jacobian matrix is as follows:
When the joint is mobile, the Jacobian matrix is as follows:
The velocity Jacobian matrix derived from the above equation can link the movement between the lower limb exoskeleton module and the mobile platform to achieve coordinated movement.
3.4. Lower Limb Workspace Analysis
According to the gait theory, it is known that the swing angle of the hip joint of normal people ranges from −25° to 30°, and the swing angle of the knee joint ranges between −60° and 0°. Based on these data, the motion space of the outer skeleton lower limb module can be simulated and analyzed to determine the motion space required for the swing of each joint when working. The motion space of the robot can be obtained by using software to build a simulation program, as shown in Figure 6. To avoid damaging the robot or the patient, the working range must be within the movement space. The blue part of Figure 6 represents the space required for the movement of lower limbs during normal human gait, and the red part represents the space required for the movement of the exoskeleton module. It can be concluded that the range of space required for the movement of the exoskeleton module meets the corresponding requirements.
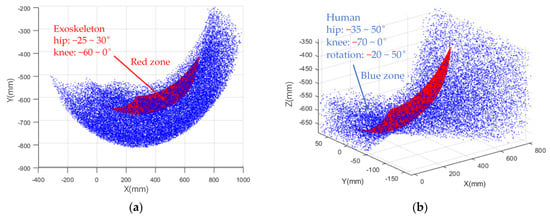
Figure 6.
Lower limb workspace: (a) motion range in 2D coordinates; (b) motion range in 3D coordinates.
4. Control Method
The rehabilitation robot can provide active and passive training for patients. The passive training mode involves the treatment of the patient’s lower limb by connecting it to the leg of the rehabilitation robot, and the mechanical lower limb provides traction to drive the movement of the affected limb to achieve rehabilitation training. During the active training mode, patients need to rely on their lower limb strength to walk, and the robot is responsible for maintaining the patient’s balance.
4.1. Control Hardware
For the rehabilitation robot, the control hardware is not only the premise and foundation of the control system platform to control the robot but also the core part of the robot’s movement. The hardware process of the rehabilitation robot control is shown in Figure 7.
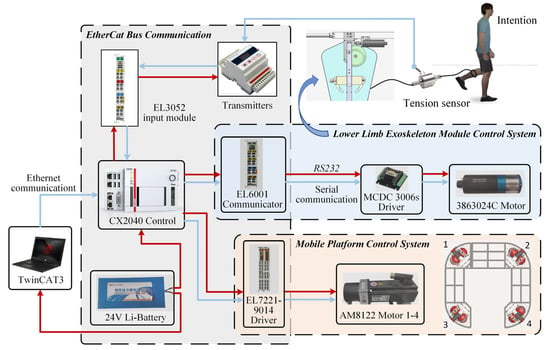
Figure 7.
Rehabilitation robot control hardware.
There is sufficient space between the top of the mobile platform and the chassis frame, and a 24 20 Li-battery, a computer, a CX2040 controller, 4 EL7221-9014 servo drive modules, 4 AM8122 servo motors(The equipment comes from Beckhoff, Shanghai, China.), and related electrical devices are placed inside. The mobile platform can be moved through Ethernet communication between the computer, the controller, and the servo motor.
The lower limb exoskeleton module uses 1 FAULHABER motor, 1 MCDC3006RS encoder, and 1 EL6001 serial port module, which communicates with the controller through RS232(The equipment comes from FAULHABER, Guangzhou, China.). The human movement intention and the contact force are collected with a tension sensor with a range of 0–30 kg and a sensitivity of 2 mV. The transmitter converts the contact force into a current analog signal and transmits it to the controller through the corresponding EL3052 module, and the current analog acceptance range is 4–20 mA.
4.2. Admittance Control
Admittance control does not directly change the force between the end effector and the external environment [30] and is a more common control method in practical applications. The inertia parameters of the robot in the admittance model parameters usually do not change, but the motion of the rehabilitation robot can reach the desired goal by adjusting the damping parameters and stiffness parameters. The contact effect between the robot admittance controller and the human body is equivalent to a “mass–spring–damping” system [31]. Then, the admittance model expression of the robot on any coordinate axis in the cartesian coordinate system is as follows:
where , , and represent the inertia, damping, and stiffness matrices of mechanical systems; represents the desired position of the rehabilitation robots in the world coordinate system; represents the actual position of the system; represents the desired velocity of the robot in the world coordinate system; represents the actual speed of the system; represents the desired acceleration of the robot in the world coordinate system; represents the actual acceleration of the system; represents the actual contact force measured by the sensor; and represents the expected contact force.
According to the relevant characteristics of the second-order system of admittance control and the overall dynamics of the robot, the robot can be regarded as a whole with four degrees of freedom for dynamic modeling of the Lagrangian equation, and the formula is as follows:
where represents the Lagrangian function; represents the kinetic energy of the system; and represents the potential energy of the system. represents the torque of the robot drive motor. represents the dissipation energy of the system, and .
The kinetic energy of the rehabilitation robot system can be regarded as the sum of the translational kinetic energy and the rotational kinetic energy of the center of mass, as shown in the following formula:
where represents the mass of the mobile platform; represents the mass of the lower limb link; represents the inertia moment of mobile platform; represents the inertia moment of the MY3 wheel; represents the lower limb link inertia; and represents the angular velocity of the lower limb.
The kinetic energy of the platform is expressed as follows:
In the calculation of lower limb dynamics, it is assumed that the mass of the link is concentrated on a microelement with a density of and a length of . Its position in the world coordinate system is , and its position in the link coordinate system is . The kinetic energy of the infinitesimal of the link in the world coordinate system is expressed as follows:
where represents the inertia matrix of the lower limb exoskeleton link.
In the whole mechanical system, only the two-link lower limb exoskeleton module generates gravitational potential energy, and the lower limb module potential energy can be expressed as follows:
The dissipated work of the mechanical system is generated by the friction of the MY3 wheel in contact with the ground and the damping work accomplished by the lower limb exoskeleton drive system, which is calculated as follows:
According to Equation (17), the system’s mass matrix, stiffness matrix, and damping matrix are calculated as follows:
The second-order “mass–spring–damping” lower limb exoskeleton impedance control model is shown in Figure 8.
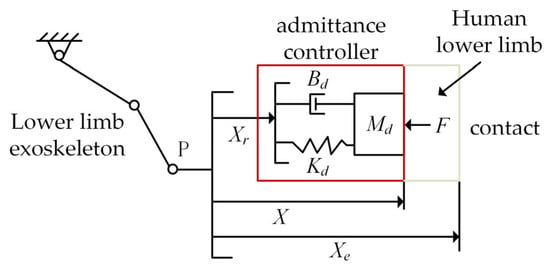
Figure 8.
Model of the interaction between the robot admittance controller and the human.
In Figure 8, represents the end of the exoskeleton of the lower limb; represents the desired position of the lower limb exoskeleton link; represents the human lower limb position; represents the actual position of the lower limb exoskeleton link; and represents the actual contact force between the exoskeleton and the human lower limb. Then, the formula for the rehabilitation robot position correction amount is as follows:
where represents the contact force with the lower limb of the human measured with the tension sensor.
Admittance control typically consists of an inner loop position controller and an outer loop admittance controller, with the inner loop using a PID control [32]. The passive and active training control strategies of the lower limb exoskeleton rehabilitation robot are shown in Figure 9. The admittance controller block diagram design is shown in Figure 10.
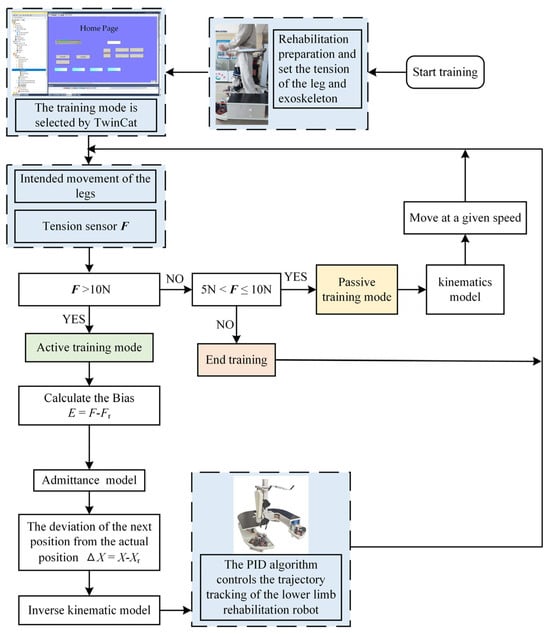
Figure 9.
The passive and active training control strategies.
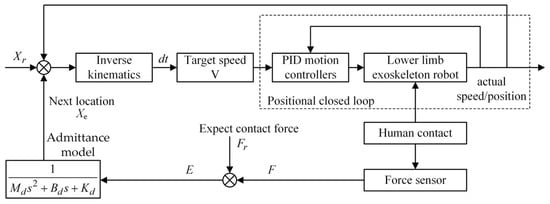
Figure 10.
Admittance controller block diagram design.
To improve the accuracy of intent detection, a force sensor with high sensitivity is used in this study, and the force sensor is mounted on an exoskeleton to connect the human lower limb with the force sensor through an elastic rope. When a person selects a training mode, the human leg should move first; then, the tension sensor reacts in a short time and passes the data to the controller for judgment. When the tensile force exceeds , the system is in the active training mode. When the tensile force is between and , the system is in the passive training mode.
In the whole process of lower limb rehabilitation training, the admittance controller first judges the movement intention of the leg according to the contact force measured by the tension sensor. indicates that the lower limb exoskeleton module is just at the critical value of being pulled, and indicates the preload tension set by the experience when the body is at rest.
When the contact force N, the active training mode is adopted, and the contact force and the expected force are substituted into the admittance model to calculate the correction value of the expected position. Then, the target velocity can be obtained by inverse kinematics and the derivation of the position correction value. Afterward, the result is transmitted to the position loop of the inner loop to control the rehabilitation robot to follow the corrected speed and position to achieve the purpose of precise control. When the contact force is 5 N 10 N, it indicates that the human lower limb strength is weak and needs some help. At this time, the lower limb exoskeleton robot will switch to the passive training mode and control the robot to assist the affected limb according to the kinematics. When the contact force N, the controller defaults that the human lower limb reaches a state of fatigue and stops training.
Figure 10 illustrates how the admittance controller can accurately control the robot’s motion based on the detected contact force. Its feedback mechanism is as follows: First, the human–computer interaction force is detected by the force sensor, and the detected force is compared with the expected force , and the output force error is given to the admittance model. Then, the position of the robot at the next moment is calculated using the admittance model, and the current position is compared with the expected position at the next moment, and the output position error is . Subsequently, the position error is calculated by inverse kinematics and derivation, and the target velocity is obtained. Finally, the motor movement is controlled by the PID controller to ensure that the movement between the robot and the human is within the expected range. In the event of an unexpected change in the contact force, the system will determine it and quickly correct it with the inner loop position controller so that the contact force changes within the desired change. Emergency stop button protection is set in the control system to prevent potential harm to the patient.
4.3. Stability Analysis
The inner ring of the lower limb exoskeleton robot control system is a classic PID control closed loop, which must be stable and convergent, and this is ignored in this study. The outer ring is admittance-controlled, and the system is treated as a second-order mass–spring–damping model. Define ; when the system is in a steady state, it can be obtained by deforming Equation (16):
To solve the above equation, two new parameters are defined as follows:
where represents the natural frequency of the system, and represents the damping ratio. Substituting (26) into (25) yields the following:
Suppose the solution of the equation is in the following form; then,
The values used for represent complex numbers. Substituting the hypothetical solution of the equation into (27) yields the characteristic equation of the parameter.
we have .
The root of the equation determines the qualitative behavior of the system, while depends on the parameters and . When , the damping form of the system is overdamping, and the system is stable but takes a long time. When , the damping form of the system is critical damping, and the system is stable. When , the damping form of the system is underdamping, and the system is unstable. The rehabilitation robot needs a stabilization system, so the parameters must be .
In this paper, the parameters obtained by simulation, namely , are used in the above analysis process, and the resulting parameters are determined as . The damping form of the system is critical damping, and the system is stable.
5. Simulation and Experiment
5.1. The Effect of Admittance Parameters on the Control
The admittance control algorithm was used to control the swing of a single joint, and the initial angle of the hip was 0 rad. The relevant parameters of the prototype were obtained from [12] and actual measurements. Experiments were carried out by varying the damping parameters separately and the stiffness parameter to obtain the step response, and the curve is shown in Figure 11.
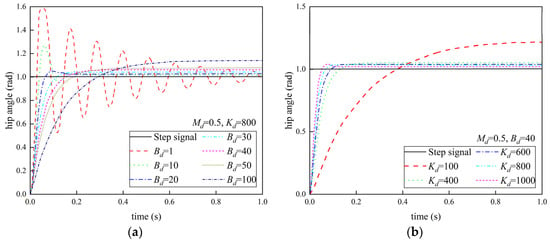
Figure 11.
The admittance controls the step response curve: (a) Md = 0.5, Kd = 800; (b) Md = 0.5, Bd = 40.
The authors of [33] used three simulation examples to verify the effectiveness and superiority of the three control methods, including the traditional impedance control method, during walking. In this study, according to the comparative simulation results and analysis, the same inertia parameter was set for optimal walking on flat ground. It can be seen from Figure 11 that the selection of impedance parameters has a great impact on the control effect of the system. When the damping parameters become small, the system responds faster, but the disadvantage is that the overshoot is larger, and the time required for stabilization also increases. With the increase in damping parameters, the steady-state error of the system increases, but the overshoot decreases, and the time required for stabilization decreases first and then increases. With the increase in stiffness parameters, the step response speed of the system becomes faster, and the overshoot increases, but the stability time of the system becomes smaller.
In this study, fixed parameters were used, and the parameters of individual patients mainly included height and leg length, which can be adapted to different patients through an adjustment mechanism in the actual test. Therefore, the parameters of the individual patient did not affect the selected admittance parameters.
Based on the simulation results, are the best try-and-error results for admittance control. The next step was to substitute the above parameters into the controller and adjust the prototype experiment according to the actual situation. The above parameters were selected for prototype experiments.
5.2. Prototype Experiment
Referring to the walking speed of the exoskeleton in passive mode, the initial speed of the robot in the admittance control mode was set to 0.21 m/s. Before the start of the prototype experiment, one healthy human subject (male, 24 years old, height 178 cm, weight 67 kg) wearing an exoskeleton for the walking action test was asked to walk a 3 m distance on flat ground. The wearing of human devices and sensors is shown in Figure 12. The affected lower limb of the volunteer was tied to the lower limb exoskeleton with a black belt. The blue elastic cord acted as a bridge between the person and the tension sensor, which could transmit the tension change generated when the person moved. Then, the system was activated, and only the control in the state of linear motion was considered in this experiment.

Figure 12.
Wear devices and sensors.
When a person subjectively intends to move, and the leg moves forward, the tension sensor collects data and transmits it to the admittance controller; then, the controller determines and provides the corresponding speed of the lower limb motor and the platform motor according to the tension condition. The experiment was divided into two parts, the first of which was a passive training walk by volunteers who simulated people with insufficient leg strength. In the second experiment, the same volunteers simulated active training walking with good leg strength.
The actual moving distance of the rehabilitation robot during the movement is shown in Figure 13a, and the following of the lower limb exoskeleton during the movement is shown in Figure 13b.

Figure 13.
The robot follows the human body as it walks: (a) walking trajectory; (b) walking training process.
During the experiment, there was a beginning phase, an intermediate phase, a deceleration phase, and an end phase. The unilateral lower limb exoskeleton module followed the movement from standing to leg lift to standing in the repetitive cycle of the human lower limb. The contact force measured with the tension sensor during the experiment is shown in Figure 14. The trajectory of the platform is shown in Figure 15.
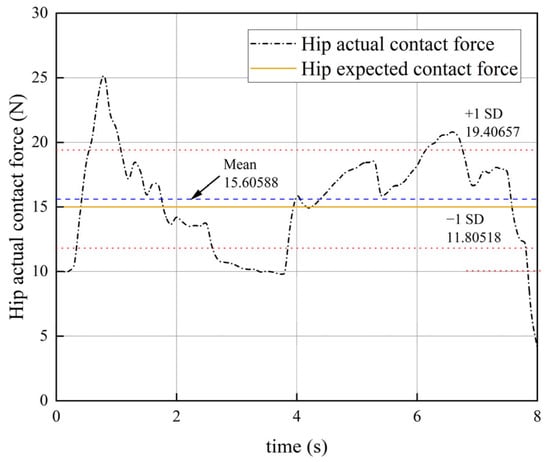
Figure 14.
Hip contact force.
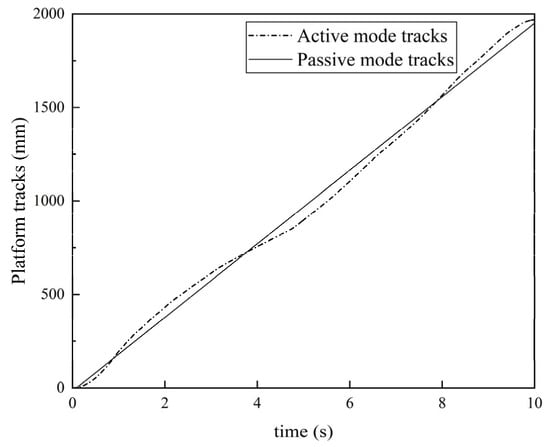
Figure 15.
Moving platform trajectory.
As can be seen from the change in the contact force in Figure 14, the contact force increased sharply at the beginning of the experiment, which is due to the use of bungee cord connection measurement between the human body and the exoskeleton. When a sudden change in force occurred, the connecting rope underwent a huge deformation, resulting in a surge in contact force. After a short period, the contact force stabilized at the average value of 15.6 N, which is close to the expected contact force of 15 N. Figure 15 shows the change in the trajectory of the moving platform during movement. The change in the trajectory of the mobile platform is related to the speed of human lower limb movement in the active training mode, and the linear change in the trajectory is relatively stable in the passive training mode.
The hip and knee trajectory tracking data were collected during the experiment. Exoskeleton data of the human lower limb in the passive assistance stage are shown in Figure 16.
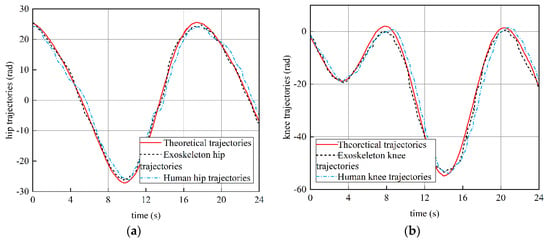
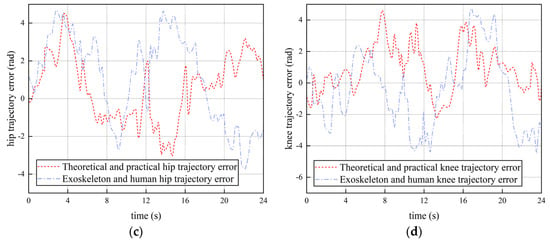
Figure 16.
Exoskeleton−assisted trajectories in passive mode: (a) hip trajectory; (b) knee trajectory; (c) hip trajectory errors; (d) knee trajectory errors.
Figure 16 shows the hip and knee data collected when the contact force was , and the human lower limb was assessed by the control system as having fatigue and needing help. In the passive mode, there is a small error between the black exoskeleton and the theoretical curve, but the theoretical curve can still be tracked well. Compared with the theoretical curve, the error of the exoskeleton and the human hip and knee is higher. The maximum angle error of the hip is , and the maximum angle error of the knee is . The error in the curve is caused by the insufficient machining accuracy of the robot and the large assembly clearance. However, the hip and knee trajectories of the robot are generally within the error range of the design and theoretical curves, which meets the test requirements. Experiment results prove that the gait trajectory of the lower limb rehabilitation robot in the passive training mode is correct, which can drive or assist the volunteers’ leg walking, so as to improve the rehabilitation of patients. The straight-line walking experiment is shown in Figure 17.
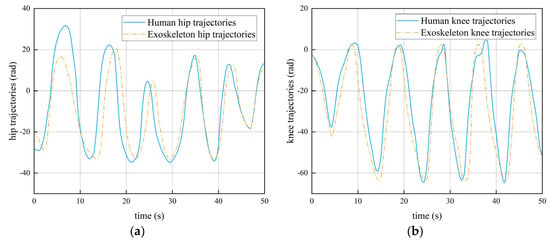
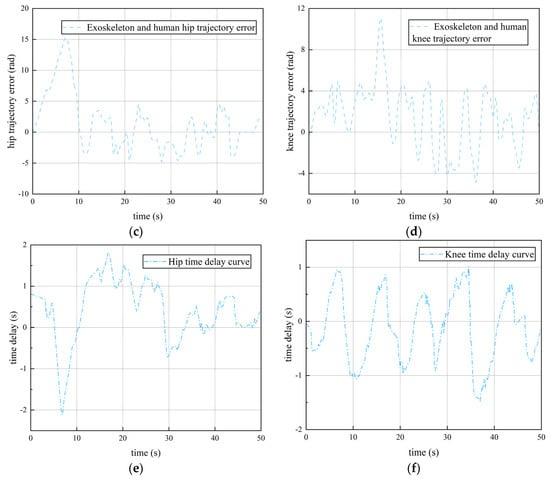
Figure 17.
Admittance −controlled exoskeleton trajectories in active mode: (a) hip trajectory; (b) knee trajectory; (c) hip trajectory error; (d) knee trajectory error; (e) hip time delay; (f) knee time delay.
After adding the optimal admittance parameters to the experiment, the error of the hip and knee tracking curve of the lower limb exoskeleton increased compared with that in the passive mode, and the response speed of the robot had a lag time of about 1–2 s. This is due to the delay in recognition of the unresponsive elastic cord when the tension was abruptly altered. The maximum error in the trajectory tracking curve occurred in the initial stage, with the maximum error of the hip being , and the knee error was about . This is due to the low machining accuracy of the lower limb exoskeleton module and the increase in the front and rear clearance due to long-term use. In addition, at the beginning of the experiment, the volunteers were not able to control the movement of the lower limbs very well. After 20 s, the trajectory error gradually stabilized, and the hip and knee errors were and , respectively. The stability error of the hip and knee with admittance control was increased by 6.52% and 1.05%, respectively, compared with that in the passive mode. The experimental results show that the lower limb exoskeleton rehabilitation robot controlled with the admittance controller can still follow the cooperative movement of the human lower limb well with fixed parameters, and the admittance control is effective.
6. Conclusions and Discussion
The experimental object in this study was a new type of rehabilitation robot that combines the MY3 omnidirectional mobile platform and the lower limb exoskeleton module. The motion control of the rehabilitation robot in the active and passive training mode was mainly studied. The admittance controller suitable for the robot was designed using the force generated by the contact between the end of the lower extremity exoskeleton and the human body. Firstly, the structure of the robot was briefly introduced. Then, the kinematics model of the robot was established, and the motion coupling relationship between the mobile platform and the exoskeleton module was calculated according to the model analysis. In the simulation software, the admittance controller was simulated to obtain the best try-and-error results for admittance parameters to deal with the change in contact force during the movement. Finally, the accuracy and effectiveness of the passive and active training control strategies were verified with prototype experiments.
From the experimental results, it was found that the passive training mode had a good gait trajectory. In the test, the robot could drive or assist the volunteer’s legs to walk. In the active training mode, the trajectory tracking effect of the robot exoskeleton was good, and it could meet the needs of human motion in the actual test. Active training mode could fully stimulate people’s willingness to exercise and accelerate physical rehabilitation. The passive training mode involves the situation when the human lower limb strength is insufficient, and the person also wants to exercise; in this mode, the lower limb movement is driven or assisted using the lower limb exoskeleton module to achieve exercise and improve the rehabilitation results. At present, the research of rehabilitation robots in our laboratory is limited in terms of mechanism and hardware. Robots can only detect the force vector of one-dimensional motion for the time being and cannot realize multi-trajectory training in the active training mode and delay in control response. There is still room for structural optimization of the robot, which has no impact on future clinical trials.
Although several devices for lower limb rehabilitation are currently under development, they have not yet been commercialized and are limited to laboratory testing. The rehabilitation robot proposed in this study is also in the stage of laboratory research and development. In the process of testing and development, human safety issues will be given priority by setting a series of safety measures. At the same time, given that rehabilitation robots involve people and medicine, they need to be supervised by a person in charge when conducting tests. In the test development stage, researchers also need to implement the feedback of patients and therapists on the availability of the device and optimize and improve the robot(This work was supported by The Research on Motion Stability of Omnidirectional Dexterous Robot of Shenyang Aerospace University (Grant no. 20180520033) and The Shandong Provincial Key Research and Development Program (Major Scientific and Technological Innovation Project) (Grant no. 2019JZZY010128).). No commercialization of the product will be carried out before it is certified by the national rehabilitation agency.
Author Contributions
Conceptualization, C.L. and S.Y.; methodology, C.L.; software, C.L.; validation, C.L., S.Y. and C.Y.; formal analysis, C.L. and S.Y.; investigation, C.L.; resources, C.L. and C.Y.; data curation, C.L. and R.F.; writing—original draft preparation, C.L.; writing—review and editing, C.L., S.Y. and C.Y.; visualization, C.L.; supervision, C.L., S.Y. and C.Y.; project administration, C.L. and R.F.; funding acquisition, C.L. and C.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by The Research on Motion Stability of Omnidirectional Dexterous Robot of Shenyang Aerospace University (Grant no. 20180520033) and The Shandong Provincial Key Research and Development Program (Major Scientific and Technological Innovation Project) (Grant no. 2019JZZY010128).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
Data are contained within the article.
Acknowledgments
Thanks to the Shenyang Aerospace University and the Shandong Provincial Key Research and Development Program (Major Scientific and Technological Innovation Project) for providing financial and equipment support.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Xu, S.Y.; Zhang, M.; Wu, X.W.; Li, L.; Li, C.X. The mechanisms of limb hemiplegia after ipsilateral brain hemisphere stroke. Int. J. Clin. Exp. Med. 2020, 13, 7386–7392. [Google Scholar]
- Zhao, Y.; Hao, Z.; Lim, J. Effects of lower limb rehabilitation training robot on balance and walking function of hemiplegic patients with ischemic stroke. Chin. J. Rehabil. Med. 2012, 27, 1015–1020. [Google Scholar]
- Langhorne, P.; Pollock, A. What are the components of effective stroke unit care? Age Aging 2002, 31, 365–371. [Google Scholar] [CrossRef] [PubMed]
- Dalleck, L.C.; Borresen, E.C.; Parker, A.L.; Abel, K.M.; Habermann, L.A.; McLaughlin, S.J.; Tischendorf, J.S. Development of a Metabolic Equation for the NuStep Recumbent Stepper in Older Adults. Percept. Mot. Ski. 2011, 112, 183–192. [Google Scholar] [CrossRef] [PubMed]
- Hu, W.; Li, G.; Sun, Y.; Jiang, G.; Kong, J.; Ju, Z.; Jiang, D. A Review of Upper and Lower Limb Rehabilitation Training Robot. In Proceedings of the International Conference on Intelligent Robotics and Applications, Wuhan, China, 16–18 August 2017; Springer: Berlin/Heidelberg, Germany, 2017; pp. 570–580. [Google Scholar]
- Métrailler, P.; Blanchard, V.; Perrin, I.; Brodard, R.; Frischknecht, R.; Schmitt, C.; Fournier, J.; Bouri, M.; Clavel, R. Improvement of rehabilitation possibilities with the MotionMaker TM. In Proceedings of the First IEEE/RAS-EMBS International Conference on Biomedical Robotics and Biomechatronics, 2006 BioRob 2006, Pisa, Italy, 20–22 February 2006; pp. 359–364. [Google Scholar]
- Feng, Y.; Wang, H.; Du, Y.; Chen, F.; Yan, H.; Yu, H. Trajectory planning of a novel lower limb rehabilitation robot for stroke patient passive training. Adv. Mech. Eng. 2017, 9, 1687814017737666. [Google Scholar] [CrossRef]
- Feng, Y.; Wang, H.; Yan, H.; Wang, X.; Jin, Z.; Vladareanu, L. Research on Safety and Compliance of a New Lower Limb Rehabilitation Robot. J. Healthc. Eng. 2017 2017, 1523068. [Google Scholar] [CrossRef] [PubMed]
- Okada, S.; Sakaki, T.; Hirata, R.; Okajima, Y.; Uchida, S.; Tomita, Y. TEM: A therapeutic exercise machine for the lower extremities of spastic patients. Adv. Robot. 2001, 14, 597–606. [Google Scholar] [CrossRef]
- Wu, Q.; Chen, Y. Development of an Intention-Based Adaptive Neural Cooperative Control Strategy for Upper-Limb Robotic Rehabilitation. IEEE Robot. Autom. Lett. 2020, 6, 335–342. [Google Scholar] [CrossRef]
- Hu, J.; Zhuang, Y.; Zhu, Y.; Meng, Q.; Yu, H. Intelligent Parametric Adaptive Hybrid Active–Passive Training Control Method for Rehabilitation Robot. Machines 2022, 10, 545. [Google Scholar] [CrossRef]
- Ye, C.; Zhang, Y.; Yu, S.; Li, D. Development of an Omni-directional Lower Limb Rehabilitation Mobile Robot. In Proceedings of the 2023 IEEE International Conference on Mechatronics and Automation (ICMA), Harbin, China, 6–9 August 2023; pp. 2045–2050. [Google Scholar]
- Meng, W.; Liu, Q.; Zhou, Z.; Ai, Q.; Sheng, B.; Xie, S. Recent development of mechanisms and control strategies for robot-assisted lower limb rehabilitation. Mechatronics 2015, 31, 132–145. [Google Scholar] [CrossRef]
- Yu, Z. Design and Research of Horizontal Lower Limb Rehabilitation Robot. Master’s Thesis, Hefei University of Technology, Hefei, China, 2015. [Google Scholar]
- Wang, Z.; Han, J.; Guo, B.; Li, X.; Du, G. Structural design and research of a novel lower limb rehabilitation robot for human-robot coupling. Int. J. Adv. Robot. Syst. 2024, 21, 17298806241238992. [Google Scholar] [CrossRef]
- Li, L.; Han, J.; Li, X.; Guo, B.; Wang, X. Customized Trajectory Optimization and Compliant Tracking Control for Passive Upper Limb Rehabilitation. Sensors 2023, 23, 6953. [Google Scholar] [CrossRef] [PubMed]
- Proietti, T.; Crocher, V.; Roby-Brami, A.; Jarrasse, N. Upper-limb robotic exoskeletons for neurorehabilitation: A review on control strategies. IEEE Rev. Biomed. Eng. 2016, 9, 4–14. [Google Scholar] [CrossRef] [PubMed]
- Chen, Q.; Cheng, H.; Yue, C.; Huang, R.; Guo, H. Dynamic balance gait for walking assistance exoskeleton. Appl. Bionics Biomech. 2018, 2018, 7847014. [Google Scholar] [CrossRef] [PubMed]
- Anneli, W.; Jorgen, B.; Susanne, P. Clinical Application of the Hybrid Assistive Limb (HAL) for Gait Training—A Systematic Review. Front. Syst. Neurosci. 2015, 9, 48–52. [Google Scholar]
- Chen, C. Research on Wearable Lower Extremity Exoskeleton System Design and Interactive Control Strategy. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2020. [Google Scholar]
- Yan, Q.; Huang, J.; Tao, C.; Chen, X.; Xu, W. Intelligent mobile walking-aids: Perception, control and safety. Adv. Robot. 2020, 34, 2–18. [Google Scholar] [CrossRef]
- Zhou, H. Research on the Structural Design and Control Method of Lower Limb Exoskeleton Rehabilitation Robot. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2015. [Google Scholar]
- Hartigan, C.; Kandilakis, C.; Dalley, S.; Clausen, M.; Wilson, E.; Morrison, S.; Etheridge, S.; Farris, R. Mobility Outcomes Following Five Training Sessions with a Powered Exoskeleton. Top. Spinal Cord. Inj. Rehabil. 2015, 21, 93–99. [Google Scholar] [CrossRef] [PubMed]
- Amiri, M.S.; Ramli, R. Admittance swarm-based adaptive controller for lower limb exoskeleton with gait trajectory shaping. J. King Saud. Univ.-Comput. Inf. Sci. 2024, 36, 101900. [Google Scholar] [CrossRef]
- Narayan, J.; Kalita, B.; Dwivedy, S.K. Adaptive backstepping human-cooperative control of a pediatric gait exoskeleton system with high-and low-level admittance. Proc. Inst. Mech. Eng. Part I J. Syst. Control. Eng. 2024, 238, 545–562. [Google Scholar] [CrossRef]
- Lu, T.W.; Chang, C.F. Biomechanics of human movement and its clinical applications. Kaohsiung J. Med. Sci. 2012, 28, S13–S25. [Google Scholar] [CrossRef]
- Aggarwal, J.K.; Cai, Q. Human motion analysis: A review. Comput. Vis. Image Underst. 1999, 73, 428–440. [Google Scholar] [CrossRef]
- Yu, S.; Ye, C.; Liu, H.; Chen, J. Development of an omnidirectional automated guided vehicle with MY3 wheels. Perspect. Sci. 2016, 7, 364–368. [Google Scholar] [CrossRef][Green Version]
- Wang, H.; Qi, H.; Xu, M.; Tang, Y.; Yao, J.; Yan, X.; Li, M. Research on the relationship between classic denavit-hartenberg and modified denavit-hartenberg. In Proceedings of the 2014 Seventh International Symposium on Computational Intelligence and Design, Hangzhou, China, 13–14 December 2014; Volume 2, pp. 26–29. [Google Scholar]
- Liang, X.; Wang, W.; Hou, Z.G.; Ren, S.; Wang, J.; Shi, W.; Peng, L.; Su, T. Position-based impedance control strategy for a lower limb rehabilitation robot. In Proceedings of the 2019 41st Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Berlin, Germany, 23–27 July 2019; pp. 437–441. [Google Scholar]
- Nikooyan, A.A.; Zadpoor, A.A. Mass–spring–damper modeling of the human body to study running and hopping–an overview. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2011, 225, 1121–1135. [Google Scholar] [CrossRef] [PubMed]
- Ba, K.; Yu, B.; Zhu, Q.; Gao, Z.; Ma, G.; Jin, Z.; Kong, X. The position-based impedance control combined with compliance-eliminated and feedforward compensation for HDU of the legged robot. J. Frankl. Inst. 2019, 356, 9232–9253. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, R.; Miao, Y.; Wang, S.; Zhang, Y. PI2-Based Adaptive Impedance Control for Gait Adaption of Lower Limb Exoskeleton. IEEE/ASME Trans. Mechatron. 2024. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).