Overvoltage Avoidance Control Strategy for Braking Process of Brushless DC Motor Drives with Small DC-Link Capacitance

Abstract

Single-phase input rectifier brushless DC motor drives with a small film capacitor have many advantages, such as high power density and high reliability. However, when the motor system operates in regenerative braking mode, the dc-link capacitor with reduced capacitance may suffer from overvoltage without adding additional hardware circuits. At the same time, the braking torque control of the motor will be affected by speed variations. In order to ensure smooth and reliable operation of the motor system, an anti-overvoltage braking torque control method is proposed in this article. The relationship among the dc-link capacitance, the dc-link capacitor voltage, and the speed during regenerative braking is analyzed quantitatively, and the speed at which the regenerative braking is switched to the plug braking is obtained, which in turn consumes the capacitor energy to avoid dc-link overvoltage. Additionally, based on the relationship between the controllability of the braking torque and the speed, a reference value of the braking current that matches the speed is designed. The proposed method makes use of the capacitor’s energy storage during regenerative braking. Meanwhile, it mitigates the impact of motor speed on braking torque. Finally, the effectiveness of the proposed method is verified on a motor platform equipped with the dc-link film capacitor.

1. Introduction

Due to the advantages of small size, simple structure, and high power density, the brushless DC motor (BLDCM) has been widely used in industrial transmission, household appliances, and other fields [1,2,3,4]. Traditional single-phase diode rectifier input motor systems usually use large-capacity electrolytic capacitors in the dc-link circuit; however, the service life of electrolytic capacitors decreases significantly under extreme high temperature and high humidity environments, and about 60% of drive circuit failures are related to the electrolytic capacitor, which reduces the reliability of the motor drive system [5,6]. Compared with an electrolytic capacitor, the film capacitor allows a higher current ripple and has a longer lifetime, enhances reliability, and reduces the failure of the drive system [7]. Hence, the electrolytic capacitor in the conventional dc-link circuit can be replaced by the film capacitor [8,9,10,11].

For the BLDCM drive with a single-phase rectifier, the dc-link circuit using a small capacitor in series with the IGBT scheme is mentioned in references [12,13,14], and the topology circuit diagram of the brushless DC motor system with the small capacitor is shown in Figure 1. In reference [14], based on the topology circuit of Figure 1, in each rectification cycle, when the capacitor voltage rises to the maximum value of the ac supply voltage, the capacitor charging vectors are applied at the same time, which will further increases the capacitor voltage, so that the motor input energy is not affected even if the dc-link capacitance is reduced.

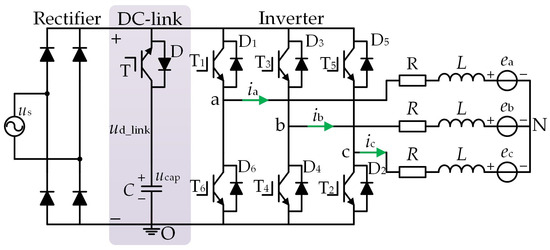
Figure 1. The equivalent circuit of BLDCM drives with small dc-link capacitance. The color-coded area in the figure is dc-link circuit.

However, when the single-phase rectifier BLDCM drives with reduced dc-link capacitance operate in regenerative braking mode, the dc-link capacitor is at risk of overvoltage. Because the dc-link capacitance in the drive system is reduced, and the diode rectifier is unable to realize the bidirectional flow of energy, the motor, during regenerative braking, can only feed energy back into the dc-link capacitor, and the capacitor voltage will rise rapidly. During regenerative braking, the copper loss of the motor can be harnessed to dissipate a portion of the motor’s mechanical energy. This serves to prevent the capacitor voltage from rapidly pumping and mitigates the occurrence of dc-link overvoltage [9,10].

Therefore, the implementation of an anti-overvoltage braking control scheme using hardware devices already available on the control system is an avenue worth exploring, which will expand the range of applications for drive systems with reduced dc-link capacitance.

In comparison to the electric mode, the braking mode represents another crucial operational state of the motor. During braking mode, the motor conducting phase current is in opposition to the phase back electromotive force (back-EMF), thereby generating an electromagnetic torque in the opposite direction of motor rotation. When the BLDCM operates in the electrical braking mode, the available electrical braking modes include regenerative braking, dynamic braking, and plug braking. Regenerative braking is a process whereby the mechanical energy of the motor system is converted into electrical energy and subsequently fed back to the energy storage elements of the power supply (e.g., batteries or supercapacitors) via a hardware circuit [15,16,17,18,19]. Dynamic braking is a technique that involves connecting switches and braking resistors in series in the dc-link circuit. This is used to prevent the dc-link voltage from exceeding a threshold value set by the control system. When the voltage reaches this threshold, the switch is turned on, and the braking resistor absorbs the energy from the motor. This helps slow down the motor and prevent any damage from the excessive dc-link voltage. During plug braking mode, the motor can reverse the input voltage or introduce specific inverter control patterns to change the motor’s conducting phase sequence, generating a braking torque in the opposite direction of the motor rotation and achieving a rapid drop in motor speed [20].

In the braking mode, the current flow circuit in the BLDCM drive is different from the normal electric mode, and the controllability of the braking torque is affected by the speed, so the control of the motor during braking is changed accordingly. Reference [20] proposes a braking torque control scheme in the whole speed range of the motor. Dynamic braking is used in the high-speed range of the motor to utilize the braking resistor to absorb the energy generated by the motor and to avoid the occurrence of dc-link overvoltage. Meanwhile, plug braking is used in the motor’s low-speed range. The hybrid application of the two braking modes realizes the smooth control of the motor braking torque at the whole speed range. In reference [21], for a hybrid energy storage system with a supercapacitor, it is proposed that combining the optimal selection of switching vectors, thereby realizing the recovery of braking energy and the control of braking torque.

In order to ensure the smooth and reliable operation of a small capacitor BLDCM system under braking mode, an anti-overvoltage braking torque control method is proposed in this paper. The relationship among the dc-link capacitance, the dc-link capacitor voltage, and the speed during regenerative braking is analyzed quantitatively, and the speed at which the regenerative braking is switched to the plug braking is obtained, which in turn consumes the capacitor energy to mitigate the phenomenon of overvoltage. Meanwhile, the braking torque controllability in different braking modes was analyzed, and the braking torque controllable speed interval was obtained. According to the obtained controllable speed interval of braking torque, a reference value of braking torque matching the motor speed is designed. The method proposed in this paper, on the one hand, makes use of the capacitor’s energy storage during regenerative braking and avoids the occurrence of capacitor overvoltage on the basis of the existing hardware of the system; on the other hand, it reduces the influence of the motor’s speed on the braking torque and takes into account the controllability of the braking torque, which ensures that the braking process of the motor is smooth and rapid.

The rest of this article is organized as follows. Section 2 introduces the operation principle of the single-phase diode rectifier brushless DC motor drive with a small capacitance. Section 3 analyzes the relationship among the dc-link capacitance, the dc-link capacitor voltage, and the speed during regenerative braking. In Section 4, the corresponding relationship between the braking torque control performance and the speed is analyzed; thus, an anti-overvoltage braking torque control method is proposed. The experimental results to verify the proposed method are given in Section 5. Section 6 concludes this paper.

2. Single-Phase Diode Rectifier BLDCM Drives with Small Dc-Link Capacitance

The equivalent circuit diagram of the single-phase diode rectifier BLDCM drives with the reduced dc-link capacitance is illustrated in Figure 1. It primarily consists of a diode rectifier, dc-link circuit, inverter, and motor three-phase windings. The inverter is composed of six IGBTs, denoted as T₁−T₆. The voltage of the dc-link capacitor is denoted as u_cap, the instantaneous voltage of the ac power source is represented as u_s, and the dc-link voltage is denoted as u_{d_link}. The phase inductance, phase resistance, and neutral point of the three-phase windings of the BLDCM are L, R, and N, respectively. Figure 1 shows the direction of the current flow. According to the direction of the phase current, the three-phase windings can be redefined as positive conducting phase p, negative conducting phase n, and nonconducting phase o (p, n, o ∈ {a, b, c}). The actual current direction of the positive conducting phase aligns with the specified positive direction. Conversely, the actual current direction of the negative conducting phase is opposite to the specified positive direction. The mathematical model of the BLDCM in the two conducting phases is expressed as follows:

$$\left\{\begin{array}{l}{u}_p=i_{p}R+L\frac{\mathrm{d}{i}_p}{\mathrm{d}t}+e_p+u_{\mathrm{N}}\\ u_n=i_{n}R+L\frac{\mathrm{d}{i}_n}{\mathrm{d}t}+e_n+u_{\mathrm{N}}\end{array}\right.$$

(1)

where e_p is back-EMF of the positive conducting phase, e_n is back-EMF of the negative conducting phase, i_p is the positive conducting phase current, i_n is the negative conducting phase current, u_p is the positive conducting phase terminal voltage, and u_n is the negative conducting phase terminal voltage.

For a single-phase diode rectifier BLDCM drive with small dc-link capacitance, the motor can achieve rated operation only if the input voltage complies with the rated voltage requirement. Taking the “p+n−” commutation period as an example, according to Equation (1), the phase current of the motor I_N = i_p = −i_n, and the back electromotive force amplitude E = e_p = −e_n. Therefore, under the rated operating conditions of the motor, it is imperative that the dc-link voltage (u_{d_link}) adhere to the following equation:

$$\left\{\begin{array}{l}{U}_{pn\mathrm{N}}\ge 2E+2I_{\mathrm{N}}R\\ u_{\mathrm{d}\_\mathrm{link}}\ge U_{pn\mathrm{N}}\end{array}\right.$$

(2)

where u_{d_link} is the dc-link voltage, U_pnN is the minimum value of dc-link voltage, E_N is the rated phase back-EMF amplitude, and I_N is the rated phase current of the motor.

To meet the requirements of Equation (2), the rectifier output voltage |u_s| can be divided into three zones based on a single rectification period T_R. Although the capacitance decreases, the motor input voltage always meets the rated voltage requirements. As depicted in Figure 2, where the amplitude of the ac power supply voltage is U_m, the frequency of the ac power source is f, and the rectification period is T_R. The logic for dividing the specific rectification period zone is as follows: Zone 1: |u_s| ≥ U_pnN where |u_s| monotonically increases until U_m. Zone 2: |u_s| ≥ U_pnN where |u_s| monotonically decreases until 0. Zone 3: |u_s| ≤ U_pnN.

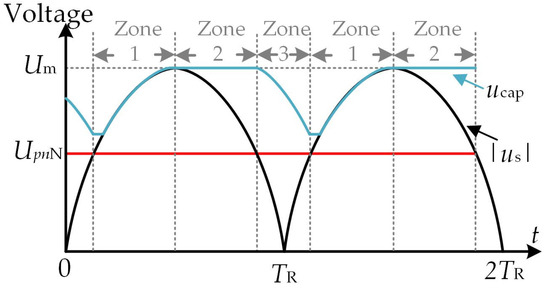
Figure 2. Regional division diagram of the output voltage of the rectifier.

The dc-link switch T is turned off in zone 1 and zone 2, while in zone 3, the switch T is turned on, and the capacitor alone supplies power to the motor. Subsequently, the capacitor voltage gradually declines until exiting zone 3. The dc-link voltage u_{d_link} is given by the following equation:

$$u_{\mathrm{d}\_\mathrm{link}}=\left\{\begin{array}{l}{u}_{\mathrm{cap}},\mathrm{T}=1\\ \left|u_{\mathrm{s}}\right|,\mathrm{T}=0\end{array}\right.$$

(3)

where T = 1 and T = 0 indicate the on and off states of the dc-link switch, u_cap is capacitor voltage, and |u_s| is the rectifier output voltage.

For the BLDCM drive with reduced dc-link capacitance, there is only one zone 3 energy release process of the capacitor under the control of the dc-link switch transistor T. Therefore, by designing the appropriate capacitance, it is possible to ensure that the dc-link voltage u_{d_link} is always greater than U_pnN in a rectification period. This guarantees a smooth and continuous motor current. Assuming the capacitor voltage is precisely U_pnN at the end of the capacitor discharge in zone 3, to simplify the analysis, the process of capacitor voltage drop is approximated to be linear. Therefore, the dc-link capacitance is designed to satisfy the following equation:

$$C\frac{\mathrm{d}{u}_{\mathrm{cap}}}{\mathrm{d}t}=I_{\mathrm{dc}}\to C\ge \frac{I_{\mathrm{N}}\arcsin \left(\frac{U_{pn\mathrm{N}}}{U_{\mathrm{m}}}\right)}{\pi f\left(U_{\mathrm{m}}-U_{pn\mathrm{N}}\right)}$$

(4)

where I_dc represents the average dc-link current, and U_m represents the amplitude of ac power supply voltage.

3. Analysis of Electrical Braking for BLDCM Drives with Small Dc-Link Capacitance

3.1. Introduction to the Braking Mode of BLDCM

When switching from electric to braking mode in BLDCM operation mode, regenerative braking or plug braking are two commonly used electrical braking modes for motors. Regenerative braking converts the mechanical energy of the motor into electrical energy, operating like a generator, while plug braking consumes energy from the power supply to accelerate the braking process. Therefore, the main difference between regenerative braking and plug braking is whether the braking consumes energy from the power supply. In braking mode, the phase back EMFs of the motor can be expressed as:

$$E=k_{\mathrm{e}}{\omega }_{\mathrm{m}}$$

(5)

where k_e and ω_m, respectively, represent the phase back-EMF coefficient and mechanical speed; E represents the amplitude of the phase back-EMF.

When the BLDCM operates in the braking mode, one electrical cycle is divided into six sectors, denoted by I to VI. The corresponding relationship between the ideal phase back-EMFs and the phase current waveform is shown in Figure 3. The conducting phase p and the conducting phase n take different values in different rotor sectors. For example, in sector I, p = b and n = a, which is the “b+a−” working state, while when the motor rotates to sector II, p = c and n = a, which is the “c+a−” working state. The conducting phase current in each sector is opposite to the direction of phase back-EMFs, resulting in a negative product. Therefore, the output braking torque of the motor is the electromagnetic torque T_e, which is opposite to the direction of motor rotation, which is different from the electric mode. As shown in Equation (6), where I_ave represents the average value of the phase current flowing through the conducting phase before commutation, the braking electromagnetic torque is expressed as:

$$T_{\mathrm{e}}=\frac{e_{\mathrm{a}}{i}_{\mathrm{a}}+e_{\mathrm{b}}{i}_{\mathrm{b}}+e_{\mathrm{c}}{i}_{\mathrm{c}}}{{\omega }_{\mathrm{m}}}=-\frac{2E{I}_{\mathrm{ave}}}{{\omega }_{\mathrm{m}}}$$

(6)

where T_e is the electromagnetic torque; i_k, ek (k = a, b, c), respectively, represent the phase current and the phase back-EMF.

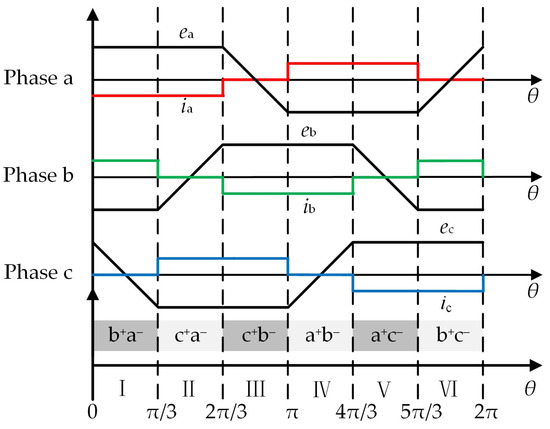
Figure 3. Correspondence between the phase back-EMFs and phase current in braking mode.

3.2. Relationship between Dc-Link Capacitor Voltage and Capacitance under Regenerative Braking

When the operating mode of the single-phase input rectifier BLDCM drives with small dc-link capacitance is shifted from the electric mode to the regenerative braking mode, a part of the mechanical energy W_m is converted into electrical energy W_C, and due to the cut-off effect of the rectifier diode, the electrical energy W_C will be stored in the dc-link capacitor, and the capacitor voltage u_cap will be increased rapidly. Because the dc-link voltage amplitude is closely related to the capacitance, the phenomenon of overvoltage is more likely to occur in the BLDCM drives with reduced dc-link capacitance. The other part of mechanical energy is converted into stator copper loss W_Cu and friction loss W_f between rotor and bearing. According to the BLDCM mechanical equation, the relationship between the regenerative braking electromagnetic torque T_e1, the dc-link capacitance C, the rotational inertia J, and the capacitor voltage during braking mode are mathematically quantitatively analyzed. The motor acceleration can be expressed as:

$$\frac{\mathrm{d}{\omega }_{\mathrm{m}}}{\mathrm{d}t}=\frac{T_{\mathrm{e}1}+T_{\mathrm{L}}+B{\omega }_{\mathrm{m}}}{J}$$

(7)

where J, T_L, and B denote the rotational inertia, load torque, and friction factor, respectively. In order to simplify the analysis, we ignore the effect of rotor bearing friction loss and load. The actual mechanical speed during regenerative braking mode is expressed as:

$${\omega }_{\mathrm{m}}=\omega -\frac{T_{\mathrm{e}1}}{J}t$$

(8)

where ω is the initial mechanical speed of motor braking, ω_m is the actual mechanical speed, and t denotes the time taken for the speed to drop from ω_m to ω.

The motor mechanical energy W_m is satisfied:

$$W_{\mathrm{m}}=\frac{1}{2}J({\omega }^2-{\omega }_{\mathrm{m}}^2)=\frac{1}{2}C\left[U_C^2-U_{C0}^2\right]+W_{\mathrm{Cu}}$$

(9)

where U_C is the voltage of the dc-link capacitor during braking mode, and U_C0 is the capacitor voltage during initial braking. The average regenerative braking torque can be expressed as T_e1 = 2I₁k_e, and as the braking process proceeds, the copper loss W_Cu can be derived as:

$$W_{\mathrm{Cu}}=2I_1^{2}Rt=\frac{T_{\mathrm{e}1}^2}{2k_{\mathrm{e}}^2}Rt$$

(10)

where T_e1 denotes the average value of regenerative braking torque; I₁ denotes the reference value of conducting phase current during regenerative braking.

According to Equation (6) to Equation (10), when the motor speed drops to the switch speed ω_c, the capacitor voltage is assumed to reach the maximum U_CM and the mathematical equation of the dc-link capacitance and the maximum value of capacitor voltage can be expressed as:

$$C=\frac{J\left(2k_{\mathrm{e}}^2{T}_{\mathrm{e}1}\omega -T_{\mathrm{e}1}^{2}R\right)t-{\left(T_{\mathrm{e}1}{k}_{\mathrm{e}}t\right)}^2}{J{k}_{\mathrm{e}}^2(U_{C\mathrm{M}}^2-U_{C0}^2)}$$

(11)

where U_CM denotes the maximum value of capacitor voltage when the motor speed drops to the speed ω_c. U_C0 denotes the initial value of the dc-link capacitor voltage when the motor speed is ω.

Assuming that the braking torque is constant during regenerative braking, we can conclude that the higher the initial mechanical speed ω, the larger capacitance that needs to be maintained so that the capacitor voltage does not exceed the threshold in order to be able to store more energy. In addition, if a larger dc-link capacitor is used, the amplitude of capacitor voltage rise will decrease.

4. Proposed Anti-Overvoltage Braking Torque Control Method for BLDCM Drives with Small Dc-Link Capacitance

This section systematically analyzes the electrical braking torque controllability of a BLDCM drive with small dc-link capacitance, providing a basis for the proposed anti-overvoltage braking torque control method. The equivalent circuit diagrams for the electrical braking modulation mode of the BLDCM drives in sectors I, III, and V are shown in Figure 4 and Figure 5 below. Figure 4a,b shows the regenerative braking OFF_PWM modulation pattern, and Figure 5a,b shows the plug braking ON_PWM modulation pattern. S_pH, S_pL, S_nH, and S_nL indicate the switching state of positive conducting phase upper bridge arm IGBTs, positive conducting phase down bridge arm IGBTs, negative conducting phase upper bridge arm IGBTs, and negative conducting phase down bridge arm IGBTs. In the following analysis, the IGBT turn-on, turn-off, and duty cycle for one modulation period are denoted as “1”, “0”, and “D”, respectively.

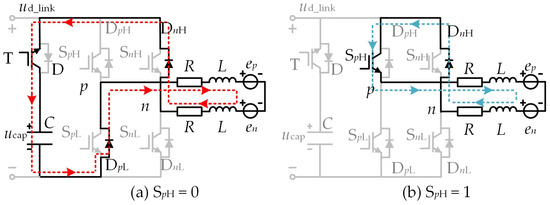
Figure 4. Equivalent circuits of regenerative braking OFF_PWM modulation pattern in an odd sector number (I, III, V). The direction of the arrow indicates the direction of current flow.

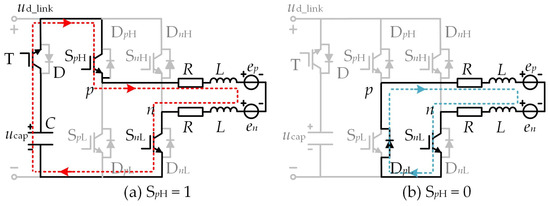
Figure 5. Equivalent circuits of plug braking ON_PWM modulation pattern in sectors (I, III, V). The direction of the arrow indicates the direction of current flow.

4.1. Controllability Analysis of Regenerative Braking Torque in Normal Conduction Period of the BLDCM

When the BLDCM drives with reduced dc-link capacitance adopt the regenerative braking OFF_PWM modulation pattern, the dc-link switch transistor T = 1. During this process, the capacitor can store a portion of the electrical energy converted from the mechanical energy. During an electrical cycle, when the rotor is located in an odd sector number (I, III, V), the switch transistor S_pH, where the positive conducting phase p is located, operates with a duty cycle D. At the same time, all other switch transistors of the inverter are turned off.

When S_pH = 1, under the excitation of the line back EMF e_pn, the positive conducting phase current i_p flows through S_pH and the antiparallel diode D_nH. Due to the presence of inductance in the phase winding, the winding inductance will store a portion of energy, forming a current path as shown in Figure 4b.

When S_pH = 0, under the action of line back EMF e_pn and inductor voltage, the positive conducting phase current i_p flows through the antiparallel diodes D_pL and D_nH and finally flows into the capacitor through the dc-link switch transistor T. At this time, the capacitor stores energy, forming another current flow path, as shown in Figure 4a. During the normal conduction period of the BLDCM, in order to simplify the analysis, we ignore the effect of the antiparallel diode freewheeling of the nonconducting phase, and the line voltage equation of the two-phase winding conduction can be expressed as:

$$u_{pn}=2R{i}_p+2L\frac{\mathrm{d}{i}_p}{\mathrm{d}t}+e_{pn}$$

(12)

where e_pn denotes the line back EMF.

When S_pH = 1, as shown in Figure 4b, in order to simplify the analysis and ignore the voltage drop effect of the diode, the line voltage u_pn = 0, combined with Equation (12), the rate of change of the positive conducting phase current i_p can be simplified as:

$$\frac{\mathrm{d}{i}_p}{\mathrm{d}t}\approx \frac{k_{\mathrm{e}}{\omega }_{\mathrm{m}}-R{I}_0}{L}$$

(13)

where I₀ is the initial value of the positive conducting current i_p and I₀ > 0. By setting Equation (13) to 0, the mechanical speed ω₀ can be derived as:

$${\omega }_0=\frac{R{I}_0}{k_{\mathrm{e}}}$$

(14)

When S_pH = 1, combining Equations (13) and (14), the mathematical relationship between the change rate of the positive conducting phase current and speed in regenerative braking mode can be expressed as:

$$\left\{\begin{array}{l}\frac{\mathrm{d}{i}_p}{\mathrm{d}t}>0,{\omega }_{\mathrm{m}}>{\omega }_0\\ \frac{\mathrm{d}{i}_p}{\mathrm{d}t}<0,{\omega }_{\mathrm{m}}<{\omega }_0\end{array}\right.$$

(15)

where ω₀ denotes the cut-off speed for the controlled rate of change of the positive conducting phase current when the conducting phase current reference is I₀, di_p/dt denotes the current change rate of the positive conducting phase during braking mode.

As illustrated in Figure 4a, when S_pH = 0, u_pn = −u_{d_link}. Similarly, according to the derivation process of Equation (12) to Equation (13), the current change rate of the positive conducting phase during the capacitor charging process can be expressed as:

$$\frac{\mathrm{d}{i}_p}{\mathrm{d}t}\approx \frac{2k_{\mathrm{e}}{\omega }_{\mathrm{m}}-2R{I}_0-u_{\mathrm{d}\_\mathrm{link}}}{2L}$$

(16)

Combining Equation (2) and Equation (16), u_{d_link} > 2(k_eω_rate + RI_N). So, when S_pH = 0, even if the motor starts braking from the rated speed ω_rate, di_p/dt < 0 satisfies any situation during the regenerative braking mode and is not affected by motor speed variations. Hence, in the capacitor charging and energy storage state illustrated in Figure 4a, the current flowing through the motor windings will gradually decrease, consequently reducing the output braking torque as well. When the rotor position is in an odd sector (I, III, V), if the motor speed satisfies the inequality ω_m > ω₀. During a modulation cycle, the change rate of conducting phase current can be controlled by chopping S_pH, achieving controllable braking torque. However, when the motor speed satisfies the inequality ω_m < ω₀, whether S_pH is turned on or turned off, the change rate of conducting phase current is always less than 0 within a modulation cycle. Therefore, the motor’s braking torque output will continuously decrease. Similarly, when the rotor is located in an even sector (II, IV, VI), the negative conduction phase down bridge arm switch transistor S_nL chops with a duty cycle D. At the same time, all other switch transistors in the inverter are turned off. According to the symmetry principle, similar results can be deduced as an odd sector (II, IV, VI).

Therefore, the controllable speed range for braking torque during regenerative braking is (ω₀, ω_rate]. If the motor speed remains within the speed range [0, ω₀], the output braking torque will continuously decrease as the speed decreases due to the uncontrollable positive or negative rate of change in the conducting phase current.

4.2. Controllability Analysis of Plug Braking Torque in Normal Conducting Period of the BLDCM

When employing plug braking in the braking mode of the BLDCM drives with reduced dc-link capacitance, taking the ON_PWM modulation pattern as an example, the speed range of torque controllability for plug braking can be derived based on the torque controllability analysis method mentioned above for the regenerative braking OFF_PWM modulation pattern.

When using the plug braking ON_PWM modulation pattern, the switching logic of the dc-link switch transistor T is consistent with the control method in the electric mode described in Chapter 1. During one electrical cycle of the motor, when the rotor is in an odd sector number (I, III, V), the positive conducting phase switch transistor S_pH chops with a duty cycle D, while the negative conducting phase switch transistor S_nL remains on. When S_pH = 1, as shown in Figure 5a, the positive conducting phase current i_p flows through S_pH and S_nL under the combined action of line back EMF e_pn and dc-link voltage u_{d_link}. When S_pH = 0, as shown in Figure 5b, due to the presence of inductance in the winding, under the action of line back EMF e_pn, the positive conducting phase current i_p flows through S_pL and the antiparallel diode D_pL.

To simplify the analysis and ignore the voltage drop effect of the diode, when S_pH = 1, u_pn = u_{d_link}, combined with Equation (12), the change rate of the positive conducting phase current of the plug braking can be expressed as:

$$\frac{\mathrm{d}{i}_p}{\mathrm{d}t}\approx \frac{u_{\mathrm{d}\_\mathrm{link}}+2k_{\mathrm{e}}{\omega }_{\mathrm{m}}-2R{I}_0}{2L}$$

(17)

When S_pH = 1, due to u_{d_link} > 2(k_eω_rate + RI_N), di_p/dt > 0 still holds even if the motor starts braking from the rated speed ω_rate, independent of the change in motor speed. Consequently, the conducting phase current will rise, causing a corresponding increase in the plug braking torque.

When S_pH = 0, as shown in Figure 5b, u_pn = 0. Analogous analysis shows that the current change rate of the conducting phase is consistent with that shown in Equation (15). Therefore, when S_pH is turned off, the increase or decrease of the motor conducting phase current is related to the speed, which affects the controllability of the motor braking torque. According to the symmetry principle, using a similar analysis method as above, when the rotor is located in even sector numbers (II, IV, VI), the same analysis results as above can be obtained. It can be seen that the controllable speed range of the plug braking torque is [0, ω₀], and within this range, the deviation between the absolute value of the output braking torque and the reference of the braking torque is small.

4.3. The Proposed Overvoltage Braking Torque Control Method for BLDCM Drives

According to the above analysis, the BLDCM drives with reduced dc-link capacitance adopt the regenerative braking mode. Due to the limitation of capacitance, the dc-link capacitor will experience overvoltage problems at a certain speed point ω_c during the regenerative braking process of the motor. To mitigate the phenomenon of overvoltage, the regenerative braking mode can be ended in advance, and the system can be switched to a plug braking mode to consume the energy of the capacitor and reduce the capacitor voltage. However, it should be noted that after switching to the plug braking, the performance of the plug braking torque control is related to the motor speed. Therefore, after switching to the plug braking, the reference of the braking torque needs to be redetermined.

When the motor performs regenerative braking with the braking torque T_e1, in a motor system with constant inertia and fixed capacitance C, after the capacitor is charged to the maximum voltage (U_CM), the motor speed is ω_c at this moment, and then the system is switched to the plug braking, and the capacitor voltage will drop rapidly, which mitigate the phenomenon of overvoltage. Combining Equations (6)–(10), the rotational speed ω_c at the end of regenerative braking satisfies the following equation.

$${\omega }_{\mathrm{c}}^2-\frac{T_{\mathrm{e}1}R}{k_{\mathrm{e}}^2}{\omega }_{\mathrm{c}}+\left[\frac{T_{\mathrm{e}1}R\omega }{k_{\mathrm{e}}^2}-{\omega }^2+\right.\left.\frac{C(U_{C\mathrm{M}}^2-U_{C0}^2)}{J}\right]=0$$

(18)

where ω_c denotes the motor speed when the capacitor voltage rises to its maximum value U_CM during regenerative braking.

By solving Equation (18), we can see that since ω_c > 0, ω_c can be deduced as:

$${\omega }_{\mathrm{c}}=\frac{R{I}_1}{k_{\mathrm{e}}}+\sqrt{\frac{R^2{I}_1^2}{k_{\mathrm{e}}^2}+\frac{J\left(k_{\mathrm{e}}{\omega }^2-2I_{1}R\omega \right)-C{k}_{\mathrm{e}}\left(U_{\mathrm{CM}}^2-U_{\mathrm{C}0}^2\right)}{J{k}_{\mathrm{e}}}}$$

(19)

According to Equation (19), when the capacitor voltage reaches U_CM, the rotational speed ω_c > (RI₁/k_e). Since the speed range of the controllable plug braking torque is [0, RI₁/k_e], and ω_c > (RI₁/k_e), that is, the rotational speed ω_c at the end of the regenerative braking exceeds the speed range of the controllable plug braking torque. If the braking torque reference remains at T_e1, then the plug braking torque will not be controllable. Thus, to maintain torque control over the plug braking, it becomes necessary to increase the torque reference of the plug braking, which entails increasing the current reference, denoted as I_ref. The requirement of I_ref > (ω_ck_e/R) needs to be met, thus expanding the speed range of the motor under the premise of controllable plug braking torque to ensure smoothness during the motor braking process.

5. Experimental Results and Analysis

In order to verify the feasibility of the proposed method above, a washing machine with a washing weight of 1 kg is built as an experimental platform, as shown in Figure 6. The relevant parameters of the BLDCM system are calculated, and the parameters are listed in Table 1. The schematic diagram and flowchart of the proposed anti-overvoltage braking torque control method are shown in Figure 7. As shown in Figure 7a, i denotes the non-commutated phase current, which is used as the feedback value for the PI current loop control. The proportional coefficient P of the PI controller is 7.0, and the integral coefficient I is 0.09.

Figure 6. Experimental platform view.

Table 1. The BLDCM system parameters.

Parameter	Symbol	Valve
Rated current	IN	0.26 A
Phase resistance	R	72 Ω
Phase inductance	L	120 mH
Back EMF coefficient	ke	0.6685 V/(rad/s)
Rated speed	nN	700 r/min
Poles pairs	P	4
Inertia	J	0.010762 kg·m²
Sampling frequency	f1	10 kHz
Mains supply voltage	Us	220 Vrms
Mains supply frequency	f	50 Hz

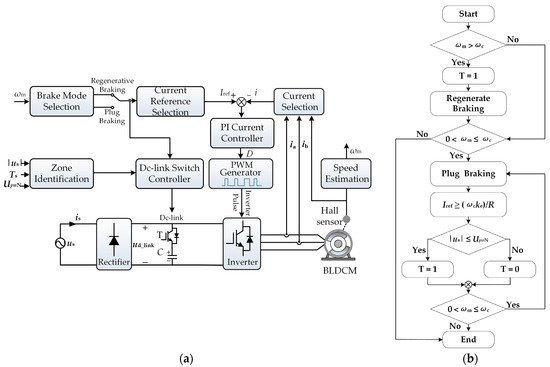
Figure 7. Control block diagram and flowchart of the proposed control method. (a) The control block diagram, and (b) the flowchart.

The control method mainly consists of the main parts such as braking mode selection, zone identification, braking current reference selection, dc-link switch controller, and PI current controller. In the experiments, the proposed method in this paper uses DSP+FPGA as the control unit. According to the parameters listed in Table 1, a film capacitor of 70 μF is used in the experiment, the braking mode switching speed ω_c = 66 rad/s (n_c = 630 rpm), the rated operating voltage of the capacitor is 450 V, the frequency of the ac power supply is 50 Hz, and the peak value of the power supply voltage U_m is 311 V. According to Equation (2), we can set U_pnN = 252 V, which can meet the requirements of the motor in the rated operating conditions.

In order to demonstrate the overvoltage problem caused by BLDCM drives with small dc-link capacitance in regenerative braking, only the regenerative braking approach is applied to the constructed washing machine experimental platform.

The washing machine was left empty, with no objects placed on it. When the speed is decelerated from 700 rpm to 0 rpm, the reference for the braking torque is −0.35 N·m. This indicates that the absolute value of the current loop reference is 0.26 A. Figure 7 illustrates the overall control process. The experimental procedure involves first maintaining the washing machine motor speed at 700 rpm using the BLDCM electric control strategy with reduced dc-link capacitance, as described in Section 1. Next, the operating mode of the washing machine should be switched to braking mode. The regenerative braking OFF_PWM modulation pattern is used in the braking control process. When the dc-link switch T is turned on during the regenerative braking process, the dc-link voltage u_{d_link} is equal to u_cap. Figure 8 shows the experimental results, with waveforms representing speed, dc-link voltage, three-phase current, and electromagnetic torque from top to bottom.

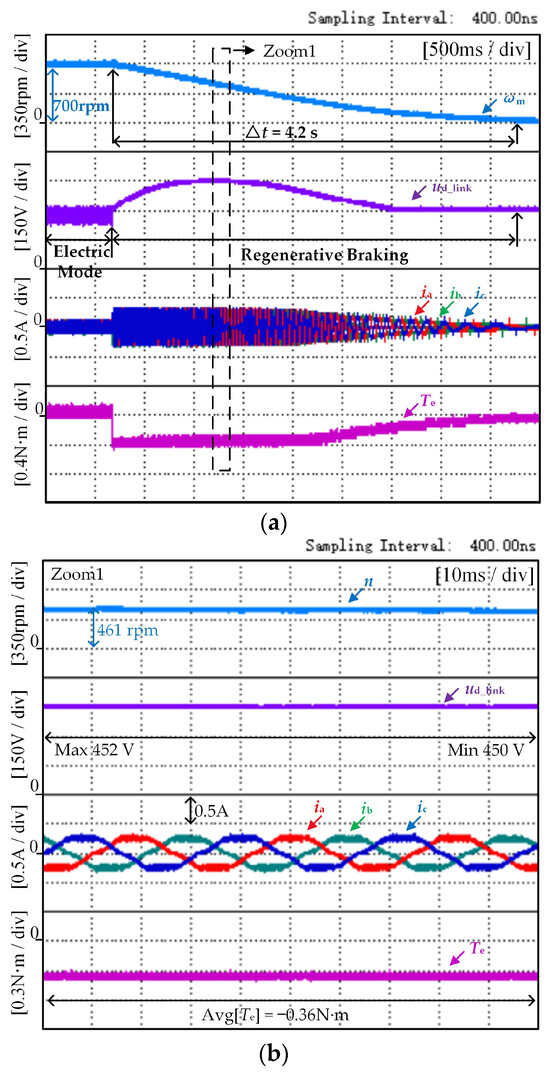
Figure 8. The experimental result with the torque reference is −0.35 N·m, and the speed decreases from 700 rpm to 0 rpm. (a) Overall view, and (b) the view of Zoom 1.

Figure 8a shows that the washing machine braking process takes approximately 4.2 s from start to finish. The initial braking torque is smooth and controllable, and the capacitor voltage increases rapidly. The regenerative braking process causes the capacitor voltage to reach its maximum value. However, during the second half of the braking process, the amplitude of the motor’s three-phase current gradually decreases while the motor’s braking torque gradually diverges from the reference.

In Figure 8b, the motor is still in the braking torque controllable region, but the maximum value of the capacitor voltage exceeds 450 V. If the rated operating voltage of the capacitor is less than 450 V, the capacitor may be degraded or even damaged, which will affect the reliability of the motor system. Therefore, to prevent capacitor overvoltage without requiring an additional mechanical braking device for the washing machine, this paper proposes an anti-overvoltage braking torque control method. Experimental waveform diagrams for this method are shown in Figure 9. By setting the switching speed n_c = 630 rpm and ensuring that there is no load weighing 1 kg inside the washing machine, the dc-link voltage and torque variation characteristics of the motor system can be reflected in the experimental waveform in Figure 9.

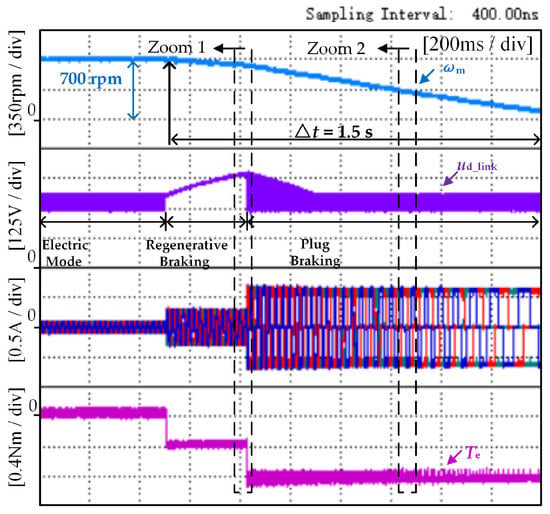
Figure 9. The overall figure of the proposed method when the speed drops from 700 rpm to 90 rpm under no-load conditions.

Figure 9 shows the experimental results of the proposed method of the washing machine under no-load conditions, in which the waveform graphs from top to bottom are the speed, three-phase current, dc-link voltage, and electromagnetic torque, respectively. During regenerative braking mode, the brake torque reference of the washing machine is −0.35 N·m. With the progress of regenerative braking, when the washing machine control system recognizes the speed ω_c and the braking mode changes to plug braking, the reference of plug braking torque is −0.83 N·m, and the modulation pattern is ON_PWM. As shown in Figure 9, three operating modes exist in the system: electric mode, regenerative braking, and plug braking. At first, the electric mode adopts a control method for the BLDCM drives with reduced capacitance, after which the control mode of the washing machine changes to regenerative braking. At the same time, once the system recognizes the rotational speed as ω_c, it will switch to the plug braking mode to consume the stored energy of the capacitor during the regenerative braking process and avoid overvoltage of the capacitor.

As can be seen from Figure 9, the washing machine takes approximately 1.5 s to decelerate from 700 rpm to 90 rpm during braking. This is a smooth and rapid braking process compared to the braking process shown in Figure 8, which only uses the regenerative braking mode. As seen in Figure 10a, the average value of regenerative braking torque is −0.36 N·m. The proposed method sets the switching speed of regenerative braking and plug braking at n_c = 630 rpm, at which time the maximum value of the capacitor voltage is 398 V, and then the braking mode is switched to plug braking. According to the previous analysis, the absolute value of the current loop reference converted from the regenerative braking torque reference of −0.35 N·m is not suitable for plug braking at this moment. Therefore, the absolute value of the plug braking current loop reference must be no less than 0.62 A; that is, the plug braking torque reference should be set to −0.83 N·m. As illustrated in Figure 10a, the average value of plug braking torque is −0.86 N·m. As the braking process continues, as depicted in Figure 10b, the average value of braking torque is −0.83 N·m. Hence, as the plug braking progresses, the final braking torque will tend to the set reference.

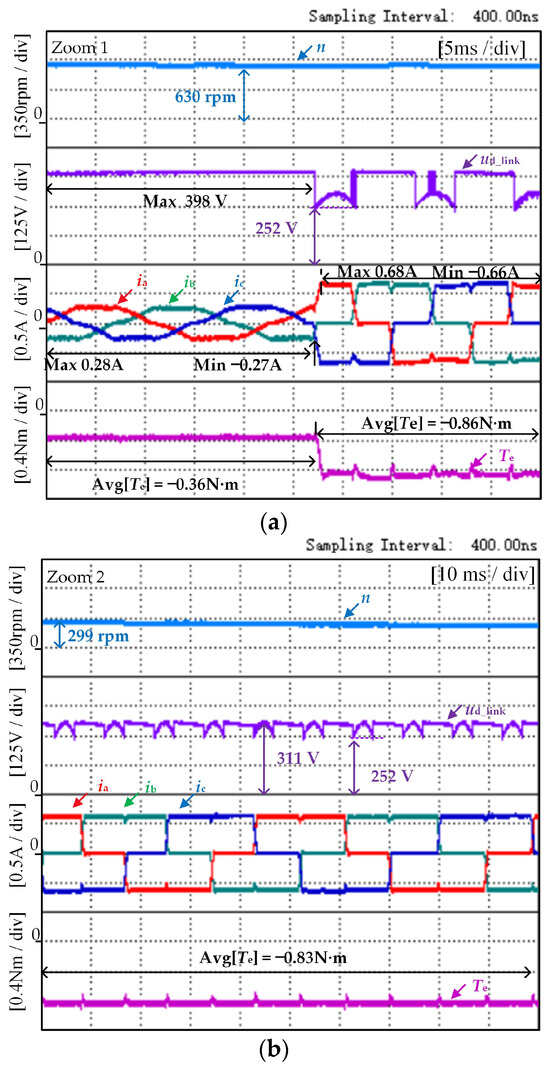
Figure 10. The experimental results of the proposed method when the speed drops from 700 rpm to 90 rpm under no-load conditions. (a) The view of Zoom 1, and (b) the view of Zoom 2.

In order to simulate the actual operating conditions of the washing machine, a 1 kg load object was added inside the washing machine, and the other experimental conditions were consistent with those mentioned in Figure 9. The results of the experiment are presented in Figure 11. Figure 11 presents the overall diagram of the system, which includes three operating modes. The washing machine takes approximately 2.4 s to brake when it decelerates from 700 rpm to 90 rpm, and the braking process remains stable. In Figure 12a, the maximum value of the capacitor voltage at the braking mode switching speed n_c = 630 rpm is 434 V, which is still within the rated range of the capacitor voltage. As seen in Figure 12b, the average value of braking torque reaches −0.83 N·m as the braking process proceeds, so the proposed method realizes prevention of capacitor overvoltage while taking into account the smoothness of braking torque.

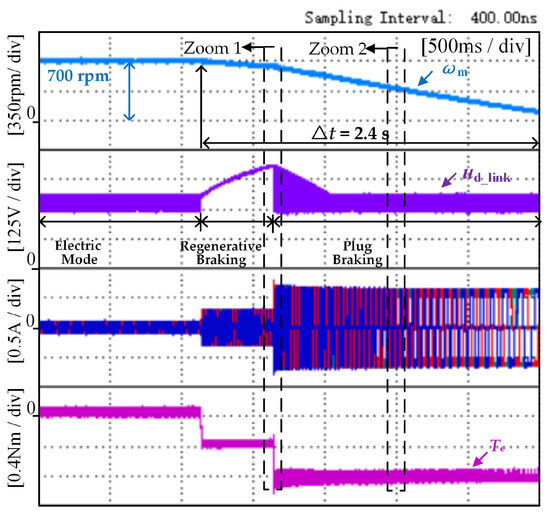
Figure 11. The experimental figure of the proposed method when the speed drops from 700 rpm to 90 rpm under a load condition of 1 kg.

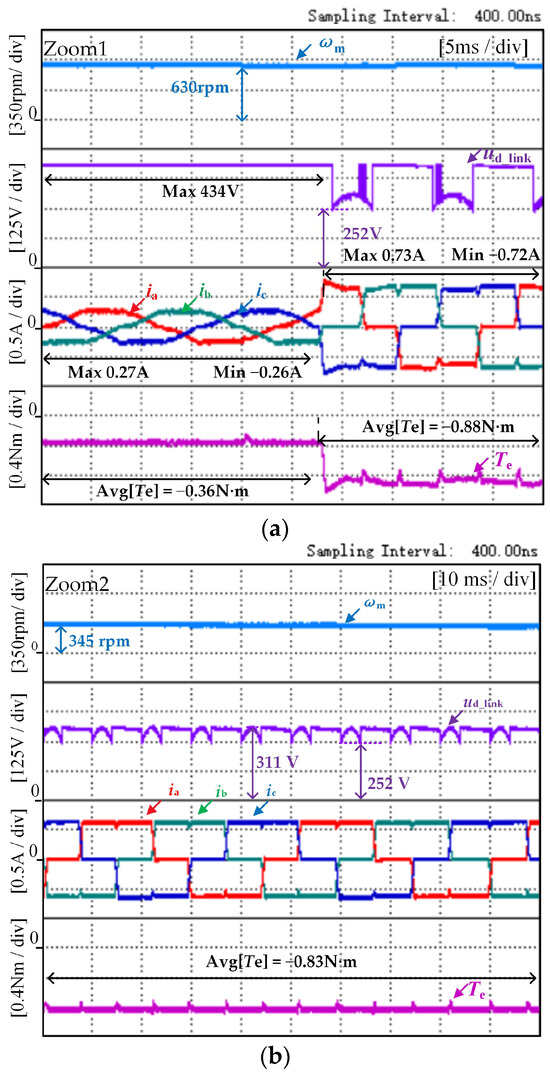
Figure 12. The experimental results of the proposed method when the speed drops from 700 rpm to 90 rpm under a load condition of 1 kg. (a) The view of Zoom 1, and (b) the view of Zoom 2.

6. Conclusions

This paper focuses on the dc-link overvoltage phenomenon in a single-phase input diode rectifier BLDCM drive with small dc-link capacitance during regenerative braking. The proposed method is designed to avoid capacitor overvoltage by detecting the motor speed at which the capacitor is overvoltage and then utilizing plug braking to reduce the energy of the capacitor and, at the same time, mitigate the impact of motor speed on braking torque controllability. The proposed anti-overvoltage braking torque control method is based on the existing hardware resources of the system, without adding additional mechanical braking devices or hardware circuits. Finally, the effectiveness of the proposed method is verified by an experimental platform of a washing machine equipped with a film capacitor.