A Novel Cooperative Control Strategy for Three-Degree-of-Freedom Pneumatic Parallel Mechanism
Abstract
1. Introduction
2. Experiment Settings
3. Modeling
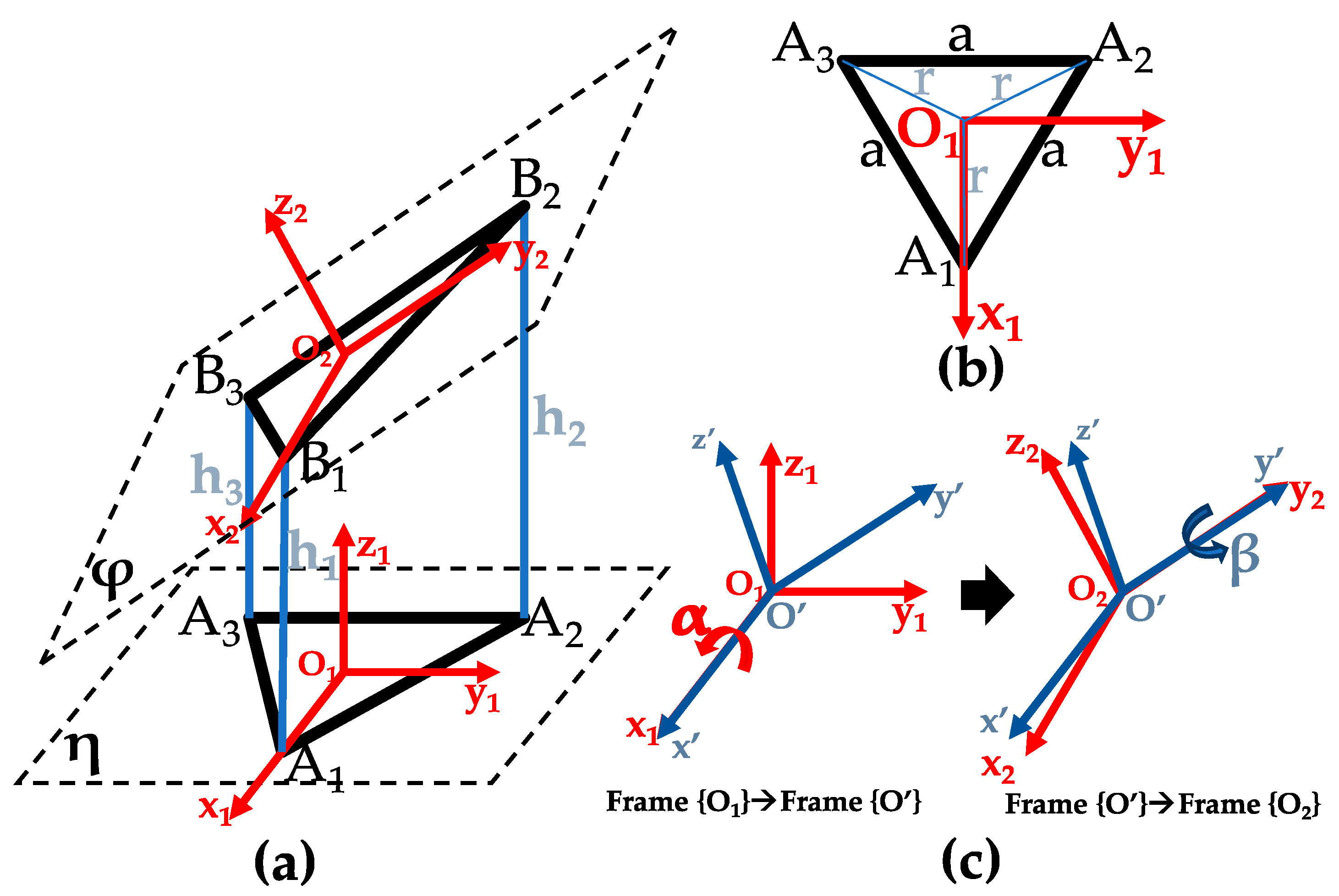
3.1. Kinematics
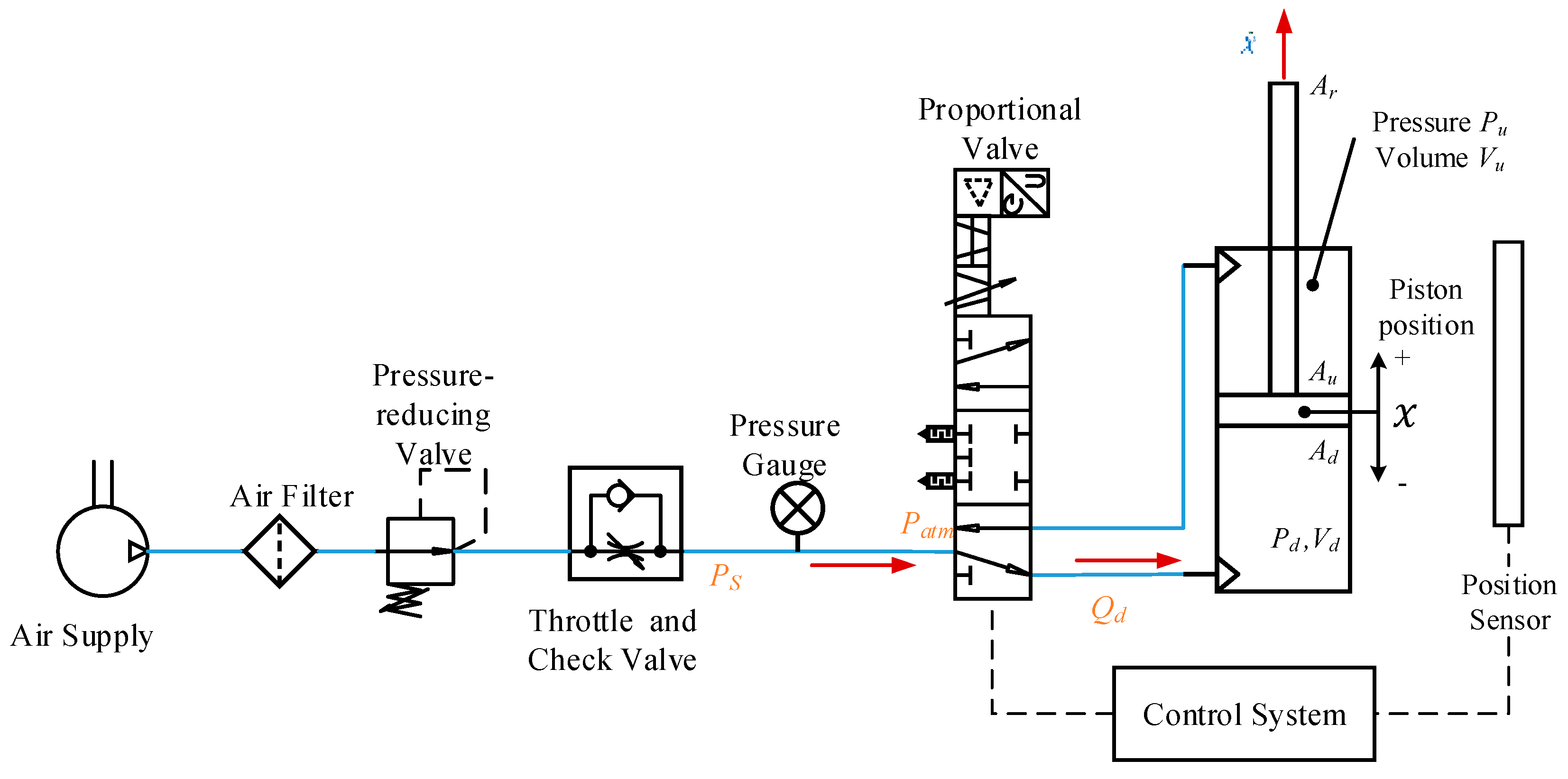
3.2. Pneumatic System Modeling
3.2.1. Pneumatic Cylinder Model
3.2.2. Valve Model
4. Design of Controller
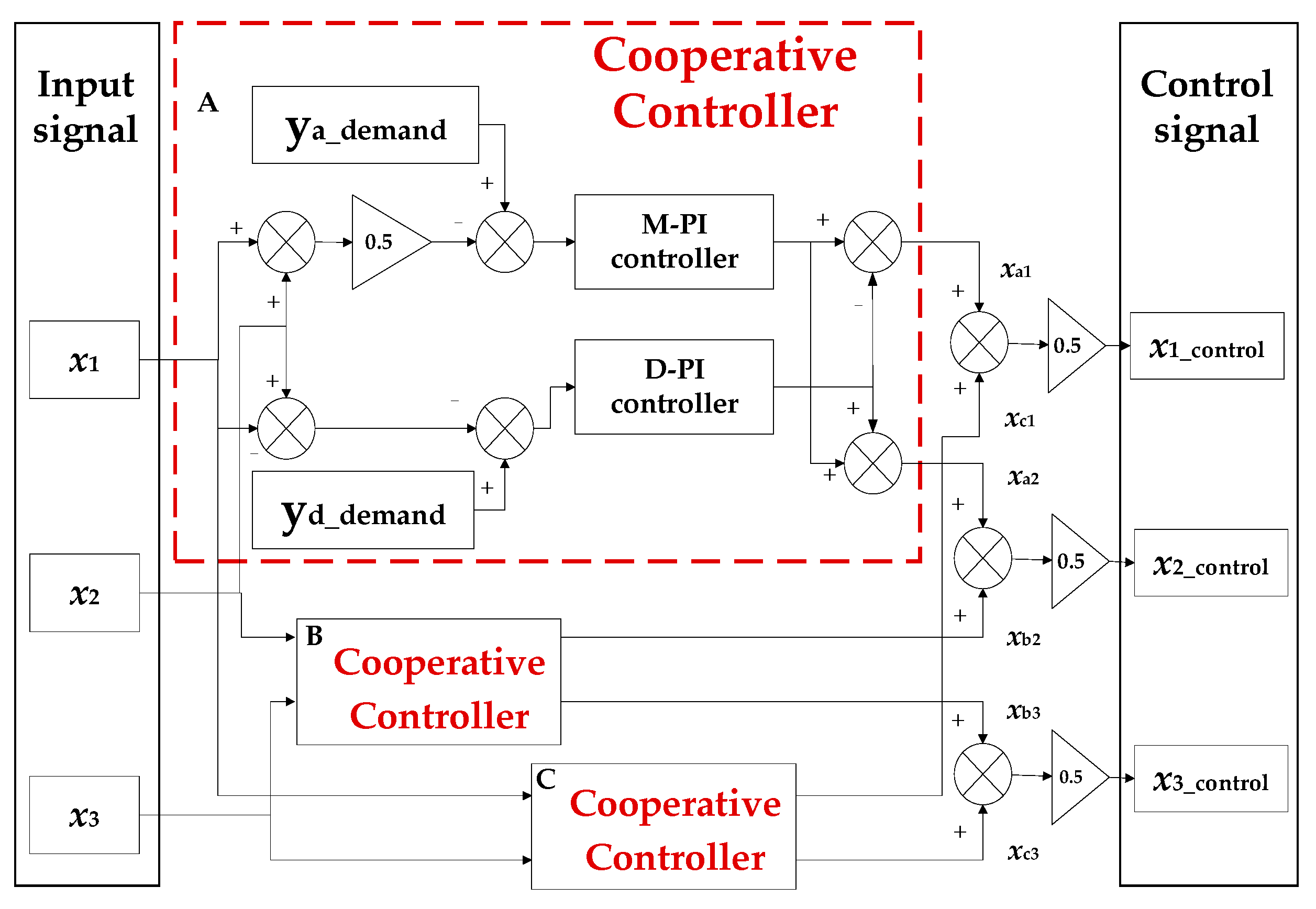
4.1. Control Strategy
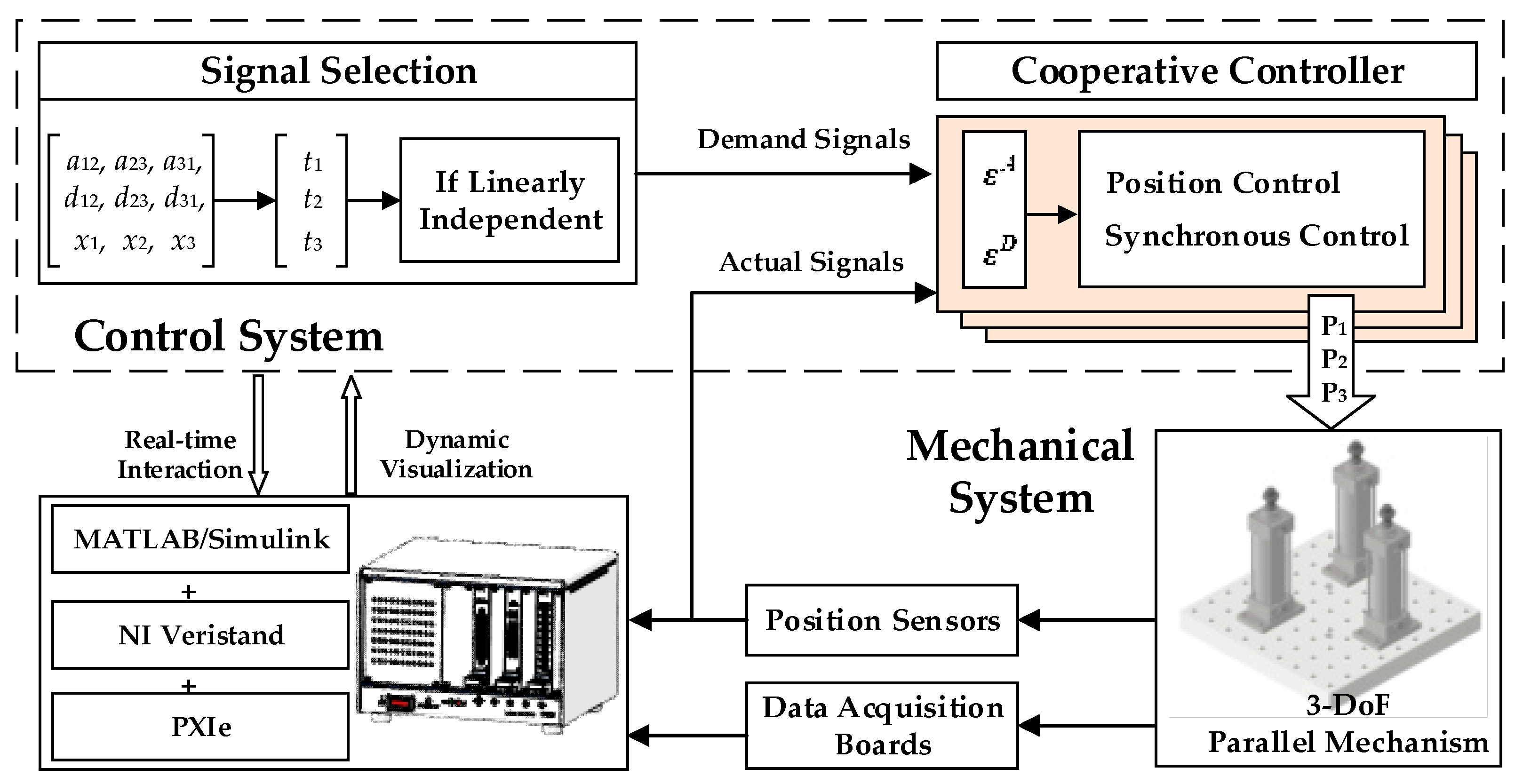
4.2. Cooperative Control System
4.2.1. Signal Selection
4.2.2. Cooperative Controller
4.2.3. Control System Framework
5. Results and Discussions
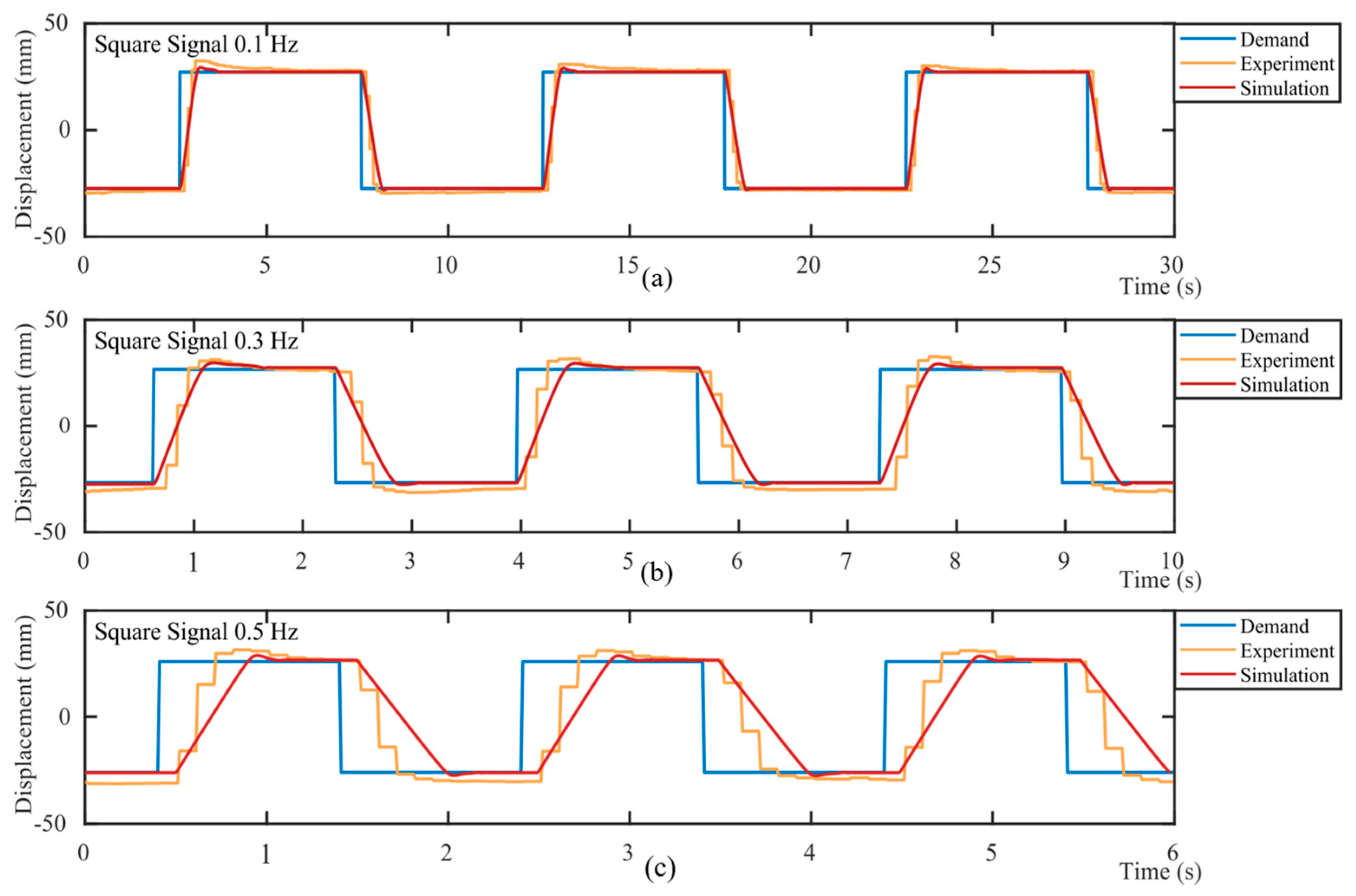
5.1. Validity of Pneumatic System Model
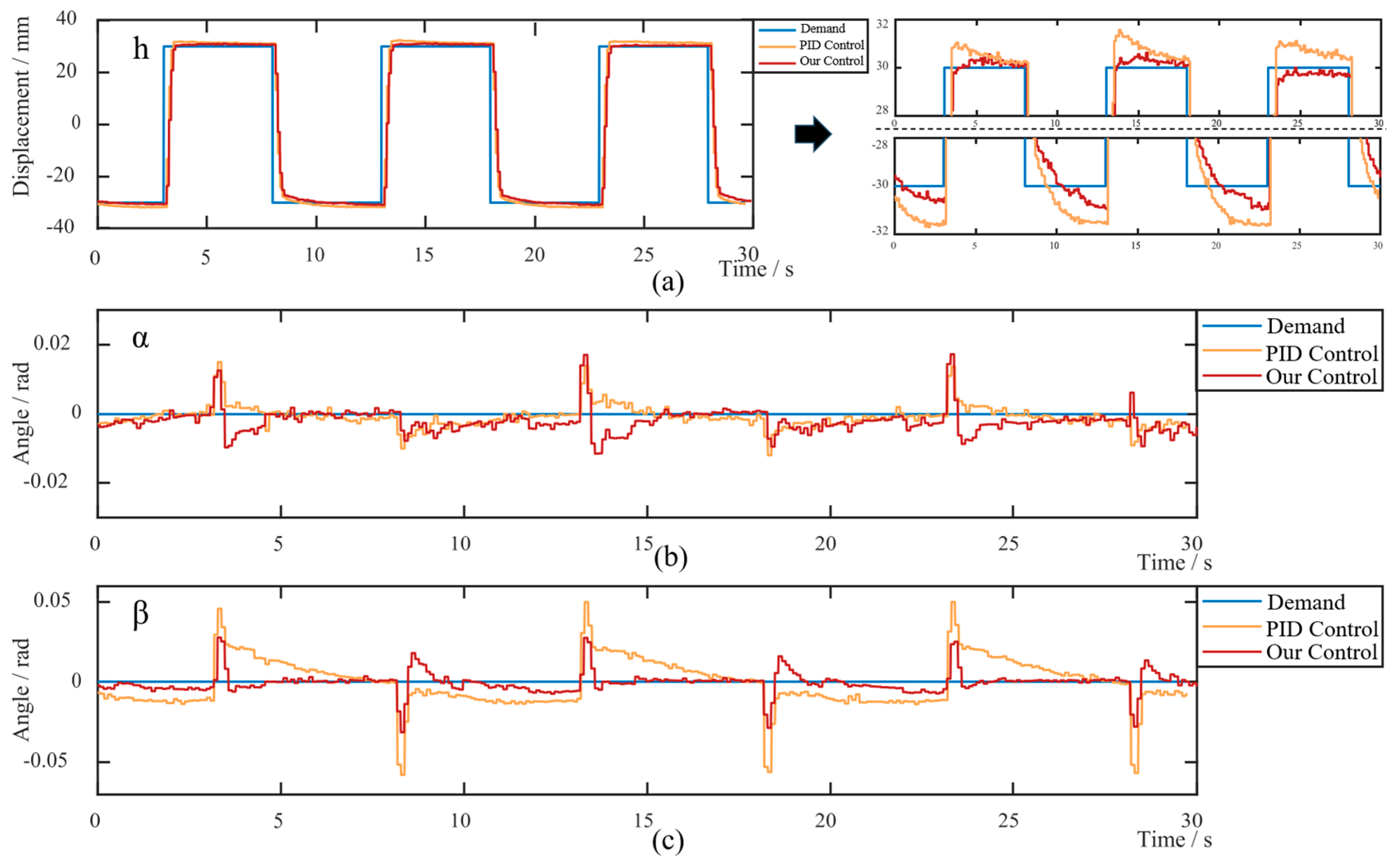
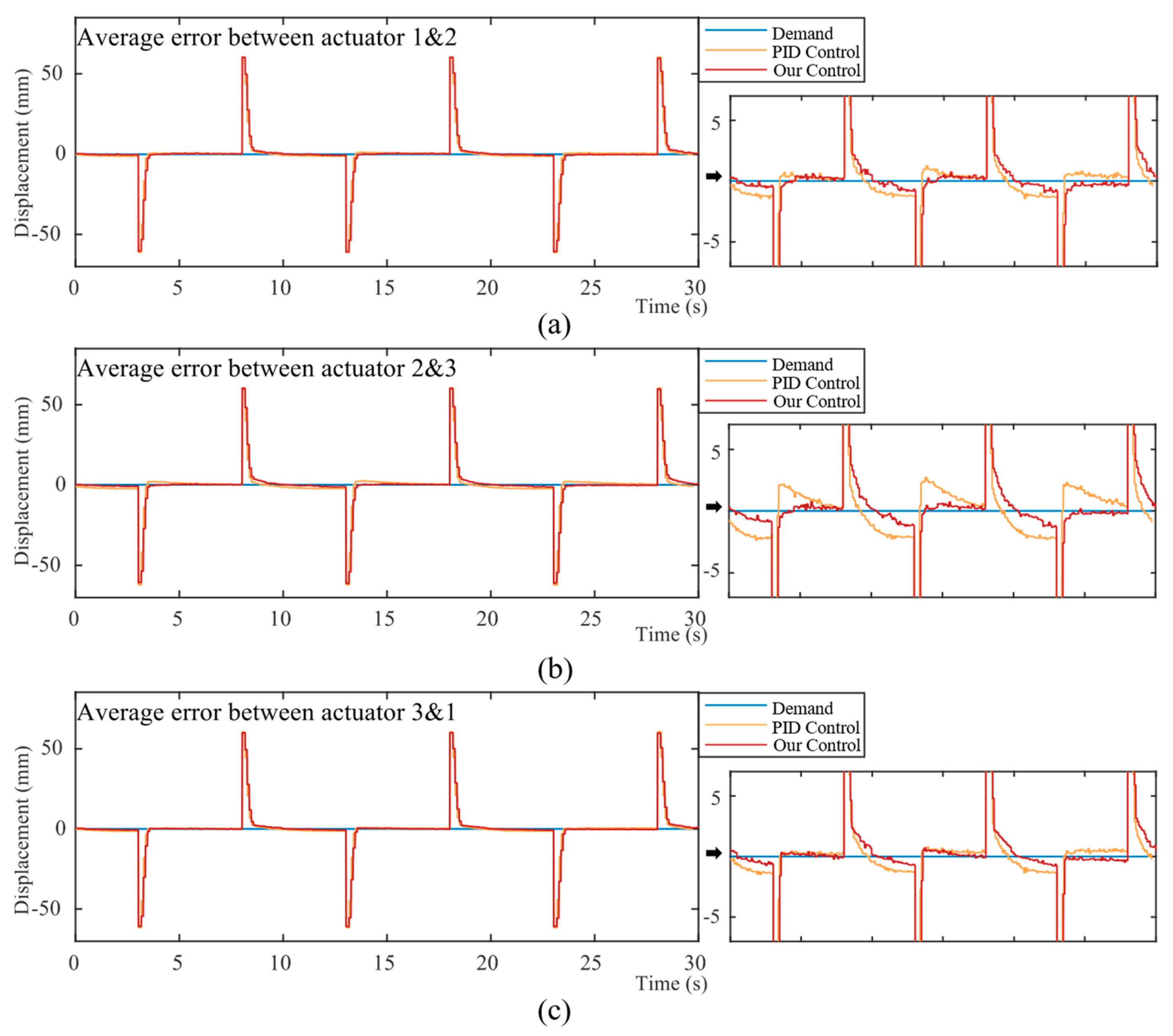
5.2. Performance of Controllers
5.3. Discussions
6. Conclusions
- Additionally, this research implemented the complete mechatronic design of a low-cost 3-DoF parallel robot that integrates mechanical, electrical, and control systems. Our self-designed parallel system with a simple and open architecture can serve as a versatile test bench for validating and comparing various methods for the 3-DoF mechanism. This can provide a controlled environment for evaluating the performances of different control algorithms under different conditions. The primary contributions of this paper can be summarized as follows. The paper introduces a novel control mechanism aimed at achieving synchronous motion and improving tracking accuracy for 3-DoF PMs.
- Unlike traditional control methods, the proposed mechanism designed a cooperative error to incorporate inter-chain communication and reduce coupling effects in PMs.
- An intuitive 3-DoF pneumatic test bench for the control methods was constructed, and comparisons with experiments with the baseline controller showed the proposed method had better tracking performance.
- In the future, it is expected to continue evaluating this cooperative controller. It is noticed that adjusting the controller for one cylinder has a certain degree of influence on the other cylinders. Subsequent research will delve into this effect and find the potential trends. Moreover, it is aimed to generalize this control approach for higher-DoF PMs, or at least, this control strategy can be employed in the motion of certain DoFs. What is more, a self-designed plate will be installed on the cylinder of the 3-DoF platform to support further research on PMs. The base of our platform is connected with an automated guided vehicle (AGV), which provides more DoF and potential research aspects.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Merlet, J.P. Parallel Robots; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006; Volume 128. [Google Scholar]
- Vallés, M.; Díaz-Rodríguez, M.; Valera, Á.; Mata, V.; Page, Á. Mechatronic development and dynamic control of a 3-DOF parallel manipulator. Mech. Based Des. Struct. Mach. 2012, 40, 434–452. [Google Scholar] [CrossRef]
- Gao, M.; Zhang, X.; Liu, H. Experiment and kinematic design of 3-RRR parallel robot with high speed. Robot 2013, 35, 716–722. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, X.; Chen, Z. Dynamic analysis of a 3-RRR parallel mechanism with multiple clearance joints. Mech. Mach. Theory 2014, 78, 105–115. [Google Scholar] [CrossRef]
- Zou, Q.; Zhang, D.; Zhang, S.; Luo, X. Kinematic and dynamic analysis of a 3-DOF parallel mechanism. Int. J. Mech. Mater. Des. 2021, 17, 587–599. [Google Scholar] [CrossRef]
- Stewart, D. A platform with six degrees of freedom. Proc. Inst. Mech. Eng. 1965, 180, 371–386. [Google Scholar] [CrossRef]
- Niu, X.-M.; Gao, G.-Q.; Liu, X.-J.; Bao, Z.-D. Dynamics and control of a novel 3-DOF parallel manipulator with actuation redundancy. Int. J. Autom. Comput. 2013, 10, 552–562. [Google Scholar] [CrossRef]
- Kumar, S.; Bongardt, B.; Simnofske, M.; Kirchner, F. Design and kinematic analysis of the novel almost spherical parallel mechanism active ankle. J. Intell. Robot. Syst. 2019, 94, 303–325. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, D.; Song, Z.; Guo, H.; Liu, R.; Kou, Z. Workspace analysis and size optimization of planar 3-DOF redundantly actuated parallel mechanism. J. Mech. Sci. Technol. 2024, 38, 1–11. [Google Scholar] [CrossRef]
- Clavel, R. DELTA, a fast robot with parallel geometry. In Proceedings of the 18th International Symposium on Industrial Robots, Lausanne, Switzerland, 26–28 April 1998; pp. 91–100. [Google Scholar]
- Liu, X.-J.; Kim, J. A new spatial three-DoF parallel manipulator with high rotational capability. IEEE/ASME Trans. Mechatron. 2005, 10, 502–512. [Google Scholar] [CrossRef]
- Wang, K.; Li, J.; Shen, H.; You, J.; Yang, T. Inverse Dynamics of A 3-DOF parallel mechanism Based on Analytical Forward Kinematics. Chin. J. Mech. Eng. 2022, 35, 119. [Google Scholar] [CrossRef]
- Xie, J.; Zuo, F.F.; Li, Y.P.; Yang, Q.Z. Mechanism design and kinematics simulation of 3-DOF parallel mechanism with low coupling degree. IOP Conf. Ser. Mater. Sci. Eng. 2020, 793, 012048. [Google Scholar] [CrossRef]
- KTalke, K.; Drotman, D.; Stroumtsos, N.; de Oliveira, M.; Bewley, T. Design and Parameter Optimization of a 3-PSR parallel mechanism for Replicating Wave and Boat Motion. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 7955–7961. [Google Scholar] [CrossRef]
- Wang, D.; Wang, L.; Wu, J.; Ye, H. An Experimental Study on the Dynamics Calibration of a 3-DOF Parallel Tool Head. IEEE/ASME Trans. Mechatron. 2019, 24, 2931–2941. [Google Scholar] [CrossRef]
- John, I.; Mohan, S.; Sudheer, A.P. Conceptual Design and Kinematic Analysis of a 1T2R Parallel Manipulator. In Proceedings of the IFToMM International Conference on Mechanisms, Transmissions and Applications, Poitiers, France, 24–26 May 2023; Springer Nature: Cham, Switzerland, 2023; Volume 124, pp. 127–137. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, X. Kinematic Analysis and Control of a 3-DOF Parallel Mechanism. In Proceedings of the Intelligent Robotics and Applications: 7th International Conference, ICIRA 2014, Guangzhou, China, 17–20 December 2014; pp. 36–47. [Google Scholar]
- de Smet, P.J.; Rivin, E.I.; Lou, Y.; Kegg, D. Robot Performance as Influenced by Mechanical System. CIRP Ann. 1990, 39, 383–386. [Google Scholar] [CrossRef]
- Guan, G.; Plummer, A. Acceleration decoupling control of 6 degrees of freedom electro-hydraulic shaking table. J. Vib. Control 2019, 25, 2758–2768. [Google Scholar] [CrossRef]
- Plummer, A.R. Model-based motion control for multi-axis servohydraulic shaking tables. Control Eng. Pract. 2016, 53, 109–122. [Google Scholar] [CrossRef]
- Zhang, L.; Cong, D.; Yang, Z.; Zhang, Y.; Han, J. Optimal Design and Hybrid Control for the Electro-Hydraulic Dual-Shaking Table System. Appl. Sci. 2016, 6, 220. [Google Scholar] [CrossRef]
- Chaudhary, G.; Ohri, J. 3-DOF Parallel manipulator control using PID controller. In Proceedings of the 2016 IEEE 1st International Conference on Power Electronics, Intelligent Control and Energy Systems (ICPEICES), Delhi, India, 4–6 July 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Sheng, L.; Li, W. Optimization design by genetic algorithm controller for trajectory control of a 3-RRR parallel robot. Algorithms 2018, 11, 7. [Google Scholar] [CrossRef]
- Dumlu, A.; Erenturk, K. Trajectory Tracking Control for a 3-DOF Parallel Manipulator Using Fractional-Order PIλDμ Control. IEEE Trans. Ind. Electron. 2014, 61, 3417–3426. [Google Scholar] [CrossRef]
- Xu, M.; Tian, W.; Zhang, X. Kinematic Calibration for the 3-UPS/S Shipborne Stabilized Platform Based on Transfer Learning. J. Mar. Sci. Eng. 2024, 12, 275. [Google Scholar] [CrossRef]
- Zhang, Z.; Hou, Z.; Li, L.; Qin, H.; Abbas, M.; Siddique, M. Design and implementation of a 2-DOF 5R parallel mechanism with a coaxial-driven layout. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2024. [Google Scholar] [CrossRef]
- Cazalilla, J.; Vallés, M.; Mata, V.; Díaz-Rodríguez, M.; Valera, A. Adaptive control of a 3-DOF parallel manipulator considering payload handling and relevant parameter models. Robot. Comput. Integr. Manuf. 2014, 30, 468–477. [Google Scholar] [CrossRef]
- Zhang, H.; Fang, H.; Zhang, D.; Luo, X.; Zou, Q. Adaptive Fuzzy Sliding Mode Control for a 3-DOF Parallel Manipulator with Parameters Uncertainties. Complexity 2020, 2020, 2565316. [Google Scholar] [CrossRef]
- Chen, Z.; Song, J.; Li, N.; Yan, W.; Zhao, C. Design and dynamics modeling of a novel 2R1T 3-DOF parallel motion simulator. J. Braz. Soc. Mech. Sci. Eng. 2023, 45, 234. [Google Scholar] [CrossRef]
- Su, Y.; Sun, D.; Ren, L.; Mills, J.K. Integration of saturated PI synchronous control and PD feedback for control of parallel manipulators. IEEE Trans. Robot. 2006, 22, 202–207. [Google Scholar] [CrossRef]
- Su, Y.X.; Sun, D. A Model Free Synchronization Approach to Controls of Parallel Manipulators. In Proceedings of the 2004 IEEE International Conference on Robotics and Biomimetics, Shenyang, China, 22–26 August 2004; pp. 523–528. [Google Scholar] [CrossRef]
- Koren, Y. Cross-Coupled Biaxial Computer Control for Manufacturing Systems. J. Dyn. Syst. Meas. Control 1980, 102, 265–272. [Google Scholar] [CrossRef]
- Doan, Q.V.; Le, T.D.; Vo, A.T. Synchronization Full-Order Terminal Sliding Mode Control for an Uncertain 3-DOF Planar Parallel Robotic Manipulator. Appl. Sci. 2019, 9, 1756. [Google Scholar] [CrossRef]
- Ren, L.; Mills, J.K.; Sun, D. Experimental Comparison of Control Approaches on Trajectory Tracking Control of a 3-DOF Parallel Robot. IEEE Trans. Control Syst. Technol. 2007, 15, 982–988. [Google Scholar] [CrossRef]
- Ren, L.; Mills, J.K.; Sun, D. Adaptive Synchronized Control for a Planar Parallel Manipulator: Theory and Experiments. J. Dyn. Syst. Meas. Control 2006, 128, 976–979. [Google Scholar] [CrossRef]
- Ren, L.; Mills, J.K.; Sun, D. Performance Improvement of Tracking Control for a Planar Parallel Robot Using Synchronized Control. In Proceedings of the 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems, Beijing, China, 9–13 October 2006; pp. 2539–2544. [Google Scholar] [CrossRef]
- Richer, E.; Hurmuzlu, Y. A High Performance Pneumatic Force Actuator System: Part I—Nonlinear Mathematical Model. J. Dyn. Syst. Meas. Control 2000, 122, 416–425. [Google Scholar] [CrossRef]
- Sanville, F.E. A new method of specifying the flow capacity of pneumatic fluid power valves. In Proceedings of the Fluid Power Symposium, Guildford, UK, 4–7 January 1971, 2nd ed.; University of Surrey: Guildford, UK, 1971. [Google Scholar]


| Components | Model | No. | Notes | Picture |
|---|---|---|---|---|
| Valves | MPYE-5-M5-010 | 3 | Proportional valve |  |
| Setpoint modules | MPZ-1-24DC-SGH-6-SW | 3 | Conjunction with valve |  |
| Cylinder | MDBB40-100Z | 3 |  | |
| Position sensor | D-MP100 | 3 | Measure piston displacement |  |
| Controller PC | JYTEK PXIe-2315 Series | 1 |  | |
| Data acquisition board | JYTEK PXIe-5510 | 1 |  |
| Vector or Point | Coordinates | Vector or Point | Coordinates |
|---|---|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Q.; He, G.; Feng, G.; Ding, B. A Novel Cooperative Control Strategy for Three-Degree-of-Freedom Pneumatic Parallel Mechanism. Actuators 2024, 13, 89. https://doi.org/10.3390/act13030089
Huang Q, He G, Feng G, Ding B. A Novel Cooperative Control Strategy for Three-Degree-of-Freedom Pneumatic Parallel Mechanism. Actuators. 2024; 13(3):89. https://doi.org/10.3390/act13030089
Chicago/Turabian StyleHuang, Qingqing, Guanwei He, Guodong Feng, and Beichen Ding. 2024. "A Novel Cooperative Control Strategy for Three-Degree-of-Freedom Pneumatic Parallel Mechanism" Actuators 13, no. 3: 89. https://doi.org/10.3390/act13030089
APA StyleHuang, Q., He, G., Feng, G., & Ding, B. (2024). A Novel Cooperative Control Strategy for Three-Degree-of-Freedom Pneumatic Parallel Mechanism. Actuators, 13(3), 89. https://doi.org/10.3390/act13030089







