Abstract
This paper provides an overview of techniques of compact modeling via model order reduction (MOR), emphasizing their application to cooperative microactuators. MOR creates highly efficient yet accurate surrogate models, facilitating design studies, optimization, closed-loop control and analyses of interacting components. This is particularly important for microactuators due to the variety of physical effects employed, their short time constants and the many nonlinear effects. Different approaches for linear, parametric and nonlinear dynamical systems are summarized. Three numerical case studies for selected methods complement the paper. The described case studies emerged from the Kick and Catch research project and within a framework of the German Research Foundation’s Priority Program, Cooperative Multistable Multistage Microactuator Systems (KOMMMA).
1. Introduction
Microactuators are the hidden facilitators of everyday life and enable devices ranging from smartphones, printers and automotives to industrial facilities. Similar diversity is found in the physical effects deployed for actuation, ranging from shape memory alloys to electrostatics. In general, these devices convert energy into mechanical motion. However, regardless of the specific design, the manufacturing of microactuators requires designated processes and takes several months. In addition, the built hardware usually cannot be repaired or modified; it can only be replaced. For these reasons, a device should be engineered to the highest extent possible prior to production. Another level of complexity is added in the case of cooperative microactuators due to the higher number of actuators and potential cross-coupling. Therefore, reliable models are crucial for this task as they allow us to study excitations, to design control schemes and to optimize the design. Numerically investigating these models is a challenging process due to their computational complexity, nonlinearities and the small time constants inherent to microactuators. This issue is addressed by methods of compact modeling, which aim for computationally efficient yet accurate surrogate models. This methodology is applicable to various physics, nonlinearities and coupling as found in cooperative microactuators. Focusing on microactuators and their potential cooperation, this paper provides an overview of a prominent branch of compact modeling: methods of model order reduction (MOR). MOR generates significantly smaller surrogate models on the basis of large-scale dynamical systems as arising from, e.g., the finite element method (FEM). It has been widely applied in the simulation of microelectromechanical systems (MEMS) and to enhance traditional simulation tools [1]. To reduce a dynamical system, it is projected onto a low-dimensional subspace that captures most of its dynamics. In a physical sense, the state vector, e.g., a displacement field, is approximated by a linear combination of inherent patterns, also known as modes, shapes or the reduced basis.
1.1. State of the Art: Projection-Based Linear Model Order Reduction for Microactuators
Extensive research has investigated this linear MOR process [2] and several methods have been proposed [3]. These methods mainly differ in how they identify the patterns, i.e., how the reduced basis and the projection are computed. More specifically, a reduced basis may be a local or global approximation, may guarantee certain system-theoretic properties or may be limited to original systems of small dimension due to the method’s computational complexity. All these reductions can be nested sequentially to combine different methods. The interested reader is referred to [4] for an intuitive overview and to [5,6,7] for a comprehensive handbook covering methods and a variety of applications. The following paragraphs consider the most established classes of these methods, namely modal truncation, substructuring, balanced truncation, Krylov subspaces and proper orthogonal decomposition (POD). Special emphasis is placed on applications to microactuators to provide starting points for interested readers.
One of the oldest methods is modal truncation [8]. Well established in structural dynamics, it approximates displacements via the superposition of vibration modes. Unlike many other methods, these modes are not purely numerical constructs but have actual physical meaning: when excited with an eigenfrequency, the device vibrates in the corresponding eigenmode. This reduced basis forms a global approximation and leads to a diagonal reduced order model (ROM), which allows for even faster computations. The consideration of modal derivatives qualifies the concept as nonlinear MOR [9,10]. Modal truncation has been widely used for MEMS, e.g., for electromechanic RF microswitches with geometrical nonlinearities [11] and fluid structural interactions [12]. Further examples include micromirror arrays [13] and MEMS gyroscopes [14,15,16,17].
Another early branch of MOR from structural mechanics is substructuring [18,19], which includes Guyan reduction or static condensation [18], Craig-Bampton reduction [20] and component mode synthesis [21,22,23]. The general idea is to decompose the domain into substructures, which are reduced individually. These reduced substructures might be collected in a library and coupled to represent a full system. Hence, this methodology is well suited for cooperative microactuators as it emphasizes coupling. For each substructure, only the degrees of freedom (DOFs) not contributing to the coupling interfaces are reduced. Therefore, the corresponding ROM’s DOFs comprise two sets: the reduced coordinates and all interface-related DOFs of the original substructure. As a result, large ROMs are required for good accuracy [24]. This concept has been applied to MEMS to investigate gas sensors [25], the failure modes of RF microswitches [26], electrothermomechanical microgrippers [27] or gyroscopes [28].
A noteworthy system-theoretic method is balanced truncation [29,30,31,32], which guarantees an optimal global reduction and, as a rather distinctive property, features an a priori error bound. Based on the control-theoretic concepts of controllabilty and observability, the system is transformed into a balanced realization. The transformed states are sorted by their Hankel singular values, which can be interpreted as the states’ energies. Truncating insignificant states achieves the reduction. While this method ensures desirable properties, it carries high computational costs and is therefore limited to small models [33]. Consequently, little research has investigated purely balanced truncation for MEMS, e.g., for a gyroscope [34]. Instead, it has often been applied as a second reduction step in combination with, e.g., Krylov-subspace-based methods [35,36].
Methods based on Krylov subspaces [37,38,39] are among the most efficient and often the only choice for large-scale models [40]. They are also known as rational interpolation or moment matching and utilize the concept of transfer functionsThey ensure that the Taylor-expanded transfer functions of both the original and the reduced model match for the first r moments. Hence, a corresponding reduced basis forms a local approximation around an expansion point in the frequency domain. The default expansion point of focuses on the steady-state behavior, while dynamic responses require higher expansion points. Specialized variants have been proposed, e.g., for second-order systems [41] or for the optimal choice of expansion points [42]. This class of methods has been deployed in numerous MEMS-related research articles, especially due to its synergy with high-dimensional FEM models. Examples include simple microstructures [43], electro-thermal MEMS [44,45,46,47,48], thermomechanical microgrippers [27], piezoelectric devices [49,50,51], electromechanical actuators [52], electromagnetic systems [53,54], gyroscopes [55] and accelerometers [56].
Another approach to the construction of a reduced basis is data-driven methods such as POD. Based on simulated data, POD finds a reduced basis via statistical methods that cover the variance in these data. While this reduced basis is limited to its training, it is easy to implement. In addition, it is commonly used for nonlinear systems as concepts from system theory might be inapplicable. An early application of POD to microactuators investigated a microswitch with squeeze-film damping [43]. Further examples include MEMS beams [57,58], resonators [59] and micromirrors [60].
Please note that it is also possible to create parametric ROMs [61,62] to conduct efficient design studies. Parametric influences might originate from, e.g., material properties or geometry. A parameter’s effect is usually either captured by an affine expression [63,64] or approximated by interpolation [65]. Additionally, the reduced basis needs to be extended to capture parametric changes. This methodology has facilitated the design process of microswitches [66], RF resonators [64], gyroscopes [64,67,68], anemometers [67], microthrusters [63,68] or thermoelectric generators [48].
1.2. State of the Art: Projection-Based Nonlinear Model Order Reduction for Microactuators
However, all these methods of projection-based MOR are limited to linear systems. In the case of nonlinearities, they cannot reduce the nonlinear terms or are not even applicable at all. This poses a major bottleneck because MEMS are often subject to nonlinear effects, ranging from large deformations, electrostatic forces, hysteresis for piezoelectric devices or shape memory alloys, to mechanical contact. A remedy is provided by additionally approximating the nonlinear forces in an efficient way. This second approximation step is also known as hyper-reduction. The following paragraphs briefly introduce relevant hyper-reduction methods, such as an approach for systems with few nonlinearities, the trajectory piecewise-linear (TPWL) approximation, polynomial tensors, discrete empirical interpolation method (DEIM) and energy conserving mesh sampling and weighting (ECSW). The first two methods are explained in detail in Section 2.3 and applied to numerical test cases in Section 3. Please note that while these methods achieve great results, they require individual treatment for each model and are often limited to load cases considered in their training. Another common challenge is to obtain the data needed from commercial simulation software, often limiting the choices.
An approach for systems with few nonlinearities is to transform them into artificial inputs [24,69]. This method is straightforward to implement, preserves the physical meaning and does not rely on training data. Further, larger numbers of nonlinearities can be lumped into fewer terms to achieve compatibility. However, this approach is limited to nonlinearities that depend on a single or a few DOFs at most, e.g., to one-dimensional electrostatic forces or mechanical contact. MEMS-related applications range from RF switches [69] and scanning-probe data storage [24] to electromechanical beam actuators [52].
The TPWL approximation is a robust method for general nonlinear systems [70]. A combination of linearized systems sampled along a training trajectory approximate a nonlinear system. The combination weights depend on the reduced state and change throughout the simulation. Therefore, a TPWL-approximated system is still nonlinear, but the corresponding terms are few and are efficient to evaluate. While the approach is robust and only requires easily obtainable data, its accuracy strongly depends on the weighting scheme and the sampling strategy. Furthermore, it relies on data generated by extensive simulation of the original model. The main work proposing this approach featured an electromechanical MEMS as a case study [70]. Later work reduced thermal actuators [71], thermal switches [47,72,73] or solenoid actuators [74] based on TPWL.
Polynomial tensors are another intuitive approach for hyper-reduction. The concept is to approximate the reduced nonlinear forces by a Taylor expansion [75,76]. However, the Taylor series’ coefficients are tensors of increasing order and, thus, the method quickly becomes inapplicable due to the amount of entries.Therefore, polynomial tensors effectively only suit nonlinearities that can be approximated by low-order Taylor expansions. One such nonlinearity is St. Venant–Kirchhoff materials, which describe linear–elastic systems at large deformations [4]. This method may be deployed to incorporate geometrical nonlinearities into substructures, as introduced in Section 2.2. A direct application to MEMS is found for an electromechanical actuator with squeeze-film damping [75].
A commonly used hyper-reduction method is the DEIM [77], which evaluates only a few of the original nonlinearities. These evaluated nonlinearities serve as weights for precomputed force patterns to approximate the whole nonlinear force vector. The approximated force vector is subsequently projected back onto the reduced space. Hence, the nonlinear vector is approximated by a reduced force basis with state-dependent weights. This scheme does not ensure stability and leads to asymmetry [4]. Constructing the reduced force basis and choosing the subset of nonlinearities to evaluate are data-driven processes and rely on training data, limiting the prediction quality. Applications to MEMS or to models featuring the same physics comprise electrothermal microgrippers [78], MEMS switches [79] and transistors [79].
A recently introduced hyper-reduction method is the ECSW procedure [80,81,82]. This approach considers the virtual work of the reduced forces over all finite elements. A subset of elements is determined so that the combination of their weighted energies approximates the original total work. The weights compensate for the energies of the numerous excluded elements [81]. This approach has similarities to the transfer of loads from a fine FEM mesh to a coarser one [81]. In contrast to the DEIM and many other hyper-reduction methods, stability and symmetry are preserved. Furthermore, the reduced force vector is approximated directly, instead of approximating the full vector and subsequently projecting it to the reduced space [81]. Again, training data are needed and this limits the prediction quality, even though there is some robustness. To our knowledge, this method is yet to be extended to the microactuator community.
1.3. Alternatives to Projection-Based Model Order Reduction
While projection-based MOR achieves highly efficient and accurate surrogate models and also preserves the original model’s structure, alternative methodologies exist. These approaches are also suitable to obtain compact models of microactuators and vary drastically in their complexity and performance. Commonly deployed methodologies for compact modeling are look-up tables, meta-modeling, generalized Kirchoffian network (GKN) and machine-learning-based or data-driven approaches. Please note that these techniques can often be combined with MOR, e.g., to update a nonlinear stiffness matrix via a look-up table [17] or to approximate nonlinear forces via artificial neural networks (ANNs) [83,84].
Look-up tables are the most basic solution and consist of precomputed outputs for sampled input combinations. While they are robust and easy to implement, they strongly depend on the sampling strategy and, potentially, an interpolation scheme. Furthermore, they are unsuitable for dynamical systems and drastically lose accuracy as the number of parameters increases.
Meta-modeling or response surfaces extend the previous approach of look-up tables with regression analysis [85]. While they also require several sampled solutions of the original models, they achieve higher accuracy and some extrapolation quality. However, their performance depends on how well the basic function matches the relation to be modeled. Usually, they are not deployed to approximate dynamical systems but relations between design variables and outputs for design optimization.
A prominent branch of compact modeling is GKNs, which transfer the concept of electrical Kirchoffian networks to other physical domains [86]. Therefore, a microactuator might be represented by a network of lumped elements. This methodology covers multiphysical problems as well as nonlinear effects while preserving the basic structure of the original model. Another advantage is the physical meaning of all components and the computational efficiency, but accuracy might be sacrificed due to the lumped nature. Furthermore, it requires expert knowledge to divide a structure into lumped elements and to fill them with an appropriate mathematical model. Applications to microsystems are common [87] and include capacitive MEMS transducers [88] and acoustic ultrasonic MEMS transducers [89], as well as magnetic, electric and acoustic transducers [87].
A novel and promising branch is machine-learning-based and data-driven approaches. This includes methods such as ANNs [90] or data-driven MOR via operator inference [91,92,93]. These methods have in common that they rely on vast amounts of training data. In the context of simulation, these data are easy to obtain without noise or outliers and are available from commercial software. Solving the original model numerous times to obtain data and subsequent training leads to high computational costs. In addition, some methods require expert knowledge to adjust the hyperparameters or choose architectures. Furthermore, the structure of the problem and the physical interpretability might not be preserved. Nevertheless, this class of methods is suitable for a wide range of problems and synergizes well with simulated data.
1.4. Outline of the Article
This paper reviews the methodology of MOR and emphasizes its application to microactuators. The aim is to further establish MOR in the microactuator community. Therefore, a brief methodological overview tailored to the microactuator community is provided. References for different actuators are intended as starting points for interested readers. Moreover, three extensive case studies demonstrate the potential of MOR.
The remainder of the paper is structured as follows. Section 2 provides the theory, describing the process from the numerical modeling of microactuators to reduced order models. Subsequently, Section 3 applies the theory from Section 2 to three microsystem-oriented case studies, covering several physics and nonlinear effects. Finally, Section 4 summarizes this work.
2. Compact Modeling by Means of Mathematical Model Order Reduction
This section describes how to derive a highly efficient surrogate model as illustrated in Figure 1. The starting point is a mathematical model given by the governing partial differential equation (PDE). Spatial discretization via, e.g., the FEM leads to an accurate but large-scale system of n ordinary differential equations (ODEs), as described in Section 2.1. Subsequently, MOR constructs a highly efficient surrogate model, i.e., an ODE system of the same form, but with much smaller dimensions , as described in Section 2.2.
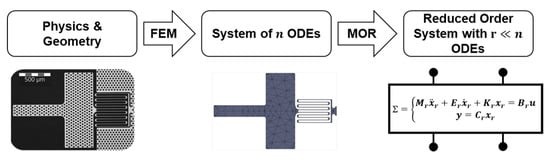
Figure 1.
Workflow of MOR-based compact modeling. Starting from a microsystem and its governing physics, the FEM assembles a high-dimensional dynamical system. This system is then reduced by methods of MOR, resulting in a surrogate model of drastically smaller dimensions.
2.1. Mathematical Modeling of Microactuators
Physical laws dictate the behavior of all microactuators. At the continuum level, these laws can be described by mathematical models (PDEs), which usually comprise two components: conservation laws and constitutive relations. The former arise from the universal conservation of quantities, such as energy or mass; the latter introduce experimentally confirmed material relations. This concept applies to numerous physical domains, including structural, thermal, acoustic and electric, as well as to their multiphysical coupling. This section deploys linear elastic dynamics as an example, since it is relevant to all microactuators. The governing PDE is Newton’s second law, which is denoted by the following second-order PDE for time-independent density:
Here, is the stress tensor, the body force per volume, the density and the displacement vector. The relevant constitutive relation is Hooke’s law given by
where is the stiffness tensor and is the strain tensor. The following strain–displacement equation from infinitesimal strain theory completes the mathematical description:
While the above equations provide the complete mathematical model, they can only be solved analytically for the most basic scenarios. An established approach to finding a remedy is numerical methods such as the FEM. The FEM subdivides the computational domain into smaller subdomains called finite elements and approximates the solution with element-wise polynomial shape functions. Mathematically, this spatial discretization converts the initial PDE into a system of linear ODEs in the form of
where , and are the system matrices and is the state vector. In contrast to Equations (1) and (3), comprises numerous nodal displacements at different positions and not continuous displacement functions. The input vector is denoted by , the user-defined output vector by . The inputs are distributed by and the outputs are computed from the state vector by . The feedthrough matrix includes the direct effect that inputs may have on outputs. As the system is linear and all matrices remain constant over time, it is referred to as linear time-invariant. Systems of this form are common in control theory and several concepts for further analysis apply. One such concept is the transfer function , which is an equivalent system representation. It relates Laplace transformations of input and output functions
where s is the complex frequency variable. For the system in Equation (4), the transfer function is given by
2.2. Projection-Based Linear Model Order Reduction
Although numerical methods such as the FEM are capable of solving sophisticated multiphysical problems, they suffer under high computational costs. These high computational costs arise from the fact that FEM-generated dynamical systems reach large dimensions up to . Therefore, these models’ dimensions impede efficient design studies and prevent application in control circuits, especially considering the small time scales of microactuators. A well-established approach to tackling this challenge is projection-based MOR [94], which creates surrogate models of the same structure but significantly smaller dimension. These surrogates enable fast prediction, more extensive analysis options, parametric investigations and feedback control.
The basic idea behind MOR is to decompose the solutions into patterns. Restricting the solution space to the most important of these patterns results in a low-dimensional surrogate model. These patterns are also known as modes, shapes or reduced basis vectors. In a mathematical sense, the state vector becomes a linear combination of predefined patterns as illustrated in Figure 2. After orthonormalizing the r most important patterns for numerical reasons, they are assembled as columns of a projection matrix . The reduced state vector comprises the weights of all these patterns. Omitting most patterns as they barely contribute introduces an approximation error , and it holds that
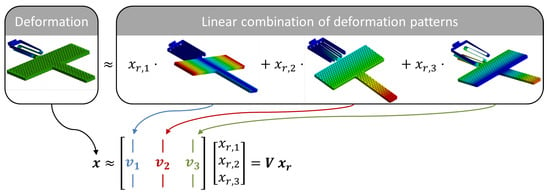
Figure 2.
General idea of MOR: approximating the state as a combination of few relevant patterns. In this example, the state corresponds to the deformation of an electrostatic beam actuator and it is approximated by three eigenmodes. Here, the color indicates deformation magnitude. The Eigenmodes are assembled as columnvectors . The corresponding weights are collected within the reduced state vector . In general, the specific vectors in depend on the method chosen for MOR.
However, substituting this approximation into the system in Equation (4) results in an overdetermined system, which also includes an approximation error. To obtain a unique solution and to eliminate the error from the equation, the system is projected onto along . The pattern-based approximation in Equation (7) and an appropriate projection reduce the system in Equation (4) to
where , , , and are the reduced system matrices. These reduced matrices only need to be computed once and can be subsequently deployed in applications. Please note that the inputs and outputs remain unchanged. This ROM contains multiple orders of magnitude less ODEs than the original FEM system in Equation (4) as . As a result, all subsequent computations are significantly faster. Specific methods to construct the reduced basis are presented and discussed in Section 1, including modal truncation, substructuring, balanced truncation, Krylov subspaces and POD.
2.3. Projection-Based Nonlinear Model Order Reduction
In general, real-world physics are nonlinear. In some cases, the nonlinearities barely contribute within the operating conditions of interest, and a linear model provides sufficient accuracy. However, the field of MEMS features several potential nonlinear effects, such as large deformations, electrostatic forces, hysteresis for piezoelectric devices or shape memory alloys or mechanical contact. Therefore, nonlinear approaches are inevitable for microactuators. In mathematical terms, a nonlinear problem depends on its solution. Hence, the solution process follows an iterative scheme until convergence criteria are eventually satisfied. Due to these iterations, nonlinearities significantly inflate the omputational demands. Considering a system as in Equation (4) but with nonlinear restoring forces leads to
Such a nonlinear system as in Equation (9) entails two great challenges for projection-based MOR. Firstly, many methods to identify reduced bases introduced in Section 2.2 leave their range of validity. Most of the related research deploys the POD because it does not rely on system-theoretic concepts, which might only be defined for linear systems. The second challenge is that the nonlinear term cannot be reduced: approximating the state by patterns and projecting the system as in Equation (8) leads to
Evaluating the nonlinear term requires us to project the reduced state vector into the original high-dimensional space, evaluating the full set of nonlinearities, and then project them back onto the reduced space. Obviously, this process is less efficient than evaluating the original model, especially with respect to the iterative solution scheme. A well-established approach is an efficient approximation of the nonlinear term, which is also known as hyper-reduction [95]. In preparation for the numerical case studies in Section 3.2 and Section 3.3, an approach for systems with few nonlinearities [69] and the TPWL [96] approximation are described.
If a system has only a few nonlinearities, a robust and straightforward approach is to isolate them and to handle them as additional inputs [24,69]. In mathematical terms, the nonlinear term is decomposed into
where is an additional input matrix that distributes nonlinear forces scaled by the nonlinear inputs . To evaluate the nonlinearities in , only a small subset of the full state vector is required. Hence, this approach performs best when the nonlinearities depend on only a few DOFs, which is the case for, e.g., electrostatic forces or simple mechanical contact. Inserting this decomposition into the system in Equation (10) gives
where collects the input matrices and summarizes the inputs. Even though this system is still nonlinear, the relocation into inputs enables the use of linear MOR methods [69]. Another noteworthy advantage is that the approximation is not limited to training data. In the case of a higher number of nonlinearities, they can be condensed by grouping schemes to require significantly fewer nonlinear evaluations. Although this step introduces another approximation, it minimizes the computational demand. Specific grouping schemes are, e.g., to approximate distributed electrostatic forces by a single lumped force [69] or by a force distribution scaled by a single nonlinear term [52].
An early and reliable approach for general nonlinear systems is the TPWL approximation [70]. The idea is to approximate a nonlinear system by a combination of linearized systems that are sampled along a training trajectory. The weights of each system depend on the reduced state and change in the course of the simulation. Due to these state-dependent weighting scheme, the TPWL-approximated system still contains nonlinearities, but they are few and are efficient to evaluate. The nonlinear force vector is expressed as a weighted sum of N linearizations and reads
where the subscript i indicates the ith sampling point, the state-dependent weight and and the linearization. Please note that the sampled systems are linear and, therefore, can be reduced by methods of linear MOR. However, a global reduced basis for all systems is required to achieve compatibility. Combining the approximation in Equation (13) with the system in Equation (10) results in a TPWL-reduced system given by
The remaining nonlinear terms are the N weights , which only depend on the reduced state vector according to Algorithm 1. First, the distance between the current state and the sampled states is computed. Based on the minimum distance m, preliminary weights are calculated. To obtain the final weights, these are normalized by their sum.
| Algorithm 1 Weighting scheme for TPWL. |
|
3. Exemplary Applications of MOR to Microactuators
This section introduces three numerical case studies of different physical domains with both linear and nonlinear setups. The first case study in Section 3.1 describes the linear MOR of a piezoelectric chip actuator based on earlier work [97]. The multiphysical coupling gives rise to a unique challenge as it potentially introduces instability to the corresponding ROMs. Applying the designated methods preserves or reintroduces stability. Section 3.2 presents the second case study, which reduces an electromechanical microactuator as demonstrated in [52]. This device corresponds to a cantilever beam actuated into electrostatic pull-in. Electrostatic forces and mechanical contact render the model nonlinear. A novel third case study in Section 3.3 reduces a geometrically nonlinear beam model via TPWL. The modeled actuator is the same as in Section 3.2, but the FEM model is coarser and exclusively composed of three-dimensional elements. All case studies deploy Ansys® Academic Research Mechanical, Release 2022 R2 for FEM modeling to compute reference solutions and to obtain system matrices. The process of MOR either uses Model Reduction inside Ansys [98] by CADFEM® and/or a Python-based implementation [99,100].
3.1. Piezoelectric Chip Actuator
This numerical case study investigates the PA3JEA piezoelectric chip actuator and is based on earlier work [97] that contains a more detailed description. Figure 3 depicts the actuator and its symmetry-exploiting FEM model. The ceramic coating houses 33 piezoelectric layers. The modeled geometry excludes the interdigitated silver electrodes since their effect on the system is insignificant. However, their electrical behavior is included and the electrical potentials of each electrode layer are coupled. Further, the cathodes are grounded. Therefore, the model is composed exclusively of THP51 ceramic [97]. Mechanical boundary conditions prevent rigid body motion and vertical deformation of the actuator’s base. The load case considered is a force acting vertically at the top surface’s center. The vertical displacement at this position and the voltage at the anode constitute the desired outputs. This model comprises 3395 nodes and corresponds to a system of 9892 differential algebraic equations (DAEs).

Figure 3.
The PA3JEA piezoelectric chip actuator and its symmetry-exploiting FEM model [97].
MOR of piezoelectric devices introduces two additional challenges: the potential loss of stability and rounding errors sensitive to the chosen unit system. The first challenge is to preserve the original system’s stability. Instability translates into a potentially unbounded output for a bounded input and, thus, renders reduced systems useless. Methods to preserve or to reintroduce stability are Schur after MOR [101], MOR after Schur [101], MOR after implicit Schur [102] and multiphysics structure-preserving MOR [38,49,101]. They differ in their approach and vary significantly in their computational efficiency. Recommended methods are either Schur after MOR or multiphysics structure-preserving MOR. The second challenge is the chosen unit system as it affects the matrices’ condition numbers, especially for multiphysical studies. For this reason, preliminary studies are recommended to determine the best-conditioned setting in order to minimize rounding errors.
The original system of DAEs representing the FEM model in Figure 3 is reduced in several settings to compare the four stability-preserving algorithms. All reductions deploy Krylov subspaces to compute the reduced basis. Further, all reduced order models are evaluated in a harmonic analysis in a frequency range of 0 kHz to 500 kHz for a unit force. The settings to be varied include the expansion point and the reduced model’s dimension. The former comprises the values 0 , 250 and 500 , while the latter is either set to 60 or 120. This setup results in six different combinations, which are evaluated for all four algorithms.
A comparison of the anode’s voltage for a reduced dimension of 60 and an expansion point of 0 is shown in Figure 4. As the curves cannot be distinguished, the figure is extended by corresponding relative errors. In general, the relative error barely surpasses , but increases towards higher frequencies due to the low expansion point. The least accurate but most efficient method is Schur after MOR. The best accuracy is achieved by multiphysics structure-preserving MOR.
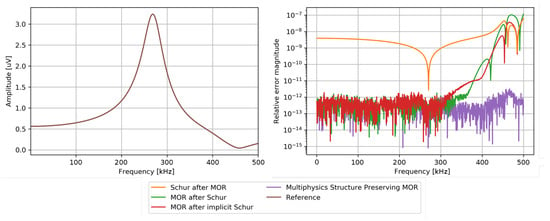
Figure 4.
Response of the anode’s voltage to a harmonic unit force computed by the FEM for reference and four reduced order models stabilized by different algorithms (left). The corresponding relative errors allow more detailed conclusions (right). This evaluation is one of six setups to compare the four stability-preserving algorithms [97].
Figure 4 compares the methods in one of the six settings and only for one of the two outputs. The remaining information is summarized in Figure 5. This plot condenses the frequency-dependent relative errors as in Figure 4 into a single number by taking the average magnitude. Although this procedure strongly depends on the chosen frequency range, it is constant for each combination and, therefore, constitutes a valid procedure. The findings coincide with the ones for Figure 4. In addition, it can be observed that the mechanical output is approximated significantly better than the electrical one.
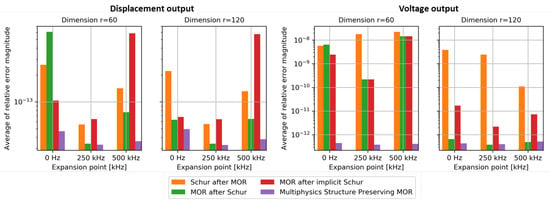
Figure 5.
Comparing the average relative error magnitude for both outputs and all six reduction settings. Multiphysics structure-preserving MOR achieves the best accuracy. MOR after Schur benefits most from increasing the reduced dimension. In general, a central expansion point leads to the best approximation quality [97].
The times required for each method with respect to the original model’s dimension are given in Figure 6. For a more detailed analysis, both the total time and the MOR-exclusive part are given. The absolute time demand as well as the scaling with model dimension vary significantly between the methods. Schur after MOR is the most efficient method, taking the least amount of time and scaling well with larger dimensions. In contrast, MOR after Schur is limited to small-sized models, as it leads to dense system matrices and high computational costs. Multiphysics structure-preserving MOR and MOR after implicit Schur perform similarly, but require more time than Schur after MOR in their stability-preserving computations. All computations were performed on an Intel® CoreTM CPU 4 × and 64 GB RAM.
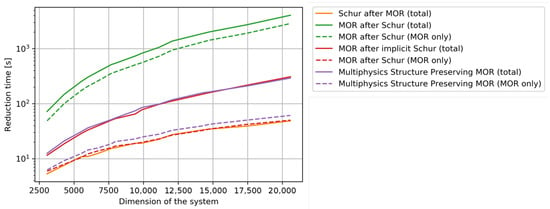
Figure 6.
The four method’s computational times vs. the original model’s dimension n. Dashed lines correspond to elapsed time due to MOR, whereas full lines provide the total demand [97].
In conclusion, MOR significantly reduces the dimension of the original model and, thus, introduces significant computational benefits. Further, all four methods preserve the original model’s stability and even the worst achieved accuracy suffices for most applications. However, Schur after MOR and multiphysics structure-preserving MOR are the methods to recommend as they are efficient and reliable. In the case of large-scale FEM models, the recommendation narrows down to Schur after MOR. Further information can be found in [97].
3.2. Electromechanical Beam Actuator
The subject of this numerical case study is a single actuator of the cooperative microsystem shown in Figure 7. An extensive description of this study is available in [52]. The design has been developed within the Kick and Catch project [52,103] and deploys multiple cooperating actuators to rotate a freely moving body. The overall goal is a multistable, quasistatic micromirror.
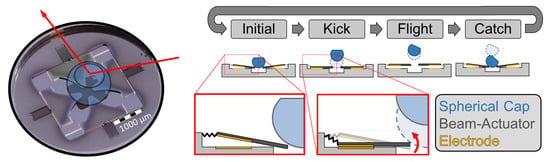
Figure 7.
The Kick and Catch actuator system [103] (left) and its operating principle (right). On the left, the indicated spherical cap rests on the four electrostatic beam actuators and is deflecting an incident light ray. As illustrated on the right, these beam actuators are actuated into pull-in to launch the spherical cap. After a free flight phase, the sphere is caught and rests stably. Consecutive flight phases allow for a high deflection angle.
One of the four electrostatic microactuators with mechanical contact constitutes the numerical case study. This actuator is highly representative because its physical principles are commonly found in a large class of microactuators. Figure 8 presents the actuator’s design, which is composed of three sections: a beam tip, an electrode and a compliant meander spring. The actuator is mounted 10 above its counter electrode, which attracts the beam when voltage is applied.
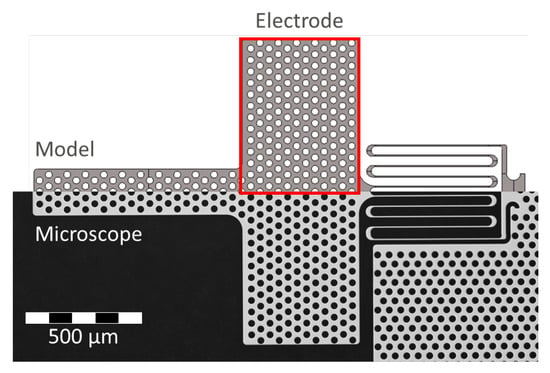
Figure 8.
The electrostatic beam actuator and its symmetry-exploiting FEM model side by side. From left to right, the beam comprises three sections: a tip for leverage, an electrode area marked in red and a compliant meander spring that enables the pull-in motion. The electrode is subject to electrostatic forces, which are nonlinear because they depend on the beam’s deformation [52].
In terms of FEM, the actuator is a linear mechanical system as in Equation (4) and of dimension . Lumped transducer elements below the electrode introduce electrostatic forces and mechanical contact. Due to the lumped nature, a nonlinear force acts on every node of the electrode area. These nonlinear forces depend on the node’s out-of-plane displacement and read
Hence, the force on node k is composed of an electrostatic part and a contact force . The electrostatic force is based on permittivity , the node’s effective area , the initial gap and the applied voltage V. The contact force has a penalty-based structure and, thus, occurs upon penetration. Its magnitude depends on the amount of penetration and the contact stiffness .
This setup is well suited for the nonlinear MOR technique for systems with few nonlinearities. As the nonlinearities only depend on a single DOF, they can be evaluated with acceptable computational costs. Furthermore, the out-of-plane displacement of adjacent nodes barely deviates. Therefore, the nonlinear forces can be grouped to reduce the number of nonlinear computations. Each group summarizes its nodes’ effective areas and their contact stiffness, respectively. In addition, a representative displacement per group is determined. This grouping procedure drastically reduces the number of nonlinear computations and can be achieved by geometric groups [69] or by clustering [52].
For the model in Figure 8, the linear part is reduced by a Krylov-subspace-based approach to a dimension of . Further, the nonlinear forces on the electrode are summarized into six groups by two approaches: geometric grouping and agglomerative clustering. The resulting two reduced order models are evaluated for a transient load case, which applies a step voltage of 30 . As a result, the beam is actuated into pull-in within less than 400 . To assess the two methods’ accuracy, the vertical tip displacement is tracked and compared to an FEM reference solution. This comparison is presented in Figure 9, in which the contact event is highlighted. Both reduced order models excellently match their reference and even provide convergence after the contact event. Although the behavior after contact differs, it cannot be compared as the FEM solution fails to converge. The speed-up factor due to MOR and the two grouping schemes is more than 250, reducing from 784 for the FEM analysis to less than 3 on an Intel® CoreTM CPU 4 x and 64 GB RAM. These computational times only indicate the efficiency, because the evaluation did not use the same solver but a less optimized one.
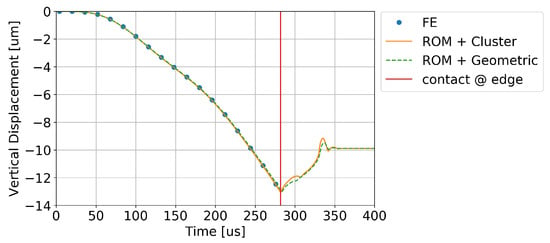
Figure 9.
Vertical displacement of the actuator’s tip after applying a step voltage of 30 , computed by two reduced order models and the FEM for reference [52].
3.3. Geometrically Nonlinear Beam Actuator
Depending on the load case, analysis of the beam actuator in Section 3.2 requires us to consider large deformations. These geometrical nonlinearities are common for microactuators and, in contrast to Section 3.2, render the whole system nonlinear. This novel numerical case study deploys a static and purely mechanical load case of the isolated beam actuator shown in Figure 8. A new FEM mesh of the homogenized actuator geometry results in a system of ODEs. A downward force on the beam’s tip is gradually increased up to 500 in steps of 10 .
Two methods are combined to reduce this setup: POD to construct the reduced basis and TPWL to handle the nonlinearities. Both rely on sampled quantities of the original model: the former requires samples of the state vector, the latter linearized system matrices. TPWL dynamically composes the current set of system matrices from a pool of linearized matrices. State-dependent weights quantify the difference between the current state and previously sampled ones. Figure 10 visualizes this procedure, illustrating selected states as deformations of the beam. Please note that TPWL can also be applied independently of MOR. Hence, this study compares the TPWL-approximated original model and its reduced version to the FEM reference solution. As a result, sources of deviation can be identified more clearly.
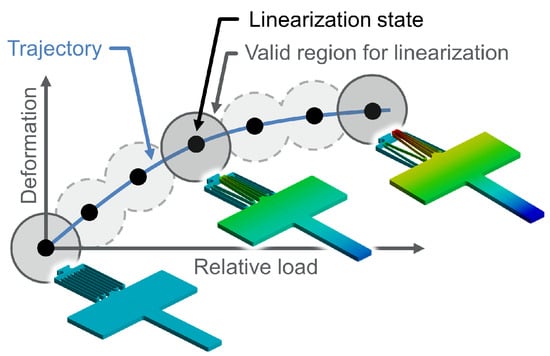
Figure 10.
TPWL approximates a nonlinear system as a weighted sum of linearized ones. These linearizations are obtained at different states along the trajectory. States correspond to physical deformations, of which three are illustrated. The color corresponds to deformation magnitude. The linearized models are valid in the vicinity of the respective linearization states, as indicated by circles.
The specific TPWL approximation uses a weighting parameter of and 11 uniformly distributed samples. The process of MOR via POD decomposes 51 snapshots obtained from the FEM reference solution. The 25 most dominant left-singular vectors form the reduced basis as the remaining singular values barely contain additional information, as illustrated in Figure 11. Therefore, they are truncated, resulting in a reduced dimension of .
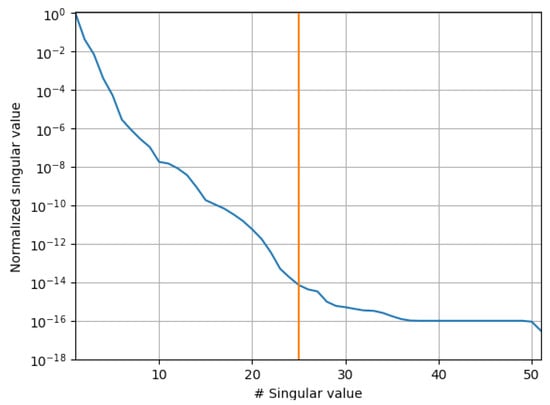
Figure 11.
Descending singular values of the FEM study’s 51 snapshots, normalized by the largest singular value. The reduced basis of left-singular vectors is truncated at indicated by the vertical line.
The TPWL-approximated model and its reduced version are then evaluated for the same 51 load steps as the original model. The output quantity assessing their performance is the beam’s tip displacement analogous to Section 3.2. Figure 12 provides the results and the relative errors of this analysis. Both models match the reference solution as the relative error barely surpasses . As with most interpolation-based methods, the error peaks between samples. The reduction step introduces negligible additional errors when compared to the TPWL approximation. Both methods are computationally more efficient and reduce the original solution time of per load step to and , respectively. Therefore, the reduced order model is faster by a factor of more than 2500. Please note that the FEM analysis uses a more optimized solver. The study was conducted on an Intel® CoreTM CPU (4 x ) and 64 GB RAM.
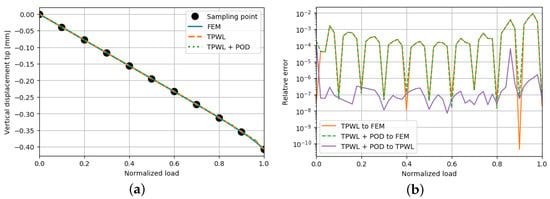
Figure 12.
(a) Comparison of the vertical tip displacement computed by the TPWL-approximated model, its reduced version and the FEM for reference. The plot also indicates sampling positions for TPWL. (b) In addition, the relative errors are shown, including the deviation of the TPWL-approximated model and its reduced version to the FEM reference solution. Further, the error between the two TPWL approximations is provided. In general, the minimum error coincides with the sampling positions and reaches maximum values in between. The coarsely sampled TPWL approximation is the main source of deviation, in contrast to the excellent match that MOR achieves.
Both the TPWL approximation and its reduced version achieve noteworthy computational benefits while losing less than 1% accuracy for this case study. This deviation predominantly originates from the TPWL approximation, while MOR to a dimension of only 25 induces a negligible error. Please note that a more sophisticated sampling strategy improves the accuracy and may even require fewer samples. Furthermore, the weighting scheme’s settings bear potential for optimization and promise better accuracy at the cost of several parameter studies. However, the aim of this numerical study is to demonstrate the basic principle and its potential, without application-dependent finetuning.
4. Conclusions and Outlook
Cooperative actuators often lead to more complex models than their independent counterparts. As a result, the model dimensions grow and limit the potential for design studies or closed-loop control. This work emphasizes the solution that MOR provides to this challenge. This methodology generates highly efficient surrogate models, as demonstrated in three numerical case studies, reaching speed-up factors of more than 250 and excellent accuracy. The gain in efficiency facilitates extensive parameter studies and design optimization. Furthermore, numerous physical effects, parametric influences and even nonlinearities can be considered with appropriate MOR methods. Reduced order models can be coupled to investigate interactions within systems. In addition, they can be conveniently combined with different model types, such as look-up tables, lumped element models or neural networks. The reduction process also preserves the model’s structure but encrypts the original model, protecting intellectual property when sharing models. Another advantage is more sophisticated closed-loop control, which becomes more feasible. However, MOR requires extra work and designated tools. Although several commercial solutions exist, consistent tool chains are rare. One reason is that most MOR methods are intrusive and need to access the underlying mathematical model. Nevertheless, the extensive literature on microsystem-related MOR suggests its potential for this field of research, accelerating if not enabling several applications.
Alternatives to MOR include look-up tables, meta-models, GKNs and data-driven approaches such as operator inference or ANNs. While look-up tables and meta-models are easy to implement, they are based on solutions of the original model. Therefore, the number of full samples grows exponentially with the number of parameters, often leading to coarse sampling. In addition, they are better suited to model relations between input parameters and outputs, rather than dynamical systems. However, these two approaches are robust and require significantly less expert knowledge. GKNs represent an original system as an equivalent network of lumped elements and are a viable alternative to projection-based MOR. They preserve the original model’s structure and physical meaning, while being capable of multiphysics and nonlinear effects. Moreover, they are established in the field of microactuators. This technique requires expert knowledge and is less accurate and flexible than MOR, e.g., regarding additional outputs. Data-driven approaches such as operator inference or ANNs are suitable for numerous tasks, but their prediction quality is limited to scenarios included in their training. They do not preserve physical meaning or the structure of the original problem, but work well with simulated data without noise or outliers.
Current trends of MOR include their combination with data-driven approaches such as ANNs. This synergy enables highly efficient training on reduced data or grey-box models incorporating physical knowledge. The former approach uses MOR to drastically reduce the dimensions of training data, which leads to faster training, easier networks and the more efficient tuning of hyperparameters. The latter concept extends linear ROMs with ANNs to include parametric influences or nonlinear effects, e.g., by updating matrices for parametric changes or nonlinearities. The potential is yet to be exploited and diffused into the microactuator community.
Author Contributions
Conceptualization, T.B. and A.S.; investigation, A.S.; writing—original draft preparation, A.S.; writing—review and editing, T.B. and A.S.; visualization, A.S.; supervision, T.B.; funding acquisition, T.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Deutsche Forschungsgemeinschaft (German Research Foundation), grant number 424616052.
Data Availability Statement
The data can be provided upon reasonable request.
Acknowledgments
Siyang Hu and Chengdong Yuan are thanked for the fruitful discussions. Further, we thank Thorlabs GmbH for supplying additional information and for their kind permission to use pictures from their website in our work.
Conflicts of Interest
The authors declare no conflict of interest. The funding institutions had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| ANN | artificial neural network |
| DAE | differential algebraic equation |
| DEIM | discrete empirical interpolation method |
| DOF | degree of freedom |
| ECSW | energy conserving mesh sampling and weighting |
| FEM | finite element method |
| GKN | generalized Kirchoffian network |
| MEMS | microelectromechanical system |
| MOR | model order reduction |
| ODE | ordinary differential equation |
| PDE | partial differential equation |
| POD | proper orthogonal decomposition |
| ROM | reduced order model |
| TPWL | trajectory piecewise-linear |
References
- Bechtold, T.; Schrag, G.; Feng, L. (Eds.) System-Level Modeling of MEMS; Wiley-VCH-Verl.: Weinheim, Germany, 2013; Advanced Micro and Nanosystems Volume 10. [Google Scholar]
- Benner, P.; Ohlberger, M.; Cohen, A.; Willcox, K. Model Reduction and Approximation; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2017. [Google Scholar]
- Baur, U.; Benner, P.; Feng, L. Model Order Reduction for Linear and Nonlinear Systems: A System-Theoretic Perspective. Arch. Comput. Methods Eng. 2014, 21, 331–358. [Google Scholar] [CrossRef]
- Rutzmoser, J. Model Order Reduction for Nonlinear Structural Dynamics: Simulation-Free Approaches. Ph.D. Thesis, Technischen Universität München, Garching, Germany, 2018. [Google Scholar]
- Benner, P.; Grivet-Talocia, S.; Quarteroni, A.; Rozza, G.; Schilders, W.; Silveira, L.M. (Eds.) Model Order Reduction: Volume 1: System- and Data-Driven Methods and Algorithms, 1st ed.; De Gruyter: Berlin, Germany, 2021; Volume 1. [Google Scholar]
- Benner, P.; Grivet-Talocia, S.; Quarteroni, A.; Rozza, G.; Schilders, W.; Silveira, L.M. (Eds.) Model Order Reduction: Volume 2: Snapshot-Based Methods and Algorithms; De Gruyter: Berlin, Germany, 2021; Volume 2. [Google Scholar]
- Benner, P.; Grivet-Talocia, S.; Quarteroni, A.; Rozza, G.; Schilders, W.; Silveira, L.M. (Eds.) Model Order Reduction: Volume 3: Applications, 1st ed.; De Gruyter: Berlin, Germany, 2021; Volume 3. [Google Scholar]
- Lord Rayleigh, J. The Theory of Sound; Macmillan: New York, NY, USA, 1894. [Google Scholar]
- Weeger, O.; Wever, U.; Simeon, B. On the use of modal derivatives for nonlinear model order reduction. Int. J. Numer. Methods Eng. 2016, 108, 1579–1602. [Google Scholar] [CrossRef]
- Vizzaccaro, A.; Salles, L.; Touzé, C. Comparison of nonlinear mappings for reduced-order modelling of vibrating structures: Normal form theory and quadratic manifold method with modal derivatives. Nonlinear Dyn. 2021, 103, 3335–3370. [Google Scholar] [CrossRef]
- Mehner, J.; Gabbay, L.D.; Senturia, S.D. Computer-aided generation of nonlinear reduced-order dynamic macromodels. II. Stress-stiffened case. J. Microelectromech. Syst. 2000, 9, 270–278. [Google Scholar] [CrossRef]
- Mehner, J.; Doetzel, W.; Schauwecker, B.; Ostergaard, D. Reduced order modeling of fluid structural interactions in MEMS based on model projection techniques. In Proceedings of the Transducers ’03, Boston, MA, USA, 8–12 June 2003; pp. 1840–1843. [Google Scholar]
- Bennini, F.; Mehner, J.; Dötzel, W. Computational Methods for Reduced Order Modeling of Coupled Domain Simulations. In Transducers ’01 Eurosensors XV; Obermeier, E., Ed.; Springer: Berlin/Heidelberg, Germany, 2001; pp. 260–263. [Google Scholar]
- Putnik, M.; Sniegucki, M.; Cardanobile, S.; Kehrberg, S.; Kuehnel, M.; Nagel, C.; Degenfeld-Schonburg, P.; Mehner, J. Incorporating geometrical nonlinearities in reduced order models for MEMS gyroscopes. In Proceedings of the IEEE Inertial Sensors 2017, Kauai, HI, USA, 28–30 March 2017; pp. 43–46. [Google Scholar]
- Putnik, M.; Sniegucki, M.; Cardanobile, S.; Kuhnel, M.; Kehrberg, S.; Mehner, J. Predicting the Resonance Frequencies in Geometric Nonlinear Actuated MEMS. J. Microelectromech. Syst. 2018, 27, 954–962. [Google Scholar] [CrossRef]
- Putnik, M.; Cardanobile, S.; Sniegucki, M.; Kehrberg, S.; Kuehnel, M.; Degenfeld-Schonburg, P.; Nagel, C.; Mehner, J. Simulation methods for generating reduced order models of MEMS sensors with geometric nonlinear drive motion. In Proceedings of the the 5th IEEE International Symposium on Inertial Sensors & Systems, Lake Como, Italy, 26–29 March 2018; pp. 1–4. [Google Scholar]
- Putnik, M. Simulation Methods for the Mechanical Nonlinearity in MEMS Gyroscopes. Ph.D. Thesis, Fakultät für Elektrotechnik und Informationstechnik, Chemnitz, Germany, 2019. [Google Scholar]
- Guyan, R.J. Reduction of Stiffness and Mass Matrices. AIAA J. 1964, 3, 380. [Google Scholar] [CrossRef]
- de Klerk, D.; Rixen, D.J.; Voormeeren, S.N. General Framework for Dynamic Substructuring: History, Review and Classification of Techniques. AIAA J. 2008, 46, 1169–1181. [Google Scholar] [CrossRef]
- Craig, R.R.; Bampton, M.C.C. Coupling of substructures for dynamic analyses. AIAA J. 1968, 6, 1313–1319. [Google Scholar] [CrossRef]
- MacNeal, R.H. A hybrid method of component mode synthesis. Comput. Struct. 1971, 1, 581–601. [Google Scholar] [CrossRef]
- Rubin, S. Improved Component-Mode Representation for Structural Dynamic Analysis. AIAA J. 1975, 13, 995–1006. [Google Scholar] [CrossRef]
- Craig, R.R.; Ni, Z. Component mode synthesis for model order reduction of nonclassicallydamped systems. J. Guid. Control. Dyn. 1989, 12, 577–584. [Google Scholar] [CrossRef]
- Lienemann, J. Complexity Reduction Techniques for Advanced MEMS Actuators Simulation. Ph.D. Thesis, Albert-Ludwigs-Universität Freiburg, Freiburg, Germany, 2006. [Google Scholar]
- Sadek, K.; Moussa, W. Application of adaptive multilevel substructuring technique to model CMOS micromachined thermistor gas sensor, part (I): A feasibility study. In Proceedings of the International Conference on MEMS, NANO and Smart Systems, Banff, AB, Canada, 20–23 July 2003; pp. 279–284. [Google Scholar]
- Sadek, K.; Lueke, J.; Moussa, W. A Coupled Field Multiphysics Modeling Approach to Investigate RF MEMS Switch Failure Modes under Various Operational Conditions. Sensors 2009, 9, 7988–8006. [Google Scholar] [CrossRef] [PubMed]
- Binion, D.; Chen, X. Coupled electrothermal–mechanical analysis for MEMS via model order reduction. Finite Elem. Anal. Des. 2010, 46, 1068–1076. [Google Scholar] [CrossRef]
- Giannini, D.; Bonaccorsi, G.; Braghin, F. Size optimization of MEMS gyroscopes using substructuring. Eur. J. Mech. A/Solids 2020, 84, 104045. [Google Scholar] [CrossRef]
- Mullis, C.; Roberts, R. Synthesis of minimum roundoff noise fixed point digital filters. IEEE Trans. Circuits Syst. 1976, 23, 551–562. [Google Scholar] [CrossRef]
- Moore, B. Principal component analysis in linear systems: Controllability, observability, and model reduction. IEEE Trans. Autom. Control 1981, 26, 17–32. [Google Scholar] [CrossRef]
- Chahlaoui, Y.; Lemonnier, D.; Vandendorpe, A.; van Dooren, P. Second-order balanced truncation. Linear Algebra Its Appl. 2006, 415, 373–384. [Google Scholar] [CrossRef]
- Reis, T.; Stykel, T. Balanced truncation model reduction of second-order systems. Math. Comput. Model. Dyn. Syst. 2008, 14, 391–406. [Google Scholar] [CrossRef]
- Wolf, T.; Castagnotto, A.; Eid, R. Moderne Methoden der Regelungstechnik 3-Teil B-Einführung in die Modellreduktion; Technische Universität München: München, Germany, 2016. [Google Scholar]
- M’Closkey, R.T.; Gibson, S.; Hui, J. System Identification of a MEMS Gyroscope. J. Dyn. Syst. Meas. Control 2001, 123, 201–210. [Google Scholar] [CrossRef]
- Kamon, M.; Wang, F.; White, J. Generating nearly optimally compact models from Krylov-subspace based reduced-order models. IEEE Trans. Circuits Syst. II Analog Digit. Signal Process. 2000, 47, 239–248. [Google Scholar] [CrossRef]
- Rudnyi, E.B.; Korvink, J.G. Review: Automatic Model Reduction for Transient Simulation of MEMS-based Devices. Sens. Update 2002, 11, 3–33. [Google Scholar] [CrossRef]
- Grimme, E.J. Krylov Projection Methods for Model Reduction. Ph.D. Thesis, University of Illinois at Urbana-Champaign, Champaign, IL, USA, 1997. [Google Scholar]
- Freund, R.W. Krylov-subspace methods for reduced-order modeling in circuit simulation. J. Comput. Appl. Math. 2000, 123, 395–421. [Google Scholar] [CrossRef]
- Freund, R.W. Model reduction methods based on Krylov subspaces. Acta Numer. 2003, 12, 267–319. [Google Scholar] [CrossRef]
- Rudnyi, E.B.; Korvink, J.G. Model Order Reduction for Large Scale Engineering Models Developed in ANSYS. In Applied Parallel Computing. State of the Art in Scientific Computing; Hutchison, D., Kanade, T., Kittler, J., Kleinberg, J.M., Mattern, F., Mitchell, J.C., Naor, M., Nierstrasz, O., Pandu Rangan, C., Steffen, B., et al., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2006; Volume 3732, pp. 349–356. [Google Scholar]
- Bai, Z.; Su, Y. SOAR: A Second-order Arnoldi Method for the Solution of the Quadratic Eigenvalue Problem. SIAM J. Matrix Anal. Appl. 2005, 26, 640–659. [Google Scholar] [CrossRef]
- Gugercin, S.; Antoulas, A.C.; Beattie, C. H2 Model Reduction for Large-Scale Linear Dynamical Systems. SIAM J. Matrix Anal. Appl. 2008, 30, 609–638. [Google Scholar] [CrossRef]
- Hung, E.S.; Yang, Y.J.; Senturia, S.D. Low-order models for fast dynamical simulation of MEMS microstructures. In Proceedings of the International Solid State Sensors and Actuators Conference (Transducers ’97), Chicago, IL, USA, 19 June 1997; pp. 1101–1104. [Google Scholar]
- Bechtold, T.; Rudnyi, E.B.; Korvink, J.G. Automatic order reduction of thermo-electric model for micro-ignition unit. In Proceedings of the International Conference on Simulation of Semiconductor Processes and Devices, Granada, Spain, 4–6 September 2002; pp. 131–134. [Google Scholar]
- Bechtold, T. Model Order Reduction of Electro-Thermal MEMS. Ph.D. Thesis, Albert-Ludwigs-Universität Freiburg, Freiburg, Germany, 2005. [Google Scholar]
- Bechtold, T.; Rudnyi, E.B.; Korvink, J.G. Fast Simulation of Electro-Thermal MEMS; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Liu, Y.; Yuan, W.; Chang, H.; Ma, B. Compact thermoelectric coupled models of micromachined thermal sensors using trajectory piecewise-linear model order reduction. Microsyst. Technol. 2014, 20, 73–82. [Google Scholar] [CrossRef]
- Yuan, C.; Kreß, S.; Sadashivaiah, G.; Rudnyi, E.B.; Hohlfeld, D.; Bechtold, T. Towards efficient design optimization of a miniaturized thermoelectric generator for electrically active implants via model order reduction and submodeling technique. Int. J. Numer. Methods Biomed. Eng. 2020, 36, e3311. [Google Scholar] [CrossRef]
- Yuan, C.; Hu, S.; Bechtold, T. Stable Compact Modeling of Piezoelectric Energy Harvester Devices. COMPEL 2020, 39, 868. [Google Scholar] [CrossRef]
- Yuan, C.; Hu, S.; Castagnotto, A.; Lohmann, B.; Bechtold, T. Implicit Schur Complement for Model Order Reduction of Second Order Piezoelectric Energy Harvester Model. In MATHMOD 2018 Extended Abstract Volume; Volume ARGESIM Report 55; ARGESIM: Vienna, Austria, 2018; pp. 77–78. ISBN 978-3-901608-91-9. [Google Scholar]
- Schütz, A.; Maeter, S.; Bechtold, T. System-Level Modelling and Simulation of a Multiphysical Kick and Catch Actuator System. Actuators 2021, 10, 279. [Google Scholar] [CrossRef]
- Schütz, A.; Farny, M.; Olbrich, M.; Hoffmann, M.; Ament, C.; Bechtold, T. Model Order Reduction of a Nonlinear Electromechanical Beam Actuator by Clustering Nonlinearities. In ACTUATOR 2022; GMM-Fachbericht, VDE VERLAG: Berlin, Germany; Offenbach, Germany, 2022; pp. 354–357. [Google Scholar]
- Pierquin, A.; Henneron, T.; Clenet, S.; Brisset, S. Model-Order Reduction of Magnetoquasi-Static Problems Based on POD and Arnoldi-Based Krylov Methods. IEEE Trans. Magn. 2015, 51, 1–4. [Google Scholar] [CrossRef]
- Bonotto, M.; Cenedese, A.; Bettini, P. Krylov Subspace Methods for Model Order Reduction in Computational Electromagnetics. IFAC-PapersOnLine 2017, 50, 6355–6360. [Google Scholar] [CrossRef]
- Chang, H.; Zhang, Y.; Xie, J.; Zhou, Z.; Yuan, W. Integrated Behavior Simulation and Verification for a MEMS Vibratory Gyroscope Using Parametric Model Order Reduction. J. Microelectromech. Syst. 2010, 19, 282–293. [Google Scholar] [CrossRef]
- Han, J.S.; Rudnyi, E.B.; Korvink, J.G. Efficient optimization of transient dynamic problems in MEMS devices using model order reduction. J. Micromech. Microeng. 2005, 15, 822–832. [Google Scholar] [CrossRef]
- Liang, Y.C.; Lin, W.Z.; Lee, H.P.; Lim, S.P.; Lee, K.H.; Sun, H. Proper Orthogonal Decomposition and Its Applications—Part II: Model Reduction for Mems Dynamical Analysis. J. Sound Vib. 2002, 256, 515–532. [Google Scholar] [CrossRef]
- Binion, D.; Chen, X. A Krylov enhanced proper orthogonal decomposition method for frequency domain model reduction. Eng. Comput. 2017, 34, 285–306. [Google Scholar] [CrossRef]
- Corigliano, A.; Dossi, M.; Mariani, S. Domain decomposition and model order reduction methods applied to the simulation of multi-physics problems in MEMS. Comput. Struct. 2013, 122, 113–127. [Google Scholar] [CrossRef]
- Gobat, G.; Opreni, A.; Fresca, S.; Manzoni, A.; Frangi, A. Reduced order modeling of nonlinear microstructures through Proper Orthogonal Decomposition. Mech. Syst. Signal Process. 2022, 171, 108864. [Google Scholar] [CrossRef]
- Benner, P.; Gugercin, S.; Willcox, K. A Survey of Projection-Based Model Reduction Methods for Parametric Dynamical Systems. SIAM Rev. 2015, 57, 483–531. [Google Scholar] [CrossRef]
- Benner, P.; Ohlberger, M.; Patera, A.; Rozza, G.; Urban, K. (Eds.) Model Reduction of Parametrized Systems; MS&A; Springer International Publishing: Cham, Switerland, 2017. [Google Scholar]
- Rudnyi, E.B.; Moosmann, C.; Greiner, A.; Bechtold, T.; Korvink, J.G. Parameter Preserving Model Reduction for MEMS System-level Simulation and Design. In MATHMOD; Vienna University of Technology: Vienna, Austria, 2006. [Google Scholar]
- Moosmann, C. ParaMOR–Model Order Reductionfor Parameterized MEMS Applications. Ph.D. Thesis, Albert-Ludwigs-Universität Freiburg, Freiburg, Germany, 2007. [Google Scholar]
- Panzer, H.; Mohring, J.; Eid, R.; Lohmann, B. Parametric Model Order Reduction by Matrix Interpolation. Automatisierungstechnik 2010, 58, 958. [Google Scholar] [CrossRef]
- Bond, B.; Daniel, L. Parameterized model order reduction of nonlinear dynamical systems. In Proceedings of the ICCAD-2005, IEEE/ACM International Conference on Computer-Aided Design, San Jose, CA, USA, 6–10 November 2005; pp. 487–494. [Google Scholar]
- Baur, U.; Benner, P.; Greiner, A.; Korvink, J.G.; Lienemann, J.; Moosmann, C. Parameter preserving model order reduction for MEMS applications. Math. Comput. Model. Dyn. Syst. 2011, 17, 297–317. [Google Scholar] [CrossRef]
- Feng, L.; Benner, P.; Korvink, J.G. Subspace recycling accelerates the parametric macro-modeling of MEMS. Int. J. Numer. Methods Eng. 2013, 94, 84–110. [Google Scholar] [CrossRef]
- del Tin, L. Reduced-Order Modelling, Circuit-Level Design and SOI Fabrication of Microelectromechanical Resonators. Ph.D. Thesis, Università di Bologna, Bologna, Italy, 2007. [Google Scholar]
- Rewieński, M.; White, J. A trajectory piecewise-linear approach to model order reduction and fast simulation of nonlinear circuits and micromachined devices. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2003, 22, 155–170. [Google Scholar] [CrossRef]
- Yang, Y.J.; Shen, K.Y. Nonlinear heat-transfer macromodeling for MEMS thermal devices. J. Micromech. Microeng. 2005, 15, 408–418. [Google Scholar] [CrossRef]
- Liu, Y.; Chang, H.; Yuan, W. A Global Maximum Error Controller-Based Method for Linearization Point Selection in Trajectory Piecewise-Linear Model Order Reduction. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2014, 33, 1100–1104. [Google Scholar]
- Liu, Y.; Wang, X. A Two-Step Global Maximum Error Controller-Based TPWL MOR with POD Basis Vectors and Its Applications to MEMS. Math. Probl. Eng. 2017, 2017, 5014235. [Google Scholar] [CrossRef]
- Albunni, M.N. Model Order Reduction of Moving Nonlinear Electromagnetic Devices. Ph.D. Thesis, Technischen Universität München, Munich, Germany, 2010. [Google Scholar]
- Chen, J.; Kang, S.M.; Zou, J.; Liu, C.; Schutt-Aine, J.E. Reduced-Order Modeling of Weakly Nonlinear MEMS Devices with Taylor-Series Expansion and Arnoldi Approach. J. Microelectrmech. Syst. 2004, 13, 441–451. [Google Scholar] [CrossRef]
- Mignolet, M.P.; Przekop, A.; Rizzi, S.A.; Spottswood, S.M. A review of indirect/non-intrusive reduced order modeling of nonlinear geometric structures. J. Sound Vib. 2013, 332, 2437–2460. [Google Scholar] [CrossRef]
- Chaturantabut, S.; Sorensen, D.C. Nonlinear Model Reduction via Discrete Empirical Interpolation. SIAM J. Sci. Comput. 2010, 32, 2737–2764. [Google Scholar] [CrossRef]
- Roy, A.; Nabi, M. Modeling of MEMS Electrothermal Microgripper employing POD-DEIM and POD method. Microelectron. Reliab. 2021, 125, 114338. [Google Scholar] [CrossRef]
- Hochman, A.; Bond, B.N.; White, J. A stabilized discrete empirical interpolation method for model reduction of electrical, thermal, and microelectromechanical systems. In Proceedings of the 48th Design Automation Conference, San Diego, CA, USA, 5–10 June 2011; Stok, L., Dutt, N., Hassoun, S., Eds.; ACM: New York, NY, USA, 2011; pp. 540–545. [Google Scholar]
- Farhat, C.; Avery, P.; Chapman, T.; Cortial, J. Dimensional reduction of nonlinear finite element dynamic models with finite rotations and energy-based mesh sampling and weighting for computational efficiency. Int. J. Numer. Methods Eng. 2014, 98, 625–662. [Google Scholar] [CrossRef]
- Farhat, C.; Chapman, T.; Avery, P. Structure-preserving, stability, and accuracy properties of the energy-conserving sampling and weighting method for the hyper reduction of nonlinear finite element dynamic models. Int. J. Numer. Methods Eng. 2015, 102, 1077–1110. [Google Scholar] [CrossRef]
- Chapman, T. Nonlinear Model Order Reduction for Structural Systems with Contact. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 2019. [Google Scholar]
- Gao, H.; Wang, J.X.; Zahr, M.J. Non-intrusive model reduction of large-scale, nonlinear dynamical systems using deep learning. Phys. D Nonlinear Phenom. 2020, 412, 132614. [Google Scholar] [CrossRef]
- Cicci, L.; Fresca, S.; Manzoni, A. Deep-HyROMnet: A deep learning-based operator approximation for hyper-reduction of nonlinear parametrized PDEs. J. Sci. Comput. 2022, 93, 57. [Google Scholar] [CrossRef]
- Simpson, T.W.; Poplinski, J.D.; Koch, P.N.; Allen, J.K. Metamodels for Computer-based Engineering Design: Survey and recommendations. Eng. Comput. 2001, 17, 129–150. [Google Scholar] [CrossRef]
- Schrag, G.; Wachutka, G. System-Level Modeling of MEMS Using Generalized Kirchhoffian Networks-Basic Principles. In System-Level Modeling of MEMS; Bechtold, T., Schrag, G., Feng, L., Eds.; Advanced Micro and Nanosystems; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2013; pp. 19–51. [Google Scholar]
- Lenk, A.; Ballas, R.G.; Werthschützky, R.; Pfeifer, G. Electromechanical Systems in Microtechnology and Mechatronics: Electrical, Mechanical and Acoustic Networks, Their Interactions and Applications; Microtechnology and MEMS; Springer: Berlin, Germany, 2010. [Google Scholar]
- Bosetti, G.; Manz, J.; Dehé, A.; Krumbein, U.; Schrag, G. Modeling and physical analysis of an out-of-plane capacitive MEMS transducer with dynamically coupled electrodes. Microsyst. Technol. 2019, 3, 81. [Google Scholar] [CrossRef]
- Bosetti, G.; Schrag, G. Efficient Modeling of Acoustic Channels – Towards Tailored Frequency Response of Airborne Ultrasonic MEMS Transducers. In Proceedings of the 2022 23rd International Conference on Thermal, Mechanical and Multi-Physics Simulation and Experiments in Microelectronics and Microsystems (EuroSimE), Graz, Austria, 25–27 April 2022; pp. 1–5. [Google Scholar]
- Gruber, A.; Gunzburger, M.; Ju, L.; Wang, Z. A comparison of neural network architectures for data-driven reduced-order modeling. Comput. Methods Appl. Mech. Eng. 2022, 393, 114764. [Google Scholar] [CrossRef]
- Peherstorfer, B.; Willcox, K. Data-driven operator inference for nonintrusive projection-based model reduction. Comput. Methods Appl. Mech. Eng. 2016, 306, 196–215. [Google Scholar] [CrossRef]
- Benner, P.; Goyal, P.; Kramer, B.; Peherstorfer, B.; Willcox, K. Operator inference for non-intrusive model reduction of systems with non-polynomial nonlinear terms. Comput. Methods Appl. Mech. Eng. 2020, 372, 113433. [Google Scholar] [CrossRef]
- Qian, E.; Kramer, B.; Peherstorfer, B.; Willcox, K. Lift & Learn: Physics-informed machine learning for large-scale nonlinear dynamical systems. Phys. D Nonlinear Phenom. 2020, 406, 132401. [Google Scholar]
- Antoulas, A.C. Approximation of Large-Scale Dynamical Systems; Advances in Design and Control; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2005. [Google Scholar]
- Ryckelynck, D. A priori hyperreduction method: An adaptive approach. J. Comput. Phys. 2005, 202, 346–366. [Google Scholar] [CrossRef]
- Rewieński, M. A Trajectory Piecewise-Linear Approach to Model Order Reduction of Nonlinear Dynamical Systems. Ph.D. Thesis, Technical University of Gdansk, Gdansk, Poland, 2003. [Google Scholar]
- Schütz, A.; Bechtold, T. Performance Comparison for Stable Compact Modelling of Piezoelectric Microactuator. In Proceedings of the 2022 23rd International Conference on Thermal, Mechanical and Multi-Physics Simulation and Experiments in Microelectronics and Microsystems (EuroSimE), Graz, Austria, 25–27 April 2022; pp. 1–8. [Google Scholar]
- Rudnyi, E.B.; Lienemann, J.; Greiner, A.; Korvink, J.G. mor4ansys: Generating Compact Models Directly from ANSYS Models; Routledge: Oxfordshire, UK, 2004. [Google Scholar]
- Harris, C.R.; Millman, K.J.; van der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J.; et al. Array programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef] [PubMed]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental algorithms for scientific computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef] [PubMed]
- Kudryavtsev, M.; Rudnyi, E.B.; Korvink, J.G.; Hohlfeld, D.; Bechtold, T. Computationally efficient and stable order reduction methods for a large-scale model of MEMS piezoelectric energy harvester. Microelectron. Reliab. 2015, 55, 747–757. [Google Scholar] [CrossRef]
- Hu, S.; Yuan, C.; Castagnotto, A.; Lohmann, B.; Bouhedma, S.; Hohlfeld, D.; Bechtold, T. Stable reduced order modeling of piezoelectric energy harvesting modules using implicit Schur complement. Microelectron. Reliab. 2018, 85, 148–155. [Google Scholar] [CrossRef]
- Farny, M.; Hoffmann, M. Kick & Catch: Elektrostatisches Rotieren einer Kugel. In MikroSystemTechnik Kongress; VDE Verlag GmbH: Stuttgart-Ludwigsburg, Germany, 2021; pp. 274–277. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).