Abstract
Inappropriate distributions of temperature and humidity will cause the failure of the spring-loaded actuators. Therefore, it is essential to understand the temperature and humidity distribution characteristics in typical spring-loaded actuators, to guarantee the safe operation of the spring-loaded actuators. In this work, a numerical simulation study on the temperature and humidity distribution characteristics in a spring-loaded actuator was conducted. The influence laws of ambient temperature, heater power, and heater size on the temperature and humidity distributions inside the spring-loaded actuator were analyzed. The practical empirical correlations for the spring-loaded actuators were fitted. The results show that the air temperature around and directly above the heater is the highest and the corresponding relative humidity is the lowest. Then, the air temperature gradually decreases, and the relative humidity increases with the lateral flow of air. When the ambient temperature increases from 233.15 K (−40 °C) to 313.15 K (40 °C), the minimum temperature inside the actuator is increased by 34%, the maximum humidity first increases and then decreases, and the maximum temperature on the heater surface is increased by 30%. When the heating power increases from 10 W to 150 W at ambient temperatures of 273.15 K and 298.15 K, the minimum temperature inside the actuator is increased by 3.40% and 3.61%, the maximum humidity is decreased by 51.97% and 58.63%, and the maximum temperature on the heater surface is increased by 30.33% and 33.25%, respectively. The influence of heater length, width, and height on the minimum temperature and maximum relative humidity inside the spring-loaded actuator is relatively small. Within the study range, the increase in heater length, width, and height makes the maximum temperature on the heater surface decrease by 9.15%, 7.59%, 4.63% at ambient temperatures of 273.15 K, and 10.74%, 9.01%, 4.73% at ambient temperature of 298.15 K, respectively. The results may provide a reference for predicting temperature and humidity distributions inside general spring-loaded actuators and provide a calculation basis for the design of their heaters.
1. Introduction
The spring-loaded actuator is widely used in high-voltage circuit breakers, switches, disconnect switches and other electrical control equipment [1]. The reliability of the spring-loaded actuator is directly related to the safe and stable operation of the national grid in China [2]. Ambient temperature is one of the key factors affecting the reliability of the spring-loaded actuator [3]. When the ambient temperature is extremely low, the output characteristics of the spring-loaded actuator will change significantly, which will affect the opening-closing time and speed of high-voltage circuit breakers and switches [4]. Due to the vastness of China, the climate differences are huge. In winter, the ambient temperature in severe cold areas of northern China can drop below −40 °C [5]. In this case, the impact of temperature on the spring-loaded actuator is more prominent, and the heating system and heating effect need to be designed and studied to ensure good thermal-mechanical properties and safe operation of the spring-loaded actuator. In recent years, with the improvement of national requirements for safe and reliable operation of the national grid in China [6], it is necessary to deeply study the heating system design, heating effect analysis, and thermal-mechanical properties analysis for spring-loaded actuators. To ensure the safe operation of high-voltage circuit breakers, high-voltage switches, etc., and ensure the stable operation of the national grid in China.
At present, several researchers have preliminarily investigated the design of heating systems, analysis of heating effects, and analysis of thermal-mechanical properties for the spring-loaded actuators [7,8]. Hyo et al. [9] studied the feedback control characteristics of a shape-memory-alloy spring-loaded actuator using a temperature follow-up test and force feedback control test. The results showed that the feedback control characteristic could be enhanced by combining the temperature follow-up method and the force feedback control method. Degeratu et al. [10,11] studied the properties and behaviors of a shape memory alloy spring-loaded actuator by thermal experiments and determined the transformation temperatures for the spring-loaded actuator. Ma et al. [12] analyzed the characteristics of output force and output displacement of a spring-loaded actuator made of shape memory alloy. They obtained the relationship of output displacement with the size parameters and temperature. Their results showed that increasing temperature can increase the output displacement of the spring-loaded actuator. Holanda et al. [13] researched the stiffness and damping properties of a typical spring-loaded actuator with a temperature control system and an unbalanced excitement force. They obtained the structural response relationship between temperature, stiffness, and damping. Auricchio et al. [14] studied the thermal-mechanical characteristics of a typical spring-loaded actuator by experimental and numerical methods and pointed out that the experimental results agree well with the numerical results. Cortez-Vega et al. [15,16] numerically and experimentally researched the thermal-mechanical characteristics of a spring-loaded actuator. Based on the numerical simulation data and experimental data, a multi-variable model was constructed to reflect the relationship between the internal force, external force, and temperature. Park et al. [17] studied the influence of heating temperature variation on the driving force of the spring-loaded actuator that was cooled and heated by cold and hot water. The results showed that the spring-loaded actuator could produce a force of 130 N with the temperature changing from 301.15 K to 355.15 K. Xiong et al. [18] analyzed the thermal-mechanical performance of a spring-loaded actuator made of shape memory alloy by the experimental method and obtained the response relationships of temperature-displacement and temperature-force. Their results showed that the spring-loaded actuator could generate the highest output displacement of 7.7 mm and the highest recovery force of 70.2 N at 373.15 K. Jiang et al. [19] studied the thermal-mechanical properties of the spring-loaded actuator at relatively low temperatures. The results showed that the tensile length of the actuator’s spring increases by 9 times at a temperature of 327 K, and at the same time, the actuator can achieve rapid rolling. Britz et al. [20] carried out an optimal design of a spring-loaded actuator under high ambient temperatures of up to 338.15 K. The results showed that the spring-loaded actuator could achieve high performance of 1 mm valve travel within 100 milliseconds at 338.15 K. Jithu et al. [21] researched the thermal-mechanical properties of a spring-loaded actuator during hydrogen absorption by numerical method. They pointed out that heat transfer enhancement methods can be used to improve the thermal-mechanical performance of the spring-loaded actuator.
Humidity can also have a significant impact on the operational performance and material characteristics of the actuator. Several scholars have studied the effect of humidity on the operational performance and material properties of various types of actuators. These results can provide a reference for studying the operational performance of typical spring-loaded actuators under different ambient humidity conditions. Wang et al. [22] fabricated a soft actuator with a two-layer structure with multiple stimulus responses, and the results showed that the actuator exhibits different actuation performance with changes in temperature and humidity. Xu et al. [23] and Arazoe et al. [24] explored the performance changes of moisture-driven actuators when the relative humidity varied, and the results showed that the actuators exhibited different performance for different relative humidity variations. Ryabchun et al. [25] explored the driving modes of an actuator material at different relative humidity and showed that the twisting, curling, and winding of the material varied with humidity. Cabuz et al. [26] showed that humidity was the main reason for the failure of a touch-mode electrostatic actuator. It is worth noting that this work explores the influence laws of ambient temperature, heater power, and heater size on the temperature and humidity distribution characteristics inside a typical spring-loaded actuator, which is also helpful for future research in the fields of micro- and nanofluidics [27,28,29], chemistry and biology [30,31], and medicine [32].
In the above-mentioned literature, several investigations have been carried out concerning analyzing the thermal-mechanical properties of typical spring-loaded actuators at various temperature conditions. However, few studies have been performed on the influence laws of various parameters on the heating effect of the heating system of typical spring-loaded actuators. Meanwhile, little attention has been paid to the distribution characteristics of temperature and relative humidity in the box of typical spring-loaded actuators.
In general, the variation in temperature and humidity will have a powerful influence on the operational performance of spring-loaded actuators. Meanwhile, unreasonable temperature and humidity distribution may lead to the failure of the operational performance of spring-loaded actuators. Therefore, it is essential to understand the temperature and humidity distribution characteristics in typical spring-loaded actuators and obtain the suitable temperature and humidity range, to guarantee the safe operation of the spring-loaded actuators. In this work, a numerical simulation study on the temperature and humidity distribution characteristics in a typical spring-loaded actuator was conducted. Then, the influence laws of ambient temperature, heater power, and heater size on the temperature and humidity distributions inside the spring-loaded actuator were analyzed. Finally, the empirical correlations of the minimum temperature and maximum relative humidity inside the spring-loaded actuator and the maximum temperature of the heater surface were fitted. The research results may provide a reference for predicting temperature and humidity distributions inside general spring-loaded actuators and provide a calculation basis for the design of their heaters.
2. Research Object
The research object is a typical spring-loaded actuator in service from a Chinese company. This spring-loaded actuator mainly consists of a box, a spring module, a heater, and other components. Figure 1 shows the schematic diagram of the overall structure of the spring-loaded actuator and gives the position of the heater. The length, width, and height of the actuator box are 784, 790, and 1225 mm. The model number of the heater is SP-409B-BY, which is made of aluminum alloy. L, W, and H are heater length, width, and height. The original values of heater length, heater width, and heater height are L0 = 169 mm, W0 = 55 mm, and H0 = 75 mm. The supply voltage of the heater is 220 V, the heating power is represented by P, and the default heating power is P0 = 100 W. The distance of the heater from the side wall of the actuator box is 84 mm, and the distance from the bottom wall of the actuator box is 150 mm. The spring-loaded actuator exchanges air with the external environment through a square vent of 80 mm × 80 mm. In this study, the working conditions and heater structural parameters were changed to study their influence laws on the temperature and humidity distributions in the box of a typical spring-loaded actuator. The details are as follows: the ambient temperature varies from 233.15 K to 313.15 K, the ambient relative humidity is 95%, the heating power ranges from 10 W to 150 W, the heater length changes from 84.5 mm to 253.5 mm, the heater width varies from 10 mm to 100 mm, and the heater height ranges from 60 mm to 90 mm. The above parameters are given according to the company’s requirements.
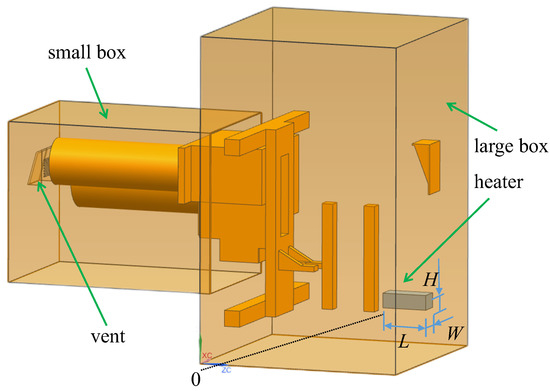
Figure 1.
Physical model of the spring-loaded actuator.
For the typical spring-loaded actuator studied in this work, according to the regulations of the State Grid of China, the relative humidity inside the actuator box needs to be less than 80%, the minimum temperature inside the actuator box needs to be greater than 278.15 K, and the maximum temperature on the heater surface needs to be less than 353.15 K. If the temperature and relative humidity inside the actuator box exceeds the above limit temperature and relative humidity, it will affect the operational performance of the spring-loaded actuator and even affect the safe and stable operation of the high-voltage switch. The extreme temperature mainly occurs on the heater surface, and of course, the temperature on the components’ surface around the heater will also be high. Extreme relative humidity mainly occurs around the components far from the heater and in multiple corners near the side walls at the bottom of the actuator box. However, due to the influence of changes in ambient temperature and ambient relative humidity, such as when the ambient temperature reaches 233.15 K (−40 °C), a very large heating power is required to ensure the temperature inside the box larger than 278.15 K. At this time, if the size of the heater is too small, the temperature of the heater surface may exceed 353.15 K (80 °C). When the ambient temperature exceeds 293.15 K (20 °C), the ambient relative humidity is greater than 90%, and the relative humidity inside the actuator box may not meet the requirement of less than 80%. Therefore, it is necessary to conduct a simulation analysis of temperature and humidity distribution characteristics in the typical spring-loaded actuator (Part 1, the research content of this paper), and reasonably optimize the power and size of the heater (Part 2, another paper under review).
This study analyzes the temperature distribution and relative humidity distribution inside the spring-loaded actuator. The equation for calculating relative humidity (RH) is as follows:
where ms is the amount of water vapor in the wet air; SH is the saturated humidity, which increases with the temperature increase.
RH = ms/SH × 100
3. Numerical Methods
3.1. Numerical Model
Figure 2a,b illustrate the numerical calculation model and the calculation flowchart of the spring-loaded actuator studied in this work, respectively. As shown in Figure 2a, the numerical calculation model mainly consists of the solid domains of the spring-loaded actuator such as the actuator box, the heater, and other parts, as well as the internal fluid domain inside the actuator box and the external fluid domain outside the actuator box. The external fluid domain is a rectangular body formed by extending the outermost wall of the actuator box outward by 1000 mm. It is constructed to simulate the atmospheric environment outside the actuator box. The outer surface of the solid domain and the inner surface of the external fluid domain were set as the fluid-solid coupling interface. The inner surface of the solid domain and the outer surface of the internal fluid domain were also set as the fluid-solid coupling interface. The inner surface of the internal fluid domain and the surfaces of the components inside the spring-loaded actuator (including the heater) were also set as the fluid-solid coupling interface. The external fluid domain and internal fluid domain were connected through the square air vent.

Figure 2.
Numerical model of the spring-loaded actuator: (a) calculation model; (b) calculation flowchart.
Figure 3 demonstrates the grid model of the typical spring-loaded actuator studied in this work. The Workbench module of ANSYS software (V19.5, ANSYS Inc., Pittsburgh, PA, United States) was used to complete the unstructured grid generation of the spring-loaded actuator. The minimum mesh size was determined according to 1/10 of the minimum structural size of each area in the spring-loaded actuator box. The maximum mesh size was initially taken as 10 mm, and the mesh growth ratio was set to 1.2. For the mesh of the internal fluid domain, the boundary layer meshes were also added. The number of boundary layers was 15, and the height of the first layer mesh was 0.1 mm. The total grid number was changed by adjusting the maximum mesh size. Finally, the appropriate total grid number was determined by the grid-independence verification.
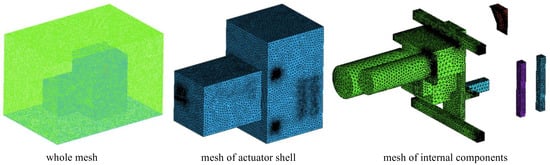
Figure 3.
Grid model of the spring-loaded actuator.
To ensure the reliability and economy of the numerical method, grid-independent verification for the spring-loaded actuator was carried out. A total of six sets of grid models were carried out for numerical calculations with total mesh numbers of 1.8 million, 2.6 million, 3.8 million, 5.0 million, 6.6 million, and 8.1 million. The variation curves of the minimum temperature and maximum relative humidity inside the actuator box with the total mesh number are given in Figure 4. It can be seen from Figure 4 that the minimum temperature inside the actuator box gradually decreases with the increase in the total mesh number, and the maximum relative humidity gradually increases with the increase in the total mesh number. It is worth noting that, the respective differences of the minimum temperature and the maximum relative humidity at the total mesh number of 6.6 million and 8.1 million are already very small. The differences between them are both close to 1%, which indicates that the requirement of grid-independent verification is achieved. Additionally, the grid convergence study results (calculated based on the minimum temperature) in Table 1 obtained by the GCI index [33] also show that the total mesh number of 6.6 million can meet the grid independence requirements, due to the GCI index being close to 1% when the total mesh number is 6.6 million. Therefore, the fifth set of grid models (total mesh number of 6.6 million, including 5.59 million in the fluid domain and 1.01 million in the solid domain) was adopted to complete the grid generation task of the typical spring-loaded actuator in this study.

Figure 4.
Grid independence verification: (a) temperature; (b) relative humidity.

Table 1.
Grid convergence study results.
3.2. Numerical Simulation Methods
In this investigation, the coupled heat transfer calculation method was used to complete the numerical calculations of the temperature and humidity inside the spring-loaded actuator. In numerical calculations, the interfaces between the fluid domain and the solid domain were all set as coupling surfaces. Both sides of the coupling surfaces have the same heat flux and temperature. The fluid domain was assumed to be a three-dimensional, gravitational, constant, incompressible flow. The finite element-based finite volume method was used to discrete the governing equations [33]. The Reynolds time-averaged N-S equations were solved by the CFX module of ANSYS software (V19.5, ANSYS Inc., Pittsburgh, PA, United States). The built-in advection schemes in CFX can be written as [34]:
where is the vector from the upwind node to the integration point (ip), and is the value at the upwind node. Specific choices for θ and yield different schemes.
The high-resolution scheme, which utilizes a specific nonlinear recipe for θ at each node as defined in Equation (2) and is calculated to be approximate to 1 as far as possible without generating new extrema, was chosen as the option of the advection scheme. Since the advection scheme for the turbulence model equations are irrespective of the advection scheme setting and depends on turbulence numerics, the high-resolution advection scheme was also chosen as the option of turbulence numerics.
Due to the need to calculate the humidity, a new material containing two components, water vapor and air, was created to form the component transport model. Due to the higher flow velocity of the fluid above the heater, the flow in this area has the characteristics of turbulent flow. Therefore, the numerical method in this study also considers the calculation of turbulent flow. Reference [35] has proven that the RNG k-ε turbulence model is more suitable for calculating temperature and humidity inside a certain space. Therefore, the RNG k-ε turbulence model was used to solve the turbulent flow inside the spring-loaded actuator box. For the solid domain, only the thermal conductivity equation was solved. The overall residual level of the numerical simulation was set to 10−6. When the residual level was equal to 10−6, the solution of the numerical simulation was stopped.
The conservation equations of continuity, momentum, and energy are as follows [36]:
According to the conservation equation for the species transport, the amount of water vapor in the air can be calculated, and then the relative humidity value can be calculated from the air temperature and saturation humidity. The conservation equation for species transport can be given as follows:
where is the local mass fraction of component A, D is the mass diffusion coefficient for component A, Scr is the turbulent Schmidt number, and RA is the net production rate caused by source term.
The mass diffusion coefficient of water vapor is computed according to the temperature-dependent empirical correlations below:
where the unit of D is m2·s−1, T is the temperature of the air-water vapor mixture.
The thermal energy equation for the air-water vapor mixture is expressed as follows:
where cp is the specific heat of the air-water vapor mixture, and kg is the thermal conductivity of the air-water vapor mixture; Prt is the turbulent Prandtl number, Ys and hs are the species mass fraction and species enthalpy, respectively.
This study solves a natural flow problem, where the driving force of fluid flow comes from gravity. Therefore, the wind speed around the actuator box was not considered in this study. According to the actual operating conditions of the spring-loaded actuator, the boundary conditions were set as follows: the body heat source was assigned to the heater domain, and the body heat flux was calculated according to the heating power (10 W to 150 W). The side and top surfaces of the external fluid domain were set as the opening conditions. The opening temperature (233.15 K to 313.15 K), opening pressure (1 atm), opening relative humidity (95%), and opening velocity (0 m·s−1) were assigned to the side and top surfaces of the external fluid domain. The relative humidity was calculated by the mass fraction of water vapor in the component transport model. For the initialization of the ambient conditions of the external fluid domain, the specific values of ambient temperature, ambient pressure, and ambient relative humidity were set according to the studied working conditions, and the corresponding ambient velocity was set to 0 m·s−1. The initialization temperature of 298.15 K, initialization pressure of 1 atm, initialization relative humidity of 0%, and initialization velocity of 0 m·s−1 were assigned to the internal fluid domain. The mass and momentum terms at the fluid-fluid interface at the square air vent are conservative flux values. The calculation of fluid-solid coupled heat transfer also follows the most basic conservation principle, which requires the conservation of variables such as temperature and heat flux at the fluid-solid interface. The conservation equation is expressed as Equation (9). The detailed boundary conditions are shown in Table 2.

Table 2.
Boundary conditions for the numerical calculations.
Equation (9) is written as follows:
where qf is the heat flux at the interface of the fluid domain side; qs is the heat flux at the interface of the solid domain side; Tf is the temperature at the interface of the fluid domain side; Ts is the temperature at the interface of the solid domain side.
3.3. Numerical Method Verification
A reliable and accurate numerical method is the basis for conducting temperature and humidity simulations of the spring-loaded actuator. Therefore, the experimental data in Reference [35] was used to verify the reliability and accuracy of the numerical method established in this study. The experimental parameters used to validate the numerical method are as follows: the dimensions of the experimental space are 4 m × 4 m × 3 m. The heater’s dimensions are 1.5 m × 0.6 m × 0.1 m. The dimensions of the inlet and outlet are both 1 m × 0.15 m. The inlet velocity is 0.15 m/s. The mass fraction of water vapor in the component at the inlet is set to 0.95%. The outlet pressure is 1 atm. The mass fraction of water vapor in the component at the outlet is set to 0%. The temperature of the heater surface is constant at 333.15 K. The temperature of the human body surface is constant at 306.15 K. The mass fraction of water vapor in the component in the experimental space is set to 1%. The outside of glass windows in the experimental space were set as the boundary condition for the convective heat transfer coefficient, with a value of 25 W·m−2·K−1.
Figure 5 compares the calculated results of the numerical method in this work and the experimental results in Reference [35]. Table 3 shows the percentage deviations between the corresponding numerical and experimental results. As shown in Figure 5a, the temperature calculated by the numerical method in this work has the same trend and similar value as the experimentally measured temperature in Reference [35], and the maximum deviation between them is 4.4%. As shown in Figure 5b, the relative humidity distribution trend calculated by the numerical method in this work is also the same as that of the experimentally measured relative humidity distribution trend in [35], and their values are also similar with a maximum deviation of 8.5%. Therefore, the numerical method for simulating the temperature and humidity distribution characteristics inside a certain space established in this study has relatively high reliability and accuracy.
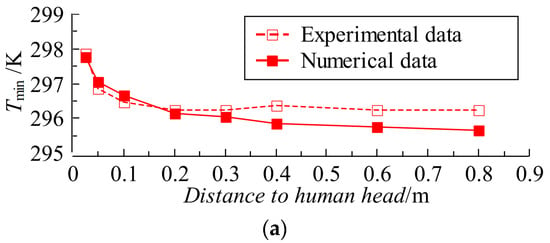
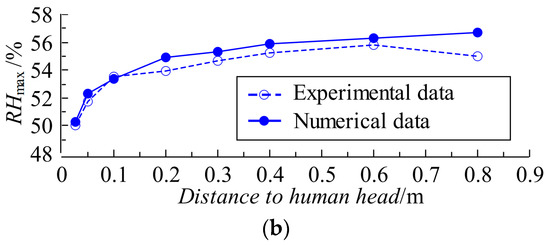
Figure 5.
Validation of numerical methods based on experimental data in Reference [35]: (a) temperature; (b) relative humidity.

Table 3.
Percentage deviations between numerical and experimental results.
4. Results Analysis and Discussion
It has been rarely seen that a heater system can control the temperature and humidity of a spring actuator and that it can be operated safely at different environmental temperatures. This study is unique: (1) the temperature and humidity distribution characteristics in a typical spring-loaded actuator are illustrated. (2) the influence laws of ambient temperature, heater power, and heater size on the temperature and humidity distributions inside the typical spring-loaded actuator were analyzed. (3) the practical empirical correlations of the minimum temperature and maximum relative humidity inside the typical spring-loaded actuator and the maximum temperature of the heater surface were fitted.
4.1. Distribution Characteristics of Velocity, Temperature, and Humidity
Figure 6 demonstrates the temperature and humidity distribution characteristics along with the flow field inside the spring-loaded actuator. The ambient temperature is 298.15 K, the ambient pressure is 1 atm, the ambient relative humidity is 95%, and the heating power is 100 W. As can be seen from Figure 6a, the air around the heater starts to move vertically upward after being heated, due to the thermal expansion and density reduction in the heated air. Then, the heated air begins to move along the width and length directions after reaching the top wall of the large box on the right side of the spring-loaded actuator. Subsequently, the heated air obliquely flows to the adjacent small box on the left side of the spring-loaded actuator. Finally, the heated air flows through the vent to the outside of the spring-loaded actuator. The air velocity above the heater is the fastest, and the maximum flow velocity is up to 0.5 m/s. Then, when the air laterally flows towards the length and width of the large box, the air velocity gradually decreases.
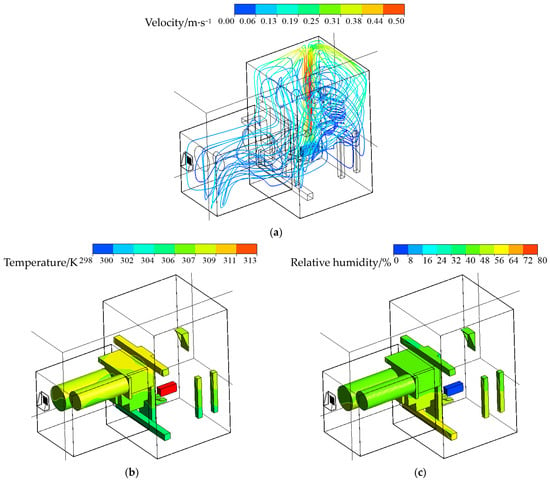
Figure 6.
Distribution characteristics of velocity, temperature, and humidity in the spring-loaded actuator: (a) velocity; (b) temperature; (c) humidity.
As seen from Figure 6b,c, the heater surface has the highest temperature and lowest relative humidity, which results in higher temperature and lower relative humidity of the air around and directly above the heater. According to the comprehensive analysis of Figure 6a,b, since the heater is located in the bottom and innermost corners of the large box, the temperature gradually decreases when the air starts flowing from the large box’s top wall directly above the heater to other components. Therefore, the air temperature around other components gradually decreases from top to bottom. As shown in Figure 6c, the corresponding relative humidity of the air around the heater is the lowest. Then, the relative humidity of the air around other components gradually increases. Overall, the relative humidity of the air around other components gradually increases from top to bottom. In addition, it can also be found from Figure 6b that, the temperature of the heater surface far exceeds the temperature of the other parts. This is because on the one hand, the size of the heater is small, and on the other hand, the heating power is relatively large (100 W). Under the condition of natural convection, the heat on the surface of the heater cannot be dissipated quickly, resulting in a high local temperature on the surface of the heater. The excessive temperature of the heater will affect the safety and reliability of the entire spring-loaded actuator. Therefore, it is necessary to study the influence laws of different working conditions and structural parameters of a heater on the temperature and humidity distributions in the spring-loaded actuator. To provide theoretical reference for the design, operation and management of the heater inside the spring-loaded actuator.
4.2. Effect of Working Conditions Parameters
Figure 7 displays the influence laws of ambient temperature on the minimum temperature, maximum relative humidity, and heater surface maximum temperature inside the spring-loaded actuator. The ambient pressure is 1 atm, the ambient relative humidity is 95%, and the heating power is 100 W. As seen in Figure 8, the effect of ambient temperature on the minimum temperature, maximum relative humidity, and heater surface maximum temperature inside the spring-loaded actuator is very significant. As shown in Figure 7a, when the ambient temperature increases from 233.15 K to 313.15 K, the minimum temperature inside the spring-loaded actuator increases from 233.86 K to 313.38 K for P = 10 W and increases from 240.32 K to 322.73 K for P = 100 W, that is, the minimum temperature inside the actuator is increased by 34.00% for P = 10 W and 34.29% for P = 100 W. As shown in Figure 7b, with the increase in ambient temperature, the maximum relative humidity shows a trend of increasing and then decreasing. Specifically, when the maximum relative humidity reaches its highest value of about 80.36% for P = 10 W and about 69.5% for P = 100 W at 273.15 K and reaches its lowest value of about 43.12% for P = 10 W and about 28.85% for P = 100 W at 313.15 K. As shown in Figure 7c, as the ambient temperature increases from 233.15 K to 313.15 K, the maximum temperature on the heater surface increases from 244.18 K to 315.54 K for P = 10 W (that is, an increase of 29.22%), and increases from 304.23 K to 398.87 K for P = 100 W (that is, an increase of 31.11%). These results show that different heating power should be used at different ambient temperatures.

Figure 7.
Effect of ambient temperature on temperature and humidity distributions inside the spring-loaded actuator: (a) minimum temperature; (b) maximum relative humidity; and (c) maximum temperature of heater surface.

Figure 8.
Effect of heater power on temperature and humidity distributions inside the spring-loaded actuator: (a) minimum temperature; (b) maximum relative humidity; (c) maximum temperature of heater surface.
Figure 8 shows the influence laws of heater power on the minimum temperature, maximum relative humidity, and heater surface maximum temperature inside the spring-loaded actuator. The ambient temperature is 298.15 K, the ambient pressure is 1 atm, and the ambient relative humidity is 95%. It can be seen from Figure 8 that, the heating power of the heater also has a significant effect on the minimum temperature, maximum relative humidity, and the heater surface maximum temperature inside the spring-loaded actuator. Specifically, when the heating power increases from 10 W to 150 W, the minimum temperature inside the spring-loaded actuator is increased from 273.64 K to 282.94 K at Ta = 273.15 K and increased from 299.54 K to 310.34 K at Ta = 298.15 K, with relative increase scales of 3.40% at Ta = 273.15 K and 3.61% at Ta = 298.15 K. The maximum relative humidity inside the spring-loaded actuator decreased from 90.81% to 57.87% at Ta = 273.15 K and decreased from 88.10% to 36.53% at Ta = 298.15 K, with relative decrease scales of 51.97% at Ta = 273.15 K and 58.63% at Ta = 298.15 K. The maximum temperature of the heater surface is increased from 280.21 K to 365.18 K at Ta = 273.15 K and increased from 311.77 K to 415.44 K at Ta = 298.15 K, with relative increase scales of 30.33% at Ta = 273.15 K and 33.25% at Ta = 298.15 K.
In summary, the influence of ambient temperature and heating power on the temperature and humidity distribution in the spring-loaded actuator is relatively significant.
4.3. Effect of Heater Size
Figure 9 illustrates the influence laws of heater length on the minimum temperature, maximum relative humidity, and heater surface maximum temperature inside the spring-loaded actuator. The width and height of the heater remain unchanged. The ambient temperature is 298.15 K, the ambient pressure is 1 atm, the ambient relative humidity is 95%, and the heating power is 100 W. As shown in Figure 9, the minimum temperature inside the spring-loaded actuator first decreases and then increases with the increase in heater length, the maximum relative humidity inside the spring-loaded actuator first increases and then decreases with the increase in heater length. However, both the minimum temperature and maximum relative humidity inside the spring-loaded actuator are little affected by the change in heater length. The heater surface maximum temperature significantly decreases with the increase in heater length. When the heater length increases from 84.5 mm to 253.5 mm, the maximum temperature of the heater surface decreases from 372.89 K to 338.77 K at Ta = 273.15 K and from 393.62 K to 351.35 K at Ta = 298.15 K, which is decreased by 9.15% at Ta = 273.15 K and 10.74% at Ta = 298.15 K.
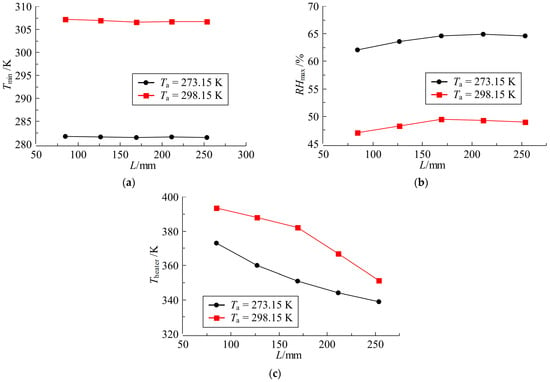
Figure 9.
Effect of heater length on temperature and humidity distributions inside the spring-loaded actuator: (a) minimum temperature; (b) maximum relative humidity; (c) maximum temperature of heater surface.
Figure 10 exhibits the influence laws of heater width on the minimum temperature, maximum relative humidity, and heater surface maximum temperature inside the spring-loaded actuator. The length and height of the heater remain unchanged. The ambient temperature is 298.15 K, the ambient pressure is 1 atm, the ambient relative humidity is 95%, and the heating power is 100 W. As shown in Figure 10, the influence rule of heater width on the minimum temperature, maximum relative humidity, and heater surface maximum temperature inside the spring-loaded actuator is almost the same as that of heater length on these characteristic parameters. The influence of heater width on the minimum temperature and maximum relative humidity inside the spring-loaded actuator is also small. The influence of heater width on the heater surface maximum temperature is also significant. When the heater width varies from 10 mm to 100 mm, the maximum temperature of the heater surface is reduced from 372.11 K to 343.86 K at Ta = 273.15 K and reduced from 396.62 K to 360.92 K at Ta = 298.15 K, i.e., reductions of 7.59% at Ta = 273.15 K and 9.01% at Ta = 298.15 K.

Figure 10.
Effect of heater width on temperature and humidity distributions inside the spring-loaded actuator: (a) minimum temperature; (b) maximum relative humidity; (c) maximum temperature of heater surface.
Figure 11 gives the influence laws of heater height on the minimum temperature, maximum relative humidity, and heater surface maximum temperature inside the spring-loaded actuator. The length and width of the heater remain unchanged. The ambient temperature is 298.15 K, the ambient pressure is 1 atm, the ambient relative humidity is 95%, and the heating power is 100 W. As can be found from Figure 11, similar to the effect laws of heater length and heater width, the effect of heater height on the minimum temperature and maximum relative humidity inside the spring-loaded actuator is not significant. In contrast, the effect of heater height on the heater surface maximum temperature is relatively significant. Unlike the effects of heater length and width, the minimum temperature inside the spring-loaded actuator slightly decreases with increasing heater height, and the maximum relative humidity slightly increases with increasing heater height. When the heater height changes from 60 mm to 90 mm, the maximum temperature of the heater surface is decreased from 360.26 K to 343.58 K at Ta = 273.15 K and decreased from 386.97 K to 368.68 K at Ta = 298.15 K, i.e., relative decrease scales of 4.63% at Ta = 273.15 K and 4.73% at Ta = 298.15 K.

Figure 11.
Effect of heater height on temperature and humidity distributions inside the spring-loaded actuator: (a) minimum temperature; (b) maximum relative humidity; (c) maximum temperature of heater surface.
In summary, the analysis results show that the heater size has little effect on the minimum temperature inside the spring-loaded actuator but has a relatively significant effect on the maximum relative humidity inside the spring-loaded actuator and the maximum temperature of the heater surface.
4.4. Empirical Correlations Fitting
To promote the practicability of the research results obtained in this investigation, the empirical correlations of the minimum temperature and maximum relative humidity inside the actuator box, as well as the maximum temperature of the heater surface, were fitted for the spring-loaded actuator under various working conditions and different heater structural parameters. To improve the fitting accuracy of the empirical correlations, the appropriate function forms are first determined based on the variation laws of various characteristic parameters of the spring-loaded actuator with the influencing parameters. This process is completed using the curve fitting function in WPS (V11.1, Kingsoft Office, Beijing, China), which involves changing the function form multiple times and selecting the function form with the highest fitting determination coefficient. Afterward, the selected function forms are weighted and multiplied together through self-programming. Finally, the final empirical correlations are fitted and obtained through self-programming in Python (V3.8, Python Software Foundation, Wilmington, DE, United States). Additionally, in order to generalize the obtained results in this work, the empirical correlation will be processed in dimensionless forms. Conduct dimensionless treatment on the ambient temperature, the minimum temperature inside the actuator box and the maximum temperature of heater surface with the maximum limit temperature (Tm = 353.15 K) of the heater surface. Conduct dimensionless treatment on the maximum relative humidity inside the actuator box with the maximum limit relative humidity (RHm = 80%). Conduct dimensionless treatment on the heating power with a rated heating power (P0 = 100 W), and conduct dimensionless treatments on the heater length, width and height with the original heater length (L0 = 169 mm), width (W0 = 55 mm) and height (H0 = 75 mm). Then, there are dimensionless ambient temperature Td = Ta/Tm, dimensionless minimum temperature inside the actuator box Tmin_d = Tmin/Tm, dimensionless maximum temperature of heater surface Theater_d = Theater/Tm, dimensionless maximum relative humidity inside the actuator box RHmax_d = RHmax/RHm, dimensionless heating power Pd = P/P0, dimensionless heater length Ld = L/L0, dimensionless heater width Wd = W/W0, and dimensionless heater width Hd = H/H0.
According to the results in Section 4.2 and Section 4.3, the minimum temperature inside the spring-loaded actuator is monotonically changed with the changing of the ambient temperature, heater power, and heater height. Therefore, the relationships between the minimum temperature and the ambient temperature, heater power, or heater height were assumed to be the power functions. Further, the minimum temperature is firstly decreased and then increased with the changing of the heater length and heater width. Therefore, the relationships between the minimum temperature and the heater length, or heater width were assumed to be the quadratic polynomial functions. Consequently, the form of the empirical correlation of the dimensionless minimum temperature is as follows:
where a1 to j1 are the parameters to be fitted for the empirical correlation of the minimum temperature of the spring-loaded actuator.
The maximum relative humidity inside the spring-loaded actuator is monotonically varied with the increase in the heater power and heater height. Thus, the relationships between the maximum relative humidity and the heater power, or heater height were assumed to be the power functions. Additionally, the maximum relative humidity is firstly increased and then decreased with the increase in the ambient temperature, heater length, and heater width. Thus, the relationships between the maximum relative humidity and the ambient temperature, heater length, and heater width were assumed to be quadratic polynomial functions. Hence, the form of the empirical correlation of the dimensionless maximum relative humidity is as follows:
where a2 to l2 are the parameters to be fitted for the empirical correlation of the maximum relative humidity of the spring-loaded actuator.
The maximum temperature of the heater surface is monotonously changed with the changing of the ambient temperature, heater power, length, width, and height. As a result, the relationships between the maximum temperature of the heater surface and the ambient temperature, heater power, length, width, or height were all assumed to be the power functions. Thus, the form of the empirical correlation of the dimensionless heater surface maximum temperature is as follows:
where a3 to f3 are the parameters to be fitted for the empirical correlation of the maximum temperature of the heater surface in the spring-loaded actuator.
Based on the numerical data from simulations, the Python language was used to fit the empirical correlations of Equations (10)–(12) by self-programming. The fitting work is completed by calling the curve fit module of the Scipy package through self-programming in Python. The curve fit module uses the non-linear least square algorithm for function fitting. The fitting results are as follows:
where 0.66 ≤ Td ≤ 0.89, 0.1 ≤ Pd ≤ 1.5, 0.5 ≤ Ld ≤ 1.5, 0.18 ≤ Wd ≤ 1.82, 0.8 ≤ Hd ≤ 1.2.
The fitting determination coefficients (R2) of Equations (13)–(15) are 0.997, 0.883, and 0.931, respectively, indicating that the fitting results of these three equations are reasonable. The validity ranges of Equations (13)–(15) are: 233.15 K ≤ Ta ≤ 313.15 K, 10 W ≤ P ≤ 150 W, 84.5 mm ≤ L ≤ 253.5 mm, 10 mm ≤ W ≤ 100 mm, 60 mm ≤ H ≤ 90 mm.
Figure 12 demonstrates the distribution curves of fitting deviations for the empirical correlations of Equations (13)–(15). As shown in Figure 12, the maximum fitting deviation and mean fitting deviation of Equation (13) for the minimum temperature inside the spring-loaded actuator are −1.05% and 0.19%, respectively. The maximum fitting deviation and mean fitting deviation of Equation (14) for the maximum relative humidity inside the spring-loaded actuator are 12.43% and 3.20%, respectively. The maximum fitting deviation and mean fitting deviation of Equation (15) for the maximum temperature of the heater surface are −5.15% and 1.38%, respectively. It can be found that Equation (14) has the largest fitting deviation and the lowest fitting accuracy, followed by Equation (15). In contrast, Equation (13) has the smallest fitting deviation and the highest fitting accuracy. On the whole, the fitting deviations of Equations (13)–(15) are small and can be used to predict the minimum temperature and maximum relative humidity inside the actuator box as well as the maximum temperature of the heater surface for a typical spring-loaded actuator.
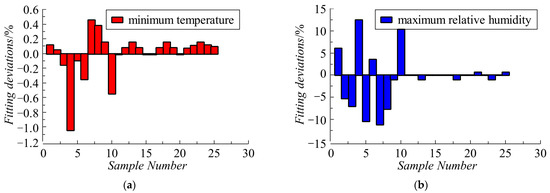
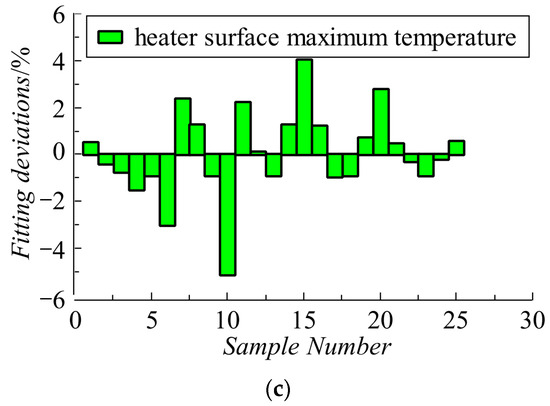
Figure 12.
Fitting deviations: (a) minimum temperature; (b) maximum relative humidity; (c) maximum temperature of heater surface.
5. Conclusions
In this work, the temperature and humidity distribution characteristics in a spring-loaded actuator were thoroughly researched by numerical methods. The main conclusions are as follows:
- (1)
- The air temperature around and directly above the heater is the highest and the corresponding relative humidity is the lowest. Then, the air temperature gradually decreases, and the relative humidity increases with the lateral flow of air.
- (2)
- When the ambient temperature increases from 233.15 K to 313.15 K, the minimum temperature inside the actuator is increased by about 34%, the maximum humidity first increases and then decreases, and the maximum temperature on the heater surface is increased by 30%.
- (3)
- When the heating power increases from 10 W to 150 W at Ta = 273.15 K and Ta = 298.15 K, the minimum temperature inside the actuator is increased by 3.40% and 3.61%, the maximum humidity is decreased by 51.97% and 58.63%, and the maximum temperature on the heater surface is increased by 30.33% and 33.25%, respectively.
- (4)
- The influence of heater length, width, and height on the minimum temperature and maximum relative humidity inside the spring-loaded actuator is relatively small. Within the study range, the increase in heater length, width, and height makes the maximum temperature on the heater surface decrease by 9.15%, 7.59%, 4.63% at Ta = 273.15 K, and 10.74%, 9.01%, 4.73% at Ta = 298.15 K, respectively.
- (5)
- The maximum fitting deviations for the empirical correlations of minimum temperature, maximum relative humidity, and heater surface maximum temperature inside the spring-loaded actuator are −1.05%, 12.43%, and −5.15%, respectively.
- (6)
- The results may provide a reference for predicting temperature and humidity distributions inside general spring-loaded actuators and provide a calculation basis for the design of their heaters.
Author Contributions
Conceptualization, L.X. (Lei Xi); methodology, L.X. (Lei Xi); validation, L.X. (Liang Xu); formal analysis, Z.Z.; investigation, Z.Y.; resources, J.G.; data curation, Q.R.; writing—original draft preparation, L.X. (Lei Xi); writing—review and editing, Q.R.; visualization, Y.L.; supervision, L.X. (Lei Xi); project administration, J.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Project Supported by Natural Science Basic Research Plan in Shaanxi Province of China (2022JQ-545), the Project funded by China Postdoctoral Science Foundation (2021M702573), and the National Natural Science Foundation of China (51876157).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| H | Heater height, mm. |
| L | Heater length, mm. |
| ms | amount of water vapor, g·m−3. |
| P | Heating power, W. |
| R | Relative humidity, %. |
| RHmax | Maximum relative humidity, %. |
| SH | Saturated humidity, g·m−3. |
| T | Temperature, K. |
| Ta | Ambient temperature, K. |
| Tmin | Minimum temperature inside the actuator, K. |
| Theater | Maximum temperature of heater surface, K. |
| W | Heater width, mm. |
References
- Kang, Y.H.; Huang, H.C.; Yang, B.Y. Optimal design and dynamic analysis of a spring-actuated cam-linkage mechanism in a vacuum circuit breaker. Machines 2023, 11, 150. [Google Scholar] [CrossRef]
- Koh, J.S. Design of shape memory alloy coil spring actuator for improving performance in cyclic actuation. Materials 2018, 11, 2324. [Google Scholar] [CrossRef]
- Shimoga, G.; Kim, T.H.; Kim, S.Y. An intermetallic niti-based shape memory coil spring for actuator technologies. Metals 2021, 11, 1212. [Google Scholar] [CrossRef]
- Hu, B.; Liu, F.; Mao, B.; Chen, Z.; Yu, H. Modeling and position control simulation research on shape memory alloy spring actuator. Micromachines 2022, 13, 178. [Google Scholar] [CrossRef]
- Wang, L.; Qiu, Y.; Han, Z.; Xu, C.; Wu, S.Y.; Wang, Y.; Xu, Z. Climate, topography and anthropogenic effects on desert greening: A 40-year satellite monitoring in the Tengger desert, northern China. Catena 2022, 209, 105851. [Google Scholar] [CrossRef]
- Xie, Q.; Meng, Q.; Yu, W.; Xu, R.; Wu, Z.; Wang, X.; Yu, H. Design of a soft bionic elbow exoskeleton based on shape memory alloy spring actuators. Mech. Sci. 2023, 14, 159–170. [Google Scholar] [CrossRef]
- Bhatt, N.; Gurung, H.; Soni, S.; Singla, A. Effect of biasing conditions on the performance of a SMA spring actuator under thermo-mechanical loading. Mech. Adv. Mater. Struc. 2022, 29, 4599–4613. [Google Scholar] [CrossRef]
- Zaman, S.; Leyva, A.; Hassan, M.S.; Valladolid, A.; Herrera, N.E.; Gomez, S.G.; Mahmud, M.S.; Tucker, D.; Haynes, C.; Lin, Y. Implementation of smart materials for actuation of traditional valve technology for hybrid energy systems. Actuators 2023, 12, 131. [Google Scholar] [CrossRef]
- Hyo Jik, L.; Jung Ju, L. Evaluation of the characteristics of a shape memory alloy spring actuator. Smart Mater. Struct. 2000, 9, 817. [Google Scholar]
- Degeratu, S.; Bizdoaca, N.G.; Manolea, G.; Diaconu, I.; Petrisor, A.; Degeratu, V. On the design of a shape memory alloy spring actuator using thermal analysis. WSEAS Trans. Syst. 2008, 7, 1281–1290. [Google Scholar]
- Degeratu, S.; Rotaru, P.; Rizescu, S.; Bîzdoacă, N.G. Thermal study of a shape memory alloy (SMA) spring actuator designed to insure the motion of a barrier structure. J. Therm. Anal. Calorim. 2013, 111, 1255–1262. [Google Scholar] [CrossRef]
- Ma, J.; Huang, H.; Huang, J. Characteristics analysis and testing of sma spring actuator. Adv. Mater. Sci. Eng. 2013, 13, 823594. [Google Scholar] [CrossRef]
- Holanda, S.A.; Silva, A.A.; de Araújo, C.J.; de Aquino, A.S. Study of the complex stiffness of a vibratory mechanical system with shape memory alloy coil spring actuator. Shock Vib. 2014, 14, 162781. [Google Scholar] [CrossRef]
- Auricchio, F.; Scalet, G.; Urbano, M. A numerical/experimental study of nitinol actuator springs. J. Mater. Eng. Perform. 2014, 23, 2420–2428. [Google Scholar] [CrossRef]
- Cortez-Vega, R.; Chairez, I.; Luviano-Juárez, A.; Feliu-Batlle, V. A hybrid dynamic model of shape memory alloy spring actuators. Measurement 2018, 114, 340–353. [Google Scholar] [CrossRef]
- Cortez-Vega, R.; Chairez, I.; Luviano-Juarez, A.; Lozada-Castillo, N.; Feliu-Batlle, V. Multi-link endoscopic manipulator robot actuated by shape memory alloys spring actuators controlled by a sliding mode. ISA Trans. 2020, 10, 010053. [Google Scholar] [CrossRef]
- Park, C.H.; Choi, K.J.; Son, Y.S. Shape memory alloy-based spring bundle actuator controlled by water temperature. IEEE/ASME Trans. Mechatron. 2019, 24, 1798–1807. [Google Scholar] [CrossRef]
- Xiong, Y.; Huang, J.; Shu, R. Thermomechanical performance analysis and experiment of electrothermal shape memory alloy helical spring actuator. Adv. Mech. Eng. 2021, 13, 16878140211044651. [Google Scholar] [CrossRef]
- Jiang, Z.C.; Xiao, Y.Y.; Cheng, R.D.; Hou, J.B.; Zhao, Y. Dynamic liquid crystalline networks for twisted fiber and spring actuators capable of fast light-driven movement with enhanced environment adaptability. Chem. Mater. 2021, 33, 6541–6552. [Google Scholar] [CrossRef]
- Britz, R.; Rizzello, G.; Motzki, P. High-speed antagonistic shape memory actuator for high ambient temperatures. Adv. Eng. Mater. 2022, 24, 2200205. [Google Scholar] [CrossRef]
- Jithu, P.V.; Mohan, G. Performance simulation of metal hydride based helical spring actuators during hydrogen sorption. Int. J. Hydrogen Energ. 2022, 47, 14942–14951. [Google Scholar] [CrossRef]
- Wang, W.; Xiang, C.; Zhu, Q.; Zhong, W.; Li, M.; Yan, K.; Wang, D. Multistimulus responsive actuator with go and carbon nanotube/pdms bilayer structure for flexible and smart devices. ACS Appl. Mater. Interfaces 2018, 10, 27215–27223. [Google Scholar] [CrossRef] [PubMed]
- Xu, G.; Chen, J.; Zhang, M.; Shi, G. An ultrasensitive moisture driven actuator based on small flakes of graphene oxide. Sens. Actuators B Chem. 2017, 242, 418–422. [Google Scholar] [CrossRef]
- Arazoe, H.; Miyajima, D.; Akaike, K.; Araoka, F.; Sato, E.; Hikima, T.; Kawamoto, M.; Aida, T. An autonomous actuator driven by fluctuations in ambient humidity. Nat. Mater. 2016, 15, 1084–1089. [Google Scholar] [CrossRef]
- Ryabchun, A.; Lancia, F.; Nguindjel, A.-D.; Katsonis, N. Humidity-responsive actuators from integrating liquid crystal networks in an orienting scaffold. Soft Matter 2017, 13, 8070–8075. [Google Scholar] [CrossRef]
- Cabuz, C.; Cabuz, E.I.; Ohnstein, T.R.; Neus, J.; Maboudian, R. Factors enhancing the reliability of touch-mode electrostatic actuators. Sens. Actuator A Phys. 2000, 79, 245–250. [Google Scholar] [CrossRef]
- Lim, A.E.; Goh, S. Effect of microchannel diameter on electroosmotic flow hysteresis. Energies 2023, 16, 2154. [Google Scholar] [CrossRef]
- Lim, A.E.; Lam, Y.C. Electroosmotic flow hysteresis for fluids with dissimilar ph and ionic species. Micromachines 2021, 12, 1031. [Google Scholar] [CrossRef]
- Ogden, S.; Bodén, R.; Hjort, K. A Latchable valve for high-pressure microfluidics. J. Microelectromech. Syst. 2010, 19, 396–401. [Google Scholar] [CrossRef]
- Mills, A.; Aissaoui, N.; Maurel, D.; Elezgaray, J.; Morvan, F.; Vasseur, J.J.; Margeat, E.; Quast, R.B.; Lai Kee-Him, J.; Saint, N.; et al. A modular spring-loaded actuator for mechanical activation of membrane proteins. Nat. Commun. 2022, 13, 3182. [Google Scholar] [CrossRef]
- Jelínek, F.; Smit, G.; Breedveld, P. Bioinspired spring-loaded biopsy harvester—Experimental prototype design and feasibility tests. J. Med. Device 2014, 8, 015002. [Google Scholar] [CrossRef]
- Hogan, N.C.; Taberner, A.J.; Jones, L.A.; Hunter, I.W. Needle-free delivery of macromolecules through the skin using controllable jet injectors. Expert Opin. Drug Deliv. 2015, 12, 1637–1648. [Google Scholar] [CrossRef] [PubMed]
- Xu, L.; Xi, L.; Zhao, Z.; Gao, J.; Li, Y. Numerical prediction of heat loss from a test ribbed rectangular channel using the conjugate calculations. Int. Commun. Heat. Mass. 2018, 96, 98–108. [Google Scholar]
- Xi, L.; Gao, J.; Xu, L.; Zhao, Z.; Ruan, Q.; Li, Y. Numerical investigation and parameter sensitivity analysis on flow and heat transfer performance of jet array impingement cooling in a quasi-leading-edge channel. Aerospace 2022, 9, 87. [Google Scholar] [CrossRef]
- Gokhan, S.; Muhsin, K. Numerical analysis of airflow, heat transfer, moisture transport and thermal comfort in a room heated by two-panel radiators. Energy Build. 2011, 43, 137–146. [Google Scholar]
- Zhang, Y.; Liu, Y.; Zhang, Y.; Wang, W.; Han, Y. Hypersonic boundary layer flow and heat transfer analysis of compressible fluid over a permeable wall with gas injection. Int. Commun. Heat. Mass. 2021, 129, 105688. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).