A Sliding Mode Control-Based Guidance Law for a Two-Dimensional Orbit Transfer with Bounded Disturbances
Abstract
:1. Introduction
2. Problem Description and Mathematical Model
3. State-Feedback Control Design
Disturbance Modeling
4. Case of an Unperturbed System
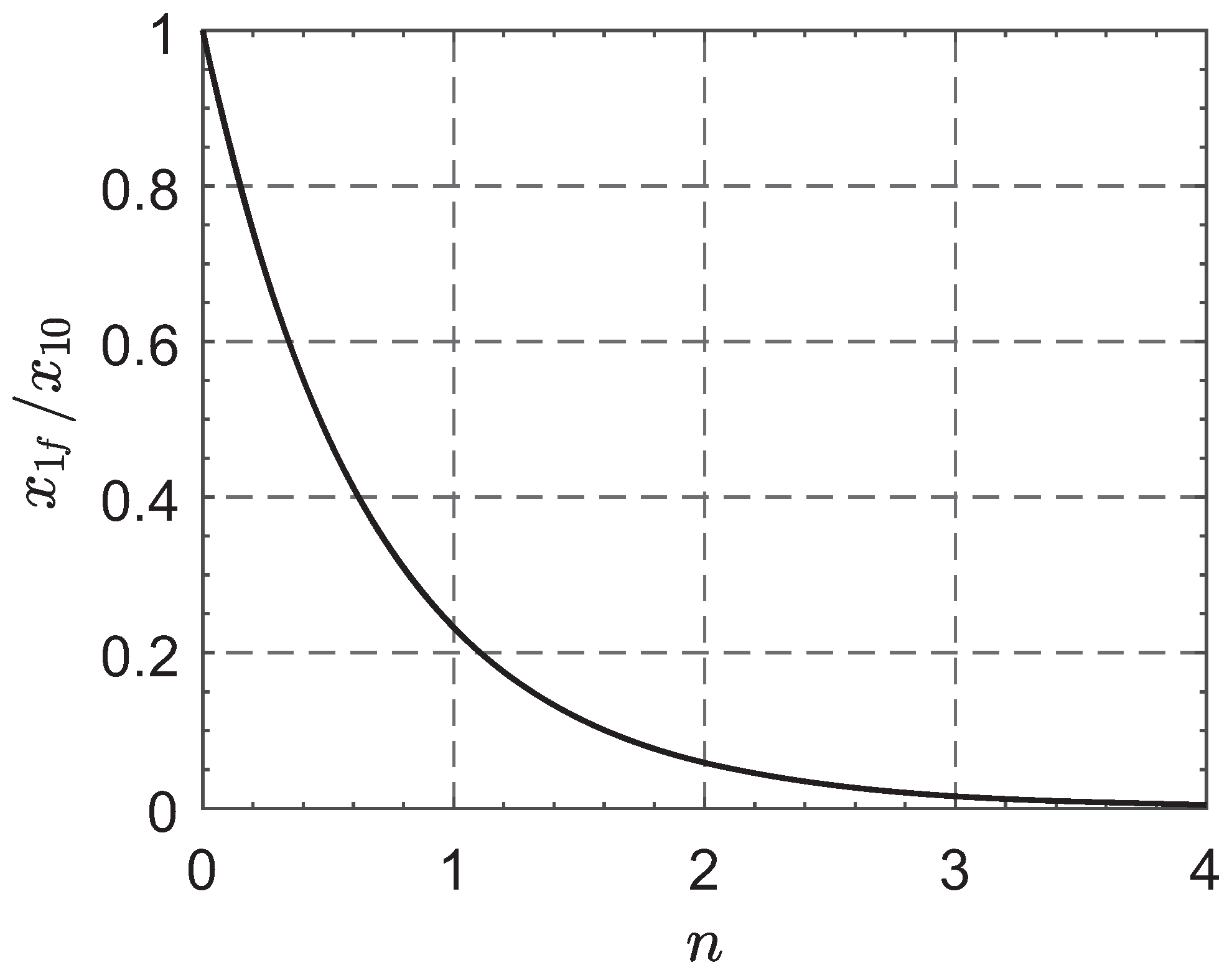
4.1. The -Variation of Tracking Errors and Controls
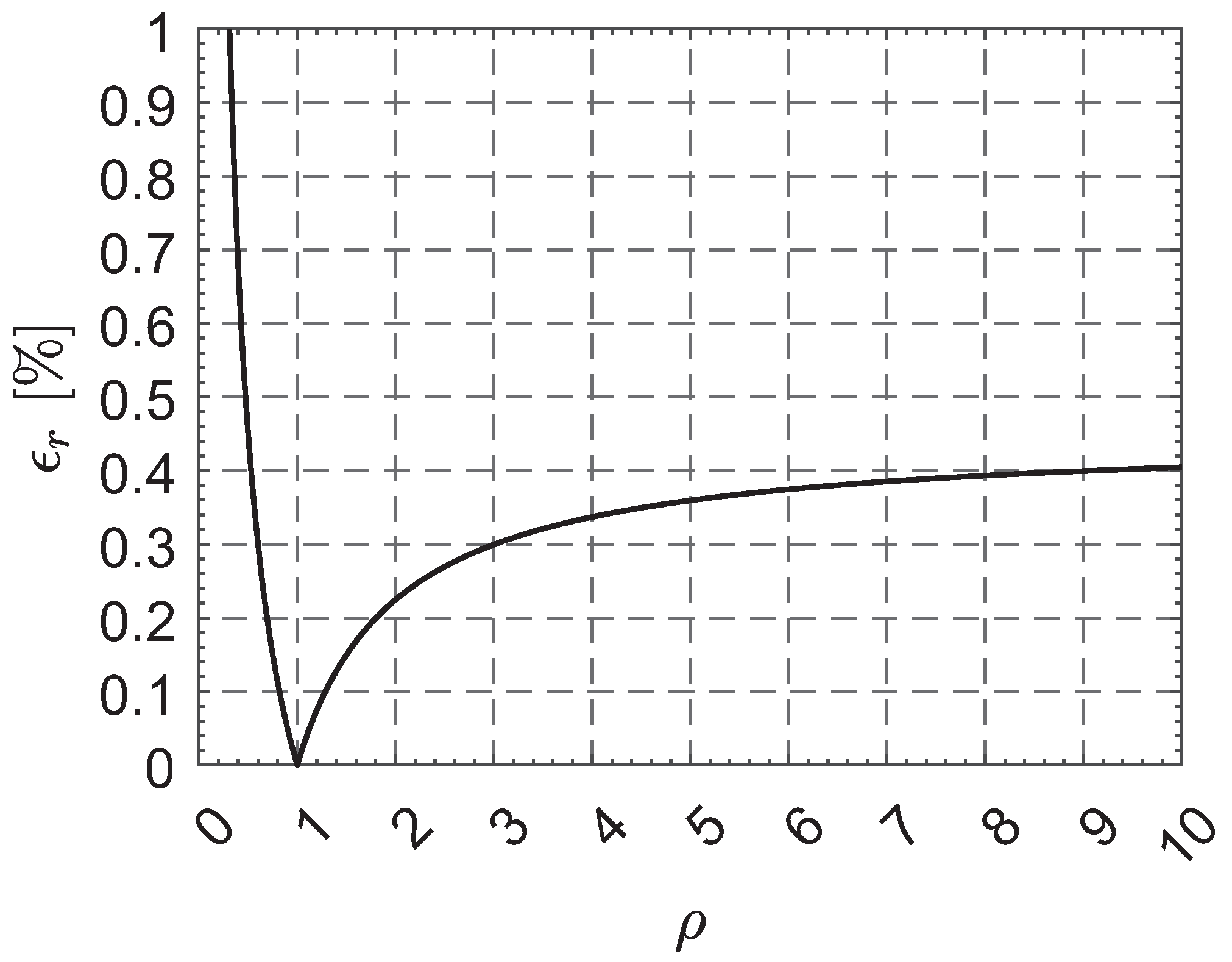
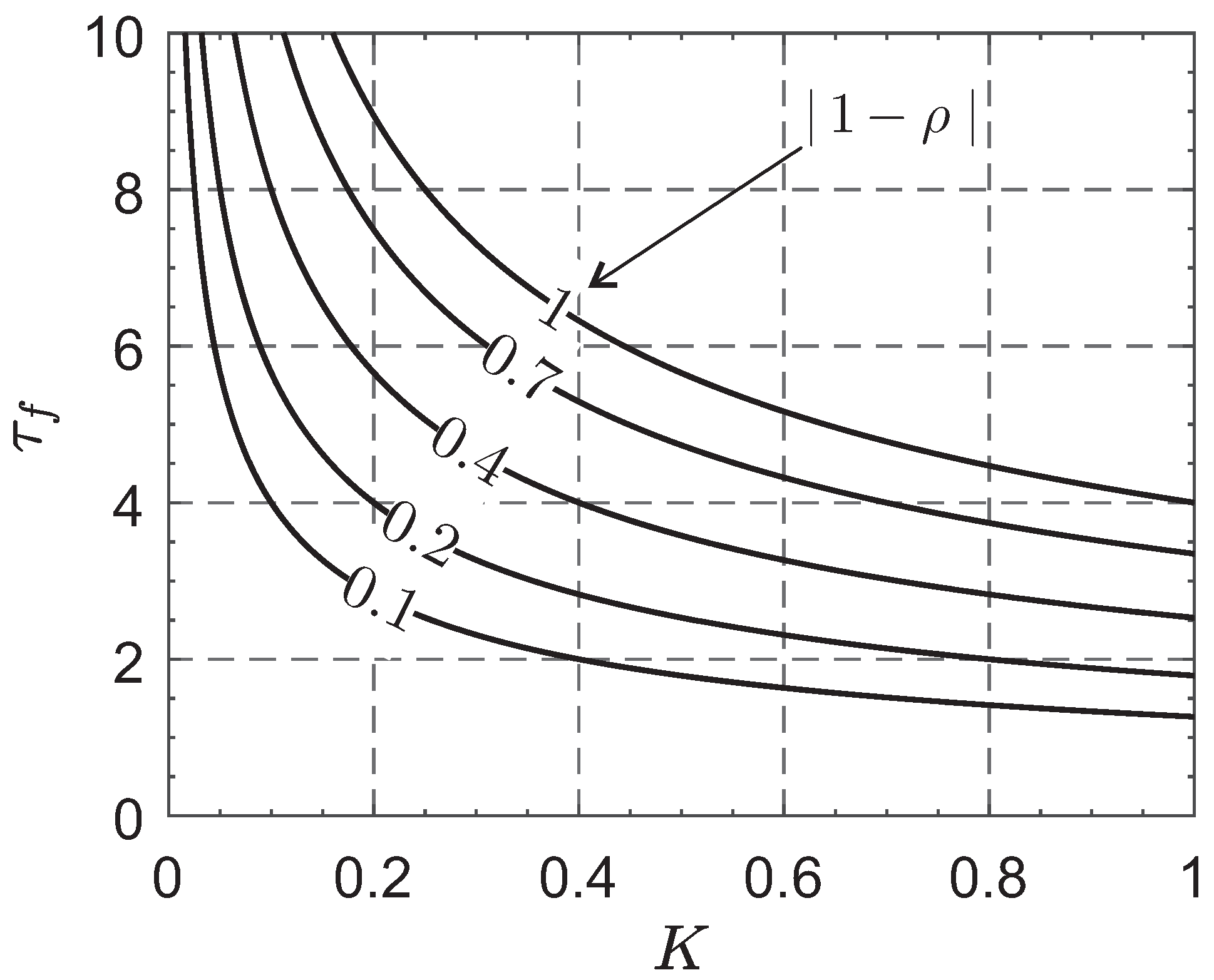
4.2. Control Parameter Selection
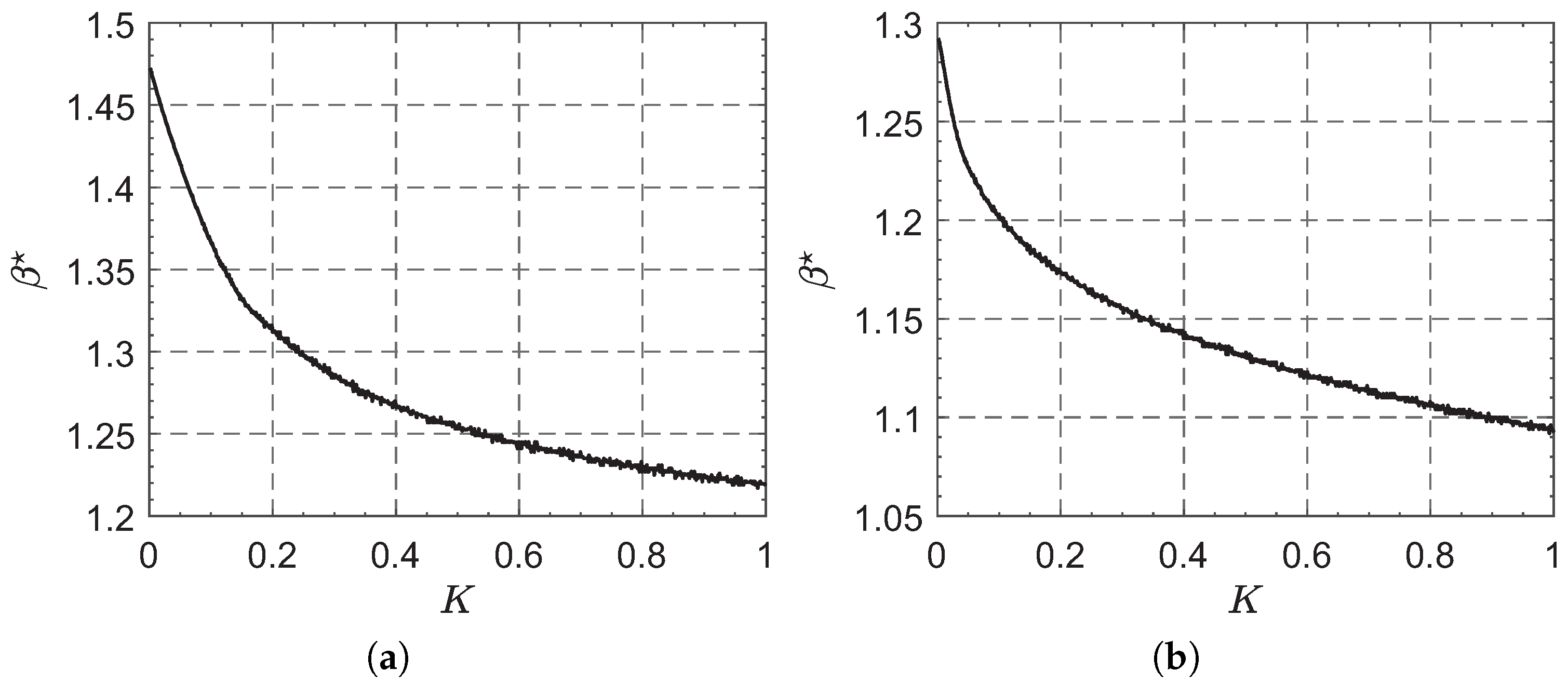
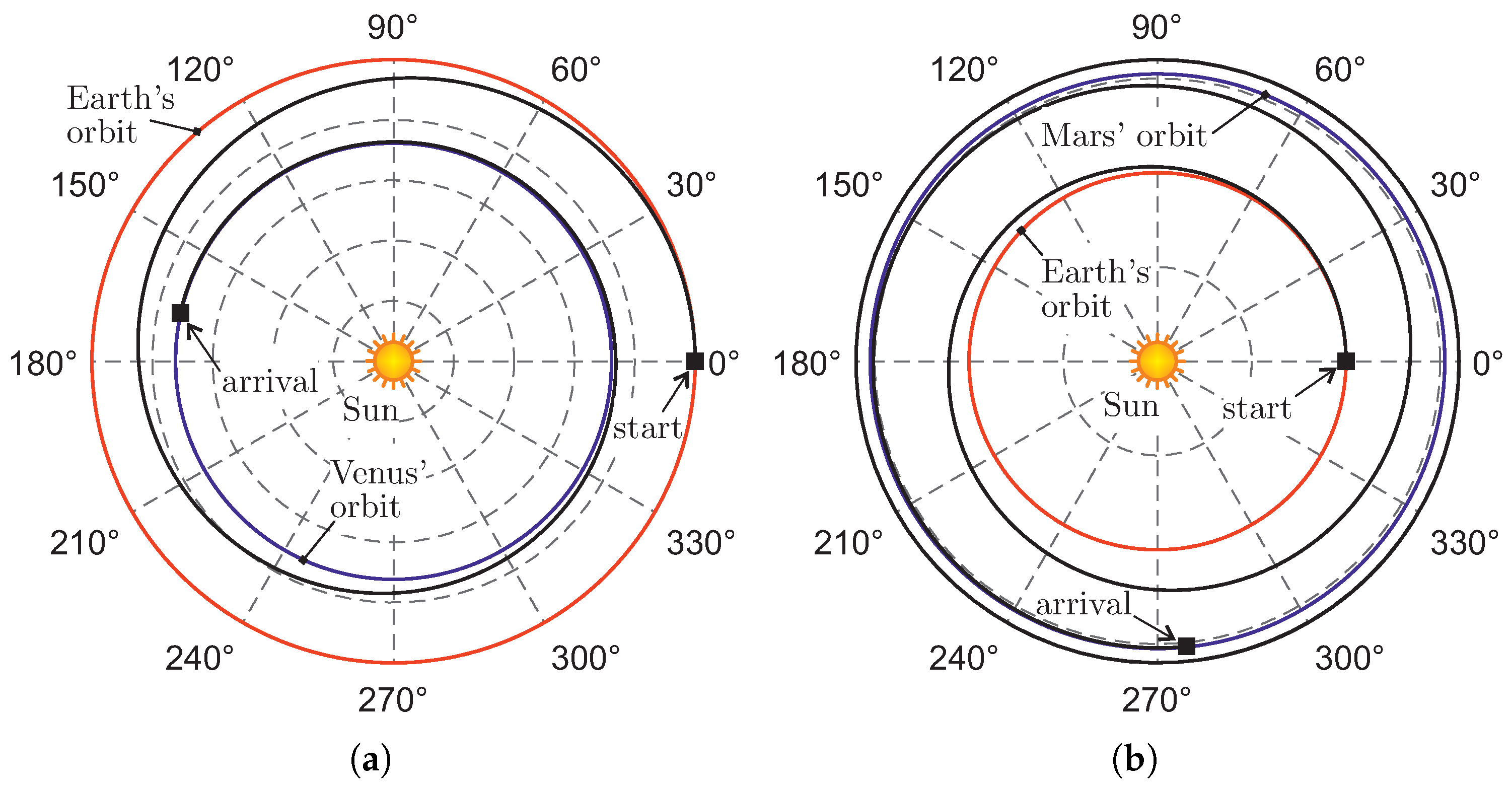
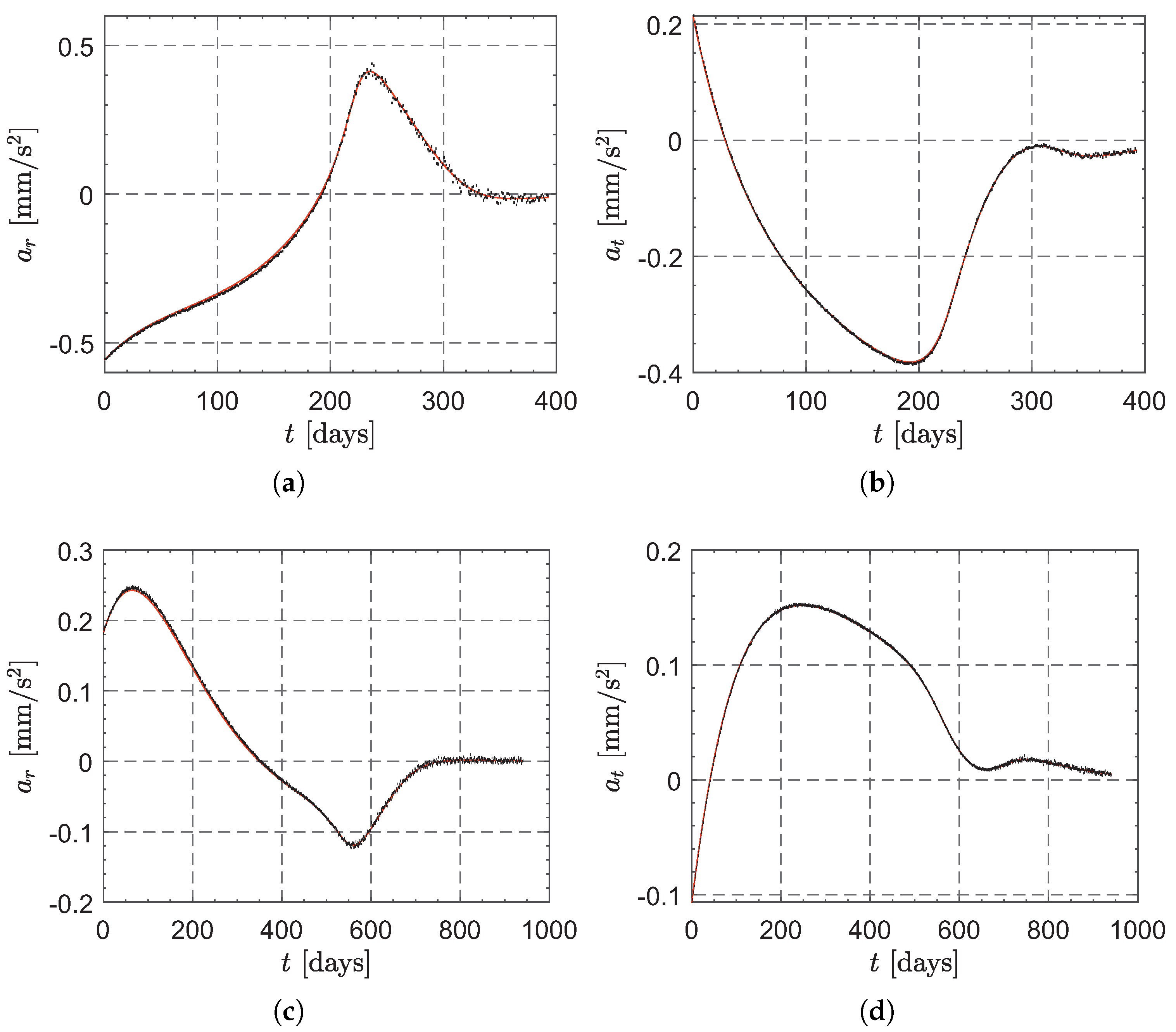
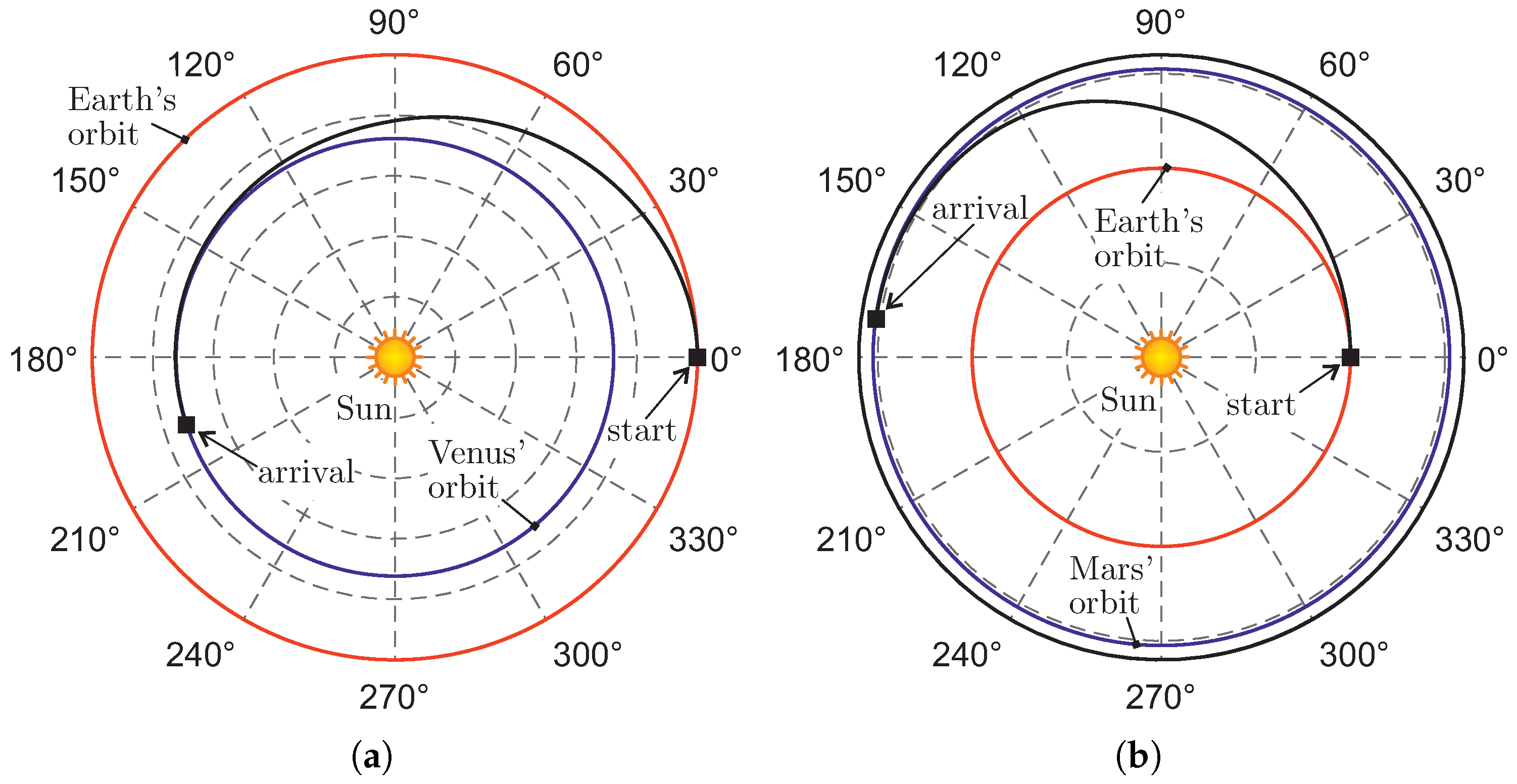
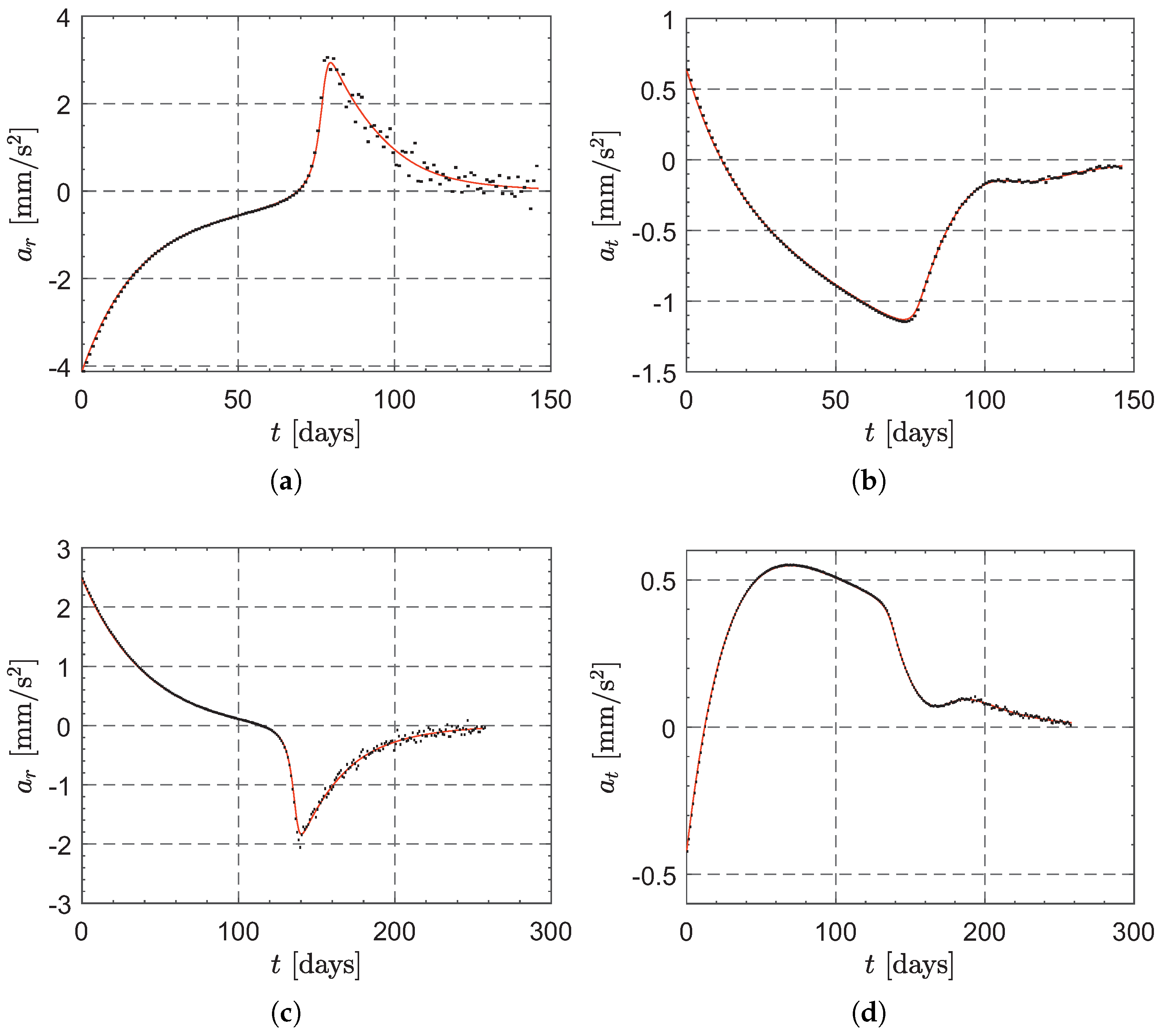
5. Numerical Simulations and Mission Application
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Notation
| a | propulsive acceleration magnitude |
| radial component of the propulsive acceleration | |
| transverse component of the propulsive acceleration | |
| c | speed of approach to when |
| radial component of the disturbance acceleration | |
| maximum of , | |
| transverse disturbance acceleration, | |
| maximum of | |
| K | speed of approach to when |
| value of K corresponding to | |
| value of K that minimizes the total velocity change | |
| n | dimensionless positive parameter; see Equation (59) |
| P | primary body center of mass |
| r | orbital radius |
| s | linear combination of ; see Equation (22) |
| S | spacecraft center of mass |
| sigmoid-like function; see Equation (35) | |
| t | time |
| u | magnitude of command signal |
| dimensionless value of | |
| dimensionless value of | |
| radial velocity component | |
| transverse velocity component | |
| X | normally distributed random number |
| dimensionless tracking errors along | |
| dimensionless radial component of the disturbance acceleration | |
| maximum magnitude of | |
| dimensionless transverse component of the disturbance acceleration | |
| maximum magnitude of | |
| thrust angle | |
| ratio of to | |
| auxiliary parameter; see Equation (27) | |
| dimensionless velocity change | |
| auxiliary parameter; see Equation (30) | |
| percentage error in orbital radius | |
| polar angle | |
| convergence rate of and | |
| value of corresponding to | |
| primary body gravitational parameter | |
| ratio of to | |
| specific standard deviation | |
| dimensionless time | |
| dimensionless Hohmann transfer time | |
| time to reach the condition | |
| time to reach the condition | |
| Subscripts | |
| 0 | initial |
| f | final |
| Superscripts | |
| · | derivative with respect to t |
| derivative with respect to | |
| ★ | design value |
| ∼ | measured |
References
- Slotine, J.J.E.; Li, W. Applied Nonlinear Control; Prentice-Hall: Englewood Cliffs, NJ, USA, 1991; Chapter 7; pp. 276–310. [Google Scholar]
- Gambhire, S.J.; Kishore, D.R.; Londhe, P.S.; Pawar, S.N. Review of sliding mode based control techniques for control system applications. Int. J. Dyn. Control 2020, 9, 363–378. [Google Scholar] [CrossRef]
- Qureshi, M.S.; Das, S.; Swarnkar, P.; Gupta, S. Design and Implementation of Sliding Mode Control for Uncertain Systems. Mater. Today Proc. 2018, 5, 4299–4308. [Google Scholar] [CrossRef]
- Hung, J.; Gao, W.; Hung, J. Variable structure control: A survey. IEEE Trans. Ind. Electron. 1993, 40, 2–22. [Google Scholar] [CrossRef]
- Utkin, V. Sliding mode control design principles and applications to electric drives. IEEE Trans. Ind. Electron. 1993, 40, 23–36. [Google Scholar] [CrossRef]
- Chen, T.; Shan, J.; Wen, H.; Xu, S. Review of attitude consensus of multiple spacecraft. Astrodynamics 2022, 6, 329–356. [Google Scholar] [CrossRef]
- Wu, B.; Wang, D.; Poh, E.K. Decentralized sliding-mode control for spacecraft attitude synchronization under actuator failures. Acta Astronaut. 2014, 105, 333–343. [Google Scholar] [CrossRef]
- Massey, T.; Shtessel, Y. Continuous Traditional and High-Order Sliding Modes for Satellite Formation Control. J. Guid. Control Dyn. 2005, 28, 826–831. [Google Scholar] [CrossRef]
- Ma, Z.; Sun, G. Adaptive sliding mode control of tethered satellite deployment with input limitation. Acta Astronaut. 2016, 127, 67–75. [Google Scholar] [CrossRef]
- Liu, S.; Huo, W. Terminal sliding mode control for space rendezvous and docking. In Proceedings of the International Conference on Computational Intelligence and Communication Networks (CICN), Jabalpur, India, 12–14 December 2015. [Google Scholar] [CrossRef]
- Dong, J.; Li, C.; Jiang, B.; Sun, Y. Fixed-time nonsingular terminal sliding mode control for spacecraft rendezvous. In Proceedings of the 29th Chinese Control and Decision Conference (CCDC), Chongqing, China, 28–30 May 2017. [Google Scholar] [CrossRef]
- Capello, E.; Punta, E.; Dabbene, F.; Guglieri, G.; Tempo, R. Sliding-mode control strategies for rendezvous and docking maneuvers. J. Guid. Control Dyn. 2017, 40, 1481–1488. [Google Scholar] [CrossRef]
- Kasaeian, S.A.; Assadian, N.; Ebrahimi, M. Sliding mode predictive guidance for terminal rendezvous in eccentric orbits. Acta Astronaut. 2017, 140, 142–155. [Google Scholar] [CrossRef]
- Li, Q.; Yuan, J.; Wang, H. Sliding mode control for autonomous spacecraft rendezvous with collision avoidance. Acta Astronaut. 2018, 151, 743–751. [Google Scholar] [CrossRef]
- Bassetto, M.; Niccolai, L.; Boni, L.; Mengali, G.; Quarta, A.A.; Circi, C.; Pizzurro, S.; Pizzarelli, M.; Pellegrini, R.C.; Cavallini, E. Sliding mode control for attitude maneuvers of Helianthus solar sail. Acta Astronaut. 2022, 198, 100–110. [Google Scholar] [CrossRef]
- Aliasi, G.; Mengali, G.; Quarta, A.A. Artificial Lagrange points for solar sail with electrochromic material panels. J. Guid. Control Dyn. 2013, 36, 1544–1550. [Google Scholar] [CrossRef]
- Boni, L.; Bassetto, M.; Niccolai, L.; Mengali, G.; Quarta, A.A.; Circi, C.; Pellegrini, R.C.; Cavallini, E. Structural response of Helianthus solar sail during attitude maneuvers. Aerosp. Sci. Technol. 2023, 133, 108152. [Google Scholar] [CrossRef]
- Quarta, A.A.; Mengali, G. Solar sail orbit raising with electro-optically controlled diffractive film. Appl. Sci. 2023, 13, 7078. [Google Scholar] [CrossRef]
- Wang, X.; Roy, S.; Farì, S.; Baldi, S. Adaptive Vector Field Guidance Without a Priori Knowledge of Course Dynamics and Wind. IEEE/ASME Trans. Mechatron. 2022, 27, 4597–4607. [Google Scholar] [CrossRef]
- Bai, Y.; Yan, T.; Fu, W.; Li, T.; Huang, J. Robust Adaptive Composite Learning Integrated Guidance and Control for Skid-to-Turn Interceptors Subjected to Multiple Uncertainties and Constraints. Actuators 2023, 12, 243. [Google Scholar] [CrossRef]
- Feng, C.; Chen, W.; Shao, M.; Ni, S. Trajectory Tracking and Adaptive Fuzzy Vibration Control of Multilink Space Manipulators with Experimental Validation. Actuators 2023, 12, 138. [Google Scholar] [CrossRef]
- Xie, R.; Dempster, A.G. An on-line deep learning framework for low-thrust trajectory optimisation. Aerosp. Sci. Technol. 2021, 118, 107002. [Google Scholar] [CrossRef]
- Peloni, A.; Rao, A.V.; Ceriotti, M. Automated Trajectory Optimizer for Solar Sailing (ATOSS). Aerosp. Sci. Technol. 2018, 72, 465–475. [Google Scholar] [CrossRef]
- Patterson, M.J.; Benson, S.W. NEXT ion propulsion system development status and performance. In Proceedings of the 43rd AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, Cincinnati, OH, USA, 8–11 July 2007. Paper AIAA-2007-5199. [Google Scholar]
- Battin, R. An Introduction to the Mathematics and Methods of Astrodynamics; AIAA education series; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 1999; Chapter 8; pp. 408–418. [Google Scholar] [CrossRef]
- Edwards, C.; Spurgeon, S.K. Sliding Mode Control: Theory and Applications; CRC Press: Boca Raton, FL, USA, 1998; Chapter 1; pp. 15–17. [Google Scholar]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bassetto, M.; Mengali, G.; Abu Salem, K.; Palaia, G.; Quarta, A.A. A Sliding Mode Control-Based Guidance Law for a Two-Dimensional Orbit Transfer with Bounded Disturbances. Actuators 2023, 12, 444. https://doi.org/10.3390/act12120444
Bassetto M, Mengali G, Abu Salem K, Palaia G, Quarta AA. A Sliding Mode Control-Based Guidance Law for a Two-Dimensional Orbit Transfer with Bounded Disturbances. Actuators. 2023; 12(12):444. https://doi.org/10.3390/act12120444
Chicago/Turabian StyleBassetto, Marco, Giovanni Mengali, Karim Abu Salem, Giuseppe Palaia, and Alessandro A. Quarta. 2023. "A Sliding Mode Control-Based Guidance Law for a Two-Dimensional Orbit Transfer with Bounded Disturbances" Actuators 12, no. 12: 444. https://doi.org/10.3390/act12120444
APA StyleBassetto, M., Mengali, G., Abu Salem, K., Palaia, G., & Quarta, A. A. (2023). A Sliding Mode Control-Based Guidance Law for a Two-Dimensional Orbit Transfer with Bounded Disturbances. Actuators, 12(12), 444. https://doi.org/10.3390/act12120444





