Fault-Estimation Design Based on an Iterative Learning Scheme for Interconnected Multi-Flexible Manipulator Systems with Arbitrary Initial Value
Abstract
:1. Introduction
- (1)
- To address the problem of arbitrary initial value offsets in each subsystem of an interconnected multi-flexible manipulator system, a novel initial value reconstruction method based on an iterative learning strategy is proposed, which eliminates the adverse effects induced by arbitrary initial value offsets within interconnected multi-flexible manipulator systems.
- (2)
- Considering the interconnections among the flexible manipulator subsystems, an iterative learning fault-estimation method is designed. This method can quickly and accurately estimate the fault signals occurring in each subsystem.
2. Problem Formulation and Preliminaries
2.1. Interconnected Nonlinear System
2.2. Fault-Estimation Design Based on Iterative Learning Control
2.3. Problem Analysis
- (1)
- How to track the fault signal well?
- (2)
- How to eliminate the effect of initial value changes?
3. Convergence Analysis
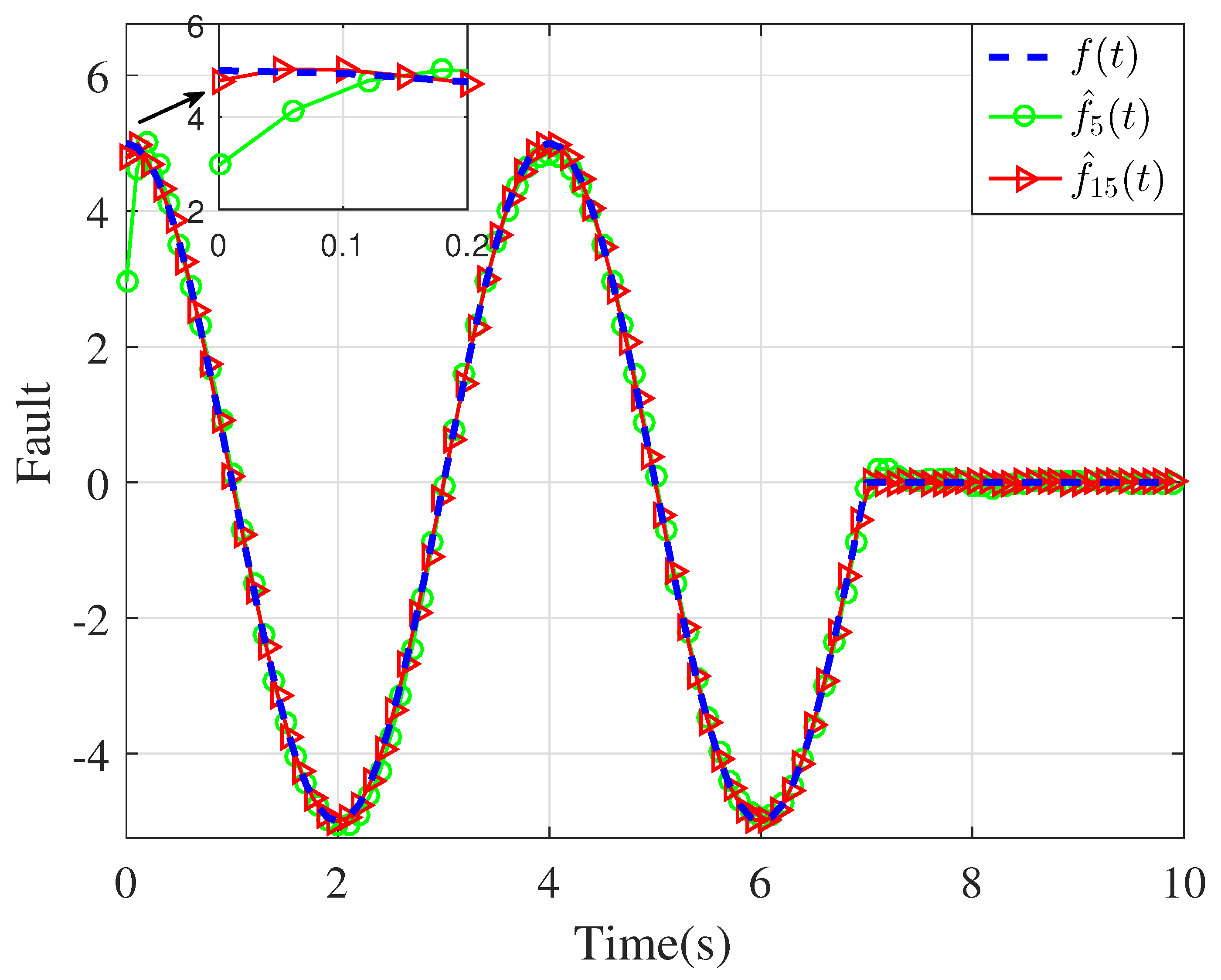
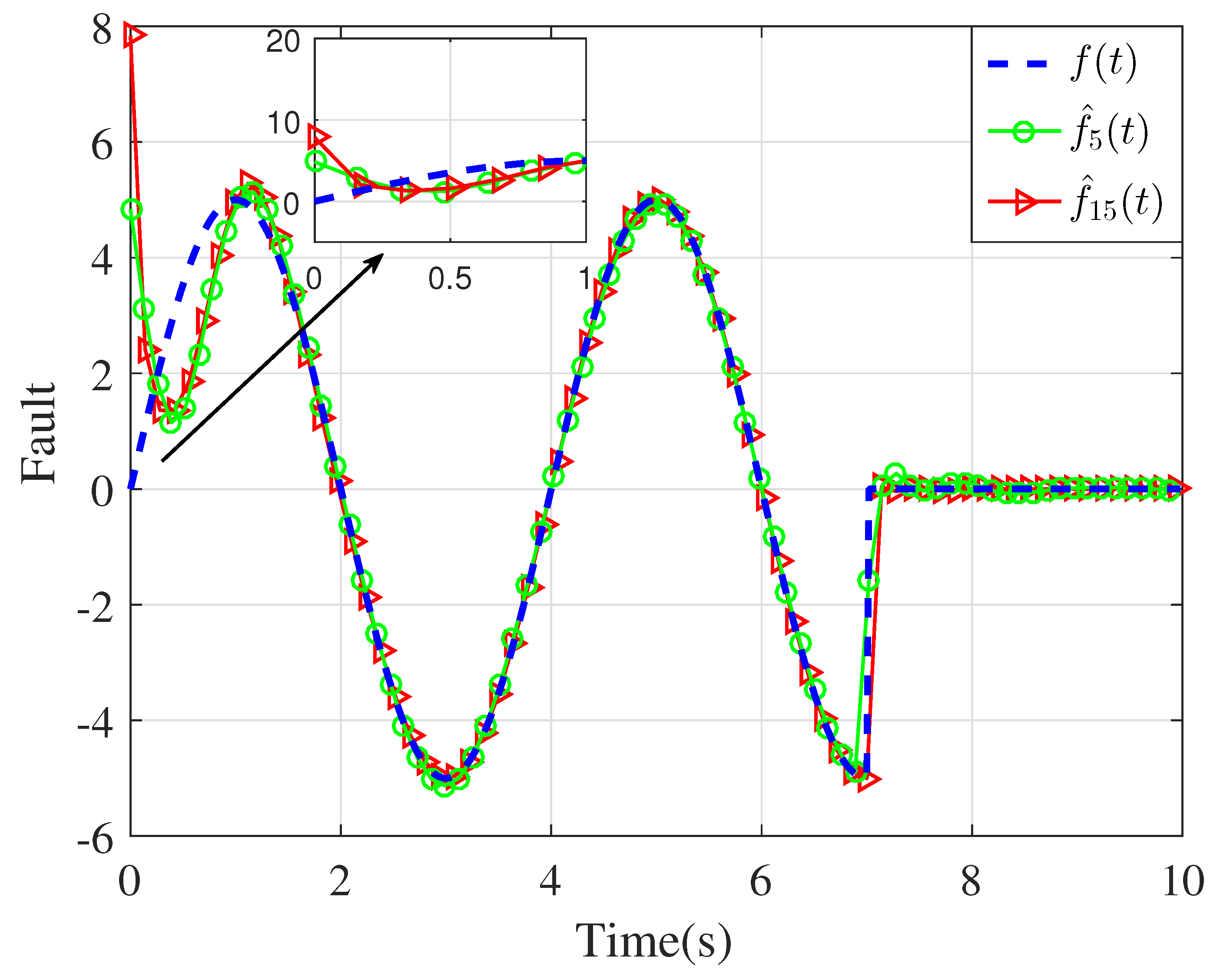
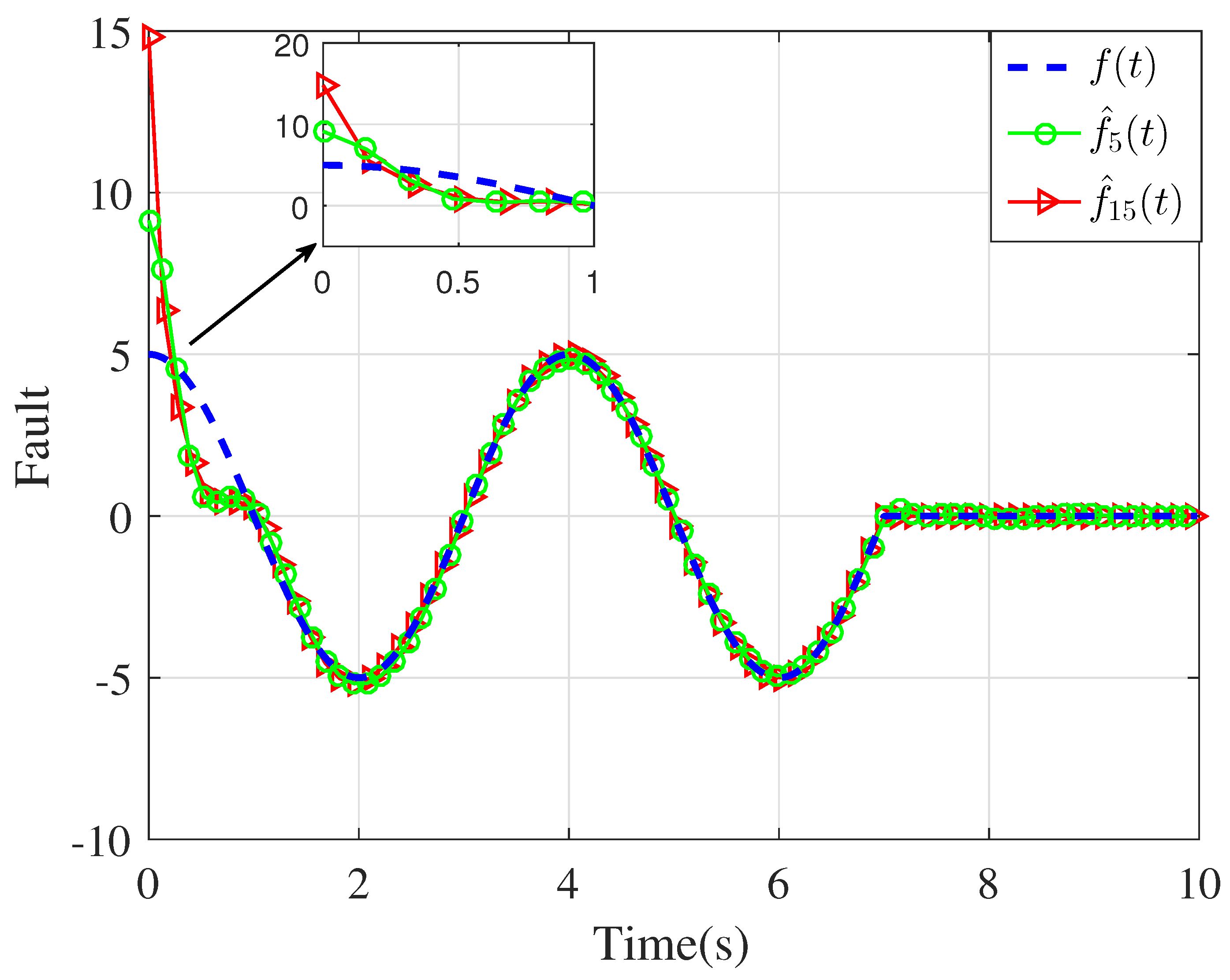
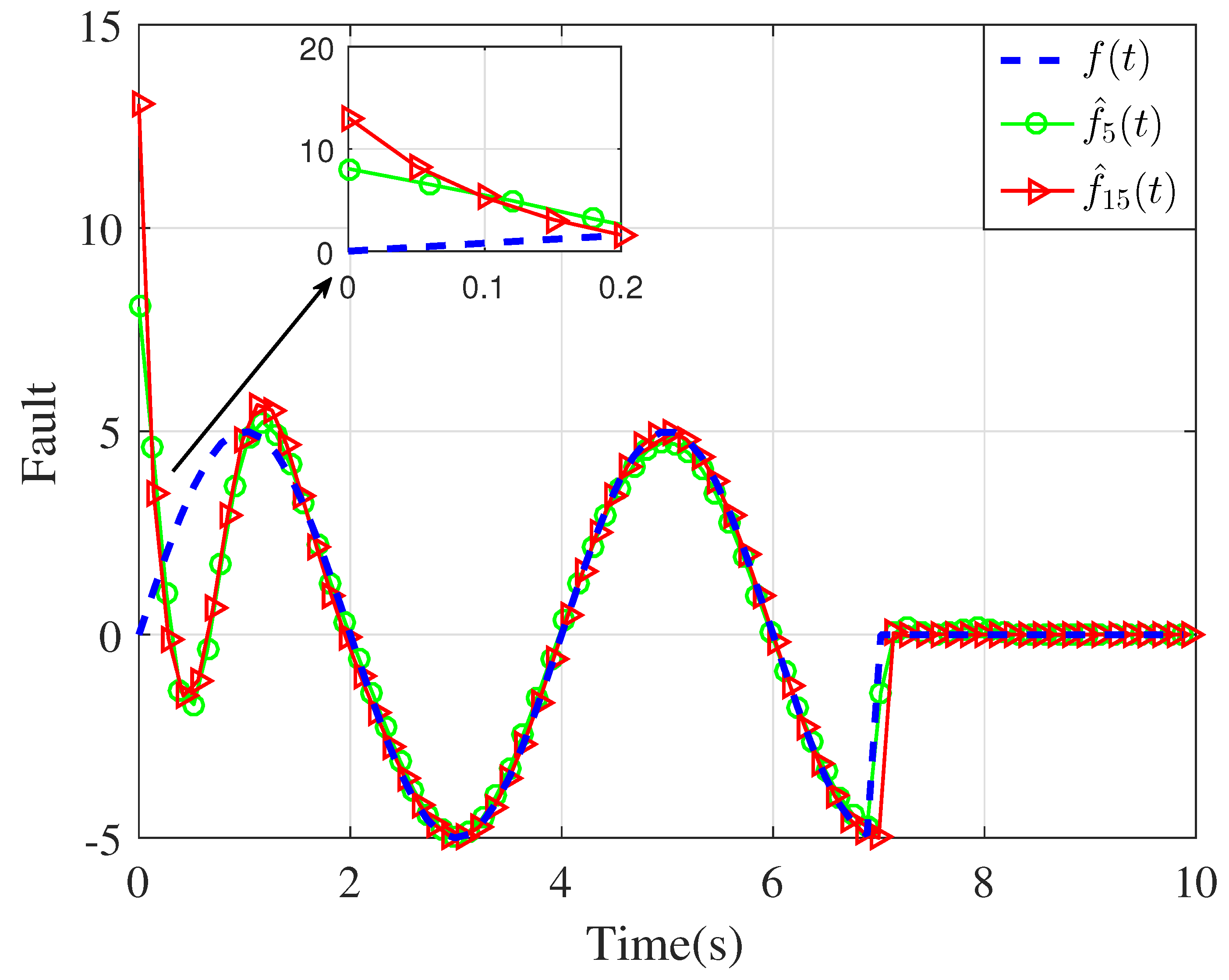
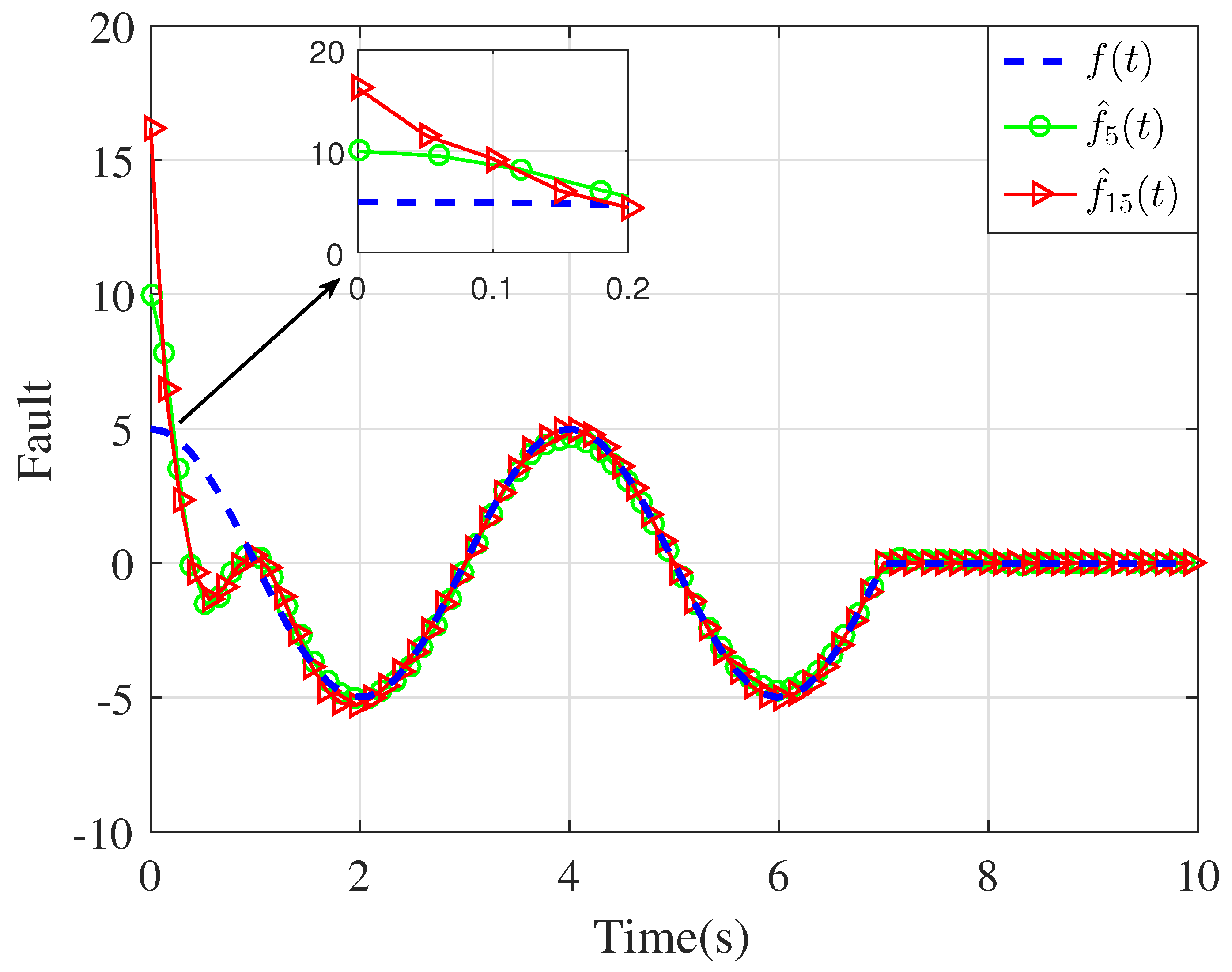
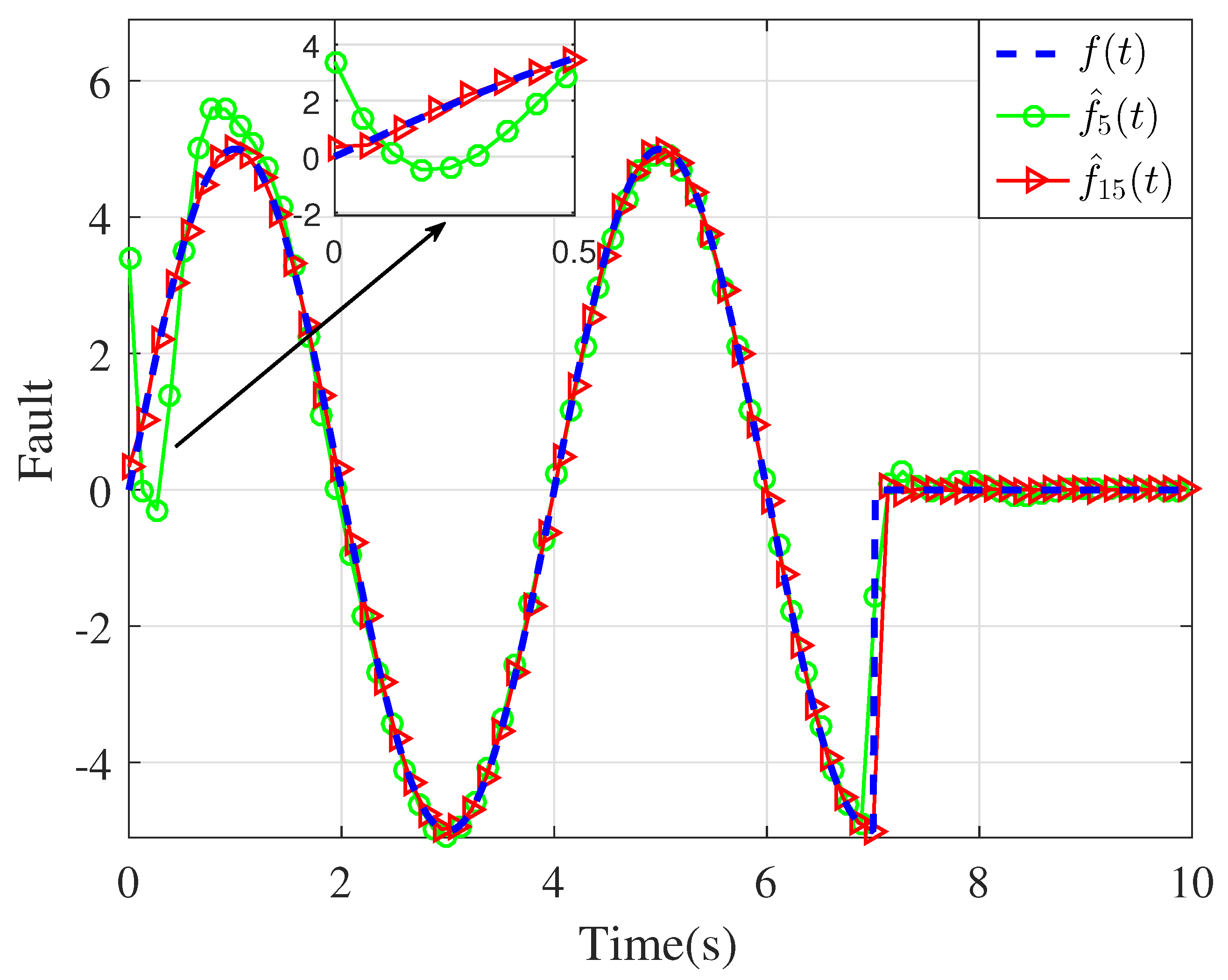
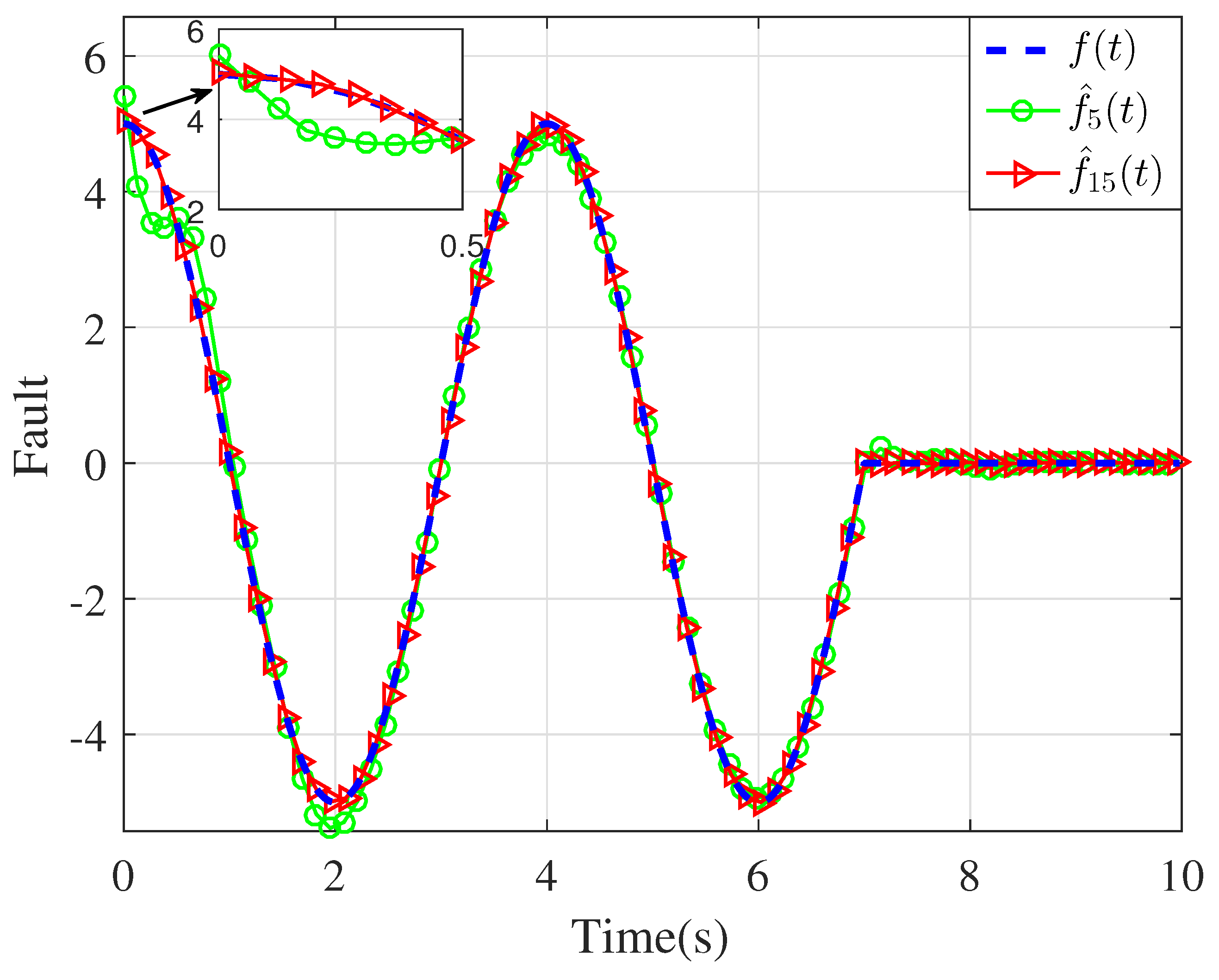
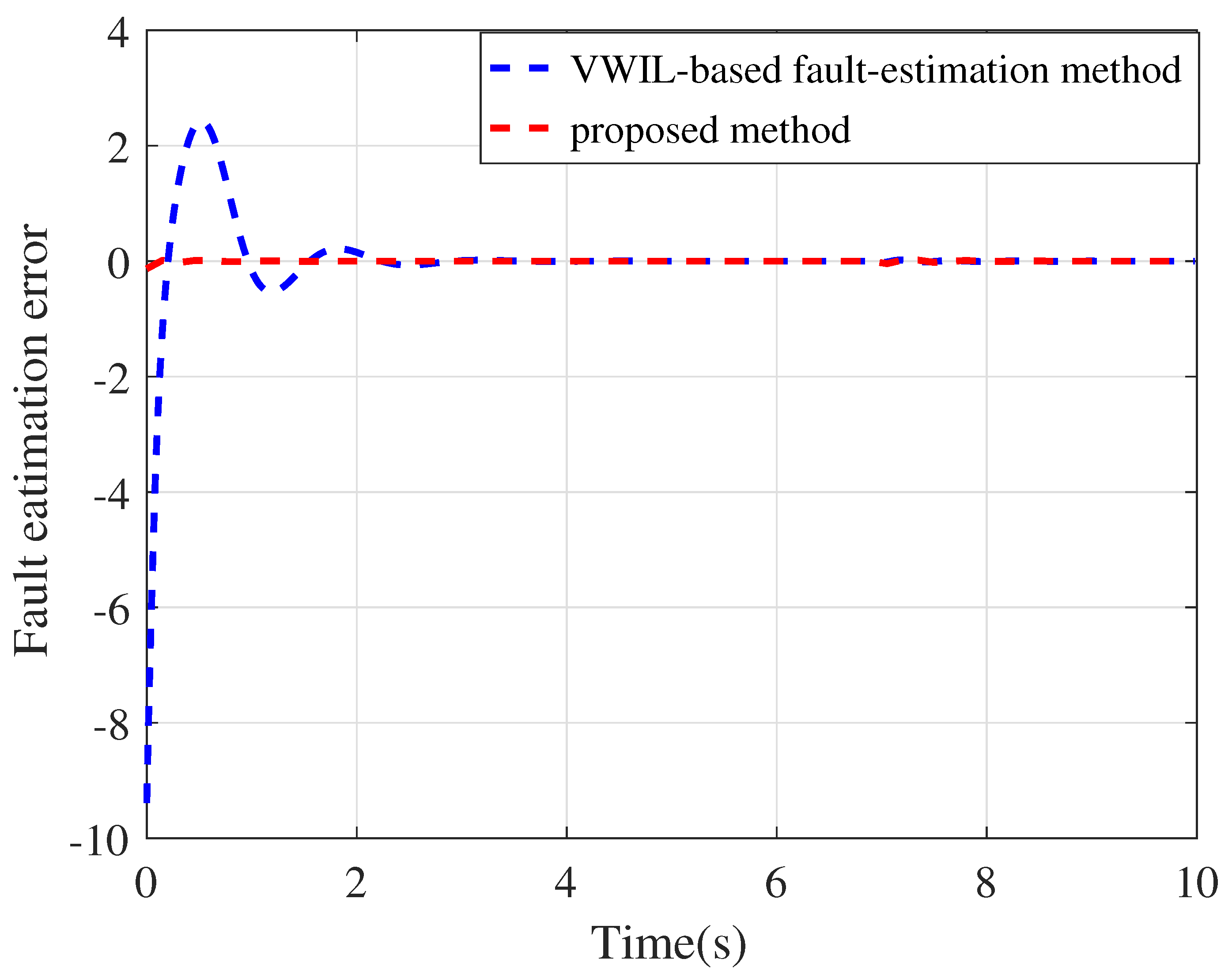
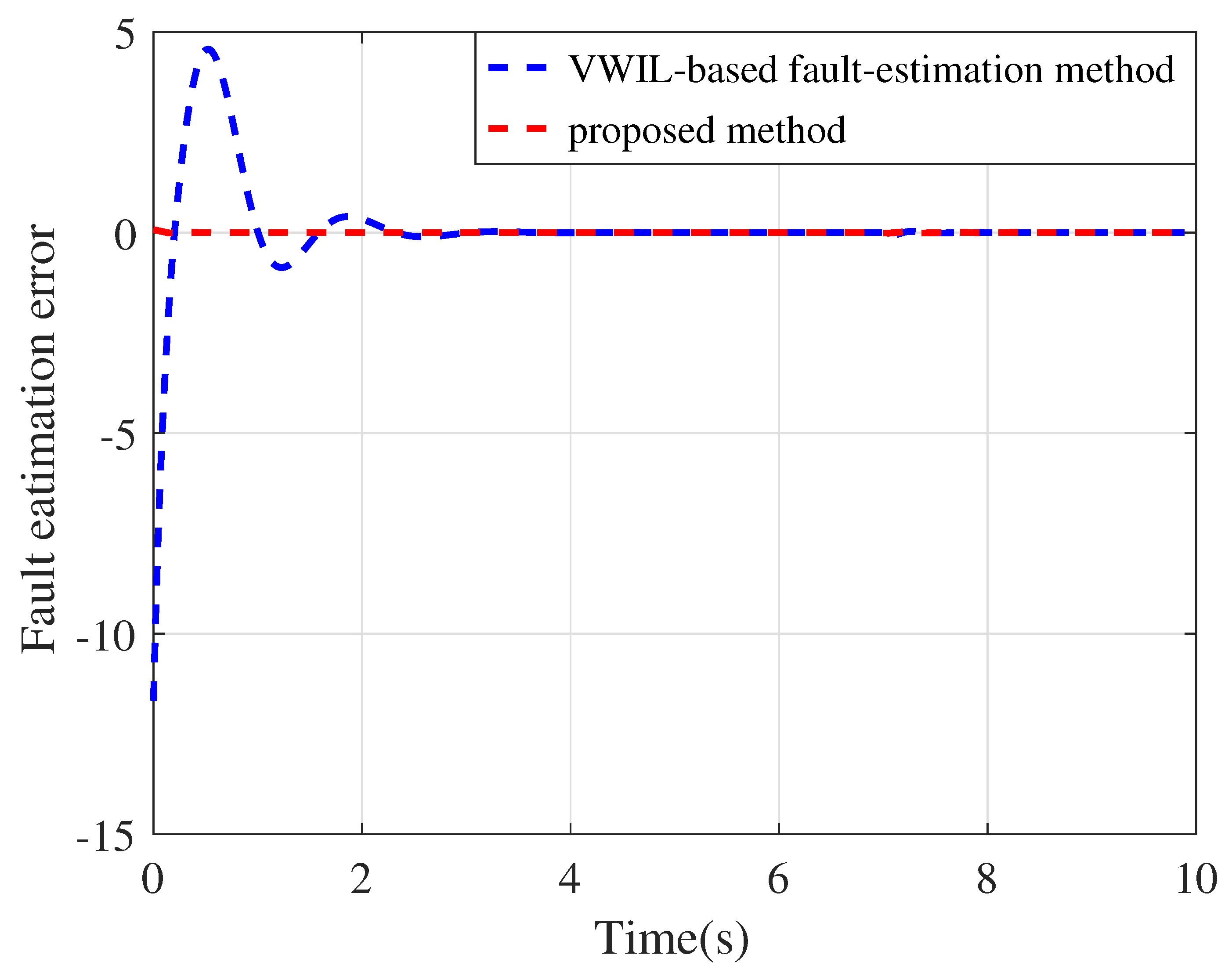
4. Simulation Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mu, Y.; Zhang, H.; Yan, Y.; Xie, X. Distributed observer-based robust fault estimation design for discrete-time interconnected systems with disturbances. IEEE Trans. Cybern. 2023, 53, 6737–6747. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Yan, J.; Yang, G. Adaptive fault estimation for T-S fuzzy interconnected systems based on persistent excitation condition via reference signals. IEEE Trans. Cybern. 2018, 49, 2822–2834. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Yang, H.; Jiang, B. Fault estimation and accommodation of fractional-order nonlinear, switched, and interconnected systems. IEEE Trans. Cybern. 2020, 52, 1443–1453. [Google Scholar] [CrossRef] [PubMed]
- Zhu, F.; Shan, Y.; Zhang, J.; Wang, F. Observer-based fault reconstructions and fault-tolerant control designs for uncertain switched systems with both actuator and sensor faults. IET Control Theory Appl. 2020, 14, 2017–2019. [Google Scholar] [CrossRef]
- Shan, Y.; Zhu, F. Interval observer fault tolerant control strategy with fault estimation and compensation. Asian J. Control 2022, 24, 895–906. [Google Scholar] [CrossRef]
- Xu, S.; Wang, L.; Feng, L.; Yang, X.; Chai, Y.; Du, H.; Zheng, W. Self-Correcting Iterative Learning-Based Fault Estimation for Parabolic Distributed Parameter Systems. IEEE Trans. Circuits Syst. II Express Briefs 2023, 1–5. [Google Scholar] [CrossRef]
- Zhang, K.; Jiang, B.; Chen, M.; Yan, X. Distributed fault estimation and fault-tolerant control of interconnected systems. IEEE Trans. Cybern. 2019, 51, 1230–1240. [Google Scholar] [CrossRef]
- Zhang, K.; Jiang, B.; Shi, P. Distributed fault estimation observer design with adjustable parameters for a class of nonlinear interconnected systems. IEEE Trans. Cybern. 2018, 49, 4219–4228. [Google Scholar] [CrossRef]
- Makni, S.; Bouattour, M.; El Hajjaji, A.; Chaabane, M. Robust fault estimation and fault-tolerant tracking control for uncertain Takagi–Sugeno fuzzy systems: Application to single link manipulator. Int. J. Adapt. Control Signal. Process. 2021, 35, 846–876. [Google Scholar] [CrossRef]
- Che, J.; Zhu, Y.; Zhou, D. Hidden Markov model-based robust H∞ fault estimation for Markov switching systems with application to a single-link robot arm. Asian J. Control 2021, 23, 2227–2238. [Google Scholar] [CrossRef]
- Wang, L.; Shen, Y.; Li, B.; Yu, J.; Zhang, R.; Gao, F. Hybrid iterative learning fault-tolerant guaranteed cost control design for multi-phase batch processes. Can. J. Chem. Eng. 2017, 96, 521–530. [Google Scholar] [CrossRef]
- Tao, H.; Paszke, W.; Rogers, E.; Yang, H.; Galkowski, K. Iterative learning fault-tolerant control for differential time-delay batch processes in finite frequency domains. J. Process Control 2017, 56, 112–128. [Google Scholar] [CrossRef]
- Feng, L.; Xu, S.; Chai, Y.; Zhang, K. Iterative learning scheme-based fault estimation design for nonlinear systems with varying trial lengths and specified constraints. Int. J. Robust Nonlinear Control 2018, 28, 4850–4864. [Google Scholar] [CrossRef]
- Cao, W.; Cong, W.; Sun, M. Iterative learning based fault detection and estimation in nonlinear systems. J. Syst. Eng. Electron. 2012, 23, 419–424. [Google Scholar] [CrossRef]
- Li, L.; Yao, L.; Wang, H.; Gao, Z. Iterative learning fault diagnosis and fault tolerant control for stochastic repetitive systems with Brownian motion. ISA Trans. 2022, 121, 171–179. [Google Scholar] [CrossRef] [PubMed]
- Zhou, F.; Wang, Y. Iterative learning control for fractional order nonlinear system with initial shift. Nonlinear Dyn. 2021, 106, 3305–3314. [Google Scholar]
- Zhao, Y.; Zhou, F.; Li, Y.; Wang, Y. A novel iterative learning path-tracking control for nonholonomic mobile robots against initial shifts. Int. J. Adv. Robot. Syst. 2017, 14, 123–140. [Google Scholar] [CrossRef]
- Li, G.; Lu, T.; Han, Y.; Xu, Z. Adaptive iterative learning control for high-order nonlinear systems with random initial state shifts. ISA Trans. 2022, 130, 205–215. [Google Scholar] [CrossRef]
- Ma, Y.; He, X.; Zhang, S.; Sun, Y.; Fu, Q. Adaptive compensation for infinite number of actuator faults and time-varying delay of a flexible manipulator system. IEEE Trans. Ind. Electron. 2022, 69, 13141–13150. [Google Scholar] [CrossRef]
- Abd Latip, S.F.; Rashid Husain, A.; Mohamed, Z.; Mohd Basri, M.A. Adaptive PID actuator fault tolerant control of single-link flexible manipulator. Trans. Inst. Meas. Control 2019, 41, 1019–1031. [Google Scholar] [CrossRef]
- Li, Y.; Tong, S.; Li, T. Fuzzy adaptive dynamic surface control for a single-link flexible-joint robot. Nonlinear Dyn. 2012, 70, 2035–2048. [Google Scholar] [CrossRef]
- Sun, L. Decentralized Adaptive Iterative Learning Control for a Class of Interconnected Systems and Applications. Ph.D. Thesis, Zhejiang University, Hangzhou, China, 2014. [Google Scholar]
- Xu, S.; Dai, H.; Feng, L.; Chen, H.; Chai, Y.; Zheng, W. Fault Estimation for Switched Interconnected Nonlinear Systems with External Disturbances via Variable Weighted Iterative Learning. IEEE Trans. Circuits Syst. II Express Briefs 2023, 70, 2011–2015. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, L.; Chen, G.; Xu, S.; Du, K. Fault-Estimation Design Based on an Iterative Learning Scheme for Interconnected Multi-Flexible Manipulator Systems with Arbitrary Initial Value. Actuators 2023, 12, 443. https://doi.org/10.3390/act12120443
Feng L, Chen G, Xu S, Du K. Fault-Estimation Design Based on an Iterative Learning Scheme for Interconnected Multi-Flexible Manipulator Systems with Arbitrary Initial Value. Actuators. 2023; 12(12):443. https://doi.org/10.3390/act12120443
Chicago/Turabian StyleFeng, Li, Guangxi Chen, Shuiqing Xu, and Kenan Du. 2023. "Fault-Estimation Design Based on an Iterative Learning Scheme for Interconnected Multi-Flexible Manipulator Systems with Arbitrary Initial Value" Actuators 12, no. 12: 443. https://doi.org/10.3390/act12120443
APA StyleFeng, L., Chen, G., Xu, S., & Du, K. (2023). Fault-Estimation Design Based on an Iterative Learning Scheme for Interconnected Multi-Flexible Manipulator Systems with Arbitrary Initial Value. Actuators, 12(12), 443. https://doi.org/10.3390/act12120443







