Integrated Development of a Topology-Optimized Compliant Mechanism for Precise Positioning
Abstract
:1. Introduction
2. Topology Optimization
| Algorithm 1 SIMP algorithm for topology optimization. SIMP Algorithm |
| Initialization: Generate mesh and boundary conditions, define material properties, initialize pseudo-density Main iteration loop: While not convergent do Finite element analysis Objective and constraints evaluation Update density End while Evaluation of results |
2.1. Boundary Conditions and Model Specifications
2.2. Topology Optimization Process
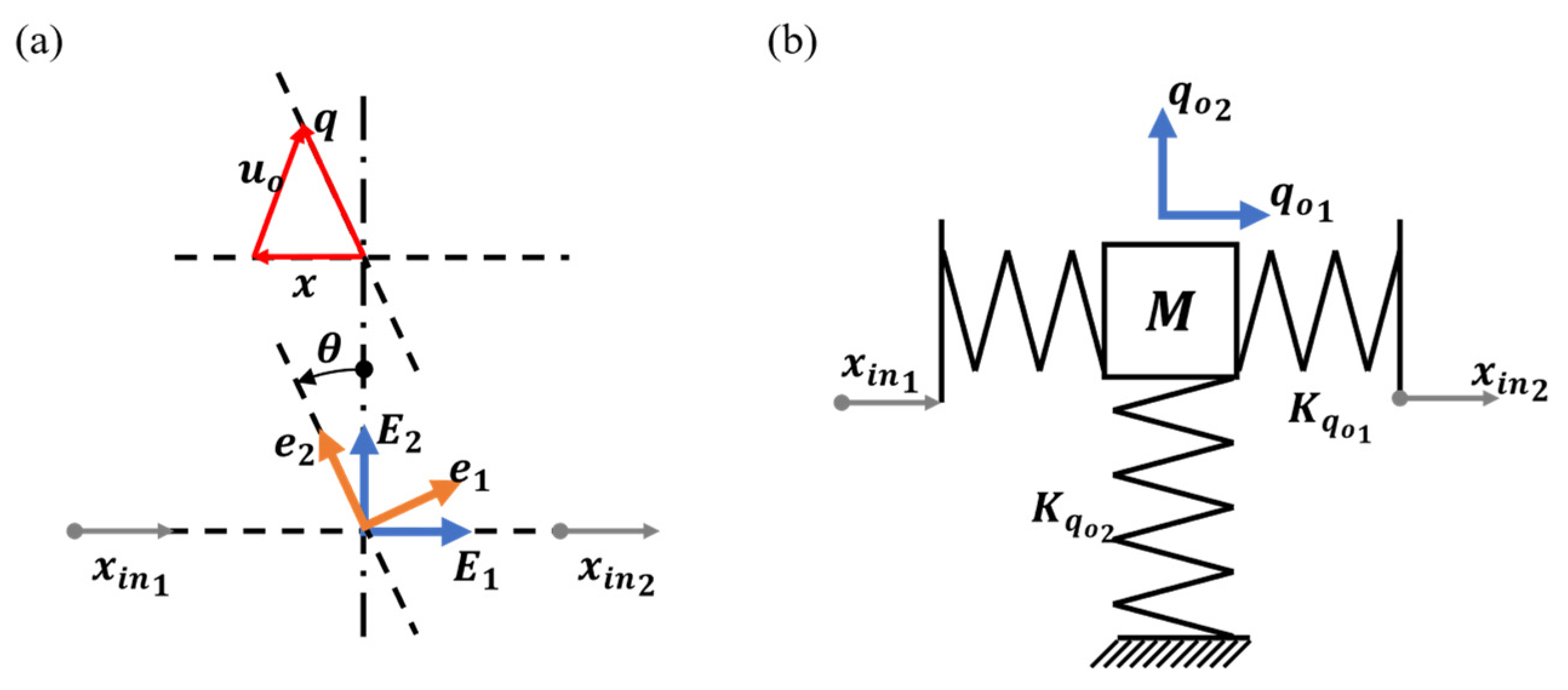
3. System Modeling and Controller Design
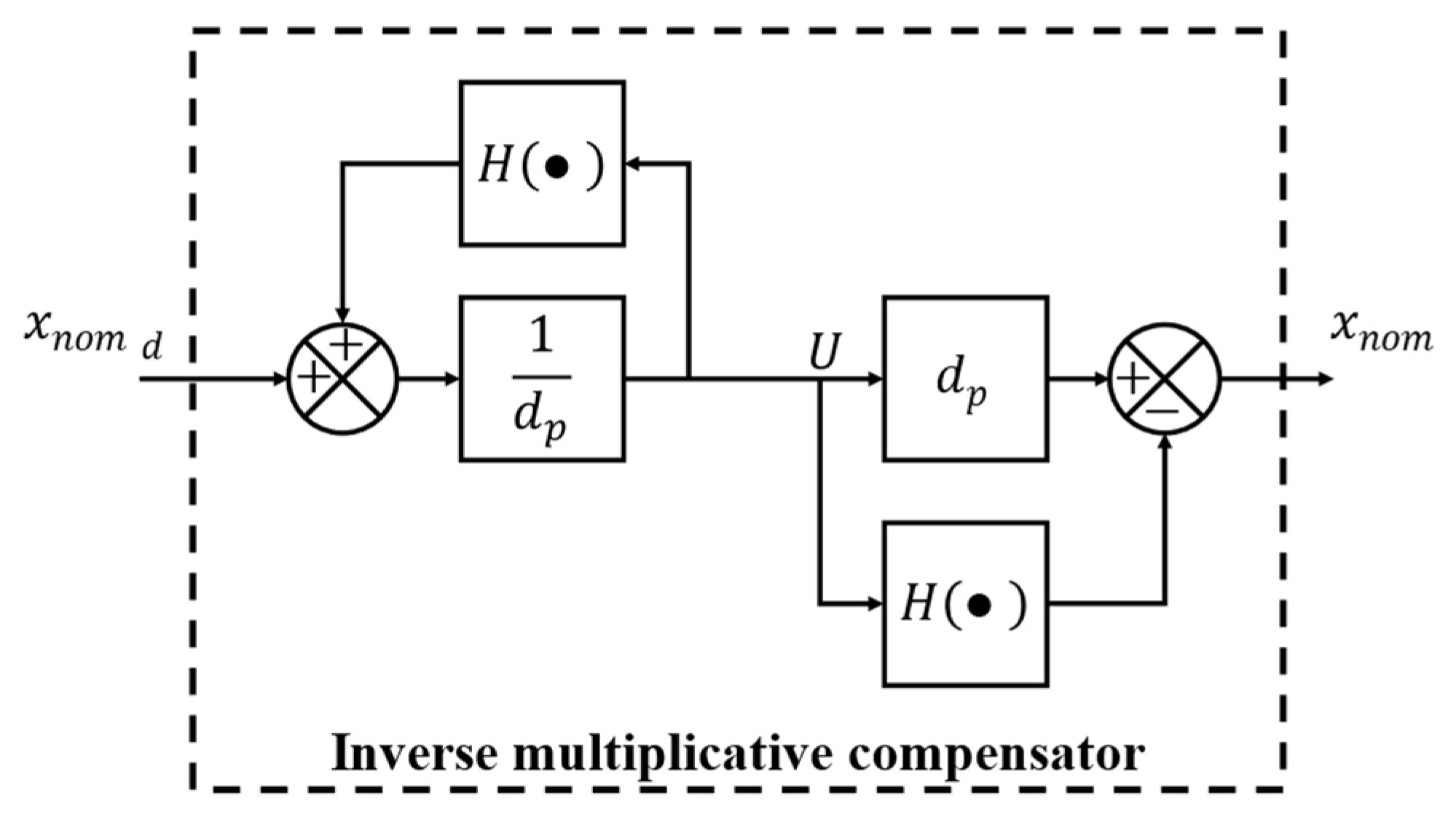
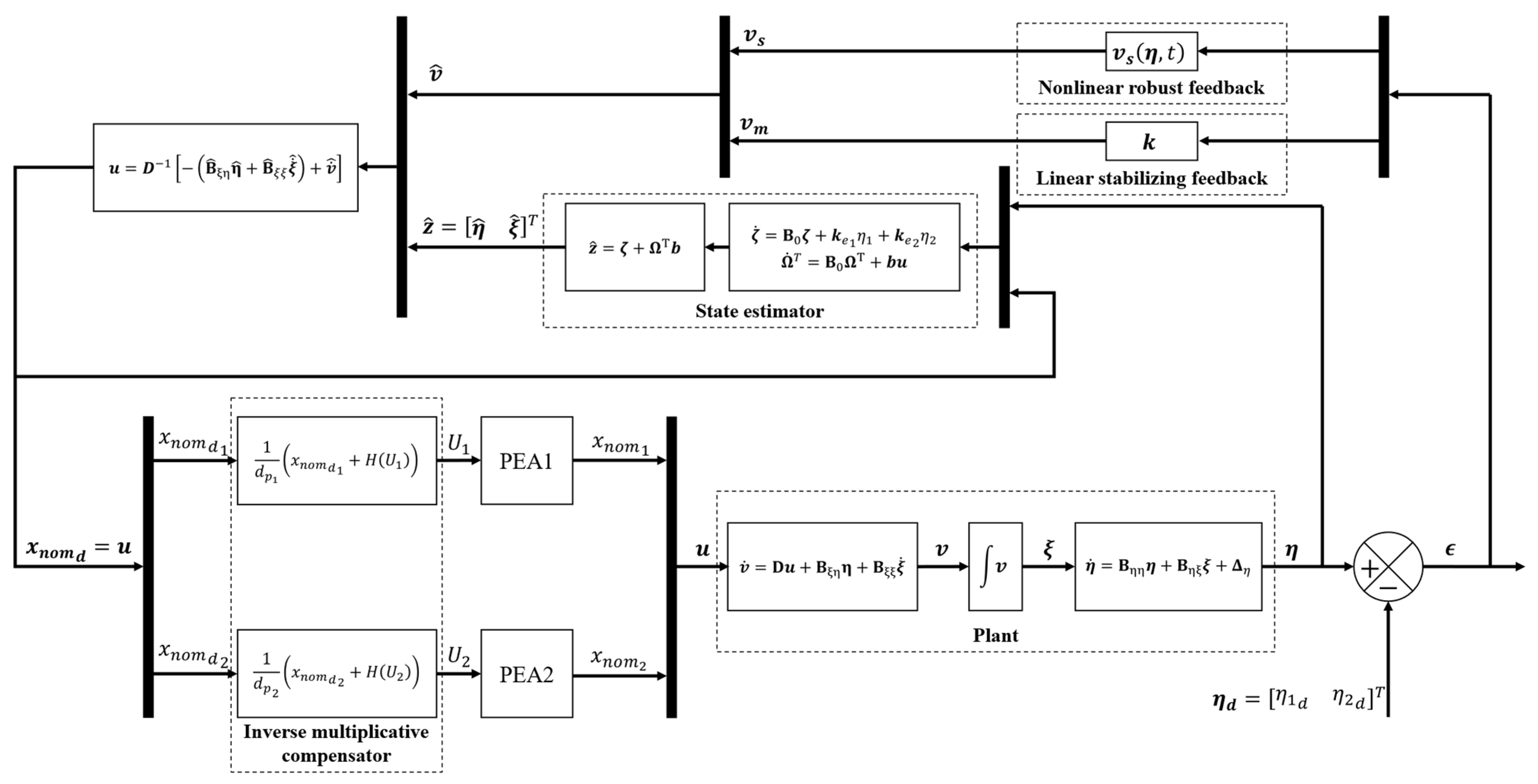
3.1. Inverse Multiplicative Compensation Scheme for PEA
3.2. Controller Design
3.2.1. Reduced Order System Dynamics
- i.
- , no compressive force exists, and ;
- ii.
- , the spatial frame , and .
- i.
- finite-element modelling error
- ii.
- piezoelectric modelling error
- iii.
- asymmetric modelling error
- iv.
- systematic noise
- v.
- measurement error .
3.2.2. Backstepping Robust Controller
- i.
- is the actual input of the first subsystem in Equation (43) and is controlled by ; is the desired input control law of the first subsystem in Equation (43). Therefore, if we can find some such that is able to track very closely, then the first subsystem in Equation (43) is automatically stabilized.
- ii.
- The same for the second subsystem in Equation (43), where the problem turns into finding from the same based on the relation given in Equation (44).
4. Experimental Results
4.1. Experimental Setup
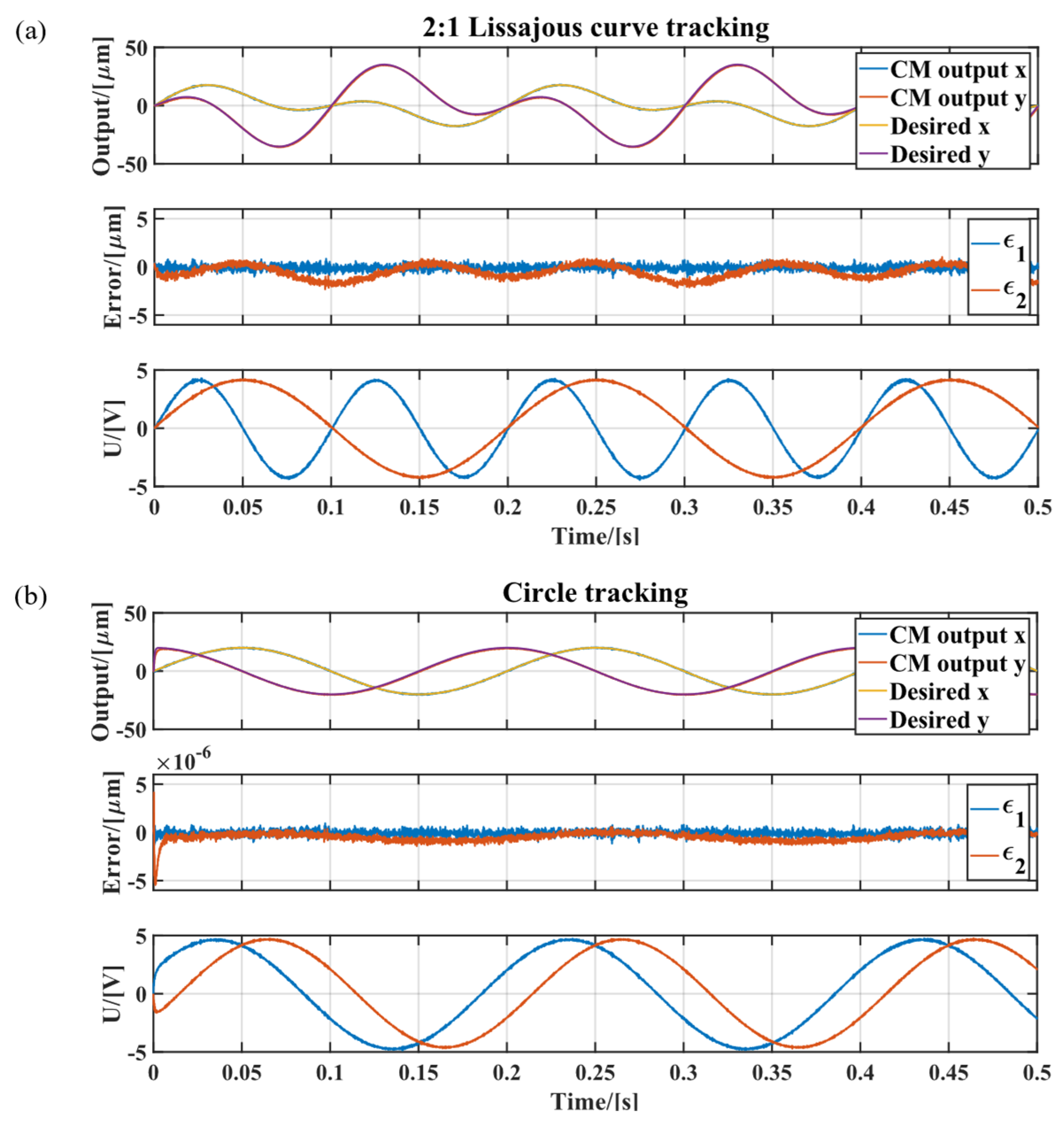
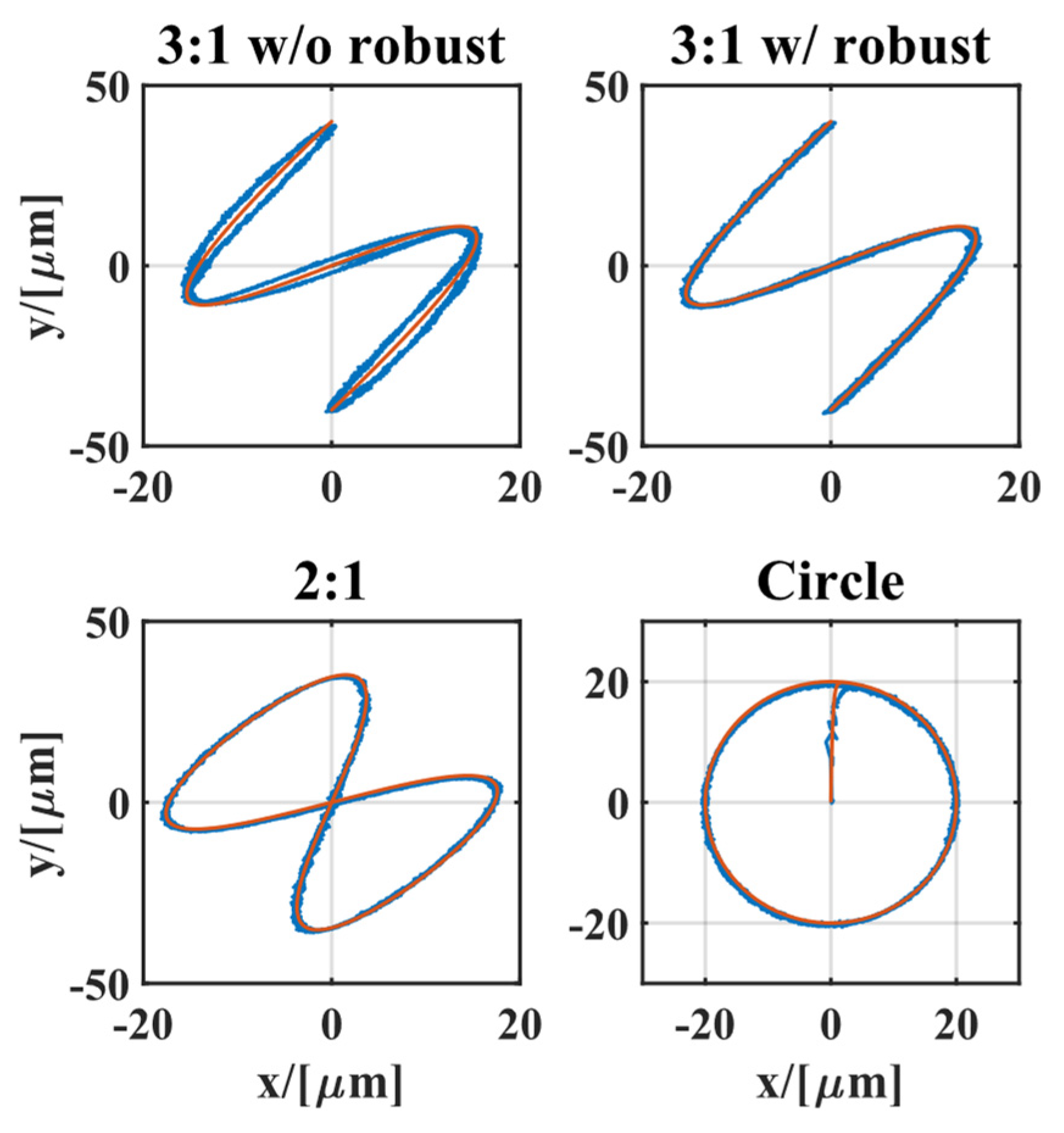
4.2. Experimental Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Nonlinear Finite-Element Method Synthesis
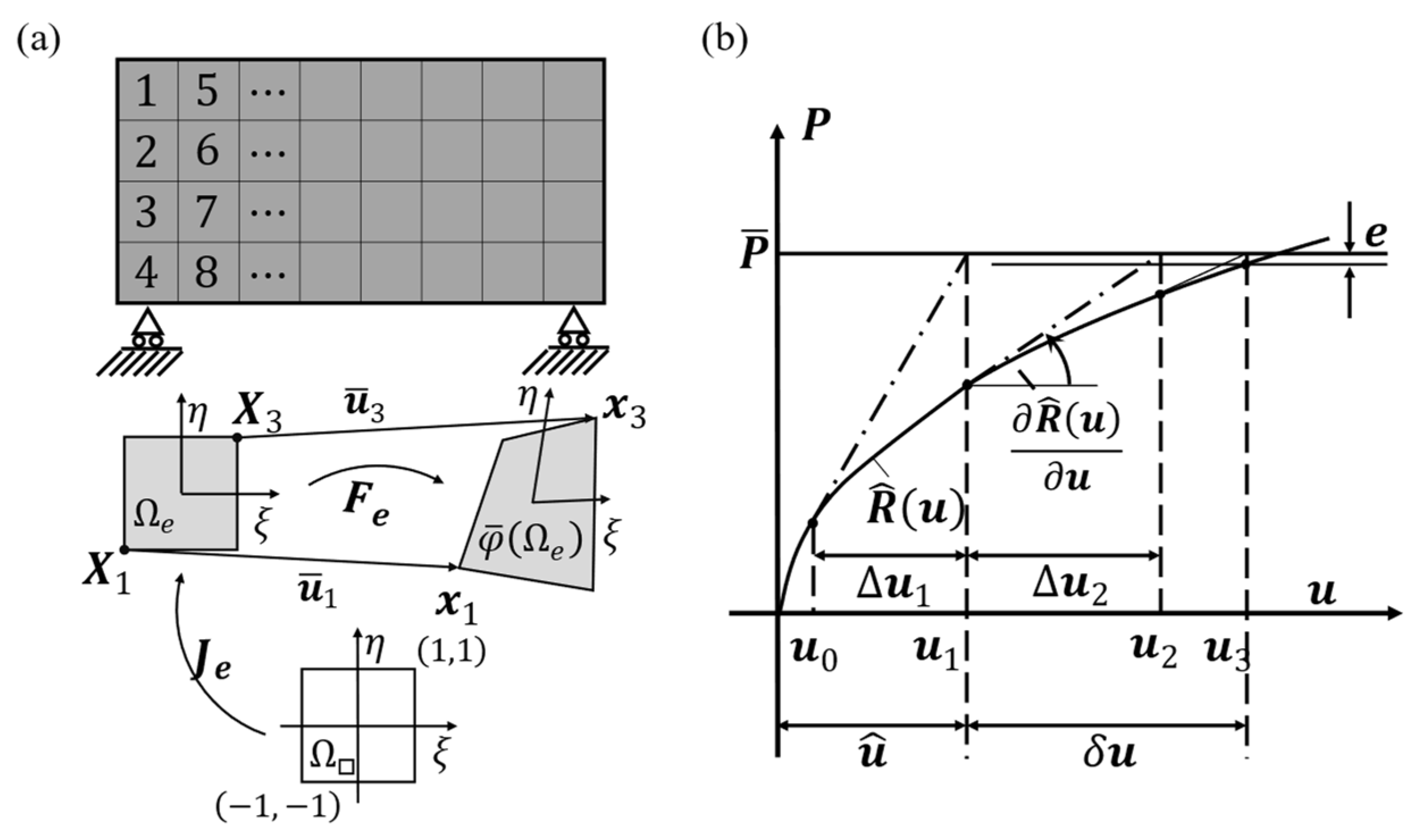
Appendix B. Identifying the Hysteresis Model of the PEAs
| Algorithm A1 Parallel recursive least square algorithm for online parameter estimation. Parallel RLSE Algorithm |
| Initialization: Make an initial guess of the coefficients, compute corresponding initial values of θ and φ Main loop: While PEA is working do Do process (A11) for regressor Equation (A8) Update state variable Do process (A11) for regressor Equation (A12) End while |
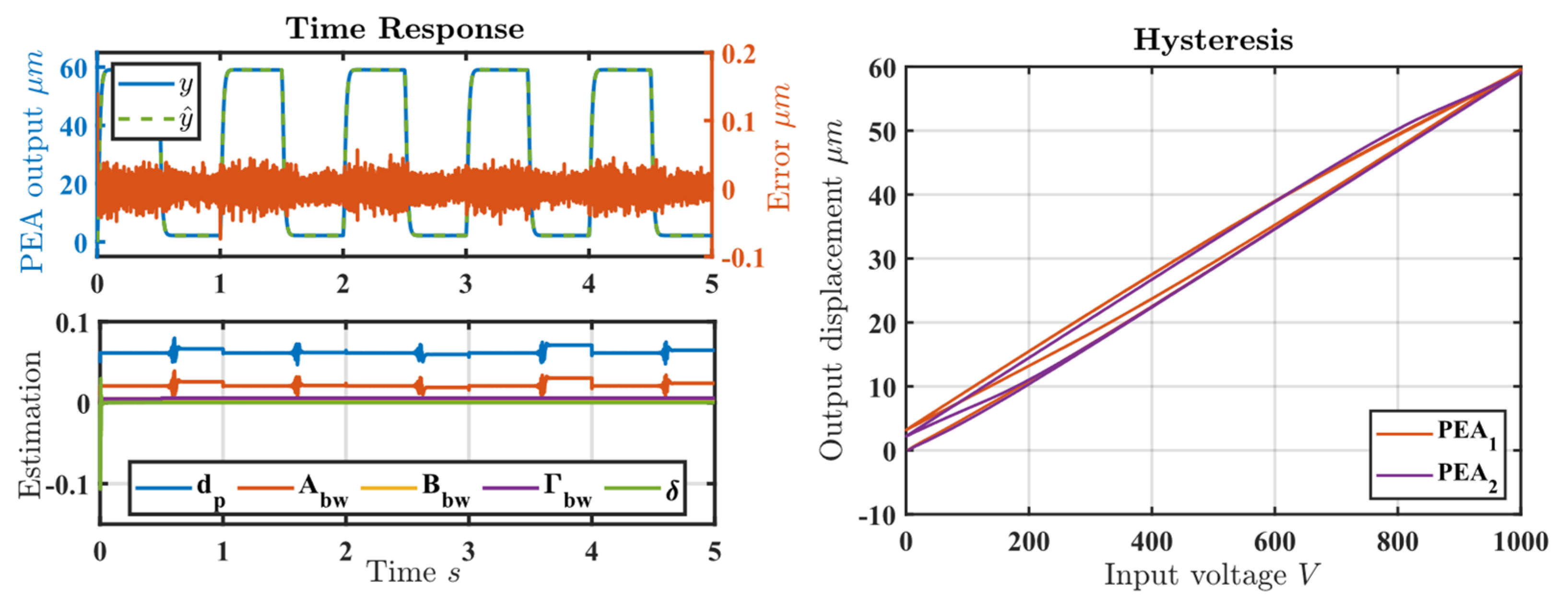
| Symbol | Initial Guess | Estimates | |
|---|---|---|---|
| PEA1 | PEA2 | ||
Appendix C. The State-Space Representation of the System Dynamics
Appendix D. Deduction of the Backstepping Controller
References
- Howell, L.L. Compliant Mechanisms. In 21st Century Kinematics; Springer: London, UK, 2013; pp. 189–216. [Google Scholar]
- Gu, G.Y.; Zhu, L.M.; Su, C.Y.; Ding, H.; Fatikow, S. Modeling and control of piezo-actuated nanopositioning stages: A survey. IEEE Trans. Autom. Sci. Eng. 2016, 13, 313–332. [Google Scholar] [CrossRef]
- Solehuddin, S.; Ridzwan, M.I.Z.; Kadarman, A.H. Methodology of Compliant Mechanisms and its Current Developments in Applications: A Review. Am. J. Appl. Sci. 2007, 4, 160–167. [Google Scholar] [CrossRef]
- Wildman, R.; Gaynor, A. 11—Topology optimization for robotics applications. In Robotic Systems and Autonomous Platforms; Walsh, S.M., Strano, M.S., Eds.; Woodhead Publishing: Sawston, UK, 2019; pp. 251–292. [Google Scholar]
- Wen, S.; Xu, Q. Design of a Novel Piezoelectric Energy Harvester Based on Integrated Multistage Force Amplification Frame. IEEE/ASME Trans. Mechatron. 2019, 24, 1228–1237. [Google Scholar] [CrossRef]
- Abdelnaby, M.A.; Arafa, M. Energy harvesting using a flextensional compliant mechanism. J. Intell. Mater. Syst. Struct. 2016, 27, 2707–2718. [Google Scholar] [CrossRef]
- Choi, K.-B.; Lee, J.J.; Hata, S. A piezo-driven compliant stage with double mechanical amplification mechanisms arranged in parallel. Sens. Actuators A Phys. 2010, 161, 173–181. [Google Scholar] [CrossRef]
- Zhu, Z.; To, S.; Zhu, W.; Li, Y.; Huang, P. Optimum Design of a Piezo-Actuated Triaxial Compliant Mechanism for Nanocutting. IEEE Trans. Ind. Electron. 2018, 65, 6362–6371. [Google Scholar] [CrossRef]
- Zhu, W.-L.; Zhu, Z.; Shi, Y.; Wang, X.; Guan, K.; Ju, B.-F. Design, modeling, analysis and testing of a novel piezo-actuated XY compliant mechanism for large workspace nano-positioning. Smart Mater. Struct. 2016, 25, 115033. [Google Scholar] [CrossRef]
- Li, L.; Chew, Z.J. 11—Microactuators: Design and technology. In Smart Sensors and Mems; Nihtianov, S., Luque, A., Eds.; Woodhead Publishing: Sawston, UK, 2014; pp. 305–348. [Google Scholar]
- Lourdes Thomas, T.; Kalpathy Venkiteswaran, V.; Ananthasuresh, G.K.; Misra, S. Surgical Applications of Compliant Mechanisms: A Review. J. Mech. Robot. 2021, 13, 020801. [Google Scholar] [CrossRef]
- Sigmund, O. On the Design of Compliant Mechanisms Using Topology Optimization*. Mech. Struct. Mach. 1997, 25, 493–524. [Google Scholar] [CrossRef]
- Lazarov, B.S.; Schevenels, M.; Sigmund, O. Robust design of large-displacement compliant mechanisms. Mech. Sci. 2011, 2, 175–182. [Google Scholar] [CrossRef] [Green Version]
- Sigmund, O. Manufacturing tolerant topology optimization. Acta Mech. Sin. 2009, 25, 227–239. [Google Scholar] [CrossRef] [Green Version]
- Guo Zhan, L.; Tat Joo, T.; Guilin, Y.; Song Huat, Y.; Sitti, M. A hybrid topological and structural optimization method to design a 3-DOF planar motion compliant mechanism. In Proceedings of the 2013 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Wollongong, NSW, Australia, 9–12 July 2013; pp. 247–254. [Google Scholar]
- Liu, C.-H.; Huang, G.-F.; Chen, T.-L. An Evolutionary Soft-Add Topology Optimization Method for Synthesis of Compliant Mechanisms With Maximum Output Displacement. J. Mech. Robot. 2017, 9, 054502. [Google Scholar] [CrossRef]
- Bendsoe, M.P.; Sigmund, O. Topology Optimization: Theory, Methods, and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Zhu, B.; Zhang, X.; Zhang, H.; Liang, J.; Zang, H.; Li, H.; Wang, R. Design of compliant mechanisms using continuum topology optimization: A review. Mech. Mach. Theory 2020, 143, 103622. [Google Scholar] [CrossRef]
- Lobontiu, N.; Garcia, E. Analytical model of displacement amplification and stiffness optimization for a class of flexure-based compliant mechanisms. Comput. Struct. 2003, 81, 2797–2810. [Google Scholar] [CrossRef]
- Li, Z.; Kota, S. Dynamic Analysis of Compliant Mechanisms. In Proceedings of the 27th Biennial Mechanisms and Robotics Conference, Montreal, QC, Canada, 29 September–2 October 2002; Volume 5, pp. 43–50. [Google Scholar]
- Li, N.; Su, H.-J.; Zhang, X.-P. Accuracy Assessment of Pseudo-Rigid-Body Model for Dynamic Analysis of Compliant Mechanisms. J. Mech. Robot. 2017, 9, 054503. [Google Scholar] [CrossRef]
- Wang, W.; Yu, Y. New Approach to the Dynamic Modeling of Compliant Mechanisms. J. Mech. Robot. 2010, 2, 021003. [Google Scholar] [CrossRef]
- Sigmund, O. Design of multiphysics actuators using topology optimization–Part I: One-material structures. J Comput. Methods Appl. Mech. Eng. 2001, 190, 6577–6604. [Google Scholar] [CrossRef]
- Sigmund, O. Design of multiphysics actuators using topology optimization–Part II: Two-material structures. J Comput. Methods Appl. Mech. Eng. 2001, 190, 6605–6627. [Google Scholar] [CrossRef]
- Saxena, A. Topology design of large displacement compliant mechanisms with multiple materials and multiple output ports. Struct. Multidiscip. Optim. 2005, 30, 477–490. [Google Scholar] [CrossRef]
- Zhao, K.; Schmiedeler, J.P. Using Rigid-Body Mechanism Topologies to Design Path Generating Compliant Mechanisms. J. Mech. Robot. 2015, 8, 014506. [Google Scholar] [CrossRef]
- Krstic, M.; Kokotovic, P.V.; Kanellakopoulos, I. Nonlinear and Adaptive Control Design; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1995. [Google Scholar]
- Bendsøe, M.P. Optimal shape design as a material distribution problem. Struct. Optim. 1989, 1, 193–202. [Google Scholar] [CrossRef]
- Sigmund, O.; Maute, K. Topology optimization approaches. Struct. Multidiscip. Optim. 2013, 48, 1031–1055. [Google Scholar] [CrossRef]
- Cheng, T.; He, M.; Li, H.; Lu, X.; Zhao, H.; Gao, H. A Novel Trapezoid-Type Stick–Slip Piezoelectric Linear Actuator Using Right Circular Flexure Hinge Mechanism. IEEE Trans. Ind. Electron. 2017, 64, 5545–5552. [Google Scholar] [CrossRef]
- Gu, G.-Y.; Zhu, L.-M.; Su, C.-Y. High-precision control of piezoelectric nanopositioning stages using hysteresis compensator and disturbance observer. Smart Mater. Struct. 2014, 23, 105007. [Google Scholar] [CrossRef]
- Liu, K.; Tovar, A. An efficient 3D topology optimization code written in Matlab. Struct. Multidiscip. Optim. 2014, 50, 1175–1196. [Google Scholar] [CrossRef] [Green Version]
- Zhu, W.-L.; Zhu, Z.; Guo, P.; Ju, B.-F. A novel hybrid actuation mechanism based XY nanopositioning stage with totally decoupled kinematics. Mech. Syst. Signal Process. 2018, 99, 747–759. [Google Scholar] [CrossRef]
- Yong, Y.K.; Aphale, S.S.; Moheimani, S.O.R. Design, identification, and control of a flexure-based XY stage for fast nanoscale positioning. IEEE Trans. Nanotechnol. 2009, 8, 46–54. [Google Scholar] [CrossRef]
- Olhoff, N. Multicriterion structural optimization via bound formulation and mathematical programming. Struct. Optim. 1989, 1, 11–17. [Google Scholar] [CrossRef]
- Radić, M. About a determinant of rectangular 2 × n matrix and its geometric interpretation. Beiträge Zur Algebra Geom. 2005, 46, 321–349. [Google Scholar]
- Capasso, G.; Morlier, J.; Charlotte, M.; Coniglio, S. Stress-based topology optimization of compliant mechanisms using nonlinear mechanics. Mech. Ind. 2020, 21, 304. [Google Scholar] [CrossRef] [Green Version]
- Andreasen, C.S.; Elingaard, M.O.; Aage, N. Level set topology and shape optimization by density methods using cut elements with length scale control. Struct. Multidiscip. Optim. 2020, 62, 685–707. [Google Scholar] [CrossRef]
- Wriggers, P. Nonlinear Finite Element Methods; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Kim, N.-H. Introduction to Nonlinear Finite Element Analysis; Springer: New York, NY, USA, 2018. [Google Scholar]
- Liu, L.; Xing, J.; Yang, Q.; Luo, Y. Design of Large-Displacement Compliant Mechanisms by Topology Optimization Incorporating Modified Additive Hyperelasticity Technique. Math. Probl. Eng. 2017, 2017, 467974. [Google Scholar] [CrossRef]
- Michaleris, P.; Tortorelli, D.A.; Vidal, C.A. Tangent operators and design sensitivity formulations for transient non-linear coupled problems with applications to elastoplasticity. Int. J. Numer. Methods Eng. 1994, 37, 2471–2499. [Google Scholar] [CrossRef]
- Dabrowski, M.; Krotkiewski, M.; Schmid, D.W. MILAMIN: MATLAB-based finite element method solver for large problems. Geochem. Geophys. Geosystems 2008, 9, Q04030. [Google Scholar] [CrossRef]
- Andreassen, E.; Clausen, A.; Schevenels, M.; Lazarov, B.S.; Sigmund, O. Efficient topology optimization in MATLAB using 88 lines of code. Struct. Multidiscip. Optim. 2010, 43, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Gu, G.-Y.; Zhu, L.-M. Comparative experiments regarding approaches to feedforward hysteresis compensation for piezoceramic actuators. Smart Mater. Struct. 2014, 23, 095029. [Google Scholar] [CrossRef] [Green Version]
- Cao, Y.; Chen, X.B. A Survey of Modeling and Control Issues for Piezo-electric Actuators. J. Dyn. Syst. Meas. Control 2014, 137, 014001. [Google Scholar] [CrossRef]
- Krejci, P.; Kuhnen, K. Inverse control of systems with hysteresis and creep. IEE Proc. Control Theory Appl. 2001, 148, 185–192. [Google Scholar] [CrossRef] [Green Version]
- Rakotondrabe, M. Bouc–Wen Modeling and Inverse Multiplicative Structure to Compensate Hysteresis Nonlinearity in Piezoelectric Actuators. IEEE Trans. Autom. Sci. Eng. 2011, 8, 428–431. [Google Scholar] [CrossRef] [Green Version]
- Zhu, W.; Wang, D.-h. Non-symmetrical Bouc–Wen model for piezoelectric ceramic actuators. Sens. Actuators A Phys. 2012, 181, 51–60. [Google Scholar] [CrossRef]
- Lin, C.-J.; Lin, P.-T. Tracking control of a biaxial piezo-actuated positioning stage using generalized Duhem model. J. Comput. Math. Appl. 2012, 64, 766–787. [Google Scholar] [CrossRef] [Green Version]
- Zhu, W.; Zhu, Z.; He, Y.; Ehmann, K.F.; Ju, B.; Li, S. Development of a Novel 2-D Vibration-Assisted Compliant Cutting System for Surface Texturing. IEEE/ASME Trans. Mechatron. 2017, 22, 1796–1806. [Google Scholar] [CrossRef]
- Wang, R.; Zhang, X. Preload characteristics identification of the piezoelectric-actuated 1-DOF compliant nanopositioning platform. Front. Mech. Eng. 2015, 10, 20–36. [Google Scholar] [CrossRef]
- Eielsen, A.A.; Vagia, M.; Gravdahl, J.T.; Pettersen, K.Y. Damping and Tracking Control Schemes for Nanopositioning. IEEE/ASME Trans. Mechatron. 2014, 19, 432–444. [Google Scholar] [CrossRef] [Green Version]
- Gu, G.; Zhu, L.; Su, C.; Ding, H. Motion Control of Piezoelectric Positioning Stages: Modeling, Controller Design, and Experimental Evaluation. IEEE/ASME Trans. Mechatron. 2013, 18, 1459–1471. [Google Scholar] [CrossRef]
- Hossein Mousavi, S.; Khayatian, A. Adaptive Control for a Class of Hysteretic Systems. J. Comput. Nonlinear Dyn. 2012, 8, 011003. [Google Scholar] [CrossRef]
- Wei, Z.; Xiang, B.L.; Ting, R.X. Online parameter identification of the asymmetrical Bouc–Wen model for piezoelectric actuators. Precis. Eng. 2014, 38, 921–927. [Google Scholar] [CrossRef]
- Tong, S.; Sui, S.; Li, Y. Fuzzy Adaptive Output Feedback Control of MIMO Nonlinear Systems With Partial Tracking Errors Constrained. IEEE Trans. Fuzzy Syst. 2015, 23, 729–742. [Google Scholar] [CrossRef]
- Nguyen, A.T.; Rath, J.; Guerra, T.M.; Palhares, R.; Zhang, H. Robust Set-Invariance Based Fuzzy Output Tracking Control for Vehicle Autonomous Driving Under Uncertain Lateral Forces and Steering Constraints. IEEE Trans. Intell. Transp. Syst. 2020, 22, 5849–5860. [Google Scholar] [CrossRef]
- Liu, G.R.; Quek, S.S. Chapter 2—Briefing on Mechanics for Solids and Structures. In The Finite Element Method, 2nd ed.; Liu, G.R., Quek, S.S., Eds.; Butterworth-Heinemann: Oxford, UK, 2014; pp. 13–41. [Google Scholar]
- McGuire, W.; Gallagher, R.H.; Ziemian, R.D. Matrix Structural Analysis; Wiley: Hoboken, NJ, USA, 1999. [Google Scholar]
- Yao, B.; Xu, L. Output Feedback Adaptive Robust Control of Uncertain Linear Systems with Disturbances. J. Dyn. Syst. Meas. Control 2006, 128, 938–945. [Google Scholar] [CrossRef]
- Li, X.; Bin, Y. Output feedback adaptive robust control of uncertain linear systems with large disturbances. In Proceedings of the 1999 American Control Conference (Cat. No. 99CH36251), San Diego, CA, USA, 2–4 June 1999; Volume 551, pp. 556–560. [Google Scholar]
- Luo, Z.; Tong, L. A level set method for shape and topology optimization of large-displacement compliant mechanisms. Int. J. Numer. Methods Eng. 2008, 76, 862–892. [Google Scholar] [CrossRef]
- Yao, B.; Tomizuka, M. Smooth Robust Adaptive Sliding Mode Control of Manipulators with Guaranteed Transient Performance. J. Dyn. Syst. Meas. Control 1996, 118, 764–775. [Google Scholar] [CrossRef]
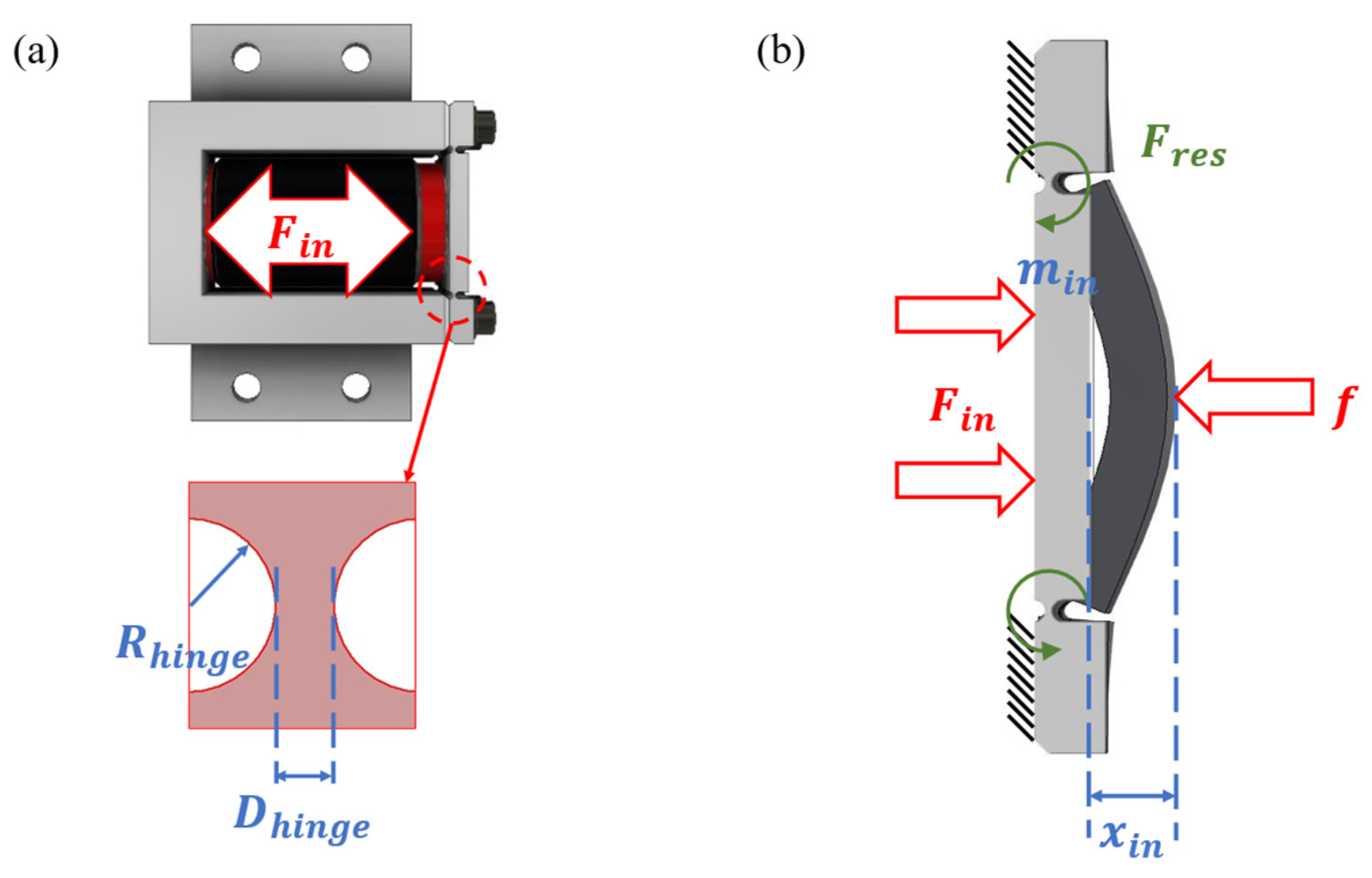





| Symbol | Quantity | Value |
|---|---|---|
| Stiffness | ||
| Max stroke a | ||
| Blocking force | ||
| Hinge radius | ||
| Hinge thickness |
| Working Conditions | |||
|---|---|---|---|
| Regular configuration | → | ← | |
| ← | → | ||
| Reversed configuration | ← | → | |
| → | ← |
| Optimization specifications | Penalty p | |
| Max iteration | 1000 | |
| Mesh specifications | Length l | |
| Width w | ||
| Thickness t | ||
| Discretization | ||
| Material properties | Young’s modulus E | |
| a | ||
| Poisson ratio ν | ||
| Part | Quantity | Guess | Estimate |
|---|---|---|---|
| CM | Horizontal stiffness | ||
| Vertical stiffness | |||
| a | |||
| Amplification ratio α | |||
| PZT set | PZT1 stiffness | ||
| PZT2 stiffness | |||
| Input plate stiffness | |||
| Input plate stiffness | |||
| State Estimator | |||
| Controller design b | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, Y.; Ju, B.; Zhu, W. Integrated Development of a Topology-Optimized Compliant Mechanism for Precise Positioning. Actuators 2022, 11, 179. https://doi.org/10.3390/act11070179
Hu Y, Ju B, Zhu W. Integrated Development of a Topology-Optimized Compliant Mechanism for Precise Positioning. Actuators. 2022; 11(7):179. https://doi.org/10.3390/act11070179
Chicago/Turabian StyleHu, Yaoyuan, Bingfeng Ju, and Wule Zhu. 2022. "Integrated Development of a Topology-Optimized Compliant Mechanism for Precise Positioning" Actuators 11, no. 7: 179. https://doi.org/10.3390/act11070179
APA StyleHu, Y., Ju, B., & Zhu, W. (2022). Integrated Development of a Topology-Optimized Compliant Mechanism for Precise Positioning. Actuators, 11(7), 179. https://doi.org/10.3390/act11070179






