Internal Rotor Actuation and Magnetic Bearings for the Active Control of Rotating Machines †
Abstract
1. Introduction
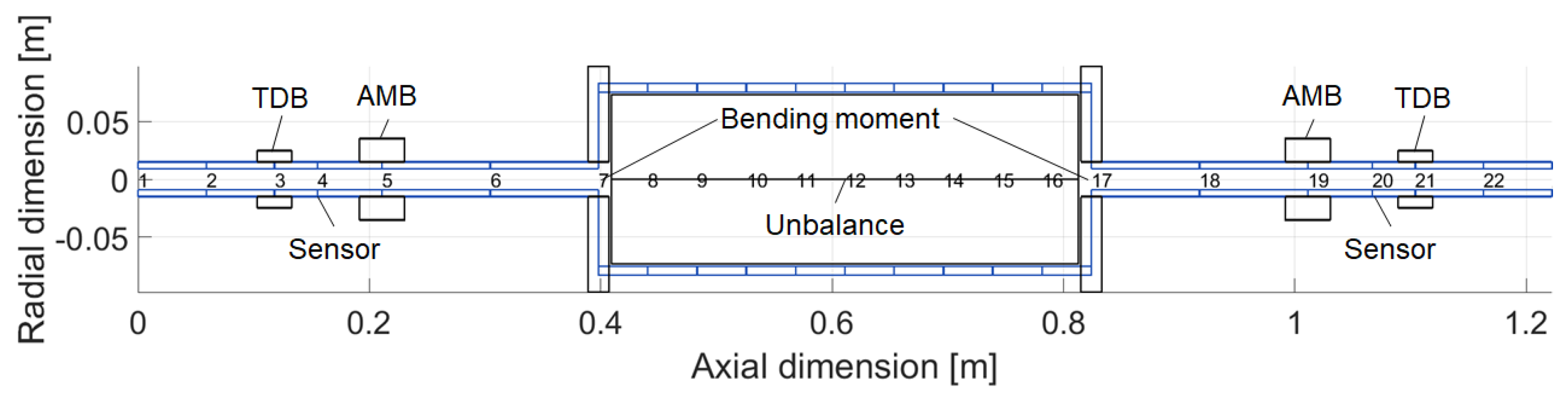
2. Modelling Methodology
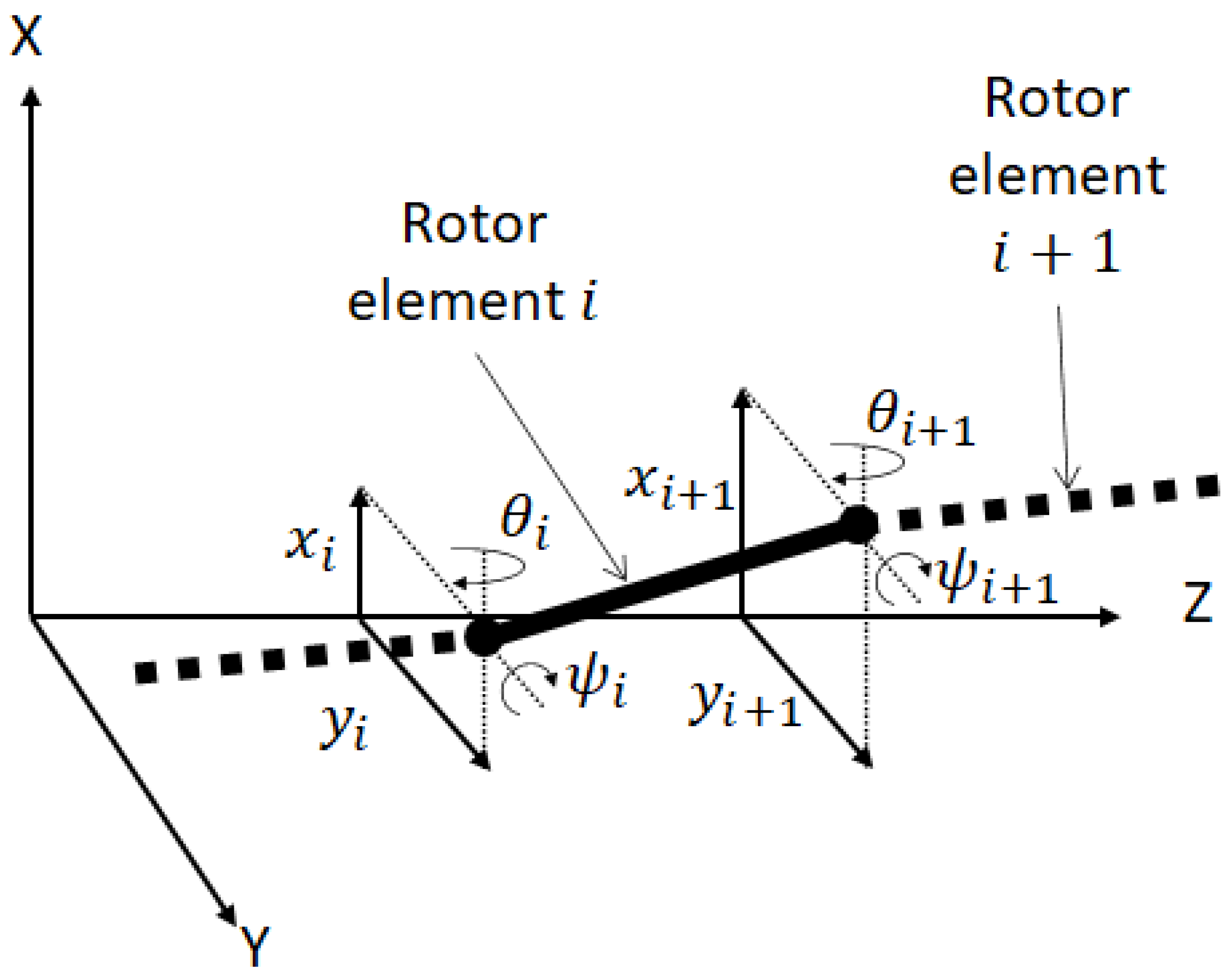
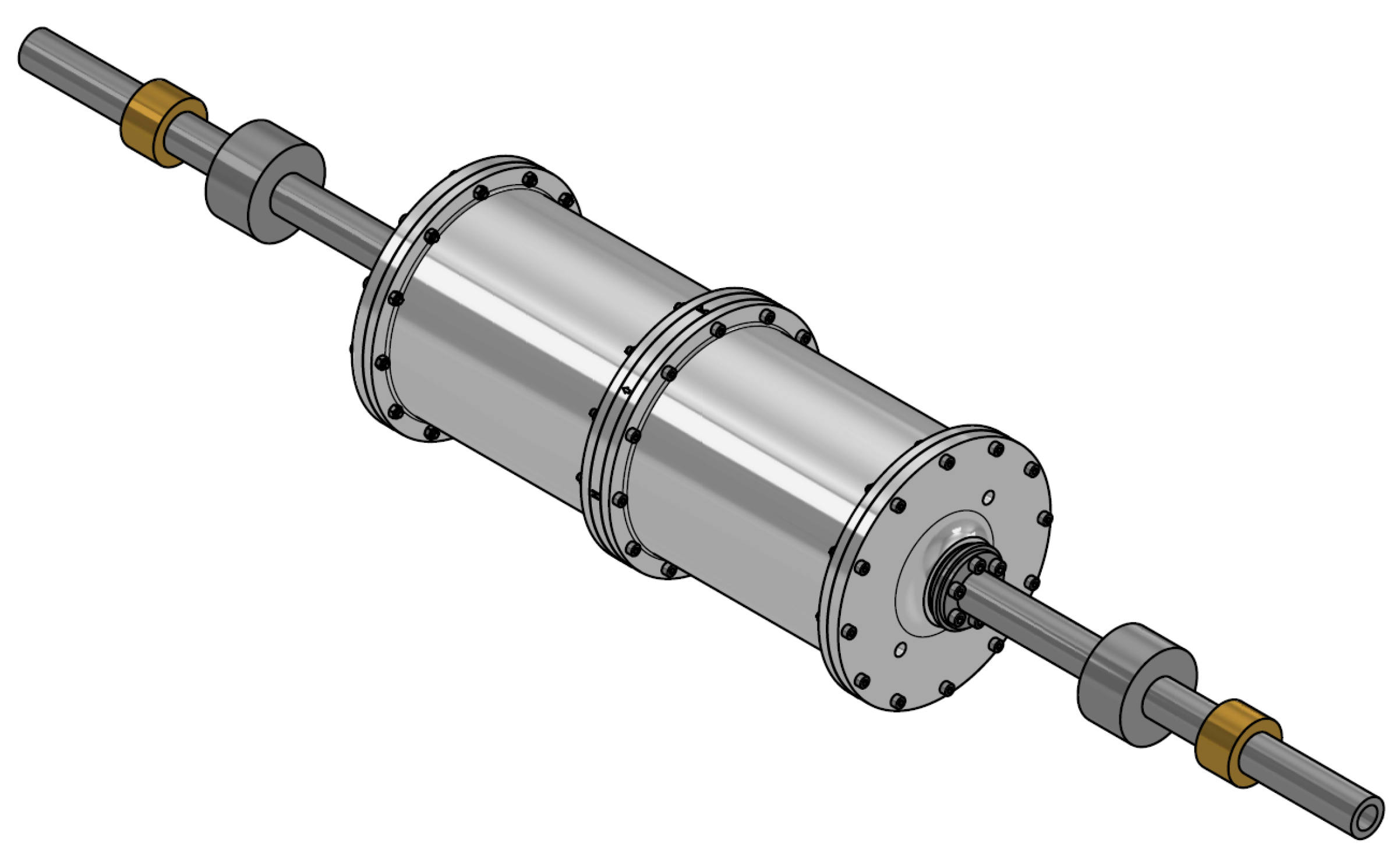
2.1. Rotor Modelling
2.2. Active Magnetic Bearing Modelling
2.3. Unbalance and Bending Actuator Modelling
3. Control Strategy
3.1. Magnetic Bearing Control
3.2. Bending Actuator Control
4. Simulated Performance
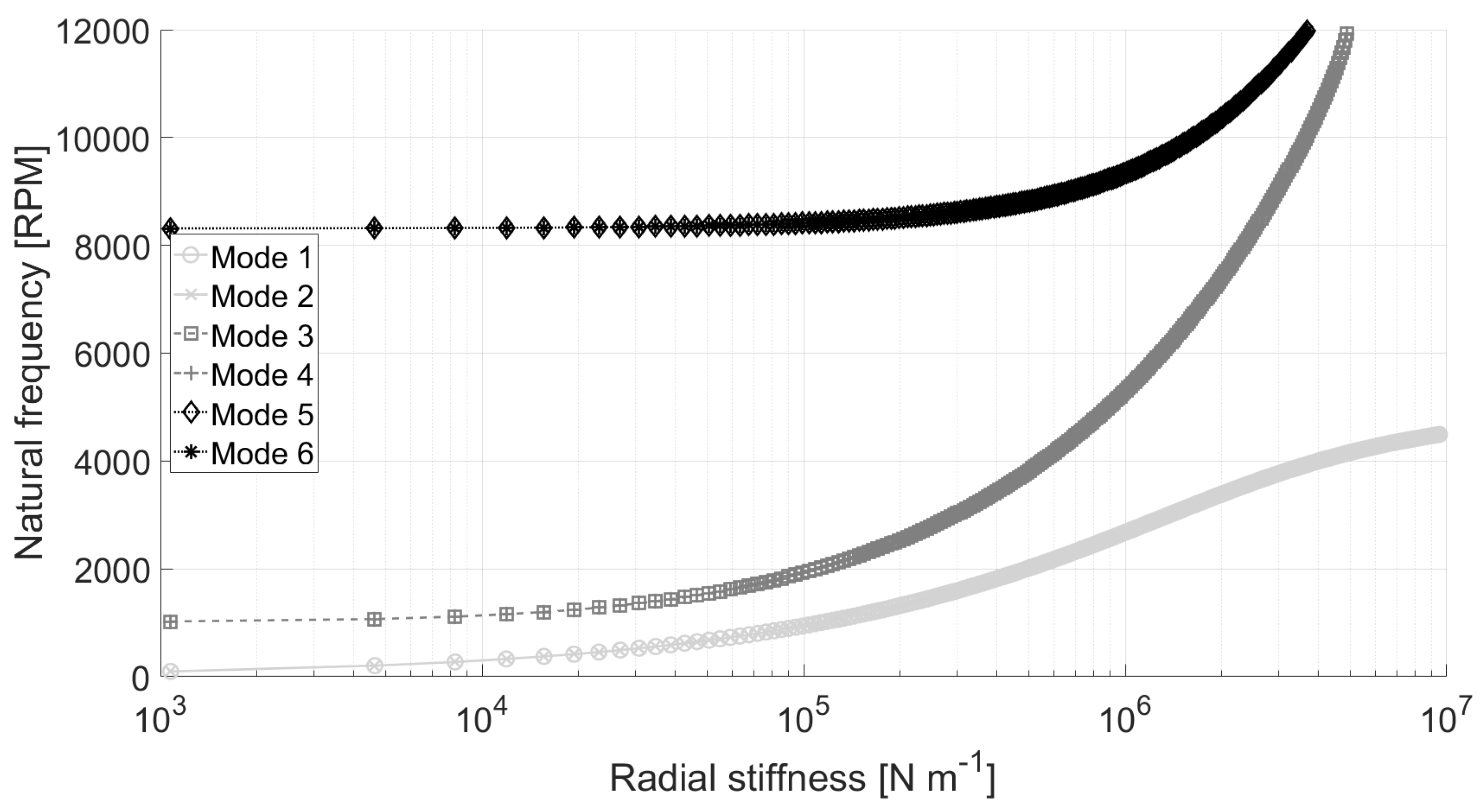
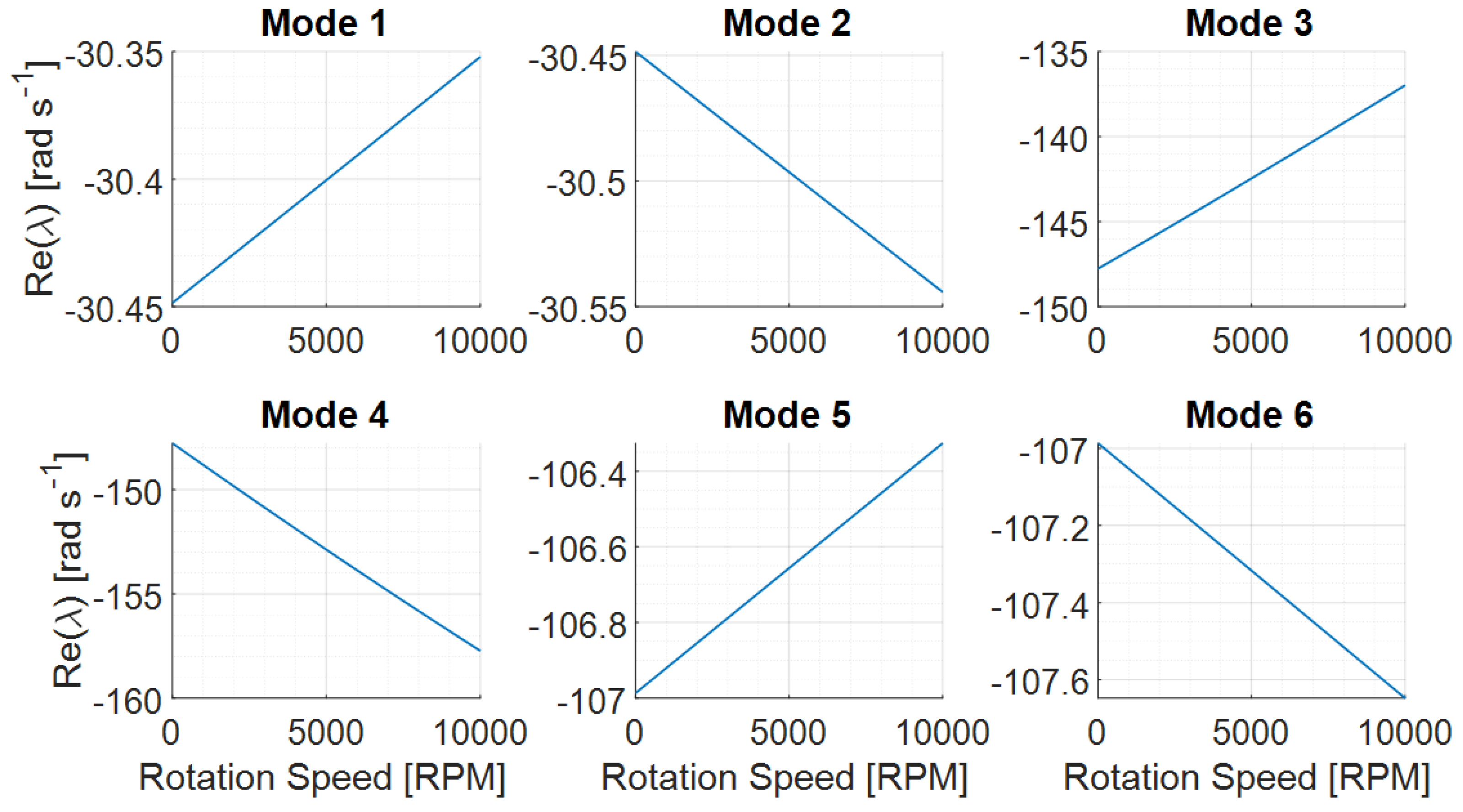
5. Modal Analysis
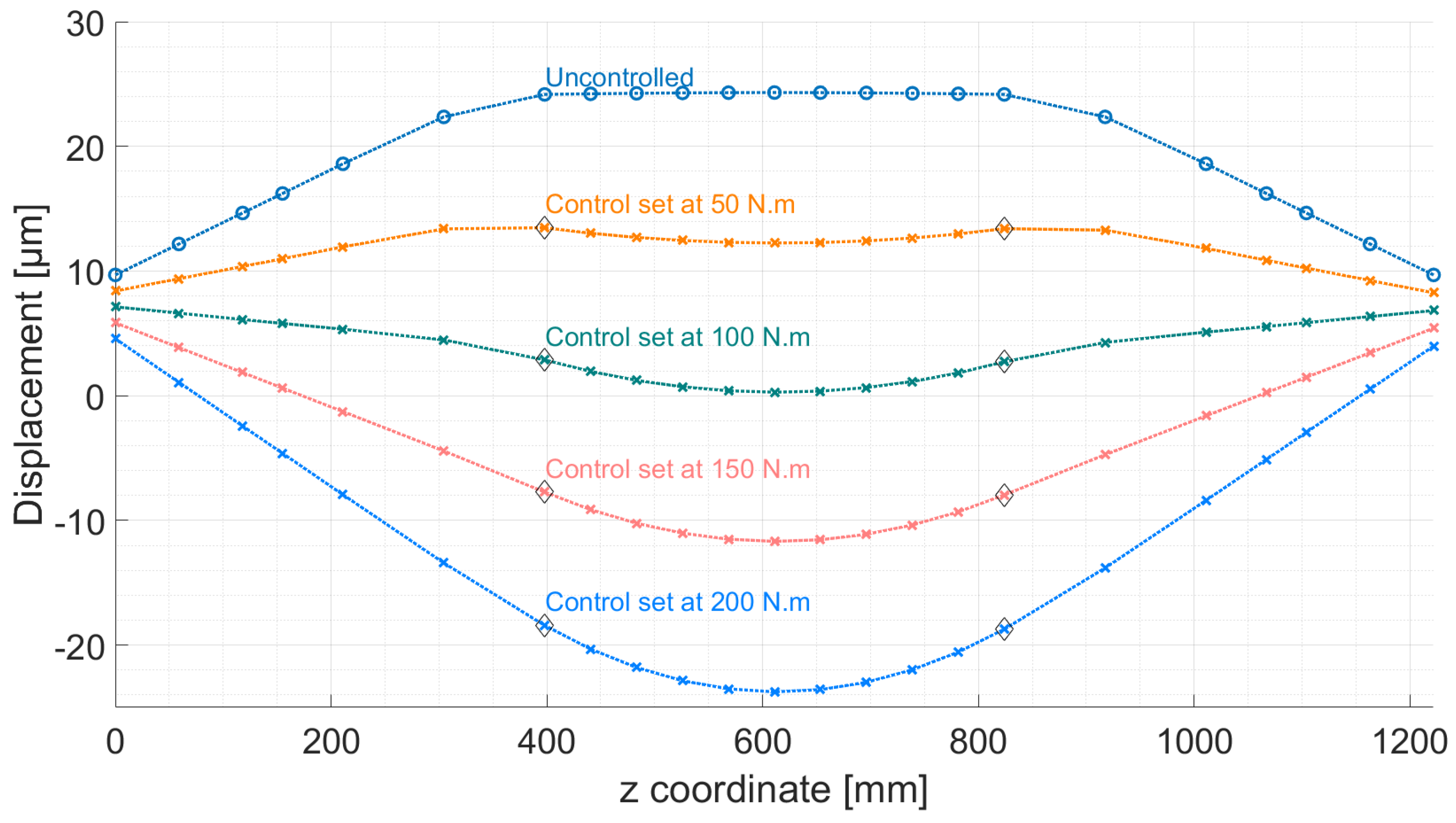
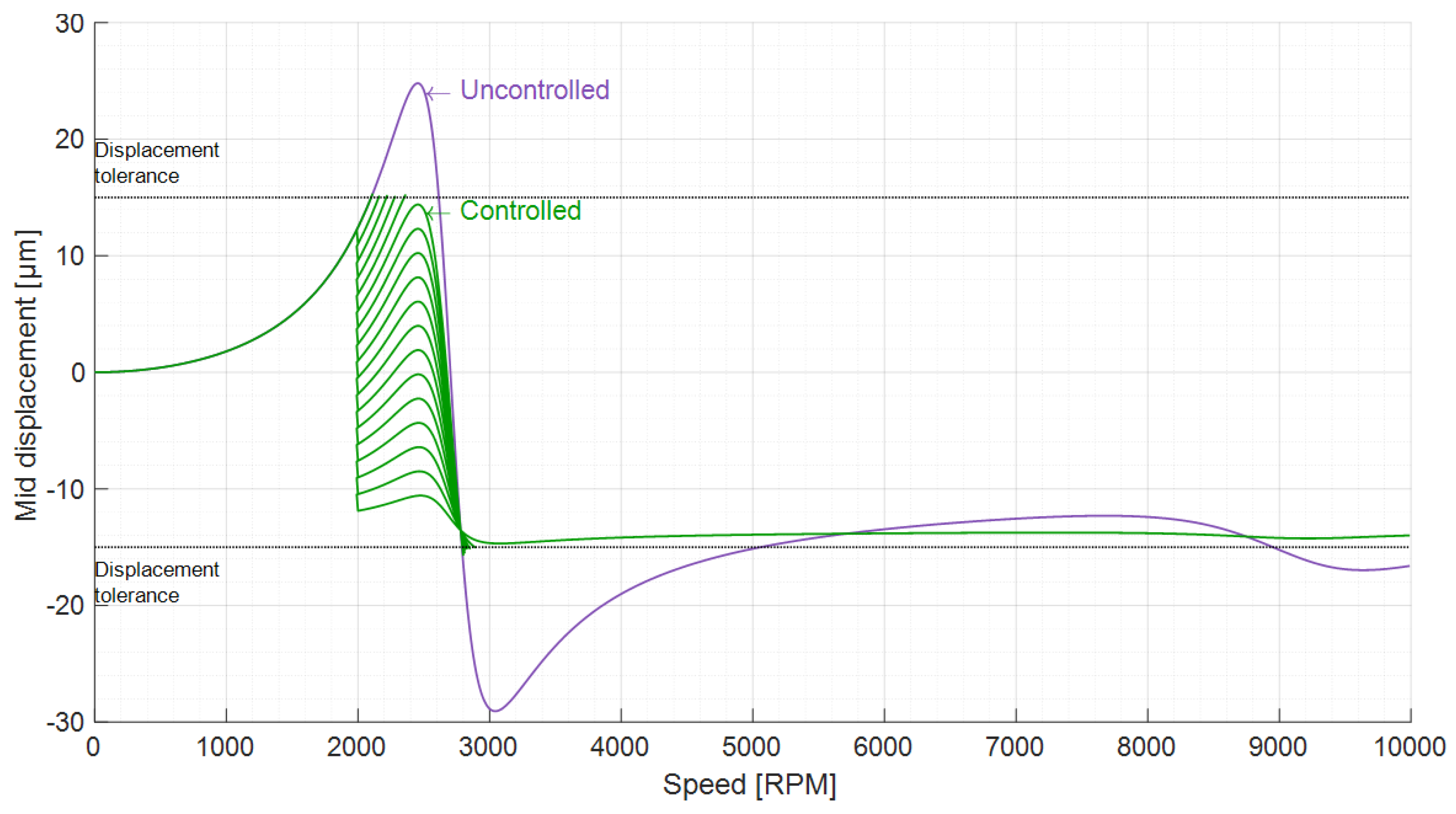
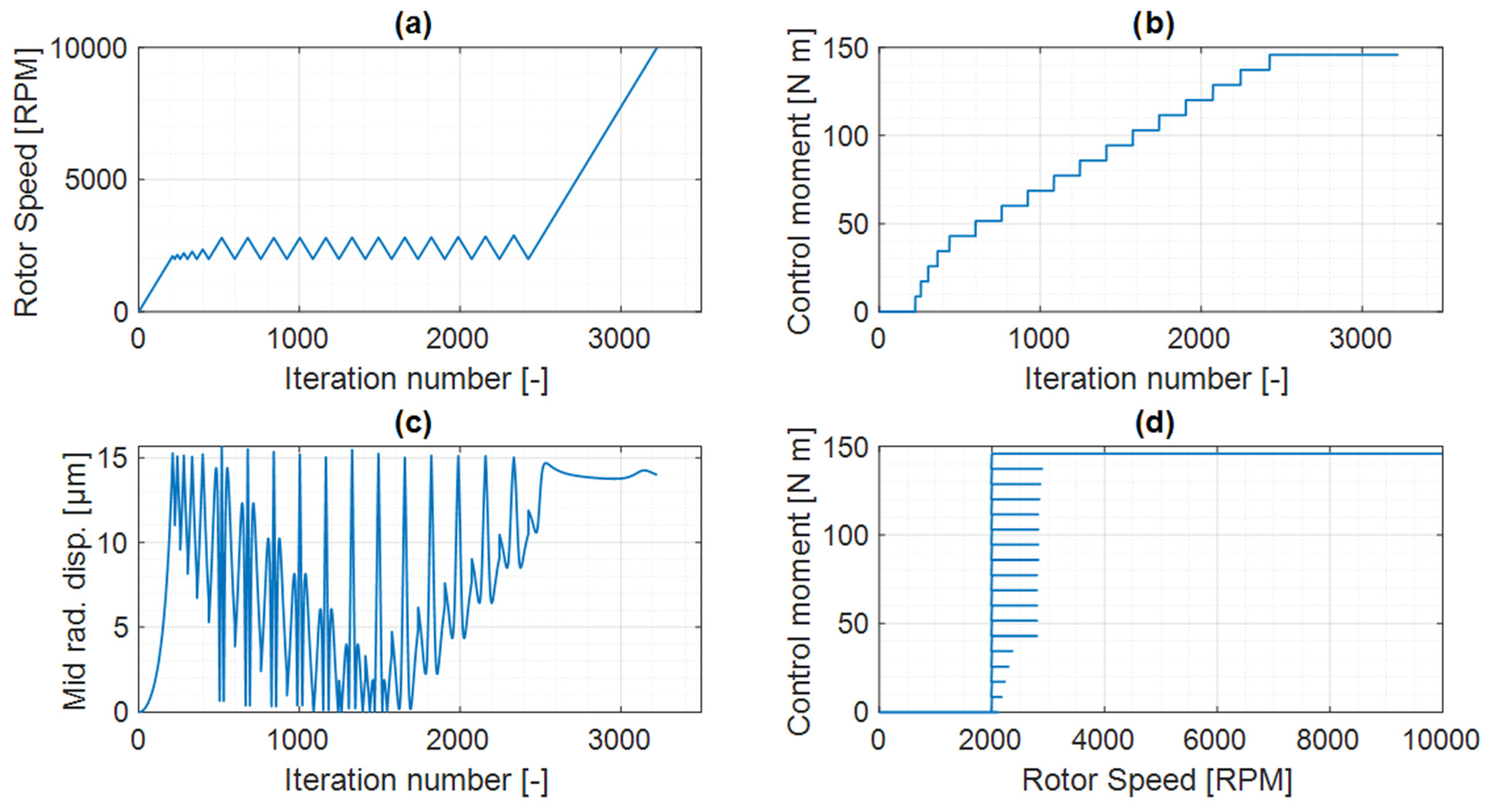
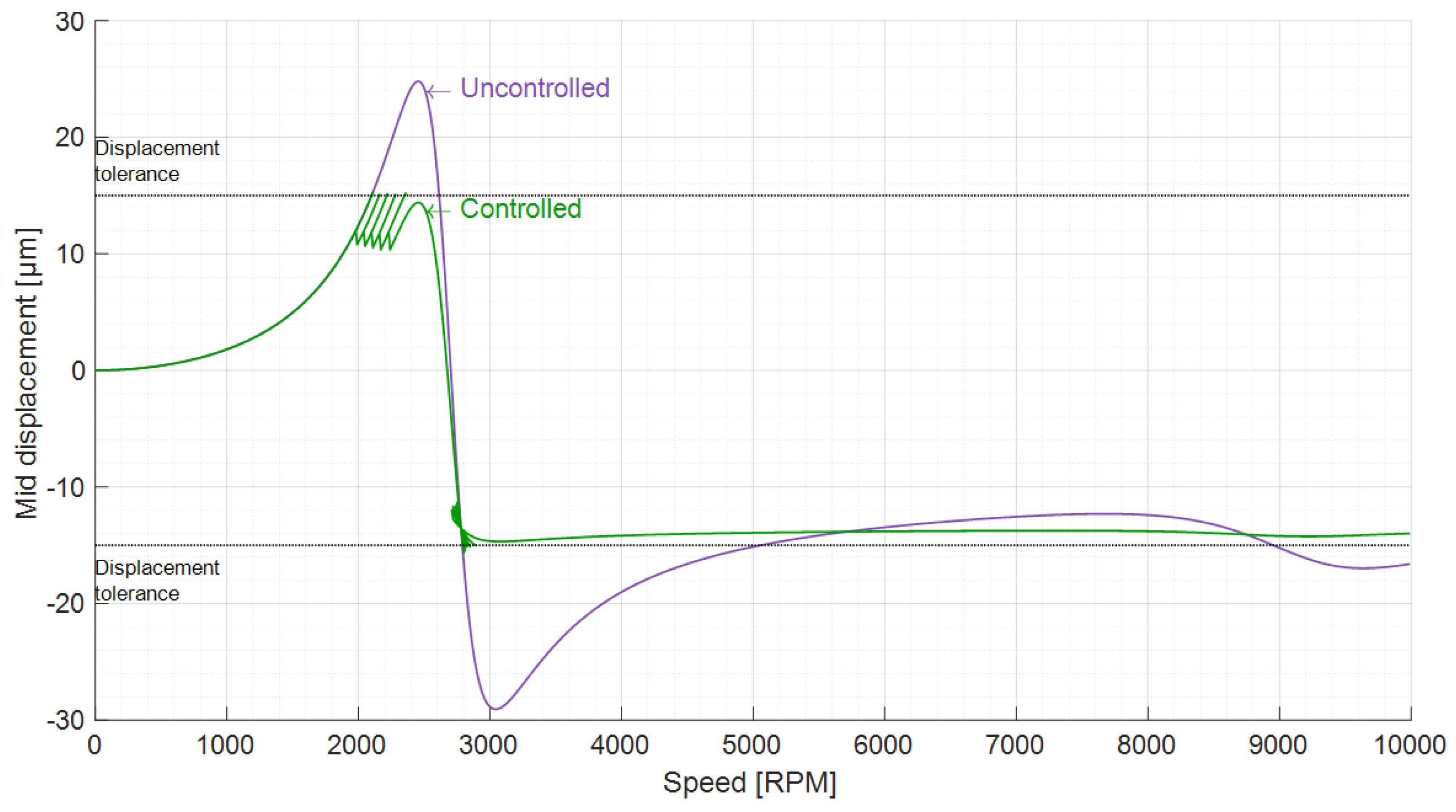
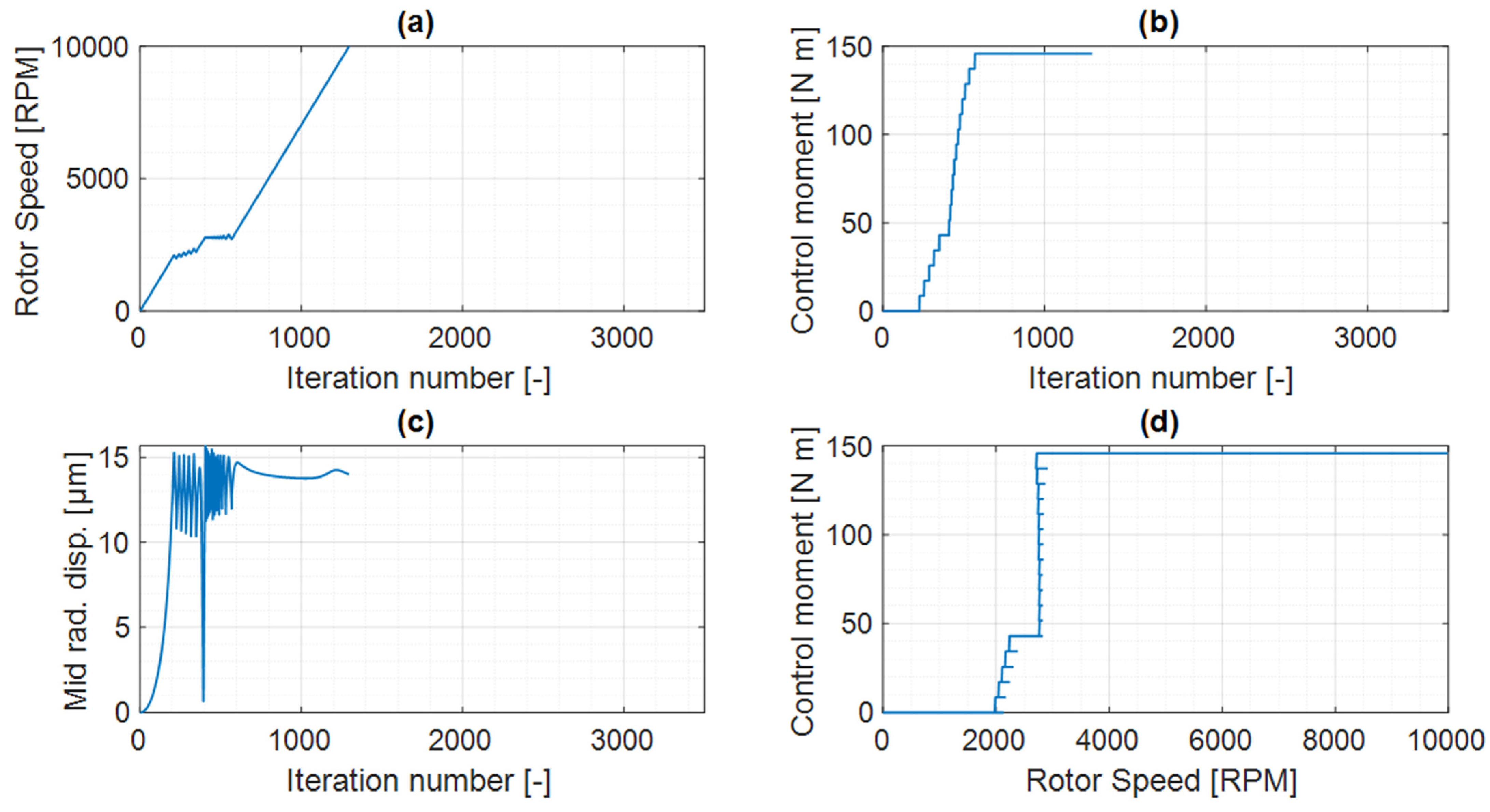
6. Control Results
7. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhou, S.; Shi, J. Active balancing and vibration control of rotating machinery: A survey. Shock Vib. Dig. 2001, 33, 361–371. [Google Scholar] [CrossRef]
- ISO 1940-1: 2003; Mechanical Vibration—Balance Quality Requirements for Rotors in a Constant (Rigid) State—Part 1: Specification and Verification of Balance Tolerances. International Organization for Standardization: Geneva, Switzerland, 2003.
- MacCamhaoil, M. Static and Dynamic Balancing of Rigid Rotors; Bruel and Kjaer: Nærum, Denmark, 2016. [Google Scholar]
- Thearle, E.L. Dynamic Balancing Machine. U.S. Patent 1876524A, 6 September 1932. [Google Scholar]
- Huang, W.Y.; Chao, C.P.; Kang, J.R.; Sung, C.K. The application of ball-type balancers for radial vibration reduction of high-speed optic disk drives. J. Sound Vib. 2002, 250, 415–430. [Google Scholar] [CrossRef]
- Green, K.; Champneys, A.; Friswell, M.; Munoz, A. Investigation of a multi-ball, automatic dynamic balancing mechanism for eccentric rotors. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2008, 366, 705–728. [Google Scholar] [CrossRef]
- Jung, D.; DeSmidt, H. A new hybrid observer based rotor imbalance vibration control via passive autobalancer and active bearing actuation. J. Sound Vib. 2018, 415, 1–24. [Google Scholar] [CrossRef]
- Van de Vegte, J.; Lake, R. Balancing of rotating systems during operation. J. Sound Vib. 1978, 57, 225–235. [Google Scholar] [CrossRef]
- Pardivala, D.N.; Dyer, S.; Bailey, C.D. Design modifications and active balancing on an integrally forged steam turbine rotor to solve serious reliability problems. In Proceedings of the 27th Turbomachinery Symposium, Houston, TX, USA, 20–24 September 1998. [Google Scholar]
- Alauze, C.; Der Hagopian, J.; Gaudiller, L.; Voinis, P. Active balancing of turbomachinery: Application to large shaft lines. JVC/J. Vib. Control 2001, 7, 249–278. [Google Scholar] [CrossRef]
- Jiménez, S.; Keogh, P.; Cole, M. Internal sensing and actuation strategies for smart machine rotors. In Proceedings of the 9th IFToMM International Conference on Rotor Dynamics, Milan, Switzerland, 22–25 September 2014; Springer International Publishing: Cham, Switherland, 2015; Volume 21, pp. 1527–1537. [Google Scholar]
- Przybylowicz, P.M. Near-critical behaviour of a rotating shaft actively stabilised by piezoelectric elements. Syst. Anal. Model. Simul. 2002, 42, 527–537. [Google Scholar] [CrossRef]
- Horst, H.G.; Wolfel, H. Active vibration control of a high speed rotor using PZT patches on the shaft surface. J. Intell. Mater. Syst. Struct. 2004, 15, 721–728. [Google Scholar] [CrossRef]
- Sloetjes, P.; De Boer, A. Vibration reduction and power generation with piezoceramic sheets mounted to a flexible shaft. J. Intell. Mater. Syst. Struct. 2008, 19, 25–34. [Google Scholar] [CrossRef]
- Naebe, M.; Shirvanimoghaddam, K. Functionally graded materials: A review of fabrication and properties. Appl. Mater. Today 2016, 5, 223–245. [Google Scholar] [CrossRef]
- Alexander, P.W.; Brei, D.; Halloran, J.W. DEPP functionally graded piezoceramics via micro-fabrication by co-extrusion. J. Mater. Sci. 2007, 42, 5805–5814. [Google Scholar] [CrossRef]
- Przybyłowicz, P. Stability of actively controlled rotating shaft made of functionally graded material. J. Theor. Appl. Mech. 2005, 43, 609–630. [Google Scholar]
- Rao, D.K.; Roy, T. Vibration analysis of functionally graded rotating shaft system. Procedia Eng. 2016, 144, 775–780. [Google Scholar] [CrossRef]
- Vadiraja, D.; Sahasrabudhe, A. Vibration analysis and optimal control of rotating pre-twisted thin-walled beams using MFC actuators and sensors. Thin-Walled Struct. 2009, 47, 555–567. [Google Scholar] [CrossRef]
- Lusty, C.; Bailey, N.Y.; Keogh, P.S. Control of flexible rotor vibration with flexibly mounted active magnetic bearings. Mech. Mach. Sci. 2019, 62, 65–73. [Google Scholar]
- Der Hagopian, J.; Mahfoud, J. Rotating machine critical speed suppressing by using electromagnetic actuators. In Proceedings of the ASME 2011 Turbo Expo: Turbine Technical Conference and Exposition, Vancouver, BC, Canada, 6–10 June 2011; Volume 6, pp. 315–319. [Google Scholar]
- Provenza, A.J.; Montague, G.T.; Jansen, M.J.; Palazzolo, A.B.; Jansen, R.H. High temperature characterization of a radial magnetic bearing for turbomachinery. J. Eng. Gas Turbines Power 2005, 127, 437–444. [Google Scholar] [CrossRef]
- Circosta, S.; Bonfitto, A.; Lusty, C.; Keogh, P.; Amati, N.; Tonoli, A. Analysis of a shaftless semi-hard magnetic material flywheel on radial hysteresis self-bearing drives. Actuators 2018, 7, 87. [Google Scholar] [CrossRef]
- Dagnaes-Hansen, N.; Santos, I.F. Magnetic bearings for non-static flywheel energy storage systems (FESS). In Proceedings of the 10th International Conference on Rotor Dynamics—IFToMM, Rio de Janeiro, Brazil, 23–27 September 2018; Springer International Publishing: Cham, Switherland, 2019; Volume 60, pp. 116–131. [Google Scholar]
- Bleuler, H.; Cole, M.; Keogh, P.; Larsonneur, R.; Maslen, E.; Nordmann, R.; Okada, Y.; Schweitzer, G.; Traxler, A. Magnetic Bearings: Theory, Design, and Application to Rotating Machinery; Springer: Berlin, Germany, 2009. [Google Scholar]
- ISO 14839-2:2004; Mechanical Vibration—Vibration of Rotating Machinery Rquipped with Active Magnetic Bearings—Part 2: Evaluation of Vibration. International Organization for Standardization: Geneva, Switzerland, 2004.
- Keogh, P.S. Contact dynamic phenomena in rotating machines: Active/passive considerations. Mech. Syst. Signal Process. 2012, 29, 19–33. [Google Scholar] [CrossRef][Green Version]
- Li, P.; Sahinkaya, M.N.; Keogh, P. Active recovery of contact-free levitation in magnetic bearing systems. Proc. ASME Des. Eng. Tech. Conf. 2012, 1, 673–680. [Google Scholar]
- Defoy, B.; Alban, T.; Mahfoud, J. Experimental assessment of a new fuzzy controller applied to a flexible rotor supported by active magnetic bearings. J. Vib. Acoust. Trans. ASME 2014, 136, 051006. [Google Scholar] [CrossRef]
- Nguyen, N.P.; Mung, N.X.; Thanh, H.L.N.N.; Huynh, T.T.; Lam, N.T.; Hong, S.K. Adaptive sliding mode control for attitude and altitude system of a quadcopter uav via neural network. IEEE Access 2021, 9, 40076–40085. [Google Scholar] [CrossRef]
- Gautam, D.; Ha, C. Control of a quadrotor using a smart self-tuning fuzzy PID controller. Int. J. Adv. Robot. Syst. 2013, 10, 380. [Google Scholar] [CrossRef]
- Lusty, C.; Keogh, P. Active vibration control of a flexible rotor by flexibly mounted internal-stator magnetic actuators. IEEE/ASME Trans. Mechatron. 2018, 23, 2870–2880. [Google Scholar] [CrossRef]
- Maslen, E.; Hermann, P.; Scott, M.; Humphris, R. Practical limits to the performance of magnetic bearings: Peak force, slew rate, and displacement sensitivity. J. Tribol. 1989, 111, 331–336. [Google Scholar] [CrossRef]
- Lalanne, M.; Ferraris, G. Rotordynamics Prediction in Engineering, 2nd ed.; John Wiley: Hoboken, NJ, USA, 1990. [Google Scholar]






| Variable | Parameter | Value | Unit |
|---|---|---|---|
| Coil turns | N | 200 | turns |
| Maximum current | 5 | A | |
| Bias current | A | ||
| Permeability of free space | N A | ||
| Pole area | m | ||
| Pole radial clearance | mm | ||
| Poles angle | ° | ||
| Maximum AMB force | 980 | N |
| Variable | Parameter | Value | Unit |
|---|---|---|---|
| AMB constant | N m A | ||
| Current stiffness | N A | ||
| Negative stiffness | N m | ||
| Equivalent stiffness | N m | ||
| Equivalent damping | N s m | ||
| Proportional gain | P | A m | |
| Derivative gain | D | 10 | A s m |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fieux, G.A.; Bailey, N.Y.; Keogh, P.S. Internal Rotor Actuation and Magnetic Bearings for the Active Control of Rotating Machines. Actuators 2022, 11, 57. https://doi.org/10.3390/act11020057
Fieux GA, Bailey NY, Keogh PS. Internal Rotor Actuation and Magnetic Bearings for the Active Control of Rotating Machines. Actuators. 2022; 11(2):57. https://doi.org/10.3390/act11020057
Chicago/Turabian StyleFieux, Gauthier A., Nicola Y. Bailey, and Patrick S. Keogh. 2022. "Internal Rotor Actuation and Magnetic Bearings for the Active Control of Rotating Machines" Actuators 11, no. 2: 57. https://doi.org/10.3390/act11020057
APA StyleFieux, G. A., Bailey, N. Y., & Keogh, P. S. (2022). Internal Rotor Actuation and Magnetic Bearings for the Active Control of Rotating Machines. Actuators, 11(2), 57. https://doi.org/10.3390/act11020057






