Abstract
The paper proposes a novel data-driven approximation kinematic (DAK) model to estimate the shape and opening level of a PneuNets soft gripper in relation to the applied pressure signal. The model offers suitable capabilities for implementing in real-time applications involving soft grasping planning and size recognition of fragile objects with different sizes and shapes. The proposed DAK model estimates the free bending behavior of a PneuNets actuator (soft gripper finger) based on a set of approximation functions derived from experimental data and an equivalent serial mechanism that mimics the shape of the actuator. The model was tested for a commercial PneuNets actuator with decreasing chamber height, produced by SoftGripping Co. (Hamburg, Germany). The model validation is accomplished through a set of experiments, where the shape and elementary displacements were measured using a digital image processing technique. The experimental data and the estimated data from the DAK model were compared and analyzed, respectively. The proposed approach has applicability in sensorless/self-sensing bending control algorithms of PneuNets actuators and in soft grasping applications where the robotic system must estimate the opening level of the gripper in order to be able to accomplish its task.
1. Introduction
Grasping is an important function when it comes to human beings and robots. In robotics, this function is performed by a grasping device called a gripper. The type of gripper depends on the task performed by the robot, and its characteristics are crucial because it is the part of the robot that is designed to interact with the environment [1,2]. Tai et al. [3] classified robotic grippers as: (1) industrial grippers for structured and unstructured environments, (2) grippers for fragile objects manipulation—soft grippers, (3) grippers for medical applications, (4) micro and nano grippers, and (5) soft fabric grippers. In this paper, we will address aspects related to soft grasping tasks (fragile object manipulation) using soft robotic grippers based on PneuNets bending actuators.
Traditional grippers are well established in the literature and are usually made from rigid elements and joints connected together. Simple parallel finger grippers or more complex anthropomorphic robotic hands with many degrees of freedom (DoF) are representative examples of this category [1,2]. Their development and requirements (DoF, number of fingers, actuation method, mechanisms used, gripping range and stroke, etc.) are closely related to industrial automation, and various manufacturers such as FESTO, SCHUNK, SMC et al. offer many commercial solutions in this matter [3,4].
Soft grippers, on the other hand, are a new class of grasping devices associated with the field of soft robotics where flexible and compliant materials are used together with new types of actuators to fulfill the grasping function [5,6]. They have the advantage of being a promising grasping solution that can be used in unstructured and dynamic working environments where interaction with soft/fragile (deformable) objects is required [7]. For example, a pick-and-place operation with a soft gripper on an assembly line can be considered a task in a structured (known) environment because the position and orientation of the grasped object are usually predefined. On the other hand, an agricultural harvesting operation can be considered a task performed in an unstructured (unknown) environment because the grasping function is performed by the robot under various uncertainties [7,8,9].
As highlighted by Fantoni et al. in the work of [10], a soft grasping task is a complex process and can be described by the following phases: (1) approaching the object with the gripper, (2) getting in touch with the object, (3) increasing the force, (4) securing the object, (5) moving the object, and (6) releasing the object. The successful completion of all phases is determined by the soft grasping technology. State-of-the-art technologies in this field are highlighted in the work of [11,12,13], respectively. The most used one is based on soft pneumatic actuators (SPA) such as: inflated silicone elastomer chambers, McKibben pneumatic muscles, pneumatic bellows, PneuNets bending structures, etc.
However, from all the enumerated SPAs, PneuNets bending actuators have attracted the attention of many researchers in the last years due to their relative simplicity of design and fabrication [14,15,16,17]. PneuNets are pneumatic actuators that have into their structure a network of pneumatic chambers (pneumatic cells), which, once pressurized, generate a preprogrammed type of motion (usually a bending motion). Material type, geometry of the chambers, and input pressure are key elements in the design of such actuators because these parameters directly influence their bending and dynamic behavior [18,19,20]. Figure 1a shows, for example, a soft gripper with two sensorless PneuNets bending actuators with decreasing chambers height produced by SoftGripping [21] that can grasp spherical, rectangular, or cubic objects between 5 and 120 mm and up to 300 g. In this example, the gripper also includes a vacuum suction cup that improves the soft grasping task. Due to its inherent compliance, this technology offers new capabilities in robotic applications [22,23,24,25].
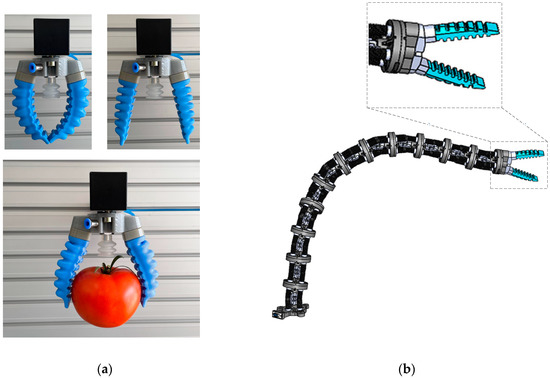
Figure 1.
Soft grippers based on PneuNets bending actuators and their robotic applications: (a) soft interaction with fragile juicy fruits such as tomatoes; (b) conceptual design of Python robot equipped with a PneuNets-based soft gripper.
Gripping range and stroke are two important parameters associated with the performance of a gripper in general [1,2]. These parameters define the overall dimensions of the gripper and are related to the bending behavior of PneuNets actuators (gripper fingers).
A kinematic model that can estimate the curvature (shape) of the gripper fingers, thus the opening level of the gripper, becomes important for designing the grasping control algorithm of grippers used in unstructured environments by robotic systems. Moreover, such a modeling approach can be viewed as a step toward applications involving real-time control of the opening level of this type of grippers.
In Figure 1b is presented the conceptual design of Python [26], a snake-like robot equipped with a soft gripper similar to the one presented in Figure 1a. Python was designed to perform various tasks in unstructured environments that involve navigation and soft grasping of fragile objects (soft and juicy fruits) of different sizes and shapes. The model is useful when the robot is approaching a fragile object up to the phase where gripper fingers get close enough to grasp the object. In this case, it is important to estimate the opening level of the gripper in relation to the size of the manipulated object. This can be accomplished by controlling the bending angle of actuators, thus the opening level of the gripper.
The applicability of the model is related especially to these types of applications where the robot is equipped with a commercial soft gripper based on sensorless PneuNets. The shape and opening level of these PneuNets actuators cannot be measured directly due to the lack of integrated sensors.
In this context, the paper proposes a model that can be used to estimate the shape and opening level of a PneuNets soft gripper in relation to the applied pressure signal. The main contribution of the paper is the data-driven approximation kinematic (DAK) model that approximates the free bending behavior of a PneuNets actuator (gripper fingers). The proposed model predicts the free bending behavior of the actuator (position and relative orientation of every pneumatic chamber) using a set of approximation functions that are derived from data-driven experimentation and an equivalent serial mechanism that mimics the shape of the actuator. The model is developed for PneuNets actuators with decreasing chamber height (variable chambers), but it can be used for PneuNets actuators with constant chamber height too (similar chambers). Through the approximation functions, the model captures material, and geometrical features of actuators (modulus of elasticity, hardness, chambers geometry), that are usually very hard to model, especially for commercial PneuNets actuators in the absence of a comprehensive datasheet.
The model is experimentally tested and validated on a commercial PneuNets actuator produced by SoftGripping [21] (Figure 1a). Numerical results are successfully compared with a set of experimental measurements obtained using a digital image processing technique, therefore confirming the effectiveness of the approach. The proposed approach is a suitable trade-off between the complexity and performance of the model, as it will be shown.
The rest of the paper is organized as follows. Section 2 continues with a review on modeling the bending angle in relation to the input pressure for PneuNets bending actuators. Next, in Section 3 is described the proposed DAK model and the experimental setup used for obtaining the approximation functions. Numerical and experimental results are compared and validated in Section 4. Finally, the paper ends up with the conclusions and future work.
2. Review on Modeling Bending Behavior of PneuNets Actuators
The bending behavior of PneuNets actuators has attracted interest for many researchers over the last years, and as a result, numerical, analytical, and empirical (statistical) models were developed to highlight the relationship between bending angle and input pressure.
Numerical methods consist mainly of finite element modeling (FEM) using software packages such as Abaqus, Ansys, COMSOL, etc. FEM simulations require much computing power, are time consuming, and are not recommended for real-time applications. The methods can be useful to validate new PneuNets actuators designs prior to the manufacturing phase. A typical FEM simulation involves the drawing of the actuator CAD model, assignment of material properties, meshing, defining boundary conditions and loads, and analysis of results. For an overview and recent developments of FEM for PneuNets bending actuators, the reader should consult [27,28].
Analytical modeling of PneuNets is still a challenging task because they are made entirely from flexible, hyper-elastic materials, and their natural bending curvature and flexural rigidity vary with the input pressure. Majidi et al. [29] developed a mathematical relationship between input pressure and bending curvature of a PneuNets actuator with constant chamber height. The mathematical model was formulated using the principle of minimum potential energy, and their results indicate that the curvature kp of the actuator linearly depends on the input pressure P as follows:
where constant D depends on the geometry of the chambers and material properties. It was considered that the modulus of elasticity E is constant, which is a simplified assumption for hyper-elastic materials, and that the effect of gravity can be neglected. Another important contribution in the field is the bending angle model proposed by Alici et al. in the work of [30]. They developed a relationship to estimate the bending angle of a PneuNets actuator with constant chamber height as a function of input pressure when the actuator is positioned as a cantilever beam. By using Euler–Bernoulli beam theory and the assumption that the actuator bends into a constant curvature shape, the following steady-state relationship was obtained:
where constants C and D depend on chamber geometry and material. Here, the bending angle varies in a nonlinear way with input pressure and could be a better choice for modeling PneuNets made from hyper-elastic materials since constant C is inversely proportional with the square of E [30]. Considering the constant curvature assumption, if a PneuNets actuator is fixed at one end and the other one can bend freely, the bending moment M generated from the pressure force and inner area of the pneumatic chambers will extend the actuator from the initial position to a final position. For each input pressure Pi will result in a different circular shape Ci(Oi,Ri), with center Oi on the Oy axis and radius Ri, as presented in Figure 2. The coordinates of point Bi(Bix, Biy) at the tip of the actuator can be calculated by using [30,31]:
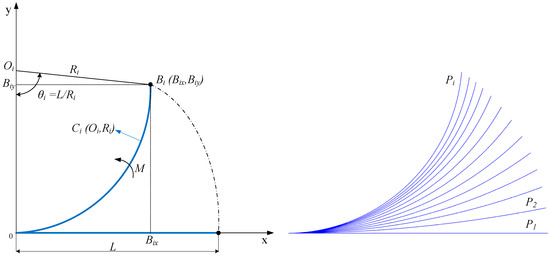
Figure 2.
Constant curvature assumption: deformation of a PneuNets bending actuator.
Shapiro et al. [32] used a similar beam deflection model for testing bi-Bellows actuators with external and internal hoops. They concluded that the model offers suitable results in predicting the curvature of actuators with external hoops, which are very similar, with PneuNets bending actuators with constant chamber height. Wang et al. [33] used a line-segment analytical model to study the dynamics of a 3D-printed SPA. The relationship between pressure and bending angle was approximated by a linear relationship.
Regarding empirical models, Wang et al. [34] developed an experimental procedure to determine the shape of three 3D-printed PneuNets actuators (gripper fingers) with constant chamber height to study the soft grasping capabilities of a soft gripper designed for automatic lunch box packing. To determine the shape of the fingers, they have integrated a flex sensor into the lower layer of the actuators, and a linear relationship between bending angle and input pressure was derived based on experimental data. Relative standard deviation (RSD) was, in general, less than 5% for an input pressure between 0 and 0.4 bar.
Chen et al. [35] used embedded air pressure and flex sensors on a PneuNets soft gripper for size recognition and adaptive grasping of spherical objects. Experimental data from the sensors were also used to fit an empirical model of the bending angle vs. input pressure using a linear relationship.
More recently, Elgeneidy et al. [36] proposed an empirical modeling approach to control the bending angle of a PneuNets actuator that integrates cheap resistive flex sensors. Their objective was to accurately estimate positioning in various grasping applications. Three empirical models were proposed and analyzed using regression analysis based on the experimental data provided by the sensors. Adjusted R2 varied between 0.880 and 0.998 and standard error S between 1.443 and 2.280 deg. A mean squared error (MSE) between 1.36 and 4.13 deg2 and a standard deviation (SD) between 1.15 and 1.94 deg was obtained compared with a set of measurements acquired with a vision system. Artificial neural networks were also used to capture the bending characteristic of the actuator, and an MSE of 1.36 deg2 and an SD of 1.15 deg were reported by the authors. They used molding techniques to fabricate the PneuNets.
This review emphasizes that analytical models and empirical models are most suited for real-time applications compared with numerical FEA models. However, analytical modeling of PneuNets by using material and geometrical parameters is challenging due to the strong nonlinear dependencies, while empirical (statistical) models use many sets of experimental data. The majority of analyzed papers deal with PneuNets with constant chamber height that are laboratory prototyped by using 3D printers or molding techniques and usually integrate a combination of different types of sensors that simplifies the estimation of bending angle. The constant curvature assumption is generally used to define the shape of PneuNets actuators, which is true only for actuators with constant chamber height. However, commercial sensorless PneuNets are becoming very popular and are usually built with a decreasing chamber height configuration (variable curvature). That means that the curvature is not constant but decreases gradually and the contact angle at the tip of the actuator is larger, which increases the grasping stability [17]. In this situation, the shape of the actuator is a nonlinear deformation curve generated by the deformation of each pneumatic chamber. If such sensorless commercial actuators are used to build a soft gripper, the use of the DAK model to approximate the opening level of the gripper in relation to the applied pressure could be a suitable solution for real-time control applications.
3. DAK Model and Experimental Setup
3.1. Description of DAK Model
The DAK model is designed to model the deformation of SPA actuators, made of elastic materials, and characterized by a deformable cellular architecture (cell network), programmed to execute a bending motion in plane. The model is not applicable for twisting, extending, or contracting SPAs.
The model associates the SPA actuator (gripper finger) with an equivalent serial mechanism, where the angular displacements of the fictitious revolute joints are approximated by regression functions, which implicitly include all the particularities of this type of actuators, such as: material properties (modulus of elasticity, hardness), manufacturing errors, unknown or hard to determine parameters such as cell geometry, wall thickness, etc.
Therefore, the DAK model addresses the kinematic modeling of SPA-type actuators regardless of their structural parameters or architecture, the application of the method requires the following steps: (a) defining the equivalent mechanism and determining its geometric parameters; (b) acquiring experimental data used to develop the DAK model; (c) numerical processing of experimental data and obtaining the DAK model; and (d) verification and validation of the DAK model by methods based on image processing techniques. The paper details the implementation steps for an actuator produced by SoftGripping [21], but these steps can be similarly applied to any type of SPA actuator with planar bending.
The schematic representation of the proposed DAK model is presented in Figure 3. The model uses pressure P as input data and returns the displacement of each element of an equivalent mechanism and the relative angles between two adjacent elements of the mechanism. The output information can be used to define a particular shape of the actuator based on the input stimulus. The model was developed considering that the cells of the actuator vary along its length (actuator with decreasing chamber height).
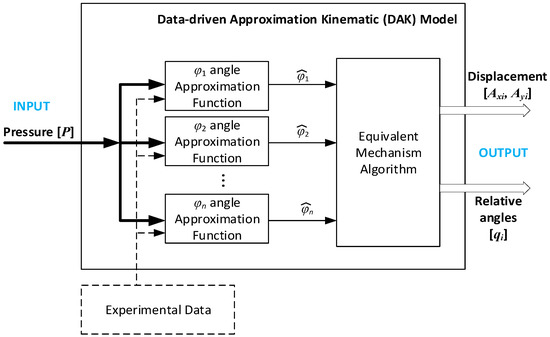
Figure 3.
DAK model—block diagram.
The equivalent mechanism is used to model the shape (deformation) of the actuator (gripper finger). The mechanism consists of a series of kinematic elements connected to each other by revolute joints that mimic the shape of the actuator. Such an approach is a suitable trade-off between the complexity of a real PneuNets actuator (nonlinear flexible structure) and the simplicity of a planar rigid body serial manipulator where the elasticity of the elements is neglected. Therefore, the number of elements of the mechanism equals the number of pneumatic chambers of the actuator. In addition, the accuracy of the model depends on the number of pneumatic chambers.
In Figure 4, an example of an equivalent mechanism for a PneuNets actuator with seven pneumatic chambers PCj {j = 1…7} is presented. Each pneumatic chamber PCj has a rigid area GPj {j = 1…7} (gripping pad), which comes in touch with the manipulated object. Each gripping pad is associated with a kinematic element of the DAK model, both components having the same orientation φj {j = 1…7}.
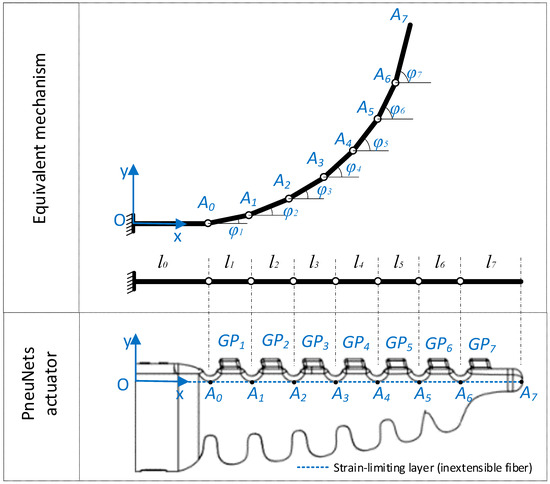
Figure 4.
Equivalent mechanism to approximate the bending shape of a PneuNets actuator with seven pneumatic chambers.
If the lengths li {i = 0…7} are known, the output values of the DAK model can be calculated in two phases. First, a set of approximation functions is used to estimate the absolute angles φj {j = 1…7} that define the orientation of each kinematic element of the mechanism with respect to the horizontal axis Ox of the global reference system. Then, in the second phase, these angles are used to calculate the position of each kinematic joint Ai {i = 0…7} and the relative angles qi {i = 1…7} between two consecutive elements, resulting in this way the approximated shape of the actuator.
Considering the research highlighted in Section 2, the deformation of each element of the actuator (pneumatic chamber) will be modeled by an approximation function of the lowest order. In the literature, the estimation errors for the approximation models are around 5%. In this study, using the DAK model, it is intended to obtain an estimation error below 3%. The approximation functions are used by the algorithm of the equivalent mechanism (Figure 3) to calculate the shape of the actuator. Preliminary experimental results lead to approximation functions of the second order (model M2), but the regression analysis was performed comparatively also for approximation functions of the first order (model M1).
where b01, b11, and b02, b12, b22 are regression coefficients of both models that can be calculated using linear and polynomial regression analysis based on the experimental data acquired from a real PneuNets actuator. Then, Equation (6) is used to calculate the cartesian position of points Ai {i = 1…7} (it is considered that the coordinates of point A0 are known):
and Equation (7) to compute the relative angles qi {i = 1…7} (where φ0 = 0) between two consecutive elements:
3.2. Experimental Setup
The experimental setup used to acquire the experimental data for obtaining the DAK model is presented in Figure 5. In Table 1, the main components are detailed. The experimental setup includes the PneuNets actuator (9) with seven pneumatic chambers (with decreasing height) produced by SoftGripping [21] that is actuated by a pneumatic control box (3) that regulates the input pressure P. The compressed air is supplied by a compressor (1) and filtered by an air service unit (2). A soft, flexible capacitive sensor (8) produced by BendLabs [37] is used to measure the absolute angles φj. This type of sensor can measure the angular displacement between its extremities without being influenced by its own elastic deformation, thus having the property of path independence [37]. The precision of the measurements provided by the sensor is 0.18 deg. The sensor was attached successively to each gripping pad GPj {j = 1…7} of the actuator, and the angular displacements φj {j = 1…7} (Figure 4) were measured with respect to the input pressure P. In Figure 5 is presented the setup for measuring the angular displacement φ7 when the sensor is mounted on GP7 (the seventh element of the equivalent mechanism). In this case, the measured angle φ7 includes the deformation of all pneumatic chambers PC1 up to PC7. Therefore, every angle φj {j = 1…7} accounts for the cumulative deformation effect of chambers PC1 up to PCj {j = 1…7}. The relative angles qi {i = 1…7} between two consecutive elements (the bending angle of each pneumatic chamber) are determined by Equation (7).
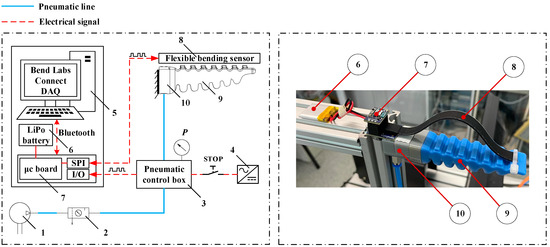
Figure 5.
Experimental setup.

Table 1.
The main components of experimental setup.
Data acquisition is accomplished with Bend Labs Connect DAQ software (5) through a Bluetooth communication interface. The microcontroller board (7) communicates with the flexible sensor (8) through a serial communication interface.
The lengths of the elements that define the equivalent mechanism are: l0 = 16.75 mm, l1…l6 = 8.5 mm, and l7 = 10.75 mm, and the element of length l0 refers to the fixed frame (10). All dimensions were measured on the PneuNets actuator presented in Figure 5 with respect to the equivalent mechanism shown in Figure 4.
4. Numerical Simulations and Experimental Results
4.1. Numerical Simulations
Using the experimental setup presented above, a set of measurements were performed to obtain the absolute values of angles φj {j = 1…7} with respect to the fixed frame based on input pressure. As shown in Figure 6, one end of the flexible bending sensor was attached successively to each gripping pad GPj {j = 1…7} of the actuator chambers PCj {j = 1…7} and the other one to the fixed element.

Figure 6.
Measuring bending angles φj of PneuNets actuator: (a) sensor positioned on the 7th pneumatic chamber (GP7); (b) sensor positioned on the 4th pneumatic chamber (GP4); (c) sensor positioned on the 1st pneumatic chamber (GP1).
For each position of the sensor, 13 measurements were made by changing the input pressure from 0 to 1.2 bar (working range of the actuator specified in datasheet [21]) with an increment of 0.1 bar. The procedure was repeated three times for each experiment, and after that, a mean value was calculated. The final numerical values are presented in Table 2. Based on these data, through a linear and polynomial regression analysis, the models M1 and M2 were obtained. The accuracy of both models was evaluated based on two metrics: adjusted coefficient of determination R2 and standard error S deg.

Table 2.
Experimental data for modeling approximation functions .
The best-fits of approximation functions {j = 1…7} using model M2 are presented in Figure 7, while the regression coefficients together with adjusted R2 and S are presented in Table 3.
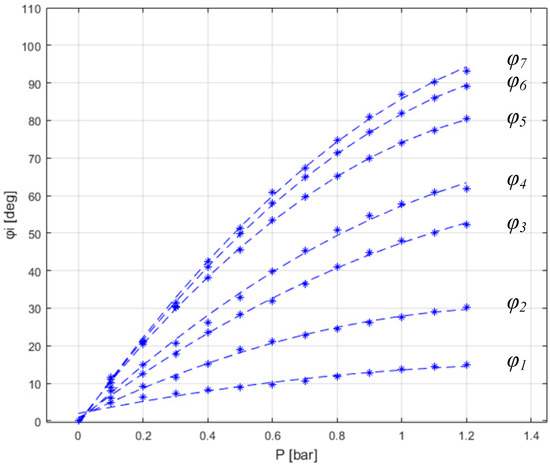
Figure 7.
Best-fits of approximation functions {j = 1…7} using model M2.

Table 3.
Regression analysis statistics for models M1 and M2.
A value of adjusted R2 close to 1 means that the variation of angle φj {j = 1…7} is well predicted, but, in this case, both models have comparable values (higher than 0.95 in general). However, S deg offers a better view of the approximation quality.
Based on the data presented in Table 3, standard error S for M1 is 1.24 up to 8.54 times higher than M2 which shows that the second model provides a better prediction in this case. Linear increase in S for model M1 suggests that a simple linear relationship cannot account for large deformations of the actuator with variable chamber height. Because the 95% prediction interval equals roughly 2ˑS [38,39], the model M1 can predict the bending angle from as low as ±2.32 deg up to ±10.11 deg, while model M2 from as low as ±0.65 deg up to ±2.42 deg. Therefore, 95% of estimations made by model M2 fall between a ±2.5 deg in general over the entire experimental data. If we consider the maximum value of φj(P) {j = 1…7} from Table 2 (93.24 deg, maximum deformation), the relative estimation error (±2.5 deg interval) is below 3%.
Based on the regression analysis results, model M2 is used to obtain the approximation functions {j = 1…7} that estimate the orientation of each kinematic element of the equivalent mechanism.
The DAK model was implemented in MATLAB/Simulink and simulated for different input pressures that cover the whole functional range. The model provides the positions of the joints Ai {i = 0…7} and relative angles qi {i = 1…7} between two consecutive elements of the equivalent mechanism, which are used to draw the bending shape of the actuator (nonlinear bending curve with variable curvature). The simulation results are presented in Figure 8.
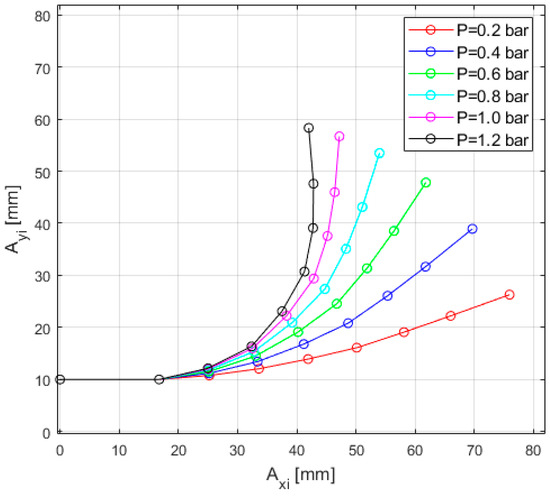
Figure 8.
Numerical simulation: estimated bending shape of the PneuNets actuator obtained with the DAK model implemented in MATLAB/Simulink.
4.2. Experimental Results
To validate the DAK model, a set of experiments that use image processing measurements were performed. To evaluate the PneuNets actuator deformation, a number of eight markers (circular shape) were added on the actuator body and one marker on the actuator fixed base. Each marker on the actuator was positioned on the strain-limiting layer (inextensible fiber) of the actuator at the point of tangency between the strain-limiting layer and the circular arc that connects two adjacent chambers (see Figure 9a).
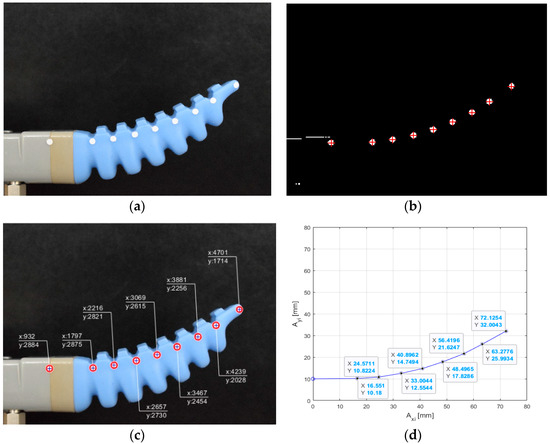
Figure 9.
Image processing steps for P = 0.3 bar: (a) original image with markers (b) identification of marker positions (c) markers’ cartesian coordinates (in pixels) (d) coordinates of Ai points in relation with the actuator reference system.
Using a high-resolution camera, the actuator deformation was recorded (images) for different input pressures: P1 = 0.3 bar, P2 = 0.6 bar, P3 = 0.9 bar, P4 = 1.1 bar. The images were then processed by using MATLAB functions in order to identify the markers (Figure 9b) and their cartesian coordinates (Figure 9c). A scale factor fk {k = 1…4} that defines the correspondence between the pixel dimension and real distances on the actuator was calculated. This scale factor is used to determine the markers position (coordinates of points Ai {i = 0…7}) in relation to the actuator reference system (Figure 9d). The results obtained through the image processing method (measured bending curve of the actuator for different input pressures) are shown in Figure 10 and are used to evaluate the accuracy of the DAK model.
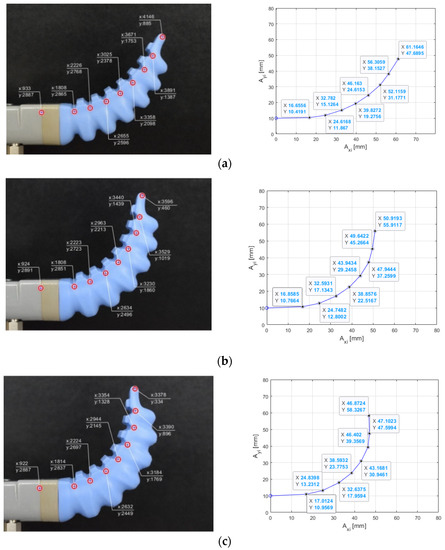
Figure 10.
Image processing results for different input pressures: (a) P = 0.6 bar; (b) P = 0.9 and (c) P = 1.1 bar.
Using the same input pressures (P1…P4), the DAK model is used to estimate the displacement of each element of the equivalent mechanism (parameters ). The numerical values of estimated () vs. measured (A1 to A7) results and the specific errors (RE, MRE, AE, MAE) are summarized in Table 4, Table 5, Table 6 and Table 7.

Table 4.
Validation of results for P = 0.3 bar.

Table 5.
Validation of results for P = 0.6 bar.

Table 6.
Validation of results for P = 0.9 bar.

Table 7.
Validation of results for P = 1.1 bar.
In Figure 11 are presented the measured and estimated shapes of the actuator. The obtained errors depend on the successful implementation of each step of the proposed method, being related to the following: the accuracy of the sensory measurement system of angles and input pressures, the algorithms used for approximation functions, markers’ positioning, image processing techniques, camera resolution, camera lens distortion.
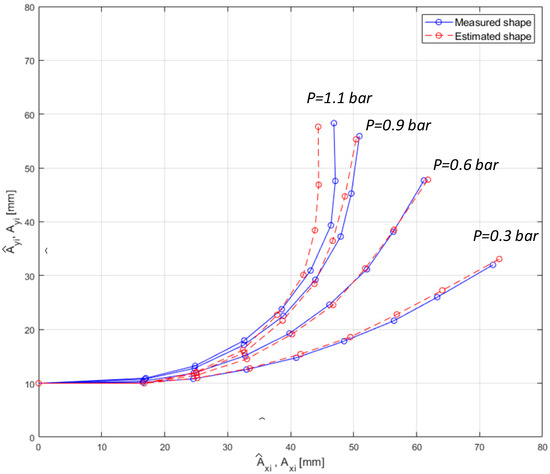
Figure 11.
Estimated vs. measured shape of PneuNets actuator (DAK model vs. experimental results).
4.3. Discussion
For DAK model efficiency analysis, four error metrics were used: relative error (RE), mean relative error (MRE), absolute error (AE), and mean absolute error (MAE). The obtained results (presented in Table 4, Table 5, Table 6 and Table 7) demonstrate that the proposed model approximates the bending deformation of the actuator through a nonlinear curve, the deviation from validation data set (captured through image processing) being characterized by the following errors: for input pressure P = 0.3 bar the MRE is 3.66% and the MAE is 0.76 mm, for input pressure P = 0.6 bar the MRE is 1.41%, and the MAE is 0.39 mm, for input pressure P = 0.9 bar the maximum MRE is 3.77% and the MAE is 0.84 mm, and for input pressure P = 1.1 bar the MRE is 4.37%, and the MAE is 1.41 mm.
The DAK model allows the modeling of the nonlinear deformation of the SPA actuators, the method implementation steps (see Section 3.1) being accompanied by specific features, advantages, and disadvantages in relation to other methods in the field.
One of the most relevant methods for modeling the kinematics of SPAs actuators uses the Euler–Bernoulli (E-B) beam theory [30]. The method based on E-B theory (E-B method) is applied for actuators with equal deformable cells (identical cells: the same geometry and equal sizes), respectively for a given pressure, it provides, as a result, a circular deformation shape (curve) with constant curvature (constant radius). Thus, for a given pressure Pi, the method E-B provides a circular deformation curve to approximate the shape of the actuator, for example: pressure P1 determines -> C1(O1,R1); pressure P2 determines -> C2(O2,R2), where O1 and O2 are the origins of circles, respectively R1, R2 are the radii of circles (see Figure 2). The alternative proposed method based on the DAK model (DAK method) aims to model the kinematics of SPA actuators with different deformable cells (different cells: similar geometry but different sizes), respectively for a given pressure Pi the method provides a nonlinear deformation curve with variable curvature.
On the other hand, the E-B method assumes that the cells are deformed identically; the angle θ that measures the arc of the deformation curve is estimated through a parabolic law θ(P) (implicitly, the deformation curve is a circular arc) [30]. The DAK model provides the angles φj {j = 1…7} of an equivalent mechanism respectively; the approximation of each angle is estimated by a parabolic approximation law (see Figure 4).
Therefore, the E-B method is recommended to be used for actuators with identical cells, while the DAK method is designed to be applied to actuators with different cell sizes. However, if the DAK method is applied to actuators with identical cells, the approximation functions {j = 1…7} will generate equal relative angles qi {i = 0…7} between kinematic elements, respectively the equivalent mechanism will have the vertices Ai {i = 0…7} inscribed on a circular arc, the same resulting from the E-B method. In this situation, the two methods, even if different, will provide similar results, the differences being determined by the ways of applying the methods and by the specific errors of each method. However, if the E-B method is applied to actuators with different cells, it would approximate the nonlinear deformation of the actuator by a circular arc (constant curvature curve) respectively; the E-B method is characterized in this case by a higher theoretical error than the DAK method.
The implementation of each method is accompanied by its own sources of errors that make the comparative analysis of the results questionable, but referring to the principles (mathematical approximation) behind the methods, based on the previous analysis, the following conclusions are drawn: (1) if the actuator cells tend to be the same size (identical cells), the results of the two methods converge to the same result, but the E-B method involves a simpler approach than the DAK method; (2) if the actuator cells tend to be very different, the results of the E-B method deviate from the truth value, while the results of the DAK method keep the accuracy of the approximation; (3) both methods have sources of errors that can affect the accuracy of the results. The error sources are related to the quality of the sensory system used to measure the deformation and the input pressure, the algorithms used in approximation, positioning errors of markers, and other specific constraints of each method.
5. Conclusions
The paper proposed a new data-driven kinematic (DAK) model, which approximates the shape of PneuNets bending actuators in relation to input pressure and thus the opening level of PneuNets-based soft grippers. The DAK model is a combination of empirical (statistical) and analytical techniques and was developed for PneuNets with decreasing chamber height (the shape of the actuator is a nonlinear deformation curve). The model was validated on a commercial PneuNets actuator produced by SoftGripping. The validation procedure involved the comparison of estimated values provided by the DAK model with the experimental values provided by a digital image processing technique when the actuator was pressurized under different input pressures. MRE errors were less than 5%, and MAE errors were less than 1.5 mm, therefore confirming the effectiveness of the approach. The obtained results offer the premise of using the DAK model in the implementation of real-time self-sensing bending control algorithms for soft grippers that integrate commercial sensorless PneuNets actuators with nonlinear deformation. Nevertheless, the model can also be used for other SPA actuators with planar bending.
The proposed approach is a suitable trade-off between complexity and performance because it captures material and geometrical features of PneuNets actuators that are usually hard to model. The advantage of the DAK model resides in its practical utility in real-time soft grasping applications where the robotic system must estimate the opening level of the gripper in order to be able to accomplish its task.
The proposed DAK model can estimate the shape and opening level of a PneuNets-based soft gripper, in relation to the applied pressure signal, up to the phase when gripper fingers get in touch with the manipulated object. When contact is accomplished, a grasping force control strategy of PneuNets-based grippers requires the control of input pressure and the development of other types of estimation algorithms, which are planned to be developed as future work.
Author Contributions
Conceptualization, O.H., C.R. and C.L.; methodology, C.R., C.L. and O.H.; software, C.R. and C.L.; validation, C.L., C.R. and O.H.; formal analysis, O.H.; investigation, C.R.; resources, C.R. and C.L.; data curation, C.R; writing—original draft preparation, C.R. and C.L.; writing—review and editing, C.R., C.L. and O.H.; visualization, C.L. and C.R.; supervision, O.H.; project administration, O.H.; funding acquisition, O.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Romanian Ministry of Education and Research, CCCDI—UEFISCDI, project number PN-III-P2-2.1-PED-2019-4939, within PNCDI III https://uefiscdi.gov.ro/proiect-experimental-demonstrativ-ped (accessed on 12 February 2022).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
This work was supported by a grant from the Romanian Ministry of Education and Research, CCCDI—UEFISCDI, project number PN-III-P2-2.1-PED-2019-4939, within PNCDI III.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study, in the collection, analyses, or interpretation of data, in the writing of the manuscript, or in the decision to publish the results.
References
- Monkman, G.J.; Hesse, S.; Schunk, H. Robot Grippers, 1st ed.; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2006; pp. 1–17. [Google Scholar]
- Staretu, I. Gripping Systems; Derc Publishing House: Tewksbury, MA, USA, 2011. [Google Scholar]
- Tai, K.; El-Sayed, A.-R.; Shahriari, M.; Biglarbegian, M.; Mahmud, S. State of the Art Robotic Grippers and Applications. Robotics 2016, 5, 11. [Google Scholar] [CrossRef]
- Zhang, B.; Xie, Y.; Zhou, J.; Wang, K.; Zhang, Z. State-of-the-art robotic grippers, grasping and control strategies, as well as their applications in agricultural robots: A review. Comput. Electron. Agric. 2020, 177, 105694. [Google Scholar] [CrossRef]
- Rad, C.; Hancu, O.; Lapusan, C. Aspects regarding “soft” grasping in smart agricultural harvesting tasks. Acta Tech. Napcensis Ser. Appl. Math. Mech. Eng. 2020, 63, 389–394. [Google Scholar]
- Shintake, J.; Cacucciolo, V.; Floreano, D.; Shea, H. Soft Robotic Grippers. Adv. Mater. 2018, 30, 1707035. [Google Scholar] [CrossRef] [PubMed]
- Gerez, L.; Chang, C.M.; Liarokapis, M. Employing Pneumatic, Telescopic Actuators for the Development of Soft and Hybrid Robotic Grippers. Front. Robot. AI 2020, 7, 601274. [Google Scholar] [CrossRef]
- Garcia, G.J.; Pomares, J.; Torres, F. Automatic robotic tasks in unstructured environments using an image path tracker. Control Eng. Pract. 2009, 17, 597–608. [Google Scholar] [CrossRef][Green Version]
- Ongaro, F.; Scheggi, S.; Yoon, C.; Brink, F.V.D.; Oh, S.H.; Gracias, D.H.; Misra, S. Autonomous planning and control of soft untethered grippers in unstructured environments. J. Micro-Bio. Robot 2017, 12, 45–52. [Google Scholar] [CrossRef]
- Fantoni, G.; Santochi, M.; Dini, G.; Tracht, K.; Scholz-Reiter, B.; Fleischer, J.; Lien, T.K.; Seliger, G.; Reinhart, G.; Franke, J.; et al. Grasping devices and methods in automated production processes. CIRP Ann. 2014, 63, 679–701. [Google Scholar] [CrossRef]
- Zaidi, S.; Maselli, M.; Laschi, C.; Cianchetti, M. Actuation Technologies for Soft Robot Grippers and Manipulators: A Review. Curr. Robot Rep. 2021, 2, 355–369. [Google Scholar] [CrossRef]
- Boyraz, P.; Runge, G.; Raatz, A. An Overview of Novel Actuators for Soft Robotics. Actuators 2018, 7, 48. [Google Scholar] [CrossRef]
- Walker, J.; Zidek, T.; Harbel, C.; Yoon, S.; Strickland, F.S.; Kumar, S.; Shin, M. Soft Robotics: A Review of Recent Developments of Pneumatic Soft Actuators. Actuators 2020, 9, 3. [Google Scholar] [CrossRef]
- Stano, G.; Arleo, L.; Percoco, G. Additive Manufacturing for Soft Robotics: Design and Fabrication of Airtight, Monolithic Bending PneuNets with Embedded Air Connectors. Micromachines 2020, 11, 485. [Google Scholar] [CrossRef] [PubMed]
- Payrebrune, K.M.; O’Reilly, O.M. On constitutive relations for a rod-based model of a pneu-net bending actuator. Extrem. Mech. Lett. 2016, 8, 38–46. [Google Scholar] [CrossRef]
- Mosadegh, B.; Polygerinos, P.; Keplinger, C.; Wennstedt, S.; Shepherd, R.F.; Gupta, U.; Shim, J.; Bertoldi, K.; Walsh, C.J.; Whitesides, G.M. Pneumatic Networks for Soft Robotics that Actuate Rapidly. Adv. Funct. Mater. 2014, 24, 2163–2170. [Google Scholar] [CrossRef]
- Liu, S.; Wang, F.; Zhang, G.W.; Liu, Z.; Zhang, W.; Tian, Y.; Zhang, D. A Novel Dual-Drive Soft Pneumatic Actuator with the Improved Output Force. In Intelligent Robotics and Applications; Yu, H., Liu, J., Liu, L., Ju, Z., Liu, Y., Zhou, D., Eds.; Springer: Cham, Switzerland, 2019; pp. 16–25. [Google Scholar] [CrossRef]
- Sun, Y.; Zhang, Q.; Chen, X.; Chen, H. An Optimum Design Method of Pneu-Net Actuators for Trajectory Matching Utilizing a Bending Model and GA. Math. Probl. Eng. 2019, 2019, 6721897. [Google Scholar] [CrossRef]
- Maruthavanan, D.; Seibel, A.; Schlattmann, J. Fluid-Structure Interaction Modelling of a Soft Pneumatic Actuator. Actuators 2021, 10, 163. [Google Scholar] [CrossRef]
- Song, E.J.; Lee, J.S.; Moon, H.; Choi, H.R.; Koo, J.C. A Multi-Curvature, Variable Stiffness Soft Gripper for Enhanced Grasping Operations. Actuators 2021, 10, 316. [Google Scholar] [CrossRef]
- SoftGripping Products, Datasheets. Available online: https://soft-gripping.com/assets/downloads/datasheets/sg_data_sheets.pdf (accessed on 7 December 2021).
- Navas, E.; Fernández, R.; Sepúlveda, D.; Armada, M.; Gonzalez-de-Santos, P. Soft Grippers for Automatic Crop Harvesting: A Review. Sensors 2021, 21, 2689. [Google Scholar] [CrossRef]
- Rodríguez, F.; Moreno, J.C.; Sánchez, J.A.; Berenguel, M. Grasping in Agriculture: State-of-the-Art and Main Characteristics. In Grasping in Robotics; Carbone, G., Ed.; Mechanisms and Machine Science; Springer: London, UK, 2013; Volume 10. [Google Scholar] [CrossRef]
- Kultongkham, A.; Kumnon, S.; Thintawornkul, T.; Chanthsopeephan, T. The design of a force feedback soft gripper for tomato harvesting. J. Agric. Eng. 2021, 52. [Google Scholar] [CrossRef]
- mGrip™—Modular Gripping System, Brochure. Available online: https://www.softroboticsinc.com/uploads/2021/03/Soft_Robotics_ModularGripping_800129_RevD_LR.pdf (accessed on 7 December 2021).
- Lapusan, C.; Hancu, O.; Rad, C. Shape Sensing of Hyper-Redundant Robots Using an AHRS IMU Sensor Network. Sensors 2022, 22, 373. [Google Scholar] [CrossRef]
- Xavier, M.S.; Fleming, A.J.; Yong, Y.K. Finite Element Modeling of Soft Fluidic Actuators: Overview and Recent Developments. Adv. Intell. Syst. 2021, 3, 2000187. [Google Scholar] [CrossRef]
- Marechal, L.; Balland, P.; Lindenroth, L.; Petrou, F.; Kontovounisios, C.; Bello, F. Toward a Common Framework and Database of Materials for Soft Robotics. Soft Robot. 2021, 8, 284–297. [Google Scholar] [CrossRef] [PubMed]
- Majidi, C.; Shepherd, R.F.; Kramer, R.K.; Whitesides, G.M.; Wood, R.J. Influence of surface traction on soft robot undulation. Int. J. Robot. Res. 2013, 32, 1577–1584. [Google Scholar] [CrossRef]
- Alici, G.; Canty, T.; Mutlu, R.; Hu, W.; Sencadas, V. Modeling and Experimental Evaluation of Bending Behavior of Soft Pneumatic Actuators Made of Discrete Actuation Chambers. Soft Robot. 2018, 5, 24–35. [Google Scholar] [CrossRef]
- Scott, W.L.; Paley, D.A. Geometric Gait Design for a Starfish-Inspired Robot Using a Planar Discrete Elastic Rod Model. Adv. Intell. Syst. 2017, 2, 1900186. [Google Scholar] [CrossRef]
- Shapiro, Y.; Wolf, A.; Gabor, K. Bi-bellows: Pneumatic bending actuator. Sens. Actuators A Phys. 2011, 166, 484–494. [Google Scholar] [CrossRef]
- Wang, Z.; Hirai, S. Soft Gripper Dynamics Using a Line-Segment Model with an Optimization-Based Parameter Identification Method. IEEE Robot. Autom. Lett. 2017, 2, 624–631. [Google Scholar] [CrossRef]
- Wang, Z.; Hirai, S. A 3D printed soft gripper integrated with curvature sensor for studying soft grasping. In Proceedings of the 2016 IEEE/SICE International Symposium on System Integration (SII), Sapporo, Japan, 13–15 December 2016; pp. 629–633. [Google Scholar] [CrossRef]
- Chen, Y.; Guo, S.; Li, C.; Yang, H.; Hao, L. Size recognition and adaptive grasping using an integration of actuating and sensing soft pneumatic gripper. Robot. Auton. Syst. 2018, 104, 14–24. [Google Scholar] [CrossRef]
- Elgeneidy, K.; Lohse, N.; Jackson, M. Bending angle prediction and control of soft pneumatic actuators with embedded flex sensors—A data-driven approach. Mechatronics 2018, 50, 234–247. [Google Scholar] [CrossRef]
- Axis Evaluation Kit, Datasheet. Available online: https://www.bendlabs.com/one_axis_datasheet.pdf (accessed on 7 December 2021).
- Ross, S.M. Introduction to Probability and Statistics for Engineers and Scientists, 6th ed.; Academic Press: Cambridge, MA, USA, 2020. [Google Scholar]
- Montgomery, D.C.; Peck, E.A.; Geoffrey, V.G. Introduction to Linear Regression Analysis, 5th ed.; Wiley: Hoboken, NJ, USA, 2012. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).