Abstract
Aiming at the efficiency and precision in micro electrical discharge machining (micro-EDM) is affected because the interpole voltage is unstable in conventional micro-EDM. This paper describes a five-degrees-of-freedom (5-DOF) controlled, wide-bandwidth, and high-precision magnetic levitation actuator. The conventional micro-EDM can install the actuator to maintain a stable interpole voltage between the electrode and workpiece to realize the high-speed micro-EDM. In this paper, the structure of the magnetic levitation actuator is designed, and the magnetic field characteristics are analyzed. On this basis, an integrator and regulator are used along with a controller with local current feedback to eliminate steady-state errors, stabilize the control system, and improve the bandwidth and positioning accuracy of the magnetic levitation actuator, and the dynamic performance of the actuator is evaluated. The experimental results show that the developed actuator has excellent positioning performance with micron-level positioning accuracy to meet the demand for the real-time, rapid, and accurate adjustment of the interpole gap during micro-EDM.
1. Introduction
A micro-EDM uses the high temperature generated by pulse discharge to melt and vaporize the material; there is no direct contact between the electrode and the workpiece during the processing, and there is no macro-cutting force in the process [1,2,3,4]. Compared with conventional machining methods, micro-EDM technology has the advantage of not being limited to the requirements of workpiece material hardness and strength and can machine any conductive material [5,6,7]. It is widely used in processing difficult materials such as those with high hardness, high toughness, high brittleness, and any conductive materials, as well as those with micro-holes and complex shapes. Overall, it has become a required processing method at this stage and is widely used in mold manufacturing [8,9,10]. However, conventional micro-EDM has low productivity [11]. When processing occurs in the case of broken or short circuits, the inter-pole gap of the micro-EDM needs to be adjusted quickly, and the conventional EDM machine tool adopts the motor and ball screw drive mode and–due to the large inertia of the mechanical transmission system–cannot ensure the ideal interpole gap in time, affecting the speed of micro-EDM and thereby limiting the efficiency and accuracy of conventional micro-EDM [12,13]. Therefore, it is necessary to improve micro-EDM’s response speed and positioning accuracy to achieve a stable discharge gap and interpole voltage.
Magnetic levitation technology has the advantages of high precision, fast response, and no pollution, which provides better technical solutions for several industries, such as magnetic levitation actuators, magnetic levitation bearings, precision positioning, magnetic levitation trains, and so on [14,15,16]. Serguei Maximov et al. [17] applied Lagrange’s equation to the analysis of a magnetic levitation system and experimentally determined the required equilibrium height of the levitated object; this method can be effectively implemented in a magnetic levitation system. Mundher H. A. [18] Yaseen utilized a microcontroller for the real-time control of Simulink functions to achieve stable control of magnetic levitation; the stability of the magnetic levitation plane was examined using phase lead compensation and linear quadratic regulator controllers. The results show that the control system with the linear quadratic regulator controller provides the same stability performance as the phase lead compensation controller. Chuan Zhao et al. [19] designed a magnetic levitation system that uses a zero-power control method, and the results show that the system levitates well and uses constant air gap control to achieve higher safety when changing the levitation mass. Kirill Poletkin [20] investigated the static pull-in of a tilt drive in a hybrid levitation micro-actuator and nonlinear modeling of the calculation of the mutual inductance and the action force between two circular filaments and experimentally verified the accuracy of the developed model, predicting the pull-in parameters of the hybrid levitation actuator with the developed analytical tool. Dongjue HE et al. [21] designed a magnetic levitation lens driving actuator, which is applied in laser processing; the actuator drives the lens to achieve real-time positioning of the laser beam focus point with good control performance and positioning accuracy. Tong Zheng et al. [22] designed a sizing optimization method to determine the magnetic levitation actuator for a rotary table and validated the effectiveness and accuracy of the method using simulation followed by experiments. Hirohisa Kato et al. [23] designed and fabricated a centrifugal pump using bearingless electrodes and permanent magnetic bearings to levitate and rotate the rotor in extremely low-temperature environments. Iwanori Murakami et al. [24] designed a superconducting magnetic bearing that combines a superconducting magnetic levitation system with a repulsive magnetic levitation system, which has a strong axial levitation force and can overcome resonance. The driving flywheel can reach 10,000 rpm by experimental verification. António J. Arsénio et al. [25] studied the optimization of the three-dimensional shape of the horizontal axis radial levitation bearing to find the optimal spacing between the Permanent magnet rings in the rotor and also between the high-temperature superconductor blocks in the stator. The guiding force is maximized while maintaining the minimum suspension force for a given size. Timo Hopf et al. [26] combined a control strategy with a flywheel system by studying an external rotor flywheel suspended by an active magnetic bearing, which improved the operating range and produced higher efficiency and a more stable power supply. Haiyue Zhu et al. [27] designed a magnetic levitation parallel actuated dual-stage motion system for the precision positioning of six axes, and the design improved the system’s dynamic characteristics in terms of reduced stage size and weight. Duan Ji An et al. [28] and Zhou Haibo et al. [29] proposed a magnetically levitated platform and combined it with a decoupled controller capable of precision motion with the ability of a comprehensive stroke. Ahn Dahoon et al. [30] designed a dual-servo mechanism, first applied to a magnetic levitation stage system, that can simultaneously achieve high precision and a long stroke with an accuracy of up to 10 nm. The platform is suitable for high-precision manufacturing processes. Feng Sun et al. [31] designed a 3-DOF permanent magnetic levitation platform with a dual closed-loop controller for stable levitation and motion control, and experimental results showed that the system achieved stable levitation and motion control of the platform with high positioning accuracy.
The magnetic levitation motion system–with the advantage of non-contact motion, where the motion target is provided by the magnetic force and both levitation and thrust forces can be generated by the same actuator in the magnetic levitation motion system–uses active control to achieve high positioning accuracy with good dynamic performance [32]. Magnetic levitation actuators can eliminate the mechanical connection between the actuator and the moving parts by remote forces, effectively overcoming frictional forces, leading to improved operability and reduced energy consumption [33]. To improve the electrode positioning response speed and efficiency during micro-EDM and to meet the requirements of high-speed, high-precision, and fine EDM, a magnetic levitation actuator with five degrees of freedom, a wide bandwidth, high accuracy, and large stroke electrode positioning has been developed by combining the magnetic levitation actuator with a micro-EDM machine tool. The actuator is compact and can be connected to the conventional micro-EDM machine tool for micro-EDM. During the machining process, when there is a broken or short circuit between the workpiece and the electrode, the magnetic levitation actuator replaces the spindle of the micro-EDM machine tool and drives the electrode to quickly adjust the interpole gap with radial and axial strokes of several millimeters so that the interpole voltage is always kept within the smooth machining voltage, realizing the rapid adjustment of abnormal discharge.
In this paper, a 5-DOF, wide-bandwidth, high-precision, large-stroke magnetic levitation actuator is introduced, and the magnetic field characteristics of this actuator are analyzed. Based on this, a local current feedback loop is used to improve the bandwidth and positioning accuracy of the magnetic levitation actuator. Finally, the characterization experiments show that the actuator has good dynamic performance and can meet the needs of micro-EDM.
2. 5-DOF Controlled Magnetic Levitation Actuator
2.1. The Structure of Magnetic Levitation Actuator
Figure 1 shows the structure diagram of the proposed 5-DOF controlled magnetic levitation actuator. It is commonly used in magnetic levitation electromagnets of electromagnets consisting of iron-core and noncore electromagnets (air-core coil). Compared with the air-core coil, the iron-core electromagnet has less magnetic leakage so that it can produce a larger electromagnetic force. However, the electromagnetic force is proportional to the square of the coil current and inversely proportional to the square of the gap, so it is highly nonlinear and difficult to control. Compared with the iron-core electromagnet, the air-core coil has more magnetic leakage and weaker electromagnetic force, but it is proportional to the coil current, easy to control, and can achieve a large stroke. Therefore, the actuator is mainly composed of two permanent magnet rings on the spindle and eight sets of air-core coils on the stator that are symmetric with the center of gravity of the spindle and with two adjacent air-core coils connected in tandem as a group. Soft iron rings are caught between two permanent magnetic rings placed opposite each other–a structure that concentrates magnetic flux. Four displacement sensors are installed in each of the X and Y directions, and one sensor in the Z direction; these sensors are used to measure the displacement of the spindle.
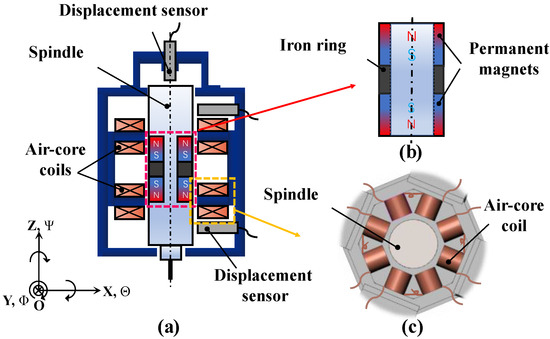
Figure 1.
The structure diagram of the 5-DOF controlled magnetic levitation actuator. (a) Actuator; (b) Permanent magnets; (c) Air-core coils.
2.2. The Principle of Magnetic Levitation Actuator
The 5-DOF motion of the spindle is controlled by the attractive or repulsive force between the energized coil and the permanent magnet. For example, in Figure 2a, the combined force generated by coil 1 and coil 2 is in the positive direction of the X-axis, and the combined force generated by coil 3 and coil 4 is in the same direction as the combined force of coils 1 and 2, so that the spindle is driven to move in the direction shown in Figure 2a. In Figure 2b, the combined force generated by coil 1 and coil 2 is in the positive direction of the X-axis, and the combined force generated by coil 3 and coil 4 is in the opposite direction to the combined force of coils 1 and 2, so the spindle is driven to rotate in the direction shown in Figure 2b. In Figure 2c, the combined force generated by coils 1 and 2 and coils 5 and 6 is in the negative Z-axis direction, and the combined force generated by coils 3 and 7 and coils 4 and 8 is in the same direction as the combined force of coils 1, 2, 3, and 4, so the driving spindle moves in the direction shown in Figure 2c.
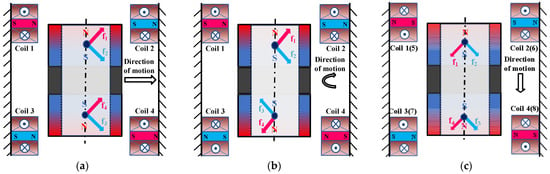
Figure 2.
Principle of spindle motion control. (a) X direction; (b) Φ direction; (c) Z direction.
2.3. Mathematical Model of 5-DOF Magnetic Levitation Actuator
The equations of motion in the Z, X, and θ directions of the spindle are shown in Equations (1)–(3). The equations of motion in the Y and Φ directions are the same as those in the X and θ directions, so they are omitted.
where m is the mass of the spindle; J is the rotational inertia in the θ direction; c is the damping coefficient; z is the distance traveled in the Z direction; x is the distance traveled in the X direction; θ is the angle of rotation back in the θ direction; kz is the air gap stiffness in the Z direction; kx is the air gap stiffness in the X direction; kθ is the air gap stiffness in the θ direction; Fz is the electromagnetic force in the Z direction; Fx is the electromagnetic force in the X direction; Mθ is the torque generated in the θ direction; l is the distance from the center of the kinematic to the force point. Meanwhile, the forces generated between the coil and the permanent magnet in the Z and X directions are Fz and Fx, and the torque generated in the θ direction is also Mθ.
In addition, the electromagnetic force between the coil and the permanent magnet is
where ki is the current stiffness factor of the coil and ik is the drive current supplied to each coil set. In addition, in this actuator, the control currents of the eight groups of coils for controlling vertical motion in the Z direction are the same and set to iz, the control currents of the four sets of coils for controlling horizontal motion in the X direction are the same and set to ix, and the control currents of the four sets of coils for controlling rotational motion in the θ direction are the same and set to iθ. The spindle’s equations of motion in the Z, X, and θ directions are
The design principle of the magnetic levitation actuator is that the coil cuts the magnetic induction line, so a counter-electromotive force is generated when the coil is energized. According to Kirchhoff’s second law, the dynamic voltage balance of this magnetic levitation actuator can be obtained.
where U is the total electric potential; UL is the inductor voltage drop; kv is the reverse electric potential coefficient; UR is the resistance voltage drop; E is the reverse electric potential; L is the coil inductance; R is the coil resistance. The electrical and mechanical models are coupled, and the Rasch transform can sort out the transfer function of the magnetic levitation actuator.
2.4. Experimental Magnetic Levitation Actuator
Figure 3 shows a physical view of the magnetic levitation actuator and its spindle. The actuator has a mass of 8 kg, a height of 190 mm, and a width of 134 mm. The hollow coil is made of copper with a wire diameter of 0.7 mm, and the number of turns per coil is 670. The mass of the spindle is 0.8 kg, with a height of 148 mm and a diameter of 45 mm. Through the experiment, the current stiffness of the magnetic levitation actuator is obtained, and the recommended value of the safe ampacity of the copper wire is 5~8 A/mm2, the cross-sectional area of the copper wire with a diameter of 0.7 mm is 0.38 mm2, and the safe ampacity is within 3.08 A. From Equation (7) in Section 2.3, it can be obtained that the load of the magnetic levitation actuator is 12.93 N. To improve the accuracy of the displacement sensor displacement detection, the detection material of both sides and the upper end of the spindle is made of stainless steel (SUS304). Considering the remanent magnetism, coercivity, maximum magnetic energy product, and economy, the permanent magnet ring is made of NdFeB–the third-generation permanent magnet material. The spindle displacement in the direction of five degrees of freedom is measured by five eddy current displacement sensors (PU-09, AEC Corp., Dallas, TX, USA), and the actuator is measured by a digital signal processor (DSP; DS1103 PPC Controller Board, dSPACE Corp., Paderborn, Germany) with a sampling rate of 10 kHz.

Figure 3.
Experimental magnetic levitation actuator and its spindle.
3. Magnetic Field Characteristic Analysis
The most important factor affecting the electromagnetic force in the magnetic levitation actuator is the air-gap magnetic induction intensity. In the actuator designed in this paper, the permanent magnet on the spindle is a circular permanent magnet. The surface current analysis method in calculating the air gap magnetic field is mainly applied to the calculation of the air gap magnetic field of the permanent magnet with a regular shape, so the surface current method is selected in this paper to calculate the air gap magnetic field. Figure 4 shows an axially magnetized cylindrical permanent magnet; the equivalent current model of the permanent magnet can be regarded as the external space magnetic field of the permanent magnet generated by the current of bound surface current on the side surface of the permanent magnet.
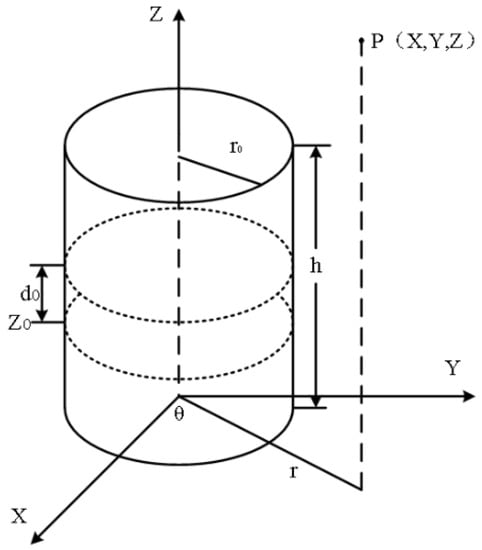
Figure 4.
Cylindrical permanent magnet.
First, the current density of the bound surface is obtained. Secondly, after obtaining the magnetic induction intensity at any point P outside the cylinder based on a cylindrical permanent magnet that has been uniformly magnetized to saturation along the same direction, the magnetic induction intensity generated by the electric current loop can be obtained. Finally, the space magnetic induction intensity of the cylindrical permanent magnet can be obtained.
The magnetic induction intensity on the X component is expressed as:
The magnetic induction intensity on the Y component is expressed as:
The magnetic induction intensity on the Z component is expressed as:
Among them:
where is the residual magnetization intensity of the permanent magnet.
According to the superposition principle, an axially magnetized magnetic ring can be used as an axially magnetized cylinder inside placed a reverse magnetized cylinder, as shown in Figure 5.
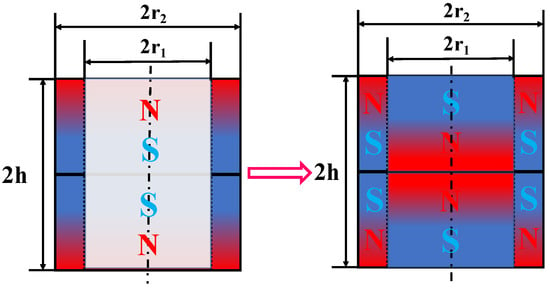
Figure 5.
Magnetic ring equivalent diagram.
Based on Equation (15) and the magnetic field superposition principle, the magnetic induction intensity on the X component of the space P point around the axially magnetized magnetic ring can be expressed as:
The magnetic induction intensity on the Y component is expressed as:
The magnetic induction intensity on the Z component is expressed as:
Among them:
Two magnetic rings placed relative to each other are combined to form the spindle of the magnetic levitation actuator designed in this paper, as shown in Figure 6.
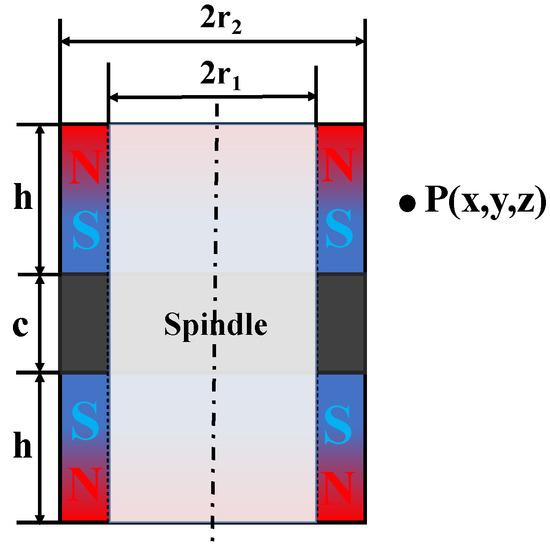
Figure 6.
Magnetic array magnetic field model.
Similarly, according to the superposition principle of the magnetic field, the magnetic induction intensity on the X component of P (x, y, z) can be expressed as:
The magnetic induction intensity on the Y component is expressed as:
The magnetic induction intensity on the Z component is expressed as:
The magnetic induction intensity in the radial direction of the spindle of the magnetic levitation actuator was simulated and analyzed using the finite element simulation software Ansoft. The magnetic induction intensity of the middle part of the spindle of the magnetic levitation actuator was measured, and the simulation model was established as shown in Figure 7. The distance range of magnetic induction intensity was within 22.5 mm~44.5 mm—that is, the maximum horizontal distance from the outer diameter of the permanent magnet to the coil. Data were collected every 0.5 mm distance, and a total of 45 groups of data were collected.
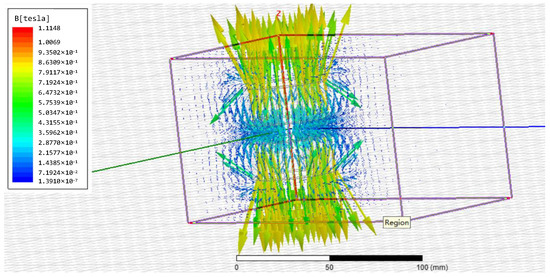
Figure 7.
Actuator simulation model diagram.
To understand the magnetic field distribution of the spindle of the magnetic levitation actuator more accurately and to verify the simulation results’ reliability and whether the spindle’s magnetic induction intensity meets this paper’s experimental requirements, a relevant experimental analysis was carried out. An experimental device for magnetic induction intensity was designed, as shown in Figure 8. The device is mainly composed of a Gauss meter (TD8600-E, measuring range 0–2 T, measuring error 0.5%), height gauge, micro platform, and magnetic suspension actuator spindle. The measurement range of magnetic induction intensity is consistent with the simulation analysis.

Figure 8.
Test platform of magnetic induction strength.
The theoretical calculation, simulation, and experiment are analyzed simultaneously. Figure 9 shows the comparison results between the theoretical calculation, simulation, and experiment of the magnetic induction intensity of the actuator. It can be seen that the curves of theory, simulation, and experiment decrease with the increase in displacement. In addition, the simulation result is larger than the experimental result because the permanent magnet ring has low magnetization and certain magnetic leakage phenomena in the experiment. The results show that the theoretical model of the magnetic induction intensity of the actuator spindle is feasible, and the magnetization intensity of the permanent magnet ring can also meet the experimental requirements. The magnetic flux and induction intensity will be increased by adding a magnetic ring to the spindle.
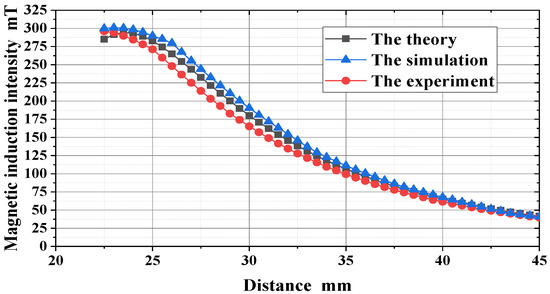
Figure 9.
Comparison of simulation and experimental results.
4. 5-DOF Magnetic Levitation Actuator Controller Design and Positioning Performance
4.1. Actuator Motion Control System
Figure 10 shows the designed 5-DOF controllable magnetic levitation actuator controller. An integral compensator is used to eliminate the steady-state error of the control system, and a regulator is used to stabilize the control system. The gain of the integrator is set to δ, a1 and a0 are the denominator parameters of the regulator, and b2, b1, and b0 are the numerator parameters of the regulator.
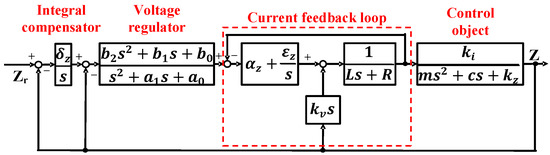
Figure 10.
Controller Designed.
In addition, a current feedback loop containing a PI controller was used to improve the response of the current in the coil, as shown in Figure 11. To simplify the controller, the transfer function from the target value of the coil current to the actual current flowing into the coil is approximated as a first-order delay system. The approximate time constant for the first-order delay system is denoted as Tdz, and the controller design for the other directions is the same as for the Z-direction. Table 1 shows the model parameters, and Table 2 shows the control parameters of the actuator, which were determined by experimental results and numerical simulations.

Figure 11.
Current feedback.

Table 1.
Model parameters.

Table 2.
Control parameters.
4.2. Composition of the Experimental System
Overall, 16 coils are used in groups of two, so eight linear amplifiers are used to amplify the coil currents, and eight current sensors are used to measure the coil currents. These amplifiers and current sensors were integrated into the amplifier box. Figure 12 shows the structure of the experimental system. The magnetic levitation is controlled by a DSP board (ds1103, dSPACE Corp.) with a sampling frequency of 10 kHz. The analog signal obtained by the displacement sensor is collected into the DSP board through the A/D converter (16 bit, ±10 V) for operational processing. The control signal after the operation is amplified by a linear amplifier through the D/A converter (16 bit, ±10 V) and applied to the magnetic levitation actuator. The designed controller was applied to the developed actuator, and the experimental results and numerical simulation parameters in Table 1 and Table 2 were used to perform the dynamic characterization experiments of the magnetic levitation actuator.
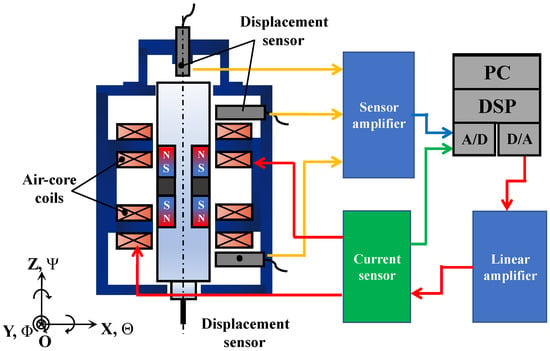
Figure 12.
Structure of the experimental system.
4.3. Performance Test
First, a 10 μm step signal was applied to the input reference points in the X, Y, and Z directions, respectively, to measure the response. Then, 1 μrad step signal was applied to the Φ direction and theta direction, respectively, measuring the response, as shown in Figure 13. To avoid the collision between the electrode and workpiece in the process of micro-EDM, the overshoot of the electrode should be set to zero. Therefore, we will adjust the controller parameters in the future to improve the step response of the actuator.
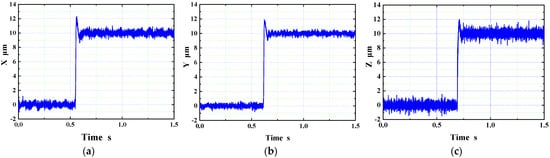
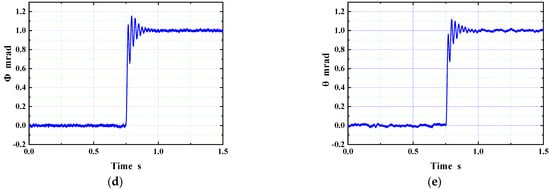
Figure 13.
Structure of the experimental system. (a) Step response in the X direction; (b) Step response in the Y direction; (c) Step response in the Z direction; (d) Step response in the Φ direction; (e) Step response in the θ direction.
Second, the positioning resolution is measured in the X, Y, and Z directions, as well as in the Φ and θ directions. As shown in Figure 14, the experimental results show that the positioning resolution of the X, Y, and Z axes was 1 μm, and the positioning resolution of the Φ, θ direction is 25 µrad and 20 µrad, respectively. The results show that the actuator has good stability, and that the actuator spindle can be maintained at the required position.
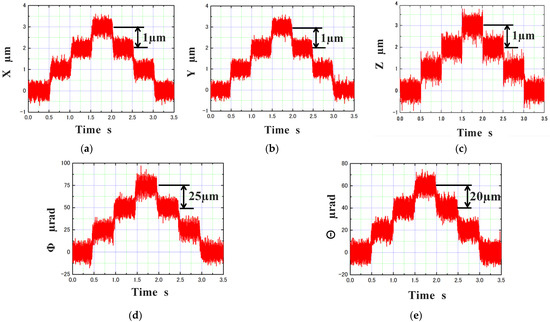
Figure 14.
Positioning resolutions. (a) Positioning resolution in the X direction; (b) Positioning resolution in the Y direction; (c) Positioning resolution in the Z direction; (d) Positioning resolution in the Φ direction; (e) Positioning resolution in the θ direction.
Third, a sine wave with an amplitude of 2 mm and a frequency of 1 Hz was applied to the X, Y, and Z axes, respectively, to measure the travel. Then, 70 mrad amplitude and a frequency of 1 Hz sine wave was applied to the Φ, θ direction measure, respectively. The experimental results are shown in Figure 15. It can be seen from the results that 4 mm of travel was achieved in the X, Y, and Z axes, and a 70 mrad stroke was achieved in the Φ, θ direction. Using the actuator’s function, the electrode can swing, the size of the machining hole can be adjusted, and a complex shape-such as the ellipse-can be finely processed.
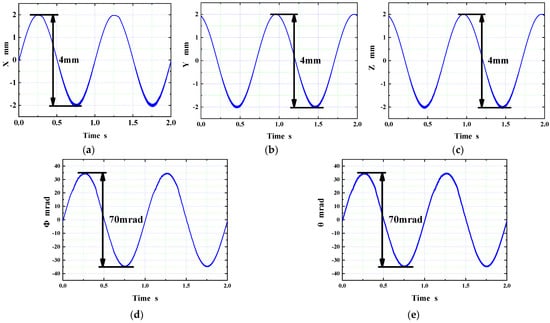
Figure 15.
Positioning resolutions. (a) The stroke in the X direction; (b) The stroke in the Y direction; (c) The stroke in the Z direction; (d) The stroke in the Φ direction; (e) The stroke in the θ direction.
Fourth, the X, Y, and Z axis directions and to evaluate the frequency response of Φ, θ directions. The frequency response was measured by a frequency response analyzer (FRA 5095, NF Corp., Yokohama, Japan), and the experimental results are shown in Figure 16. Actuator X, Y, and Z direction of the bandwidth is 101 Hz, 101 Hz, and 51 Hz, respectively. The bandwidth of Φ, θ direction was, respectively, 42 Hz, 45 Hz. Based on the above experimental results, the performance evaluation results of the brake are shown in Table 3.
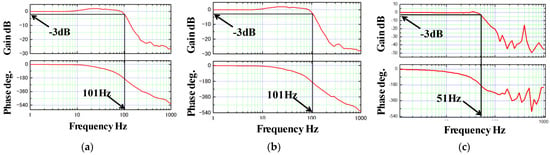
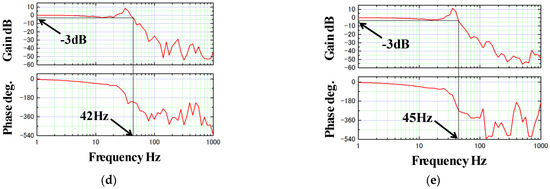
Figure 16.
Frequency responses. (a) The bandwidth in the X direction; (b) The bandwidth in the Y direction; (c) The bandwidth in the Z direction; (d) The bandwidth in the Φ direction; (e) The bandwidth in the θ direction.

Table 3.
Performance evaluation results table.
Finally, a multi-axis linkage control was performed. The target values in the X and Y directions were set as sine and cosine waves with frequencies of 0.5 Hz and amplitudes of 0.5, 1.0, and 1.5 mm, respectively. This linkage control caused the spindle to move in a circular manner. The motion trajectory is shown in Figure 17.
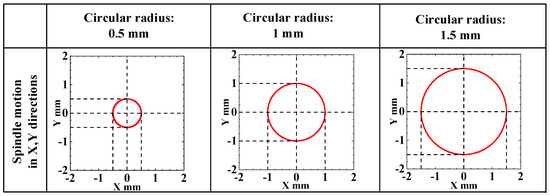
Figure 17.
Spindle circular motion.
5. Conclusions
In this paper, a wide-band, high-precision, and large-stroke 5-DOF magnetic levitation actuator is proposed and manufactured, which can be installed in a conventional micro-EDM machine tool. The magnetic field model of the magnetic levitation drive was established, the magnetic field simulation analysis of the magnetic levitation drive was carried out, the related experiments were carried out by building an experimental device, and the magnetic field characteristics of the magnetic levitation drive were analyzed. The controller of the actuator was also designed and evaluated for its response speed, positioning accuracy, motion range, frequency band width, and multi-axis linkage control effect. The developed magnetic levitation actuator has millisecond response speed in all five degrees of freedom; the motion range is up to 4 mm in the translational direction and 70 mrad in the rotational direction; the positioning resolution is up to 1 μm in the translational direction and 25 μrad in the rotational direction; the frequency bandwidth of the actuator is 101 Hz in the radial direction, 51 Hz in the axial direction, and about 40 Hz in the rotational direction. The experimental results show that the developed actuator can achieve a fast response and stable suspension, which can meet the demand for real-time, fast, and accurate adjustment of the interpole gap during micro-EDM processing, thus maintaining the stability of the interpole voltage. It improves the discharge probability of microelectronic processing, thus increasing the processing efficiency.
Author Contributions
B.L.: Conceptualization, Methodology, Software, Validation, Investigation, Data curation, Formal analysis, Writing—original draft, Visualization, Funding acquisition; X.Z.: Supervision, Funding acquisition, Resources, Project administration, Writing—review & editing; F.X.: writing—review & editing; G.Y.: writing-review & editing; J.J.: writing—review & editing; C.X.: writing—review & editing; F.S.: writing—review & editing; K.O.: writing-review & editing. All authors have read and agreed to the published version of the manuscript.
Funding
This research is supported by National Natural Science Fund of China (No. 52005345, No. 52005344), National Key Research and Development Project (No. 2020YFC2006701), China Scholarship Council (No. 202208210073), Scientific Research Fund Project of Liaoning Provincial Department of Education (No. LFGD2020002), Major Project of the Ministry of Science and Technology of Liaoning Province (No. 2022JH1/10400027).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
We thank Chuan Zhao, Wenzhe Pei, Fucheng Zhang and Jian Zhang for their suggestions.
Conflicts of Interest
The authors declare no competing interest.
References
- Prakash, V.; Kumare, P.; Singh, P.K.; Hussain, M.; Das, A.K.; Chattopadhyaya, S. Micro-electrical discharge machining of difficult-to-machine materials: A review. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2019, 233, 339–370. Available online: https://journals.sagepub.com/doi/10.1177/0954405417718591 (accessed on 5 June 2022). [CrossRef]
- Urso, D.G.; Giardini, C.; Ravasio, C. Effects of Electrode and Workpiece Materials on the Sustainability of Micro-EDM Drilling Process. Int. J. Precis. Eng. Manuf. 2018, 19, 1727–1734. Available online: https://link.springer.com/article/10.1007/s12541-018-0200-2 (accessed on 5 June 2022).
- Suganthi, X.H.; Natarajan, U.; Sathiyamurthy, S.; Chidambaram, K. Prediction of quality responses in micro-EDM process using an adaptive neuro-fuzzy inference system (ANFIS) model. Int. J. Adv. Manuf. Technol. 2013, 68, 339–347. Available online: https://link.springer.com/article/10.1007/s00170-013-4731-5 (accessed on 5 June 2022). [CrossRef]
- Yang, F.; Yang, J.; Yao, K.; Hua, H. Adaptive Voltage Position Control for Pulse Power Supply in Electrical Discharge Machining. IEEE Trans. Ind. Electron. 2019, 66, 5895–5906. Available online: https://ieeexplore.ieee.org/document/8480869 (accessed on 5 June 2022). [CrossRef]
- Kumar, D.; Singh, N.K.; Bajpai, V. Recent trends, opportunities and other aspects of micro-EDM for advanced manufacturing: A comprehensive review. J. Braz. Soc. Mech. Sci. Eng. 2020, 42, 2172–2191. Available online: https://link.springer.com/article/10.1007/s40430-020-02296-4 (accessed on 10 July 2022). [CrossRef]
- Shabgard, M.R.; Gholipoor, A.; Baseri, H. A review on recent developments in machining methods based on electrical discharge phenomena. Int. J. Adv. Manuf. Technol. 2016, 87, 2081–2097. Available online: https://link.springer.com/article/10.1007/s00170-016-8554-z (accessed on 10 July 2022). [CrossRef]
- Gostimirovic, M.; Pucovsky, V.; Sekulic, M.; Radovanovic, M.; Madic, M. Evolutionary multi-objective optimization of energy efficiency in electrical discharge machining. J. Mech. Sci. Technol. 2018, 32, 4775–4785. Available online: https://link.springer.com/article/10.1007/s12206-018-0925-y (accessed on 10 July 2022). [CrossRef]
- Macedo, F.T.B.; Wiessner, M.; Hollenstein, C.; Kustera, F.; Wegenera, K. Dependence of Crater Formation in Dry EDM on Electrical Breakdown Mechanism. Procedia CIRP 2016, 42, 161–166. Available online: https://linkinghub.elsevier.com/retrieve/pii/S2212827116004960 (accessed on 12 June 2022). [CrossRef]
- Nahak, B.; Gupta, A. A review on optimization of machining performances and recent developments in electro discharge machining. Manuf. Rev. 2019, 6, 2. Available online: https://mfr.edp-open.org/articles/mfreview/full_html/2019/01/mfreview180009/mfreview180009.html (accessed on 12 June 2022). [CrossRef]
- Gohil, V.; Puri, Y.M. Turning by electrical discharge machining: A review. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2017, 231, 195–208. Available online: https://journals.sagepub.com/doi/10.1177/0954405415590560 (accessed on 12 June 2022). [CrossRef]
- Lee, C.H.; Lai, T.S. An Intelligent System for Improving Electric Discharge Machining Efficiency Using Artificial Neural Network and Adaptive Control of Debris Removal Operations. IEEE Access 2021, 9, 75302–75312. Available online: https://ieeexplore.ieee.org/document/9431212 (accessed on 25 June 2022). [CrossRef]
- Zhang, Z.; Zhang, Y.; Ming, W.Y.; Zhang, Y.M.; Cao, C.; Zhang, G.J. A review on magnetic field assisted electrical discharge machining. J. Manuf. Process. 2021, 64, 694–722. Available online: https://www.sciencedirect.com/science/article/abs/pii/S1526612521000955?via%3Dihub (accessed on 18 June 2022). [CrossRef]
- Guo, Y.F.; Ling, Z.B.; Zhang, X.Y.; Feng, Y.R. A magnetic suspension spindle system for small and micro holes EDM. Int. J. Adv. Manuf. Technol. 2018, 94, 1911–1923. Available online: https://link.springer.com/article/10.1007/s00170-017-0990-x (accessed on 18 June 2022). [CrossRef]
- Chen, C.H.; Hu, Y.F.; Wu, H.C.; Song, C.S. Parametric design and experiment of maglev actuators for microgravity vibration isolation system. Int. J. Appl. Electromagn. Mech. 2018, 58, 319–335. Available online: https://content.iospress.com/articles/international-journal-of-applied-electromagnetics-and-mechanics/jae180037 (accessed on 12 July 2022). [CrossRef]
- Zhang, T.; Le, Q.Y.; Zhu, W.G. Structure and Suspension Force Analysis of Six-Pole Five Degrees of Freedom AC Hybrid Magnetic Bearing. IEEE Trans. Magn. 2021, 57, 6. Available online: https://ieeexplore.ieee.org/document/9386118 (accessed on 12 July 2022). [CrossRef]
- Lee, H.R.; Kim, K.C.; Lee, J. Review of Maglev Train Technologies. IEEE Trans. Magn. 2006, 42, 1917–1925. Available online: https://ieeexplore.ieee.org/document/1644911 (accessed on 12 July 2022).
- Maximov, S.; Montañez, F.G.; Perez, R.E.; Galvan, J.C.O.; Mestiza, H.A. Analytical Analysis of Magnetic Levitation Systems with Harmonic Voltage Input. Actuators 2020, 9, 82. [Google Scholar] [CrossRef]
- Yaseen, M.H.A. Investigation on planar electromagnetic levitation system using lead compensation and LQR controllers. Electr. Eng. 2020, 102, 725–736. Available online: https://link.springer.com/article/10.1007/s00202-019-00905-7 (accessed on 12 July 2022). [CrossRef]
- Zhao, C.; Sun, F.; Jin, J.J.; Tang, J.H.; Xu, F.C.; Li, Q. Analysis of Quasi-Zero Power Characteristic for a Permanent Magnetic Levitation System with a Variable Flux Path Control Mechanism. IEEE/ASME Trans. Mechatron. 2021, 26, 437–447. Available online: https://ieeexplore.ieee.org/document/9204846 (accessed on 14 July 2022). [CrossRef]
- Poletkin, K. On the Static Pull-In of Tilting Actuation in Electromagnetically Levitating Hybrid Micro-Actuator: Theory and Experiment. Actuators 2021, 10, 256. [Google Scholar] [CrossRef]
- He, D.J.; Shinshi, T.; Nakai, T. Development of a Lens Driving Maglev Actuator for ep Piercing. Key Eng. Mater. 2012, 523–524, 774–779. Available online: https://www.scientific.net/KEM.523-524.774 (accessed on 14 July 2022).
- Zheng, T.; Lu, X.; Xu, F.Q.; Xu, X.Z. Optimisation method of magnetic levitation actuator for rotary table. IET Electr. Power Appl. 2020, 14, 893–900. Available online: https://ietresearch.onlinelibrary.wiley.com/doi/10.1049/iet-epa.2019.0788 (accessed on 14 July 2022). [CrossRef]
- Kato, H.; Komori, M.; Asami, K.; Sakai, N. Development of one-axis controlled bearingless motor and its application to a centrifugal pump for extremely low temperature. Int. J. Appl. Electromagn. Mech. 2020, 64, 1287–1294. Available online: https://content.iospress.com/articles/international-journal-of-applied-electromagnetics-and-mechanics/jae209447 (accessed on 18 July 2022). [CrossRef]
- Murakami, I.; Zhao, Y.M.; Tashiro, T. Stabilization of a Magnetic Repulsive Levitation Flywheel System Using a High-Efficiency Superconducting Magnetic Bearing. Actuators 2022, 11, 180. [Google Scholar] [CrossRef]
- Arsénio, A.J.; Silva, F.F.; Fernands, J.F.P.; Branco, P.J.C. Optimization of the Guiding Stability of a Horizontal Axis HTS ZFC Radial Levitation Bearing. Actuators 2021, 10, 311. [Google Scholar] [CrossRef]
- Hopf, T.; Richter, M.; Schüßler, B.; Rinderknecht, S. Control Strategies for Highly Gyroscopic Outer Rotors with Diametral Enlargement in Active Magnetic Bearings. Actuators 2022, 11, 91. [Google Scholar] [CrossRef]
- Zhu, H.Y.; Teo, T.J.; Pang, C.K. Magnetically Levitated Parallel Actuated Dual-Stage (Maglev-PAD) System for Six-Axis Precision Positioning. IEEE/ASME Trans. Mechatron. 2019, 24, 1829–1838. Available online: https://ieeexplore.ieee.org/document/8764447 (accessed on 14 July 2022). [CrossRef]
- Duan, J.A.; Zhou, H.B.; Guo, N.P. Electromagnetic Design of a Novel Linear Maglev Transportation Platform with Finite-Element Analysis. IEEE Trans. Magn. 2011, 47, 260–263. Available online: https://ieeexplore.ieee.org/document/5601781 (accessed on 14 July 2022). [CrossRef]
- Zhou, H.B.; Deng, H.; Duan, J. Hybrid Fuzzy Decoupling Control for a Precision Maglev Motion System. IEEE/ASME Trans. Mechatron. 2018, 23, 389–401. Available online: https://ieeexplore.ieee.org/document/8100985 (accessed on 20 July 2022). [CrossRef]
- Ahn, D.; Jin, J.W.; Yun, H.; Jeong, J. Development of a Novel Dual Servo Magnetic Levitation Stage. Actuators 2022, 11, 147. [Google Scholar] [CrossRef]
- Sun, F.; Pei, W.Z.; Zhao, C.; Jin, J.J.; Xu, F.C.; Zhang, X.Y. Permanent Maglev Platform Using a Variable Flux Path Mechanism: Stable Levitation and Motion Control. IEEE Trans. Magn. 2022, 58, 8300410. Available online: https://ieeexplore.ieee.org/document/9772652 (accessed on 20 July 2022). [CrossRef]
- Zhou, L.; Wu, J.J. Magnetic Levitation Technology for Precision Motion Systems: A Review and Future Perspectives. Int. J. Autom. Technol. 2022, 16, 386–402. Available online: https://www.fujipress.jp/ijat/au/ijate001600040386/ (accessed on 22 July 2022). [CrossRef]
- Poletkin, K.V.; Asadollahbaik, A.; Kampmann, R.; Korvink, J.G. Levitating Micro-Actuators: A Review. Actuators 2018, 7, 17. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).