Image Servo Tracking of a Flexible Manipulator Prototype with Connected Continuum Kinematic Modules
Abstract
1. Introduction
1.1. Motivation
1.2. Related Works
1.3. Contribution
- This paper presents a three-segment CKM-based continuum robot design that is convenient for the fabrication of a continuum robot and efficient at obtaining the overall kinematic model for control purposes.
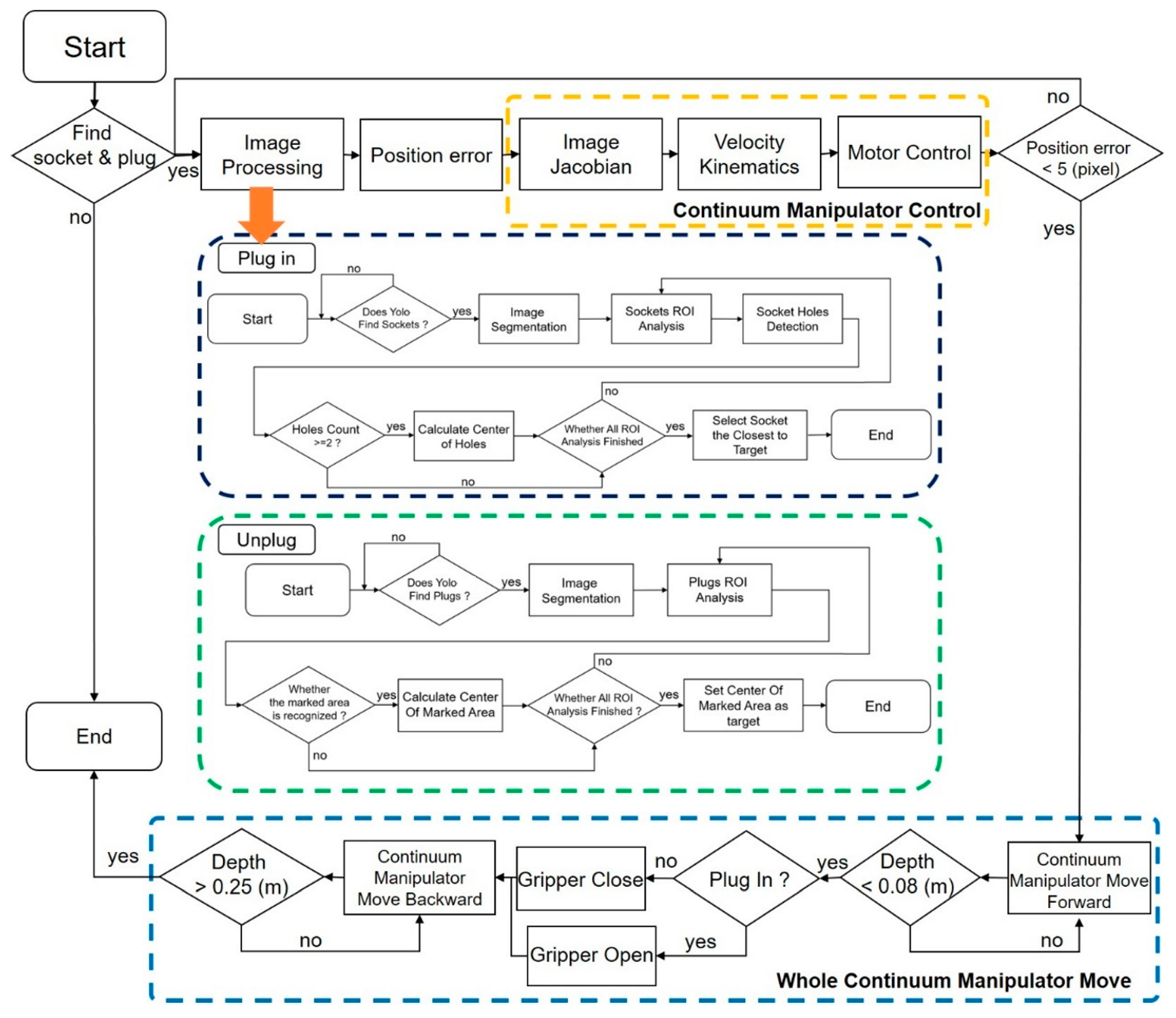
- For the proposed design and control validation, experiments of image-based servoing path tracking and autonomous manipulation are established, utilizing Jacobian images to track the desired image targets by controlling the continuum robot. In the eye-to-hand (ETH) experiment, a heart shape trajectory was tracked to verify the precision of the kinematics with acceptably low endpoint errors. In the eye-in-hand (EIH) experiment, a stereo vision-based object detection algorithm was developed for the power socket grasping task with high accuracy and efficient operation in real-time.
1.4. Limitation
2. Proposed Method
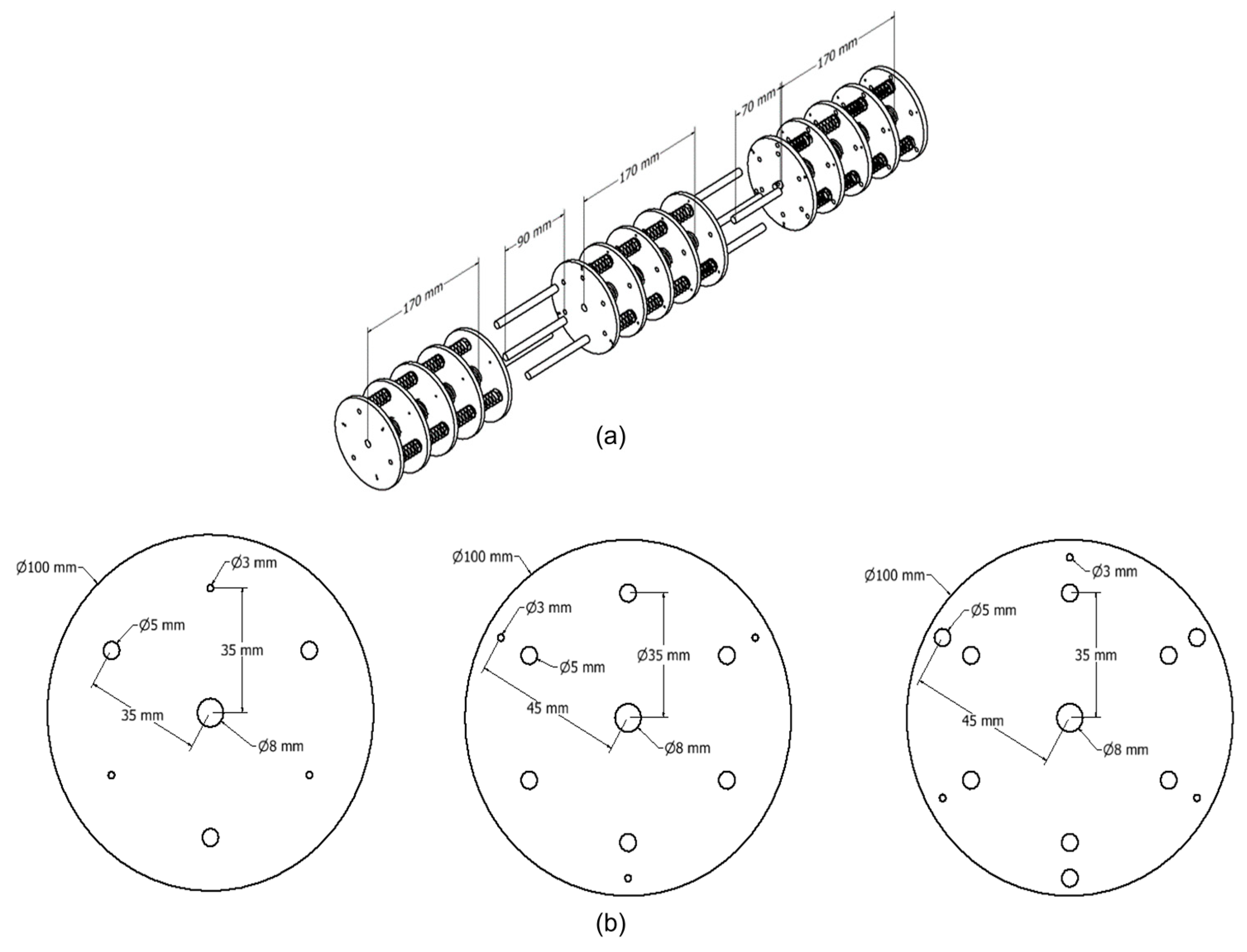
2.1. Design and Kinematics of A Continuum Kinematic Module (CKM)
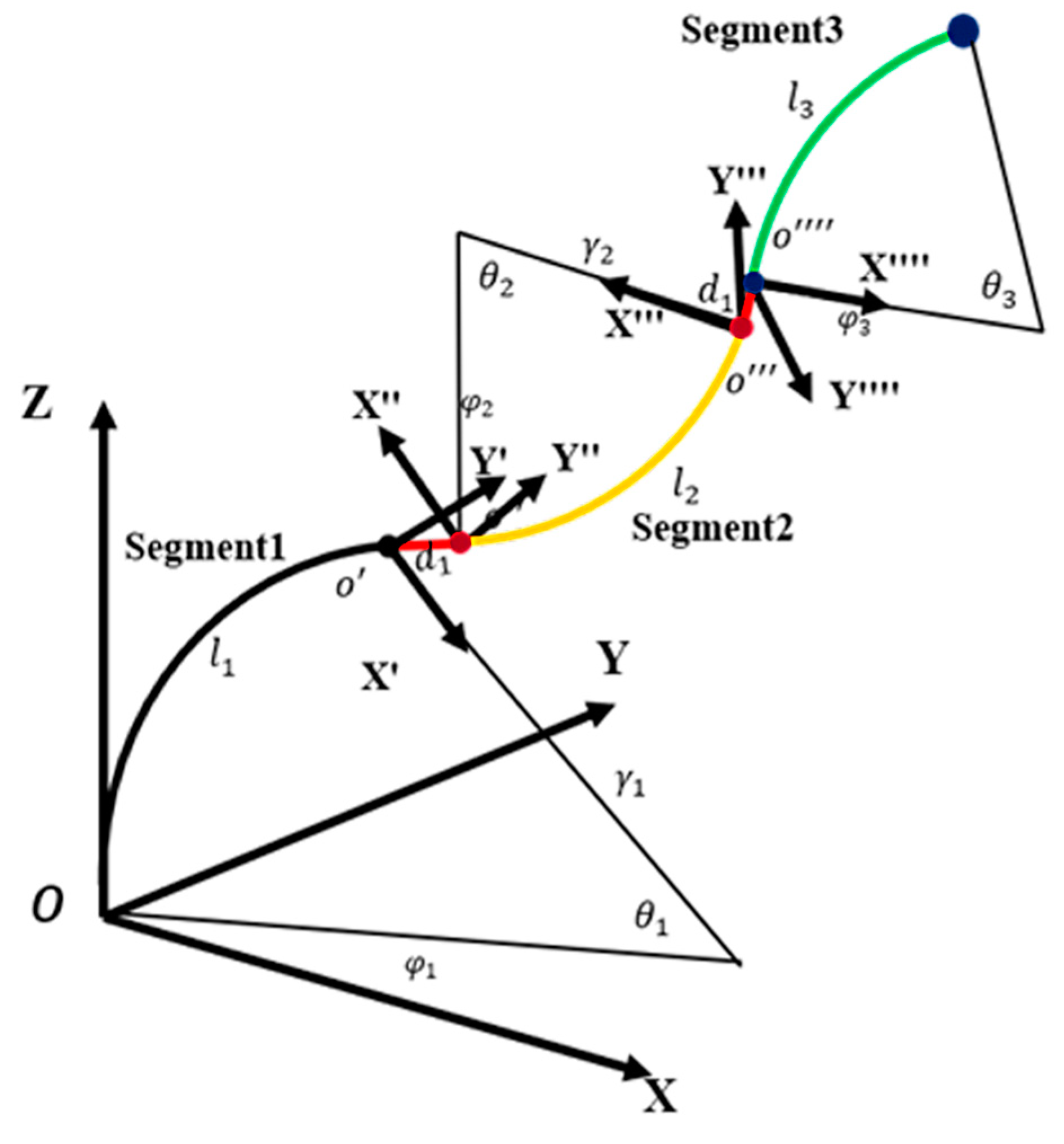
2.2. Design and Kinematics of the Flexible Manipulator Formed with Three CKMs
2.3. Implementation of the Image Servo Tracking Systems
2.3.1. Eye-To-Hand (ETH) Visual Servoing Configuration
2.3.2. Eye-In-Hand (EIH) Visual Servoing Configuration
3. Experimental Results
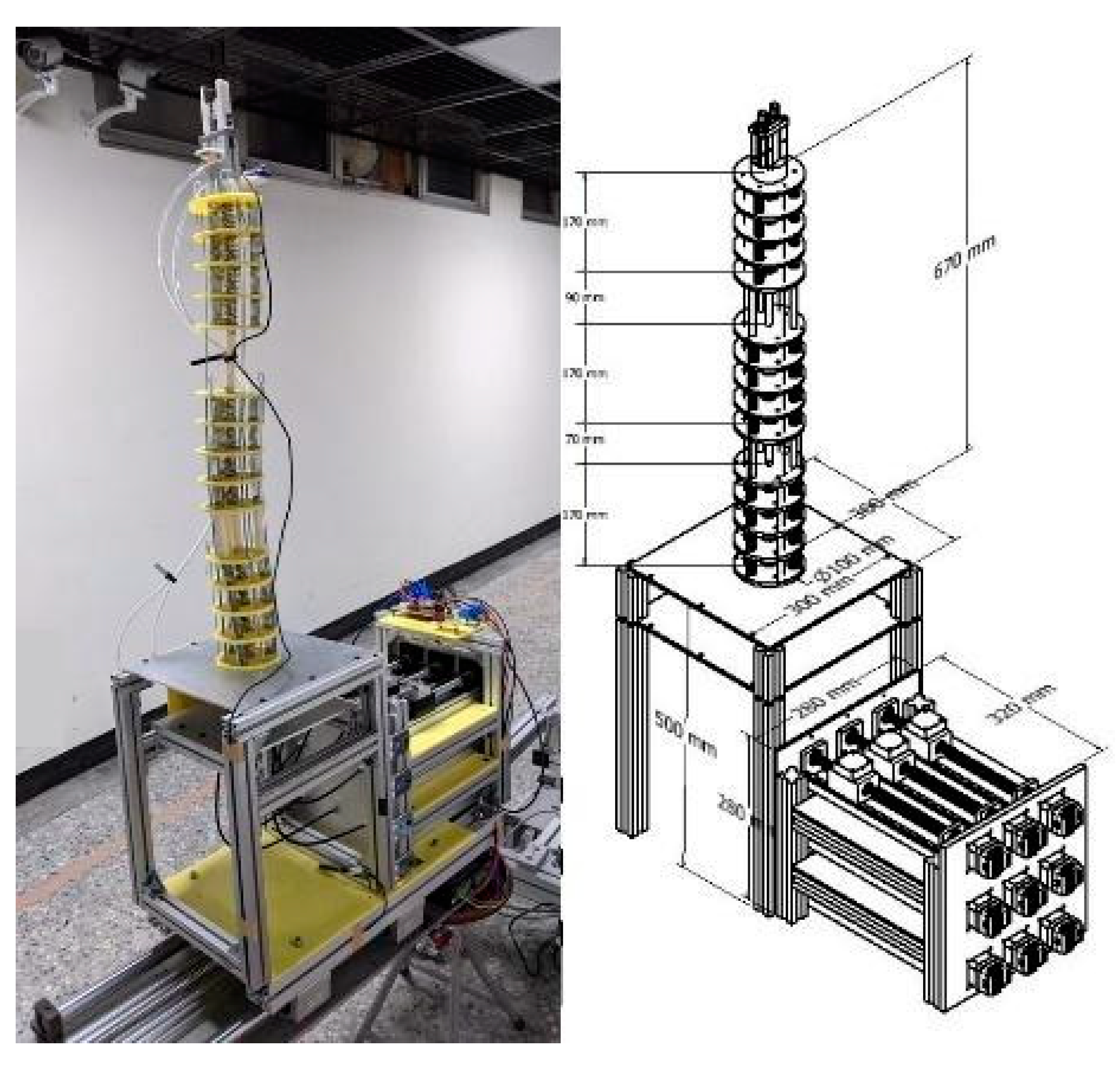
3.1. CKM-Based Continuum Robot Implementation
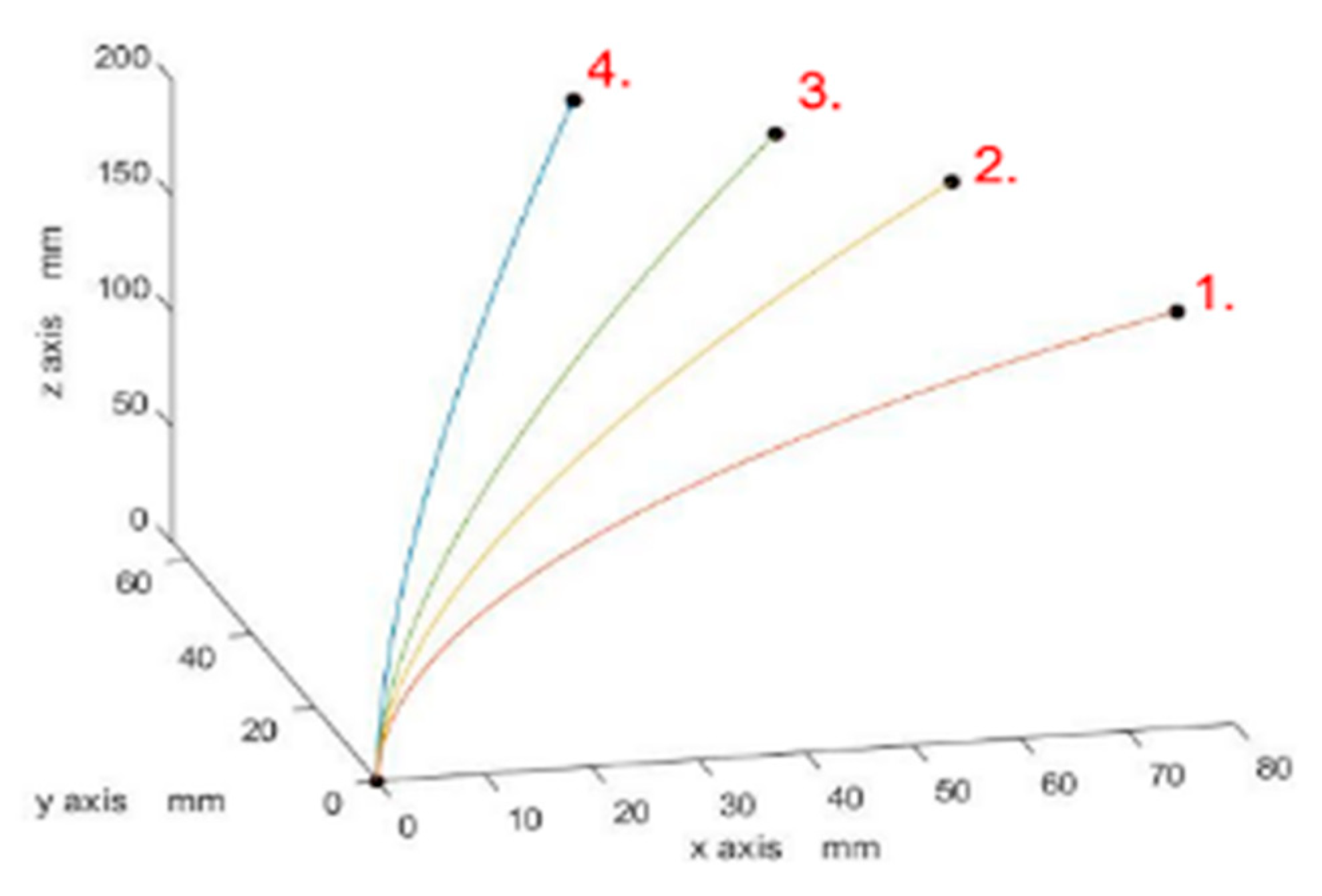
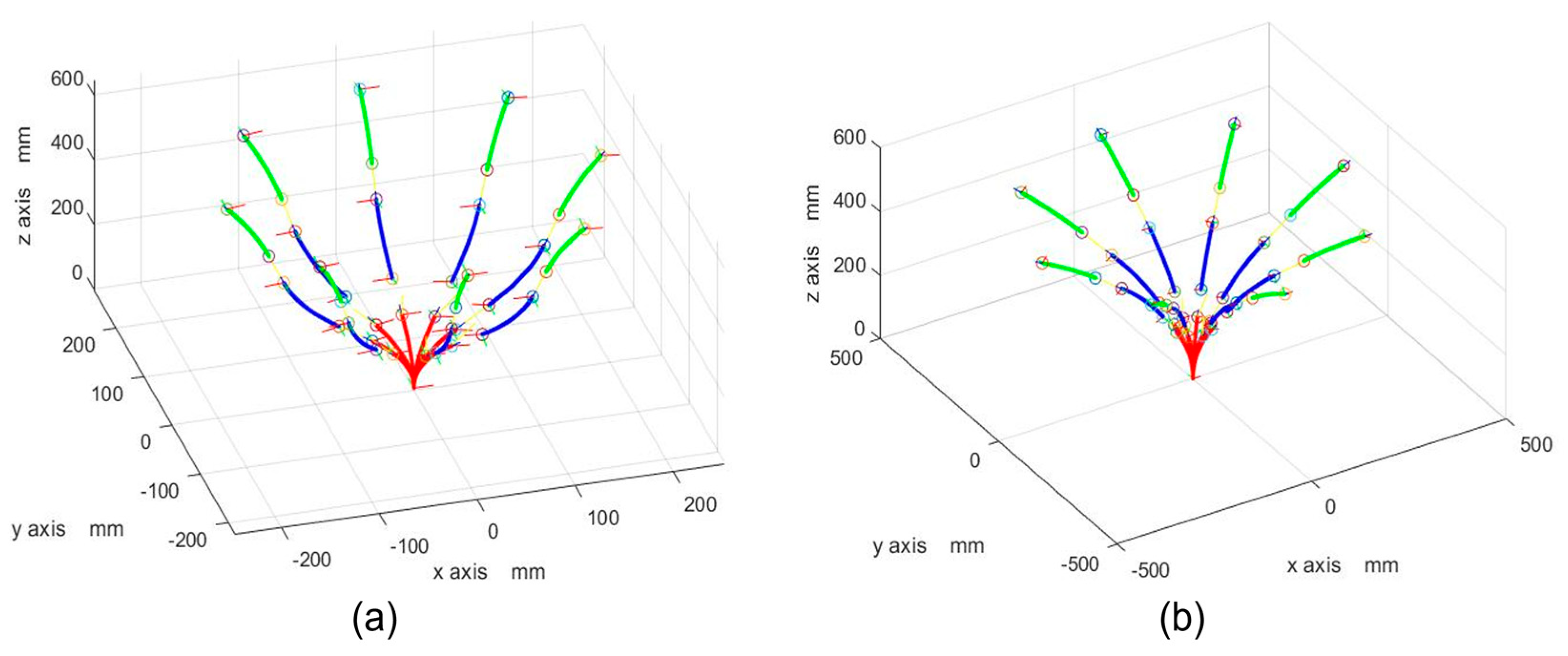
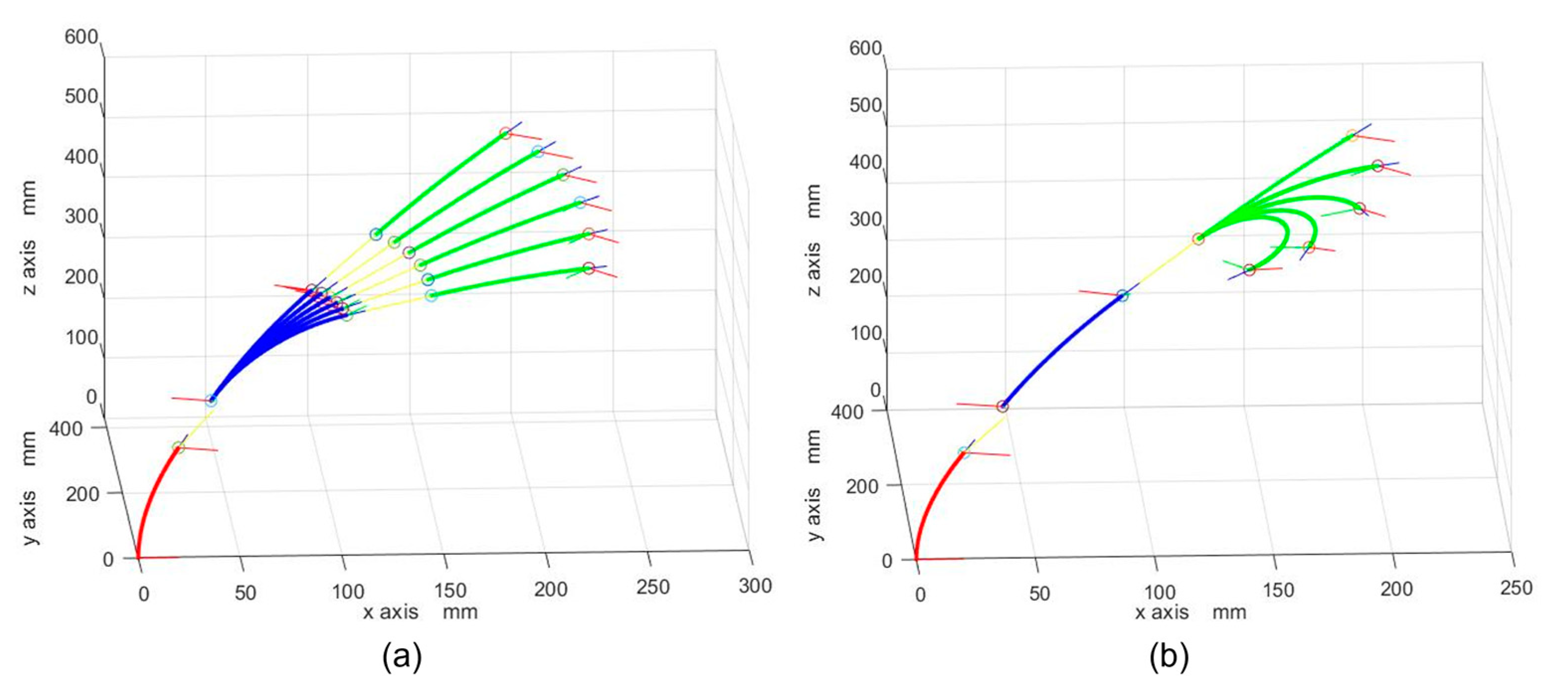
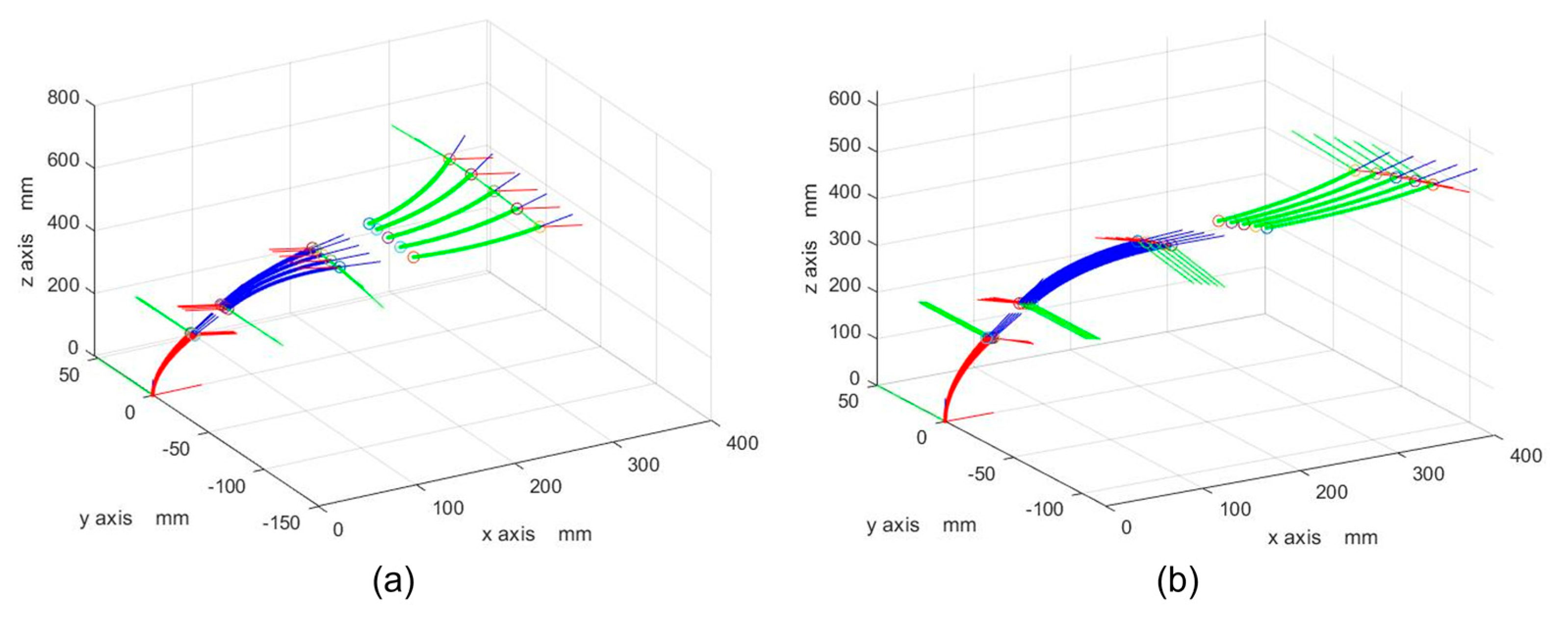
3.2. Kinematic Simulations
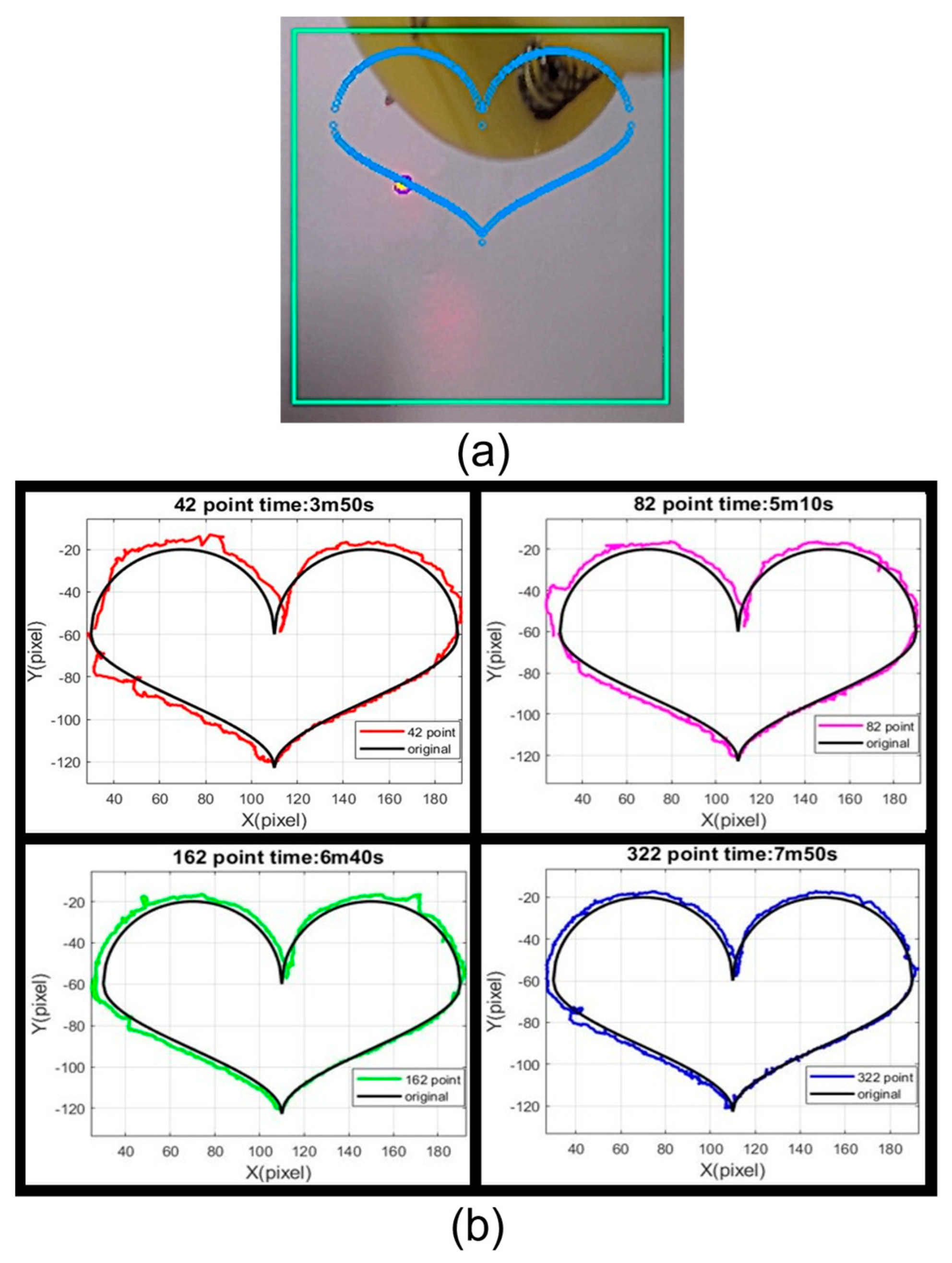
3.3. Heart Shape Trajectory Tracking
3.4. Image-based Servo Tracking Experiment
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Angrisani, L.; Grazioso, S.; Gironimo, G.D.; Panariello, D.; Tedesco, A. On the use of soft continuum robots for remote measurement tasks in constrained environments: A brief overview of applications. In Proceedings of the 2019 IEEE International Symposium on Measurements & Networking (M&N), Catania, Italy, 8–10 July 2019; pp. 1–5. [Google Scholar]
- Boonchai, P.; Tuchinda, K. Design and Control of Continuum Robot for Using with Solar Cell System. In Proceedings of the 3rd International Conference on Vision, Image and Signal Processing (ICVISP 2019), Vancouver, BC, Canada, 26–28 August 2019. [Google Scholar]
- Burgner-Kahrs, J.; Rucker, D.C.; Choset, H. Continuum Robots for Medical Applications: A Survey. IEEE Trans. Robot. 2015, 31, 1261–1280. [Google Scholar] [CrossRef]
- Yamauchi, Y.; Ambe, Y.; Nagano, H.; Konyo, M.; Bando, Y.; Ito, E.; Arnold, S.; Yamazaki, K.; Itoyama, K.; Okatani, T.; et al. Development of a continuum robot enhanced with distributed sensors for search and rescue. ROBOMECH J. 2022, 9, 8. [Google Scholar] [CrossRef]
- Zhang, J.; Sheng, J.; O’Neill, C.T.; Walsh, C.J.; Wood, R.J.; Ryu, J.H.; Desai, J.P.; Yip, M.C. Robotic Artificial Muscles: Current Progress and Future Perspectives. IEEE Trans. Robot. 2019, 35, 761–781. [Google Scholar] [CrossRef]
- Li, S.; Hao, G. Current Trends and Prospects in Compliant Continuum Robots: A Survey. Actuators 2021, 10, 145. [Google Scholar] [CrossRef]
- Dong, X.; Wang, M.; Mohammad, A.; Ba, W.; Russo, M.; Norton, A.; Kell, J.; Axinte, D. Continuum Robots Collaborate for Safe Manipulation of High-Temperature Flame to Enable Repairs in Challenging Environments. IEEE/ASME Trans. Mechatron. 2022, 27, 4217–4220. [Google Scholar] [CrossRef]
- Wooten, M.; Frazelle, C.; Walker, I.D.; Kapadia, A.; Lee, J.H. Exploration and Inspection with Vine-Inspired Continuum Robots. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, QLD, Australia, 21–25 May 2018; pp. 5526–5533. [Google Scholar]
- Hannan, M.W.; Walker, I.D. Kinematics and the implementation of an elephant’s trunk manipulator and other continuum style robots. J. Robot. Syst. 2003, 20, 45–63. [Google Scholar] [CrossRef]
- Jones, B.A.; Walker, I.D. Kinematics for multi-section continuum robots. IEEE Trans. Robot. 2006, 22, 43–55. [Google Scholar] [CrossRef]
- Yoon, H.S.; Yi, B.J. A 4-DOF flexible continuum robot using a spring backbone. In Proceedings of the International Conference on Mechatronics and Automation, Changchun, China, 9–12 August 2009; pp. 1249–1254. [Google Scholar]
- Tokunaga, T.; Oka, K.; Harada, A. 1segment continuum manipulator for automatic harvesting robot-prototype and modeling. In Proceedings of the IEEE International Conference on Mechatronics and Automation (ICMA), Takamatsu, Japan, 6–9 August 2017; pp. 1655–1659. [Google Scholar]
- Liu, Y.; Yang, Y.; Peng, Y.; Zhong, S.; Liu, N.; Pu, H. A Light Soft Manipulator With Continuously Controllable Stiffness Actuated by a Thin McKibben Pneumatic Artificial Muscle. IEEE/ASME Trans. Mechatron. 2020, 25, 1944–1952. [Google Scholar] [CrossRef]
- Dalvand, M.M.; Nahavandi, S.; Howe, R.D. An Analytical Loading Model for n-Tendon Continuum Robots. IEEE Trans. Robot. 2018, 34, 1215–1225. [Google Scholar] [CrossRef]
- Hassan, T.; Cianchetti, M.; Mazzolai, B.; Laschi, C.; Dario, P. Active-Braid, a Bioinspired Continuum Manipulator. IEEE Robot. Autom. Lett. 2017, 2, 2104–2110. [Google Scholar] [CrossRef]
- Zhang, G.; Du, F.; Xue, S.; Cheng, H.; Zhang, X.; Song, R.; Li, Y. Design and Modeling of a Bio-Inspired Compound Continuum Robot for Minimally Invasive Surgery. Machines 2022, 10, 468. [Google Scholar] [CrossRef]
- Comin, F.J.; Saaj, C.M.; Mustaza, S.M.; Saaj, R. Safe Testing of Electrical Diathermy Cutting Using a New Generation Soft Manipulator. IEEE Trans. Robot. 2018, 34, 1659–1666. [Google Scholar] [CrossRef]
- Zhao, B.; Zhang, W.; Zhang, Z.; Zhu, X.; Xu, K. Continuum Manipulator with Redundant Backbones and Constrained Bending Curvature for Continuously Variable Stiffness. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 7492–7499. [Google Scholar]
- Qu, T.; Chen, J.; Shen, S.; Xiao, Z.; Yue, Z.; Lau, H.Y.K. Motion control of a bio-inspired wire-driven multi-backbone continuum minimally invasive surgical manipulator. In Proceedings of the IEEE International Conference on Robotics and Biomimetics (ROBIO), Qingdao, China, 3–7 December 2016; pp. 1989–1995. [Google Scholar]
- Hwang, M.; Kwon, D. Strong Continuum Manipulator for Flexible Endoscopic Surgery. IEEE/ASME Trans. Mechatron. 2019, 24, 2193–2203. [Google Scholar] [CrossRef]
- Zhang, S.; Li, Q.; Yang, H.; Zhao, J.; Xu, K. Configuration Transition Control of a Continuum Surgical Manipulator for Improved Kinematic Performance. IEEE Robot. Autom. Lett. 2019, 4, 3750–3757. [Google Scholar] [CrossRef]
- Wang, T.; Wang, Z.; Wu, G.; Lei, L.; Zhao, B.; Zhang, P.; Shang, P. Design and Analysis of a Snake-like Surgical Robot with Continuum Joints. In Proceedings of the 5th International Conference on Advanced Robotics and Mechatronics (ICARM), Shenzhen, China, 18–21 December 2020; pp. 178–183. [Google Scholar]
- Li, J.; Zhou, Y.; Tan, J.; Wang, Z.; Liu, H. Design and Modeling of a Parallel Shifted-Routing Cable-Driven Continuum Manipulator for Endometrial Regeneration Surgery. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 24 October 2020–24 January 2021; pp. 3178–3183. [Google Scholar]
- Shen, W.; Yang, G.; Zheng, T.; Wang, Y.; Yang, K.; Fang, Z. An Accuracy Enhancement Method for a Cable-Driven Continuum Robot With a Flexible Backbone. IEEE Access 2020, 8, 37474–37481. [Google Scholar] [CrossRef]
- Seleem, I.A.; El-Hussieny, H.; Assal, S.F.M.; Ishii, H. Development and Stability Analysis of an Imitation Learning-Based Pose Planning Approach for Multi-Section Continuum Robot. IEEE Access 2020, 8, 99366–99379. [Google Scholar] [CrossRef]
- Li, Q.; Yang, H.; Chen, Y.; Xu, K. Closed Loop Control of a Continuum Surgical Manipulator for Improved Absolute Positioning Accuracy. In Proceedings of the IEEE International Conference on Robotics and Biomimetics (ROBIO), Dali, China, 6–8 December 2019; pp. 1551–1556. [Google Scholar]
- Lai, J.; Huang, K.; Lu, B.; Chu, H.K. Toward Vision-based Adaptive Configuring of A Bidirectional Two-Segment Soft Continuum Manipulator. In Proceedings of the IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Boston, MA, USA, 6–9 July 2020; pp. 934–939. [Google Scholar]
- Yang, H.; Wu, B.; Liu, X.; Xu, K. A Closed-Loop Controller for a Continuum Surgical Manipulator Based on a Specially Designed Wrist Marker and Stereo Tracking. In Proceedings of the IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Boston, MA, USA, 6–9 July 2020; pp. 335–340. [Google Scholar]
- Song, K.; Tsai, H. Visual Servoing and Compliant Motion Control of a Continuum Robot. In Proceedings of the 18th International Conference on Control, Automation and Systems (ICCAS), PyeongChang, Republic of Korea, 17–20 October 2018; pp. 734–739. [Google Scholar]
- Mo, H.; Wei, R.; Ouyang, B.; Xing, L.; Shan, Y.; Liu, Y.; Sun, D. Control of a Flexible Continuum Manipulator for Laser Beam Steering. IEEE Robot. Autom. Lett. 2021, 6, 1074–1081. [Google Scholar] [CrossRef]
- Wu, K.; Zhu, G.; Wu, L.; Gao, W.; Song, S.; Lim, C.M.; Ren, H. Safety-Enhanced Model-Free Visual Servoing for Continuum Tubular Robots Through Singularity Avoidance in Confined Environments. IEEE Access 2019, 7, 21539–21558. [Google Scholar] [CrossRef]
- del Giudice, G.; Orekhov, A.; Shen, J.; Joos, K.; Simaan, N. Investigation of Micro-motion Kinematics of Continuum Robots for Volumetric OCT and OCT-guided Visual Servoing. IEEE/ASME Trans. Mechatron. 2020, 26, 2604–2615. [Google Scholar] [CrossRef]
- Lindenroth, L.; Merlin, J.; Bano, S.; Manjaly, J.G.; Mehta, N.; Stoyanov, D. Intrinsic Force Sensing for Motion Estimation in a Parallel, Fluidic Soft Robot for Endoluminal Interventions. IEEE Robot. Autom. Lett. 2022, 7, 10581–10588. [Google Scholar] [CrossRef]
- Xu, F.; Wang, H.; Chen, W.; Miao, Y. Visual Servoing of a Cable-Driven Soft Robot Manipulator With Shape Feature. IEEE Robot. Autom. Lett. 2021, 6, 4281–4288. [Google Scholar] [CrossRef]
- AlBeladi, A.; Ripperger, E.; Hutchinson, S.; Krishnan, G. Hybrid Eye-in-Hand/Eye-to-Hand Image Based Visual Servoing for Soft Continuum Arms. IEEE Robot. Autom. Lett. 2022, 7, 11298–11305. [Google Scholar] [CrossRef]
- Zhang, Z.; Rosa, B.; Caravaca-Mora, O.; Zanne, P.; Gora, M.J.; Nageotte, F. Image-Guided Control of an Endoscopic Robot for OCT Path Scanning. IEEE Robot. Autom. Lett. 2021, 6, 5881–5888. [Google Scholar] [CrossRef]
- Webster, R.J., III; Jones, B.A. Design and Kinematic Modeling of Constant Curvature Continuum Robots: A Review. Int. J. Robot. Res. 2010, 29, 1661–1683. [Google Scholar] [CrossRef]
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You Only Look Once: Unified, Real-Time Object Detection. arXiv 2016, arXiv:1506.02640. [Google Scholar]
- Redmon, J.; Farhadi, A. YOLOv3: An Incremental Improvement. arXiv 2018, arXiv:1804.02767. [Google Scholar]
- Bochkovskiy, A.; Wang, C.Y.; Liao, H.Y.M. YOLOv4: Optimal Speed and Accuracy of Object Detection. arXiv 2020, arXiv:2004.10934. [Google Scholar]
- Wang, H.; Lin, Y.; Xu, X.; Chen, Z.; Wu, Z.; Tang, Y. A Study on Long-Close Distance Coordination Control Strategy for Litchi Picking. Agronomy 2022, 12, 1520. [Google Scholar] [CrossRef]
- Tang, Y.; Zhou, H.; Wang, H.; Zhang, Y. Fruit detection and positioning technology for a Camellia oleifera C. Abel orchard based on improved YOLOv4-tiny model and binocular stereo vision. Expert Syst. Appl. 2023, 211, 118573. [Google Scholar] [CrossRef]













| Transform Turn | ||||
|---|---|---|---|---|
| 1 | ||||
| 2 | ||||
| 3 | ||||
| 4 | ||||
| 5 |
| Speed Variation | ||||||
|---|---|---|---|---|---|---|
| X | Y | Z | X_error | Y_error | Z_error | |
| Start point | 279.6 | −101.5 | 586.8 | - | - | - |
| 1 | 281.6 | −79.38 | 591.0 | −1.8 | −2.12 | −4.2 |
| 2 | 282.7 | −57.43 | 594.4 | −3.1 | −4.07 | −7.6 |
| 3 | 283.5 | −36.03 | 596.8 | −3.9 | −5.47 | −10.0 |
| 4 | 283.6 | −16.42 | 598.4 | −4.0 | −5.08 | −11.5 |
| Speed variation | ||||||
| X | Y | Z | X_error | Y_error | Z_error | |
| Start point | 279.6 | −101.5 | 586.8 | - | - | - |
| 1 | 298.4 | −103.5 | 575.5 | 1.2 | −2.0 | 11.3 |
| 2 | 316.7 | −105.3 | 563.3 | 2.9 | −3.8 | 23.5 |
| 3 | 334.3 | −106.7 | 551.2 | 5.3 | −1.4 | 35.6 |
| 4 | 351.2 | −107.7 | 538.4 | 8.4 | −2.4 | 48.4 |
| Number of Points | Test | Max Error (pixel) | Min Error (pixel) | Average Error (pixel) | RMSE | |||
|---|---|---|---|---|---|---|---|---|
| X | Y | X | Y | X | Y | |||
| 42 | 1 | 14.43 | 27.00 | 0.10 | 0.04 | 3.70 | 5.21 | 7.80 |
| 2 | 15.23 | 32.30 | 0.02 | 0.41 | 3.89 | 5.34 | 7.67 | |
| 3 | 16.34 | 35.05 | 0.04 | 0.10 | 3.64 | 5.17 | 7.63 | |
| 4 | 15.69 | 28.31 | 0.03 | 0.39 | 3.77 | 5.26 | 7.74 | |
| 5 | 16.89 | 33.41 | 0.21 | 0.19 | 3.98 | 5.31 | 7.87 | |
| Average | 15.72 | 31.21 | 0.08 | 0.22 | 3.80 | 5.26 | 7.74 | |
| 82 | 1 | 40.00 | 19.24 | 0.00 | 0.33 | 2.82 | 4.08 | 6.05 |
| 2 | 38.20 | 20.45 | 0.00 | 0.33 | 2.79 | 3.99 | 6.08 | |
| 3 | 42.32 | 18.78 | 0.08 | 0.07 | 2.67 | 4.12 | 6.13 | |
| 4 | 39.64 | 19.67 | 0.02 | 0.09 | 2.37 | 4.05 | 6.09 | |
| 5 | 37.25 | 20.26 | 0.07 | 0.05 | 2.88 | 3.98 | 6.03 | |
| Average | 39.50 | 19.68 | 0.03 | 0.17 | 2.71 | 4.04 | 6.08 | |
| 162 | 1 | 36.00 | 14.42 | 0.00 | 0.06 | 1.81 | 3.09 | 4.26 |
| 2 | 37.23 | 14.36 | 0.02 | 0.02 | 1.86 | 3.07 | 4.32 | |
| 3 | 34.05 | 13.96 | 0.00 | 0.03 | 1.82 | 3.08 | 4.23 | |
| 4 | 32.35 | 14.85 | 0.00 | 0.04 | 1.83 | 3.02 | 4.36 | |
| 5 | 35.87 | 13.56 | 0.02 | 0.01 | 1.79 | 3.08 | 4.33 | |
| Average | 35.10 | 14.23 | 0.01 | 0.03 | 1.82 | 3.07 | 4.30 | |
| 322 | 1 | 6.02 | 11.09 | 0.02 | 0.00 | 1.79 | 3.10 | 3.97 |
| 2 | 6.04 | 11.05 | 0.01 | 0.02 | 1.80 | 2.97 | 4.07 | |
| 3 | 5.98 | 11.09 | 0.00 | 0.03 | 1.73 | 2.99 | 4.05 | |
| 4 | 6.06 | 11.12 | 0.00 | 0.01 | 1.75 | 3.12 | 4.01 | |
| 5 | 6.03 | 10.99 | 0.00 | 0.01 | 1.76 | 3.08 | 4.03 | |
| Average | 6.03 | 11.07 | 0.01 | 0.02 | 1.77 | 3.05 | 4.03 | |
| Unplugging Task | Plugging Task | |||
|---|---|---|---|---|
| Time (s) | Mission Completion | Time (s) | Mission Completion | |
| 1 | 61 | Success | 88 | success |
| 2 | 55 | Success | 80 | success |
| 3 | 62 | Success | - | fail |
| 4 | 58 | Success | 75 | success |
| 5 | 57 | Success | - | fail |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hsu, M.-H.; Nguyen, P.T.-T.; Nguyen, D.-D.; Kuo, C.-H. Image Servo Tracking of a Flexible Manipulator Prototype with Connected Continuum Kinematic Modules. Actuators 2022, 11, 360. https://doi.org/10.3390/act11120360
Hsu M-H, Nguyen PT-T, Nguyen D-D, Kuo C-H. Image Servo Tracking of a Flexible Manipulator Prototype with Connected Continuum Kinematic Modules. Actuators. 2022; 11(12):360. https://doi.org/10.3390/act11120360
Chicago/Turabian StyleHsu, Ming-Hong, Phuc Thanh-Thien Nguyen, Dai-Dong Nguyen, and Chung-Hsien Kuo. 2022. "Image Servo Tracking of a Flexible Manipulator Prototype with Connected Continuum Kinematic Modules" Actuators 11, no. 12: 360. https://doi.org/10.3390/act11120360
APA StyleHsu, M.-H., Nguyen, P. T.-T., Nguyen, D.-D., & Kuo, C.-H. (2022). Image Servo Tracking of a Flexible Manipulator Prototype with Connected Continuum Kinematic Modules. Actuators, 11(12), 360. https://doi.org/10.3390/act11120360









