Adaptive Fault Tolerant Non-Singular Sliding Mode Control for Robotic Manipulators Based on Fixed-Time Control Law

Abstract

This paper presents a fault tolerant scheme employing adaptive non-singular fixed-time terminal sliding mode control (AFxNTSM) for the application of robotic manipulators under uncertainties, external disturbances, and actuator faults. To begin, non-singular fixed-time terminal sliding mode control (FxNTSM) is put forth. This control method uses non-singular terminal sliding mode control to quickly reach fixed-time convergence, accomplish satisfactory performance in tracking, and produce non-singular and non-chatter control inputs. Then, without knowing the upper bounds beforehand, AFxNTSM is used as a reliable fault tolerant control (FTC) to estimate actuator faults and unknown dynamics. The fixed-time stability of the closed-loop system is established by the theory of Lyapunov analysis. The computer simulation results of the position tracking, control inputs, and adaptive parameters are presented to verify and illustrate the performance of the proposed strategy.

1. Introduction

Recent developments in the field of control systems are having a profound impact on the fields of mechatronics and robotic systems. The problem of the robotic manipulator is one that is explored in the area of control theory. It is a highly unstable mechanical system that is nonlinear to a high degree. As a consequence of this, such a system must have a robust control law and must be capable of maintaining strong stability and trajectory tracking capabilities in the face of external disturbance and uncertainty [1]. In spite of the fact that a range of robust solutions have been offered for uncertain robotic systems, an additional problem arises when joint actuators fail to function properly. In this scenario, FTC is utilized to compensate for controller failures in order to ensure that the system continues to function correctly. Under real-world conditions, it is impossible to prevent the control failure from occurring. Therefore, an accurately functioning controlled system is impossible if the controller cannot tolerate faults in the system being regulated. As a consequence of this, there is a growing interest in the development of FTC methodologies, which have been subjected to extensive research and are being utilized in a variety of industries. The fundamental theory of FTC is that the designed controller needs to be robust in order to guarantee the achievement of the optimal level of stability and robustness in the event that the actuators fail to do their jobs [2].

The family of nonlinear controllers includes the sliding mode control (SMC). It is able to manage nonlinear systems with uncertainties, bounded disturbances, and low sensitivity to parameter variations in an effective manner. Terminal sliding mode control (TSM), which provides robust tracking and better precision, was created in [3] with the purpose of achieving finite-time stability. However, it suffers from slow convergence and singularity concerns. Then, SMC techniques were proposed as solutions to these challenges in order to meet the aims of attaining rapid convergence through the use of fast terminal SMC (FTSM), and getting rid of singularities through the use of fast non-singular terminal SMC (FNTSM) [4,5]. In addition, the amount of time required for the finite-time system to converge is highly dependent on the initial values of the nonlinear system, and this amount of time would unquestionably increase as the initial values of the nonlinear system were raised. Therefore, fixed-time stability is an alternative, which may be utilized to precisely calculate the time of convergence regardless of the initial conditions [6,7]. Concerning finite-time convergence, several FTC algorithms have been proposed for robotic applications using adaptive control scheme to estimate the actuator faults [8].

Adaptive control is a well-known nonlinear control method that is gaining popularity in control engineering applications. It exhibits extraordinary adaptability to system uncertainty, external disturbances, and actuator failures, and improve the closed-loop system’s tracking performance [9]. Various adaptive finite time SMC schemes have been proposed for the robotic manipulator with uncertainties and actuator failures. In [10], FTC using adaptive finite-time FTSM was designed for the robotic system under faults, in which faults were estimated using adaptive gains. A finite-time SMC based active FTC was proposed to estimate the unknown dynamics of the nonlinear robot with joint faults [11]. Another FTC scheme based on a class of third-order SMC was developed for the second-order nonlinear system in the presence of actuator faults [12]. Furthermore, a robust adaptive control approach with a quasi-continuous high-order SMC and neural network has been proposed for the unknown dynamics of the nonlinear system under joint actuator faults [13].

Interestingly, all of the aforementioned publications focused primarily on the adaptive scheme for the estimation of the upper bounds of uncertain dynamics and actuator faults utilizing finite-time FNTSM control [11,12,13]. According to our understanding, few works offer adaptive FxNTSM control [14,15], but none of them examined the FTC based on adaptive FxNTSM method under actuator failures. It is recognized that the primary advantage of FxNTSM control is singularity avoidance, strong robustness under system uncertainty and external disturbances; and convergence time does not depend on the initial values. In this study, we examine the fixed-time convergence and FTC for the nonlinear system in the presence of unknown dynamics. Therefore, we are proposing the adaptive fixed-time non-singular terminal SMC (AFxNTSM) for the application of uncertain and disturb robotic manipulators under actuator failures. The following is a summary of the key contributions of this work: (1) A sliding surface derived from the characteristics of non-singular fixed-time terminal SMC is devised. This sliding surface is designed to provide exceptional tracking performance, fixed-time convergence, and reduced chatter in the control torque. (2) Adaptive FTC approach is proposed with FxNTSM; bounded unknown dynamics and actuator failure are estimated to obtain the robust and sustainable performance for the robotic system. (3) The fixed-time stability analysis of the system is studied using the Lyapunov synthesis.

The other sections of this work are structured as follows: Section 2 presents the related works. Section 3 provides the system modelling and problem formulations. In Section 4 and Section 5, respectively, the control design and stability analysis based on the Lyapunov theorem are described in detail. Section 6 then provides the numerical simulations to validate and demonstrate the performance of proposed scheme, and Section 7 addressed the discussion on the simulation results. The conclusions of the paper are presented in Section 8.

2. Related Work

In recent years, a significant number of researchers have focused their attention on the issue of the SMC schemes for nonlinear systems, which are distinguished by a fixed-time convergence. In [16], the authors proposed a singularity-free fixed-time SMC scheme for an uncertain robotic system with disturbances. The research that was published in [17] involved the creation of a new fixed-time sliding surface using constant and variable exponent coefficients for the second-order system. For the autonomous underwater vehicle, an event-triggered scheme using an integral fixed-time SMC technique has been presented in [18], and the formation control was constructed with the help of a fixed-time SMC, and disturbance was dealt with the assistance of a disturbance observer in [19]. Moreover, the author in [20] presented fast exponential fixed-time super-twisting SMC for the robotic manipulator and the finite-time high-order sliding mode observer to estimate the angular velocity and lumped disturbances. A fixed-time super-twisting sliding mode method subject to control input limitations was developed for a symmetric chaotic supply chain system [21]. A third-order fixed-time super-twisting-like SMC scheme was designed for the piezoelectric nanopositioning stage [22]. Another fixed-time control strategy based on robust observer was presented for $n-DOF$ robot manipulators with uncertainty [23].

Faulty actuators can be compensated for by employing a variety of different adaptive techniques, which were presented in order to build FTC for a wide range of nonlinear systems. An adaptive non-singular TSM (AFTSMC) has been used in [10] to achieve fast response and lessen chattering and singularity problems, and adaptive control based FTC has been used to estimate uncertainties and actuator faults. Actuator failure compensation for an underactuated nonlinear system utilising an adaptive fuzzy SMC approach to adjust the uncertainties caused by actuator faults has been addressed in [24]. In [25], another adaptive technique has been developed for wind turbine under constant and variable actuator faults. In [26], FNTSM was designed and paired with adaptive control for attitude tracking of spacecraft in the presence of actuator faults, actuator saturations, external disturbances, and inertia uncertainty. Robust fault tolerant tracking control using fixed-time SMC and observer has been presented for an uncertain robotic manipulator [27].

3. Robot Dynamics and Problem Statement

The robotic manipulator’s dynamic equation can be described as follows [28]:

$$M_0\left(q\right)\ddot{q}+\overline{M}\left(q\right)\ddot{q}+C_0(q,\dot{q})\dot{q}+\overline{C}(q,\dot{q})\dot{q}+G_0\left(q\right)+\overline{G}\left(q\right)=u\left(t\right)+T_d+f(t-t_f)\mathcal{F}(q,\dot{q},\tau )$$

(1)

$$⟹M_0\left(q\right)\ddot{q}+C_0(q,\dot{q})\dot{q}+G_0\left(q\right)=u\left(t\right)+\Xi (q,\dot{q},\ddot{q},T_d,\mathcal{F})$$

(2)

where $\Xi (q,\dot{q},\ddot{q},T_d,\mathcal{F})=T_d+f(t-t_f)\mathcal{F}(q,\dot{q},\tau )-\overline{M}\left(q\right)\ddot{q}-\overline{C}(q,\dot{q})\dot{q}-\overline{G}\left(q\right)$. The (2) can be rewritten as

$$\ddot{q}=M_0^{-1}\left(q\right)[u\left(t\right)-C_0(q,\dot{q})\dot{q}-G_0\left(q\right)+\Xi (q,\dot{q},\ddot{q},T_d,\mathcal{F})]$$

(3)

where $q\in \mathbb{R}{}^n$ is joints position, $\dot{q}\in \mathbb{R}{}^n$ is joint velocity and $\ddot{q}\in \mathbb{R}{}^n$ is joint acceleration. $M\left(q\right)\in \mathbb{R}{}^{n\times n}$ represents the inertia matrix and satisfies that $0<{\lambda }_1\left(M\left(q\right)\right)\le ∥M\left(q\right)∥\le {\lambda }_2\left(M\left(q\right)\right)$ with ${\lambda }_1$ and ${\lambda }_2$ illustrate the min and the max eigenvalues of matrix $M\left(q\right)$. $C(q,\dot{q})\in \mathbb{R}{}^{n\times n}$ denotes the coriolis, centripetal, and friction forces matrix; $G\left(q\right)\in \mathbb{R}{}^n$ is the gravitational vector. $M_0\left(q\right),C_0(q,\dot{q}),G_0\left(q\right)$ are nominal and $\overline{M}\left(q\right),\overline{C}(q,\dot{q}),\overline{G}\left(q\right)$ are uncertain parameters. $T_d\in \mathbb{R}{}^n$ is a representation of the external disturbance, $u\left(t\right)\in \mathbb{R}{}^n$ is the input torque at the joints, the fault vector for a constant and/or time-varying actuator is defined by $\mathcal{F}(q,\dot{q},\tau )\in \mathbb{R}{}^n$, and the fault time profile is indicated by $f(t-Tf)$, where $tf$ is the time at which the fault first occurs. The following notations throughout the paper will be used.

In addition, the following is the time profile of the faults that were discussed earlier, $f(·)$, is defined:

$$f(t-t_f)=diag\left\{f_1(t-t_f),f_2(t-t_f),\cdots ,f_n(t-t_f)\right\}$$

(4)

The time profile fault model is as follows, where $f_i$ is the $i_{th}$ state equation affected by the fault:

$$f_i(t-t_f)=\left\{\begin{array}{cc}0& ift<t_f\\ 1-e^{-{\varsigma }_i(t-t_f)}& ift\ge t_f\end{array}\right.$$

(5)

where ${\varsigma }_i>0$ is the time constant that characterizes the unknown actuator fault’s development. When ${\varsigma }_i$ is minor, the fault is referred to as an incipient fault. When ${\varsigma }_i\to \infty$, the $f_i$ function begins to grow as a step, and the fault that was in the process of developing becomes an abrupt fault.

Using (3), we can express the trajectory tracking error as

$$\ddot{e}=M_0^{-1}\left(q\right)[u\left(t\right)-C_0(q,\dot{q})\dot{q}-G_0\left(q\right)+\Xi (q,\dot{q},\ddot{q},T_d,\mathcal{F})]-{\ddot{q}}_d$$

(6)

$$\Rightarrow \ddot{e}=M_0^{-1}\left(q\right)u\left(t\right)+\Omega (q,\dot{q})+\tilde{\Xi }(q,\dot{q},\ddot{q},T_d,\mathcal{F})$$

(7)

where $\Omega (q,\dot{q})=-M_0^{-1}\left(q\right)[C_0(q,\dot{q})\dot{q}+G_0\left(q\right)]-{\ddot{q}}_d$ denotes the known nominal system dynamics and $\tilde{\Xi }(q,\dot{q},\ddot{q},T_d,\mathcal{F})=M_0^{-1}\left(q\right)\Xi (q,\dot{q},\ddot{q},T_d,\mathcal{F})$. The tracking error $e=q-q_d$, where q is the actual and $q_d$ is the desired position vector.

4. Control Design

This section begins with a discussion of the features of nonsingular fixed-time sliding surface and control design named FxNTSM. Moreover, the important Lemma and Assumption are given in this section.

4.1. Fixed-Time Non-Singular Terminal Sliding Manifold

In literature, sliding surfaces have been constructed to obtain the benefits of TSM while avoiding the singularity problem. Motivated by the aforementioned methodologies discussed in Section 1, the proposed FxNTSM surface can be designed as providing robust and precise trajectory tracking of the $n-DOF$ robotic manipulators in fixed-time:

$$s\left(t\right)=\dot{e}\left(t\right)+{\theta }_{1}si{g}^{{\eta }_1}\left(e\left(t\right)\right)+{\theta }_{2}si{g}^{{\eta }_2}\left(e\left(t\right)\right)$$

(8)

where $s\left(t\right)\in \mathbb{R}{}^n$ is the sliding surface, $si{g}^y(·)={\left|·\right|}^{y}sign(·)$, ${\theta }_1\in \mathbb{R}{}^{+}$ and ${\theta }_2\in \mathbb{R}{}^{+}$ are positive constants, and the ${\eta }_1$ and ${\eta }_2$ are constants satisfying the relation $0<{\eta }_1<1$ and $1<{\eta }_2$.

The development of the sliding manifold is completed; now, the robustness against uncertainty and actuator faults will be achieved through the FxNTSM design for $n-DOF$ robotic manipulators.

Assumption 1.

Conditional bounds on the uncertainty, external disturbance and fault vector are expressed by (9) that are shown below:

$$∥\tilde{\Xi }(q,\dot{q},\ddot{q},T_d,\mathcal{F})∥\le {\Xi }_1+{\Xi }_2∥q∥+{\Xi }_3{∥\dot{q}∥}^2$$

(9)

where ${\Xi }_1$, ${\Xi }_2$ and ${\Xi }_3$ are unknown constants of uncertainties, disturbances and actuator faults’ upper bounds.

Lemma 1

([29,30]). Consider the following nonlinear system:

$$\dot{x}\left(t\right)=f(t,x),x\left(0\right)=x_0$$

(10)

where $f(t,x)$ is a continuous nonlinear function. For fixed-time stability with fast time convergence, Lyapunov function $V\left(x\right)$ that satisfies

a.

$V\left(x\right)=0\iff x=0$

b.

$\dot{V}\left(x\right)\le -{\beta }_1{V}^{{\alpha }_1}\left(x\right)-{\beta }_{2}V{\left(x\right)}^{{\alpha }_2}$

where ${\beta }_1,{\beta }_2>0,0<{\alpha }_1<1and{\alpha }_2>1$. Then, the system is fixed-time stable and the convergence time can be computed as

$$T\le \frac{1}{{\beta }_1(1-{\alpha }_1)}+\frac{1}{{\beta }_2({\alpha }_2-1)}$$

(11)

During the sliding motion, we have $s\left(t\right)=0$. Thus, the following dynamics can be obtained according to (8) as

$$\dot{e}\left(t\right)=-{\theta }_{1}si{g}^{{\eta }_1}\left(e\left(t\right)\right)-{\theta }_{2}si{g}^{{\eta }_2}\left(e\left(t\right)\right)$$

(12)

The Lyapunov function is considered as follows:

$$V_e\left(t\right)=\frac{1}{2}e{\left(t\right)}^{T}e\left(t\right)$$

(13)

The derivative of $V_e\left(t\right)$ can be obtained with (12) as

$${\dot{V}}_e\left(t\right)=e{\left(t\right)}^T\dot{e}\left(t\right)=e{\left(t\right)}^T\left[-{\theta }_{1}si{g}^{{\eta }_1}\left(e\left(t\right)\right)-{\theta }_{2}si{g}^{{\eta }_2}\left(e\left(t\right)\right)\right]$$

(14)

$$\begin{array}{c}{\dot{V}}_e\left(t\right)\le -{\theta }_1{∥e\left(t\right)∥}^{{\eta }_1+1}-{\theta }_2{∥e\left(t\right)∥}^{{\eta }_2+1}\hfill \\ \le -2^{\frac{{\eta }_1+1}{2}}{\theta }_1{V_e}^{\frac{{\eta }_1+1}{2}}-2^{\frac{{\eta }_2+1}{2}}{\theta }_2{V_e}^{\frac{{\eta }_2+1}{2}}\hfill \end{array}$$

(15)

According to Lemma 1, the sliding surface (8) will reach zero in a fixed-time, and the time it takes to converge is bounded by

$$\begin{array}{c}{T}_1=\frac{1}{2^{\frac{{\eta }_1+1}{2}}{\theta }_1\left(1-\frac{{\eta }_1+1}{2}\right)}+\frac{1}{2^{\frac{{\eta }_2+1}{2}}{\theta }_2\left(\frac{{\eta }_2+1}{2}-1\right)}\hfill \\ =\frac{\sqrt{2}}{2^{{\eta }_1/2}{\theta }_1\left(1-{\eta }_1\right)}+\frac{\sqrt{2}}{2^{{\eta }_2/2}{\theta }_2\left({\eta }_2-1\right)}\hfill \end{array}$$

(16)

4.2. Fxntsm Control Design

To control a robotic manipulator in the presence of known bounded uncertainties, external disturbances, and actuator failures, the FxNTSM control law can be defined as follows:

$$u\left(t\right)=u_1\left(t\right)+u_2\left(t\right)$$

(17)

where $u_1\left(t\right)$ is the control input that is utilized in the control of the nominal dynamics, and $u_2\left(t\right)$ is used to mitigate the uncertainties and actuator fault:

$$u_1\left(t\right)=-M_0^{}\left(q\right)\left(\Omega (q,\dot{q})+{\theta }_1\Pi \left(q\right)\dot{e}\left(t\right)+{\theta }_2{\eta }_2{\left|e\left(t\right)\right|}^{{\eta }_2-1}\dot{e}\left(t\right)\right)$$

(18)

where $\Pi \left(e\left(t\right)\right)=\left\{\begin{array}{cc}{\eta }_1{\left|e\left(t\right)\right|}^{{\eta }_1-1}& ife\left(t\right)\ne 0\\ 0& ife\left(t\right)=0\end{array}\right.$ satisfies the non-singularity in the control input:

$$u_2\left(t\right)=-M_0^{}\left(q\right)\left(({\Xi }_1+{\Xi }_2∥q∥+{\Xi }_3{∥\dot{q}∥}^2)sign\left(s\right)+{\gamma }_{1}si{g}^{{\gamma }_{10}}\left(s\left(t\right)\right)+{\gamma }_{2}si{g}^{{\gamma }_{20}}\left(s\left(t\right)\right)\right)$$

(19)

where ${\gamma }_1\in \mathbb{R}{}^{+}$ and ${\gamma }_2\in \mathbb{R}{}^{+}$ are positive constants, and ${\gamma }_{10}$ and ${\gamma }_{20}$ are constants satisfying the relation $0<{\gamma }_{10}<1$ and $1<{\gamma }_{20}$, respectively.

5. Stability Analysis

In this section, the stability of the overall system using FxNTSM scheme is established through the application of the Lyapunov theorem. Afterward, the fault tolerant control structure with adaptive laws is subsequently designed to provide AFxNTSM for uncertain robotic manipulators under varying actuator faults at joint(s). Then, stability analysis using AFxNTSM method is investigated by the Lyapunov theorem.

Theorem 1.

Taking into account the defined robotic manipulator (3), the proposed sliding manifold (8) and the proposed FxNTSM controller (17) allow for the desired augular position of the uncertain robotic manipulator to converge in a fixed-time along with (9).

Proof .

The following is the Lyapunov function selected as

$$V_s\left(t\right)=\frac{1}{2}s{\left(t\right)}^{T}s\left(t\right)$$

(20)

The calculation for the derivative of $V_s\left(t\right)$ can be written as

$${\dot{V}}_s\left(t\right)=s{\left(t\right)}^T\dot{s}\left(t\right)$$

(21)

The derivative of (8) when substituted into Equation (21) yields

$${\dot{V}}_s\left(t\right)=s{\left(t\right)}^T\left[\ddot{e}\left(t\right)+{\theta }_1\Pi \left(q\right)\dot{e}\left(t\right)+{\theta }_2{\eta }_2{\left|e\left(t\right)\right|}^{{\eta }_2-1}\dot{e}\left(t\right)\right]$$

(22)

By substituting error Equation (7) in (22), one has

$$\dot{V}\left(t\right)=s{\left(t\right)}^T\left\{\begin{array}{c}{M}_0^{-1}\left(q\right)u+\Omega (q,\dot{q})+\tilde{\Xi }(q,\dot{q},\ddot{q},T_d,\mathcal{F})\hfill \\ +{\theta }_1\Pi \left(q\right)\dot{e}\left(t\right)+{\theta }_2{\eta }_2{\left|e\left(t\right)\right|}^{{\eta }_2-1}\dot{e}\left(t\right)\hfill \end{array}\right\}$$

(23)

By substituting control input (17) in (23), one obtains

$${\dot{V}}_s\left(t\right)=s{\left(t\right)}^T\left\{\begin{array}{c}(-{\Xi }_1-{\Xi }_2∥q∥-{\Xi }_3{∥\dot{q}∥}^2)sign\left(s\left(t\right)\right)-\Omega (q,\dot{q})\hfill \\ -{\gamma }_{1}si{g}^{{\gamma }_{10}}\left(s\left(t\right)\right)-{\gamma }_{2}si{g}^{{\gamma }_{20}}\left(s\left(t\right)\right)\hfill \\ -{\theta }_1\Pi \left(q\right)\dot{e}\left(t\right)-{\theta }_2{\eta }_2{\left|e\left(t\right)\right|}^{{\eta }_2-1}\dot{e}\left(t\right)+\Omega (q,\dot{q})\hfill \\ +\tilde{\Xi }(q,\dot{q},\ddot{q},T_d,F)+{\theta }_1\Pi \left(q\right)\dot{e}\left(t\right)+{\theta }_2{\eta }_2{\left|e\left(t\right)\right|}^{{\eta }_2-1}\dot{e}\left(t\right)\hfill \end{array}\right\}$$

(24)

$$\begin{array}{c}{\dot{V}}_s\left(t\right)=s{\left(t\right)}^T\left\{\begin{array}{c}(-{\Xi }_1-{\Xi }_2∥q∥-{\Xi }_3{∥\dot{q}∥}^2)sign\left(s\left(t\right)\right)+\tilde{\Xi }(q,\dot{q},\ddot{q},T_d,\mathcal{F})\hfill \\ -{\gamma }_{1}si{g}^{{\gamma }_{10}}\left(s\left(t\right)\right)-{\gamma }_{2}si{g}^{{\gamma }_{20}}\left(s\left(t\right)\right)\hfill \end{array}\right\}\hfill \\ \le (-{\Xi }_1-{\Xi }_2∥q∥-{\Xi }_3{∥\dot{q}∥}^2)∥s\left(t\right)∥+\parallel \tilde{\Xi }(q,\dot{q},\ddot{q},T_d,\mathcal{F})\parallel ∥s\left(t\right)∥\hfill \\ -{\gamma }_1{∥s\left(t\right)∥}^{{\gamma }_{10}+1}-{\gamma }_2{∥s\left(t\right)∥}^{{\gamma }_{20}+1}\hfill \end{array}$$

(25)

According to Assumption 1, one can obtain

$${\dot{V}}_s\left(t\right)\le -{\gamma }_1{∥s\left(t\right)∥}^{{\gamma }_{10}+1}-{\gamma }_2{∥s\left(t\right)∥}^{{\gamma }_{20}+1}$$

(26)

$${\dot{V}}_s\left(t\right)\le -2^{\frac{{\gamma }_{10}+1}{2}}{\gamma }_1{\left\{V_s\left(t\right)\right\}}^{\frac{{\gamma }_{10}+1}{2}}-2^{\frac{{\gamma }_{20}+1}{2}}{\gamma }_2{\left\{V_s\left(t\right)\right\}}^{\frac{{\gamma }_{20}+1}{2}}$$

(27)

Thus, the system trajectory approaches to $s\left(t\right)$ in a fixed-time. According to Lemma 1, the convergence time can be formulated as

$$T_2=\frac{1}{2^{\frac{{\gamma }_{10}+1}{2}}{\gamma }_1\left(1-\frac{{\gamma }_{10}+1}{2}\right)}+\frac{1}{2^{\frac{{\gamma }_{20}+1}{2}}{\gamma }_2\left(\frac{{\gamma }_{20}+1}{2}-1\right)}$$

(28)

By the combination of $T_1$ and $T_2$, the total fixed settling time can be calculated as

$$T_{10}=T_1+T_2=\frac{\sqrt{2}}{2^{{\gamma }_{10}/2}{\gamma }_1\left(1-{\gamma }_{10}\right)}+\frac{\sqrt{2}}{2^{{\gamma }_{20}/2}{\gamma }_2\left({\gamma }_{20}-1\right)}+\frac{\sqrt{2}}{2^{{\eta }_1/2}{\theta }_1\left(1-{\eta }_1\right)}+\frac{\sqrt{2}}{2^{{\eta }_2/2}{\theta }_2\left({\eta }_2-1\right)}$$

(29)

Hence, this shows that the proposed scheme is fixed-time SMC. □

AFxNTSM Based FTC Control Design

For the unknown dynamics and actuator faults, the control input using adaptive scheme is designed as follows:

$$u\left(t\right)=u_3\left(t\right)$$

(30)

where

$$u_3\left(t\right)=-M_0^{}\left(q\right)\left(\begin{array}{c}({\widehat{\Xi }}_1+{\widehat{\Xi }}_2∥q∥+{\widehat{\Xi }}_3{∥\dot{q}∥}^2)sign\left(s\left(t\right)\right)+\Omega (q,\dot{q})\hfill \\ +{\gamma }_{1}si{g}^{{\gamma }_{10}}\left(s\left(t\right)\right)+{\gamma }_{2}si{g}^{{\gamma }_{20}}\left(s\left(t\right)\right)\hfill \\ +{\theta }_1\Pi \left(q\right)\dot{e}\left(t\right)+{\theta }_2{\eta }_2{\left|e\left(t\right)\right|}^{{\eta }_2-1}\dot{e}\left(t\right)\hfill \end{array}\right)$$

(31)

where ${\widehat{\Xi }}_1$, ${\widehat{\Xi }}_2$ and ${\widehat{\Xi }}_3$ represent the estimates of ${\Xi }_1,{\Xi }_2$ and ${\Xi }_3$, respectively.

For the compensation of uncertainties, external disturbances and actuator faults, adaptive laws are designed as follows:

$$\left\{\begin{array}{c}{\dot{\widehat{\Xi }}}_1^{}=\frac{1}{{\lambda }_1}∥s∥\hfill \\ {\dot{\widehat{\Xi }}}_2^{}=\frac{1}{{\lambda }_2}∥q∥∥s∥\hfill \\ {\dot{\widehat{\Xi }}}_3^{}=\frac{1}{{\lambda }_3}{∥\dot{q}∥}^2∥s∥\hfill \end{array}\right.$$

(32)

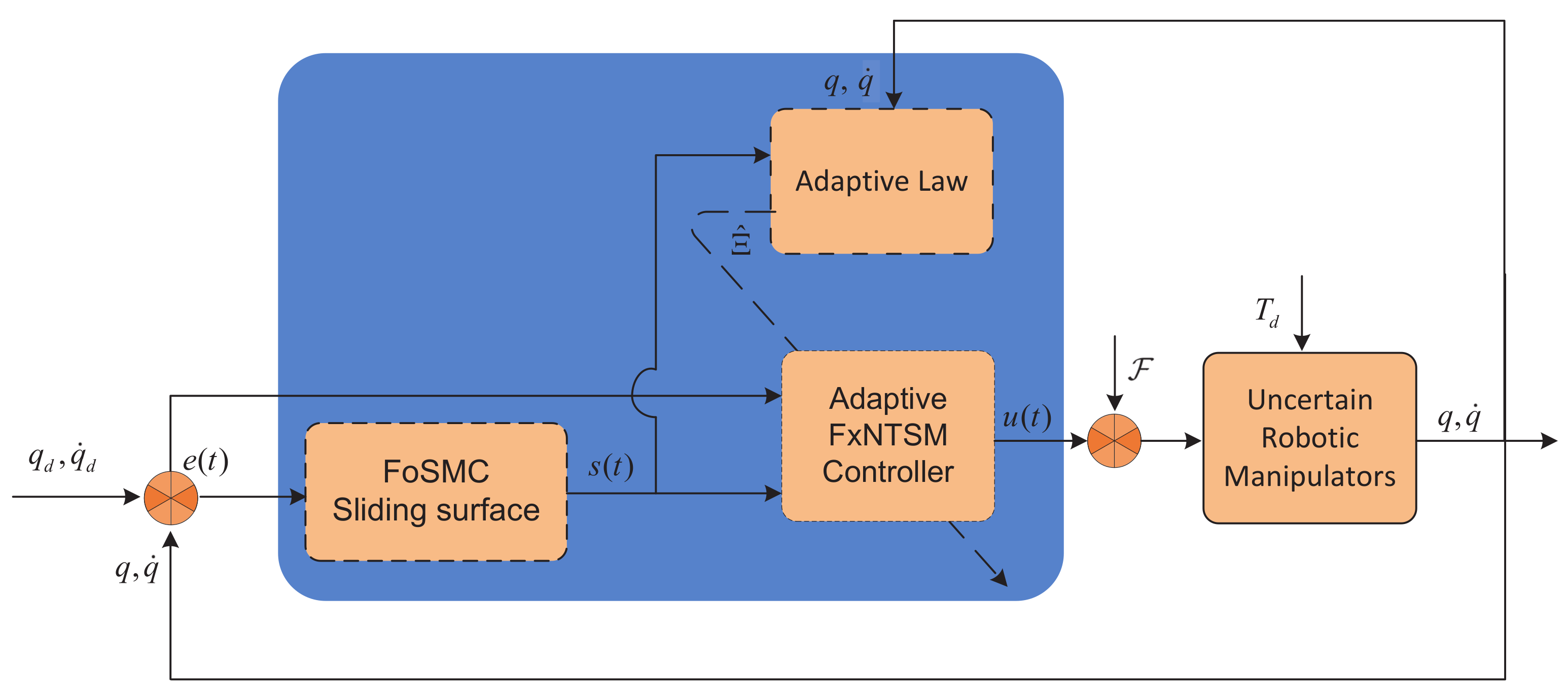
where ${\lambda }_1,{\lambda }_{2}and{\lambda }_3$ are positive constants, and the proposed model is given in Figure 1.

The upper bounds of the uncertainties, external disturbances and actuator faults can be compensated using (32). Hence, the AFxNTSM scheme formulates the tracking performance of the uncertain robotic manipulators under actuator faults.

Theorem 2.

Taking into account the defined robotic manipulator (3), which is subject to a number of problems such as uncertainties, external disturbances and joint actuator failures. Therefore, the proposed sliding surface (8), AFxNTSM control input (30) and adaptive laws (32) make it possible for the desired angular position of the robotic manipulator to converge in a fixed-time with the condition of Assumption 1.

Proof .

The Lyapunov functional candidate is chosen as follows:

$$V_a\left(t\right)=\frac{1}{2}s{\left(t\right)}^{T}s\left(t\right)+\frac{1}{2}{\lambda }_1\Delta {\Xi }_1^2+\frac{1}{2}{\lambda }_2\Delta {\Xi }_2^2+\frac{1}{2}{\lambda }_3\Delta {\Xi }_3^2$$

(33)

where $\Delta {\Xi }_1={\widehat{\Xi }}_1-{\Xi }_1,\Delta {\Xi }_2={\widehat{\Xi }}_2-{\Xi }_2,\Delta {\Xi }_3={\widehat{\Xi }}_3-{\Xi }_3$ are adaptation errors.

The derivative of $V_a\left(t\right)$ can be obtained as

$${\dot{V}}_a\left(t\right)=s{\left(t\right)}^T\dot{s}\left(t\right)+{\lambda }_1\Delta {\Xi }_1^{}{\dot{\widehat{\Xi }}}_1^{}+{\lambda }_2\Delta {\Xi }_2^{}{\dot{\widehat{\Xi }}}_2^{}+{\lambda }_2\Delta {\Xi }_3^{}{\dot{\widehat{\Xi }}}_3^{}$$

(34)

The substitution of derivative of (8) into (34), one obtains

$$\begin{array}{c}{\dot{V}}_a\left(t\right)=s{\left(t\right)}^T\left\{\begin{array}{c}{M}_0^{-1}\left(q\right)u\left(t\right)+\Omega (q,\dot{q})+\tilde{\Xi }(q,\dot{q},\ddot{q},T_d,\mathcal{F})\hfill \\ +{\theta }_1\Pi \left(q\right)\dot{e}\left(t\right)+{\theta }_2{\eta }_2{\left|e\left(t\right)\right|}^{{\eta }_2-1}\dot{e}\left(t\right)\hfill \end{array}\right\}\\ +{\lambda }_1\Delta {\Xi }_1^{}{\dot{\widehat{\Xi }}}_1^{}+{\lambda }_2\Delta {\Xi }_2^{}{\dot{\widehat{\Xi }}}_2^{}+{\lambda }_3\Delta {\Xi }_3^{}{\dot{\widehat{\Xi }}}_3^{}\end{array}$$

(35)

The substitution of control input (30) into (35), one obtains

$$\begin{array}{c}{\dot{V}}_a\left(t\right)=s{\left(t\right)}^T\left\{\begin{array}{c}(-{\widehat{\Xi }}_1-{\widehat{\Xi }}_2∥q∥-{\widehat{\Xi }}_3{∥\dot{q}∥}^2)sign\left(s\left(t\right)\right)-\Omega (q,\dot{q})\hfill \\ -{\gamma }_{1}si{g}^{{\gamma }_{10}}\left(s\left(t\right)\right)-{\gamma }_{2}si{g}^{{\gamma }_{20}}\left(s\left(t\right)\right)\hfill \\ -{\theta }_1\Pi \left(q\right)\dot{e}\left(t\right)-{\theta }_2{\eta }_2{\left|e\left(t\right)\right|}^{{\eta }_2-1}\dot{e}\left(t\right)+\Omega (q,\dot{q})\hfill \\ +\tilde{\Xi }(q,\dot{q},\ddot{q},T_d,\mathcal{F})+{\theta }_1\Pi \left(q\right)\dot{e}\left(t\right)+{\theta }_2{\eta }_2{\left|e\left(t\right)\right|}^{{\eta }_2-1}\dot{e}\left(t\right)\hfill \end{array}\right\}\\ +{\lambda }_1\Delta {\Xi }_1^{}{\dot{\widehat{\Xi }}}_1^{}+{\lambda }_2\Delta {\Xi }_2^{}{\dot{\widehat{\Xi }}}_2^{}+{\lambda }_3\Delta {\Xi }_3^{}{\dot{\widehat{\Xi }}}_3^{}\end{array}$$

(36)

$$\begin{array}{c}{\dot{V}}_a\left(t\right)=s{\left(t\right)}^T\left\{\begin{array}{c}(-{\widehat{\Xi }}_1-{\widehat{\Xi }}_2∥q∥-{\widehat{\Xi }}_3{∥\dot{q}∥}^2)sign\left(s\left(t\right)\right)\hfill \\ -{\gamma }_{1}si{g}^{{\gamma }_{10}}\left(s\left(t\right)\right)-{\gamma }_{2}si{g}^{{\gamma }_{20}}\left(s\left(t\right)\right)+\tilde{\Xi }(q,\dot{q},\ddot{q},T_d,\mathcal{F})\hfill \end{array}\right\}\\ +{\lambda }_1\Delta {\Xi }_1^{}{\dot{\widehat{\Xi }}}_1^{}+{\lambda }_2\Delta {\Xi }_2^{}{\dot{\widehat{\Xi }}}_2^{}+{\lambda }_3\Delta {\Xi }_3^{}{\dot{\widehat{\Xi }}}_3^{}\end{array}$$

(37)

$$\begin{array}{c}{\dot{V}}_a\left(t\right)\le -{\gamma }_1{∥s\left(t\right)∥}^{{\gamma }_{10}+1}-{\gamma }_2{∥s\left(t\right)∥}^{{\gamma }_{20}+1}\hfill \\ -{\widehat{\Xi }}_1∥\left(s\right(t\left)\right)∥-{\widehat{\Xi }}_2∥q∥∥\left(s\right(t\left)\right)∥-{\widehat{\Xi }}_3{∥\dot{q}∥}^2∥\left(s\right(t\left)\right)∥\hfill \\ +\parallel \tilde{\Xi }(q,\dot{q},\ddot{q},T_d,\mathcal{F})\parallel ∥s\left(t\right)∥+{\lambda }_1\Delta {\Xi }_1^{}{\dot{\widehat{\Xi }}}_1^{}+{\lambda }_2\Delta {\Xi }_2^{}{\dot{\widehat{\Xi }}}_2^{}+{\lambda }_3\Delta {\Xi }_3^{}{\dot{\widehat{\Xi }}}_3^{}\hfill \end{array}$$

(38)

Using (32), (38) can be simplified as follows:

$${\dot{V}}_a\left(t\right)\le -{\gamma }_1{∥s\left(t\right)∥}^{{\gamma }_{10}+1}-{\gamma }_2{∥s\left(t\right)∥}^{{\gamma }_{20}+1}$$

(39)

Hence, the robotic manipulator that is used for the precise trajectory tracking is fixed-time stable if and only if certain conditions are met. As a result, the proof of stability is thoroughly examined. □

Now, we will determine the fixed settling time, and the preceding equation can be represented as [26]

$${\dot{V}}_a\left(t\right)\le -{\gamma }_1{\left\{2(V_a\left(t\right)-\Phi )\right\}}^{\frac{{\gamma }_{10}+1}{2}}-{\gamma }_2{\left\{2(V_a\left(t\right)-\Phi )\right\}}^{\frac{{\gamma }_{20}+1}{2}}$$

(40)

where $\Phi =\frac{1}{2}{\lambda }_1\Delta {\Xi }_1^2+\frac{1}{2}{\lambda }_2\Delta {\Xi }_2^2+\frac{1}{2}{\lambda }_3\Delta {\Xi }_3^2$.

$${\dot{V}}_a\left(t\right)\le -2^{\frac{{\gamma }_{10}+1}{2}}{\gamma }_1{\left\{1-\frac{\Phi }{V_a\left(t\right)}\right\}}^{\frac{{\gamma }_{10}+1}{2}}{V}_a{\left(t\right)}^{\frac{{\gamma }_{10}+1}{2}}-2^{\frac{{\gamma }_{20}+1}{2}}{\gamma }_2{\left\{1-\frac{\Phi }{V_a\left(t\right)}\right\}}^{\frac{{\gamma }_{20}+1}{2}}{V}_a{\left(t\right)}^{\frac{{\gamma }_{20}+1}{2}}$$

(41)

Using Lemma 1, the fixed-time can be computed as

$$T_3=\frac{1}{{\sigma }_1\left(1-\frac{{\gamma }_{10}+1}{2}\right)}+\frac{1}{{\sigma }_2\left(\frac{{\gamma }_{20}+1}{2}-1\right)}=\frac{2}{{\sigma }_1\left(1-{\gamma }_{10}\right)}+\frac{2}{{\sigma }_2\left({\gamma }_{20}-1\right)}$$

(42)

where ${\sigma }_1=2^{\frac{{\gamma }_{10}+1}{2}}{\gamma }_1{\left\{1-\frac{\Phi }{V_a\left(t\right)}\right\}}^{\frac{{\gamma }_{10}+1}{2}},{\sigma }_2=2^{\frac{{\gamma }_{20}+1}{2}}{\gamma }_2{\left\{1-\frac{\Phi }{V_a\left(t\right)}\right\}}^{\frac{{\gamma }_{20}+1}{2}}$.

By the combination of of $T_1$ and $T_3$, the fixed time convergence can be computed as

$$T_{20}=\frac{2}{{\sigma }_1\left(1-{\gamma }_{10}\right)}+\frac{2}{{\sigma }_2\left({\gamma }_{20}-1\right)}+\frac{\sqrt{2}}{2^{{\eta }_1/2}{\theta }_1\left(1-{\eta }_1\right)}+\frac{\sqrt{2}}{2^{{\eta }_2/2}{\theta }_2\left({\eta }_2-1\right)}$$

(43)

As a result, the state trajectory will approach to zero in fixed-time.

Remark 1.

Applying the proposed method to the uncertain dynamics of robotic system (1), which includes the sliding surface (8), the proposed control input (30) and the adaptive laws (32), implies the tracking error tends to zero. In the following part, the numerical simulation will be provided.

6. Simulation Results and Comparative Analyses

In order to validate the proposed FxNTSM and AFxNTSM methods, a 2DOF manipulator is used to show the simulation performance. A 2DOF robotic manipulator under actuator faults with external disturbances and uncertainty will be used. Therefore, there are two cases that are presented with and without actuator faults to demonstrate the high performance of FxNTSM and AFxNTSM, and simulations using MATLAB/Simulink are illustrated. Their model parameters, intended trajectories and uncertainties are given, and the dynamic of 2DOF robotic manipulators is described as:

$$\begin{array}{cc}& M\left(q\right)=\left[\begin{array}{cc}{M}_{11}& M_{12}\\ M_{21}& M_{22}\end{array}\right], C(q,\dot{q})=\left[\begin{array}{c}{C}_1\\ C_2\end{array}\right], G\left(q\right)=\left[\begin{array}{c}{G}_1\\ G_2\end{array}\right],\hfill \\ & u\left(t\right)=\left[\begin{array}{c}{u}_1\\ u_2\end{array}\right], q_d=\left[\begin{array}{c}1.45-1.4e^{-t}+0.6e^{-4t}\\ 1.25+e^{-t}-0.5e^{-4t}\end{array}\right], T_d=\left[\begin{array}{c}1-e^{-t}\\ 1-e^{-t}\end{array}\right].\hfill \end{array}$$

where $M_{11}=m_1{r}_1^2+m_1(r_1^2+l_1^2)+2cos\left(q_2\right)m_2{l}_1{r}_2^{}+J_2+J_1$, $M_{12}=m_2{r}_2^2+cos\left(q_2\right)m_2{r}_2^{}{l}_1+J_2$, $M_{21}=M_{12}$, $M_{22}=m_2{r}_2^2+J_2$, $C_1=-sin\left(q_2\right)m_2{r}_2^{}{l}_1{\dot{q}}_1{\dot{q}}_2-sin\left(q_2\right)m_2{r}_2^{}{l}_1({\dot{q}}_1+{\dot{q}}_2){\dot{q}}_2$, $C_2=sin\left(q_2\right)m_2{r}_2^{}{l}_1{\dot{q}}_1{\dot{q}}_1$, $G_1=cos\left(q_1\right)(m_1{r}_1^{}+m_2{l}_1^{})g+cos(q_1+q_2)m_2{r}_2^{}g$, $G_2=cos(q_1+q_2)m_2{r}_2^{}g$.

The length of the links $l_1$ = 1 m, $l_2$ = 1 m, centroid length of joints $r_1$ = 0.5 m, $r_2$ = 0.85 m, mass of the links ${\overline{m}}_1$ = 0.5 kg, ${\overline{m}}_2$ = 1.5 kg, nominal mass of links $m_{10}$ = 0.4 kg, $m_{20}$ = 1.2 kg, moment of inertia $J_1=J_2$ = 5 kg·m² and gravitational constant g = 9.8 m/s². In addition, the physical model of $2-DOF$ robotic manipulator is given in Figure 2.

6.1. Case-1: Proposed Scheme without Actuator Faults

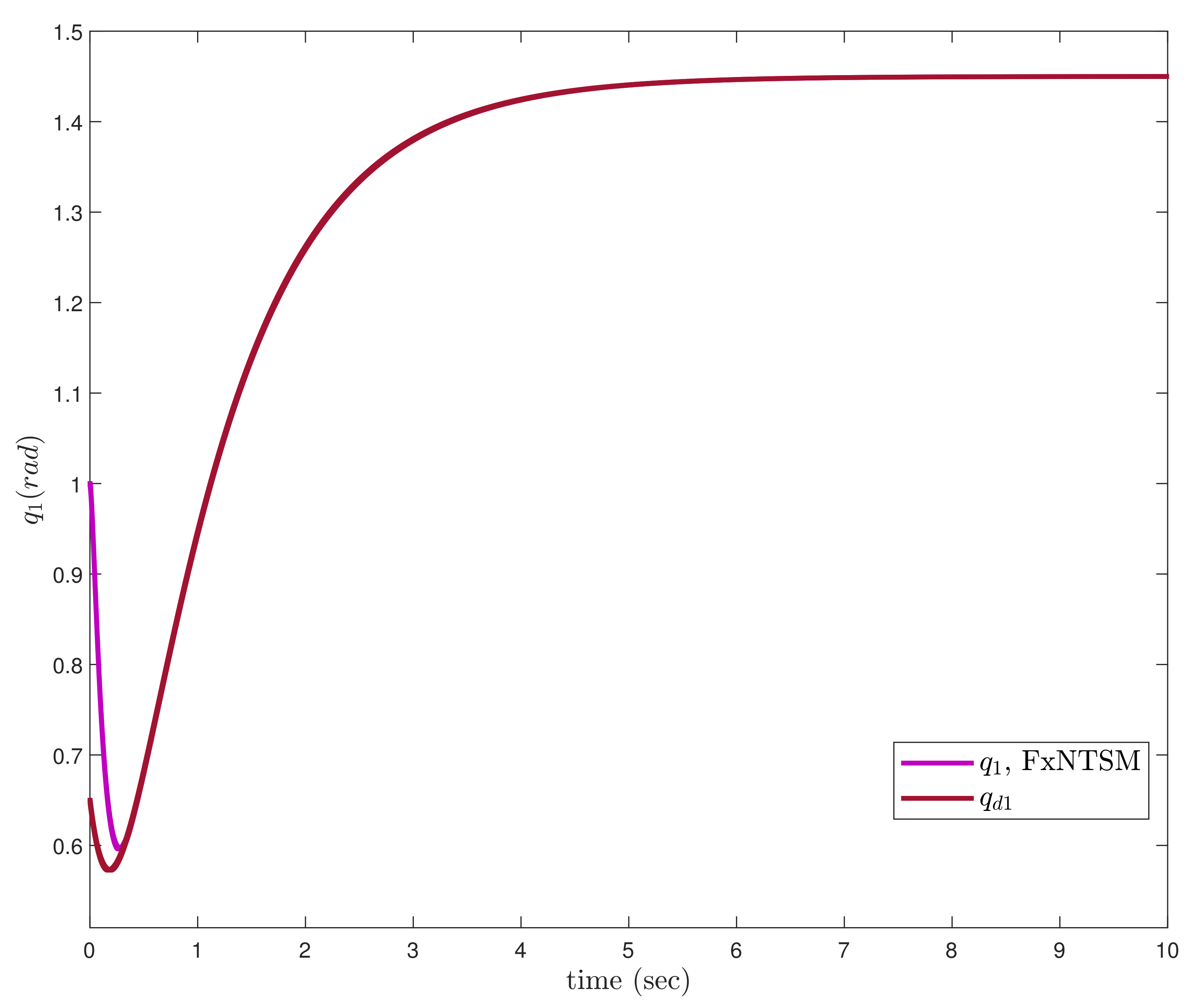
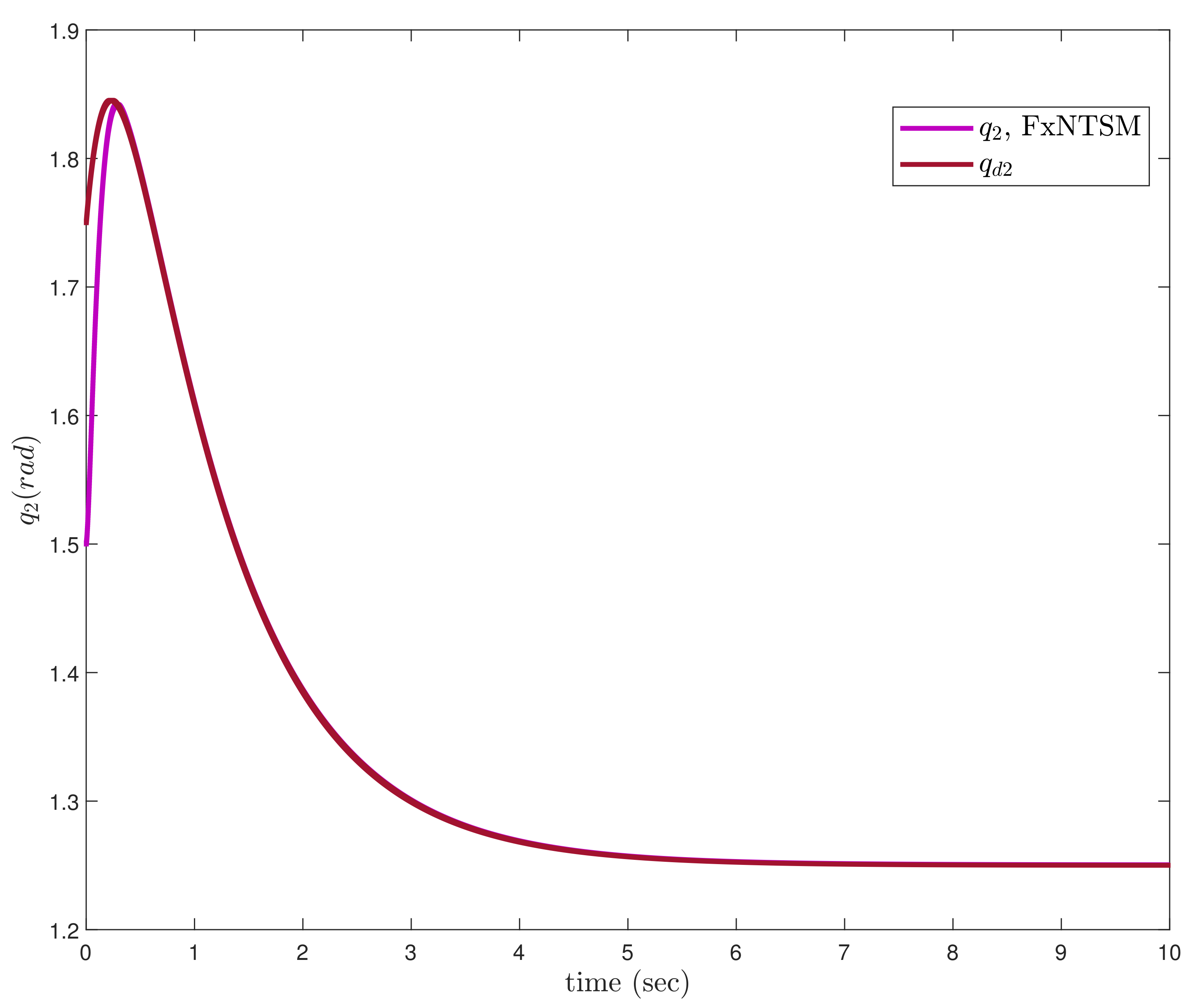
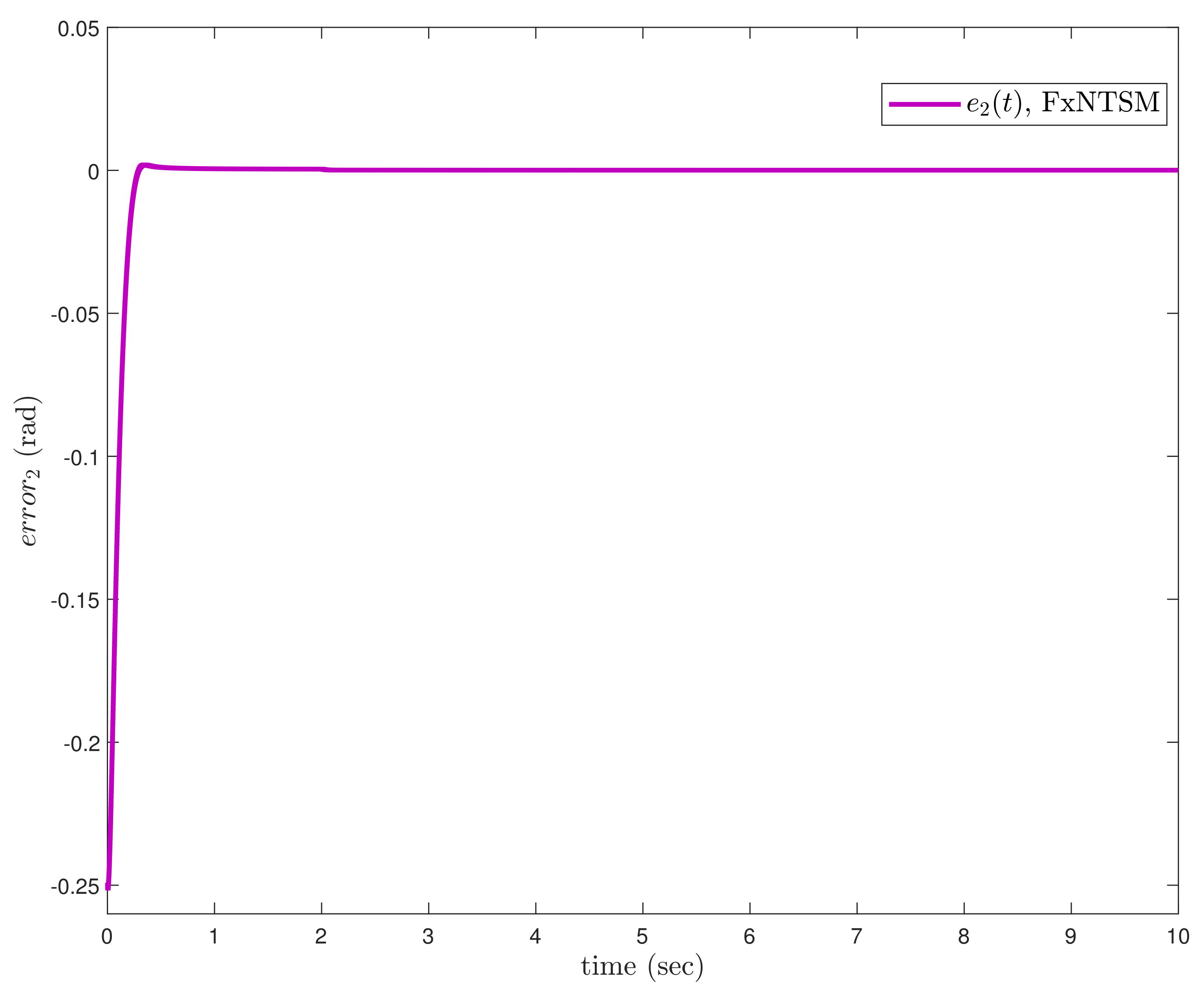
In this subsection, the proposed FxNTSM method is applied on the $2-DOF$ robotic manipulator with known uncertainties and external disturbances and the joint actuator faults are not considered. The parameters of FxNTSM are selected as follows: for (8), parameters are chosen as ${\theta }_1=6$, ${\theta }_2=1$, ${\eta }_1=0.8$, ${\eta }_2=1.5$. The parameters of (17) are selected as ${\gamma }_1=50$, ${\gamma }_2=50$, ${\gamma }_{10}=0.65$, ${\gamma }_{20}=1.5$. The initial conditions of joint positions are chosen as $q_1\left(0\right)=1$ and $q_2\left(0\right)=1.5$.

Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10 exhibit, accordingly, the position tracking performance, tracking errors, control inputs, and sliding mode surfaces, which correspond to the simulation findings of the proposed method on $2-DOF$ robotic manipulators.

Taking into consideration the high tracking and robustness against the known bounded system’s uncertainties, the proposed FxNTSM has superior performance and obtains angular position fast tracking performance in Figure 3 and Figure 4, smaller tracking errors in Figure 5 and Figure 6, and chatter-free control inputs in Figure 7 and Figure 8.

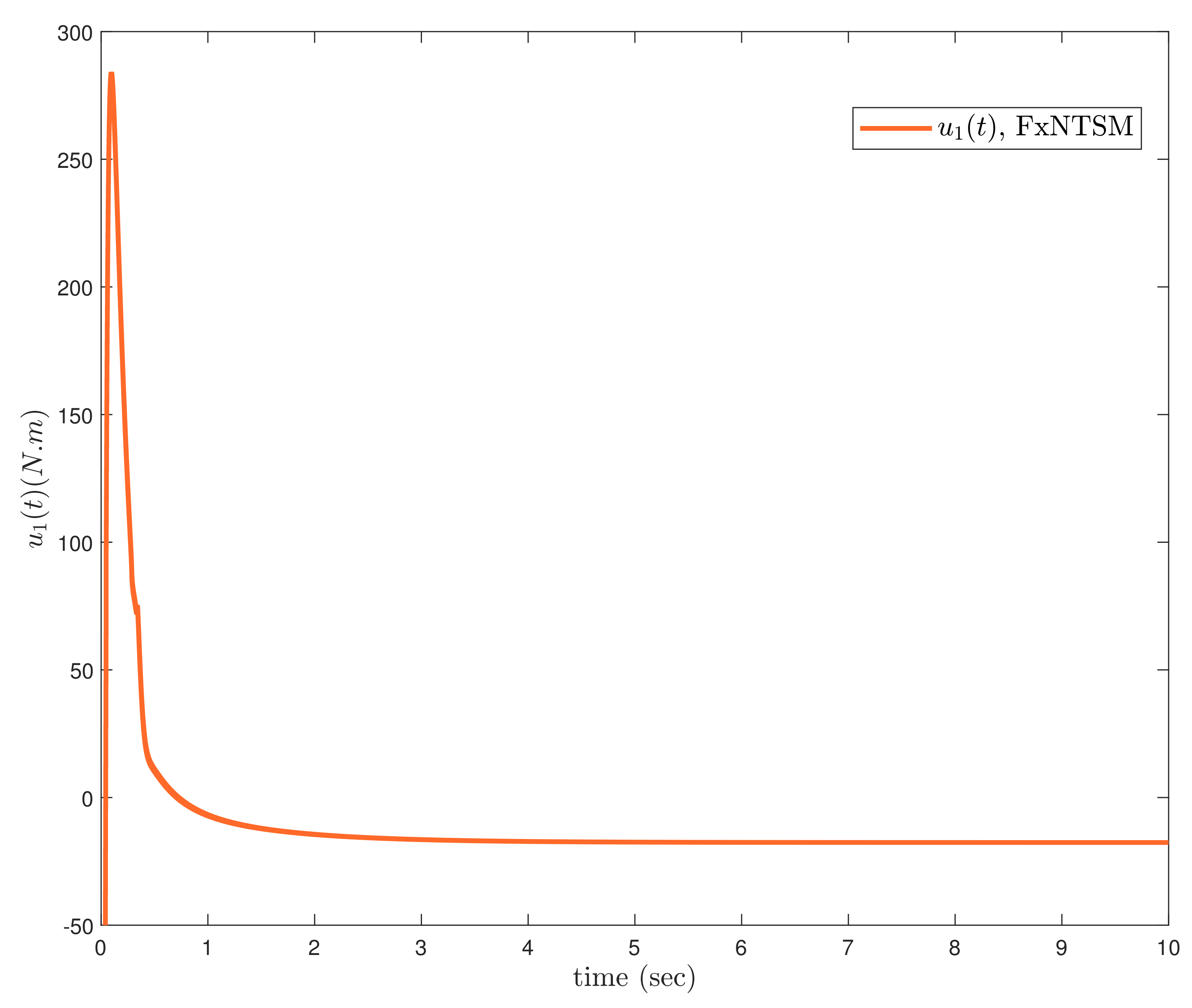
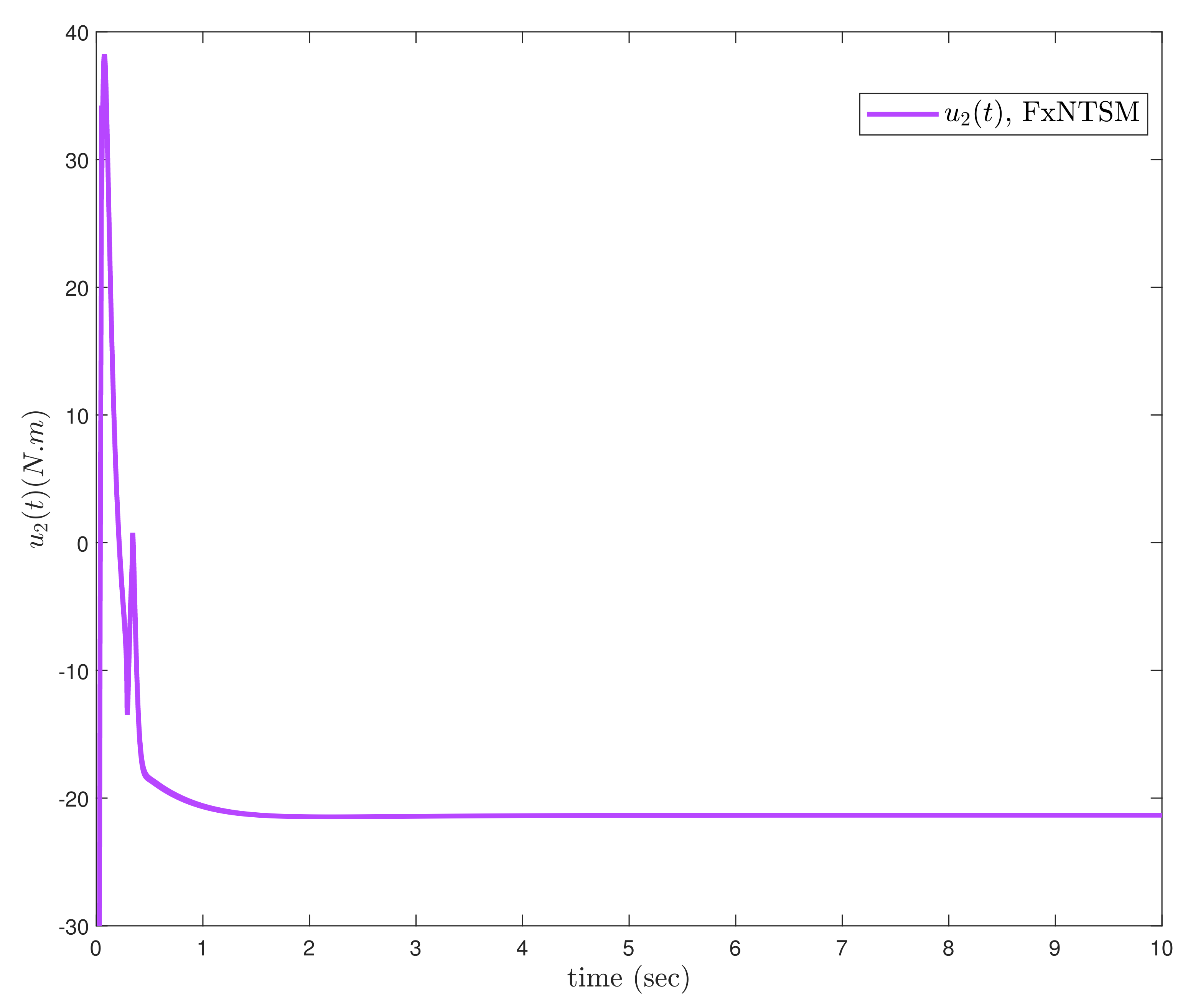
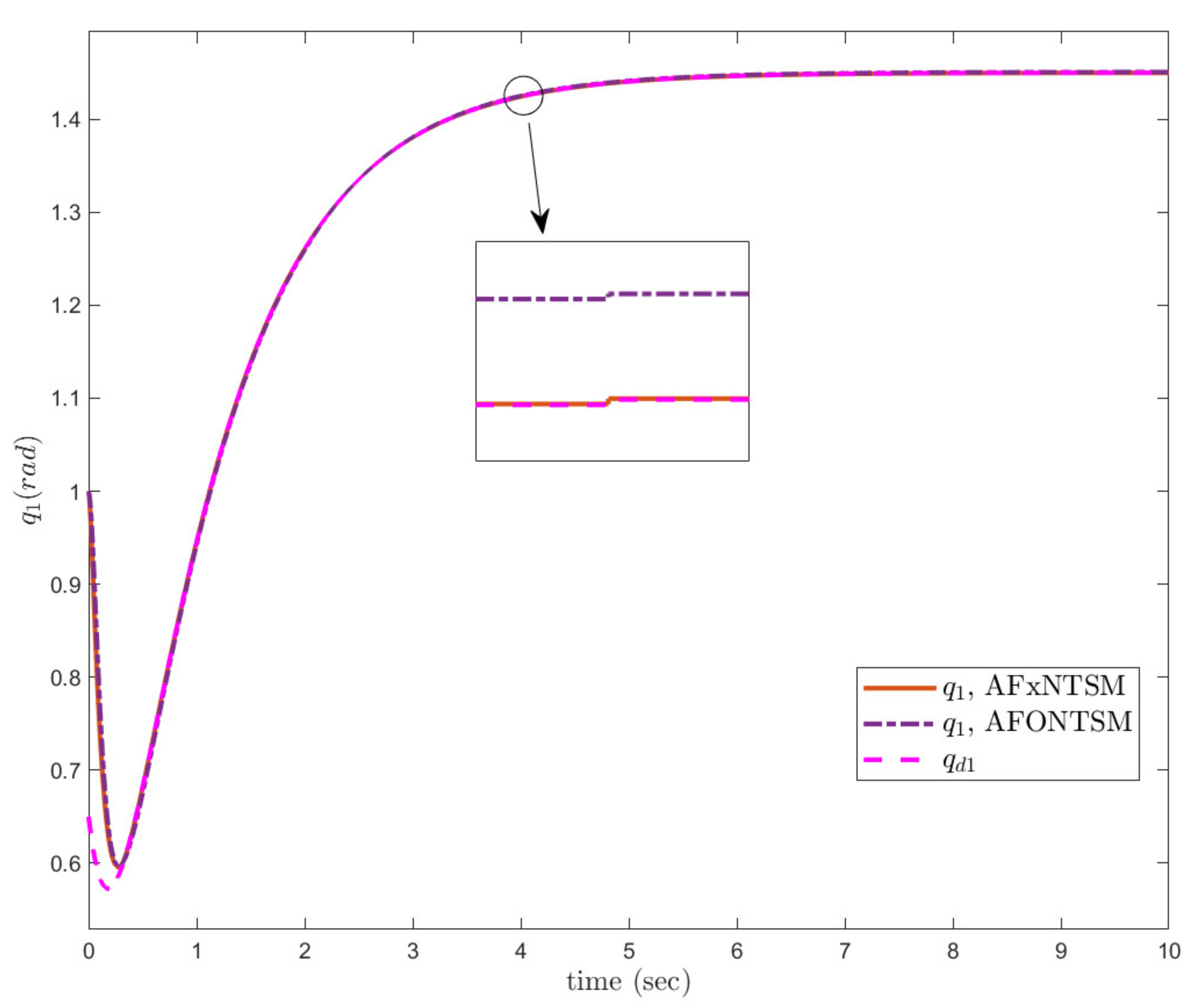
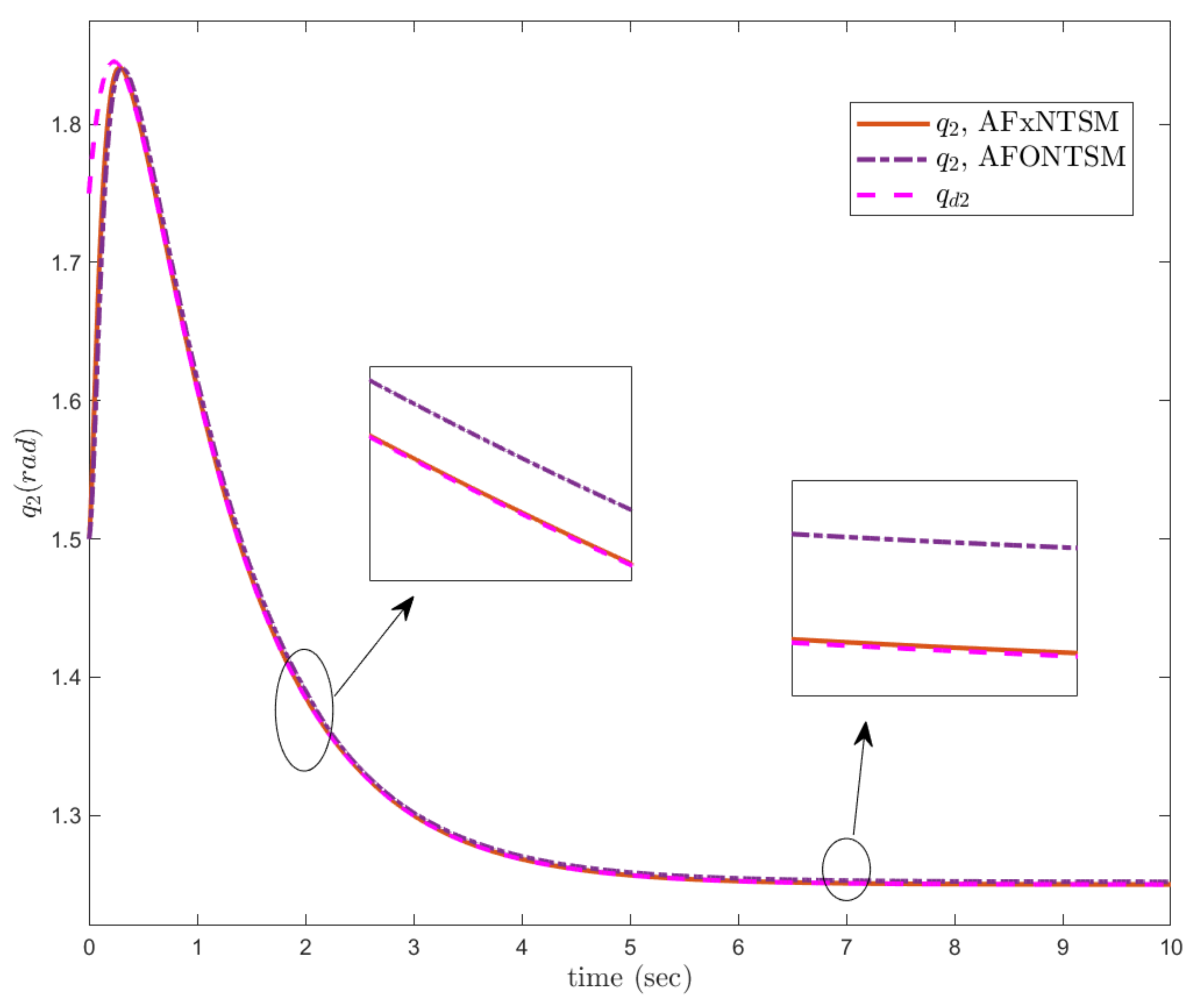
6.2. Case-2: Comparative Analysis under Unknown Dynamics and Actuator Faults

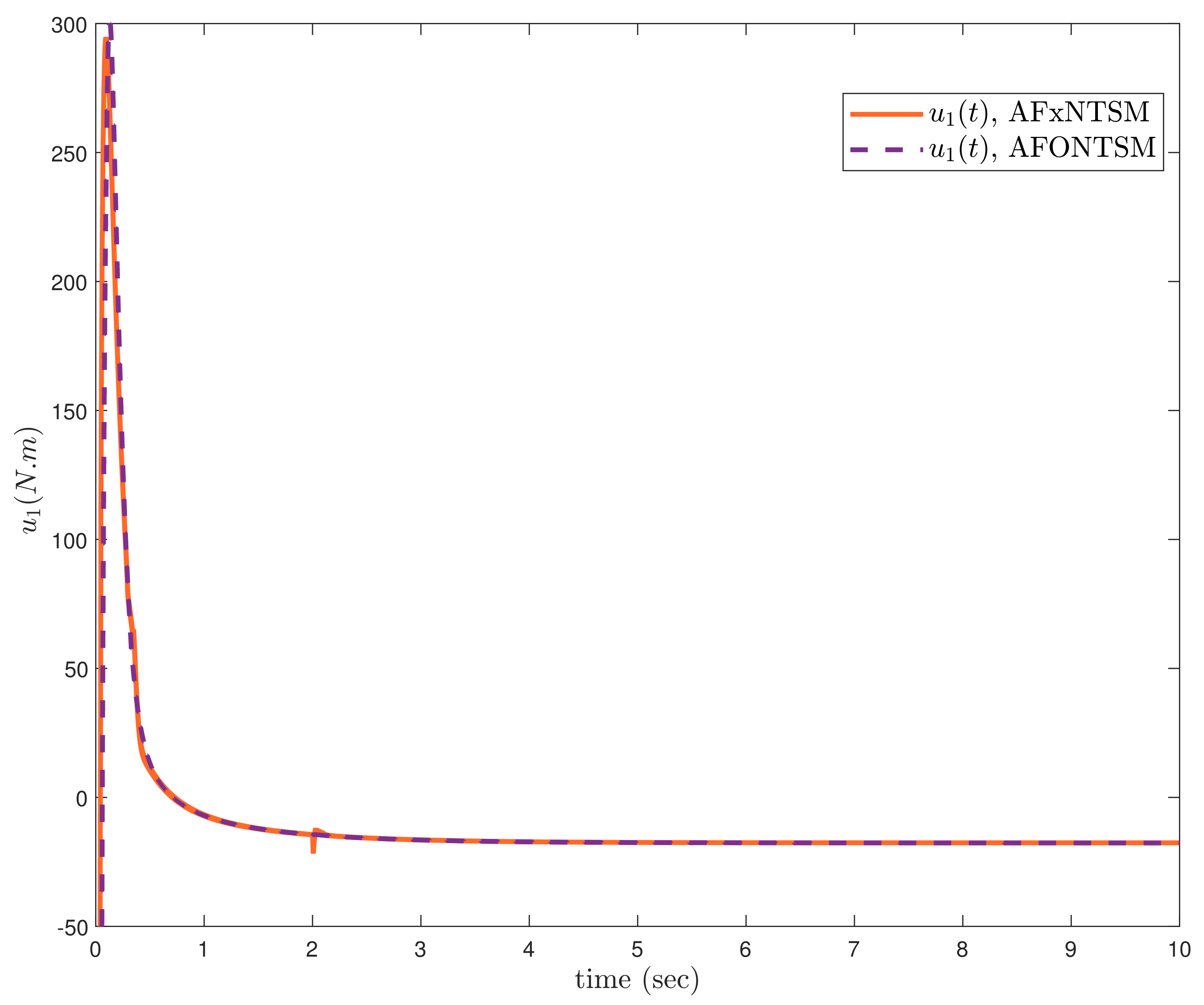
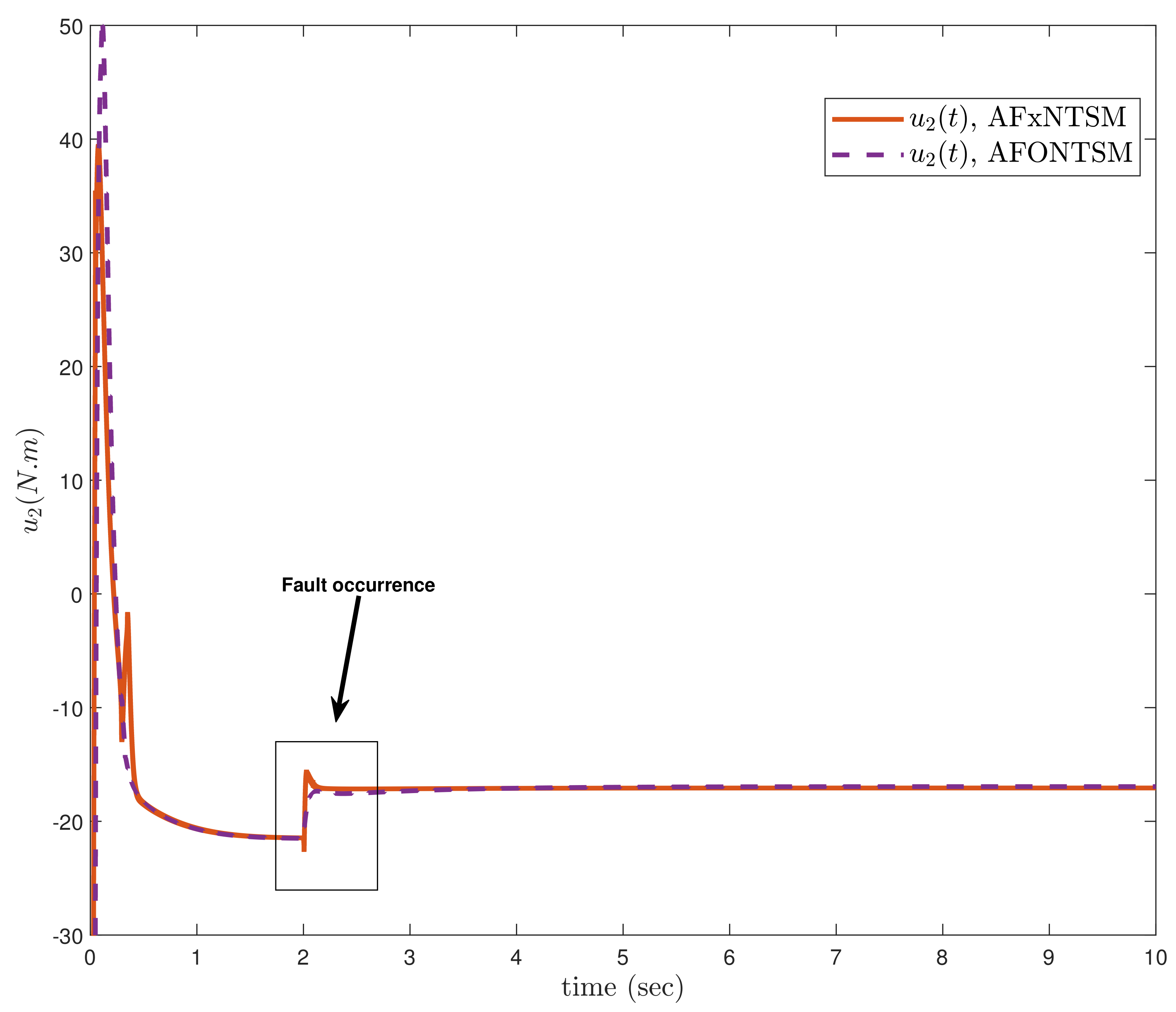
In this subsection, the proposed adaptive approach with FxNTSM method is employed to compensate the unknown dynamics of the uncertain $2-DOF$ robotic manipulator in the existence of unknown bounded external disturbances and actuator faults. Moreover, it is compared with adaptive fractional-order non-singular terminal sliding mode control (AFONTSM) [10] to show the effectiveness of the proposed method. The fault occurs at 2 s for joint-2 such as $\mathcal{F}={\left[0,0.7u_2\left(2s\right)\right]}^T$, the parameters of (30) are selected the same as (17), and the parameters of (32) are selected as ${\lambda }_1=20$, ${\lambda }_2=20$ and ${\lambda }_3=20$. 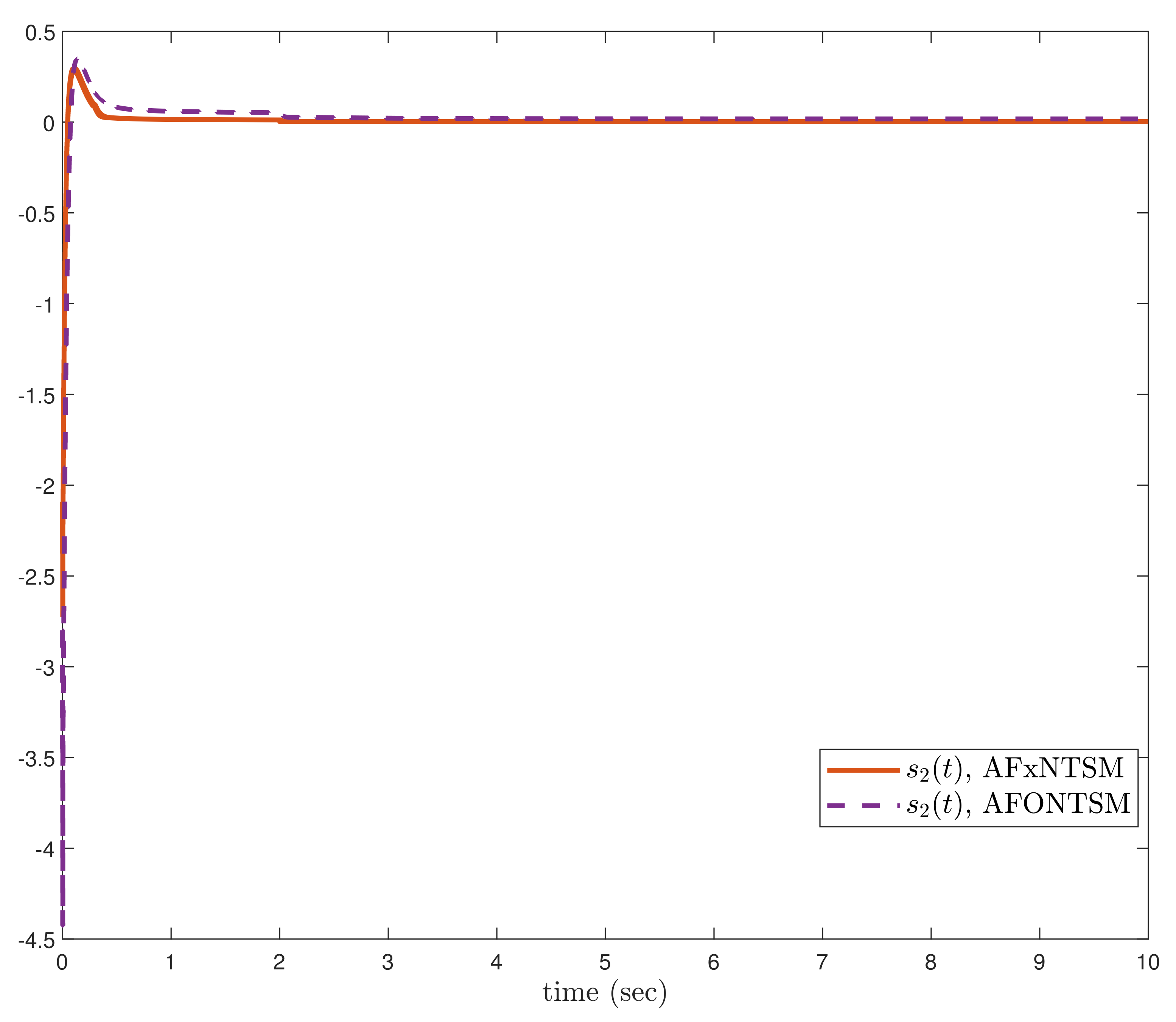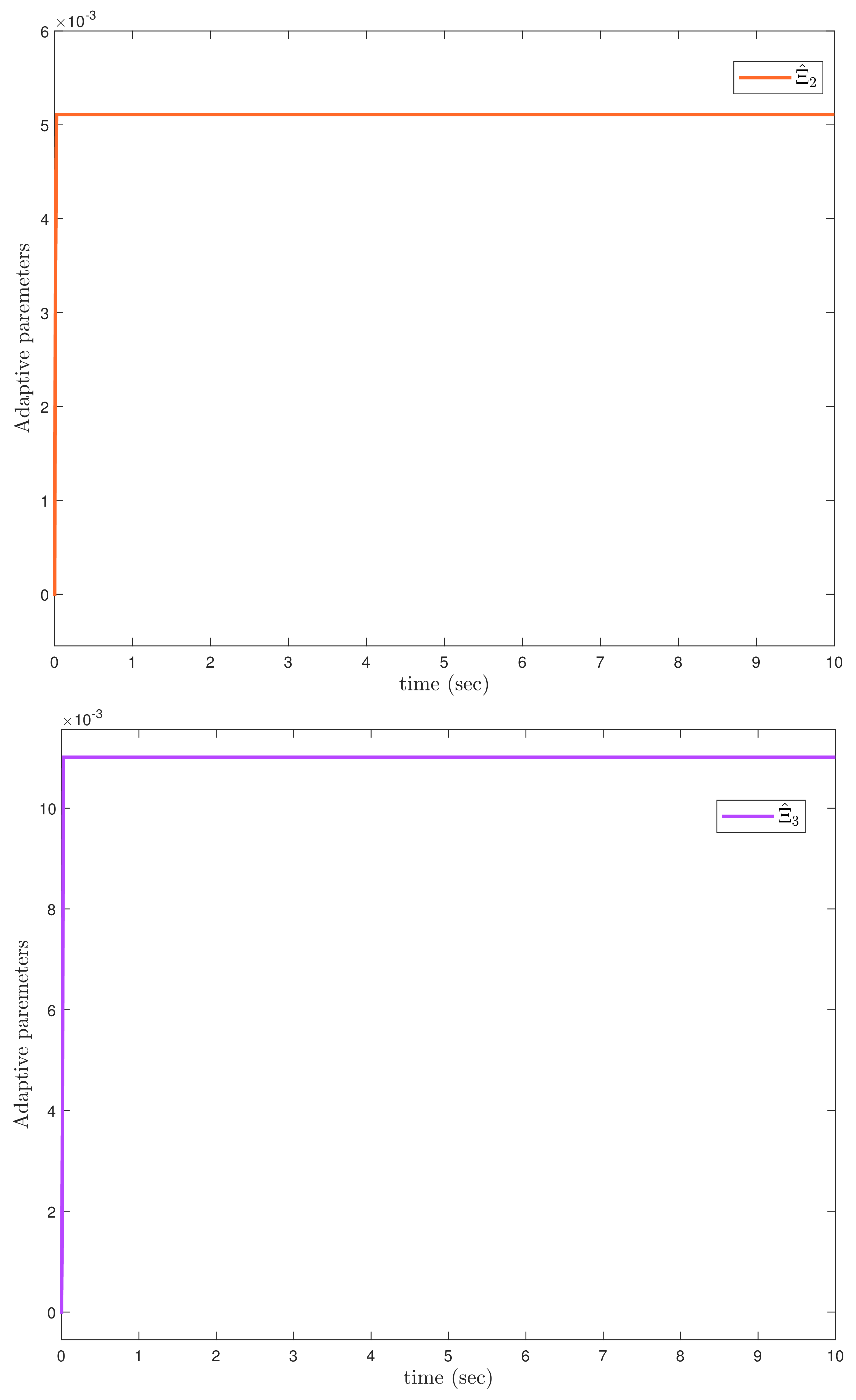The performances under unknown dynamics and actuator faults, the compared benchmark simulations of trajectories, control inputs and sliding surfaces of the proposed AFxNTSM scheme with AFONTSM are given in Figure 11, Figure 12, Figure 13, Figure 14, Figure 15 and Figure 16. In addition, the adaptive parameter estimations of unknown dynamics are illustrated in Figure 17.

The compared obtained results show that the AFxNTSM has enhanced tracking performance, chatter-free control inputs and precise adaptive values in the presence of uncertainties, external disturbances and actuator failures. In Figure 11, Figure 12, Figure 13 and Figure 14, it is clearly seen that the proposed method under external disturbances and at the occurrence of actuator faults provides the better convergence and trajectory tracking performance while the AFONTSM method shows the large angular position error and the less robust to unknown dynamics. Moreover, the root mean square (RMS) error of the proposed AFxNTSM method and AFONTSM technique are computed as $e_{1RMS}=0.0294$, $e_{2RMS}=0.0208$ and $e_{1RMS}=0.0320$, $e_{2RMS}=0.0237$, respectively.

7. Discussion

In this section, the discussion related to the simulated results of the proposed FxNTSM and AFxNTSM are presented. In addition, the limitations of the suggested controller are briefly discussed in terms parameters and stability analyses. Moreover, the future aspects of the proposed method with the nonlinear system are also discussed.

A comparison is made between the suggested control approach and the AFONTSM and the parameters of both schemes are fairly selected. Thus, it is evident from Figure 11 and Figure 12 that the suggested controller has the minimum tracking error and the shortest time to converge. In addition, the control inputs of the two joints can be seen in Figure 13 and Figure 14, and it can be observed that the suggested solution provides the smoothest and efficient control input. Moreover, the adaptive estimation is given in Figure 17, which estimates the unknown parameters and compensates the effects of uncertainties, external disturbance and actuator faults, and shows that there is no drifting problem in adaptive control laws.

The parameters of the suggested control strategy are selected according to the range that was stated, such as ${\theta }_1>0$, ${\theta }_2>0$, $0<{\eta }_1<1$, ${\eta }_2>1$, ${\gamma }_1>0$, ${\gamma }_2>0$, $0<{\gamma }_{10}<1$ and ${\gamma }_{20}>1$. If these are not taken care of, the closed-loop system will not remain fixed-time stable. It is easy to see, based on the results of (29) and (43) that $T_{10}$ and $T_{20}$ are inversely proportional to ${\theta }_i$ and ${\gamma }_i$, whereas ${\theta }_i$ and ${\gamma }_i$ are directly proportional to $u\left(t\right)$ in (17) and (30). Therefore, the appropriate values of ${\theta }_i$ and ${\gamma }_i$ need to be chosen in order to obtain fixed-time convergence as well as closed-loop system stability at the same time. Furthermore, the ranges of the other parameters are known, which enables one to choose the suitable value in a manner that is appropriate. In addition, this work can further be extended to consider the non-smooth nonlinearities for the nonlinear robotic systems such as a robotic manipulator, inverted pendulum, mobile robots etc.

8. Conclusions

For robotic manipulator trajectory tracking with uncertainties, external disturbances and actuator faults, an AFxNTSM based FTC is developed. In order to estimate the unknown bounds of actuator faults, uncertainties and disturbances, fixed-time sliding surface is developed and then the FxNTSM control is designed utilising an adaptive approach, allowing for fixed-time convergence and tracking performance. FxNTSM and AFxNTSM are applied on the $2-DOF$ manipulator with and without actuator faults to show and justify the efficacy of the proposed approach. Simulation results show that the proposed FxNTSM and AFxNTSM outperform in terms of response time, trajectory tracking error, faults control, and better uncertainties and disturbances rejection capability.