Secure Control of Networked Inverted Pendulum Visual Servo Systems Based on Active Disturbance Rejection Control

Abstract

This paper investigates secure control of Networked Inverted Pendulum Visual Servo Systems (NIPVSSs) based on Active Disturbance Rejection Control (ADRC). Firstly, considering the network- and image-induced delays in conjuction with computational errors caused by image processing and image attacks, the model of NIPVSSs is established. Secondly, the limitations of the traditional Single-Input-Single-Output (SISO) ADRC used in NIPVSSs with disturbance are revealed. The limitations are that the ESO used in the traditional SISO ADRC brings large steady-state error, and the NLSEF used in the traditional SISO ADRC can achieve stable control of pendulum angle, but cannot achieve stable control of cart position. Thirdly, a new Single-Input-Multi-Output (SIMO) ADRC method is proposed for NIPVSSs with disturbance. In the new SIMO ADRC method, the new ESO is designed by introducing additional first and second derivatives of error to reduce the steady-state error. In addition, the new NLSEF is developed by taking both the calculated cart position and pendulum angle as inputs to achieve dual stable control of pendulum angle and cart position. Finally, combined with the designed ADRC parameter-tuning strategy, the results from simulation and real-world experiments confirm the effectiveness and feasibility of the proposed method.

1. Introduction

The inverted pendulum has strong coupling, multivariable, nonlinear characteristics, etc., [1,2,3]. This can reflect many core problems, (e.g., robustness, follow-up, stabilization, tracking) in control theory and engineering, and is thus used as a typical control experiment platform. When the designed control algorithms are verified on the inverted pendulum, they can be applied to control spacecraft attitude [4], robot balance [5], ship self-balance [6] and so forth. With the rapid development of machine vision [7,8,9] and network communication [10,11,12], visual sensing has facilitated improvements in control quality owing to its excellent characteristics, particularly regarding non-contact and comprehensive information. This transforms the traditional inverted pendulum system into networked inverted pendulum visual servo systems (NIPVSSs) [13].

The application of network and visual sensing increases the flexibility of NIPVSSs, but introduces disturbances. The disturbances include delays caused by information transmission via network, and image computational errors caused by image processing and image attacks [14] (, i.e., attacks against images, such as pepper and salt attacks, shearing attacks). In this case, the system performance will be degraded, or even cause system instability.

To cope with the disturbances, several works have developed techniques to control the inverted pendulum. For instance, in view of the unknown periodic external disturbance, an adaptive tracking controller is given [15]; In view of the nonlinear disturbance as a form of external disturbance or uncertainty, a disturbance-observer-based dynamic surface control is given [16]; In view of a disturbance manifested as time-varying delay, a sliding mode controller is given [17]; In view of the disturbance manifesting as time-varying input delay and external disturbance, a Fuzzy adaptive control is given for the inverted pendulum [18]; In view of the disturbance as a form of structured uncertainty caused by measurement error, a robust controller is given [19]; In view of the disturbance as form of multiple time-varying delays from network and computational errors from image processing, an $H_{\infty }$ controller is given [13]. However, the existing techniques are often constrained by range of disturbances. In particular, when wide-range disturbance is caused by image attacks, the feasible controller bears certain limitations. Therefore, it is necessary to search for a disturbance rejection mechanism to control the inverted pendulum.

Active Disturbance Rejection Control (ADRC) [20] is a popular disturbance rejection mechanism. The core idea of ADRC is to take the simple integral series as the standard type and treat the parts of the system dynamics that differ from the standard type as the total disturbance. ADRC adopts Extended State Observer (ESO) to estimate and eliminate the total disturbance in real time, and then relies on NonLinear State Error Feedback (NLSEF) control law to achieve system stability. ADRC has gradually been applied to the active suspension system of motor trains [21], dynamic parafoil control [22], hydraulic servo systems [23], speed control of stepping motors and permanent magnet motors [24], etc.

This paper investigates the ADRC-based anti-disturbance secure control of NIPVSSs. The main contributions of this paper are summarized as follows:

(1)

The limitations of the traditional Single-Input-Single-Output (SISO) ADRC employed in NIPVSSs with disturbance are revealed. The limitations are that the ESO used in the traditional SISO ADRC brings large steady-state error, and the NLSEF employed in the traditional SISO ADRC can achieve stable control of pendulum angle, but cannot achieve stable control of cart position.

(2)

A new Single-Input-Multi-Output (SIMO) ADRC method is proposed for NIPVSSs with disturbance. In the new SIMO ADRC method, the new ESO is designed by introducing additional first and second derivatives of error to reduce the steady-state error, and the new NLSEF is developed by taking both the calculated cart position and pendulum angle as its inputs to achieve dual stable control of pendulum angle and cart position.

To simplify for the sake of understanding the problem of concern in this paper, Figure 1 summarizes the problem and the proposed mechanism. Regarding the problem of secure control of NIPVSSs with disturbance caused by delays and computational errors, the traditional SISO ADRC can achieve stable control of pendulum angle, but cannot achieve stable control of cart position. The proposed SIMO can achieve dual stable control of pendulum angle and cart position even under image attacks.

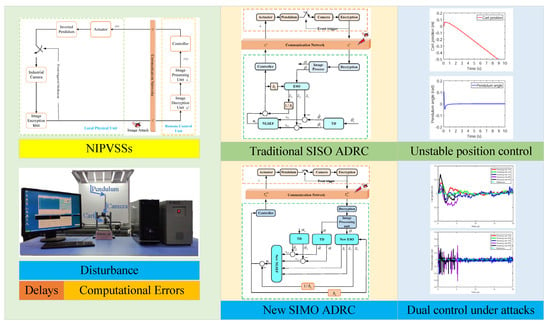
Figure 1. A summary of the problem and the proposed mechanism in this paper.

2. NIPVSSs and Traditional ADRC

2.1. NIPVSSs

The NIPVSSs framework is shown in Figure 2, and the model is shown in Figure 3. Firstly, the industrial camera captures the inverted pendulum image in real-time motion. The image is then encrypted via an image encryption unit and the next image is captured by an industrial camera through an event-triggered mechanism. Secondly, the encrypted image is sent to a remote control unit through the network, and the image encryption unit encrypts the image. Furthermore, the image-processing unit calculates the state of the inverted pendulum and then sends it to the controller that calculates the corresponding control input according to the state. Finally, the calculated control input is transmitted to an actuator through the network, and the actuator gives the corresponding drive pulse to the inverted pendulum according to the control input, thus allowing the inverted pendulum to run smoothly at the balance point.

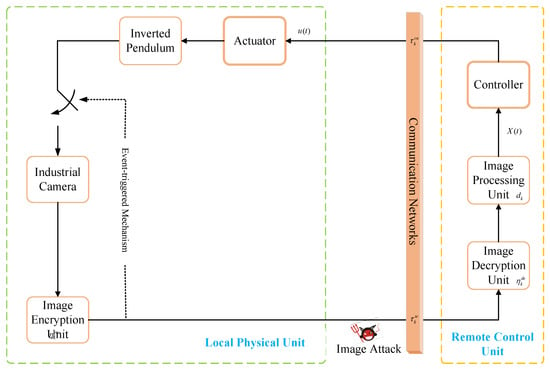
Figure 2. Structure of NIPVSSs’ Fused Image Encryption and Decryption.

Figure 3. NIPVSSs Model.

Remark 1. 

The image encryption unit adopts the image encryption algorithm employed in [25]. It firstly uses the bilinear difference method to scale the image for reducing the initial amount of image data. Then, Hough transform is used to determine the pendulum of the inverted pendulum image, and the encrypted area is set to further reduce the computational complexity. Finally, according to the key area, a small number of random rows and columns are generated by chaotic mapping, and these rows and columns are rotated to encrypt the image. This algorithm not only guarantees the security of image transmission through the network, but also meets the high real-time requirements of NIPVSSs.

The model of inverted pendulum based on acceleration is, cf. [13],

$$\left\{\begin{array}{c}\dot{X}=AX+Bu,\hfill \\ Y=CX+Du,\hfill \end{array}\right.$$

(1)

where $X=\left[\alpha ;\theta ;\dot{\alpha };\dot{\theta }\right]$ is system state; $\alpha$, $\theta$, $\dot{\alpha }$ and $\dot{\theta }$, respectively, represent the cart position, pendulum angle, cart velocity and pendulum angle velocity of the inverted pendulum; u is control input; Y is system output; A, B, C and D are constant matrices. Further considering the delays (including image-encryption- and decryption-induced delay, image-processing-induced delay, network-induced delay) and the external disturbance (e.g., image-processing errors caused by environmental noise and image attacks), the above (1) is further rewritten as, cf. [26],

$$\left\{\begin{array}{c}\dot{X}\left(t\right)=(A+\mathsf{\Delta }A)X\left(t\right)+Bu(t-\lambda \left(t\right)-\tau \left(t\right)),\hfill \\ t\in \left[t_k+{\eta }_k^{en}+{\tau }_k^{sc}+{\eta }_k^{de}+d_k+{\tau }_k^{ca},t_{k+1}+{\eta }_{k+1}^{en}+{\tau }_{k+1}^{sc}+{\eta }_{k+1}^{de}+d_{k+1}+{\tau }_{k+1}^{ca}\right),\hfill \end{array}\right.$$

(2)

where $\mathsf{\Delta }A=DFE$, $D=diag\left\{1,1,1,1\right\}$ and

$$\begin{array}{cc}\hfill \mathsf{\Delta }A& =diag\left\{{\mathsf{\Delta }}_1={\mathsf{\Delta }}_{1,n}+{\mathsf{\Delta }}_{1,a},{\mathsf{\Delta }}_2={\mathsf{\Delta }}_{2,n}+{\mathsf{\Delta }}_{2,a},0,0\right\},F=diag\left\{r_1,r_2,0,0\right\},\hfill \\ \hfill E& =diag\left\{{\left|{\mathsf{\Delta }}_{1,n}\right|}_{max}+{\left|{\mathsf{\Delta }}_{1,a}\right|}_{max},{\left|{\mathsf{\Delta }}_{2,n}\right|}_{max}+{\left|{\mathsf{\Delta }}_{2,a}\right|}_{max},1,1\right\},-1⩽r_1⩽1,-1⩽r_2⩽1,\hfill \end{array}$$

${\mathsf{\Delta }}_{1,n}$ and ${\mathsf{\Delta }}_{2,n}$ are the uncertainties of the original cart position and pendulum angle caused by um-modeled dynamics and other external disturbances (e.g., environmental noise), ${\mathsf{\Delta }}_{1,a}$ and ${\mathsf{\Delta }}_{2,a}$ are the uncertainties of the cart position and pendulum angle caused by the image attack; $\lambda \left(t\right)$ is image-induced delay, $\tau \left(t\right)$ is network-induced delay; $t_k$ is the k-th image-sampling instant, ${\eta }_k^{en}$ is the k-th image encryption time, ${\tau }_k^{sc}$ is the k-th network transmission time from sensor to controller, ${\eta }_k^{de}$ is the k-th image decryption time, $d_k$ is the k-th image-processing time, ${\tau }_k^{ca}$ is the k-th network transmission time from controller to actuator.

Remark 2. 

The general nonlinear differential equation of a single inverted pendulum is

$$lmucos\theta +lmgsin\theta =J\ddot{\theta },$$

(3)

where l is the length from the pivot to the center of the pendulum, m represents the mass of the pendulum, g is the acceleration of the gravity, J denotes the moment of the inertia about the pivot of the pendulum, the values of l, m, g, J can be found in [13], and $u=\ddot{\alpha }$ is the control input. By linearizing (3) in $\left|\theta \right|⩽0.2rad$ (i.e., $cos\theta \approx 1$ and $sin\theta \approx \theta$ in $\left|\theta \right|⩽0.2rad$), A and B of (1) can be obtained, i.e.,

$$A=\left[\begin{array}{cccc}0& 0& 1& 0\\ 0& 0& 0& 1\\ 0& 0& 0& 0\\ 0& \frac{lmg}{J}& 0& 0\end{array}\right],B=\left[\begin{array}{c}0\\ 0\\ 1\\ \frac{lm}{J}\end{array}\right].$$

The cart position α and pendulum angle θ can be extracted from the image captured by the industrial camera (i.e., $Y=[\alpha ;\theta ]$), and thus C and D of (1) can be obtained, i.e.,

$$C=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\end{array}\right],D=\left[\begin{array}{c}0\\ 0\end{array}\right].$$

Remark 3. 

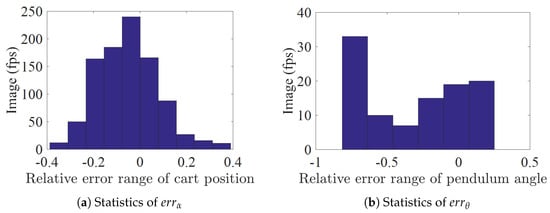
The values of ${\left|{\mathsf{\Delta }}_{1,n}\right|}_{max}$ and ${\left|{\mathsf{\Delta }}_{2,n}\right|}_{max}$ when ${\left|{\mathsf{\Delta }}_{1,a}\right|}_{max}=0$ and ${\left|{\mathsf{\Delta }}_{2,a}\right|}_{max}=0$ can be obtained according to statistical analysis. For example, in the NIPVSSs experiment, 2000 image frames are collected and the relative errors $er{r}_{\alpha }$ and $er{r}_{\theta }$ between cart position in addition to pendulum angle from the encoder and those from the image extraction are obtained in Figure 4. Considering ${\mathsf{\Delta }}_{1,n}\alpha =er{r}_{\alpha }$ and ${\mathsf{\Delta }}_{2,n}\theta =er{r}_{\theta }$, it can be observed from Figure 4 that ${\left|{\mathsf{\Delta }}_{1,n}\right|}_{max}=0.4$ and ${\left|{\mathsf{\Delta }}_{2,n}\right|}_{max}=0.82$ when ${\left|{\mathsf{\Delta }}_{1,a}\right|}_{max}=0$ and ${\left|{\mathsf{\Delta }}_{2,a}\right|}_{max}=0$.

Figure 4. Statistics of $er{r}_{\alpha }$ and $er{r}_{\theta }$.

Remark 4. 

Since the inverted pendulum swings violently back and forth at the balance point, resulting in rapid changes of the cart velocity and pendulum angle velocity, their uncertainties are ignored.

Remark 5. 

The control of (2) belongs to secure control. The difference between traditional control and secure control lies on whether the uncertainties ${\mathsf{\Delta }}_{1,a}$ and ${\mathsf{\Delta }}_{2,a}$ caused by image attacks are zero. In the traditional control, the uncertainties ${\mathsf{\Delta }}_{1,a}$ and ${\mathsf{\Delta }}_{2,a}$ are zero. However, in the secure control, the uncertainties ${\mathsf{\Delta }}_{1,a}$ and ${\mathsf{\Delta }}_{2,a}$ are not zero, and thus a better disturbance rejection mechanism should be adopted.

2.2. Traditional ADRC

ADRC [27] mainly includes: Tracking Differentiator (TD), Extened State Observer (ESO), Nonlinear State Error Feedback (NLSEF) and disturbance compensation. A typical second-order ADRC structure is shown in Figure 5.

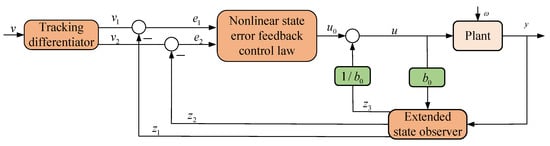
Figure 5. Typical second-order ADRC structure.

(1) Plant. The general second-order plant in Figure 5 is, cf. [28],

$$\left\{\begin{array}{c}{\dot{x}}_1=x_2,\hfill \\ {\dot{x}}_2=f(x_1,x_2,\omega ,t)+bu,\hfill \\ y=x_1,\hfill \end{array}\right.$$

(4)

where $x_1$ and $x_2$ are system state; y is system output; $\omega$ is the disturbance; $f(x_1,x_2,\omega ,t)$ is the total disturbance; b is a constant scalar. Let $x_3=f(x_1,x_2,\omega ,t)$ and denote ${\dot{x}}_3=\Im$, and the above (4) becomes

$$\left\{\begin{array}{c}{\dot{x}}_1=x_2,\hfill \\ {\dot{x}}_2=x_3+bu,\hfill \\ {\dot{x}}_3=\Im ,\hfill \\ y=x_1.\hfill \end{array}\right.$$

(5)

The traditional ADRC [27] is shown in the following (6)–(11).

(2) TD [27]. Set v as the given value of the system, and the form of the second-order TD is

$$\left\{\begin{array}{c}{\dot{v}}_1=v_2,\hfill \\ {\dot{v}}_2=-1.76r{v}_2-r^2(v_1-v),\hfill \end{array}\right.$$

(6)

where $v_1$ is the tracking value, $v_2$ is the differential value, and r is the speed factor.

(3) ESO [27]. The second-order ADRC requires the third-order ESO, i.e.,

$$\left\{\begin{array}{c}{\widehat{e}}_1=z_1-x_1,\hfill \\ {\dot{z}}_1=z_2-{\beta }_{01}{\widehat{e}}_1,\hfill \\ {\dot{z}}_2=z_3-{\beta }_{02}fal({\widehat{e}}_1,{\gamma }_{01},\delta )+b_{0}u,\hfill \\ {\dot{z}}_3=-{\beta }_{03}fal({\widehat{e}}_1,{\gamma }_{02},\delta )),\hfill \end{array}\right.$$

(7)

where $z_1$, $z_2$ and $z_3$ are, respectively, the estimated value of $x_1$, $x_2$ and $f(x_1,x_2,\omega ,t)$;

$$fal({\widehat{e}}_1,\gamma ,\delta )=\left\{\begin{array}{c}{\left|{\widehat{e}}_1\right|}^{2}sgn\left({\widehat{e}}_1\right),\left|{\widehat{e}}_1\right|>\delta \hfill \\ {\widehat{e}}_1/{\delta }^{1-\gamma },\left|{\widehat{e}}_1\right|⩽\delta \hfill \end{array}\right.$$

$b_0$ is the estimated value of b; ${\beta }_{01}$, ${\beta }_{02}$ and ${\beta }_{03}$ are parameters with respect to ESO bandwidth.

Remark 6. 

According to the findings in [29], the values of ${\beta }_{01}$, ${\beta }_{02}$ and ${\beta }_{03}$ are

$${\beta }_{01}=3{\omega }_0,{\beta }_{02}=\frac{3{\omega }_0^2}{5},{\beta }_{03}=\frac{{\omega }_0^3}{9}.$$

(8)

where ${\omega }_0$ is ESO bandwidth.

(4) NLSEF [27]. According to the given value and actual output value of the system, the classical PID control is formed by simple linear-weighting combination of proportion, integral and differential. However, since the ESO estimates the total disturbance of the system, including the disturbance caused by the steady-state error, the integration link can be ignored. Therefore, the NLSEF becomes the error combination between TD and ESO, i.e.,

$$u_0={\beta }_{1}fal(e_1,{\gamma }_1,\delta )+{\beta }_{2}fal(e_2,{\gamma }_2,\delta ).$$

(9)

where $e_1=z_1-v_1$ and $e_2=z_2-v_2$.

(5) Disturbance compensation [27]. To compensate the total disturbance of the system estimated by ESO, it follows that

$$u=u_0-\frac{z_3}{b_0},$$

(10)

Finally, the compensated system becomes

$$\left\{\begin{array}{c}{\dot{x}}_1=x_2,\hfill \\ {\dot{x}}_2=x_3+b(u_0-\frac{z_3}{b_0})=x_3-\frac{b}{b_0}{z}_3+b{u}_0.\hfill \end{array}\right.$$

(11)

3. ADRC-Based Secure Control of NIPVSSs

3.1. Traditional SISO ADRC-Based Secure Control of NIPVSSs

ADRC has the ability to suppress the uncertainties ${\mathsf{\Delta }}_1$ and ${\mathsf{\Delta }}_2$ in (2), especially ${\mathsf{\Delta }}_{1,a}$ and ${\mathsf{\Delta }}_{2,a}$ caused by image attacks. For the delays ${\tau }_k$, $d_k$ and ${\eta }_k$, this paper mainly uses the delay-free method, i.e., these delays are transformed as a part of the total system disturbance. Therefore, ${\mathsf{\Delta }}_1$, ${\mathsf{\Delta }}_2$, ${\tau }_k$, $d_k$ and ${\eta }_k$ in the system comprise all the total disturbances of the system, and can be estimated directly through ESO and compensated accordingly. Even if the image is attacked, ESO can still estimate the total disturbances and compensate that.

The traditional ADRC is a single-input-single-output system, while the inverted pendulum is a single-input-multiple-output system. To apply ADRC in the form of (4), the cart position can be treated as the internal disturbance of the system [30], as shown in Figure 6.

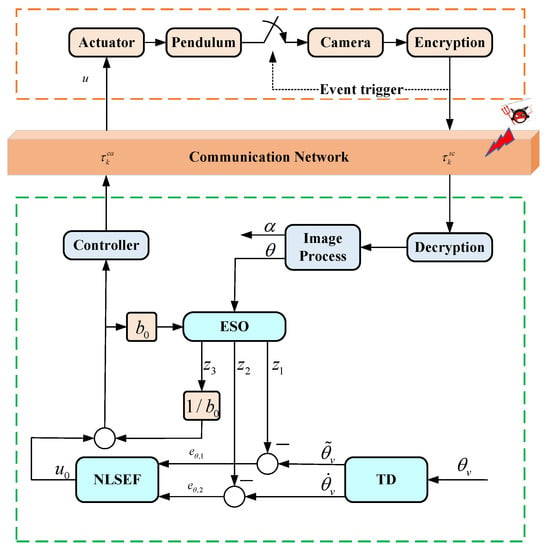
Figure 6. Single-input-single-output ADRC with single target of pendulum angle.

(1) Plant. From (2), we can know that u is with the delay $\lambda \left(t\right)+\tau \left(t\right)$ and the pendulum angle is with uncertainty ${\mathsf{\Delta }}_2$, so it follows that

$$\begin{array}{cc}\hfill \ddot{\theta }& =\frac{lmg}{J}\theta +{\mathsf{\Delta }}_2\theta +bu(t-\lambda \left(t\right)-\tau \left(t\right))\hfill \\ \hfill & =\underset{f(\theta ,\omega ,t)}{\underbrace{\frac{lmg}{J}\theta +{\mathsf{\Delta }}_2\theta +bu(t-\lambda \left(t\right)-\tau \left(t\right))-bu\left(t\right)}}+bu\left(t\right).\hfill \end{array}$$

(12)

where $b=\frac{lm}{J}$, $\omega ={\mathsf{\Delta }}_2\theta +bu(t-\lambda \left(t\right)-\tau \left(t\right))-bu\left(t\right)$ is the disturbance caused by the parameter uncertainty and multiple time-varying time delays in the system, $f(\theta ,\omega ,t)$ is the total disturbance.

The above (12) becomes

$$\left\{\begin{array}{c}{\dot{x}}_1=x_2,\hfill \\ {\dot{x}}_2=x_3+bu,\hfill \\ {\dot{x}}_3=\Im ,\hfill \end{array}\right.$$

(13)

where $x_1=\theta$, $x_2=\dot{\theta }$ and $x_3=f(x_1,\omega ,t)$. The system (13) uses ADRC to estimate and compensate the disturbance.

(2) TD for pendulum angle reference. Set ${\theta }_v$ as the reference of the pendulum angle, and the second-order TD for the pendulum angle is

$$\left\{\begin{array}{c}{\dot{\tilde{\theta }}}_v={\dot{\theta }}_v,\hfill \\ {\ddot{\theta }}_v=-1.76r{\dot{\theta }}_v-r^2({\tilde{\theta }}_v-{\theta }_v),\hfill \end{array}\right.$$

(14)

where ${\tilde{\theta }}_v$ is the tracking value of ${\theta }_v$ and ${\dot{\theta }}_v$ is the differential value of ${\theta }_v$.

(3) ESO for pendulum angle. The third-order ESO for pendulum angle is

$$\left\{\begin{array}{c}{\widehat{e}}_1=z_1-x_1,\hfill \\ {\dot{z}}_1=z_2-{\beta }_{01}{\widehat{e}}_1,\hfill \\ {\dot{z}}_2=z_3-{\beta }_{02}fal({\widehat{e}}_1,{\gamma }_{01},\delta )+b_{0}u,\hfill \\ {\dot{z}}_3=-{\beta }_{03}fal({\widehat{e}}_1,{\gamma }_{02},\delta )),\hfill \end{array}\right.$$

(15)

(4) NLSEF for pendulum angle. The NLSEF for pendulum angle is

$$u_0={\beta }_{1}fal(e_{\theta ,1},{\gamma }_1,\delta )+{\beta }_{2}fal(e_{\theta ,2},{\gamma }_2,\delta ).$$

(16)

where $e_{\theta ,1}=z_1-{\tilde{\theta }}_v$ and $e_{\theta ,2}=z_2-{\dot{\theta }}_v$.

(5) Disturbance compensation. To compensate the total disturbance of the system estimated by ESO, it follows that (10). Finally, the compensated system becomes (11).

According to the previous analysis, it can be known that the controller of the form (9) can control the pendulum angle, but cannot control the cart position. After using traditional ADRC, the subsequent simulation results are shown in Figure 7. The simulation results show that the pendulum angle can be stabilized at the balance point; however, the cart position tends infinitely in the negative direction, and it is difficult to control the cart position. Therefore, to achieve dual control of the cart position and pendulum angle, it is necessary to further improve ADRC.

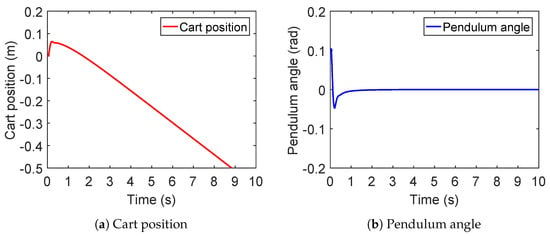
Figure 7. Simulation results of traditional ADRC.

3.2. New SIMO ADRC-Based Secure Control of NIPVSSs

The traditional SISO ADRC is analyzed above, and the results show that stable control cannot be achieved. Therefore, to solve the problem of dual control over the cart position and pendulum angle, the new ADRC is shown in Figure 8 by adding the cart position control to NLSEF.

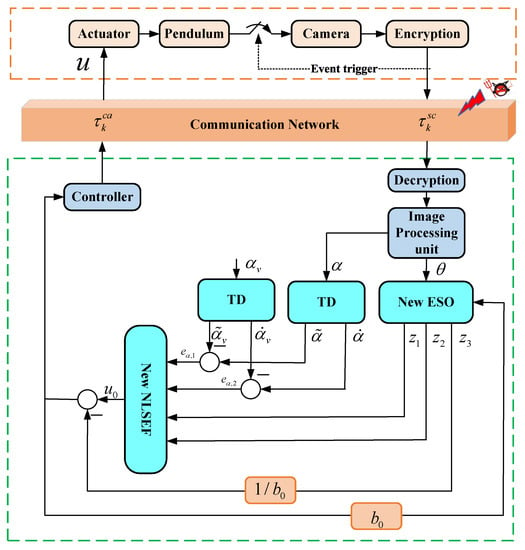
Figure 8. Single-input-multi-output ADRC considering cart position and pendulum angle.

Plant. Consider (12) and (13).

TDs for pendulum angle reference, cart position reference and cart position. The TD for the pendulum reference is (14). The TD for cart position reference is

$$\left\{\begin{array}{c}{\dot{\tilde{\alpha }}}_v={\dot{\alpha }}_v,\hfill \\ {\ddot{\alpha }}_v=-1.76r{\dot{\alpha }}_v-r^2({\tilde{\alpha }}_v-{\alpha }_v),\hfill \end{array}\right.$$

(17)

where ${\tilde{\alpha }}_v$ is the tracking value of ${\alpha }_v$ and ${\dot{\alpha }}_v$ is the differential value of ${\alpha }_v$. The TD for cart position is

$$\left\{\begin{array}{c}\dot{\tilde{\alpha }}=\dot{\alpha },\hfill \\ \ddot{\alpha }=-1.76r\dot{\alpha }-r^2(\tilde{\alpha }-\alpha ),\hfill \end{array}\right.$$

(18)

where $\tilde{\alpha }$ is the tracking value of $\alpha$ and $\dot{\alpha }$ is the differential value of $\alpha$.

Remark 7. 

Considering the control objective of NIPVSSs is to stabilize the cart position and pendulum angle at the origin, i.e., ${\theta }_v=0$ and ${\alpha }_v=0$, to make ${\tilde{\theta }}_v$, ${\dot{\theta }}_v$, ${\tilde{\alpha }}_v$ and ${\dot{\alpha }}_v$ equal to 0. Therefore, the TD (14) of pendulum angle reference and the TD (17) cart position reference can be omitted, and thus further reducing the calculation time of TD.

3.2.1. The New ESO

(1) Design of the new ESO. In the traditional ESO, all $z_1$, $z_2$ and $z_3$ tracking $x_1$, $x_2$ and $x_3$ are based on the error ${\widehat{e}}_1$, thereby leading to a defect: excessive steady-state error will reduce the system performance, or even destabilize the system. Therefore, this paper proposes a new ESO to reduce the steady-state error.

Re-write (15) as

$$\left\{\begin{array}{c}{z}_1=x_1+{\widehat{e}}_1,\hfill \\ z_2={\dot{z}}_1+{\beta }_{01}{\widehat{e}}_1,\hfill \\ z_3={\dot{z}}_2+{\beta }_{02}fal({\widehat{e}}_1,{\gamma }_{01},\delta )-b_{0}u.\hfill \end{array}\right.$$

(19)

Combining (13) and (15) and deriving the first and second terms of (19), we can get

$$\left\{\begin{array}{c}{\dot{z}}_1={\dot{x}}_1+{\dot{\widehat{e}}}_1=x_2+{\dot{\widehat{e}}}_1,\hfill \\ {\dot{z}}_2={\ddot{z}}_1+{\beta }_{01}{\dot{\widehat{e}}}_1=\ddot{y}+{\ddot{\widehat{e}}}_1+{\beta }_{01}{\dot{\widehat{e}}}_1=x_3+{\ddot{\widehat{e}}}_1+{\beta }_{01}{\dot{\widehat{e}}}_1+b_{0}u.\hfill \end{array}\right.$$

(20)

Substituting the above (20) into the third item of (19), we can get

$$\left\{\begin{array}{c}{\dot{z}}_1={\dot{x}}_1+{\dot{\widehat{e}}}_1=x_2+{\dot{\widehat{e}}}_1,\hfill \\ {\dot{z}}_2=x_3+{\ddot{\widehat{e}}}_1+{\beta }_{01}{\dot{\widehat{e}}}_1+b_{0}u,\hfill \\ z_3=x_3+{\ddot{\widehat{e}}}_1+{\beta }_{01}{\dot{\widehat{e}}}_1+{\beta }_{02}fal({\widehat{e}}_1,{\gamma }_{01},\delta ).\hfill \end{array}\right.$$

(21)

Combining (19) and (21), we can get

$$\left\{\begin{array}{c}{z}_1=x_1+{\widehat{e}}_1,\hfill \\ z_2=x_2+{\dot{\widehat{e}}}_1+{\beta }_{01}{\widehat{e}}_1,\hfill \\ z_3=x_3+{\ddot{\widehat{e}}}_1+{\beta }_{01}{\dot{\widehat{e}}}_1+{\beta }_{02}fal({\widehat{e}}_1,{\gamma }_{01},\delta ).\hfill \end{array}\right.$$

(22)

Let ${\widehat{e}}_2=z_2-x_2$ and ${\widehat{e}}_3=z_3-x_3$. In (22), there are

$$\left\{\begin{array}{c}{\widehat{e}}_2={\dot{\widehat{e}}}_1+{\beta }_{01}{\widehat{e}}_1\hfill \\ {\widehat{e}}_3={\ddot{\widehat{e}}}_1+{\beta }_{01}{\dot{\widehat{e}}}_1+{\beta }_{02}fal({\widehat{e}}_1,{\gamma }_{01},\delta )\hfill \end{array}\right.$$

Therefore, the new ESO can be given by

$$\left\{\begin{array}{c}{\widehat{e}}_1=z_1-x_1,\hfill \\ {\widehat{e}}_2=z_2-x_2,\hfill \\ {\widehat{e}}_3=z_3-x_3,\hfill \\ {\dot{z}}_1=z_2-{\beta }_{01}{\widehat{e}}_1,\hfill \\ {\dot{z}}_2=z_3-{\beta }_{02}fal({\widehat{e}}_2,{\gamma }_{01},\delta )+b_{0}u,\hfill \\ {\dot{z}}_3=-{\beta }_{03}fal({\widehat{e}}_3,{\gamma }_{02},\delta ).\hfill \end{array}\right.$$

(23)

Remark 8. 

In the traditional ESO, $z_1$, $z_2$ and $z_3$ tracking $x_1$, $x_2$ and $x_3$ are based on the error ${\widehat{e}}_1$, thus leading to large excessive steady-state error. To solve this problem, ${\widehat{e}}_2$ and ${\widehat{e}}_3$ are obtained by using (19)–(22). Finally, the new ESO (23) has the form where $z_1$, $z_2$ and $z_3$ tracking $x_1$, $x_2$ and $x_3$ are based on the error ${\widehat{e}}_1$, ${\widehat{e}}_2$ and ${\widehat{e}}_3$, respectively.

(2) Comparison of steady-state error between the new and traditional ESO. To compare the steady-state error of (23) and (15), it is necessary to calculate them separately. However, both (23) and (15) contain nonlinear terms $fal(·)$, which is not conducive for the calculation of steady-state error. However, it is continuous and smooth at any small range, so the function can be converted into a linear function. Therefore, the above (23) can be simplified into a linear form, and the new linear ESO is

$$\left\{\begin{array}{c}{\widehat{e}}_1=z_1-x_1,\hfill \\ {\widehat{e}}_2=z_2-x_2,\hfill \\ {\widehat{e}}_3=z_3-x_3,\hfill \\ {\dot{z}}_1=z_2\left(t\right)-c_1{\widehat{e}}_1,\hfill \\ {\dot{z}}_2=z_3-c_2({\dot{\widehat{e}}}_1+c_1{\widehat{e}}_1)+b_{0}u,\hfill \\ {\dot{z}}_3=-c_3({\ddot{\widehat{e}}}_1+c_1{\dot{\widehat{e}}}_1+c_2{\widehat{e}}_1),\hfill \end{array}\right.$$

(24)

where $c_1={\beta }_{01}$; $c_2$ is composed of ${\beta }_{02}$ and $fal(·)$; $c_3$ is composed of ${\beta }_{03}$ and $fal(·)$. Since the control gain parameters in linear ADRC generally take values greater than 1 [31], there are $c_1$, $c_2$ and $c_3$ being greater than 1.

Then, the system-state equation containing errors of the improved ESO is

$$\left\{\begin{array}{c}{\dot{\widehat{e}}}_1={\dot{z}}_1-{\dot{x}}_1=z_2-c_1{\widehat{e}}_1-x_2={\widehat{e}}_2-c_1{\widehat{e}}_1,\hfill \\ {\dot{\widehat{e}}}_2={\dot{z}}_2-{\dot{x}}_2=z_3-c_2({\dot{\widehat{e}}}_1+c_1{\widehat{e}}_1)+b_{0}u-x_3-bu={\widehat{e}}_3-c_2{\widehat{e}}_2,\hfill \\ {\dot{\widehat{e}}}_3={\dot{z}}_3-{\dot{x}}_3=-c_3({\ddot{\widehat{e}}}_1+c_1{\dot{\widehat{e}}}_1+c_2{\widehat{e}}_1)-\Im =-c_3({\widehat{e}}_3+c_2{\widehat{e}}_1-c_2{\widehat{e}}_2)-\Im .\hfill \end{array}\right.$$

(25)

Furthermore, the above (25) can be expressed as

$$\dot{\widehat{e}}=\mathcal{A}\widehat{e}+\mathcal{B}\Im ,$$

(26)

where $\widehat{e}=[{\widehat{e}}_1;{\widehat{e}}_2;{\widehat{e}}_3]$,

$$\mathcal{A}=\left[\begin{array}{ccc}-c_1& 1& 0\\ 0& -c_2& 1\\ -c_2{c}_3& c_2{c}_3& -c_3\end{array}\right],\mathcal{B}=\left[\begin{array}{c}0\\ 0\\ -1\end{array}\right].$$

Assumption 1. 

$max\left\{\left|x_3=f(x_1,\omega ,t)\right|,\left|{\dot{x}}_3=\Im \right|\right\}⩽{\omega }_o$, ${\omega }_o$ is ESO bandwidth.

Theorem 1. 

Given appropriate parameters for $c_1$, $c_2$ and $c_3$ making the eigenvalue of matrix $\mathcal{A}$ of the system (26) located in the left half-plane, the errors of the system (25) are then bounded and the steady-state error is

$${\widehat{e}}_1⩽\frac{{\omega }_0}{c_2{c}_3},{\widehat{e}}_2⩽\frac{c_1{\omega }_0}{c_2{c}_3},{\widehat{e}}_3⩽\frac{{\omega }_0}{c_3}.$$

(27)

Proof of Theorem 1. 

The solution of (26) is

$$\widehat{e}=exp(-\mathcal{A}t)\widehat{e}\left(0\right)+{\int }_0^{t}exp\left(-\mathcal{A}(t-\tau )\right)\mathcal{B}\Im \left(\tau \right)d\tau .$$

(28)

Taking the norm on both sides of the above (28) leads to

$$\begin{array}{cc}\hfill ∥\widehat{e}∥& ⩽∥exp(-\mathcal{A}t)\widehat{e}\left(0\right)∥+∥{\int }_0^{t}exp\left(-\mathcal{A}(t-\tau )\right)\mathcal{B}\Im \left(\tau \right)d\tau ∥\hfill \\ \hfill & ⩽∥exp(-\mathcal{A}t)∥∥\widehat{e}\left(0\right)∥+∥\mathcal{B}∥{\int }_0^t∥exp\left(-\mathcal{A}(t-\tau )\right)\Im \left(\tau \right)∥d\tau \hfill \\ \hfill & ⩽∥exp(-\mathcal{A}t)∥∥\widehat{e}\left(0\right)∥+∥\mathcal{B}∥{\int }_0^t∥exp\left(-\mathcal{A}(t-\tau )\right)∥∥\Im \left(\tau \right)∥d\tau .\hfill \end{array}$$

(29)

Since the matrix $\mathcal{A}$ is Schur stable and according to [32], it follows that

$$∥exp(-\mathcal{A}t)∥⩽\kappa exp(-\chi t),$$

(30)

where $\kappa$ and $\chi$ are given positive constants.

Further, according to (29) and (30) and letting $\left|\Im \right|<{\omega }_0$, it can be obtained that

$$\begin{array}{cc}\hfill ∥\widehat{e}∥& ⩽\kappa ∥\widehat{e}\left(0\right)∥exp(-\chi t)+\kappa ∥\mathcal{B}∥{\int }_0^{t}exp(-\chi (t-\tau ))∥\Im \left(\tau \right)∥d\tau \hfill \\ \hfill & ⩽\kappa ∥\widehat{e}\left(0\right)∥exp(-\chi t)+\kappa ∥\mathcal{B}∥∥{\omega }_0∥{\int }_0^{t}exp(-\chi (t-\tau \left)\right)d\tau \hfill \\ \hfill & ⩽\kappa ∥\widehat{e}\left(0\right)∥+\kappa ∥\mathcal{B}∥∥{\omega }_0∥{\chi }^{-1}\left(1-exp(-\chi t)\right)\hfill \\ \hfill & ⩽\kappa ∥\widehat{e}\left(0\right)∥+\kappa ∥{\omega }_0∥{\chi }^{-1}.\hfill \end{array}$$

(31)

According to (30), the error of system (25) is bounded.

Furthermore, when (25) enters the steady state, the left-hand of the system (25) converges to zero, i.e., when the system (25) enters the steady state, there is

$$\left\{\begin{array}{c}{\widehat{e}}_2-c_1{\widehat{e}}_1=0,\hfill \\ {\widehat{e}}_3-c_2{\widehat{e}}_2=0,\hfill \\ -c_3({\widehat{e}}_3+c_2{\widehat{e}}_1-c_2{\widehat{e}}_2)-\Im =0.\hfill \end{array}\right.$$

(32)

According to (25), the steady-state error of the improved ESO is

$${\widehat{e}}_1=-\frac{\Im }{c_2{c}_3},{\widehat{e}}_2=-\frac{c_1\Im }{c_2{c}_3},{\widehat{e}}_3=-\frac{\Im }{c_3}.$$

(33)

Due to Assumption 1, taking the absolute value of (33) yields (27). □

Similarly, according to [33], the steady-state error of traditional ESO is

$$\left|{\widehat{e}}_1\right|⩽\frac{{\omega }_0}{c_3},\left|{\widehat{e}}_2\right|⩽\frac{c_1{\omega }_0}{c_3},\left|{\widehat{e}}_3\right|⩽\frac{c_2{\omega }_0}{c_3}.$$

(34)

The steady-state errors of traditional ESO and new ESO are shown in Table 1. Since the gains $c_1$, $c_2$ and $c_3$ of ESO are greater than 1, when the coefficient values are the same, the steady-state errors of new ESO are clearly smaller than those of traditional ESO.

Table 1. Comparison of steady-state errors between new ESO and traditional ESO.

New ESO	$\left|{\widehat{e}}_1\right|⩽\frac{{\omega }_0}{c_1{c}_2{c}_3}$	$\left|{\widehat{e}}_2\right|⩽\frac{{\omega }_0}{c_2{c}_3}$	$\left|{\widehat{e}}_3\right|⩽\frac{{\omega }_0}{c_3}$
Traditional ESO	$\left|{\widehat{e}}_1\right|⩽\frac{{\omega }_0}{c_3}$	$\left|{\widehat{e}}_2\right|⩽\frac{c_1{\omega }_0}{c_3}$	$\left|{\widehat{e}}_3\right|⩽\frac{c_2{\omega }_0}{c_3}$

Remark 9. 

It is acknowledged that the steady state of nonlinear ESO cannot be reduced to a linear state directly. However, on the one hand, it is expected that the steady-state error of nonlinear ESO bears almost the same characteristics as that of linear ESO since the nonlinear function $fal(·)$ is continuous and smooth at any small range. On the other hand, the main purpose of this subsection is to compare the steady-state error between the linear new ESO and linear traditional ESO, and thus the nonlinear new ESO is converted into the linear new ESO.

3.2.2. The New NLSEF

Due to the addition of the control of the cart position, the traditional second-order ADRC NLSEF (16) is re-written as

$$u_0={\beta }_{1}fal(e_{\alpha ,1},{\gamma }_1,\delta )+{\beta }_{2}fal(e_{\alpha ,2},{\gamma }_2,\delta )+{\beta }_3{e}_{\theta ,1}+{\beta }_4{e}_{\theta ,2},$$

(35)

where $e_{\alpha ,1}=\tilde{\alpha }-{\tilde{\alpha }}_v$, $e_{\alpha ,2}=\dot{\alpha }-{\dot{\alpha }}_v$, $e_{\theta ,1}=z_1-{\tilde{\theta }}_v$ and $e_{\theta ,2}=z_2-{\dot{\theta }}_v$; ${\beta }_1$ and ${\beta }_2$ are repectively the control component of controlling the cart position $\alpha$ and cart velocity $\dot{\alpha }$; ${\beta }_3$ and ${\beta }_4$ are repectively the control component of controlling the pendulum angle $\theta$ and pendulum angular velocity $\dot{\theta }$; the control gain tuning formulas ${\beta }_1={\omega }_{c1}^2$, ${\beta }_2=2{\omega }_{c1}$, ${\beta }_3=-{\omega }_{c2}^2/2$, ${\beta }_2=-2{\omega }_{c2}$ and ${\omega }_{c1}$ and ${\omega }_{c2}$ are the bandwidth of the controller gain.

Remark 10. 

The above (35) controls both the cart position and pendulum angle, avoiding single-variable control of the pendulum angle in (16) and overcoming the limitation of (16) that the cart position is used as a disturbance variable. Therefore, it control the stability of both the cart position and pendulum angle of NIPVSSs.

To compensate the total disturbance of the system estimated by ESO, it follows that (10). Finally, the compensated system becomes (11).

3.2.3. Stability of Closed-Loop System

For simplicity, we will analyse the stability of new SIMO ADRC-based NIPVSSs with new linear ESO and new linear NLSEF. The new ESO is (24). The new linear NLSEF can be converted from (35), i.e.,

$$u_0=c_4{e}_{\alpha ,1}+c_5{e}_{\alpha ,2}+{\beta }_3{e}_{\theta ,1}+{\beta }_4{e}_{\theta ,2},$$

(36)

where $c_4$ is composed of ${\beta }_1$ and $fal(·)$; $c_5$ is composed of ${\beta }_2$ and $fal(·)$. The following Assumption 2 guarantees that the stability of new SIMO ADRC-based NIPVSSs with new linear ESO and new linear NLSEF will approaches that of new SIMO ADRC-based NIPVSSs with new nonlinear ESO and new nonlinear NLSEF.

Assumption 2. 

The bounds of errors between the nonlinear function and linear equation are bounded: ${\beta }_{02}fal({\widehat{e}}_2,{\gamma }_{01},\delta )-c_2({\dot{\widehat{e}}}_1+c_1{\widehat{e}}_1)<\infty$, ${\beta }_{03}fal({\widehat{e}}_3,{\gamma }_{02},\delta )-c_3({\ddot{\widehat{e}}}_1+c_1{\dot{\widehat{e}}}_1+c_2{\widehat{e}}_1)<\infty$, ${\beta }_{1}fal(e_{\alpha ,1},{\gamma }_1,\delta )-c_4{e}_{\alpha ,1}<\infty$, ${\beta }_{2}fal(e_{\alpha ,2},{\gamma }_2,\delta )-c_5{e}_{\alpha ,2}<\infty$.

To analyse the closed-loop system, the closed-loop model should be established. For simplicity, consider the following Assumption 3.

Assumption 3. 

The control objective of NIPVSSs is to make the cart position and pendulum angle stable at the origin, i.e., ${\theta }_v=0$ and ${\alpha }_v=0$, to make ${\tilde{\theta }}_v$, ${\dot{\theta }}_v$, ${\tilde{\alpha }}_v$ and ${\dot{\alpha }}_v$ equal to 0.

According to the above Assumption 3 and considering (12), (13) and (17)–(36) and $u=\ddot{\alpha }$, the closed-loop model of new SIMO ADRC-based NIPVSSs with new linear ESO and new linear NLSEF is

$$\dot{X}=\mathbb{A}X+\mathbb{B}\xi$$

(37)

where $X=[\alpha ;\theta ;\dot{\alpha };\dot{\theta }]$, $\xi =[x_3;{\widehat{e}}_1;{\widehat{e}}_2;{\widehat{e}}_3]$,

$$\mathbb{A}=\left[\begin{array}{cccc}0& 0& 1& 0\\ 0& 0& 0& 1\\ c_4& {\beta }_3& c_5& {\beta }_4\\ b{c}_4& b{c}_4& b{c}_4& b{c}_4\end{array}\right],\mathbb{B}=\left[\begin{array}{cccc}0& 0& 0& 0\\ 0& 0& 0& 0\\ 1-\frac{b}{b_0}& b{\beta }_3& b{\beta }_4& -\frac{b}{b_0}\\ -\frac{1}{b_0}& {\beta }_3& {\beta }_4& -\frac{1}{b_0}\end{array}\right]$$

Theorem 2. 

Given the appropriate parameters for $c_1$, $c_2$, $c_3$, $c_4$ and $c_5$ making the eigenvalue of matrix $\mathbb{A}$ of the system (37) located in the left-half closed plane, then the state X of the system (37) is bounded.

Proof of Theorem 2. 

The proof is similar to that of Theorem 1, and is thus omitted. □

4. Simulation and Real-Time Control Experiment

In the practical application of ADRC, since the computer control system cannot achieve continuous ADRC, it needs to be discretized [34,35]. In combination with the improved ESO and the discrete form of the second-order fastest TD in [36], Figure 9 shows the complete discrete form of ADRC algorithm.

Figure 9. Complete discrete-time improved ADRC algorithm.

Remark 11. 

The discrete-time TD, improved ESO, new NLSEF and disturbance compensation originate from the continuous TD (6), the new ESO (23), the new NLSEF (35), and disturbance compensation (10). Note that $v_1$ represents ${\tilde{\theta }}_v$, ${\tilde{\alpha }}_v$ and $\tilde{\alpha }$; $v_2$ represents ${\tilde{\dot{\theta }}}_v$, ${\tilde{\dot{\alpha }}}_v$ and $\dot{\alpha }$; v represents ${\theta }_v$, ${\alpha }_v$ and α in the above TD.

4.1. Parameter Tuning

According to the second-order ADRC algorithm introduced earlier, the parameters to be set include the speed factor r and h of TD link, ${\beta }_{01}$, ${\beta }_{02}$, ${\beta }_{03}$, ${\gamma }_{01}$ and ${\gamma }_{02}$ of ESO link, ${\beta }_1$, ${\beta }_2$, ${\beta }_3$, ${\beta }_4$, ${\gamma }_1$ and ${\gamma }_2$ of NLSEF link. Since ${\gamma }_{01}$, ${\gamma }_{02}$, ${\gamma }_1$ and ${\gamma }_2$ are nonlinear parameters, small changes to a parameter will greatly affect the tuning of other parameters. Therefore, once these parameters are determined, they are not easy to modify, and the other parameters can be tuned online. Since the three parts of ADRC are designed, the separation principle [36] is adopted. Each link is set separately, and the relevant parameters are then adjusted slightly. To achieve real-time control of ADRC, first set a buffer in the image-processing unit to store the state information obtained by the image-processing unit, then set $h=0.01s$ to update state information, and save the control input in the zero-order hold until the next control input arrives. The parameters of the entire NIPVSSs controller are shown in Table 2.

Table 2. ADRC-based NIPVSSs parameters.

Links	ESO Link	NLSEF Link
Parameters	${\beta }_{01}=180$, ${\beta }_{02}=2160$, ${\beta }_{03}=24000$, ${\gamma }_{01}=0.75$${\gamma }_{02}=1.5$	${\beta }_1=8$, ${\beta }_2=45$, ${\beta }_3=-125$, ${\beta }_4=-30$, ${\gamma }_1=0.75$${\gamma }_2=1.5$

Remark 12. 

The separation principle [36], control variates method, and trial-and-error method are used to obtain the parameters displayed in Table 2. Separation principle details that the parameters of ESO and NLSEF are set separately, and the relevant parameters are then adjusted slightly. The control variates method defines that the nonlinear parameters ${\gamma }_{01}$, ${\gamma }_{02}$, ${\gamma }_1$ and ${\gamma }_2$ will be first determined, and the other parameters can be tuned online. The trial-and-error method details the testing of numerous parameter values until the expected control performance is achieved. Although the trial-and-error method cannot guarantee optimal parameters, the parameters set in Table 2 are sufficient for stabilizing the NIPVSSs.

Remark 13. 

In the process of ESO parameter tuning, the first step is to tune $b_0$ (that is close to b when the model is known). Then, tune ${\beta }_{01}$, ${\beta }_{02}$ and ${\beta }_{03}$ under the condition of keeping the system stable. The larger the value of ${\beta }_{03}$, the smaller the disturbance lag of the system. However, if the value of ${\beta }_{03}$ is excessively large, the estimated value of the total disturbance will overshoot and oscillate. The values of ${\beta }_{01}$ and ${\beta }_{02}$ bear little impact on the performance of the control system, but if the values are too large, the system will oscillate.

Remark 14. 

The experiments shows that the total disturbance of the system with $r=10$ is conspicously smaller than that of the system with $r=15/20/25$. In addition, if TD is not used, the total disturbance of the system with $r=10$ is clearly smaller than that of the system with $r=10$ when TD is used. Based on the above analysis, TD link may not be used in subsequent experiments for the following reasons: (1) The total system disturbance without TD is less than that with TD; (2) Removal of TD link can appropriately reduce calculation delay, thus improving the robustness of the system.

4.2. Experiment Analysis

In the previous section, single-input-multiple-output ADRC was designed for NIPVSSs and a group of parameters was given, with the simulation results verifying the effectiveness of this group of parameters. To further verify the effectiveness of parameters under real-time control, the simulation and experimental results are shown in Figure 10 and Figure 11. The simulation and experimental results show that the system can still operate stably after the ADRC method is employed to estimate and compensate the total disturbance under parameter uncertainty and multiple time-varying delays.

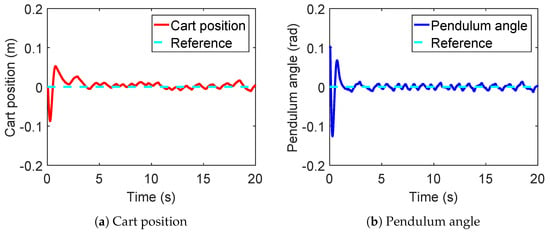
Figure 10. Simulation results of single-input-multiple-output ADRC.

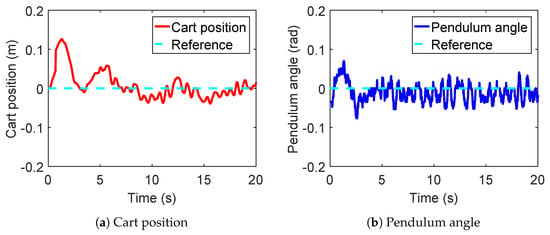
Figure 11. Experimental results of single-input-multiple-output ADRC.

Remark 15. 

The simulation results in Figure 10 are superior to the experimental results in Figure 11, where the control system in Figure 10 requires about 3 or 4 s to reach zero while the time in Figure 11 increases to 10 s. The reasons behind this include that the simulation does not account for many real-world factors, including parameters drift of the inverted pendulum, real-time distributions of multiple time-varying delay and image-processing error, the usage of a digital controller, saturation characteristics of the actuator, etc.

Next, we will further analyze the tolerance of different anti-image-attack systems under ADRC.

4.2.1. Analysis of the Influence of Salt and Pepper Attack on the Performance of NIPVSSs

A salt and pepper attack refers to the injection of salt and pepper noise into an image by an attacker, thus degrading the image with pure white or black pixels of a certain intensity. Salt and pepper attacks of different intensities (0.1%, 0.9%, 1.3%, 1.4%, 1.5%) are injected into the inverted pendulum image, and the ADRC method is used to conduct the inverted pendulum real-time control experiment in turn. The cart position and pendulum angle of the real-time control experiment are shown in Figure 12 and Figure 13. These figures demonstrate that when the salt and pepper salt attack intensity is 0.1%, 0.9% or 1.3%, there is no significant difference in cart position and pendulum angle; however, when the intensity is 1.4% or 1.5%, the cart position stops with the violent movement of the pendulum angle. Meanwhile, the mean and standard deviation of cart position and pendulum angle are used to display the stability performance of the inverted pendulum, as shown in Table 3. It can be seen from Table 3 that: When the salt and pepper attack intensity is less than or equal to 1.3%, the cart position and pendulum angle are in stable operation; However, with an increase in salt and pepper attack intensity, the mean cart position gradually shifts away from the balance point 0 m, the pendulum angle gradually moves away from the balance point 0 rad, and the standard deviation of the cart position and pendulum angle gradually increases. However, there is no sharp increase when; the salt and pepper attack intensity starts at 1.4%; the mean and standard deviation of the cart position and pendulum angle increase sharply. To more intuitively display the impact of salt and pepper attacks of different intensities on the cart position and pendulum angle, the mean and standard deviation of cart position and pendulum angle are shown in Figure 14 and Figure 15. Figure 12, Figure 13, Figure 14 and Figure 15 show that after the system suffers from a salt and pepper attack of a certain intensity, and with the intensity gradually increasing, the control law designed by ADRC can achieve stable control of the NIPVSSs, and although its stability can suffer slightly, there is no obvious fluctuation. When the salt and pepper attack intensity is greater than 1.3%, the designed control law cannot achieve stable control of NIPVSSs, resulting in the divergence of NIPVSSs. The real-time control experiment shows that NIPVSSs can tolerate a maximum salt and pepper attack intensity of 1.3% after adopting ADRC method.

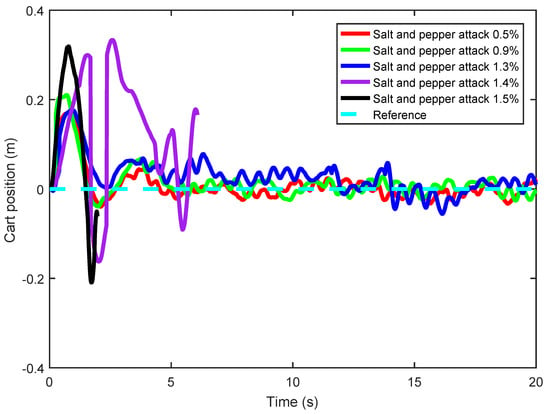
Figure 12. Cart position (real-time control) under different intensities of salt and pepper attack.

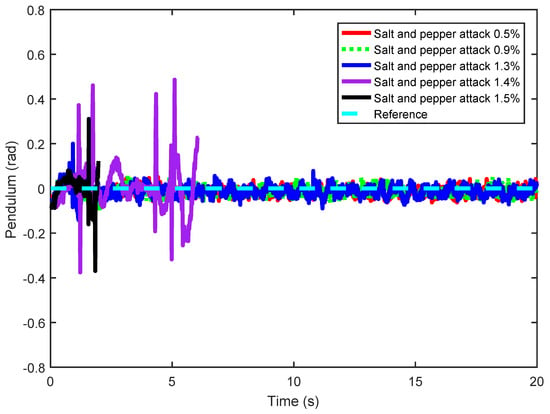
Figure 13. Pendulum angle (real-time control) under different intensities of salt and pepper attack.

Table 3. Mean and standard deviation of cart position and pendulum angle under different intensities of salt and pepper attack.

Intensities of Salt and Pepper Attack	0.5%	0.9%	1.3%	1.4%	1.5%
MCP ${}^1$ (m)	0.0036	0.0150	0.0276	0.1097	0.1168
SCP ${}^2$ (m)	0.0366	0.0397	0.0424	0.1338	0.1638
MPA ${}^3$ (rad)	−0.0121	−0.0124	−0.0124	0.0458	0.0564
MPA ${}^4$ (rad)	0.0214	0.0245	0.0247	0.0865	0.1029

¹ Mean of cart position ² Standard deviation of cart position ³ Mean of pendulum angle ⁴ Standard deviation of pendulum angle.

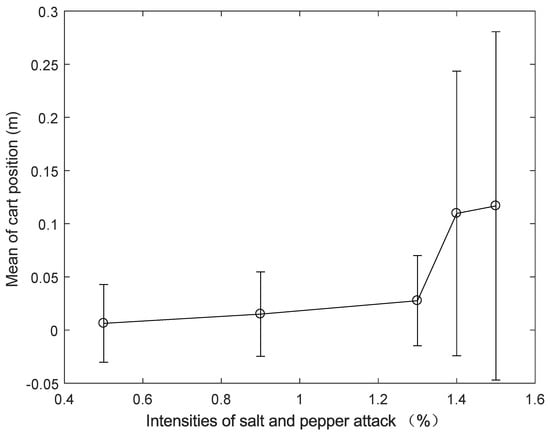
Figure 14. Mean and standard deviation of cart position (real-time control) under different intensities of salt and pepper attack.

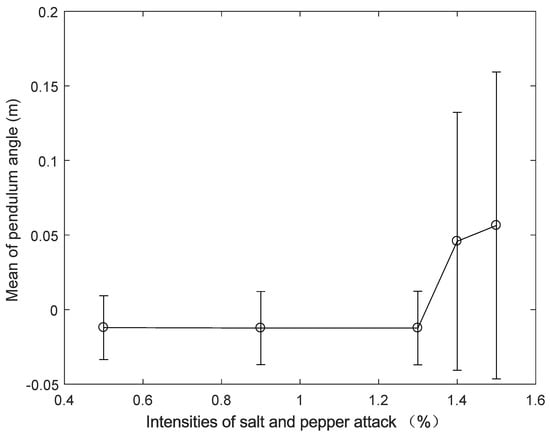
Figure 15. Mean and standard deviation of pendulum angle (real-time control) under different intensities of salt and pepper attack.

Remark 16. 

The salt and pepper attack intensity is decided by the attacker whose aim is to destabilize the system. Figure 12 and Figure 13, and Table 3, show that (1) the intensities of 0.1%, 0.9% or 1.3% are slight and the system remains stable, and (2) the intensities of 1.4% or 1.5% are unmanageable and lead to system destabilization.

4.2.2. Analysis of the Influence of Shearing Attack on the Performance of NIPVSSs

Shearing attacks at different shearing rates (1%, 4%, 7%, 8%, 9%) are injected into the inverted pendulum image, and the ADRC method is used to conduct real-time control experiments of the inverted pendulum in turn. The cart position and pendulum angle of the real-time control experiment are shown in Figure 16 and Figure 17, where one can observe there is no significant difference between the cart position and pendulum angle when the shearing rate is 1%, 4% or 7%. However, when the shearing rate is 8% or 9%, the cart position stops with violent movement of the pendulum angle. Meanwhile, the mean value and standard deviation of cart position and pendulum angle are shown in Table 4. It can be seen from Table 4 that: When the shearing rate is less than or equal to 7%, both cart position and pendulum angle are in stable operation. However, with the increase of shearing rate, the mean value of cart position is gradually away from the balance point 0 m, and the mean value of pendulum angle is gradually away from the balance point 0 rad, and the standard deviation of cart position and pendulum angle is gradually increased, but there is no sharp increase; When the shearing rate starts from 8%, the mean and standard deviation of cart position and pendulum angle increase sharply. To more intuitively display the impact of different shearing attacks on the cart position and pendulum angle, the mean and standard deviation of cart position and pendulum angle are shown in Figure 18 and Figure 19. Figure 16, Figure 17, Figure 18 and Figure 19 show that after the system is subjected to a shearing attack at a certain shearing rate, with the shear rate gradually increasing, the control law designed by ADRC can achieve the stability control of NIPVSSs, and its stability can be slightly worse, but there is no obvious fluctuation; When the shearing rate is greater than 7%, the designed control law cannot achieve the stable control of NIPVSSs, resulting in the divergence of NIPVSSs. The real-time control experiment shows that NVIPCS can tolerate 7% of the maximum shearing rate after using ADRC method.

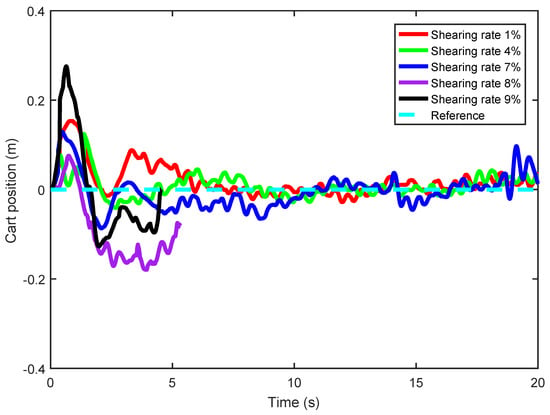
Figure 16. Cart position (real-time control) under different intensities shearing rates.

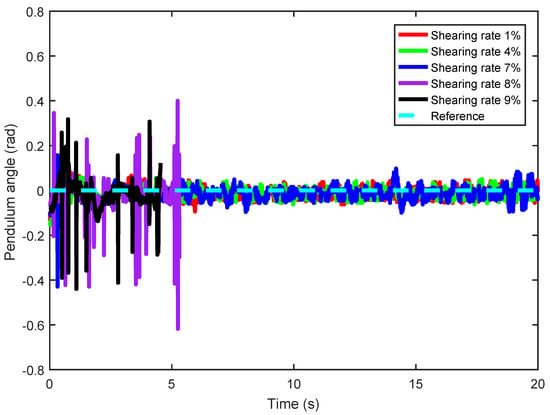
Figure 17. Pendulum angle (real-time control) under different intensities shearing rates.

Table 4. Mean and standard deviation of cart position and pendulum angle under different shearing rate.

Shearing Rate	1%	4%	7%	8%	9%
MCP ${}^1$ (m)	−0.0062	0.0073	0.0194	−0.0825	−0.0993
SCP ${}^2$ (m)	0.0239	0.0360	0.0377	0.0967	0.1173
MPA ${}^3$ (rad)	−0.0105	−0.0127	−0.0129	0.0424	0.0467
MPA ${}^4$ (rad)	0.0257	0.0284	0.0366	0.0756	0.0790

¹ Mean of cart position ² Standard deviation of cart position ³ Mean of pendulum angle ⁴ Standard deviation of pendulum angle.

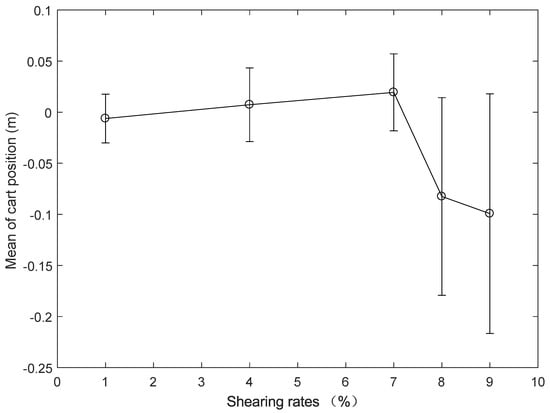
Figure 18. Mean and standard deviation of cart position (real-time control) under different intensities shearing rates.

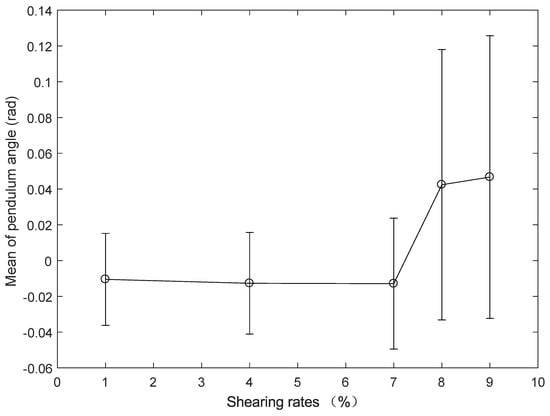
Figure 19. Mean and standard deviation of pendulum angle (real-time control) under different intensities shearing rates.

4.2.3. Analysis of the Influence of Gaussian Attack on the Performance of NIPVSSs

Gaussian attacks with different distributions $(\mu ,\sigma )=(0,1)$, $(\mu ,\sigma )=(0,2)$, $(\mu ,\sigma )=(2,2)$, $(\mu ,\sigma )=(2,5)$ and $(\mu ,\sigma )=(5,5)$ are injected into the inverted pendulum image, and the ADRC method is used to conduct the inverted pendulum real-time control experiment in turn. The cart position and pendulum angle of the real-time control experiment are shown in Figure 20 and Figure 21, demonstrating that when the Gaussian attack obeys $(\mu ,\sigma )=(0,1)$, $(\mu ,\sigma )=(0,2)$, $(\mu ,\sigma )=(2,2)$, or $(\mu ,\sigma )=(2,5)$, there is no significant difference between the cart position and pendulum angle; however, when the Gaussian attack obeys $(\mu ,\sigma )=(2,5)$ or $(\mu ,\sigma )=(5,5)$, the cart position stops with violent movement of the pendulum angle. Meanwhile, the mean and standard deviation of cart position and pendulum angle are shown in Table 5. It can be seen from Table 5 that: when $\mu$ or $\sigma$ increases, both the mean and standard deviation of cart position increase, while the mean of the pendulum angle does not increase; however, the standard deviation increases rapidly, which indicates that with an increase in $\mu$ or $\sigma$ of Gaussian attack, the pendulum angle becomes increasingly divergent, leading to system instability. To more intuitively display the influence of Gaussian attacks subject to different distributions on the cart position and pendulum angle, the mean and standard deviation of cart position and pendulum angle are shown in Figure 22 and Figure 23. Figure 20, Figure 21, Figure 22 and Figure 23 show that when the system is subjected to a Gaussian attack with a certain Gaussian distribution, the control law designed by ADRC can achieve stable control of NIPVSSs with an increase in the Gaussian attack, and its stability can be slightly affected; however, there is no conspicuous fluctuation. When $\mu$ or $\sigma$ of the Gaussian attack increases, the designed controller cannot achieve stable control of NIPVSSs, resulting in the divergence of NIPVSSs. The real-time control experiment shows that the system can operate stably with ADRC method under the Gaussian attack obeying $(\mu ,\sigma )=(0,2)$ and $(\mu ,\sigma )=(2,2)$.

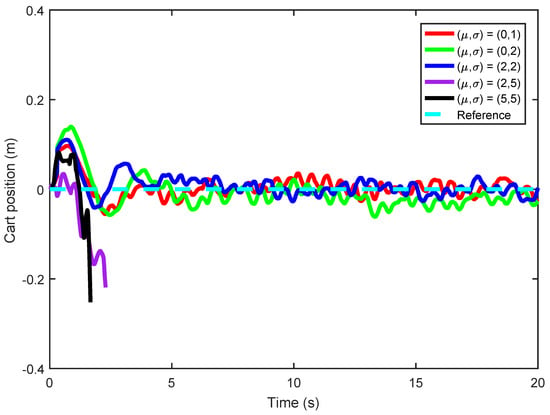
Figure 20. Cart position (real-time control) under different distributions.

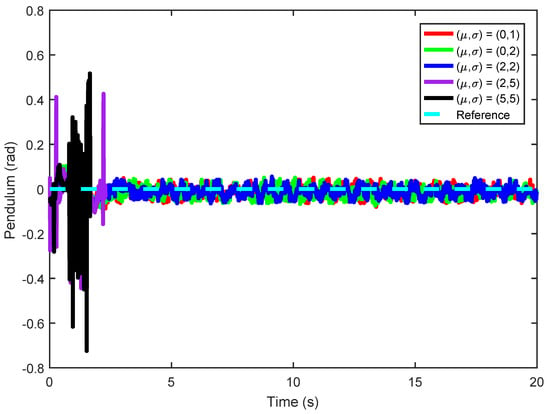
Figure 21. Pendulum angle (real-time control) under different distributions.

Table 5. Mean and standard deviation of cart position and pendulum angle under Gaussian attack with distributions.

$(\mathit{\mu },\mathit{\sigma })$	(0,1)	(0,2)	(2,2)	(2,5)	(5,5)
MCP ${}^1$ (m)	0.0041	-0.0079	0.0085	−0.0552	−0.0606
SCP ${}^2$ (m)	0.0246	0.0260	0.0374	0.0707	0.0705
MPA ${}^3$ (rad)	−0.0126	−0.0128	−0.0145	0.0106	0.0162
MPA ${}^4$ (rad)	0.0252	0.0256	0.0280	0.0811	0.1750

¹ Mean of cart position ² Standard deviation of cart position ³ Mean of pendulum angle ⁴ Standard deviation of pendulum angle.

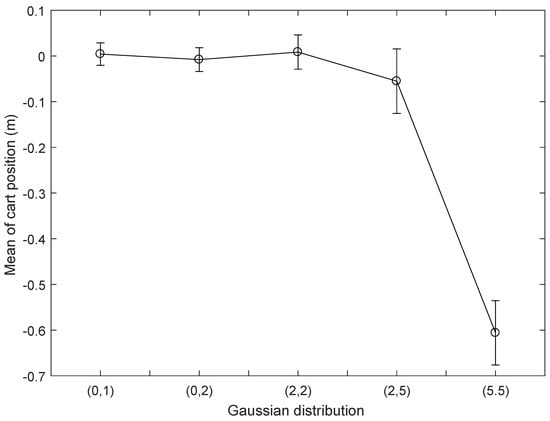
Figure 22. Mean and standard deviation of cart position (real-time control) under different distributions.

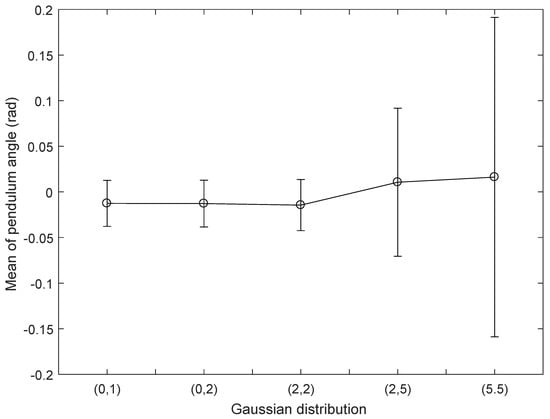
Figure 23. Mean and standard deviation of pendulum angle (real-time control) under different distributions.

4.2.4. Analysis of the Influence of Salt and Pepper Attack and Gaussian Attack Simultaneously on the Performance of NIPVSSs

Figure 24 shows the experimental results of NIPVSSs under a salt and pepper attack of intensity 0.5% and Gaussian attack $(\mu ,\sigma )=(0,1)$ simultaneously, with consequent destablization of NIPVSSs.

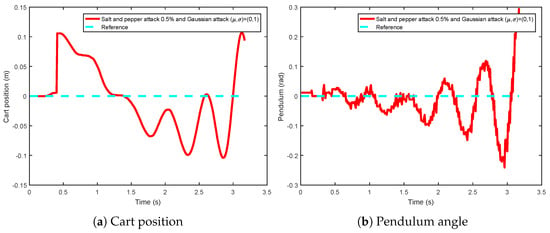
Figure 24. Experimental results of NIPVSSs under salt and pepper attack at intensity of 0.5% and Gaussian attack $(\mu ,\sigma )=(0,1)$ simultaneously.

4.2.5. Comparison of $H_{\infty }$ Control [13], Sliding Mode Control [17] and the Proposed SIMO ADRC Control

To more intuitively compare the $H_{\infty }$ control [13], sliding mode control [17] and the proposed SIMO ADRC control, the results of $H_{\infty }$ control [13] and sliding mode control [17] on NIPVSSs are shown in Figure 25 and Figure 26. It can be seen from Figure 11, Figure 25 and Figure 26 that $H_{\infty }$ control [13] and sliding mode control [17] cannot achieve stable control of NIPVSSs, while the proposed SIMO ADRC control can achieve stable control of NIPVSSs.

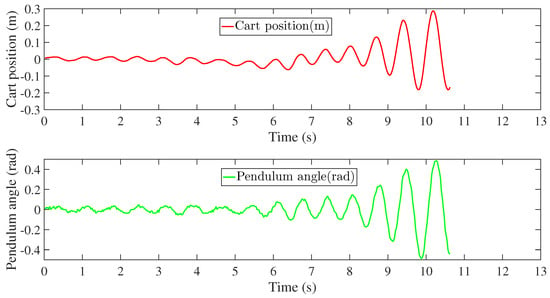
Figure 25. Cart position and pendulum angle of the NIPVSSs with the $H_{\infty }$ controller in [13].

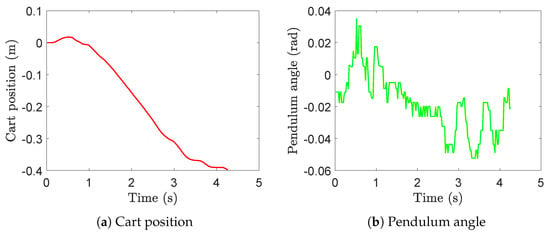
Figure 26. Cart position and pendulum angle of the NIPVSSs with the sliding mode controller in [17].

5. Conclusions

This paper investigated the ADRC-based secure control of NIPVSSs. The main contributions are: (1) The limitations of the traditional SISO ADRC used in NIPVSSs with disturbance are revealed. These limitations are that the ESO used in the traditional SISO ADRC leads to large steady-state error, while the NLSEF employed in the traditional SISO ADRC can achieve stable control of pendulum angle, but cannot achieve stable control of cart position. (2) A new SIMO ADRC method is proposed for the NIPVSSs with disturbance. In the new SIMO ADRC method, the new ESO is designed by introducing additional first and second derivatives of error to reduce the steady-state error. Additionally, the new NLSEF is developed by taking both the calculated cart position and pendulum angle as inputs to achieve dual stable control of pendulum angle and cart position.

The simulation and real-time control verify the effectiveness and feasibility of the proposed method, i.e., NIPVSSs bear a certain ability to resist image attacks after adopting the new SIMO ADRC method. Furthermore, the new SIMO ADRC method has low computational cost since the mathematical functions employed (e.g., addition, subtraction, multiplication, division, sign function and exponential function) are common, and include finite as well as small numbers. Moreover, the new SIMO ADRC method is achieved via software coding, and thus no additional facilities are used in the experiment. However, the main difficulty of using the new SIMO ADRC method concerns parameter tuning. By using the separation principle, control variates method and trial-and-error method, a large number of parameter values are tested until the expected control system is obtained.

To better solve real-world disturbance rejection problem, some meta-heuristic learning algorithms have been widely utilized, e.g., neuroadaptive learning [37], output feedback adaptive control [38] and multilayer neuroadaptive force control [39]. The application of meta-heuristic learning algorithms to NIPVSSs presents an interesting idea for future work.