Robust Stabilization of Underactuated Two-Wheeled Balancing Vehicles on Uncertain Terrains with Nonlinear-Model-Based Disturbance Compensation
Abstract
1. Introduction
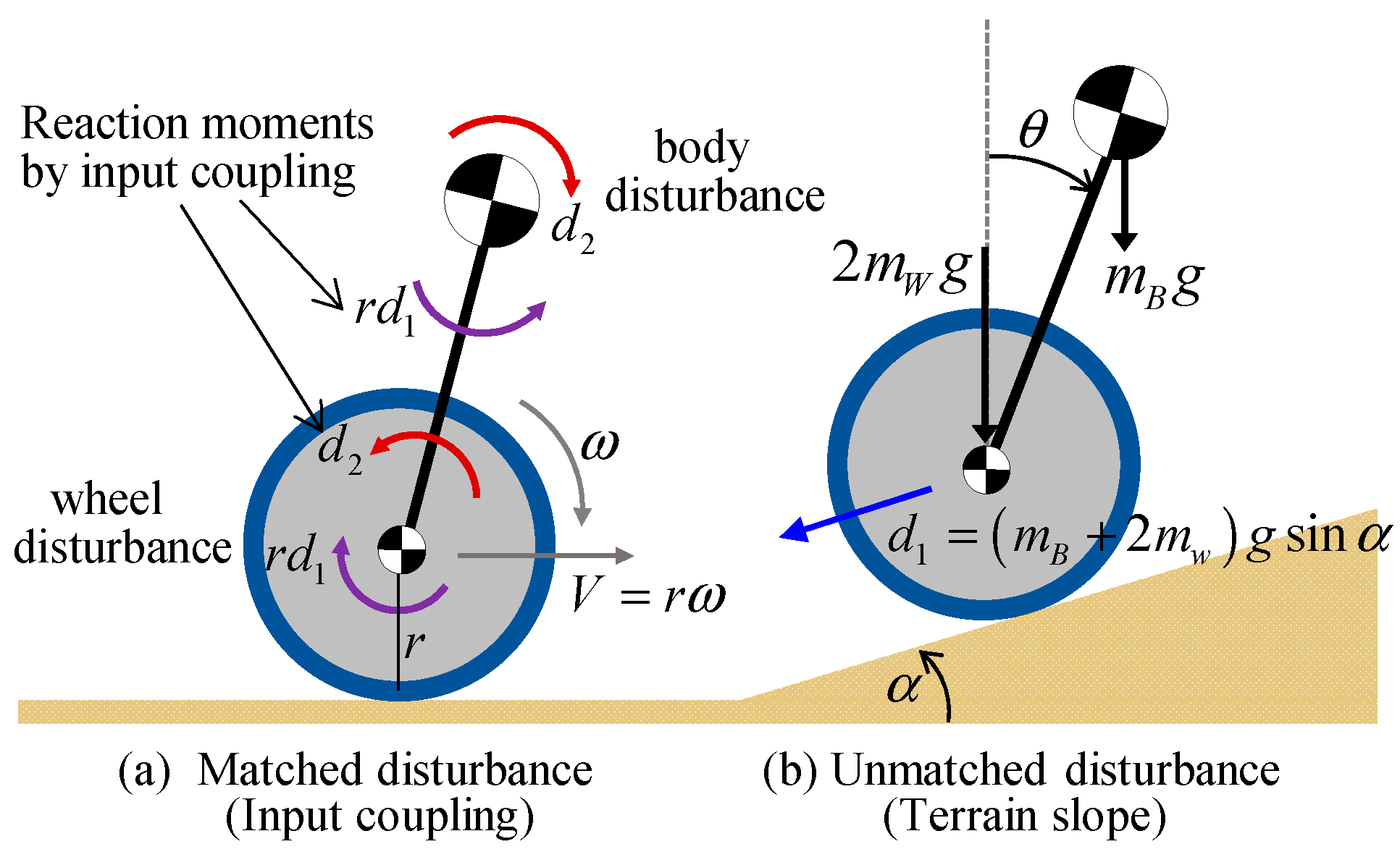
2. Dynamic Characteristics of TWIP on Inclined Surfaces
2.1. Dynamic Model
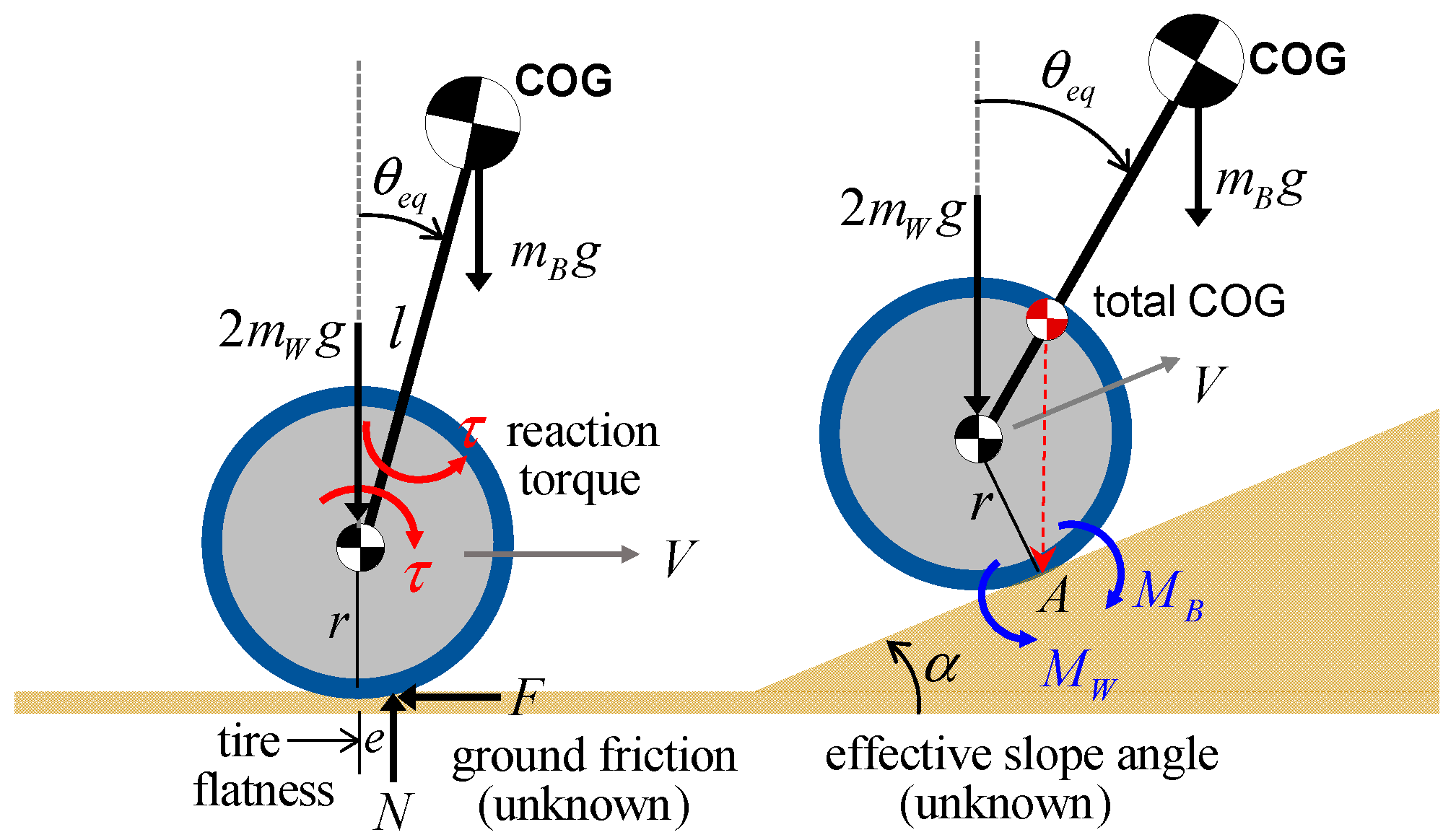
2.2. Finding Static Equilibrium Point on Inclined Surfaces
2.3. Limit of Error-Based Feedback Control
3. NDOB-Based Disturbance Compensation
3.1. NDOB Application to Underactuated TWIPs
3.2. Disturbance Rejection by Input Matrix Modulation
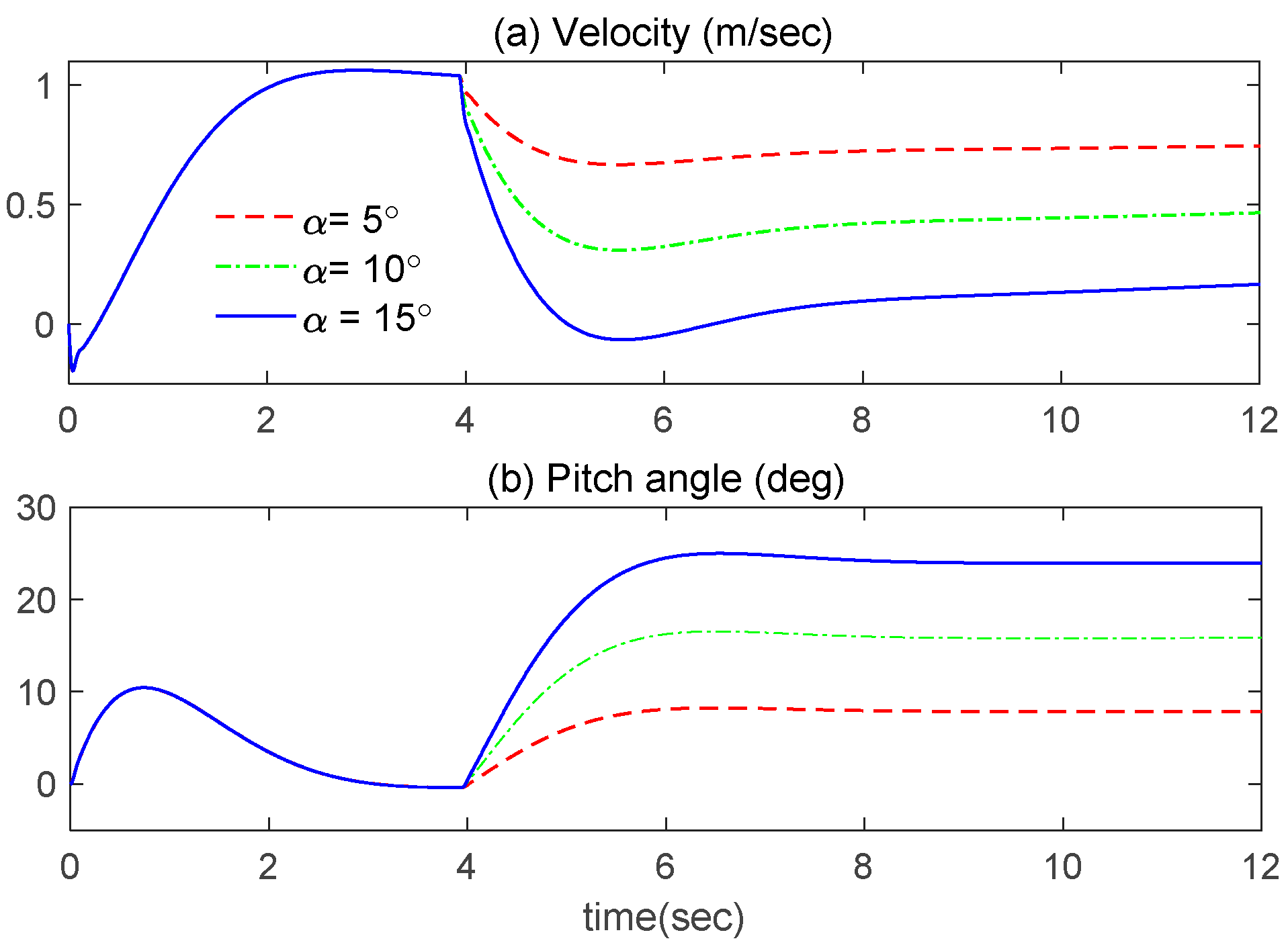
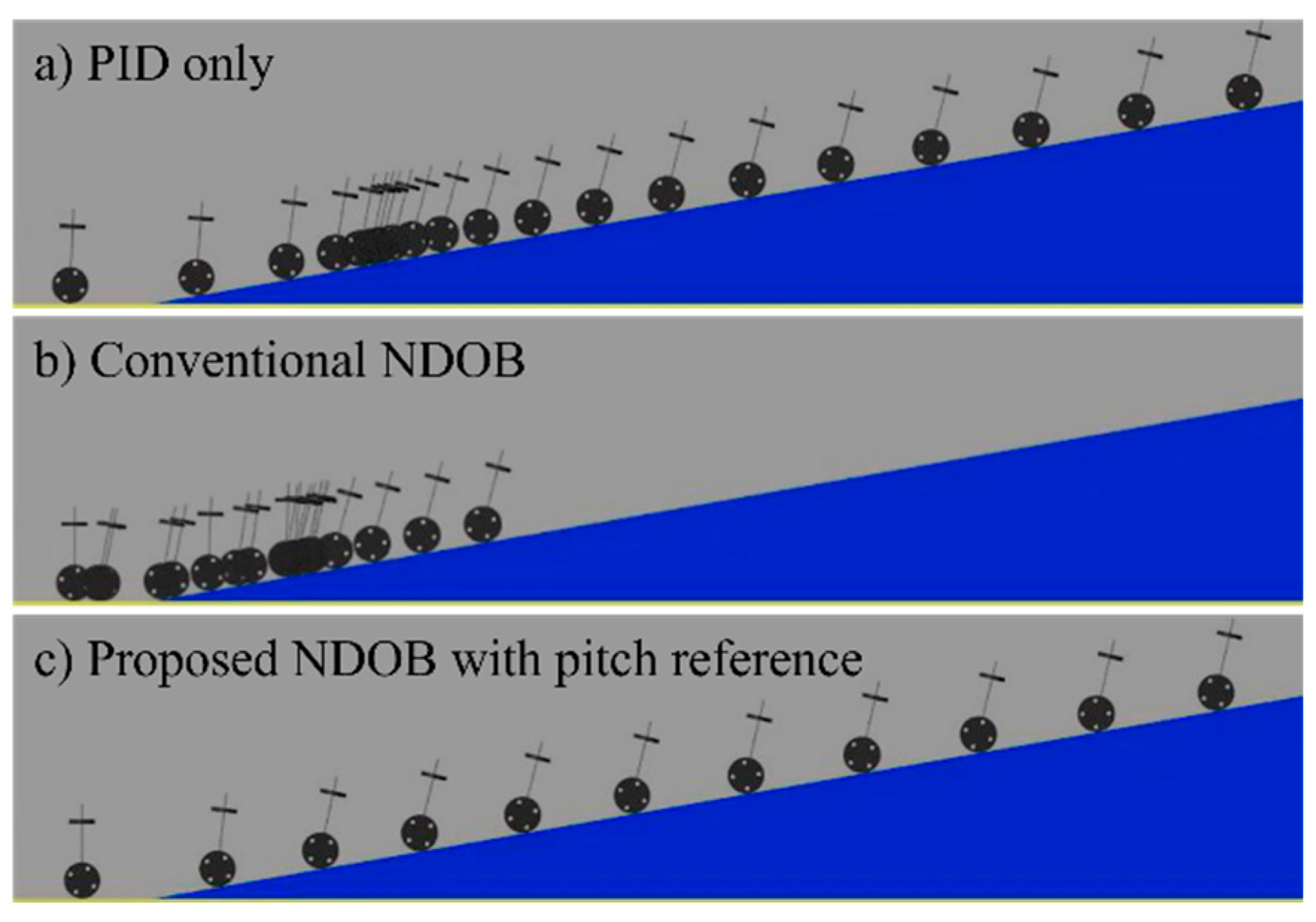
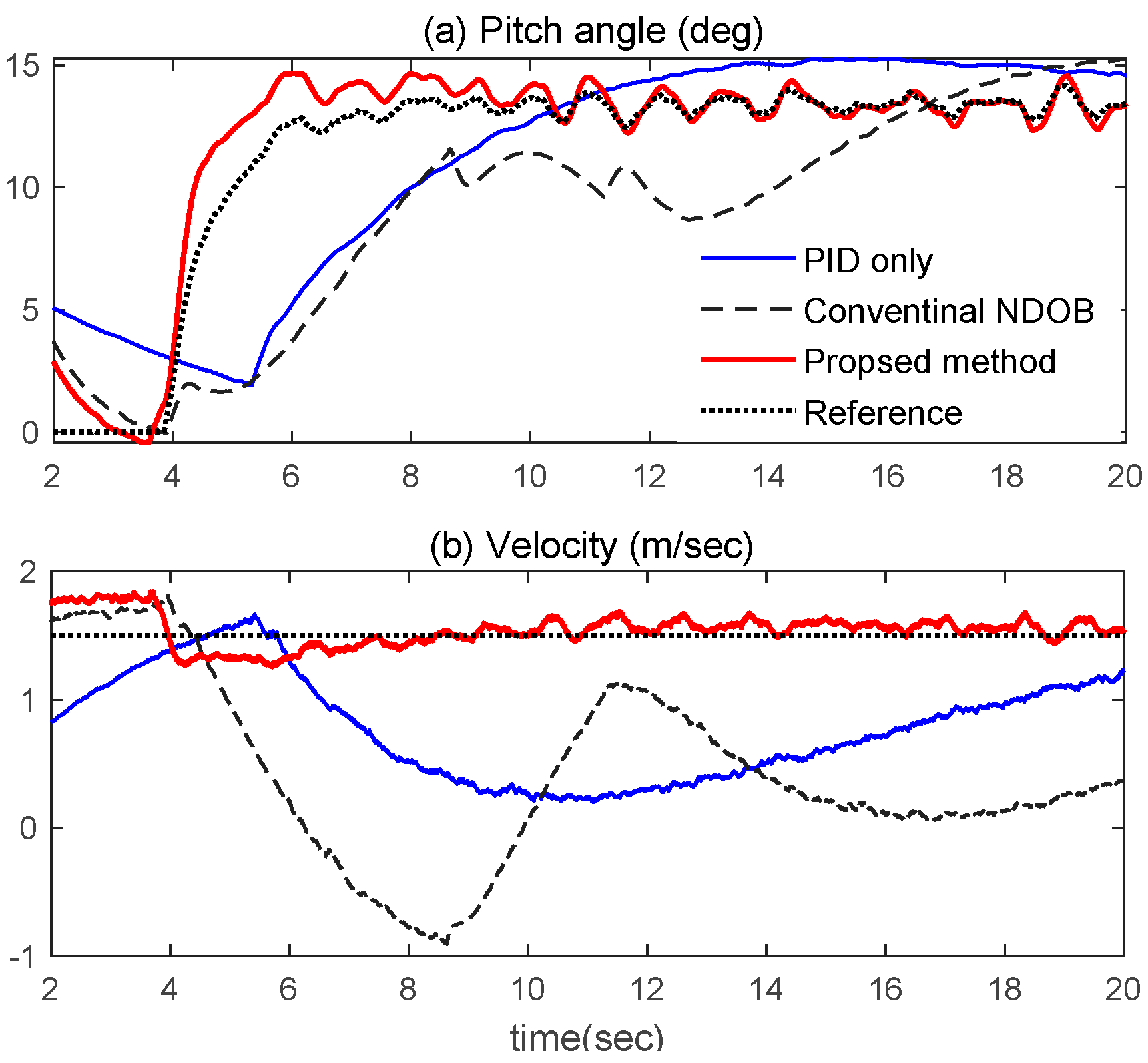
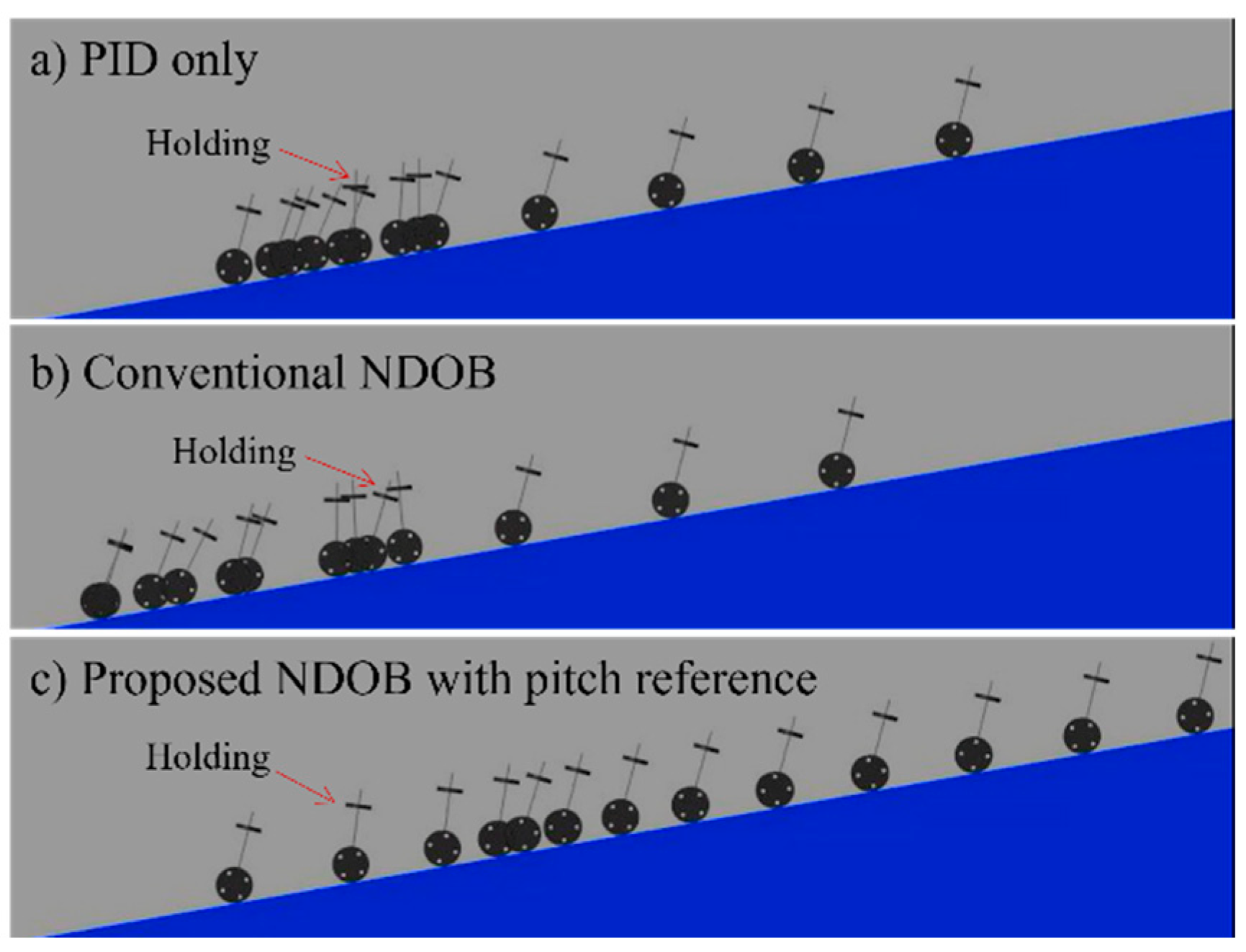
4. Numerical Simulations
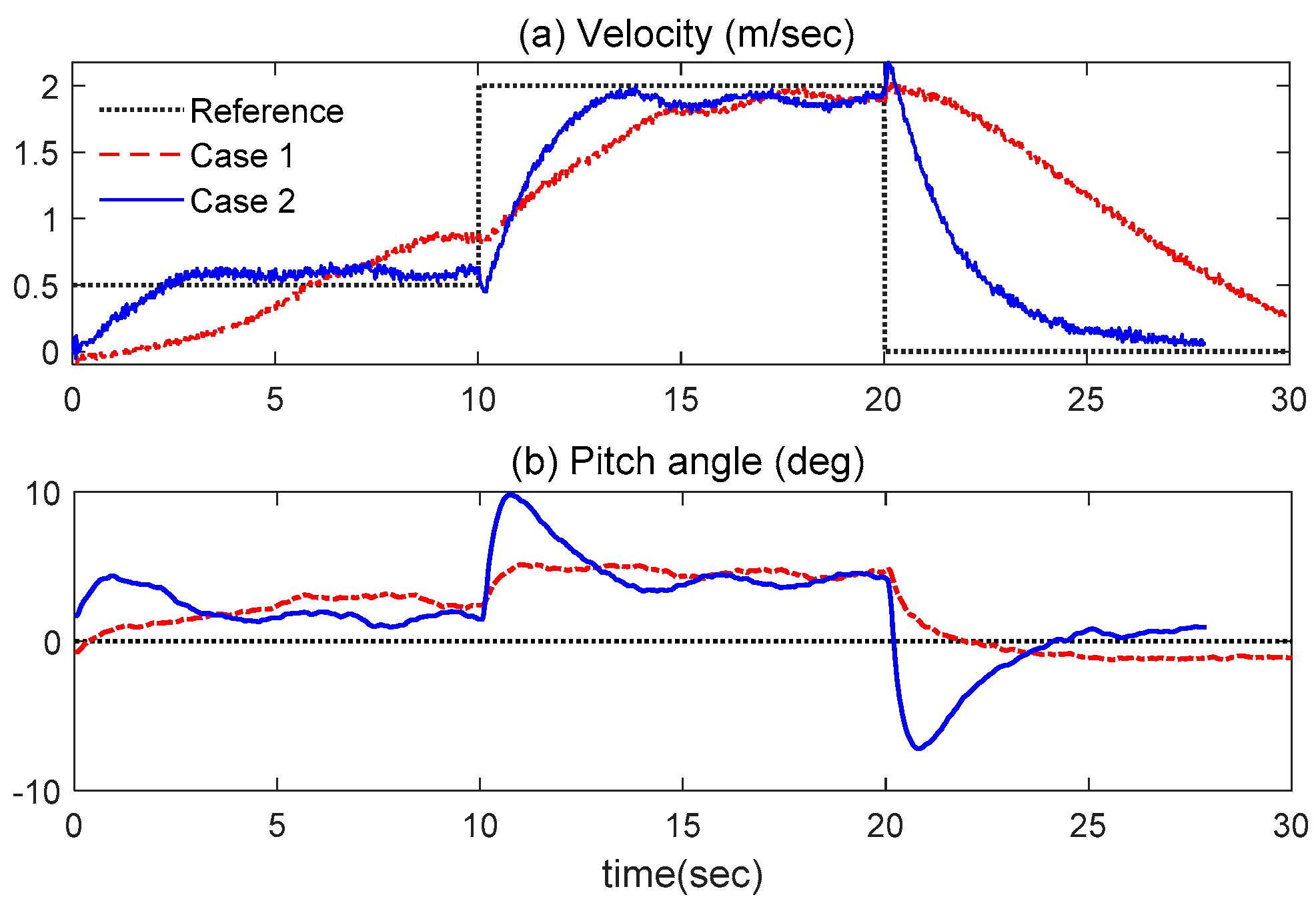
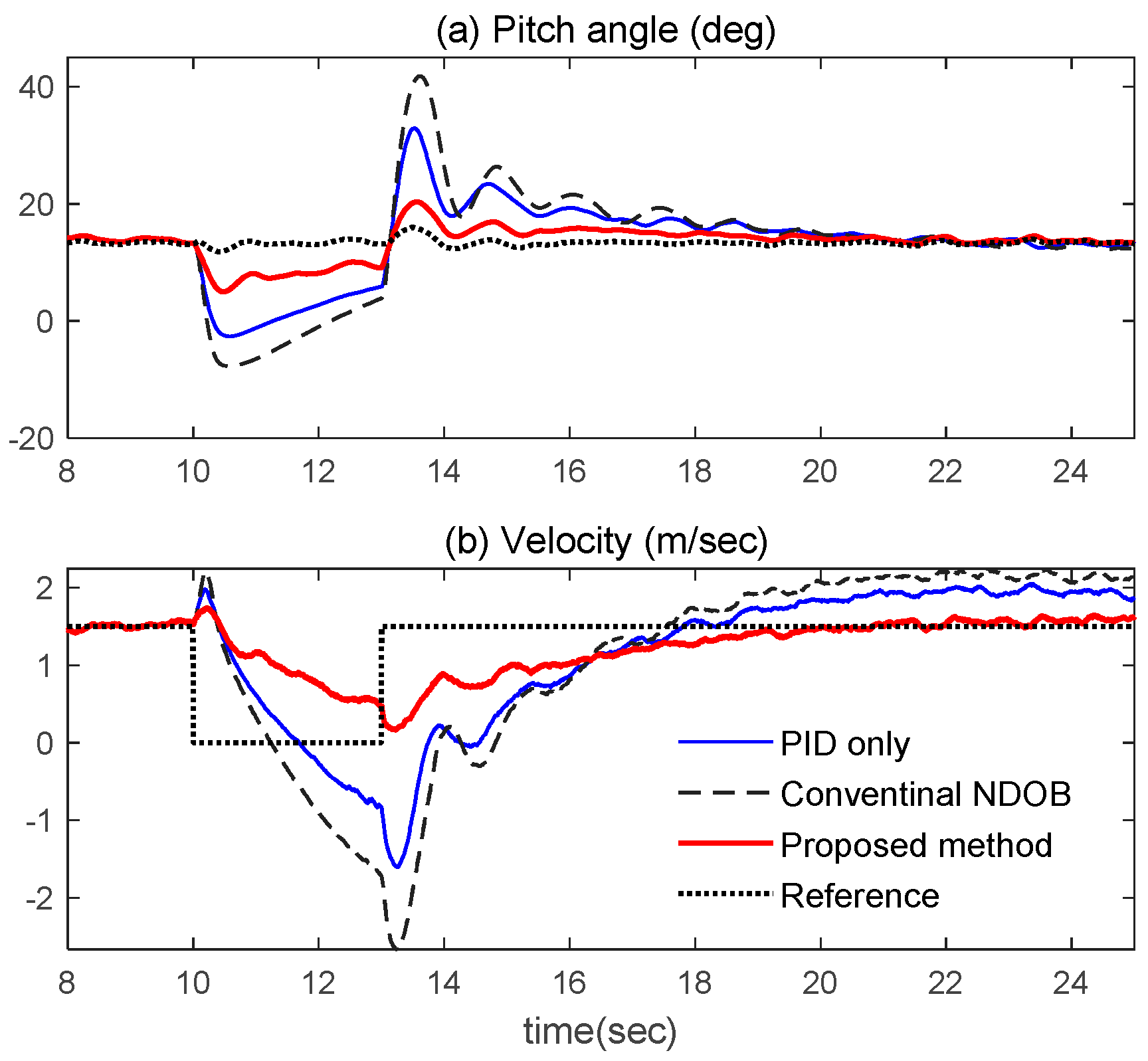
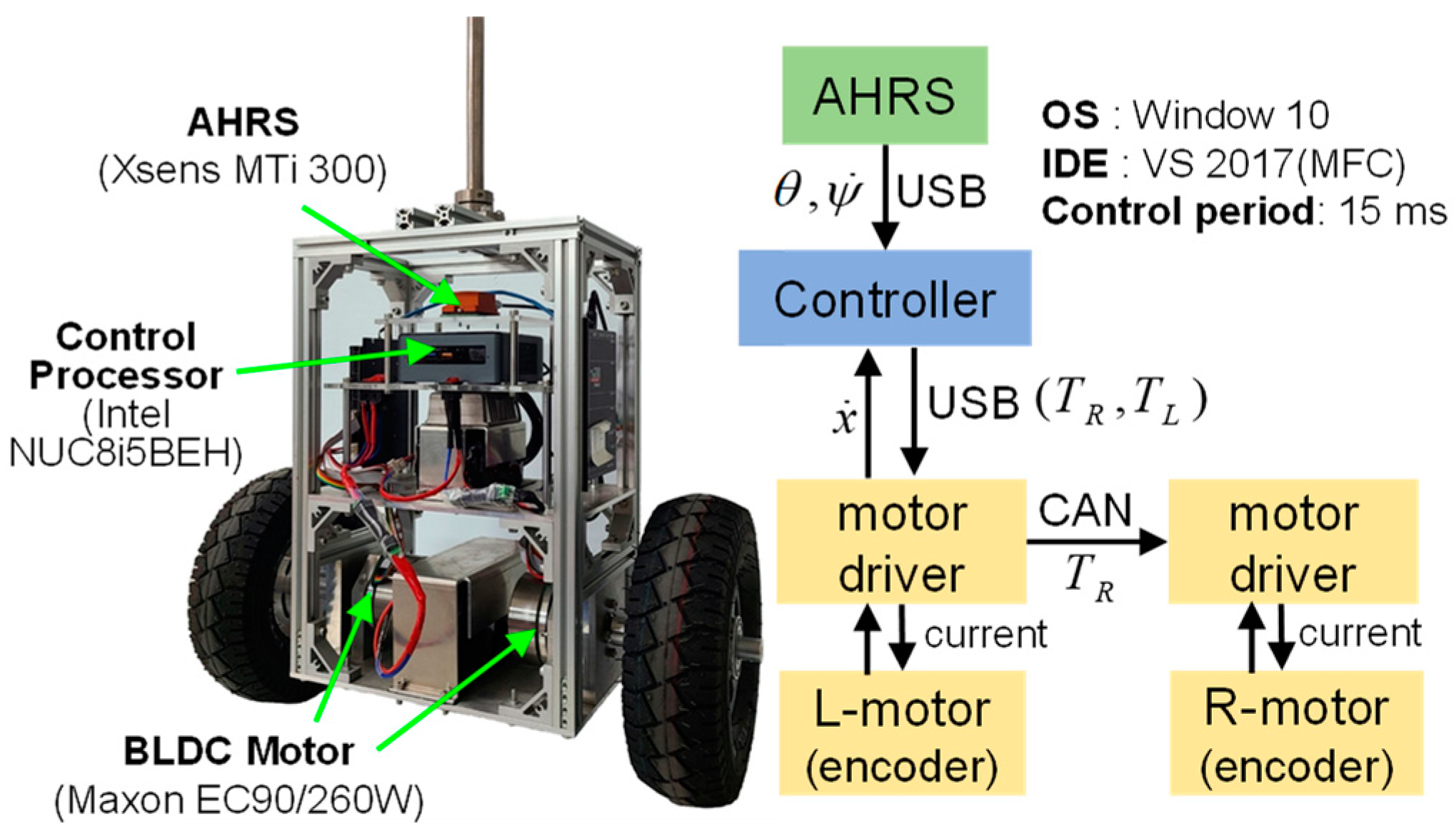
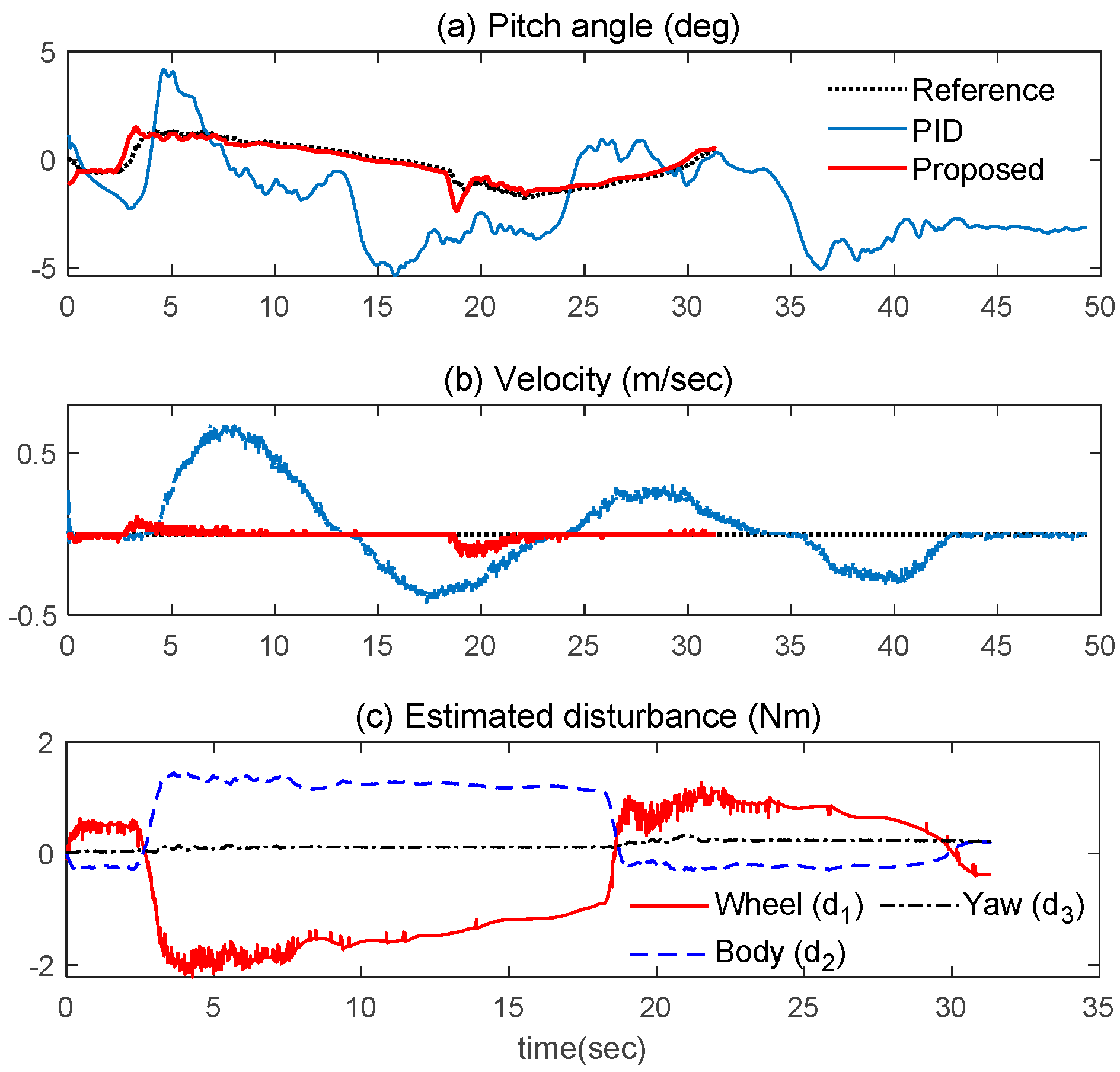
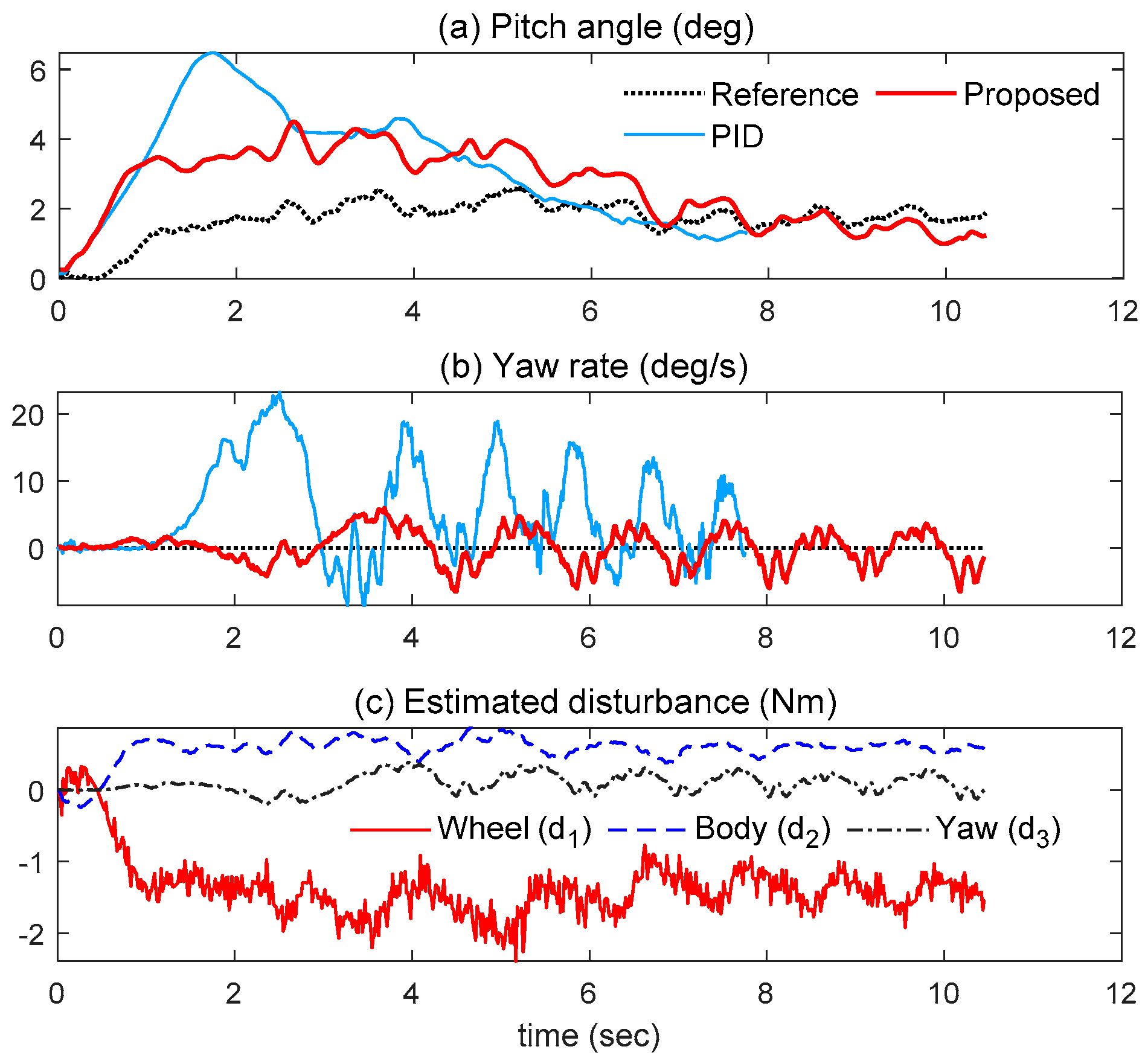
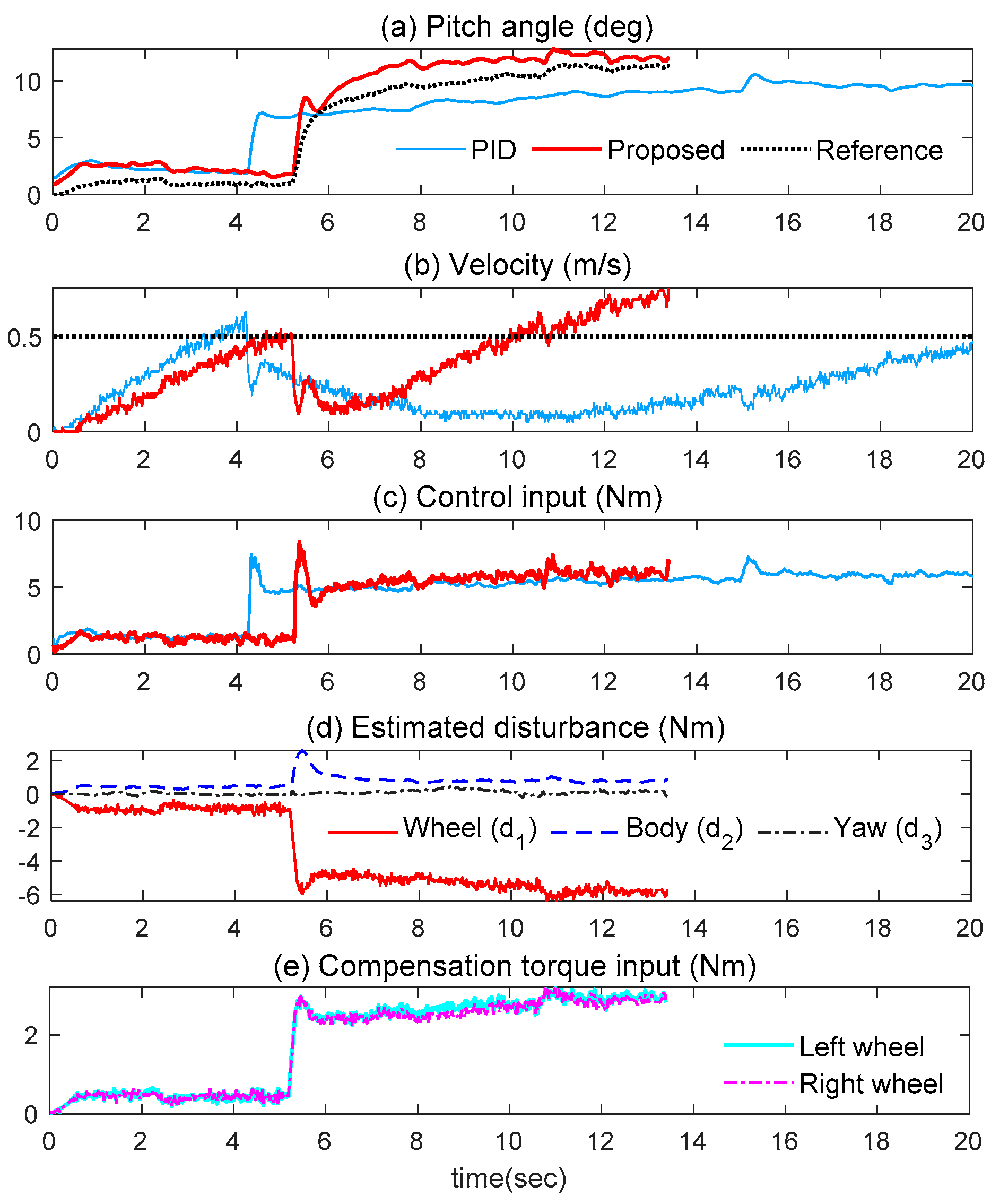
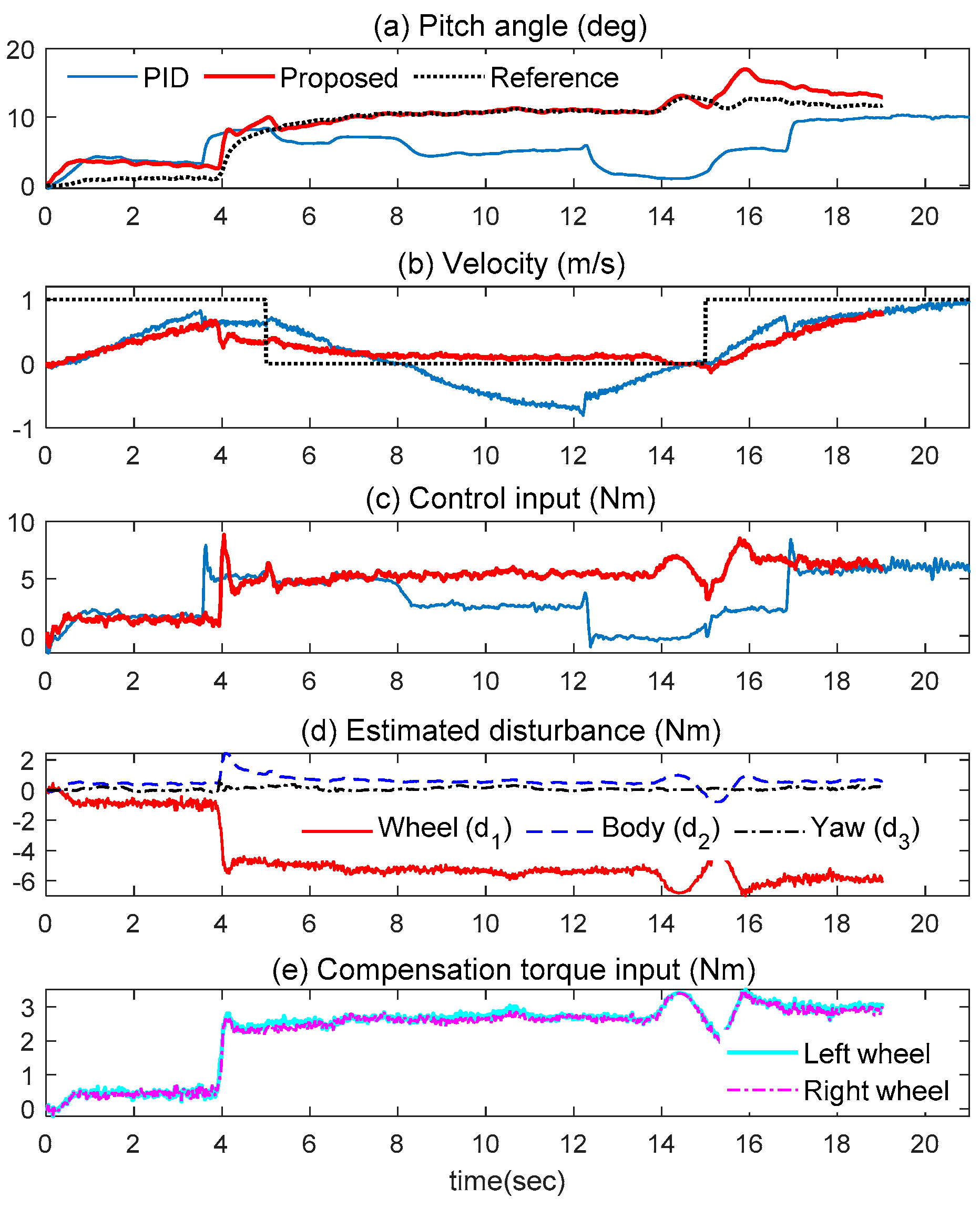
5. Experimental Results
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
Elements of the Matrices and Vectors in Equation (A1)
References
- Segway, A. Two-Wheeled Self-Balancing Personal Transporter. Available online: https://en.wikipedia.org/wiki/Segway (accessed on 25 May 2022).
- Personal Urban Mobility and Accessibility (PUMA). Available online: https://en.wikipedia.org/wiki/Personal_Urban_Mobility_and_Accessibility (accessed on 17 November 2022).
- Vermeiren, L.; Dequidt, A.; Guerra, T.M.; Rago-Tirmant, H.; Parent, M. Modeling, control and experimental verification on a two-wheeled vehicle with free inclination: An urban transportation system. Control Eng. Pract. 2011, 19, 744–756. [Google Scholar] [CrossRef]
- Takahashi, Y.; Kohda, M. Human riding experiments on soft front wheel raising of robotic wheelchair with inverse pendulum control. In Proceedings of the 2005 IEEE International Conference on Industrial Technology, Hong Kong, China, 14–17 December 2005; pp. 266–271. [Google Scholar]
- Boston Dynamics. Available online: https://www.bostondynamics.com/legacy (accessed on 25 May 2022).
- Zafar, M.; Hutchinson, S.; Theodorou, E.A. Hierarchical optimization for whole-body control of wheeled inverted pendulum humanoids. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 7535–7542. [Google Scholar]
- Klemm, V.; Morra, A.; Gulich, L.; Mannhart, D.; Rohr, D.; Kamel, M.; de Viragh, Y.; Siegwart, R. LQR-Assisted Whole-Body Control of a Wheeled Bipedal Robot With Kinematic Loops. IEEE Robot. Autom. Lett. 2020, 5, 3745–3752. [Google Scholar] [CrossRef]
- Huang, J.; Ding, F.; Fukuda, T.; Matsuno, T. Modeling and velocity control for a novel narrow vehicle based on mobile wheeled inverted pendulum. IEEE Trans. Control Syst. Technol. 2013, 22, 1607–1617. [Google Scholar] [CrossRef]
- Larimi, S.R.; Zarafshan, P.; Moosavian, S.A.A. A New Stabilization Algorithm for a Two-Wheeled Mobile Robot Aided by Reaction Wheel. J. Dyn. Syst. Meas. Control 2014, 137, 011009. [Google Scholar] [CrossRef]
- Chan, R.P.M.; Stol, K.A.; Halkyard, C.R. Review of modelling and control of two-wheeled robots. Annu. Rev. Control 2013, 37, 89–103. [Google Scholar] [CrossRef]
- Li, Z.; Yang, C. Neural-Adaptive Output Feedback Control of a Class of Transportation Vehicles Based on Wheeled Inverted Pendulum Models. IEEE Trans. Control Syst. Technol. 2011, 20, 1583–1591. [Google Scholar] [CrossRef]
- Ravichandran, M.T.; Mahindrakar, A. Robust Stabilization of a Class of Underactuated Mechanical Systems Using Time Scaling and Lyapunov Redesign. IEEE Trans. Ind. Electron. 2010, 58, 4299–4313. [Google Scholar] [CrossRef]
- Kim, S.; Kwon, S. Nonlinear Optimal Control Design for Underactuated Two-Wheeled Inverted Pendulum Mobile Platform. IEEE/ASME Trans. Mechatron. 2017, 22, 2803–2808. [Google Scholar] [CrossRef]
- Canete, L.; Takahashi, T. Disturbance compensation in pushing, pulling, and lifting for load transporting control of a wheeled inverted pendulum type assistant robot using the extended state observer. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, Vilamoura-Algarve, Portugal, 7–12 October 2012; pp. 5373–5380. [Google Scholar]
- Huang, J.; Ri, S.; Liu, L.; Wang, Y.; Kim, J.; Pak, G. Nonlinear Disturbance Observer-Based Dynamic Surface Control of Mobile Wheeled Inverted Pendulum. IEEE Trans. Control Syst. Technol. 2015, 23, 2400–2407. [Google Scholar] [CrossRef]
- Huang, J.; Guan, Z.-H.; Matsuno, T.; Fukuda, T.; Sekiyama, K. Sliding-Mode Velocity Control of Mobile-Wheeled Inverted-Pendulum Systems. IEEE Trans. Robot. 2010, 26, 750–758. [Google Scholar] [CrossRef]
- Xu, J.-X.; Guo, Z.-Q.; Lee, T.H. Design and Implementation of Integral Sliding-Mode Control on an Underactuated Two-Wheeled Mobile Robot. IEEE Trans. Ind. Electron. 2013, 61, 3671–3681. [Google Scholar] [CrossRef]
- Huang, J.; Zhang, M.; Ri, S.; Xiong, C.; Li, Z.; Kang, Y. High-order disturbance-observer-based sliding model control for mobile wheeled inverted pendulum systems. IEEE Trans. Ind. Electron. 2020, 67, 2030–2041. [Google Scholar] [CrossRef]
- Dai, F.; Gao, X.; Jiang, S.; Liu, Y.; Li, J. A multi-DOF two wheeled inverted pendulum robot climbing on a slope. In Proceedings of the 2014 IEEE International Conference on Robotics and Biomimetics (ROBIO 2014), Bali, Indonesia, 5–10 December 2014; pp. 1958–1963. [Google Scholar]
- Peng, K.; Ruan, X.; Zuo, G. Dynamic model and balancing control for two-wheeled self-balancing mobile robot on the slopes. In Proceedings of the 10th World Congress on Intelligent Control and Automation, Beijing, China, 6–8 July 2012; pp. 3681–3685. [Google Scholar]
- Takei, T.; Matsumoto, O.; Komoriya, K. Simultaneous estimation of slope angle and handling force when getting on and off a human-riding wheeled inverted pendulum vehicle. In Proceedings of the 2009 IEEE/RSJ International Conference on Intelligent Robots and Systems, St. Louis, MO, USA, 10–15 October 2009; pp. 4553–4558. [Google Scholar]
- Kausar, Z.; Stol, K.; Patel, N. The Effect of Terrain Inclination on Performance and the Stability Region of Two-Wheeled Mobile Robots. Int. J. Adv. Robot. Syst. 2012, 9, 218. [Google Scholar] [CrossRef]
- Hirata, K.; Kamatani, M.; Murakami, T. Advanced motion control of two-wheel wheelchair for slope environment. In Proceedings of the IECON 2013-39th Annual Conference of the IEEE Industrial Electronics Society, Vienna, Austria, 10–13 November 2013; pp. 6436–6441. [Google Scholar]
- Kim, S.; Kwon, S. Dynamic modeling of a two-wheeled inverted pendulum balancing mobile robot. Int. J. Control Autom. Syst. 2015, 13, 926–933. [Google Scholar] [CrossRef]
- Liu, Y.; Yu, H. A survey of underactuated mechanical systems. IET Control Theory Appl. 2013, 7, 921–935. [Google Scholar] [CrossRef]
- Dinale, A.; Hirata, K.; Zoppi, M.; Murakami, T. Parameter Design of Disturbance Observer for a Robust Control of Two-Wheeled Wheelchair System. J. Intell. Robot. Syst. 2014, 77, 135–148. [Google Scholar] [CrossRef]
- Chen, W.-H.; Yang, J.; Guo, L.; Li, S. Disturbance-Observer-Based Control and Related Methods—An Overview. IEEE Trans. Ind. Electron. 2015, 63, 1083–1095. [Google Scholar] [CrossRef]
- Chen, W.-H. Disturbance Observer Based Control for Nonlinear Systems. IEEE/ASME Trans. Mechatron. 2004, 9, 706–710. [Google Scholar] [CrossRef]
- Chen, W.-H.; Ballance, D.J.; Gawthrop, P.J.; Gribble, J.J.; Reilly, J.O. A nonlinear disturbance observer for two link robotic manipulators. IEEE Trans. Ind. Electron. 2000, 47, 932–938. [Google Scholar] [CrossRef]
- Riachy, S.; Orlov, Y.; Floquet, T.; Santiesteban, R.; Richard, J. Second order sliding mode control of underactuated me-chanical systems I: Local stabilization with application to an inverted pendulum. Int. J. Robust Nonlinear Control 2008, 18, 529–543. [Google Scholar] [CrossRef]
- Kim, S.; Kwon, S.J. Robust transition control of underactuated two-wheeled self-balancing vehicle with semi-online dy-namic trajectory planning. Mechatronics 2020, 68, 102366. [Google Scholar] [CrossRef]
- Simscape. Available online: https://mathworks.com/products/simscape-multibody.html (accessed on 25 May 2022).
- Tariq, M.; Bhattacharya, T.K.; Varshney, N.; Rajapan, D. Fast response Anti windup PI speed controller of Brushless DC motor drive: Modeling, simulation and implementation on DSP. J. Electr. Syst. Inf. Technol. 2016, 3, 1–13. [Google Scholar] [CrossRef]
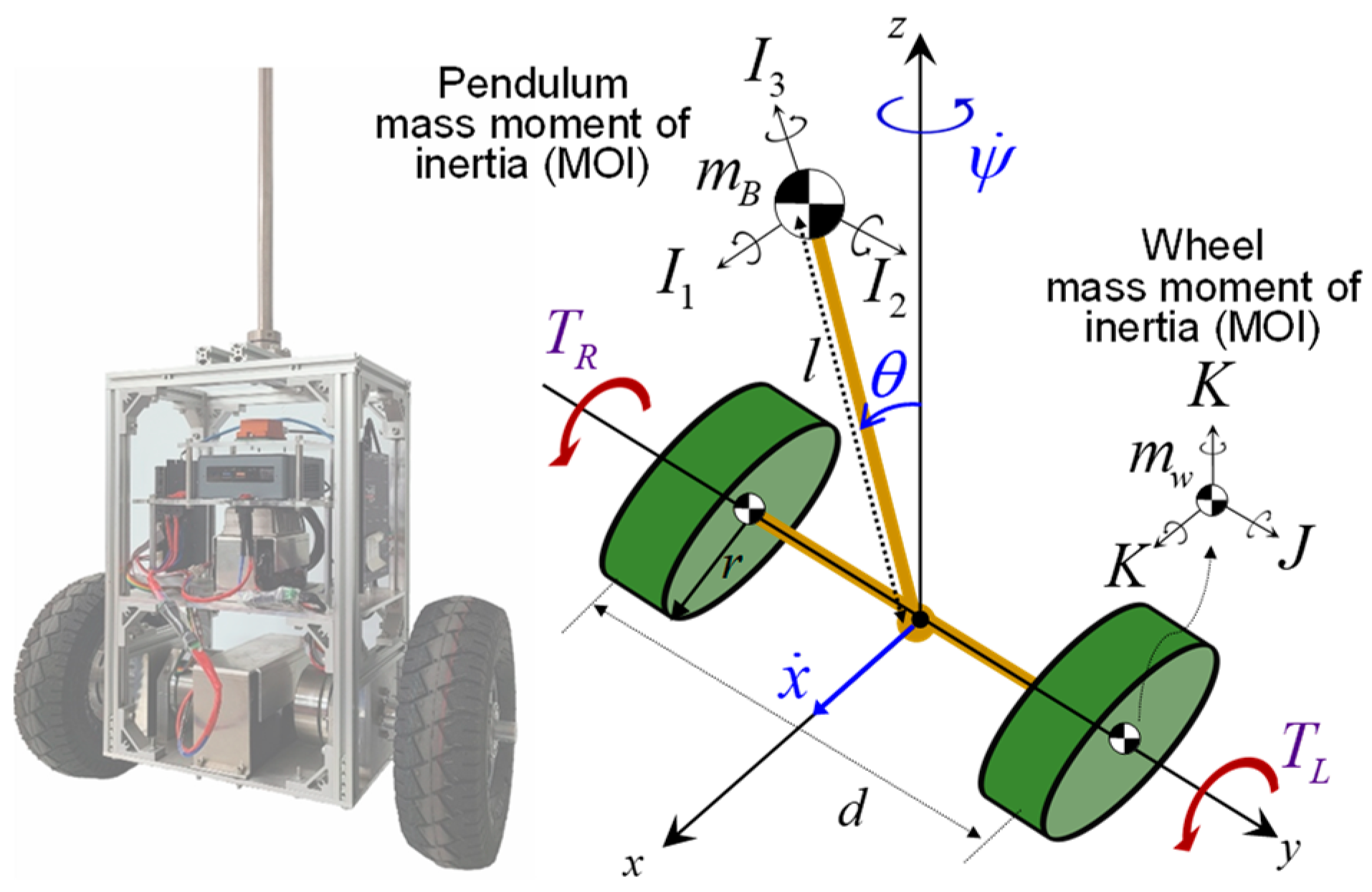



| Displacement along the forward direction | |
| Pitch angle of inverted pendulum | |
| Yaw rate of the entire TWIP robot | |
| Torque of left and right wheels | |
| Distance between the parallel wheels | |
| Distance from the wheel axis to the center of gravity (length of inverted pendulum) | |
| Mass of inverted pendulum and each wheel | |
| MOI of inverted pendulum body | |
| MOI of each wheel body | |
| Radius of wheel |
| 17.6, 2.2 (kg) | |
| 0.15, 0.47, 0.127 (m) | |
| 0.4032, 0.3297, 0.1907 (kg m2) | |
| 0.010, 0.018 (kg m2) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, Y.; Kwon, S. Robust Stabilization of Underactuated Two-Wheeled Balancing Vehicles on Uncertain Terrains with Nonlinear-Model-Based Disturbance Compensation. Actuators 2022, 11, 339. https://doi.org/10.3390/act11110339
Kim Y, Kwon S. Robust Stabilization of Underactuated Two-Wheeled Balancing Vehicles on Uncertain Terrains with Nonlinear-Model-Based Disturbance Compensation. Actuators. 2022; 11(11):339. https://doi.org/10.3390/act11110339
Chicago/Turabian StyleKim, Yongkuk, and SangJoo Kwon. 2022. "Robust Stabilization of Underactuated Two-Wheeled Balancing Vehicles on Uncertain Terrains with Nonlinear-Model-Based Disturbance Compensation" Actuators 11, no. 11: 339. https://doi.org/10.3390/act11110339
APA StyleKim, Y., & Kwon, S. (2022). Robust Stabilization of Underactuated Two-Wheeled Balancing Vehicles on Uncertain Terrains with Nonlinear-Model-Based Disturbance Compensation. Actuators, 11(11), 339. https://doi.org/10.3390/act11110339





