Design and Implementation of an Asynchronous Finite State Controller for Wheeled Mobile Robots

Abstract

Wheeled mobile robots (WMRs) can navigate in uncontrolled environments with the assistance of electronic or physical devices. Several works have been conducted on the control and management of the path-tracking of a vehicle in different road scenarios. This paper aims to create an asynchronous finite state control law for a WMR. The control law is based on a proportional–integral–derivative controller, and the performance of the proposed model is evaluated in virtual and real environments in two different scenarios. In the first one, the WMR must perform a zig-zag maneuver between obstacles, while the second one involves a double left lane change. In the proposed scenarios, the WMR drives along a path until an obstacle is detected at less than 50 cm, causing the WMR to check whether the first lane is free to go and move on. These scenarios and the related required engineering approaches seem particularly suitable for system engineering in a student’s laboratory for the design and implementation of automated guidance system modeling.

1. Introduction

Mobile robots can navigate in uncontrolled environments with the assistance of Information Communication Technology (ICT). Nowadays, in Industry 4.0, there is an increasing interest in the use of these mobile robots for industrial applications, and they are essential parts of their manufacturing execution systems too [1].

Wheeled mobile robots (WMRs) are easy to manage with kinematic models, but they present some issues related to the design of stabilizing control laws, due to the nonholonomic constraints [2].

The use of mobile robots is associated with some problems related to the terrain and environment where the robot must be moved and complete the tasks assigned [3]. The locomotion is therefore fundamental for a robot’s movement through the working environment and not only depends on the nature of the environment or path of the robot’s movement but also on vital factors. To solve these issues, it is important to investigate how it is designed. The advantages of using tracked locomotion on soft and yielding terrains and wheeled locomotion on flat and compact grounds are known [4]. Based on these ideas, a novel hybrid leg-wheel track ground mobile robot for surveillance and inspection was proposed [5]. The model was designed to combine the advantages of tracked locomotion on soft and yielding terrains and wheeled locomotion on flat and compact grounds. In recent work, the authors described three possible parallel taxonomies based on body architecture, track profile, and track type to give more details to the designers so that they can select the most suitable architecture on the basis of the operative necessities [6]. Another issue in the mobile robot design is related to input delays and limited communication. An adjustable event-triggered mechanism based on Lyapunov analysis was proposed to reduce the communication burden in the controller-to-robot channel [7]. The results of the proposed method are consistent with simulations and show a significant saving of bandwidth usage compared with traditional time-triggered implementation.

To evaluate and perform the proper control law to track a default path, different algorithms, such as proportional–integral–derivative (PID) controllers, model predictive control (MPC), and fuzzy neural controllers have been proposed [8].

More works have been related to the control and management of the path-tracking of vehicles in different road scenarios. Recent works have studied different control laws, even for vehicle platoons in simulated environments.

An MPC approach to control the intervehicular distance and the speed in a vehicle platoon in order to improve road safety and to minimize fuel consumption was developed [9]. A similar problem was solved using a robust decentralized controller based on a linear control law that provides the speed profile for each component of the platoon [10].

The trajectory tracking problem was solved using two approaches: nonlinear MPC and linear MPC [2]. The results show the effectiveness of both methods. Considerations related to the computational effort of the MPC were developed with the purpose of analyzing the proposed methods in real time.

An adaptive nonlinear trajectory tracking control law based on the use of an input–output feedback linearization technique to get asymptotically exact cancellation for the uncertainty in the given system parameters was designed [11]. The results of the proposed model were compared using an adaptive controller in a simulated environment.

Other applications of the WMRs are related to the guarantee that the wheeled mobile robot can efficiently track its desired trajectory specified by the desired image trajectory. A new adaptive image-based trajectory tracking control approach without the exact camera intrinsic and extrinsic knowledge parameters and the position of the feature point was developed [12].

A two-wheeled robot using a PID controller was used in [13]. The PID algorithm was adopted to control the speed of two DC motors to achieve precise control of the speed of the mobile platform. Thanks to its advantages, such as simplicity, robustness, and familiarity in the control community, a robust PID algorithm was proposed for use as a path tracking controller [14].

A comparison between a nonlinear PID controller and a genetic learning algorithm was proposed for controlling the trajectory tracking [15]. In this work, the comparison between the two methods demonstrated better performance with the PID algorithm due to the minimization of tracking error and improved control smoothness following the application of an external disturbance. As remarked previously, the control system proposed in this work is not the only one that could be implemented to follow a line through a line sensor. Indeed, in solving this problem, different control system approaches can be tested. A Linear Quadratic Tracking and Dynamic Programming method to evaluate which system performs better in terms of avoiding obstacles has been tested [16]. A fuzzy controller combined with a dynamic window approach was implemented to reach a goal through some obstacles [17]. These works, as in many other ones, show a fast and efficient algorithm that can be used on a mobile robot. However, the goal is not to demonstrate the most efficient control method but to show to undergraduate students a possible solution and be able to implement it and understand the strong and weak points of this approach. An increasing number of articles and other materials are using the term "Educational Robotics" to refer to the use of robots in education [18]. Such articles also provide some suggestions about the components and the methods that could be used in the educational robot approach. A study related to intervention methods that foster Computational thinking competence in the context of Educational robot activities for 66 students, aged 8–9 years old, was performed [19]. During the work carried out, the students were divided into four groups and attended a science class for 1 h per week for 12 weeks.

The aim of this paper was to create an asynchronous finite state control law for a WMR. The control law is based on a PID controller, and the performance of the proposed model was evaluated in virtual and real environments in two different scenarios. In the first, the WMR had to perform a zig-zag maneuver between obstacles, while the second involved a double left lane change.

In the proposed scenarios, the WMR drove on a three-lane road and only changed its lane when it detected an obstacle at less than 50 cm away.

2. Material and Methods

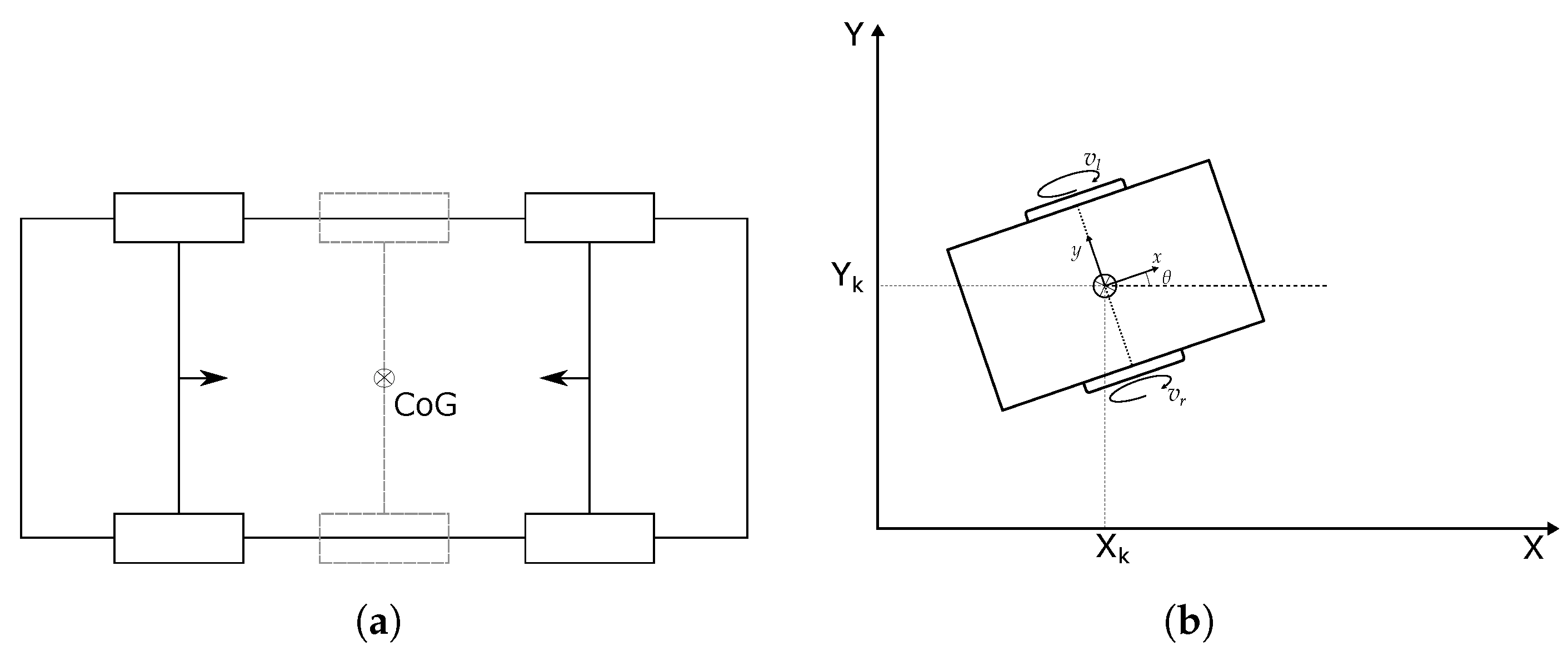
The mobile robot was a four-wheeled, non-steering mini car equipped with an ultrasonic sensor, wheel encoders, and line sensors. Each wheel had its own DC motor, but the controller provided the same power to the wheels on the same side. Thus, the mini car was able to rotate itself to change direction. The mini car was 21 cm long and 15 cm wide with a mass of 400 g.

Due to hardware architecture, the wheels on the same side of the mini car received the same power, which translated into the same angular speed.

Thus, it was possible to represent the wheels by using only one wheel per side located near the Center of Gravity (CoG), as shown in Figure 1a.

With these assumptions, the model describing the dynamics of the mini car is as follows (Figure 1b) is:

$$\left\{\begin{array}{c}\dot{x}=\frac{R}{2}(v_r+v_l)cos\theta \hfill \\ \dot{y}=\frac{R}{2}(v_r+v_l)sin\theta \hfill \\ \dot{\theta }=\frac{R}{L}(v_r-v_l)\hfill \end{array}\right.$$

(1)

where:

• x is the longitudinal position of the robot (with respect to the CoG)
• y is the lateral position of the robot (with respect to the CoG)
• $\theta$ is the head of the robot
• R is the wheel radius
• L is the distance between the the wheels
• $v_l$ and $v_r$ are, respectively, the left and right angular wheel velocities

2.1. System Design

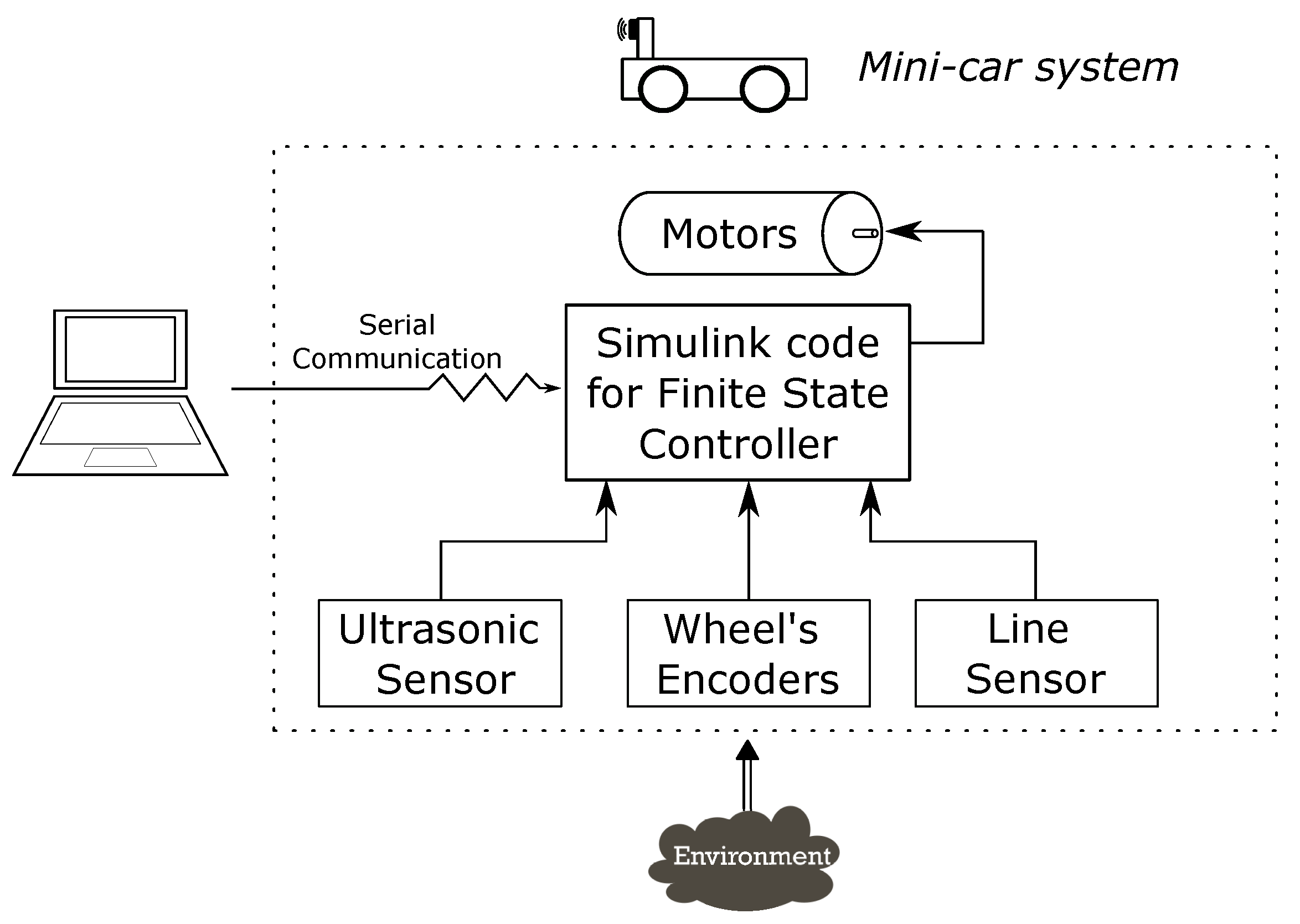
The system consisted of a Freenove 4WD Car with a Nucleo F411RE board witha microcontroller and serial communication with a laptop to allow continuous communication between the hardware and simulink software (useful during testing, debugging, and deploying of the firmware), as shown in Figure 2.

The WMR was equipped with a Nucleo board microcontroller (Figure 3d) with a frequency of 32 kHz and various sensors:

• Ultrasonic sensor:
  • The HC-SR04 Ultrasonic Ranging Module (Figure 3a) integrates both an ultrasonic transmitter and a receiver. The transmitter was used to convert electrical signals (electrical energy) into high-frequency (beyond human hearing) sound waves (mechanical energy), and the function of the receiver was the opposite of this.
• Line-tracking sensor:
  • This sensor (Figure 3b) has three reflective optical photodiodes that emit and receive infrared light that reflects on a surface and detect color through the intensity of the light.
• Wheel encoders:
  • The encoders (Figure 3c) used were rotary incremental with an optical interrupter that detects the rotation of a holed wheel.

The WMR was also equipped with four 5V DC motors and one Tower Pro Micro Servo SG90 that were used, respectively, to move the WMR and rotate its ultrasonic sensor. After assembly, the minicar looks like in Figure 4.

On the software side, Matlab/Simulink was used to design and develop the controller to move and react to the environment. To simulate the WMR and the environment, the “Mobile Robotics Training Library” was used. This provided various blocks to emulate motors, encoders, line sensors, and tracks to follow.

Moreover, thanks to the Simulink Coders, code was converted to C++ and uploaded to the Nucleo board through serial communication.

2.2. Software Design

The control algorithm was designed on Simulink through the Stateflow API and deployed on the onboard STM Nucleo32 through the STMicroelectronics Matlab package.

Thus, data from the mini vehicle could be acquired and used as input for the Simulink blocks that handle the movement of the car. In detail, values retrieved regarding the distance traveled by left and right wheels are used to estimate the vehicle’s orientation, the distance measured by the ultrasonic sensors, and the angle of the servomotor that commands its rotation.

These values are then processed and provided as input to the finite state machine controller. Each state has code to either keep the current lane or to turn in order to change lane, depending on the distance measured by the nearest obstacle ahead. The transition between states happens because of guard conditions on the measured distance and on the orientation of the vehicle with respect to the direction of the road.

Finally, the rotation of the ultrasonic sensor to detect obstacles on the adjacent lanes is managed by a pulse width modulation that acts on the servomotor.

Figure 5 summarizes the event-based evolution of the vehicle overtime.

2.3. Hardware-Software Integration

Sensors do not have any internal algorithm to convert the signals into useful information such as traveled distance, speed, and distance from objects.

In order to have all of the necessary data to develop a control algorithm, we needed to elaborate the signals from each sensor.

• Ultrasonic sensor:
  • The Ultrasonic Ranging Module uses the principle that ultrasonic waves will reflect when they encounter any obstacles. This is possible by counting the time interval between the time at which the ultrasonic wave is transmitted to when the ultrasonic wave reflects back after encountering an obstacle. The time interval counting ends after an ultrasonic wave is received, and the time difference is the total time taken for the ultrasonic wave’s journey from being transmitted to being received. Knowing that the speed of sound in air is a constant (v = 343 m/s), it is possible to calculate the distance d between the Ultrasonic Ranging Module and the obstacle: $d=vt/2$.
• Line-tracking sensor:
  • Each optical sensor sends a high level signal every time it detects a black surface and a low level signal when the surface is white. Knowing this, it is possible to build a look-up table to convert a three-bit value into a value that can be used in the controller (

    Table 1. Look-up table used for the line-tracking sensor.

    Left	Center	Right	Control Intensity
    0	0	0	0
    0	0	1	2
    0	1	0	0
    0	1	1	1
    1	0	0	−2
    1	0	1	0
    1	1	0	−1
    1	1	1	0

    ), where negative values indicate control actions toward the left and positive values indicate control actions toward the right. The control intensity is a proportional gain applied to the final value provided by the PID, and it is used to enforce staying in the lane when the robot happens to be far from the centerline.
• Wheel encoders:
  • The encoders send an interruption signal each time a hole is detected in the drilled wheel. By counting the number of ticks during a specific time interval, it is possible to compute the traveled distance, speed, and wheel rotation speed. Given the total number of ticks at time k as $ticks\left(k\right)$, the rate is

    $$\Delta ticks\left(k\right)=ticks\left(k\right)-ticks(k-1)$$

    (2)

The traveled distance, speed, and rotational speed are

$$\begin{array}{cc}\hfill & traveledDistance\left(k\right)=\frac{2\pi R}{N_{ticks}}ticks\left(k\right)\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill & speed\left(k\right)=\frac{\Delta ticks\left(k\right)}{Ts}\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill & \omega \left(k\right)=\frac{2\pi }{N_{ticks}}\Delta ticks\left(k\right)\hfill \end{array}$$

(5)

where $N_{ticks}$ represents the number of holes in the wheel, and $T_s$ is the sampling time.

All information received from sensors is used to compute the motor’s behavior in terms of its goal. Motors require a Pulse-Width Modulation (PWM) signal to work, so the controller was tuned accordingly to give the correct duty cycle so that the motor used the right amount of voltage in the range of 0–5 V).

2.4. WMR Control

The WMR works on two basic operations: following the current line and changing line if an obstacle is detected. In order to implement this behavior, two different controllers were implemented.

2.4.1. Line-Tracking Control

A PID controller manages the voltage given to the motors in function of the line-tracking sensor.

It receives the result from the line-tracking sensor according to Table 1. It uses a value of 0 as a reference, which means that the central optical sensor detects a black surface.

The PID was chosen due to its simplicity and repeatability. In the considered scenario, in fact, lane keeping was a minimum requirement to validate our approach. However, considering that the straight lane does not require the vehicle to perform an important control action, a basic controller can fit the request, allowing a quick and reliable value to be achieved even without deep tuning of its constants.

In the analyzed scenarios, a trial and error tuning was sufficient to obtain trustworthy values to make the vehicle stay on the track. Nevertheless, suboptimal gains are still suitable for handling this type of control.

This is enforced by the fact that the standard tuning methods (e.g., as explained by Ziegler-Nichols in [20]) require the response of the system to be measured in order to adjust the gains coherently, and this was not possible with the chosen configuration.

2.4.2. Line Change Control

Line change is based on the following discrete time equation of the evolution of the WMR’s direction:

$$\theta (k+1)=\theta \left(k\right)+\frac{\Delta D_R\left(k\right)-\Delta D_L\left(k\right)}{L}$$

(6)

where $\theta$ is the orientation of the WMR, $D_R\left(k\right)$ and $D_L\left(k\right)$ are the distances traveled by the right and left wheels at time k, and L is the distance between the wheels.

The motors mounted on the WMR have some physical constraints that prevent them from applying any desired voltage; in fact, they require a minimum amount of power to work. To turn around this issue, a proportional controller with a bounded output was used. Moreover, the WMR was designed to stop turning automatically if an overshoot over a specific threshold was detected.

3. Case Study

The case study analyzed a three-lane road with fixed obstacles. The vehicle started in the rightmost lane and changed track only when it was obliged to due to the presence of an obstacle in front of itself. It was assumed that at least one lane was free from obstacles for a sufficiently long stretch in order to allow the settling of the vehicle in that lane before moving to avoid a subsequent obstacle in its path.

The aforementioned case study was treated in both a simulated environment and with a real car kit that broadly reproduced the behavior of an unmanned vehicle. Performances were compared to verify the correctness of the theoretical model and the reliability of the physical robot.

3.1. Flowchart Design

For both the simulated and the real tests, a flowchart was designed in order to describe the behavior of the vehicle over time.

Within the flowchart, there are states that require the robot to perform certain actions, such as following the road, while continuously monitoring the environment to detect the presence of in-front obstacles. When this happens, the vehicle has to check whether the other lanes are free and move into one of them. To simplify the flowchart while maintaining a realistic evolution of the scenario, the following assumptions were made:

• When in an external lane, in correspondence of an object, it is assumed that the central lane is free
• When in a central lane, in correspondence of an object, it is assumed that at least one of the external lanes is free; if both are free, preference is given to the rightmost lane

The intensity of the control action to keep the robot on the lane is regulated by a PID controller, taking into account that between a virtual and real case study, there should be minor differences in tuning the gains due to the physical characteristics of the WMR. However, these modifications only influence the derivative part of the controller, as summarized in

Table 2. Values of the PID in the real and virtual simulation.

	Kp	Ki	Kd
Real	65	1	2
Virtual	65	1	0.2

. Other values are possible without compromising the overall objective. However, tests have shown that higher values of the derivative term in the simulated environment cause the robot to stop and oscillate when approaching a lane. On the other hand, the lane-changing maneuver is performed by a high-gain proportional controller paired with a constraint that stops the rotation of the WMR at a predefined angle (about 45°). High gain is needed to accomplish the physical constraints of the WMR, as its motors require a minimum power to overcome the friction and make the robot rotate.

The inputs of the flowchart were measurements retrieved from sensors described in Section 2.3, while the outputs were the pulse width modulation to supply to the motors that command the velocity and the rotation of the robot, together with the heading of the servomotor linked to the ultrasonic sensor.

3.2. Virtual Tests

Tests in the virtual environment were performed on Simulink with built-in toolboxes to simulate the movement of an autonomous robot. Even through the model slightly differed from the actual robot (i.e., it represents a unicycle, thus simplifying some dynamics of the WMR), it is a good approximation to predict the behavior of the autonomous vehicle before deploying the control algorithm on it.

In particular, the Matlab toolbox used was the Mobile Robot Toolbox which contains the Mobile Robotics Training Library and details about the architecture and design of the model, as shown in Equation (1). Sensors were simulated with the help of Simulink blocks that reproduced the main properties of each WMR component. The main difference with respect to the physical device is that the virtual ultrasonic sensor had to have the same heading as the vehicle. Thus when rotating it, the simulation performed a rotation of the whole robot. However, this did not affect the overall performance.

3.3. Real World Environment

To perform tests with a real vehicle, a longitudinal track composed of three lanes, drawn with a black spray can on a long white sheet of paper, was designed. This choice was revealed to be, in place of the use of black tape to draw the road, the best option to reduce friction between the wheels and the floor and increase the reliability of the WMR’s behavior. To represent undesired obstacles, boxes were put on the road with the only rule being to separate them longitudinally by at least half a meter. This procedure facilitated the settling of the vehicle after a change in lane.

The car moved at 40% of its own maximum speed (around 1 m/s), and the critical distance required to detect an obstacle was set at 0.5 m, which was revealed to be a suitable distance for the ultrasonic sensor to operate with high precision and for the vehicle to have enough space to avoid the object fluently.

3.4. Comparison between the Virtual and Real Environments

As already remarked, this work is intended for undergraduate students as the first approach to control system engineering and implementation of control on physical hardware. In particular, the differences between the simulation and real-world experiments can be used to open up a broad discussion, since the physical properties of the environment and hardware have to be included in the defining process of a system model.

The WMR used in this work does not have powerful motors or any low-level controller on the motors’ torque or angular speed. Thus, there is a need to not only define a path-tracking control but also a low-level controller that could output a PWM according to the readings on the wheel encoder. Moreover, physical differences between the WMRs may slightly change the result of the same controller on two different WMRs. In the same way, the friction involved among components and with the floor plays a relevant role in the effectiveness of the control. A WMR turns on the z-axis thanks to the slipping of all four wheels. Not considering the slip or not estimating the amount of it during a turn will introduce inaccuracy and differences between simulation and real-world scenarios.

Students must consider these complications, which are usually not addressed in control courses, as difficulties related to control system engineering.

4. Results

The simulation results were attained with Matlab/Simulink, which was used to simulate the behaviour of the WMR and carry out the appropriate modifications to the system. Through this program, it is possible to understand and even correct inaccuracies that have been introduced through modelization and controller design.

Figure 6 shows the simulation results of the control system in the two scenarios, while in Figure 7, the real-world test is shown. The results obtained with the WMR are represented as a photo sequence of the path route by the WMR itself.

The two scenarios present a three-lane map with obstacles placed on each lane. The positions of the obstacles change the behavior of the WMR. Their spots are defined as follows:

• Scenario 1: Zig-zagging
  • Three obstacles were placed at 0.7, 1.5, and 2.4 m from the starting point in the bottom left corner of the sheet of paper.
    The first and last obstacles were placed in the rightmost lane; meanwhile, the second obstacle was placed in the center lane (Figure 7a). The expected result from this configuration was to have a zig-zag movement starting from the right lane and ending in the center lane.
• Scenario 2: Double left lane change
  • This scenario had four obstacles: the first one was placed at 0.7 m, two were at 1.5 m and the last one was at 2.2 m from the starting point.
    The first obstacle was in the right lane, the second and third obstacles were in the right and center lane, respectively, and the last obstacle was in the left lane (Figure 7b).
    The expected result was a double left lane change due to the presence of obstacles in the other lanes and final repositioning in the center lane.

These two scenarios ensured the replication of every possible maneuver in a three-lane road environment.

In the next sections, the results obtained from one of the many trials of the control system are shown. In general, the test results were good with small differences among them that did not affect the overall behavior.

The efficiency of the control varied according to the initial state of the WMR (position and direction with respect to the right lane) and the friction of the wheels with the paper sheet. The sensitivity to the initial state was due to the precision and efficiency of the hardware, particularly the motors, which require a minimum voltage to operate and therefore a minimum rotation speed.

4.1. Scenario 1

The simulation results show that the WMR is able to perform the zig-zag maneuver, thereby avoiding obstacles. The WMR chose the best direction according to its current lane and the information coming from the ultrasonic sensor. As explained in Section 2.4, the lane change control consisted of a 45° rotation of the WMR towards the target lane. Figure 8a shows the direction of the WMR during the test.

At the beginning of the simulation, the WMR stabilized on the current line. After a few centimeters, it detected the first obstacle, turned 45° to the left and drove straight until it found a black line to follow.

When it was around 1 m on the center lane, it found another obstacle, checked whether there was space to the right of it and decided to turn right. It finally repeated this operation for the last obstacle at 2.4 m and stopped. The movements of the WMR were clean and smooth and it easily navigated through this simulated scenario.

As predicted, the real-world implementation had dynamics that were not considered in the simulation, such as friction. As shown in Figure 7a, the WMR did not turn 45° to the left due to the greater degree of friction, resulting in a longer path being taken to reach the center lane. As a consequence, the WMR detected an obstacle while reaching the target lane, resulting in a turn to the right to change lane again.

It is easy to notice how the behavior changed the second time it turns left. The lower level of friction allowed the WMR to turn more and reduce the traveling time from the left and center lanes, similar to in the simulation.

4.2. Scenario 2

Figure 7b shows the path route of the WMR when two out of three lines were occupied. The simulation result demonstrates the effectiveness of the flowchart-based controller in a more complex scenario with respect to the zig-zag movement. Each lane change was performed in about 30 cm, giving the WMR enough time to stabilize on the new line before detecting another obstacle. Figure 8b indicates the effectiveness of the rotation control and sequence of the movements performed by the WMR during the simulation.

The real-world application presented significant differences to the simulation. In the beginning, the MWR detected the obstacle and turned left, but the amount of friction meant that the WMR turned less than 45 degrees. The distance traveled to switch lanes increased as a consequence, and the WMR detected the obstacle on the center lane when it was still switching lanes. Thus, due to the higher initial friction of the wheels, the WMR started to change lanes and proceeded straight to the third lane while checking if there was space to come back to the right lane. The last obstacle on the left lane was detected even before the WMR had finished switching lanes, so it turned right halfway and stabilized on the center lane.

4.3. Application as Training for Systems Engineering Students

These scenarios were designed in a competition for two different summer schools organized by the University of Genoa for bachelor students in Computer Engineering, supported by the SysE2021 project (2021–2023), “Centre d’excellence transfrontalier pour la formation en ingénierie de systèmes” developed in the framework of the Interreg V-A France-Italie (ALCOTRA) (2014–2020). During these events, the students assembled the minicar for the tests. Consequently, they programmed, deployed, and tested the code in a real scenario. It was a valuable way to provide students with a combination of practical and theoretical lessons that are useful from a pedagogical point of view. Figure 9 presents the brainstorming section completed bye staff during the Summer School SysE2021.

The authors are available to share their code and provide support for this kind of educational activity.

5. Conclusions

In this paper, we demonstrated how to design and implement an event-based controller to handle the displacement of a WMR on a three-lane road with the presence of obstacles.

The case study was analyzed on both a virtual environment, with the help of Matlab/Simulink toolboxes to reproduce the WMR’s behavior as reliably as possible, and on a real scenario by making use of the Freenove 4WD car kit.

The results denote the dissimilarities between the virtual displacement scenario, which was free from uncertainties such as friction and the physical constraints of the vehicle, and the real experiment. In the latter, the WMR behaved well as it was able to broadly imitate the virtual evolution of the system, even though there were non-negligible differences such as the steering angle and line following, which can slightly vary from test to test due to the unreliability of the hardware.

In future work, we aim to improve the WMR equipment in order to acquire data with higher fidelity from both the ultrasonic sensor and the vehicle’s components responsible for its displacement over time. This will increase the complexity of the model but should allow the analysis of more heterogeneous scenarios, even those involving more than one WMR at a time.

Moreover, this kind of activity is suitable for educational purposes, as it was adapted for bachelor students from the SysE2021 Summer School, organized in Imperia in September 2021. On that occasion, students focused only on the use of one sensor at a time, but depending on their level of knowledge, it could cover more difficult problems. Based on feedback, these car kits are likely to be part of the following Summer School planned in September 2022.

This experiment demonstrates the feasibility of analyzing qualitatively complex scenarios using cheap hardware, which opens a world of possibilities for integrating virtual WMR toolboxes with easy-to-assemble robots to instantly verify the correctness of theoretical research.

To enhance future research in this area, the authors are available to provide their own software and assistance.