Analysis of Trajectory Tracking Characteristics of a Magnetically Driven Oil-Free Scroll Compressor
Abstract
:1. Introduction
2. Description of the System
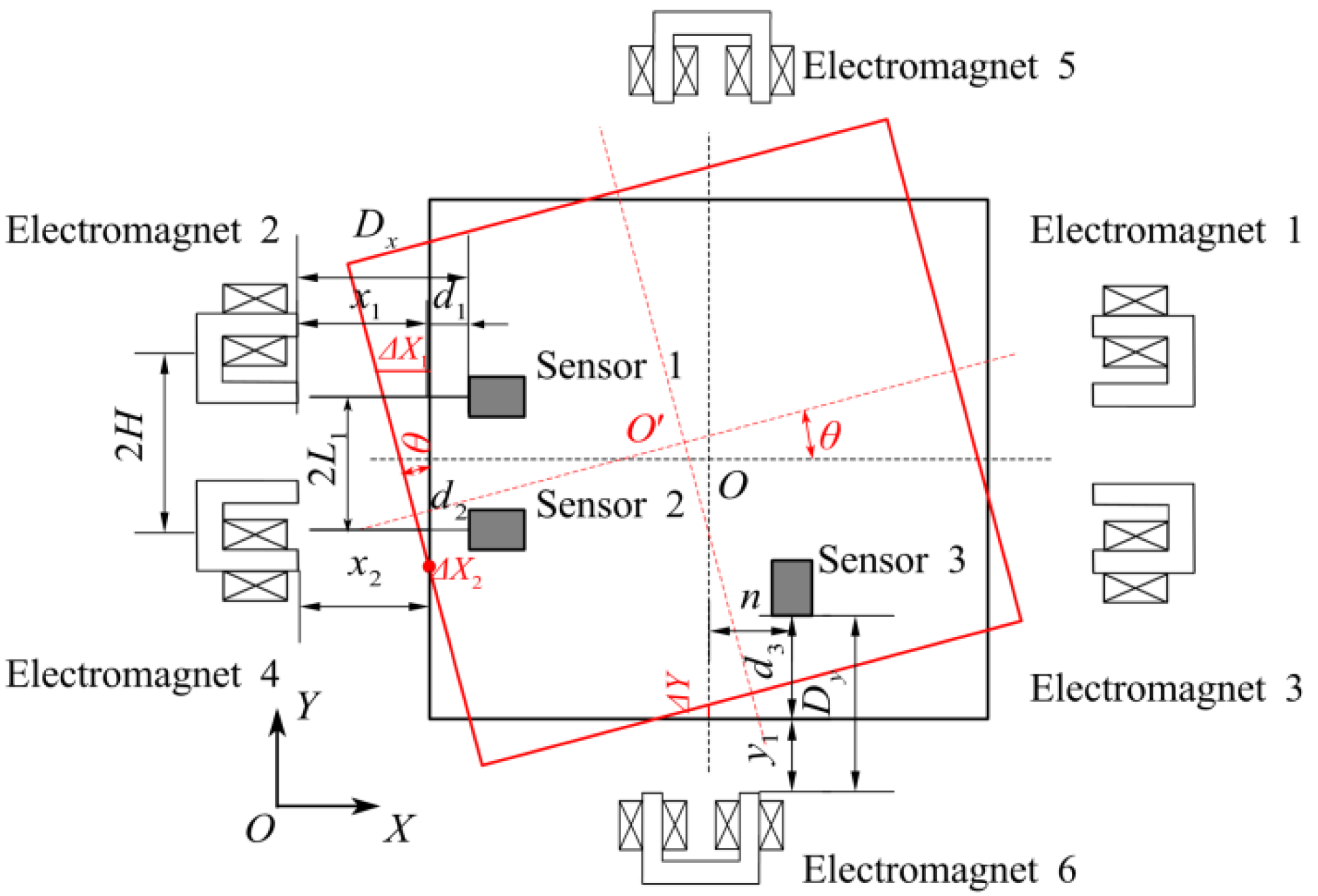
2.1. Structure and Principle
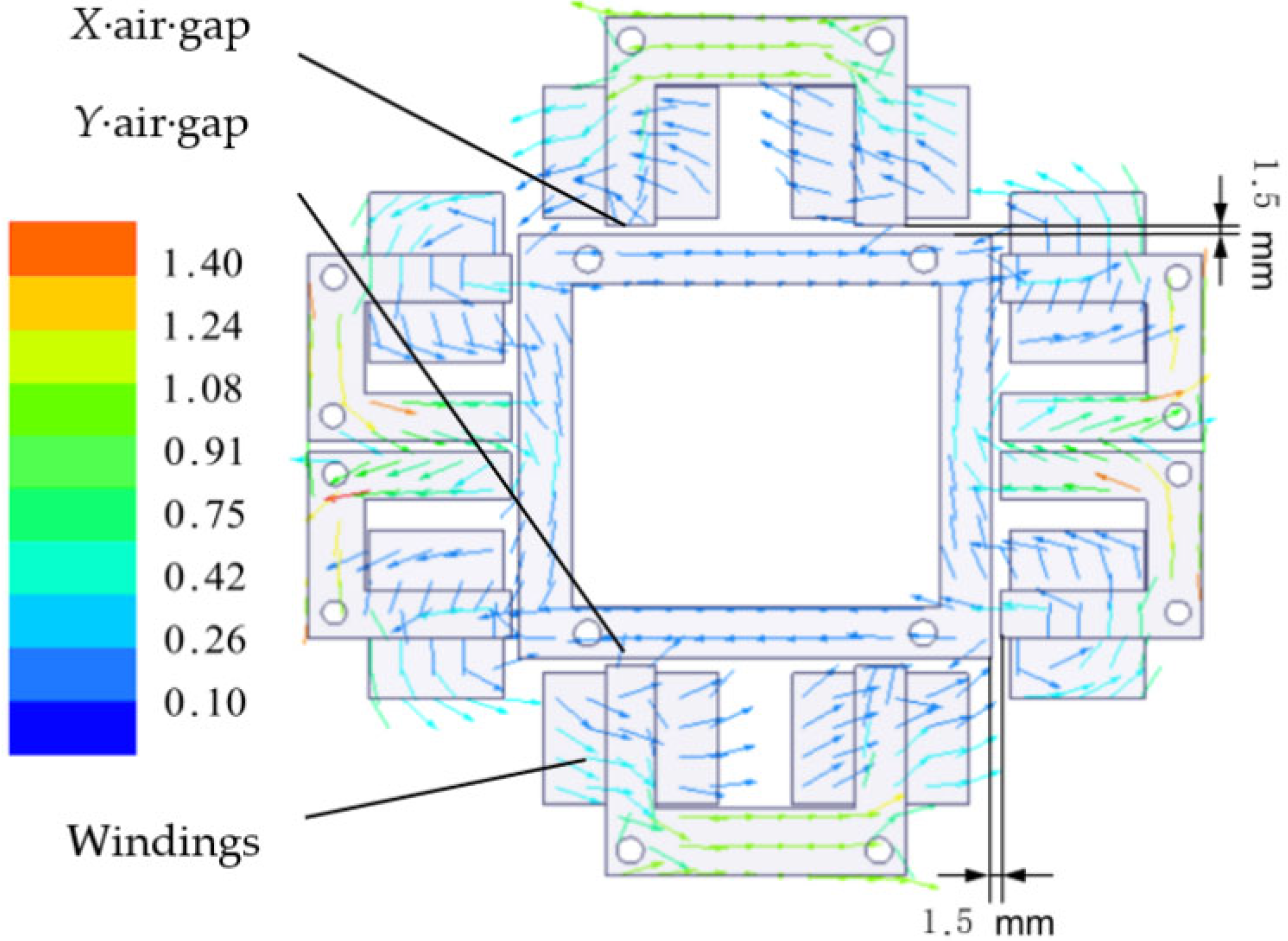
2.2. Magnetic Circuit Analysis
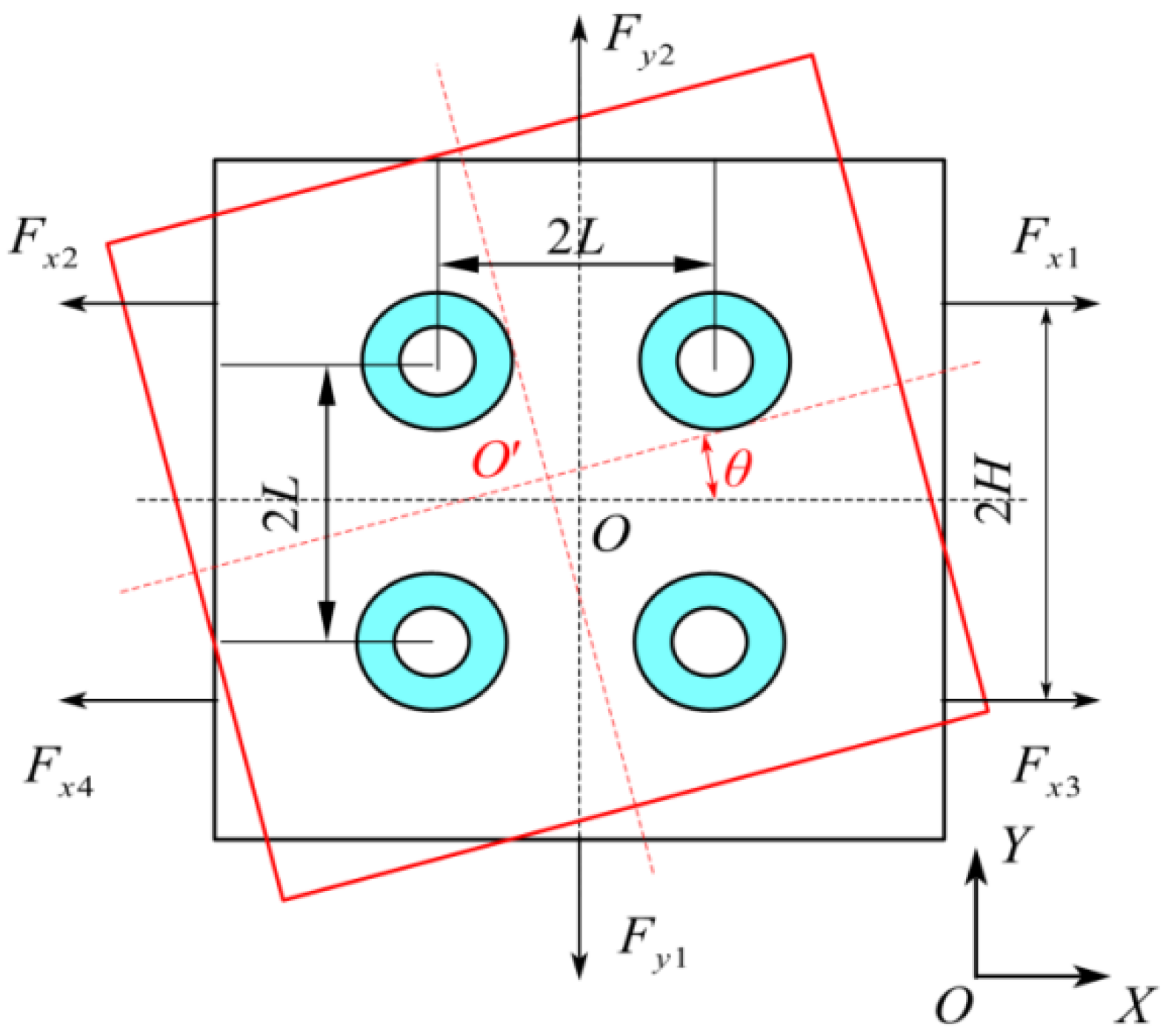
2.3. System Model
3. Controller Design and System Simulation
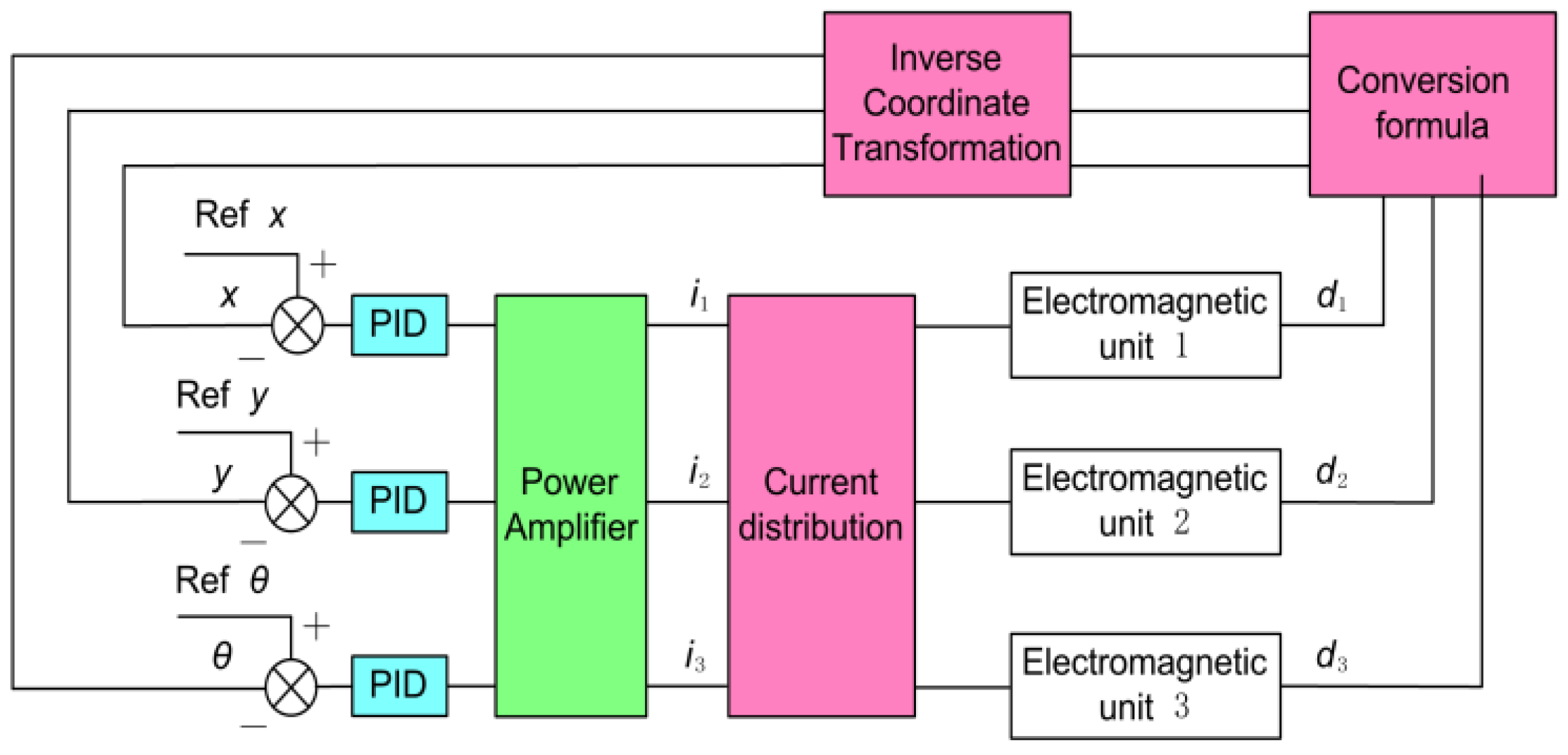
3.1. Motion Controller Design
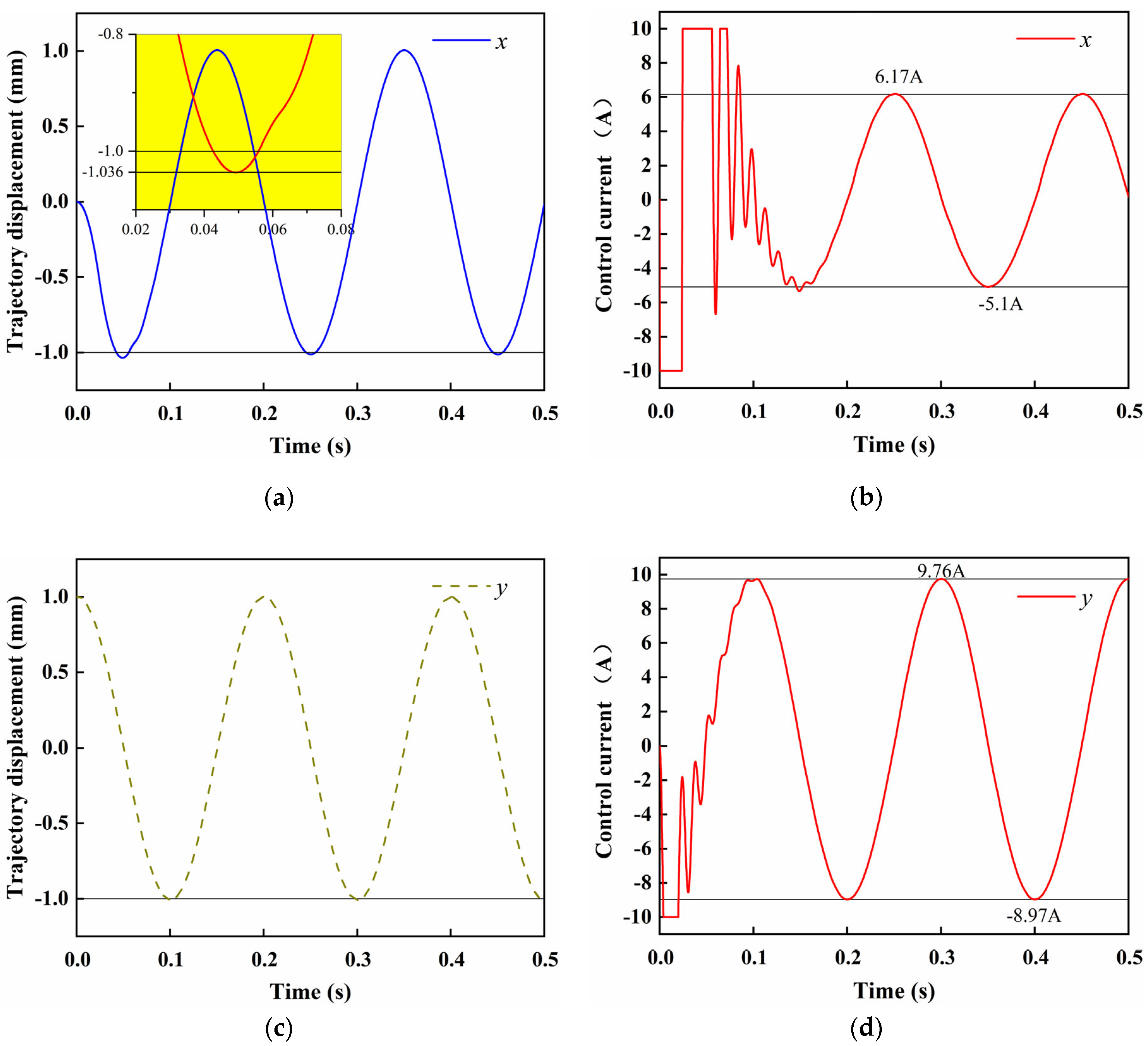
3.2. Control System Simulation
4. Experiment and Analysis
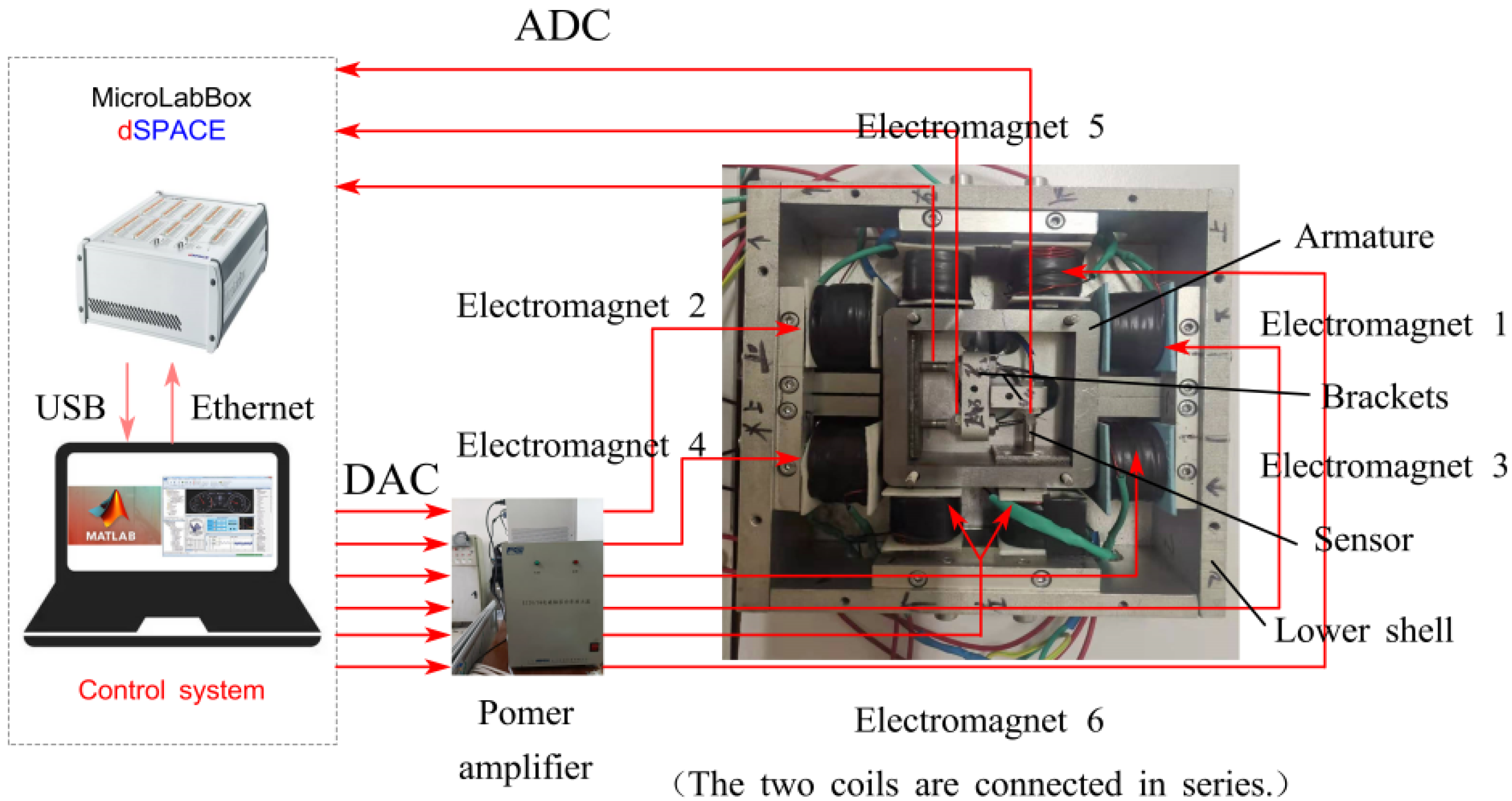
4.1. Experimental System
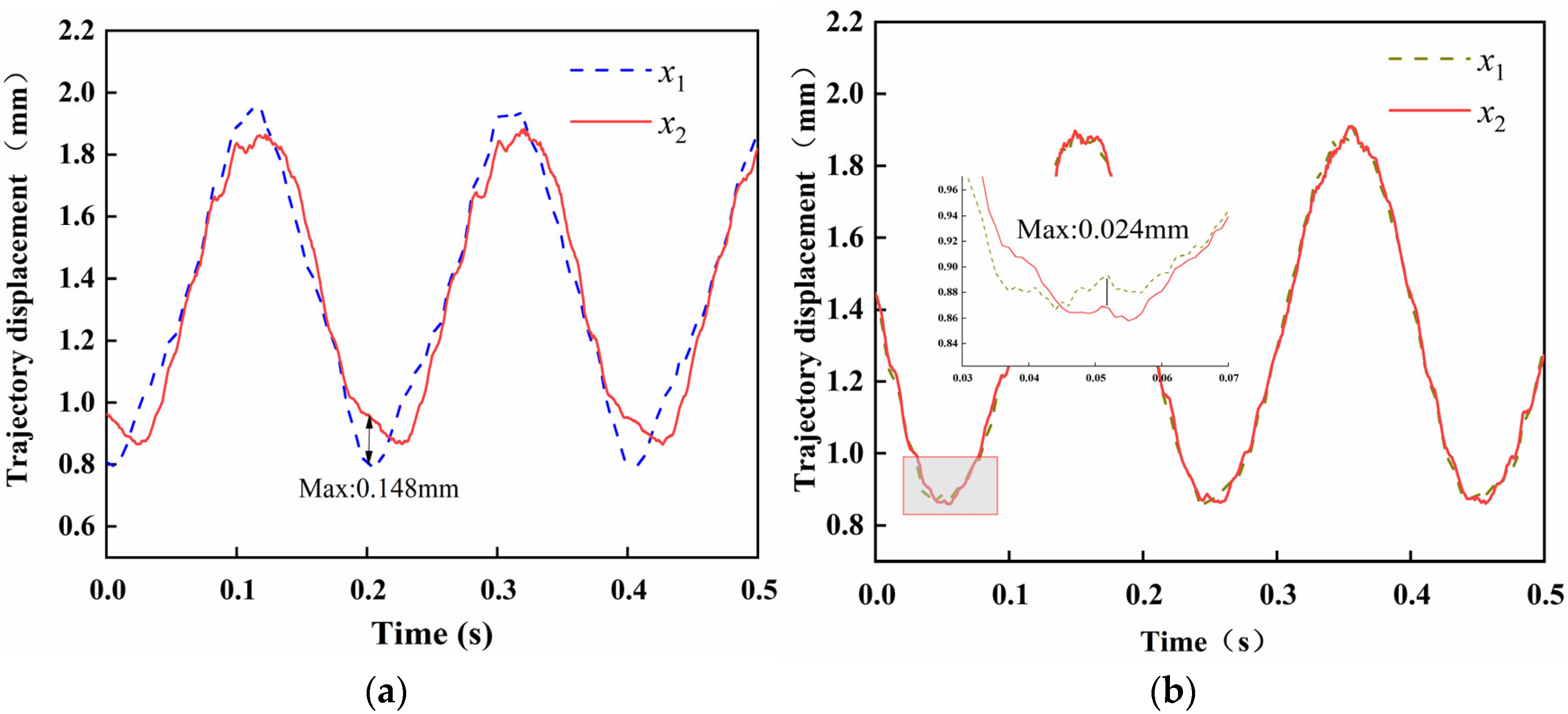
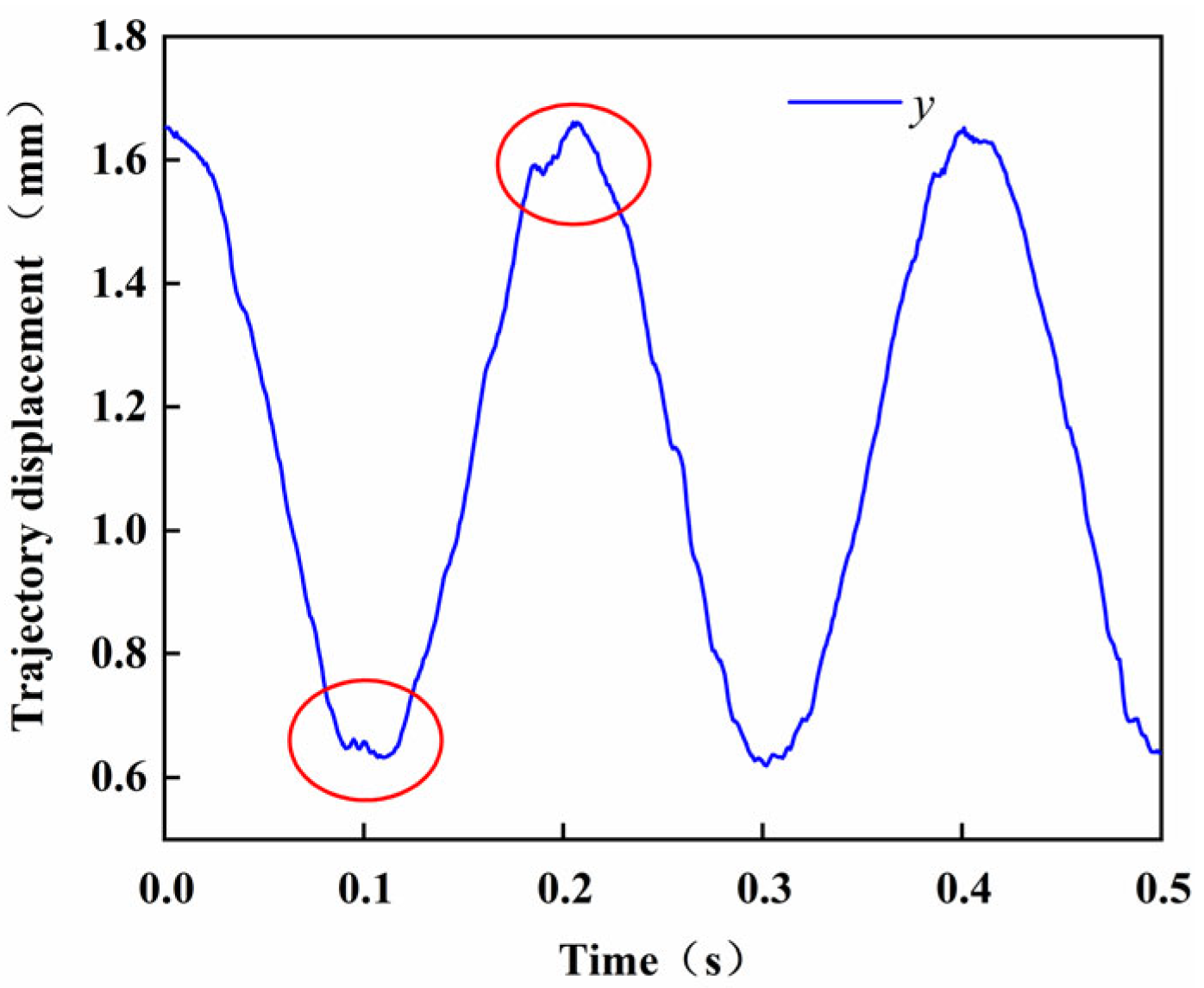
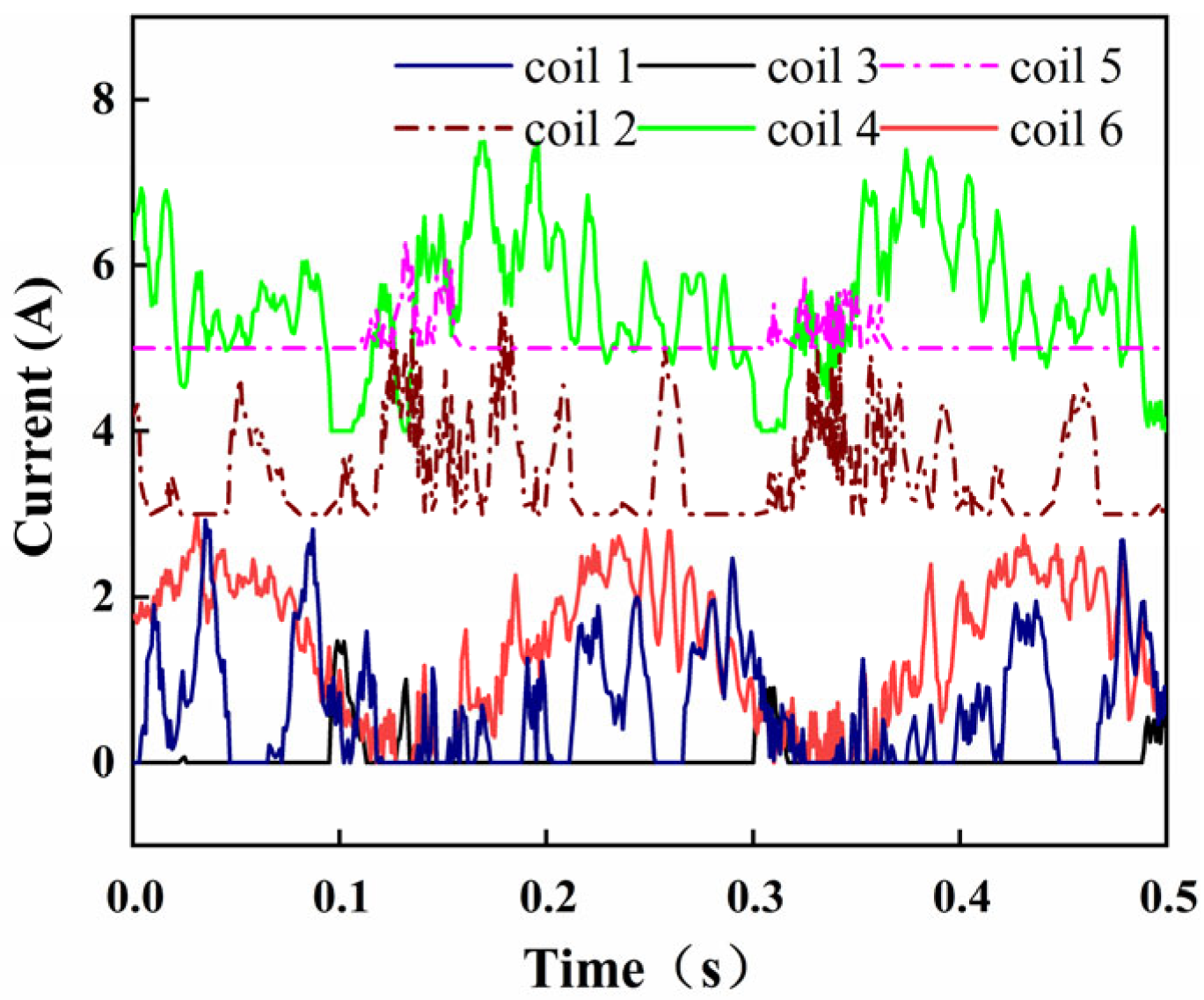
4.2. Experimental Result
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Li, B.R.; Zhang, X.; Yang, G.Y. Numerical simulation of interior flow field for oil-free scroll vacuum pump. Vacuum 2016, 53, 7–10. [Google Scholar]
- Cardone, M.; Gargiulo, B. Numerical Simulation and Experimental Validation of an Oil Free Scroll Compressor. Energies 2020, 13, 5863. [Google Scholar] [CrossRef]
- Li, H.S.; Chen, Y.H.; Wu, K.B.; Zhang, X.W.; Wang, J.S. Structural Design on Tooth Seal of Oil-Free Scroll Compressor. Lubr. Eng. 2015, 40, 13–16. [Google Scholar]
- Shi, C.; Sun, F.; Dou, R.; Ren, H.; Li, Q.; Xu, F.; Zhang, X. Modeling and simulation analysis of oil-free scroll compressor driven by magnetic force. Int. J. Appl. Electromagn. Mech. 2020, 64, 1269–1278. [Google Scholar] [CrossRef]
- Shi, C.; Xu, F.C.; Sun, F. Mechanical Properties of Scroll Compressor with Permanent Magnetic Compliance Mechanism. J. Southwest Jiaotong Univ. 2022, 57, 597–603. [Google Scholar]
- Wang, X.N.; Hu, Y.F.; Wu, H.C.; Dong, R. Research of bearing capacity model of large-air-gap hybrid magnetic bearings. J. Mech. Eng. 2015, 51, 153–160. [Google Scholar] [CrossRef]
- Deng, Z. Research and Development Status of High Temperature Superconducting Magnetic Bearings. Trans. China Electrotech. Soc. 2009, 24, 1–8. [Google Scholar]
- Li, H.; Deng, Z.; Huang, H.; Liao, H.; Yuan, Y.; Zhang, W. Experiments and Simulations of the secondary suspension system to improve the dynamic characteristics of HTS maglev. IEEE Trans. Appl. Supercond. 2021, 31, 1–8. [Google Scholar] [CrossRef]
- Zhu, H.Y.; Teo, D.; Pang, C.K. Magnetically levitated parallel actuated dual-stage (Maglev-PAD) system for six-axis precision positioning. IEEE/ASME Trans. Mechatron. 2019, 24, 1829–1838. [Google Scholar] [CrossRef]
- Zhao, C.; Oka, K.; Sun, F.; Harada, A.; Jin, J.; Zhang, M. Design of Zero-Power Control Strategy with Resisting Tilt of Hybrid Magnetic Levitation System. IEEE Trans. Ind. Electron. 2022, 69, 11. [Google Scholar] [CrossRef]
- Soni, T.; Dutt, J.K.; Das, A.S. Dynamic Behavior and Stability of Energy Efficient Electro-Magnetic Suspension of Rotors Involving Time Delay. Energy 2021, 231, 120906. [Google Scholar] [CrossRef]
- Zhang, X.; Trakarnchaiyo, C.; Zhang, H.; Khamesee, M.B. MagTable: A tabletop system for 6-DOF large range and completely contactless operation using magnetic levitation. Mechatronics 2021, 77, 102600. [Google Scholar] [CrossRef]
- Chao, N.; Feng, L.; Wang, Z.M.; Bao, J.; Hu, J. Graphene levitation and orientation control using a magnetic field. J. Appl. Phys. 2018, 123, 044302. [Google Scholar]
- Han, B.C.; Qin, J.; Yuan, Q. Multi-objective Optimization of a Combined Radial-Axial Magnetic Bearing for Magnetically Suspended Compressor. IEEE Trans. Ind. Electron. 2016, 63, 2284–2293. [Google Scholar] [CrossRef]
- Xu, S.; Sun, J.; Wang, Z. Improved design and analysis of a radial magnetic bearing with paired-pole or alternating-pole configurations. IET Electr. Power Appl. 2022, 16, 382–393. [Google Scholar] [CrossRef]
- Yun, L.; Sun, J.; Han, B. Modeling and design of 3-DOF Magnetic Bearing for High-Speed Motor Including Eddy-Current Effects and Leakage Effects. IEEE Trans. Ind. Electron. 2016, 63, 3656–3665. [Google Scholar]
- Hosseinzadeh, R.; Martin, F.; Hinkkanen, M. A Dynamic Model for Six-Degree-of-Freedom Bearingless Linear Motor Systems. IEEE Trans. Ind. Appl. 2021, 57, 6921–6930. [Google Scholar] [CrossRef]
- Miric, S.; Kuttel, P.; Tuysuz, A.; Kolar, J.W. Design and Experimental Analysis of a New Magnetically Levitated Tubular Linear Actuator. IEEE Trans. Ind. Electron. 2019, 66, 4816–4825. [Google Scholar] [CrossRef]
- Zhao, C.; Sun, F.; Pei, W.Z.; Jin, J.J.; Xu, F.C.; Zhang, X.Y. Independent Cascade Control Method for Permanent Magnetic Levitation Platform. J. Southwest Jiaotong Univ. 2022, 57, 618–626. [Google Scholar]
- Sun, F.; Pei, W.Z.; Jin, J.J.; Zhao, C.; Xu, F.C.; Zhang, M. Research on Floating Control Method for Permanent Magnetic Levitation Platform Using a Variable Flux Path Mechanism. J. Southwest Jiaotong Univ. 2022, 57, 531–539. [Google Scholar]
- Sun, F.; Pei, W.Z.; Zhao, C.; Jin, J.; Xu, F.; Zhang, X. Permanent Maglev Platform Using a Variable Flux Path Mechanism: Stable Levitation and Motion Control. IEEE Trans. Magn. 2022, 58, 7. [Google Scholar] [CrossRef]
- Ke, L.; Yan, G.; Yan, S.; Wang, Z.; Li, X. Optimal Design of Litz Wire Coils With Sandwich Structure Wirelessly Powering an Artificial Anal Sphincter System. Artif. Organs 2015, 39, 615–626. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Z.; Yan, G.; Wang, Z.; Jiang, P.; Hua, F.; Yao, S.; Ding, Z. Design and Evaluation of Puborectalis﹍ike Artificial Anal Sphincter That Replicates Rectal Perception. Artif. Organs 2020, 44, E300–E312. [Google Scholar] [CrossRef] [PubMed]
- Luciani, G.B.; Hoxha, S.; Torre, S.; Rungatscher, A.; Menon, T.; Barozzi, L.; Faggian, G. Improved Outcome of Cardiac Extracorporeal Membrane Oxygenation in Infants and Children Using Magnetic Levitation Centrifugal Pumps. Artif. Organs 2016, 40, 27–33. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, S.; Qin, Y.; Guo, H.; Li, Z.; Li, Y.; Tang, J.; Ma, Z.; Liu, J. 5 nm-scale surface evenness movement measurement method based on the electron spin in diamond. Laser Phys. Lett. 2021, 18, 015202. [Google Scholar] [CrossRef]
- Yuhki, A.; Nogawa, M.; Takatani, S. Development of a compact, sealless, tripod supported, magnetically driven centrifugal blood pump. Artif. Organs 2015, 24, 501–505. [Google Scholar] [CrossRef]
- Forrai, A.; Ueda, T.; Yumura, T. Electromagnetic Actuator Control: A Linear Parameter-Varying (LPV) Approach. IEEE Trans. Ind. Electron. 2007, 54, 1430–1441. [Google Scholar] [CrossRef]
- Haisler, W.L.; Timm, D.M.; Gage, J.A.; Tseng, H.; Killian, T.C.; Souza, G.R. Three-dimensional cell culturing by magnetic levitation. Nat. Protoc. 2013, 8, 1940–1949. [Google Scholar] [CrossRef]
- Parfenov, V.A.; Mironov, V.A.; Koudan, E.V.; Nezhurina, E.K.; Karalkin, P.A.; Pereira, F.D.; Petrov, S.V.; Krokhmal, A.A.; Aydemir, T.; Vakhrushev, I.V.; et al. Fabrication of calcium phosphate 3D scaffolds for bone repair using magnetic levitational assembly. Sci. Rep. 2020, 10, 4013. [Google Scholar] [CrossRef] [Green Version]
- Yaman, S.; Tekin, H.C. Magnetic Susceptibility-Based Protein Detection Using Magnetic Levitation. Anal. Chem. 2020, 92, 12556. [Google Scholar] [CrossRef]



| Description | Parameter | Quantity |
|---|---|---|
| Moment of inertia | J | 0.0015097 kg·m2 |
| Mass of suspended solids | m | 1.7 kg |
| Current stiffness coefficient in the X direction | kix | 150 |
| Displacement stiffness coefficient in the X direction | kdx | −75 |
| Current stiffness coefficient in the Y direction | kiy | 180 |
| Displacement stiffness coefficient in the Y direction | kdy | −57 |
| Magnetic stiffness coefficient of a magnetic ring group | km | 4.544 N/mm |
| Damping of the system | c | 0.015 N/(mm/s) |
| Center distance between two electromagnets in the X direction | H | 19.5 mm |
| Center distance of adjacent magnetic rings | L | 21 mm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, C.; Sun, F.; Xu, F.; Jin, J.; Tong, L.; Zhou, Q.; Oka, K. Analysis of Trajectory Tracking Characteristics of a Magnetically Driven Oil-Free Scroll Compressor. Actuators 2022, 11, 312. https://doi.org/10.3390/act11110312
Shi C, Sun F, Xu F, Jin J, Tong L, Zhou Q, Oka K. Analysis of Trajectory Tracking Characteristics of a Magnetically Driven Oil-Free Scroll Compressor. Actuators. 2022; 11(11):312. https://doi.org/10.3390/act11110312
Chicago/Turabian StyleShi, Ce, Feng Sun, Fangchao Xu, Junjie Jin, Ling Tong, Qing Zhou, and Koichi Oka. 2022. "Analysis of Trajectory Tracking Characteristics of a Magnetically Driven Oil-Free Scroll Compressor" Actuators 11, no. 11: 312. https://doi.org/10.3390/act11110312
APA StyleShi, C., Sun, F., Xu, F., Jin, J., Tong, L., Zhou, Q., & Oka, K. (2022). Analysis of Trajectory Tracking Characteristics of a Magnetically Driven Oil-Free Scroll Compressor. Actuators, 11(11), 312. https://doi.org/10.3390/act11110312







