Selection for Plastic, Pathogen-Inducible Recombination in a Red Queen Model with Diploid Antagonists
Abstract
:1. Introduction
2. Model and Methods
2.1. Life Cycles
2.2. Species Interaction
2.3. Recombination Strategies
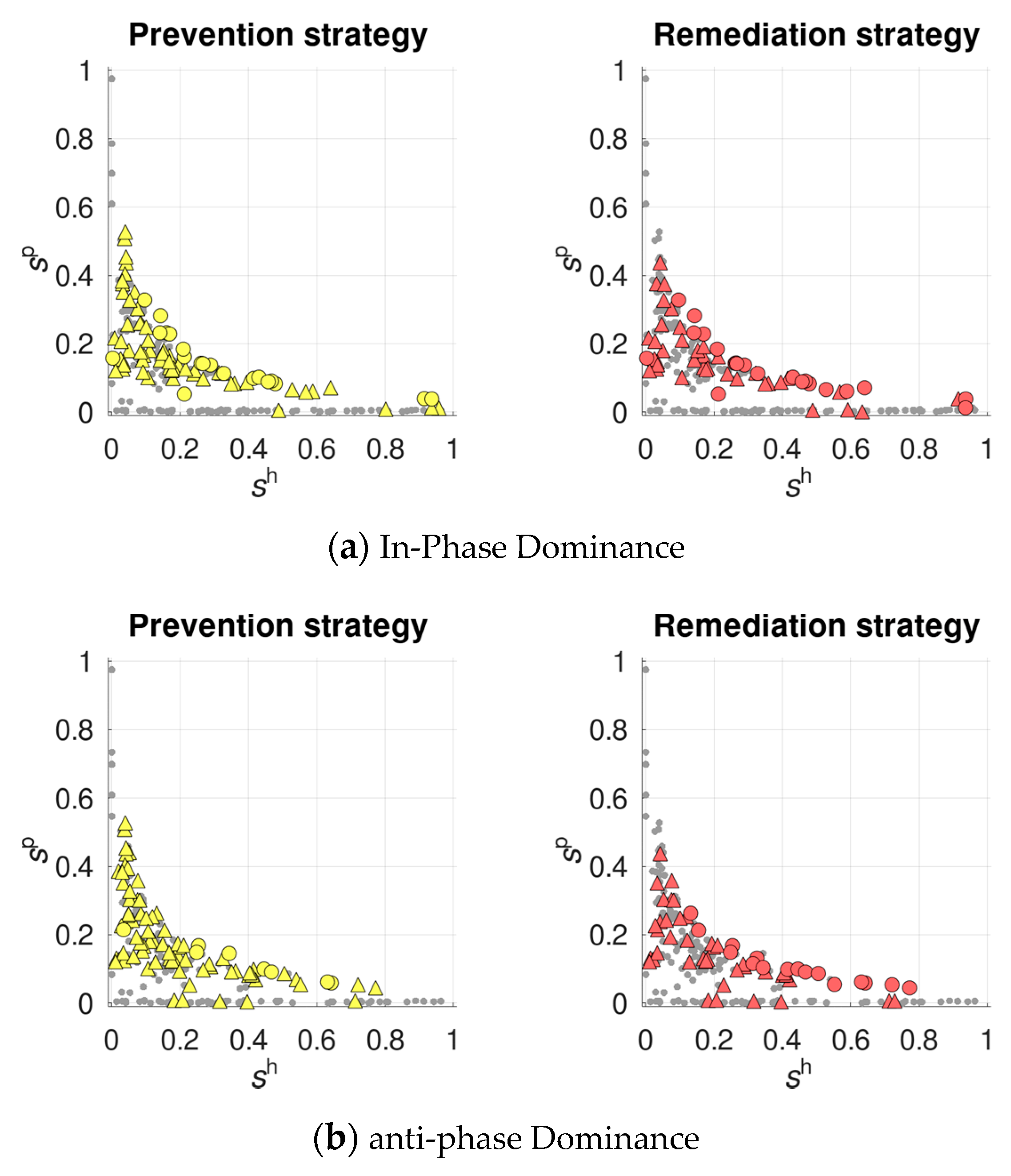
- prevention strategy—with recombination sensitive to the potential infection risk, so that recombination rate of each host class increases proportionally to the frequency of the dangerous (exactly for this class) parasite class:
- remediation strategy—with recombination sensitive to the actual infection status, so that the infected hosts display an increased recombination rate () compared to their resistant counterparts ():
2.4. Experimental Design
3. Results
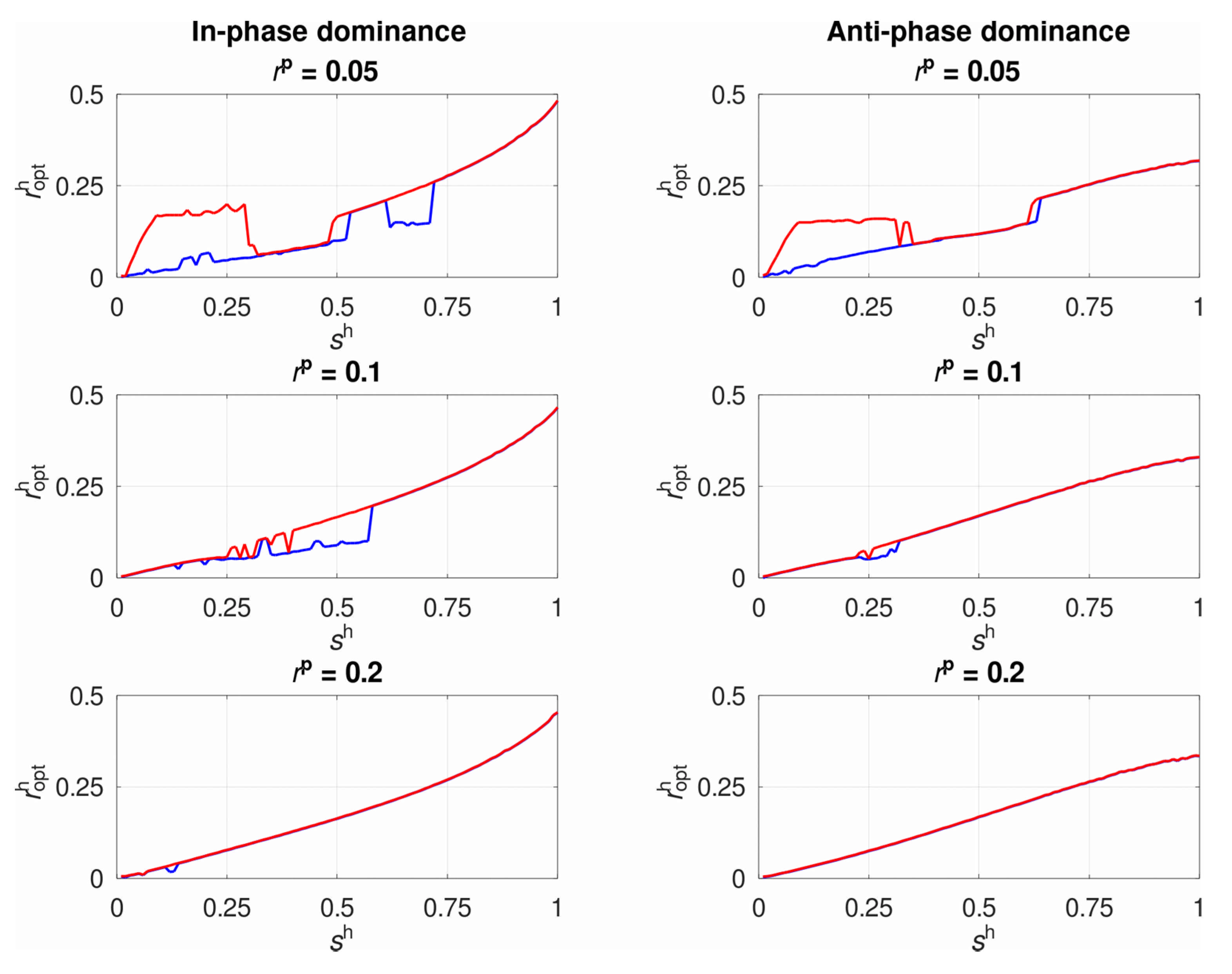
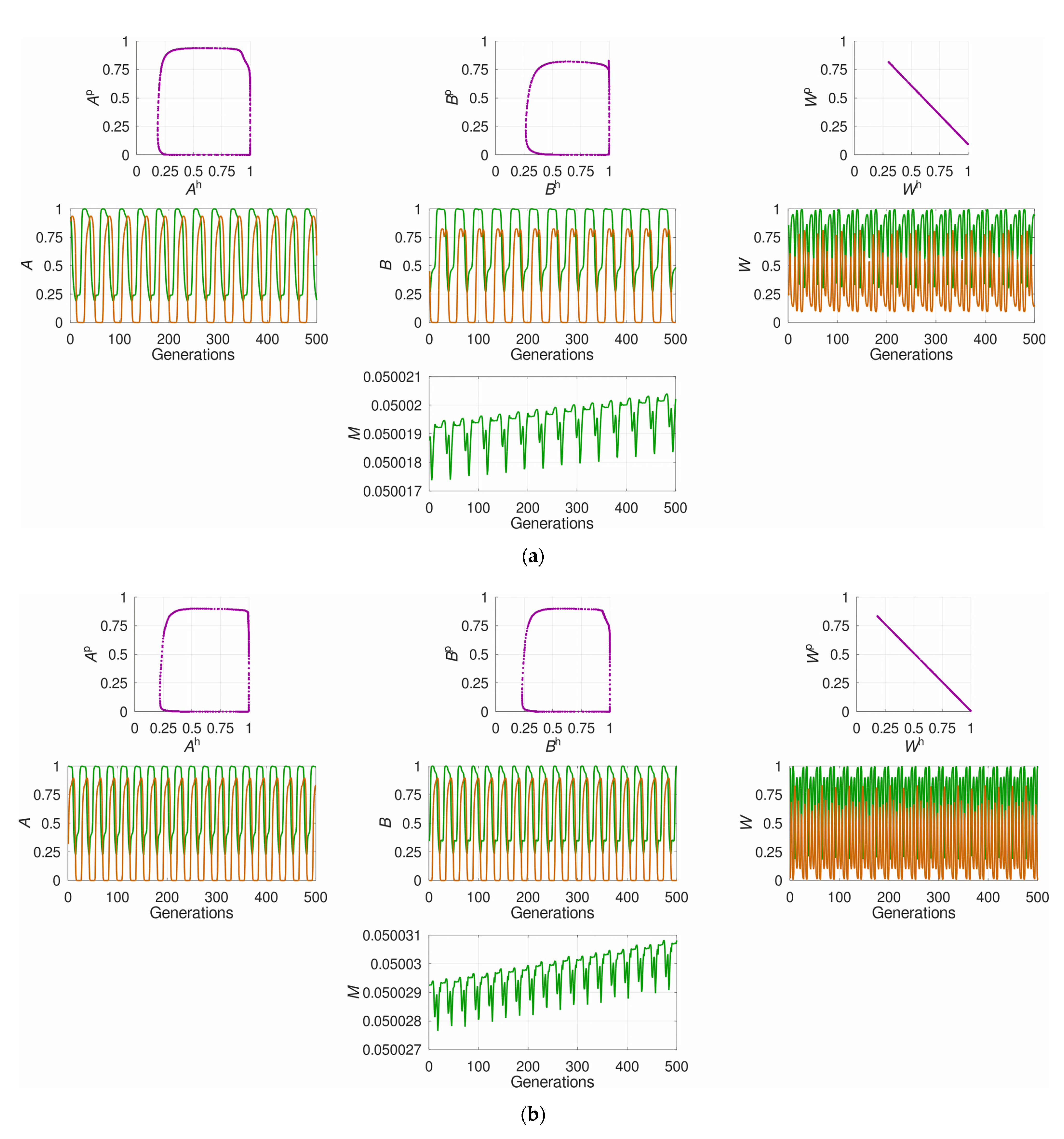
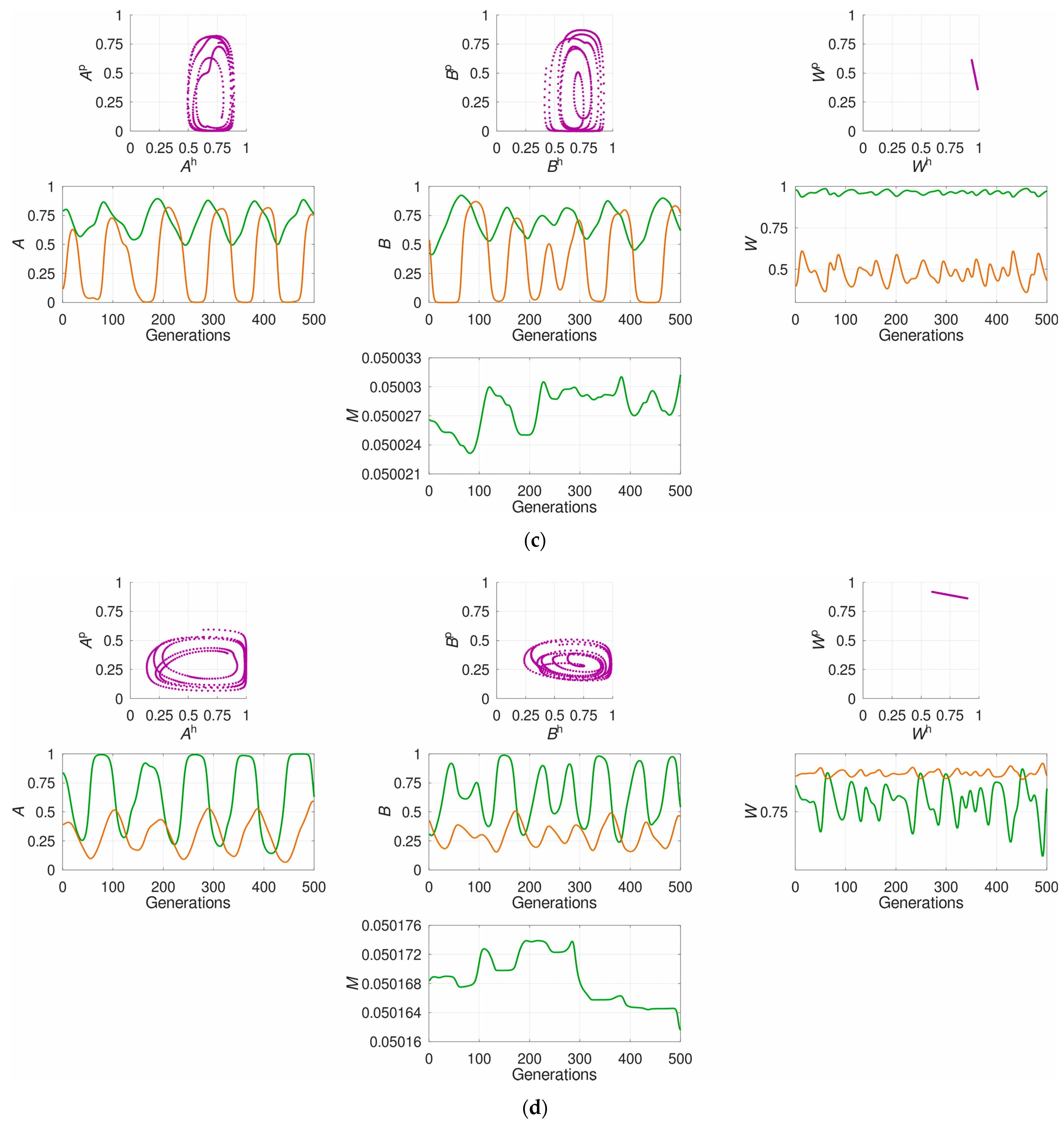
3.1. The System’s Dynamics and the Optimal Constant Recombination in the Host
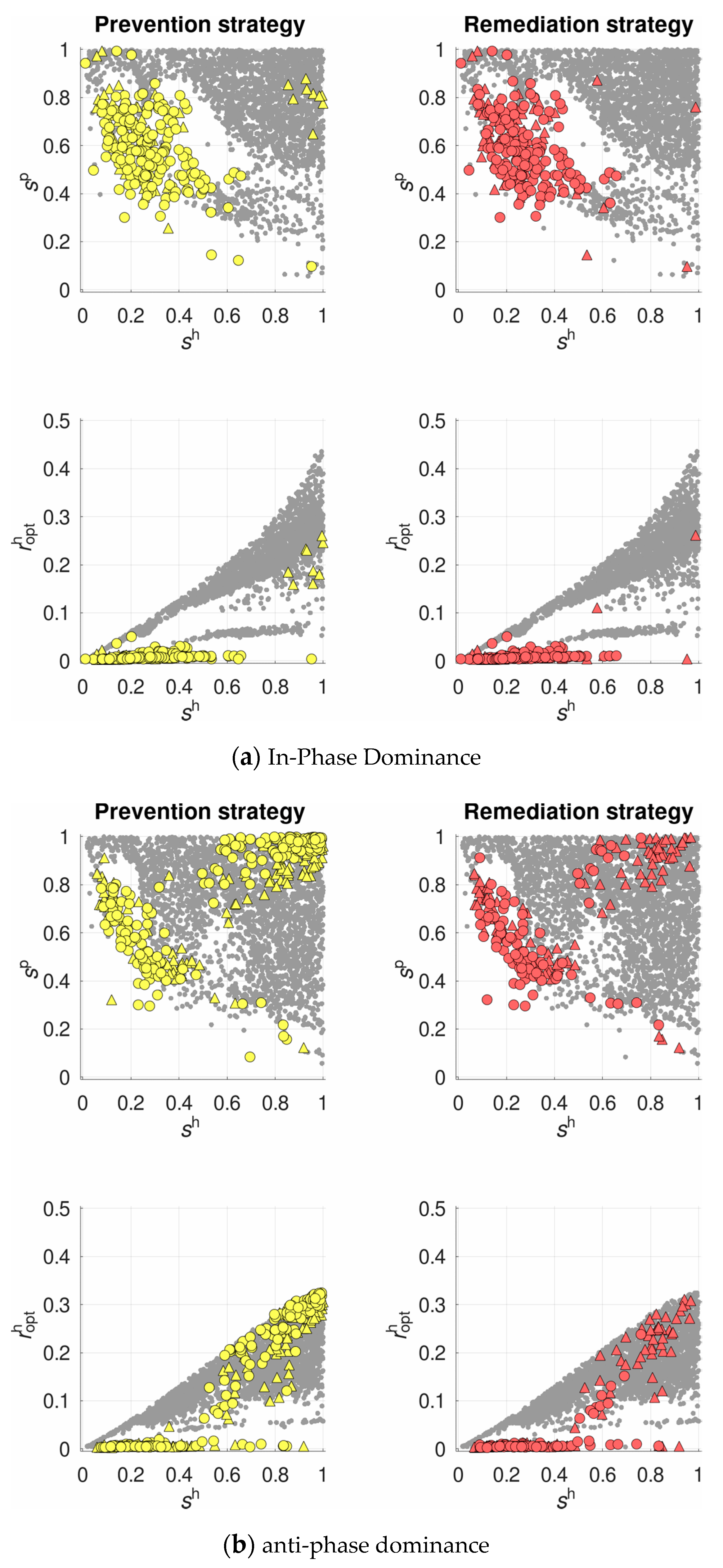
3.2. Selection for Plastic Recombination in the Host
4. Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability
Acknowledgments
Conflicts of Interest
References
- Lotka, A.J. Analytical Note on Certain Rhythmic Relations in Organic Systems. Proc. Natl. Acad. Sci. USA 1920, 6, 410–415. [Google Scholar] [CrossRef]
- Volterra, V. Fluctuations in the Abundance of a Species considered Mathematically1. Nat. Cell Biol. 1926, 118, 558–560. [Google Scholar] [CrossRef]
- De Bach, P.; Smith, H.S. Are population oscillations inherent in the host-parasite relation? Ecology 1941, 22, 363–369. [Google Scholar] [CrossRef]
- Stiven, A.E. Experimental Studies on the Epidemiology of the Host Parasite System, Hydra and Hydramoeba hydroxena (Entz). II. The Components of a Simple Epidemic. Ecol. Monogr. 1964, 34, 119–142. [Google Scholar] [CrossRef]
- Van den Bosch, R.; Schlinger, E.I.; Lagace, C.F.; Hall, J.C. Parasitization of Acyrthosiphon pisum by Aphidius smithi, a density-dependent process in nature (Homoptera: Aphidae) (Hymenoptera: Aphidiidae). Ecology 1966, 47, 1049–1055. [Google Scholar] [CrossRef]
- Haldane, J.B.S. Disease and Evolution. In Malaria: Genetic and Evolutionary Aspects; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Van Valen, L. A new evolutionary law. Evol. Theor. 1973, 1, 1–30. [Google Scholar]
- Bell, G. The Masterpiece of Nature: The Evolution and Genetics of Sexuality; University of California Press: Berkeley, CA, USA, 1982. [Google Scholar]
- Decaestecker, E.; Gaba, S.; Raeymaekers, J.A.M.; Stoks, R.; Van Kerckhoven, L.; Ebert, D.; De Meester, L. Host-parasite ‘Rd Queen’ dynamics archived in pond sediment. Nature 2007, 450, 870–873. [Google Scholar] [CrossRef]
- Ebert, D. Host–parasite coevolution: Insights from the Daphnia–parasite model system. Curr. Opin. Microbiol. 2008, 11, 290–301. [Google Scholar] [CrossRef]
- Dybdahl, M.F.; Lively, C.M. Host-parasite coevolution: Evidence for rare advantage and time-lagged selection in a natural population. Evolution 1998, 52, 1057–1066. [Google Scholar] [CrossRef] [PubMed]
- Koskella, B.; Lively, C.M. Evidence for negative frequency-dependent selection during experimental coevolution of a freshwater snail and a sterilizing trematode. Evolution 2009, 63, 2213–2221. [Google Scholar] [CrossRef]
- Wolinska, J.; Spaak, P. The cost of being common: Evidence from natural daphnia populations. Evolution 2009, 63, 1893–1901. [Google Scholar] [CrossRef] [PubMed]
- Lively, C.M. A Review of Red Queen Models for the Persistence of Obligate Sexual Reproduction. J. Hered. 2010, 101, S13–S20. [Google Scholar] [CrossRef]
- Hamilton, W.D. Sex versus Non-Sex versus Parasite. Oikos 1980, 35, 282. [Google Scholar] [CrossRef]
- May, R.M.; Anderson, R. Epidemiology and genetics in the coevolution of parasites and hosts. Proc. R. Soc. London. Ser. B Boil. Sci. 1983, 219, 281–313. [Google Scholar] [CrossRef]
- Hamilton, W.D.; Axelrod, R.; Tanese, R. Sexual reproduction as an adaptation to resist parasites (a review). Proc. Natl. Acad. Sci. USA 1990, 87, 3566–3573. [Google Scholar] [CrossRef]
- Agrawal, A.F.; Lively, C.M. Infection genetics: Gene-for-gene versus matching-alleles models and all points in between. Evol. Ecol. Res. 2002, 4, 79–90. [Google Scholar]
- Otto, S.P.; Nuismer, S.L. Species interactions and the evolution of sex. Science 2004, 304, 1018–1020. [Google Scholar] [CrossRef]
- Engelstädter, J.; Bonhoeffer, S. Red Queen Dynamics with Non-Standard Fitness Interactions. PLoS Comput. Biol. 2009, 5, e1000469. [Google Scholar] [CrossRef]
- Salathé, M.; Kouyos, R.D.; Bonhoeffer, S. The state of affairs in the kingdom of the Red Queen. Trends Ecol. Evol. 2008, 23, 439–445. [Google Scholar] [CrossRef]
- Lively, C.M. Coevolutionary Epidemiology: Disease Spread, Local Adaptation, and Sex. Am. Nat. 2016, 187, E77–E82. [Google Scholar] [CrossRef]
- Lively, C.M. Evidence from a New Zealand snail for the maintenance of sex by parasitism. Nat. Cell Biol. 1987, 328, 519–521. [Google Scholar] [CrossRef]
- Lively, C.M.; Craddock, C.; Vrijenhoek, R.C. Red Queen hypothesis supported by parasitism in sexual and clonal fish. Nat. Cell Biol. 1990, 344, 864–866. [Google Scholar] [CrossRef]
- Busch, J.W.; Neiman, M.; Koslow, J.M. Evidence for maintenance of sex by pathogens in plants. Evolution 2004, 58, 2584. [Google Scholar] [CrossRef]
- Kumpulainen, T.; Grapputo, A.; Mappes, J. Parasites and sexual reproduction in psychid moths. Evolution 2004, 58, 1511–1520. [Google Scholar] [CrossRef] [PubMed]
- Jokela, J.; Dybdahl, M.F.; Lively, C.M. The Maintenance of Sex, Clonal Dynamics, and Host-Parasite Coevolution in a Mixed Population of Sexual and Asexual Snails. Am. Nat. 2009, 174, S43–S53. [Google Scholar] [CrossRef]
- Vergara, D.; Jokela, J.; Lively, C.M. Data from: Infection dynamics in coexisting sexual and asexual host populations: Support for the Red Queen hypothesis. Am. Nat. 2017, 184, 22–30. [Google Scholar] [CrossRef]
- Koch, H.R.; Wagner, S.; Becks, L. Antagonistic species interaction drives selection for sex in a predator–prey system. J. Evol. Biol. 2020, 33, 1180–1191. [Google Scholar] [CrossRef] [PubMed]
- Fischer, O.; Schmid-Hempel, P. Selection by parasites may increase host recombination frequency. Biol. Lett. 2005, 1, 193–195. [Google Scholar] [CrossRef]
- Kerstes, N.A.G.; Bérénos, C.; Schmid-Hempel, P.; Wegner, K.M. Antagonistic experimental coevolution with a parasite increases host recombination frequency. BMC Evol. Biol. 2012, 12, 18. [Google Scholar] [CrossRef] [PubMed]
- Plough, H.H. The effect of temperature on crossingover in Drosophila. J. Exp. Zool. 1917, 24, 147–209. [Google Scholar] [CrossRef]
- Plough, H.H. Further studies on the effect of temperature on crossing over. J. Exp. Zool. 1921, 32, 187–202. [Google Scholar] [CrossRef]
- Bomblies, K.; Higgins, J.; Yant, L. Meiosis evolves: Adaptation to external and internal environments. New Phytol. 2015, 208, 306–323. [Google Scholar] [CrossRef]
- Modliszewski, J.L.; Copenhaver, G. Meiotic recombination gets stressed out: CO frequency is plastic under pressure. Curr. Opin. Plant Biol. 2017, 36, 95–102. [Google Scholar] [CrossRef] [PubMed]
- Kathiria, P.; Sidler, C.; Golubov, A.; Kalischuk, M.; Kawchuk, L.; Kovalchuk, I. Tobacco Mosaic Virus Infection Results in an Increase in Recombination Frequency and Resistance to Viral, Bacterial, and Fungal Pathogens in the Progeny of Infected Tobacco Plants. Plant Physiol. 2010, 153, 1859–1870. [Google Scholar] [CrossRef]
- Singh, N.D.; Criscoe, D.R.; Skolfield, S.; Kohl, K.P.; Keebaugh, E.S.; Schlenke, T.A. Data from: Fruit flies diversify their offspring in response to parasite infection. Science 2016, 349, 747–750. [Google Scholar] [CrossRef]
- Zilio, G.; Moesch, L.; Bovet, N.; Sarr, A.; Koella, J.C. The effect of parasite infection on the recombination rate of the mosquito Aedes aegypti. PLoS ONE 2018, 13, e0203481. [Google Scholar] [CrossRef]
- Singh, N.D. Wolbachia Infection Associated with Increased Recombination in Drosophila. G3 Genes Genomes Genet. 2019, 9, 229–237. [Google Scholar] [CrossRef]
- Zhuchenko, A.A.; Korol, A.B.; Preigel, I.A.; Bronstein, S.I. The evolutionary role of the dependence of recombination on environment: Two and three loci models. Theor. Appl. Genet. 1985, 69, 617–624. [Google Scholar] [CrossRef]
- Rybnikov, S.R.; Frenkel, Z.M.; Korol, A.B. What drives the evolution of condition-dependent recombination in diploids? Some insights from simulation modelling. Philos. Trans. R. Soc. B Biol. Sci. 2017, 372, 20160460. [Google Scholar] [CrossRef]
- Otto, S.P. The Advantages of Segregation and the Evolution of Sex. Genetics 2003, 164, 1099–1118. [Google Scholar] [CrossRef] [PubMed]
- Agrawal, A.F. Differences between selection on sex versus recombination in red queen models with diploid hosts. Evolution 2009, 63, 2131–2141. [Google Scholar] [CrossRef] [PubMed]
- Mostowy, R.; Engelstädter, J. Host-parasite coevolution induces selection for condition-dependent sex. J. Evol. Biol. 2012, 25, 2033–2046. [Google Scholar] [CrossRef]
- Kimura, M. A model of a genetic system which leads to closer linkage by natural selection. Evolution 1956, 10, 278–287. [Google Scholar] [CrossRef]
- Nei, M. Modification of linkage intensity by natural selection. Genetics 1967, 57, 625–641. [Google Scholar] [CrossRef]
- Jeffreys, A.J.; Kauppi, L.; Neumann, R. Intensely punctate meiotic recombination in the class II region of the major histocompatibility complex. Nat. Genet. 2001, 29, 217–222. [Google Scholar] [CrossRef]
- Wegner, K.M. Clustering of Drosophila melanogaster Immune Genes in Interplay with Recombination Rate. PLoS ONE 2008, 3, e2835. [Google Scholar] [CrossRef]
- Choi, K.; Reinhard, C.; Serra, H.; Ziolkowski, P.A.; Underwood, C.J.; Zhao, X.; Hardcastle, T.J.; Yelina, N.E.; Griffin, C.; Jackson, M.; et al. Recombination rate heterogeneity within Arabidopsis disease resistance genes. PLoS Genet. 2016, 12, e1006179. [Google Scholar] [CrossRef]
- Dong, S.; Raffaele, S.; Kamoun, S. The two-speed genomes of filamentous pathogens: Waltz with plants. Curr. Opin. Genet. Dev. 2015, 35, 57–65. [Google Scholar] [CrossRef]
- Dumont, B.L.; Devlin, A.A.; Truempy, D.M.; Miller, J.C.; Singh, N.D. No Evidence that Infection Alters Global Recombination Rate in House Mice. PLoS ONE 2015, 10, e0142266. [Google Scholar] [CrossRef]
- Gratias, A.; Geffroy, V. Deciphering the Impact of a Bacterial Infection on Meiotic Recombination in Arabidopsis with Fluorescence Tagged Lines. Genes 2020, 11, 832. [Google Scholar] [CrossRef]
- Holsinger, K.; Feldman, M.W. Linkage modification with mixed random mating and selfing: A numerical study. Genetics 1983, 103, 323–333. [Google Scholar] [CrossRef]
- Sasaki, A.; Iwasa, Y. Optimal Recombination Rate in Fluctuating Environments. Genetics 1987, 115, 377–388. [Google Scholar] [CrossRef]
- Hadany, L.; Beker, T. On the Evolutionary Advantage of Fitness-Associated Recombination. Genetics 2003, 165, 2167–2179. [Google Scholar] [CrossRef]
- Agrawal, A.F.; Hadany, L.; Otto, S. The Evolution of Plastic Recombination. Genetics 2005, 171, 803–812. [Google Scholar] [CrossRef]
- Korol, A.B.; Preigel, S.I. Host-parasite interaction as a factor of evolution of genetic recombination. Genetika 1988, 24, 1113–1120. (In Russian) [Google Scholar]
- Preigel, S.I.; Korol, A.B. Evolution of recombination in systems of ‘host-parasite’ type: Multilocus models. Genetika 1990, 26, 349–358. (In Russian) [Google Scholar]
- Agrawal, A.F. Similarity Selection and the Evolution of Sex: Revisiting the Red Queen. PLoS Biol. 2006, 4, e265. [Google Scholar] [CrossRef]
- Hodgson, E.E.; Otto, S.P. The red queen coupled with directional selection favours the evolution of sex. J. Evol. Biol. 2012, 25, 797–802. [Google Scholar] [CrossRef]
- Frenkel, V.; Ronin, Y.; Korol, A. The dynamics of the rec-system in variable environments: Haploid selection in a cyclical two-state environment. Theor. Popul. Biol. 2006, 70, 111–124. [Google Scholar] [CrossRef]
- Rybnikov, S.; Frenkel, Z.; Korol, A.B. The evolutionary advantage of fitness-dependent recombination in diploids: A deterministic mutation–selection balance model. Ecol. Evol. 2020, 10, 2074–2084. [Google Scholar] [CrossRef]
- Rybnikov, S.; Weissman, D.B.; Hübner, S.; Korol, A.B. Fitness dependence preserves selection for recombination across diverse mixed mating systems. bioRxiv 2020, 318238. [Google Scholar] [CrossRef]

| Parasite Genotype | Host Genotype | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| In-Phase Dominance () | |||||||||
| I | R | R | R | R | R | R | R | R | |
| R | I | I | R | R | R | R | R | R | |
| R | I | I | R | R | R | R | R | R | |
| R | R | R | I | R | R | I | R | R | |
| R | R | R | R | I | I | R | I | I | |
| R | R | R | R | I | I | R | I | I | |
| R | R | R | I | R | R | I | R | R | |
| R | R | R | R | I | I | R | I | I | |
| R | R | R | R | I | I | R | I | I | |
| Anti-Phase Dominance () | |||||||||
| I | I | R | I | I | R | R | R | R | |
| R | R | I | R | R | I | R | R | R | |
| R | R | I | R | R | I | R | R | R | |
| R | R | R | R | R | R | I | I | R | |
| R | R | R | R | R | R | R | R | I | |
| R | R | R | R | R | R | R | R | I | |
| R | R | R | R | R | R | I | I | R | |
| R | R | R | R | R | R | R | R | I | |
| R | R | R | R | R | R | R | R | I | |
| Parameters/Combinations | In-Phase Dominance (n = 2856) | Anti-Phase Dominance (n = 3307) | ||||
|---|---|---|---|---|---|---|
| Model A | Model B | Model C | Model A | Model B | Model C | |
| Selection Intensity in the Host () | 0.787 | - | 0.137 | 0.810 | - | 0.238 |
| Selection Intensity in the Parasite () | 0.425 | - | −0.040 | 0.479 | - | 0.029 |
| Recombination Rate in the Parasite () | 0.023 | 0.022 | 0.037 | 0.032 | 0.040 | 0.049 |
| Overall Selection Intensity () | - | 0.974 | 0.889 | - | 0.970 | 0.775 |
| R2-Adjusted | 0.891 | 0.949 | 0.961 | 0.901 | 0.942 | 0.962 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rybnikov, S.; Frenkel, Z.; Korol, A.B.; Fahima, T. Selection for Plastic, Pathogen-Inducible Recombination in a Red Queen Model with Diploid Antagonists. Pathogens 2021, 10, 898. https://doi.org/10.3390/pathogens10070898
Rybnikov S, Frenkel Z, Korol AB, Fahima T. Selection for Plastic, Pathogen-Inducible Recombination in a Red Queen Model with Diploid Antagonists. Pathogens. 2021; 10(7):898. https://doi.org/10.3390/pathogens10070898
Chicago/Turabian StyleRybnikov, Sviatoslav, Zeev Frenkel, Abraham B. Korol, and Tzion Fahima. 2021. "Selection for Plastic, Pathogen-Inducible Recombination in a Red Queen Model with Diploid Antagonists" Pathogens 10, no. 7: 898. https://doi.org/10.3390/pathogens10070898
APA StyleRybnikov, S., Frenkel, Z., Korol, A. B., & Fahima, T. (2021). Selection for Plastic, Pathogen-Inducible Recombination in a Red Queen Model with Diploid Antagonists. Pathogens, 10(7), 898. https://doi.org/10.3390/pathogens10070898






