1. Introduction
In many fields, such as biology, technology, or management, there is a need for understanding the prediction of the aging process of an analyzed object. Prospective familiarity with the degradation process over the entire cycle of the existence of an object will enable the analysis of repair works. The problem of maintaining residential buildings in adequate technical condition also imposes providing for optimal planning of maintenance works, while the proper determination of the scope and program of refurbishment requires a diagnosis of the technical condition to be carried out. Accurate determination of the state of the building, the reasons behind damage, and above all, the prediction of unfavorable changes make it possible specify refurbishment needs.
Diagnosis comprises the basis for properly carried out refurbishment activity in every technical object. It pertains to both issues of assessing the technical state and its causes, as well as the prediction of the degradation process. The diagnosis of the technical condition of buildings can be carried out using two methods. The one most frequently applied is the assessment of unfavorable changes in the objects on the basis of site inspections, nondestructive testing, measurements, and calculations. Another course of action that can be taken is the predictive method, relying on predicting the degradation of a building.
Predicting the aging process of residential buildings carried out using traditional technologies is necessary when planning maintenance works in these buildings [
1,
2,
3,
4,
5,
6,
7]. A better understanding of the service life of buildings results in more efficient building maintenance and reduced environmental costs [
8,
9]. Service life analysis aims at establishing and explaining the performance-over-time functions [
10,
11,
12,
13]. Reference [
14] developed three design proposals that target different service lives (30 years, 50 years, 100 years) based on the building’s expected life and uses BIM technology to simulate the life cycle cost and design performance as based on the renovation scenario analysis of the building’s life cycle.
In accordance with the recommendations of ISO 7162:1992 standards [
15], an assessment of the performance characteristics of a building should be carried out. The changes in these characteristics should be predicted over time using a method simulating the predicted degradation of a good over time known as Predicted Service Life Distribution of the Component (PSLDC). The ISO standards “Planning the Service Life of a Building” [
16,
17] provide general standards regarding the issues of predicting the service life of a building. These guidelines contain an introduction to predicting performance characteristics, but lack details regarding forecasting. These standards highlight difficulties in indicating degradation, even in the case of similar buildings, as there are many variables influencing the service lives in practice. The variety of buildings, environments, quality of construction works, and future conditions of maintenance lead to uncertainty in forecasting service life. In one of the ISO standards “Planning the Service Life of a Building” [
17], there is an entry that the course of the service life runs in accordance with the Weibull distribution and its possible modifications.
References [
8,
18,
19] were given the classification of methods for predicting the service life of buildings (PSLDC). The classification is comprised of deterministic, probabilistic, and simulation methods. Deterministic methods based on the ISO standard provide merely approximated results. However, probabilistic methods based on indicating variables of the service model as random values with a known probability distribution are labor-intensive. The other group of probabilistic methods for describing the course of the destruction process are methods containing Markov chains. Markov chains are often applied for describing the destruction process of bridges and technical infrastructure. The example of applying discrete Markov [
18] chains is the description of the destruction process of a residential building described in four states.
The simulation methods [
8,
18] are comprised of methods for determining the service life of a building, somewhere between the not-very-accurate deterministic methods and probabilistic methods, requiring a high quantity of data. The simulation methods are based on developing a mathematical model using probability distributions for determining the individual variables of the model. Reference [
20] presented problems related to exploitation reliability, which was defined as the probability of exploiting a building without any interference (failure) in a given period of time. The author evaluated the construction technologies of residential buildings in terms of their reliability, and buildings erected in traditional technologies occurred to be the best.
Service Life Prediction is necessary to evaluate Life Cycle Assessment for a sustainable construction process [
21]. In Reference [
22], the time behavior of building components is simulated using time dependent environmental models thanks to the correlation between performance characteristics’ decay (measured by lab programs) and the conditions established by users’ requirements. The analysis in Reference [
23] shows that the environmental performance of buildings is affected by the service life of a building and the replacement intervals of building components.
The study on service life prediction of building components is presented in References [
24,
25,
26,
27]. Artificial Neural Network, with its back-propagation learning algorithm, was used in developing model of service life prediction. The simulation results using trained neural network model indicated that implementation of the neural network model is important for future application of service life prediction of building components.
Building management [
28] is a particular economic activity comprising a set of property maintenance, operation, and repair. This is a technical set of operations required for building maintenance and preservation of usable condition, as well as functionally required for the maintenance of the land to ensure that property is used in accordance with the purpose.
Reference [
29] proposes a new stochastic dynamic programming model where optimality conditions are derived through the Hamilton-Jacobi-Bellman equations. The model defined the joint production and repair, which are major maintenance switching strategies that minimize the total cost over an infinite planning horizon. Two probabilistic approaches are described in Reference [
30], one approach using a mathematical function (Weibull) to describe the performance of a component over time and one approach using discrete Markov chains.
The purpose of the research reported in Reference [
31] was to develop a model that allows for the identification of the owner’s needs in all phases of the building life cycle. A six-level classification system for the information required in the project and a two-dimensional model that maps the life cycle were corroborated and improved by applying the Delphi technique to a panel of 10 experts in two rounds. Reference [
32] concluded that the planning and the application of the condition-based maintenance strategy its significant characteristics and make reference to the resulting prediction model.
Assessments of materials degradation require that methods be available to aid prediction of service life. Researchers in advanced aerospace, nuclear, electronics, and medicine have been more successful than researchers in building and construction technology in responding to the need for reliable predictions of service life [
33].
In Reference [
34], a proposed method combines the use of failure mode and effect analysis to permit identifying likely failure modes from which maintenance actions could be planned and the limit states method to assess the durability of the given retrofit action. In Reference [
35], the model of the lifespan curve for a residential building was presented, where the Pareto principle was applied as the strategy for undertaking maintenance works.
Obsolescence presents a serious threat to built property [
36], as it rarely accounts for the immobile, long-lasting, and (financial and natural resource) capital-intensive characteristics of property, nor for its societal and cultural significance. Minimizing obsolescence and extending longevity are therefore indispensable for maintaining the physical, economic, and societal investments.
The research aim is to present the method of diagnosing the aging process of a building and its components. Ensuring an adequate technical condition of residential buildings is one of the most important problems over the course of their service life. Prognostic familiarity of the aging process of buildings over the entire period of their existence is helpful when analyzing repair works. The proper development of the range and program of maintenance works requires the diagnosis of the technical condition to be carried out. Proper determination of the condition of the building, the reasons behind damage, and above all, the forecast of unfavorable changes will make it possible to determine repair needs.
2. Methods of Functions Describing the Aging Process of a Building
The problem of ensuring an adequate the technical condition of a building occurs over the entire period it is in service. The technical condition of a building changes as a result of the aging process. In solving problems connected with developing a prediction of changes in performance characteristics of a residential building, using algorithms to determine changes in the reliability of technical devices is proposed. The prognosis of unfavorable processes will make it possible to determine the time frame in which the technical condition of a building will be unsatisfactory in the future and will necessitate repair works.
The problem of the wear of objects is an increase in damage and partial defects [
37]. A model presented in Reference [
38] allows for different kinds of obsolescence to be characterized and distinguished. To improve the representation of service life in life cycle assessments and the evaluation of environmental impacts, building service life prediction modelling was examined.
The object’s reliability is defined as the ability to fulfil the task resulting from the purpose it was intended [
39]. The object is demanded to fulfill a determined function in determined time t in determined conditions of operation. The measure of the reliability of an object is the probability of the task completing. Such defined reliability measure is a function of time of the building’s reliable performance and is called reliability function [
40].
For modeling situations in survival analysis, when the probability of failure changes over time, the Weibull distribution is most often applied as the distribution of the random variable of the time a building is fit for service. This distribution has been applied for many years, as a strength distribution as well as a distribution of the time of the proper operation and durability of analyzed goods [
41,
42,
43,
44,
45,
46,
47].
The probability density function for the Weilbull distribution is determined with relation:
where:
- t
the exploitation period,
- α
scale parameter (a real number) α > 0,
- β
the shape parameter (real number), β > 0.
Parameter α of the distribution determines the probability of a breakdown in time:
for α < 1, the probability of breakdown decreases in time, which indicates the fact, when the object breakdown is modeled, that some specimens may have production defects and slowly fall out of the population,
for α = 1 (exponential distribution), the probability is constant, which suggests that that breakdowns are caused by external random events,
for α > 1, the probability grows in time, it indicates the fact time-related technical wear of elements is the main cause of breakdowns,
for α = 2 (the Rayleigh distribution), the probability grows in time.
The distributions function for the Weilbull distribution:
A measure of the reliability of technical devices is the R(t) function, also referred to as the survival function. The distribution function is called the probability of damage, a destruction function, breakdown, or a failure function, and is determined with the relation:
- TR
period of object durability,
- R(t)
reliability function, also called the probability of proper operation, or durability function.
The specific example of the Weibull distribution, when the shape parameter is α = 1, is the exponential distribution. The characteristic for the exponential distribution is a constant intensity of damage throughout the whole period of the object exploitation [
42,
45,
47]. Exponential distribution is frequently used in the examination of a proper performance time of mechanical and electronic devices.
3. Assumptions Made Regarding the PRRD Method
In business planning of repairing the buildings, one should determine the scope of works. There are no reliable mathematical models that allow the estimation of the operational reliability of a building, often referred to as changes in the building performance. In the case of technical appliances (mechanical and electronic), attempts are undertaken to determine the prediction of their operational reliability. However, for buildings, only indicative graphs of changes in performance are presented.
Literature [
41,
42,
43,
44,
45,
46,
47] gives the general form of Weibull as a model for describing the prognoses of the aging. In the case of mechanical and electronic devices, a particular case of Weibull distribution—exponential distribution—is used. The distribution function of exponential distribution is treated as a function of the damage of a device. The damage function, also referred to as unreliability, is a complement of reliability, which is the R(t) function.
The developed model of predicting changes in the performance characteristics of buildings—Prediction of Reliability according to Exponentials Distribution (PRED) [
46,
48]—is based on the principles applied for technical devices. However, large approximations are accepted in exponential distribution. The negligible influence of wear processes is assumed. The exponential model of degradation curves of objects is based on a constant intensity of damage, which, according to the author, is not precise in the case of building structures.
Another specific case of Weibull distribution is Rayleigh distribution. In this distribution, the wear of the object along with the passing of time is considered to be a significant cause of failure. The author proposes using this distribution for the mathematical description of the aging process of a residential building. In the aging process of a building, its wear increases continuously, which is why the author believes that, in assessing the changes in the performance characteristics of residential buildings, formulas based on Rayleigh distribution are more accurate relationships.
The general form of the function describing the course of changes in the performance characteristics over time t based on the Weibull distribution is expressed by the relationship (1). In Rayleigh distribution, parameters α and β are equal to: α = 2, β = 1/T.
The proposed [
48,
49,
50] model PRRD (Prediction of Reliability according to Raleigh Distribution) of changes in the performance characteristics R
i(t) of the i-th building component in time t, based on the Raleigh distribution, and using durability periods of component T
Ri from data found in literature [
51,
52,
53,
54], is described by the relationship [
45,
46]:
The disabilities of building components are given in literature [
51,
52,
53,
54] as ranges of periods which result from the different conditions concerning location, maintenance, variability in properties of materials, the level of workmanship, and the level of design.
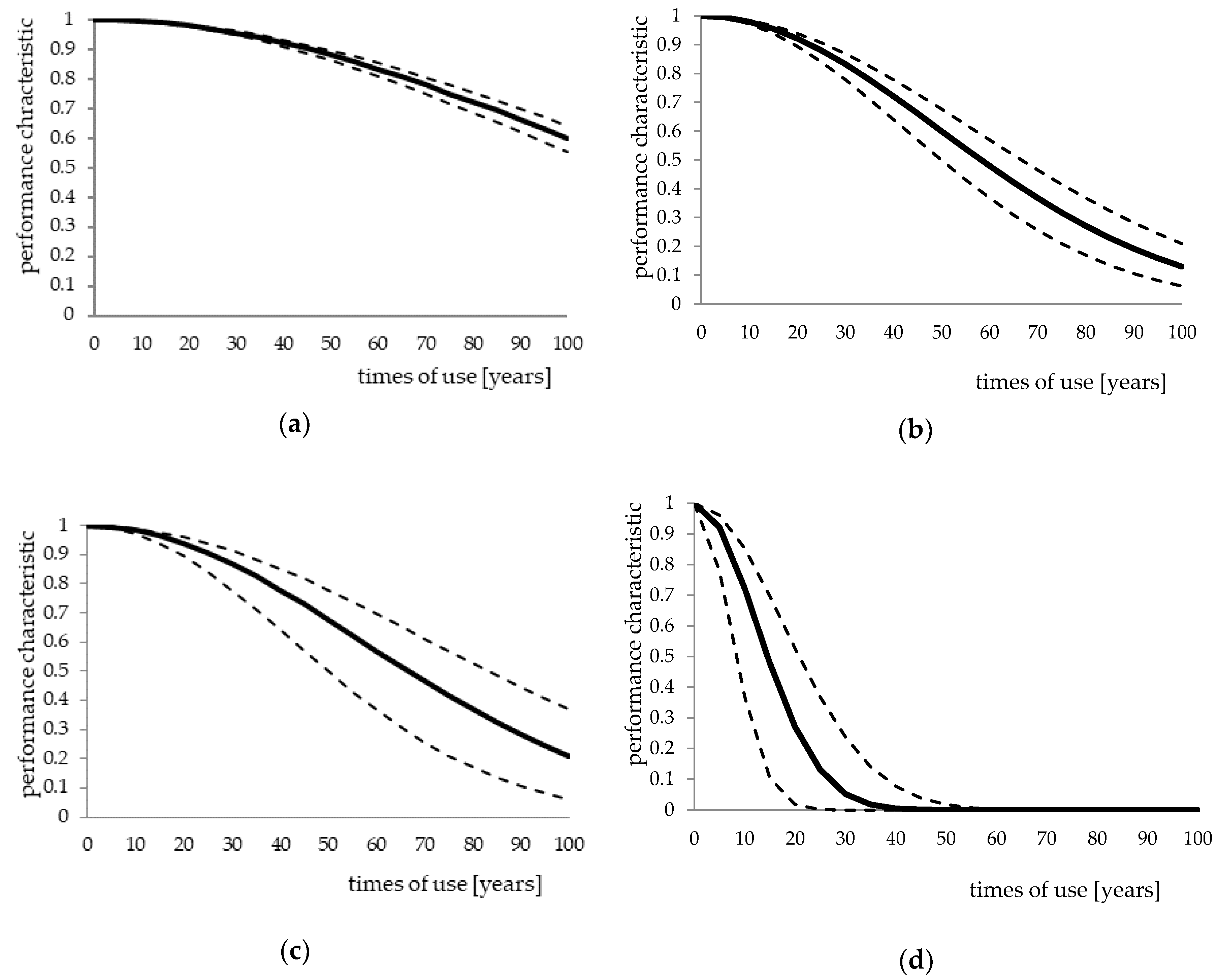
The selected results of calculations are presented in
Figure 1.
Buildings are made up from many elements with a difficult to define and determine homogeneity of materials. They have a complex structure and are subject to wear as a result of many processes. In addition to this, building structures are exposed to outside factors, often with a very diverse intensity. Indicating changes in the technical state over the entire course of the use of a building is a process requiring many generalizations to be made.
Each building is made up of many components. These elements serve various functions and are created from dissimilar construction materials, with each being characterized by different properties and different service lives. The initial stage of the diagnostic analysis of a building is its decomposition.
A building constructed using traditional technology with exemplary material and construction solutions was subjected to decomposition into diagnostic levels. The depth of diagnosis, as well as level p of probing into the structure of the building, were assumed. The components of level p were listed in
Table 1. Each component is characterized by its own service life. Studies pertaining to the service lives of building components were carried out at research centers in Poland. As a result of the analysis of literature data pertaining to the service lives minimum T
Rmin, maximum T
Rmax, and average T
Rsr values were established. These values are compiled in
Table 1. Under comprehensive analysis of changes in the service properties of a building, the problem ought to be looked into accounting for the phenomena accompanying the long-term use of the object. Among them are: Wear, frequency of carrying out maintenance works, manner of use, the type of use, the influence of outside factors, the correctness of the design process, the quality of the applied materials, and the precision with which it had been made. In the case of buildings which have been used for a few dozen years, there is no possibility of checking the conditions derived from the design and construction period of the building. The long period of use to date points to the fact that design and construction processes were correct and high-quality building materials were used. The assumption was also made that the type of use of the objects (all are residential buildings), as well as external factors (similar atmospheric conditions due to the same climate, close geographical location), for all objects are at an equal level and do not influence the diversification of their performance characteristics.
Each building component serves a specific function. Structural elements have the most significant influence on the service life of a building. Other elements influence the performance characteristics of a building to a lesser degree, with their influence resulting from the fact that damaged auxiliary elements can lead to changes in the parameters of basic elements. The intensities of the influence of performance characteristics of the i-th components (
Figure 1) in the form of a scale of weights of elements A
i (importance weight) based on scale serving to assess the quality of a building were accounted for when determining the performance characteristics of the entire building, which is a collection of n components. Changes in the performance characteristics of building R
A(t) in time t are determined by the relationship [
48]:
4. Verification of the Mathematical Model
The examined material comprises 592 residential buildings performed in the traditional technology, situated within the area of the town of Zielona Gora [
55]. The buildings were built between 1915—2015. The buildings were divided into subgroups research buildings 5, 10, 15, ..., 100 years.
The buildings covered by the analysis are characterized by similar solutions in terms of their construction and materials used. All of them are two stories high with full basements. The walls of the analyzed buildings were made of full brick and the floors over the basements are brick infill floors, with the remaining floors constructed on wooden beams construction. The stairs and roof trusses are wooden with a collar beam roof structure, and roof covering is comprised of plain type pantile or roofing felt.
The technical states of all the buildings were periodically (every five years) inspected by experts. The periodic monitoring, consisting in the examination of technical wear, resulted in the reports containing the information on the percentage wear of 25 components of the 592 buildings.
For each building element, it is possible to determine the prediction of the technical wear in any arbitrary exploitation period. The durability periods of building elements of determined material-structure solutions are given in [
49,
50,
51,
52], and after substituting them into Formula (4), the prediction of the degree of technical wear may be obtained according to the Rayleigh distribution.
The bibliography on reliability of electronic a device attributes the intensity of failure to technical wear as described in:
where S
z(t)—the rate of the product wear.
Often [
41], a different definition of the intensity of damage λ(t) is given, described as the speed at which unreliability F(t) increases in relation to R(t):
Based on the above dependencies, the degree of consumption in the PRRD model is a function dependent on time:
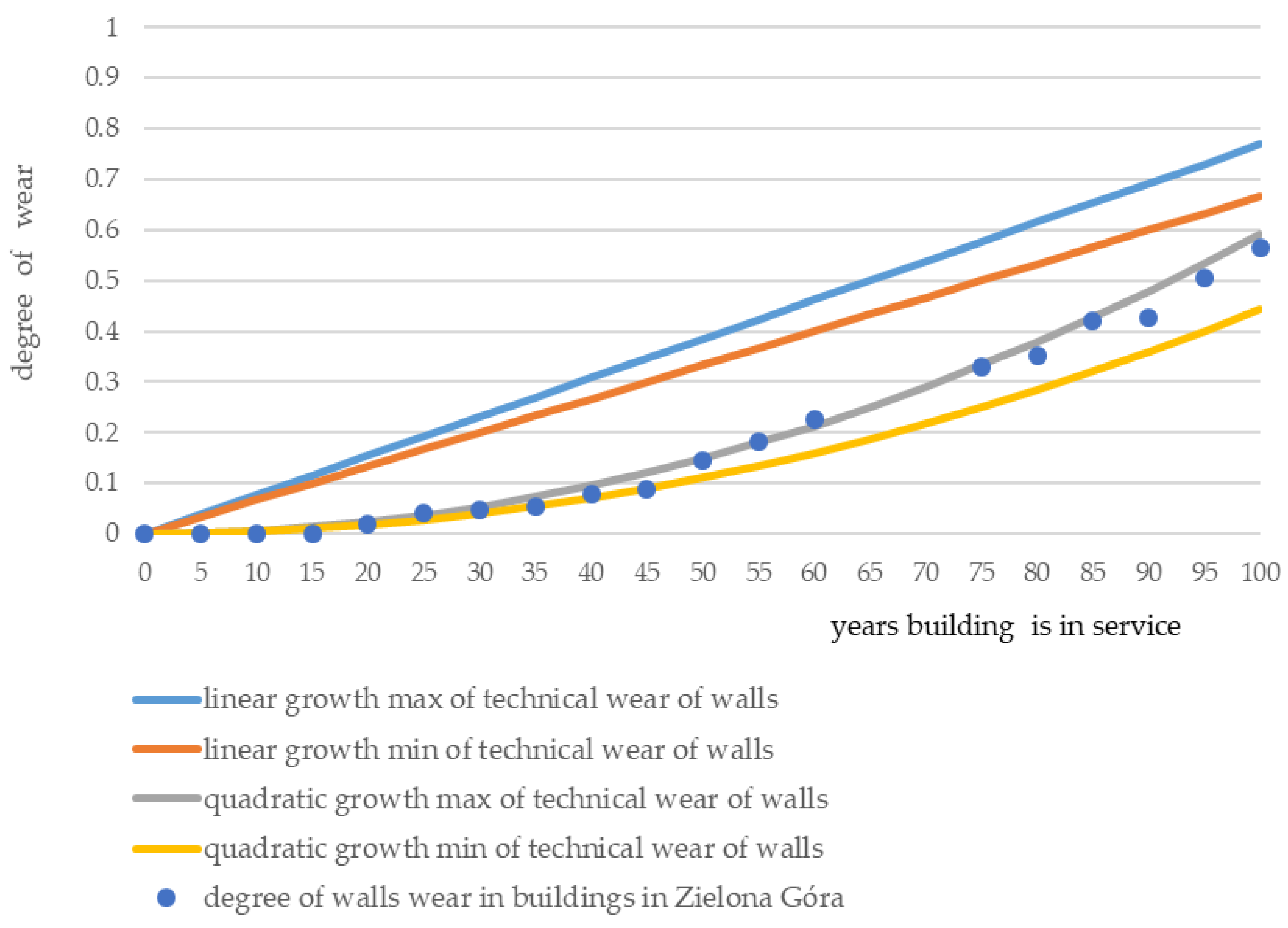
Out of the results of periodic inspections (every five years) of building elements, the results for walls were selected. For each subgroup of buildings (5, 10, 15, ..., 100 years old), average values of wall wear were calculated. The results are presented in
Table 2 and
Figure 2.
According to the relationship (8), changes in the consumption of masonry brick walls in the full period of their use have been determined. For brick masonry walls, the durability period is determined within the limits 130–150 years. The degrees of technical wear were determined for the minimum (130) and the maximum (150) values, with the use of the according to Rayleigh distribution (Formula (8)). The obtained results are presented in
Table 2 and
Figure 2. The analysis adopts the same class of use for all buildings.
The values of the degree of wear of walls by the Rayleigh distribution during a 100-year period of building exploitation, as well as the average values of the degree of wear, obtained in periodic inspections of buildings five-year, 10, 15, ..., 100-year, were verified with the use of Student t-test for independent samples. The maximum probability of an allowable error, which could be made while drawing conclusions, was assumed to be equal α = 0.05. For this level of significance, a critical area was determined. For buildings included in the analysis, the number of degrees of freedom equal to n = 19, the critical value of the test is p = 2.0930. In examining buildings with the t-test, the test result was 2.2957. This value is greater than p = 2.0930, which means that the results by the Rayleigh distribution are statistically significant. It can be assumed, therefore, that the reliability of predictions of buildings determined by the Rayleigh distribution is close to reality.
The prediction of the degree of wear of the walls is an example of the methodology of prediction of technical condition of building elements. In an analogous way, it is possible to elaborate predictive changes in the degree of wear of all building components.
5. Applying the PRRD Model in Planning Maintenance Works
Ensuring the proper technical condition of a building in over the course of its use can only be done by properly carried out refurbishment activities. The proposed PRRD model can be applied to modeling situations in the analysis of changes in the performance characteristics of a building which had not undergone refurbishment. The PRRD method of predicting changes in the performance characteristics can support activities aimed at avoiding an inadequate technical condition of a building. The accurate prediction of unfavorable changes and preventive repairs and maintenance works will make it possible to ensure the proper technical condition of the object.
The effective use of a building ought to be based on maintaining an adequate level of performance characteristics of the building, with refurbishment processes serving to fulfill this task. All types of refurbishment activities have a significant influence on the technical condition of a building over the course of its continued use. The full characterization of a refurbished object must account for the initial state and the scope of maintenance works. On this basis, the course of changes in the performance characteristics over time, prior to and after the refurbishment, can be determined.
The prediction of changes in the performance characteristics R
M(t) of a building which had undergone refurbishment, where tp is the date of the refurbishment, is expressed by the Formula (9):
where:
r—the number of refurbished components in a given inter-repair cycle,
m—number of all components,
Ai—weight of i-th component,
tpi—time of carrying out refurbishment on component i,
TRi—life cycle of i-th component.
The following assumptions were made:
- (1)
The building is constructed using traditional technology, and the material and building solutions taken from
Table 1;
- (2)
The frequencies of maintenance works for building components are:
- c1 = 5
five-year cycle—including wall and ceiling paint coats, oil paint coats on windows, and doors,
- c2 = 15
gutters and downpipes, electrical installations,
- c3 = 30
wooden stairs, plumbing pipes and pipe fittings, gas lines,
- c4 = 60
wooden ceilings, roof trusses, ceramic tile roof cover, outside plaster, window and door frames, glazing, floors and floor covers, furnaces and radiators, electrical installation cables.
- (3)
The times of carrying out maintenance works on building components stem from the life cycles of these elements nearing their end.
Proposals of times of carrying out planned-preventive maintenance works were initially indicated based on experiments and the life cycles of building components nearing their end. The proposed maintenance works aim to maintain the building in good, satisfactory, or average technical condition, and rely on prophylactic action and preventing the premature emergence of unfavorable changes.
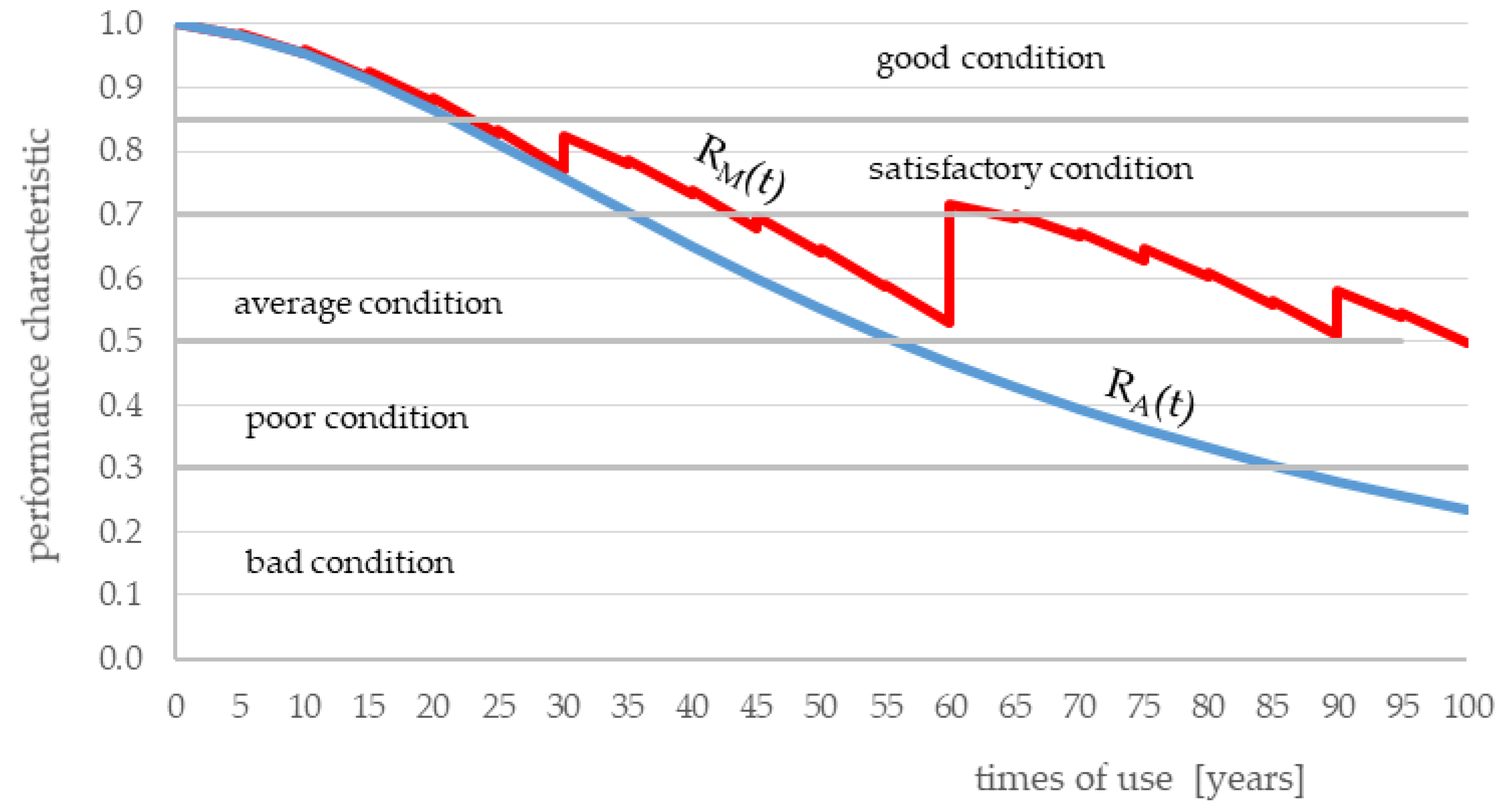
The obtained results of predictions of changes in the performance characteristics of a renovated building according to Rule (9) for the earlier accepted assumptions are presented in
Figure 3. For purposes of comparison, a dashed line is used to also present changes in the performance characteristics over the course of use of a building which had not undergone maintenance works.
Modeling various possible usage scenarios of a building according to the proposed method will allow for the optimal planning of building maintenance works undertakings. The changes in the performance characteristics of the building shown in
Figure 3 illustrate the application of a sample strategy of maintenance works of selected building components at the assumed times.
The characteristics of various strategies of choosing refurbishment activities have an influence on the shape of the life curve of a building. The obtained data allow for the comparative analysis of the reliability effectiveness of a building and choice of the most adequate material and structural solutions.
6. Discussion of Proposal to Assess the Date of the Complete Maintenance Works
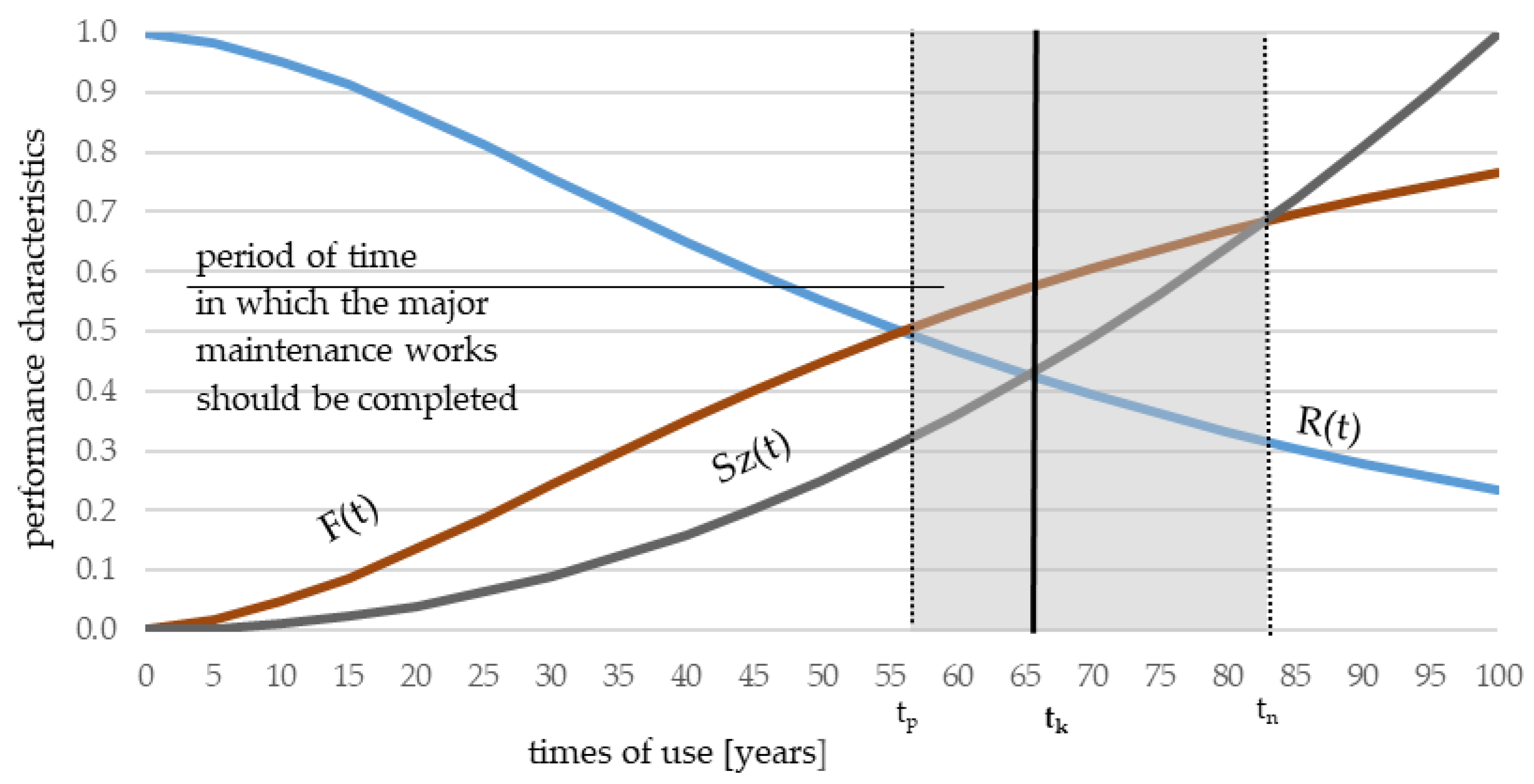
Changes in the performance characteristics of a building R(t), changes in the failure of a building (F(t), and its level of wear SZ(t) during subsequent years of its use are a picture of the changes in the technical condition of a building over the course of subsequent years of service.
The performance characteristics of a building along with its failure over the course of its use can assume values from 0 to 1. The level of wear of a building, given as a percentage, increases over time, from 0 to the maximum value.
The performance characteristics of a building in which maintenance works had not been carried out decrease in subsequent years of use, whereas the failure of a building continually increases. It is assumed that an important moment is term t
p, when the performance characteristics are so poor, that they are equal to the failure of the building. Starting from term t
p, complete maintenance works of the building ought to be carried out due to its bad technical condition (
Figure 4).
A more critical term is the moment tk. The function of changes in the performance characteristics lessens and reaches lower values than the constantly increasing failure function. Term tk is assumed as a critical term when the performance characteristics function is equal to the level of wear function. It is assumed that term tk is a term requiring the unconditional carrying out of major maintenance works of the building.
Term tn, on the other hand, indicates the limit of the unprofitability of carrying out any maintenance works. It is a date when the level of wear begins to exceed the failure of the building.
The proposed model of changes in the operational properties of a building and its components over time is a method of predicting unfavorable changes to the technical condition of a building. The aging process of residential buildings is an inevitable problem. Familiarity with the course of the damage process for the entire period a building is in use is helpful when planning maintenance works.
In this method, the value of the level of wear equal to 70% is given as the limit for carrying out maintenance works; due to the high costs of repairs, provided the demolition of the building is recommended if the level of wear is higher than 70%. The carried-out analysis does not account for the costs of remodeling and regards only the technical state of the building. Thanks to the indicated changes of the aging function over time, it can be stated that residential buildings whose level of wear is higher than 70% are to be demolished due to their bad technical state.
The exponential distribution is applied often to assess the distribution of the time of proper operation, however the exponential model of the reliability distribution does not exist in reality. In the exponential distribution, significant approximations are accepted, assuming the negligible influence of wear processes. Another specific example of the Weibull distribution is the Rayleigh distribution. This distribution occurs when the wear of the object with the passing of time is the main reason behind failure. It is the author’s opinion that the choice of the Rayleigh distribution for modelling the aging process in buildings seems to be the most accurate. All buildings and their components undergo wear over the course of their use, with the Rayleigh distribution applied in cases when the wear of the building increases along with the passing of time.
The model of the distribution of the time during which a building operates properly presented as the prognosis of changes in the technical condition can be applied to solve problems occurring in practice. The approach directed at predicting the occurrence of damage will make it possible to plan maintenance works on buildings in an optimal manner over the entire course of their service lives.
The proposed method of determining the terms of complete maintenance works should be treated as a warning. The terms of maintenance work according to this method stem from the bad technical condition of the building. The additional operating costs accounted for result from the lack of maintenance works, and will surely lead the terms being moved to earlier.
The proposed prognostic models of the aging process of residential buildings can be effectively used by real estate managers for planning the maintenance of buildings.
7. Conclusions
Over the entire course of use, the performance characteristics of a building are increasingly lower, decreasing with usage and deteriorating as a result of technical wear. The increase in the performance characteristics can take place as a result of conservation, preventive measures, modernization, the replacement of components, or overhaul or rebuilding. In all periods of the life cycle of a technical object, the needs for predicting damage occur. Determining the changes in the performance characteristics of a building, in accordance with the recommendations set out by standards, requires the application of Predicted Service Life of a Component (PSLDC) danger curves as support tools in the planning the times of maintenance works. The proposed model of changes in the performance characteristics of a residential building in the Prediction of Reliability according to Rayleigh Distribution (PRRD) function of time facilitates the prediction of changes in the technical state of a building.
The next stages of research will concern the analysis of conservation strategies to control the degradation of the building. The decision-making process will include models of deterioration of conditions in the building and problems related to maintenance works costs.
The prediction of the degradation of a building should prove useful in processes of reacting to aging-related damage of buildings, while applying danger curves by administrators can be valuable as a means of supporting the planning of maintenance works.