Shear Performance Assessment of Timber Log-House Walls under In-Plane Lateral Loads via Numerical and Analytical Modelling
Abstract
:1. Introduction
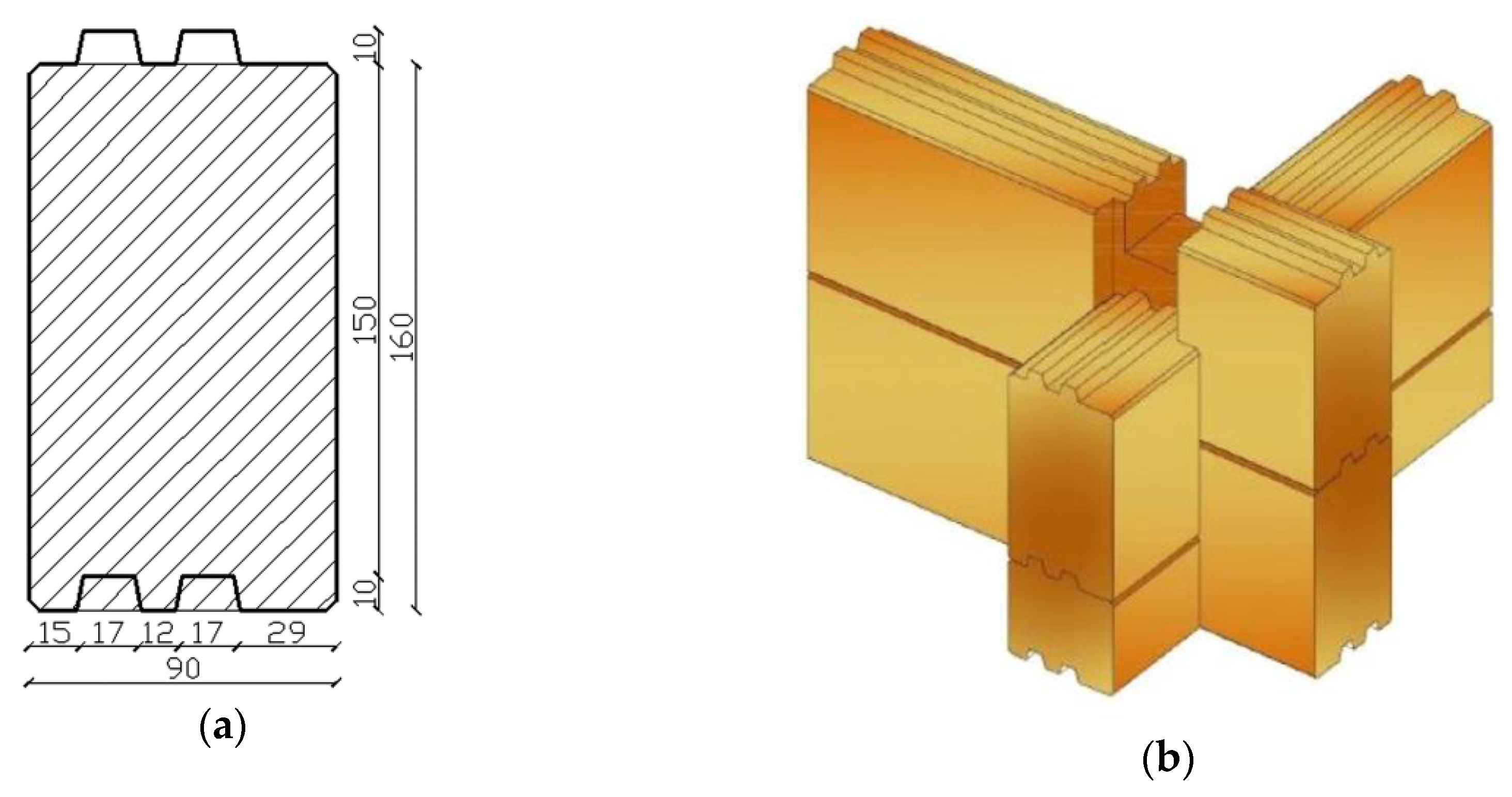
2. Past Experimental Studies on Log-House Corner Joints: Summary of Test Methods and Results
3. Finite-Element Numerical Investigation
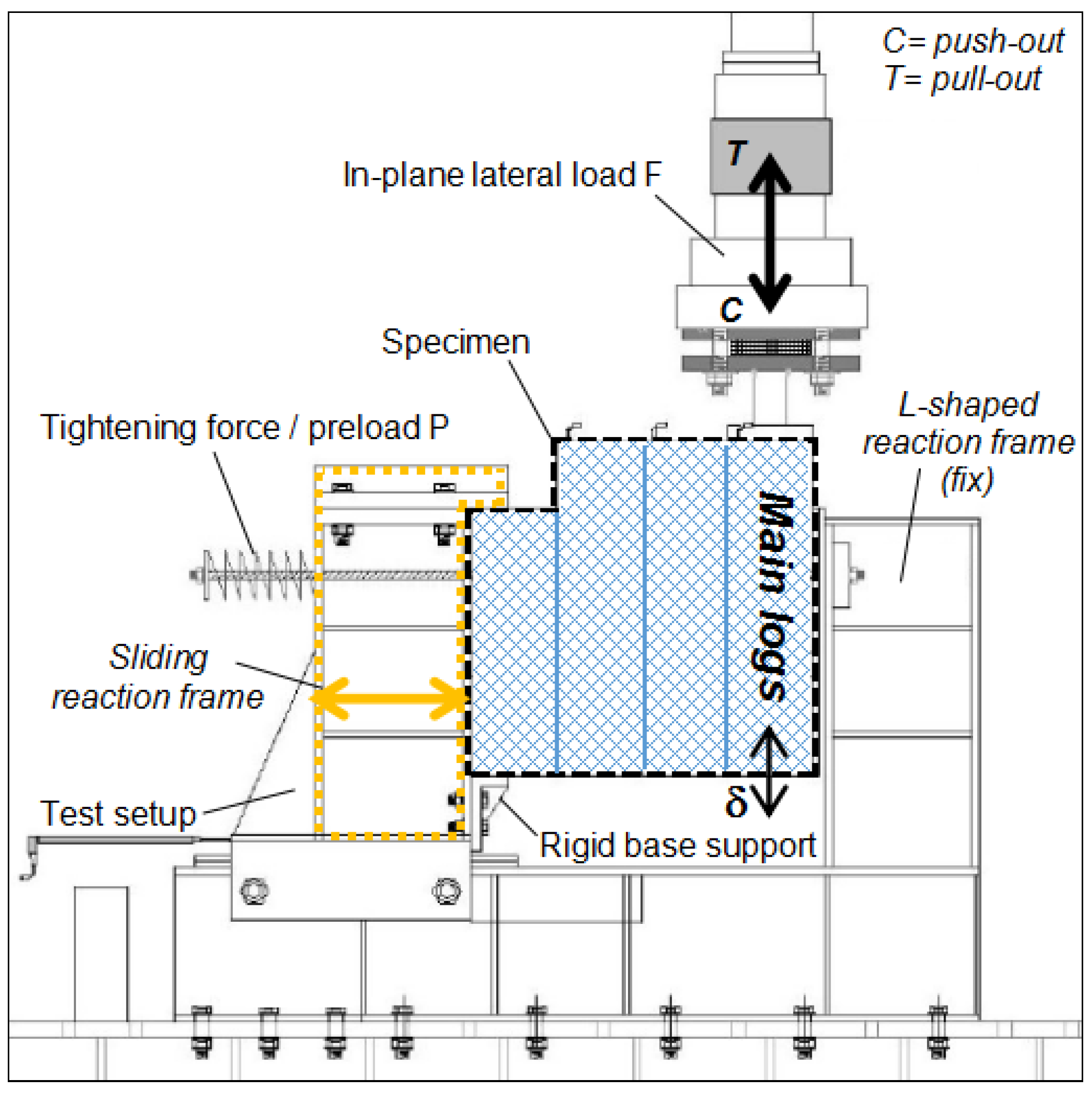
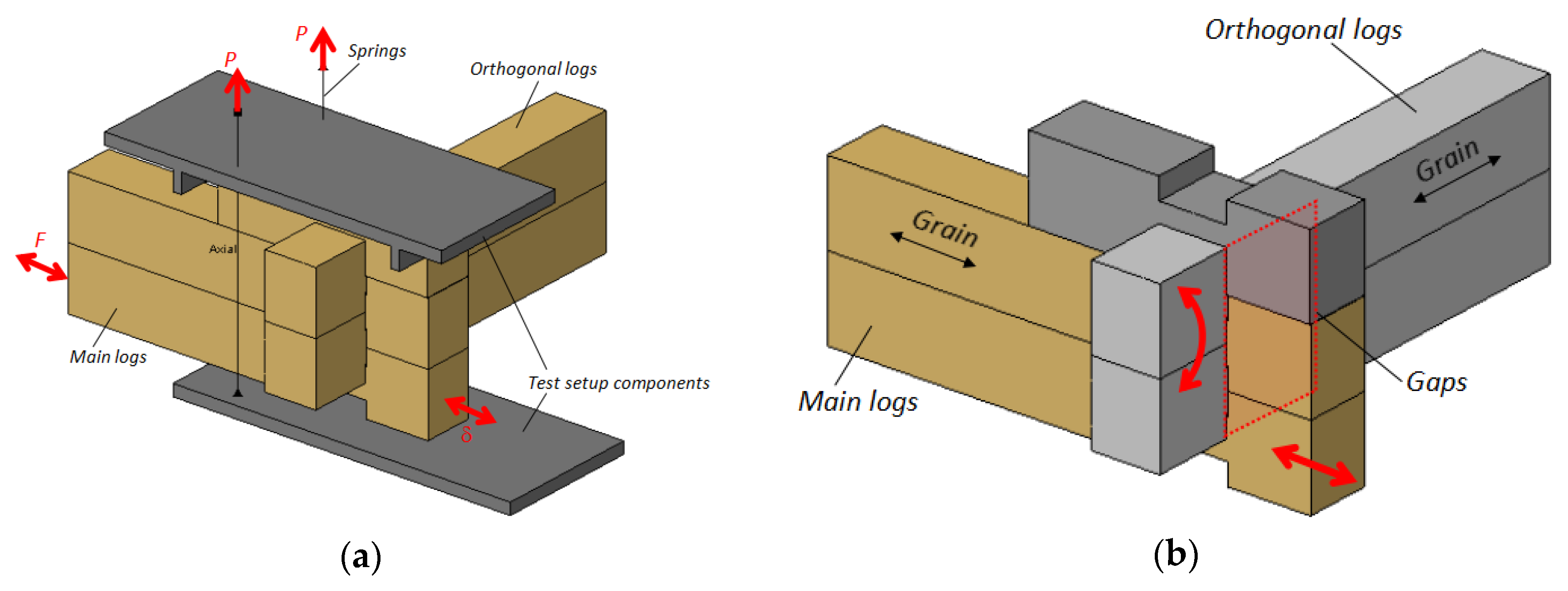
3.1. Model Assembly and Solving Approach
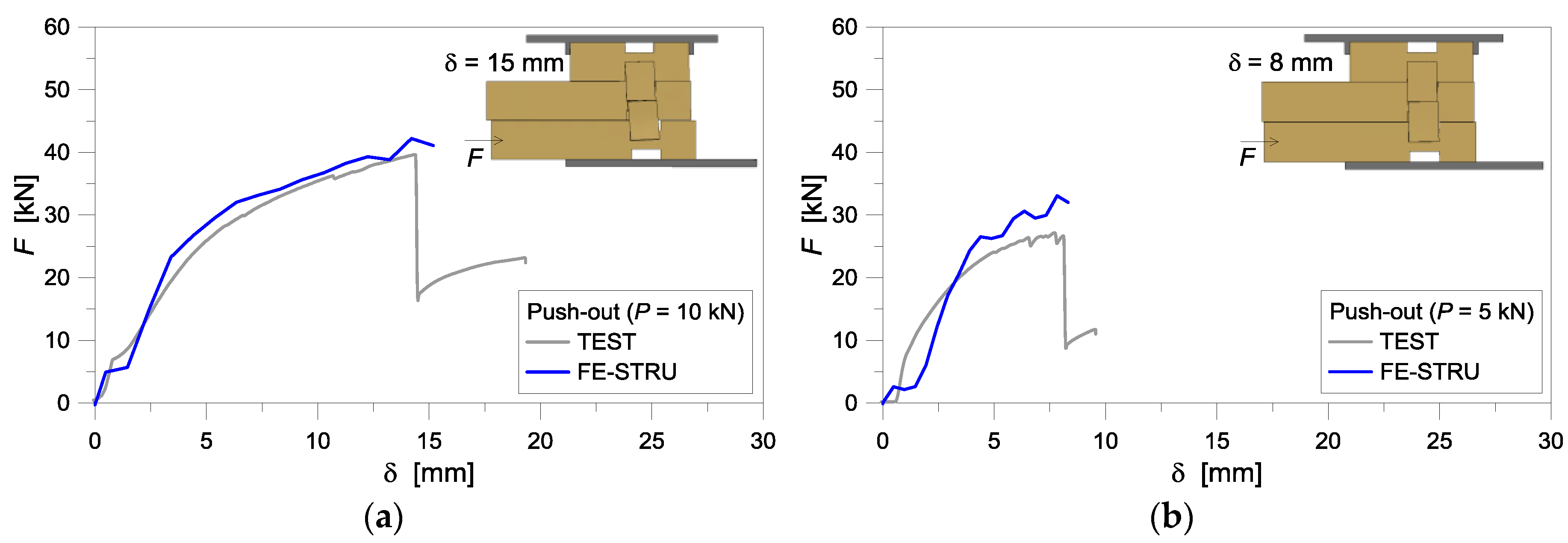
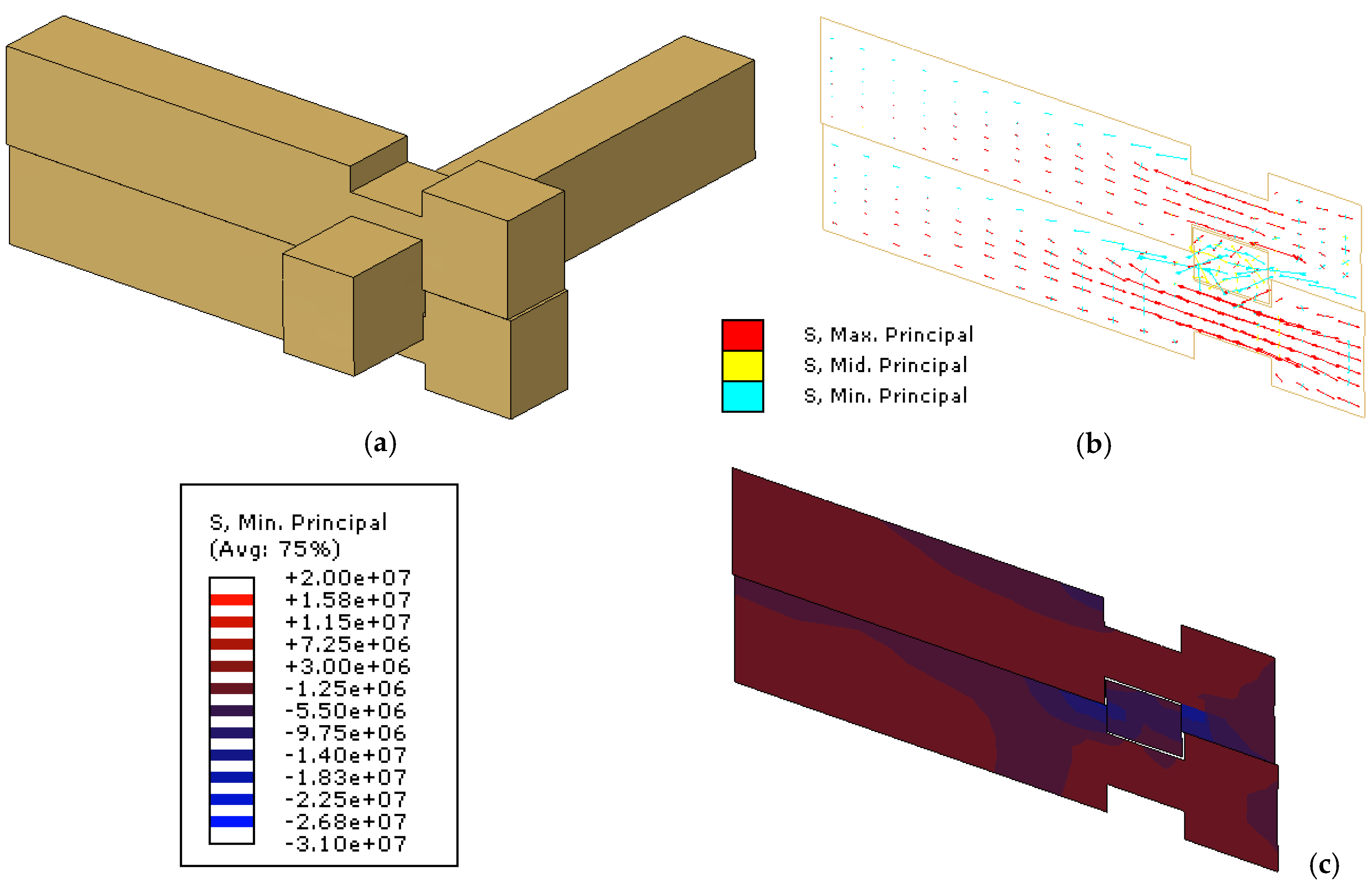
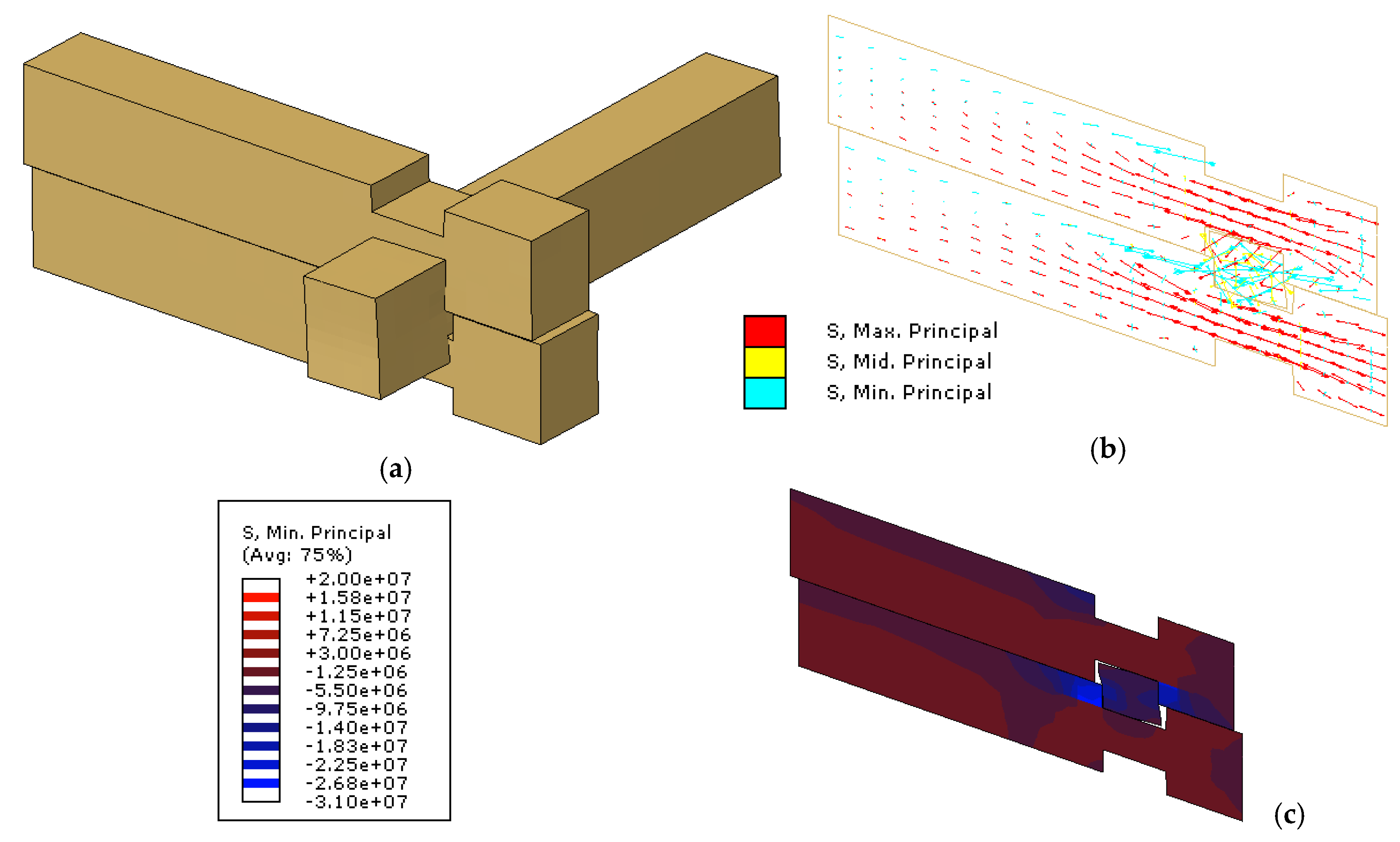
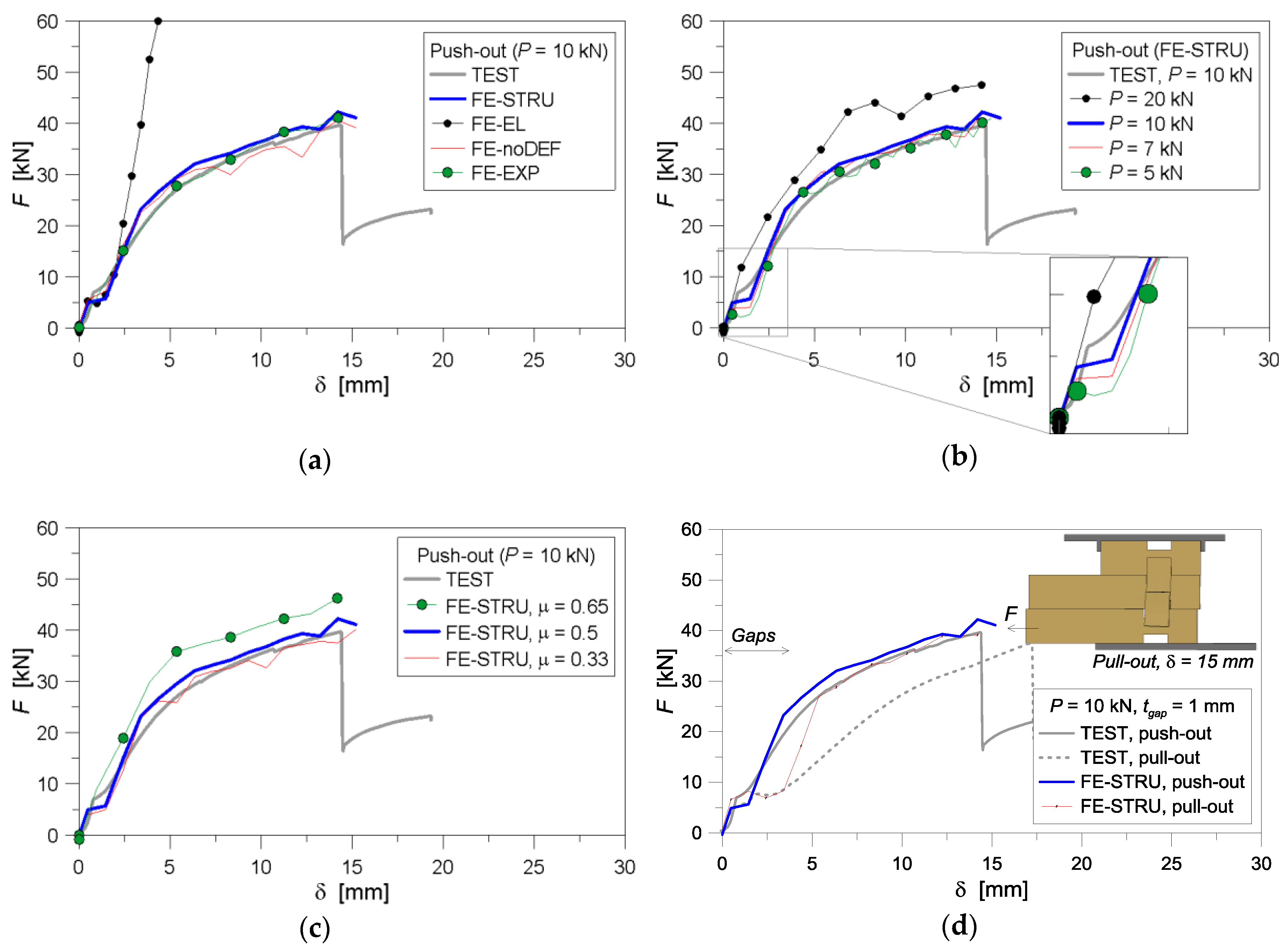
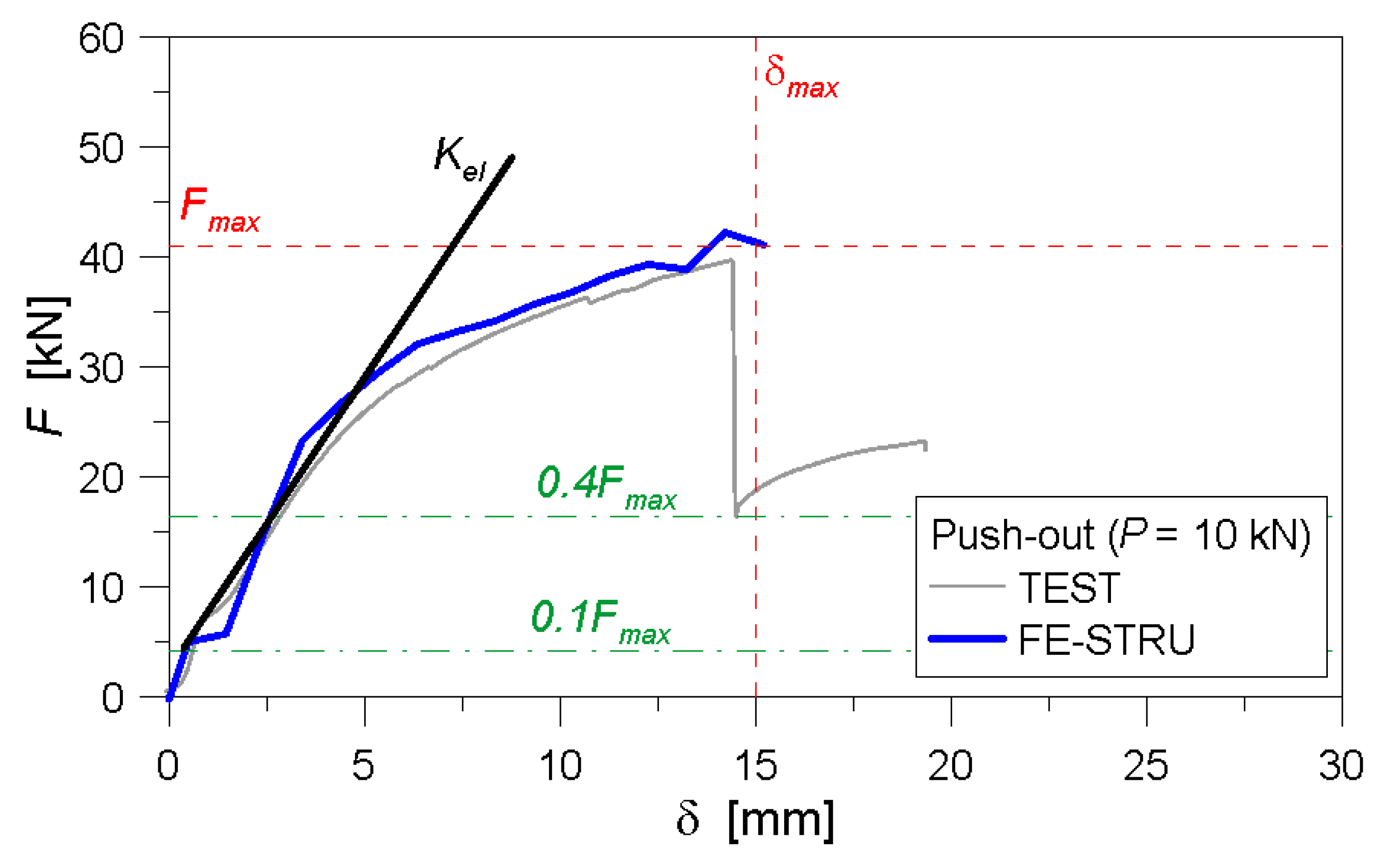
3.2. Validation of FE Models towards the Past Experiments
3.3. Discussion of Push-Out Parametric FE Results and Influencing Parameters
3.3.1. Timber Properties
- an ideal, orthotropic, linear elastic behaviour (FE-EL);
- an orthotropic, elasto-plastic material with resistance parameters available in the literature for small-scale timber specimens without defects (FE-noDEF, with average values provided in Reference [23]);
- an orthotropic, elasto-plastic material with stiffness and resistance properties experimentally derived from small-scale log-house components (FE-EXP, see Reference [7]).
3.3.2. Preload and Friction Coefficient
3.3.3. Loading Configuration and Gaps
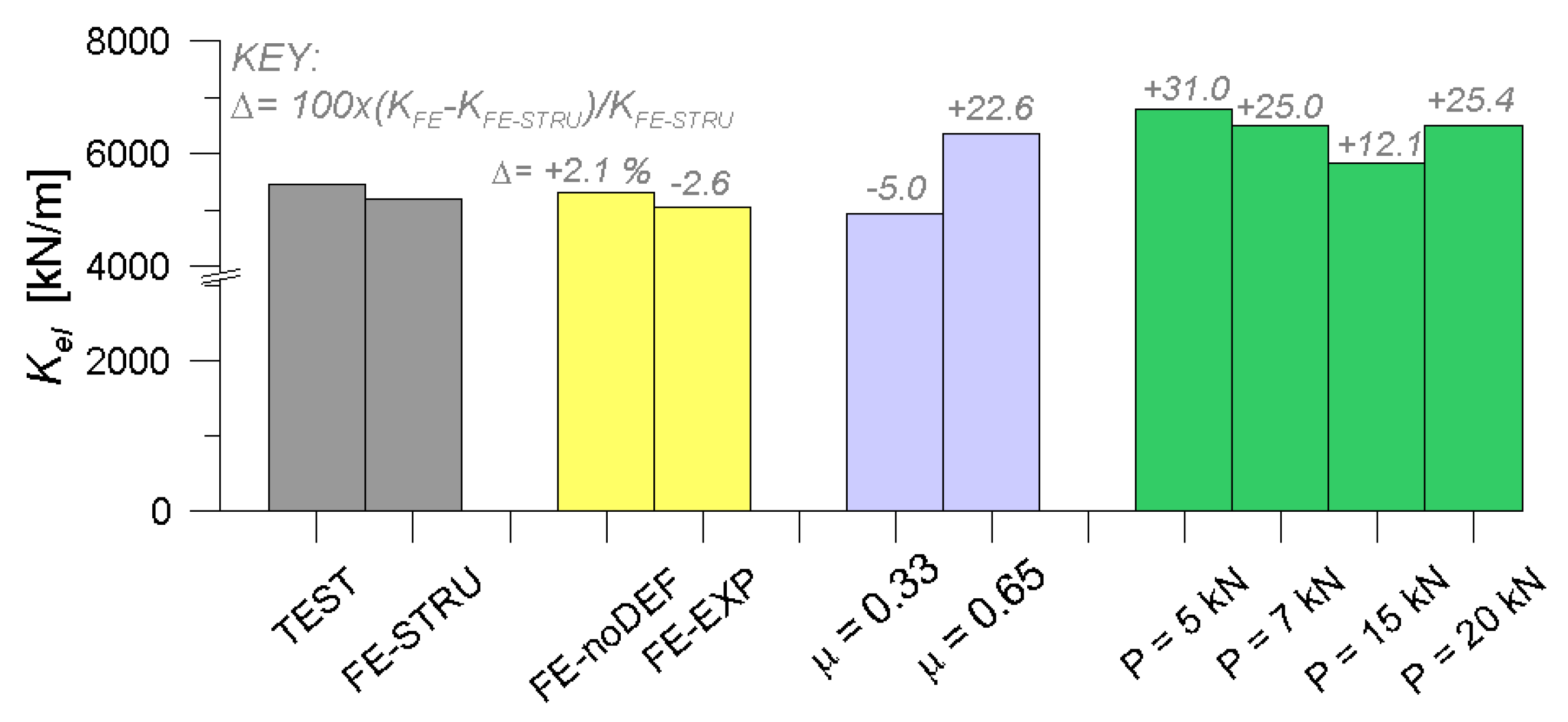
3.4. FE Derivation of the Corner Joint Stiffness
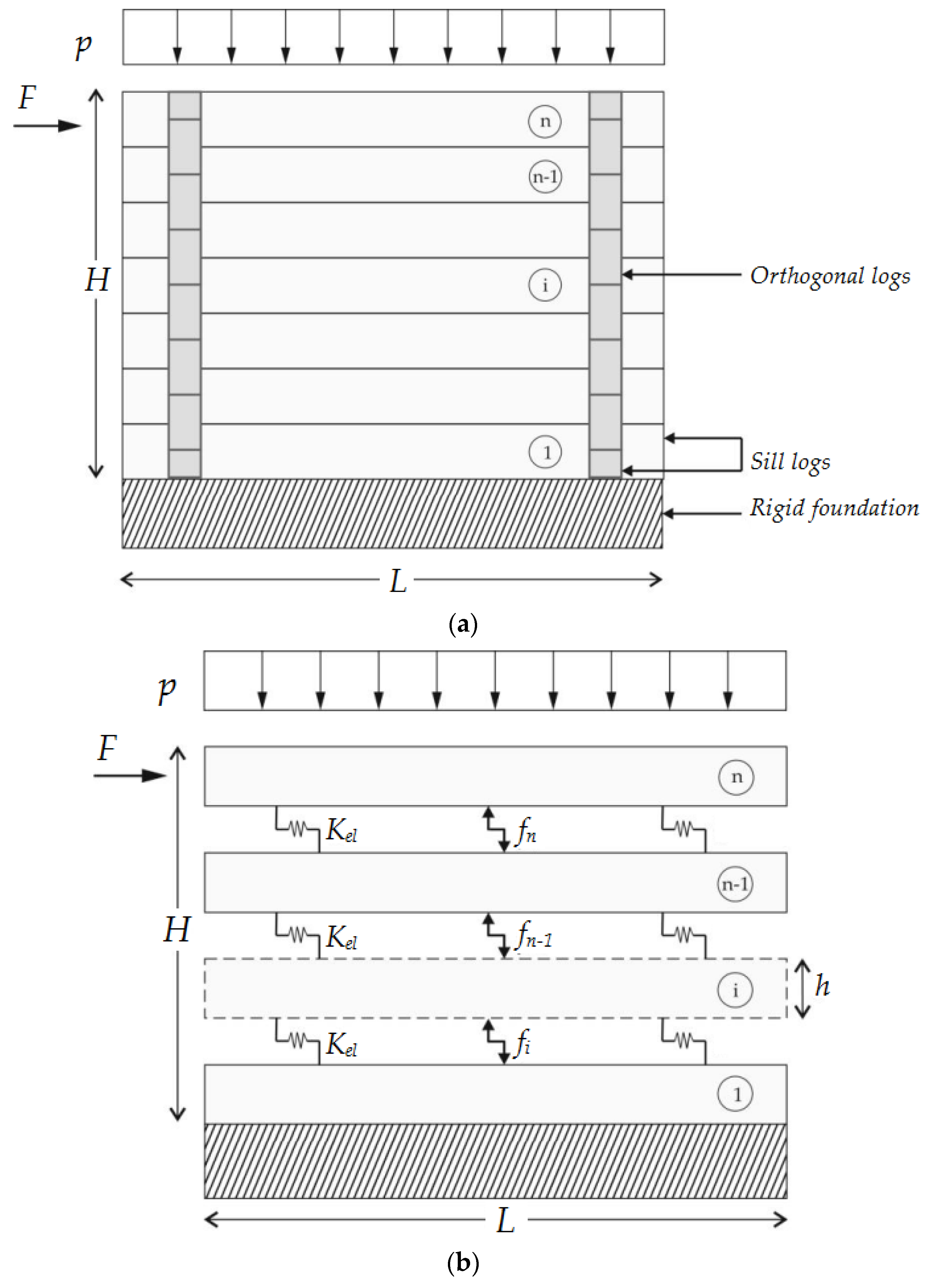
4. Simplified Analytical Model for the Design of In-Plane Loaded Log-House Walls
4.1. Basic Assumptions
- static friction effects are accounted, at the level of each log, in the form of fi Coulomb forces, with i = 1,…n − 1;
- the presence of n tolerance gaps in the region of corner joints is also considered, as an additional contribution for the total displacement estimation. At this stage, given the structural system of Figure 10, the carpentry joints are considered at the logs ends only (i.e., possible internal joints and restraints are disregarded).
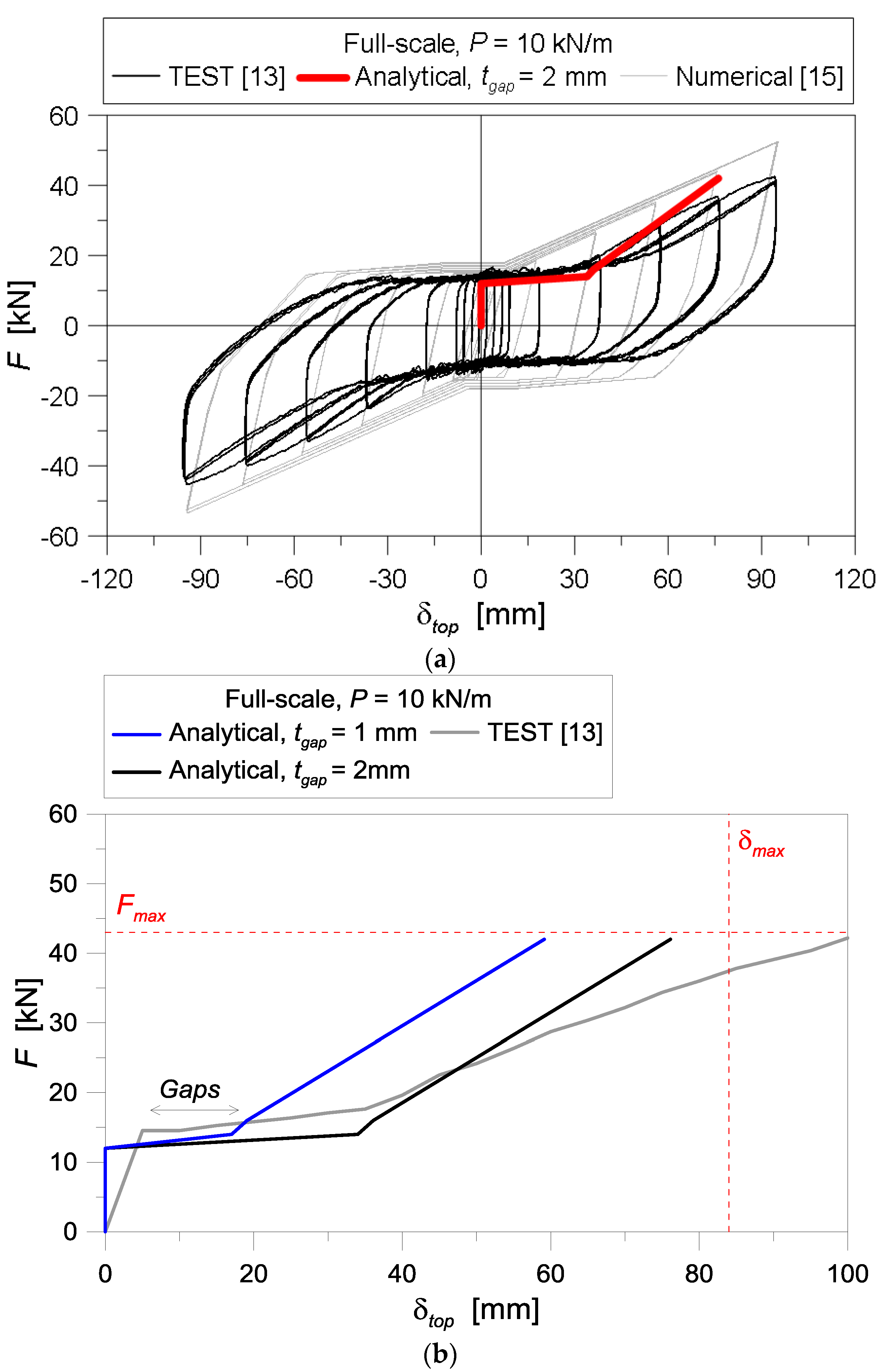
4.2. Validation of the Analytical Model
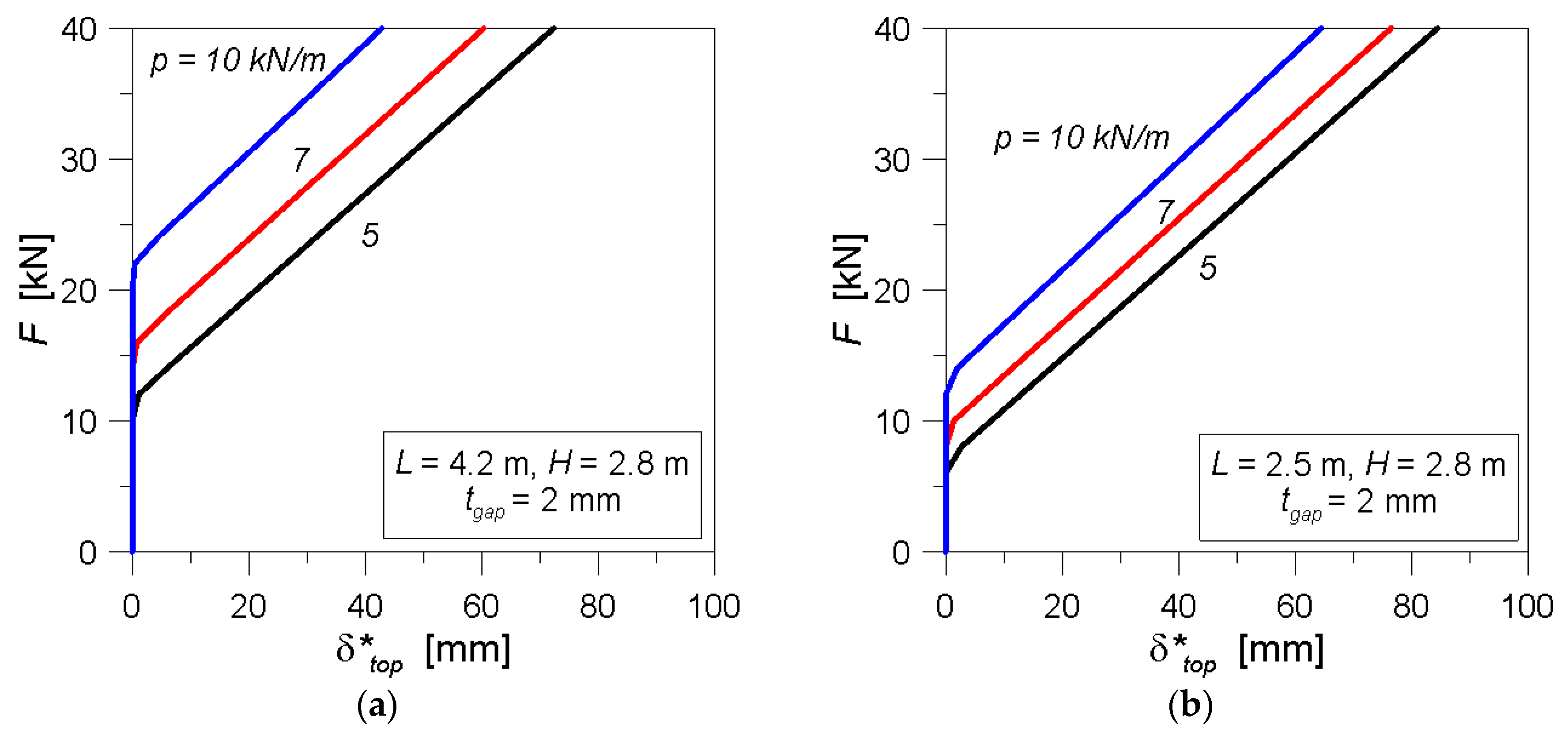
4.3. Derivation of Force-Preload-Displacement Charts
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Eurocode 8—Design of Structures for Earthquake Resistance—Part 1: General Rules, Seismic Actions and Rules for Buildings; EN 1998-1:2004; European Committee for Standardization (CEN): Brussels, Belgium, 2009.
- Eurocode 5—Design of Timber Structures—Part 1-1: General-Common Rules and Rules for Buildings; EN 1995-1-1:2009; European Committee for Standardization (CEN): Brussels, Belgium, 2009.
- Heimeshoff, B.; Kneidl, R. Zur Abtragung vertikaler Lasten in Blockwänden—Experimentelle Untersuchungen (Carrying of vertical loads by walls of log houses). Holz Roh Werkst. 1992, 50, 173–180. (In German) [Google Scholar] [CrossRef]
- Heimeshoff, B.; Kneidl, R. Bemessungsverfahren zur Abtragung vertikaler Lasten in Blockwänden. (Methods of calculation for walls of log houses under vertical loads). Holz Roh Werkst. 1992, 50, 441–448. (In German) [Google Scholar] [CrossRef]
- Bedon, C.; Fragiacomo, M. Derivation of buckling design curves via FE modelling for in-plane compressed timber log-walls in accordance with the Eurocode 5. Eur. J. Wood Prod. 2017, 75, 449–465. [Google Scholar] [CrossRef] [Green Version]
- Bedon, C.; Fragiacomo, M. Numerical and analytical assessment of the buckling behavior of Blockhaus log-walls under in-plane compression. Eng. Struct. 2015, 82, 134–150. [Google Scholar] [CrossRef] [Green Version]
- Bedon, C.; Rinaldin, G.; Izzi, M.; Fragiacomo, M.; Amadio, C. Assessment of the structural stability of Blockhaus timber log-walls under in-plane compression via full-scale experiments. Constr. Build. Mater. 2015, 78, 474–490. [Google Scholar] [CrossRef] [Green Version]
- Bedon, C.; Fragiacomo, M. Experimental and numerical analysis of in-plane compressed unprotected log-haus timber walls in fire conditions. Fire Saf. J. 2018. [Google Scholar] [CrossRef]
- Bedon, C.; Fragiacomo, M.; Amadio, C.; Sadoch, C. Experimental study and numerical investigation of ‘Blockhaus’ shear walls subjected to in-plane seismic loads. J. Struct. Eng. 2014, 141, 04014118. [Google Scholar] [CrossRef]
- Branco, J.; Araújo, J.P. Structural behavior of log timber walls under lateral in-plane loads. Eng. Struct. 2012, 40, 371–382. [Google Scholar] [CrossRef] [Green Version]
- Leichti, R.J.; Scott, R.J.; Miller, T.H. An experimental investigation of foundation anchorage details and base shear capacity for log buildings. For. Prod. J. 2001, 55, 4. [Google Scholar]
- Giovannini, T.; Grossi, P.; Sartori, T.; Tomasi, R. Blockhaus system: Experimental characterization of corner joints and shear walls. In Proceedings of the World Conference on Timber Engineering—WCTE2014, Quebec City, QC, Canada, 10–14 August 2014. [Google Scholar]
- Grossi, P.; Sartori, T.; Giongo, I.; Tomasi, R. Analysis of timber log-house construction systems via experimental testing and analytical modelling. Constr. Build. Mater. 2016, 102, 1127–1144. [Google Scholar] [CrossRef]
- Branco, J.M.; Lourenço, P.B.; Aranha, C. Seismic analysis of a 2-storey log-house. Adv. Mater. Res. 2013, 778, 478–485. [Google Scholar] [CrossRef]
- Bedon, C.; Rinaldin, G.; Fragiacomo, M. Non-linear modelling of the in-plane seismic behaviour of timber Blockhaus log-walls. Eng. Struct. 2015, 91, 112–124. [Google Scholar] [CrossRef] [Green Version]
- Bedon, C.; Rinaldin, G.; Fragiacomo, M.; Noé, S. Finite element assessment of the seismic performance of three dimensional Blockhaus buildings. In Proceedings of the World Conference on Timber Engineering—WCTE 2016, Vienna, Austria, 22–25 August 2016; ISBN 9783903039001. [Google Scholar]
- Bedon, C.; Fragiacomo, M. Numerical Investigation of Timber Log-Haus Walls with Steel Dovetail Reinforcements under In-Plane Seismic Loads. Adv. Civ. Eng. 2018, 2018. [Google Scholar] [CrossRef]
- Abaqus, F.E.A. V. 6.12 Computer Software; Dassault Systèmes: Providence, RI, USA, 2015. [Google Scholar]
- Structural Timber—Strength Classes; EN 338; European Committee for Standardization (CEN): Brussels, Belgium, 2009.
- FIP®—Technical Data Sheet—Plastic Materials. Available online: http://www.fipitaly.it (accessed on 31 July 2018).
- Murase, Y. Friction of wood sliding on various materials. J. Fac. Agric. Kyushu Univ. 1984, 28, 147–160. [Google Scholar]
- Flatscher, G.; Bratulic, K.; Schickhofer, G. Screwed joints in cross laminated timber structures. In Proceedings of the WCTE2014—World Conference on Timber Engineering, Quebec City, QC, Canada, 10–14 August 2014. [Google Scholar]
- Eberhardsteiner, J. Mechanisches Verhalten Von Fichtenholz; Springer: Wien, Austria, 2002; ISBN 978-3-211-83763-4. [Google Scholar] [CrossRef]
- Bodig, J.; Jayne, B.A. Mechanics of Wood and Wood Composites; Van Nostrand Reinhold: New York, NY, USA, 1982. [Google Scholar]
- Tomasi, R.; Sartori, T.; Grossi, P.; Wenzell, L. Blockhaus Structural System: Experiments on Corner Carpentry Joints; Internal Technical Report; University of Trento: Trento, Italy, 2012. (In Italian) [Google Scholar]
- Giovannini, T.; Grossi, P.; Sartori, T.; Tomasi, R. Blockhaus Structural System: Experiments on Full-Scale Walls; Internal Technical Report; University of Trento: Trento, Italy, 2012. (In Italian) [Google Scholar]
- Izzi, M.; Flatscher, G.; Fragiacomo, M.; Schickhofer, G. Experimental investigations and design provisions of steel-to-timber joints with annular-ringed shank nails for Cross-Laminated Timber structures. Constr. Build. Mater. 2016, 122, 446–457. [Google Scholar] [CrossRef]
- Timber Structures. Test Methods. Cyclic Testing of Joints Made with Mechanical Fasteners; EN 12512:2001/A1; CEN: Brussels, Belgium, 2005.
- Timber Structures. Joints Made with Mechanical Fasteners. General Principles for the Determination of Strength and Deformation Characteristics; EN 26891; CEN: Brussels, Belgium, 1991.
- Prestandard and Commentary for the Seismic Rehabilitation of Buildings; FEMA 356; Federal Emergency Management Agency: Washington, DC, USA, 2000.
| Parameter | FE Model | ||||
|---|---|---|---|---|---|
| FE-STRU [19] | FE-EL | FE-noDEF [23] | FE-EXP [7] | ||
| E0,mean | MPa | 11,000 | 11,000 | 13,000 | 11,556 |
| E90,mean | MPa | 370 | 370 | 450 | 192 |
| G | MPa | 690 | 690 | 812 ** | 617 |
| fc,90 | MPa | 2.94 | − | 3 | 3.39 |
| fc,0 | MPa | 24.70 | − | 45 | 33.59 |
| fv | MPa | 2.82 | − | 2.82 * | 2.82 * |
| Reference Configuration | |||
|---|---|---|---|
| TEST | FE-STRU | FE-noDEF | FE-EXP |
| 5471 | 5195 | 5306 | 5062 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sciomenta, M.; Bedon, C.; Fragiacomo, M.; Luongo, A. Shear Performance Assessment of Timber Log-House Walls under In-Plane Lateral Loads via Numerical and Analytical Modelling. Buildings 2018, 8, 99. https://doi.org/10.3390/buildings8080099
Sciomenta M, Bedon C, Fragiacomo M, Luongo A. Shear Performance Assessment of Timber Log-House Walls under In-Plane Lateral Loads via Numerical and Analytical Modelling. Buildings. 2018; 8(8):99. https://doi.org/10.3390/buildings8080099
Chicago/Turabian StyleSciomenta, Martina, Chiara Bedon, Massimo Fragiacomo, and Angelo Luongo. 2018. "Shear Performance Assessment of Timber Log-House Walls under In-Plane Lateral Loads via Numerical and Analytical Modelling" Buildings 8, no. 8: 99. https://doi.org/10.3390/buildings8080099







