1. Introduction
Remote sensing is the science and art of obtaining information about an object, area, or phenomenon through the analysis of data acquired by a device that is not in contact with the subject under investigation. Object extraction from remote sensing acquired data has been an important research topic in computer vision for many years. Some useful applications of this subject include map creation, urban city planning, and land use analysis. For instance, building extraction and delineation is one of the most important tasks in map feature extraction. Obviously, the automation of such tasks can lead to greater productivity, resulting in reduced timelines for map production.
High-resolution satellite imaging sensors provide a new data source for building extraction that is of low cost or even free of charge. The high spatial resolution of the imagery reveals very fine details in urban areas and greatly facilitates the classification and extraction of urban-related features such as roads.
Many techniques have been developed to extract buildings from high-resolution satellite imagery. These techniques can be classified, according to the need for involvement of human experts, into three main categories as follows: (1) manual; (2) semi-autonomous; and (3) autonomous.
Manual techniques for the extraction of buildings from high-resolution satellite imagery are slow and require huge amounts of time. Thus, semi-autonomous and autonomous techniques have been proposed to improve the speed and utility of various applications such as urban map production.
One can easily observe that high-resolution satellite imagery contains two categories of buildings: (1) buildings with sloped roof tiles; and (2) non-tile flat roof buildings. Most existing studies and proposed techniques in the literature focus on the detection of either roof tile buildings, or non-tile flat buildings which have standard rectangular structures. It is rare to find studies on both types.
The contributions of this paper are as follows. Firstly, we present a thorough review and classification of all available techniques for building detection using satellite images. Secondly, we introduce an autonomous and highly accurate approach for roof tile and flat building detection, known as Building Detection with Shadow Verification (). This approach depends on both color and shape information extracted from satellite/aerial images. Color information is used to detect roof tile buildings using our defined color invariant threshold.
Shape information is based mainly on edge detection followed by line generation technique where generated lines are grouped into: (1) parallel and (2) perpendicular line sets. Non-tile flat building candidates are identified from the treatment of these two line sets. In addition, shadow information is used to verify the generated building hypotheses. Our proposed approach to detect and verify the presence of both roof tile buildings and non-tile flat buildings is robust and accurate due to the fusion of results obtained from both algorithms.
Moreover, we benchmarked our proposed approach with state-of-the-art building detection algorithms such as Markov random field model segmentation [
1], and the multi temporal marked point processes proposed in [
2]. Results reveal that BDSV records the highest overall quality percentage (
), in addition to the lowest execution time.
The remainder of this paper is organized as follows.
Section 2 presents a review of published work on building detection, including: (1) edge-based detection techniques; (2) object-based detection techniques; and (3) thresholding-based detection techniques.
Section 3 introduces the framework of our proposed
approach and discusses in depth both the roof tile and non-tile flat building detection algorithms that constitute the main components in
. The fine-tuning of various parameters is shown in
Section 3.
Section 4 presents performance analysis with benchmarking against state-of-the-art existing algorithms over the SztaKi–Inria and Istanbul building datasets using the RGB color format with 1.5 m/pixel and 0.3 m/pixel resolution, respectively. Finally, conclusions are given in
Section 5.
2. Literature Review
Building extraction from high-resolution satellite imagery is an active research topic in the photogrammetry and computer vision fields. Comprehensive surveys of research in this area can be found in [
3,
4,
5].
Considering both radiometry and geometry, many of these algorithms are edge-based detection techniques [
6,
7,
8] consisting of linear feature detection and grouping for parallelogram structure hypotheses extraction [
9]. In addition to linear feature detection approaches, other edge-based detection approaches rely on building polygons verification using the geometric structure of buildings [
7], shadow [
6,
10,
11,
12], and illuminating angles [
6], among others.
Park et al. [
13] use a rectangular building model to search and find missing lines relaying on detected lines by creating pairs of antiparallel lines over the roof using a line-rolling algorithm. A rectangular shape model can also be estimated using shadow information [
14], implementing a novel Markov random field (MRF)-based region-growing segmentation technique. An iterative classification is applied, and the final buildings are determined using a recursive minimum bounding rectangle.
The dominant orientation angle in a building cluster is studied in [
15], where local Fourier analysis is used to generate a building unit shape (BUS) space by recursive partitioning of regions using a hyperine in two-dimensional (2D) image space. A seeded BUS then searches for its neighbors and is grown until the predefined homogeneous criteria are satisfied.
Providing an approximate position and shape for candidate building objects is explored by Lee et al. [
16]. This method is based on classification on multispectral IKONOS imagery. Fine extraction is then carried out in the corresponding panchromatic image through ISODATA segmentation and squaring based on the Hough transform.
Segl and Kaufmann [
17] combined both supervised and unsupervised image segmentation for detection of buildings in suburban areas. A series of image classification results was generated by applying the thresholding technique with different values within a pre-defined range. The buildings were classified by shape matching with the database model. If the correct shape parameter is greater than an optimal threshold, then the object is classified as a building unit.
A region-growing algorithm on gray-scale images followed by using the edge map for the building presence verification is implemented in [
18]. Another approach is discussed in [
19], where the authors propose a low-level solution that effectively merges bi-dimensional and three-dimensional information to detect and analyze edges in satellite images.
A different group of building detection techniques is based on the combination of imagery and three-dimensional data. The use of two complementary sources of data usually improves the results. Most of these studies are based on two main approaches: object-based classification techniques and thresholding-based detection techniques.
In object-based classification techniques, image objects are created using automatic segmentation techniques. Then, the objects are characterized by means of spectral and height features, among others [
20,
21]. Approaches based on thresholding consist of the application of a threshold value to the normalized digital surface model (
) to discriminate buildings and vegetation, combined with a threshold applied to the normalized difference vegetation index (
) image in order to mask the vegetation. Then, buildings can be accepted or rejected according to different conditions, such as size and shape [
18,
22], spectral values [
23], or texture features [
24,
25].
A thresholding algorithm with the application of the
is implemented in [
26] , with a subsequent correction of the shape of the detected building based on alignments extracted from the imagery. Moreover, height data, active contours, and spectral information to extract the buildings are discussed in [
27].
In [
28], the authors propose a novel approach which depends on shadow information and color features to detect buildings. Finally, building shapes are determined using a novel box-fitting algorithm. Moreover, color information is also introduced in [
29] where the author apply a segmentation technique on the HSV color space in addition to edge features in order to extract buildings.
Besides the discussed building detection techniques, another approach based on a novel probabilistic model is presented in [
2]. The author introduces a new method which integrates building extraction with change detection in remotely-sensed image pairs. The method incorporates object recognition and low-level change information in a joint probabilistic approach. The accuracy is ensured by Bayesian object model verification, showing high accuracy percentages over several datasets.
The authors in [
1] propose a novel segmentation algorithm based on a Markov random field model. In addition, they present a novel feature-selection approach useful for detecting both roads and buildings. Experimental results reveal that the proposed framework is solid, robust, and unsupervised, with promising quantitative and qualitative results compared to other building detection methods.
On the other hand, it is observed that principal component analysis (PCA) is also utilized in building detection tasks. The authors in [
30] propose a building detection algorithm from pan-sharpened satellite color images, through eliminating non-building objects. First of all, vegetation and shadow regions are eliminated using the normalized difference vegetation index (NDVI) and the YIQ color space intensity ratio, respectively. Secondly, roads are masked out using a thinning morphological operation. Finally, PCA is implemented, resulting in false object removal, and thus buildings are retained. The proposed algorithm performance analysis is conducted over several study areas with different properties.
Dong [
31] presents an approach for building detection in high-resolution satellite images. This approach utilizes the automatic histogram-based fuzzy C-means (AHFCM) technique as an image segmentation task. Vegetation and shadow regions are masked out using NDVI and a ratio map in the HIS model, respectively. Finally, buildings are detected and classified through PCA.
3. BDSV Approach
Based on what we have reviewed in the previous section, we note that integrating multiple features such as color, geometrical structure, and reflectance shadow can improve the detection process reliability and robustness, especially in complex real scenes. In this section, we will discuss in depth our proposed approach for building detection known as Building Detection with Shadow Verification (), which is useful for extracting both roof tile and non-tile flat buildings.
Extraction of buildings with sloped roof tiles mainly depends on the color information contained in the image. Based on a color invariant defined as a color ratio later in
Section 3.1.1, the roof tile building identification task can be accomplished. Non-tile flat building extraction is more complex since it depends on the geometrical shape of the buildings. This task can be done using the edge and line features of the rectangular structural formation of buildings in the image.
Finally, in order to verify candidate detected buildings, shadow information is integrated. Candidate buildings with close shadows will be considered as actual buildings, otherwise they will be neglected.
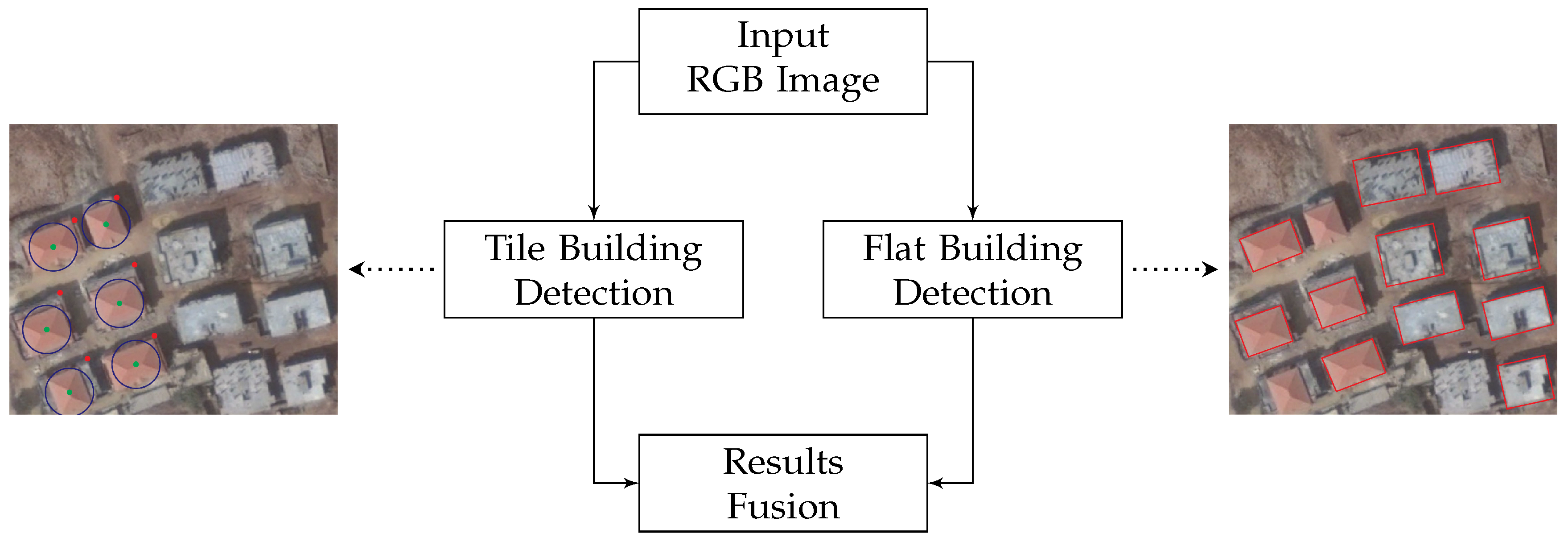
Figure 1 illustrates the overall block diagram of our proposed Building Detection with Shadow Verification (
) approach, which is composed of three main pillars as follows:
The tile building detection () algorithm: A proposed algorithm for the detection of roof tile buildings using color invariants.
The flat building detection () algorithm: A proposed algorithm for the detection of non-tile flat buildings based on edge and line features.
Results fusion: A fusion algorithm to integrate the results obtained by the algorithms above and select candidate buildings.
Figure 1 shows the result of applying
and
to the Jiyyeh area in Mount Lebanon where both roof tile and non-tile buildings exist.
was able to successfully detect roof tile buildings marked with a blue circle with the green dot referring to the detected building centroid and the red dot representing the shadow centroid. A red rectangle is used to illustrate buildings detected by
which are mainly non-tile buildings and some of the roof tile ones.
Although by design focuses on the detection of flat buildings, in the previous study area it was able to detect some roof tile buildings with rectangular shapes. Moreover, although is focused by design on detecting roof tile buildings, theoretically it would be able to detect a flat building with a red-colored roof. The choice of algorithm names ( and ) is only meant to reflect the type of buildings upon which each algorithm is focused. Further details about both algorithms will be presented in the following sections.
3.1. The Tile Building Detection (TBD) Algorithm
Roof tile building detection algorithm is mainly based on the color features extracted from satellite/aerial image. For the scope of this work, we focus on red roof tiles, which are commonly available in our country and the region. The proposed technique can be easily extended to account for other tile colors.
A new color invariant to detect vegetation areas has been suggested in [
32]. In this work, we define a color ratio (
) related to red roof tile building, and then a thresholding technique is applied using the calculated
. After that, different morphological operations are performed in order to verify the presence of buildings.
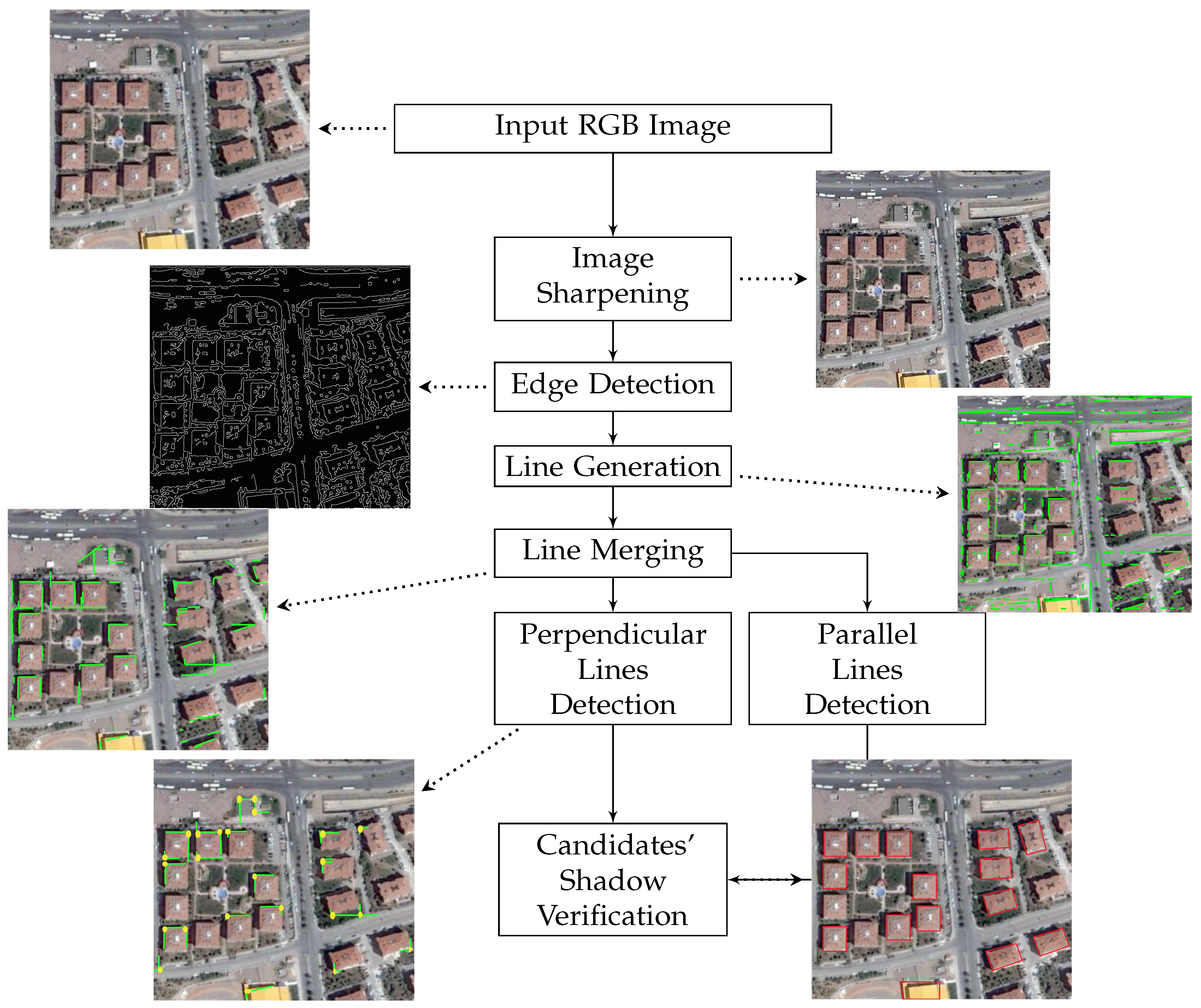
Figure 2 illustrates the block diagram of this algorithm to be discussed thoroughly in the coming subsections.
3.1.1. Image Color Invariant
Color invariants help to extract color properties of objects without being affected by imaging conditions. We extract the color information in the aerial image using a specific color index based on a study [
33] where red and near-infrared bands are used. We follow here the same strategy to define a color invariant, using red and green bands of the color aerial image as shown in Equation (
1) [
28]:
where
R stands for the red band and
G stands for the green band of the color image. This color invariant has a value of unity for red-colored objects independent of their intensity values. Similarly, it has a value of minus unity for green-colored objects in the image. The fraction aims to increase the contrast of red objects within the image. As discussed in [
33], the
is a nonlinear transformation and the normalization by
/4 is used to give values between −1 and 1.
Generally, the most popular roof tiles used in our country and the region are red, so it can be easily segmented using the proposed color ratio with great accuracy. can be easily extended to detect other roof tile colors like blue and green.
3.1.2. Image Thresholding and Hole Filling
Image thresholding is the principle of applying a useful operation in order to separate out the regions of the image corresponding to objects in which we are interested from the regions of the image that correspond to background. Thresholding often provides an easy and convenient way to perform this segmentation on the basis of the different intensities or colors in the foreground and background regions of an image.
Image thresholding results in a binary image that consists mainly of two regions: objects of interest and the background region. There are a lot of techniques used in image processing, but the common thread among these different techniques is that all of them use a threshold as an input for the thresholding operation. For the sake of tile building detection (
), we use the color ratio image generated in the previous step as a input image to the local thresholding technique, which transforms the color ratio image into a binary image using a
color invariant threshold as depicted in
Figure 2. The obtained binary image contains the regions of interest (red roof tile buildings), but these regions are not closed regions, i.e., there are some holes in each object. Hence, in order to eliminate these holes and get enclosed building candidates, we must apply traditional hole-filling technique.
3.1.3. The Area Verification and Shadow–Building Pair Hypothesis
After applying the holes filing step, we get a resultant image that contains building candidates and some non-building objects that have the same color as buildings rooftops. In order to eliminate non-building objects, we apply a disc erosion morphological operation. The structuring element (SE) disc size is calculated based on the average area of building candidates since in general, buildings within the same region usually have a similar size.
Moreover, building candidates are verified according to the area criterion (building area), which is represented by the number of pixels per building. This area is defined as the average area of a building in the study area.
The final operation in the algorithm is to eliminate falsely detected building candidates. This is achieved by calculating the distance between each building candidate centroid represented by a green dot, and its relative shadows centroid represented by a red dot. This distance must be below a pre-defined building–shadow distance threshold. Any building candidate with no relative shadow that adheres to this hypothesis is eliminated. For illustration purposes, -detected buildings are delineated by a blue circle and -detected buildings will be highlighted using a red rectangle.
It is worth mentioning that shadows can be segmented using any robust algorithm from the literature. For the scope of this work, we relied on HSV shadow detection technique proposed in [
34]. Since we rely on the shadow centroid, the time of day where the image is taken is not of high impact. However, if the building shadow is missing, then it will result in a false positive.
3.2. The Flat Building Detection (FBD) Algorithm
In this section, we will discuss our proposed algorithm, known as flat building detection (), used to detect all types of buildings that have the regular rectangular shape, but also buildings that have at least one right angle. depends mainly on edge detection and line generation techniques. Resultant lines need to be filtered and processed to eliminate non-relevant lines, only keeping those representing building boundaries.
In our line-merging routine, we first divide detected lines into two classes: (1) perpendicular lines and (2) parallel lines. In the first class, for treatment we consider that every right angle is a building candidate, while in the second one we consider that every two parallel lines separated by a predefined distance are building boundaries. Finally, the results obtained by the two classes are merged, and thus building candidates are obtained.
Figure 3 shows the block diagram for this algorithm.
3.2.1. Image Sharpening and Edge Detection
mainly relies on the edge properties of buildings. That is why in the preprocessing stage of the proposed algorithm the sharpening filter is applied to show fine details and improve the edge detection performance.
Of the several known edge detection algorithms (Sobel, Canny, LoG, Roberts) [
35], Canny edge detection is used in this study. The Canny algorithm provides several advantages over other edge detection techniques where it produces one pixel wide edges and connects broken lines. Those lines are crucial for the remaining blocks in this algorithm.
3.2.2. Line Generation and Merging
Detected edges in the previous block are the points with a zero second derivative in the input image. In order to detect buildings, these discrete points must be grouped using the Hough transform to form straight lines [
36]. For each edge pixel, the Hough transform searches for other nearby pixels that will form straight lines taking into account a threshold distance so that pixels with a distance larger than the threshold value are discarded.
As shown in
Figure 4a, generated lines are not connected and suffer from gaps and discontinuities. In our line-merging block, if the gap between the lines’ segment is below a threshold (the
line-merging distance), then these lines are merged. The line-merging procedure calculates the Euclidean distance between each line starting/ending point and all other line starting/ending points. Therefore, in every iteration, we get a pair of two nearest lines, and we obtain also a new line which represents the two merged lines.
Figure 4b shows a sample output of the introduced line-merging technique. By the end of the iterations, non-merged lines are eliminated, reducing the search space and improving the runtime of subsequent blocks.
It is worth noting that previous blocks were implemented using existing libraries in Matlab (off-the-shelf), however the line-merging block and all remaining ones were designed and implemented by the authors.
3.2.3. Perpendicular Line Detection
Buildings usually have at least one right-angle, and thus we assume that every two perpendicular lines form a building’s corner. In this block, we iterate over merged lines and calculate the angle between each pair (perpendicular line angle). If the calculated angle is between 80 and 100 degrees, then we consider that these two lines are perpendicular. Perpendicular line pairs are merged to form a right-angle. Each right-angle is considered as a seed point for a building candidate.
In order to calculate the angle between two lines, first we obtain the vector representation of each line. Using the vector representation, we calculate the norm of each vector. The last step before calculating the angle between the two vectors is to calculate their dot product. Finally, the angle between vectors
and
is given by :
3.2.4. Parallel Line Detection
As part of the parallel line pairs detection, two conditions must be verified: (1) the angle between the two lines must be less than 10 degrees, (
parallel line angle) and (2) the distance between those two lines must be bounded within certain thresholds that represent the distance of building’s parallel sides (
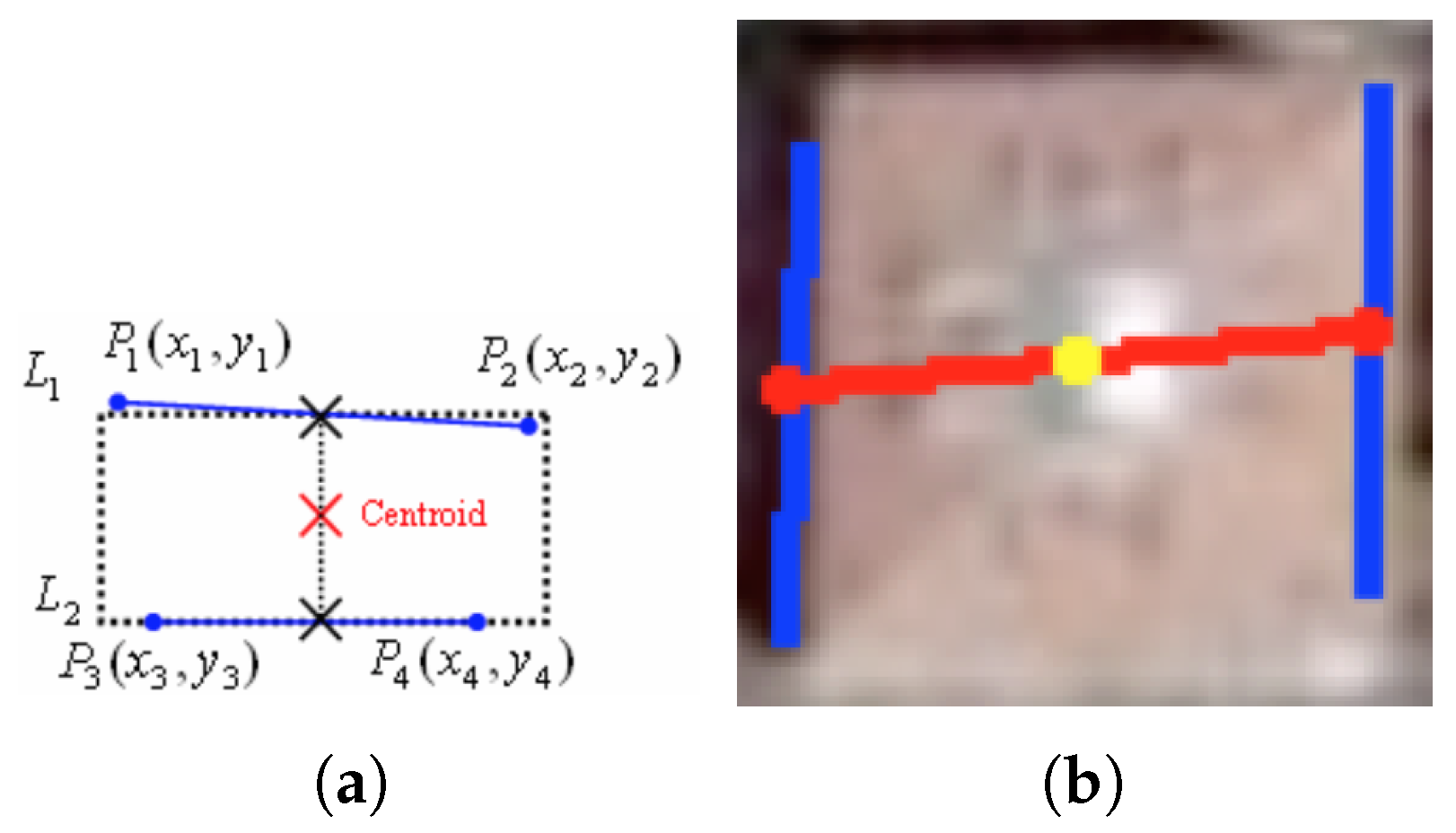
parallel line distance). For each pair of detected parallel lines, a new virtual line connecting their midpoints is generated. The midpoint of the newly generated line is considered as a seed point for building candidate.
Figure 5a,b show an illustration of the theoretical and real case implementation of generating building candidate seed point from a pair of parallel lines.
3.2.5. Candidates’ Shadow Verification
In this final step, we consider all the resulting right angles from the perpendicular line treatment, and all the resulting midpoints from the parallel lins treatment as seeds points for building candidates. It is worth mentioning here that a building structure could be detected via both parallel and perpendicular verification conditions where parallel line detection and perpendicular line detection complement each other.
For parallel line building candidates, we apply the same verification condition as for buildings candidates through calculating the building–shadow distance distance, and any parallel lines building candidate with no relative shadow will be eliminated.
On the other hand, the distance between buildings candidates right corner and shadows centroid is referred to as the right corner–shadow distance. If this distance is less than a specific threshold, then the presence of a building is verified.
This verification block is important to eliminate non-building candidates such as parked cars or swimming pools. These structures could be detected as buildings due to their standard rectangular shape, however they usually do not have a corresponding shadow centroid.
3.3. Results Fusion
Integrating multiple cues and characteristics of buildings can leads to better results in building detection operation. The results obtained by both building detection algorithms ( and ) are combined using a simple OR operation. Detected buildings are marked by a tick that can be either red, green, or black, as illustrated in the following.
In the last block, we define the following five states:
State 1: true buildings detected by both , and . These buildings will be highlighted by red and green ticks in the results section.
State 2: true buildings detected by , but not by . These buildings will be highlighted by red ticks only in the results section.
State 3: true buildings detected by , but not by . These buildings will be highlighted by green ticks only in the results section.
State 4: true buildings not detected by both and . These buildings will be highlighted by black crosses in the results section.
State 5: false buildings detected by either or . These buildings will be highlighted by black ticks in the results section.
We use a simple logical operator for , where candidates belonging to States 1, 2 and 3 are considered real buildings.
4. Parameter Tuning
In this section, the numerical values of different thresholds used in and will be presented and discussed.
The algorithm contains three thresholds: (1) the area condition threshold building area to eliminate falsely-detected objects; (2) the color invariant threshold by which the color invariant image is transformed into a binary image, where all pixels with values greater than the threshold are rounded up to one; and (3) the building–shadow distance threshold used for building candidate verification. This threshold represents the distance between building centroid and corresponding shadow centroid.
With respect to the
algorithm, five thresholds were defined in this manuscript. Firstly, in the line-merging routine, the minimum distance between two lines to be merged must be less than a pre-defined
line-merging distance threshold. Secondly,
parallel line angle represents the value of the angle between two lines in order to be considered as a pair of parallel lines. Thirdly, the distance that separates a pair of parallel lines as discussed in
Figure 5 must belong to the
parallel line distance threshold interval. Fourthly, the angle between two perpendicular lines must be bounded within the
perpendicular line angle. Fifthly, the
right corner–shadow distance represents the distance threshold between right corner building candidate and its relative shadow centroid.
and
sub-routines and relative thresholds are summarized in
Table 1.
Two approaches can be followed to assign values for various thresholds: (1) a static approach where these values are manually assigned and tuned according to the environmental conditions of the study area; and (2) a dynamic unsupervised approach that relies on the existing study area to learn how to set these thresholds. For instance, the average area of all detected building candidates under consideration in the study area can be used to set the value of building area.
For the scope of this work, we will stick to the static approach where we manually assign the thresholds’ values based on the study area environmental conditions. Future work will focus on devising unsupervised approach to learn how to set these thresholds.
Table 2 presents a description of all used thresholds throughout this manuscript and corresponding values used over Istanbul dataset in
Section 5.
5. Result Analysis
In this section, we will benchmark results with several state-of-the-art buildings datasets used in the literature. Performance metrics used in the Istanbul Dataset benchmark will be based on a set of parameters including the miss factor (MF), branching factor (BF), and the quality percentage (QP), for reporting algorithm performances. Many researchers use these definitions to report the efficiency of their systems. Based on these definitions, all objects in the image are categorized into four types.
True positive (TP). Both manual and automated methods label the object belonging to the buildings regions.
True negative (TN). Both manual and automated methods label the object belonging to the background.
False positive (FP). The automated method incorrectly labels the object as belonging to the building regions.
False negative (FN). The automated method does not correctly label a pixel truly belonging to the building regions.
To evaluate performance, the numbers of objects that fall into each of the four categories TP, TN, FP, and FN are determined, and the following measures are computed:
The interpretation of the above measures is as follows. The branching factor is a measure of the commission error where the system incorrectly labels background objects as buildings. The miss factor measures the omission error where the system incorrectly labels buildings objects as background. Among these statistics, the quality percentage measures the absolute quality of the extraction and is the most important measure. To obtain 100% quality, the extraction algorithm must correctly label every building (FN = 0) without mislabeling any background objects (FP = 0).
Moreover, the following performance parameters will be used in evaluating the SztaKi–Inria dataset benchmark, in accordance with other works.
5.1. The SztaKi–Inria Dataset
In this section,
will be benchmarked with various building detection algorithms studied in [
2], where the authors propose a new framework for building detection and introduce a comprehensive analysis between their algorithm, and other state-of-the-art algorithms over the
SztaKi–Inria dataset which includes eight study areas satellite images in RGB color format with a resolution of 1.5 m/pixel.
The benchmarked algorithms used are defined as follows:
key point-based method [
37]: a supervised building detection algorithm, where the input image must be characterized by a couple of template buildings which are used for training. Its main drawback is that for images containing a high variety of buildings may need a huge template library, which is hard to control.
method [
38]: detects buildings according to joint probability density functions of four different local feature vectors, and performs data and decision fusion in a probabilistic framework to detect building locations.
Edge-verification (
) method [
28]: depends on edge information, where an edge map is produced. Fitting the building rectangles and verification of the proposals are based purely on the Canny edge map of the obtained candidate regions. For dense urban areas the processing time and the appearance of false edge patterns.
Segment–Merge (
) method [
39]: considers building detection as a regional-level or image segmentation problem. This method assumes that buildings are homogeneous areas w.r.t. either color or texture. It can fail if the background and building areas cannot be efficiently separated with the chosen color or texture descriptors.
method [
2]: is an object-change modeling approach based on multi temporal marked point processes, which simultaneously exploit low-level change information between the time layers and object level building descriptions to recognize and separate changed and unaltered buildings.
method [
1]: is based on Markov random field model segmentation. This segmentation algorithm is based on class-driven vector data quantization and clustering and the estimation of the likelihoods given the resulting clusters. The main contribution depends on the estimation of likelihoods in order to reach higher accuracy percentages in the building detection operation.
The benchmarking process will be be applied at three levels: (1) object-level performance analysis; (2) as a pixel-level performance benchmark; and (3) for computational time analysis. The results for SZADA1, SZADA2 and SZADA3 will be combined and reported in the following tables as SZADA. Similarly, results for COTE D’AZUR1 and COTE D’AZUR2 study areas will be merged and reported as COTE D’AZUR.
resultant output on SztaKi–Inria dataset dataset is shown in
Figure 6 where subfigures
Figure 6a–h show the resultant output of applying DBSV , respectively, on the SZADA1, SZADA2, SZADA3, Budapest, Bodensee, Normandy, COTE D’AZUR1, and COTE D’AZUR2 study areas. The resultant output shows the efficiency of
in roof tile building detection. Even though
records some false positives among different study areas, it succeeds in improving the overall accuracy by detecting several non-tile flat buildings.
Object-level performance analysis is done over SztaKi–Inria dataset using missing objects (
) and false objects (
) performance metrics, in addition to the
F–Score metric defined in Equation (
7) which represents the overall accuracy of the algorithm.
Table 3 shows the object-level accuracy assessment results of benchmarking
against the
,
,
,
, and
algorithms. It is worth mentioning that
records the lowest
and
values, thus outperforming all the benchmarked algorithms with an overall F-score of
.
The authors of [
1] use pixel-level accuracy assessment to compare their unsupervised building and road classification algorithm against existing ones in the literature. Pixel-level performance benchmark and accuracy assessment rely on the
(
) metric defined earlier in Equation (
9),
(
) shown in Equation (
6), and the
F1-score defined in Equation (
8).
In
Table 4, we benchmarked
in addition to several algorithms. It is clearly shown that
records the highest
and
values for all study areas, indicating the high efficiency of our proposed building detection approach. As a result,
ranked first in terms of overall
F1-score with a value equal to (
).
Finally,
Table 5 shows the computational time of applying several benchmarked algorithms over each study area separately.
outperforms all the benchmarked algorithms in recording the lowest computational time, which makes it more faster in execution even in study areas containing large number of buildings as in the case in the
and
.
5.2. Istanbul Dataset
The authors of [
28] propose a novel method for building detection by defining a set of parameters used in shadow detection, in addition to determining shapes of the buildings using edge information. They present the Istanbul dataset which includes 12 study areas: five of them contain only red roof tile buildings, while the remaining seven study areas contain both roof tile and non-tile flat buildings.
For the scope of this work, we will focus in particular on three study areas that contain both roof tile and non-tile buildings, since the remaining study areas have similar environmental characteristics. The chosen images are: (1)
which includes buildings having various sizes; (2)
, a suburban study area including vegetation zones; and finally, (3)
, a study area that contains highway, cars, and trees, in addition to target buildings. The Istanbul dataset is described in
Table 6. The aerial images used are in
color format with a 0.3 m/pixel resolution.
The
study area contains two non-tile flat buildings and the resultant images of applying
are shown in
Figure 7. As can be noted from
Figure 7a,
detected 9 roof tile buildings, whereas
Study Area contains 11 roof tile buildings.
did not detect the two buildings located on the right top of the
study area, due to their small area as compared to the other buildings.
detected 10 of 13 buildings, and it classified a garden wall as a building due to its rectangular shape as shown in
Figure 7b. The
in
Figure 7c ensures that all buildings in the
study area are detected with only one
classified object. Therefore, we can observe that
outperforms algorithm suggested in [
28] for the
study area.
Table 7 shows a detailed accuracy assessment of applying
on the
study area. Analysis of
results reveal two important issues. First, for study areas which contains buildings with great variation in sizes,
will fail in detecting all colored rooftop buildings. Future work will focus on handling this drawback. Second, the garden detected as a building by
is due to the enclosure wall shadow. Usually, rectangular-shaped structures such as parking lots, swimming pools, tennis courts, and gardens will have no relative shadows in most cases.
The
study area has the same environmental conditions as the
study area with much more complexity due to the non-uniform distribution of buildings. The results of applying
on the
study area are shown in
Figure 8.
missed only one green-tiled roof building located in left-bottom corner of the study area, as seen in
Figure 8a. This issue will be addressed in the future work since currently
focuses on red-rooftop buildings only. Output results reported in
Table 8 reveals that
has zero
objects, while algorithm suggested in [
28] scored six
objects, as we will see later.
is an urban area that contains additional objects classes such as cars and roads.
in
Figure 9a succeeded in detecting all 16 red roof tile buildings, while
detected 11 buildings, as shown in
Figure 9b. With results fusion in
Figure 9c,
records only one false negative,
. The accuracy results of the
study area are tabulated in
Table 9 where
detected 23 buildings out of 24 with
, and the algorithm suggested in [
28] detected 20 buildings with
as we will see next.
Table 10 shows a detailed comparison of
and the algorithm suggested in [
28] for the three images from Istanbul dataset. The
metric defined in Equation (
9) is utilized for this comparison as reported in [
28]. It is obvious that
records higher precision for the three areas, which reveals the superiority of our proposed approach in detecting both roof tile and non-tile buildings. Moreover
records lower
, which indicates that
have less commission error in labeling background objects as buildings.
Finally,
Table 11 shows the frequency of occurrence of various states in the
block for all five study areas considered so far. The recorded states for the various areas used in the results analysis clearly show the importance of using multiple criterion, i.e., the color and shape properties of a building unit.
State 5 shows the high efficiency of in detecting true buildings, where it records only one false building in the study area. As is clear from the State 4 column, rarely fails in detecting target objects. It missed two buildings in Study Area 2 and only one in both and due to building closeness and overlapping. The between , and increase the robustness of our building detection technique, which is clear from State 1 being mostly lower than the sum of both State 2 and State 3. This results in more accurate detection, especially in mixed urban areas that contain both roof tile and non-tile flat buildings.
6. Conclusions
In this paper we present an approach known as Building Detection with Shadow Verification to detect buildings from RGB aerial images. We suggest to extract roof tile buildings based on color features. We also present to detect non-tile flat buildings with rectangular shapes based on edge information. The algorithm shows a great efficiency in detecting colored rooftop buildings. has some limitations in complex environments where we have a non-uniform distribution of buildings, since right corner estimation becomes a difficult task.
Experimental results reveal the high performance of the proposed method on a 11 different study areas belonging to the SztaKi–Inria dataset and the Istanbul dataset, where outperforms state-of-the-art algorithms in terms of the overall quality percentage (), the overall executional time (15.97 s), and the precision metric. The integration of machine learning techniques will be applied in future work, leading to more accurate results, especially for improving performance in detecting and validating different building shapes, thus improving overall BDSV performance.