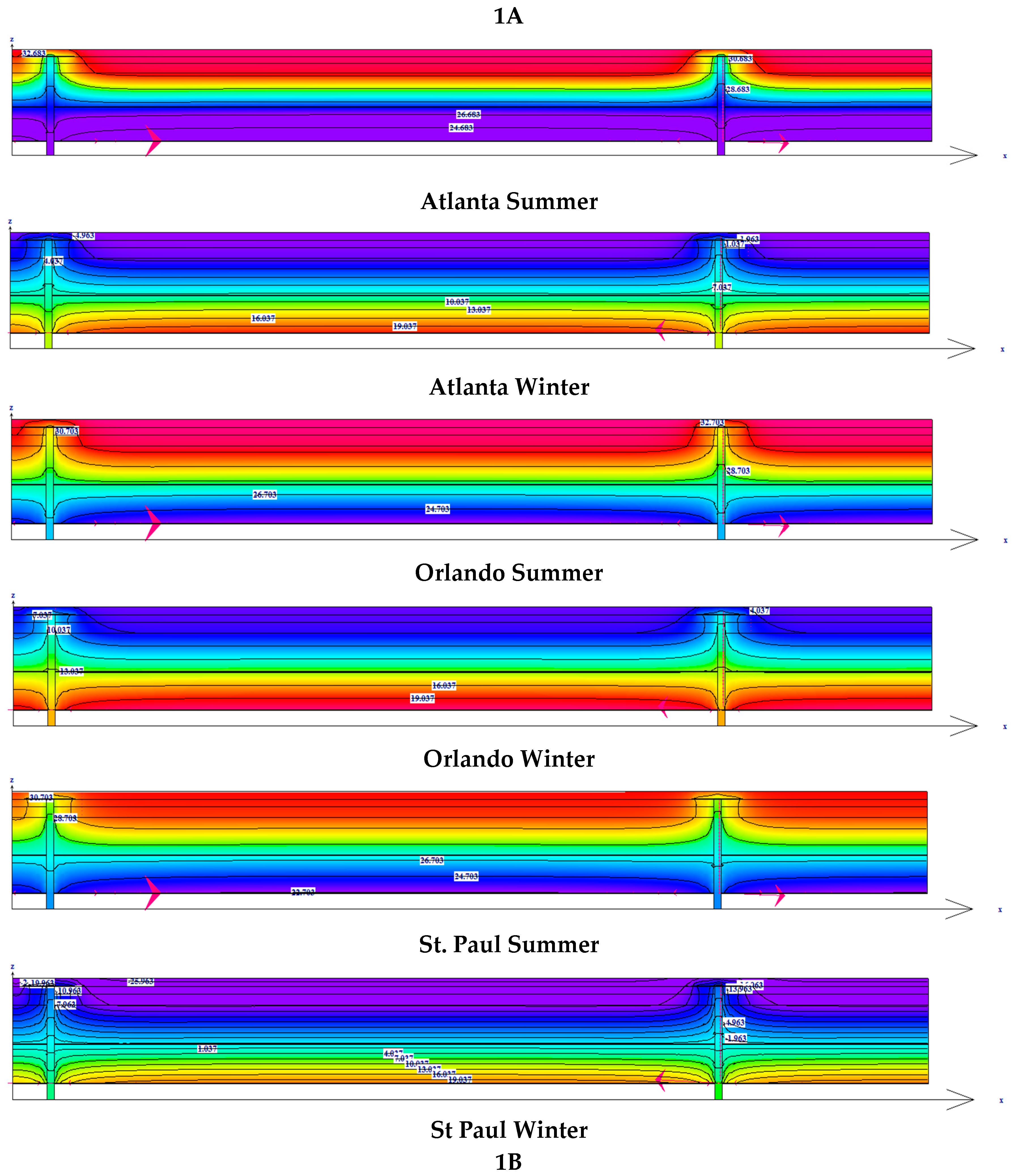
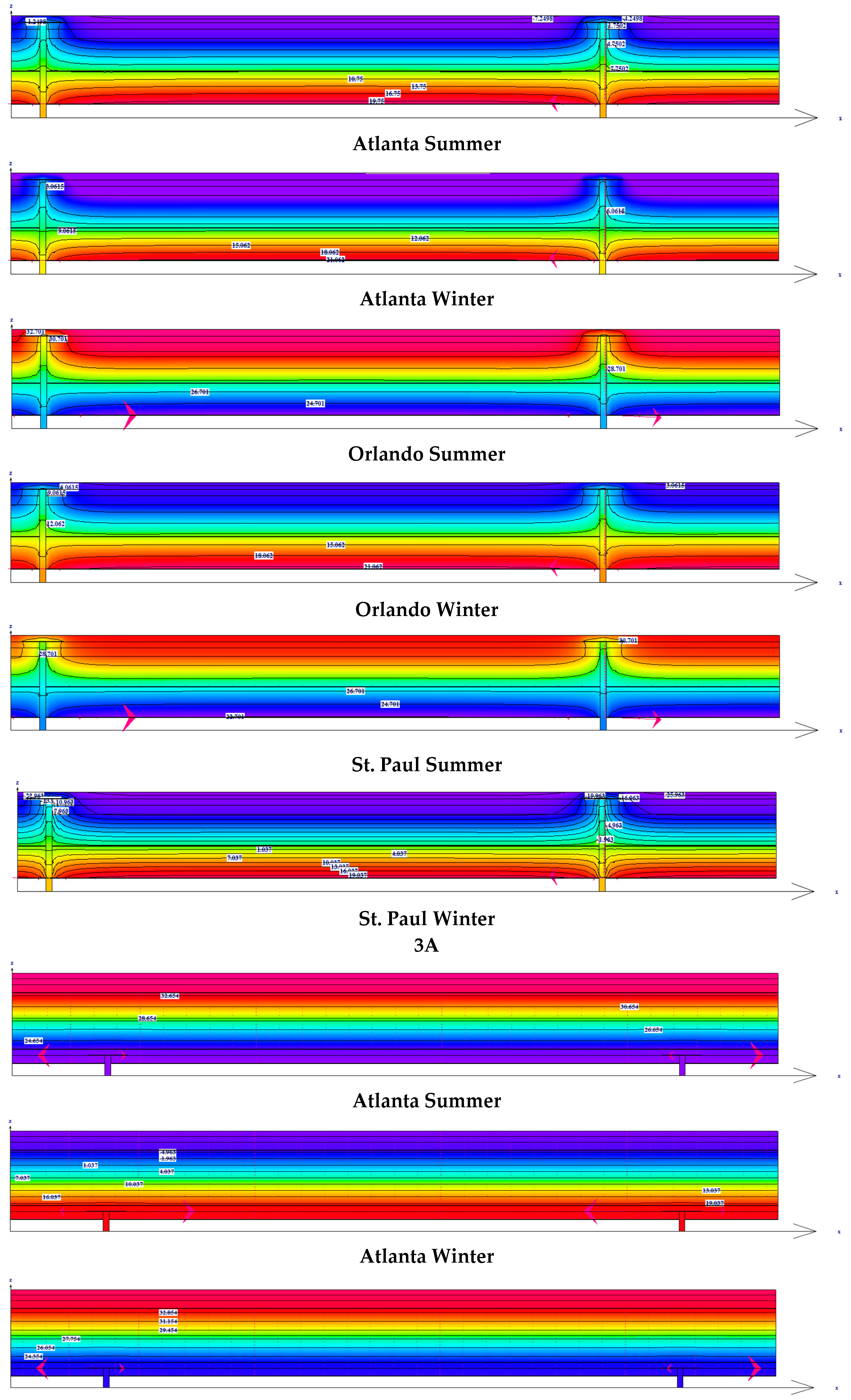
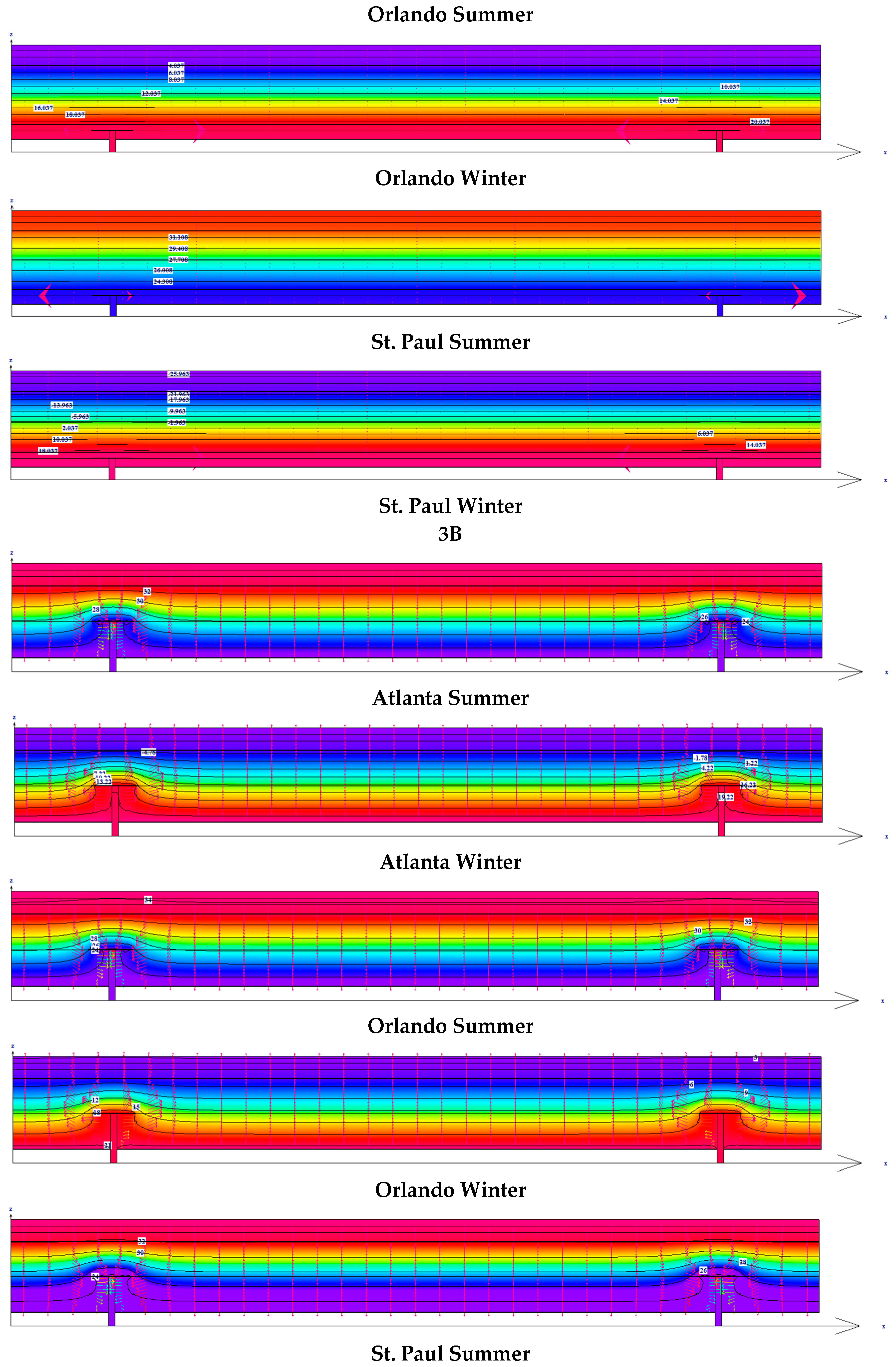
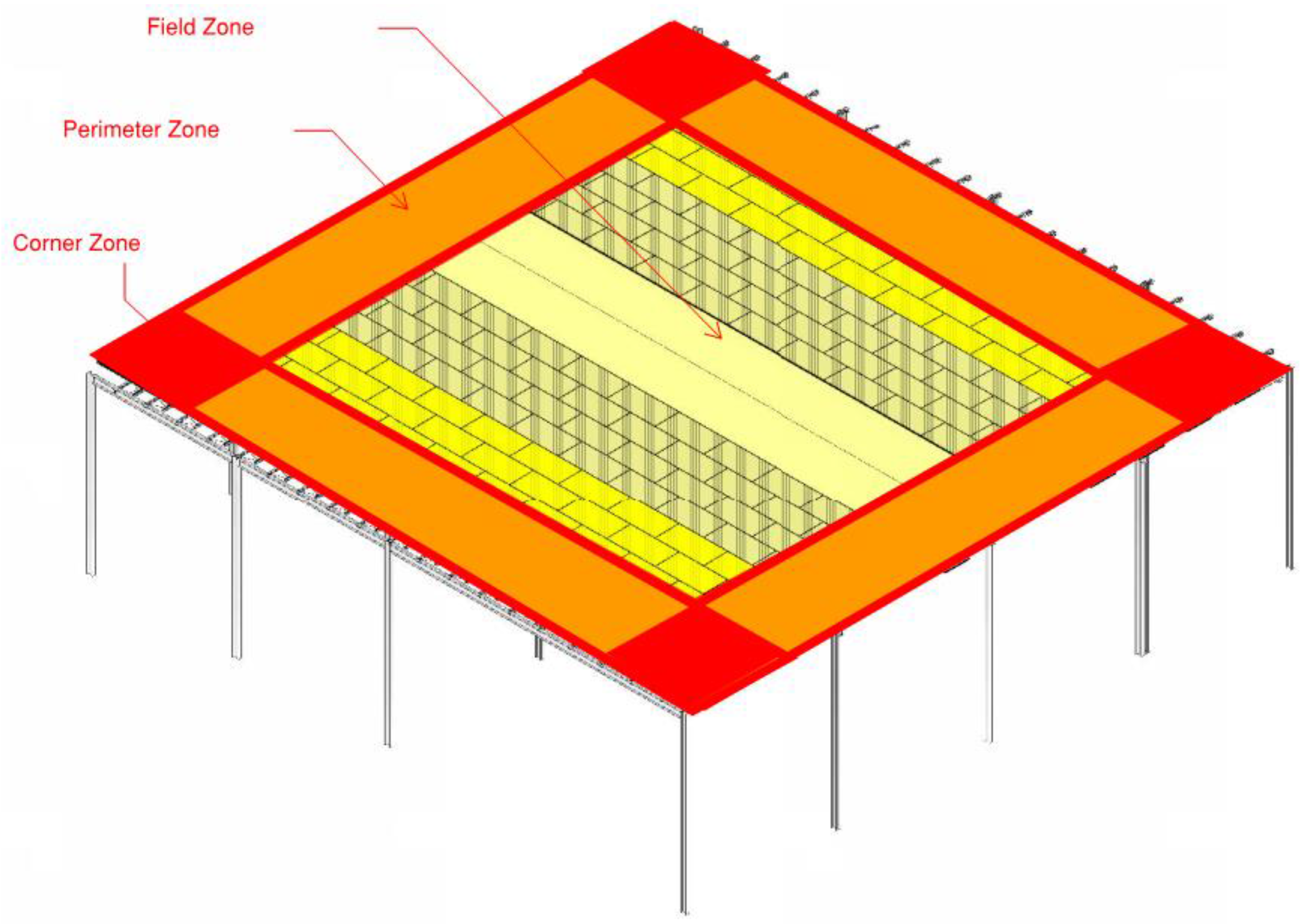
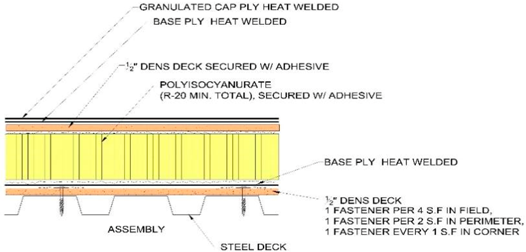
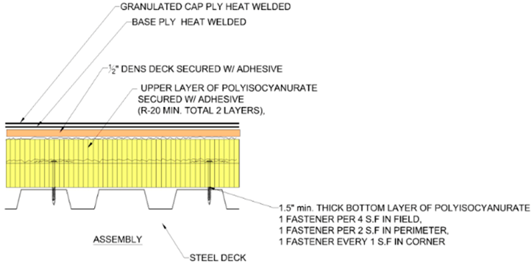
The entire assembly is modeled in zones as the Field, Perimeter and the Corner zone separately with fastener density specified in the standards for the specific areas.
Figure 3 below shows the isometric view of one of the models to get a clear understanding of the assembly analyzed. The results are presented in three sections emphasizing on comparing the effect of metal fasteners in a single assembly, the comparison of different roofing assemblies with standard fastener arrangements and graphical analysis of the impacts of thermal bridging on the basis of heat transfer.
4.1. Analysis of the Effect of Fastener Density on Heat Transfer through the Roofing Assemblies
In this section, the effect of thermal bridging on a particular assembly is analyzed. In other words, the heat transfer through the roofing assembly is quantified and tabulated as per different zones under different climatic conditions. These different zones are basically the measure of fastener density with the field zone having minimum and the corner zone having the maximum number of fastener per unit area. Heat transfer per unit area is tabulated in
Table 5 below along with the metal deck temperatures for all 3 zones of Assembly 1B, taken as example, under different climatic conditions. The “total” heat loss per unit area calculated in each case is based on the averaged value of heat transfer over a 10,000 sq. ft. roof with 6400 sq. ft. as field zone, 3200 sq. ft. as perimeter zone and 400 sq. ft. at the corner zone.
In order to understand the results, Assembly 1B is emphasized (12″ O.C.) and the heat transfer data is tabulated. It is clearly evident from
Table 5, that as the fastener density increases, the heat loss also increases which can be attributed to the much higher thermal conductivity of metal fasteners as compared to the insulation and other roofing materials. The heat flowing through the assembly tends to take the route with the least resistance and thus the major portion of heat flows through the metal fasteners instead of going through the insulation layers. As a result of this process, the majority of heat transfer occurs through the metal fasteners. This hypothesis can be clearly understood with
Figure 4.
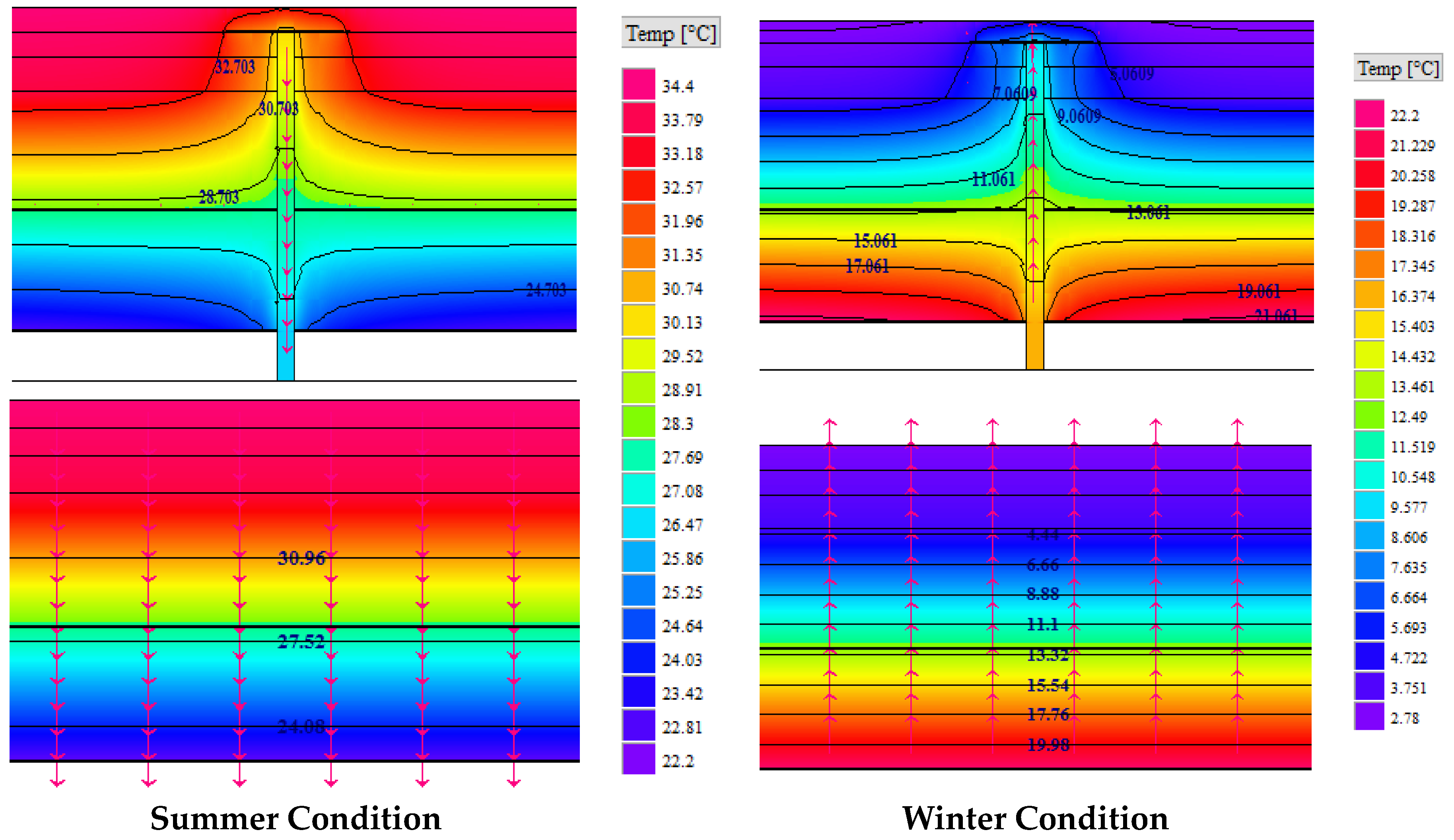
As can be seen from
Figure 4, in case of summer, the heat flows from outside towards inside through the route of metal fasteners. In addition, the temperature around the fastener is seen to be higher than the rest of the assembly. On the other hand, in case of “no fasteners”, the heat flow and the temperature distribution is uniform throughout the assembly. This figure clearly indicates the mechanism of heat flow through an assembly with metal fasteners acting as the major career of heat flow and also provides an evident justification that why there is a sudden increase in heat loss going from cases of “No Fasteners” to the Field zone with fasteners. For in-depth understanding, isotherms for each case analyzed are provided in
Appendix A.
In addition, the percentage change in
R-Value is calculated through the difference between the case of “No Fasteners” and the “Total” including all three zones with their areas according to the ASHRAE standards. The following formula is used to calculate the effective
R-Value of the entire assembly.
where Δ
T is the temperature difference between inside and outside of the assembly;
q is the heat transferred per unit area.
The percentage
R-Value change is calculated taking the effective
R-Value using the given formula in case of “No Fasteners” as baseline.
Using this formula, the percentage change in effective R-Value for Assembly 1B is about 35% in total (including field, perimeter and corner zones). A change of this magnitude in overall effective resistance can be understood practically on the basis of the fact that in case of the 1B assembly considered, the length of the fastener runs almost through the entire section of the assembly thus providing a considerably low resistance pathway for the heat to travel and avoiding the high thermal resistance path through the insulation.
When noted separately in the field zone of 1B, where the fastener density is 1 fastener per ft
2, the change in
Reffective was found to be 32%. These results coincide with the previous work of Olson et al. (
Table 2) [
3] where the percentage change in
Reffective came out to be around 28% when 1 fastener per ft
2 was considered. The 4% difference in the results can be attributed to the different fastener sizes used in the Olsen et al., (2015) study. This work used the # 14 (0.245″ thread diameter) fasteners as opposed to # 12 fasteners (0.22″ thread diameter) used in case of Olson et al., (2015) which directly infers an increase in cross-sectional area of fasteners by about 24%.
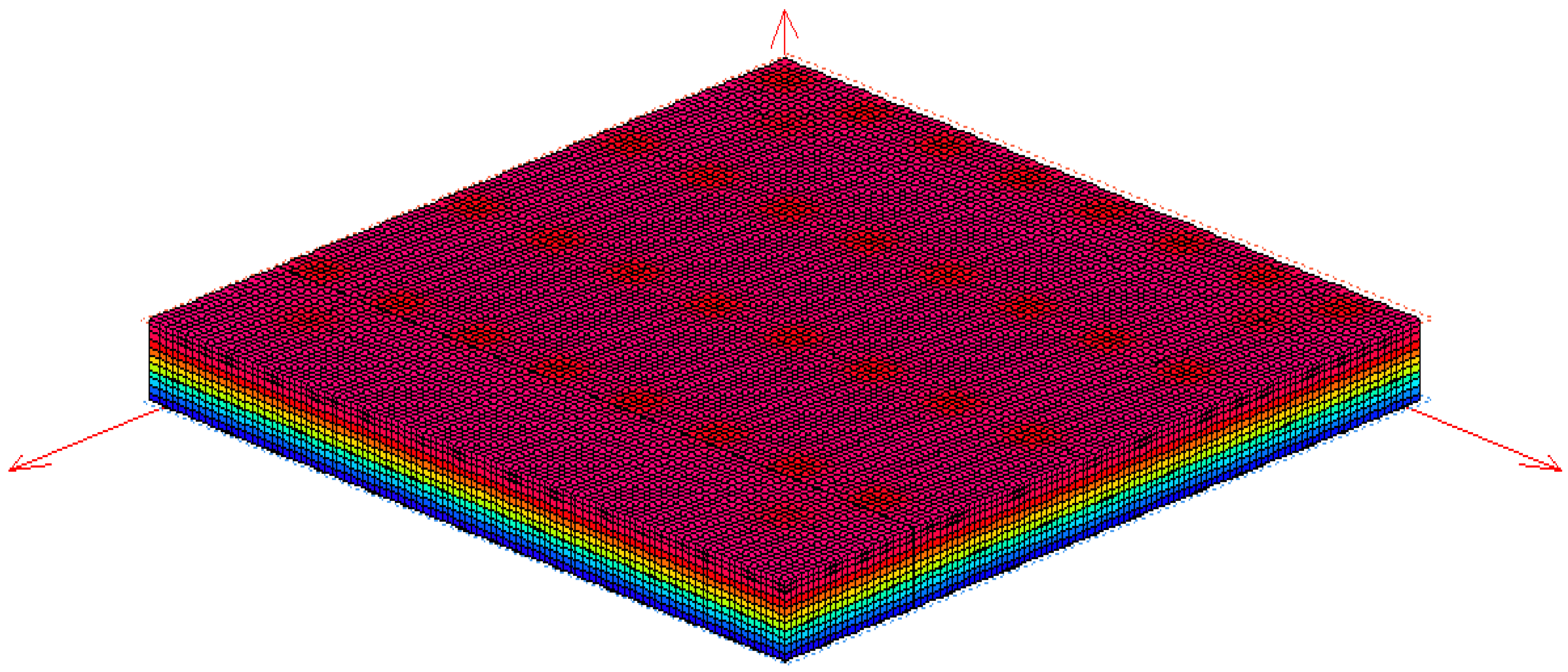
A cut out section from the corner zone assembly is shown in
Figure 5 to provide a graphical representation of how the temperature varies through various layers.
4.2. Comparative Analysis of Different Roofing Assemblies with Fasteners
In this section, different roofing assemblies and the extent of change in
Reffective (h·ft
2·°F/Btu) due to fasteners in each case are discussed. The only case considered here for explanation is for CZ2 (Orlando Summer) and all the data in
Table 6 is based on total area of 10,000 sq. ft. containing the field, perimeter, and corner zones.
The “Prescribed design value” case mentioned in
Table 6 denotes the
Reffective value of the entire assembly where R-20 insulation is used and no effect of fasteners is considered, as is prescribed by the Standards. On the other hand, the “Actual Value” is calculated with taking into account the effect of thermal bridging due to metal fasteners arranged accordingly in the Field, Perimeter and Corner zones of a 10,000 ft
2 roof.
The data in
Table 6 shows a much higher change in
Reffective in case of assemblies 1A and 1B as compared to 3A and 3B assemblies. In addition to the fact that assemblies 3A and 3B has comparatively less fastener density than 1A and 1B, this difference can be understood by the composition of the two assemblies, as in case of 1A and 1B the fasteners run through the entire thickness of the roof and connects two very different boundary conditions with their high thermal conductivity and thus transfers more heat. On the other hand, in case of Assembly 3A and 3B the fasteners cover only a small fraction of the thickness of the assembly with not so different boundary conditions on their two ends. For this reason, very low amount of heat transfers through them and the majority of the heat loss has to go through the insulation with extremely less thermal conductivity. The difference between the cases of Assembly 1A and 1B can be understood on the basis of the density of fasteners as in case of 1A the fasteners are 6″ O.C. as compared to 12″ O.C. and it is already established under section 1 that heat loss and thus the percentage change in
Reffective is directly proportional to the fastener density.
Also if a single assembly is considered under different climatic conditions, there is a slight difference among the percentage
Reffective change values for summer and winter conditions but the change is not prominent and can be explained on the basis of the fact that there is higher temperature difference in case of winter conditions. This variation is shown in the
Table 7 below.
The percentage Reffective change is seen to slightly higher in case of winter condition due to higher temperature difference between inside and outside design conditions and the metal plate present on the inside of the assembly i.e., high conductivity metal in exposure to the warmer region.
4.3. Energy Loss Analysis
Now in order to get a better understanding of the practical impacts of this thermal bridging, the energy loss is quantified in case of each assembly under all three design conditions. As discussed earlier, the total area here is 10,000 ft
2 with standard Field, Perimeter, and Corner zones in case of “Actual Value”. Where else the case of “Prescribed Design Value” depicts the energy loss where no effect of thermal bridging is considered as in case of Standards. The data presented in
Table 8 consists of heat transfer per unit area averaged over a total area of 10,000 sq. ft.
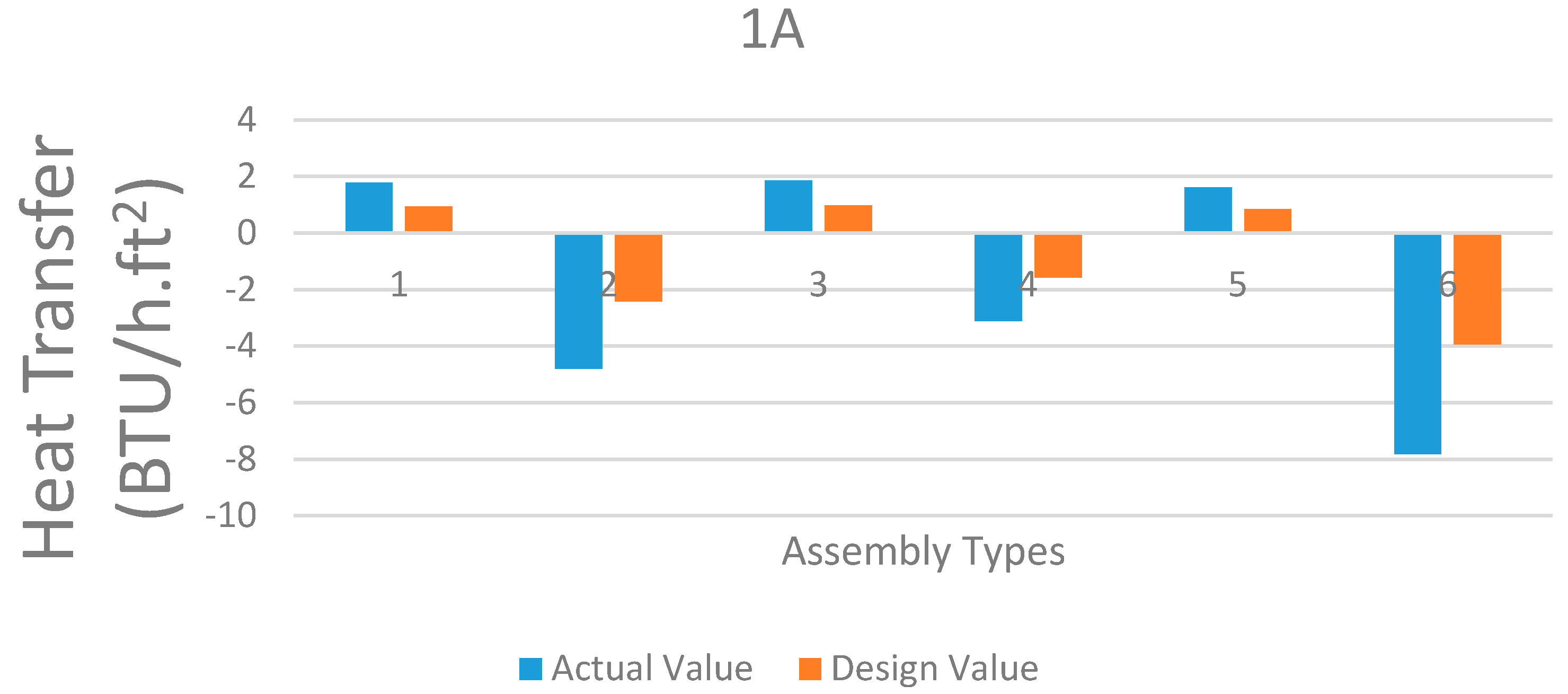
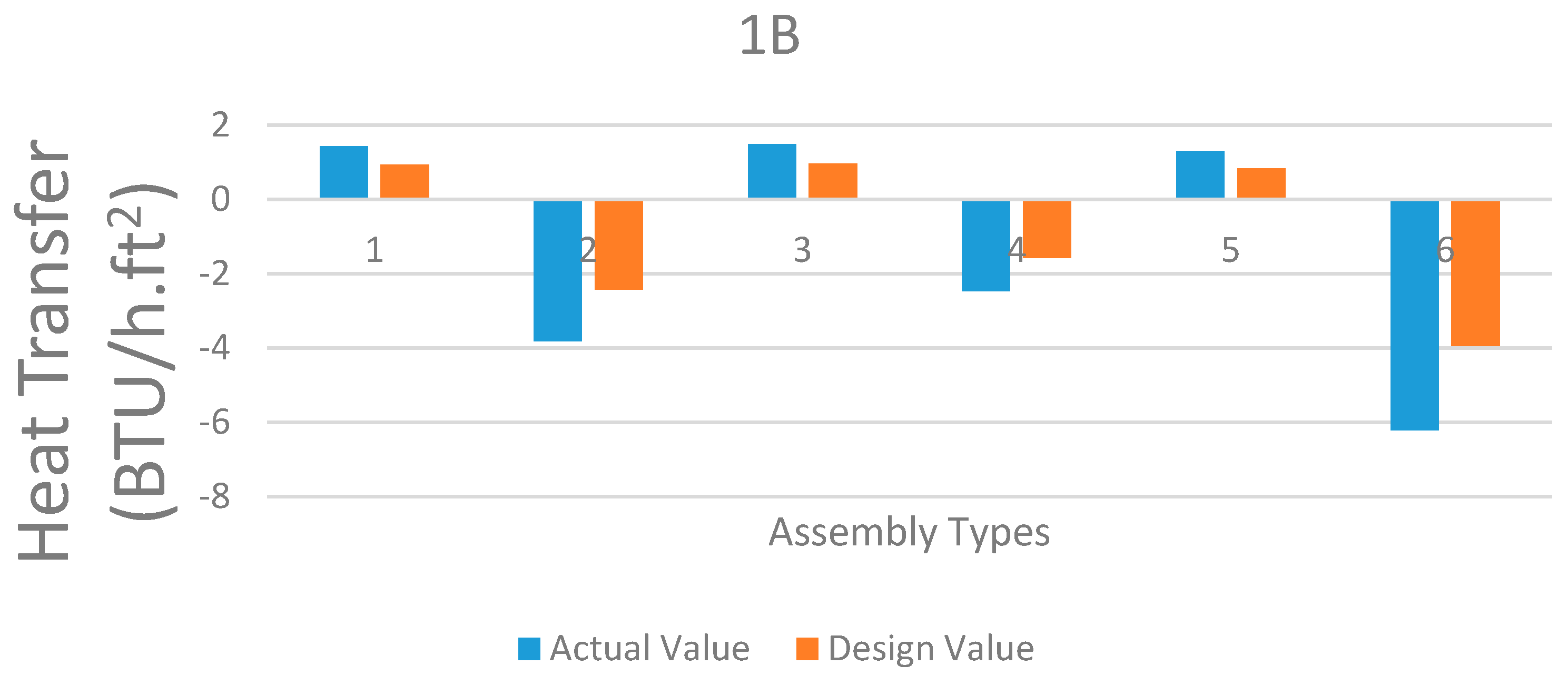
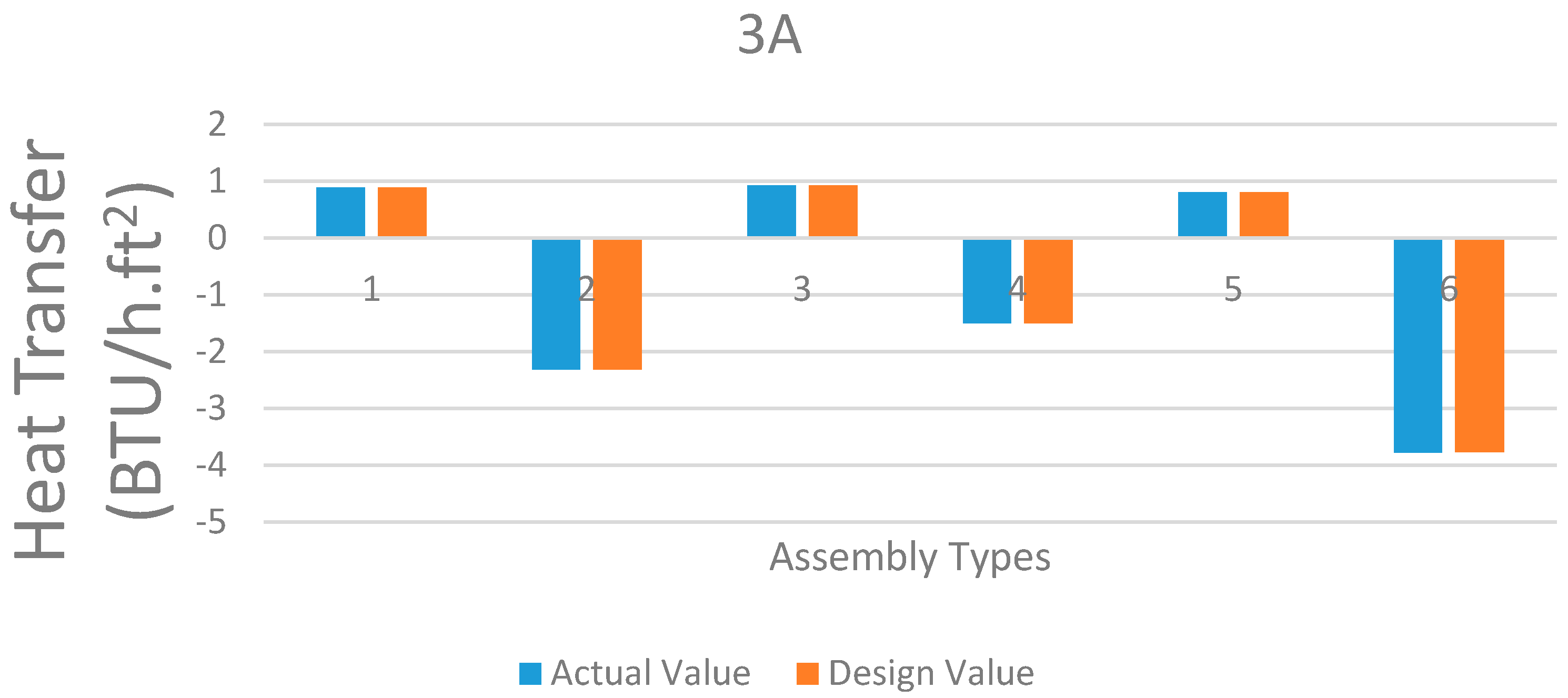
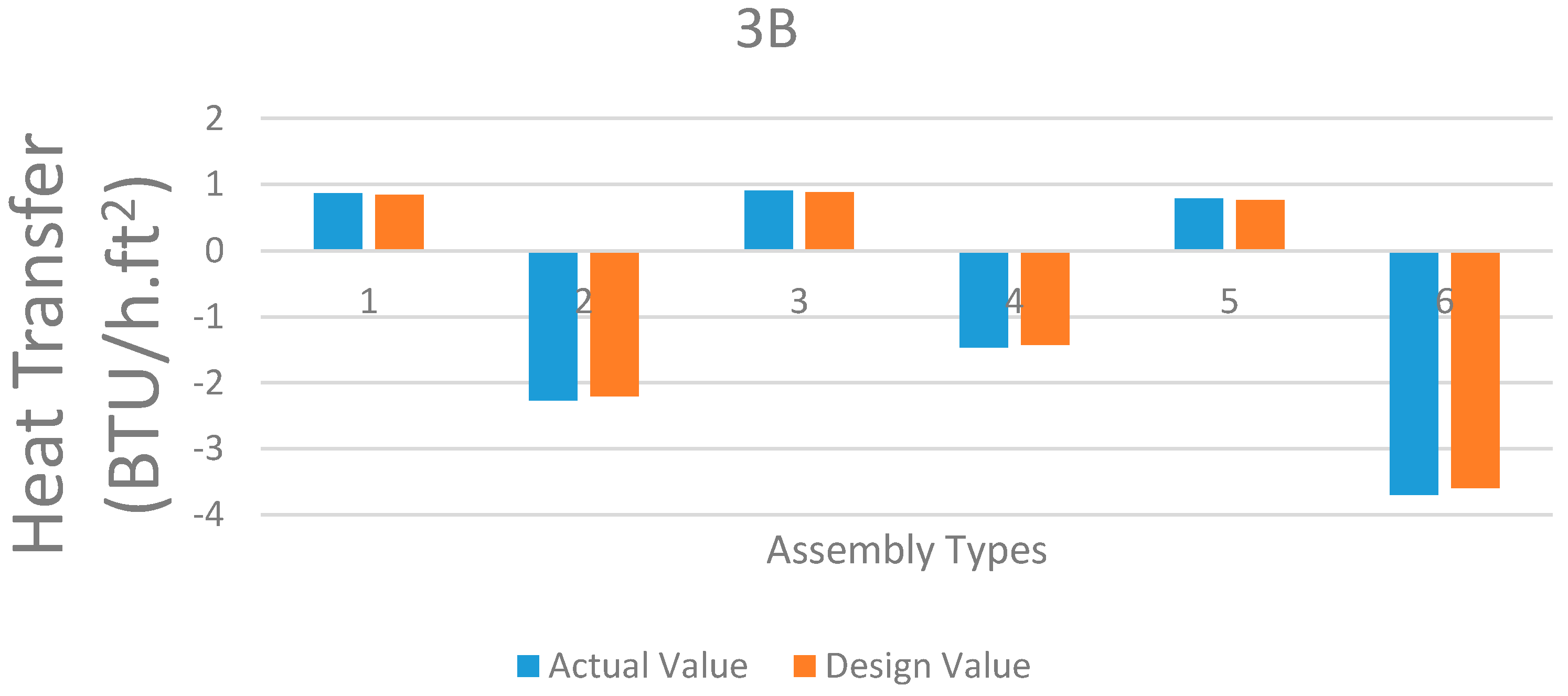
The data in
Table 8 is plotted separately for each assembly, depicting the difference between the heat loss values inducted due to the presence of metal fastener. The six weather conditions depicted in
Table 8 are represented as different bar charts numbered from 1 through 6.
Figure 6,
Figure 7,
Figure 8 and
Figure 9 shows the comparative study of heat transfer through the roofing assemblies under different design conditions. It also provides a graphical representation of the extra heat wastage in the practical/actual case compared with the ideal design case without considering any effect of metal fasteners. It is clearly visible that a large amount of heat losses incurred due to the phenomenon of Thermal Bridging due to metal fasteners and plates. Another notable synopsis is that the heat losses in case of Assemblies 3A and 3B are not only much lower than 1A and 1B but also the relative change in heat loss due to Thermal Bridging is minimal.
4.4. Comparison of 2D (THERM) and 3D (HEAT3) Analysis
However, the results when compared with those of Gulati et al., (2016) [
4] and Suddappalli et al., (2016) [
5], turned out to be substantially different. The net heat transfer in case of 3D analysis turned out to be comparatively less and the metal deck temperatures were moderate as compared to the 2D THERM analysis. The following
Table 9 summarizes the comparison of metal deck temperatures in case of CZ2 (Orlando, FL) zone.
The reason for this difference can be accredited to the limitations of two-dimensional analysis. In case of Gulati et al., (2016) and Suddappalli et al., (2016), the net energy loss is calculated using Convective Heat Transfer Equations based on the metal deck and fastener tip temperatures where else in this analysis the heat loss is obtained by direct simulations through the software. In order to understand the difference, another single fastener assembly was modeled in HEAT3 with minimizing the depth (dimension in y-direction) to a minimum possible value i.e., less than the depth of the fastener and thus eliminating one dimension for heat dissipation through the fastener. This was done to make the three-dimensional model as similar as possible to the two-dimensional model. The results of this simulation in three-dimensional came out to be almost similar and tending towards the two-dimensional analysis as the metal deck temperatures came to coincide. The results of this analysis proved the reason for difference in results to be the transition from two to three Dimensions. To understand the practical difference in the two cases, in case of two-dimensional, there is one less direction for dissipation of heat and thus more heat travels through the assembly via fasteners. In addition, in case of two-dimensional, there is no surface area for fasteners to dissipate heat in any direction other than upwards and downwards through the Assembly which results in much more heat flux flowing through the fastener. As opposed to this mechanism, the fasteners in case of three-dimensional model have surface area in each direction and thus heat flows in all three directions. This heat flow system is coincident with the actual heat flow mechanism through the Assembly.