Robust Optimization of Hospital Regional Integrated Energy Systems Based on Multi-Scenario Weight Scanning

Abstract

Regional Integrated Energy Systems (RIESs) are pivotal in the low-carbon transition of energy-intensive hospital campuses. However, traditional multi-objective optimization for RIES planning often suffers from the subjective selection of weights, leading to configurations that lack robustness against varying decision-maker preferences. To address this, this paper proposes a robust optimization methodology integrating shadow cost theory and multi-scenario weight scanning. A high-fidelity dynamic simulation model of a hospital in Beijing was constructed using TRNSYS. By monetizing environmental externalities into shadow costs, a comprehensive objective function, including annual cost savings rate, primary energy savings rate, and environmental shadow cost savings rate, was established, and the Hooke–Jeeves algorithm was employed to scan ten distinct weight scenarios, ranging from profit-driven to eco-centric preferences. The results reveal that solar collectors lack economic competitiveness under current boundary conditions due to cooling–heating coupling constraints. Instead, a configuration featuring a large-capacity gas turbine (2790 kW) coupled with a moderate GSHP was identified as the optimal solution in over 80% of the scenarios, demonstrating high preference robustness. Crucially, this configuration achieves net-negative emissions by maximizing clean power exports to displace carbon-intensive grid electricity. Compared to the reference system, the optimized RIES reduces primary energy consumption by 82.7% and achieves substantial environmental benefits, subject to grid emission factors. These findings confirm that prioritizing clean power export is a resilient pathway for hospitals to balance economic feasibility with environmental goals under current policy frameworks, providing scientific guidance for policymakers and engineers.

1. Introduction

Driven by the escalating global energy crisis and environmental degradation, there is a widespread consensus on the urgent need to enhance energy efficiency and mitigate carbon emissions [1]. Regional Integrated Energy Systems (RIESs) have emerged as a pivotal solution for low-carbon transition, enabling the cascade utilization and synergistic carbon sink complementation among different energy forms [2,3]. Hospitals, with their continuous 24/7 demands, substantial load volatility, and stringent reliability standards, are ideal candidates for RIES deployment [4,5].

In recent years, extensive research has been conducted on RIES optimization. Early work primarily focused on single economic objectives [6,7,8,9], which failed to meet increasingly stringent environmental regulations. Subsequent research shifted towards multi-objective optimization (MOO) to balance economic costs, energy consumption, and environmental emissions. MOO methods are generally categorized into no-preference, a priori, and a posteriori methods [10]. No-preference methods (e.g., global criterion method) do not rely on decision-maker preferences but focus on neutral compromise solutions, thus having limited application in energy systems. A priori methods require preference articulation before solving, commonly using the weighted sum or ε-constraint methods. For example, Zeng et al. [11] combined the weighted sum method with genetic algorithms for CCHP optimization. Liu et al. [12] used the ε-constraint method to quantify the trade-off between economic and environmental goals, finding that a 57% reduction in carbon emissions increased costs by 15.1%, while also highlighting that shared energy storage can significantly reduce both investment and emissions. A posteriori methods aim to generate a Pareto solution set [13]. For example, Qiao et al. [14] achieved an 8.16% emission reduction and 2.25% efficiency improvement using the Fruit Fly Optimization Algorithm. Chen et al. [15] proposed a gas turbine/PV/storage system, using multi-objective optimization to achieve a balance among energy efficiency (PESR up to 53.08%), power supply reliability (EMR reaching 99.88%), and environmental economy. While comprehensive, they leave the difficult task of selecting the final “best” solution to the decision-maker, often leading to confusion when the Pareto front is dense [16,17].

Despite these advancements, critical gaps remain in the existing literature regarding the handling of objective weights and environmental valuation. First, traditional weighted sum methods rely heavily on expert experience or the Analytic Hierarchy Process (AHP), where minor subjective fluctuations in weights can lead to vastly different “optimal” configurations. Second, most studies optimize for a fixed set of weights, failing to account for preference robustness. In practice, decision preferences often shift due to external policy changes (e.g., carbon tax implementation) or internal budget constraints, and a configuration optimized for a single weight set may perform poorly if priorities change. Third, environmental objectives are often treated as physical quantities (e.g., tons of CO₂), making them mathematically incommensurable with economic objectives, which leads to the use of arbitrary scaling factors.

To address these limitations, this paper proposes an optimization method that quantifies environmental value based on “shadow costs” and ensures robustness through “multi-scenario weight scanning.” First, a dynamic simulation model of the hospital Renewable Integrated Energy System (RIES) was constructed using TRNSYS 17. Shadow cost theory is introduced to monetize the emissions of CO₂, NO_x, and SO₂ into social marginal abatement costs. A weighted optimization model is established targeting the Annualized Cost Saving Rate (ACSR), Primary Energy Saving Rate (PESR), and Shadow Cost Saving Rate (SCSR). Second, to address the lack of preference robustness, a multi-scenario weight scanning strategy is implemented. Instead of identifying a single optimal point based on fixed weights, the system is optimized across ten distinct preference scenarios spanning the decision space to identify a configuration that remains optimal regardless of whether the priority is cost or environment. Finally, the Hooke–Jeeves algorithm is employed to identify the configuration that appears most frequently and is least sensitive to weight changes. This solution is proposed as the robust optimal configuration balancing economy, energy saving, and environmental protection, and is compared and analyzed with the reference system.

2. Methodology

2.1. RIES Construction and TRNSYS Modeling

This study selected a general hospital in Beijing as the case study to construct a RIES encompassing energy generation, conversion, storage, and consumption. The core of the system consists of a Combined Cooling, Heating, and Power (CCHP) subsystem and a Ground Source Heat Pump (GSHP) subsystem, integrated with auxiliary equipment, such as solar collectors (SC) and Electric Chillers (EC). The overall system architecture is illustrated in Figure 1.

During the heating season, the building’s thermal load is met by the joint operation of CCHP, GSHP, and SC. Heat generated by the CCHP serves as the base load; meanwhile, the GSHP and SC act as peak-shaving and supplementary sources, with their on-off status and output dynamically adjusted based on real-time solar irradiance and load demand. During the cooling season, the cooling load is supplied jointly by CCHP, GSHP, and EC. Specifically, the high-temperature exhaust gas from the gas turbine (GT) first drives the Lithium Bromide (LiBr) Absorption Chiller (AC); the GSHP and EC are then utilized to satisfy the residual load and handle load fluctuations. Regarding electricity, power generated by the CCHP is prioritized for self-consumption. Any deficit is purchased from the grid, while surplus electricity is sold to the grid.

The TRNSYS 17 transient simulation platform was employed for full-condition modeling, simulation, and performance analysis. Utilizing its modular component library, a high-fidelity physical model was constructed to ensure the accuracy of thermodynamic calculations (

Table 1. The main components used in the simulation.

Component	Type
ASHP	Type236
GSHP	Type927
EC	Type666
Boiler	Type700
Cooling Tower	Type162
AC	Type107
SC	Type71
GT	Type120a
Control	Type666
Heat Exchanger	Type5b
Buried Pipe	Type557a
Meteorological Parameters	Type15-2
Load Calculation	Type682
Quantity Integrator	Type24
Online Graphical Plotter	Type65c

). Simulations were conducted with a 1 h time step over 8760 h. The interaction between the optimization algorithm (MATLAB 2016) and TRNSYS was handled via the text-based modification of the input file (.dck), allowing iterative variation in component capacities. The operation strategy of the RIES, established based on multi-energy complementarity and coordination, is shown in Figure 2.

2.2. Mathematical Model of Main Equipment in RIES

2.2.1. CCHP Model

The CCHP system serves as the core energy supply unit in the RIES, primarily consisting of a prime mover, heating devices, and cooling equipment. GT, acting as the core prime mover, is modeled as follows:

$$E_{\mathrm{GT},i}=G_i{\eta }_{\mathrm{GT},i}^e$$

(1)

$$Q_{\mathrm{GT},i}^h=G_i{\eta }_{\mathrm{GT},i}^h$$

(2)

Based on operational data from a typical commercial GT, the functional relationship between power generation, outdoor ambient temperature, and exhaust waste heat is obtained through data fitting:

$$E_{\mathrm{GT},i}=1.758Q_{\mathrm{GT},i}^h+1620T_i-1003932$$

(3)

where E_GT,i denotes the power generation of the gas turbine at time i, kJ/h; G_i is the heat value of natural gas input at time i, kJ/h; ${\eta }_{\mathrm{GT},i}^e$ represents the power generation efficiency at time i; $Q_{\mathrm{GT},i}^h$ is the exhaust waste heat of the gas turbine at time i, kJ/h; ${\eta }_{\mathrm{GT},i}^h$ is the waste heat recovery efficiency; and T_i is the outdoor dry-bulb temperature at time i,°C.

2.2.2. AC Model

The Lithium Bromide (LiBr) AC is the primary device for waste heat recovery in the CCHP system. Its energy conversion efficiency is characterized by the coefficient of performance (COP). The relationship between heat consumption and cooling output at any given time is expressed as:

$$Q_{\mathrm{AC},i}^c=CO{P}_{\mathrm{AC},i}{Q}_{\mathrm{GT},i}^h{\eta }_{\mathrm{B},i}$$

(4)

where $Q_{\mathrm{AC},i}^c$ is the cooling capacity of the AC unit at time i, kJ/h; COP_AC,i is the COP of the unit at time i; and η_B,i denotes the waste heat recovery efficiency.

2.2.3. GSHP Model

A GSHP is a crucial device for both winter heating and summer cooling, utilizing borehole heat exchangers. Its performance is characterized by the heating coefficient of performance (COP^h) and cooling coefficient of performance (COP^c), modeled as follows:

$$Q_{HP,i}^h=E_{HP,i}^{h}CO{P}_{HP,i}^h$$

(5)

$$Q_{HP,i}^c=E_{HP,i}^{c}CO{P}_{HP,i}^c$$

(6)

where $Q_{HP,i}^h$ and $Q_{HP,i}^c$ represent the heating and cooling output of the GSHP at time i, kJ/h, respectively; $E_{HP,i}^h$ and $E_{HP,i}^c$ denote the power consumption of the GSHP under heating and cooling modes at time i, kJ/h; and $CO{P}_{HP,i}^h$ and $CO{P}_{HP,i}^c$ are the COPs for heating and cooling modes, respectively.

2.3. Optimization Model

2.3.1. Comprehensive Evaluation Index System

To achieve a multi-dimensional evaluation, a dimensionless comprehensive objective function F is defined as the weighted sum of ACSR, PESR, and SCSR. The expression of F is shown in Equation (7):

$$F=\alpha ACSR+\beta PESR+\gamma SCSR$$

(7)

where ACSR, PESR, and SCSR compare with the reference system (Gas Boiler + Electric Chiller). A higher value indicates better performance. α, β, and γ are the corresponding weighting coefficients, satisfying α + β + γ = 1 and 0 ≤ α, β, γ ≤ 1.

In this study, robustness is defined as “preference robustness”: the ability of a system configuration to remain the optimal choice across a wide range of subjective weight preferences. This differs from “parameter robustness” (sensitivity to load/weather). A configuration that appears most frequently across diverse weight scenarios is considered the most robust choice for decision-makers with uncertain priorities. To mitigate subjectivity, ten representative weight scenarios are established (

Table 2. Weight scenarios for multi-objective optimization.

Number	α	β	γ
1	0	0	1
2	1	0	0
3	0	1	0
4	1/3	1/3	1/3
5	0	2/3	1/3
6	0	1/3	2/3
7	1/3	0	2/3
8	2/3	0	1/3
9	1/3	2/3	0
10	2/3	1/3	0

), effectively mapping the vertices and the center of the decision simplex. The optimization algorithm is executed for each weight scenario to obtain a set of optimal configurations $X_{opt,i}$. Finally, the frequency of each configuration across all scenarios is statistically analyzed. The configuration with the highest frequency is selected as the final recommendation.

Economic Indicator (ACSR)

The Annualized Total Cost (ATC) is adopted as the evaluation criterion, which includes the annualized value of initial capital investment, annual operating costs (fuel, electricity purchase, and maintenance), minus revenue from electricity sales.

$$ACSR=1-{\displaystyle \frac{AT{C}_{RIES}}{AT{C}_{Ref}}}$$

(8)

$$ATC={\displaystyle \frac{p·i}{1-{(1+i)}^{-n}}}+C_g{V}_g+C_{el,b}{\displaystyle \sum _{i=1}^{8760}\frac{E_{b,i}}{3600}}-C_{el,s}{\displaystyle \sum _{i=1}^{8760}\frac{E_{GT,i}}{3600}}+\mu P$$

(9)

where ATC is the annualized total cost, CNY; P is the total initial investment, CNY; i is the annual interest rate (6.5%); n is the system lifespan (20 years); c_g is the natural gas price, CNY/m³; V_g is the gas consumption, m³; C_e,s and C_e,b are the grid feed-in price and electricity purchase price, CNY/kWh, respectively; μ is the maintenance factor (0.03); and subscripts ATC_RIES and ATC_Ref denote the RIES and reference system, respectively.

Energy Efficiency Indicator (PESR)

The primary energy consumption (PEC) is used for evaluation, converting electricity and natural gas into standard primary energy.

$$PESR=1-{\displaystyle \frac{PE{C}_{RIES}}{PE{C}_{Ref}}}$$

(10)

$$PEC={\displaystyle \sum _{i=1}^{8760}\frac{E_{b,i}}{{\eta }_{grid}{\eta }_e}}+35588V_g$$

(11)

where PEC denotes primary energy consumption, kJ; η_grid is the average power generation efficiency (0.92); and η_e is the grid transmission efficiency (0.35).

Environmental Indicator (SCSR)

Unlike traditional assessments that only count physical emissions, this study introduces shadow cost theory to internalize the marginal social cost of pollution abatement. The calculation is as follows:

$$SCSR=1-{\displaystyle \frac{PS{C}_{RIES}}{PS{C}_{Ref}}}$$

(12)

$$PSC={\displaystyle \sum _{k\in \left\{{\mathrm{CO}}_2,{\mathrm{NO}}_x\right\}}{T}_k·E_k}$$

(13)

where PSC is the pollutant shadow cost, CNY, and T_k is the social marginal abatement cost, CNY/t. Specifically, the value for CO₂ is adopted as 20.83 CNY/t, and for NO_x as 8006.84 CNY/t [18]. It is important to note that these values represent a societal perspective and are subject to policy variations. E_k is the emission quantity. Notably, the model considers the offset effect of exported electricity on regional grid emissions, which is critical for assessing the true environmental benefit of RIESs.

2.3.2. Constraints

Energy Balance Constraints

To avoid energy waste or shortage, the hourly output of cooling, heating, and electricity must equal the hourly demand:

$$Q_{GP,i}^h+Q_{HX,i}^h+Q_{SC,i}^h=L_{user,i}^h$$

(14)

$$Q_{GP,i}^c+Q_{AC,i}^c+Q_{EC,i}^c=L_{user,i}^c$$

(15)

$$E_{GT,i}+E_{b,i}=E_{GP,i}^c+E_{GP,i}^h+E_{EC,i}^c+E_{pump}+L_{user,i}^e$$

(16)

where $Q_{HX,i}^h$ is the energy output, kW, and $L_{user,i}$ is the load demand, kW.

Operational Constraints

The energy output must remain within the minimum and maximum capacity limits of equipment k:

$$P_{k,\min }\le P_k\le P_{k,\max }$$

(17)

2.3.3. Optimization Algorithm

The Hooke–Jeeves algorithm, a robust derivative-free direct search method, is employed. Compared to population-based methods (e.g., NSGA-II), this approach offers superior computational efficiency for the five continuous variables involved. Additionally, since the weight scanning method is used to solve scalarized weighted-sum problems, a single-objective solver proves sufficient and more efficient than Pareto front generation. To address non-convexity and avoid local optima, preliminary runs with randomized initial points were conducted to ensure robust convergence. The optimization flowchart is shown in Figure 3. The decision variables include GT capacity, GSHP capacity, EC capacity, SC area, and water tank volume. The optimization variable vector is defined as:

$$X=[Ca{p}_{GT},Ca{p}_{GSHP},Ca{p}_{EC},A_{solar},V_{tank}]$$

(18)

3. Description of Case Study

3.1. Case Description and Load Characteristics

The case study centers on a General Hospital in Beijing. Spanning a total area of 75,337 m², the facility includes outpatient, emergency, and inpatient units. This paper specifically considers the cooling, heating, and electrical loads during the heating and cooling seasons, where the electrical load accounts solely for the self-consumption of the energy supply system. To capture dynamic load profiles, Dest 3.0 software [19] was utilized for hourly simulations, yielding a full-year dataset of 8760 h (Figure 4).

Simulation outputs reveal a peak heating load of 4916 kW and a peak cooling load of 7975 kW. The cumulative annual thermal demands are 30,592 GJ for heating and 30,827 GJ for cooling.

3.2. Computational Boundary Conditions

(1)

Natural Gas Price: The price for natural gas used for power generation is set at 2.71 CNY/m³ [20], while the price for heating and cooling is 2.77 CNY/m³.

(2)

Electricity Price: Commercial electricity use in Beijing is subject to a Time-of-Use (ToU) tariff. According to the latest policy, the specific peak, flat, and valley prices for non-residential use are detailed in

Table 3. Time-of-Use (ToU) electricity prices for commercial users in Beijing.

Period Type	Time Slot	Price (CNY/kWh)
Critical Peak	11:00–13:00 (July–Aug.)	1.2421
	16:00–17:00 (July–Aug.)
	18:00–21:00 (Jan., Dec.)
Peak	10:00–13:00	1.0351
	17:00–22:00
Flat	07:00–10:00	0.7180
	13:00–17:00
	22:00–23:00
Valley	23:00–07:00 (Next day)	0.4407

. The feed-in tariff for natural gas power generation is set at 0.4155 CNY/kWh, adopting the Shanghai standard as a proxy due to local data unavailability [21].

(3)

Equipment Reference Costs: Equipment cost is a critical factor influencing system investment and the annualized cost. The economic parameters for all equipment involved, including lifetime, capital cost, and Operation & Maintenance (O&M) cost, are determined as shown in

Table 4. Economic parameters of system equipment.

Equipment	Lifetime (Year)	Capital Cost	O&M Cost (CNY/kWh)
GT	20	4500 CNY/kW	0.05
AC	20	455 CNY/kW	0.04
Heat Exchanger (HX)	20	200 CNY/kW	0.02
Waste Heat Boiler (WHB)	20	120 CNY/kW	0.03
GSHP	20	600 CNY/kW	0.06
Geothermal Well	20	7500 CNY/Well	0.02
SC	20	600 CNY/m2	0.03
Water Tank	20	450 CNY/m3	0.015
GB	20	145 CNY/kW	0.03
EC	20	635 CNY/kW	0.04

.

(4)

Optimization Parameter Settings: The Hooke–Jeeves algorithm is utilized for optimization. The algorithm parameters are initialized as follows: initial step size δ = 0.5, acceleration factor α = 1, step reduction rate ω = 0.5, and precision tolerance ε = 0.2. The range, initial values, and step sizes for the decision variables are listed in

Table 5. Settings for optimization variables.

Variable Name	Initial Value	Range	Step Size
GT Capacity	0	0–2790 kW	310
SC Area	0	0–1800 m2	100
Ratio of SC Area to Tank Volume	50	50–80 m2/m3	2
GSHP Capacity	0	0–5400 kW	354
EC Capacity	0	0–4000 kW	200

.

4. Results and Discussion

4.1. Sensitivity Analysis of Weights and Configurations

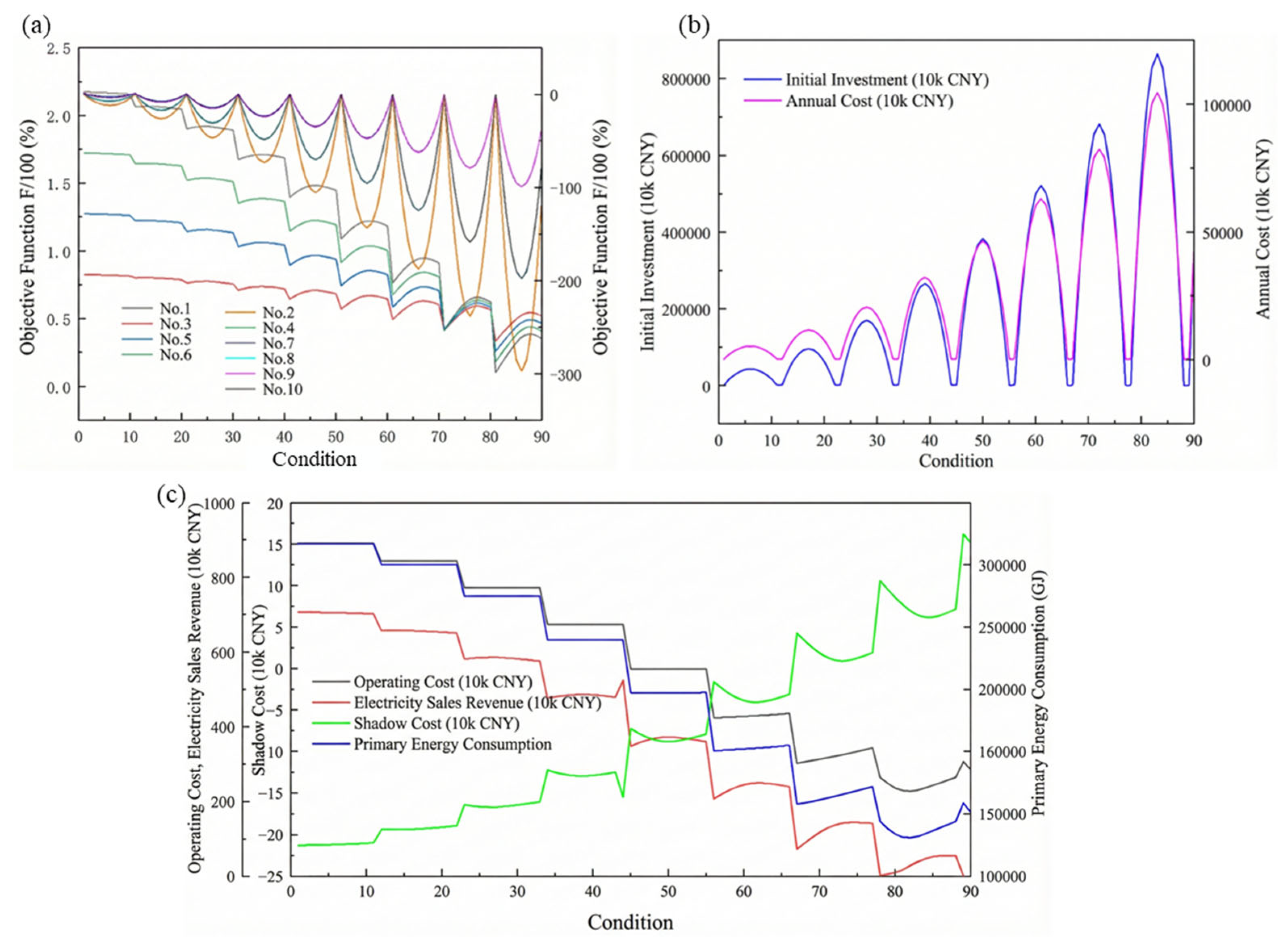
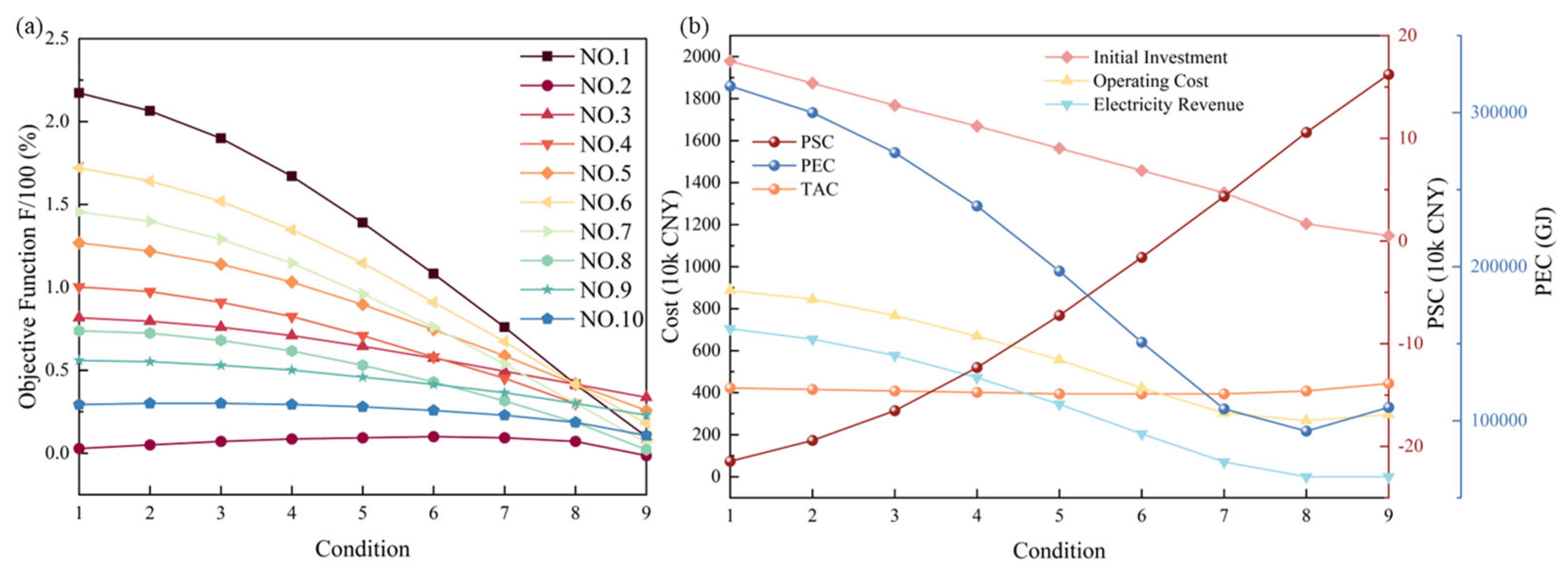
The trends of the comprehensive objective function values under different weight combinations, with respect to system configurations (centered on GT rated power), are illustrated in Figure 5a. Generally, as the gas turbine (GT) power decreases (corresponding to operating conditions 1 to 90), the objective function F shows a downward trend. It is worth noting that the rate of decline and the position of inflection points vary across different weight preferences. For instance, in economy-oriented scenarios (where weights favor cost saving), the objective function is highly sensitive to the reduction in GT power; conversely, in environment-oriented scenarios, the curve is relatively flat, indicating that the system maintains environmental benefits within a certain range through the compensation of other low-carbon equipment.

The intricate trade-off between economics and primary energy consumption is depicted in Figure 5c. As GT power decreases, annual operating costs, electricity sales revenue, and primary energy consumption all exhibit a fluctuating downward trend; in contrast, the environmental shadow cost gradually increases. Unlike operating costs, the initial investment and annual cost of the system generally show a fluctuating upward trend (Figure 5b). This is primarily because, to compensate for the power and heat deficit caused by GT downsizing, the system must rely on or enlarge other equipment (e.g., GSHPs, ECs), which often possess higher unit capital costs or operational electricity expenses. Notably, under most weight combinations, the local optimum for annualized cost occurs when the SC area is 0 m². This indicates that under the current boundary conditions (investment costs vs. energy prices), solar heating lacks a competitive advantage. This is attributed to the cooling–heating coupling constraint. The crowding-out effect of solar energy on winter heating reduces the requisite GSHP capacity. However, this downsizing constrains the GSHP’s cooling potential in summer, necessitating a compensatory expansion of the EC capacity. Consequently, the incremental costs for summer cooling negate the winter heating savings, eroding overall system viability.

Consequently, configurations with SC were discarded. The remaining nine distinct configurations are summarized in

Table 6. Equipment configuration of 9 candidate integrated energy systems.

Number	GT Capacity (kW)	GSHP Capacity (kW)	EC Capacity (kW)
1	2790	1056	3479.3
2	2436	1596	3533.31
3	2087	2136	3587.32
4	1739	2678	3640.45
5	1391	3217	3695.45
6	1043	3757	3749.46
7	695	4298	3803.58
8	290	4838	3520.99
9	0	5404	3908.63

.

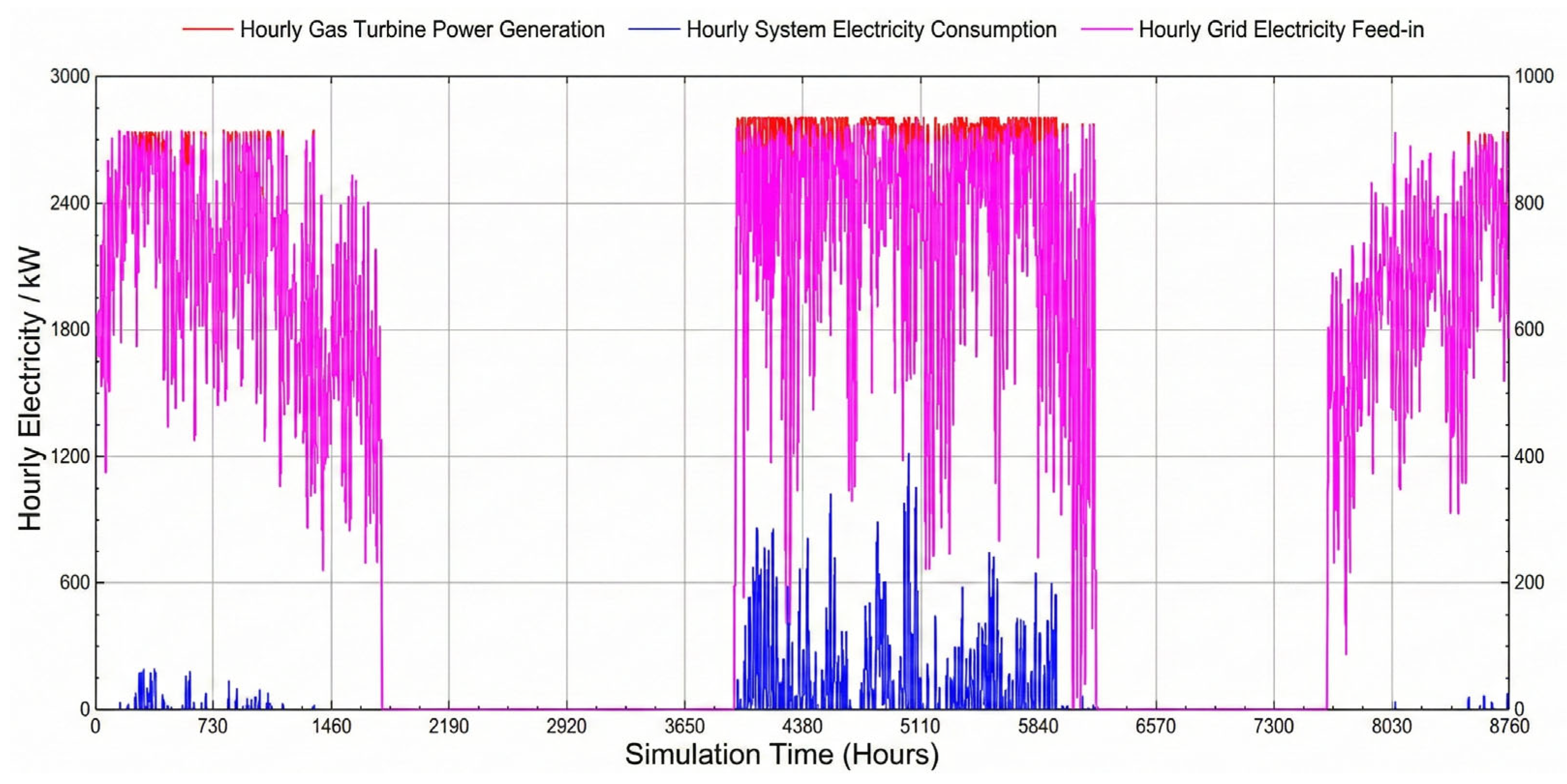
Figure 6 presents the multi-scenario weight scanning results. As seen in Figure 6a, a robust positive correlation is evident between the objective function F and GT-rated power across all weight scenarios. The monotonic decline in F with reduced GT power implies that, within the defined constraints, maximizing GT capacity optimizes the comprehensive utility of the RIES. This phenomenon is driven by the grid-interaction mechanism. Maximizing GT capacity amplifies grid-exported electricity (Figure 6b). On one hand, high electricity sales revenue offsets operating costs; on the other hand, exporting clean electricity (substituting conventional coal power) generates significant environmental benefits (negative shadow costs). Although natural gas consumption increases, the electricity revenue and emission reduction benefits dominate the comprehensive evaluation.

Statistical analysis of the 10 weight scenarios reveals that Configuration 1 (GT 2790 kW, GSHP 1056 kW, EC 3479 kW) is identified as the optimal solution in over 80% of the scenarios. This confirms the preference robustness of this configuration, implying that regardless of whether the decision-maker prioritizes economy or environment, the “large-capacity GT + moderate-scale GSHP” scheme is the best choice for this hospital campus.

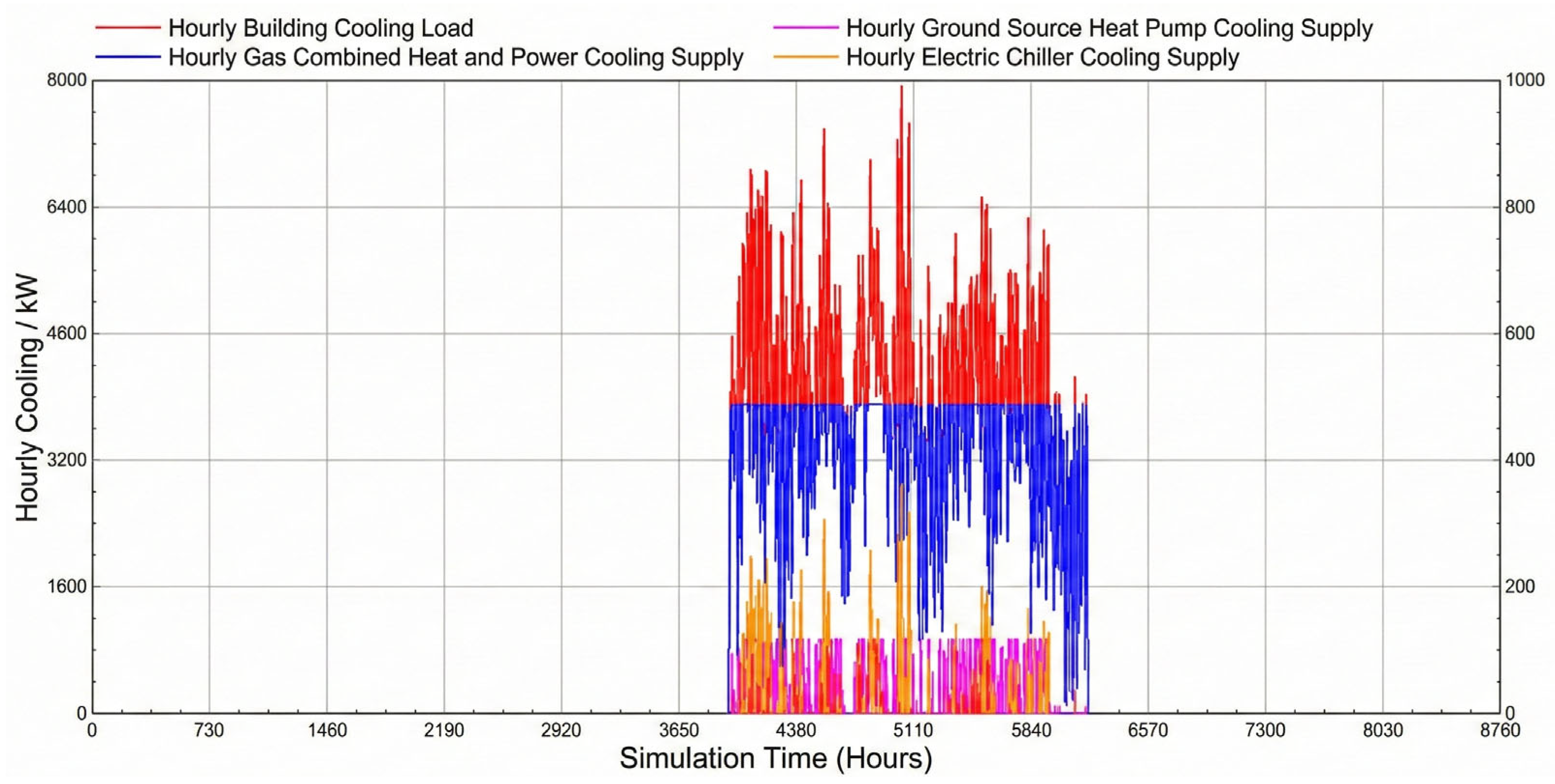
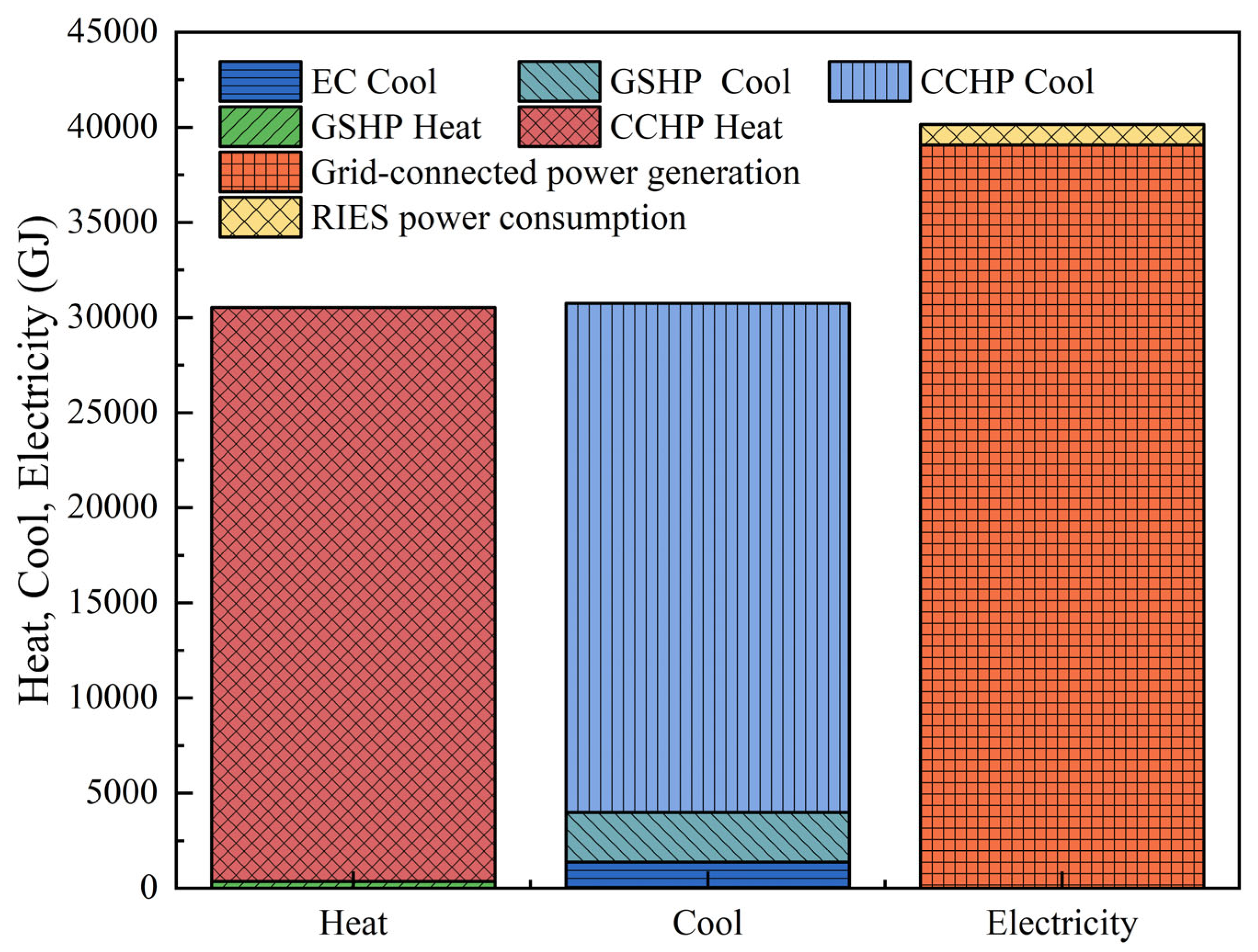
The load distribution under this optimal configuration is detailed in Appendix A. As shown in Figure 7, the CCHP system covers the vast majority of loads: 99% of the heating load and 86% of the cooling load. Of the remaining cooling load, the GSHP contributes 8.6%, with the rest supplemented by the EC. Notably, the high GT capacity enables the system to export 94% of its generation, functioning effectively as a distributed power plant.

4.2. Comprehensive Benefit Comparison

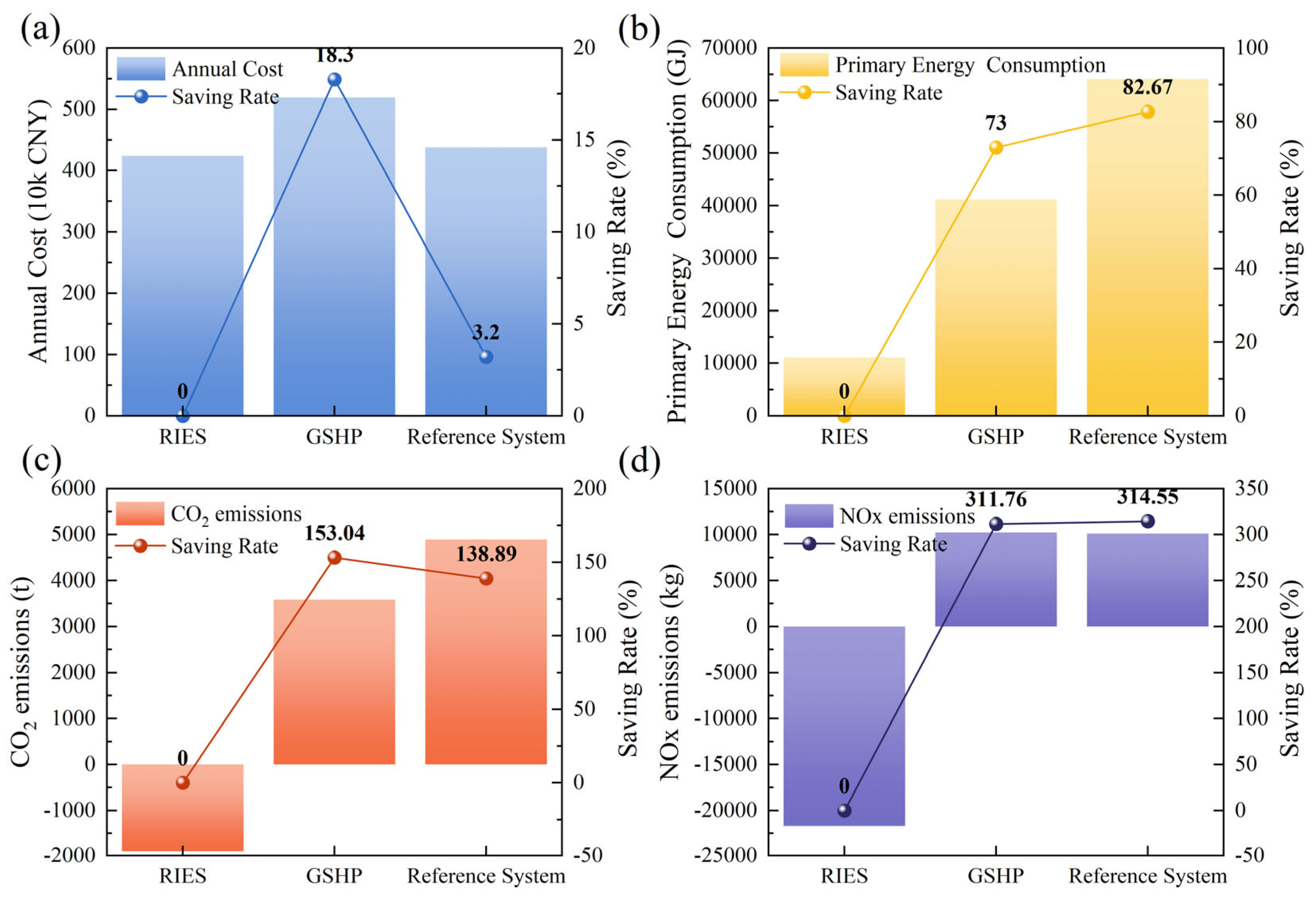
A comparative assessment of the robustly optimized RIES (Configuration 1) against the Standalone GSHP and reference systems was conducted to quantify annual performance. The results are summarized in

Table 7. Annual cost, primary energy consumption, and pollutant emissions of different systems.

Number	RIES (Optimized)	Standalone GSHP	Reference System
ATC (10k CNY)	424	519	438
PEC (GJ)	11,113	41,158	64,113
CO2 Emissions (t)	−1903	3588	4893
NOx Emissions (kg)	−21,676	10,234	10,106

Note: The negative values indicate a “net environmental benefit” generated by exporting clean electricity to the grid. This effectively offsets the pollutant emissions associated with an equivalent amount of grid electricity based on the average grid emission factor.

and Figure 8.

The comparison results demonstrate that the proposed RIES achieves a balance of “economic feasibility and environmental excellence.” Although the Annualized Total Cost (ATC) of the RIES is only slightly reduced by 3.2% compared to the reference system (constrained by higher initial capital costs), it still outperforms the Standalone GSHP System, verifying its economic viability. However, the environmental benefits are transformative. After accounting for the offset effect of exported electricity on the regional grid, the RIES effectively achieves net-negative emissions. Compared to the reference system and the Standalone GSHP System, the RIES achieves CO₂ reduction rates of 153.04% and 138.89%, respectively. Furthermore, the NO_x reduction rates reach remarkable levels of 311.76% and 314.55%. These significant reductions are primarily attributed to the cascade utilization of energy and the substitution of grid electricity (with higher marginal emissions) by efficient distributed generation. In addition, the energy-saving effect is substantial. The PESR is 82.67% and 73.00% relative to the reference system and Standalone GSHP System, respectively. This makes the system highly attractive for medical institutions committed to achieving ESG (environmental, social, and governance) goals.

4.3. Limitations and Sensitivity Analysis

While the “large-capacity GT + moderate-scale GSHP” configuration demonstrates superior performance, the interpretation of these results requires a critical examination of underlying assumptions and boundary conditions. First, the reported “net-negative emissions” are heavily predicated on the current carbon intensity of the regional grid, where exported electricity is assumed to displace high-carbon, coal-dominated power. Consequently, this environmental benefit represents a theoretical maximum. As the grid progressively decarbonizes with increased renewable penetration, the “offset” credit inevitably diminishes. Second, the economic robustness of the proposed configuration is sensitive to the spread (the margin between electricity feed-in tariffs and natural gas prices). The optimization currently favors maximizing exports under the assumption of unconstrained grid access; however, significant fluctuations in gas prices, reductions in distributed generation subsidies, or local grid export limits could shift the optimal capacity of the GT downwards. Finally, the exclusion of SC reflects current cost structures, the specific load characteristics of medical building campuses (high reliability and continuous thermal demand), and specific load-coupling dynamics. The economic viability of SCs remains subject to potential capital cost reductions or policy subsidies.

5. Conclusions

Focusing on the energy demand of hospital campuses, this paper proposes a robust optimization design method for RIES based on the Hooke–Jeeves algorithm and multi-scenario weight analysis. An empirical study was conducted on a general hospital in Beijing by coupling a high-fidelity TRNSYS dynamic simulation model with the optimization algorithm. The main conclusions are as follows:

(1)

A comprehensive scan of 10 decision preference scenarios reveals that the “High-capacity gas turbine (2790 kW) + Ground Source Heat Pump” configuration is the optimal solution in over 80% of cases. The configuration’s insensitivity to weight perturbations demonstrates that, within the current techno-economic landscape, a strategy prioritizing clean power export represents the most robust pathway for maximizing the comprehensive utility of medical campuses.

(2)

The optimized RIES achieves remarkable net-negative emissions. Benefiting from efficient cascade utilization and the carbon offset mechanism of exported electricity, the primary energy consumption is reduced by 82.7%. Remarkably, it achieves net reduction rates of 153.04% for CO₂ and 311.8% for NO_x after accounting for grid offsets. Despite the higher initial investment, the 3.2% reduction in ATC confirms the economic viability of this low-carbon transition. These findings underscore the need for policymakers to incentivize feed-in mechanisms and mature carbon trading schemes to accelerate RIES adoption.

(3)

The proposed framework, integrating shadow cost theory and multi-scenario weight scanning, effectively avoids the subjectivity defect of traditional multi-objective optimization. By internalizing environmental externalities, this approach offers a resilient decision-making tool adaptable to dynamic market prices and policies. Future research will extend this framework to assess the long-term impact of climate change on load profiles and investigate the role of energy storage systems in enhancing temporal flexibility.

This study assumes static energy policies and current technology costs. Furthermore, the specific optimal configuration is case-dependent, particularly for medical building campuses in cold zones. Application to other climates or grid mixes requires re-optimization using the proposed framework. Future work should incorporate long-term uncertainties in energy prices and climate change impacts on load profiles.