Impact of University Building Thermal Environments on Thermal Comfort and Learning Efficiency: A Study Under Conditions of Hot Summer and Cold Winter

Abstract

Learning efficiency in a university context is predicated on a conducive learning environment. This in turn requires settings offering thermal comfort. In this study, we experimentally explored the relationship between the thermal environment of colleges and universities in hot-summer and cold-winter regions on the thermal comfort and learning efficiency of Chinese college students. Findings are intriguing in that temperatures delivering optimal thermal comfort and optimal learning efficiency differ. Specifically: (1) Students generally feel most comfortable when the room temperature is approximately 24 °C; (2) Combined studies comparing temperature on thermal comfort and learning efficiency found that college students learn better in slightly colder environments; (3) Based on the comprehensive value of satisfying the best thermal comfort and high learning efficiency, the optimal temperature range is 20.6 °C to 22.2 °C.

1. Introduction

With the evolution of modern educational concepts and concurrent rising expectations for improved quality of life, the impact of the architectural environment on learning efficiency has gained increasing attention. In China, students spend about a third of their time in the classroom, while the physical environment of the classroom is closely related to students’ comfort and learning outcomes [1]. College students face unrelenting academic pressure, with the quality of their learning environment directly affecting their academic performance [2,3].

Currently, many colleges and universities in China do not adequately consider thermal comfort in the design and use of their buildings. School buildings tend to overheat in summer and overcool in winter, making it difficult for students to concentrate on their studies [4,5]. In addition, with the intensification of global climate change and the frequent occurrence of extreme weather events, higher requirements for building thermal comfort have emerged as a priority [6,7]. Given this background, the importance of understanding the relationship between the influence of the built environment on thermal comfort and learning efficiency of university students is clear, though as yet untested in China.

A number of scholars have carried out research on environmental thermal comfort-related issues [8,9,10,11,12,13,14,15,16,17,18]. For example, Lu and Wang [15]. applied machine learning to forecast urban air pollution, providing methodological insights into understanding composite environmental factors; while Ravindra et al. [16]. assessed the impact of air pollution on public health, thereby broadening the health dimension of environmental comfort. Many have also established thermal evaluation models and design standards. As a result, codes and standards related to indoor thermal comfort have emerged internationally. For example, ASHRAE Standard 55-2017 [19], amongst others. By studying the thermal comfort of students and teachers in the classroom context, children have been shown to be more sensitive to higher temperatures than adults under the same conditions [20]. Research on the thermal comfort of primary and secondary school teachers has found that students’ neutral and ideal temperature values are lower than those of adults. In addition to age, some studies indicate that when the temperature in the classroom is slightly elevated, students feel more comfortable [21,22]. This indicates that the temperature acceptable to students may be higher than the standard recommendation. However, for school buildings in China, it is relatively difficult to maintain adequate thermal comfort conditions. Therefore, some scholars have proposed indicators such as ePMV and aPMV as suitable for different experimental conditions [23,24,25,26,27]. Most scholars, however, have tended to focus primarily on the thermal comfort of residents in residential and office buildings. For example, Zhao Shengkai analyzed the thermal comfort needs of occupants in open-plan office buildings in the Xi’an area [28]. In order to improve work efficiency and improve the indoor thermal environment of office buildings, Chen Chuxin et al. studied the indoor thermal environment of office buildings over the transition season in Northern China [29]. Chen Shuqin et al. studied human thermal comfort and energy consumption of Hangzhou residential buildings in winter, based on a personal comfort system [30].

Apart from the issue of students’ thermal comfort in the indoor classroom environment, there is also the matter of the impact of thermal settings on student learning efficiency. This study focuses specifically on university classroom buildings due to their unique functional and operational significance. Unlike offices or residences, classrooms host prolonged, high-intensity cognitive activities where environmental quality directly impacts learning outcomes-a core institutional mission. The young adult student population also presents distinct thermal perception and adaptive behaviors. Furthermore, optimizing the thermal environment in these densely occupied spaces carries substantial implications for both educational performance and energy efficiency, given the scale of university building stocks. Currently, there are many studies on the impact of indoor temperature and ventilation conditions in classrooms on learning efficiency, most of which employ subjective evaluations and experimental methods [31,32,33,34]. In addition, Cho [31] found that high temperatures in summer have a negative impact on exam scores. In their study on ‘The Relationship Between Comfort Perception in University Classroom Buildings and Academic Performance,’ Hoque and Weil concluded that students’ concentration and academic performance improve under a comfortable learning environment [35]. Sarbu et al. [34] stated that learning performance was highest at 27 °C, when the experimental temperature was in the range of 22–29 °C. These findings indicate that temperature does indeed affect learning efficiency [34].

However, for university classrooms in hot-summer and cold-winter (HSCW) regions, there remains a lack of systematic experimental research aimed at determining an optimal temperature range that simultaneously accommodates both student thermal comfort and learning efficiency. Existing studies tend to either focus predominantly on subjective comfort evaluation or employ relatively simplistic cognitive assessment methods, failing to provide temperature parameters based on dual-objective optimization that could offer practical operational guidance.

In summary, while the significance of the thermal environment for occupant well-being is established, research specific to educational settings reveals critical gaps. First, extant studies often generalize findings across vastly different climate zones, neglecting the distinctive bioclimatic challenges of regions like China’s hot-summer and cold-winter zone [36], where buildings face dual demands of summer heat and winter cold. Second, methodologies for assessing learning efficiency frequently rely on oversimplified metrics, such as self-reported memory or single cognitive tasks, failing to capture its multidimensional nature encompassing attention, perception, memory, and reasoning [37]. Consequently, there is a lack of targeted, quantitative evidence from this specific climate zone that (a) employs a composite, multi-faceted cognitive assessment to evaluate learning efficiency, and (b) explicitly analyzes the trade-off between the thermal conditions conducive to optimal learning and those preferred for thermal comfort. To address these gaps, this study investigates the relationship between indoor temperature, thermal comfort, and learning efficiency in a controlled environment simulating a university classroom in the Sichuan Province hot-summer and cold-winter region. By integrating a detailed thermal comfort questionnaire with a battery of four cognitive ability tests, the study aims to quantify these relationships and propose a reconciled temperature range that balances both objectives, thereby providing evidence-based guidance for the design and operation of campus buildings in similar climates.

2. Materials and Methods

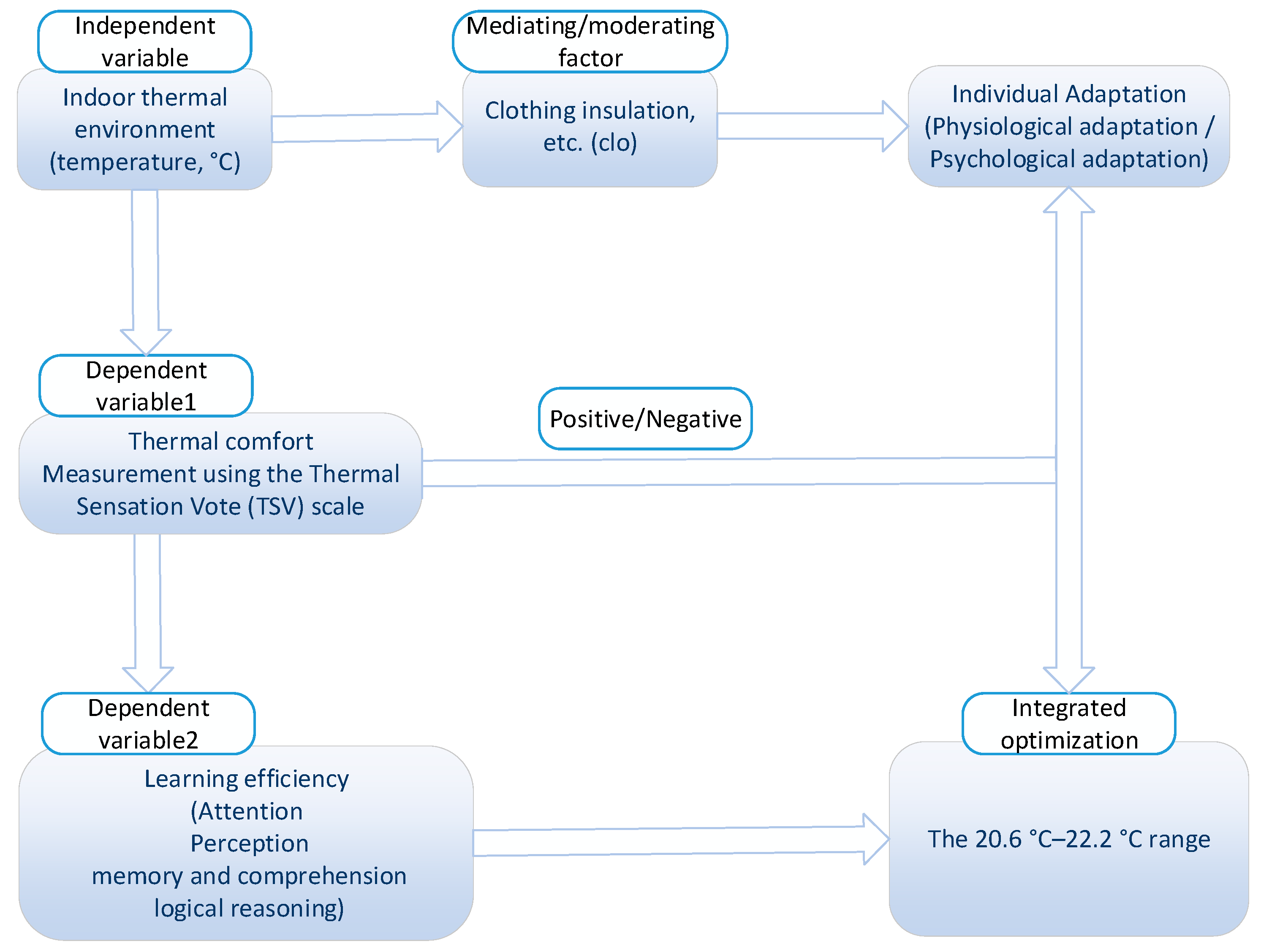
2.1. Study Framework

The research framework is shown in Figure 1. A literature review is undertaken in order to analyze and master the relevant factors affecting thermal comfort and learning efficiency, as well as to determine and select the appropriate measurement parameters and test methods. The effects of thermal environment parameters on thermal comfort and learning efficiency in different classrooms were analyzed through experiments, and the quantitative relationship between thermal environment parameters and thermal comfort and learning efficiency was established. Next, the thermal environment parameters for evaluating thermal comfort and learning efficiency are established through theoretical reference. Finally, the range of thermal environment parameters of college students’ classrooms in hot summer and cold winter areas under comprehensive needs is determined.

2.2. Thermal Comfort Research Methods

For the scientific assessment of the impact of indoor thermal environments on the human body, researchers have developed multiple evaluation systems, which can be broadly categorized into the following three types:

• Theoretical models based on heat balance, represented by the Predicted Mean Vote (PMV) and its derivative, the Predicted Percentage of Dissatisfied (PPD). Originating from Professor Fanger’s steady-state heat balance equation [38], this model objectively predicts the average thermal sensation (PMV) of most people in a given environment and the expected percentage feeling dissatisfied (PPD) by calculating the balance between human heat production and dissipation. Its strength lies in a complete theoretical framework, making it a core component of international standards. It is particularly suited for fully air-conditioned, steady-state environments with low air velocity, stable metabolic rates, and relatively uniform clothing. However, the model requires high precision in input parameters and has limitations in reflecting individual differences, dynamic environments, or the actual adaptive behaviors of occupants in naturally ventilated buildings.
• Adaptive models based on behavioral adaptation. This model posits that thermal comfort is not determined solely by physical parameters but is significantly influenced by behavioral adjustments, psychological expectations, and past thermal experiences. It typically establishes regression relationships between outdoor temperature and the actual acceptable or neutral indoor temperature through field studies. Adaptive models are more aligned with naturally ventilated, semi-open, or user-adjustable indoor environments and are used to define comfort zones for such contexts. Their limitation is a stronger dependency on regional and cultural factors, resulting in relatively lower model universality.
• Direct subjective evaluation metrics. These methods obtain immediate feedback from users via questionnaires and form the cornerstone of empirical research. Commonly used metrics include:

Thermal Sensation Vote (TSV): Uses the ASHRAE 7-point scale (cold, cool, slightly cool, neutral, slightly warm, warm, hot) to measure immediate thermal perception.

Thermal Comfort Vote (TCV): Typically uses a 4-point scale (comfortable, slightly uncomfortable, uncomfortable, very uncomfortable) to evaluate overall comfort.

Thermal Acceptability Vote (TAV): Directly asks whether the environment is acceptable (yes/no).

These subjective metrics are interrelated and offer the advantages of being direct and flexible, effectively capturing individual differences and momentary perceptions. They are widely used in various experiments and field studies.

This study was conducted in a controlled artificial climate chamber with the core objective of investigating the short-term impact of specific temperature setpoints on immediate thermal sensation and cognitive performance. Consequently, the experimental environment involved strictly controlled steady-state conditions, yet the participants were real individuals with a background of autonomous adaptation. Furthermore, the research required a tool that could synchronize with short-term cognitive testing and efficiently gather immediate subjective feedback. Therefore, we selected the Thermal Sensation Vote (TSV) as the primary thermal comfort evaluation metric. TSV is a fundamental, internationally recognized subjective scale. Its simplicity and immediacy perfectly match the short-term exposure design of this experiment, providing the most direct and reliable subjective data for subsequent analysis of the synchronous relationship between the thermal environment and learning efficiency. Simultaneously, we calculated thermal acceptability from the TSV to supplement the evaluation of overall environmental satisfaction.

This study designs a questionnaire based on previous surveys [1,35,39,40,41,42], which are then tailored to the characteristics of Chinese university students. The substance of the questionnaire solicits personal demographic information, thermal sensation votes, thermal environment change votes, and thermal comfort satisfaction votes. Questions 2 to 4 all use a five-point Likert scale. The test scale is shown in Appendix A.

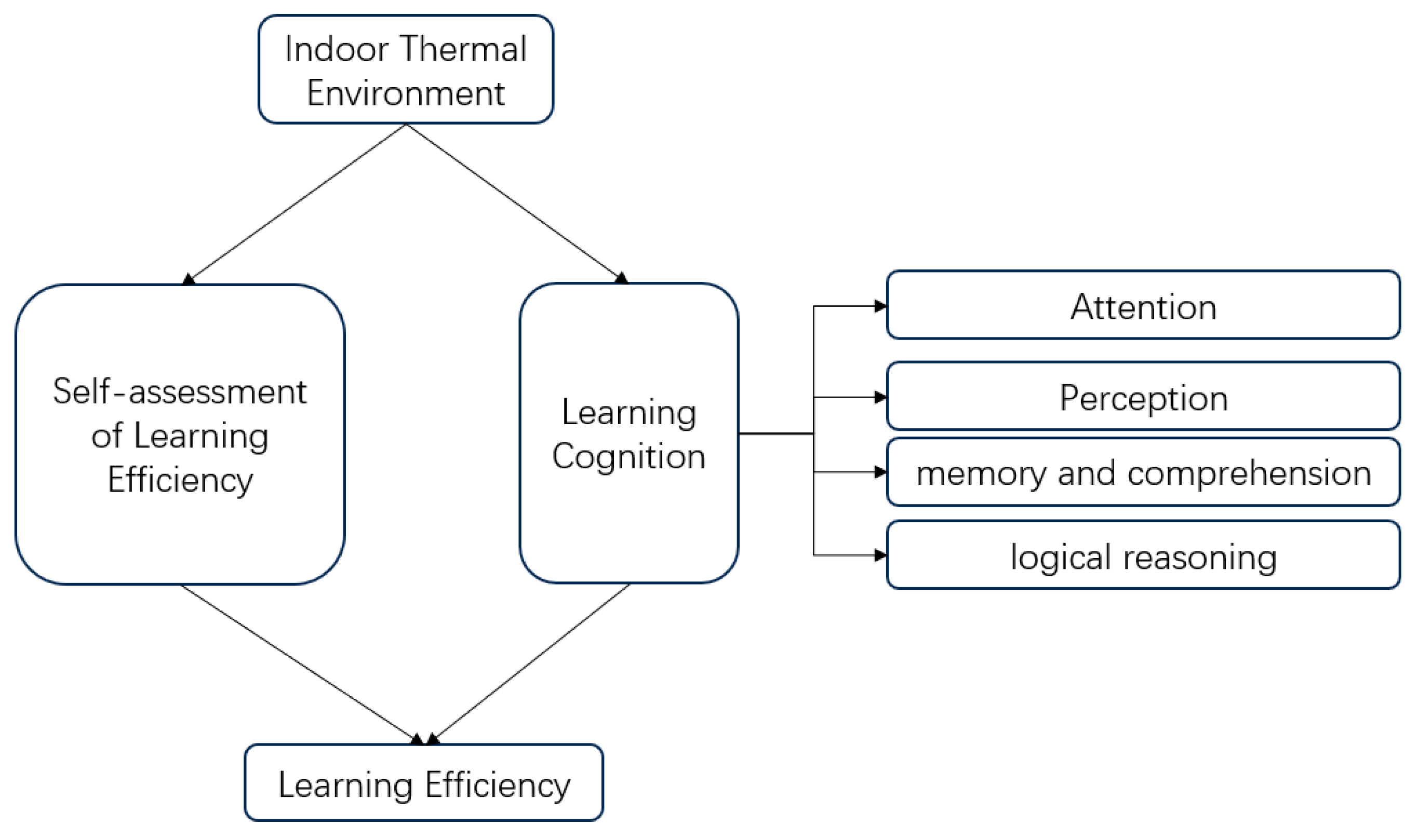
2.3. Methods of Evaluating Learning Efficiency

Mechanisms of the Effect of Indoor Thermal Environments on Learning Efficiency

The impact of the environment on individuals is characterized by subjective agency. Students generally do not passively accept environmental changes, but rather adopt different coping strategies based on their learning experience to respond to changes in the environment [43]. When they focus on a learning task, students tend to engage in self-regulation to ensure the timely completion of the task. However, when students prioritize their personal experiences, this may lead to an extension of the task duration, a decline in learning motivation, or even a diversion of attention.

During the learning process, learning conditions can be assessed not only through subjective psychological experiences but also through the physiological and psychological adjustments influenced by the environment. These adjustments occupy cognitive resources, which in turn affect individuals’ learning cognition and thought processes [44]. Both psychological and physiological adjustments concurrently influence students’ subjective sensations. Therefore, it is essential to first understand students’ subjective experiences, and then, through the study of their actual learning cognitive abilities, provide a more objective and comprehensive evaluation of the relationship between the thermal environment and learning efficiency.

In summary, the relationship between the indoor thermal environment and learning efficiency can be explored through two pathways. Firstly, a self-evaluation of learning efficiency and cognitive performance assessments, along with a self-evaluation of learning efficiency is undertaken through a questionnaire survey. Secondly, cognitive processes are examined through four testing domains: attention, perception, memory and comprehension, and logical reasoning. The approach is illustrated in Figure 2.

• Self-evaluation of Learning Efficiency

The self-evaluation of learning efficiency is particularly important for students who primarily rely on their personal experiences. Such students are more likely to adjust their strategies in response to changes in the external environment by extending study time, reducing learning motivation, or pursuing disengagement behaviors. These responses are likely to result in a decrease in learning efficiency. In light of this, this study utilizes a questionnaire to collect data on students’ self-evaluation of learning efficiency. The assessment scale is provided in Appendix A.

2.

Evaluation of Cognitive Learning Abilities

This study also employs simple tests of four cognitive abilities aimed at comprehensively assessing the extent to which learning efficiency is affected. These four abilities are attention, perception, memory and comprehension, and logical reasoning.

To effectively translate laboratory-based cognitive tests into indicators of real-world classroom learning efficiency, this study selected tasks grounded in the research paradigms of cognitive psychology and environmental ergonomics [45]. The four chosen tests were designed to accurately assess the following core cognitive functions: (1) The Digit-Symbol Substitution Test (DEST) primarily measures sustained attention, perceptual-motor speed, and working memory—functions critical for real-time note-taking and keeping pace with instructional delivery in the classroom [46]; (2) The Amfimov Table—Digit Recognition test assesses perceptual vigilance and selective attention, a cognitive process analogous to filtering key information from complex visual materials during lectures [47]; (3) The Meaningless Figure Recognition test targets visual short-term memory and encoding efficiency, which are fundamental for memorizing diagrams, formulas, and new concepts [48]; (4) The Verbal Deductive Reasoning test evaluates logical thinking and executive function, directly related to problem-solving, critical analysis, and knowledge integration in learning contexts [49]. Thus, although no single test can replicate the full complexity of classroom teaching, this integrated battery systematically captures the core cognitive capacities underlying classroom learning efficiency. See

Table 1. Cognitive Learning Abilities Testing Items.

Classification	Testing Tasks
Attention	Digit-Symbol Substitution Test (DEST) [49]
Perception	Amfimov Table—Digit Recognition [50]
memory and comprehension	Meaningless Figure Recognition [51]
logical reasoning	Verbal Deductive Reasoning [52]

.

The scales for each testing item are provided in Appendix A.

3.

Factor Analysis of Cognitive Learning Abilities Evaluation

Establishing a quantitative relationship between the indoor thermal environment and learning performance is essential for determining the optimal temperature range conducive to university students’ ability to study effectively. However, cognitive learning abilities encompass four distinct dimensions. In order to arrive at a quantitative relationship, it is necessary to integrate these four abilities into a fitting curve that represents the relationship between indoor temperature and cognitive learning performance. Consequently, the relative weight of each ability is of particular importance. In previous studies, most weightings have been set using equal proportions. In contrast, this study employs the Ordinal Priority Approach (OPA) to determine the weights. The Ordinal Priority Approach (OPA) is a multi-criteria decision analysis method that helps address group decision-making problems involving preference relationships. It was first proposed by Younes Ataei and Amin Mahmoudi in 2020 to address common issues inherent in existing multi-attribute decision-making methods [50].

The weighting process involved an expert panel comprising eleven industry specialists. These experts were selected from fields closely related to this study to ensure professional judgment in weight determination. Rankings were obtained through a structured anonymous questionnaire. The questionnaire first explained the connotations of the four cognitive abilities—attention, perception, memory and comprehension, and logical reasoning and their relevance to classroom learning tasks. Subsequently, experts were asked to independently rank these four abilities based on their professional judgment regarding their relative importance for achieving efficient classroom learning. No preset options were provided in the questionnaire to minimize leading bias.

4.

Calculation of Effect Size

To evaluate the practical significance of statistically significant results, effect sizes (ES) were calculated. For analyses of variance (ANOVA), the effect size was estimated using the following formula [51]:

$$\mathrm{E}\mathrm{S}=\sqrt{{\displaystyle \frac{\mathrm{F}}{\mathrm{n}}}}$$

(1)

where F is the F-statistic from the ANOVA, and n is the sample size per group (the mean sample size was used when group sizes were unequal).

This effect size metric corresponds to Cohen’s f. According to the benchmarks proposed by Cohen [52], an f value ≥ 0.1 indicates a small effect, ≥0.25 indicates a medium effect, and ≥0.4 indicates a large effect.

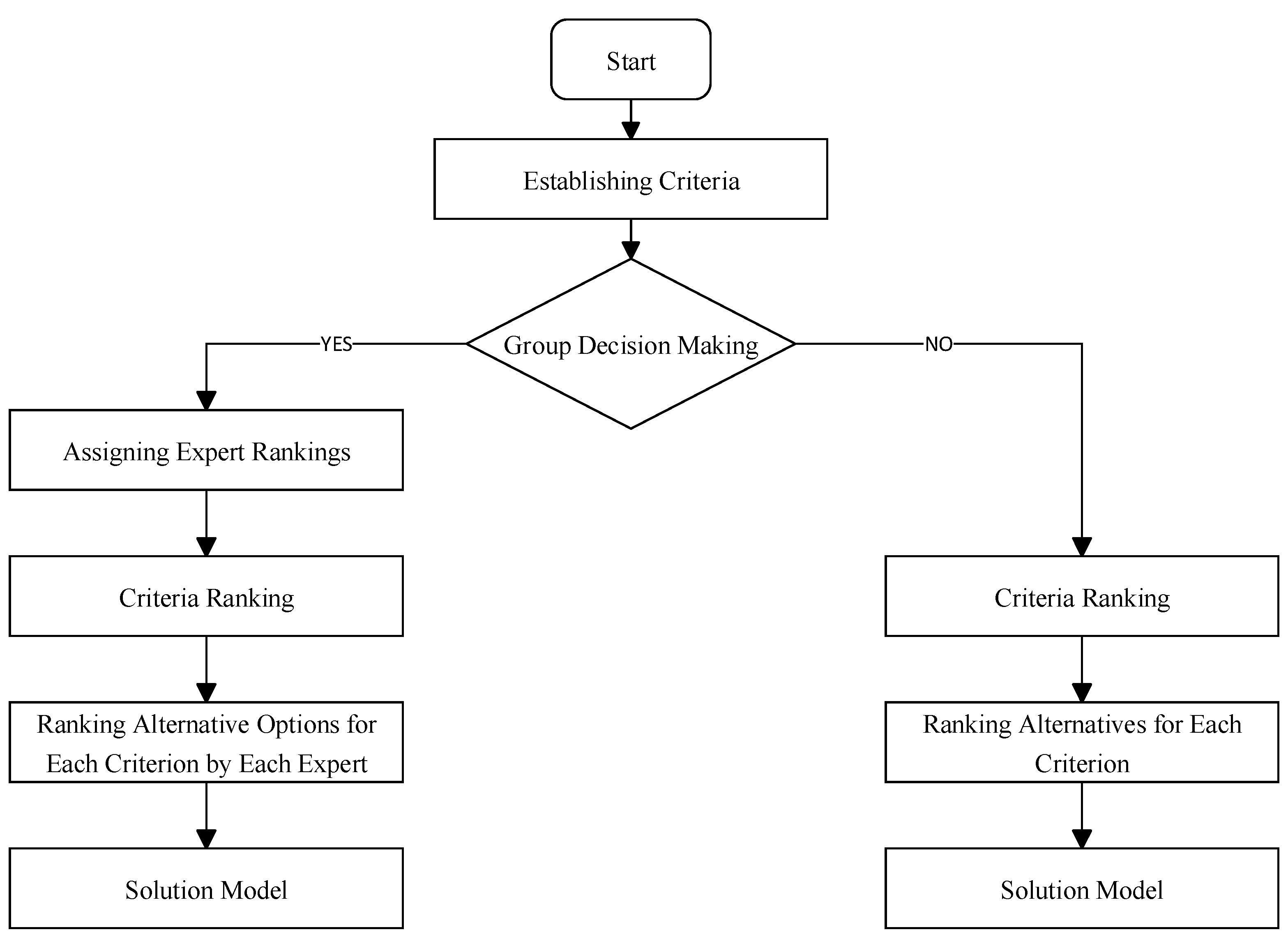
2.4. Comprehensive Analysis of the Impact of Thermal Comfort on Learning Efficiency

Unlike certain earlier studies that focus on a single objective, such as improving thermal comfort or enhancing students’ learning efficiency, this study aims to determine the optimal indoor temperature range under the combined influence of both thermal comfort and learning efficiency. This is achieved by separately establishing functional relationships between thermal comfort and temperature, as well as between learning efficiency and temperature. This is done in order to identify the optimal temperature range under their combined effect. Subsequently, environmental parameter grading methods for both thermal comfort and learning efficiency are applied to determine the corresponding temperature ranges. When determining the temperature range, the goal is to simultaneously ensure that both thermal comfort and learning efficiency are maintained at their optimal levels, thereby identifying the temperature range that satisfies the needs of regions with hot summers and cold winters under different comfort and learning conditions.

• Method of Determination

When the thermal comfort requirement reaches a certain percentage (e.g., a), the corresponding indoor temperature range is denoted as a′ (as shown in the blue section of Figure 3). When learning efficiency reaches b, the temperature range is represented by b′ (as shown in the yellow section of Figure 3). By integrating the optimal thermal comfort temperature range and the temperature range for high learning efficiency, an appropriate temperature range for the indoor thermal environment design parameters of university teaching buildings can be proposed, as illustrated in the green area of Figure 3.

Since optimal thermal comfort and high learning efficiency are not achieved within the same temperature range, the values of a and b are particularly crucial. The comfort zone defined in ASHRAE 55 [19] is based on the principle that the environment is considered comfortable when 90% of the population finds it satisfactory. Robert C. et al. found that when the training accuracy of the learning content approaches 85%, learning efficiency reaches its optimal level, with the top 85% of performance indicating high learning efficiency [53]. Based on the aforementioned standards, the thermal comfort satisfaction rate (a) in this study is determined by values of 94%, 90%, and 85%. The learning efficiency value (b) is defined as 85% of the difference between the highest and lowest values of the final composite index.

2.5. Overview of the Experiment

All experiments in this study were conducted at Chengdu University of Technology (Yibin Campus), Sichuan Province, in the People’s Republic of China. The data collection took place from 24 April 2024 to 21 May 2024, with a total of 165 valid responses gathered.

Prior to the experiment, all experiment coordinators received training, which covered the experimental procedures, the determination of thermal environment parameters, and important considerations regarding the questionnaires. Additionally, during the experiment, detailed explanations and guidance were provided to the participating students. Furthermore, all participants were students from Chengdu University of Technology (Yibin Campus), who had been residing in the area for at least one year.

The experiment was conducted in Yibin City, Sichuan Province, which is located in a hot summer and cold winter region. During the summer, the weather is humid and hot, with average temperatures ranging from 25 °C to 35 °C, while winter temperatures average between 4 °C and 10 °C. Based on the annual average temperature of regions with hot summers and cold winters, the experimental temperatures were set at four levels: 17 °C, 22 °C, 26 °C, and 30 °C.

The experiment was conducted in a standard, windowless interior classroom at Chengdu University of Technology (Yibin Campus) to eliminate the influence of direct solar radiation and variable outdoor conditions. The rectangular room measured approximately 11 m (length) × 9 m (width) × 3.5 m (height). The walls were constructed of brick with plaster finish. The room was furnished with typical student desks and chairs arranged in rows. A commercially available split-type air conditioning unit was used to precisely control the indoor air temperature to the four target setpoints: 17 °C, 22 °C, 26 °C, and 30 °C.

To ensure a stable and uniform thermal environment for the participants, the air conditioning system was activated for at least 60 min prior to each experimental session to achieve a steady-state condition. The horizontal temperature distribution was verified through spot measurements at multiple locations, including room corners, using a handheld anemometer-thermometer. Temperature variations across these points were confirmed to be within ±0.8 °C of the target setpoint, a range deemed acceptable for controlled environment studies of this nature.

Indoor relative humidity was not actively controlled or continuously logged during the experiments. Based on local meteorological data for Yibin City during the experimental period (April–May 2024) and considering the dehumidifying effect of the air conditioning system, the indoor relative humidity is estimated to have ranged between 50% and 70%.

Participants were instructed to wear their normal, season-appropriate indoor campus attire. Standardized clothing was not provided.

It should be noted that the experiments were scheduled in April and May due to practical constraints regarding participant availability and academic calendar. While this period represents a transitional season in the HSCW region, and all participants were long-term local residents, the specific effects of peak summer or winter acclimatization on the responses were not captured in this study design. This consideration is further discussed in the Limitations section.

This experiment consists of three components: adaptation time, learning efficiency testing, and thermal comfort subjective evaluation. First, the experimental room was prepared and the temperature was calibrated to ensure that it remained within the required range for the experiment, meeting all environmental criteria. Next, the participants entered the experimental room and underwent a ten-minute adaptation period, during which the experiment coordinator explained the testing procedure. Following this, participants were provided with the learning efficiency testing questionnaire and were instructed to complete it according to the experimental guidelines. After finishing the learning efficiency test, participants completed the subjective thermal comfort questionnaire. The entire experiment lasted approximately 25 min.

To ensure the validity and reliability of the learning efficiency testing data, this study introduces a composite index (LP: Learning Performance) for calculation [54], as follows:

$$\mathrm{L}\mathrm{P}={\left[{\mathrm{A}\mathrm{C}}^{0.5}\times {\left({\displaystyle \frac{1}{\mathrm{R}\mathrm{T}}}\right)}^{0.5}\right]}^2$$

(2)

AC refers to the accuracy. RT refers to the response time.

3. Results and Analysis

3.1. Descriptive Statistics

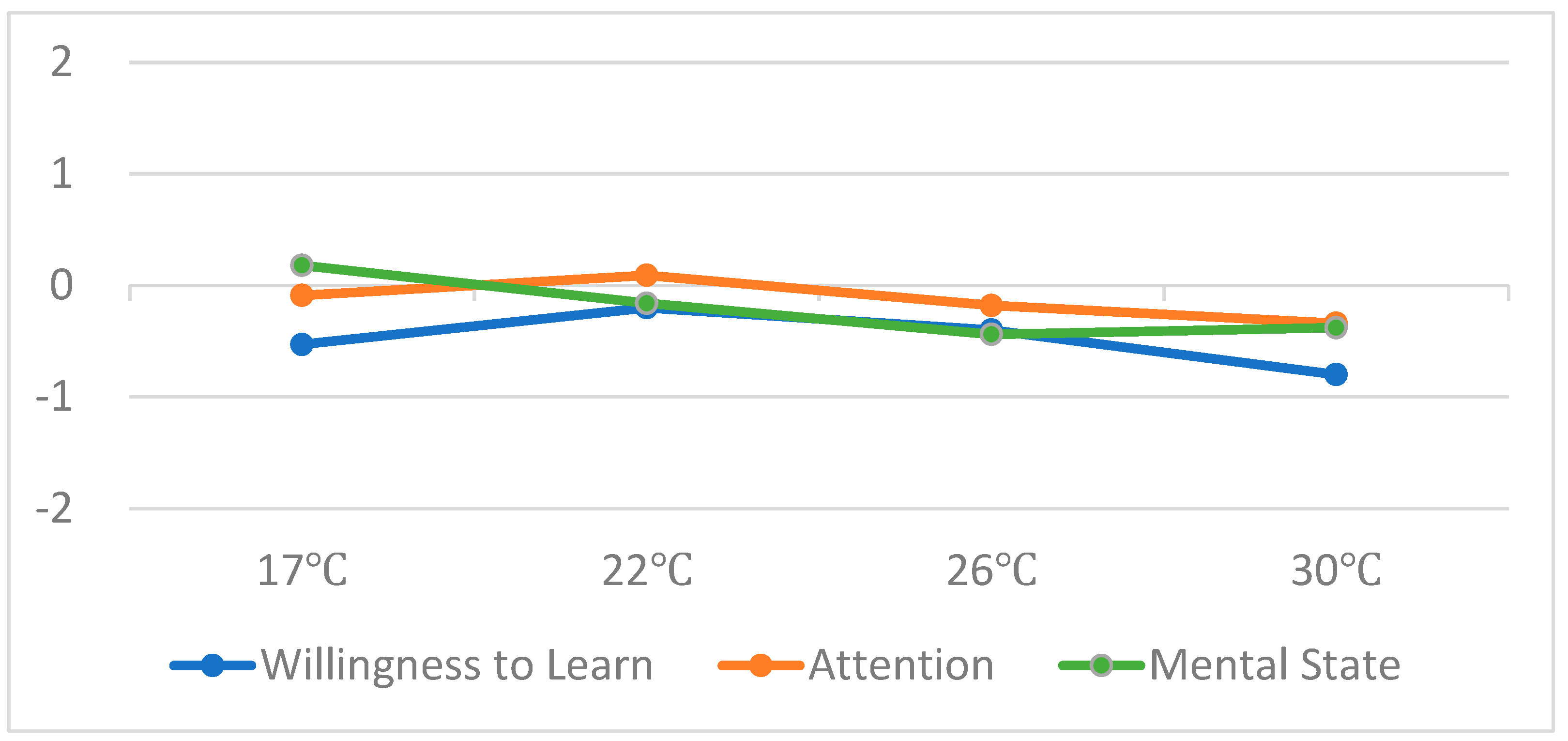
3.1.1. Subjective Thermal Comfort Evaluation

The thermal sensation data at different temperatures were analyzed using SPSS 27 software, with temperature as the independent variable and thermal sensation votes as the dependent variable. It was found that thermal neutrality occurs between 22 °C and 26 °C. The results of one-way ANOVA revealed significant differences in thermal sensation votes across different temperatures (p < 0.001), with the optimal thermal sensation occurring at 24.1 °C. The equation obtained after fitting the data using Origin software is as follows:

$$\mathrm{Y}=-3.37+0.14\mathrm{X},$$

(3)

3.1.2. Self-Evaluation of Learning Efficiency

The data on learning willingness, attention, and mental state at different temperatures were analyzed using SPSS 27 software. The results showed that there were no significant differences in learning willingness, attention, and mental state across different temperatures (p > 0.05). Therefore, in this experiment, the effects of learning willingness, attention, and mental state on learning efficiency are not considered. See Figure 4.

3.1.3. Results of Cognitive Learning Abilities Testing

The results of the learning task tests at four different temperatures, including accuracy (AC), response time (RT), and the Learning Performance (LP), were processed using SPSS software and presented in tabular form for visual analysis. The results show that indoor temperature significantly affects the accuracy of the meaningless figures test, but has no significant impact on the accuracy of the other test items. Additionally, indoor temperature significantly affects the response time for the digit-symbol test, digit recognition, meaningless figure recognition, and logical reasoning. However, indoor temperature only has a significant effect on the composite index for the digit-symbol test. However, for all test tasks, only the effect size (ES) value for the accuracy of the digit-symbol test was smaller than 0.1, while the effect sizes for the other tests were greater than 0.1, with nearly half of them exceeding 0.25. This suggests that temperature does have an impact on all test tasks, although the degree of influence varies across different tasks.

The specific data, including effect sizes (ES), are shown in

Table 2. Learning Efficiency Test Results at Different Temperatures (Mean ± Standard Deviation).

Test Task	Indicator	17 °C	22 °C	26 °C	30 °C	p	ES
Digit-Symbol Substitution Test (DEST)	AC (%)	98.04 ± 7.97	97.28 ± 7.75	98.28 ± 6.94	98.10 ± 7.34	0.916	0.064
	RT (s)	79.94 ± 13.17	78.76 ± 18.30	87.44 ± 17.01	91.32 ± 26.95	<0.05	0.312
	LP (AC/AT)	1.25 ± 0.20	1.30 ± 0.31	1.16 ± 0.19	1.15 ± 0.29	<0.05	0.286
Digit Recognition	AC (%)	88.67 ± 6.82	86.38 ± 9.31	86.64 ± 8.02	88.58 ± 7.83	0.434	0.149
	RT (s)	93.88 ± 22.17	94.02 ± 23.08	98.67 ± 27.74	114.16 ± 36.07	<0.05	0.342
	LP (AC/AT)	0.98 ± 0.20	0.97 ± 0.23	0.93 ± 0.24	0.84 ± 0.26	0.057	0.249
Meaningless Figure Recognition	AC (%)	60.30 ± 16.96	71.00 ± 18.79	73.60 ± 20.44	72.50 ± 20.09	<0.05	0.287
	RT (s)	25.32 ± 7.26	28.65 ± 13.78	24.94 ± 6.49	32.31 ± 14.18	<0.05	0.273
	LP (AC/AT)	2.56 ± 0.98	2.90 ± 1.33	3.06 ± 0.96	2.57 ± 1.13	0.166	0.204
Logical Reasoning	AC (%)	68.38 ± 24.08	69.76 ± 24.44	75.00 ± 23.39	74.31 ± 22.75	0.547	0.131
	RT (s)	328.96 ± 114.14	325.42 ± 98.94	394.22 ± 155.28	324.46 ± 99.12	<0.05	0.273
	LP(AC/AT)	0.23 ± 0.12	0.23 ± 0.10	0.21 ± 0.10	0.25 ± 0.11	0.573	0.127

. According to Cohen’s criteria, the ES values for response time in the Digit-Symbol Substitution Test (0.312) and Digit Recognition (0.342) indicate medium-to-large practical effects of temperature, suggesting meaningful differences in cognitive processing speed across thermal conditions.

Based on the above statistical findings, the influence of temperature varies across different test tasks, and the degree of impact on accuracy, response time, and the composite index for the same test task is not consistent. Therefore, evaluating the learning efficiency of university students using a single test task alone would introduce substantial error, making it impossible to accurately measure the effect of temperature on learning efficiency. Thus, it is necessary to integrate these four abilities in order to conduct a comprehensive analysis of the quantitative impact of temperature on thermal comfort.

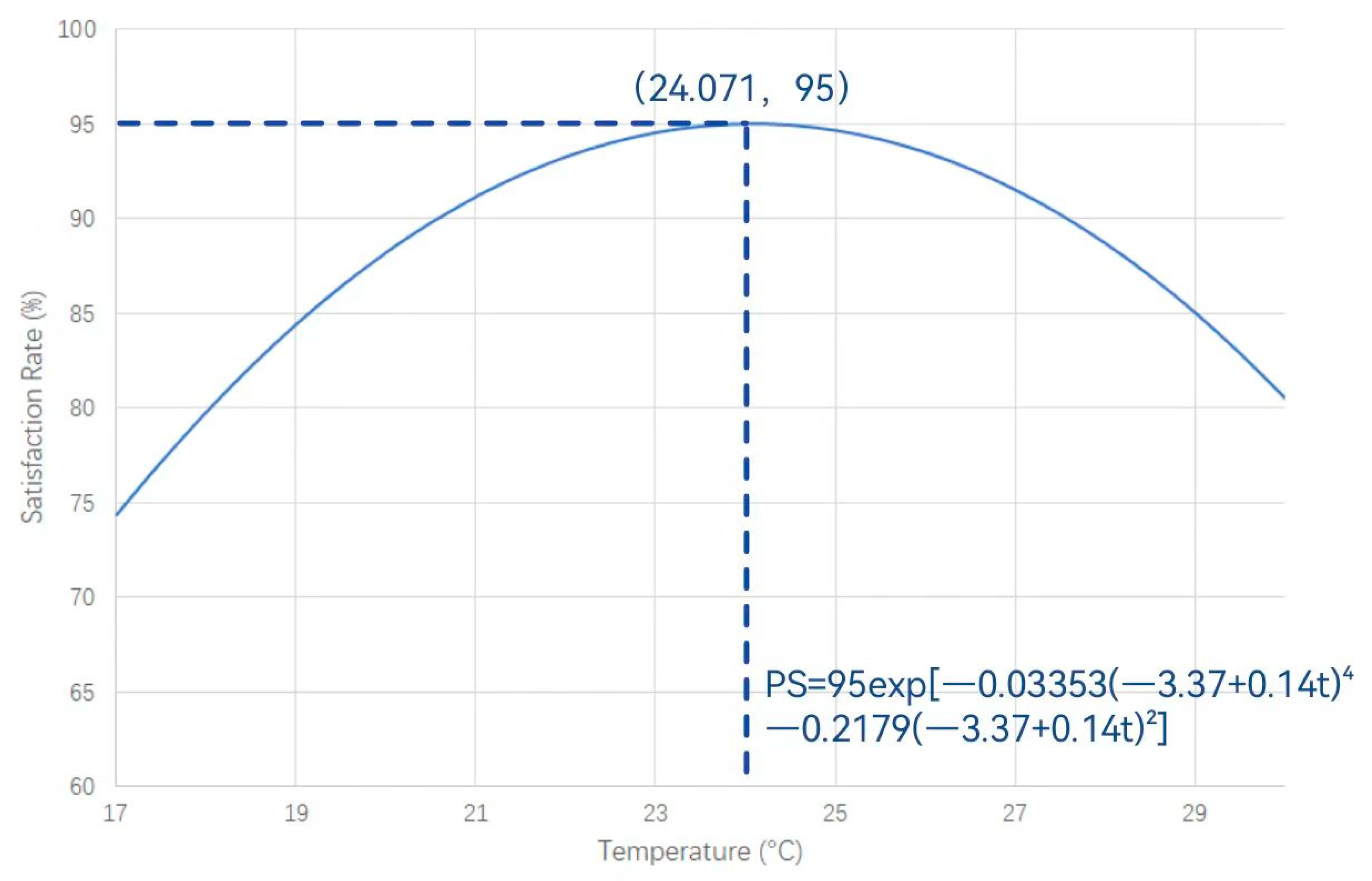
3.2. Quantitative Analysis of the Impact of Temperature on Thermal Comfort

After obtaining the data, it is important to note that individual differences among people exist, meaning the results cannot directly represent the feelings or perceptions of the entire population [55]. However, in order to assess the thermal comfort conditions in classrooms for university students, this study evaluates the group using a satisfaction rate indicator, PS (Percentage of Satisfied) [56]. At the same time, due to individual differences, a 5% dissatisfaction rate is allowed when the classroom environment is considered comfortable, resulting in a PS of 95%. The formula for PS is as follows:

$$\mathrm{P}\mathrm{S}=95\mathrm{e}\mathrm{x}\mathrm{p}[-(0.03353{\mathrm{T}\mathrm{S}\mathrm{V}}^4+0.2179{\mathrm{T}\mathrm{S}\mathrm{V}}^2\left)\right],$$

(4)

where

• PS refers to Percentage of Satisfied.
• TSV refers to the actual thermal sensation vote curve.

Based on the group satisfaction rate formula (4) and combining it with the previous Equation (3) TSV = −3.37 + 0.14 t, the relationship between thermal comfort satisfaction rate and temperature can be derived. As shown in Figure 5, the highest satisfaction rate occurs at 24 °C.

The comfort zone defined in ASHRAE 55 [19] is based on the principle that an environment is considered comfortable when 90% of the population finds it satisfactory. Based on these standards, this study determines the thermal comfort satisfaction rate (a) at 94%, 90%, and 85%. According to these satisfaction rates, different temperature ranges are derived. The results are shown in

Table 3. Temperature Ranges at Different Satisfaction Rates.

Satisfaction Rate (%)	Temperature Range (°C)
a > 94	22.5–25.6
a > 90	20.6–27.6
a > 85	19.1–28.9

.

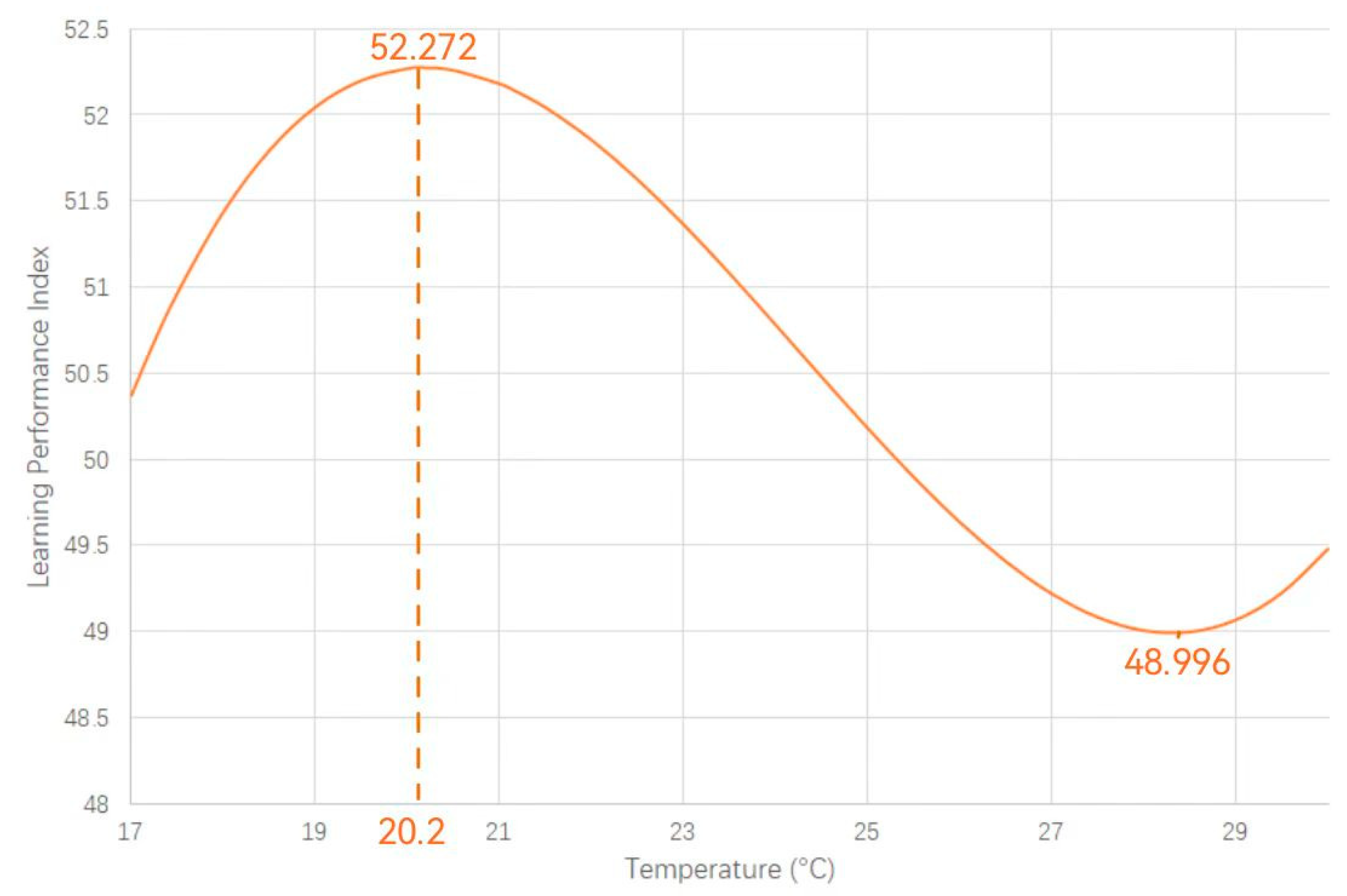
3.3. Quantitative Analysis of the Impact of Temperature on Learning Efficiency

Previous analyses have examined the effects of temperature on participants’ attention, perception, memory, and logical reasoning abilities. However, learning efficiency is a composite ability that requires the combined influence of these four factors. Therefore, to comprehensively assess the impact of temperature on learning efficiency, it is necessary to standardize the test scores across these four proxies. These standardized scores are then weighted according to the proportions derived from the Ordinal Priority Approach (OPA) in order to construct a composite analysis, ultimately yielding a quantitative assessment of the impact of temperature on learning efficiency.

The test data were standardized using the following formula:

$$\mathrm{p}\mathrm{i}={\displaystyle \frac{\mathrm{x}\mathrm{i}}{\mathrm{m}\mathrm{a}\mathrm{x}\left\{\mathrm{x}\mathrm{i}\right\}}}\times 100\mathrm{\%}$$

(5)

where

• Pi refers to the Percentage Normalized Score.
• xi refers to the composite index of the i-th participant.

After standardizing the data using the above formula, the data were fitted using Origin2021 software. Linear, quadratic, and cubic polynomial models were tested to fit the composite index. The cubic polynomial form was ultimately selected as it provided the most statistically appropriate fit, enabling the modeling of the observed inflection point and the potential asymmetry in performance decline on either side of the optimum features that simpler models could not adequately capture. The fitting equation is as follows:

Digit-Symbol Test: F₁(t) = 0.027t³ − 1.975t² + 45.910t − 294.327

Digit Recognition Test: F₂(t) = −0.0063t³ + 0.383t² − 7.949t + 116.787

Meaningless Figure Recognition: F₃(t) = −0.0168t³ + 1.053t² − 20.948t + 166.276

Logical Reasoning: F₄(t) = 0.027t³ − 1.828t² + 40.435t − 252.333

In the context of the entire learning process, all four abilities are essential; thus, determining their respective proportions is crucial. Based on the analysis in Chapter 2 and the theoretical research, this study will employ the Ordinal Priority Approach (OPA) to determine these proportions. The OPA-solver1.4 software will be used for this purpose, and the testing flowchart for the OPA-solver is shown below. See Figure 6.

The final proportions are as follows: W (Attention) = 0.263258, W (Perceptual Ability) = 0.259470, W (Memory and Understanding) = 0.138258, W (Logical Reasoning) = 0.339015.

The combined equation is:

F(t) = 0.26F₁(t) + 0.26F₂(t) + 0.14F₃(t) + 0.34F₄(t)

After organizing the data, the final quantitative impact equation of temperature on learning efficiency is:

F(t) = 0.01221t³ − 0.88802t² + 20.92351t − 108.67498

To provide a clearer and more intuitive visualization of the relationship between the participants’ composite learning index and temperature, this study used Excel2019 software to present the fitted equation in graphical form, as shown in Figure 7. It was observed that the composite learning index reaches its maximum at 20.2 °C, indicating that learning efficiency is highest at this temperature.

As previously discussed, a learning efficiency of 85% is considered high. As Figure 8 shows, the maximum composite learning index value is 52.272, and the minimum value is 48.996. Therefore, the value corresponding to 85% efficiency is calculated as follows: (52.272 − 48.996) × 0.85 + 48.996 = 51.78. Based on the learning efficiency equation, the temperature range is derived and shown in

Table 4. Temperature Range for High Learning Efficiency.

Learning Efficiency Range	Temperature Range
b > 85%	18.5–22.2 °C

.

In summary, the temperature range of 18.5 °C to 22.2 °C satisfies the thermal conditions required for high learning efficiency among university students. It is acknowledged that this optimal range is derived from the fitted model and is subject to the model’s estimation uncertainty.

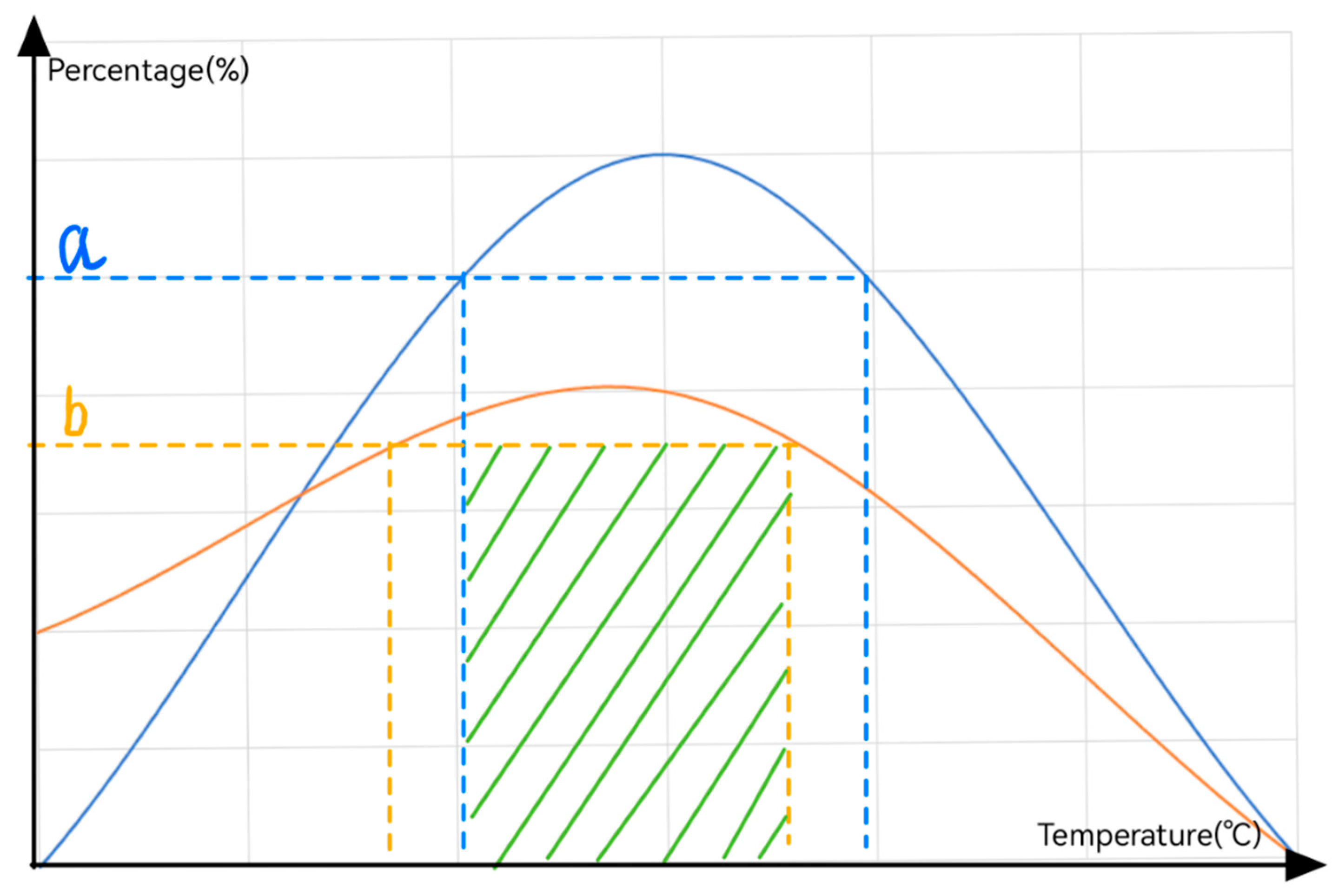
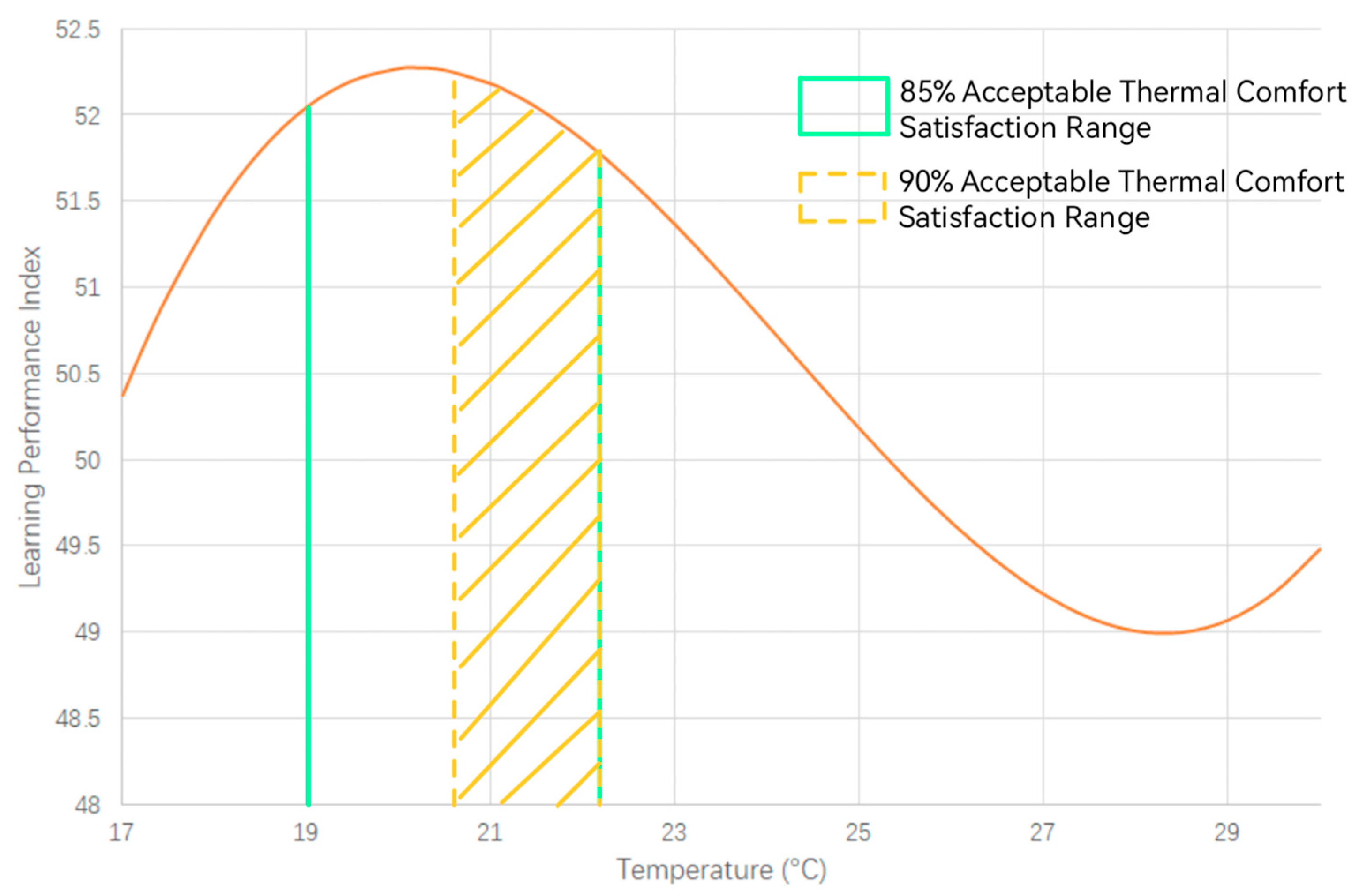
3.4. Analysis of Indoor Temperature Values Based on the Requirements for Thermal Comfort and Learning Efficiency

University classrooms differ from residential environments in that they not only need to meet the thermal comfort requirements of the occupants but also must support the learning efficiency of students to fulfill the functional demands of the classroom.

When the thermal comfort satisfaction rate for the population is set at 94%, the temperature range is 22.5 °C to 25.6 °C. However, when considering both the high learning efficiency range and the thermal comfort range simultaneously, it is found that there is no overlap between the two when the thermal comfort rate is 94%. In this case, it becomes a decision-making issue whether to prioritize the students’ thermal comfort or their learning efficiency when setting the temperature range. This study will not engage in further discussion on this matter. When the thermal comfort satisfaction rate for the population is set at 90%, the temperature range is 20.6 °C to 27.6 °C. When this range is combined with the high learning efficiency range, the optimal temperature range is 20.6 °C to 22.2 °C. Similarly, when the thermal comfort satisfaction rate is set at 85%, the temperature range is 19.1 °C to 28.9 °C. When this range is combined with the high learning efficiency range, the optimal temperature range is 19.1 °C to 22.2 °C, as shown in Figure 8.

Based on the findings from the above research, considering the combined values of different thermal comfort satisfaction levels and high learning efficiency, the temperature range of 20.6 °C to 22.2 °C is the optimal range that ensures 90% of students are in a thermally comfortable environment while maintaining high learning efficiency.

4. Discussion

According to the subjective thermal sensation votes provided by students across different temperature conditions, at 17 °C, the majority of students reported feeling “cool” or “very cool.” At 22 °C, nearly 80% of students felt “neutral” in terms of thermal comfort. At 26 °C, the overall thermal sensation shifted slightly towards “warm.” Finally, at 30 °C, most students considered the environment to be “warm” or “very warm.” By analyzing the thermal sensation data of students at different temperatures using SPSS software, the results showed significant differences in thermal sensation votes across the various temperatures (p < 0.001). The optimal thermal comfort temperature was found to be 24.1 °C, which is quite close to the 24.7 °C indoor thermal comfort temperature predicted for university classrooms by Yan Xufeng et al. [57].

The analysis of the learning cognitive ability test results revealed that individually analyzing the accuracy (AC), response time (RT), and thermal comfort yields significant errors in assessing learning efficiency. Only by selecting the Learning Performance (LP) metric can a more accurate representation of the students’ learning efficiency be obtained [58]. Some studies [59,60] suggest that within a certain temperature range, temperature changes have no significant effect on work efficiency. However, the results of this study indicate that certain tasks are significantly affected. For example, the attention test showed significant differences across temperatures (p < 0.05). As the temperature increased, the average value of the composite indicator first increased and then decreased, with the highest value observed at 22 °C. This suggests that students’ attention levels were highest at 22 °C. At the same time, as the temperature increased, accuracy did not shift significantly. However, response time increased with rising temperatures, with the lowest response time observed at 22 °C, and the highest at 30 °C. This suggests that as the temperature increased, students experienced a sense of fatigue.

Beyond statistical significance, the effect sizes (ES) reported in Table 2 provide insights into the practical importance of temperature effects on cognitive performance. The medium-to-large effect sizes observed for response time measures (e.g., ES = 0.342 for Digit Recognition) suggest that temperature variations have meaningful impacts on processing speed that would likely translate to noticeable differences in real classroom settings. In contrast, the generally smaller effect sizes for accuracy measures (e.g., ES = 0.064 for DEST accuracy) indicate that while temperature affects how quickly students process information, it may have less impact on their ultimate accuracy when tasks are untimed. This pattern aligns with the speed-accuracy trade-off phenomenon in cognitive psychology [61], where participants may sacrifice speed to maintain accuracy under suboptimal conditions.

The study found that, under controlled experimental conditions, the temperature for optimal learning efficiency among university students (20.2 °C) was notably lower than their subjectively preferred optimal thermal comfort temperature (approximately 24.1 °C), with a difference of about 4 °C. This finding directly raises a central question: In managing the thermal environment of classrooms, should priority be given to satisfying students’ comfort preferences, or to maximizing their cognitive performance?

From the perspectives of physiological and cognitive mechanisms, this discrepancy may be reasonable. Slight thermal discomfort (in a slightly cool state) might enhance physiological arousal and alertness, thereby promoting higher levels of cognitive engagement and attention focus. Conversely, being in a state of complete thermal neutrality could lead to relaxation, which may be detrimental to learning tasks requiring high concentration. This aligns with the observed phenomenon in this study of faster reaction times in slightly cool environments (e.g., 22 °C) and is consistent with findings in some literature indicating that students prefer slightly cooler classrooms [41,62,63].

However, this does not imply that comfort should be entirely sacrificed for the sake of efficiency. Prolonged exposure to significantly uncomfortable environments may induce negative emotions and increase mental load, potentially offsetting or even reversing the advantages observed in short-term cognitive tasks. Therefore, an ideal teaching environment design should seek a pragmatic balance, rather than optimization along a single dimension.

Accordingly, the temperature range of 20.6–22.2 °C proposed in this study should be understood as such a balanced solution: it is not an absolute, single-point optimum, but rather a compromise range that simultaneously satisfies two key constraints. Specifically, it ensures a thermal comfort satisfaction rate of at least 90% (according to standards such as ASHRAE 55), while maintaining student learning efficiency at a high level (with a composite index exceeding 85% of peak performance). This range is lower than the 24 °C driven purely by thermal comfort, yet significantly higher than the lower limit of discomfort that might result from solely pursuing learning efficiency. It aims to provide practical guidance for classroom environment settings that balances both learning efficiency and thermal comfort. This finding is similar to the research of Seppanen et al., which suggests that the optimal performance in terms of both thermal comfort and learning efficiency occurs around 22 °C [64].

This study has several limitations. First, the experiments were conducted during the spring (April and May) and therefore did not account for full seasonal thermal acclimatization that might occur in peak summer or winter. Although all participants were long-term local residents (≥1 year) in Yibin, ensuring a baseline acclimatization to the local Hot-Summer-Cold-Winter climate, the specific physiological and psychological adjustments linked to extreme seasonal exposure may not have been fully engaged. For instance, tolerance to 30 °C might be higher in a true summer context, while sensitivity to 17 °C might be more pronounced in deep winter. This potential acclimatization difference suggests that the absolute values of the identified optimal temperature range (20.6–22.2 °C) could shift marginally across seasons. It is important to note, however, that the primary aim of this work was to establish a general functional relationship between indoor temperature and learning efficiency; this core mechanistic finding is likely less sensitive to the specific season of data collection. Future research should aim to replicate this experiment in summer and winter to directly quantify the effect of seasonal acclimatization on thermal comfort and cognitive performance in classroom settings, thereby validating and refining the present model under varied climatic exposures.

Furthermore, when evaluating the practical implications of the findings from this study, it is necessary to consider the inherent limitations of the experimental design itself. To precisely parse the causal relationship between temperature and cognitive performance, the experiment employed a short-term, controlled exposure protocol along with standardized cognitive test tasks. This design effectively isolates the temperature variable and controls for confounding factors, making it an ideal method for establishing causal mechanisms. However, authentic classroom learning constitutes a dynamic process involving prolonged concentration, complex knowledge integration, social interaction, and intrinsic motivation. Consequently, the short-term effects of temperature on foundational cognitive abilities (such as processing speed and short-term memory) observed in this study may not fully equate to its impact on long-term academic outcomes in real educational settings.

Although the self-assessment indicators of learning efficiency showed no statistically significant differences in the direct analysis of this study, this does not imply that they are irrelevant within the chain of relationships linking the thermal environment to learning efficiency. On the contrary, they may play the roles of mediating or moderating variables [65]. For instance, prolonged exposure to a suboptimal thermal environment could subtly influence learning motivation, which in turn affects cognitive performance; alternatively, an individual’s psychological state might moderate their sensitivity to thermal stimuli. Future research could employ larger samples, longitudinal designs, or structural equation modeling to further investigate the roles of these subjective factors within complex pathways of influence. The findings of this study underscore the significant value of employing a multi-method assessment strategy—integrating subjective questionnaires with objective cognitive measures—in research on thermal comfort and learning efficiency, as it enables a more comprehensive and deeper understanding of the holistic impact of the environment on human occupants.

5. Conclusions

5.1. Summary and Recommendations

This study summarizes the current research progress and findings on student thermal comfort and learning efficiency from both domestic and international scholars. Most studies have rarely considered the differentiation of building climate zones, while extant methods for evaluating learning efficiency are relatively simplistic. In supplementing the research data and understanding in this field, this study analyzes the relationship between thermal environment, thermal comfort, and learning efficiency in university classrooms under conditions of summer-hot and winter-cold climates, as experienced in Sichuan Province, China, through thermal comfort questionnaires and four ability tests. The following conclusions are drawn.

• Between 17 °C and 24 °C, as the temperature increases, the thermal sensation shifts from −1 to 0 (subjectively feeling cold to comfortable). Between 24 °C and 30 °C, with further temperature rise, the thermal sensation changes from 0 to 1 (subjectively feeling comfortable to warm). The most comfortable thermal sensation is reported at 24 °C.
• The analysis shows that the optimal thermal comfort temperature corresponds to 24 °C, while the optimal learning efficiency temperature is 20.2 °C, with a temperature difference of 3.8 °C. A comprehensive comparison reveals that university students exhibit better learning efficiency in slightly cooler environments.
• Based on the combined optimal values for both thermal comfort and high learning efficiency, the ideal temperature range lies between 20.6 °C and 22.2 °C.

In response to the aforementioned issues, it is incumbent to consider the climate and architectural characteristics of universities located in summer-hot and winter-cold regions. Reasonable design of classroom orientations and ventilation systems should be prioritized, with targeted adjustments to the indoor temperature. The indoor temperature can be slightly lowered to create a cooler environment, which may help improve the learning efficiency of university students.

5.2. Future Research

This study only examined the impact of temperature on university students’ thermal comfort and learning efficiency. However, there are many other factors that can influence learning efficiency. Future research could consider investigating the effects of other environmental parameters, such as humidity, noise levels, lighting, and carbon dioxide concentration, as well as psychological factors.