Numerical Modelling and Experimental Validation of FRCM-Reinforced Concrete Beams Using Macro-Modelling Techniques

Abstract

Fibre reinforced cementitious matrix (FRCM) systems are composite materials that are increasingly used for retrofitting masonry and reinforced concrete structures. Their behaviour does not depend only on the mechanical properties of the fibres and the matrix. Therefore, it is essential to perform tensile tests on FRCM coupons, as well as additional tests to investigate whether the interaction between the FRCM system and the substrate can be considered a perfect bond. The aim of this paper is to numerically simulate the behaviour of concrete beams retrofitted with two FRCM composite systems assuming perfect bond. The results of the numerical simulations were compared with experimental data, and it was observed that the adopted models successfully capture the cracking behaviour of both the concrete and the FRCM, as well as overall structural response of the specimens. The main finding was that the behaviour of concrete beams retrofitted with FRCM can be effectively estimated using a macro-modelling approach in numerical simulations. The ultimate load obtained experimentally is between 2% and 20% higher than the numerical value. This is safe and accurate enough for engineering purposes.

1. Introduction

Societal concern for sustainability has led to a growing emphasis on the conservation of existing structures in order to maintain their functionality of constructions by means of repair and retrofitting, thereby extending their service life [1,2]. The use of externally applied composite materials made of high-strength fibres embedded in a matrix has emerged as an alternative to traditional reinforcement methods. The main types of such composites are fibre-reinforced polymers (FRPs) and fibre-reinforced cementitious matrix (FRCM), both of which are employed for structural applications due to their efficiency and high strength-to-weight ratio [3,4,5].

FRCM systems offer several advantages over the more widespread FRPs, including the applicability to wet supports, vapour permeability, enhanced compatibility with masonry substrates, and greater resistance to high temperatures [6,7,8,9,10,11,12,13,14,15].

A FRCM system is composed of a fibre mesh embedded in an inorganic matrix. The mesh typically consists of an orthogonal grid made from carbon fibres, alkaline resistance (AR) glass, basalt, aramid, or synthetic polymeric reinforcements such as PBO. Matrices can be made of cement mortars or lime-based ones (particularly in heritage buildings), and can include additives or additions such as polymers, fly ash, and fibres [5,16,17,18,19,20,21,22].

The mechanical behaviour of FRCM depends not only on the properties of the mesh and matrix but also on the performance of the interfaces—between the mesh and the matrix, and between the matrix and the substrate. Under uniaxial tensile loading, FRCM composites typically exhibit a trilinear idealised stress–strain response, with each phase corresponding to a distinct cracking state. The first phase (Stage A) represents the initial elastic behaviour, dominated by the mortar, prior to the onset of cracking. The second phase (Stage B) begins when the tensile strength of the matrix is reached and the first crack appears, resulting in a reduction in the slope of the stress–strain curve. The last phase (Stage C) begins when no new cracks form, and existing cracks widen. In stage C, the load is primarily carried by the fibres, and the composite’s strength and stiffness are governed by the mesh [5,17,23,24]. However, the last phase may not be present due to the possible premature slippage of fibres [5,22,24,25,26,27,28,29]. Furthermore, the gripping system employed in uniaxial tensile tests significantly affects the stress–strain response [26,27,28,30].

Both American and Italian Guidelines [29,31,32] recommend characterising the properties of the FRCM composites through uniaxial tensile tests. Additionally, other tests are advised to evaluate the bond between the FRCM and the substrate. One such method is the bending test of concrete beams reinforced with FRCM. However, these tests are not standardised, and the comparisons are hindered by significant variations in parameters such as beam length, number of load points, and arrangement of the reinforcement and reinforcement type, among others [33,34,35,36,37,38,39,40,41,42]. As previously noted, the mechanical performance of FRCM systems depends not only on the strength of the textile and the matrix, but is also affected by their interaction with each other and with the substrate, as well as by the testing method. While tensile tests on FRCM are relatively simple, cost-effective and informative, adhesion tests and bending tests are more complex and expensive. For this reason, a simplified numerical model using only the values from tensile tests of the composite is proposed in this paper. This will allow estimating the behaviour of reinforced beams without the need for expensive experimental testing, provided that ultimate limit states remain on the safe side.

Relying on the values from tensile tests of the FRCM requires adopting the hypothesis of perfect bond between the composite and the concrete substrate. The suitability of such simplification is supported by the fact that the most common failure mode of FRCM applied to a substrate is debonding at the matrix-to-textile interface. This makes the interfacial behaviour within the FRCM highly relevant [3,43,44,45,46], as it affects the presence or absence of the third branch of the stress–strain curve. Bencardino et al. (2018) [47] reviewed concrete beams reinforced with carbon FRCM and found that, among 25 tested beams, 13 failed due to debonding at the matrix-to-textile interface, 5 exhibited debonding without an interface being identified, and only 2 failed due to textile rupture. Similar observations arose the authors’ own experimental tests on beams [48].

When using complex numerical or analytical models to study FRCM-reinforced members, it is necessary to characterise tensile adhesion through a cohesive material law (CML) that describes the fibre–matrix slip behaviour [47,49,50]. Provided that maximum adherence between the FRCM and substrate is achieved, the most probable failure mode is the slippage in the fibre–matrix interface [34,45,51,52,53,54]. On its part, achieving maximum adherence between the FRCM and the support required at least a minimum bonded length, similar to FRP. According to various studies [34,45,51,52,53,54], this length (known as effective bond length) is between 150 mm and 300 mm for FRCM. Specifically for carbon FRCMs, Awani et al. (2015) [54] estimates the effective bond length to be between 250 and 300 mm, and D’Antino et al. (2020) [37] suggests a value of 300 mm.

Flexural testing of concrete beams reinforced with FRCM subjected to flexure is a method used to study the bond between the composite and the substrate. The beams may be pre-damaged [55,56], or constructed with a low reinforcement ratio [50,57,58]. Recent research also explores the adherence of FRCM systems with coated textiles [48,59] and with fibre-reinforced matrices [50,60]. These research lines are consistent with the fact that failure often occurs at the fibre–matrix interface within the composite. Consequently, improving this bond enhances the effectiveness of the reinforcement.

Simulations of concrete beams retrofitted with FRCM can serve different purposes [58,60,61,62,63,64,65,66,67], namely to study the interface between concrete and FRCM [68,69], to analyse the influence of reinforcement [70], or to estimate the global structural behaviour [71]. Elsanadedy et al. [71] conducted 3D simulations of reinforced concrete beams under four-point bending, modelling the textile as shell elements and estimating interface behaviour based on pull-out tests and literature and calibrating with experimental results. Aljazaeri and Al-Jaberi [69] modelled FRCM as a laminated system using tensile test data and different interface conditions between mortar ad textile obtained from the literature. Concrete parameters were obtained from the literature and calibrated. Interface between FRCM and concrete is considered a critical parameter and different interfacial cohesive models were considered. Mercedes et al. [72] used truss elements for steel, shell elements for the reinforcement and solid elements for the concrete. Previously, FRCM is simulated as a fabric (truss elements) embedded in the matrix (solid elements) to obtain modulus of elasticity of the composite. Concrete reinforced beams are estimated with concrete damage plasticity and calibrated with experimental results. Feng et al. [73] used a 3D model to study the size effect of fully wrapped reinforcements of beam, together with the degree of corrosion of steel rebars. FRCM is modelled as a yarn inside of a matrix bond with spring elements that were calibrated against experimental results by the trial-and-error method. Khattak et al. [74] simulated five-point bending of reinforced concrete beams with FRCM in both sagging and hogging regions, using two or four layers of PBO or carbon, assuming perfect bond and a predefined bond–slip law at the matrix–textile interface. In general, proposed numerical models are calibrated using results from bending tests. Therefore, when using different textiles, matrices or concretes, new experimental campaigns are necessary before using these models to estimate beams reinforced with FRCM.

The aim of this research is to develop a numerical macro-model for engineering applications. The model should be capable of estimating the ultimate load of concrete beams reinforced with FRCM by using the results from direct tensile tests on the composite (i.e., a specific matrix and textile combination). Therefore, the need to conduct flexural tests of each individual composite is eliminated, as well as that of any other test for bond interface characterisation. The purpose is to estimate the ultimate load for design purposes, relying on tensile characterisation of the FRCM and calculations based on strength class for the concrete beam, without requiring model calibration. Notched reinforced concrete beams are used, even though they do not represent real applications. The reason to employ them in this study was the fact that, in these beams, the contribution of the steel is suppressed. This allows a simplification when estimating ultimate load capacity in retrofitting applications. The main limitations of the approach would affect serviceability limit state, as the model would not evaluate whether the existing reinforcement of the beam may yield at low loads, not the deflection at different load stages.

2. Review of Experimental Tests

As part of a research project on the structural performance of concrete reinforced with FRCM conducted as the Universidad Politécnica de Madrid, two series of concrete beams were retrofitted with different externally bonded FRCM composites and tested to investigate the influence of the matrix type on the overall structural behaviour [48]. In parallel, the FRCM systems were characterised through uniaxial tensile tests to determine their mechanical properties under tension [61]. The results from these tests have been used to define and calibrate the numerical model of beams retrofitted with FRCM presented in this publication. This section provides an overview of the materials employed in the experimental work and summarises the key findings relevant to the numerical simulation of three-point bending tests.

2.1. Materials

Two different FRCM systems were selected for the experimental campaign, both incorporating the same high-strength coated carbon balanced grid but differing in the type of mortar used: a conventional masonry mortar (M1) and a structural repair mortar containing additives and fibres (M2). Although both mortars exhibit a similar compressive strength, their compositions differ significantly. The purpose of selecting these two mortars was to investigate whether the matrix properties influence the overall behaviour of FRCM-reinforced beams and, in particular, their failure mode.

The carbon mesh, noted for its high geometrical stability, has an equivalent thickness of 0.057 mm, a nominal ultimate tensile strength (f_f,u) of 3600 MPa, a Young’s modulus (Ef) of 223 GPa, and an ultimate tensile strain (ε_f,u) of 1.55%. These values are provided by the manufacturer [75].

Mortar M1 is a conventional normalised mortar in accordance with standard EN 197-1:2011 [76] with a cement–sand–water ratio of 2:6:1. It is made of 551 kg of Portland cement type 42.5 MPa CEM II, 1583 kg of aggregate size up 4 mm, and 263 kg of water per cubic metre. Mortar M2 is a pre-dosed, bicomponent, thixotropic R4 repair mortar compliant to UNE-EN 1504-3:2006 [77], containing short fibres up to 7 mm in length. One component is a cementitious mixture based on white Portland cement (52.5 MPa) and CSA cement with 35% of binder approximately, combined with silicious sand (maximum size of 2 mm), metakaolin, anti-corrosive and anti-shrinkage additives, and a snubbing agent. The second component is a water-based polyurethane dispersant.

The average values of compressive strength (f_m,c), flexural strength (f_m,f) and modulus of elasticity (E_m) of the mortars at 28 days were obtained from tests according to UNE-EN 12190:1999 [78] and UNE-EN 13412:2008 [79] and are collected in

Table 1. Mechanical properties of mortars.

Mortar	M1 (Conventional)	M2 (Repair)
fm,c [MPa]	41.2	51.9
fm,f [MPa]	7.2	10.0
Em [GPa]	15.0	20.0

. Four specimens were used to determine the flexural strength and modulus of elasticity, while eight were used to determine the compressive strength.

Reinforced concrete beams were used as substrates in bending tests. The concrete was made of 300 kg of Portland cement type CEM II (42.5 MPa), 1055 kg of aggregate with a maximum size of 4 mm, 260 kg of aggregate with sizes between 4 mm and 8 mm, 600 kg of aggregate with sizes between 6 mm and 12 mm and 170 kg of water. The cement–aggregates–water ratio is 2:6:1. The concrete, designed to have a compressive strength of 30 MPa, was tested at 28 days according to UNE-EN 12390-3:2020 [80] using cube specimens with a resulting average compressive strength of 31.7 MPa. The reinforcement was made with 8 mm diameter rebars of standard steel. The yield strength and modulus of elasticity of the steel were 545 MPa and 210 GPa, respectively.

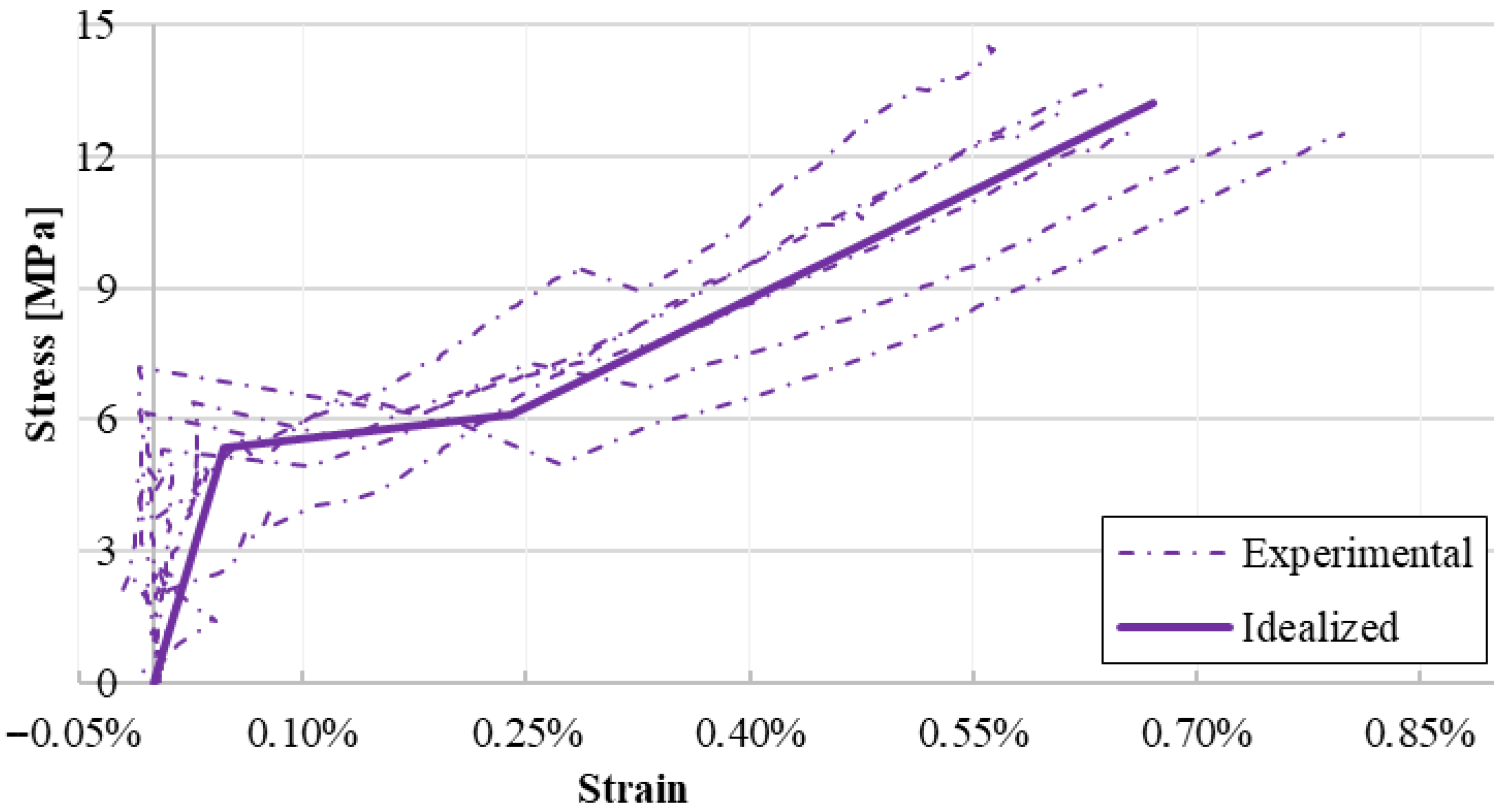
2.2. Direct Tensile Tests

The mechanical performance of FRCM composites under tension is strongly influenced by factors including the geometry of specimens [4,68,70,81,82,83,84,85], gripping method [5,69,73,74,86,87,88,89,90,91,92], test setup [5,69,73,74,86,87,88,89,90,91,92], and material properties. The geometry of the FRCM test specimens was selected in accordance with the recommendations of ACI 549.4R-20 [34], ACI 549.6R-20 [35], AC434 (2018) [30], CNR-DT 215/2018 [25], and RILEM TC 250-CSM [93]. The manufacturing process and the number of specimens were also determined based on these guidelines. Each specimen measured 40 mm in width and 8 mm in thickness, formed by two layers of matrix, each with a thickness of 4 mm, and had a total length of 300 mm. A gripping length of 75 mm was provided at each end, and specimens were tested after a curing period of 28 days. The clamping grid method, as recommended by CNR-DT 215/2018 [25], was selected for gripping. This method facilitates textile rupture under tension and, according to previous research, enables the observation of a trilinear stress–strain response [5,22,24,43,61,86,87,94,95]. The test setup followed the specifications outlined in CNR-DT 215/2018 [25].

The electromechanical test machine used for tensile tests was a Servosis ME-405/50/5 with a load cell REP Traducer Type TC4 50 kN. The grids were designed ad hoc after MTS Model XSA 304A to adapt them to the geometry of specimens (see also Figure 1). A constant crosshead displacement rate of 0.5 kN/min was applied during testing.

Data acquisition was performed using digital image correlation (DIC), a non-contact optical technique that enables full-field measurements of displacement and strains within a predefined region of interest (ROI) [96]. A low-cost 2D-DIC prototype, similar to the one developed by Garcia et al. [97,98] was employed for image acquisition (Figure 1). Sample preparation followed the procedure described in [26]. The DIC setup was carefully chosen to ensure optimal accuracy and minimise errors, with the acquisition prototype (camera) placed at 1 m from the specimen, achieving a GSD of 0.07 mm/px. A lens aperture of f8 was used, and images were acquired at a rate of 1 frame per second (FPS) with a shutter speed of 1/100 s.

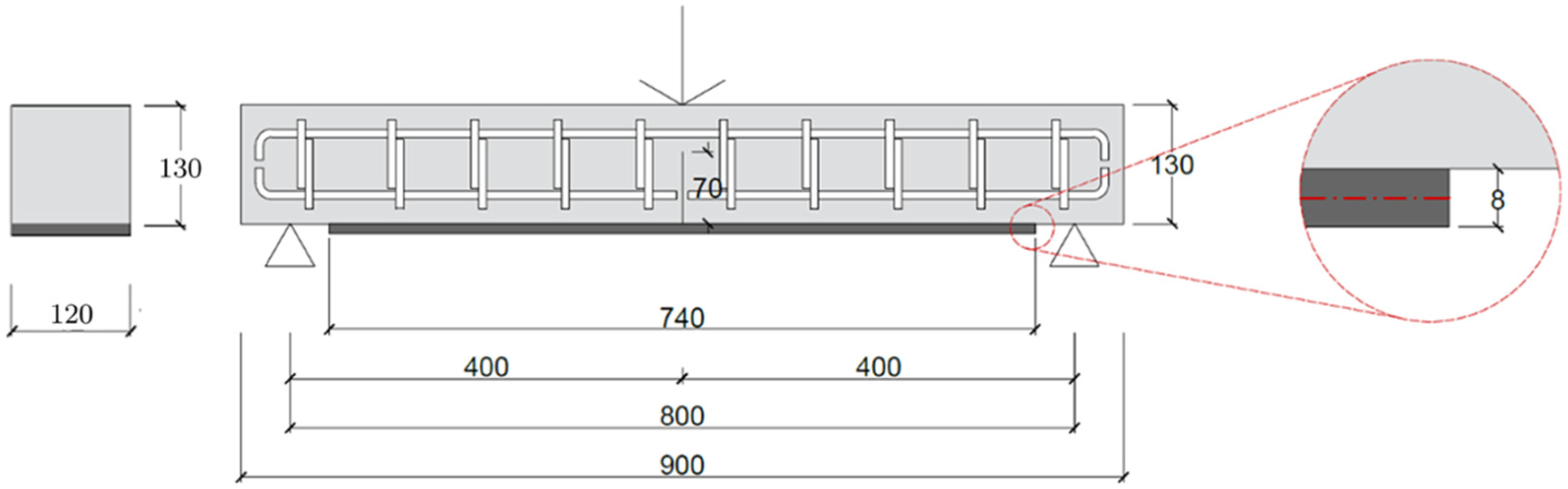
2.3. Bending Tests

Three-point bending tests were conducted to assess the behaviour of FRCM composites bonded to concrete and to study potential failure modes. In addition to a notched reinforced concrete beam used as a control beam, three notched beams reinforced with FRCM made of mortar M1 (system 1) and two notched beams reinforced with FRCM made of mortar M2 (system 2) were tested. It is important to note that the notch introduced in the control beam reduces its stiffness compared to the FRCM-reinforced beams.

All beams were internally reinforced with steel rebars to prevent shear failure. Minimal longitudinal reinforcement was added for constructive reasons and to avoid localised concrete crushing. The lower longitudinal reinforcement was interrupted by a 70 mm deep notch, which facilitated cracking development at the midspan and ensured that the longitudinal reinforcement did not contribute to the flexural capacity. Figure 2 illustrates the beam dimensions and the reinforcement layout.

Concrete beams measuring 900 mm in length, 120 mm in depth, and 130 mm in height were tested under a span of 800 mm (Figure 2). An ad hoc bending platform was designed to adapt the test machine to the test procedure. This setup included a custom bench constructed from structural profiles to support the specimens, with two 45 mm roller serving as point supports and a 20 mm roller used to apply the load at the centre of the span. The electromechanical test machine Servosis ME-405/50/5 was equipped with a REP Transducer Type TC 50 kN. The static load was applied under displacement control at a rate of 1.2 mm/min, a value consistent with those reported in the literature for quasi-static loading of beams reinforced with carbon FRCM [99].

As in the tensile tests, DIC was employed for data acquisition. A dual 2D-DIC approach was adopted, as out-of-plane deformation was negligible. The first (macro) approach focused on beam deformation around the notch, while the second (micro) approach provided a detailed analysis of the FRCM behaviour. A customised and ad hoc design 2D-DIC prototype based on a standard configuration for mechanical tests [97,100] was used to acquire the images. Two aligned cameras were positioned at distances of 1.25 mm (macro) and 0.5 mm (micro) from the measurement plane. For the macro approach, the ROI measured 350 mm × 120 mm, with a ground sampling distance (GSD) of 0.11 mm/px. In the micro approach, the ROI was 125 mm × 7 mm. A shutter speed of 1/100 s and a lens aperture of f8 were selected to ensure adequate illumination, depth of field, and image sharpness.

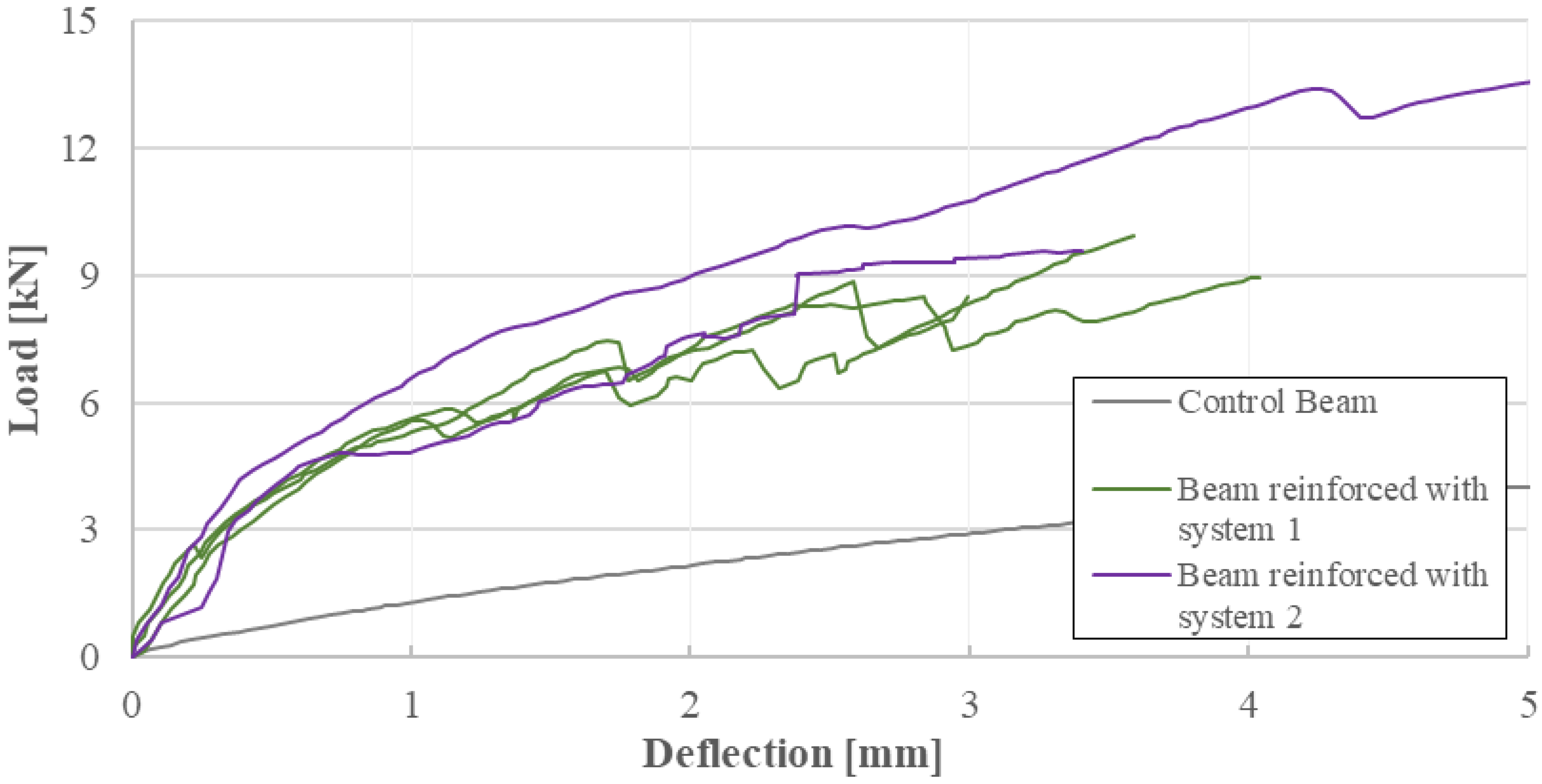
2.4. Main Results

To monitor displacement and strain, a 2D digital image correlation (DIC) system was integrated into the experimental setup. Data processing was conducted using the open-source software Ncorr v1.2, while strain extraction and visualisation were managed through the Ncorr Post CSTool. By synchronising the image acquisition system with specific loading intervals, each captured frame was associated with a corresponding stress level. In this way, it was possible to calculate the strain in each of the images and, accordingly, to obtain the stress–strain curves for each of the tests performed.

The stress–strain curves obtained from uniaxial tensile tests on FRCM coupons are shown in Figure 3 and Figure 4 for system 1 and system 2, respectively. The idealised curves of the FRCM systems are calculated following the recommendations of the Italian Guidelines CNR-DT 215/2018 [25], considering the cross-sectional area of the reinforcing fibres. Then, they are converted into idealised curves based on the total cross-sectional area of the composite for further application in the numerical simulation. Figure 3 and Figure 4 show the curves obtained experimentally and the idealised curves based on the total cross-sectional area of the composite. The curves of system 1, the one with mortar M1, show a bilinear evolution, whereas curves from system 2 are trilinear.

Strength (f_FRCM), maximum strain (ε_FRCM) and modulus of elasticity (E_FRCM) for each stage and system are presented in

Table 2. Results of tensile tests on FRCM composite specimens.

System	Stage	fFRCM	εFRCM	EFRCM
		(MPa)	(%)	(GPa)
System 1 Mortar M1	A	2.47	0.03	8724
	B	12.62	0.77	1363
	C, ultimate
System 2 Mortar M2	A	5.35	0.05	11,321
	B	6.10	0.24	389
	C, ultimate	13.20	0.67	1650

. The values were calculated with the composite cross-section. Both systems exhibit similar ultimate tensile strength; however, the crack initiation stress (f_FRCM,A) in system 2 is more than twice that of system 1, which is attributable to the higher tensile strength of mortar M2. These findings support previous conclusions that mortar composition significantly affects the cracking process and the textile–matrix bond. This, in turn, has a substantial impact on the overall behaviour of the composite, which cannot be predicted solely from the mechanical properties of the mortars [101].

The results of the bending tests of beams are summarised in

Table 3. Experimental results from bending tests.

Beam	Load Pu	Deflection	Stress Max FRCM	Peak Strain FRCM	Load Increment	Failure Mode
	(kN)	(mm)	(MPa)	(%)	(%)
Control beam	4.53	5.13	-	-	-	-
Reinforcement with system 1	9.17 ± 0.55	3.49 ± 0.50	15.04 ± 0.91	1.71 ± 0.05	203 ± 12	Debonding at the matrix-to-textile interface
Reinforcement with system 2	12.19 ± 2.58	4.17 ± 0.89	19.97 ± 4.21	1.51 ± 0.93	269 ± 57	Debonding at the matrix-to-textile interface

, which presents the average values and statistical deviation for each system. The load increment is calculated relative to the ultimate load of the control beam (i.e., the beam without the FRCM reinforcement).

The experimental load–deflection curves of all 6 beams are shown in Figure 5, where three families of curves are clearly visible, corresponding to each type of beam.

The failure modes were classified according to the typologies listed in CNR-DT 215 [25]. All tested beams exhibited the same failure mode, characterised by debonding at the textile–matrix interface. This failure occurs within the composite material itself, without involving the interface between the support and the reinforcement. Figure 6 illustrates the described failure mode. These observations support the validity of assuming a perfect bond in engineering numerical models, as this assumption proves to be both feasible and accurate in this context.

3. Modelling of the FRCM-Reinforced Beams

A two-dimensional finite element model is employed to simulate the nonlinear behaviour of concrete beams, following a macro-modelling approach. The nonlinear numerical model adhered to standard advanced procedures. All static nonlinear numerical analysis were conducted under a plane stress assumption using a refined finite element mesh. The model geometry was designed to closely replicate the bespoke experimental setup.

DIANA FEA software Version 10.7. was selected for its specialised elements and constitutive models tailored to concrete, steel reinforcement, and FRCM [102]. Three types of numerical models were developed: a reinforced concrete notched beam for comparison with the control beam’s experimental results and two distinct reinforced concrete notched beams with different FRCM composites for comparison with experimental data. All three models employ the same constitutive model for concrete with the primary differences being the inclusion of FRCM reinforcement elements. Also, a plain concrete notched beam was previously modelled to study the concrete behaviour independently, although this was not associated with any experimental test.

The mechanical behaviour of both the RC beam and the FRCM was described using suitable nonlinear constitutive laws based on the total strain rotating crack approach, calibrated against available experimental data. The system of nonlinear equations was solved using the modified Newton–Raphson algorithm, with the arch length control method to improve convergence.

3.1. Element Type and Size

The adopted mesh is illustrated in Figure 7. Both the RC beam and the FRCM were modelled using eight-node quadrilateral isoparametric plane stress elements (CQ16M). Additionally, six-node triangular isoparametric plane stress elements (CT12M) incorporated into the beam model to better capture pronounced strain gradients near the beam–FRCM interface and the notched region, facilitating smooth transitions between elements of varying sizes. This led to the employment of three different sizes of elements: 15 mm for the macroscale regions of the beam, 4 mm for the FRCM, and a refined mesh of up to 3 mm for the concrete area above the notch. To model the interaction between the matrix and the beam, a two-dimensional interface element (CL12I) was used.

The interaction between concrete and FRCM is defined as linear elastic with a normal stiffness of 1000 MPa/mm and a shear stiffness of 1000 MPa/mm, as recommended for a rigid and perfect bond [103,104]. A sensitivity analysis was performed for normal and shear stiffness using 10 MPa/mm, 100 MPa/mm, 1000 MPa/mm, 1000 MPa/mm, and 10,000 MPa/mm, and no significant effects in the results were found.

3.2. Boundary Conditions

Steel blocks (6 mm × 6 mm) were used to transfer the load and support the beam under the three-point bending tests. These blocks were connected to the beam via an elastic interface that restricted normal displacement while allowing shear movements. The interface was defined with a normal stiffness of 1000 MPa/mm and a shear stiffness of 10 MPa/mm.

The two blocks were positioned at the bottom of the beam to prevent vertical displacement, with the right block additionally restraining horizontal displacements. At the top of the beam, above the notch, a third block was placed to transfer the load. In this case, the load was applied through an imposed vertical displacement.

3.3. Loading Scheme

The load was applied as a vertical displacement of the upper steel block. To ensure convergence of the simulation, the load was applied in different step. The Newton–Raphson iteration method was employed, updating the tangential stiffness at each iteration, with a maximum of 30 iterations. The convergence criterion was defined by internal energy limited to 0.001.

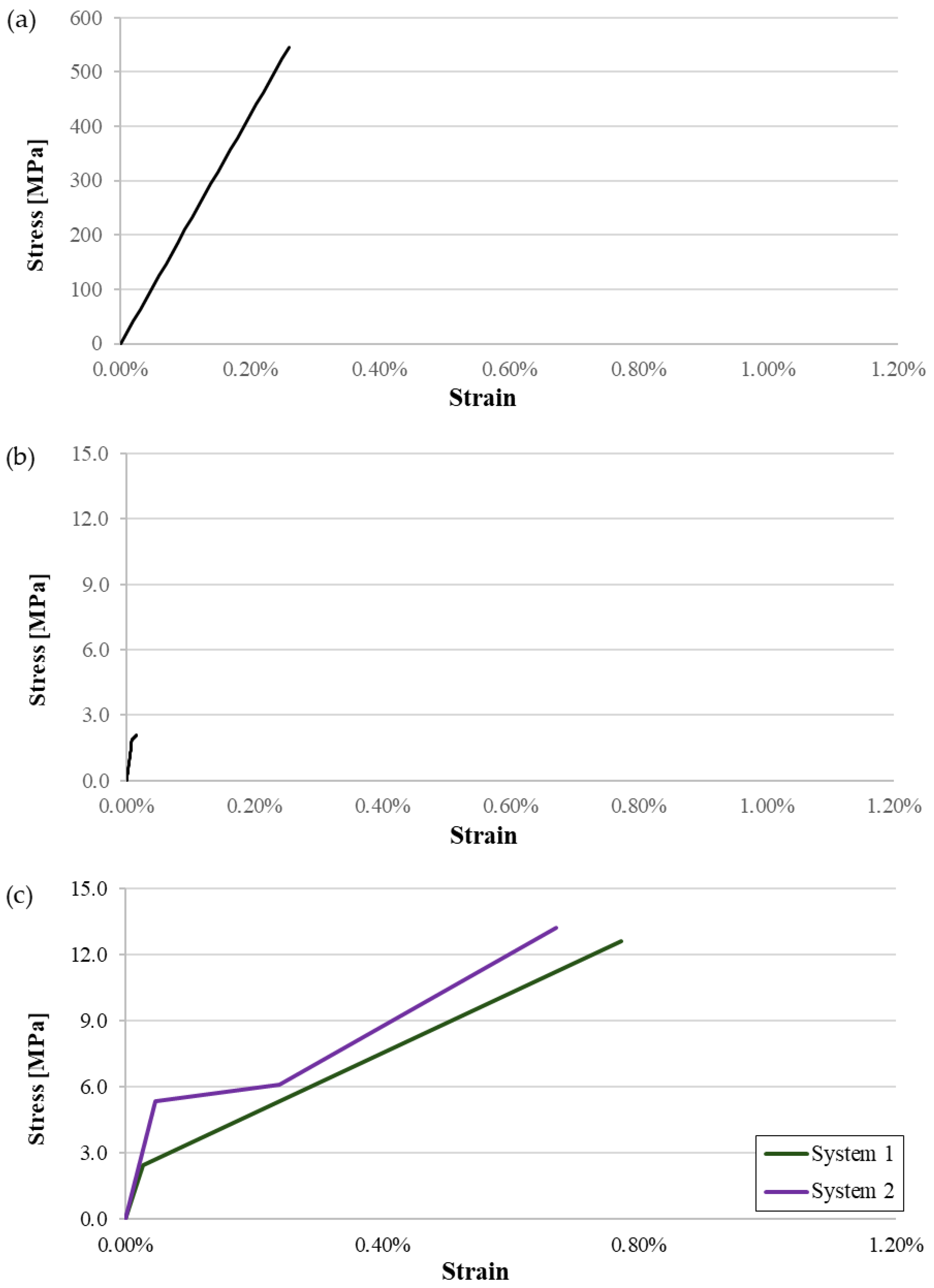
3.4. Constitutive Material Models

Three constitutive models were implemented in the numerical simulation to reproduce the nonlinear behaviour of steel reinforcement bars, concrete, and FRCM composites (Figure 8). Steel was idealised through an elastoplastic constitutive law, with Young’s modulus of 210 GPa and a yield stress of 545 MPa, as specified in Section 2.1.

The concrete described in Section 2.1 exhibited a compressive strength of 31.7 MPa and a density of 2445 kg/m³. Additional parameters required for the simulation were obtained according to fib Model Code for Concrete Structures 2010 [105]. Tensile strength was set to 2.1 MPa, fracture energy to 136 N/m, and the elastic modulus to 23,410 MPa. The concrete behaviour was modelled using a total strain-based crack model with a rotating crack approach. The tensile curve from fib Model Code for Concrete Structures 2010 [105] and an ideal compressive curve were chosen to simulate tensile and compressive behaviour.

FRCM composites were also modelled with total strain-based crack with a rotating crack approach. The elastic phase corresponds to the first branch of the idealised curves obtained with tensile tests, with a Young’s modulus of 8724 MPa for system 1 and 11,321 MPa for system 2. The compressive behaviour was assumed to be elastic; however, its influence was considered negligible due to the tensile nature of the stresses in the composite. The tensile response was defined by a multi-linear curve with transition points derived from tensile tests (see also Table 2).

4. Numerical Performance of FRCM-Reinforced Beams

The results from the three numerical simulations are analysed individually. Each model’s performance is illustrated using load–deflection curves, principal compressive stresses, and principal tensile strains at three key stages. The curves obtained from the simulations are compared with corresponding experimental results, and failure patterns were evaluated both numerically and experimentally. The model of the plain concrete notched beam is excluded from the presented results, as it was used solely to check the behaviour of concrete and does not correspond to any experimental test.

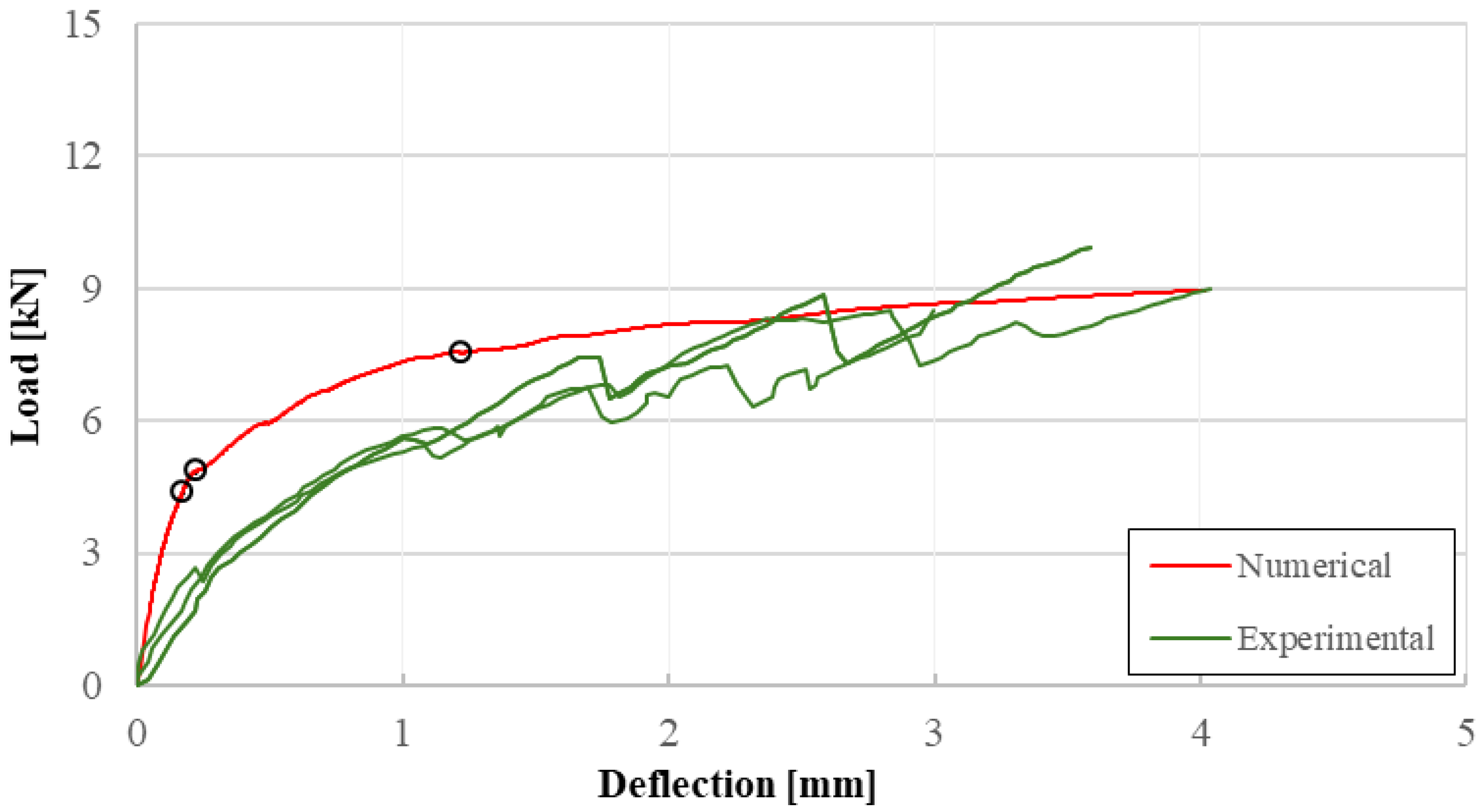
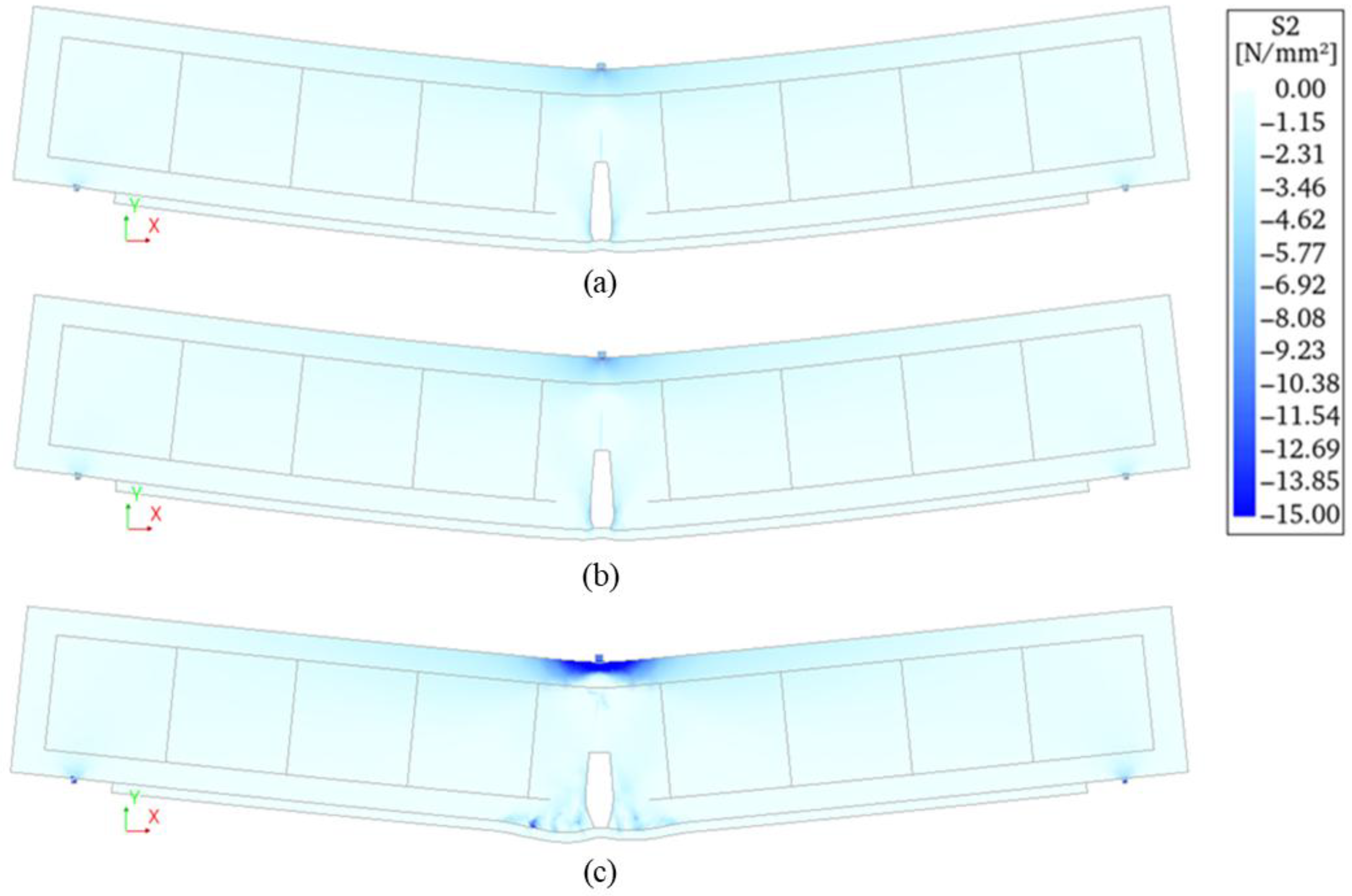
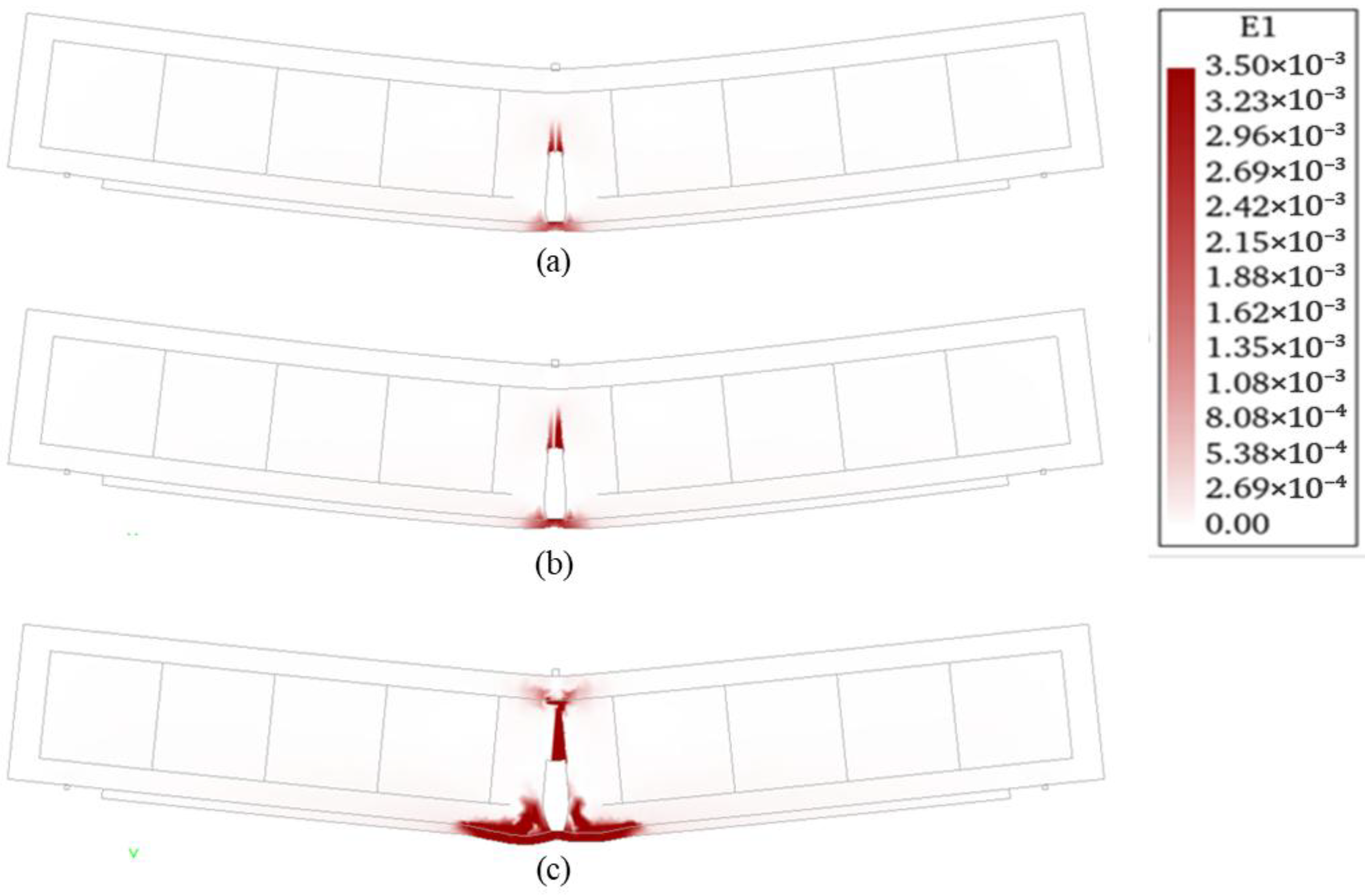
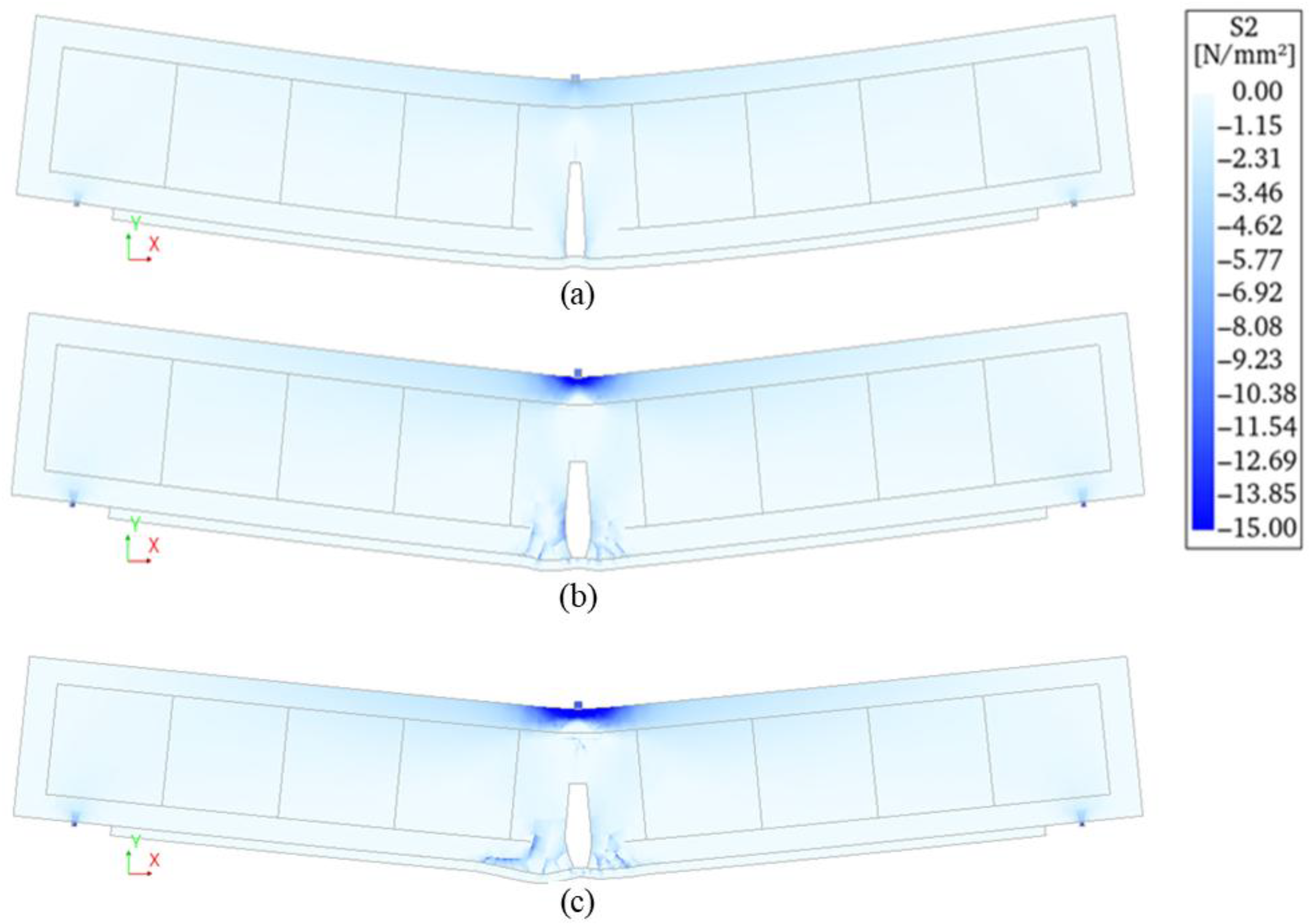
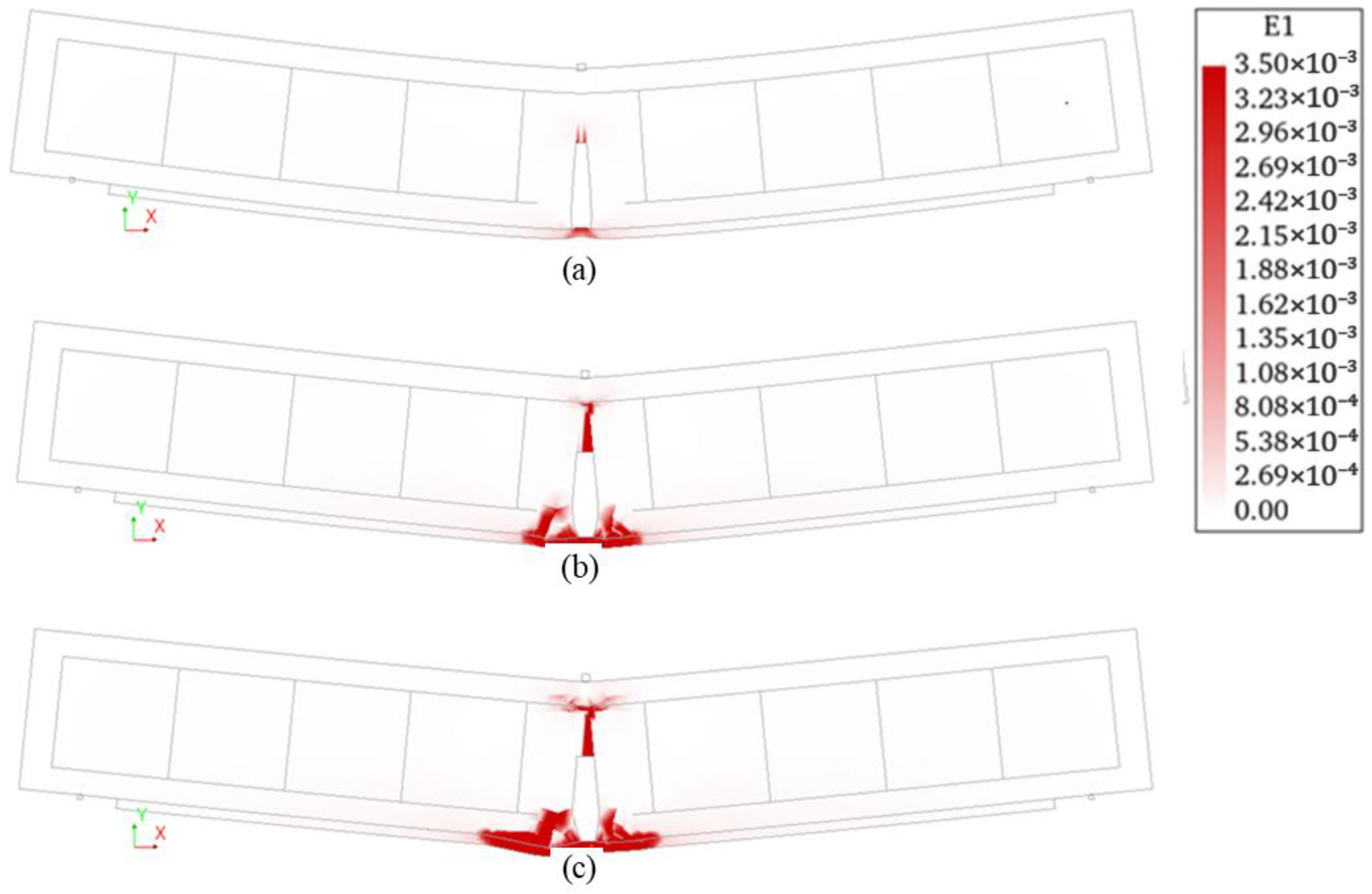
4.1. Reinforced Concrete Beam

The results of the numerical simulation for the reinforced concrete beam are compared with experimental data using load–deflection curves (see Figure 9). The potential scatter of experimental results in similar beams was plotted through 20% above and below load for each displacement, added in dotted lines. This comparison aims at evaluating the accuracy and performance of the model in replicating the behaviour of the control beam. The numerical simulation produced a response that closely matches the experimental data. Three key points were identified on the load–deflection curve to define the beam’s behaviour: (1) the end of the elastic branch, (2) the peak load, and (3) a pronounced post-peak response. At each of these points, the principal compressive stresses (Figure 10) and principal tensile strains (Figure 11) were extracted for further analysis. It is worth noting that the initial peak load observed in the numerical simulation could not be clearly identified in the experimental curve due to limitations in the data acquisition frequency curding testing. Load–deflection curves obtained through numerical simulation differ from the experimental model. This can be explained by the tensile behaviour assumed in the concrete. Although concrete reinforced beams model does not allow to obtain better fit curves without calibration, the simplification was accepted in this study within the framework of a design approach. In this sense, engineers usually employ the concrete strength class for real applications. The lack of a better curve adjustment is an indicator of the limitations of the model for serviceability limit state.

Figure 10 presents the principal compressive stress distribution at three stages of vertical imposed displacement: 0.05 mm, 0.13 mm, and 2.6 mm. The area under compression is located in the central upper region of the beam. At the initial load stage (Figure 10a), the stress levels are minimal and barely visible. In the second stage (Figure 10b), the compressive zone becomes more pronounced. By the final stage (Figure 10c), the compressive area has expanded laterally, while appearing narrower in the vertical direction, and the stress values have significantly increased.

Figure 11 illustrates the principal tensile strain distributions at the same vertical imposed displacement used for the compressive principal stress analysis: 0.04 mm, 0.13 mm, and 2.6 mm. In the elastic phase (Figure 11a), both strain and stress levels are minimal and concentrated around the edge of the notch. At peak load (Figure 11b), the strain exceeds 0.0035 and visible cracking has already occurred. In the post-peak stage (Figure 11c), the crack has propagated upward, reaching the zone of the upper steel reinforcement zone, and the strain field extends horizontally along this region.

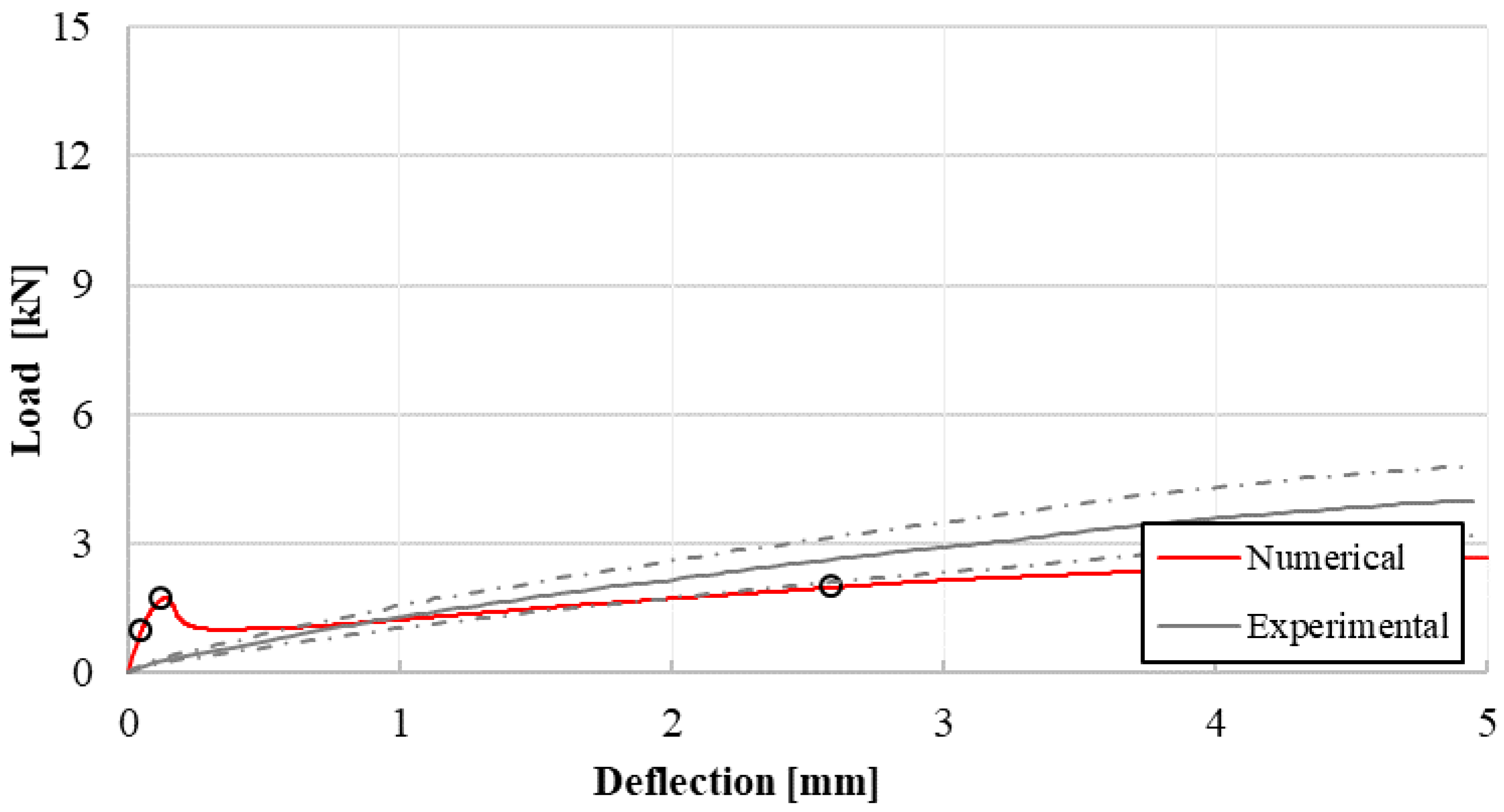
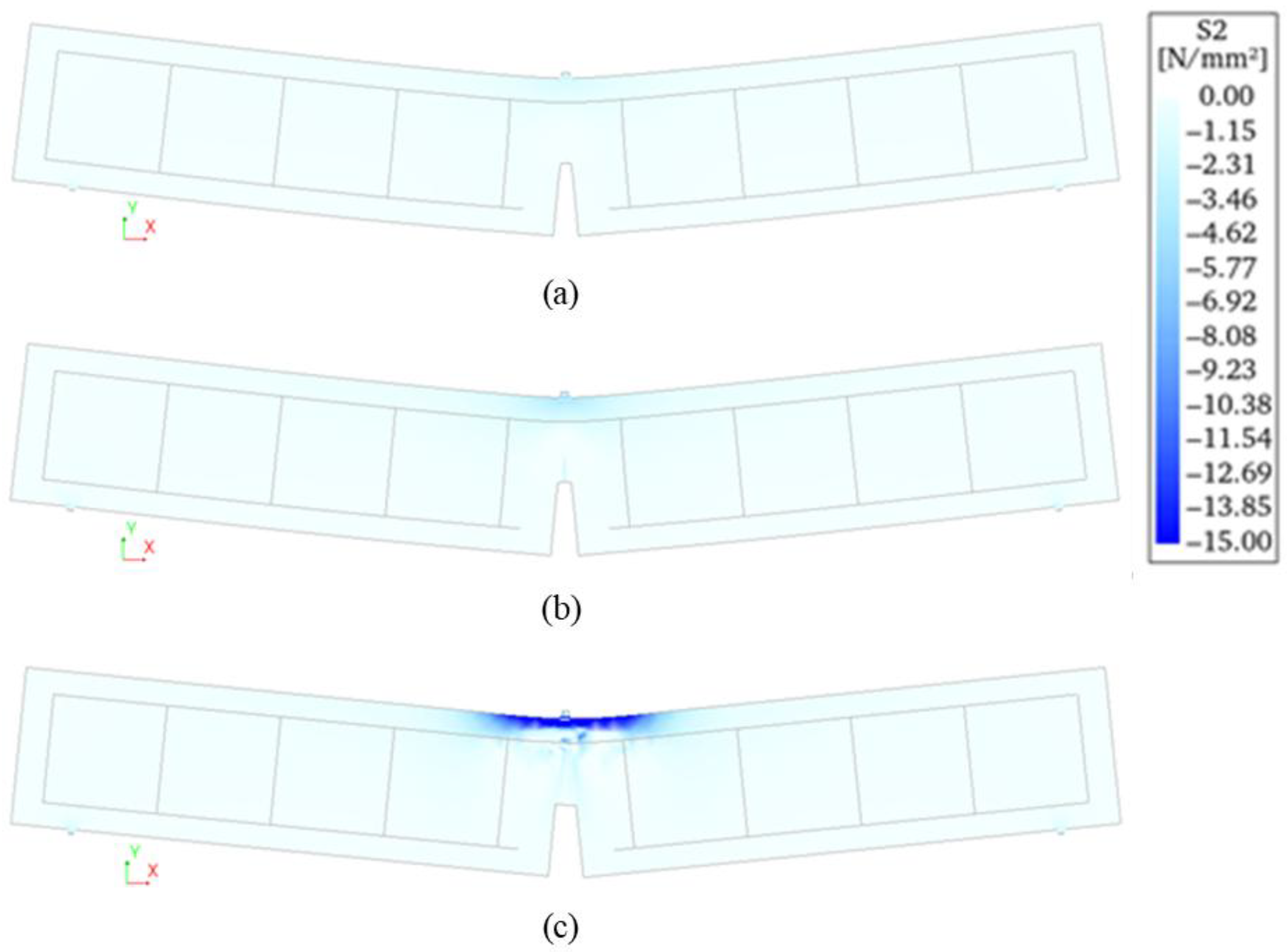
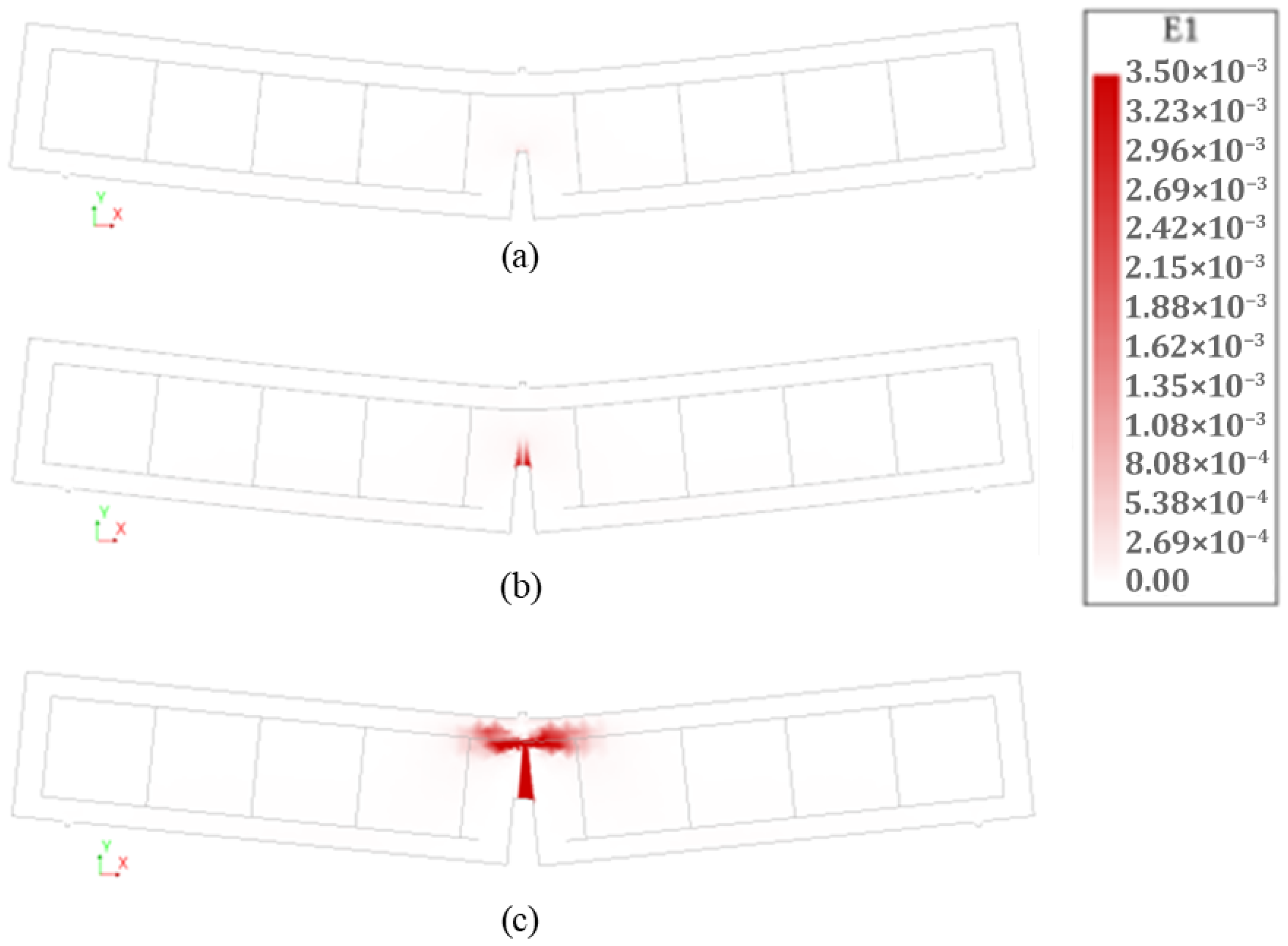
4.2. Reinforced Concrete Beam Retrofitted with FRCM System 1

The load–deflection curves obtained experimentally using DIANA 10.7 software are compared in Figure 12. The initial stiffness of the simulation curve is noticeably higher; at a deflection of 1.5 mm, the simulated load is approximately 130% of the experimental load; however, at a deflection of 4 mm, both curves converge, with the load reaching approximately 9 kN in both cases. The higher initial stiffness is mainly due to the simulation of the support beam, whose stiffness is also greater in the serviceability limit state (Figure 9). Also, reinforced concrete specimens are vulnerable to microcracks due to drying shrinkage or handling prior to testing. This could explain why tested specimens tended to exhibit lower stiffness and greater deflection at ultimate load that those predicted numerically.

Once again, three key points are used to characterise the beam’s behaviour. The first point marks the onset of concrete cracking at the notch. The second point corresponds to the cracking of FRCM, which is the transition point A in the tensile response curve. The third point represents the behaviour along the second branch of the FRCM composite’s idealised tensile curve.

Figure 13 displays the principal compressive stresses at vertical imposed displacements of 0.18 mm, 0.23 mm, and 1.21 mm. Initially, compressive stresses are concentrated in the central upper area of the beam, which is consistent with a stress distribution in which the neutral axis lies in the upper portion of the concrete and the tensile force is primarily carried by the FRCM. As the imposed displacement increases, both the magnitude and extent of the compressive stresses grow. At the third point, the central upper area of the beam remains under compression, while small compressive stress lines appear near the FRCM–concrete interface, corresponding to areas affected by cracking.

Tensile principal strains are displayed in Figure 14. At the first point, a crack in the concrete above the notch is already visible. At the second point, the cracking of the FRCM composite is evident, with tensile strains exceeding 0.03%. By the third stage, both the concrete beam and the FRCM are fully cracked. The strain field extends around the upper steel rebar, indicating that the FRCM is working within the second branch of its idealised tensile stress–strain curve.

The strain value of FRCM in the numerical model is higher than that obtained in the direct tensile tests. Therefore, the failure in the simulation occurs within the FRCM reinforcement, as it occurred in the flexural test.

4.3. Reinforced Concrete Beam Retrofitted with FRCM System 2

Figure 15 compares the load–deflection curves obtained from numerical simulation and bending tests. As in the case of the beam retrofitted with FRCM system 1, three key points are marked on the curve: the first indicates the onset of concrete cracking, the second corresponds to the cracking of the FRCM (transition point A in the tensile response of the composite), and the third represents the stage where the composite operates within the third branch of its idealised tensile curve. The curve generated by DIANA software exhibits higher initial stiffness than the experimental curves up to the first point. The main reason for this, as well as in the case of the beam retrofitted with system 1, is the initial stiffness in the simulation of the support beam. Beyond the third point, its stiffness lies between the experimental curves of the two tested beams.

Figure 16a, 16b and 16c present the principal compressive stress distributions at vertical imposed displacements of 0.16 mm, 0.66 mm, and 1.21 mm, respectively. The compressive stresses are primarily concentrated in the concrete beam, particularly in the central upper area. As displacement increases, some compressive stress lines also appear near the interface area, likely associated with the development of cracks. These localised compressive zones suggest the redistribution of stresses as damage progresses in the composite.

Figure 17 illustrates the distribution of tensile principal strains at the three key points. At the first point, the strain levels observed in both the composite and the beam are notably higher than those recorded in the beam retrofitted with system 1 (Figure 14), indicating the greater deformation required to initiate cracking the composite. At the third stage, the tensile strain zones expand within the beam, with a more pronounced increase observed in the composite material and at the FRCM–concrete interface.

The numerical simulation of the beam fails in the composite due to the high strain values reached in the material. This failure mode corresponds to what has been observed experimentally in beams of the same type. Furthermore, a comparison of the load–deflection curves obtained for beams reinforced with systems 1 (Figure 12) and 2 (Figure 15) reveals that their stiffnesses differ at intermediate loads, particularly for the deflection range of 0.5 to 1.5 mm. This phenomenon was captured by the numerical model through the different properties assigned to the FRCM systems, system 1 exhibiting a lower stiffness between key points two and three.

5. Conclusions

A comprehensive numerical analysis was conducted to investigate the behaviour of concrete beams retrofitted with two distinct types of FRCM systems (using the same carbon mesh and two types of mortars for the matrices). Three types of notched concrete beams were modelled to assess the influence of several parameters, the accuracy of reinforced concrete beam simulations and, primarily, the overall performance of beams retrofitted with FRCM. In all simulations, the von Mises plasticity law was applied to steel rebars, while the total strain crack model was used for both concrete and FRCM. The adopted modelling approach successfully captured the cracking of both concrete and FRCM, as well as the global structural response of the beams at the ultimate limit state. The debonding at the FRCM–concrete interface is not considered explicitly in the model, given that the most common failure mode involves internal delamination of fibres from the matrix within the FRCM composite, so potentiality of debonding between support and composite should be carefully consider prior to applying the model. The main goal of the simulation was to evaluate whether such simplification of the interfacial behaviour significantly affects the accuracy of predicted overall response of FRCM-reinforced beams and the possibility of creating a model to estimate ultimate loads of concrete beams reinforced with FRCM composites.

Numerical results from all models were compared with experimental data, focusing on load–deflection curves. Additionally, compressive principal stresses and tensile principal strains were analysed at critical stages of beam behaviour. The following conclusions can be drawn:

• The adopted macro-modelling approach enables a reliable estimation of the behaviour of concrete beams retrofitted with FRCM systems when the failure initiates within the composite.
• The model demonstrates sufficient accuracy for beam simulation at the ultimate limit state. The material characterisation of FRCM through idealised stress–strain from tensile tests of coupons provide a cost-effective and practical alternative to bending tests on retrofitted beams.
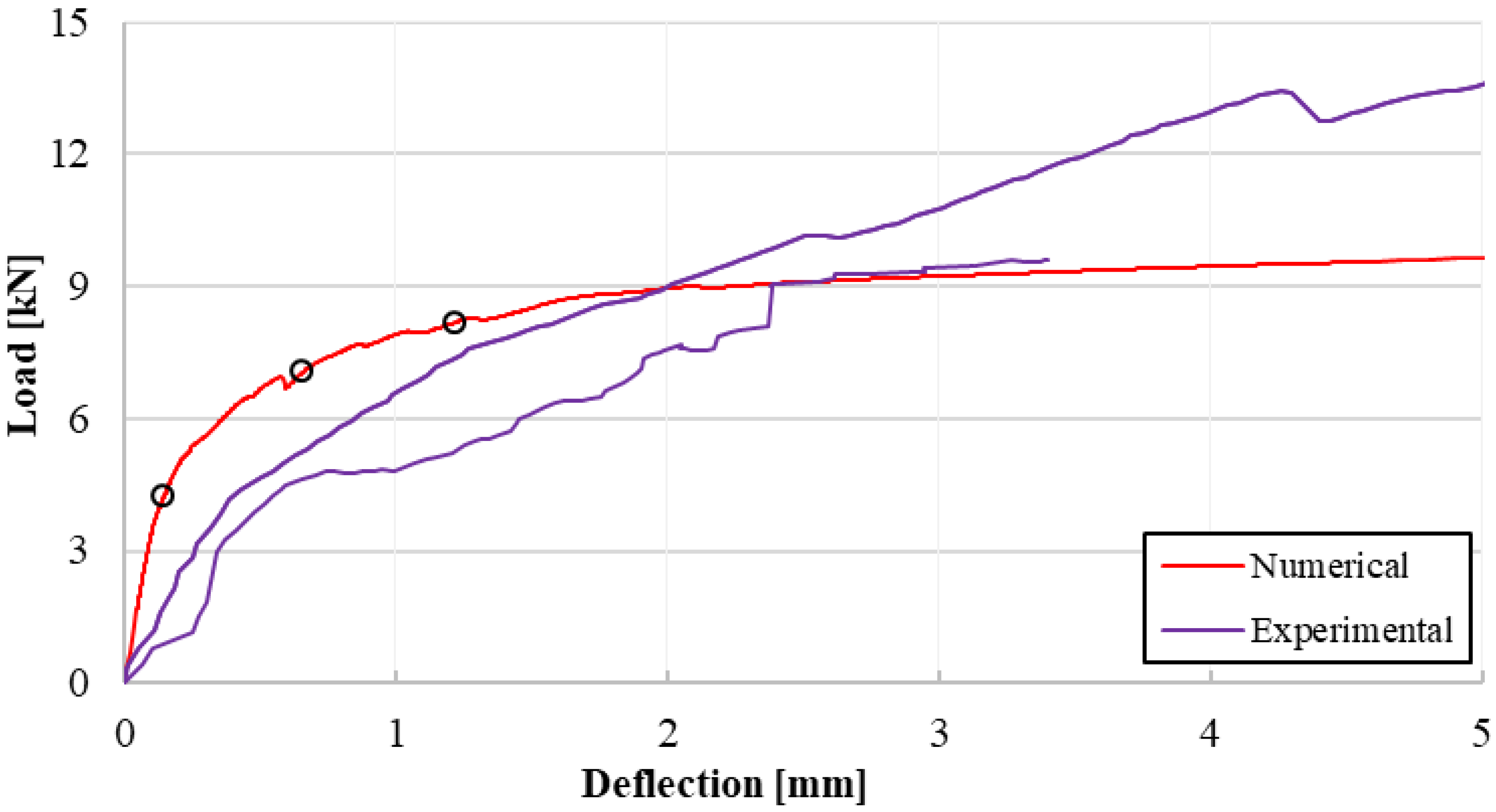
• For the control beam, the load drops when the concrete tensile strength is reached and then it starts to rise slightly. In beams strengthened with FRCM, there is no decrease in load; the stiffness simply decreases. Comparing the two FRCM systems, both show similar load–deflection curve shapes, but beams retrofitted with system 2 support higher loads, which is consistent with tensile test results and experimental results on beams.
• The model achieves a sufficient level of accuracy in simulating the beam behaviour, adequate for engineering applications, relying solely on the constitutive models of concrete and FRCM and assuming a perfect bond between the reinforcement and the substrate.
• The tailored combination of macro-modelling approach, perfect bond assumption between concrete and FRCM, and use of tensile test data for each composite system, significantly reduces computational cost and the need for extensive bending tests.

The proposed numerical model has been validated through a limited number of flexural tests conducted on beams reinforced with two distinct FRCM composites. Consequently, the conclusions are limited, and the research represents an initial step in a broader validation process involving diverse concrete beams and FRCM systems.

These conclusions are not only limited by the size of the experimental campaign, but also by the limitations of the compared composite systems. A perfect bond in the interface between the beam and concrete needs to be considered before using the proposed numerical simulation, as it constitutes a key assumption of the model. Some parameters of flexural applications are required for this assumption to be of application, such as sufficient bond length, preparation of the support, and employment of mortar with additives to improve adhesion. However, these parameters are not the focus of the investigation. The model, then, will require further research before it can be applied more widely.