The Effect of Sewer-Derived Airflows on Air Pressure Dynamics in Building Drainage Systems

Abstract

The performance of a building drainage system, “BDS”, is determined by the complexity of internal airflow and pressure dynamics, governed by unsteady wastewater flows from randomly discharging appliances such as WCs, sinks, and baths. Designers attempt to optimise system safety by equalising pressure and incorporating ventilation pipes and active devices such as AAVs and positive pressure reduction devices (PPRDs). However, failures within these systems can lead to foul gases and potentially hazardous microbes entering habitable spaces and posing a risk to public health. This study, for the first time, develops a novel model that simulates the effect of air from the sewer on BDS performance, which describes the correlation between system airflow and air pressure under the influence of air from the sewer. A combination of full-scale laboratory experiments representing a 3-storey building and real-world data from a 32-storey test rig configured as a building demonstrated that sewer air significantly modifies airflow and air pressure within a BDS. These findings are crucial for modern urban environments, where the prevalence of tall buildings amplifies the risks associated with air pressure transients. This work paves the way for updating codes to more effectively address real-world challenges.

1. Introduction and Background

The development of sanitation systems has been a fundamental aspect of urban infrastructure, evolving over the past 5500 years to achieve efficient wastewater management and air pressure control and safeguarding public health. Despite these advancements, modern urbanisation and the increasing height of buildings present new challenges for both BDSs and sewer systems (SS); urbanisation compounded by the effects of climate change, including flash floods, further exacerbates these challenges [1]. One of these challenges exerts significant pressure on sewer systems, which struggle to accommodate such extensive changes [2]. As a result, the sewer system becomes pressurised, leading to excess pressure and airflow from the sewer into the BDS under certain conditions, impacting air pressure changes within the BDS.

Previous studies and standards have typically examined BDSs and SSs independently. For example, design codes such as BS EN 752:2017 [3] for drain and sewer systems outside buildings and BS EN 12056-2:2000 [4] for gravity drainage systems inside buildings address different requirements and design considerations, reflecting the fundamentally distinct functions and operational environments of these systems. However, there has been little recognition, if any, of how these systems influence each other, particularly with respect to airflow and pressure dynamics [5].

In sewer networks, airflow is a critical concern, as it influences odour, corrosion, and air–water interactions within the system [6]. It can enter the system as wastewater travels from buildings or when exterior manholes are opened, allowing air to move through the network. Once inside, the direction of air is influenced by multiple factors, such as local ventilation characteristics and transient pressure variations associated with hydraulic loading, including conditions arising from undersized or capacity-limited wastewater sewers, rapid flow transitions and surcharge, temperature-related density effects, wind shear at roof terminals, and site-specific geographical and operational conditions. Under such unsteady conditions, particularly in combined sewer systems during wet-weather events, pressure transients may be transmitted to the building interface and, where sewer air-relief capacity is limited or BDS resilience is reduced (e.g., inadequate venting or diminished trap-seal retention), can promote pressure imbalance and the backflow or ingress of sewer air into the BDS. Accordingly, some regulatory and code frameworks explicitly recognise the ventilation of drainage and sewer systems as a means of managing adverse pressure regimes [7].

As uncovered in this research, the inflow of air backflow from the sewer [8,9,10,11,12] generates excess air pressure within the BDS, which can significantly impact system performance. These influences become more pronounced with the increasing number of tall buildings. As building height increases, the flow rate also increases, necessitating larger pipes or additional vent systems to equalise pressure [13,14]. Even with the same flow rate, the risk of trap seal depletion escalates with the height of the buildings.

For the first time, this study provides evidence-based experiments showing how updraft air (air coming from the sewer) alters the air pressure regime in the BDS, including its effect on the entrained air and pressure regime.

2. Introduction of New Terms for Building Drainage Systems

2.1. Modified Entrained Air (Qmea)

Based on extensive historical data spanning half a century [1], it is assumed that the entrained air (Qea) generated by water discharge is the sole source of air within a building drainage system. When water is discharged from the inlet at the top of the stack, it draws air along the length of the stack to maintain airflow. This air is then drawn through the wet stack due to the shear force between the inside surface of the water annulus and the central air core [15,16]. Figure 1a is a vertical section of a typical unscaled single-stack system with an active branch in normal operation conditions.

Based on a simple central core calculation [17], it can be seen that the volumetric flow of entrained air may be expressed as

$$Q_{ea}={\displaystyle \frac{\pi }{4}}{(D-2t)}^2{v}_a$$

(1)

where Qea is the entrained airflow rate (L/s), V_a is the mean air velocity in the pipe (m/s), t is the film thickness (m), and D is the internal diameter of the pipe (m).

When the system is exposed to the air that originates from the sewer (Qas), which is updraft airflow ranging up to 28 L/s under normal conditions [9,10,11], as shown in Figure 1b, it alters the system characteristics of the drainage system.

When allowing both the inflow of water and the introduction of updraft air into the system, a transformation of the system occurs, resulting in alterations in pressure and entrained air and even modifications to the characteristics of air deriving from the sewer, as shown in Figure 1c. In the theoretical calculation, it is assumed that the modified entrained air (Qmea) is the result of the combination of water and sewer air within the system. If Qea and Qas are different, the net airflow rate (modified entrained air Qmea) would be different between the two, with the direction determined by the larger flow rate. The relationship between the measured and calculated values of $Q_{\mathrm{mea}}$ was determined from laboratory experiments (Section 3.2) and is shown in Figure 2 and defined by Equation (2):

$${\left(Q_{mea}\right)}_{Measured}=0.72{\left(Q_{mea}\right)}_{Calculated}-1.34$$

(2)

where

• ${{(Q}_{mea})}_{Measured}$ is modified entrained air from measurement = ${{(Q}_{ea}-Q_{as})}_{Measured}$; ${{(Q}_{mea})}_{Calculated}$ is modified entrained air from calculation = ${{(Q}_{ea}-Q_{as})}_{Calculated}$;
• Qea is the entrained air associated with water flow (L/s);
• Qas is the airflow from the sewer (L/s).

Figure 2. Comparison of measured versus theoretically calculated modified entrained airflow rate.

Figure 2. Comparison of measured versus theoretically calculated modified entrained airflow rate.

Due to the dynamics of air–water interaction, and if the flow regime is turbulent, the interaction between the water and air can become complex. The Qmea yellow colour represents modified measured entrained air and can be positive or negative depending on the water flow rate and updraft airflow rate. In order to find out the direction of air movements, it is assumed that the entrained airflow downward is negative and airflow upward is positive.

To replicate normal airflow from a sewer, a centrifugal inline fan model (Xpelair XID125- 90102AA, Xpelair, Southampton, UK) was used and connected to an inline fan controller (XIC1/21858AW, Xpelair, Southampton, UK). It was necessary to use a fan that could produce adequate airflow. The fan was placed inside a chamber to induce airflow with no real power. If there was any change in the pressure drop inside the system, putting the fan inside the chamber would prevent the fan from compensating for it. The fan therefore acted like a low-power pressure differential across the system, simulating low power entering from the sewer. The concept of the fan analogy in airflow dynamics within the building drainage vent system is that used by [18,19]. These studies found that it is convenient to represent all the driving force of the vertical column of water, which entrains the airflow rate from upper stack termination as a centrifugal fan positioned at the base of the stack. This established knowledge was instrumental in the current research, albeit with a different focus.

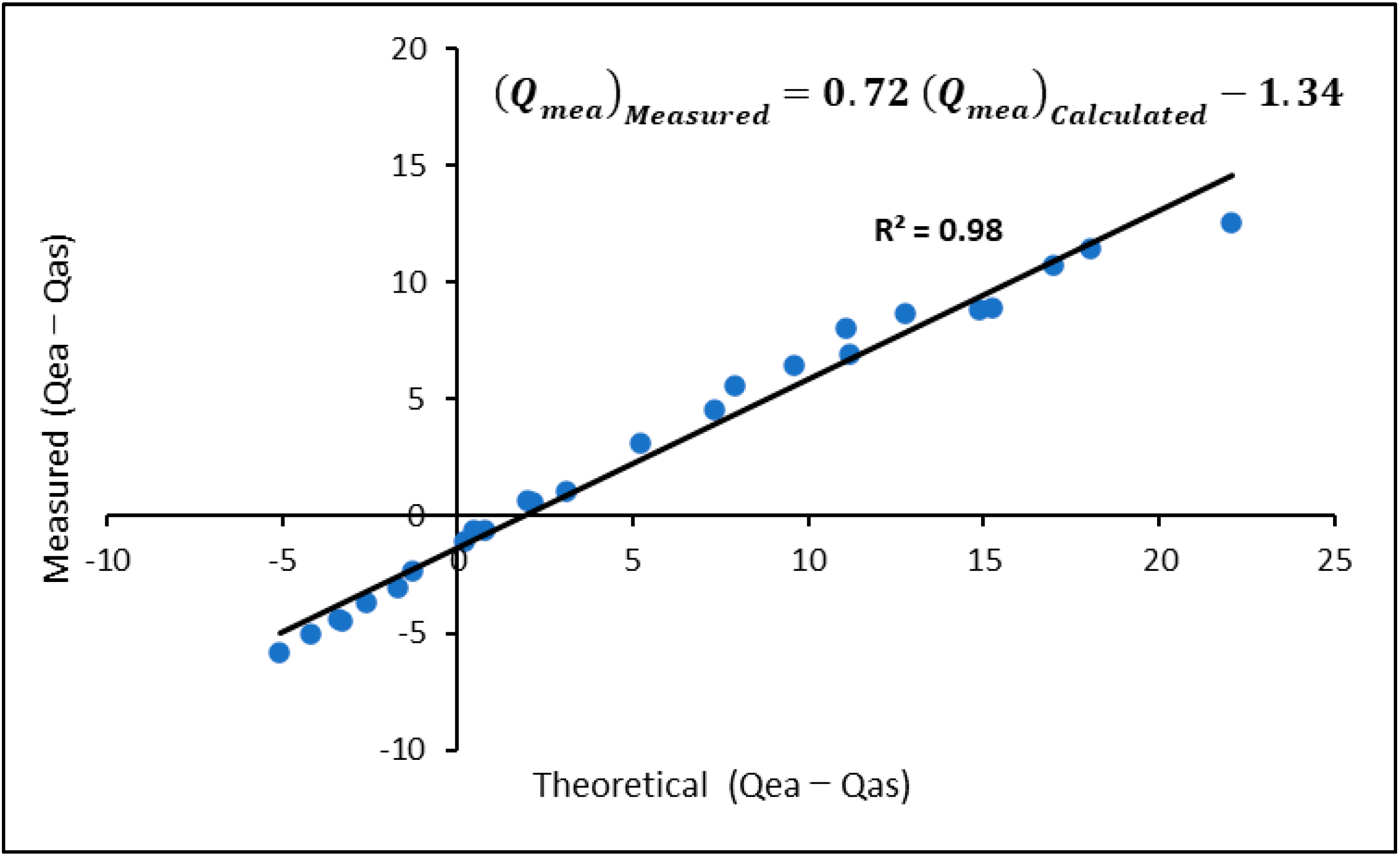
2.2. Classical Pressure Profile and Modified Air Pressure Due to Sewer Air (${\mathit{\Delta }P}_{\mathit{updraft\; air}}$)

Classical pressure profiles within building drainage systems highlight the key critical pressure phenomena that occur during water discharge from a branch. As the air travels down the pipe, cumulative losses occur, as shown in Figure 3. These include entry losses, ${\Delta P}_{entry}$, which arise as water enters the drainage stack; frictional losses are encountered as water flows through the pipe walls, ${\Delta P}_{dry pipe friction}$. Losses due to fittings and inlets also occur, ${\Delta P}_{branch junction}$ (such as bends and elbows), and the impact of back pressure ${\Delta P}_{back pressure}$ is at the base of the stack. Moreover, pressure loss due to sewer air has been established in this research, ${\Delta P}_{updraft air}$, thereby modifying the internal system pressure.

The pressure loss due to sewer air ${\mathbf{\Delta }\mathit{P}}_{\mathit{u}\mathit{p}\mathit{d}\mathit{r}\mathit{a}\mathit{f}\mathit{t} \mathit{a}\mathit{i}\mathit{r}}$ should be added to the steady flow energy equation for previously developed pressure losses along the drainage pipe [20], which are induced by the motive force of the work downward on the air by water.

$${\mathit{\Delta }P}_{total}={ \Delta P}_{entry}+{\Delta P}_{dry pipe friction}+{\Delta P}_{branch junction}+{\Delta P}_{back pressure}+{\mathbf{\Delta }\mathit{P}}_{\mathit{u}\mathit{p}\mathit{d}\mathit{r}\mathit{a}\mathit{f}\mathit{t} \mathit{a}\mathit{i}\mathit{r}}$$

(3)

The classical pressure profile provides a time-specific snapshot of the internal pressure regime following an appliance discharge (Figure 3b). However, with sewer air and for a given discharge event (such as a toilet flush), a range of possible pressures can occur within the stack, depending on the amount of air travelling upward from the sewer, which leads to the modification of air pressure distribution along the drainage stack.

Modified air pressure due to sewer air underlines the complexity of pressure interactions in drainage systems and highlights the importance of accounting for all pressure losses in the system to ensure proper system functionality and efficiency.

3. Methods and Procedures

This research addresses a significant gap in understanding in building drainage systems (BDSs) and their interaction with sewer systems (SSs). This study focuses on investigating these interactions by simulating sewer air and developing novel model-based equations to find the impacts on the air pressure regime inside a BDS, leading to the development of new conceptual understandings that describe the correlation between newly introduced terms such as modified entrained air and modified air pressure when the system is subjected to both BDS operation and sewer air.

To achieve this, a full-scale laboratory test rig was constructed to analyse the pressure loss when the system is exposed to sewer air, with a specific focus on air passage. The model equations derived from these experiments were validated using a 3-floor test rig and a 32-floor real-world test rig at the National Lift Tower (NLT) in Northampton, UK, ensuring robustness and applicability across a range of building drainage system types and configurations. The workflow of the method is outlined below:

• Build laboratory test rig;
• Conduct experiments;
• Develop model equations based on experiments;
• Validate model using 3-floor test rig;
• Validate model using 32-floor test rig NLT;
• Confirm applicability of the model and its impact on air pressure regimes.

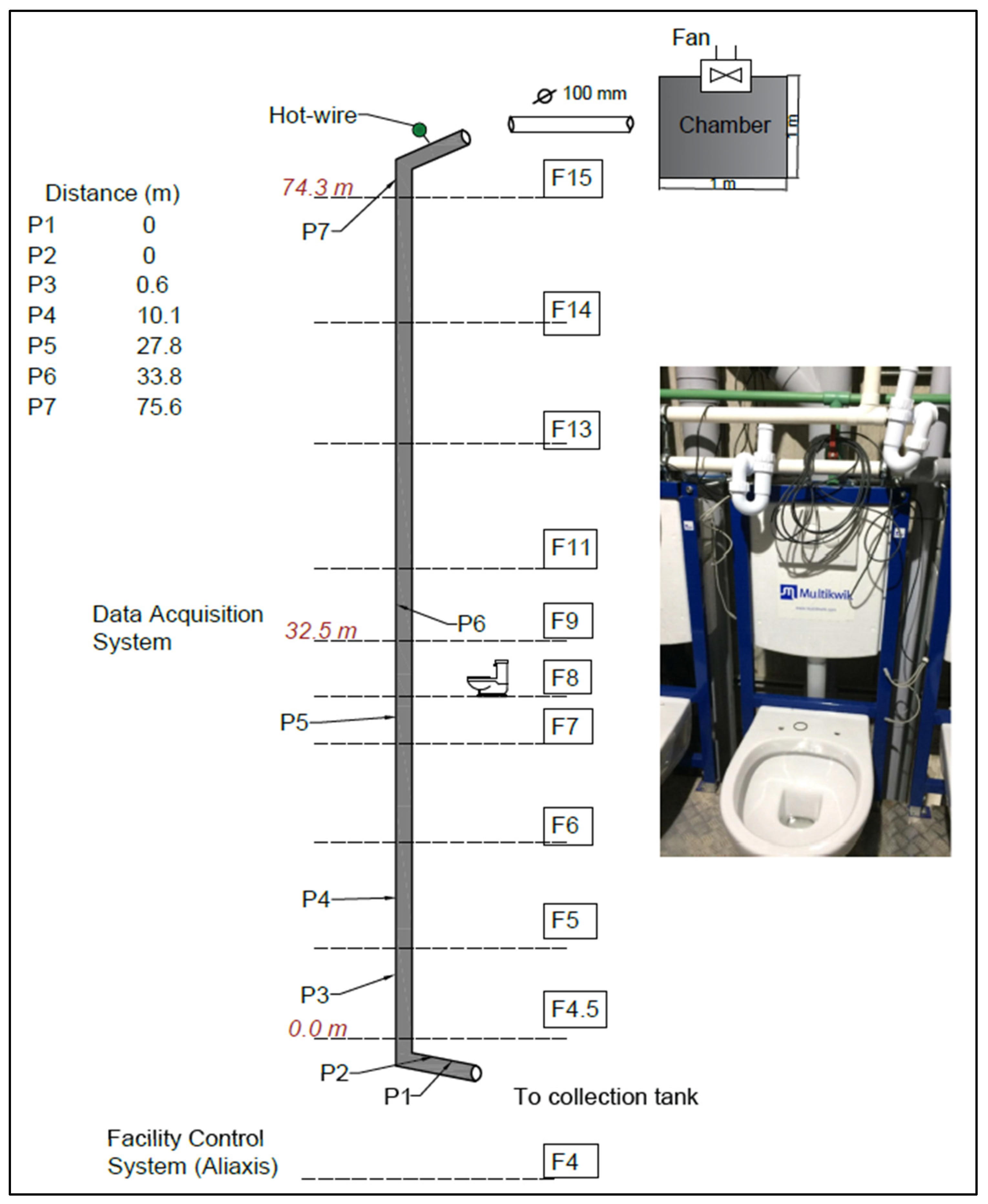
3.1. Experiment 1: Methodological Approach for Investigating Pressure Losses Due to Sewer Air

In this study, by creating a steady airflow that was adjusted to match the system losses, it was possible to effectively simulate and represent the airflow from the sewer to the building. This simulation allowed for a better understanding of the airflow characteristics and facilitates the study of its impact on various aspects of the system. A novel model-based experiment for continuous updraft airflow in a dry stack was designed and developed to be applicable to buildings of various heights. The model was therefore applied and validated to a 3-storey building and 32-storey real-world test rig (NLT); see Section 4.3.

Test Procedure

The investigation involved setting up a centrifugal fan as the primary flow driver, providing a precisely controllable and repeatable volumetric flow rate with sufficient static pressure head to overcome distributed losses across the system. The fan was set to match system losses for realistic sewer-to-building airflow. It was then connected to a horizontal loop 100 mm diameter pipe with varying lengths of 9, 30, and 40 m, as shown in Figure 4, with the following objectives:

(i)

To measure the induced continuous airflow within the system;

(ii)

To measure pressure fluctuations along different pipe lengths;

(iii)

To analyse the system’s response to these changes in pipe length.

Pressure transducers were installed at different locations throughout the piping system. A transducer (P1) was utilised to measure the pressure differential across the fan. Another transducer (P2) was located at the inlet side of the fan and served as the baseline measurement against which pressures measured at other locations (P3, P4, and P5) along the pipe lengths of 9, 30, and 40 m were compared. Data was collected at a frequency of 1000 samples per second.

The pressure changes are expressed as a function of the airflow rate and system length, ${\Delta P}_{updraft air}=f\{Q_{as}, L\}$. Considering the correlation among the three variables, the corresponding results are presented in Figure 5, which shows that as the length of the pipe increases, the pressure change also increases consistently across different updraft airflow rates.

By analysing the data collected of the three parameters (${\Delta P}_{updraft air},Q_{as}, and L)$, novel equations were developed for the first time to quantify the pressure loss along the drainage stack when the system is exposed to sewer air. L is the pipe length, ${∆P}_{updraft}$ is the change in pressure in the system due to sewer air, ${∆P}_{min}$ is pressure changes per metre length, ${∆P}_C$ is the rate of pressure changes due to increasing the pipe length, and Qas is updraft airflow rate.

$${∆P}_{updraft}/L={∆P}_{min}+L{∆P}_C$$

(4)

$${∆P}_{min}={{K_1(Q}_{as})}^2$$

(5)

$${∆P}_C={K_2{(Q}_{as})}^2$$

(6)

where $K_1$ and $K_2$ are experimentally determined constants specifically for a 100 mm PVC pipe. The corresponding values used in this study are $K_1={2.5\ast 10}^{-4}$ and $K_2={3\ast 10}^{-6}$.

3.2. Experiment 2: Three-Storey Single-Stack Test Rig—Steady Flow Conditions

Following the development of the model-based equations presenting pressure loss due to sewer air (${\Delta P}_{updraft air}$), a second experiment was carried out to validate its applicability under controlled laboratory conditions. This experiment utilised a three-storey single-stack test rig, enabling systematic evaluation of the interaction between water discharge and airflow within a vertical drainage system. The primary objective was to observe airflow behaviour, pressure variations, and water–air interactions under steady flow conditions. To create steady flow conditions, water was supplied by a centrifugal pump that was used to deliver the flow from the laboratory underground storage tank to the overhead water closets utilising a (75 mm) diameter pipeline. This work involved an evaluation of

(i)

How the entrained airflow rate is modified by airflow from the sewer;

(ii)

The influence of sewer air on air pressures across the bend at the base of the stack.

The data was recorded at a frequency of 100 Hz while varying the updraft airflow rates up to 20 L/s (considering five different updraft airflow rates) and water flow rates, ranging from 1 to 4 L/s. The measurements were conducted while the system was exposed to sewer air without any water supply, and then measurements were taken when the system was exposed to both updraft air and water. To ensure consistency in the results, each test consisted of 10 repetitions. Figure 6 is a sketch of the laboratory single-stack test rig with dimensions and necessary devices connected to it.

Test Procedure

Data collection was based on measuring the airflow rate using an anemometer positioned at the top of the stack in the dry section to monitor air movements within the system. Additionally, pressures were measured at the base of the stack by placing two pressure sensors 1 m away from the vertical and horizontal axes in order to minimise the influence of highly disturbed near-bend hydrodynamics and to obtain stable and repeatable pressure measurements. The first step involves operating the system under normal conditions without updraft airflow. The second step requires measuring updraft airflow rates for a minimum of one minute with the system inactive, followed by measuring the airflow rate when the system is exposed to sewer air and a water supply. Figure 7 provides an example of the results obtained for a water flow rate of 1 L/s.

Figure 7 represents a different updraft airflow (Qas) at a constant water flow rate of 1 L/s, showing the system’s recording of the specific updraft airflow before initiating the water flow. Once the water is turned on, the recording continues for over one minute, capturing the dynamic behaviour of the system during this period (blue line). Subsequently, the data capturing the changes in airflow rate, referred to as entrained airflow (Qea), and the modified entrained airflow profile (Qmea) resulting from the discharge of water are collected. This technique was applied to other water flow rates of 2, 3, and 4 L/s.

3.3. Experiment 3: Thirty-Two-Storey Single-Stack Test Rig—Unsteady Flow Conditions

The NLT in the Northampton, UK, test facility comprises a test rig 76.3 m high and a 100 mm diameter drainage system. In this research, the drainage system in the NLT was used to study the impact of sewer connections on the system, with floor heights detailed in Figure 8. Testing involved automated flushing, full toilet traps, and measurements using a hot-wire anemometer and seven pressure transducers (p1–p7, Figure 8).

Test Procedure

A fan generated airflow in a 1 m³ chamber at the top of the stack and sensors recorded data at 500 Hz during 1 min tests for single flushes. Experiments were conducted at a height of 29 m, with dry and wet conditions. For accuracy in the test, the average of the three peak drops from the flushes was calculated. This work involved an evaluation of

(i)

How the entrained airflow rate is modified by airflow from the sewer;

(ii)

How a single water flow event results in a range of pressure changes along the drainage stack under varying updraft airflow conditions.

4. Results and Discussions

As stated in the methodology section, analysing changes in the air pressure regime within the BDS necessitates the measurement of entrained air and the pressure variations occurring within the system when the system operation is exposed to sewer air, in addition to introducing new terms such as modified entrained air and modified air pressure.

4.1. Modification of Entrained Air (Qmea) by Updraft Air (Qas)

Comparing five different updraft airflow rates (Qas), ranging from 0 to 20 L/s, with water flow rates varying from 1 to 4 L/s, tests were conducted on a three-storey single-stack test rig under steady flow conditions to measure entrained air and changes in entrained air. The results are presented in Figure 9.

Figure 9 plots the measured airflow rate (y-axis) versus different updraft airflow from the sewer, Qas (x-axis), for water flow rates Qw = 1, 2, 3, and 4 L/s. At Qas = 0 (fan off), the baseline entrained airflow for Qw = 1 L/s is around−6.65 L/s. As Qas increases, the measured modified airflow Qmea becomes less negative (i.e., the magnitude of entrainment decreases), and for Qw = 1 L/s it eventually crosses zero at a high Qas. For a fixed Qas, increasing Qw shifts the curve downward, indicating larger entrainment (more negative airflow).

To measure the net airflow changes inside the BDS due to sewer air, the new parameter $\overline{Qmea}$ was introduced, as shown in Figure 10, which involves zeroing the data by subtracting the measured updraft airflow rate Qas from the measured modified entrained airflow rate Qmea. The blue line represents the baseline scenario without any updraft airflow: Qas = 0. The other lines represent different updraft airflow rates, Qas > 0, in conjunction with varying water flow rates. It is evident that the $\overline{Qmea}$ value are more obvious for updraft airflow rates of 17 and 20 L/s compared to the baseline scenario. These findings highlight the significant impact of updraft airflow on the modification of entrained airflow, particularly at higher updraft airflow rates.

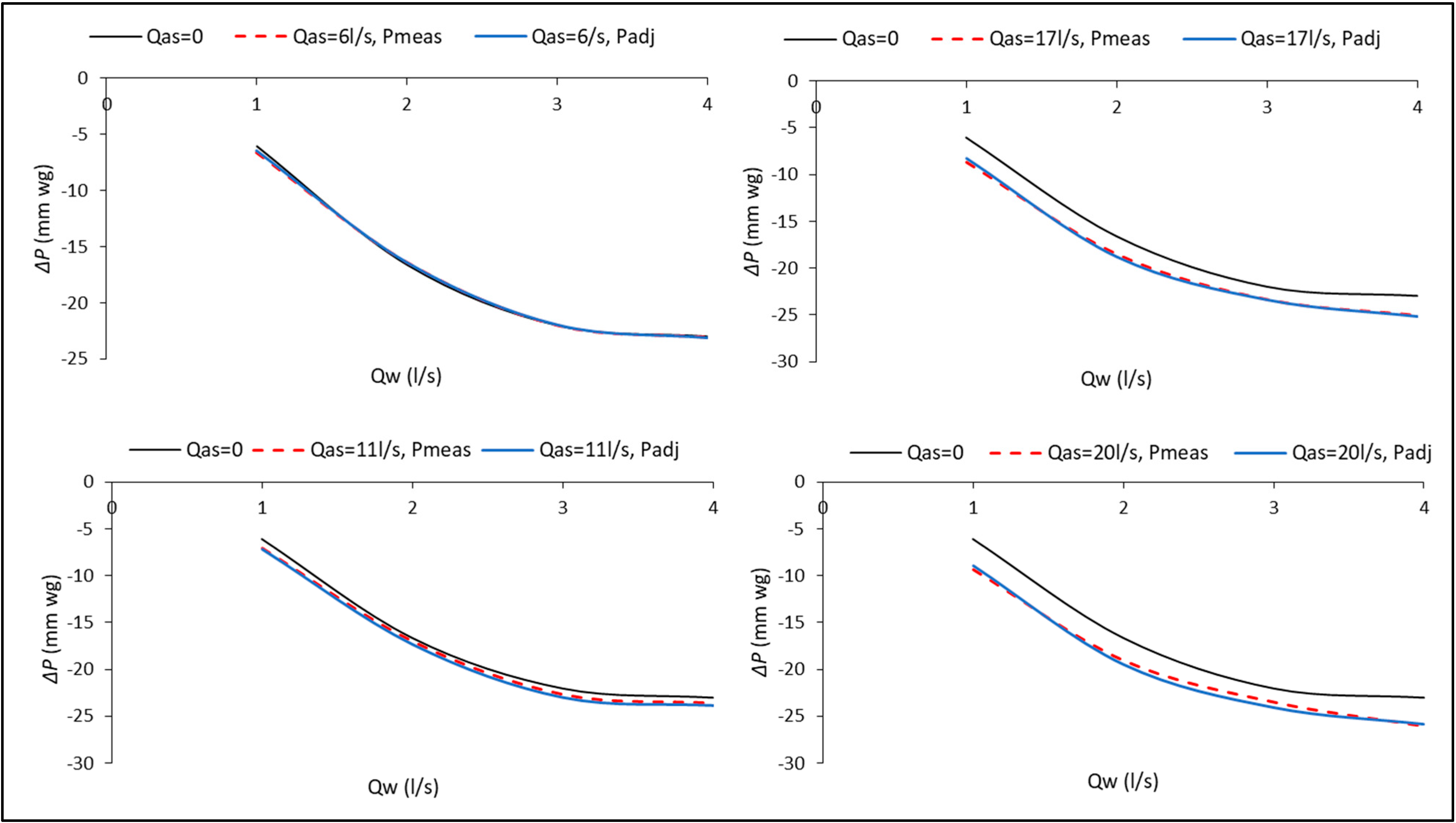
4.2. Modified Air Pressure Distribution

Comparing pressure changes between two systems under both steady and unsteady flow conditions showed that sewer–air effects caused significant pressure fluctuations in the low- and high-rise test rigs. The result from both tests are shown in Figure 11, where an increase in updraft airflow rates corresponds to an increase in positive and negative pressure changes. In addition, the higher water flow rates were associated with larger positive and negative pressure changes along the stack.

4.3. Applied Developed Model Equations for the Dry Stack Exposed to Sewer Air

The developed model equations (Equations (4)–(6), as described in Section 3.1) were validated using test rigs, both the 3-storey test rig at HWU and the 32-storey test rig at the NLT. The measured pressure data, referred to as ($P_{mea}$), were compared to the adjusted data obtained using the equations, referred to as ($P_{adj}$).

4.3.1. Laboratory Test Rig: Three-Storey Building

Various updraft airflow rates (6 L/s, 11 L/s, 17 L/s, and 20 L/s) combined with different water flow rates ranging from 1 to 4 L/s were used to compare the laboratory pressure measurements ($P_{mea}$) with adjusted pressure ($P_{adj}$) based on the baseline (solid black line) using the developed equations, as shown in Figure 12.

The solid black lines for all graphs represent the measurement of pressure changes across the bend at the base of the stack with no updraft airflow rate, Qas = 0, and for water discharge rates of 1–4 L/s. The dashed lines are the measured pressure changes across the base of the stack with water discharge and updraft air Qas > 0. And the blue solid lines are the adjusted pressure changes using the developed equations.

The figure reveals a very close match between ($P_{mea}$) and ($P_{adj}$) across almost all updraft airflow rates, highlighting the accuracy of both the experimental data and the developed model. This means that measuring the pressure along the pipe generated by continuous airflow passing through it can effectively represent the variations in pressure caused by air from the sewer, ${\mathbf{\Delta }\mathit{P}}_{\mathit{u}\mathit{p}\mathit{d}\mathit{r}\mathit{a}\mathit{f}\mathit{t} \mathit{a}\mathit{i}\mathit{r}}$.

Figure 13 illustrates the comparison between air pressure values in a mm water gauge between the measured and adjusted baseline data using Equations (4)–(6). Different colours of best fit lines represent different updraft airflow rates (Qas). The data show a strong linear relationship, with a coefficient of determination (R²) of 0.99 for almost all updraft air.

4.3.2. NLT Test Rig

The data measured at the National Lift Tower (NLT) was compared with the results obtained from model-based equations on the horizontal dry stack configuration; see Section 3.1. This model simulates the pressure changes along the drainage stack when exposed to sewer air. In both the measured and modelled data, the base points mentioned previously were used in the measurements. Three separate equations were employed sequentially along the stack: one for the dry, another for the wet part, and the third for the horizontal part. Although the equation itself remains constant (4, 5, and 6), the length of the pipe differs among these segments. The analysis incorporates losses associated with a fan connected inside a chamber, which is then linked to the top of the stack via a duct. Additionally, the calculations take into account the length of the main horizontal pipe, which is also open to the atmosphere at the outlet, as shown in Figure 8.

Figure 14a illustrates the pressure changes across various elevations along the stack ($P_{meas}$). The measurements are based on placing pressure sensors P1 to P7 at different locations along the stack, as specified in Figure 8. The solid black line charts the baseline pressure measurement, with natural updraft measurements recorded around 8.17 L/s that might be due to stack height or other factors, based on just a single flush at floor 8. The subsequent coloured dashed lines trace the pressure measurements at different updraft airflow rates ranging from 22 L/s to 38 L/s, achieved using a fan located at the top of the stack.

Additionally, the solid-coloured lines represent the calculated pressure changes derived from the model and based on the baseline data (solid black line) referred to as adjusted pressure changes ($P_{adj}$). This comparison between the measured ($P_{meas}$) and adjusted pressure changes ($P_{adj}$) provides insights into the model’s effectiveness in capturing the impact of updraft airflow rates on the pressure distribution within the system.

Two key considerations are crucial when applying the developed equations for the dry part of the stack and the main horizontal pipe. Firstly, measurements are calculated starting from the open top termination and progressing downward, meaning the length at the top is zero and increases as one moves down the stack. Similarly, for the main horizontal pipe, measurement starts at zero at the outlet open to the atmosphere, and the length of the horizontal pipe is calculated up to the point where the pressure sensor is located.

The experimental results highlight the influence of sewer air on stack pressure behaviour. As shown in Figure 14b, for a given discharge event (such as a toilet flush), a range of possible pressures can occur within the stack, depending on the amount of air travelling upward from the sewer

Figure 15 shows a comparison between air pressure values in the mm water gauge between the measured and adjusted baseline data using Equations (4)–(6). The red line represents the best-fit regression. The results show a strong linear relationship, with a coefficient of determination (R²) of 0.98 for just a single flush.

The small discrepancies between some measured and predicted values in the horizontal pipe’s wet section can likely be explained by several factors [21]. First, the BDS test rig used to obtain the measurements is not connected to the public sewer, which may change the stack pressure regime. Second, the limited number of pressure sensors along the rig may miss localised pressure variations at specific elevations, and the test was based on a single flush.

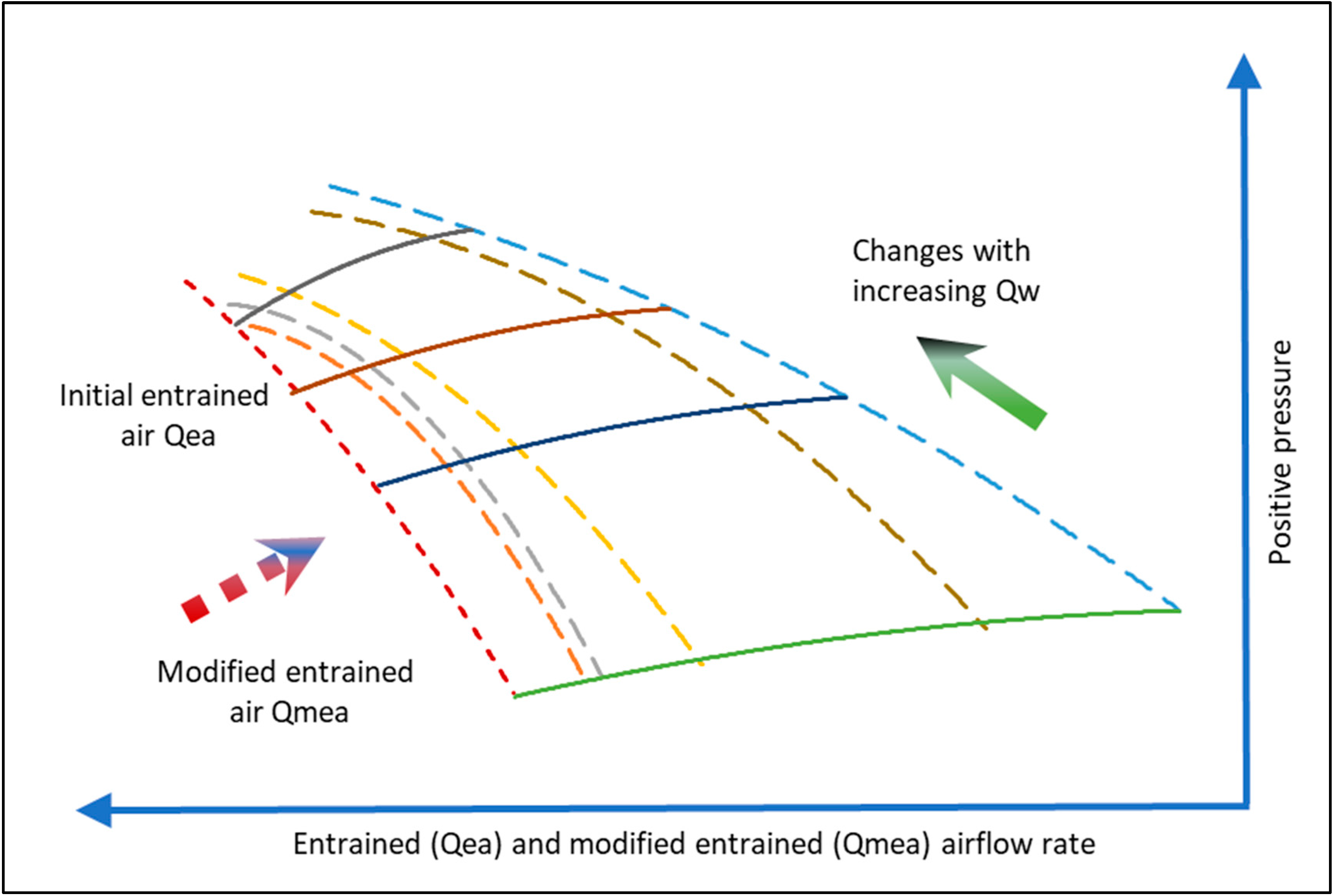
4.4. Development of a New Conceptual Diagram for Building Drainage Systems Exposed to Sewer Air

In normal conditions, as can be seen in the classical pressure profile, two zones can be identified, representing positive and negative pressure air zones with respect to the heights of the discharge points shown in Figure 2, which are the key elements in forming a drainage monitoring system of a real building. When the building drainage system is exposed to sewer air, there is no change in the zones within the BDS; however, the quantity of the pressure along the stack will be different. Two distinct trendlines are observed.

The first trendline illustrates the negative pressure, which was measured and observed across the bend at the base of the stack. Figure 16 presents a conceptual diagram illustrating the correlation between pressure variations at the base of the stack, measured 1 m away from the bend in both vertical and horizontal directions. The pressures shown are negative values recorded at a specific location on the test rig with a discharge point 5 m above the base. These correlations are intended to represent the behaviour of a drainage stack when influenced by sewer air. However, the specific numerical values associated with these correlations may vary depending on factors such as the water flow rate, pipe diameter, stack height, and sewer conditions.

Experimental analyses incorporating updraft airflows of up to 20 L/s demonstrate that the direction of the modified entrained air remains consistently negative.

Figure 17 depicts the positive pressure region observed under normal conditions, with the onset of positive pressure depending on both stack height and the water flow rate. In Figure 16 and Figure 17, the red dashed line represents the entrained air measured with no updraft airflow, while the other dashed lines correspond to modified entrained air at five different updraft airflow rates (6, 7, 11, 17, and 20 L/s). The solid lines, ranging from green to black, represent water flow rates from 1 L/s to 4 L/s. Four key observations can be drawn from these graphs, as outlined below:

• The modification of entrained air due to sewer air;
• The reduction in initial entrained air with higher updraft air rates;
• The increase in positive or negative pressure with increasing water flow;
• The increase in positive and negative pressure with adjusted modified entrained air.

5. Conclusions

Understanding and considering the integration between a building drainage system and a sewer system is essential for achieving effective and reliable design. Of particular importance is the influence of updraft air originating from the sewer on the air pressure regime inside the BDS, as above-ground and below-ground drainage systems are often treated in isolation. Accurately accounting for the bidirectional movement of air between the sewer and the building is especially important for simulating system pressures, which becomes increasingly critical in tall buildings. For any given appliance discharge, a range of possible pressures can occur within the stack, depending on the amount of air travelling upward from the sewer.

A set of equations was developed to calculate air pressure regimes when the system is exposed to updraft air from the sewer. Applying this model to both a simulated three-storey building and a real test rig (NLT) demonstrated the significant impact of sewer air on the air pressure regime within the BDS.

This study introduces the novel concept of modified entrained air (Qmea), which becomes particularly significant when the building drainage system is influenced by air from the sewer system, altering the overall system response. In parallel, the concept of a modified pressure profile is proposed, emphasising the need to account for pressure variations induced by sewer air within the conventional pressure profile. Experimental and field work observations from both steady and unsteady flow conditions confirm that increasing updraft airflow (Qas) modifies the entrained air (Qmea), coupled with increases in pressure drops along the stack.