A Review of the Soil–Geosynthetic Interface Direct Shear Test and Numerical Modelling

Abstract

The use of geosynthetics in reinforced soil structures (RSSs) requires the experimental and numerical modelling of the soil–geosynthetic interaction to support the design and analysis and deepen the knowledge of RSS systems. Direct shear testing has served as a fundamental laboratory choice for soil–geosynthetic interface testing, with the benefits being its availability, simplicity, and straightforward shear strength acquisition. This review paper pays attention to the direct shear testing and modelling of soil–geosynthetic interfaces. A brief laboratory interface experiment overview is presented, summarising the adopted soil–geosynthetic types, as well as the influences of various factors regarding soil–geosynthetic properties and loading/environmental conditions. Development of the finite element method to model interfaces is introduced, concentrating on the commonly adopted zero-thickness element, the thin-layer element, and continuum elements. As a result, emphasis is given to the comparison of the three element methodologies for the analysis of their advantages and limitations in accuracy, stability, and applicability for interface modelling. Based on the retrospective analysis, a summary and visions for the research progress of soil–geosynthetic interface testing and modelling are proposed to provide suggestions for future research topics.

1. Introduction

The common use of geosynthetics in reinforced soil structures (RSSs), such as a reinforced soil wall (RSW) [1,2,3], entails the soil–geosynthetic interaction analysis to support the relevant design and stress/deformation analysis within the geo-media. The interaction mechanism has been proven to be highly dependent on the thin soil–geosynthetic contact area, which is mainly characterised as an “interface” for the purpose of analytical and numerical analyses [4,5,6]. Restrained by the nearby geosynthetic element, the interface exhibits significantly distinguished loading responses from those of the surrounding soils [7]. Thus, the interest aroused by this topic has produced massive experimental programmes, mainly through the laboratory direct shear test and pullout test [8,9,10]. Both of these tests are capable of reflecting the global performance of an RSS system, although they show different soil–geosynthetic interaction response mechanisms. Compared with the pullout test, the direct shear test typically features a simpler set-up, lower expenses, and straightforward acquisition of the interface’s strength and stiffness parameters required for the optimisation of an RSS design. This paper aims to discuss the current literature on the soil–geosynthetic direct shear test from experimental and numerical viewpoints and to propose some future developments on this topic.

Hitherto, direct shear tests on various geosynthetic materials and shape configurations (e.g., geogrids, geostrips, geotextiles, and geomembranes) have been carried out to study the interfacial mechanical behaviour between these materials and soils [11,12,13,14,15,16]. The important factors influencing the interface’s direct shear response were also investigated for better understanding, and these factors could be accordingly categorised as soil–geosynthetic properties (e.g., soil density, soil particle size/shape/orientation, and geosynthetic configuration) [17,18,19,20,21], loading conditions (e.g., cyclic loading and confining stiffness) [13,18,22], and environmental variables (e.g., in-soil moisture and temperature) [23,24,25,26]. Usually, the studied soil is mainly of the sand/granular type; investigations on other soils (clay, silt, gravel, etc.) and geosynthetic formats (e.g., geomat/-strip/-foam) are rarely reported. Extending the studied soil and geosynthetic material to a wider range of categories can essentially enrich the interface direct shear database and provide complementary information or necessary strength parameters for the analyses of corresponding reinforced soil structures (e.g., pullout test and RSW analyses on the sand–polymeric strip interface) [27,28,29,30,31], where empirical equations for interface parameters are used as a result of the lack of direct shear data.

Meanwhile, numerical methods have also been developed to analyse soil–geosynthetic interaction problems, either by the discrete element method (DEM) [32,33] or the finite element method (FEM) [34,35,36], where the latter is the primary approach adopted by researchers. The existing FEM analysis generally involves two types of elements, namely, interface elements and continuum elements. The well-known zero-thickness element [37] and the thin-layer element proposed by Desai et al. [38] are the two prevalent types of interface elements that were used for interface modelling (e.g., [39,40,41,42]). However, previous interface element studies typically used the particular interface constitutive laws that require up to a dozen parameters, which greatly increases the difficulty of the calibration process. While the continuum element is compatible with various practical constitutive laws (e.g., the Mohr–Coulomb law) and has been shown to perform well in simulating soil–geosynthetic interactions (e.g., [43,44,45]), it has been mostly applied in pullout and RSW scenarios rather than in a direct shear case.

Therefore, considering the points mentioned, the present study includes the following two divisions: (1) a brief and detailed retrospective analysis of the current status of the soil–geosynthetic direct shear test, where (i) the features of reported soil and geosynthetics are concluded and, more importantly, (ii) emphasis is given to discussion of the influences of important factors, including soil and geosynthetic properties, loading conditions, and environmental conditions; (2) a review of the development of numerical methods for interface modelling, (i) including the zero-thickness element, the thin-layer element, and the continuum/solid element in FEM analysis, where constitutive law type, simulation scenarios, numerical software, and the number of modelling parameters are summarised, (ii) along with a comparison of the three interface elements. The present study may be useful for researchers interested in the state of the art of soil–geosynthetic interface experiments and numerical simulations and particularly for readers who are searching for novel topics, data sources, and modelling strategies.

2. Soil–Geosynthetic Direct Shear Test Overview

A fundamental procedure for soil–geosynthetic interaction analysis is the laboratory direct shear test. This test mainly includes four different types of shear apparatus: a direct shear box (DSB), direct simple shear (DSS), a large direct shear box (LDSB), and rotational shear ring devices [46]. Experiments for soil–geosynthetic interfaces have been widely carried out, with most of them being of the direct shear type (i.e., DSB or LDSB). For the purpose of literature analysis, this section collects the reported soil–geosynthetic direct shear test references over the past two decades, i.e., [11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71] (41 in total). Emphasis is given to the influence of various factors regarding soil–geosynthetic interface testing materials (i.e., soil type and geosynthetic product features) and boundary conditions.

2.1. Soil and Geosynthetic Features

Table 1. Summary of soil–geosynthetic features/types for literature-selected direct shear tests.

Reference	Ref. No.	Soil		Geosynthetic Product
		Type	Classification a (USCS)	Type b	Material c
					Raw	Coating
Lee and Manjunath (2000)	[12]	Beach sand	SP	GT	PET, PP	–
Xenaki and Athanasopoulos (2001)	[16]	Ottawa sand beach sand	– –	Geofoam	PS	–
Fleming et al. (2006)	[15]	Ottawa sand Sand–Bentonite mix silty sand	– – –	GM	HDPE	–
Abu-Farsakh et al. (2007)	[17]	Sand Clay-1 Clay-2	SP CL, CH ML-CL	GT GG	PP PET, PP	– –
Liu et al. (2009)	[47,48]	Ottawa sand Gravel Laterite clay	– GP –	GT, GG	PET	PVC
Pitanga et al. (2009)	[49]	Silty sand	–	GM GT Geomat	HDPE PP –	– – –
Hsieh et al. (2011)	[50]	Quartz sand Riverbed gravel Crushed stone	SP GP GP	GT GG	PP PET	– PVC
Khoury et al. (2011)	[51]	Sand–glass bead mix	–	GT	PP	–
Vieira et al. (2013)	[13]	Silica sand	SP	GT	PET, PP	–
Kwak et al. (2013)	[52]	Jumunjin sand	–	GT	HDPE	–
Bacas et al. (2015)	[21]	Spain landfills	–	GT GM GC	PP, PE HDPE PP, HDPE	– – – –
Ferreira et al. (2015)	[53]	Granite residual soil	SW-SM	GG GT GC	HDPE, PET PP PET, PP	– – –
Wang et al. (2016)	[18]	Silica sand Gravel	SP GP	GG	PP	–
Chai and Saito (2016)	[54]	Mixed clayey soil Bentonite Decomposed granite	– – –	GM GT GCL	PE, PVC, HDPE PET	– – –
Choudhary and Krishna (2016)	[55]	Sand	SP	GT, GG	–	–
Infante et al. (2016)	[56]	River sand River sand	SW SM	GG GT	PVA, PP PP, PET	– –
Liu et al. (2016)	[57]	Fujian sand	–	GG	PP	–
Afzali-Nejad et al. (2017)	[19]	Angular sand	–	GT	PP	–
Punetha et al. (2017)	[58]	River sand	SP	GM GT	HDPE –	– –
Fowmes et al. (2017)	[59]	Uniform sand Mudstone clay	– CL	GM	HDPE	–
Markou and Evangelou (2018)	[14]	Ottawa sand Cohesive soil	SP –	GM	PVC, PET, HDPE	–
Afzali-Nejad et al. (2018)	[20]	Crushed sand	SP	GM GT	PVC –	– –
Jotisankasa and Rurgchaisri (2018)	[23]	Sand Silt Clay	SM ML CH	GT	PP, PET	–
Markou (2018)	[60]	Uniform sand	–	GT GT	PP, PET PET	– PVC
Hassanikhah et al. (2020)	[24]	Clay–silt mixture	–	GM	HDPE	–
Namjoo et al. (2020)	[61]	Sand	SP	GT GG GC	PP HDPE PP, HDPE	– – – –
Afzali-Nejad et al. (2021)	[22]	Angular sand	SP	GT GM	PP PVC	– –
Chao and Fowmes (2021)	[25]	Mudstone clay	CL	GDL	PP, HDPE	– –
Lashkari and Jamali (2021)	[62]	Sand	–	GT GM	– PVC	– –
Liu et al. (2021)	[63]	Crushed limestone Quartz/round gravel Spherical granular	– – –	GG	PP	–
Qannadizadeh et al. (2022)	[64]	Angular sand	SP	GRP	–	–
Razeghi and Ensani (2023)	[11]	Sand-1 Sand-2 Clay	SW, SC SP-SC CH	GT GG	PE PE	– PVC
Muluti et al. (2023)	[65]	River sand Clay	SP –	GT GCL	– PP	– –
Kayadelen et al. (2023)	[66]	Spherical sand Crushed sand Sand mixture	– – –	GT	PP	–
Khan and Latha (2023)	[67]	River sand Manufactured sand	SP SP	GT GM	– HDPE	– –
Chao et al. (2024)	[26]	Quartz sand Silica sand	– –	GM GG	– –	– –
Kommanamanchi et al. (2024)	[68]	Natural sand Recycled sand	SP SP	GG GT	PP, PET PET	– –
Ying et al. (2025)	[69]	Crushed limestone Spherical granular	– –	GG	PP	–
He et al. (2025)	[70]	Frozen soil	CL-ML	GT	–	–
Gao et al. (2025)	[71]	Saline soil	–	GT	PP	–

^a The tested soils are classified according to the USCS standard as poorly graded sand (SP), well-graded sand (SW), silty sand (SM), sand with clayey fines (SC), high-plasticity clay (CH), low-plasticity clay (CL), low-plasticity silt (ML), and poorly graded gravel (GW). ^b The abbreviations for geosynthetic types: geogrid (GG), geotextile (GT), geomembrane (GM), geo-composite (GC), geosynthetic clay liner (GCL), geosynthetic drainage layer (GDL), and glass bead-reinforced polymer (GRP). ^c The geosynthetic product materials used in the literature: polypropylene (PP), polyethylene (PE), polyester (PET), polystyrene (PS), polyvinyl chloride (PVC), polyvinyl alcohol (PVA), high-density polyethylene (HDPE), and low-density polyethylene (LDPE).

summarises all soil and geosynthetic features used by the selected experiments in chronological order. In the table, general soil types (i.e., sand, clay, silt, and gravel) and common geosynthetic configuration features (i.e., geogrid, geotextile, geomembrane, etc.) are specified. Also, the particular type of geosynthetic raw/body material (PP, PE, PET, PVC, etc.) and the standard soil classification (SP, SW, SM, etc.; as per the Unified Soil Classification System USCS) are detailed.

As shown, the sandy soil type is the one tested in the largest number of experiments on soil–geosynthetic interfaces, whereas few investigations have been currently performed on other types of soil (such as clay, gravel, silt, and/or soil mixtures). One noteworthy fact is that for tested granular soils like sand and gravel, mainly poor gradation (SP or GP), i.e., uniform particle distribution, was incorporated, whereas tests on geosynthetic and well-graded sand (SW) or well-graded gravel (GW) soil types are still rarely reported. The geosynthetic configurations being considered are mainly of the grid, textile, and membrane types, but other geometries, such as strip, mat, or foam, could be further taken into account to extend the knowledge on soil–geosynthetic direct shear behaviour and to amplify the current testing database.

2.2. Influence of Soil and Geosynthetic Properties

Experimental evidence has demonstrated that depending on various factors regarding soil and geosynthetic properties, loading conditions, and environmental conditions, the direct shear failure mechanism can be difficult to analyse.

Table 2. Summary of influencing factors investigated by selected soil–geosynthetic direct shear tests.

Category	Key Factor	Reference	Related Interface Parameters
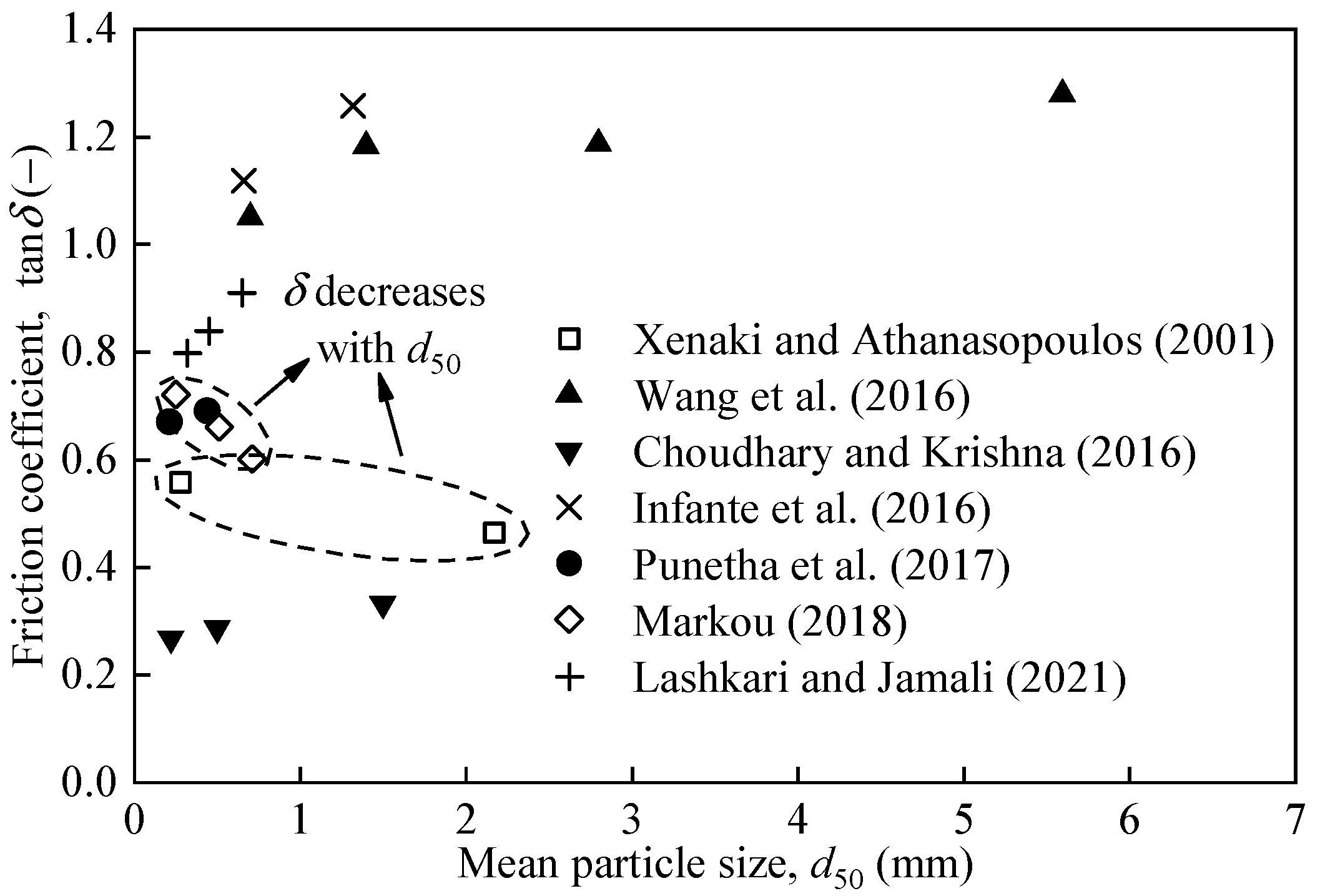
Soil properties	Particle size	[16,18,55,56,58,60,62]	δp, δr, ψ, ts
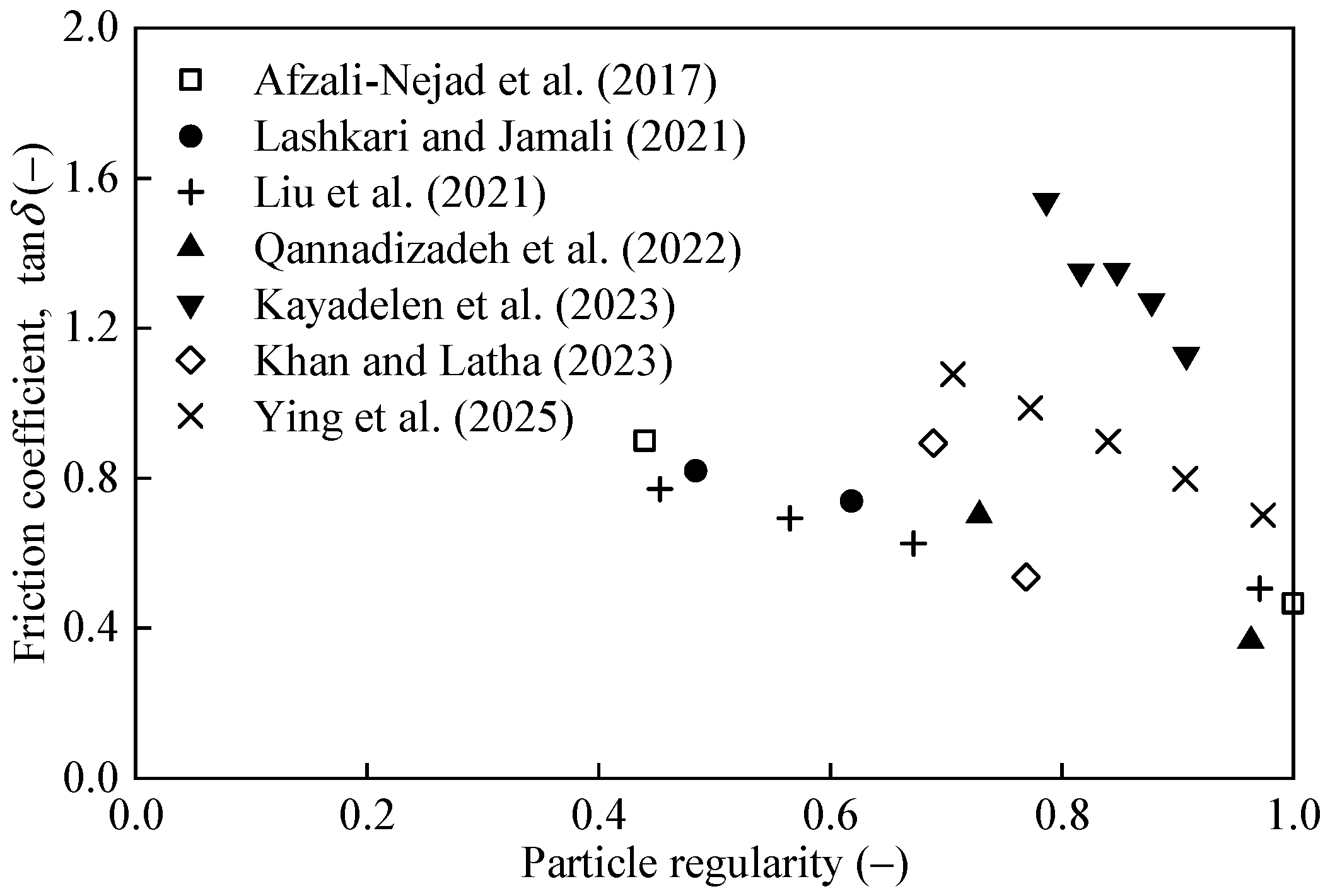
	Particle shape	[14,16,19,60,62,63,64,66,67,69]	δp, δr, ψ, ts
	Density	[16,17,19,22,53,56,58,62,64]	δp, ψ, ts
	Fine content	[11,57]	δp, δr
	Anisotropy	[20,49]	δp
Geosynthetic properties	Surface roughness	[21,24,59,60,64]	δp, ψ, ts
	Configuration	[47,48,50,53,55,56,59,68]	δp, δr, ψ, ts
	Density	[16,54]	δp, δr
Loading conditions	Cyclic loading	[12,13,18,52,57,63,71]	δp, δr, ψ, ts
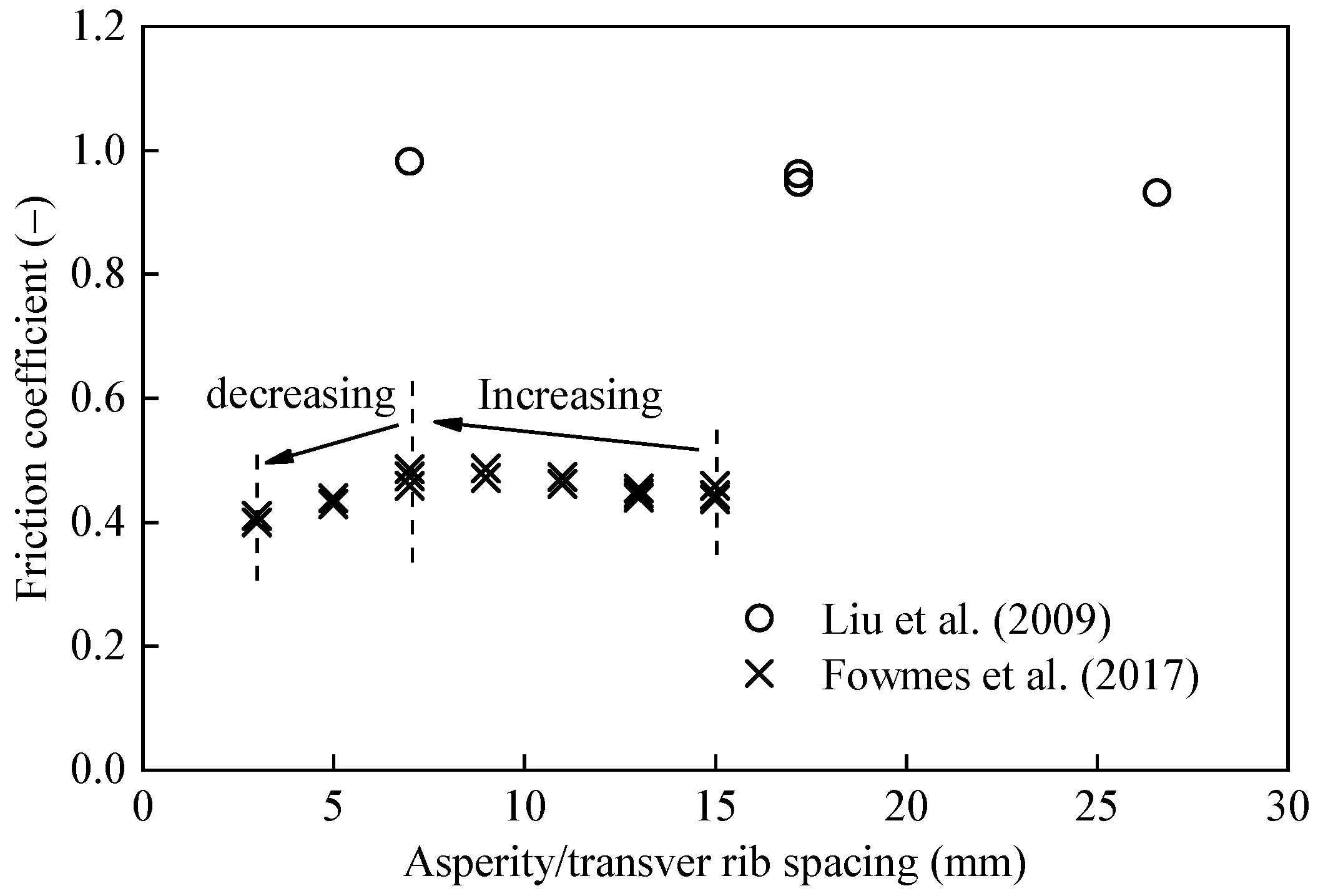
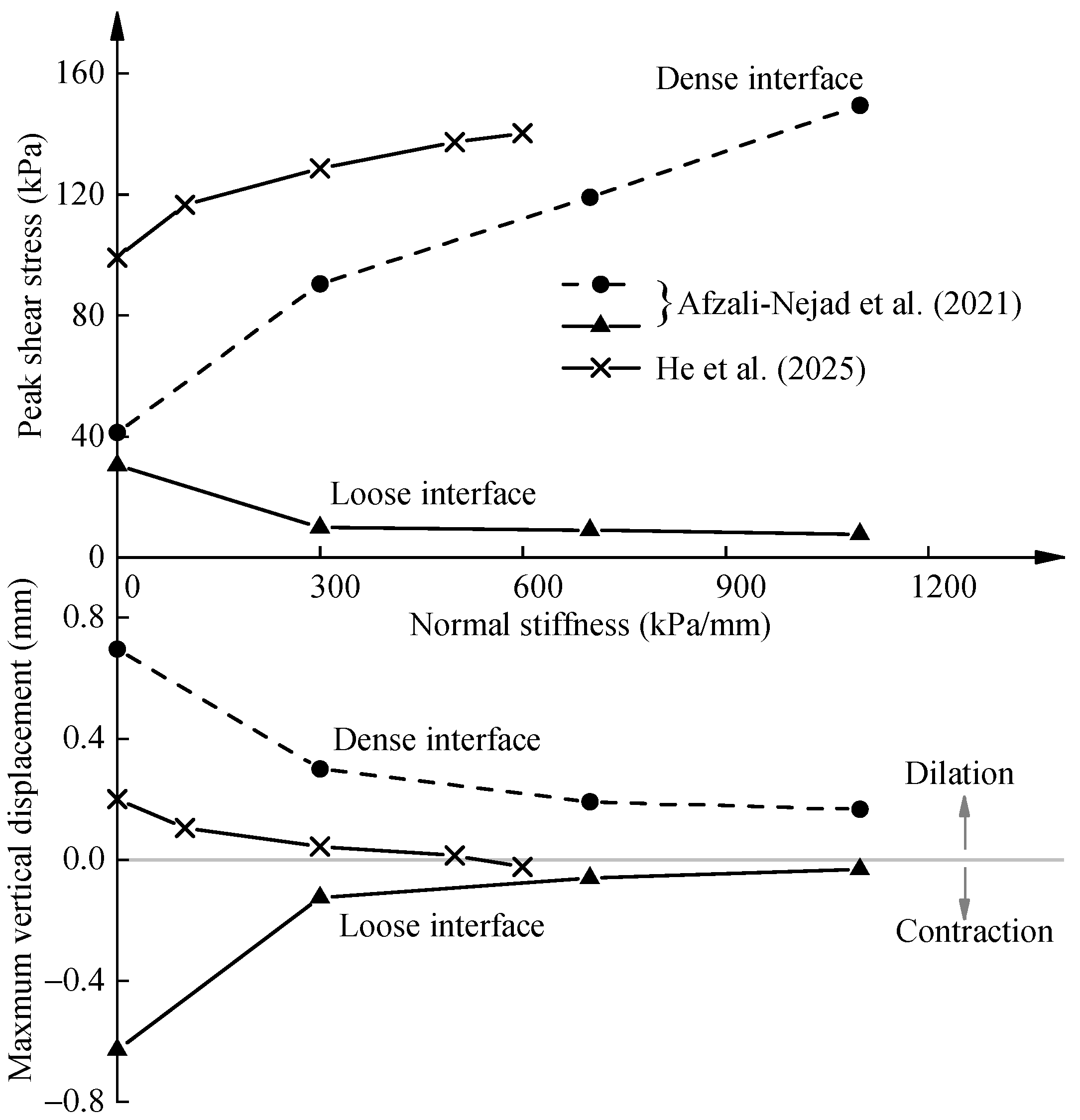
	Confining stiffness	[22,70]	δp, δr, ψ, ks, kn, ts
	Shearing rate	[24,58]	δp, δr, ψ, ks
	Shear box size	[56,60]	–
Environmental conditions	Suction/moisture	[11,15,17,23,24,25,26,51,53,54,58,70]	δp, δr, ψ, ts
	Temperature	[25,26,70,71]	δp, δr, ψ, ts
	Chemical/pH	[52]	δp, δr, ψ

summarises the specific key influencing factors and related research references found in the literature. The interface parameters for numerical modelling related to each factor are also listed; thus, the commonly recognised interface parameters (i.e., the peak and residual friction angles δ_p and δ_r, the dilatancy angle ψ, the shear and normal stiffnesses k_s and k_n, and the shear band thickness t_s) are also incorporated in this table. This numerical connection part is fully described later in Section 3.

Soil particle features greatly influence the interface behaviour between soil and geosynthetics, mainly through particle size and shape. Approaches to estimate the particle size and shape are typically based on the mean particle size d₅₀ and particle regularity, respectively. Figure 1 collects the measured experimental data from the literature [16,18,55,56,57,58,60,62], with horizontal and vertical coordinates representing friction coefficient and mean particle size, respectively. As shown in the figure, the friction angle generally exhibited an increasing tendency with regards to d₅₀ (i.e., soils with larger particles provided more shear resistance in interaction with geosynthetics). However, the opposite conclusion was found in the studies by Xenaki and Athanasopoulos [16] and Markou [60], who revealed a decrease in shear strength with particle size. The possible reason may be the more efficient mobilisation of soil friction by the larger number of grains in contact with the geosynthetic as the sand grain size decreases [60]. Regarding the influence of particle shape, some investigations [14,16,60] suggested that a sub-angular/sharp shape of sand grains mobilises more shearing resistance than rounded sand at the sand–geosynthetic interface. Recently, several documented research works [19,62,63,64,66,67,69] studied the effects of particle shape, where granular soils with identical particle size distributions and relative density were used to avoid interferences. Particle regularity, defined as the mean value of particle roundness and sphericity, was used in the studies to quantify the shape of soil particles. Figure 2 shows the measured relationships between interface friction coefficient and particle regularity. As expected, an increase in regularity reduced the shear resistance of the soil–geosynthetic interface due to the reduction in contact area and friction. Besides this, larger particle size or lower regularity of the particles could also strengthen the interface dilatant effect [19,62,66]. With the use of digital image analysis techniques [62,66], the interface shear/dilatant zone thickness turned out to be reduced by the increase in sand particles’ regularity.

Ample attention has also been paid to the influence of soil density, which has been proven to exhibit a positive correlation with the interface’s peak strength, dilatancy, and strain softening [16,17,19,22,53,56,58,62,64]. The possible reason is the interlocking within dense soils [56]. One exception is the study by Xenaki and Athanasopoulos [16], where, by comparing two different sands (Ottawa sand and beach sand) with different particle sizes and angularities, a negligible influence by soil density was found. Another important concern is soil grain composition: test evidence indicates that no explicit relations exist between the interface’s shear strength and grain fine content in soils [11,57]. Razeghi and Ensani [11] found that increasing the percentage of soil fines improves or reduces the soil-geotextile interface’s shear strength, depending on the moisture content (i.e., there is a coupled effect between soil moisture and fine content). In addition, special concern has been given to the inherent soil anisotropy, which was investigated through the method of compacting the soil sample in an inclined bedding pane, suitable to assess the interface’s friction under low normal pressure [49]. A further study performed by Afzali-Nejad [20] explored the influences of bedding plane inclination orientation; the interface’s peak strength was found to be affected by the inherent anisotropy, although residual strength and stress–dilation law showed low sensitivity.

A geosynthetic’s geometric properties substantially impact the soil–geosynthetic interface behaviour. This is mainly due to the geosynthetic’s surface roughness, configuration (i.e., layout and/or shape) as well as geosynthetic material product density. Test-based comparisons between rough- and smooth-textured geosynthetic surfaces have been made (e.g., [21,24,60], among others), indicating, as expected, that shear strength rises when smooth geosynthetic products are replaced with equivalent rough-textured ones. This is in line with further findings revealing that the interface’s strength and dilation increase with surface asperity thickness [21,59,64]. In addition, soil interlocking and related interface passive resistance have been shown to play the predominant roles controlling an interface’s mechanical behaviour. For example, experimental evidence indicated that geotextiles with openings which allowed for soil particle penetration showed higher interface friction angle than regular flat geotextiles [50,55] and geogrids provided more interface shear resistance than geotextiles [47,48,53,56,68]. The reason identified was that soil particles’ interlocking with geotextiles’ openings or geogrids’ ribs mobilised the internal soil shear strength (typically larger than the soil–geosynthetic interface shear strength), in addition to the passive resistance of the transverse ribs or openings. Interestingly, Ferreira et al. [53] revealed that this internal soil shear strength mobilisation strongly enhances the positive relation between interface strength and soil density. Additionally, a closer spacing of transverse ribs or surface asperities caused higher peak strength [47,48,59,68], yet Fowmes et al. [59] found that an overly closed spacing could decrease the shear resistance due to the over-sliding of soil particles atop the ribs or asperities, as depicted in Figure 3, where the measured data from [48,59] are collected, showing the relations between the friction coefficient and the spacing of transversal ribs. Geosynthetic product density has also been taken into consideration. Experimental observations demonstrated that HDPE geomembrane provided lower shear strength than soft expanded PS geofoam [16] and PVC geomembrane [54], meaning that increasing geosynthetic density may reduce interface shear resistance. However, the number of samples was not high enough, and more experimental evidence should be provided to demonstrate this phenomenon.

2.3. Influence of Loading Conditions

The loading conditions for soil–geosynthetic direct shear tests mainly include boundary conditions (e.g., confining pressure and stiffness), shear box configuration (e.g., size and dimensions/set-up), and shear movement type (cyclic shear, shearing rate, etc.). Note that confining pressure is not listed in Table 2 because multiple stress levels are required to determine the shear strength envelope. Confining stiffness, applied through a spring analogy [22] or normal stiffness spring [70] on the top boundary, also plays an important role in the direct shear mechanism. Experimental observations on sand–geotextile [22] and silty clay–geotextile [70] revealed that increasing the confining stiffness improved interface shear strength and reduced dilatant deformation (see Figure 4). However, this phenomenon may be significantly different if the soil is in a loose state; shear stress and contactant displacement in loose interfaces are reduced by the increase in normal stiffness. This may be attributed to the stress relief caused by weakened contactant deformation, as confining stiffness always suppresses volumetric deformation. Therefore, future research on this topic is encouraged to clarify the influence mechanism of normal stiffness, especially considering low-density soils.

General test results show that cyclic loadings induce positive effects on interface shear strength. For instance, cyclic loading tests on PET–yarned geotextile [13] and geogrids [18,57,63] revealed that no cyclic stress degradation occurred at peak shear strength; further, as the number of cycles increased, the interface shear strength also increased, and the hysteretic curve underwent insignificant changes. The possible reason is that cyclic shearing intensifies soil–geosynthetic interface dilatancy due to sand grain rearrangement and crushing [18]. However, this may not be valid once damage occurs in the geosynthetic product/material. It was found that if geotextile damage occurred, this led to soil particles clogging the openings created during damage, resulting in a decrease in peak strength with cyclic performance, up to steady residual strength [12]. Another study [52] also demonstrated that damage from chemical/pH decay also led to a negligible relation between shear strength and the number of cycles applied. Additionally, the cyclic behaviour of the soil–geosynthetic interface may be also influenced by the shape of soil particles and thermal conditions. In this regard, Liu et al. [63] found that the damping ratio (one of the key dynamic parameters for assessing interface performance under seismic loading) became lower when particle regularity increased. Temperature coupled effects also changed the interface phenomenon. Gao et al. [71] found that the freeze–thaw cycles became dominant in affecting interface strength, rather than the number of cycles applied, reducing the damping ratio.

Special attention has also been paid to the influence of the shearing rate. Hassanikhah et al. [24] found that an increase in shearing rate causes peak strength to rise and that a more significant dilatancy effect was obtained in rough-textured geosynthetics, with insignificant impacts on smooth-shaped ones. This was attributed to the incomplete dissipation of pore pressure. Nevertheless, another study by Punetha et al. [58] revealed a contrary tendency (i.e., a higher shearing rate led to lower shear strength). According to their analyses, a potential reason was the time reduction required for sand particle rearrangement. The two opposite conclusions are possibly due to the different drainage conditions, i.e., how much time for pore pressure dissipation. As the shearing rate influences the drainage of fine-grained soils, the corresponding rate threshold of drained and undrained conditions may have been different for the soils and geosynthetics used in the two studies. A greater number of relevant experiments need to be performed to further investigate the influence of the shearing rate on soil–geosynthetic interfaces.

The influence of the shear box configuration has also attracted some research interest. According to Infante et al. [56] and Markou [60], who performed soil–nonwoven geotextile shear tests with different shear box sizes, comparable peak shear strengths were obtained in tests using standard shear boxes and small/large shear boxes (approximately only 3% and 6% differences were obtained, respectively). From the obtained results and for the particular soil, tested samples, and boundary conditions applied, insignificant effects were caused by the shear box dimensions. It seems that the soil–geosynthetic shear experiments performed thus far are still not enough to fully explain the influences of the shearing rate, shear box size, and shear test set-up, and further studies are necessary for clearer interpretations.

2.4. Influence of Environmental Conditions

The in-soil environmental conditions, corresponding to hydraulic, thermal, and chemical aspects, have significant influence on the soil–geosynthetic interaction behaviour. A well-known fact is that an increase in moisture/saturation/water content (i.e., a decrease in suction) leads to significant reduction in soil–geosynthetic interface peak friction angle and dilatancy [11,15,17,23,24,25,26,51,53,54,58,70]. The increase in suction derived from shear-induced drainage may also influence the test phenomenon, as obtained by suction-monitored direct shear tests [23]. To eliminate the effects of shear-induced drainage, suction-controlled shear apparatus was developed to maintain a constant suction condition during the test process [24,51], where pore air/water pressure control was obtained through the axis transformation technique, and quantitative analyses were performed for determining a more precise relation between suction and interface shear resistance.

Studies on temperature effects [25,26,70,71] have proved that the thermal environment significantly influences the mechanical responses of geosynthetics-soil interfaces. An increase in temperature decreased the interface’s peak shear strength and even reduced creep displacement in creep shear tests [25,26]. The hydraulic performance was also affected by the thermal conditions of the soil–geosynthetic interface, indicating that moisture–temperature coupled effects occurred upon interaction at the interface. Chao and Fowmes [25] found that enough heating significantly increased interface creep deformation during drying cycles, while He et al. [70] revealed that the influence of moisture was greatly weakened by higher temperature in tests under constant normal stiffness. The 14° difference in friction angle caused by water content change (9%) at freezing temperature (−5 °C) was reduced to 1.5° after the sample was heated to in-air ambient temperature (20 °C). Moreover, Gao et al. [71] investigated the influence of freeze–thaw cycles on a saline soil–geotextile interface. It was found that as the freeze–thaw cycles increased, significant shear stress degradation occurred, accompanied by shear stiffness enhancement and damping ratio reduction. When discussing chemical effects (pH), Kwak et al. [52] found that both acid and basic conditions induced the decay of soil particles near the soil–geosynthetic interface, leading to considerable degradation of the interface shear strength, which was more significant if low normal pressure was applied.

2.5. Summary of Soil–Geosynthetic Direct Shear Tests

In summary, the currently available literature on soil–geosynthetic direct shear tests mainly focuses on the interaction between poorly graded sand and geogrid, geotextile, and geomembrane geosynthetic product types. Experimental analyses on well-graded sand, other soil types (like clay, silt, and gravel), and other geosynthetic geometric configurations (strips, mats, foams, etc.) are still rarely reported. The following points can be addressed: (1) Soil properties: Soil density, particle size, and angularity have been found to directly affect interface shear strength, but studies targeting soil anisotropy and fine content influences are still limited. (2) Regarding the geosynthetic product properties, the role of surface roughness and geometries/configuration of geotextile, geomembrane, and geogrid products are investigated the most, whereas geosynthetic density has received less attention. (3) Regarding the loading conditions, the mechanical interface shear performance sensitivity due to different confining pressure and cyclic loading scenarios has been clarified, whereas the effects of confining stiffness, shear box size, and shearing rate remain unclear and, in some conditions, disputable. (4) Regarding the environmental conditions, the in-soil water content or suction change definitely alters the interface mechanism, but temperature or chemical effects need to be further elucidated with more experiments.

3. Development of Numerical Modelling

Numerical modelling, if calibrated and validated, is extremely useful to support the analysis and design of reinforced soil structures. In this regard, an accurate prediction of soil–reinforcement interaction behaviour is fundamental. Current soil–structure interface modelling methods mainly include finite element (FE) (e.g., [35,36,37,38,39,40,41,42,43,44,45]), discrete element (e.g., [32,33]), and contact analysis (e.g., [72,73]). Nonetheless, this study will mainly focus on FE analysis because of its widest use in the literature on soil–geosynthetics, even though the other two methods show unique advantages in modelling microscale behaviour and interface separation, respectively.

The primarily involved finite elements for interface modelling are the specially developed interface element and continuum element methods. The idea of the interface element firstly originated from finite element implementation to represent rock joint discontinuities (Goodman et al. [37]). This implementation/method is well known as the “zero-thickness” interface method with the Goodman zero-thickness element. Later, the thin-layer element (Desai et al. [38]) was proposed to overcome the issue of ill-conditioning in the Goodman element due to large normal stiffness, showing better load transfer because an element continuity was considered. With the exception of these two special interface elements, the conventional continuum element has also attracted research interest (e.g., [44,45,74]). Unlike the special interface elements, which generally involve particular interface constitutive laws and require multiple definition parameters, the continuum element, as a material, may be a user-friendly choice due to its compatibility with general soil material constitutive laws commonly available in commercial FE software platforms (linear elastic with Mohr–Coulomb or Drucker–Prager failure criterion, etc.).

To provide direct insights into the development of interface modelling,

Table 3. Summary of numerical studies on soil–geosynthetic/structure interface modelling since 2000.

Element Type	Reference and Ref. No.	Constitutive Law	Modelling Scenario	Platform	Para. No.
Zero-thickness element	Hu and Pu (2003) [40]	Damage Elastoplasticity	Direct shear test and pullout test	–	9
	Zhang and Zhang (2009) [41]	Damage Elastoplasticity	Slide block test, direct shear test, and CFRD	–	12
	Yu et al. (2015) [43]	Mohr–Coulomb criterion	Unit cells and concrete panel segment	FLAC, PLAXIS	5
	Yu and Bathurst (2017) [6]	Mohr–Coulomb criterion	Pullout test and GT-reinforced soil layer over a void	FLAC	5
	Abu-Farsakh et al. (2018) [36]	Mohr–Coulomb criterion	Integrated bridge system	PLAXIS	5
	Hegde and Roy (2018) [75]	Mohr–Coulomb criterion	Direct shear test and pullout test	PLAXIS	5
	Cui et al. (2019) [76]	Two-surface hardening	Triaxial heating test	ICFEP	17
	Liu et al. (2021) [77]	Elastic–perfectly plastic	Slide block test, T-bar penetration, and embedded chain link	ABAQUS	4
	Ghalamzan Esfahani and Gajo (2024) [78]	Chemo-mechanical coupled Cam-Clay	Casagrande direct shear test	ABAQUS	23
Thin-layer element	Karabatakis and Hatzigogos (2002) [79]	Elasto- viscoplasticity	Creep shear test	FORTRAN	7
	Qian et al. (2013) [73]	Linear elasticity	CFRD	–	2
	Saberi et al. (2019) [42]	Two-surface plasticity	Slide block test, pullout test, and CFRD	ABAQUS	11
Continuum element	Damians et al. (2021) [45]	Mohr–Coulomb criterion	MSE wall	CODE_BRIGHT	5
	Damians et al. (2022) [44]	Drucker–Prager criterion	Soil–facing interaction	CODE_BRIGHT	5
	Damians et al. (2024) [29]	Mohr–Coulomb criterion	Steel/PET trip pullout test	CODE_BRIGHT	5

summarises the main references on soil–geosynthetic interface modelling over the past two decades, according to the element types used. Note that some studies on methods to study the interface between soil and other structural materials are also listed, since the soil–structure modelling method is universal, regardless of the particular structure subject to interaction, and is thus also applicable in the soil–geosynthetic interface case study. Attention is also paid to interface constitutive laws, modelling scenarios, numerical platform (i.e., software/code), and the number of interface parameters required.

3.1. Zero-Thickness Element (Goodman Element)

Being the earliest interface element in FE analysis, the zero-thickness element has aroused massive research interest since its presentation by Goodman et al. in 1968 [37]. The Goodman interface element is featured by zero thickness due to the assumption that common nodes are shared by the neighbouring elements near the interface (i.e., identical coordinates for the nodes along the normal direction). However, numerical errors may occur because of the ill-conditioning of the stiffness matrix, in cases where the normal stiffness and element meshing are inappropriately defined [80,81,82,83]. Aiming to improve numerical performance and stability, similar but modified versions of the zero-thickness element have been proposed successively. Herrmann [81] formulated a “link” element for the purpose of modelling different interface acting modes—such as slip, bond, and separation—where fictitious springs were adopted to establish the element equations. A comparative study carried out by Kaliakin and Li [82] revealed that the deficiency of tangential force oscillations within the Goodman element was eliminated by this new element definition; however, this led to unreliable prediction of the normal response. They presented a linear zero-thickness element by employing tangential and normal responses similar to the Goodman and Herrmann elements, respectively, eliminating the deficiencies of both previous elements and improving interface behaviour.

Introducing finite thickness to the Goodman element was also considered a good solution for mesh overlapping and ill-conditioning. As concluded by Ng et al. [83], who numerically compared the DRCRISP element (Goodman element type) and CRISP90 element [84] (constant strain with finite interface element thickness), the CRISP90 interface element was considered more appropriate to model soil–pipe interfaces. A modified version of the CRISP90 interface element was also developed in the study, dedicated to overcoming the re-bonding issues of the original CRISP90 element, through introducing an initial and limited normal adhesion. Yuan and Chua [85] assumed “virtual” non-zero thickness to overcome the issues caused by the normal stiffness definition in the zero-thickness element. The “virtual” thickness was initially set to provide normal stiffness and then set to vanish in the final formulation stage, through which the element stiffness matrix possessed the same form as the Goodman element. Hu and Pu [40] also formulated a constant-strain interface element with finite thickness well capturing the interface behaviour of the soil–steel direct shear test and geotextile pullout test. Zhang and Zhang [41] proposed a uniform format between the constant-strain interface element and the zero-thickness element; i.e., the element equations for the two elements could transfer mutually, which was then demonstrated through multiple numerical simulations consisting of the slide block test, the direct shear test, and concrete-faced rockfill dam (CFRDs). Nonetheless, unlike previous studies [6,37,80,81,82,83,84,85] which involved elastic or elastic–perfectly plastic laws containing no more than 5 parameters (shear stiffness, normal stiffness, cohesion, friction angle, dilatancy angle, etc.), both studies employed damage-based elastoplastic models for describing complex interface behaviour, at the cost of up to 10 parameters.

Commenced already several years ago, the development of commercial software greatly facilitates numerical modelling concerning interfaces. The most renowned computational platforms for geotechnical researchers and geotechnical engineers are finite difference (FD) code FLAC [86], as well as FE code PLAXIS [87], ABAQUS [88], and CODE_BRIGHT [89]. Geotechnical problems are more efficiently analysed through the well-built elements/models and the user interface tools provided by these numerical platforms.

In reinforced soil structures, for example, Yu and Bathurst [6] systematically discussed the influence of the choice of soil and interface properties through two examples in FLAC; soil modulus E = 10–100 MPa, soil–reinforcement interface stiffnesses k_normal = 10 kN/m³, k_shear = 100 kN/m³, and a friction reduction ratio R_i = 0.67 were recommended for when physical test data of the soil–reinforcement interface are not available. Abu-Farsakh et al. [36] and Hegde and Roy [75] performed FE analysis of a geosynthetic-reinforced soil integrated bridge system and a geotextile pullout test by using PLAXIS, respectively. The former suggested that 2D-FE modelling can be an alternative to 3D-FE modelling with appropriate accuracy, even if the 3D bridge model geometry could not be rigorously simplified to the plane strain case, while the latter indicated that the interface friction efficiency calibrated by the pullout test was much smaller than that of the direct shear test due to the development of the progressive interface failure mechanism in the pullout test. The influence of the choice of the FD method (FLAC) or FE method (PLAXIS) was also investigated by Yu et al. [43], who found that both programmes exhibited acceptable accuracy in reproducing the measured performance of reinforced soil structures if the soil and soil–reinforcement interface parameter values were adjusted within reasonable limits. Moreover, FE analyses using the ABAQUS zero-thickness element also emerged recently, yet mostly through various user-defined subroutines [88] (FRIC, UMAT, UEL, etc.). For example, Liu et al. [77] implemented an interface model to consider the shear response under tensile normal stress through FRIC (user-defined friction), which was difficult to represent with the ABAQUS built-in Coulomb friction law. The number of parameters for this 3D tensile stress analysis was four. Ghalamzan Esfahani and Gajo [78] performed numerical analyses of hydro-chemo-mechanical (HCM) behaviour of interfaces based on a chemo-mechanical (CM) coupled Cam-Clay model implemented in UMAT (user-defined material) code. The element format of the zero-thickness element proposed by Kaliakin and Li [82] was compiled to the UEL (user-defined element) subroutine to prevent numerical instability. Stress- and displacement-controlled Casagrande direct shear tests under varied mechanical, hydraulic, and chemical conditions was selected to validate the HCM coupled analysis method proposed. The HCM coupled analysis required up to 23 parameters for multi-field calculation scenarios. Among them, the salt concentration parameters played a key role in the modelling process. A 3D zero-thickness element was also presented by Cui et al. [76], who considered the fully coupled thermo-hydro-mechanical (THM) behaviour of interfaces. A THM coupled interface element was implemented into the FEM program ICFEP [90] on the basis of the zero-thickness element previously formulated by Day and Potts [80]. An undrained triaxial heating test on fissured clay was simulated to capture the coupled THM response of the pre-existing fissure. Due to the complexity of multi-field constitutive laws, 17 parameters were needed to simulate the THM coupled behaviour of the interface, increasing the calibration cost of the model.

3.2. Thin-Layer Element (Desai Element)

As a result of the encountered numerical difficulties in the “zero-thickness” interface element method, some researchers have attempted to overcome the issues mentioned before by developing the thin-layer interface element. The element was firstly proposed by Desai et al. [38] in 1984 and contained six nodes with two degrees of freedom (DoF) for each node. This element was actually a solid element with real entities (i.e., physical properties with weight and geometric dimensions) and was reasonably able to model interface behaviour by assuming very small thickness. The selection of appropriate thickness is of major importance for these elements to obtain adequate and representative performance of the problem to be modelled. In comparison with the element’s length, too large a thickness would inevitably make the thin-layer element behave like a solid element, while too small a thickness may give rise to computational difficulties. After parametric analyses conducted by Desai et al. [38], a thickness/length ratio between 0.01 and 0.1 was recommended to maintain interface nature and numerical stability. More importantly, instead of using conventional constitutive models for solid elements, particular constitutive relationships were also needed to incorporate various interface deformation modes, such as stick, slip, debonding and (if required) re-bonding behaviours. The performance of the thin-layer interface element was also examined by a series of numerical studies targeting different application scenarios [91,92,93]. The element was proved to be more computationally reliable than the zero-thickness element due to its improved definition of normal and shear behaviour [38]. Successive studies were also performed by Zaman et al. [91] and Desai et al. [92,93]; in the studies, the thin-layer element was successfully applied to nuclear-contaminated structures, soil–anchor systems, and cyclic interface shear tests. The abovementioned studies were limited to the elastic description of the interface only; thus, further consideration was required to reproduce the typical nonlinear elastoplastic behaviour of the interface. Sharma and Desai [94] implemented a hierarchical single-surface (HISS) model into the thin-layer element [95]. This elastoplastic model for soils was slightly modified to conform to regular interface constitutive laws. Based on the disturbed state concept (DSC) and the HISS formulation, damage or disturbance caused by shearing or nearby structures was also considered by Desai and Rigby [96], who formulated an elastoplastic model in the element equations. By further incorporating the DSC and viscoplastic terms into the HISS model, Samtani et al. [97] applied the thin-layer element to simulate the viscoplastic or time-dependent strain behaviour of the interface. Note that the elastic analyses under monotonic loads needed no more than 5 parameters [38,90,91,92], while the plastic analyses through the DSC [94], DSC-HISS [96], and viscoplastic-HISS [97] models involved 7, 14, and 9 parameters, respectively.

However, even though the thin-layer element has attracted lots of research interest, numerical studies based on this element have reported limited samples since 2000. Karabatakis and Hatzigogos [79] formulated an elastic–viscoplastic model to capture the creep behaviour of interfaces, and the thin-layer element [38] and “virtual” thickness element [85] were used through FORTRAN code implementations for comparison. It was revealed that thickness t exerted more pronounced impacts on the creep response in the thin-layer element than in the “virtual” thickness element. The reason was attributed to the only partial contribution of thickness t to the “virtual” thickness element formulation, while for the thin-layer element, thickness t is engaged in the whole formulating process. Qian et al. [73] also performed a comparative study regarding the elastic analysis of concrete-faced rockfill dams (CFRDs), where commonly adopted interface modelling approaches were compared (i.e., the Goodman element, the thin-layer element, and the contact analysis method). The three numerical methods produced similar settlement and horizontal displacement, agreeing well with observed in situ data, although the contact analysis method was considered the best choice when large separation was involved (in this case, the zero-thickness and thin-layer elements were not applicable). Another contribution was made by Saberi et al. [42], who implemented an advanced two-surface elastoplastic model [98] into the ABAQUS thin-layer interface element to incorporate strain softening, dilatancy, particle breakage, and stress degradation (e.g., due to cyclic loading). Numerical applications in the slide block test, shaft pullout test, and CFRDs demonstrated its accuracy and advancement in capturing sophisticated interface behaviour. The numbers of modelling parameters for the above three studies [42,73,79] were 11, 2, and 7, respectively.

3.3. Continuum Element (Solid Element)

Instead of using a specific interface element (which, as previously commented, requires novel or particular element format and constitutive law), conventional continuum elements or “solid” elements also attract research interest in modelling soil–structure interface problems with minor—or even no modification—to the available numerical coding, mesh tool, or regular constitutive models. Griffith [99] proposed a simple interface method to model the slip of the interface, and the continuum element was used without any modification, as it was able to cover the full range of interface behaviour (i.e., perfectly rough to perfectly smooth interfaces were numerically analysed). Pande and Sharma [74] performed a comparative study on modified and normal eight-node continuum elements, where relative displacements were set as independent degrees of freedom in the modified element formulation. They revealed that the two elements gave almost identical results up to a very high aspect ratio (i.e., length/thickness ratio) of 100,000. The use of continuum elements with lower aspect ratios (e.g., up to 5000) could be calculated without creating any numerical problems. As elastic analysis was conducted by both studies, and only a minor calibration of the Young’s modulus and the Poisson’s ratio was required.

Inspired by this continuum element methodology, nonlinear plastic analyses of the interface have also been performed based on an elastic–perfectly plastic material definition for the interfaces [74,99]. Ng et al. [83] examined the performance of an eight-node continuum element by three numerical examples, where the interface was defined as a material based on the classic linear elastic model with the Mohr–Coulomb yield criterion. They found that an aspect ratio of up to 100,000 did not cause numerical issues, which was in accordance with the findings proposed by [74], and recommended an aspect ratio of at least 100 when adopting the conventional continuum element to model soil–structure interface behaviour. The continuum element method has been revealed to be excellent in modelling shearing behaviour, despite it being unable to model explicit separation that may occur at the interface (i.e., physical contact loss). Recent studies by Damians et al. [29,44,45] analysed both soil–facing and soil–reinforcement interfaces for reinforced soil (RE) wall applications, including also calibrated reinforcement pullout responses, through 3D numerical models by using CODE_BRIGHT [89]. The influence of reinforcement types was investigated through examples assuming steel or polymeric-based strips. The interface between soil and steel/polymeric strips was represented by continuum elements with a five-parameter definition for the linear elastic–perfectly plastic Mohr–Coulomb failure criterion. Both pullout and full-scale RE wall models were able to capture typical mechanical behaviour of this type of wall systems, where it is crucial to represent both soil–structure interfaces (i.e., soil–facing and soil–reinforcement).

3.4. Comparison of Zero-Thickness, Thin-Layer, and Continuum/Solid Interface Elements

As aforementioned, the zero-thickness element, thin-layer element, and continuum element primarily compose the finite element (FE) library for the interface modelling scope. The selection of an appropriate numerical method is of great importance to achieve the desired accurate prediction and to reduce computational costs. A summary of the main features of these three interface elements is presented in

Table 4. Summary on the features of three element types for interface modelling.

Element Type	2D Representation	Stress Components	Advantages	Limitations
Zero-thickness element		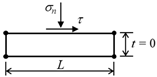Normal stress σn and tangential stress τ	Simple and practicable, commonly available in FE codes, able to model complex shear behaviour	Numerical instability, particular constitutive law, hard to model separation
Thin-layer element		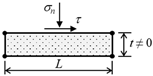Normal stress σn and tangential stress τ	Physical representation, numerical stability, able to model complex shear behaviour	Requiring small thickness (0.01 < t/L < 0.1), particular constitutive law, hard to model separation
Continuum element		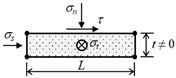Normal stress σn, horizontal stress σs, out-of-plane stress σt, and tangential stress τ	Physical representation, numerical stability, compatible with general constitutive laws	Careful selection of material law and parameters, hard to model separation

(a 2D representation of a four-node element is schematically depicted in each interface element case). The stress components involved, advantages, and limitations of the three elements are also included for comparative purposes based on the relative references which performed comparative analyses on these types of interface elements (i.e., [7,44,73,79,83,94]).

Zhang and Zhang [7] systematically reviewed the numerical approaches of interface modelling and stated that the interface element could be categorised into two types, namely, “shear element” and “entity element”, according to the element’s inherent configuration. The shear element considers only two stress components in the 2D plane (i.e., one is the stress perpendicular to the interface, and the other is the stress tangential to the interface plane), while the entity element possesses a uniform format, like the conventional continuum element (i.e., four stress components for the 2D case, as shown in Table 4). Thus, the zero-thickness element [37,82], the Goodman type with finite thickness [40,41,84], and the “virtual” thickness element [85] might fall into the domain of shear elements, whereas the thin-layer element [38] is an entity element. It is noteworthy that despite having a uniform format, the thin-layer element behaves significantly differently from the continuum element of neighbouring soil. The two normal stress components at the lateral surface (i.e., σ_s and σ_t in Table 4) are ignored due to the small-thickness assumption, indicating that a particular constitutive relationship is required. This is similar to the zero-thickness element, which also incorporates two stress components at the longitudinal or interface plane surface.

In comparison, the zero-thickness element has been usually implemented through surface-to-surface contact in FE platforms (PLAXIS, ABAQUS, CODE_BRIGHT, etc.), where the nodes are acquiescently defined by the neighbouring elements where the interface is in contact. This requires a consistent mesh between the elements on the two sides (i.e., identical mesh length L in Table 4) and appropriate normal stiffness to avoid numerical instability. When using the continuum element, the interface has been treated as an individual entity based on the continuous material concept defined by traditional soil-based constitutive laws. The continuum element has mostly been used with elastic or elastic–perfectly plastic laws like the Mohr–Coulomb or Drucker–Prager criterion (e.g., [29,44,45,82,93]), which is simple and practical. To model the complex shear behaviour of the interface (strain softening, creep, suction dependency, etc.), advanced elastoplastic constitutive models may be used for the continuum element method, but they face the challenges of calibrating the parameters with only direct shear test (or pullout test, in case of soil–reinforcement problems) data available. By absorbing the advantages of both elements (i.e., physical representation of the continuum element and particular constitutive law of the zero-thickness element), the thin-layer element is numerically stable and able to model complicated behaviour once an advanced interface model is adopted, for example, the recent, specially developed elastoplastic constitutive models for interface modelling [100,101,102,103,104,105,106,107], which target different aspects of interface behaviour, such as critical state, boundary surface plasticity, state-dependency, damage, suction and temperature effects, etc. Implementing these advanced material laws into numerical codes may make it possible to model realistic interface behaviour under complex and variable-loading conditions, despite the cost of increasing parameter numbers and calibration difficulty. However, to use the thin-layer element, novel FE implementations should still be fully developed (which is not the case for elements commonly available in commercial software packages), which challenges the user’s knowledge and deep understanding of both geomechanics and numerical computation fields.

Moreover, Qian et al. [73] obtained almost the same CFRD (concrete-faced rockfill dam) settlement with the zero-thickness element and the thin-layer element and recommended using the contact analysis method to model separation, in which case the two interface elements were inapplicable. Damians et al. [44] also revealed that the zero-thickness element and the continuum element achieved quite close results in soil–facing interaction systems when maintaining the same interface shear strength parameters. These findings demonstrated that all the three element types can reasonably model shearing behaviour, even while facing difficulties in modelling debonding or separation. Considerations of the anisotropy or cohesion loss in de-bonding mode may solve this issue for the thin-layer and continuum elements, since they are intrinsically implemented as continuum media. According to Sharma and Desai [94], the thin-layer element could include the zero-thickness element as a special case of thickness t → 0. This idea was later developed by Karabatakis and Hatzigogos [79], in whose work the thin-layer element was regarded as a “flexible” interface element, behaving as either a zero-thickness element or a solid element when the thickness t was relatively small or large, respectively.

It should be noted that there are also some simulation strategies not using interface elements for soil–structure interactions (e.g., [108,109]). For instance, Bagheri et al. [108] assessed the seismic resilience of reinforced concrete (RC) superstructures on long–short combined piled raft foundations by FE modelling. It was found that neglecting the soil–structure interaction underestimates the displacement and drift ratio by up to 48% and 80%, respectively. Patrício et al. [109] emphasised the influence of superstructure and construction stages. Elastic analyses on concrete-wall buildings were performed by calibrating the elastic modulus on field monitoring data. Applying the interface elements to these practical problems is promising and could provide more numerical insights, even though difficulties in linking laboratory-scale observations with actual field-scale implications may be encountered.

3.5. Summary of the Numerical Modelling of Soil–Geosynthetic Interfaces

To summarise, the FE modelling of interfaces has been concentrated on the use of the zero-thickness element, thin-layer element, and continuum element methods. All these three element types are proved to produce acceptable prediction of the interface shear response, yet mainly the zero-thickness element has been subject to ample developments and applications so far, based on the literature search applied in this study. As aforementioned, the following can be concluded for the three elements: (1) Approach availability: The zero-thickness element and the continuum element are available in most FE codes, whereas the use of thin-layer element requires novel formulations during numerical implementation. (2) Element capacity: The continuum element is mostly used to model simple shearing behaviour with elastic or elastic–perfectly plastic laws for solids, while the zero-thickness and thin-layer elements have the potential to model complex interface phenomena when adopting advanced constitutive models particularly designed for interface applications. (3) Calibration difficulty: Model parameters for the zero-thickness and thin-layer elements can be direct calibrated by measured curves from direct shear tests because of the consistency between constitutive and measured variables, while for the continuum element, parameter transformation is needed to conform to its intrinsic constitutive mechanical definition.

4. Concluding Remarks

This work presented an overview of the soil–reinforcement interface direct shear test and numerical modelling. From the experimental and numerical review of the current literature, the following concluding remarks are considered:

(1)

The interaction between poorly graded sand and geogrids/-textile/-membranes has mainly been studied; experimental extension to cohesive soils, gravelly soils, well-graded granular soils, reinforced strips, and other emerging geosynthetic materials is encouraged.

(2)

Test findings on the effects of soil anisotropy and fine content, geosynthetic hardness and aperture, confining stiffness, shear rate and size, temperature, and chemical aspects need to be supplemented to clarify the influencing mechanism within the interface phenomenon.

(3)

Among the three interface elements, the zero-thickness element has undergone the most rapid development and has been employed in wide applications, while the thin-layer element and the continuum element are still young topics with potential development ahead.

(4)

The thin-layer and continuum elements are capable to obtain stress/deformation distribution within the interface, yet they exhibit sensitivity to the selection of numerical modelling parameters.

(5)

The primary constitutive formulations used remain conventional elastic or elastoplastic models; numerical implementations of recently developed bounding surface plasticity, hypo-plasticity, critical state laws, or machine learning-based models should be taken into consideration.

(6)

The zero-thickness and continuum elements are recommended for starters, given their common availability in most commercial software platforms, while researchers pursuing high-accuracy and realistic modelling may refer to thin-layer elements or newly self-developed zero-thickness elements.

This study can provide useful information for the readers aiming to know the state of the art of soil–reinforcement/soil–geotextile interface direct shear tests and related numerical modelling strategies. Studies reported in the literature of the last two decades are highlighted to provide readers with a source for research to which they can refer directly. More importantly, the features of different numerical approaches are elucidated, which can be helpful for the readers to determine the modelling strategy suited for their own needs.