Research on Construction Duration Optimization of High-Rise Residential Buildings Based on an Integrated Platform

Abstract

The integrated platform provides a safe operating environment for high-rise residential construction and enables the simultaneous advancement of main structural works and facade operations. However, the construction workflow based on an integrated platform is highly complex, with tightly interlinked processes, making construction duration optimization an urgent issue. Focusing on the construction characteristics of the integrated platform for facade operations and the coordinated execution of structural and facade works, this study investigates the problem of construction duration optimization. With the objective of minimizing the overall construction period, the logical relationships among various processes are systematically sorted out, and a mathematical optimization model is established that considers precedence constraints, overlapping relationships, and labor resource conditions. By introducing a genetic algorithm, the optimal construction scheme under the shortest possible duration is obtained. An empirical analysis based on an actual engineering project demonstrates that the construction cycle of a standard floor was shortened from the original 6 days to 5 days, effectively reducing technical interruptions on site and lowering labor resource demand by 10–15%. This improvement enhances lean construction performance at the project level. The research results provide theoretical support and methodological reference for construction duration optimization using integrated construction equipment and hold significant engineering value and practical significance for promoting the digitalization, systematization, and efficiency of building construction.

1. Introduction

1.1. Background

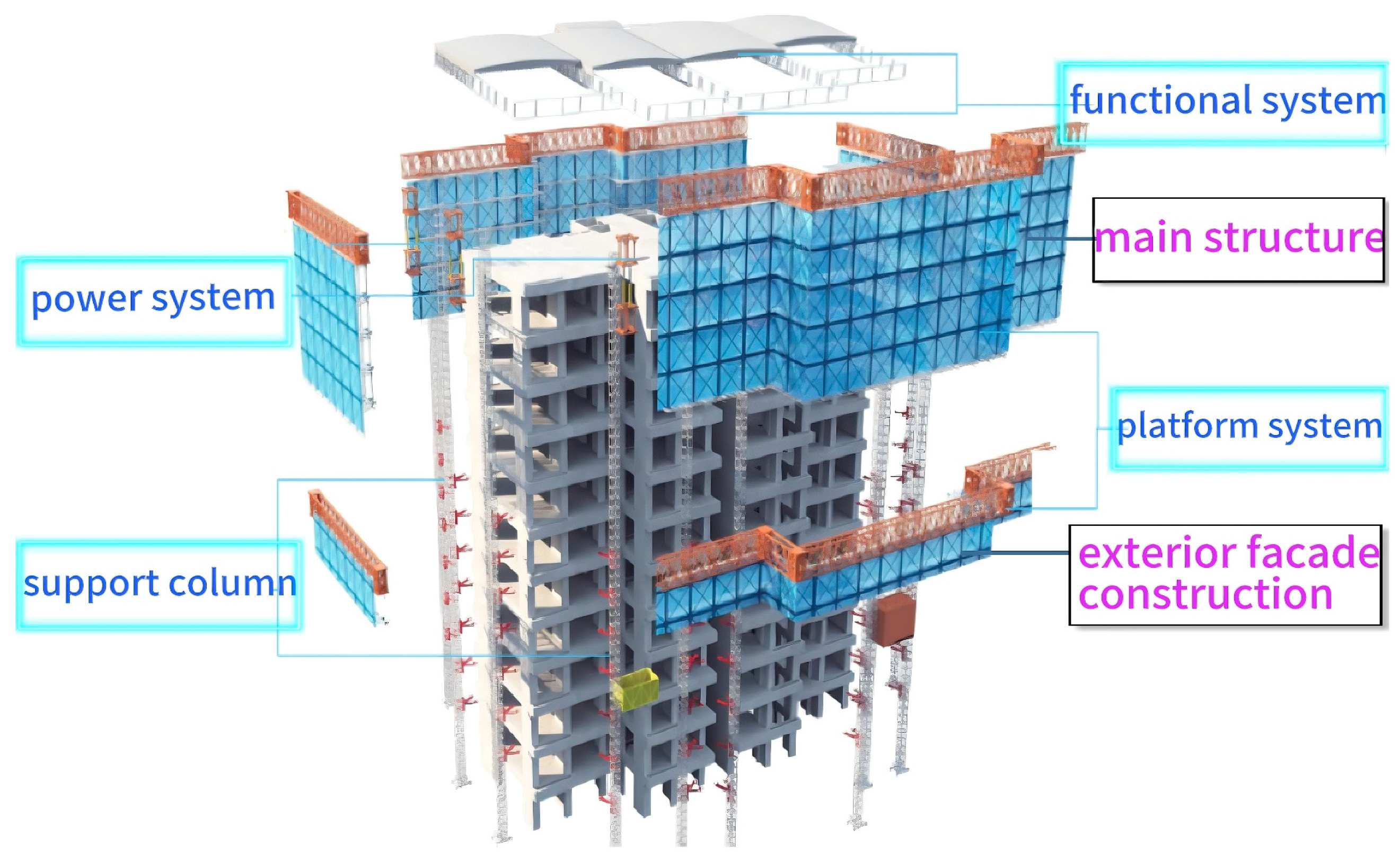
With the rapid increase in the number of high-rise and super high-rise buildings in China, the demand for efficient, safe, and intelligent construction equipment on job sites has grown significantly. Traditional scaffolding systems and single-platform integrated platforms are increasingly unable to meet the requirements of modern construction industrialization in terms of efficiency, space utilization, and safety assurance. The traditional single-platform integrated system is characterized by having only one lifting platform, where construction activities are carried out sequentially on the same level, resulting in a relatively simple workflow. Although this approach features a straightforward structure and intuitive management, it has notable limitations. In contrast, the dual-platform integrated system is equipped with two vertically arranged platforms that can operate independently within the same lifting system, enabling spatial separation and temporal overlap of structural and facade operations. The upper platform is primarily responsible for main structural construction, while the lower platform is used for facade operations, thereby achieving concurrent progress of structural works and facade installation. The system consists of four major components: the supporting system, power system, platform system, and functional system, collectively creating a factory-like construction environment on site. By coordinating two simultaneous workfaces, the dual-platform system transforms traditional high-altitude operations into standardized, factory-style production. Compared with conventional single-platform systems used in high-rise construction, it offers significant advantages in construction efficiency, safety, adaptability, and intelligent operation. The construction diagram of the dual-platform integrated platform is shown in Figure 1.

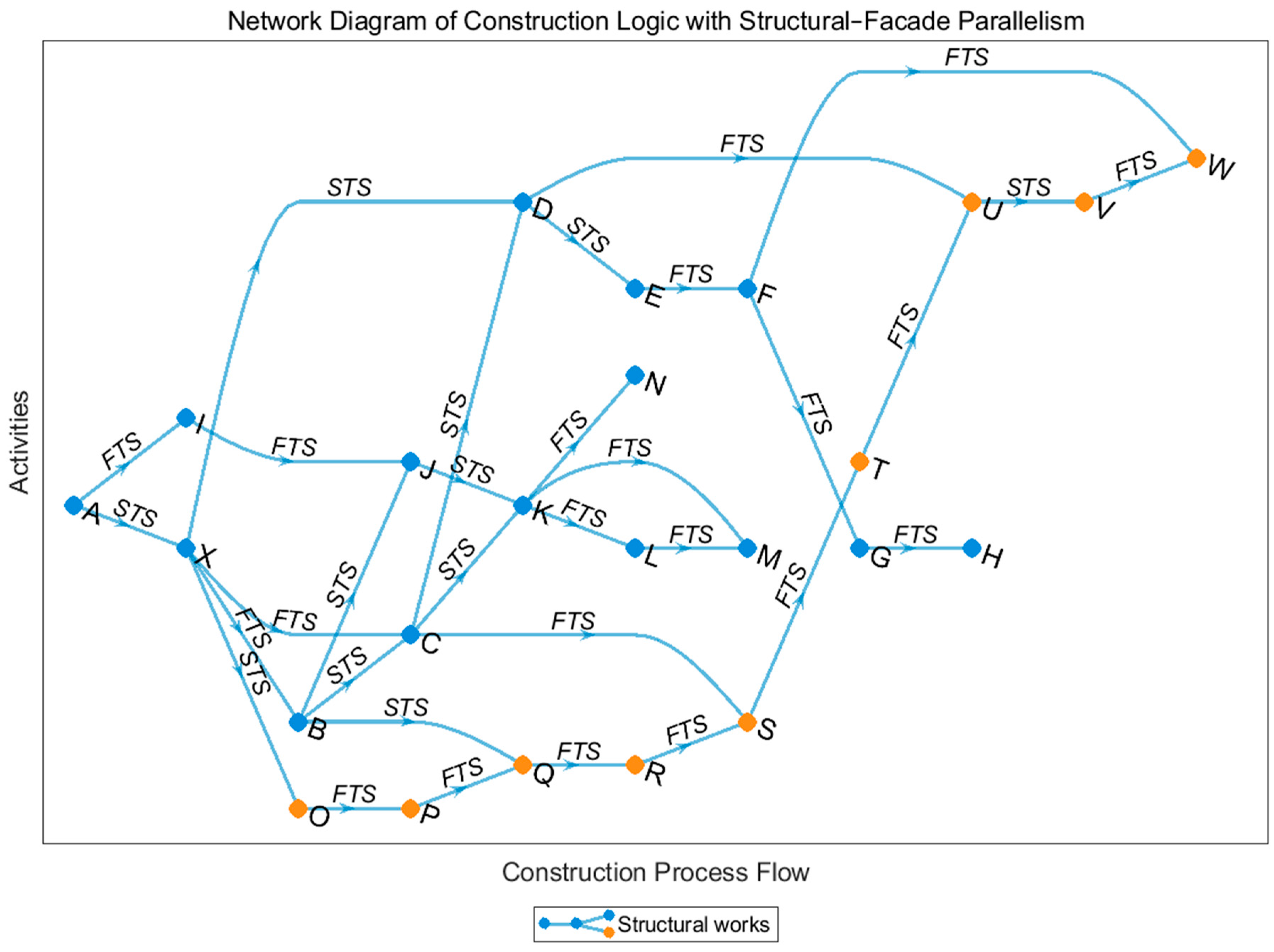
However, in actual engineering projects, the construction process of dual-platform integrated systems still largely follows the traditional serial-oriented approach, resulting in poor coordination between the two platforms. Currently, how to achieve optimized construction scheduling under multi-platform collaborative conditions has become a critical issue in high-rise construction management. Traditional schedules typically treat each “floor” as a single construction unit, overlooking the parallelism and interleaving relationships both between floors and within each floor. Meanwhile, the lack of precise temporal and spatial coordination between structural works and facade operations leads to process interruptions and resource waste. With the development of intelligent algorithms, construction schedule optimization based on genetic algorithms has gradually become an important method for improving construction organization efficiency.

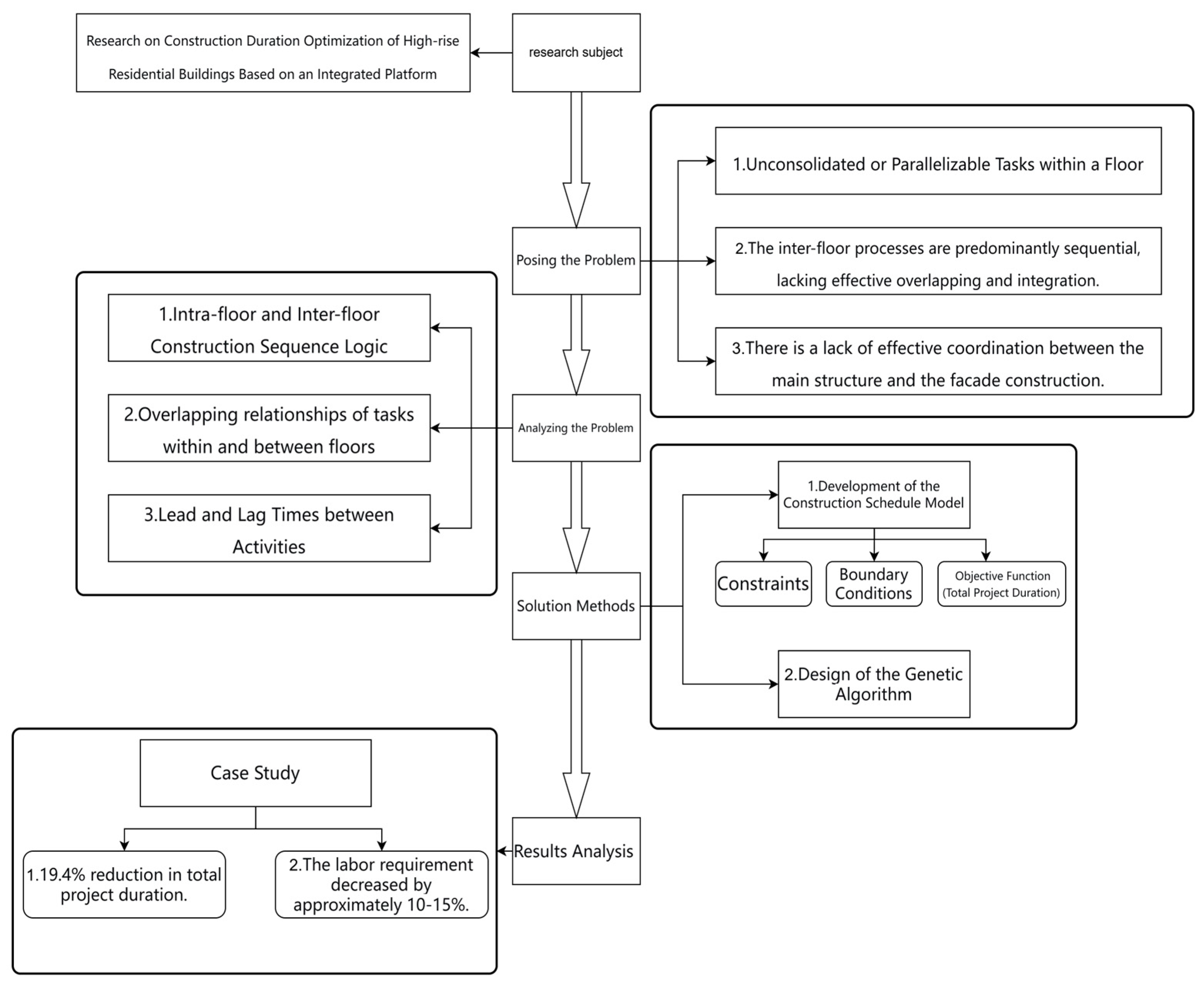
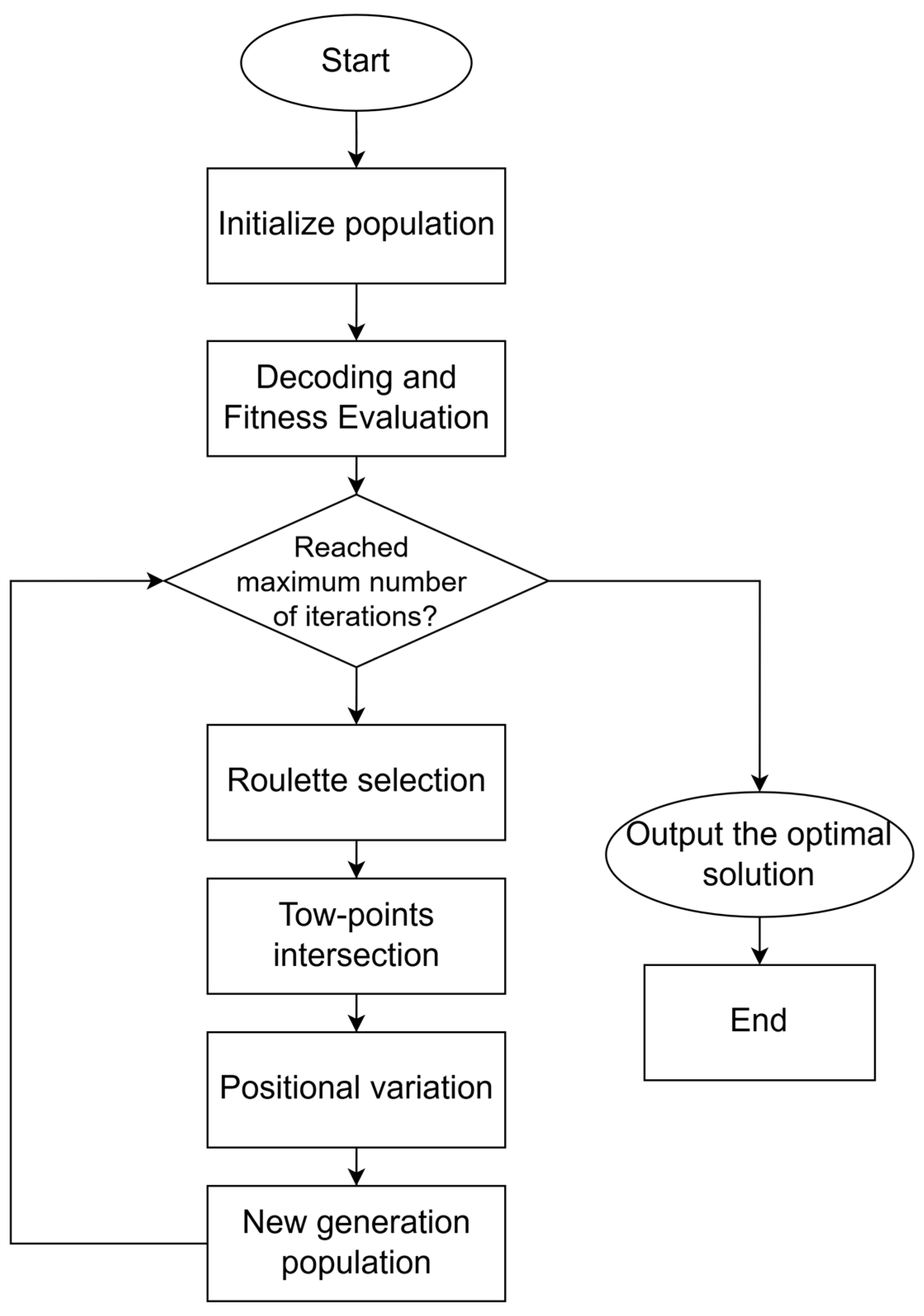
This study focuses on the construction duration of high-rise residential buildings using an integrated platform and investigates duration optimization issues for standard floors. A genetic-algorithm-based mathematical model is developed to optimize the construction schedule. By analyzing the logical relationships, overlapping conditions, and time-lag constraints among construction activities, an optimization objective function is formulated and solved to obtain the optimal schedule. The research aims to promote coordinated progress between structural and facade operations, enhance resource utilization efficiency of the integrated platform, and provide both theoretical support and practical guidance for construction schedule optimization in high-rise buildings.

1.2. Literature Review

In the field of construction project management, time optimization has long been a central research topic. As project scales grow and construction processes become more complex, traditional methods such as the Critical Path Method (CPM) and Linear Planning Method (LPM) are increasingly unable to meet optimal scheduling requirements under multiple constraints. ElSahly [1] conducted a systematic review of time–cost optimization models in construction management, categorizing existing research into exact algorithms, approximate algorithms, and hybrid intelligent algorithms, and noting that exact algorithms suffer from low computational efficiency, whereas intelligent algorithms perform better in large-scale problems. Warne [2] addressed large-scale time–cost trade-off problems using genetic algorithms, demonstrating the computational efficiency and accuracy of metaheuristic approaches in complex project networks and highlighting the advantages of GA for rapid optimization. Liu [3] proposed a Discrete Symbiotic Organisms Search (DSOS) algorithm to solve large-scale TCTP problems, further illustrating that traditional mathematical methods struggle to deal with nonlinear relationships between project duration and cost. Overall, research on time optimization has evolved from deterministic models to stochastic/fuzzy models and, more recently, to intelligent optimization models, with optimization objectives shifting from simple duration minimization toward multi-objective balancing.

Among the major models and methods for duration optimization, the time–cost trade-off (TCT) problem is one of the earliest systematically studied. Warne developed a large-scale TCT model using genetic algorithms, achieving high-precision optimization across 630 activity variables and demonstrating the strong parallel computing capability and robustness of GA. Turkoglu and Arditi [4] further proposed a multi-objective TCT model based on particle swarm optimization (PSO), integrating project duration, cost, resource fluctuations, and quality into a unified framework, which significantly advanced the development of multi-objective scheduling optimization. In recent years, multi-objective optimization has become increasingly comprehensive. For example, Yuan Zhenmin [5] introduced a multi-objective optimization method for prefabricated buildings that combines ECRS techniques with intelligent simulation, simultaneously considering time, cost, quality, and CO₂ emissions, while addressing uncertainties such as material supply and weather conditions to achieve holistic trade-offs among performance objectives. Elbeltagi [6] developed an integrated multi-objective optimization model encompassing time, cost, resources, and cash flow and applied particle swarm optimization (PSO) together with Pareto trade-off strategies to achieve unified scheduling under multiple decision criteria. These studies demonstrate that high-dimensional, multi-objective collaborative optimization has become a mainstream direction in large-scale engineering projects. Tran [7] introduced a Multi-Objective Social Group Optimization (MOSGO) algorithm, generating time–cost trade-off curves through a multi-criteria decision-making mechanism to provide efficient solutions for complex projects. Huang [8] developed an uncertainty-informed time–cost optimization model for high-rise buildings based on the NSGA-II algorithm, integrating Monte Carlo simulation with GA to enhance convergence accuracy under uncertain conditions. These studies collectively promote the TCT model toward a more intelligent direction involving multi-constraint and multi-factor coordination.

In complex construction systems, resource constraints are a critical factor limiting schedule optimization. Gonçalves [9] proposed a Biased Random-Key Genetic Algorithm (BRKGA) to solve RCPSP problems and introduced a forward–backward improvement mechanism that significantly enhances search efficiency. Chen and Lee [10] developed a hybrid genetic algorithm (HGA) for solving multi-mode resource-constrained multi-project scheduling problems (MMRCMPSPs), outperforming traditional GA approaches, particularly in highly complex projects. Damci [11] further examined the problem from the perspective of resource leveling and systematically compared the performance of nine different resource-leveling objective functions in a real steel structure project. The study showed that different objective functions produce different resource histograms and that the optimal objective function is project-dependent. Therefore, contractors need to select an appropriate resource-leveling criterion based on the specific characteristics of the project. Abdel-Basset [12] introduced a heuristic priority-rule scheduling model (PHR) for uncertain environments that can dynamically respond to fluctuations in resource availability. Xie et al. [13] established an integrated scheduling model for multi-mode construction in prefabricated buildings, coordinating component supply and onsite installation to achieve joint optimization of resource constraints and duration minimization. These findings suggest that future research on time optimization should focus more on resource sharing, synchronized construction, and supply-chain coordination.

In studies on construction duration optimization based on intelligent algorithms, methods such as genetic algorithms (GAs), particle swarm optimization (PSO), and ant colony optimization (ACO) have been widely applied due to advancements in artificial intelligence. Among them, GA is most widely used owing to its strong global search capability and robust parameter performance. Yoonseok Shin [14] proposed a hybrid model combining simulation and a genetic algorithm (GA) to achieve the optimal arrangement of temporary hoists in high-rise building construction. This approach overcomes the limitations of traditional formula-based methods, which struggle with multiple hoist combinations and the high time cost of pure simulation methods. In real projects, it produced results superior to conventional approaches, demonstrating the strong adaptability of GA in equipment scheduling. Fan Zesen [15] applied GA to the automated layout of high-rise modular residential buildings, enabling the automatic generation of module units and core circulation arrangements. This study broadened the application boundary of GA in design-oriented architectural optimization and demonstrated its advantages in handling complex combinatorial search spaces. Faghihi [16], using BIM, proposed a GA-based automatic generation method for construction sequences that ensures structural safety through stability constraints. Razavi-Alavi [17] integrated GA with simulation frameworks to optimize site layout and scheduling simultaneously, achieving dual coordination of construction resources and onsite space. Xie [18] developed a GA optimization model that accounts for resource constraints and component supply, significantly shortening the construction duration. Hu [19] combined GA and PSO to form a hybrid GA–PSO model that outperforms single algorithms by 4–8%, demonstrating the superiority of hybrid intelligent approaches. Overall, GA has become one of the core algorithms in construction duration optimization.

In recent years, the integration of Building Information Modeling (BIM) with intelligent algorithms has provided data support and dynamic visualization capabilities for schedule optimization. Wefki [20] constructed an integrated BIM–GA–5D simulation framework enabling automated schedule optimization and visual feedback. Yang [21] proposed a BIM-based automated construction site layout planning method that leverages GA and PSO to reduce transportation time and cost. Essam [22] further developed a BIM-based multi-objective optimization model to coordinate time, cost, and resource utilization. However, existing studies mainly focus on planar workflow scheduling or single-scenario optimization, with limited attention to spatiotemporal collaborative optimization involving multiple workspaces and parallelized tasks under integrated platform conditions. A dynamic optimization mechanism tailored for dual-platform vertical construction systems remains lacking.

As modular construction becomes a key direction of construction industrialization, its schedule optimization challenges have become increasingly prominent. Thai [23] reviewed modular high-rise systems and connection technologies, highlighting their rapid construction and standardization advantages, which form the technical basis for duration optimization. Lee [24] applied GA to schedule multi-module building projects, achieving integrated optimization of module production, transportation, and installation and significantly shortening overall duration. Yuan [25] introduced fuzzy theory and a Hybrid Cooperative Evolutionary Algorithm (HCOEA) to enhance the robustness of prefabricated building scheduling under uncertainty. Xu [26] achieved automated optimization of prefabricated component production using GA and IFC models, improving integration between offsite manufacturing and onsite assembly. These studies offer valuable insights for schedule optimization in industrialized construction.

Modern building project optimization objectives now extend beyond time alone. He Wei [27] developed a multi-objective time–cost–energy consumption model and used principal component analysis to reveal correlations among the three factors. Wang [28] built a four-objective model incorporating time, cost, quality, and carbon emissions and applied ACO to obtain Pareto-optimal solutions, enabling coordination between green construction and scheduling. Ekici [29] and Faghihi [30] explored multi-objective balance in sustainable high-rise construction from artificial intelligence and Pareto-front perspectives, providing theoretical foundations for future intelligent scheduling. Collectively, these studies illustrate that time optimization is evolving toward intelligent, low-carbon, and collaborative directions.

Compared with previous studies, this research does not limit its focus to scheduling optimization for a single task or a single platform. Wang Shuqiang et al. [31] optimized the process path of a single-platform building integration platform to explore and study the best construction results in order to save construction time and improve efficiency, thereby minimizing construction time. Instead, it is based on a dual-platform integrated construction system and comprehensively analyzes the logical relationships, overlapping activities, and time-lag constraints between structural works and facade operations. A construction duration optimization model under multiple constraints is established. By introducing a genetic algorithm, this study enables global search and intelligent optimization of the construction process and develops an optimization model with project duration minimization as the objective function, thereby obtaining the optimal construction schedule.

The main innovations of this study are as follows:

(1) It breaks away from the traditional single-platform serial construction approach by treating structural and facade construction as a dynamic collaborative system. Through an analysis of their spatiotemporal relationships, this study achieves synchronized progress between the upper and lower platforms.

(2) It develops a multi-constraint optimization model that simultaneously considers logical constraints, resource constraints, platform load-bearing constraints, and other influencing factors, thus significantly enhancing the model’s practical applicability. It applies a genetic algorithm to obtain solutions, achieving global optimization and dynamic adjustment of the construction schedule, which greatly improves construction efficiency.

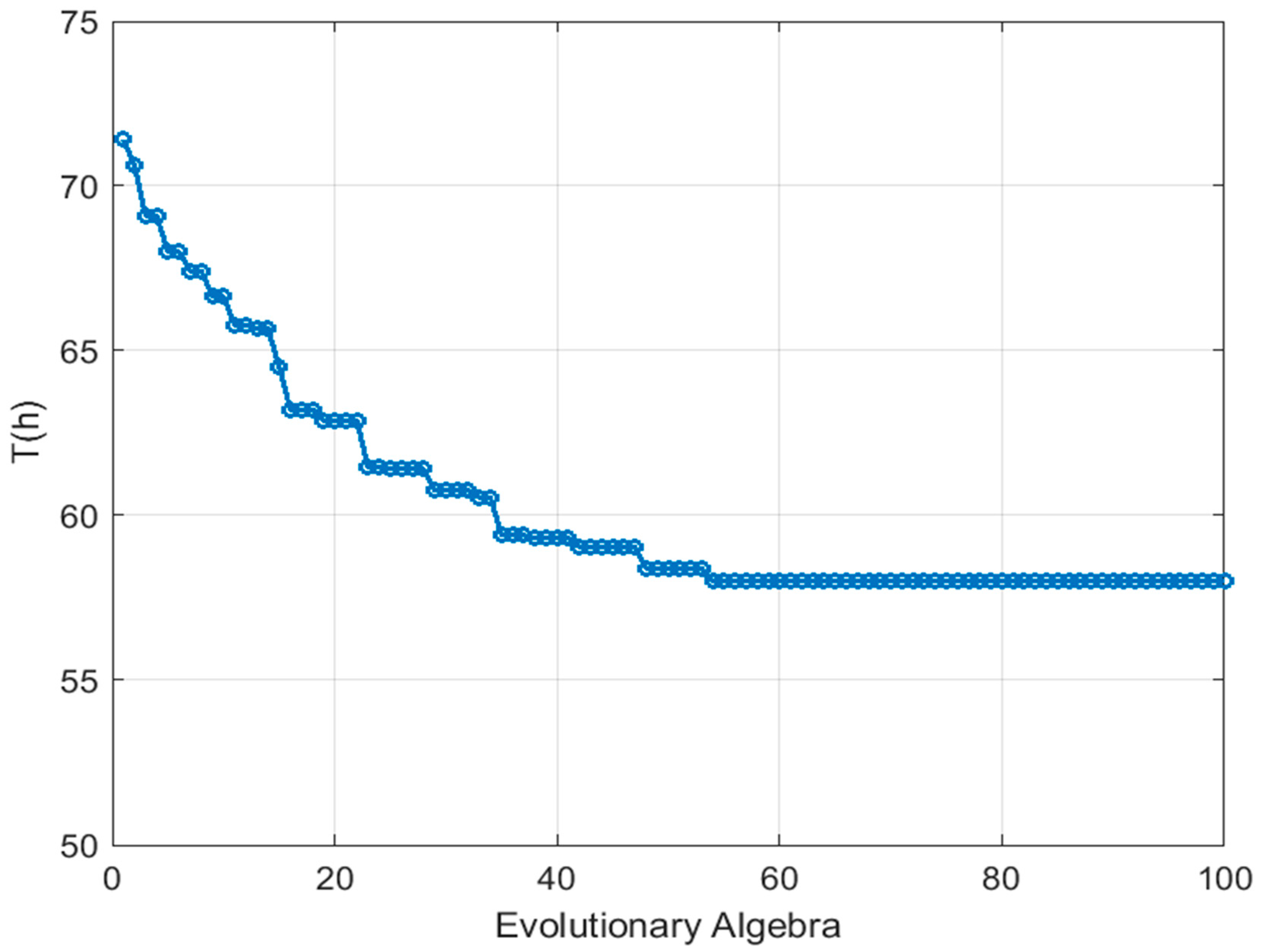
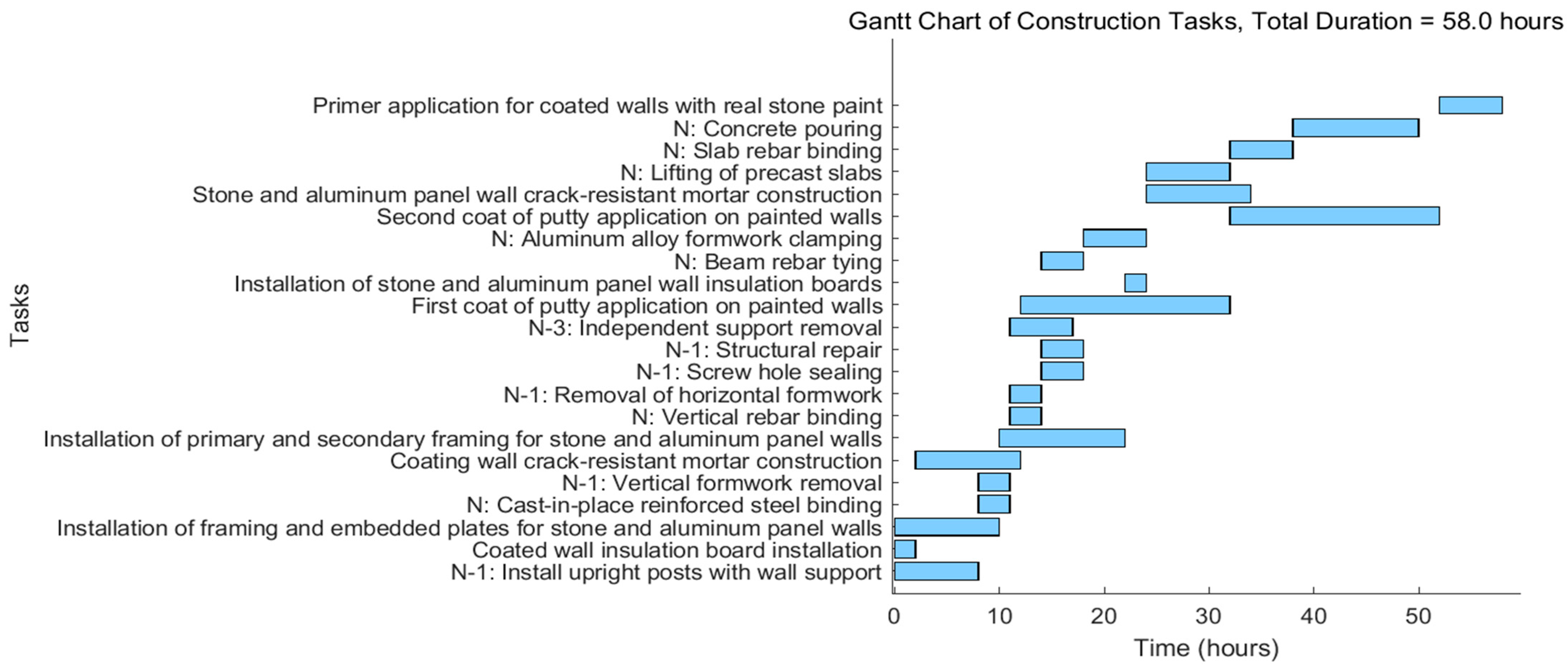
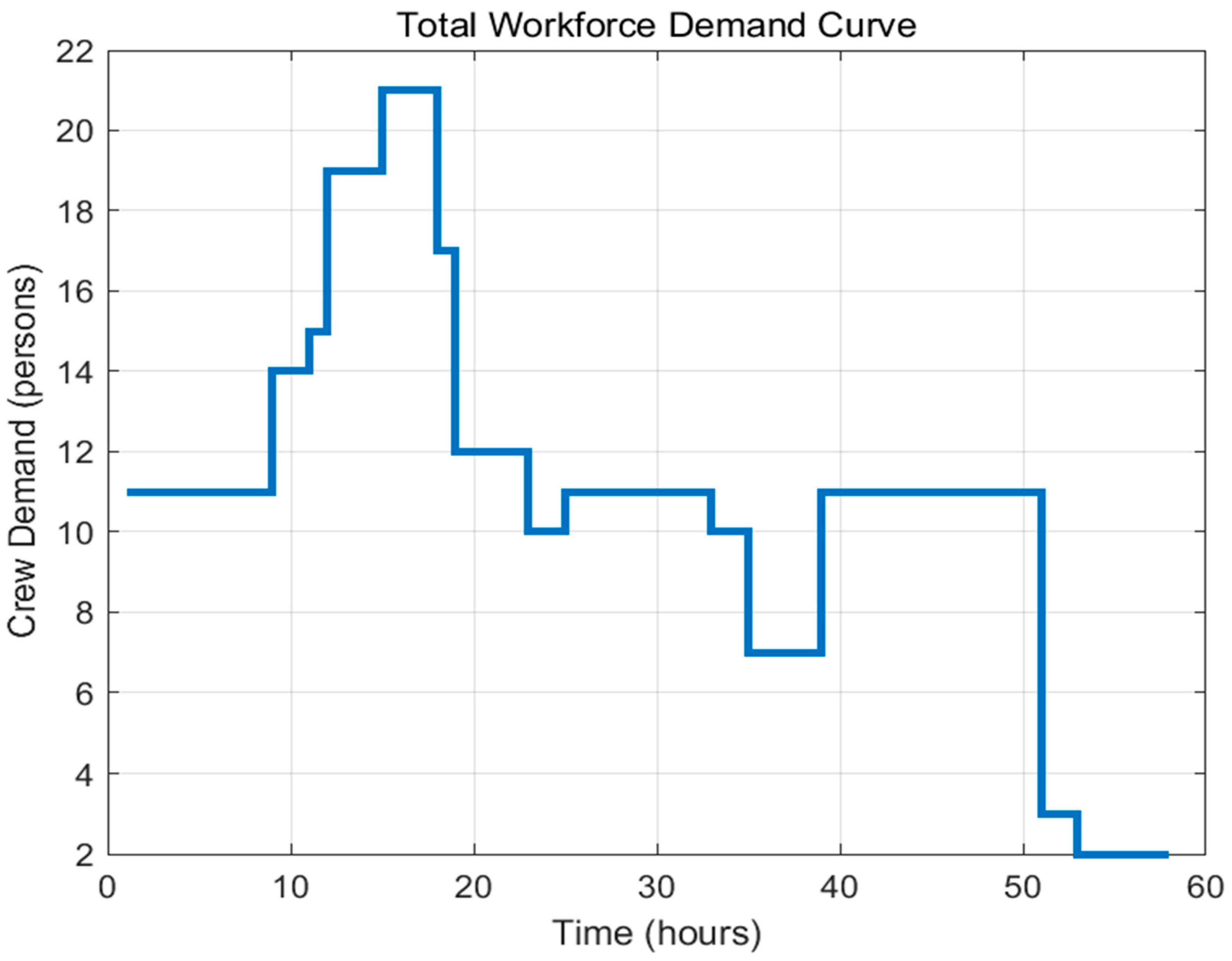
The results of the optimization model and simulation analysis show that, while shortening the construction duration, labor resource input is also effectively reduced, construction organization becomes more balanced and efficient, and platform utilization is significantly improved. This research not only fills the gap in previous studies regarding collaborative optimization for integrated platform operations but also provides a new technical pathway and theoretical foundation for intelligent scheduling and duration management in high-rise residential construction.

2. Methods

2.1. Definition of the Problem

This study takes the construction duration of high-rise residential buildings using an integrated platform as its research focus and investigates optimization strategies for integrated-platform construction schedules. The technology roadmap is shown in Figure 2.

In practical engineering applications, however, traditional integrated platform construction schemes rely heavily on empirical experience and are still predominantly based on serial operations. For example, main structural construction typically follows a sequence such as concrete pouring–waiting rebar–tying–formwork installation–precast slab hoisting–second concrete pouring. Facade construction is often disconnected from the structural works, lacking effective interleaving and parallel arrangements. As a result, equipment and labor experience extended idle periods, process constraints are not sufficiently detailed, and the advantages of the integrated platform cannot be fully realized. This study first analyzes the shortcomings of traditional construction schemes and then examines the logical precedence relationships and adjustable dependencies within the integrated-platform construction process. It further investigates the overlapping time constraints between activities. Finally, under the condition of meeting minimum labor requirements, a mathematical model is developed with the objective of minimizing the overall construction duration. A genetic algorithm is employed to search for the optimal construction schedule, thereby achieving the shortest possible project duration.

2.2. Logical Relationship Analysis

By analyzing the construction tasks performed in each operating state of the integrated platform, a deeper understanding of its workflow can be achieved, which facilitates the analysis of the logical sequence among construction procedures. The construction workflow diagram is shown in

Table 1. The construction workflow diagram.

Status of the Integrated Platform	Work Content: Main Structure	Work Content: Facade (Floors N-5)
State 1: Initial State	Concrete pour on N-1 complete; pending rebar work on upper floor.	Coated wall insulation board installation;
		Installation of framing and embedded plates for stone and aluminum panel walls.
State 2: Ready to Lift	N-1: Installation of wall-connected columns;	Coating wall crack-resistant mortar construction;
	Column: Section addition;	Installation of primary and secondary framing for stone and aluminum panel walls.
	At the column: Catwalk panels flipped up, and flip-up plates raised in preparation for jacking.
State 3: Lifting State	Rack: Close the walkway panels at the columns, lower the flip panels to seal.
State 4: Operation Status	N: Cast-in-place reinforced steel binding;	First coat of putty application on painted walls;
	N: Vertical rebar binding;	Installation of stone and aluminum panel wall insulation boards.
	N: Beam rebar tying;
	N: Aluminum alloy formwork clamping.
State 5: Resting State 1	N: Lifting of precast slabs;	Second coat of putty application on painted walls;
	N: Slab rebar binding;	Stone and aluminum panel wall crack-resistant mortar construction.
	N: Concrete pouring.
Resting State 2	N-1: Vertical formwork removal;	Primer application for coated walls with real stone paint.
	N-1: Removal of horizontal formwork;
	N-1: Screw hole sealing;
	N-1: Structural repair.
Resting State 3	N-2: Waterproof mortar construction.

.

Based on the analysis of the construction tasks described above, the work contents of each operating state of the integrated climbing platform are clearly understood. The logical sequence of construction procedures is analyzed from the following two aspects:

(1) Analysis of the logical sequence of construction procedures within each structural floor

Rebar tying of floor N is the prerequisite for in situ rebar tying of floor N; in situ rebar tying of floor N is the prerequisite for vertical rebar tying of floor N; vertical rebar tying of floor N is the prerequisite for beam rebar tying of floor N; beam rebar tying of floor N is the prerequisite for aluminum formwork assembly of floor N. Subsequently, the following operations are carried out: precast composite slab installation for floor N, slab rebar tying for floor N, and concrete pouring for floor N.

After concrete pouring is completed on floor N–1 and the required strength is reached, vertical formwork removal on floor N–1 can be performed; this is followed by horizontal formwork removal, tie-hole grouting, and structural patching.

The construction task on floor N–2 is waterproof mortar application.

On floor N–5, exterior insulation panel installation for painted facades is carried out first, which serves as the prerequisite for embedded bracket installation of stone/aluminum panel facades. The subsequent operations include anti-cracking mortar application for painted facades on floor N–5, installation of primary and secondary facade brackets for stone/aluminum panels, first putty application for painted facades, installation of insulation panels for stone/aluminum facades, second putty application for painted facades, anti-cracking mortar application for stone/aluminum facades, and finally, primer application for textured coatings on painted facades.

(2) Analysis of the logical sequence of construction procedures between structural floors

After concrete pouring is completed on floor N–1 and the required strength is achieved, rebar tying of floor N may begin. The prerequisites for vertical formwork removal on floor N–1 include both the concrete strength achievement on floor N–1 and the completion of rebar tying on floor N.

In summary, the logical flow of construction procedures for the standard floors of both the main structure and facade works can be obtained as shown in

Table 2. The sequential logical relationship between the construction of the main structure and the standard floor construction of the exterior facade.

Structural Layer	Number	Process Name	Preceding Process
N floors	A	N: Structural steel reinforcement tying	/
	B	N: Cast-in-place reinforced steel binding	A, X
	C	N: Vertical rebar binding	B
	D	N: Beam rebar tying	C
	E	N: Aluminum alloy formwork clamping	D
	F	N: Lifting of precast slabs	D,E
	G	N: Slab rebar binding	F
	H	N: Concrete pouring	F,G
N-1 floors	I	N-1: Install upright posts with wall support	A
	J	N-1: Vertical formwork removal	I
	K	N-1: Removal of horizontal formwork	I,J
	L	N-1: Screw hole sealing	K
	M	N-1: Structural repair	K
N-2 floors	N	N-2: Waterproof mortar construction	K
N-5 floors	O	N-5: Coated wall insulation board installation	X
	P	N-5: Installation of framing and embedded plates for stone and aluminum panel walls	O
	Q	N-5: Coating wall crack-resistant mortar construction	P
	R	N-5: Installation of primary and secondary framing for stone and aluminum panel walls	Q
	S	N-5: First coat of putty application on painted walls	R
	T	N-5: Installation of stone and aluminum panel wall insulation boards	S
	U	N-5: Second coat of putty application on painted walls	S,T
	V	N-5: Stone and aluminum panel wall crack-resistant mortar construction	T,V
	W	N-5: Primer application for coated walls with real stone paint	U,V
	X	Integrated platform jacking	A, I

.

In network planning techniques, four basic types of activity precedence relationships are commonly used: Finish-to-Start (FTS), Start-to-Start (STS), Finish-to-Finish (FTF), and Start-to-Finish (STF).

Based on the earlier analysis of construction procedure sequences, the next step is to further examine the overlapping relationships between activities, identify their specific precedence types, and determine which relationships can be adjusted. The analysis is conducted from two perspectives: within the same structural floor and between different floors.

(1) Analysis of work-overlap relationships within a structural floor

After concrete pouring is completed on floor N–1 and while waiting for rebar tying on floor N, the integrated platform is lifted. Since rebar tying on floor N does not interfere with platform lifting, these two operations can proceed simultaneously; thus, the relationship between them is STS. Only after the platform has been lifted can the following operations on floor N be carried out: in situ slab rebar tying, vertical rebar tying, and beam rebar tying. Therefore, the relationship between platform lifting and each of these three tasks is FTS. These three tasks may start concurrently, meaning that the relationships among them are STS. The subsequent operations—formwork assembly, precast slab installation, slab rebar tying, and concrete pouring—must each begin only after the preceding operation is completed; therefore, all of these are FTS relationships. The detailed work-overlap logic within floor N is shown in

Table 3. The detailed work-overlap logic within floor N.

Process	Process Number	Lapping Work	Overlapping Logical Relationships
N: Structural steel reinforcement tying	A	X	STS
Integrated platform jacking	X	B	FTS
		C	FTS
		D	FTS
N: Cast-in-place reinforced steel binding	B	C	STS
N: Vertical rebar binding	C	D	STS
N: Beam rebar tying	D	E	FTS
N: Aluminum alloy formwork clamping	E	F	FTS
N: Lifting of precast slabs	F	G	FTS
N: Slab rebar binding	G	H	FTS
N: Concrete pouring	H	/	/

.

The vertical formwork on floor N–1 can only be installed after the column bracing is completed, which corresponds to an FTS (Finish-to-Start) relationship. The tie-rod hole sealing and structural patching on floor N–1 must begin only after the horizontal formwork has been removed; therefore, both tasks have an FTS relationship with the horizontal formwork removal. Since tie-rod hole sealing and structural patching can be carried out simultaneously, the relationship between these two tasks is STS (Start-to-Start). The detailed work-overlap logic within floor N–1 is shown in

Table 4. The detailed work-overlap logic within floor N–1.

Process	Process Number	Lapping Work	Overlapping Logical Relationships
N-1: Install upright posts with wall support	I	J	FTS
N-1: Vertical formwork removal	J	K	FTS
N-1: Removal of horizontal formwork	K	L	FTS
		M	FTS
N-1: Screw hole sealing	L	M	STS
N-1: Structural repair	M	/	/

.

Floor N–5 is designated for exterior facade finishing works. Since the logical relationships among its procedures are predominantly sequential, they follow FTS (Finish-to-Start) dependencies. The detailed work-overlap logic within floor N–5 is shown in

Table 5. The detailed work-overlap logic within floor N–5.

Process	Process Number	Lapping Work	Overlapping Logical Relationships
N-5: Coated wall insulation board installation	O	P	FTS
N-5: Installation of framing and embedded plates for stone and aluminum panel walls	P	Q	FTS
N-5: Coating wall crack-resistant mortar construction	Q	R	FTS
N-5: Installation of primary and secondary framing for stone and aluminum panel walls	R	S	FTS
N-5: First coat of putty application on painted walls	S	T	FTS
N-5: Installation of stone and aluminum panel wall insulation boards	T	U	FTS
N-5: Second coat of putty application on painted walls	U	V	FTS
N-5: Stone and aluminum panel wall crack-resistant mortar construction	V	W	FTS
N-5: Primer application for coated walls with real stone paint	W	/	/

.

(2) Analysis of Work-Overlap Relationships Between Structural Floors

Based on the three core factors—structural load-transfer logic, construction safety, and process coordination—the installation of column supports on floor N–1 must be carried out only after the rebar binding of the Nth-floor structural components is completed, forming an FTS (Finish-to-Start) relationship. The rebar binding of vertical components on floor N, the removal of vertical formwork on floor N–1, and the application of crack-resistant mortar on the coating facade at floor N–5 do not interfere with one another and therefore can be performed simultaneously, indicating an STS (Start-to-Start) relationship. The vertical rebar binding on floor N, the removal of horizontal formwork on floor N–1, and the first coat of putty on the coating facade at floor N–5 is located on different floors and do not affect each other, meaning they can also proceed simultaneously—an STS relationship. Similarly, the rebar binding of beams on floor N and the second coat of putty on the coating facade at floor N–5 belong to the structural and finishing stages, respectively, and their relationship is STS. By the same reasoning, the installation of composite slabs on floor N and the application of primer for the real-stone coating on floor N–5 also form an STS relationship. Performing the waterproof mortar construction on floor N–2 only after the horizontal formwork removal on floor N–1 is essential to ensuring structural quality, construction safety, and coordination between processes; therefore, these two operations follow an FTS relationship. The lifting of the integrated platform and the installation of insulation boards for the coating facade on floor N–5 can occur simultaneously, forming an STS relationship. The detailed analysis of the inter-floor work-overlap relationships for the structural layers is shown in

Table 6. The detailed analysis of the inter-floor work-overlap relationships for the structural layers.

Process	Process Number	Lapping Work	Overlapping Logical Relationships
N: Structural steel reinforcement tying	A	I	FST
N: Cast-in-place reinforced steel binding	B	J	STS
		Q	STS
N: Vertical rebar binding	C	K	STS
		S	STS
N: Beam rebar tying	D	U	STS
N: Aluminum alloy formwork clamping	E	/	/
N: Lifting of precast slabs	F	W	STS
N: Slab rebar binding	G	/	/
N: Concrete pouring	H	/	/
N-1: Install upright posts with wall support	I	/	/
N-1: Vertical formwork removal	J	/	/
N-1: Removal of horizontal formwork	K	N	FTS
N-1: Screw hole sealing	L	/	/
N-1: Structural repair	M	/	/
N-2: Waterproof mortar construction	N	/	/
N-5: Coated wall insulation board installation	O	/	/
N-5: Installation of framing and embedded plates for stone and aluminum panel walls	P	/	/
N-5: Coating wall crack-resistant mortar construction	Q	/	/
N-5: Installation of primary and secondary framing for stone and aluminum panel walls	R	/	/
N-5: First coat of putty application on painted walls	S	/	/
N-5: Installation of stone and aluminum panel wall insulation boards	T	/	/
N-5: Second coat of putty application on painted walls	U	/	/
N-5: Stone and aluminum panel wall crack-resistant mortar construction	V	/	/
N-5: Primer application for coated walls with real stone paint	W	/	/
N: Concrete pouring	X	O	STS

.

(3) Time-Lag Constraints Between Construction Activities

In the construction process using the dual-platform building machine, the minimum time lag and maximum time lag are the key parameters governing the logical relationships between activities. The minimum time lag refers to the shortest waiting time required after the predecessor activity is completed before the successor activity can start or finish. The maximum time lag refers to the longest allowable delay after the predecessor activity is completed before the successor activity must start or finish. The minimum time lag represents the boundary of technical feasibility, while the maximum time lag represents the boundary of managerial effectiveness. Together, they define the “time corridor” for activity scheduling, within which resource balancing must be achieved during dual-platform building-machine construction.

Based on the above analysis of activity-overlap relationships and on-site construction data, the time-lag constraints for the activities within and between structural floors are determined as shown in

Table 7. The time-lag constraints for the activities within and between structural floors.

Process Number	Lapping Work	Overlapping Logical Relationships	${\mathbf{\delta }}_{\mathbf{i}\mathbf{j}}^{\mathbf{m}\mathbf{i}\mathbf{n}}$/h	${\mathbf{\delta }}_{\mathbf{i}\mathbf{j}}^{\mathbf{m}\mathbf{a}\mathbf{x}}$/h
A	I	FTS	0	24
A	X	STS	0	/
X	B	FTS	0	/
X	C	FTS	0	/
X	D	FTS	0	/
X	O	STS	0	/
B	C	STS	0	12
B	J	STS	0	/
B	Q	STS	0	/
C	D	STS	0	12
C	K	STS	0	/
C	S	STS	0	/
D	E	FTS	12	48
D	U	STS	0	/
E	F	FTS	4	24
F	G	FTS	0	24
F	W	STS	0	/
G	H	FTS	0	4
I	J	FTS	0	/
J	K	FTS	0	12
K	L	FTS	0	/
K	M	FTS	0	/
K	N	FTS	0	/
L	M	STS	0	24
O	P	FTS	0	/
P	Q	FTS	0	/
Q	R	FTS	0	/
R	S	FTS	0	/
S	T	FTS	0	/
T	U	FTS	0	/
U	V	FTS	0	/
V	W	FTS	0	/

. The network diagram illustrating the precedence logic sequence of the construction process is shown in Figure 3.

2.3. Construction Duration Model Development

Based on the analysis of the construction-duration optimization strategies for the main structure and exterior facade works, an optimization model for the standard-floor construction duration is established. The symbols used in the model and their corresponding meanings are presented in

Table 8. The symbols used in the model and their corresponding meanings.

Notation	Hidden Meaning
i	Process i
j	Process j
Si	Start time of process i
Sj	Start time of process j
Di	Duration of process i
Dj	Duration of process j
Rir	The demand of process i for resource r
Cr	The total amount of labor resource r
At	The set of processes that are under construction at time t
δij	The overlap time between process i and process j
T	Standard floor construction period

.

(1) Constraint Analysis

➀ Overlapping-relation constraints

For each pair of activities i and j with an overlapping relationship, the corresponding constraint is defined according to the overlap type:

STS (Start-to-Start) relationship:

$$S_j\ge S_i+{\delta }_{ij},STS\left(i,j\right)$$

(1)

FTS (Finish-to-Start) relationship:

$$S_j\ge S_i+D_i+{\delta }_{ij},FTS\left(i,j\right)$$

(2)

FTF (Finish-to-Finish) relationship:

$$S_j+D_j\ge S_i+D_i+{\delta }_{ij},FTF\left(i,j\right)$$

(3)

STF (Start-to-Finish) relationship:

$$S_j+D_j\ge S_j+{\delta }_{ij},STF\left(i,j\right)$$

(4)

➁ Time-window constraints for overlapping lags

The overlapping lag between two activities must fall within the given minimum and maximum lag boundaries. The mathematical expression is as follows:

$${\delta }_{ij}^{min}\le {\delta }_{ij}\le {\delta }_{ij}^{max}$$

(5)

➂ Resource constraints

Resource constraints refer to limits on labor, equipment, and other resources required during construction. Here, the focus is on labor resources: at any time, the total labor demand of ongoing activities cannot exceed the available labor capacity.

$$\sum R_{ir}\le C_r,i\in Active\left(t\right)$$

(6)

(2) Schedule Boundary Conditions

Activity-duration boundaries require each duration to remain within its allowable minimum and maximum limits:

$$D_i^{min}\le D_i\le D_i^{max}$$

(7)

Upper bound on total construction duration:

$$T\le T_{\mathit{max}}$$

(8)

(3) Objective Function

Under the given constraints and boundaries, the objective is to minimize the total duration of the standard-floor construction for both the main structure and the facade works:

$$minT=\max \left(S_i+D_i\right)i\in Active\left(t\right)$$

(9)

(4) Optimization Model for Standard-Floor Construction Duration

Based on the objective function, the constraints, and the boundary conditions described above, the optimization model for the standard-floor construction duration—covering both main structure works and facade works—is established as follows:

$$minT=\max \left(S_i+D_i\right)i\in Active\left(t\right)$$

(10)

$$s.t.\left\{\begin{array}{c}\begin{array}{c}{S}_j\ge S_i+{\delta }_{ij},STS\left(i,j\right)\\ S_j\ge S_i+D_i+{\delta }_{ij},FTS\left(i,j\right)\\ S_j+D_j\ge S_i+D_i+{\delta }_{ij},FTF\left(i,j\right)\\ S_j+D_j\ge S_j+{\delta }_{ij},STF\left(i,j\right)\\ {\delta }_{ij}^{min}\le {\delta }_{ij}\le {\delta }_{ij}^{max}\\ \sum R_{ir}\le C_r,i\in Active\left(t\right)\\ D_i^{min}\le D_i\le D_i^{max}\\ T\le T_{max}\end{array}\end{array}\right.$$

(11)

2.4. Algorithm Selection and Comparison

In the optimization of construction duration for high-rise residential buildings—particularly when involving integrated platform construction—the problem is a typical combinatorial optimization problem. This study compares several commonly used intelligent optimization algorithms, including particle swarm optimization (PSO), ant colony optimization (ACO), and simulated annealing (SA). Their main characteristics are summarized in

Table 9. Comparative analysis of various optimization algorithms in construction schedule optimization.

Comparison Item	GA	PSO	ACO	SA
Search mechanism	Population-based parallel search, crossover and mutation evolution	Individual speed and position iteration	Pheromone-inspired search	Single-point random search
Global optimization capability	Strong	Medium	Relatively strong	Weak
Convergence speed	Moderate (stable)	Fast (early maturing)	Slow (parameter dependent)	Slow
Parameter complexity	Medium (crossover rate, mutation rate)	Few	Many (pheromone related)	Few
Is it prone to getting stuck in a local optimum	No	Yes	No	Yes
Adapt construction optimization	Complex process scheduling and resource constraints	Suitable for continuous variable problems	Suitable for path optimization problems	For local fine-tuning
Stability	High	Medium	General	Low
Scalability	Strong	General	General	Weak

.

Considering the stability, solution accuracy, and computational efficiency of various algorithms, this study selects the genetic algorithm (GA) as the core optimization method for construction-duration optimization of high-rise residential projects using an integrated platform.

The genetic algorithm simulates the biological evolution process through selection, crossover, and mutation operations. It is capable of maintaining population diversity in large-scale nonlinear solution spaces, thereby avoiding premature convergence to local optima. Its main advantages include the following:

Strong global search capability: As a population-based search method, GA can effectively locate global optima in multi-modal functions.

Flexible encoding: Priority-based encoding can be used to represent construction activity sequences, making GA naturally suitable for construction scheduling optimization.

High robustness: GA is insensitive to initial solutions and parameter settings, ensuring stable computational performance.

Strong scalability: It can be easily integrated with other optimization techniques to form hybrid genetic algorithms, further enhancing optimization accuracy.

The flowchart of the genetic algorithm is shown in Figure 4.

3. Case Study

3.1. Project Overview

This study takes the construction application of the integrated platform in Building #5 of a project in Chengdu, Sichuan Province, as an example. The building has a total of 25 floors, with a standard floor height of 3.1 m and a structural layer height of 3.2 m. The project employs a lightweight building construction machine as the core construction equipment, focusing on the collaborative application of its integrated platform for main structure construction and facade work during standard floor construction. The project is part of a large-scale high-rise residential group in the Chengdu area, characterized by a high number of floors, strong structural repetitiveness, short standard floor construction cycles, and typical high-rise residential features. It adopts innovative construction equipment—the integrated platform—with complete and analyzable data, aligning with the principle of combining research objectives with engineering practice.

3.2. Construction Scheme for Main Structure and Facade Work

The integrated platform, through its unique design, enables simultaneous operations across multiple structural layers. Specifically, during the main structure construction phase, the platform’s working surface covers Layer N, Layer N-1, and Layer N-2, totaling three consecutive structural layers. During the facade work phase, its effective working range is located at Layer N-5. In the platform design, there is typically a two-layer interval between the upper and lower working platforms. This spacing is primarily determined by safety protection requirements while also considering construction space needs and equipment operating conditions.

Based on project practice, the standard construction cycle for both main structure construction and facade work using this integrated platform in standard floors is 6 days. The construction work for each standard floor is shown in Figure 5.

The allocation of labor resources is shown in

Table 10. The allocation of labor resources.

Construction Work Content	All Types of Work	Number of People
N layer template support	Carpenter	8
N layer steel bar binding	Steel Fixer	6
N layer laminated plywood hoisting	Hoisting Worker + Carpenter	2 + 4
N layer plate surface steel bar binding	Steel Fixer	5
N layer concrete pouring	Concrete Worker	10
N-1 layer vertical and horizontal formwork removal	Carpenter	6
N-1 layer attached wall fittings are installed	Welder + Installer	2 + 4
N-1 layer hole sealing	Plasterer	4
N-1 layer structural repair	Plasterer	4
N-2 layer waterproof mortar construction	Plasterer	6
N-5 layer insulation board construction	Insulation Worker	4
N-5 layer keel burial plate construction	Welder + Installer	2 + 3
N-5 layer primary and secondary keel construction	Installer	8
N-5 layer crack-resistant mortar construction	Plasterer	4
N-5 layer putty construction	Plasterer	4
N-5 layer real stone paint construction	Spray Paint	6

.

Based on the aforementioned labor resource allocation and the fact that the handover between construction processes is not strictly idealized—typically involving short-term parallel operations during the transition and acceptance phases—this study explicitly incorporates such parallel processes in the pre-optimization model. Total workforce demand curve before optimization is shown in Figure 6.

The standard floor construction cycle for the integrated platform is 6 days, with working hours from 6:00 to 18:00, totaling 12 h per day. In this study, the activity durations of each construction process are set as deterministic parameters. The listed process durations are determined primarily based on two aspects: (1) historical construction data of similar high-rise residential projects, particularly the standard-floor construction records from projects employing dual-platform building machines or integrated platform construction modes, and (2) current construction quota standards and labor productivity indicators for building engineering, which are then converted in combination with the standard crew size. The detailed construction schedule for the main structure and facade work of the standard floor is shown in

Table 11. The detailed construction schedule for the main structure and facade work of the standard floor.

Construction Work Content	Start Time to End Time
N layer template support	1d/06:00–1d/18:00
N layer steel bar binding	2d/06:00–2d/16:00
N layer laminated plywood hoisting	2d/16:00–3d/12:00
N layer plate surface steel bar binding	3d/12:00–3d/18:00
N layer concrete pouring	4d/06:00–4d/18:00
N-1 layer vertical and horizontal formwork removal	5d/06:00–5d/12:00
N-1 layer attached wall fittings are installed	5d/12:00–6d/08:00
N-1 layer hole sealing	6d/08:00–6d/12:00
N-1 layer structural repair	6d/12:00–6d/18:00
N-2 layer waterproof mortar construction	6d/10:00–6d/18:00
N-5 layer insulation board construction	1d/06:00–2d/10:00
N-5 layer keel burial plate construction	2d/10:00–3d/08:00
N-5 layer primary and secondary keel construction	3d/08:00–4d/10:00
N-5 layer crack-resistant mortar construction	4d/10:00–5d/08:00
N-5 layer putty construction	5d/08:00–6d/16:00
N-5 layer real stone paint construction	6d/16:00–6d/18:00

.

The original plan exhibits deficiencies in three key aspects:

(1) Although equipped with an integrated platform system, the original plan only implements dual platforms physically while maintaining the linear operational logic of traditional single-platform approaches. The workflow design for upper and lower platforms follows conventional processes without leveraging the parallel processing capacity of dual platforms. The construction schedule adopts a per-floor sequential mindset with serialized inter-floor task arrangements. Furthermore, the coarse process division prevents decomposition into smaller, flexible work packages, resulting in ineffective task overlapping and interfacing between floors, ultimately failing to achieve comprehensive three-dimensional cross-operation.

(2) The plan demonstrates excessive serialization of processes within individual floors without consolidating parallelizable tasks. Most intra-floor operations follow a “finish-to-start” sequence, neglecting potential parallel execution across different sub-areas or work groups. The broad process categorization obscures parallelizable tasks as the concept of “work units/operation zones” remains unimplemented. Even spatially independent activities (e.g., formwork installation and rebar binding in different zones) are sequentially scheduled, resulting in low operational time overlap.

(3) There is a lack of effective connection and coordination between the main structure construction and facade work. Although the project employs an integrated platform with physical conditions for dual-platform collaborative construction, the original construction plan continues to follow traditional single-platform patterns in both process logic and scheduling, failing to leverage the parallel advantages and synergistic potential of the dual-platform system. In the original plan, main structure construction and facade work are treated as two essentially independent workflows with only a basic sequential relationship (“structure completion --facade follow-up”). However, there is no coordination mechanism based on precise spatiotemporal relationships, causing different specialties to progress vertically according to their own operational logic.

3.3. Optimization Results and Analysis Based on Genetic Algorithm

This study utilized MATLAB 2024b software to implement the genetic algorithm for schedule optimization. The program was executed on a computer with an Intel(R) Core(TM)i5-1135G7 CPU (2.40 GHz base frequency) and 16 GB RAM.

In the genetic parameter configuration, the population size was set to 50, evolution generations to 100, crossover rate to 0.8, mutation rate to 0.1, and γ to 0.5. The selection operation employed the roulette wheel method to maintain survival-of-the-fittest while preserving diversity, ensuring both effective transmission of superior task combinations and computational efficiency. For crossover operations, a two-point crossover based on mapping relationships was adopted, which not only guaranteed validity of task sequences but also enhanced the global search capability of the genetic algorithm while inheriting favorable sequential structures from parent generations. Finally, the optimized scheme was used to derive corresponding labor requirements.

The algorithm outputs after optimization include the following:

(1) Objective function iteration curve diagram (Figure 7)

(2) Optimized Gantt chart for standard floor construction of main structure and facade works (Figure 8)

(3) Total labor demand curve diagram for the construction process (Figure 9)

(1) Analysis of the Objective Function Iteration Curve

The optimization process and convergence characteristics of the genetic algorithm are intuitively reflected in the iteration curve of the objective function.

The curve clearly demonstrates the algorithm’s “exploration” and “exploitation” capabilities. In the early stages of evolution (approximately the first 30 generations), the curve shows a rapid, step-like decline, indicating that the algorithm effectively conducts a global search in the solution space, quickly eliminating inferior solutions and discovering key optimization paths that significantly shorten the construction period. Subsequently, the curve enters a phase of gentle convergence, where the algorithm shifts to localized fine-tuning, gradually approaching the optimal solution through adjustments to task sequences and platform allocations. Ultimately, the total duration was optimized from the baseline of 72 h to 58 h, achieving an efficiency improvement of 19.4%, validating the model’s effectiveness.

The iteration curve is generally smooth, without significant oscillations or premature convergence, indicating that the parameter settings—such as population size, crossover rate, and mutation rate—are well balanced. The crossover operation ensures the inheritance and recombination of superior gene patterns, while moderate mutation effectively maintains population diversity, preventing the algorithm from settling into local optima. This convergence behavior demonstrates the algorithm’s strong stability and robustness when addressing complex construction constraints, enabling it to provide reliable optimal or near-optimal solutions for decision-making.

(2) Analysis of the Optimized Gantt Chart

A comparison of the Gantt charts before and after optimization reveals a fundamental shift in the construction organization model from “serial” to “parallel and collaborative.”

The pre-optimization Gantt chart displays typical sequential task characteristics. Main structure tasks and facade work are separated, forming two independent long sequences. This not only results in an extended total duration but also leads to low resource utilization.

The post-optimization Gantt chart demonstrates a clear advanced model of “three-dimensional overlapping and parallel progression.” Through the intelligent scheduling of the genetic algorithm, rigid dependencies between tasks are successfully decoupled, allowing facade work to be integrated at an earlier stage. This arrangement enables the dual platforms to function like two collaborative workstations in an assembly line, maximizing the utilization of spatial and temporal resources. This is the fundamental reason for the significant reduction in the construction period.

(3) Analysis of Total Labor Demand Curve

The optimization process not only focused on schedule compression but also significantly improved resource management, which is fully reflected in the total labor demand curve.

By comparing the total construction labor demand curves before and after optimization, it can be concluded that after optimization by the genetic algorithm, the labor demand curve has become more balanced and continuous. By intelligently adjusting the start times of various tasks, the algorithm effectively distributed the originally concentrated labor requirements more evenly throughout the project duration.

Peak Reduction: By staggering high labor-demand tasks along the timeline and scheduling them in parallel with low-demand tasks, the maximum peak labor demand was successfully reduced from approximately 30 workers to about 22 workers, representing a 26.7% decrease.

Trough Filling: Through precise task overlapping (such as executing structural construction at level N concurrently with work at level N-2), unnecessary waiting periods were eliminated, raising the minimum labor demand to over 14 workers.

Balancing Effect: After optimization, the labor demand fluctuates within a reasonable range of 14–22 workers for most of the duration, achieving refined and intensive utilization of human resources.

4. Discussion

This study successfully optimized the construction schedule of the integrated platform using a genetic algorithm, significantly reducing the standard floor cycle time from 72 h to 58 h. The specific improvements include partial overlapping in the timeline of formwork installation, rebar binding, composite slab hoisting, and exterior wall insulation work; earlier initiation of facade construction with substantially reduced platform waiting time; and tighter coordination between the upper and lower working surfaces of the platform. To clarify how the proposed optimization reduces the overall construction duration, a comparative analysis of idle times for critical activities before and after optimization is conducted.

Table 12. Detailed analysis of idle time reduction by activity.

Process	Original Start (h)	Optimized Start (h)	Idle Time Reduced (h)
N: Structural steel reinforcement tying	12	8	4
N-1: Vertical formwork removal	48	8	40
N-1: Screw hole sealing	62	14	48
N-1: Structural repair	66	14	52
N-5: Installation of primary and secondary framing for stone and aluminum panel walls	26	10	16
N-5: First coat of putty application on painted walls	48	12	36
N-5: Stone and aluminum panel wall crack-resistant mortar construction	38	24	14
N-5: Primer application for coated walls with real stone paint	70	52	18

summarizes the start times of selected critical activities under the original and optimized schedules, as well as the corresponding reductions in organizational idle time. The idle time refers to the organizational waiting time between the earliest technically feasible start and the actual scheduled start in the original plan. The idle time reduction is calculated as the difference between the original and optimized start times of the same activity.

Under the constraints of construction sequence logic and platform limitations, the genetic algorithm continuously enhanced construction efficiency by automatically identifying superior task sequences. The optimization results demonstrate strict compliance with all critical logical relationships, such as the requirement that beam rebar installation at level N must follow the completion of vertical rebar work at the same level.

In addition to process logic and platform constraints, human resource allocation also significantly impacts construction efficiency during schedule optimization. Based on the total construction labor demand curves before and after optimization, the cumulative labor hours for the entire construction process were calculated by summing the hourly labor demand. It was found that the optimized solution reduced overall labor input by approximately 10–15%. This reduction enables more rational allocation of platform resources and ensures enhanced continuity and stability of the construction process.

Compared with traditional Critical Path Method (CPM) and experience-based scheduling approaches, the genetic algorithm demonstrates stronger adaptability and global search capabilities when addressing large-scale task sequencing and multi-platform parallel constraints. Relative to ant colony optimization and simulated annealing algorithms employed in existing studies, the genetic algorithm utilized in this research shows satisfactory performance in convergence speed and solution stability, achieving satisfactory scheduling outcomes with relatively few iterations. This indicates that genetic algorithms hold significant application value for schedule optimization in integrated platform systems.

From a practical engineering perspective, the optimization results not only reduce the project duration but also provide contractors with valuable references for resource allocation. While rationalizing task sequences, the approach reduces platform idle time and improves the utilization rates of both labor and machinery. This has positive implications for project cost control, safe construction practices, and balanced resource configuration.

The construction duration optimization model proposed in this paper is not limited to reinforced concrete structures alone. Its core lies in the modeling and optimization of activity representation, precedence relationships, resource constraints, and parallel construction modes under integrated platform conditions for construction processes. Theoretically, this method possesses strong generalizability.

The primary reason for selecting reinforced concrete structures as the research object in this study is that they remain the most common structural form in high-rise residential buildings. Furthermore, the dual-platform building machine and its integrated construction mode offer well-defined engineering application scenarios for typical processes such as formwork erection, rebar installation, and concrete pouring. For other concrete-based structural forms, or even building projects with different structural systems, the model can be effectively applied by redefining the set of construction activities, their logical relationships, and resource parameters based on their specific construction process characteristics—all while keeping the optimization framework and solution method unchanged. Therefore, from a methodological perspective, this model is particularly suitable for duration planning and optimization in concrete construction processes, with the reinforced concrete structure serving as a representative application case in this study.

However, this study has certain limitations. On the one hand, the genetic algorithm may occasionally converge prematurely, resulting in locally rather than globally optimal solutions. On the other hand, the model developed in this paper primarily focuses on analyzing the influence of reconstructing construction process logic, overlapping relationships between processes, and the coordination mechanism of the dual platforms on construction duration. The model assumes that resources can be supplied as planned with certainty, without considering uncertainties such as material shortages, worker absenteeism, or equipment failures. Practical complex factors, such as weather impacts or material delivery delays, have not yet been incorporated. Additionally, the duration parameters are determined based on historical data and construction quotas, which are inherently deterministic assumptions. In actual construction, process durations may deviate due to fluctuations in material supply, labor organization efficiency, equipment operational status, and on-site environmental conditions. Furthermore, algorithm parameters (crossover rate, mutation rate) significantly influence the results and require further experimental optimization. Finally, it should be noted that the current optimization results are obtained based on simulation models and have not yet been implemented in actual construction sites. Although the models incorporate real construction data and constraints, practical validation remains a critical direction for future work. On-site testing will help assess feasibility, identify potential issues, and further refine the construction plan.

Future research could develop in the following directions: First, combining genetic algorithms with other intelligent optimization methods (e.g., ant colony optimization, particle swarm optimization, reinforcement learning) to enhance optimization performance. Second, the incorporation of uncertainties related to resource supply and duration parameters during the construction process, as well as their impact on the robustness of optimization results, will serve as an important direction for future research. Third, developing an intelligent construction scheduling system integrated with BIM technology to enable visualization and dynamic optimization. Fourth, applying the research findings to facade-integrated platforms and smart construction systems to verify their versatility and effectiveness across different construction scenarios.

5. Conclusions

This study employed a genetic algorithm to optimize the construction sequence for high-rise residential projects using an integrated platform. Through priority-based encoding, decoding rules, and genetic operator configuration, a fitness function was established to achieve schedule optimization. The research findings are as follows:

(1) Significant reduction in construction time: The optimization results indicate that, while maintaining the logical constraints of the processes and the coordinated operation of the two platforms, the total construction time was reduced from the original 72 h to 58 h, a reduction of 19.4%, demonstrating the effectiveness of the genetic algorithm in optimizing construction schedules.

(2) Improved Human Resource Allocation: The optimized plan reduces overall labor input by approximately 10–15%, a conclusion derived from cumulative labor-hour analysis based on the summation of hourly labor demand throughout the entire construction process before and after optimization. Inputs for peak processes (such as formwork erection and steel reinforcement binding) have been reduced, while critical processes (such as concrete pouring) maintain stable inputs. This indicates that the optimization not only enhances construction efficiency but also improves the balanced allocation and utilization of human resources.

(3) Satisfactory Algorithm Performance: The objective function decreased from approximately 70 to 64 within the first 20 generations, and further dropped to 59 within 40 generations, stabilizing after the 55th generation. The minimal fluctuation in the objective function during later iterations demonstrates the algorithm’s strong convergence and stability. Crossover and mutation operations effectively maintained population diversity, preventing premature convergence to local optima.

(4) Managerial and Practical Implications: This research provides quantitative decision-making support for high-rise residential construction planning, offering valuable references for schedule control, labor allocation, and platform scheduling, ultimately contributing to cost reduction and construction efficiency improvement.

However, limitations remain: the study does not account for external site conditions (e.g., weather, material supply fluctuations) affecting schedules and resources and assumes uniform worker skill levels without considering individual differences. Future research could incorporate real-time field data to develop multi-objective optimization models addressing integrated optimization of schedule, cost, and resources. Although this study takes reinforced concrete construction as a representative case, the proposed optimization framework is extensible to other concrete construction scenarios through appropriate redefinition of activity sets and constraints.