Numerical Prediction for Reinforced Concrete Beams Subjected to Monotonic Fatigue Loading Using Various Concrete Damage Models
Abstract
1. Introduction
1.1. Fatigue Behavior of Concrete
1.2. Fatigue Behavior of Reinforcement
1.3. Literature Review on Numerical Modeling of Fatigue Behavior of RC Beams
2. Finite Element Simulation
2.1. Material Modeling
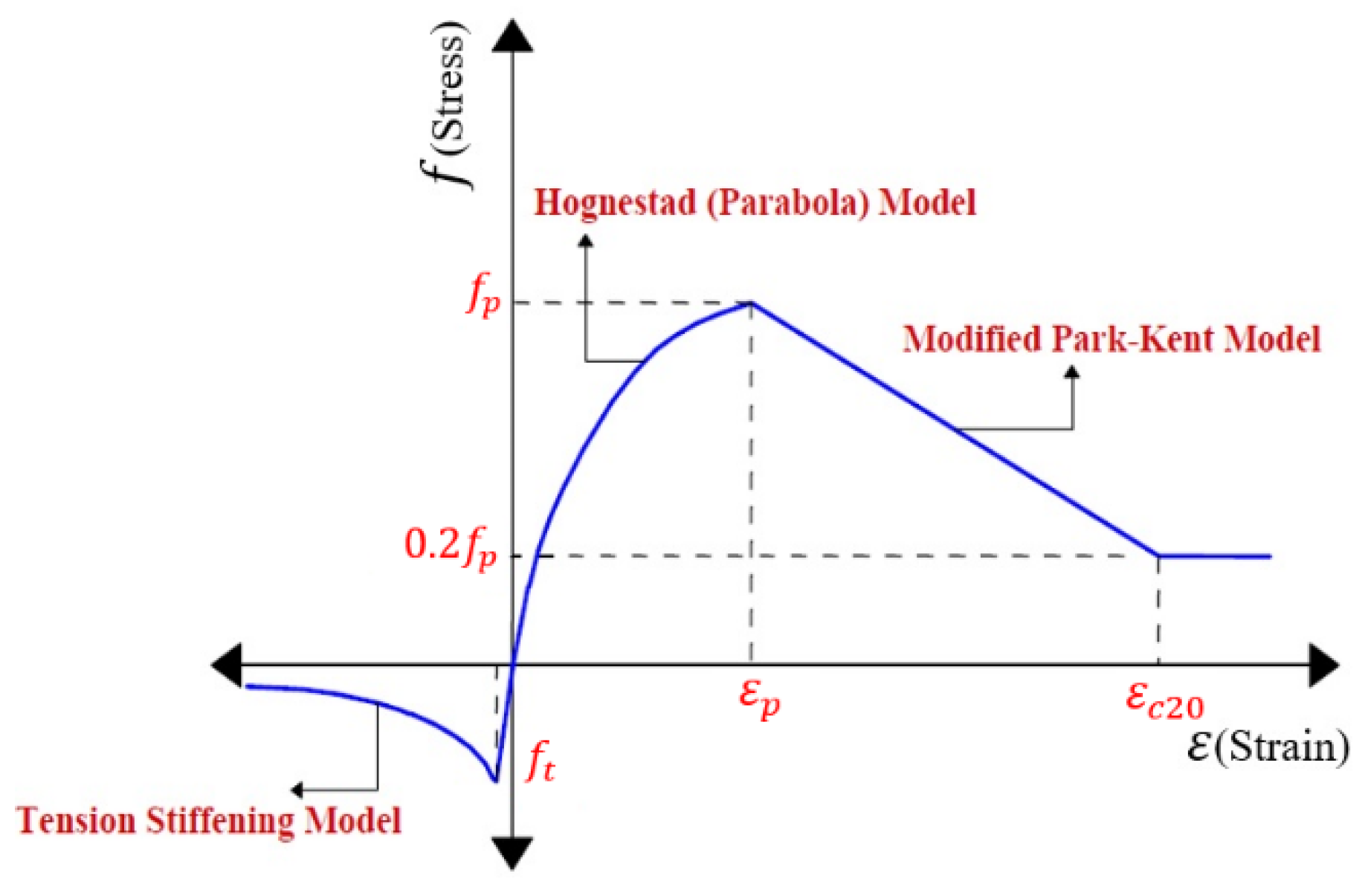
2.1.1. Concrete
2.1.2. Steel Reinforcement
2.2. Structural Modeling
2.3. Concrete Damage Models
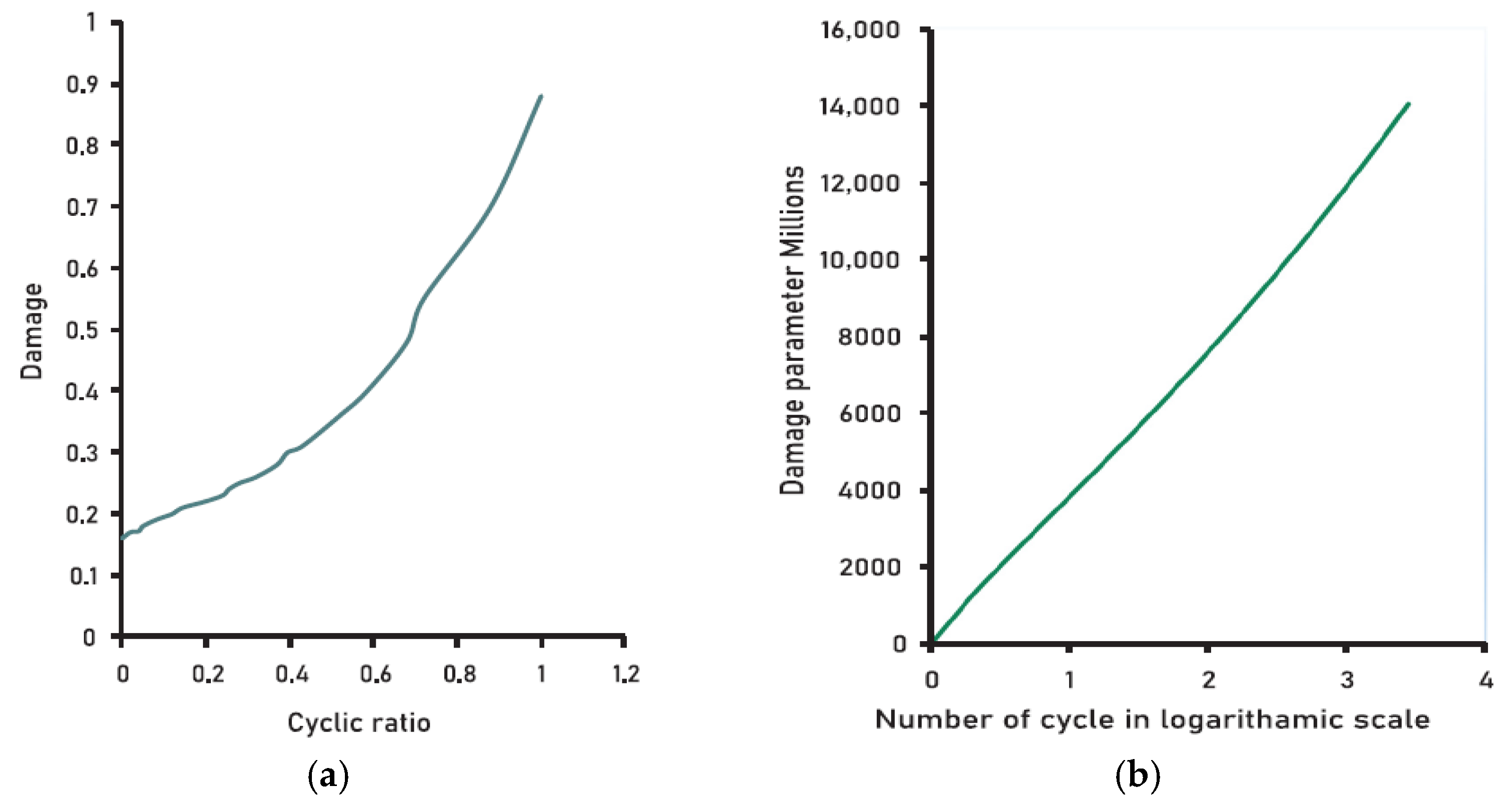
2.3.1. VecTor2 Concrete Damage Model
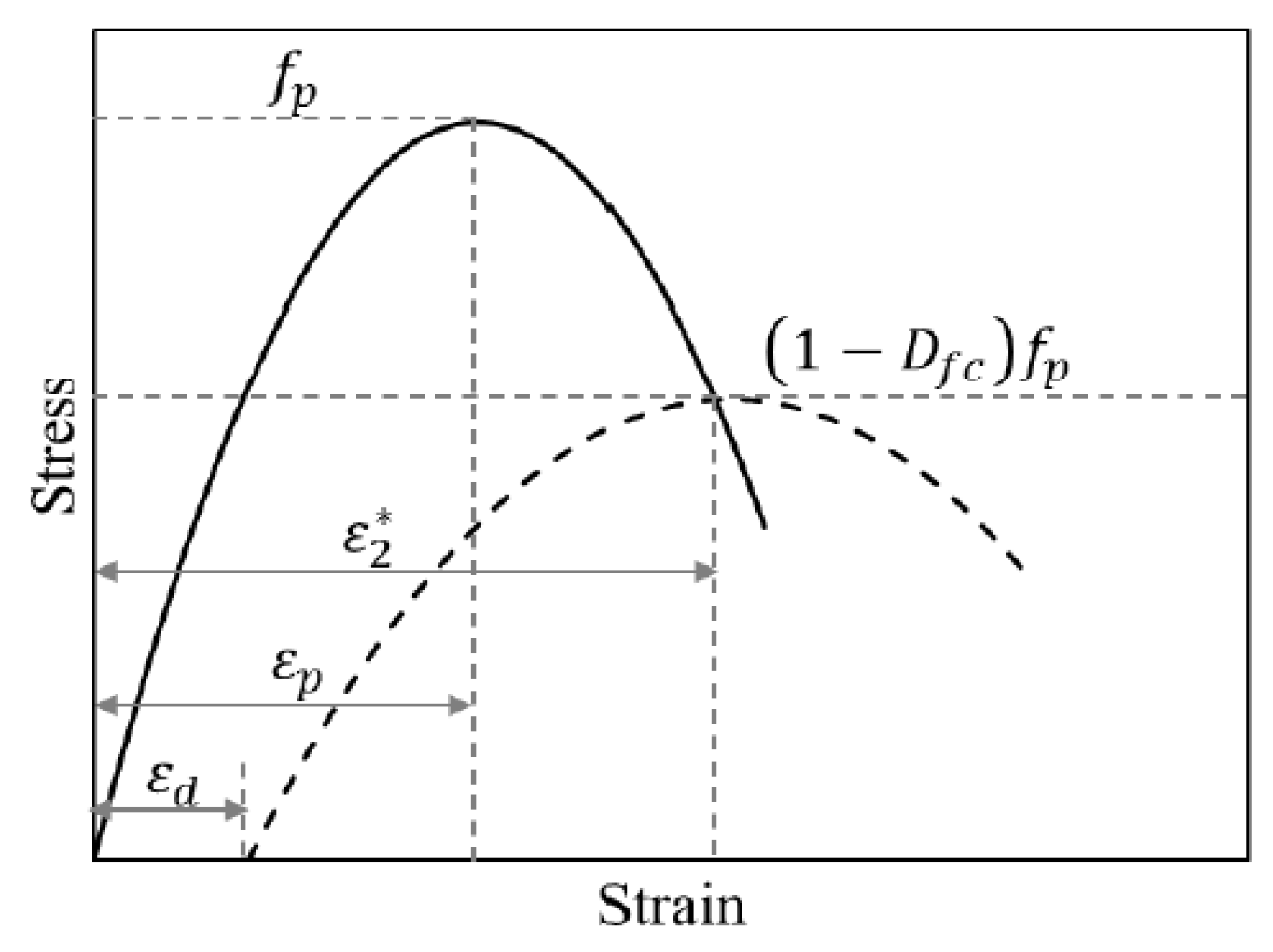
2.3.2. Lü et al. Concrete Damage Model
2.4. Experimentally Modeled Specimens
2.5. Sensitivity Analysis
3. Numerical Results and Discussion
3.1. Deflection vs. Number of Load Cycles Response
3.1.1. VecTor2 Damage Model
3.1.2. Lü et al. Damage Model
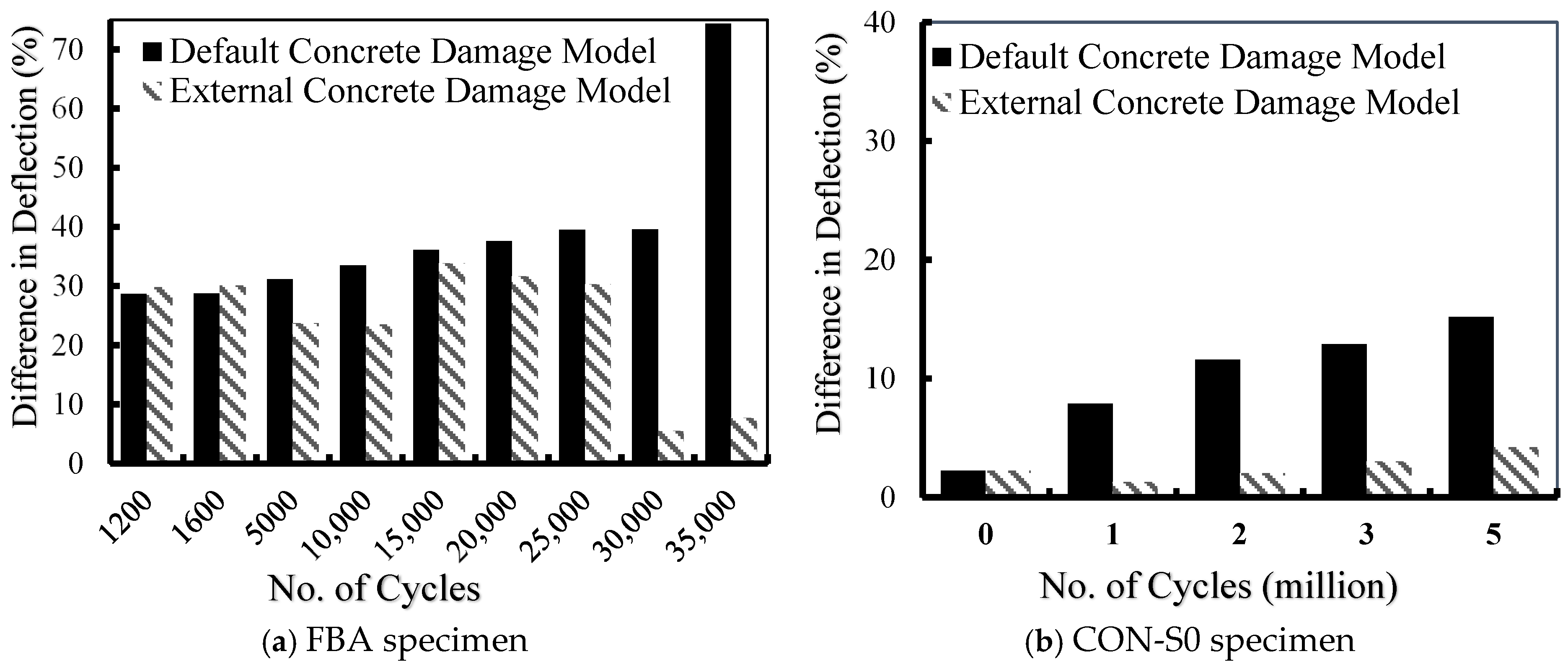
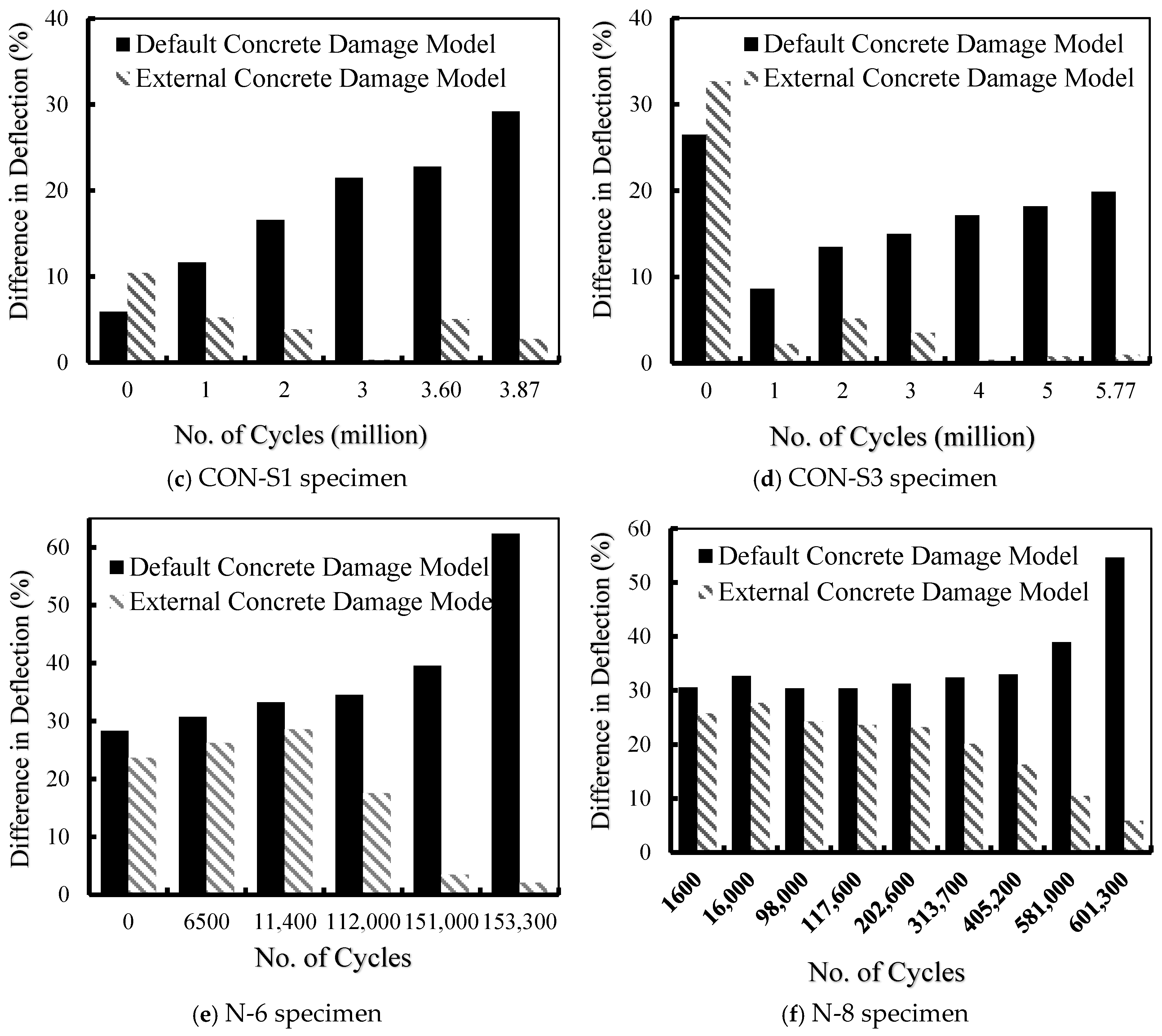
3.1.3. Comparison Between Concrete Damage Models
3.2. Strain Response
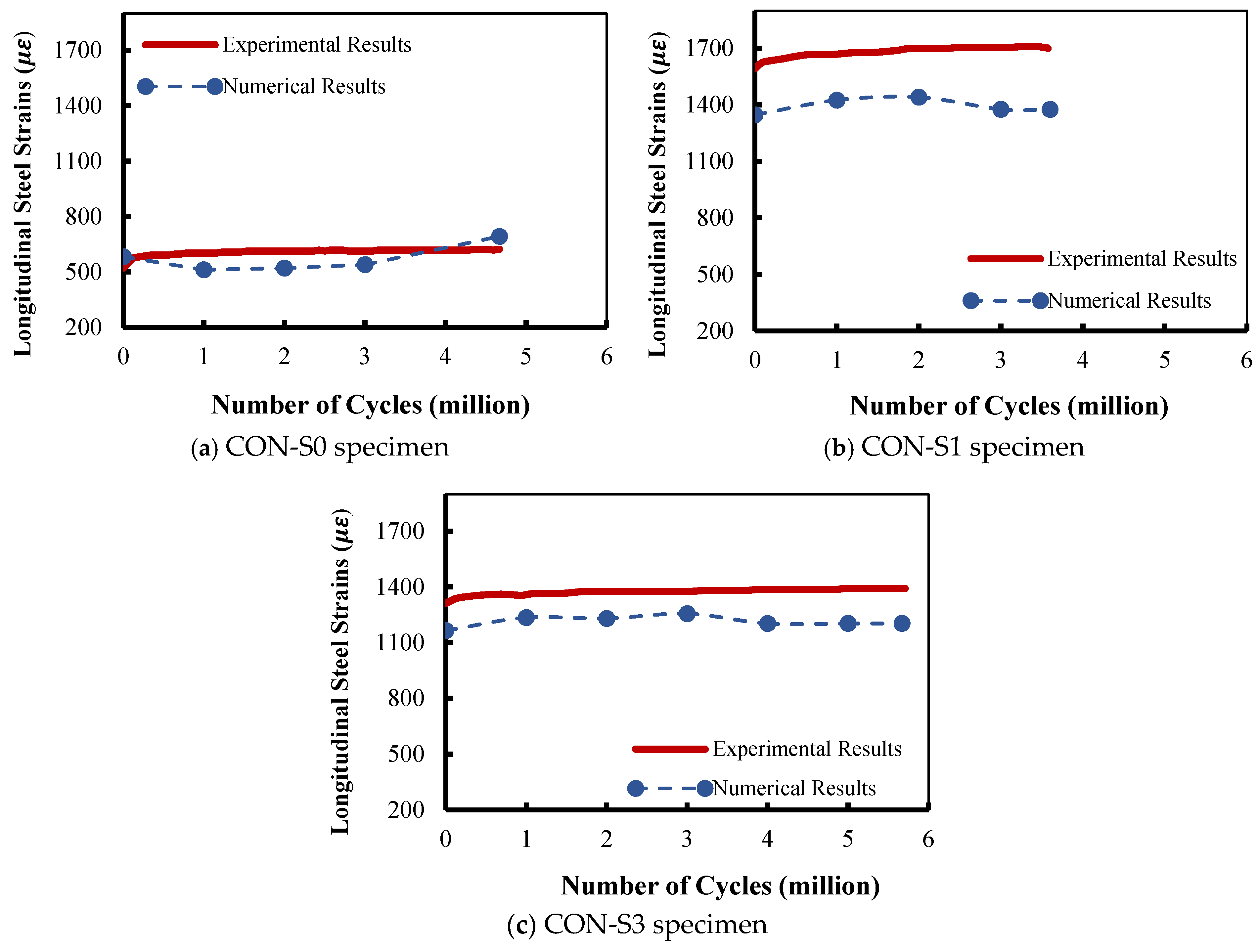
3.2.1. Strain in Longitudinal Steel
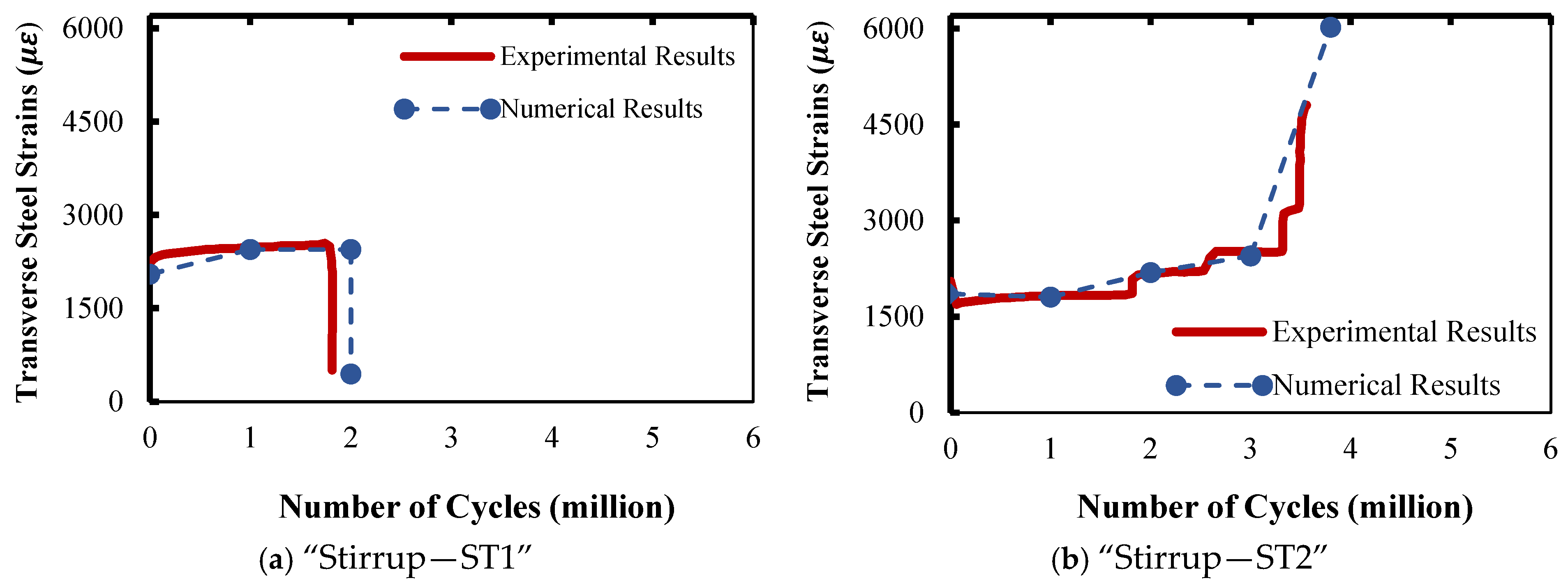
3.2.2. Strain in Transverse Steel
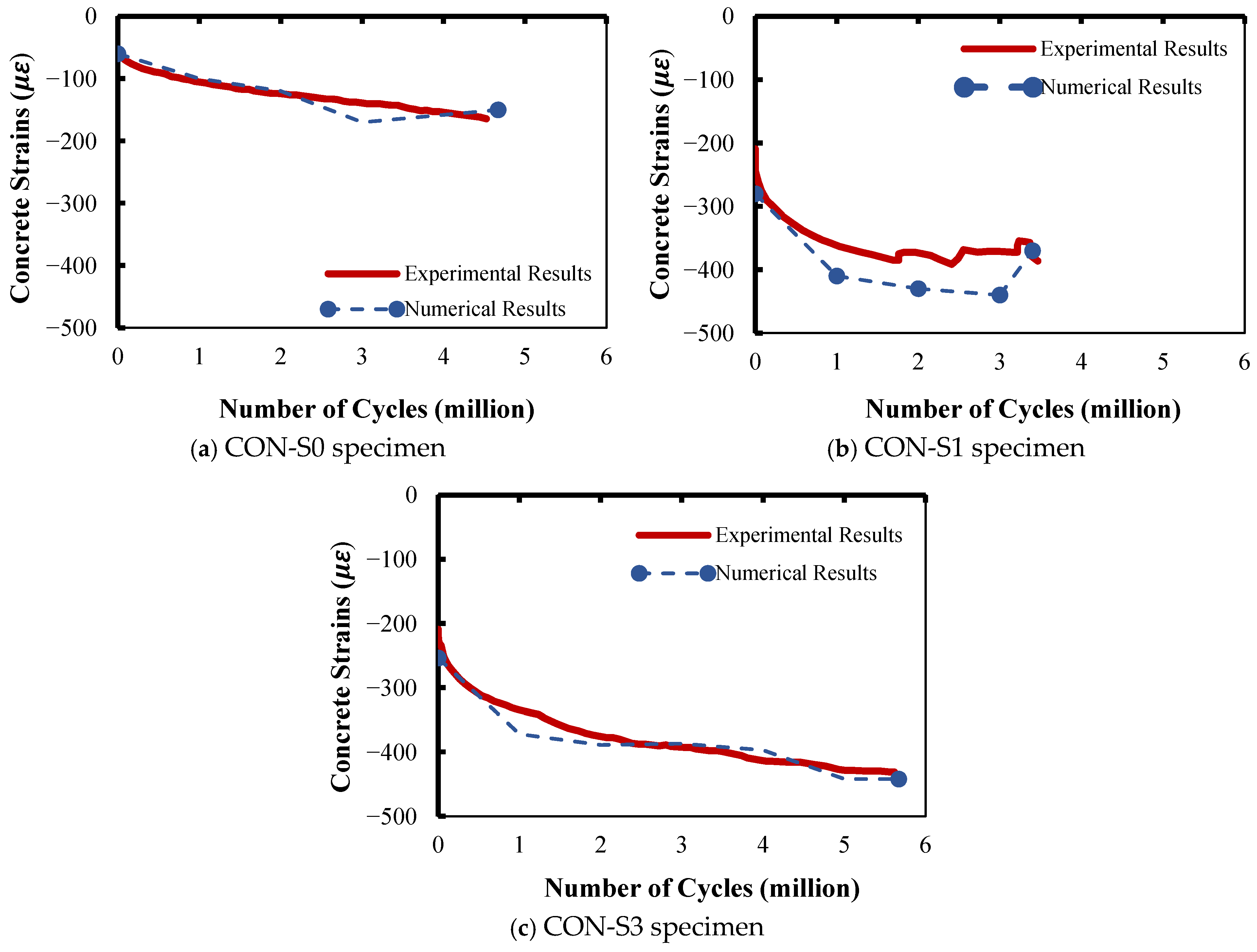
3.2.3. Strain in Concrete
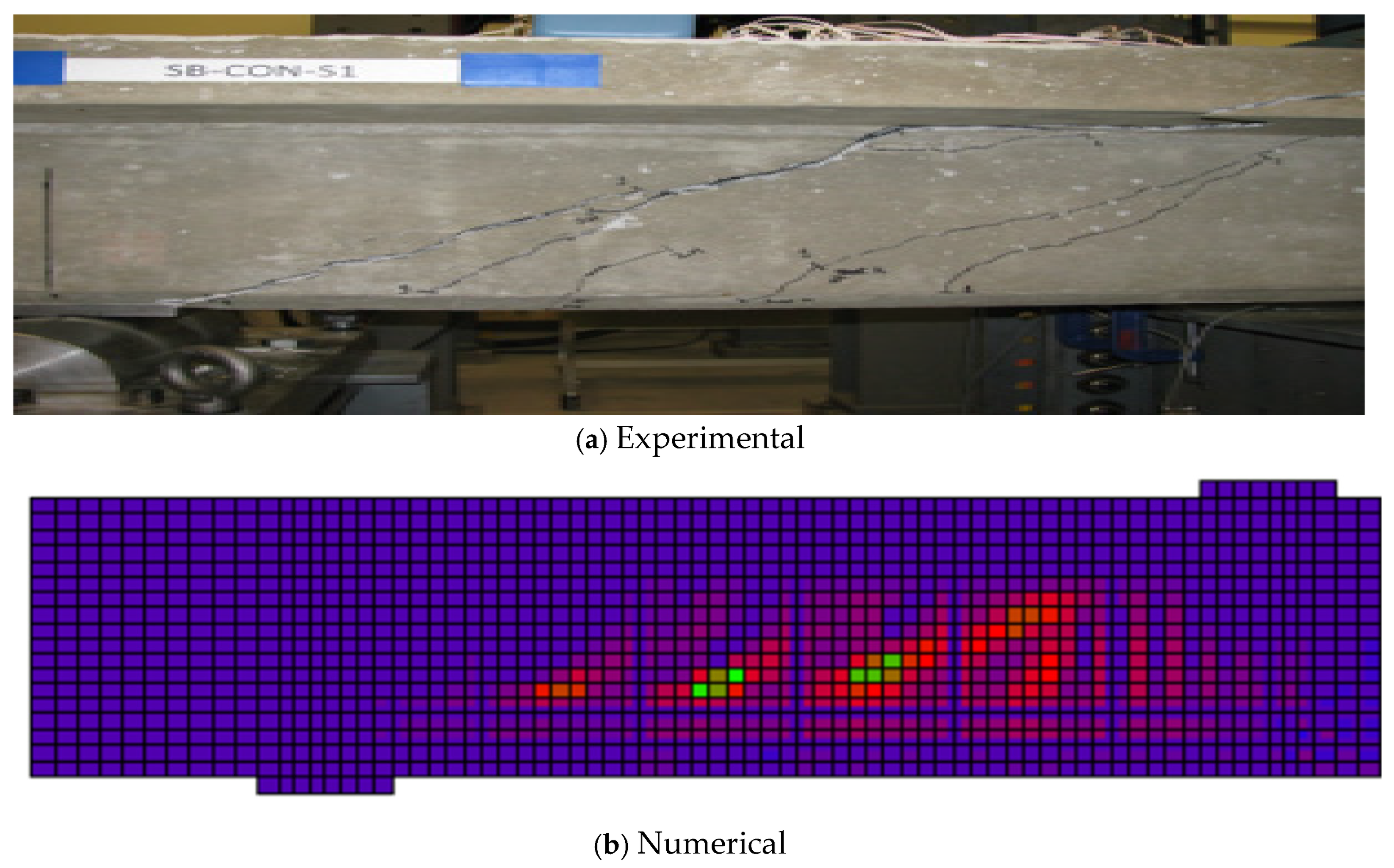
3.3. Failure Modes
4. Conclusions
- (i)
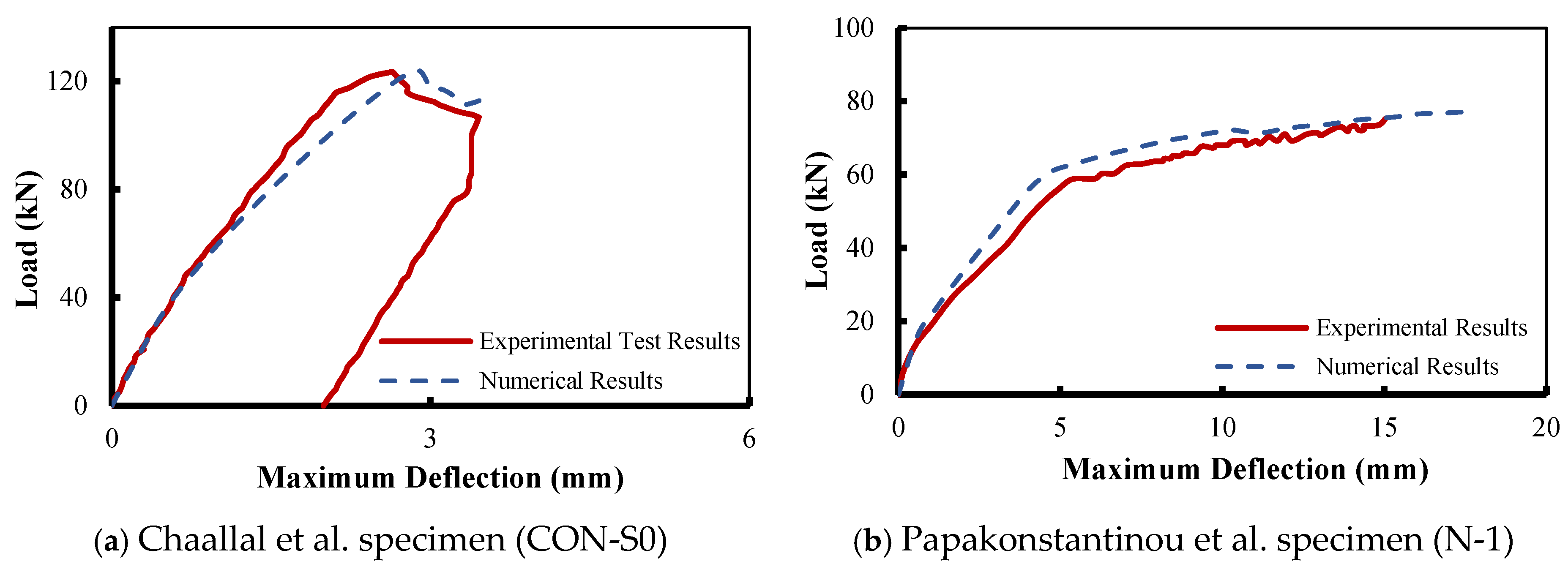
- Generally, the numerical model was capable of simulating the behavior of RC beams under monotonic fatigue loading. The numerical model was successful in predicting the response of experimental beams in terms of the maximum deflection versus the number of loading cycles and failure modes.
- (ii)
- The VecTor2 concrete damage model was able to capture the fatigue behavior at early load cycles. Wide discrepancies between the FE model results and the experimental ones were observed when the number of cycles increased. This can be attributed to the rotating smeared crack assumption, which affected the stiffness and crack opening under constant-amplitude cyclic loading, resulting in almost constant deflection responses with an increasing number of cycles.
- (iii)
- The external damage model (Lü et al.) adopted in this study provided a response identical to the experimental response when the specimens were subjected to monotonic fatigue loading. However, the Lü et al. concrete damage model showed differences in predicting strain behavior in the early cycles due to microcracking and early stiffness deterioration, and the average stress–strain relationships adopted by the MCFT.
- (iv)
- When implementing the Lü et al. damage model, comparisons between the numerical and experimental results showed strong correlations in terms of the strain in longitudinal reinforcement, transverse reinforcement, and concrete. This research has demonstrated that accurate FE models are valuable resources for obtaining information about the useful quantitative characteristics of RC beams.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Glucklich, J. Static Fatigue in Concrete. Rheol. Acta 1961, 1, 356–361. [Google Scholar] [CrossRef]
- Junior, S.; Parvin, A. Performance of Continuous Concrete Beams with Reinforced FRP Bars and Sheets. In Proceedings of the Fifth Conference on Smart Monitoring, Assessment and Rehabilitation of Civil Structures (SMAR), Potsdam, Germany, 27–29 August 2019; pp. 27–29. [Google Scholar]
- ACI Committee 215. Considerations for Design of Concrete Structures Subjected to Fatigue Loading; Report No. PRC-215-21; American Concrete Institute: Framington Hills, MI, USA, 2021. [Google Scholar]
- Dineshkumar, R.; Ramkumar, S. Review paper on fatigue behavior of reinforced concrete beams. Mater. Today Proc. 2020, 21, 19–23. [Google Scholar] [CrossRef]
- Banjara, N.K.; Ramanjaneyulu, K. Experimental Investigations and Numerical Simulations on the Flexural Fatigue Behavior of Plain and Fiber-Reinforced Concrete. J. Mater. Civ. Eng. 2018, 30, 04018151. [Google Scholar] [CrossRef]
- Banjara, N.; Ramanjaneyulu, K. Investigations on Behaviour of Flexural Deficient and CFRP Strengthened Reinforced Concrete Beams under Static and Fatigue Loading. Constr. Build. Mater. 2019, 201, 746–762. [Google Scholar] [CrossRef]
- Bastidas-Arteaga, E.; Bressolette, P.; Chateauneuf, A.; Sánchez-Silva, M. Probabilistic lifetime assessment of RC structures under coupled corrosion–fatigue deterioration processes. Struct. Saf. 2009, 31, 84–96. [Google Scholar] [CrossRef]
- Papakonstantinou, C.; Petrou, M.; Harries, K. Fatigue Behavior of RC Beams Strengthened with GFRP Sheets. J. Compos. Constr. 2001, 5, 246–253. [Google Scholar] [CrossRef]
- Kim, J.; Kim, Y. Experimental study of the fatigue behavior of high strength concrete. Cem. Concr. Res. 1996, 26, 1513–1523. [Google Scholar] [CrossRef]
- Meneghetti, L.C.; Garcez, M.R.; da Silva Filho, L.C.P.; Gastal, F.d.P.S.L.; Bittencourt, T.N. Fatigue life of RC beams strengthened with FRP systems. Struct. Concr. 2014, 15, 219–228. [Google Scholar] [CrossRef]
- Heffernan, P.J.; Erki, M.A. Fatigue Behavior of Reinforced Concrete Beams Strengthened with Carbon Fiber Reinforced Plastic Laminates. J. Compos. Constr. 2004, 8, 132–140. [Google Scholar] [CrossRef]
- Wang, Y.; Li, Y.; Lu, L.; Wang, F.; Wang, L.; Liu, Z.; Jiang, J. Numerical prediction for life of damaged concrete under the action of fatigue loads. Eng. Fail. Anal. 2024, 162, 108368. [Google Scholar] [CrossRef]
- Haghighi, M.; Asadi, P.; Hashemolhosseini, H.; Baghbanan, A. An experimental study on the bending fatigue behavior of concrete beams by a proposed machine. Mech. Based Des. Struct. Mach. 2024, 52, 9082–9098. [Google Scholar] [CrossRef]
- Maljaars, J.; Leonetti, D.; Hashemi, B.; Snijder, H.H. Systematic derivation of safety factors for the fatigue design of steel bridges. Struct. Saf. 2022, 97, 102229. [Google Scholar] [CrossRef]
- El-Saikaly, G.; Chaallal, O. Extending the Fatigue Life of Reinforced Concrete T-Beams Strengthened in Shear with Externally Bonded FRP: Upgrading versus Repairing. J. Compos. Constr. 2015, 19, 04014027. [Google Scholar] [CrossRef]
- Ekenel, M.; Myers, J. Fatigue Performance of CFRP Strengthened RC Beams under Environmental Conditioning and Sustained Load. J. Compos. Constr. 2009, 13, 93–102. [Google Scholar] [CrossRef]
- Barnes, R.A.; Mays, G.C. Fatigue Performance of Concrete Beams Strengthened with CFRP Plates. J. Compos. Constr. 1999, 3, 63–72. [Google Scholar] [CrossRef]
- El-Tawil, S.; Ogunc, C.; Okeil, A.; Shahawy, M. Static and Fatigue Analyses of RC Beams Strengthened with CFRP Laminates. J. Compos. Constr. 2001, 5, 258–267. [Google Scholar] [CrossRef]
- Isojeh, B.; El-Zeghayar, M.; Vecchio, F. Numerical Analysis of Reinforced Concrete and Steel-Fiber Concrete Elements under Fatigue Loading. J. Struct. Eng. 2019, 145. [Google Scholar] [CrossRef]
- Ray, S.; Kishen, J.M. Analysis of fatigue crack growth in reinforced concrete beams. Mater. Struct. 2013, 47, 183–198. [Google Scholar] [CrossRef]
- Williams, G.; Higgins, C. Fatigue of Diagonally Cracked RC Girders Repaired with CFRP. J. Bridge Eng. 2008, 13, 24–33. [Google Scholar] [CrossRef]
- American Association of State Highway and Transportation Officials (AASHTO). Standard Specifications for Highway Bridges, 41st ed.; AASHTO: Frederick, MD, USA, 2021. [Google Scholar]
- ACI Committee 440. Guide for Design and Construction of Structural Concrete Reinforced with Fiber-Reinforced Polymer (FRP) Bars; Report No. 440 1R-15; American Concrete Institute: Farmington Hills, MI, USA, 2015. [Google Scholar]
- Chaallal, O.; Boussaha, F.; Bousselham, A. Fatigue Performance of RC Beams Strengthened in Shear with CFRP Fabrics. J. Compos. Constr. 2010, 14, 415–423. [Google Scholar] [CrossRef]
- El-Saikaly, G.; Chaallal, O. Fatigue behavior of RC T-beams strengthened in shear with EB CFRP L-shaped laminates. Compos. Part B Eng. 2015, 68, 100–112. [Google Scholar] [CrossRef]
- EAR fib Working Group and Stijn Matthys (UGent). Externally Applied FRP Reinforcement for Concrete Structures; International Federation for Structural Concrete: Lausanne, Switzerland, 2019; Volume 90, ISSN 1562-3610. Available online: https://hdl.handle.net/1854/LU-8657278 (accessed on 1 July 2019).
- Alliche, A. Damage model for fatigue loading of concrete. Int. J. Fatigue 2004, 26, 915–921. [Google Scholar] [CrossRef]
- Breitenbücher, R.; Ibuk, H. Experimentally Based Investigations on the Degradation-Process of Concrete Under Cyclic Load. Mater. Struct. 2006, 39, 717–724. [Google Scholar] [CrossRef]
- Göringer, J.; Foglar, M.; Jiříček, P. Impact performance of specimens subjected to fatigue loading—Experimental investigation. EPJ Web Conf. 2015, 94, 01058. [Google Scholar] [CrossRef]
- Liu, F.; Zhou, J. Fatigue Strain and Damage Analysis of Concrete in Reinforced Concrete Beams under Constant Amplitude Fatigue Loading. Shock Vib. 2016, 2016, 1–7. [Google Scholar] [CrossRef]
- Yadav, I.; Thapa, K. Fatigue Damage Model of Concrete Materials. Theor. Appl. Fract. Mech. 2020, 108. [Google Scholar] [CrossRef]
- Huang, W.; Gong, F.; Jin, W.; Maekawa, K. Numerical analysis of high and low-cycle flexural fatigue for reinforced concrete beams under full-range of varying amplitudes. Struct. Concr. 2021, 22, 2167–2183. [Google Scholar] [CrossRef]
- Huang, C.; Zhang, R.; Zhang, J.; Guo, X.; Wei, P.; Wang, L.; Huang, P.; Li, W.; Wang, Y. A novel method for fatigue design of FRP-strengthened RC beams based on machine learning. Compos. Struct. 2025, 359, 118867. [Google Scholar] [CrossRef]
- Maekawa, K.; Toongoenthong, K.; Gebreyouhannes, E.; Kishi, T. Direct Path-Integral Scheme for Fatigue Simulation of Reinforced Concrete in Shear. J. Adv. Concr. Technol. 2006, 4, 159–177. [Google Scholar] [CrossRef]
- Ibrahim, N.; Elkholy, S.; Godat, A. Finite Element Simulation of Reinforced Concrete Beams under Fatigue Loading. In Proceedings of the Seventh World Congress on Civil, Structural, and Environmental Engineering (ICSECT’22). 2022, Seventh World Congress on Civil, Structural, and Environmental Engineering (ICSECT’22), Lisbon, Portugal, 10–12 April 2022. [Google Scholar]
- Elkholy, S.; Salem, M.; Godat, A. Finite Element Models on Shear Behavior of Deep Beams Prepared Using Steel Fiber-Reinforced Recycled Coarse Aggregate Concrete. Fibers 2025, 13, 160. [Google Scholar] [CrossRef]
- Isojeh, B. Fatigue Damage Analysis of Reinforced Concrete Structural Elements. Ph.D. Thesis, University of Toronto, Toronto, ON, Canada, 2017. [Google Scholar]
- Isojeh, B.; Vecchio, F. Manual for Fatigue Analysis of RC Structural Elements Using Vector 2; Safe Technology Limited: Singapore, 2017. [Google Scholar]
- Wong, P.S.; Vecchio, F.J.; Trommels, H. Vector2 Formworks User’s Manual, 2nd ed.; University of Toronto: Toronto, ON, Canada, 2013. [Google Scholar]
- Baingo, D. A Framework for Stochastic Finite Element Analysis of Reinforced Concrete Beams Affected by Reinforcement Corrosion. Ph.D. Thesis, University of Ottawa, Ottawa, ON, Canada, 2012. [Google Scholar] [CrossRef]
- Mohamed, K.A. Performance and Strut Efficiency Factor of Concrete Deep Beams Reinforced with GFRP Bars. Ph.D. Thesis, Université De Sherbrooke, Sherbrooke, QC, Canada, 2015. [Google Scholar]
- Rezvanisharif, M.; Ketabi, M.S. FE Modeling and Seismic Performance Evaluation of Hybrid SMA-Steel RC Beam-Column Joints. Lat. Am. J. Solids Struct. 2019, 16, e192. [Google Scholar] [CrossRef]
- CSA A23.3-19; Design of Concrete Structures. Standard CSA-A23.3-19. Canadian Standards Association: Toronto, ON, Canada, 2019.
- Vecchio, F.; Collins, M. The Modified Compression-Field Theory for RC Elements Subjected to Shear. J. Am. Concr. Inst. 1986, 83, 219–281. [Google Scholar]
- Habibi, S. Finite Element Modelling of Corrosion-Damaged Reinforced Concrete Structures. Master’s Thesis, University of Toronto, Toronto, ON, Canada, 2017. Available online: https://www.proquest.com/docview/1934400235?pq-origsite=gscholar&fromopenview=true (accessed on 1 January 2017).
- Salgado, R.; Guner, S. A Numerical Analysis Methodology for the Strengthening of Deep Cap Beams. Spec. Publ. Adv. Concr. Bridges Des. Constr. Eval. Rehabil. 2019, 333, 1–18. [Google Scholar] [CrossRef]
- Baji, H.; Eslami, A.; Ronagh, H.R. Development of a nonlinear FE modelling approach for FRP-strengthened RC beam-column connections. Structures 2015, 3, 272–281. [Google Scholar] [CrossRef]
- Dutta, B.; Nath Nayak, A.; Nanda, B.; Dirar, S. Reinforced concrete deep beam shear retrofitted with deep embedded bars: A numerical investigation. Mater. Today Proc. 2022, 60, 281–287. [Google Scholar] [CrossRef]
- Isojeh, B.; Vecchio, F. Parametric Damage of Concrete under High-Cycle Fatigue Loading in Compression. In Proceedings of the 9th International Conference on Fracture Mechanics of Concrete and Concrete Structures, Berkeley, CA, USA, 29–1 May–June 2016. [Google Scholar] [CrossRef]
- Al-Rousan, R.; Issa, M. Fatigue performance of reinforced concrete beams strengthened with CFRP sheets. Constr. Build. Mater. 2011, 25, 3520–3529. [Google Scholar] [CrossRef]
- Arafa, A.; Ahmed, N.; Farghaly, A.S.; Chaallal, O.; Benmokrane, B. Exploratory Study on Incorporating Glass FRP Reinforcement to Control Damage in Steel-Reinforced Concrete Bridge Pier Walls. J. Bridge Eng. 2021, 26, 04020116. [Google Scholar] [CrossRef]
- Kent, D.C.; Park, R. Flexural Members with Confined Concrete. J. Struct. Div. 1971, 97, 1969–1990. [Google Scholar] [CrossRef]
- Hordijk, D.A. Local Approach to Fatigue of Concrete. Ph.D. Thesis, Technische Universiteit Delft, Delft, The Netherlands, 1993; p. 0368. Available online: https://www.elibrary.ru/item.asp?id=6852485 (accessed on 29 October 1993).
- IS 456; Plain and Reinforced Concrete—Code of Practice. Bureau of Indian Standards: New Delhi, India, 2000.
- Menin, R.; Trautwein, L.; Bittencourt, T. Smeared Crack Models for Reinforced Concrete Beams by Finite Element Method. Rev. Ibracon Estrut. E Mater. 2009, 2, 166–200. [Google Scholar] [CrossRef]
- Isojeh, B.; El-Zeghayar, M.; Vecchio, F. Concrete Damage under Fatigue Loading in Uniaxial Compression. ACI Mater. J. 2017, 114, 225–235. [Google Scholar] [CrossRef]
- Isojeh, B.; El-Zeghayar, M.; Vecchio, F. Simplified Constitutive Model for Fatigue Behavior of Concrete in Compression. J. Mater. Civ. Eng. 2017, 29. [Google Scholar] [CrossRef]
- Vecchio, F. Disturbed Stress Field Model for RC: Validation. J. Struct. Eng. 2001, 127, 350–358. [Google Scholar] [CrossRef]
- Lü, P.; Li, Q.; Song, Y. Damage Constitutive of Concrete under Uniaxial Alternate Tension–Compression Fatigue Loading Based on Double Bounding Surfaces. Int. J. Solids Struct. 2004, 41, 3151–3166. [Google Scholar] [CrossRef]
- Yu, S.; Sun, Z.; Yu, J.; Yang, J.; Zhu, C. An improved meshless method for modeling the mesoscale cracking processes of concrete containing random aggregates and initial defects. Constr. Build. Mater. 2023, 363, 129770. [Google Scholar] [CrossRef]
- Murthy, A.R.; Karihaloo, B.L.; Vindhya Rani, P.; Shanmuga Priya, D. Fatigue behaviour of damaged RC beams strengthened with ultra high performance fibre reinforced concrete. Int. J. Fatigue 2018, 116, 659–668. [Google Scholar] [CrossRef]
- Papakonstantinou, C.; Balaguru, P.; Petrou, M. Analysis of Reinforced Concrete Beams Strengthened with Composites Subjected to Fatigue Loading. ACI Spec. Publ. SP 2002, 206, 41–60. [Google Scholar] [CrossRef]
- Asgari, B.; Osman, S.; Adnan, A. Sensitivity Analysis of the Influence of Structural Parameters on Dynamic Behaviour of Highly Redundant Cable-Stayed Bridges. Adv. Civ. Eng. 2013, 2013, 1–11. [Google Scholar] [CrossRef]
- Vass, G. Finite Element Modelling of Different Strengthening Strategies for Reinforced Concrete Deep Beams. [Université de Liège > conv Erasmus en sc Appl]. Master’s Thesis, Université de Liège, Liège, Belgium, 2018. Available online: https://matheo.uliege.be/handle/2268.2/4439 (accessed on 1 January 2018).
- Baktheer, A.; Chudoba, R. Experimental and theoretical evidence for the load sequence effect in the compressive fatigue behavior of concrete. Mater. Struct. 2021, 54, 82. [Google Scholar] [CrossRef]
- Godat, A.; Qu, Z.; Lu, X.Z.; Labossière, P.; Ye, L.P.; Neale, K.W. Size Effects for Reinforced Concrete Beams Strengthened in Shear with CFRP Strips. J. Compos. Constr. 2010, 14, 260–271. [Google Scholar] [CrossRef]
- Luo, C.; Yang, P.; Niu, Y.; Zhang, Y.; Cheng, C. Analytical method of incorporating failure probability to predict the fatigue life of ultra-high-performance concrete (UHPC). Front. Built. Environ. 2024, 10, 1403245. [Google Scholar] [CrossRef]
- Al-musawi, H.; Figueiredo, F.P.; Guadagnini, M.; Pilakoutas, K. Shrinkage properties of plain and recycled steel–fibre-reinforced rapid hardening mortars for repairs. Constr. Build. Mater. 2019, 197, 369–384. [Google Scholar] [CrossRef]
- Ding, Y.; Fang, Y.; Jin, W.; Zhang, J.; Li, B.; Mao, J. Numerical Method for Creep Analysis of Strengthened Fatigue-Damaged Concrete Beams. Buildings 2023, 13, 968. [Google Scholar] [CrossRef]
- Zhu, L.; Wang, J.; Li, X.; Zhao, G.Y.; Huo, X.J. Experimental and numerical study on creep and shrinkage effects of ultra high-performance concrete beam. Compos. Part B 2020, 184, 107713. [Google Scholar] [CrossRef]
- Dellepiani, M.G.; Vega, C.R.; Pina, J.C.; Flores, E.I. Numerical investigation on the creep response of concrete structures by means of a multi-scale strategy. Constr. Build. Mater. 2020, 263, 119867. [Google Scholar] [CrossRef]




| Material | Factor | Constitutive Model |
|---|---|---|
| Concrete | Compression Pre-Peak | Hognestad (Parabola) |
| Compression Post-Peak | Modified Park-Kent | |
| Compression Softening | Vecchio 1992-A | |
| Tension-Stiffening | Modified Bentz 2005 | |
| Tension-Softening | Nonlinear (Hordjik) | |
| Steel Reinforcement | Hysteretic Response | Bauschinger Effect (Seckin) |
| No. | Beam Sets | Specimen | Beam Dimensions (mm) | a/d 1 | Cross-Section Type | ||||
|---|---|---|---|---|---|---|---|---|---|
| Span Length | Web Width | Flange Width | Web Height | Flange Depth | |||||
| 1 | Murthy et al. [61] | FBA | 1200 | 100 | - | 200 | - | 2.00 | R-section 2 beam |
| 2 | Chaallal et al. [15,25] | CON-S0 | 3110 | 152 | 508 | 304 | 406 | 3.00 | T-section beam |
| 3 | Chaallal et al. [15,25] | CON-S1 | 3110 | 152 | 508 | 304 | 406 | 3.00 | T-section beam |
| 4 | Chaallal et al. [15,25] | CON-S3 | 3110 | 152 | 508 | 304 | 406 | 3.00 | T-section beam |
| 5 | Papakonstantinou et al. [8,62] | N-1 | 1220 | 152.4 | - | 152.4 | - | 2.67 | R-section beam |
| 6 | Papakonstantinou et al. [8,62] | N-6 | 1220 | 152.4 | - | 152.4 | - | 2.67 | R-section beam |
| 7 | Papakonstantinou et al. [8,62] | N-8 | 1220 | 152.4 | - | 152.4 | - | 2.67 | R-section beam |
| No. | Beam Sets | Specimen | fc’ (MPa) | Longitudinal Steel | Transverse Steel | ||||
|---|---|---|---|---|---|---|---|---|---|
| Top | Bottom | ||||||||
| Diameter (mm) | Yield Stress (MPa) | Diameter (mm) | Yield Stress (MPa) | Diameter (mm) and Spacing (mm) | Yield Stress (MPa) | ||||
| 1 | Murthy et al. [61] | FBA | 35 | 2 Φ8 | 300 | 2 Φ10 | 590 | 6 @ 100 | 240 |
| 2 | Chaallal et al. [15,25] | CON-S0 | 31 | 6 Φ10 | 480 | 4 Φ25 | 500 | None | - |
| 3 | Chaallal et al. [15,25] | CON-S1 | 31 | 6 Φ10 | 480 | 4 Φ25 | 500 | 8 @ 175 | 540 |
| 4 | Chaallal et al. [15,25] | CON-S3 | 31 | 6 Φ10 | 480 | 4 Φ25 | 500 | 8 @ 260 | 540 |
| 5 | Papakonstantinou et al. [8,62] | N-1 | 39.3 | 2 Φ13 | 427 | 2 Φ13 | 427 | 10 @ 50 | 320 |
| 6 | Papakonstantinou et al. [8,62] | N-6 | 39.3 | 2 Φ13 | 427 | 2 Φ13 | 427 | 10 @ 50 | 320 |
| 7 | Papakonstantinou et al. [8,62] | N-8 | 39.3 | 2 Φ13 | 427 | 2 Φ13 | 427 | 10 @ 50 | 320 |
| No. | Beam Sets | Specimen | Applied Load | Load Amplitude | Frequency (Hz) | |||
|---|---|---|---|---|---|---|---|---|
| Load Level 1 (%) | Loads (kN) | |||||||
| Max. | Min | Max | Min | (%) | ||||
| 1 | Murthy et al. [61] | FBA | 87 | 8.7 | 68.0 | 6.8 | 10 | 2 |
| 2 | Chaallal et al. [15,25] | CON-S0 | 65 | 35 | 89.0 | 48.0 | 54 | 3 |
| 3 | Chaallal et al. [15,25] | CON-S1 | 65 | 35 | 273.0 | 128.0 | 47 | 3 |
| 4 | Chaallal et al. [15,25] | CON-S3 | 65 | 35 | 191.0 | 103.0 | 54 | 3 |
| 5 | Papakonstantinou et al. [8,62] | N-1 | ---- 2 | ---- | ---- | ---- | ---- | ---- |
| 6 | Papakonstantinou et al. [8,62] | N-6 | 73 | 6 | 53.4 | 4.4 | 8 | 2 |
| 7 | Papakonstantinou et al. [8,62] | N-8 | 85 | 4 | 40.0 | 3.3 | 8 | 3 |
| Specimen | Experimental Results | Numerical Results (VecTor2 Damage Model) | Numerical Results (External Damage Model) | Cycle Number | ||
|---|---|---|---|---|---|---|
| Max. Def. (mm) 1 | Max. Def. (mm) | Difference (%) * | Max. Def. (mm) | Difference (%) * | ||
| FBA [61] | 5.36 | 3.83 | −28.71 | 3.77 | −29.79 | 1200 |
| 5.37 | 3.83 | −28.72 | 3.75 | −30.10 | 1600 | |
| 5.56 | 3.83 | −31.16 | 4.24 | −23.73 | 5000 | |
| 5.75 | 3.83 | −33.47 | 4.40 | −23.50 | 10,000 | |
| 5.99 | 3.83 | −36.13 | 3.96 | −33.89 | 15,000 | |
| 6.13 | 3.83 | −37.64 | 4.19 | −31.64 | 20,000 | |
| 6.33 | 3.83 | −39.54 | 4.41 | −30.34 | 25,000 | |
| 6.33 | 3.83 | −39.59 | 6.00 | −5.51 | 30,000 | |
| 14.92 | 3.83 | −74.36 | 13.76 | −7.74 | 35,000 | |
| CON-S0 [15,25] | 1.60 | 1.63 | 2.26 | 1.63 | 2.26 | 0 |
| 2.03 | 1.87 | −7.87 | 2.01 | −1.28 | 1,000,000 | |
| 2.12 | 1.87 | −11.57 | 2.07 | −2.03 | 2,000,000 | |
| 2.15 | 1.87 | −12.89 | 2.21 | 3.03 | 3,000,000 | |
| 2.21 | 1.87 | −15.18 | 2.30 | 4.21 | 4,688,000 | |
| CON-S1 [15,25] | 6.02 | 6.38 | 5.91 | 6.65 | 10.42 | 0 |
| 7.26 | 6.41 | −11.63 | 6.88 | −5.24 | 1,000,000 | |
| 7.69 | 6.41 | −16.57 | 7.39 | −3.85 | 2,000,000 | |
| 8.17 | 6.41 | −21.49 | 8.14 | −0.34 | 3,000,000 | |
| 8.31 | 6.41 | −22.78 | 8.73 | 5.06 | 3,600,000 | |
| 9.06 | 6.41 | −29.20 | 9.31 | 2.73 | 3,870,000 | |
| CON-S3 [15,25] | 4.22 | 5.33 | 26.30 | 5.59 | 32.46 | 0 |
| 5.78 | 5.28 | −8.65 | 5.65 | −2.25 | 1,000,000 | |
| 6.11 | 5.28 | −13.49 | 5.79 | −5.19 | 2,000,000 | |
| 6.22 | 5.28 | −14.99 | 6.00 | −3.54 | 3,000,000 | |
| 6.38 | 5.28 | −17.15 | 6.40 | 0.41 | 4,000,000 | |
| 6.46 | 5.28 | −18.19 | 6.51 | 0.81 | 5,000,000 | |
| 6.60 | 5.28 | −19.88 | 6.66 | 1.00 | 5,766,000 | |
| N-6 [8,62] | 5.32 | 3.81 | −28.38 | 4.06 | −23.63 | 0 |
| 5.48 | 3.80 | −30.66 | 4.04 | −26.22 | 6500 | |
| 5.70 | 3.80 | −33.33 | 4.07 | −28.58 | 11,400 | |
| 5.80 | 3.80 | −34.48 | 4.79 | −17.53 | 112,000 | |
| 6.29 | 3.80 | −39.59 | 6.50 | 3.45 | 151,000 | |
| 10.10 | 3.80 | −62.38 | 10.31 | 2.08 | 153,000 | |
| N-8 [8,62] | 3.69 | 2.56 | −30.56 | 2.74 | −25.75 | 1600 |
| 3.79 | 2.55 | −32.66 | 2.74 | −27.70 | 163,000 | |
| 3.68 | 2.56 | −30.35 | 2.79 | −24.27 | 980,000 | |
| 3.68 | 2.56 | −30.33 | 2.81 | −23.65 | 1,176,000 | |
| 3.73 | 2.56 | −31.25 | 2.86 | −23.26 | 2,026,000 | |
| 3.78 | 2.55 | −32.39 | 3.02 | −20.13 | 3,137,000 | |
| 3.82 | 2.56 | −32.98 | 3.20 | −16.29 | 4,052,000 | |
| 4.19 | 2.56 | −38.96 | 3.75 | −10.47 | 5,180,000 | |
| 5.63 | 2.55 | −54.65 | 5.30 | −5.88 | 6,013,000 | |
| Average | 26.11 | 10.60 | ||||
| STDV | 17.37 | 14.63 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license.
Share and Cite
Ibrahim, N.; Elkholy, S.; Godat, A. Numerical Prediction for Reinforced Concrete Beams Subjected to Monotonic Fatigue Loading Using Various Concrete Damage Models. Buildings 2026, 16, 175. https://doi.org/10.3390/buildings16010175
Ibrahim N, Elkholy S, Godat A. Numerical Prediction for Reinforced Concrete Beams Subjected to Monotonic Fatigue Loading Using Various Concrete Damage Models. Buildings. 2026; 16(1):175. https://doi.org/10.3390/buildings16010175
Chicago/Turabian StyleIbrahim, Nagwa, Said Elkholy, and Ahmed Godat. 2026. "Numerical Prediction for Reinforced Concrete Beams Subjected to Monotonic Fatigue Loading Using Various Concrete Damage Models" Buildings 16, no. 1: 175. https://doi.org/10.3390/buildings16010175
APA StyleIbrahim, N., Elkholy, S., & Godat, A. (2026). Numerical Prediction for Reinforced Concrete Beams Subjected to Monotonic Fatigue Loading Using Various Concrete Damage Models. Buildings, 16(1), 175. https://doi.org/10.3390/buildings16010175