Experimental Study on the Mechanical Performance of Cast-in-Place Base Joints for X-Shaped Columns in Cooling Towers

Abstract

The supporting system of super-large cooling towers is crucial for the structural safety of nuclear power plants. The X-shaped reinforced concrete column has emerged as a promising solution due to its superior stability. However, the performance of the cast-in-place base joint, which is a key force-transfer component, requires thorough investigation. This study experimentally investigates the mechanical performance of the joints under ultimate vertical compressive and tensile loads. The loads represent gravity-dominated and extreme wind uplift scenarios, respectively. A comprehensive testing program monitored load–displacement responses, strain distributions, crack propagation, and failure modes. The compression specimen failed in a ductile flexural compression manner with plastic hinge formation above the column base. In contrast, the tension specimen exhibited a tension-controlled failure pattern. Crucially, the joint remained stable after column yielding in both loading scenarios. The result validates the “strong connection–weak member” design principle. The findings confirm that the proposed cast-in-place joint possesses excellent load-bearing capacity and ductility. Therefore, the study provides a reliable design basis for the supporting structures of super-large cooling towers.

1. Introduction

The transformation of the energy structure represents a critical issue for contemporary society. Traditional energy sources with high pollution and emission levels are gradually being replaced by cleaner alternatives. As an economical and efficient energy source, nuclear power plays a significant role in driving this energy transition and achieving green, low-carbon development. During operation, nuclear power plants generate substantial amounts of heat, which must be dissipated into the environment via cooling systems to maintain normal reactor function. As the core component of cooling system, the cooling tower bears the crucial responsibility of transferring heat from the circulating water to the atmosphere [1]. However, numerous challenges persist in the design and construction of cooling towers. For most inland nuclear power plants, limited to circulating water systems of conventional thermal power plants, the construction of large-scale cooling towers is essential to ensure adequate heat rejection. In the future, nuclear plants will require even taller and larger cooling towers to meet enhanced cooling demands and support the reliable application of nuclear energy. Consequently, it is necessary to conduct in-depth research on the design and construction of super-large cooling towers.

Currently, the main structures of cooling towers are predominantly constructed from reinforced concrete. Based on the structural behavior, cooling tower structures can be divided into the bottom supporting columns and the upper hyperbolic shell, typically built using full scaffolding, cast-in-place and slip-form construction techniques, respectively [2,3]. Large cooling towers are recognized as some of the largest reinforced concrete thin-shell structures in the world, and wind loads are the primary design consideration [4]. With the advancement of nuclear power, research focus must extend beyond the upper shell to critically examine the supporting columns. By supporting the shell and transferring gravity loads, wind loads, and other forces, the strength and stiffness of the supporting columns significantly influence the overall performance of the cooling tower. Historical incidents, such as the collapse of cooling towers at the Ferry Bridge Power Plant in 1965 and the Fiddlers Ferry Power Plant in 1984 in the UK, underscore the critical impact of wind on these structures [5]. Furthermore, multiple cooling tower failures throughout history demonstrate that the wind resistance is closely linked to the performance of the supporting columns [6,7,8]. Currently, the tower heights specified in existing cooling tower design codes [9,10,11,12] are insufficient to meet the requirements of modern engineering projects, making research on the supporting columns for super-large cooling towers a pressing issue. Therefore, to better fulfill the cooling demands of nuclear power plants, this study focuses on a detailed investigation of the supporting columns for super-large cooling towers.

Rajashekhar et al. [13] analyzed the static and dynamic performance of the cooling tower. Considering different column support systems, the relationship between the throat height and the total height was explored. Zhu et al. [14] investigated the effects of different cross-sectional shapes and types of support columns on the dynamic characteristics, load-bearing capacity, and stability of cooling tower structures. The findings indicated that X-shaped columns exhibit superior structural stability and wind resistance, while inverted V-shaped columns offer construction simplicity while meeting code requirements. Chen has conducted a series of studies on cooling tower support column selection. In 2021, Chen et al. [15] investigated the stability of slender concrete-filled steel tubular (CFST) X-shaped columns through combined experimental and numerical analysis, leading to an improved design method for conservatively predicting the axial compressive capacity. In 2022, Chen [16] conducted integrated theoretical, experimental, and finite element studies on the mechanical behavior of crossed CFST columns. The structural responses of cooling towers employing crossed CFST columns were analyzed under various load combinations. Section design and selection for the CFST members were performed according to the specific characteristics of cooling tower structures and the forms of loading. Furthermore, in 2023, Chen et al. [17] conducted theoretical and experimental investigations into the stability of CFST X-shaped columns considering variations in flexural rigidity. The study highlighted that the concrete infill and the irregular, longitudinally varying cross-sections are responsible for significant changes in bending stiffness. Beyond static and wind loads, the mechanical performance of cooling tower support columns under seismic loading also significantly influences the overall structural stability and safety. In 1980, Wolf et al. [18] conducted a parametric analysis of concrete cooling towers, revealing that the support columns and the foundations constitute the most vulnerable structural components, playing a decisive role in the seismic response. The study recommended maximizing the inclination angle of the inclined columns in the plan to enhance seismic performance. In 1981, Nelson [19] found that the angle between the lower support columns and the horizontal ground plane has a considerable effect on the lower-order vibration frequencies of large hyperbolic cooling towers, while changes in Poisson’s ratio have a minimal effect. Sabouri-Ghomi et al. [20] performed finite element analyses focusing on stress concentration, nonlinear behavior, stability, and safety factors of cooling tower structures under seismic action. The results demonstrated that plastic hinges form in the X-shaped support columns during earthquakes, leading to a reduction in the structural safety factor. Ziraoui et al. [21] utilized SAP2000 (SPA2000, 2011) to analyze the seismic behavior of a reinforced concrete cooling tower, simulating and evaluating the structural response to seismic loads from both near-field and far-field ground motions. Recently, in 2025, Zheng et al. [22] investigated the seismic response of concrete cooling towers with corroded shell reinforcement, demonstrating that corrosion-induced stiffness loss alters dynamic properties, intensifies stress concentration, and redirects energy dissipation.

The review shows that although CFST and steel X-shaped members have been proposed as supporting columns [23,24], the practical application in super-large cooling towers faces significant challenges. The challenges include demanding corrosion protection requirements leading to high maintenance costs [25,26], potential concrete placement and steel tube deformation issues during construction for CFST [27], and complex joint details with stringent installation precision for steel structures [28]. Consequently, the reinforced concrete X-shaped column emerges as a more viable solution. However, the column base connection has been identified as a critical and potentially vulnerable region. Therefore, this study aims to evaluate the mechanical performance and validate the reliability of cast-in-place reinforced concrete X-shaped column base joints. The research focuses on analyzing the behavior of cooling tower column base joints under both the vertical compressive loads induced by gravity and the vertical tensile loads generated under extreme wind conditions.

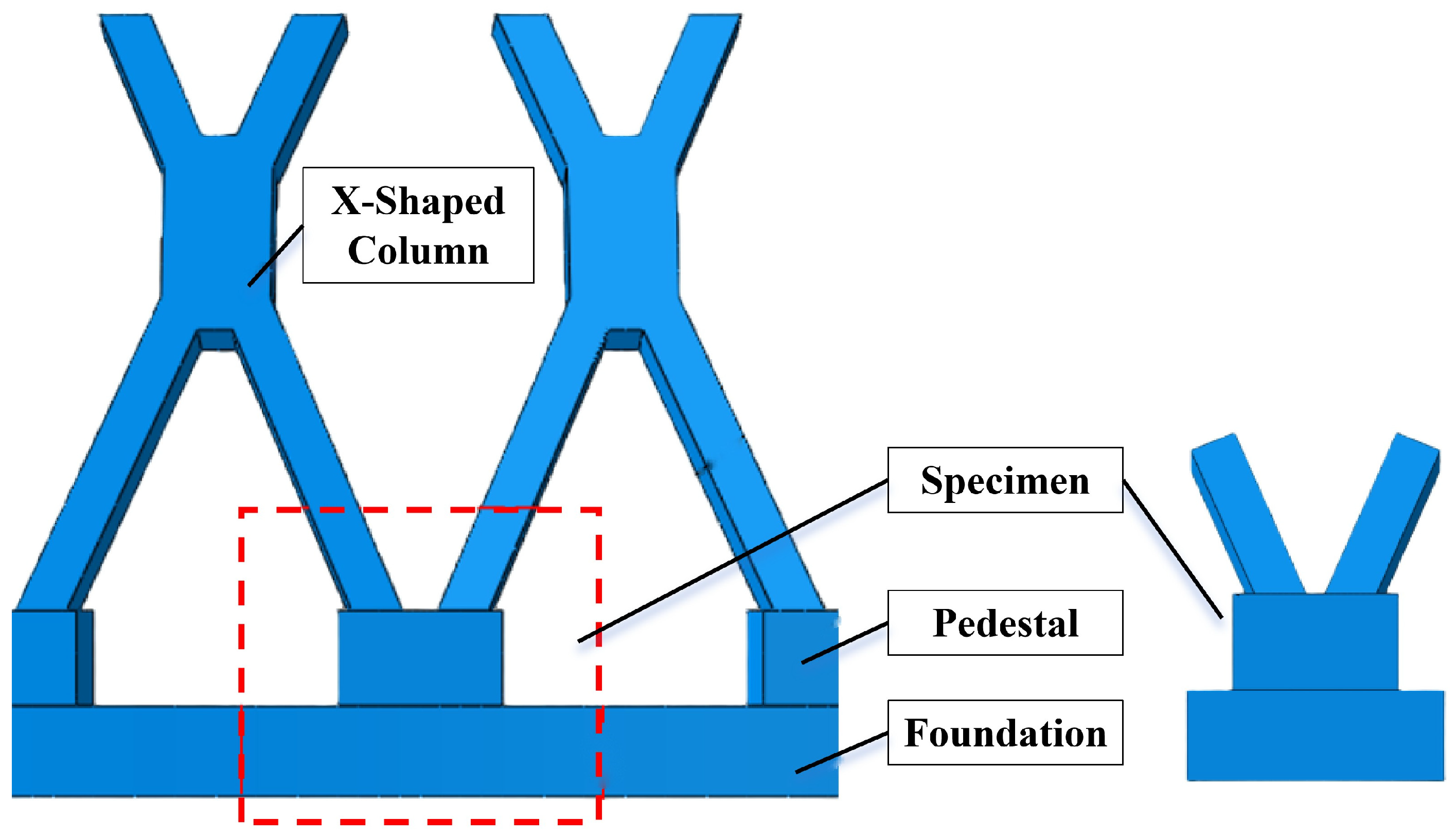
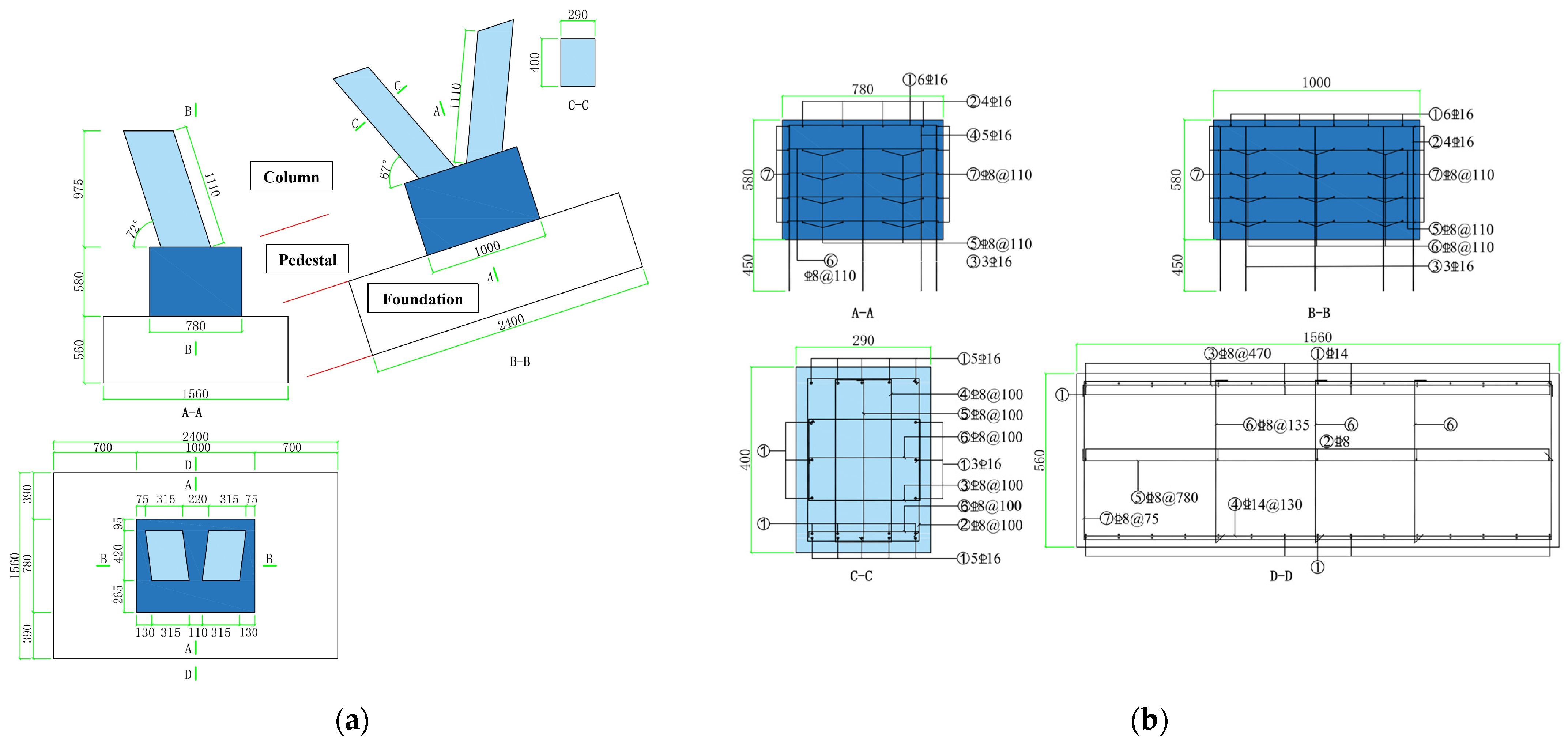
2. Experimental Program

2.1. Specimens and Material

The physical test models in this study were developed based on a large nuclear power plant cooling tower. Selecting the column base as the core, an isolated “single pedestal–dual column” substructure was selected as the research subject, as shown in Figure 1. Two test specimens were designed: specimen JD-1 for vertical compression and specimen JD-2 for vertical tension. The physical model consisted of a ring foundation, a central pedestal, and two inclined legs from two X-shaped columns, all cast monolithically from bottom to top during construction. To facilitate the application of the vertical uplift load, a connecting beam was designed at the top of the columns in the tension specimen JD-2. Both specimens were identical in geometric dimensions and concrete cover thickness. The detailed dimensions and reinforcement arrangement of the cast-in-place joint are shown in Figure 2.

The concrete material testing was conducted in accordance with the Chinese standard “Standard for Test Methods of Concrete Physical and Mechanical Properties” [29]. During each concrete casting process, samples were reserved to fabricate nine standard 150 mm cubes for compressive strength testing. The main mechanical properties of the cast-in-place concrete were measured, with the material properties of concrete at different structural locations summarized in

Table 1. Material properties of concrete (Unit: MPa).

Part	fcu	fc	ft	E
Column	51.3	39.0	3.5	35,770.8
Pedestal	46.0	35.0	3.3	33,854.7
Foundation	45.6	34.7	3.2	33,772.7

.

The testing of reinforcement mechanical properties was conducted in accordance with the Chinese standard “Metallic materials—Tensile testing—Part 1: Method of test at room temperature” [30]. Tensile tests were performed on reinforcement to determine the key mechanical properties. The material characteristics of reinforcement with different diameters are presented in

Table 2. Material properties of reinforcement.

Diameter (mm)	δ (%)	fy (MPa)	ft (MPa)
8	16.0	473	645
14	17.5	433	621
16	15.0	443	630

.

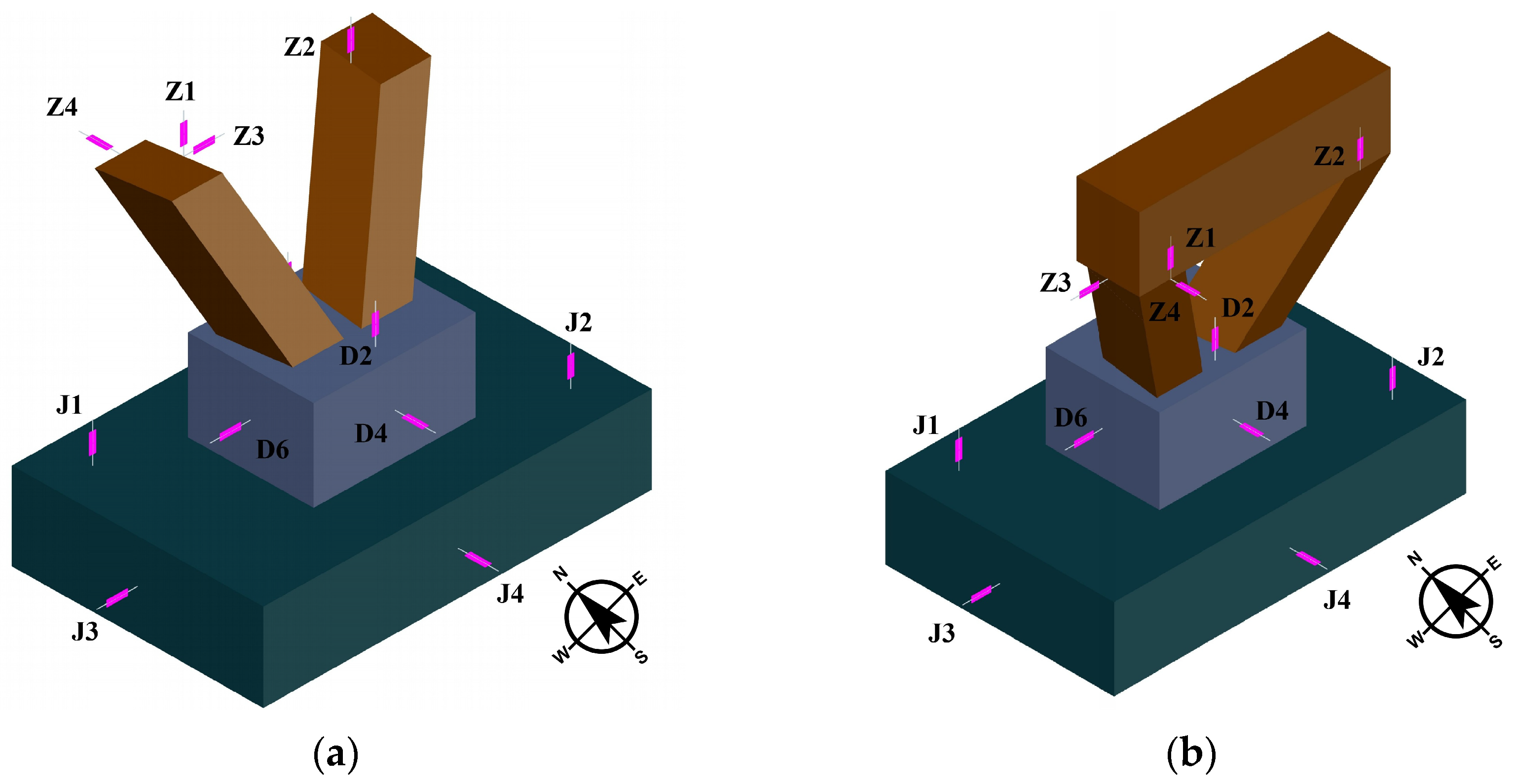
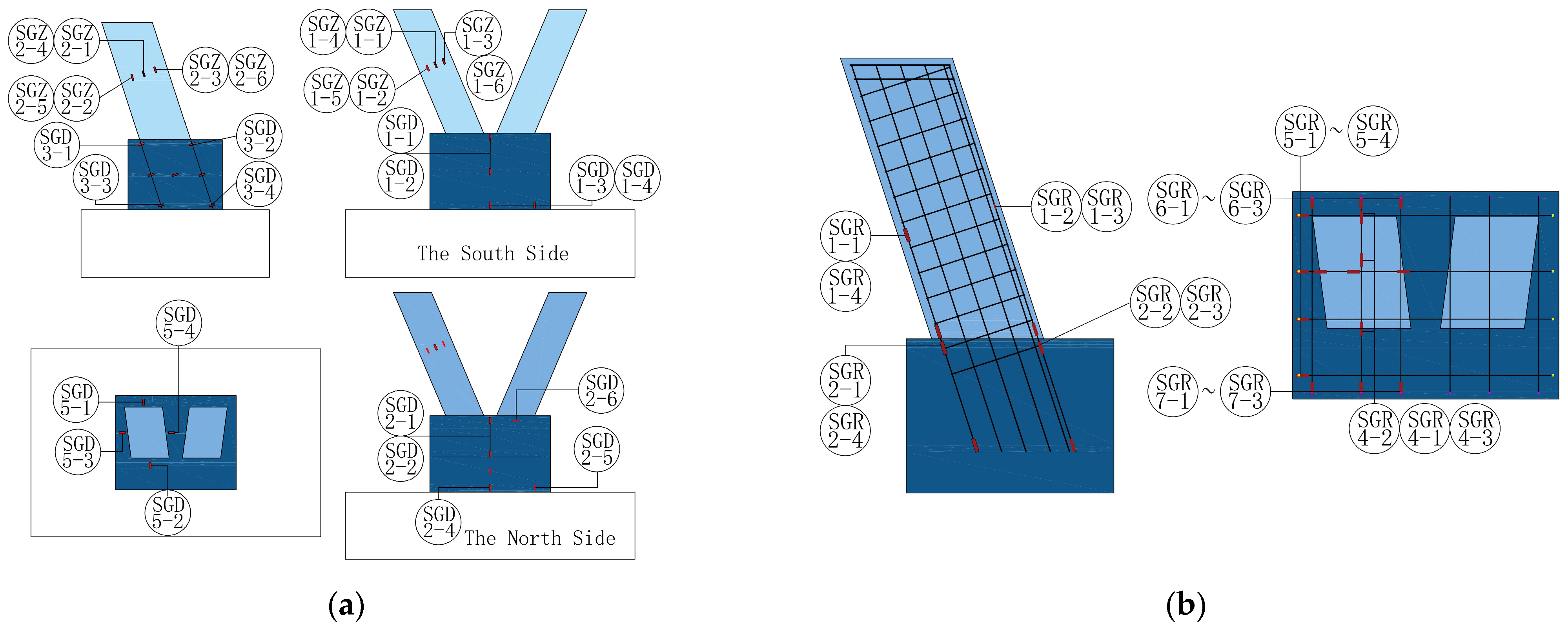
2.2. Test Setup and Loading History

The specimens were tested through a 4000 kN reaction frame, as illustrated in Figure 3. The ring foundation of the specimen was secured at both ends by fixed beams, which were anchored to the laboratory’s strong floor using ground anchor bolts. The loading system consisted of two 2000 kN hydraulic jacks. For the compression test on specimen JD-1, one jack was positioned on each inclined column to apply synchronized vertical downward compression. For the tension test on specimen JD-2, both jacks were placed beneath the connecting beam, enabling synchronized vertical upward tension through jack lifting.

To analyze the load-bearing capacity and stiffness variation in the specimens, linear variable differential transformers (LVDTs) were installed at the column tops, pedestal, and ring foundation. Four LVDTs (Z1–Z4) were positioned at the top of the columns to measure displacements in three directions during loading. Six LVDTs (D1–D6) were arranged on the top and around the pedestal to monitor the displacement and potential expansion and contraction. Another four LVDTs (J1–J4) were placed on the top and sides of the ring foundation to record the overall displacement of the specimen. The specific arrangement is detailed in Figure 4.

The strain state of the specimens during loading was monitored using strain gauges installed at corresponding locations. The instrumentation included both concrete surface strain gauges and reinforcement strain gauges, with the arrangement detailed in Figure 5.

Specimens were coated with white aqueous paint and marked with 100 mm spaced black grids using permanent markers. This grid system enabled precise documentation of crack dimensions, locations, and damage progression. Cracks were traced with color-coded markers: red for west column and blue for east column.

Prior to formal testing, a preloading procedure was implemented to verify the proper functioning of the data acquisition system and to eliminate any systemic gaps between the specimen and the test setup. Following preloading, the specimens were unloaded, and all measurement channels were subjected to zero-drift correction. The formal loading protocol subsequently employed a combined load–displacement control scheme, conducted in accordance with the procedures specified in the Chinese standard “Standard for Test Methods of Concrete Structures” [31]. During the elastic stage, load control was applied at a rate of 1 kN/s, with load increments of 100 kN and a holding time of 10 min at each level. Upon reaching the inelastic stage, displacement control was implemented at a rate of 0.5 mm/min, using displacement increments of 2 mm and maintaining a 10-min holding period at each level.

Test termination criteria included either (a) degradation to 85% of peak load capacity P_max or (b) observable severe damage modes.

3. Test Results and Analysis

3.1. Crack Propagation and Failure State

3.1.1. Compression Specimen

Based on experimental observations of the compression specimen of cast-in-place column base joint, the loading process was categorized into six distinct phases:

Phase 1:

Initial loading showed no visible deformation, though pre-existing microcracks from construction and curing were observed on concrete surfaces.

Phase 2:

Fine cracks developed in both the east and west columns. The cracks initially appeared at the common edge on the south side of the X-shaped columns and subsequently propagated across both adjacent surfaces, as shown in Figure 6. Concurrently, cracks emerged at the interface between the top surface of the pedestal and the columns.

Figure 6. Failure morphology diagram of specimen JD-1 in phase 2. (a) Phase 2 integral structure. (b) Phase 2 partial view.

Figure 6. Failure morphology diagram of specimen JD-1 in phase 2. (a) Phase 2 integral structure. (b) Phase 2 partial view.

Phase 3:

The loading mode was switched to displacement control. Superficial cement peeling was observed on the concrete surface at the bottom of the columns on north side. Meanwhile, the cracks on the top surface of the pedestal began to extend radially.

Phase 4:

Concrete crushing occurred at the bottom of the north side of the columns. A pronounced, elongated crack developed on the pedestal’s top surface, accompanied by the appearance of fine cracks on the south face, as depicted in Figure 7.

Figure 7. Failure morphology diagram of specimen JD-1 in phase 4. (a) Phase 4 integral structure. (b) Phase 4 partial view.

Figure 7. Failure morphology diagram of specimen JD-1 in phase 4. (a) Phase 4 integral structure. (b) Phase 4 partial view.

Phase 5:

Localized concrete spalling was observed at the bottom of the north side of the inclined columns. A prominent transverse crack developed on the south face of the pedestal, while fine cracks initiated on its east and west sides.

Phase 6:

The crack patterns in the columns fully developed. Extensive concrete spalling occurred at the bottom of the north side of the columns, with a visible separation gap appearing between the column bases and the pedestal top surface. The pedestal top surface showed slight upward bulging, while the cracks on the east and west sides remained relatively narrow, as shown in Figure 8.

Figure 8. Failure morphology diagram of specimen JD-1 in phase 6. (a) Phase 6 integral structure. (b) Phase 6 partial view.

Figure 8. Failure morphology diagram of specimen JD-1 in phase 6. (a) Phase 6 integral structure. (b) Phase 6 partial view.

Based on the experimental observations described above, it can be concluded that the failure mode of the JD-1 joint is characterized by eccentric compression failure of the X-shaped columns, exhibiting typical features of large eccentricity. The initial failure occurred at the base of the columns. Cracks developed in the tensile zone, showing a direct correlation with the magnitude of the bending moment within the columns. As the load increased, plastic hinges formed after the reinforcement yielded, transitioning the column from the elastic to the plastic stage, and the concrete in the compression zone was crushed eventually. This column–pedestal joint effectively realized a column–hinge energy dissipation mechanism. As the load increased, damage to the pedestal remained relatively minor, primarily manifesting as cracks on the top surface and horizontal cracks on the south face. The top-surface cracks in the pedestal, located between the two column roots, resulted from tensile stresses generated at the bases of the columns. The horizontal cracks on the front face of the pedestal aligned with the anchorage edge of the main longitudinal reinforcement from the columns, which is attributed to the abrupt change in cross-section caused by the embedded column reinforcement. Additionally, upward arching of the concrete at the top of the pedestal was observed. Overall, damage was predominantly concentrated in the columns. The connection at the pedestal was proven reliable, with minimal damage. The main findings demonstrate that the cast-in-place reinforced concrete column base joint provides a reliable fixity effect and adheres to the “strong connection–weak member” design principle.

3.1.2. Tension Specimen

Based on experimental observations of the tension specimen of cast-in-place column base joint, the loading process was categorized into six distinct phases:

Phase 1:

During the initial loading stage, no significant deformation was observed in the east and west columns, and no new cracks appeared on the concrete surfaces of either the inclined columns or the pedestal.

Phase 2:

Cracks developed in both columns, initiating from the edge on the south side of the X-shaped columns and subsequently propagating across both adjacent surfaces. The widest crack was observed at the interface between the top surface of the pedestal and the columns, as shown in Figure 9.

Figure 9. Failure morphology diagram of specimen JD-2 in phase 2. (a) Phase 2 integral structure. (b) Phase 2 partial view.

Figure 9. Failure morphology diagram of specimen JD-2 in phase 2. (a) Phase 2 integral structure. (b) Phase 2 partial view.

Phase 3:

Cracks on the surfaces of the X-shaped inclined columns continued to propagate. Cracks emerged on the top surface of the pedestal, initiating from the midpoint between the two column bases and extending towards the south face, where they developed into vertical cracks. A limited number of transverse cracks appeared on the south face of the pedestal, while minor diagonal cracks formed on its east and west sides.

Phase 4:

The loading mode was switched to displacement control. The crack pattern in the columns stabilized, with further development primarily manifesting as crack width enlargement. On the south face of the pedestal, the transverse cracks propagated completely across the surface and intersected with the vertical cracks, as shown in Figure 10.

Figure 10. Failure morphology diagram of specimen JD-2 in phase 4. (a) Phase 4 integral structure. (b) Phase 4 partial view.

Figure 10. Failure morphology diagram of specimen JD-2 in phase 4. (a) Phase 4 integral structure. (b) Phase 4 partial view.

Phase 5:

The crack patterns in the columns remained. A prominent transverse crack developed at the bottom of the south face of the pedestal, while additional vertical cracks formed at the top of the same face and propagated downward. The diagonal cracks on the east and west sides of the pedestal continued to extend.

Phase 6:

The cracks were fully developed, parallel to each other along the direction of the column sections. On the south face of the pedestal, transverse and vertical cracks intersected, forming a grid-like pattern. The diagonal cracks on the east and west sides propagated from the south edge toward the mid-section of the pedestal, as shown in Figure 11.

Figure 11. Failure morphology diagram of JD-2 specimen, phase 6. (a) Phase 6 integral structure. (b) Phase 6 partial view.

Figure 11. Failure morphology diagram of JD-2 specimen, phase 6. (a) Phase 6 integral structure. (b) Phase 6 partial view.

Based on the experimental observations, the failure mode of the JD-2 joint is identified as eccentric tension failure of the X-shaped inclined columns, exhibiting characteristic features of small eccentricity. Cracks initially developed in the mid-height region of the columns and subsequently propagated towards both ends. As the load increased, the tensile reinforcement at the column bases yielded first. After the structure entered the inelastic stage, extensive cracking occurred in the pedestal concrete, primarily manifesting as cracks on the top surface, front face, and east and west sides. The top-surface cracks were induced by tensile forces transferred from the columns; the horizontal cracks on the front face corresponded to the anchorage depth of the main column reinforcement; and the cracks on the east and west sides originated from the splitting effect of the anchored column reinforcement on the surrounding pedestal concrete.

Compared to the JD-1 specimen, the cracks in the columns of JD-2 were more uniform, while the pedestal experienced more significant damage. The main findings indicate that under tensile loading, the failure of the cast-in-place joint is dominated by damage to both the columns and the pedestal, while still maintaining the fundamental “strong connection–weak member” mechanism.

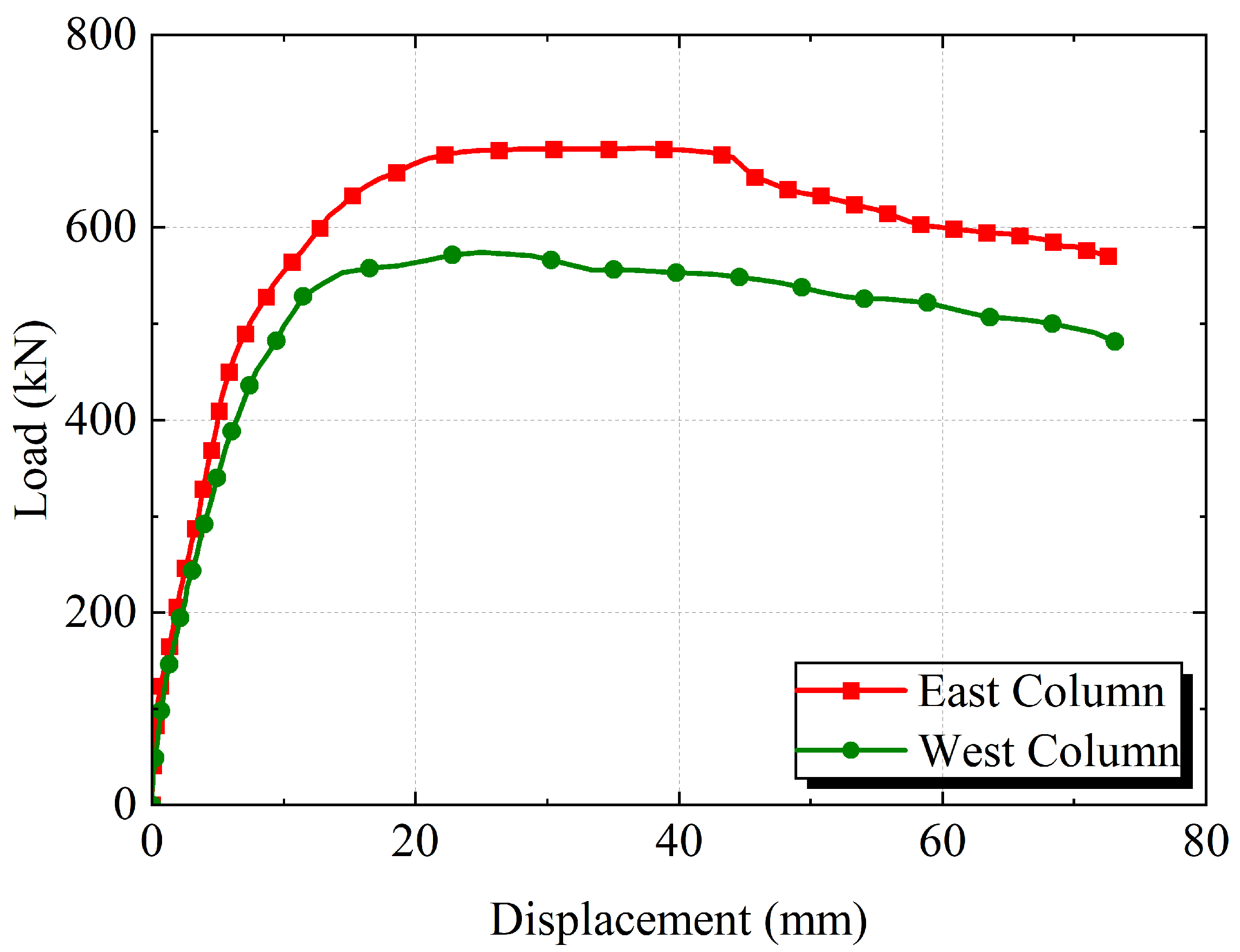
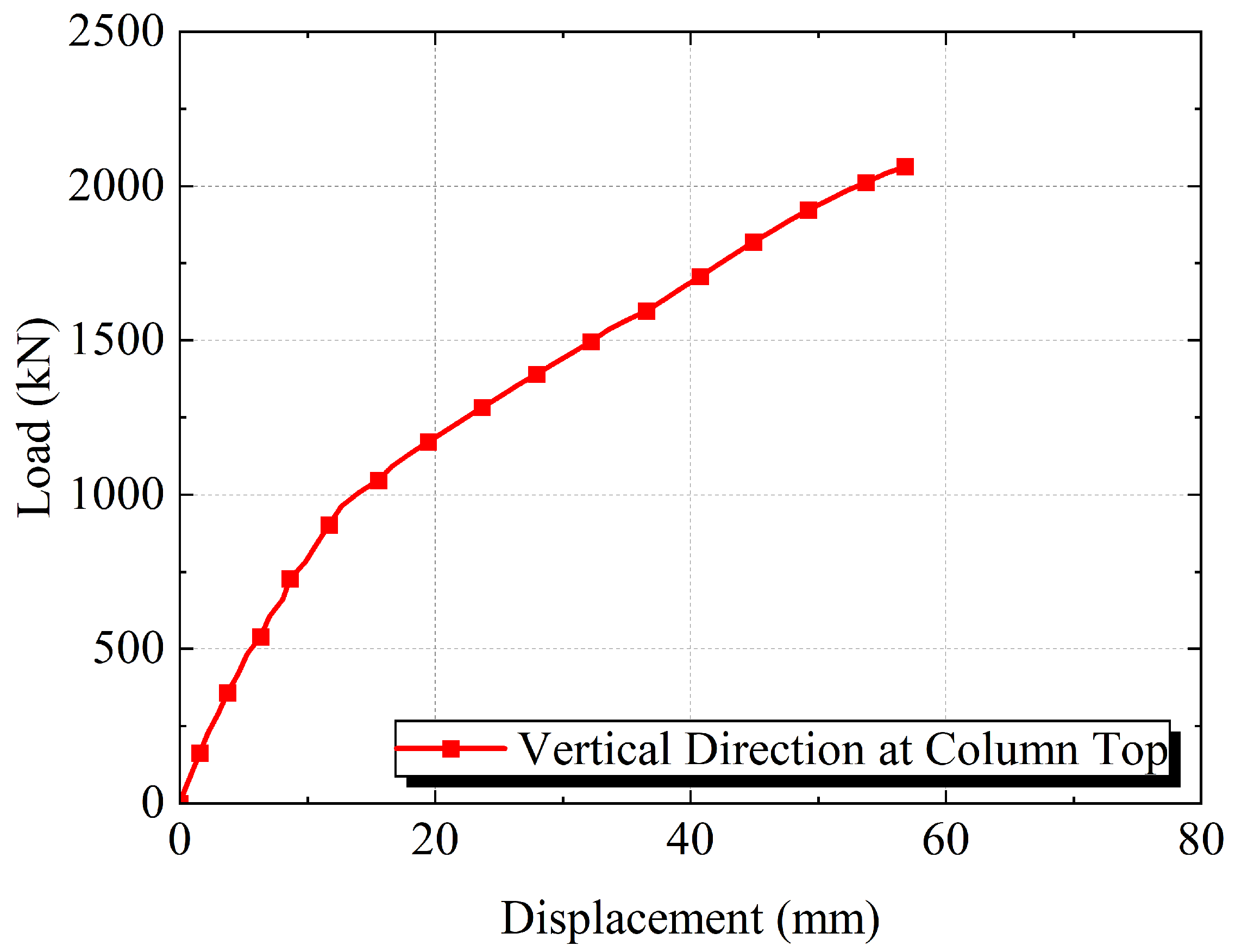
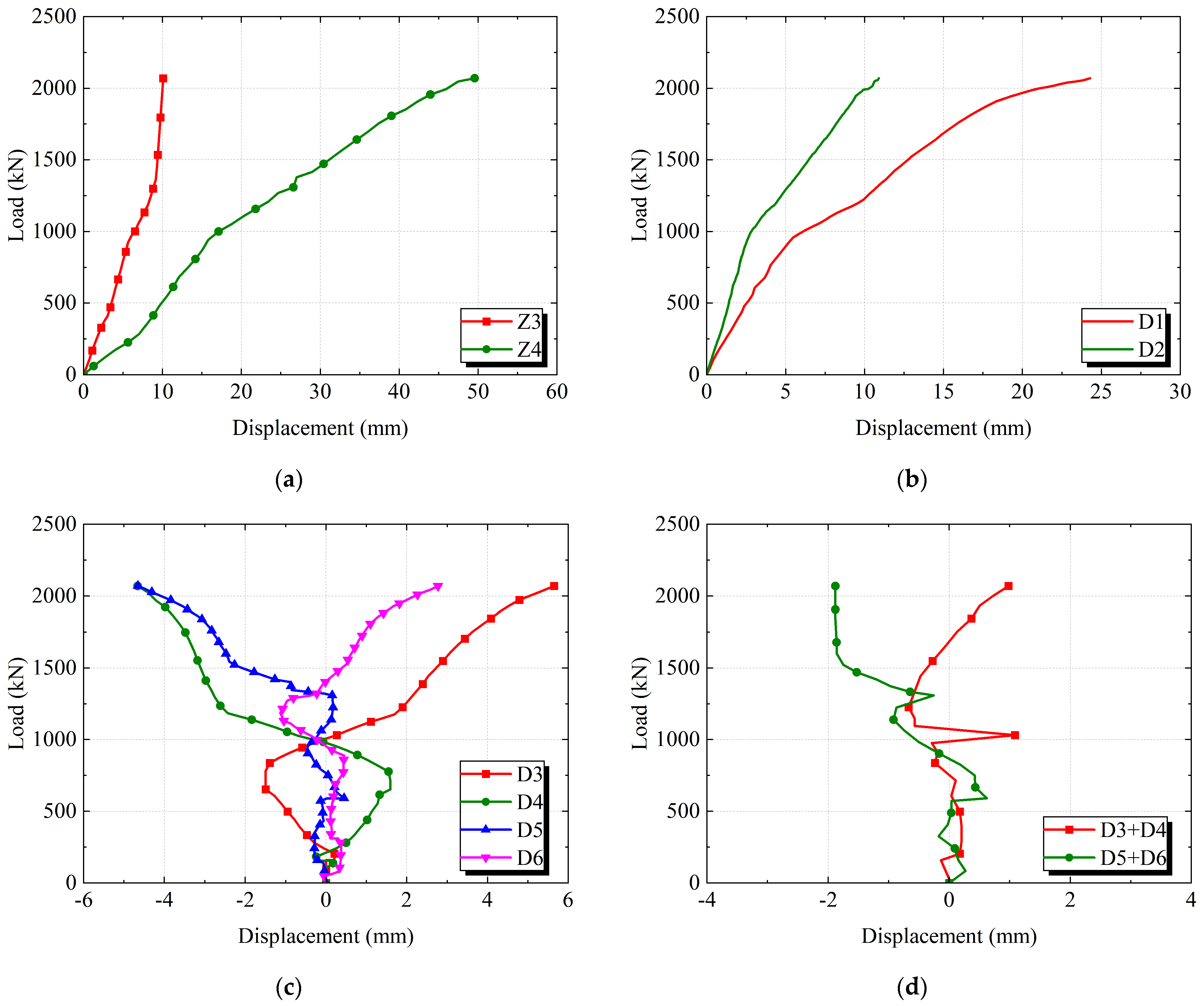
3.2. Load–Displacement Relationships

Figure 12 presents the load versus net vertical displacement curves at the column tops for the cast-in-place joint JD-1 under compression. The net displacement was obtained by subtracting the vertical displacement of the ring foundation from the measured vertical displacement at the column top, thereby eliminating boundary condition effects and focusing on the joint deformation. As shown in the figure, the east column demonstrated higher load-bearing capacity and stiffness than the west column, although both exhibited similar curve shapes and general trends. Prior to reaching a load of 100 kN, the stiffness of both columns was nearly identical, with the load–displacement curves appearing almost linear. Between approximately 100 kN and 400 kN, a minor change in slope occurred in the curves for both columns, yet the response remained essentially linear. This indicates that both columns behaved elastically up to 400 kN, with the slight slope change around 100 kN likely attributable to the closure of initial gaps within the loading system. The load–displacement curves for both columns reached the peak values within the net vertical displacement range of 20 mm to 40 mm. Following the peak load, both curves exhibited a gradual strength degradation without sudden loss of bearing capacity. The overall shape of the load–displacement relationships indicates that the cast-in-place joint JD-1 possessed good ductility and stable deformation capacity.

Figure 13a shows the load versus lateral displacement curves at the column tops for specimen JD-1. The hoop-direction displacements at the column tops were significantly larger than the radial-direction displacements, with maximum values reaching 72 mm and 12 mm, respectively. Figure 13b presents the load versus vertical displacement relationship at the top of the pedestal, where the total load represents the sum of the loads applied to the east and west columns. As the pedestal load increased from 200 kN to 900 kN, the vertical displacement at the pedestal top increased linearly and gradually, indicating that the joint remained in the elastic stage during this phase. The measured column top displacements during this period included the downward displacement component due to pedestal compression. The north side of the pedestal top exhibited continuously increasing displacement until specimen failure, while the south side showed displacement reduction and even reversal (upward lifting) when the total load reached approximately 1000 kN. This lifting phenomenon occurred because the radial inclination of the X-shaped columns was oriented toward the north side. Notably, the onset of displacement reversal at the south side coincided with the yielding stage of the columns. Figure 13c displays the load versus horizontal displacement curves at the pedestal sides. The north and south sides of the pedestal showed negative and positive horizontal displacements, respectively, forming essentially symmetric patterns. This indicates that the pedestal underwent a rigid body translation of approximately 3 mm toward the north, rather than horizontal expansion. Figure 13d shows the development of the sum of displacements on opposite faces of the pedestal, confirming the absence of significant transverse geometric deformation in the north–south direction and validating the characteristic of rigid body displacement.

Figure 14 shows the load versus net vertical displacement relationship at the column tops for cast-in-place joint JD-2 under tension. The load–displacement curve remains essentially linear until the load reaches 900 kN, indicating elastic behavior within this range. During the yield transition phase, continuous stiffness degradation occurs. Loading was terminated at a column top displacement of 56.8 mm, corresponding to significant damage development in the specimen.

Figure 15a presents the load versus lateral displacement curves at the column tops for specimen JD-2. The radial displacements at the column tops substantially exceed the hoop-direction displacements, reaching 50 mm and 10 mm, respectively. This is attributed to the restraining effect of the connecting beam provided in the hoop direction. Figure 15b shows the load versus vertical displacement relationship at the pedestal top. As the load increases from 0 to 1000 kN, the vertical displacement at the pedestal top increases linearly and gradually, consistent with the column top load–displacement relationship in Figure 12. The measured column top displacements include the upward displacement component due to pedestal tension. Both the north and south sides of the pedestal top show continuously increasing displacement until failure, with the south side exhibiting greater displacement (24 mm) than the north side (11 mm) due to the radial inclination of the X-shaped columns toward the south. Figure 15c displays the load versus horizontal displacement curves at the pedestal sides. The north and south sides show positive and negative horizontal displacements, respectively, forming approximately symmetric patterns. The pedestal underwent a net translation of approximately 4.6 mm toward the north, accompanied by approximately 1 mm of horizontal expansion. Figure 15d shows the development of displacements on opposite faces of the pedestal. The sum of north and south side displacements indicates transverse geometric deformation in the north–south direction, while the horizontal displacements at the east and west sides reveal approximately 2 mm of expansion deformation.

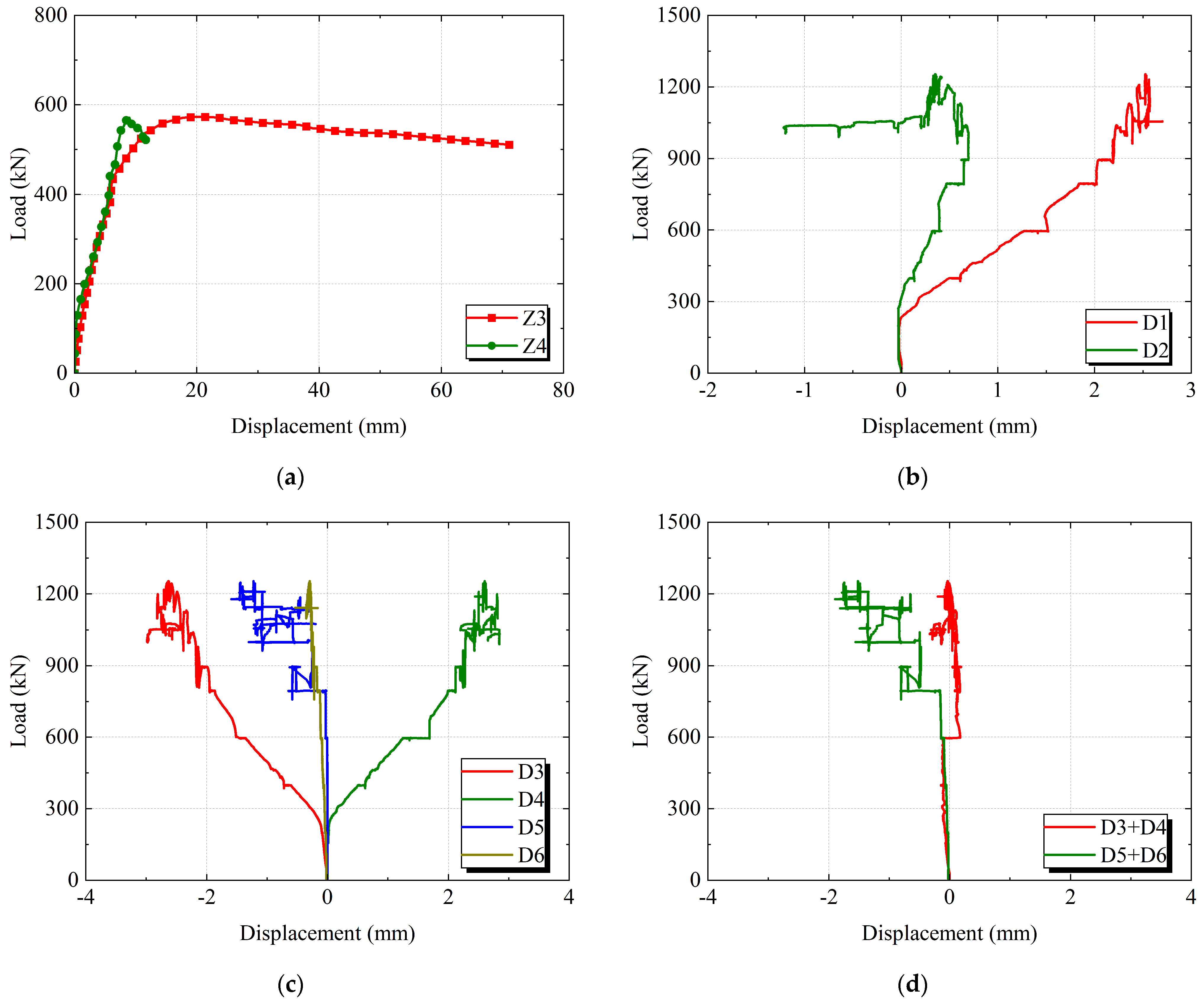
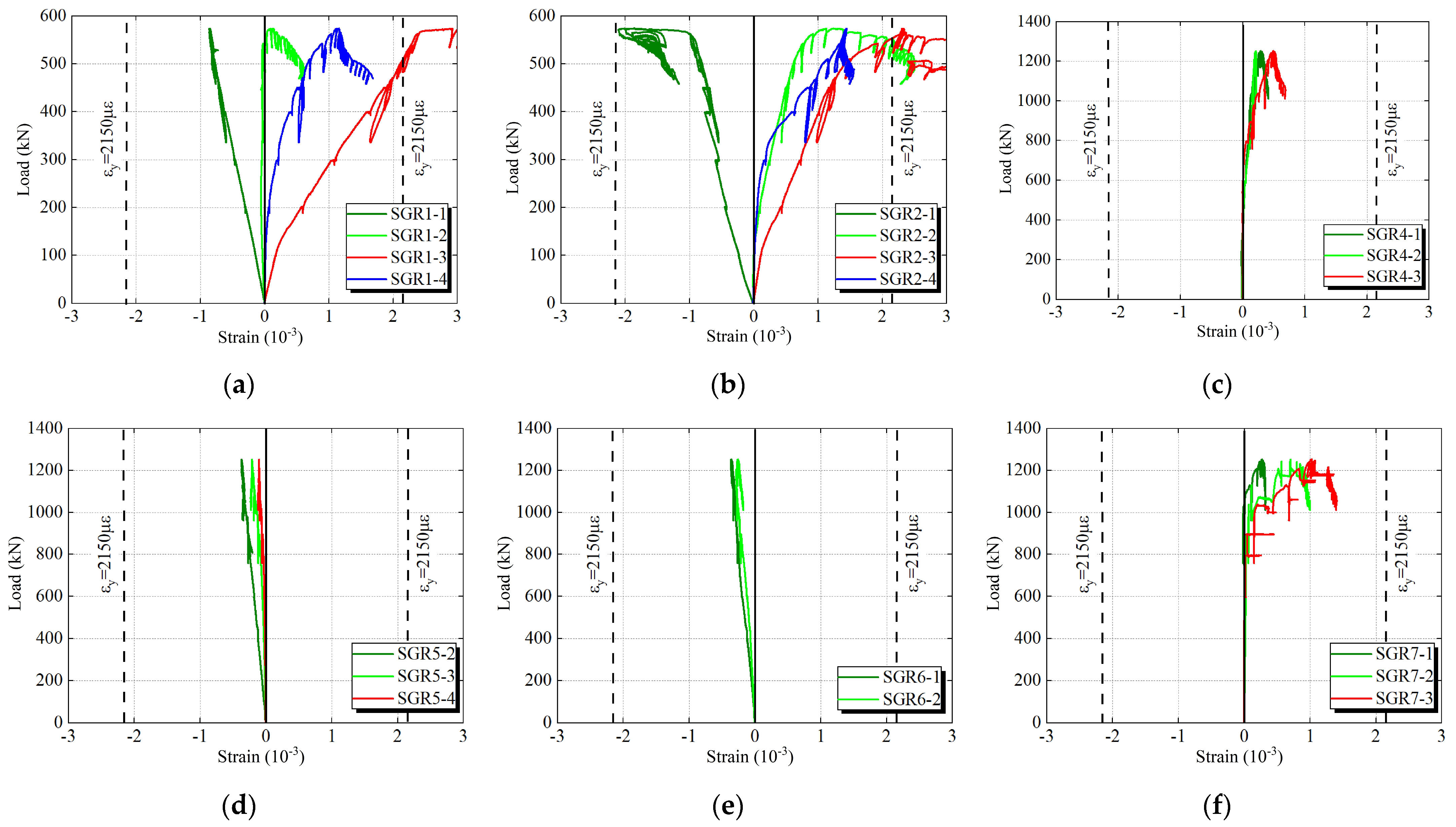
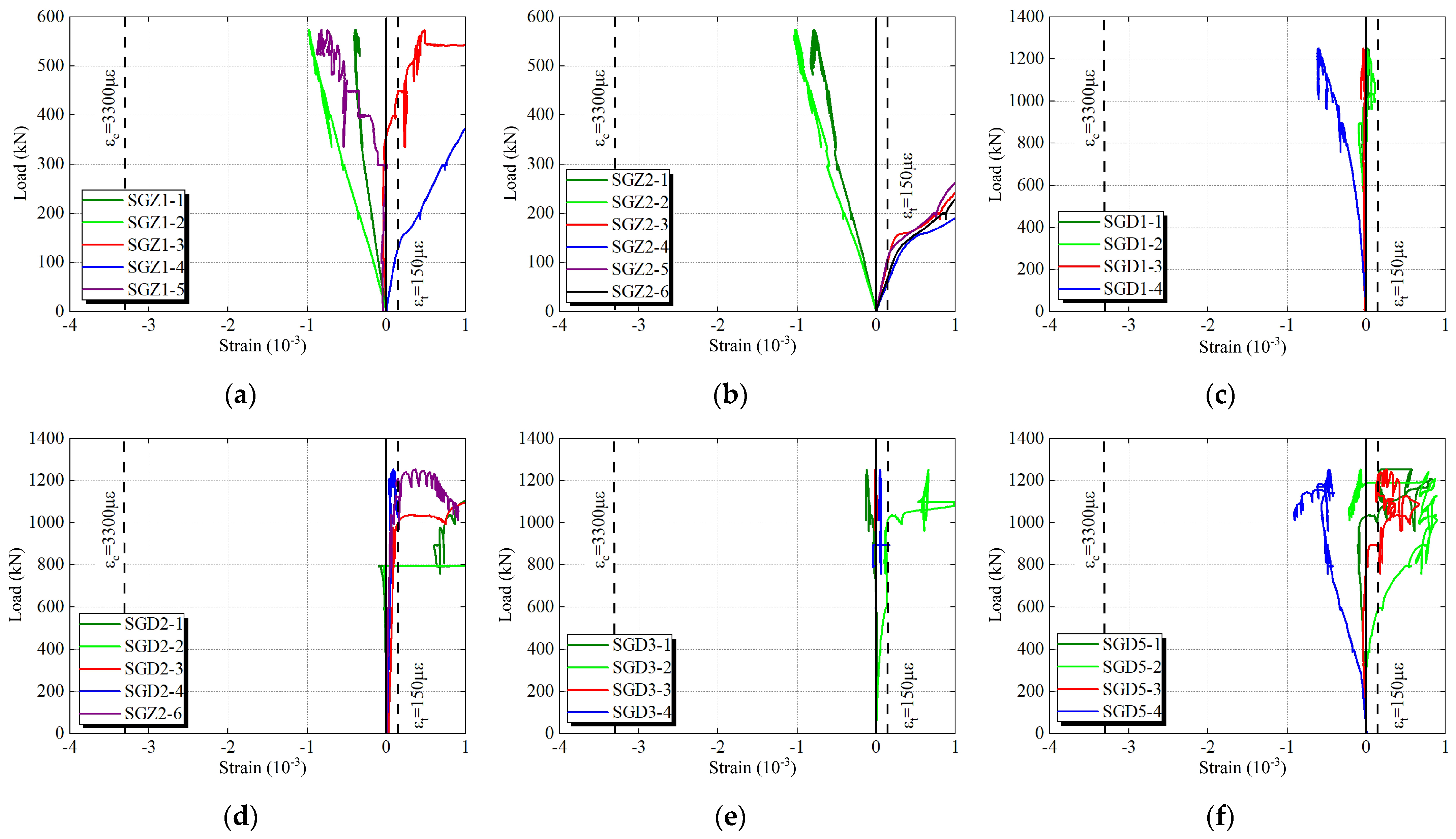
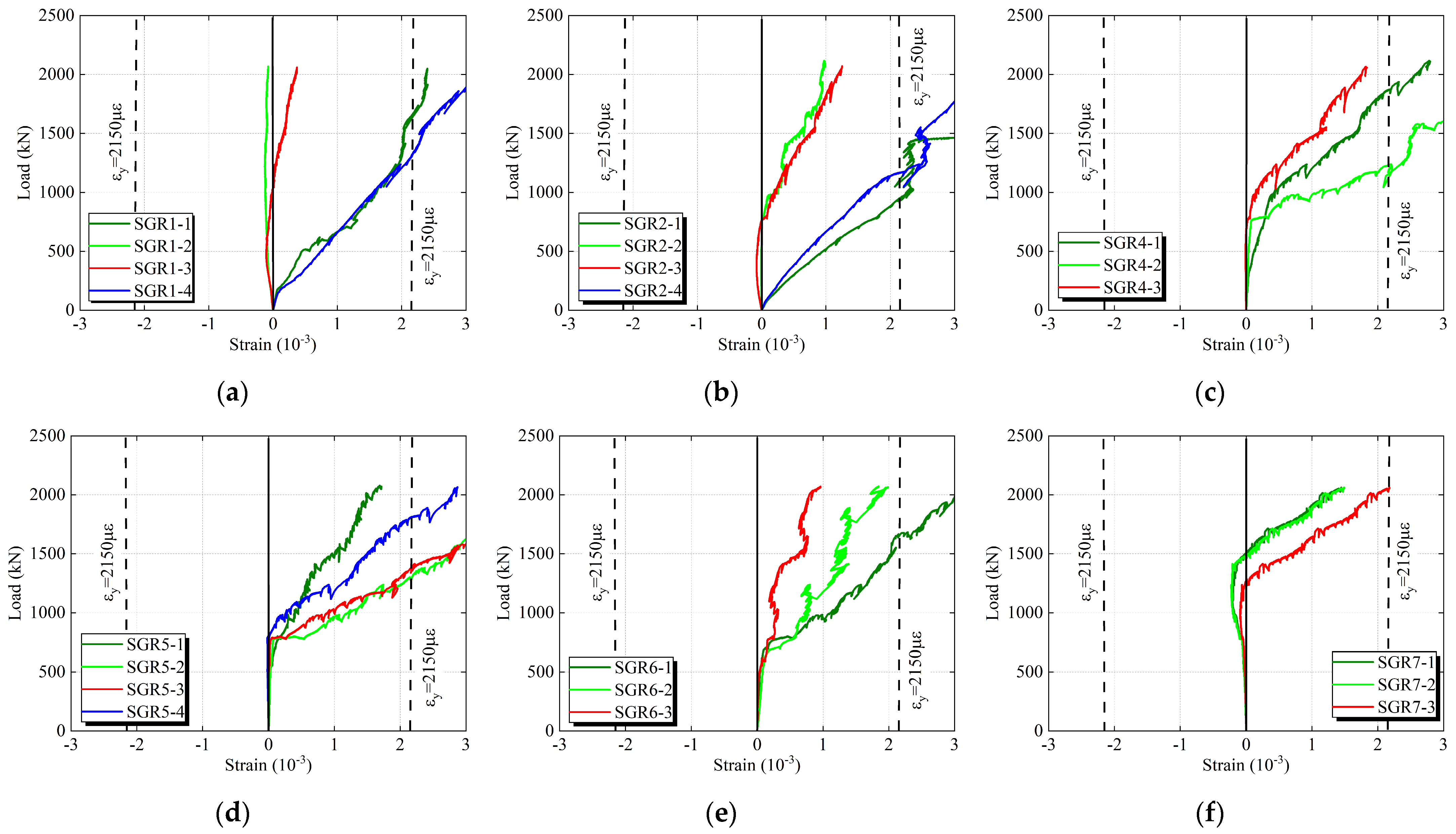
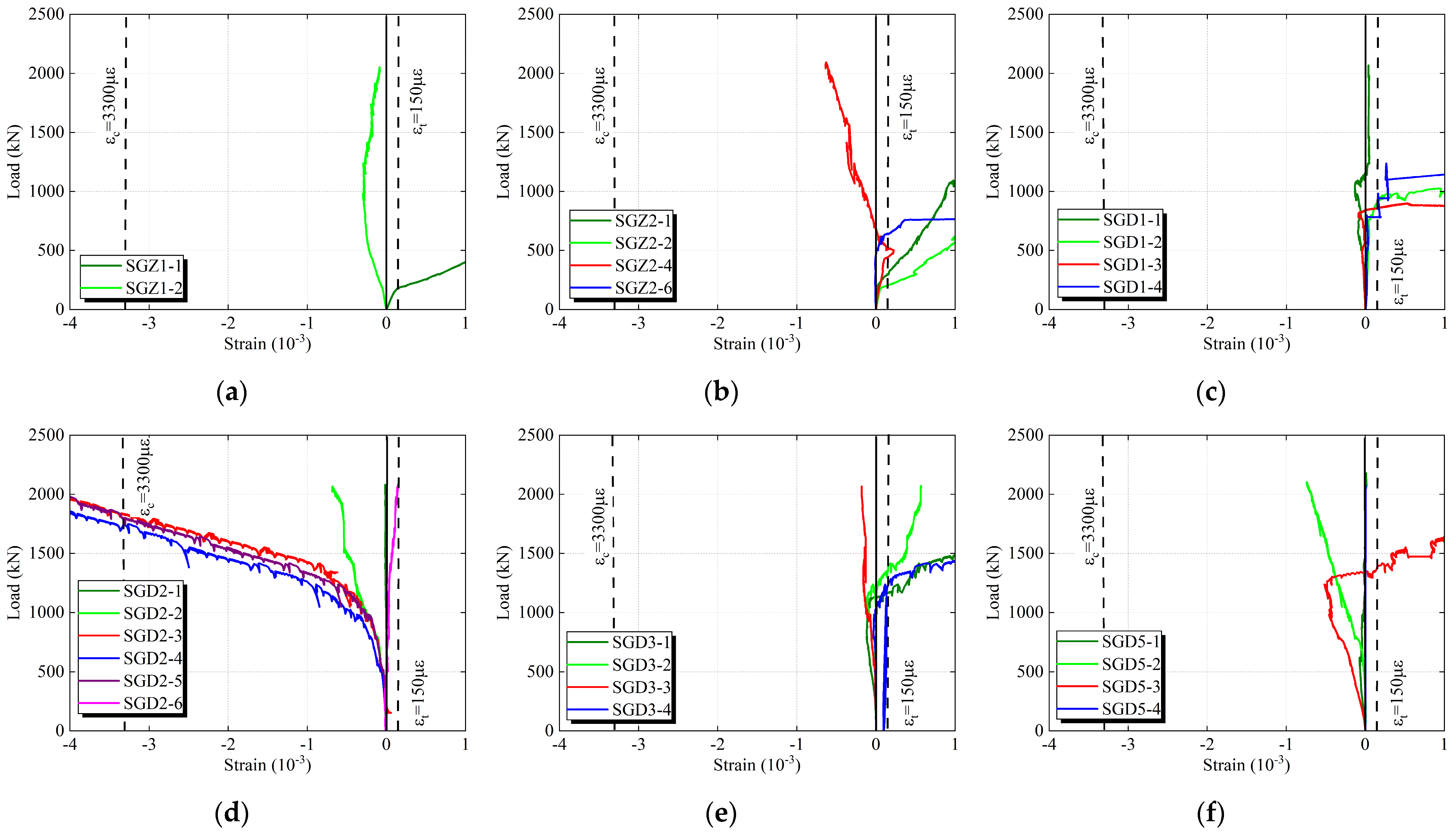
3.3. Load–Strain Relationships

Strain data of the concrete surface and reinforcement for each specimen corresponding to each load level were recorded automatically by the strain acquisition system. The strain evolution of reinforcement and concrete during the loading process of JD-1 specimen is presented in Figure 16 and Figure 17, respectively.

As shown in Figure 16, the reinforcement yielded at 2150 µε. When the column load reached approximately 500 kN, the longitudinal reinforcement on the south side of the inclined columns yielded, which was in tension. Subsequently, the strain in the reinforcement increased rapidly, confirming the formation of a plastic hinge at the column base. In contrast, the reinforcement on the north side and within the pedestal anchorage zone remained largely below the yield point until much higher load levels. The sequential yielding pattern, where the tensile reinforcement in the column yields first and is followed much later by only limited yielding in the pedestal, quantitatively validates the intended “strong connection–weak member” hierarchy. The strain in the reinforcement at other locations remained relatively small and below the yield point.

Figure 17 indicates that concrete surface cracking initiated when the tensile strain reached 150 µε, while crushing occurred at a compressive strain of 3300 µε. At a column top load of 100 kN, cracks first appeared in the columns. When the pedestal load reached approximately 600 kN, cracks appeared at the top and on the south side of the pedestal. In the load–strain relationship curves, concrete cracking occurs earlier than the corresponding phenomenon noted during the test, since the initial crack widths are too small to be detected visually.

The strain evolution of reinforcement and concrete during the loading process of JD-2 specimen is presented in Figure 18 and Figure 19, respectively.

Figure 18 demonstrates that the south side of the columns acted as the primary tension zone. The longitudinal reinforcement in the columns yielded when the load reached approximately 1000 kN, while the longitudinal reinforcement in the pedestal yielded at approximately 1300 kN. The force transfer under uplift mobilizes the column reinforcement and actively engages the reinforcement network within the pedestal. The resulting more distributed yield pattern explains the more extensive cracking observed in the pedestal concrete. According to Figure 19, initial cracking in the columns occurred at about 100 kN, while the pedestal began cracking at approximately 1000 kN.

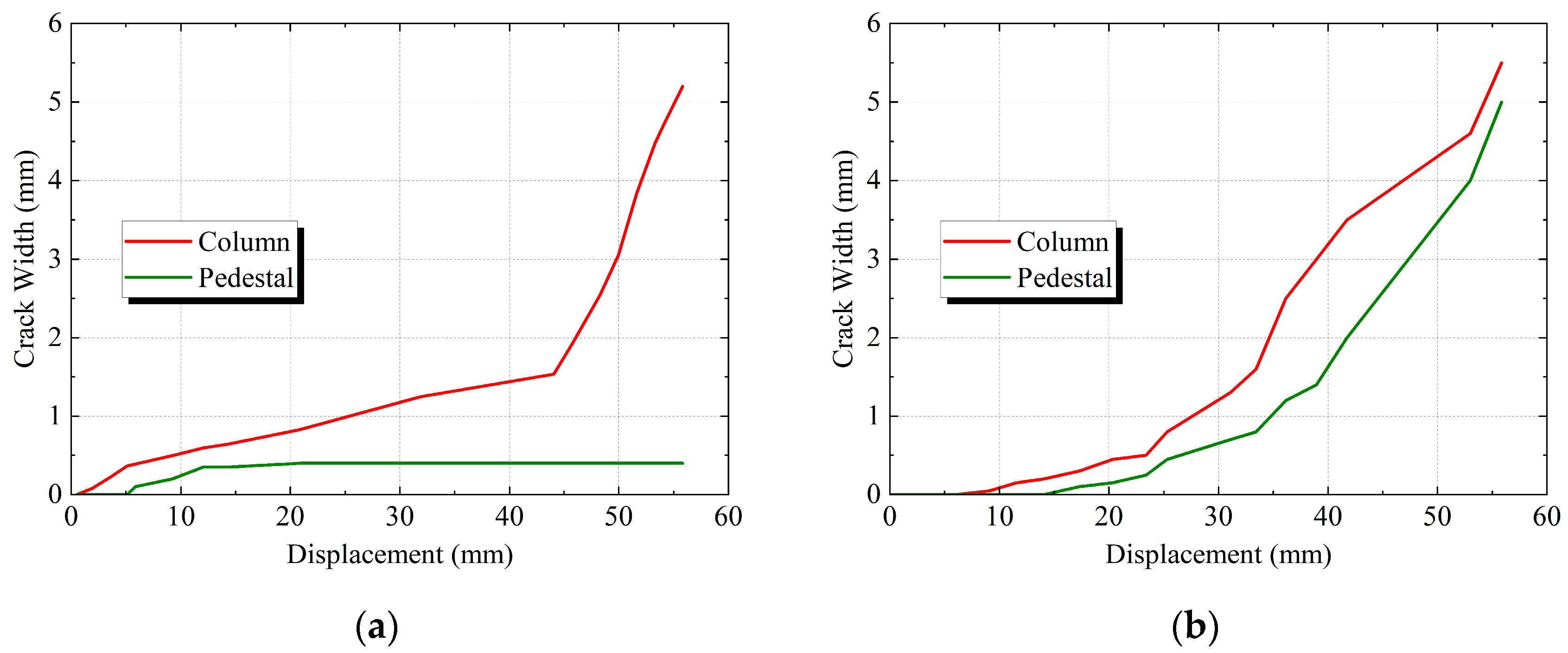
3.4. Crack Width Progression Curve

To quantify the damage evolution, the development of characteristic crack widths with respect to the net vertical displacement at the column top was monitored during testing. Crack widths were measured on the column and the pedestal surface using a crack width gauge with an accuracy of 0.05 mm. Key cracks, representative of the major failure patterns described in Section 3.1, were tracked at each load stage.

The progression of crack width with displacement for the compression specimen is presented in Figure 20a. Cracks in the column initiated at a displacement of approximately 3.5 mm, with widths below 0.1 mm. As the displacement increased, these cracks developed steadily. A significant acceleration in crack widening was observed after a displacement of about 5 mm, corresponding to the yielding of the longitudinal reinforcement and the formation of a plastic hinge. The most critical crack, located at the interface between the column base and the top surface of the pedestal, exhibited the most pronounced growth, ultimately exceeding 2.5 mm at the ultimate displacement. This aligns with the observed separation gap and concrete crushing in that region.

The development of crack width with displacement for the tension specimen is shown in Figure 20b. Cracks in the column initiated at a smaller net displacement of approximately 6 mm, while cracks in the pedestal formed later, at a displacement of about 14 mm. The initial crack widths in both components were below 0.1 mm. The growth of crack widths exhibited a distinct two-stage pattern. Prior to a displacement of about 35 mm, corresponding to the elastic and early yield transition phase in the load–displacement response, the crack width increased gradually and nearly linearly for both components. Beyond this point, the crack width progression accelerated markedly. The cracks in the pedestal demonstrated a more pronounced increase in width compared to those in the column in this later stage. This quantitative data confirms the significant tensile engagement and damage accumulation within the pedestal under uplift forces.

The quantitative crack width data substantiate the qualitative failure mode descriptions. JD-1 demonstrated localized, severe cracking at the column–pedestal junction, consistent with a flexural compression failure. In contrast, JD-2 exhibited more distributed but still significant cracking within the pedestal body, quantifying its active role in resisting tensile forces.

4. Discussion

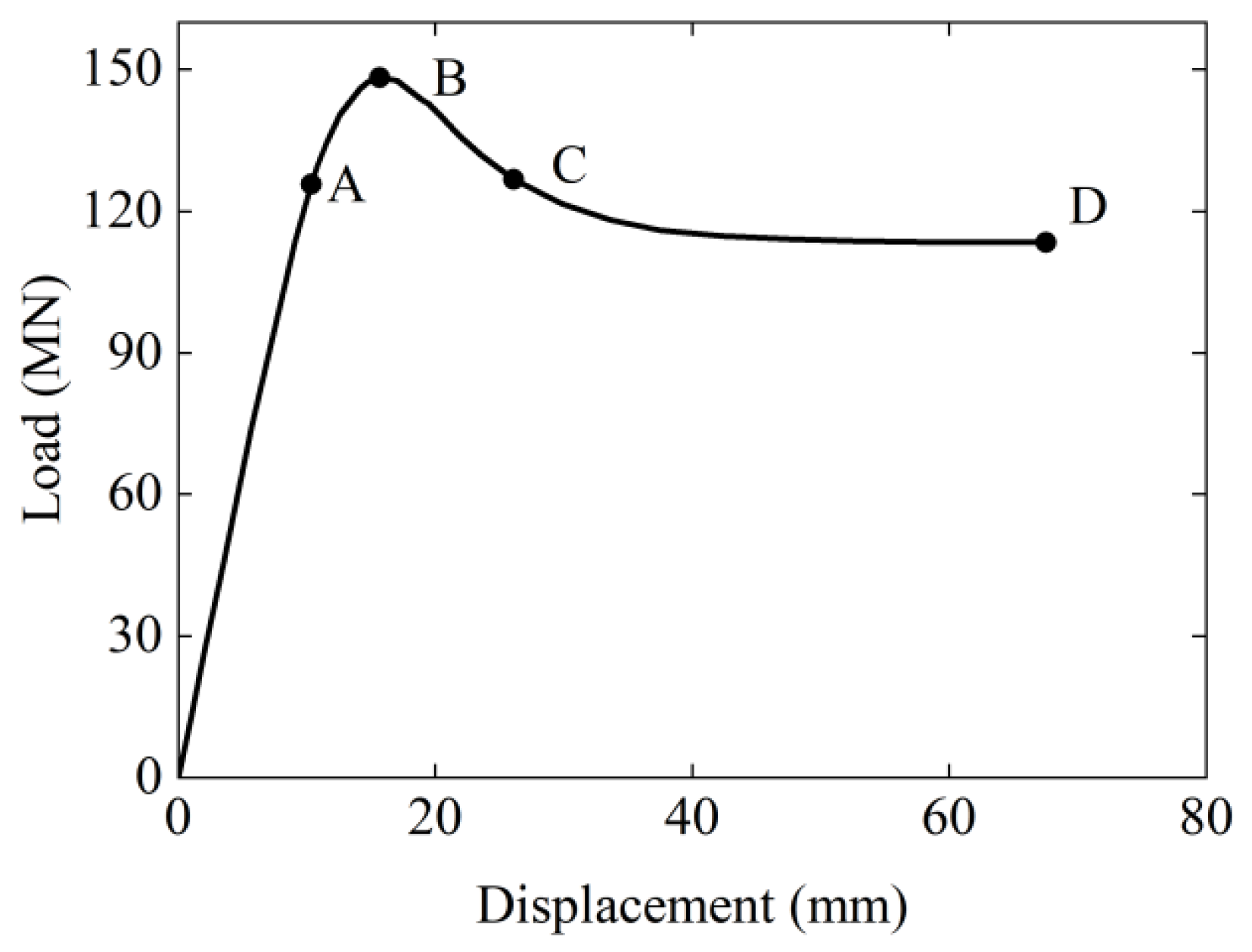
4.1. Mechanical Response

The typical load versus top vertical displacement curve for the concrete X-shaped column is shown in Figure 21, which includes four characteristic points. Point A is the yield point, Point B is the peak load point, Point C is the ultimate load point, and Point D marks the test termination. The load–displacement relationship exhibits four distinct stages: 0A, AB, BC, and CD.

Stage 1:

Elastic Stage (0A). Point A represents the yield point of the specimen. During this stage, the load increases linearly. The concrete and reinforcement work in concert with good bond integrity, jointly resisting the external force. No cracking occurs in the concrete, and the overall structure remains intact.

Stage 2:

Elasto-plastic Stage (AB). In this stage, the curve begins to deviate from linearity, and the relationship between load and displacement becomes nonlinear, although the load continues to increase. After the reinforcement yields, the bond between the reinforcement and concrete begins to degrade, and the slip of the reinforcement within the concrete occurs. The load reaches its peak at Point B.

Stage 3:

Descending Stage (BC). After Point B, the curve enters the descending branch. A pronounced decline is observed in the stage: the load begins to decrease while the displacement continues to increase. The compressive stress in the concrete compression zone reaches the ultimate compressive strain, initiating failure phenomena such as crushing or diagonal cracking. Consequently, the load-bearing capacity of the concrete declines rapidly. Point C indicates the ultimate load.

Stage 4:

Failure Stage (CD). Point D, where the load has decreased to 0.85 times the peak load, defines the end of the test.

1.

Compression Specimen

The mechanical characteristic values of JD-1 were analyzed based on the load–displacement relationship curve shown in Figure 12, with the results summarized in

Table 3. Characteristic values of JD-1.

Method	Part	K (kN/mm)	Fy (kN)	Δy (mm)	μ	Fmax (kN)	Δmax (mm)	Fu (kN)	Δu (mm)
Geometric Graphic Method	West column	78.25	499.80	10.08	7.14	574.17	24.95	484.32	72.00
	East Column	86.60	567.62	10.80	6.42	682.83	37.42	580.44	69.32
Equivalent Elasto-Plastic Energy Method	West column	78.25	502.26	10.20	7.06	574.17	24.95	484.32	72.00
	East Column	86.60	575.43	11.37	6.09	682.83	37.42	580.44	69.32
Park Method	West column	78.25	498.96	10.03	7.18	574.17	24.95	484.32	72.00
	East Column	86.60	570.49	10.86	6.38	682.83	37.42	580.44	69.32
Mean	West column	78.25	500.34	10.10	7.13	574.17	24.95	484.32	72.00
	East Column	86.60	571.18	11.01	6.30	682.83	37.42	580.44	69.32

. The table presents the joint performance characteristics obtained through three different methods: the geometric graphic method [32], the equivalent elasto-plastic energy method [33], and Park method [34]. The joint initial stiffness was defined as the secant stiffness at 0.1 times the yield load. The yield point was determined using the above three methods, resulting in three sets of yield loads and corresponding yield displacements. The highest point on the load–displacement curve is defined as the peak load and the peak displacement. The point at which the load has fallen to 85% of the peak load is designated as the ultimate load and the ultimate displacement. The ductility coefficient, calculated as the ratio of ultimate displacement to yield displacement, is consequently influenced by the method used to determine the yield point.

As shown in Table 3, the characteristic values obtained from the three different yield point determination methods show close agreement, permitting the average values for analysis. The east column demonstrated 10.7%, 14.0%, and 18.9% higher values than the west column in initial stiffness, yield load, and peak load, respectively. Conversely, the ductility coefficient and ultimate displacement of east column were 11.6% and 3.7% lower. The variations are attributable to construction tolerances, including but not limited to concrete compaction quality, formwork dimensions, and reinforcement positioning.

For the JD-1 specimen under vertical compression, both columns exhibited a four-stage ductile failure process: yielding, hardening, plastic hinge rotation, and concrete crushing. This behavior satisfies the “collapse prevention” performance objective for tall structures under rare earthquake scenarios. After reaching peak load, the specimen showed no abrupt strength degradation, failing through a mixed mode of reinforcement yielding and concrete crushing, which falls within the category of ductile failure. The peak bearing capacity of the east column increased by 18.9%, and the ultimate displacement slightly decreased, reflecting the strength-ductility trade-off associated with higher strength and enhanced confinement.

2.

Tension Specimen

The mechanical characteristic values of JD-2 were analyzed based on the load–displacement relationship curve shown in Figure 14, with the joint initial stiffness defined as the secant stiffness at 0.1 times the yield load. The results are summarized in

Table 4. Characteristic values of JD-2.

Method	K (kN/mm)	Fy (kN)	Δy (mm)
Geometric Graphic Method	101.83	1575.71	35.54
Equivalent Elastic-Plastic Energy Method	101.83	1715.79	41.05
Park Method	101.83	1849.18	46.16
Mean	101.83	1713.55	40.92

.

As indicated in Table 4, the maximum deviations in yield load and yield displacement determined by the three methods are 8.04% and 13.15%, respectively. The close agreement among the characteristic values obtained from the three yield point determination methods justifies using the average values for subsequent analysis.

For the JD-2 specimen subjected to vertical tension, the load–displacement curve exhibited a three-stage characteristic: gradual elasticity, steep plasticity, and strength stabilization. During the elastic stage, the curve demonstrated excellent linearity, indicating that the specimen remained macroscopically uncracked. The yield transition stage was marked by continuous stiffness degradation, corresponding to progressive development of concrete cracks, sequential yielding of longitudinal reinforcement rows, and stable propagation of microcracks in the concrete tensile zone. In the strength stabilization stage, the nearly horizontal curve slope reflected a typical coupled failure mechanism involving steel hardening and concrete spalling. After the peak load, no significant strength reduction was observed, although severe damage occurred in the concrete.

In summary, the X-shaped column specimen under tension exhibited reinforcement-controlled behavior over the entire cross-section with stable crack propagation. Consequently, the initial stiffness, yield load, and yield displacement of the tension specimen exceeded the values recorded under compression.

4.2. Load–Strain Response

• Compression Specimen

Under the ultimate vertical compression scenario of the X-shaped columns in the cooling tower, specimen JD-1 exhibited a failure sequence characterized by zonal yielding and layered force transfer. The corner longitudinal reinforcement in the tensile zone of the mid-height section (SGR 1-3) first yielded at a column top load of 500 kN, triggering an abrupt shift of the sectional neutral axis and a sharp reduction in the compression zone height. Subsequently, all four corner longitudinal reinforcements at the column root yielded, with the tensile reinforcement experiencing a steep strain increase after peak load, forming a plastic hinge at the base. In the pedestal anchorage zone, only localized yielding occurred in the corner reinforcement (SGR 2-2, 2-3), while the remaining reinforcement stayed below the yield threshold due to bond-friction stress redistribution in the concrete. The analysis of strain gradients along the height of the joint and between different reinforcement layers reveals the load-transfer path. A sharp strain gradient was observed from the yielded longitudinal reinforcement in the column to the anchored extensions within the pedestal. At the column–pedestal interface, the strain exhibits abrupt attenuation, indicating that the force from the yielded column section is effectively diffused into the more rigid pedestal through bond stress, while the pedestal itself remains predominantly elastic. This demonstrated that the pedestal acted as a second line of defense through localized reinforcement yielding and concrete stress diffusion, effectively delaying global structural collapse.

The concrete strain field revealed a significant “compression–bending–punching” coupling effect at the column–pedestal interface. When the load reached 100 kN, the concrete on the south side of the column attained its cracking strain, exhibiting large eccentric compression characteristics. The concrete on the west side and top surface of the pedestal transitioned from compression to tension after peak load, resulting from increased bending moment transmission depth.

These results confirm that the pedestal localizes the extreme deformations in the column plastic hinge region through the synergistic action of elastic reinforcement constraint and concrete stress diffusion at both material and structural scales. This mechanism ensures progressive energy dissipation and maintains global stability of the cooling tower support columns under ultimate vertical compression conditions.

2.

Tension Specimen

Under the ultimate vertical tension scenario of the X-shaped columns in the cooling tower, specimen JD-2 exhibited progressive zonal yielding and abrupt neutral axis migration. The corner longitudinal reinforcement at the mid-height and base sections of the columns (SGR1-1, SGR1-4, SGR1-5, SGR1-8) yielded sequentially, leading to rapid expansion of the tensile zone. Meanwhile, the compression reinforcement in the same sections (SGR1-2, SGR1-7) maintained compressive strain without yielding. The strain fields in the pedestal surface reinforcement and concrete revealed a complex, multi-directional stress state combining circumferential tension and radial crushing. Along the height of the pedestal, a clear strain gradient was observed in the vertical reinforcement; strain levels were highest near the interface with the column base and diminished with increasing distance downward. The gradient signifies the effective diffusion of tensile force from the yielded column into the pedestal body through bond and anchorage. The east–west distributed reinforcement reached peak tensile strains exceeding 2150 µε, while the north–south reinforcement yielded at 1235 kN, indicating the formation of circumferential cracking bands on the pedestal top surface. In the east and west faces of the pedestal, mid-span longitudinal reinforcement developed higher strain than outer longitudinal reinforcement. South-face longitudinal reinforcement developed higher strain than north-face longitudinal reinforcement. The comparison indicated an overall tensile stress state within the pedestal.

Concrete strain distribution on the pedestal surface showed edge-tension and crushing characteristics. The south face (SGD1-2–SGD1-4) cracked in tension, while the north face (SGD2-3–SGD2-5) reached the ultimate compressive strain. The south side of the pedestal developed a transverse main crack at 900 kN due to eccentric loading. These patterns demonstrate that the pedestal formed a conical failure mode under uplift forces, ultimately losing load-bearing capacity due to combined reinforcement yielding and concrete crushing at the base.

5. Conclusions

This study conducted an experimental investigation on the mechanical behavior of cast-in-place X-shaped reinforced concrete column base joints under ultimate vertical compression and tension loads. The main conclusions are drawn as follows:

(1)

The cast-in-place joint design for X-shaped reinforced concrete columns was validated as feasible and reliable for application in super-large cooling towers. The joints exhibited excellent mechanical performance, including substantial load-bearing capacity and pronounced ductility under both compressive and tensile loading regimes.

(2)

The failure mechanism confirmed the design principle of a strong joint–weak component. Specifically, the plastic hinge formed in the column section above the base, while the joint remained intact and stable even after the column yielded. This ensures progressive failure, which is crucial for structural safety under extreme conditions.

(3)

Under compression, the joint failed in a ductile flexural compression manner, whereas the failure was tension-controlled under uplift. The tensile specimen demonstrated higher initial stiffness and yield load compared to the compressive specimen, which experienced earlier stiffness degradation due to concrete crushing under combined compression and bending.

(4)

The strain analysis revealed a sequential yielding process of the longitudinal reinforcement and a complex internal stress distribution within the pedestal, which effectively facilitated stress diffusion and delayed catastrophic failure.

The monotonic tests conducted in this study serve as confirmatory experiments, aiming to validate the reliability of the joints and to elucidate the damage progression process. Future work will focus on developing high-fidelity finite element models for parametric studies. These models will be used to further optimize the joint design and to investigate its mechanical performance under complex loading conditions, including combined axial-moment loading, seismic behavior, and long-term durability. This will require expanded experimental programs and refined numerical models to develop comprehensive design guidelines.