Experimental Study on Shear Behavior of 30 m Pre-Tensioned T-Beam with Polygonal Tendons Under Shear-Span Ratio of 2.5

Abstract

Pre-tensioned T-beams with polygonal tendons offer high load-bearing capacity and suitability for large spans, demonstrating broad application potential in bridge engineering. The cracking state of a prestressed beam is a crucial indicator for assessing its service state, while the ultimate bearing capacity is a key metric for structural safety. In this study, we designed a novel 30 m pre-tensioned T-beam with polygonal tendons and investigated its shear cracking performance and ultimate bearing capacity under a shear-span ratio of 2.5 through a full-scale test. A graded loading protocol was employed. The results indicate that during the initial loading stage, the shear cracking load of the inclined section was 1766 kN. A distinct inflection point appeared on the load–displacement curve, accompanied by a significant reduction in stiffness. Cracks initially developed at the junctions between the web and the top flange, as well as the diaphragm, and subsequently propagated towards the shear–flexural region, exhibiting typical shear–compression failure characteristics. During the secondary loading to the ultimate state, the beam demonstrated good ductility and stress redistribution capability. The ultimate shear capacity reached 3868 kN. Failure occurred by crushing of the concrete in the compression zone after the critical inclined crack penetrated the web, with the member ultimately reaching its ultimate capacity through a plastic hinge mechanism. Strain analysis revealed that the polygonal tendons effectively restrained the premature development of inclined cracks, thereby enhancing the overall shear performance and deformation capacity. This study verifies the mechanical performance of the new T-beam under a shear span-to-depth ratio of 2.5 through calculations based on different codes and finite element numerical analysis, providing experimental evidence and theoretical references for its engineering application.

1. Introduction

Precast pre-tensioned concrete beams have been widely used in various engineering structures worldwide due to their advantages, such as high load-bearing capacity and convenient installation [1,2,3]. For small and medium-span bridges, precast pre-tensioned concrete T-beams, I-beams, and small box girders are commonly adopted. However, the application of small box girders is limited in industrial production owing to issues such as operational difficulties during fabrication caused by their narrow internal cavities, as well as problems like formwork bulging and concrete step-offs at formwork joints [4,5]. In contrast, pre-tensioned concrete T-beams and I-beams offer benefits such as rapid fabrication and better quality control [6,7,8,9,10]. Particularly, the pre-tensioning method is characterized by lower construction costs and the absence of reserved ducts, thereby avoiding issues associated with post-tensioning, such as inadequate grouting compaction leading to steel corrosion and reduced durability. Based on the arrangement of pre-tensioned tendons, pre-tensioned beams can be classified into those with straight tendons and those with polygonal tendons. Straight tendons are aligned along the longitudinal axis of the beam, primarily resisting axial tensile stresses to counteract positive moments, with limited contribution to shear resistance. In contrast, polygonal tendons, as an innovative tendon configuration, are typically arranged near the ends and in the tension zone at midspan, forming a polygonal profile. The inclined layout of polygonal tendons at the beam ends aligns with the direction of principal tensile stresses, effectively restraining the development of diagonal cracks and enhancing the member’s shear capacity [11]. Additionally, polygonal tendons provide a longer effective bond length, ensuring compatibility of sectional deformation while further reducing the risk of tendon corrosion and improving the durability of the member.

For prestressed beams, shear behavior is one of the key factors controlling the design of the member. Numerous scholars have conducted research on the shear performance of prestressed beams. For example, Zhang et al. [12] conducted a full-scale test on the flexure–shear coupling performance of a pre-tensioned T-beam with polygonal tendons, verifying its cracking resistance and shear capacity at normal and inclined sections, providing an experimental basis for its use as an alternative to voided slab beams, which are difficult to prefabricate and maintain. Zhang et al. [13] performed shear tests on nine prestressed concrete T-beams to study the influence of the number of prestressing tendons, the bending angle, and the flange width on the shear performance. The results indicated that increasing the number of prestressing tendons and the bending angle significantly improves the ultimate shear capacity, while the influence of flange width is relatively minor, providing an experimental basis for the design optimization of prestressed concrete T-beams. Feng et al. [14], through theoretical analysis and experimental design, focused on the beneficial effect of the horizontal component of the prestressing tendon force on the shear capacity, proposed a recommended formula considering the contribution of the horizontal component, and conducted shear tests on T-beams with different prestressing levels and bending angles, verifying the accuracy of the proposed formula and providing a basis for code revision. Zhi et al. [15], through comparative tests on nine T-shaped concrete beams and 21 prestressed high-strength concrete beams, systematically studied the influence of parameters such as concrete strength, shear-span ratio, and prestressing level on shear performance, revealed the development law of diagonal cracks in prestressed T-beams, and proposed a formula for calculating the shear capacity of T-shaped/I-shaped sectional beams applicable to a concrete strength range of 25.5–84.3 MPa, based on test data from 66 beams. Feng et al. [16], based on the Modified Compression Field Theory (MCFT), established an MCFT analysis model for prestressed concrete beams under combined bending and shear, investigated the influence of the shear-span ratio on the failure mode and shear capacity of test beams through three sets of shear tests, and proposed a simplified calculation formula for the shear capacity of prestressed concrete beams through regression analysis. Hansol Jang et al. [17], based on the Strut-and-Tie Model (STM), proposed an optimized STM model that comprehensively considers the web bearing capacity and confinement effects, incorporates anchorage capacity and horizontal shear strength analysis, achieving a more comprehensive bearing capacity assessment. Qi et al. [18], addressing the issue of underestimating the shear capacity of concrete T-beams due to neglecting the shear contribution of the flange, proposed a method for calculating the effective shear width of the web based on the concept of the effective shear area, established a theoretical formula for calculating the shear capacity of T-beams considering the influence of the flange, and verified its correctness using test data from 157 concrete T-beams. Wei et al. [19], through four-point bending and flexure–shear coupling tests on full-scale pre-tensioned prestressed concrete double T-beams, combined with numerical analysis, verified the enhancing effect of the combined configuration of straight and bent tendons on the shear performance of the beam. The results showed that this configuration can significantly improve the cracking load, ultimate capacity, and deformation performance of the prestressed beam. Alsomiri Mujahed et al. [20], by constructing multiple sub-stress fields, proposed a combined stress field model to reveal potential failure modes at different locations in the shear-span region. Through shear tests on two sets of full-scale prestressed concrete T-beams with different shear-span ratios, they derived a formula for calculating the ultimate shear strength of prestressed concrete beams.

It should be noted that for pre-tensioned prestressed beams, the formation of cracks may allow corrosive agents to penetrate the beam and come into contact with the prestressing tendons. This can lead to corrosion of the tendons and a reduction in bond performance between the tendons and concrete, subsequently causing issues such as premature yielding of the tendons and loss of prestress [21,22,23,24,25,26]. Furthermore, current research on the shear behavior of prestressed T-beams predominantly focuses on those with straight tendons, while studies on the shear performance along inclined sections of T-beams with polygonal tendons remain relatively limited. Additionally, most experiments are conducted only on scaled models, and the resulting conclusions have primarily qualitative significance for full-scale members. Additionally, parabolic or undulating tendon layouts are common and effective configurations in post-tensioned prestressed concrete for optimizing internal force distribution. Post-tensioning, which involves tensioning tendons through preformed ducts, readily accommodates curved tendon profiles. However, this method inherently introduces common issues such as incomplete grouting of ducts, significant uncertainties in prestress losses, and challenges in anchorage protection. This study focuses on the pre-tensioning prestressed system, which fundamentally differs in its construction process from post-tensioning. In contrast, pre-tensioning achieves bond anchorage by tensioning tendons on a bed prior to concrete casting. It offers distinct advantages, including reliable prestress transfer, superior durability, and high production efficiency. However, its tendons are typically limited to straight or polygonal layouts. Therefore, the three-segment polygonal tendon arrangement scheme proposed in this paper aims to accurately simulate the advantageous effects of continuous curved tendons typically achieved in post-tensioned systems. Based on the second-phase reconstruction and expansion project of the Chang–Zhang Expressway, this paper presents the design of a novel 30 m pre-tensioned T-beam with polygonal tendons. A full-scale shear test was conducted on the beam under a shear-span ratio of 2.5. Through incremental loading, key results such as the load–displacement curve, crack propagation patterns, and strain characteristics of the test beam were obtained, providing valuable references for engineering practice. This study presents, for the first time, a full-scale shear test on a novel pre-tensioned T-beam with polygonal tendons, effectively overcoming the limitations of scaled models in quantitatively predicting the performance of actual structures. Furthermore, while most existing research focuses on shear–compression failure under small shear-span ratios or diagonal tension failure under large shear-span ratios, this investigation selects a typical shear–compression zone with a shear-span ratio (λ) of 2.5 for testing. This fills a critical gap in experimental data on the shear behavior of prestressed T-beams under shear–compression failure conditions. The findings hold significant practical importance for refining the shear design theory of prestressed beams and enhancing the safety and durability of engineering structures.

2. Overview of a Full-Scale 30 m Pre-Tensioned T-Beam with Polygonal Tendons

2.1. Specimen Parameters

The test utilized a full-scale T-shaped test beam with a calculated span of 28,280 mm and a depth of 1800 mm. The top flange had a total width of 1750 mm, with edge and root thicknesses of 200 mm and 250 mm, respectively. The web thickness was 280 mm, and the bottom flange width was 600 mm. Additionally, diaphragms with a thickness of 420 mm were provided at both ends. The test beam was cast using C55 concrete. The longitudinal reinforcement consisted of HRB400 rebars with diameters of 14 mm and 28 mm, while the stirrups were made of 12 mm diameter HRB400 rebars. The longitudinal rebars beneath the top flange and within the web were HPB300 rebars with a diameter of 10 mm. Prestressing strands employed high-strength strands, categorized into straight prestressing strands and harped prestressing strands. Each prestressing strand had a diameter of 15.2 mm, a cross-sectional area of 140 mm², a yield strength of 1383.3 MPa, and an ultimate strength of 1834.6 MPa. The detailed configuration of the test beam is illustrated in Figure 1.

2.2. Material Properties

Prior to the test, performance tests were conducted on the various types of rebars and prestressing strands used for the beam, and the mechanical property parameters of the rebars were obtained, as shown in

Table 1. Mechanical properties of steel rebars.

Rebar Type	Yield Strength/MPa	Ultimate Strength/MPa	Modulus of Elasticity/GPa
HRB300A10	332.0	461.2	200
HRB400C12	418.0	595.4	200
HRB400C14	446.0	580.4	200
HRB400C28	432.0	614.1	200

. Ordinary Portland cement P.O 52.5 was used, with fine sand as fine aggregate and crushed stone with a maximum particle size of 19 mm as coarse aggregate. To ensure the workability of the concrete, a high-range water reducer was employed. During the casting process, three standard 150 mm cube specimens were cast. After 28 days of curing, the cube specimens were tested for compressive strength, yielding an average compressive strength of 64.6 MPa.

2.3. Harping of Prestressing Strands with Polygonal Profile

The polygonal prestressing tendons are bent at a point 5 m from the midspan using a deflector, with an average bending angle of 4.4°. Prior to tensioning, a bending jack is installed at the bending point inside the beam, and an anchorage abutment is set up at the end of the tensioning bed. The former is used to control the alignment of the strands within the beam, while the latter adjusts the tensioning direction and the height at the strand ends. Together, they form the bending and displacement system, which serves to guide and position the prestressing strands during tensioning.

During the tensioning process, the strands were tensioned twice sequentially. The initial prestressing stress of the strands was 465 MPa, and the final tensioning stress was 1339 MPa. After concrete casting, the beam was covered with tarpaulins following a 6-h standing period, and steam curing was carried out using a phased temperature-raising process. Seven days later, prestress release was performed after confirming that the actual concrete strength and modulus of elasticity were not less than 90% of the theoretical values specified in the design code. The half-section configuration of the prestressing strands within the test beam and their harping process are illustrated in Figure 2.

3. Test Plan

3.1. Loading Plan

Considering the constraints of the test site and the cracking patterns of the specimen under shear–compression failure, the shear-span ratio was set as λ = 2.5 for this test. (The cases such as diagonal compression failure with a shear-span ratio close to 1 or diagonal tension failure with a shear-span ratio greater than 3 were not covered.) Accordingly, the loading setup shown in Figure 3 was designed. An uplift-resistant foundation was constructed below the test floor. Threaded bars and anchor bolts were then used to connect the reaction beam and the restrained beam to the foundation. Finally, pressure was applied via a hydraulic jack installed between the reaction beam and the test beam to load the test T-beam. Additionally, restrained beams were set at the beam ends to prevent the test beam from overturning during the experiment. Within the entire loading system, the load is supplied by the hydraulic jack. The pressure is transmitted through the reaction beam and a series of other fixture components to the foundation, ensuring stable and graded application of the load.

A graded loading procedure was adopted, wherein concentrated loads were applied incrementally. The initial loading stage was conducted until visible cracking occurred in the test specimen, which was subsequently unloaded. After the stabilization of all residual deformations, the specimen was reloaded until the ultimate limit state was reached. Following complete yielding of the specimen, it was unloaded again. The load values for each step during the two loading stages and the corresponding shear force values in the test beam segment are presented in

Table 2. Loading protocol for crack resistance test (initial loading).

Loading Level	Load/kN	Shear Force/kN	Loading Level	Load/kN	Shear Force/kN
LC1	200	168	LC13	1750	1472
LC2	400	336	LC14	1800	1514
LC3	600	505	LC15	1900	1598
LC4	800	673	LC16	2000	1682
LC5	1000	841	LC17	2100	1766
LC6	1100	925	LC18	2200	1850
LC7	1200	1009	LC19	2300	1934
LC8	1300	1093	LC20	2400	2018
LC9	1400	1177	LC21	2500	2102
LC10	1500	1261	LC22	2600	2186
LC11	1600	1345	LC23	2700	2270
LC12	1700	1429	LC24	2800	2354

and

Table 3. Loading protocol for bearing capacity test (secondary loading).

Loading Level	Load/kN	Shear Force/kN	Loading Level	Load/kN	Shear Force/kN
LU1	500	420	LU10	3000	2523
LU2	800	673	LU11	3200	2691
LU3	1200	1009	LU12	3400	2859
LU4	1600	1345	LU13	3600	3027
LU5	2000	1682	LU14	3800	3195
LU6	2200	1850	LU15	4000	3364
LU7	2400	2018	LU16	4200	3532
LU8	2600	2186	LU17	4400	3700
LU9	2800	2354	LU18	4600	3868

, respectively. This graded loading protocol was established with reference to the relevant provisions of the “Standard for Test Methods of Concrete Structures” (GB/T 50152-2012) [27]. This paper primarily focuses on the cracking resistance under static loading and the ultimate bearing capacity, without addressing complex stress conditions such as low-cycle reversed loading or fatigue loading.

Before formal loading, preloading is first conducted to inspect the test setup, eliminate gaps between the specimen and loading devices, and ensure the loading system enters normal working condition. During the initial loading phase, graded loading with relatively large increments is applied until the specimen cracks. After cracking, the increment size is reduced while loading continues until significant cracking occurs, after which the specimen is unloaded. Subsequently, loading is resumed with larger increments up to the cracking load, followed by smaller increments until the specimen fully yields, after which unloading is performed. In both loading phases, larger increments are used initially to allow the specimen to pass rapidly through the elastic stage. Thereafter, the load increment per step is reduced based on actual conditions to improve data accuracy in the nonlinear stage. To obtain stable measurement point data and observe crack development and failure mode, each load stage is maintained for at least 5 min. Unloading continues until the force transducer reading stabilizes near zero load, at which point data acquisition is stopped.

3.2. Measurement Plan

To investigate the crack development patterns, failure mode, load–displacement relationship at the loading section, and characteristics of concrete strain variation in the test beams under a shear-span ratio of λ = 2.5, this experiment adopted the following procedures: white latex paint was applied to the shear-span zone of the specimen web, and square grids were marked to facilitate clear observation and recording of crack propagation and the variation in maximum crack width using a handheld high-precision crack observation device; at the loading section shown in Figure 3, a pressure transducer and a draw-wire electronic displacement sensor were installed to monitor load and displacement data; concrete strain gauges were arranged on one side of the web to obtain the concrete strain at local measurement points on the beam surface.

Additionally, an optical three-dimensional dynamic tracking system was set up beside the test beam segment to capture the minute displacements of target points arranged on the concrete surface within the shear-span zone. Based on the principles of the finite element method, the strains of the rectangular two-dimensional plane elements formed by these target points were calculated. The optical 3D dynamic tracking system employed was the Optotrak Certus system (a portable optical 3D dynamic tracking and vibration measurement system designed and manufactured by Northern Digital Inc., hereafter referred to as the NDI device) [28]. This system detects infrared light emitted by multiple target points on the object’s surface through an array of infrared cameras and acquires their spatial coordinates using triangulation and frequency identification techniques. The measurement accuracy of the instrument is approximately 1 × 10⁻² mm. The positions of the target points and the corresponding computation units are illustrated in Figure 4. The Optotrak Certus system can simultaneously measure the specific spatial positions of multiple target points, offering real-time capability, high accuracy, and strong anti-interference performance.

4. Analysis of Test Results

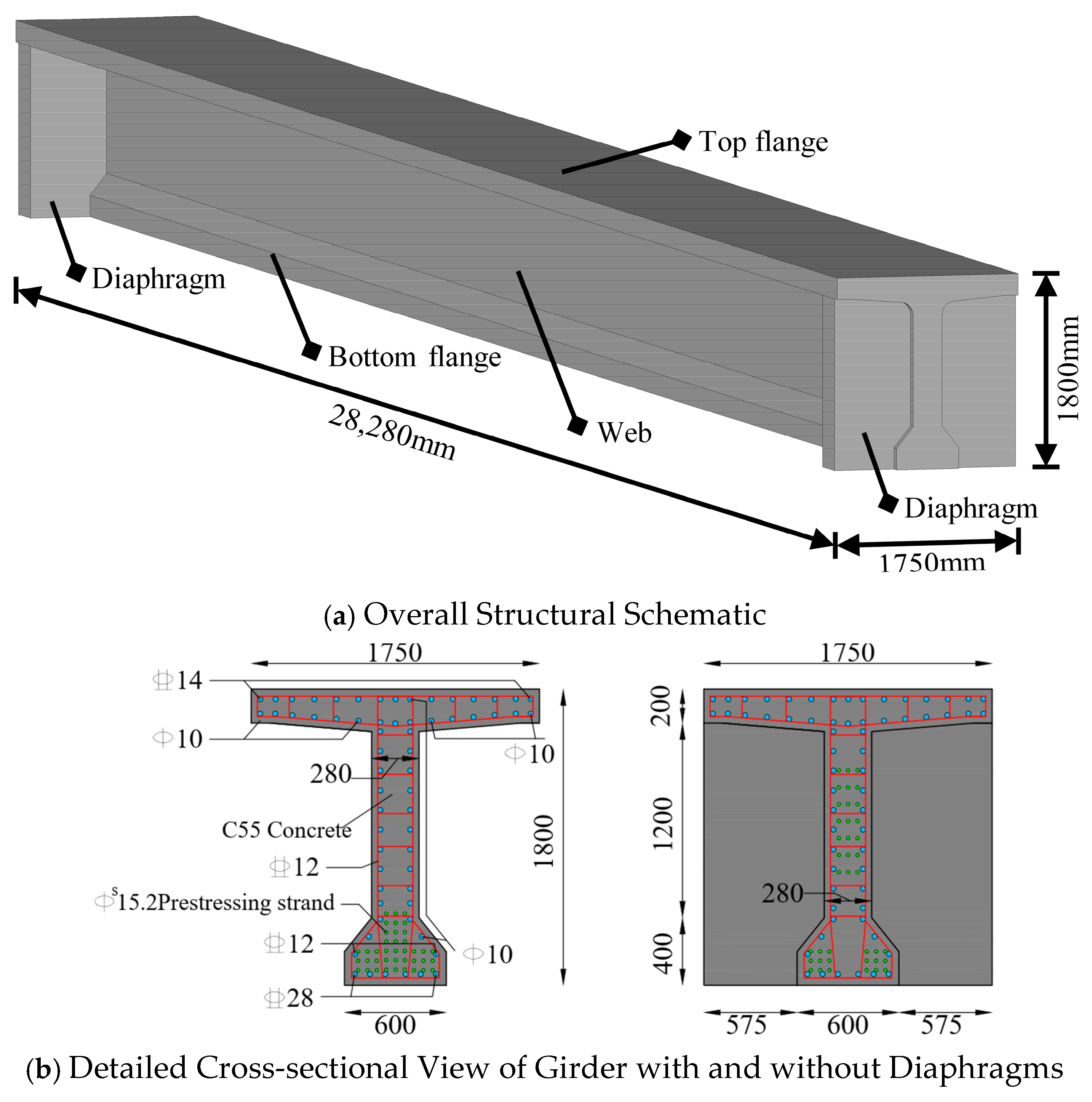
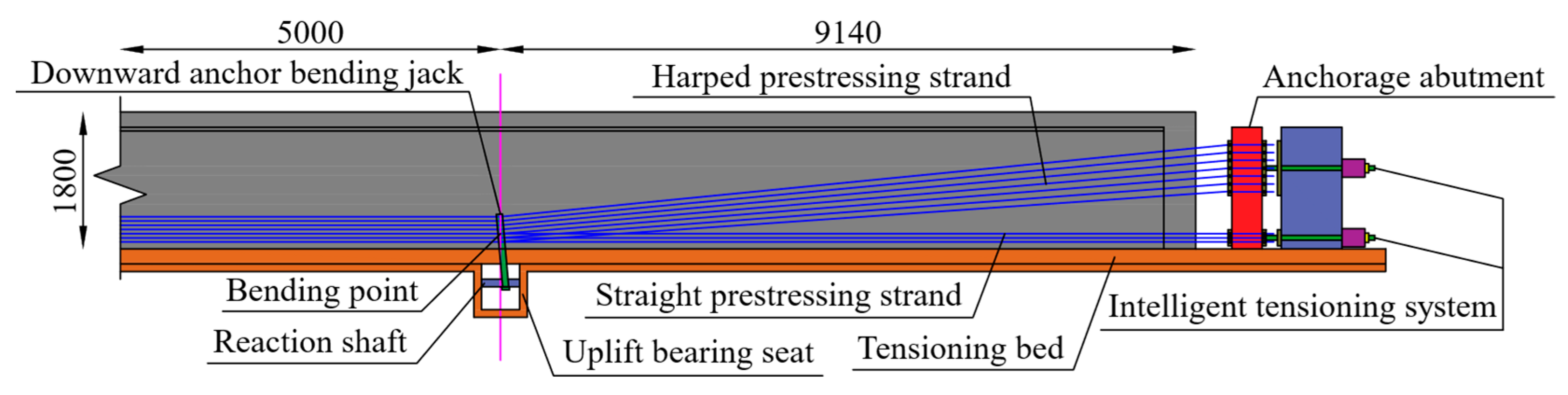
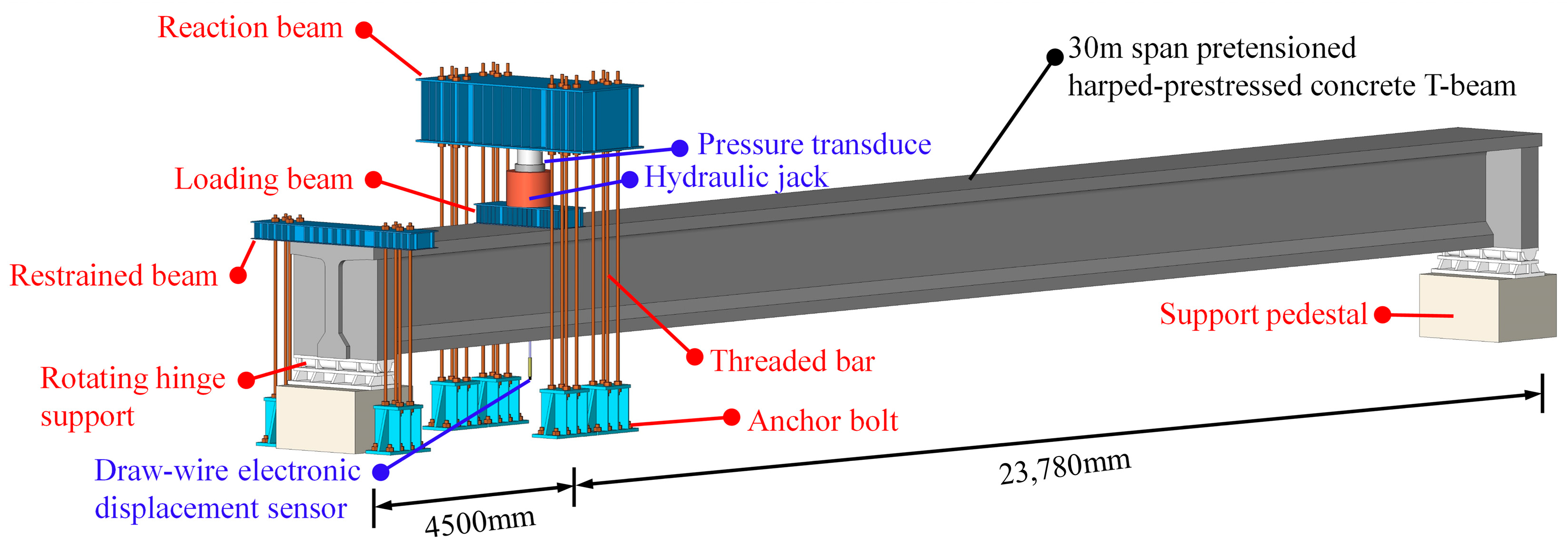
4.1. Shear Force and Vertical Displacement

This study adopts the shear force value of the test beam segment as the representative value of the beam loading and plots the relationship curve between the shear force of the test beam segment and the displacement measurement points under a shear-span ratio (λ) of 2.5, as shown in Figure 5.

From the shear force–displacement curve illustrated in Figure 5, the entire process of the first loading can be broadly divided into the following three stages: the elastic stage, the cracking stage, and the unloading stage.

During the elastic stage, the load–displacement curve is essentially linear, with high shear stiffness and small deformation in the beam. When loading reached Load Case LC17 (corresponding to a load of 2100 kN and a shear force of 1766 kN in the test beam segment), a distinct inflection point appeared in the load–displacement curve. The stiffness of the test beam segment decreased, and significant nonlinear deformation occurred. At this point, fine vertical cracks began to form in the concrete near the loading section. The measured displacement at the loading section after completing this load case was 20.1 mm, indicating that the reduction in beam stiffness and the nonlinear deformation were primarily induced by crack propagation. Based on the previously described crack development, extensive shear diagonal cracks began to appear in the test beam after this load case. Therefore, this paper defines the shear force value of the test beam segment corresponding to LC17 as the experimental diagonal cracking shear force for the beam under a shear-span ratio (λ) of 2.5.

After cracking, the beam deformation increased more rapidly with further loading. Flexural–shear diagonal cracks emerged and developed quickly, while the concrete in the loading section gradually lost its load-carrying capacity. The tangent slope of the shear force–displacement curve gradually decreased but did not reach a plateau, indicating that the internal reinforcement and prestressing strands had not yielded. After completing Load Case LC24 (corresponding to a load of 2800 kN and a shear force of 2354 kN in the test beam segment), the measured displacement at the loading section was 35.9 mm, and the unloading process commenced.

During the unloading stage, the beam deformation gradually recovered. Cracks concentrated at the junctions of the web, top flange, and diaphragm, as well as flexural–shear diagonal cracks propagating from the bottom of the bottom flange, gradually closed. When the shear force at the loading section reduced to near zero, the residual displacement at the loading section was 5 mm, as shown in Figure 5.

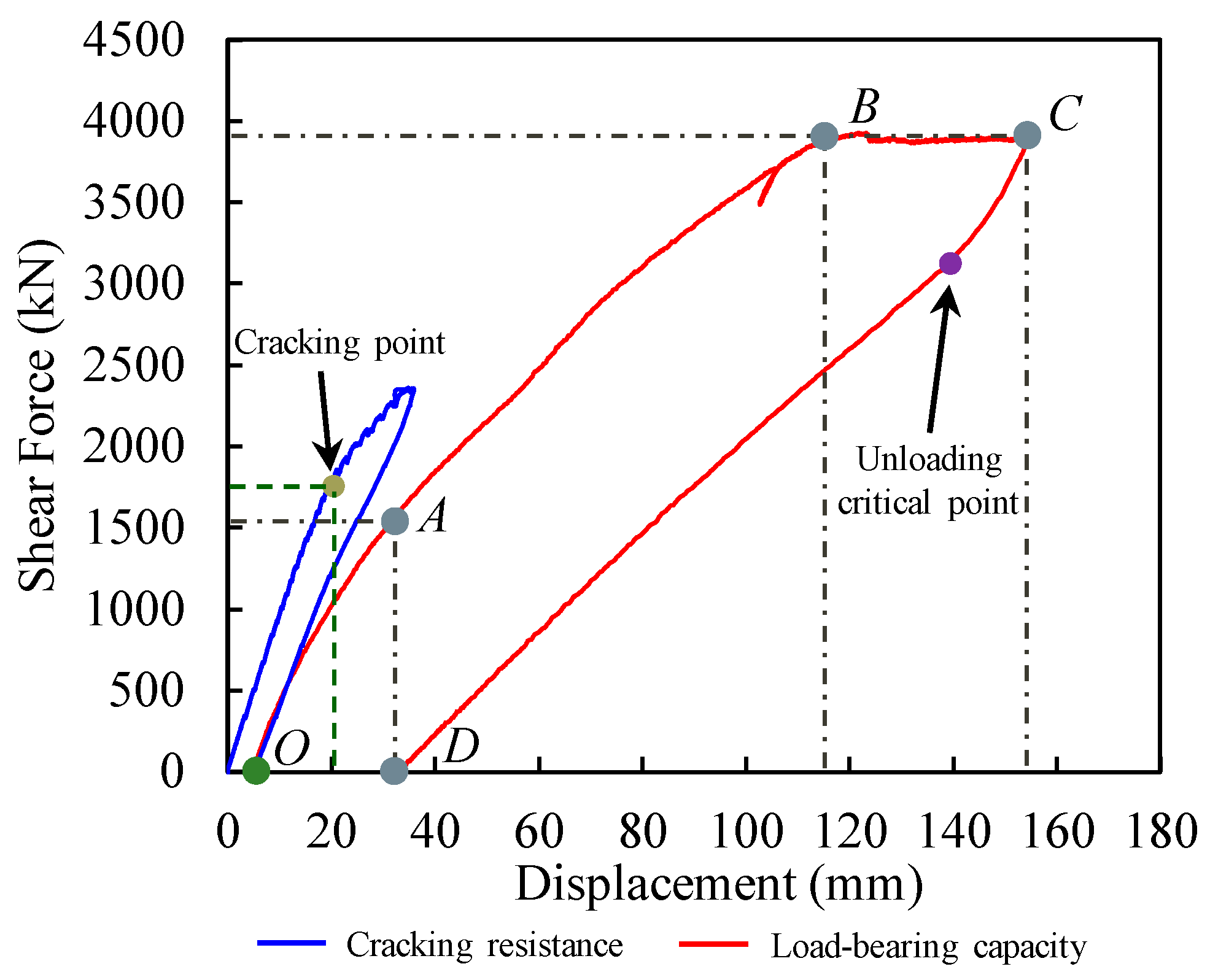
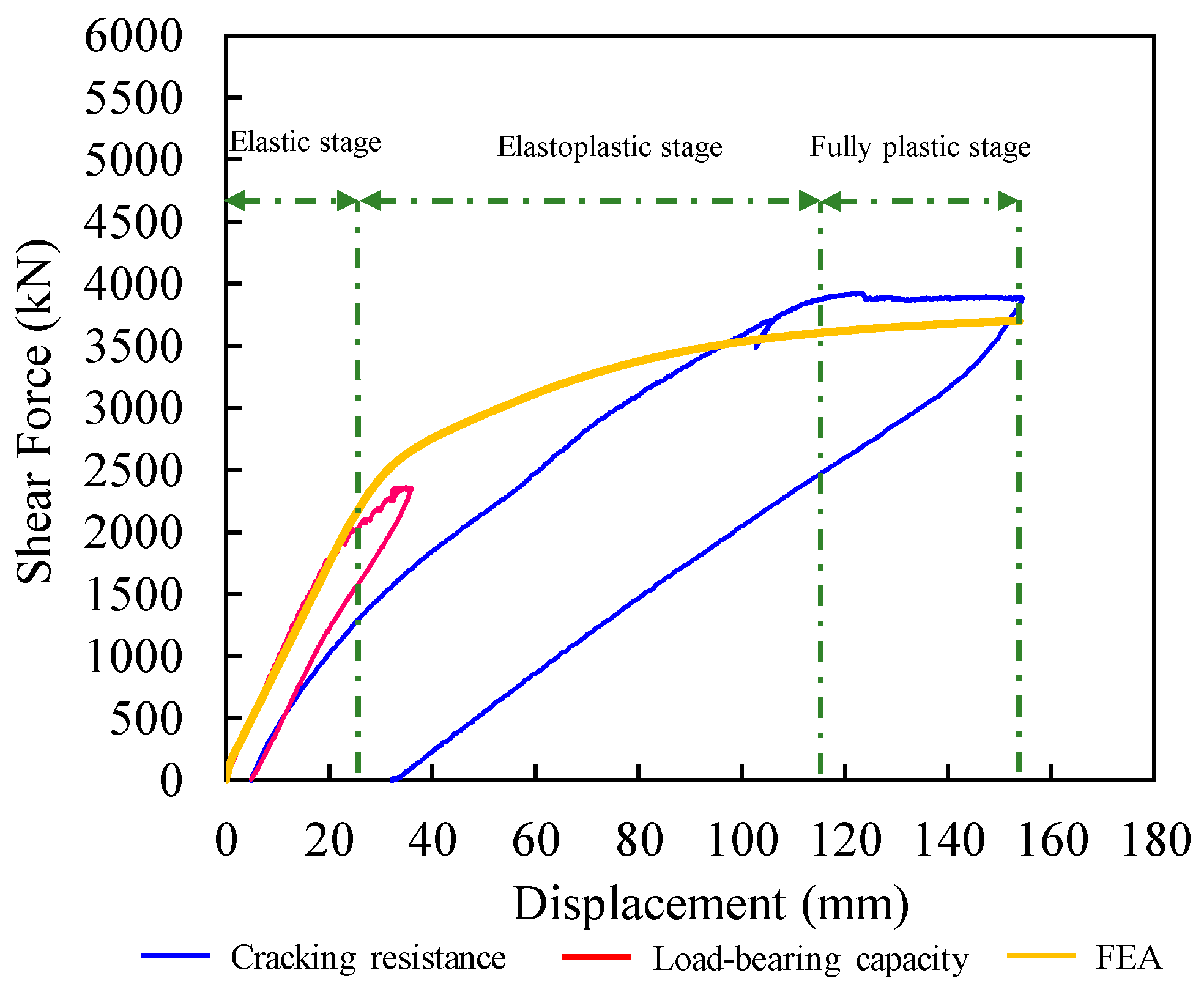
As shown in Figure 6, the shear force–displacement relationship obtained from the bearing capacity test can be divided into the following stages: the slight nonlinear stage (Points O–A), the elastoplastic deformation stage (Points A–B), the plastic yielding stage (Points B–C), and the unloading stage (Points C–D).

At the initial loading stage (Points O–A), the specimen was essentially in an elastic state. However, as indicated by the reloading curve in Figure 6, the load–displacement relationship was not perfectly linear elastic; instead, a slight degradation in stiffness gradually occurred as loading progressed. Furthermore, the shear force corresponding to the first inflection point of the curve decreased. Around loading case LU4 (corresponding to a total load of 1562 kN and a shear force of 1313 kN in the test beam segment), the specimen began to enter the elastoplastic stage, with a corresponding displacement of 26.25 mm at the loaded section. Compared to the initial loading during the crack resistance test, the shear force value at which the test beam segment entered the elastoplastic stage decreased by 11.55%. The equivalent stiffness decreased by 16.34% compared to the tangent stiffness of the initial loading.

This is primarily attributed to the irreversible changes that had already occurred in the internal structure of the test beam after the first loading cycle. During the initial loading, a concrete damage zone filled with micro-cracks had formed at the tips of macroscopic cracks, and this damage could not be fully recovered. Simultaneously, even in regions without visible cracks, multiple micro-slips and defects had developed within the concrete matrix. Although the macroscopic cracks partially closed upon initial unloading, they could not return to their original state. These micro-cracks, formed during the initial loading, created multiple stress concentration zones during the reloading process. Even though these zones experienced mutual extrusion, friction, interlocking, and shear during reloading, their mechanical performance was already compromised compared to the initial loading. All these factors contributed to the gradual development of a slight nonlinear state in the member during the early phase of reloading and a reduction in the shear force corresponding to the first inflection point.

After the member entered the elastoplastic deformation stage (Points A–B), the test beam segment exhibited significant nonlinear behavior overall. The tangent stiffness decreased markedly compared to the initial loading stage but remained relatively stable. This behavior results from several factors. Firstly, in the cracked sections, the tensile force was primarily carried by the reinforcing bars and prestressing strands, both of which exhibited essentially linear elastic behavior until reaching their yield strength. Secondly, the concrete in the compression zone had not yet reached its compressive strength during this stage, behaving approximately in a linear elastic manner. The combination of these two aspects formed a relatively stable load-bearing framework. Additionally, the existing cracks formed during the initial loading only needed to gradually reopen, eliminating the need to overcome the concrete’s tensile strength again to form new cracks. Compared to the nonlinear stage during initial loading, the equivalent shear stiffness in this stage decreased by 27.91%, indicating a reduction in the fracture energy required to propagate the cracks. Consequently, although the test beam entered the elastoplastic stage overall, the global shear stiffness remained at a relatively stable level.

When the loading reached case LU18 (corresponding to a total load of 4600 kN and a shear force of 3868 kN in the test beam segment), the specimen reached its ultimate limit state and entered the plastic yielding stage (Points B–C). At this point, the load–displacement curve reached a plateau, with the tangent stiffness essentially zero. The primary characteristic of the mechanical behavior was deformation rather than load-bearing capacity. The specimen dissipated the energy input by the loading apparatus through substantial plastic deformation, thereby achieving the intended ductile failure mode. Within the test beam segment, a plastic hinge had formed at the loaded section, leading to redistribution of internal forces, while the shear force remained essentially constant.

After undergoing significant deformation at the ultimate state, the specimen began to unload (Points C–D). During the initial phase of unloading, the recovery stiffness was high. At this time, the test beam segment was under high stress, and no significant relative slip rebound had occurred at the cracked sections. The concrete on both sides of the cracks was in tight contact, with aggregate interlock providing high contact stiffness and shear resistance. As unloading continued and the load decreased to a critical unloading point, the load was no longer sufficient to keep the crack surfaces tightly pressed together to overcome their frictional and mechanical interlocking resistance. The concrete then began to exhibit significant relative slip rebound, and the aggregate interlock effect was broken. Beyond this critical point, the crack surfaces disengaged from full interlock and entered a stage dominated by sliding friction. Subsequently, as the load continued to decrease, the frictional resistance decreased at an almost constant rate. Therefore, the unloading curve maintained a low and stable value in the subsequent range until the load was completely removed. The residual displacement at the loaded section was 32.2 mm, as shown in Figure 6.

In addition, the design shear force of a single beam under the action of Highway Class I and secondary dead loads was calculated in accordance with the General Specifications for Design of Highway Bridges and Culverts (JTG D60-2015) [29]. The uniformly distributed lane load was taken as 10.5 kN/m, and the pedestrian load as 3.0 kN/m. The secondary dead load was accounted for by considering a 2 cm thick asphalt surface treatment, a 6–12 cm thick C25 concrete cushion layer, and crash barriers on both sides. The lateral distribution coefficients for the Highway Class I lane load and pedestrian load were computed using the lever rule method and the eccentric pressure method, respectively, with the number of traffic lanes taken as four. After incorporating the self-weight of the structure and performing load combinations, the design shear force at the support section was determined to be 962.6 kN. The ratio of the measured cracking load to the design value was 1.835, indicating that the new type of T-beam possesses relatively excellent crack resistance.

Additionally, by inputting the relevant material, geometric, and detailing parameters of the test beam into the Specifications for Design of Highway Reinforced Concrete and Prestressed Concrete Bridges and Culverts (JTG 3362-2018) [30] and the Design Specifications for Highway Prefabricated Concrete Bridges (JTGT 3365-05-2022) [31], the calculated shear capacities were 2946 kN and 2925 kN, respectively. Both calculation results are conservative, with deviations from the experimental result of approximately 25%. Similarly, inputting the relevant parameters into a variable-angle truss model—which allows for setting the corresponding inclination angle of the compressive strut based on the different mechanical characteristics of the beam—yielded a calculated shear capacity of 3966 kN for the test beam. This value is in close agreement with the measured result, showing a deviation of only 2.5%. The above findings demonstrate, on one hand, that this structural form provides an increased safety margin within the current design codes. On the other hand, they indicate that the variable-angle truss model, by setting the strut inclination angle according to the specific mechanical characteristics of the beam, enables a more accurate calculation of the beam’s shear capacity. Therefore, it is recommended to adopt this model for shear capacity analysis of beams.

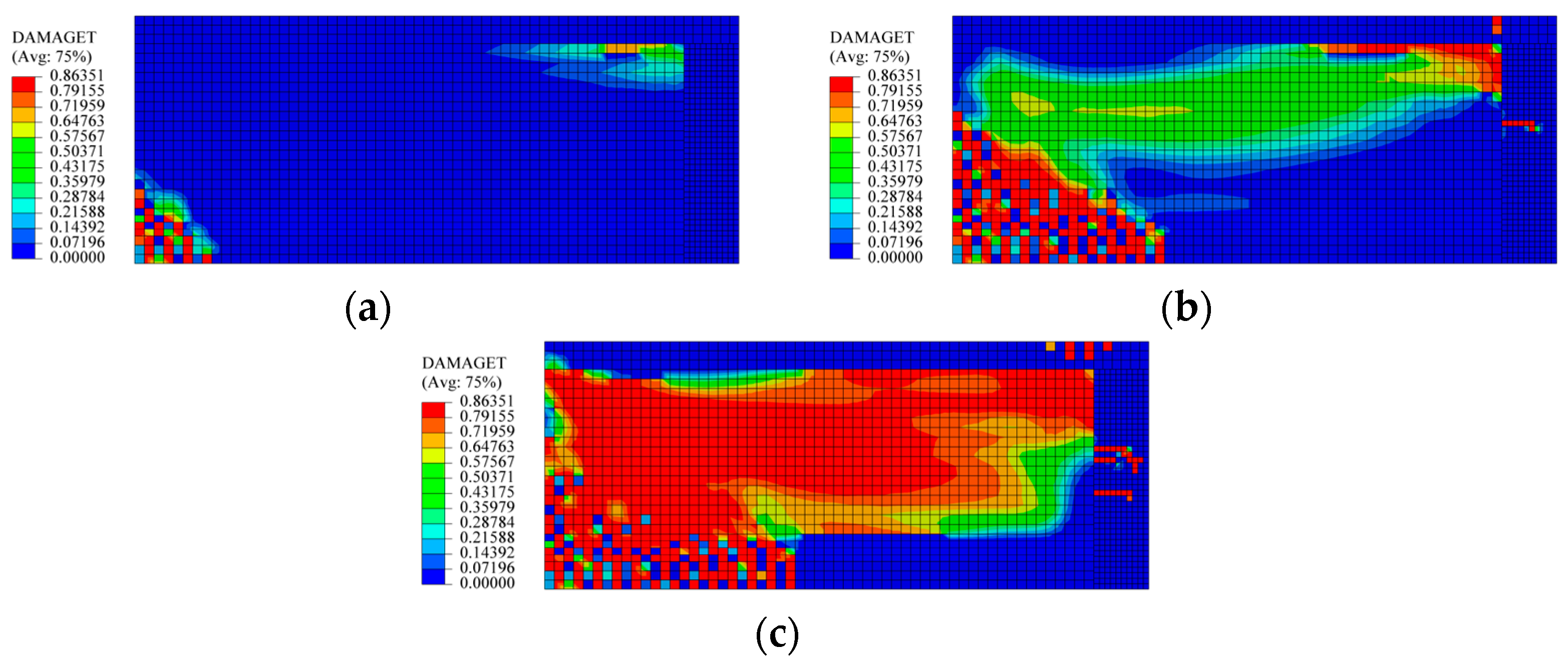
4.2. Crack Propagation State and Member Failure Mode

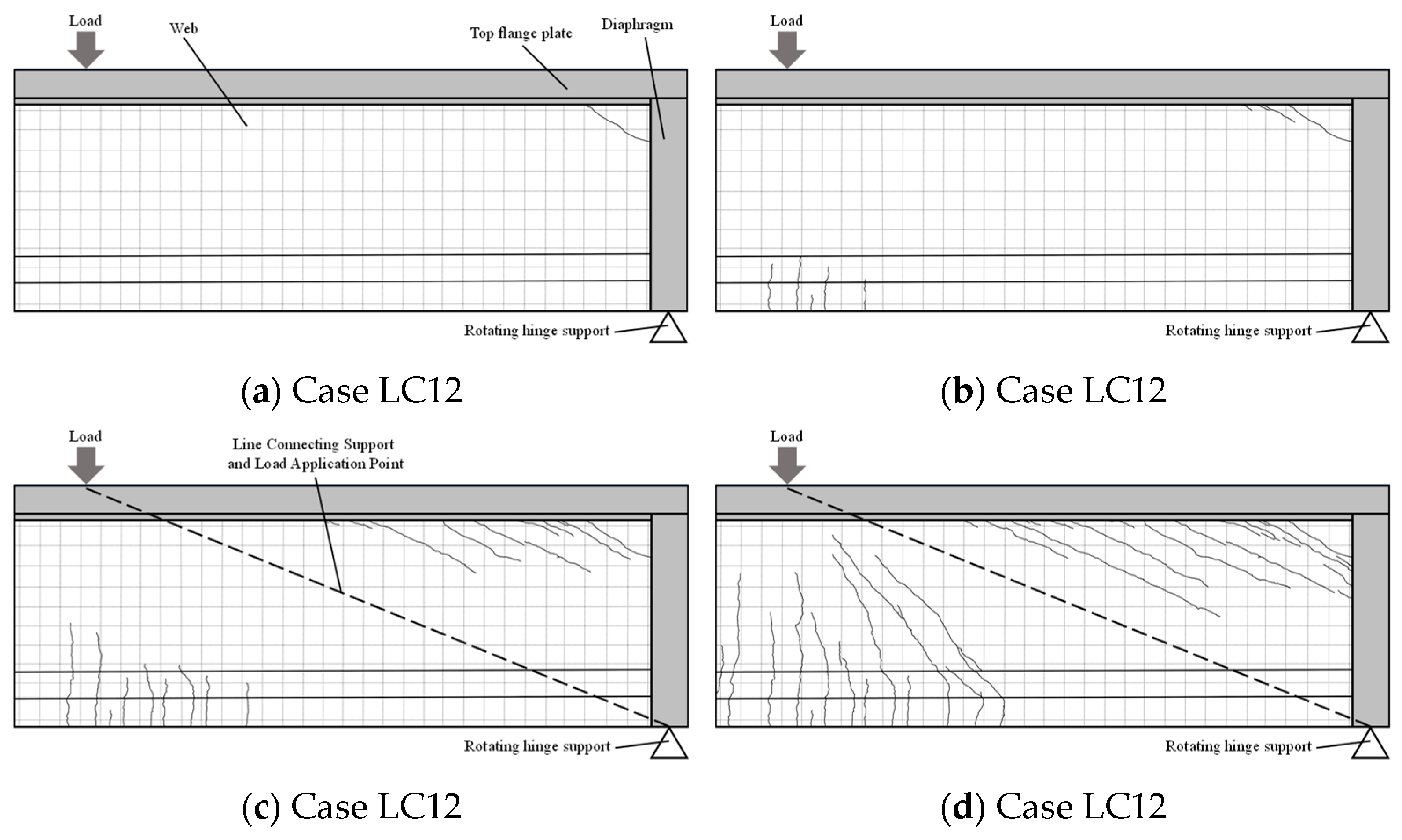
In the initial stage of the shear test loading, the test beam exhibited significant elastic characteristics, with minimal deformation observed in the beam segment. As the load was incrementally increased, a small number of micro-cracks first appeared at the junctions of the web, top flange, and diaphragm (under Working Condition LC12). The maximum crack width reached 0.12 mm, and these cracks developed obliquely from the root of the top flange toward the diaphragm, as illustrated in Figure 7a.

With further increase in load, fine vertical flexural cracks began to emerge in the tension zone near the loading section (under Working Condition LC17). The maximum crack width in this region was 0.02 mm. However, at this stage, the widest cracks in the test beam segment were still located at the junctions of the web, top flange, and diaphragm, with a maximum crack width of 0.23 mm, as shown in Figure 7b.

As the load continued to increase, the cracks at the junctions of the web, top flange, and diaphragm not only propagated further at their original locations (under Working Condition LC20) but also extended gradually toward the line connecting the support and the load application point. The crack paths aligned with this line, as depicted in Figure 7c. With ongoing loading, the fine concrete cracks in the tension zone of the flexural–shear segment began to extend vertically for a short distance before developing obliquely toward the load application point. Some of these cracks approached the junction of the top flange and the web (under Working Condition LC24), demonstrating typical shear–compression failure behavior, as shown in Figure 7d. At this point, distinct cracks had appeared in various regions of the test beam segment. The widest cracks remained at the junctions of the web, top flange, and diaphragm, with a maximum width of 0.24 mm. Additionally, as seen in Figure 7, no oblique cracks were observed near the line connecting the support and the load application point throughout the test. Figure 8 shows the photograph of crack development after the completion of loading in the bearing capacity test.

During the initial stage of the bearing capacity test up to the peak load of the previous shear test (2800 kN), no new crack propagation was observed in the test beam segment. Only the gradual reopening of existing cracks with increasing load was noted, reflecting the elastic recovery capability of the prestressing strands and ordinary reinforcement, as well as the crack closure effect of the concrete.

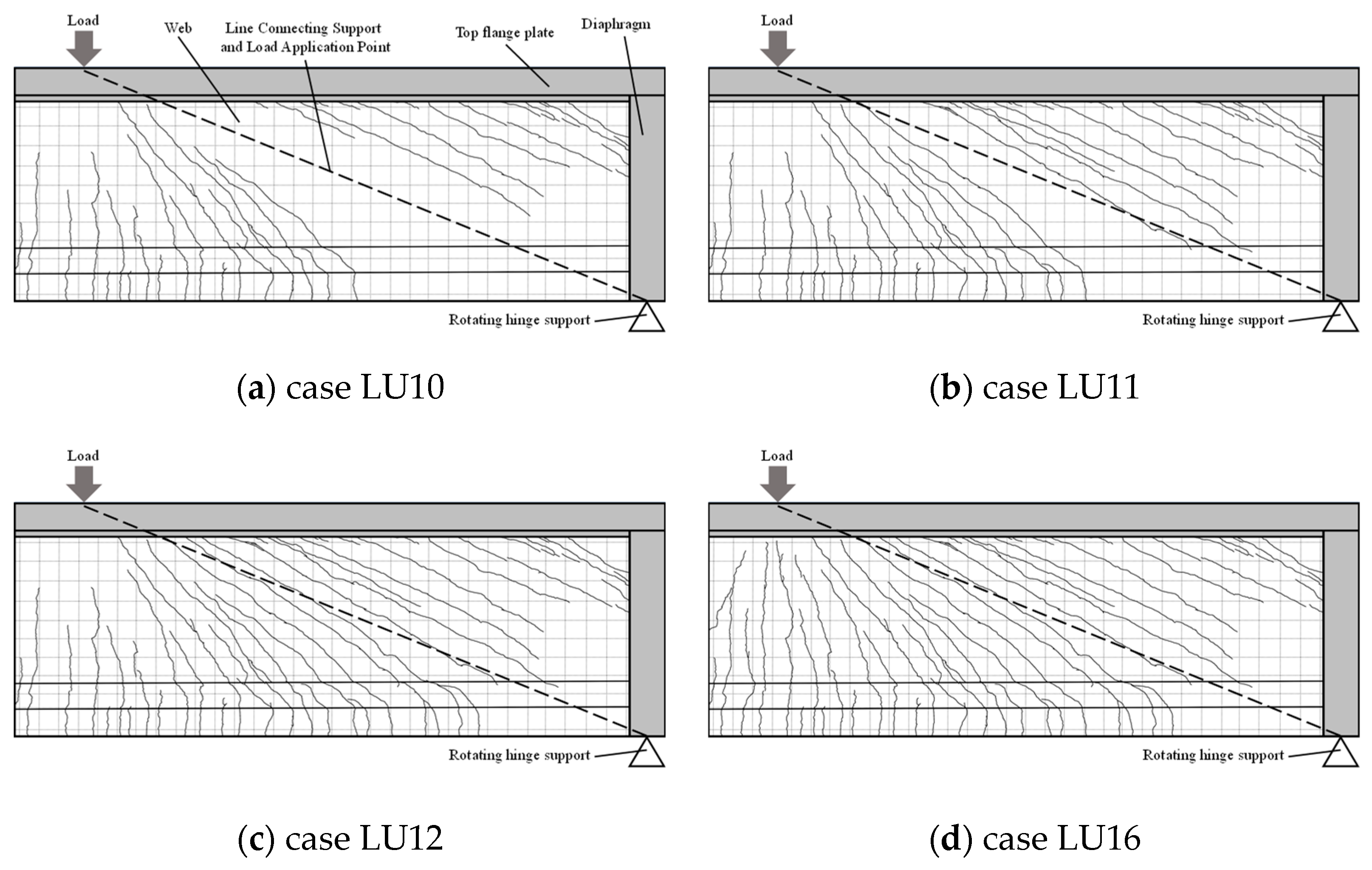
As the load exceeded the peak value of the first loading cycle, the cracks entered a propagation phase. The existing cracks extended further, gradually approaching the line connecting the support and the load application point. Inclined cracks originating from the bottom flange and extending towards the load application point reached the junction of the top flange and the web (Case LU10), as shown in Figure 9a.

With further increase in load, inclined cracks generated from both the top and bottom flanges extended towards the respective ends of the line connecting the support and the load application point. An inclined short strut formed within the web region, while the concrete in the compression zone remained uncracked (Case LU11), as shown in Figure 9b.

Upon additional loading, a critical diagonal crack penetrated the web formed along the line connecting the support and the load application point. Concurrently, the concrete in the web region gradually lost its load-bearing capacity, and the load was primarily resisted by the combined action of the concrete in the compression zone, ordinary reinforcement, and prestressing strands. Throughout this process, the crack widths continuously increased, yet the concrete in the compression zone remained intact until relatively high load levels were reached (Case LU12), as shown in Figure 9c. This demonstrates the effective contribution of the polygonal tendons to the shear capacity of the structure and their restraining effect on crack development.

At the ultimate limit state, the concrete in the compressed zone of the web crushed, accompanied by a sharp increase in the overall displacement of the test beam. The load–displacement curve entered an approximately flat plateau segment, where the bearing capacity remained essentially stable while deformations continued to develop. The width of the critical diagonal crack increased rapidly, and a distinct plastic hinge mechanism formed near the loading section, indicating that the structure had entered the plastic yielding stage (Case LU16), as shown in Figure 9d. This failure mode exhibits typical shear–compression failure characteristics. It also reflects the role of polygonal tendons in improving member ductility and shear performance. The mechanical behavior demonstrated significant stress redistribution capability and sustained shear capacity maintenance, illustrating the balance between the inherent brittle failure tendency of prestressed members and the requirement for ductility. A photograph of crack development after the completion of the bearing capacity test is shown in Figure 10.

In conventional reinforced concrete beams, the propagation of diagonal cracks is primarily governed by the principal tensile stress exceeding the concrete’s tensile strength. The trajectory of the principal stress intuitively predicts the development path of diagonal cracks. Under the combined action of external shear and bending moments, the principal compressive stress trajectories are approximately parallel to the line connecting the load application point and the support, while the principal tensile stress trajectories are orthogonal to them. This region exhibits the highest level of principal tensile stress and is susceptible to the initiation and propagation of diagonal cracks.

Polygonal prestressing tendons apply a concentrated vertical force towards the centroid at the bending points of the concrete member. This vertical component acts in the opposite direction to the shear force induced by external loads, and its mechanical effect can be understood as introducing a reverse shear field in the web beforehand. The modification of the principal stress trajectories is specifically manifested as follows: the vertical component causes the principal compressive stress trajectories to become more “arched,” while the curvature of the principal tensile stress trajectories correspondingly decreases, becoming flatter. Most critically, this effectively reduces the principal tensile stress value along the potential diagonal crack development path and directly alters the direction of the principal stresses.

In the shear test (Figure 7), the absence of diagonal cracks near the line connecting the support and load application point provides direct evidence that the vertical component of the prestressing force alters the principal stress distribution. The maximum principal tensile stress generated by external loads in this region is partially counteracted by the reverse effect of prestressing, preventing its value from reaching the concrete’s tensile strength for most of the loading stages. Consequently, the early appearance of diagonal cracks in this critical region is suppressed. Instead, diagonal cracks first appear in regions where the prestressing effect is weaker, such as the web, top flange, and junctions with the diaphragm.

In the bearing capacity test (Figure 9), the formation path of critical diagonal cracks (extending from the top and bottom flanges toward the support and loading point, respectively) was also influenced by the vertical component of the prestressing force. This component, together with the internal reinforcement, established a more efficient force transfer path. Even as the concrete in the web gradually ceased to contribute, the concrete in the compression zone remained intact until higher load levels. This demonstrates that the vertical component effectively shared shear forces, delayed the crushing of the concrete in the compression zone, and allowed the member to undergo a longer plastic deformation process before failure (evident as a plateau in the load–displacement curve). This phenomenon results from an optimized internal force transfer mechanism following the redistribution of principal stresses.

4.3. Beam Strain

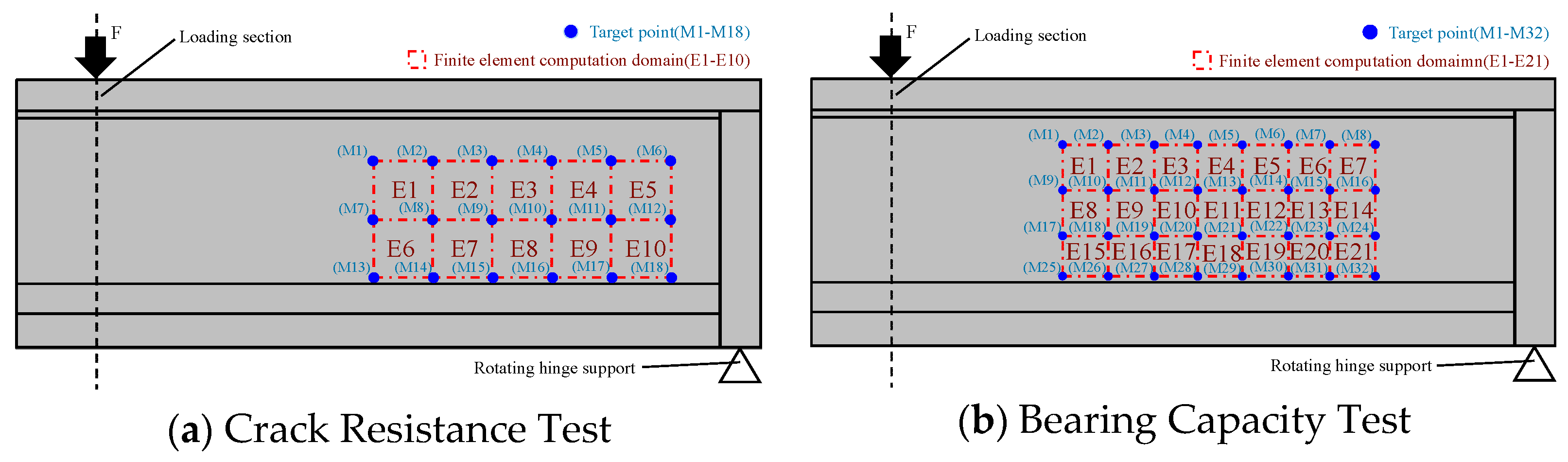
In this test, target points of the NDI device were placed on the surface of the concrete web within the shear-span region to capture the specific displacements of each point during the step-by-step loading process. The average principal strain of the rectangle formed by the target points was calculated based on the theory of the 4-node rectangular element. For a 4-node rectangular element, each node has two degrees of freedom (displacements in the x and y directions), so the total displacement vector of the element is

$$\{\delta \}={\left[u_i v_i u_j v_j u_k v_k u_m v_m\right]}^T$$

(1)

In the above equation, u_i and v_i represent the displacements of the i-th node in the x and y directions, respectively. For a 4-node rectangular element, the shape function N is defined in the natural coordinate system (ξ,η) as follows:

$$\begin{gathered} N_i=\left(1-\xi \right)\left(1-\eta \right)/4, N_j=\left(1+\xi \right)\left(1-\eta \right)/4 \\ {N}_k=\left(1+\xi \right)\left(1+\eta \right)/4, N_m=\left(1-\xi \right)\left(1+\eta \right)/4 \end{gathered}$$

(2)

For plane problems, the nodal displacements can be related to the strains within an element through the strain–displacement matrix B [32]. By taking the centroid of the element as the calculation point for strain, the strain vector at this point and the corresponding form of the B matrix are expressed as follows:

$$\epsilon ={\left[{\epsilon }_x {\epsilon }_y {\gamma }_{xy}\right]}^T=B\left\{\delta \right\}$$

(3)

$$B=\left[\left[B_i\right]\left[B_j\right]\left[B_k\right]\left[B_m\right]\right]$$

(4)

$$\begin{gathered} B_n=\left[\begin{array}{cc}{\displaystyle \frac{\partial N_n}{\partial x}}& 0\\ 0& {\displaystyle \frac{\partial N_n}{\partial y}}\\ {\displaystyle \frac{\partial N_n}{\partial y}}& {\displaystyle \frac{\partial N_n}{\partial x}}\end{array}\right]={\displaystyle \frac{1}{4ab}}\left[\begin{array}{cc}b{\xi }_n\left(1+{\eta }_0\right)& 0\\ 0& a{\eta }_n\left(1+{\xi }_0\right)\\ a{\eta }_n\left(1+{\xi }_0\right)& b{\xi }_n\left(1+{\eta }_0\right)\end{array}\right] \\ \left(n=i,j,k,m; {\xi }_0={\xi }_n\xi ; {\eta }_0={\eta }_n\eta \right) \end{gathered}$$

(5)

In this equation, a and b represent the side lengths of the rectangular element along the x and y axes, respectively; ξ_n, η_n denote the natural coordinate system coordinates of the four corner points, which are i (−1, −1), j (1, −1), k(1, 1), and m (−1, 1); the coordinate at the centroid is (ξ, η) = (0, 0).

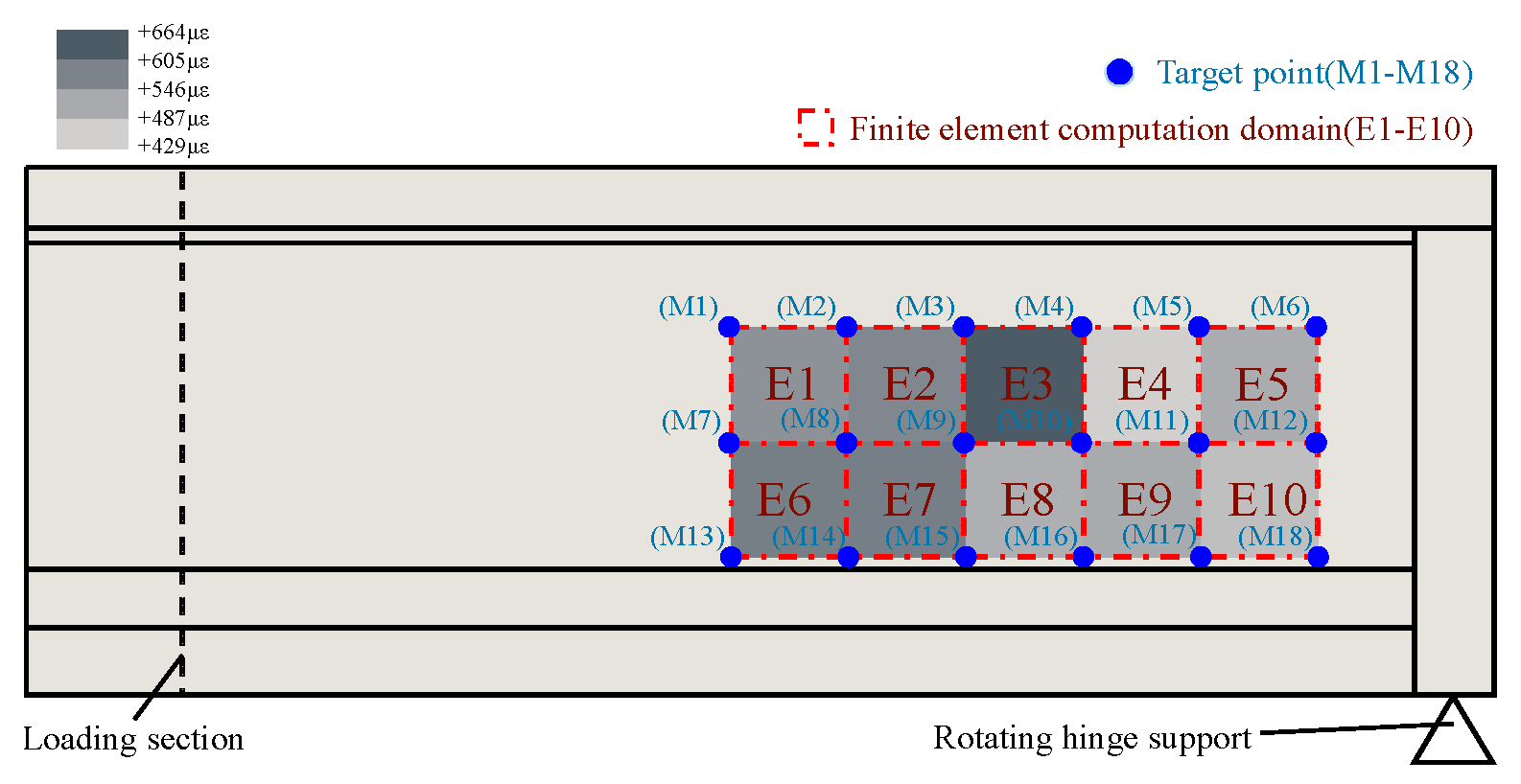
The principal strains of the rectangular elements in the web can be calculated by substituting the strain components ε_x, ε_y, and γ_xy into the principal strain formula. The cloud diagrams of the principal strains for elements numbered E1 to E10 under the cracking load are shown in Figure 11.

Since the computational domains of elements E1–E5 are largely covered by the crack propagation zone in the upper part of the beam web, their variation trends are generally similar. A sudden strain change occurs between load case LC17 (shear force of the test beam segment: 1766 kN) and LC18 (shear force of the test beam segment: 1850 kN), indicating that the concrete in this region exhibits significant nonlinear characteristics in its average strain trend due to cracking.

The strain variations of elements E6–E10 remain essentially consistent throughout the entire loading process. Their computational domains hardly overlap with the crack propagation zone. Therefore, the average principal strain of these elements is always much smaller than that of elements E1–E5 under the same load cases, and only minor abrupt changes occur in some final load cases. This indicates that no significant cracking occurred in the concrete of this region during loading.

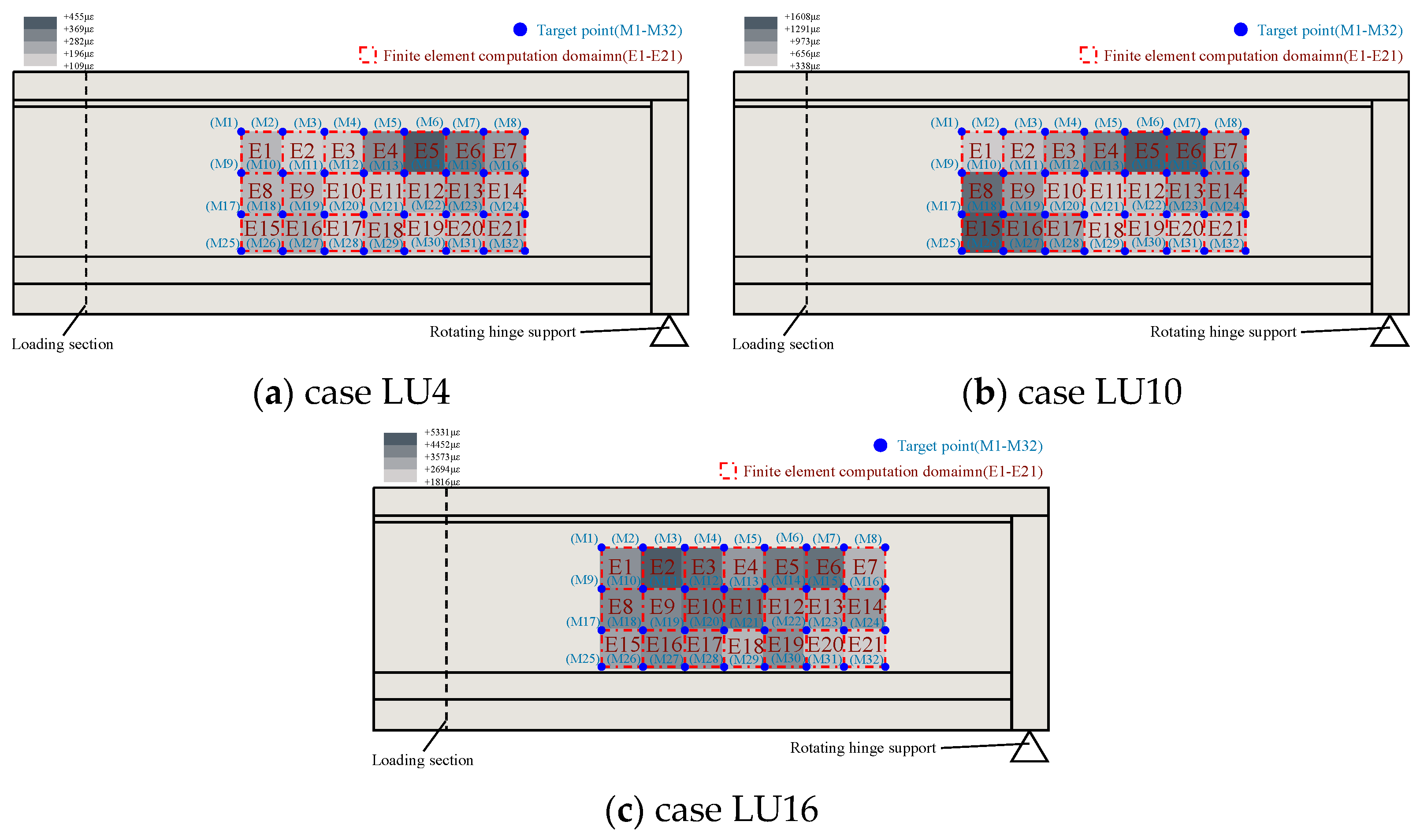
The minute displacements of target points (M1–M32) measured by the NDI equipment during the bearing capacity test were substituted into Equations (1)–(5) for calculation, yielding the average principal strains of each 4-node rectangular element (E1–E21) throughout loading cases LU1 to LU16. The cloud diagrams of average principal strain for each element under loading cases LU4, LU10, and LU16 are shown in Figure 12. Throughout the entire loading process, the evolution of average principal strain in the rectangular elements of the test beam’s web exhibited distinct stages, closely associated with damage accumulation and internal force redistribution.

From no-load to Load Case LU4 (shear force in the test beam segment is approximately 1313 kN), the member exhibited primarily elastic behavior. The average principal strains of all elements increased slowly and linearly, indicating no significant degradation in the overall structural stiffness during this loading stage. The specific response is illustrated in Figure 12a.

As the load increased and the member entered the elastoplastic stage, existing cracks gradually reopened. This led to a notable acceleration in the strain growth rate of elements directly intersected by the initial cracks (such as E4 to E7 and E15). However, the overall strain values were slightly lower than those during the first loading. This can be attributed to the fact that, although friction and aggregate interlock along the original crack surfaces provided some shear resistance, the overall stiffness was significantly lower than that of the intact concrete.

When the load further increased to Load Case LU10, the majority of the original cracks had fully reopened, and new cracks began to propagate outward from the vicinity of the original crack zones. Consequently, elements previously not directly affected by cracking (such as E2, E3, E16, E17, and elements in the mid-height of the web except E10) experienced a sudden increase in strain. This reflects the progressive spread of damage and the intensification of internal force redistribution, as shown in Figure 12b.

By Load Case LU12 and beyond, critical diagonal cracks had fully developed and propagated through elements such as E10. These elements, located in key regions of the shear transfer path, exhibited a sharp increase in strain. After the concrete ceased to contribute effectively, shear forces were primarily resisted by the reinforcing bars and prestressing strands, leading to significant strain concentration.

Throughout the loading process, the evolution of the average principal strain in the rectangular elements of the test beam’s web displayed distinct stages closely associated with damage accumulation and internal force redistribution. During secondary loading, the premature reopening of cracks reduced the fracture energy demand and accelerated strain development. In the plastic stage, reinforcing bars and prestressing strands carried the majority of the tensile forces, resulting in strain concentration along the critical main crack paths. Ultimately, concrete crushing and the formation of plastic hinges led to deformation localization in critical regions. The overall behavior was characterized by a combined response of shear stiffness degradation, strain localization, and internal force redistribution.

Furthermore, from the perspective of quantitative strain analysis, the elements with the most concentrated and rapidly increasing strain (such as E10) are located along the path of the ultimately formed critical diagonal crack. This phenomenon quantitatively demonstrates that after the redistribution of internal forces, the transfer of forces eventually concentrates along the critical path dominated by reinforcing bars and prestressing tendons. The vertical component of the prestressing force alters the principal stress trajectories in the early stages, delaying the initiation of cracks; in the later stages, it works in conjunction with conventional reinforcement to form a more effective shear resistance mechanism.

5. Finite Element Analysis

5.1. Establishment of the Finite Element Model

To investigate the cracking resistance and bearing capacity behavior of a 30 m pre-tensioned T-beam with polygonal tendons under a shear-span ratio of λ = 2.5, and considering that a single experimental test may not fully reflect the mechanical response of the member under different parameters and boundary conditions while being susceptible to random factors, this study performed a numerical simulation of the test beam. A conventional numerical analysis model of the beam was established using the finite element software Abaqus/CAE Release 2022, as shown in Figure 13.

A partitioned modeling approach was adopted for the numerical model. The concrete and the shear loading bearing blocks were modeled using 8-node reduced-integration solid elements (C3D8R). Longitudinal reinforcement and stirrups, which primarily resist axial stresses and strains, were assembled into a reinforcement skeleton and modeled using 2-node three-dimensional truss elements (T3D2). Considering the mechanical behavior of prestressing strands during both prestressing application and subsequent test loading, two-node linear space beam elements (B31) were selected. Schematic diagrams of the models for the concrete, rebar, and prestressing strand components are shown in Figure 14.

Relative slip between solid components was neglected during model assembly. The reinforcement skeleton and prestressing strands were embedded within the concrete elements using the embedded constraint. Prestress application in both straight and harped prestressing strands was simulated using the cooling method to replicate the prestress release process. The boundary condition at the bottom bearing block of the loading end was defined as a fixed rotating hinge support, while that at the non-loading end was defined as a sliding rotating hinge support. Shear force was applied by controlling the vertical displacement of the loading block on top of the flange plate. During the analysis, gravity load was first applied to simulate self-weight. All calculations were performed using a static implicit solver.

The constitutive model for concrete adopts the concrete damage plasticity (CDP) model, which is described by effective stress and damage variables, enabling a decoupled algorithm for effective stress calculation and degradation evaluation. The tensile damage $d_t$ and compressive damage $d_c$ of concrete are used to characterize the damage behavior of concrete under tensile and compressive conditions during plastic deformation. In this study, the Sidoroff energy equivalence damage model is employed to calculate the compressive damage parameter $d_c$ and tensile damage parameter $d_t$ for concrete. The specific calculation process is as follows: In these equations, ${\sigma }_c$ and ${\sigma }_t$ represent the compressive and tensile stresses of concrete, respectively, while ${\epsilon }_c$ and ${\epsilon }_t$ denote the compressive and tensile strains of concrete, respectively [33].

$$d_c or d_t=1-\sqrt{{\displaystyle \frac{{\sigma }_{c or t}}{E_0{\epsilon }_{c or t}}}}$$

(6)

The model is primarily defined by elastic parameters (including the modulus of elasticity and Poisson’s ratio of concrete), plastic parameters, compression hardening and damage, and tension hardening and damage parameters. Within the plastic parameters, the dilation angle (ψ) and eccentricity (e) govern the shape of the non-associated flow potential function. The ratio of initial biaxial to uniaxial compressive yield stress (σ_b0/σ_c0, typically defaulted to 1.16) and the invariant stress ratio (K_c, typically defaulted to 2/3) control the concrete’s yield surface. The viscosity parameter (ν) serves as a viscoplastic regularization parameter intended to improve numerical convergence when the material exhibits softening and stiffness degradation behaviors. The values of the relevant parameters for the concrete damaged plasticity (CDP) model used in this test are presented in

Table 4. Loading protocol for crack resistance test (initial loading).

Dilation Angle (ψ)	Eccentricity (e)	Ultimate Compressive Strength Ratio (σb0/σc0)	Invariant Stress Ratio (Kc)	Viscosity Parameter (ν)
38	0.1	1.16	0.667	1.5 × 10−3

.

Furthermore, the uniaxial tensile and compressive constitutive relationships for concrete were defined in accordance with the Code for Design of Concrete Structures (GB50010-2010) [34]. The concrete’s uniaxial compressive strength was assigned the average value obtained from actual material tests.

Both the reinforcing steel and prestressing strands were modeled using an ideal elastic–plastic constitutive model. The yield strength and modulus of elasticity for the reinforcement, as well as the relevant parameters for the prestressing strands, were assigned values based on actual test results.

In addition, as part of a series of studies adopting the same modeling methodology as this paper, reference [35] conducted a comparative verification under the condition of a small shear-span ratio of 1. The bearing capacity of the beam obtained from the numerical model within the same series was 6530 kN, while the average bearing capacity of the corresponding test beam was 6931 kN. The error between the two is less than 6%, confirming the computational accuracy of the numerical simulation method employed in this paper in validating the shear bearing capacity of this new type of T-beam.

5.2. Shear–Displacement Comparison

As the critical load-bearing region of the beam within the combined bending–shear span, the displacement variation at the bottom of the loading section can represent the overall response characteristics of the beam segment. To clarify the mechanical behavior of this region under load, a concentrated single-point load was applied at the top of this section in the model. The computed load–displacement curve is compared with the experimental results in Figure 15. This curve clearly reflects the deformation development and load-bearing characteristics of the model beam under monotonic loading, exhibiting three typical phases: the elastic stage, the elastoplastic stage, and the fully plastic stage.

In the elastic stage, the beam’s load–displacement relationship is linear. The concrete, reinforcing steel, and prestressing strands all remain in an elastic state. The overall stiffness of the beam closely matches the initial stiffness observed in the test.

During the elastoplastic stage, as the load gradually increases, significant damage initiates and propagates in the concrete at the bottom of the bending-shear region. Significant redistribution of internal forces within the cross-section occurs: compressive forces are primarily borne by the concrete in the top compression zone, while tensile forces at the bottom are mainly carried by the prestressing strands and the ordinary tensile reinforcement. The load–displacement curve exhibits an enveloping trend relative to the cracking test and the plastic phase of the bearing capacity test. The reduction in stiffness falls within a reasonable range compared to the actual test.

Upon entering the fully plastic stage, the prestressing strands at mid-span approach yield, and the beam reaches its ultimate limit state. Concurrently, the load–displacement curve enters a plateau. With continued loading, the load-bearing capacity remains nearly constant at 3702 kN. This value is nearly equivalent to the experimental bearing capacity of 3868 kN, with an error of approximately 4%. Displacement continues to increase, indicating that the bending–shear region of the test beam has approached a state of nearly complete plasticity.

These results demonstrate that the numerical model can effectively replicate the entire process of the beam’s response, from linear elasticity through damage initiation and propagation, to final plastic development. In particular, the patterns of internal force redistribution and stiffness degradation during the elastoplastic transition phase show good agreement with the experimental observations. This mutual validation confirms the reliability of both the test and the model in capturing the key mechanical behaviors of the beam within the bending–shear span.

In this study, the constitutive relationship of the concrete material was modeled using the concrete damaged plasticity (CDP) model. Existing research has confirmed that the computational accuracy of this model is significantly correlated with the finite element mesh size. In general, for finite element analysis of concrete structures, the mesh size is typically selected within a range of 1 to 6 times the maximum aggregate size, with 3 times the maximum aggregate size being considered as a recommended mesh size that balances accuracy and efficiency [36]. For the 30 m pre-tensioned T-beam with polygonal tendons investigated in this case, the maximum concrete aggregate size is 20 mm. Accordingly, the recommended mesh size range for the finite element modeling of this member should be 20–120 mm.

To investigate the influence of mesh sensitivity on the numerical simulation results, a baseline numerical model with a mesh size of 70 mm was established. Four comparative models with overall mesh sizes of 40 mm, 100 mm, 120 mm, and 200 mm were subsequently developed. The computed shear force–displacement curves are presented in Figure 16.

As shown in the figure, the mesh size of 200 mm exceeds the aforementioned recommended range, and its computational results exhibit significant deviations. In contrast, the mesh sizes within the recommended range yield load-bearing capacities and force–displacement curve trends that are relatively consistent, with minor differences in the computational outcomes. A comprehensive analysis indicates that, for this case, a mesh size of approximately 70 mm can achieve stable and reliable numerical solutions while ensuring computational efficiency.

5.3. Tensile Damage Comparison

To thoroughly investigate the predictive capability of the finite element model regarding the crack propagation behavior of the test beams, Figure 17a–c present the tensile damage cloud diagrams corresponding to the cracking test case LC17 (Figure 7b), case LC24 (Figure 7d), and the ultimate limit state case LU16 (Figure 9d) from the bearing capacity test, respectively. It can be seen from Figure 17a that during the initial loading stage, the tensile damage of the numerical model primarily concentrates at the junction regions of the web, top flange, and diaphragm, as well as the tension zone near the loading section. This is consistent with that observed in the test, as shown in Figure 7b. As the load increased to LC24, the calculated tensile damage cloud diagram (Figure 17b) shows a significant expansion of the damaged area, which is coincident with the expansion of the area where cracks occurred. In addition, both numerical calculation and experimental observation indicate that no cracking was observed in the bottom region of the web near the supports. Moreover, at the ultimate limit state LU16, the numerical simulation demonstrates that extensive tensile damage occurred in the web of the test beam segment (Figure 17c), which is in agreement with the widespread cracking observed in the web during the test (Figure 9d and Figure 10).

In summary, the finite element model effectively simulated the complete spatial evolution of cracks, from their local initiation and propagation to final coalescence. Moreover, from the perspective of damage mechanics, it visually elucidated the intrinsic mechanism by which the vertical component force introduced by the polygonal tendons influences the failure mode. This mechanism operates by altering the internal stress field distribution, thereby suppressing early cracking in critical regions, optimizing the internal force transfer path, and ultimately affecting the failure pattern. The model thus provided robust numerical validation and a meso-mechanical explanation for the theoretical analysis based on experimental observations presented in the paper.

6. Conclusions

This study systematically investigates the mechanical response, damage evolution, and failure modes of a 30 m pre-tensioned T-beam with polygonal tendons throughout the entire shear loading process, via a full-scale shear test conducted under a shear-span ratio of 2.5. Complete load–displacement data, crack development processes, and web strain distribution characteristics were obtained from the test. The main conclusions are as follows:

The pre-tensioned T-beam with polygonal tendons exhibited excellent shear capacity and good ductility. Its inclined section cracking shear force was 1766 kN, and the ultimate shear capacity reached 3868 kN, validating the effectiveness and reliability of the structure under high shear forces. The vertical component provided by the polygonal tendons directly counteracts a portion of the principal tensile stress, significantly delaying the initiation and propagation of diagonal cracks. This changes the failure mode to a more predictable shear–compression failure, thereby enhancing structural ductility and safety redundancy.

The test revealed the stiffness degradation pattern of the specimen at different loading stages. The shear force–displacement curve during initial loading displayed typical elastic, cracking, and nonlinear phases, with a significant reduction in stiffness after cracking. During secondary loading, the specimen entered the elastic–plastic stage earlier, with an approximately 16.34% decrease in equivalent shear stiffness and an approximately 11.55% reduction in the shear force corresponding to the cracking load. These results reflect the irreversible damage caused by the initial loading and can serve as a basis for the design and assessment of similar T-beams.

Regarding crack development and the failure mechanism, cracks initiated at the geometric discontinuity regions where the web intersects with the top flange and diaphragm. Under the restraint provided by the polygonal tendons, these cracks gradually aligned with the direction of the principal tensile stress and propagated slowly. A critical diagonal crack only formed and penetrated when the load approached the ultimate capacity, with final failure occurring due to crushing of the concrete at the top of the diagonal crack. The polygonal tendons effectively enhanced the crack resistance of the web, altered the path and propagation rate of the diagonal cracks, and made the failure process more controllable. Cloud maps of the web strain field further quantitatively revealed the process of damage localization and internal force redistribution. The strain concentration zones coincided with the crack paths. During secondary loading, the strain increase exhibited distinct stages, clearly reflecting the complete process of damage propagation from the initial regions to the formation of a critical shear band.