Experimental and Numerical Study on Seismic Performance of Steel Reinforced Concrete Inclined Column Under Cyclic Loading

Abstract

As the requirements for structural functionality increase, designers frequently opt for inclined columns instead of traditional vertical columns. This choice enhances the spatial dynamics, esthetic appeal, and lighting effects of the structure. However, the research on the failure mechanism and seismic performance of inclined columns under cyclic loading is not systematic. To promote the application of inclined columns in earthquake-prone areas, quasi-static tests were conducted on steel-reinforced concrete inclined columns (SRCIC). The study analyzed the elastic and elastic-plastic development trend, failure mechanism, second-order effect, deformation and energy dissipation of the inclined columns. Traditional vertical columns often experience bending or shear failure, while SRCIC exhibited a new failure pattern characterized by bending failure on one side and compression failure on the other. Based on the experimental design, the nonlinear finite element analysis model of SRCIC is established. The finite element model was validated for horizontal peak load, ductility coefficient, and damage area at various inclination angles, providing a foundation for further parameter analysis. In the numerical analysis section, the effects of inclination angle, steel ratio, reinforcement ratio, and stirrup ratio on the skeleton curve and ductility coefficient were studied in detail, leading to the application of SRCIC.

1. Introduction

To fulfill functional requirements such as structural lighting and ventilation, inclined columns are frequently employed as primary supporting elements. To enhance the mechanical properties and seismic performance of these inclined columns, steel can be integrated into the concrete, resulting in a steel-concrete composite structure. This approach maximizes the benefits of high bearing capacity, favorable deformation characteristics, robust seismic performance, as well as fire resistance and corrosion resistance [1,2,3]. Consequently, it is suitable for promotion and application in multi-layer, long-span, and uniquely shaped structures located in earthquake-prone regions [4,5,6].

Recent research has yielded numerous beneficial insights into the seismic behavior of steel-reinforced concrete columns. Yang [7] and Xue [8] developed two innovative types of prefabricated steel reinforced concrete columns: one being partially prefabricated and the other consisting of prefabricated hollow steel reinforced concrete columns. The influence of cross-sectional shape, stirrup spacing, axial compression ratio, cast-in-place concrete strength, and other factors on the seismic behavior of columns was investigated through quasi-static tests conducted on ten column specimens. The findings revealed that the hysteretic behavior of certain prefabricated steel reinforced concrete columns, in terms of performance, strength degradation, ductility, and energy dissipation, is superior to that of prefabricated hollow steel reinforced concrete columns. Leveraging plastic stress theory, this research presents a calculation technique for determining the bending and shear bearing capacity of the two innovative types of steel columns. This method offers an effective predictive framework for their practical engineering design and application. Zhao [9] examined the restraining mechanism and effects of steel and hoop stirrups on concrete, segmenting the concrete within the steel-concrete column into four distinct areas. Utilizing the Mander model [10], he proposed a theoretical framework for the stress–strain relationship in each concrete area, which offers valuable theoretical guidance for the refined numerical model analysis of steel-concrete columns. Dong [11] extended the restraint mechanism of section steel and steel bars to high-strength recycled concrete columns. He calculated the cracking, yielding, and peak loads of the concrete, which correlated well with the experimental results. Liu [12] conducted a scaled model test on a 2-span, 5-story steel-concrete special-shaped column space frame structure to investigate its seismic performance. The results suggest that the structure follows the design concept of “strong columns and weak beams,” displaying remarkable energy dissipation and deformation capacities, along with substantial collapse resistance. The evaluation of the space frame’s seismic performance utilized the OpenSees 3.3 platform. Additionally, the findings from the numerical analysis indicate that an increase in both the aspect ratio and the axial compression ratio of the column limbs can improve the bearing capacity and stiffness of the special-shaped frame, although this may lead to a reduction in ductility. Ma [13] reached conclusions similar to those of Liu [12] regarding the steel high-strength concrete frame, which follows the concepts of robust columns and vulnerable beams, along with strong joints and weaker components. Additionally, Ma determined the limit of the axial compression ratio to be 0.75. Gautham [14] utilized the software ABAQUS 2021 to carry out a parametric study on steel-reinforced concrete columns. The results revealed that increasing the hoop ratio and steel ratio significantly improves both the displacement ratio and the lateral displacement of the column at failure, leading to a change in the failure mode from shear to bending. Furthermore, a predictive method for assessing the interaction response of axial load and bending moment concerning bearing capacity was introduced. In comparison to the results obtained from the design principles outlined in Eurocode 4 (2004) and AISC 360-16 (2016) design guidelines, it was observed that Eurocode 4 (2004) adversely affects column bending failure, while the proposed prediction method for carrying capacity demonstrates greater reliability. Wang [15] conducted an analysis of the damage test outcomes for steel-reinforced concrete columns that were exposed to low cyclic reciprocating loads. He combined mechanical analysis with regression analysis to summarize a simplified three-line skeleton curve model for the columns. Additionally, a cyclic damage index was established to reflect the performance degradation of the columns. Furthermore, a multi-line hysteresis model for steel-reinforced concrete columns was developed, which can accurately predict their cyclic response. The research findings indicate that the incorporation of steel within concrete columns can effectively leverage the advantages of both materials. These composite steel-concrete columns show a considerable improvement in load-carrying capacity, stiffness, and ductility.

With the improvement of the national economic level, residents have increasingly higher expectations for the esthetics of buildings. Designers may incorporate inclinations into the columns of structures for esthetic enhancement, thereby improving the architectural space and overall visual appeal. Additionally, irregular architectural styles and steeply inclined columns have gradually been adopted in actual construction projects [16,17,18]. Due to the presence of the inclination angle, the mechanical properties and seismic performance of inclined columns differ from those of vertical columns. For instance, Hassan [19] conducted an analysis on how the angle of inclination affects the stiffness and strength of columns. The findings indicated that as the inclination angle increases, there is a corresponding decrease in both the axial stiffness and strength of the column, with a greater reduction in strength observed at higher inclination angles. Allouzi [20] developed nonlinear finite element models for three double-layer concrete-filled steel tube columns that had different inclination angles. The study revealed that as the inclination angle rises, the maximum bearing capacity of the columns diminishes. After quantifying this relationship, double-layer columns were analyzed, leading to the formulation of a column compressive strength prediction formula that effectively estimates the compression strength of inclined columns with angles ranging from 0° to 30°. Han [21] and Ren [22] conducted numerous vertical monotonic loading tests on short slanted concrete-filled steel tube columns. Their findings revealed that, as the angle of inclination rises, there is a slight reduction in the vertical load-bearing capacity of these columns. Building on Han’s experiments [21], Lam [23] extended the column inclination angle to a range of 0° to 15° through numerical simulations. He employed regression analysis to derive the reduction coefficient associated with the inclination angle and the compressive load-bearing capacity of short slanted concrete-filled steel tube columns. A linear relationship was established between these variables, which can accurately forecast the compressive load-bearing capacity of slanted columns. Hansapinyo [24] investigated the mechanical characteristics of hollow steel tubes filled with concrete, specifically focusing on columns that are inclined and subjected to vertical reciprocal loads. The study found that the angle of inclination significantly reduces the vertical compressive load-bearing capability of these columns; however, filling them with concrete or thickening the steel tube wall can substantially alleviate the negative impact of the inclination on their bearing capacity. Zhang [25] proposed a theoretical estimation model for the shear strength of inclined column-beam joints, which is founded on the softened tension and compression rod model. The findings reveal that the column inclination angle influences the initial shear force at the joint, leading to variations in the joint’s stress under both positive and negative loading conditions. Notably, the mechanical properties are contingent on the inclination direction: the shear strength increases in the direction of inclination while decreasing in the opposite direction. Furthermore, a larger inclination angle correlates with a more significant strength effect. In summary, the column inclination angle can diminish the compression or shear bearing capacity of the component to varying extents. However, in practice, steel-reinforced concrete inclined columns (SRCIC) are typically designed using the same procedures as conventional vertical columns. To date, there has been limited research on the seismic performance of SRCIC under cyclic loading. To enhance the safety of inclined column structures, further investigation is required regarding the seismic behavior of SRCIC when subjected to the simultaneous influences of vertical pressure and lateral cyclic loading.

This research investigates the seismic performance of highly inclined SRCIC and steel reinforced concrete vertical column (SRCVC) through a quasi-static test. Based on the results of the quasi-static test, a finite element analysis model was established. Utilizing this validated and robust finite element model, a parametric analysis was conducted on various factors, including inclination angle, steel ratio, reinforcement ratio, and stirrup ratio. The resulting changes in the ductility coefficient were systematically summarized, thereby enhancing the theoretical framework for SRCIC and offering theoretical guidance for their application in practical engineering projects.

2. Experimental Procedure

2.1. General Information of Specimens

The test is based on the large-scale underground hub project in Huangmugang, Shenzhen, China. The structural middle column adopts steel reinforced concrete columns with an inclination of 0° to 11°. In this paper, the most unfavorable condition, namely 11° inclined column, is selected as the main research object. The specimen can be considered as half of a typical frame column, that is, the height of the main body of the specimen column is the distance from the inflection point in the column to the bottom of the column.

The test involves the design of two SRCIC specimens and one SRCVC specimen for the experiment. The geometric measurements and reinforcement parameters of the three specimens are completely uniform, with the sole difference being the angle formed between the axis of the column and the plumb line, as illustrated in Figure 1. Specifically, SRCIC-11 and SRCIC-18 correspond to specimens with inclination angles $\theta$ of 11° and 18°, respectively, while SRCVC-0 denotes specimens where the column axis aligns with the plumb line. Each specimen has a vertical height of 2000 mm, an effective height of 1200 mm, and a diameter of the column at 350 mm. Centrally located within the column cross-section is a cross-shaped steel component with a cross-sectional size of 200 × 100 × 8 × 14 mm, which contains 8.62% steel ratio. Additionally, 16φ12 longitudinal bars are uniformly spread around the column’s circumference, leading to a longitudinal reinforcement ratio of 1.88%. Stirrups labeled φ10 are positioned at a consistent spacing of 175 mm throughout the column’s height, yielding a volume stirrup ratio of 1.18%, while the concrete protective layer has a thickness of 20 mm. The structural and reinforcement design of the specimens adheres to the specifications outlined in GB50010-2010 [26]. Furthermore, to ensure that the loading of the specimens conforms to the cantilever column model, a reinforced concrete pedestal is designed at the base of the column. This pedestal is connected to the reserved hole for the ground anchor via screw rods and pressure beams, ensuring complete fixation of the column’s base during the loading process.

2.2. Materials

C60 Concrete provided by the mixing station was utilized to create the specimens, and three standard cube test blocks were formed to assess the compressive strength of the concrete. After conducting the compression test, it was determined that the average compressive strength of the cubes at 28 days was 69.3 MPa. The longitudinal bars are of HRB400 grade, while the stirrups are made from HPB300 grade steel. Additionally, the section steel utilized is of Q235 grade.

2.3. Experimental Apparatus

The apparatus used to load the specimen is depicted in Figure 2. To the solid ground, the specimen’s base is fixed with screws and pressure beams, which limit both translational and rotational movements along the X, Y, and Z axes. At the upper end of the specimen, two actuators designed for servo loading are placed. Actuator 1 applies a vertical downward force, denoted as N, on the specimen through a rubber bearing. One end of actuator 2 is anchored to the reaction wall, while the other end is affixed to the steel plate. This device is connected to the specimen to deliver a lateral reciprocating push-pull load, labeled as P.

Due to the inconsistency in the thrust and tensile stiffness of the inclined column, we establish a convention to facilitate the analysis of test phenomena and data. Specifically, the movement of actuator 2 away from the reaction wall is defined as the north direction, while movement toward the reaction wall is designated as the south direction. Furthermore, we designate the semicircular surface of the column that is farthest from the reaction wall as the north side, and the semicircular surface closest to the reaction wall as the south side.

2.4. Loading Scheme

The specimen is subjected to loading in two distinct stages. In the initial stage, a constant vertical pressure, denoted as N, is exerted on the upper part of the column to replicate the gravity experienced by the structure. Here, N is set at 390 kN, leading to an axial pressure ratio, n, of 0.1. In the subsequent stage, while maintaining the vertical pressure N constant, a lateral reciprocating push-pull load P is applied in accordance with JGJ/T101-2015 [27], using a displacement control method. The drift ratio cycle for each level is depicted in Figure 3. For the initial ten levels of cyclic loading, the drift ratio, $\delta$, which is defined as the ratio of the top displacement of the column to the effective height ($∆/h$), begins at 0.1% and incrementally increases to 1.0% in steps of 0.1%. Each phase undergoes a single cycle, following which the increase for every phase of cyclic loading is established at 0.5%, with three cycles executed for each phase. The loading process concludes when the specimen shows considerable damage and is unable to withstand the vertical pressure, or when the horizontal load drops to 85% of the respective peak load.

3. Experimental Analysis and Discussion

3.1. Failure Progression

The phenomenon of damage observed in the specimen is concentrated within 200 mm from the base of the column. Figure 4 illustrates the main milestones and key points of damage at the base of the specimen throughout the loading procedure. The failure process of SRCIC-11 resembles that of SRCIC-18. When the drift ratio $\delta$ reaches 1.5%, a transverse main crack emerges in the concrete on the specimen’s north side due to tensile stress. As the drift ratio increases, this transverse main crack extends toward the east and west sides, while new horizontal and vertical cracks continue to develop, forming a network. When the drift ratio $\delta$ reaches 3.5% to 4.0%, portions of the concrete are compromised by the network of cracks, gradually breaking and falling off. The concrete on the north side exhibits typical bending failure characteristics. Conversely, there are no notable cracks detected in the concrete on the south side of the specimen at $\delta$ = 1.5%. When $\delta$ increases to 2.5%, no major cracks are evident on the south side, although several areas of broken concrete appear. As the drift ratio continues to rise, the area of the crushing zone expands. By the time the drift ratio $\delta$ reaches 3.5% to 4.0%, several broken concrete areas merge into a single piece, resulting in complete concrete failure and detachment, exposing the longitudinal bars. Consequently, the specimen’s load-bearing ability is diminished, and the concrete on the south side exhibits characteristics of compression failure. Therefore, due to the influence of the inclination angle, the combined effects of vertical pressure and lateral reciprocating push-pull forces lead to a failure mechanism characterized by bending failure on the northern side and compression failure on the southern side.

SRCVC-0 exhibits distinct failure processes, with similar concrete failure mechanisms observed on both the north and south sides. When the drift ratio $\delta$ reaches 2.5%, a transverse main crack first appears approximately 100 mm from the base of the column. As the drift ratio increases, this main crack extends from east to west, and numerous transverse and vertical cracks continue to develop, resulting in a dense network of cracks. The concrete becomes fragmented due to this network of cracks, and by the time the drift ratio $\delta$ reaches 5.0%, the concrete is completely shattered and has fallen off, rendering it incapable of bearing any load. Both the northern and southern sides of the specimen exhibit typical bending failure characteristics.

The specimens designed for this study are primarily subjected to bending failure; however, the failure modes of SRCIC differ from those of SRCVC. SRCIC exhibits an initial eccentricity, ${∆}_0$, as illustrated in Figure 5. Consequently, the concrete on the north side experiences rapid failure due to the combined effects of tensile stress from the lateral load P and vertical pressure N. Specifically, when the drift ratio is relatively small ($\delta$ = 1.5%), a transverse bending main crack develops. In contrast, SRCVC lacks initial eccentricity ${∆}_0$, resulting in a smaller tensile stress from the vertical pressure N when the drift ratio is still relatively small. As a result, SRCVC primarily relies on the tensile stress generated by the lateral load P, leading to a slower failure process compared to SRCIC. When $\delta$ reaches 2.5%, lateral main cracks begin to appear. Similarly, under the combined effects of compressive stress from lateral load P and vertical pressure N, the concrete on the south side of SRCIC does not exhibit significant transverse main cracks, remaining predominantly under compression. However, the stress distribution between the concrete on the south and north sides of SRCVC is completely symmetrical, leading to the appearance of transverse main cracks due to the tensile stress induced by the lateral load P.

Due to the combined effects of lateral load P and vertical pressure N, which accelerate the concrete damage process, SRCIC loses its bearing capacity at a drift ratio of 4.0%. In contrast, SRCVC can continue to bear load until the drift ratio reaches 5.0%. This exceeds the elastoplastic drift ratio limit specified in specification GB50011-2010 [28]. This finding demonstrates that the deformation capacity of SRCIC under earthquake action is inferior to that of SRCVC. Nevertheless, SRCIC still exhibits good plastic deformation ability and can be effectively utilized in structures located in earthquake-prone areas.

3.2. Second-Order Effect

The bending member experiences significant lateral displacement when subjected to earthquake forces. Consequently, the actual bending moment experienced by the member section increases, resulting in a second-order effect. This second-order effect diminishes the load-bearing capacity and stability of the column, highlighting the necessity to investigate the second-order effects of SRCIC. The study adopts a quasi-static cyclic loading method based on existing research results [7,11], which has practical advantages of controllable operation and strong repeatability. This method can effectively separate dynamic factors such as load history and inertial coupling, thereby clearly quantifying the influence mechanism of second-order effects on the basic performance of structures, providing direct and reliable basis for design and evaluation. Although it is difficult to fully simulate dynamic phenomena such as high-frequency and cumulative effects in ground motions, the conclusions obtained still have important engineering benchmark value.

The loading process of SRCIC is depicted in Figure 5, which shows the stress and deformation involved. In this figure, the constant vertical pressure is denoted as N, the lateral reciprocating push-pull load is represented as P, the inclination angle of the inclined column is $\theta$, the effective height is $h$, the initial displacement caused by the inclination angle is ${∆}_0$, and the lateral reciprocating displacement during loading is $∆$. Based on static balance analysis, it is essential to ensure that the bending moment at the column’s base is balanced, resulting in the formulation of the subsequent balance equation:

Bending moment equilibrium equation without considering the second-order effect:

$$\mathrm{Northward} \mathrm{loading}: P_1·h-N·{∆}_0=M$$

(1)

$$\mathrm{Southward} \mathrm{loading}: P_1·h+N·{∆}_0=M$$

(2)

Bending moment equilibrium equation considering second-order effect:

$$\mathrm{Northward} \mathrm{loading}: P_2·h-N·({∆}_0-∆)=M$$

(3)

$$\mathrm{Southward} \mathrm{loading}: P_2·h+N·({∆}_0+∆)=M$$

(4)

In Formulas (3) and (4), $P_2·h$ represents the first-order bending moment effect, while $N·({∆}_0-∆)$ and $N·({∆}_0+∆)$ denote the second-order bending moment effects resulting from northward and southward loading, respectively. During the loading process, the lateral reciprocating displacement $∆$ continues to change as the drift ratio increases. Consequently, only the ratios of the second-order to first-order bending moments at the three characteristic points (yield, peak, and failure) are calculated, as shown in

Table 1. Ratio of second-order bending moment to first-order bending moment for each characteristic point.

Specimen		Second-Order Bending Moment/First-Order Bending Moment (%)
		Yield Point	Peak Point	Failure Point
SRCIC-11	North	5.22	5.88	12.71
	South	3.56	4.21	6.80
	Average	4.39	5.05	9.76
SRCIC-18	North	4.32	6.58	10.91
	South	2.76	3.66	4.48
	Average	3.54	5.12	7.70
SRCVC-0	North	3.14	4.45	7.68
	South	4.76	6.15	9.62
	Average	3.95	5.30	8.65

.

Table 1 shows that at both the yield and peak points, the ratio of the second-order bending moment to the first-order bending moment for the specimen is approximately 5%, suggesting that the second-order effect has a minimal impact. However, as the drift ratio increases, the impact of the second-order effect becomes significantly more pronounced. At the failure point, the second-order effect reaches about 10%, indicating that it can no longer be disregarded. Furthermore, the inclination angle of the inclined column exacerbates the second-order effect of the specimen when subjected to northward loading, while it mitigates the second-order effect during southward loading, demonstrating an asymmetrical behavior. This asymmetry is a primary reason why the inclined column experiences bending damage on the front side and compression on the back side.

In Equations (1)–(4), $P_1$ and $P_2$ are the lateral loads of the specimen without considering and considering second-order effects, respectively. By substituting the column end bending moment M in Equations (3) and (4) into Equations (1) and (2), we can obtain:

$$\mathrm{Northward} \mathrm{loading}: P_1·h-N·{∆}_0=P_2·h-N·({∆}_0-∆)$$

(5)

$$\mathrm{Southward} \mathrm{loading}: P_1·h+N·{∆}_0=P_2·h+N·({∆}_0+∆)$$

(6)

According to Equations (5) and (6),

$$P_1=P_2+{\displaystyle \frac{N·∆}{h}}=P_2+\alpha ·P_2=(1+\alpha )·P_2$$

(7)

In Equation (7), $\alpha$ represents the improvement coefficient of the lateral load-bearing capacity of the specimen, excluding the influence of the second-order bending moment effect. It indicates that, in practical engineering applications, the presence of the second-order effect diminishes the lateral load-bearing capacity of the component. To account for this influence, the strength reduction coefficient $\beta$ is defined as $\beta ={\displaystyle \frac{P_1-P_2}{P_1}}$.

By substituting Equation (7) into the strength reduction coefficient $\beta$, we can derive the necessary results:

$$\beta ={\displaystyle \frac{P_1-P_2}{P_1}}={\displaystyle \frac{\alpha ·P_2}{(1+\alpha )·P_2}}={\displaystyle \frac{\alpha }{1+\alpha }}$$

(8)

By substituting the experimentally measured values at the three characteristic points into Equations (7) and (8), one can compute the lateral load-bearing capacity improvement coefficient $\alpha$ and the strength reduction coefficient $\beta$ of the specimen, as presented in

Table 2. Second-order bending moment effect influence coefficient.

Specimen		$\mathit{\alpha }$ (%)			$\mathit{\beta }$ (%)
		Yield Point	Peak Point	Failure Point	Yield Point	Peak Point	Failure Point
SRCIC-11	North	3.68	4.26	8.59	3.55	4.09	7.91
	South	4.99	5.77	9.78	4.75	5.46	8.91
	Average	4.34	5.02	9.19	4.15	4.78	8.41
SRCIC-18	North	2.54	4.09	6.05	2.48	3.93	5.70
	South	4.70	6.06	7.93	4.49	5.71	7.35
	Average	3.62	5.08	6.99	3.49	4.83	6.53
SRCVC-0	North	3.14	4.45	7.68	3.04	4.26	7.13
	South	4.76	6.15	9.62	4.54	5.79	8.78
	Average	3.95	5.30	8.65	3.80	5.03	7.96

.

Table 2 demonstrates that as the drift ratio increases, both the lateral load-bearing capacity improvement coefficient $\alpha$ and the strength reduction coefficient $\beta$ of the specimen exhibit an upward trend. Notably, at the failure point, both $\alpha$ and $\beta$ approach 10%, indicating that during the declining stage, the second-order effect accelerates the damage process of the specimen. However, in conjunction with the definitions and derivation processes of $\alpha$ and $\beta$, inclination angle of the specimen does not influence the values of $\alpha$ and $\beta$.

3.3. Horizontal Load vs. Drift Ratio Response

Figure 6 illustrates the response curve (i.e., hysteresis curve) of the horizontal load and drift ratio for each specimen. Both SRCIC and SRCVC demonstrate commendable hysteretic performance. In comparison to the hysteretic curve of reinforced concrete columns, only a minor pinching phenomenon is observed [29], indicating that the inclusion of section steel in the specimens significantly enhances the hysteretic performance of the columns, enabling them to withstand strong earthquakes. Additionally, Figure 6 highlights the concrete crack point, yield point, peak point, and failure point of the specimens. It reveals that prior to concrete cracking, the horizontal load and drift ratio exhibit a nearly linear relationship, suggesting that the specimens remain in the elastic stage. As the drift ratio increases, the specimens transition into the elastic-plastic phase, where cracks propagate and develop, resulting in a decrease in stiffness while simultaneously producing plasticity. After surpassing the peak point, the specimens gradually enter the failure stage, characterized by a substantial reduction in stiffness, a significant increase in plastic deformation, and a widening of the hysteresis loop, until either the concrete completely fails or the longitudinal reinforcement yields, thereby reaching the failure point.

In contrast, SRCIC exhibits hysteretic performance that differs from that of SRCVC. The hysteresis curve of SRCVC is approximately centrally symmetrical around the origin, whereas the hysteresis curve of SRCIC is distinctly asymmetric. The area of the hysteresis curve corresponding to northward loading (i.e., the segment of the curve located above $y=0$) is significantly larger than that for southward loading (i.e., the segment of the curve situated below $y=0$). To conveniently quantify the degree of asymmetry in inclined columns with varying inclination angles, we define the asymmetry coefficient $\omega$ as the ratio of the peak horizontal load applied in the north direction to that applied in the south direction. Calculations reveal that the asymmetry coefficients $\omega$ for SRCIC-11, SRCIC-18, and SRCVC-0 are 1.36, 1.73, and 1.03, respectively. This suggests that with a rise in the inclination angle, the asymmetry coefficient $\omega$ of the specimen also increases, thereby enhancing the hysteretic performance during northward loading while weakening it during southward loading. The failure mode of the specimen is primarily governed by the crushing of the concrete on the south side.

3.4. Deformation Capacity

The ability of a structure or component to deform under seismic forces can be assessed through the ductility coefficient $\mathsf{\mu }$ [28]. Specifically, $\mathsf{\mu }$ is defined as $\mathsf{\mu }={\mathsf{\Delta }}_u∕{\mathsf{\Delta }}_y$.

Table 3. Ductility coefficient from the tests and from the FEM analysis (FEM analysis to be discussed in Section 4).

Test Specimen	Calculation Result	Loading Direction	Py/kN	Δy/mm	Pm/kN	Δm/mm	Pu/kN	Δu/mm	$\mathsf{\mu }$	$\overline{\mathsf{\mu }}$	Relative Error/%
SRCIC-11	Experimental value	North	256.3	29.0	275.1	36.1	233.8	61.8	2.13	1.97	17.3
		South	188.4	28.9	202.9	36.1	172.5	51.9	1.80
	Simulated value	North	267.0	23.0	269.3	30.0	228.9	68.7	2.98	2.31
		South	194.3	31.0	214.0	36.0	181.9	50.7	1.64
SRCIC-18	Experimental value	North	307.4	24.0	335.0	42.1	284.8	53.0	2.21	1.88	16.5
		South	179.8	26.0	193.6	36.1	164.6	40.2	1.54
	Simulated value	North	315.6	19.8	328.2	29.9	279.0	59.9	3.02	2.19
		South	175.3	30.8	187.2	36.0	159.1	42.0	1.36
SRCVC-0	Experimental value	North	250.5	24.2	263.6	36.1	224.1	53.0	2.19	2.06	16.5
		South	226.0	33.1	254.5	48.2	216.3	64.0	1.93
	Simulated value	North	240.7	20.6	259.7	35.8	220.7	52.3	2.54	2.40
		South	220.6	22.8	260.2	36.0	221.2	51.3	2.25

displays the values obtained from tests and simulations for the ductility coefficient. In this table, ${\mathsf{\Delta }}_y$, ${\mathsf{\Delta }}_m$ and ${\mathsf{\Delta }}_u$ refer to the yield displacement, peak displacement, and failure displacement, respectively, while $P_y$, $P_m$ and $P_u$ denote the yield load, peak load, and failure load, respectively. Due to the absence of a distinct yield point in the specimen, ${\mathsf{\Delta }}_y$ is typically determined using the energy equivalent method [30,31], as illustrated in Figure 7. This method involves drawing a secant line on the skeleton curve to ensure that the areas of regions I and II are equal. The point where this secant line intersects the skeleton curve signifies the yield point. Furthermore, $P_u$ is defined as 0.85 times $P_m$ [27], and the remaining characteristic parameters can be derived from Figure 7.

The calculation results of the ductility coefficient reveal that the average ductility coefficients for the north and south sides of SRCVC-0 are 1.05 and 1.10 times greater than those of SRCIC-11 and SRCIC-18, respectively. This indicates that the inclination angle of the column adversely affects its ductility coefficient. Specifically, a greater inclination angle correlates with a lower ductility coefficient. Moreover, the reduction in ductility coefficient becomes increasingly pronounced with higher angles of inclination. Additionally, the northward ductility coefficients of SRCIC-11, SRCIC-18, and SRCVC-0 are 1.18, 1.44, and 1.13 times their respective southward ductility coefficients. This suggests that the reduction effect on the ductility coefficient is more pronounced in the southward loading direction. This phenomenon can be attributed to the bending failure characteristics exhibited by the north side of the inclined column, which retains good ductility, leading to a less significant reduction in the ductility coefficient. In contrast, the south side of the inclined column consistently experiences compressive stress during loading, which causes the concrete to crush and sustain damage at an earlier stage. This significantly reduces the stiffness of the specimen, thereby resulting in a marked decrease in the ductility coefficient.

3.5. Dissipated Energy

Energy dissipation serves as an essential measure for assessing the seismic behavior of a structure or its components. This performance can be evaluated using parameters such as the equivalent viscous damping coefficient ${\xi }_{ep}$ [27], the energy consumption $E_i$ of each cycle, and the cumulative energy consumption $E_{sum}$. The equivalent viscous damping coefficient ${\xi }_{ep}$ is calculated using Equation (9).

$${\xi }_{ep}={\displaystyle \frac{1}{2\pi }}·{\displaystyle \frac{S_{(ABC+CDA)}}{S_{(OBE+ODF)}}}$$

(9)

In this formula, $S_{(ABC+CDA)}$ represents the area contained within the hysteresis loop ABCD, while $S_{(OBE+ODF)}$ denotes the sum of the areas of the triangles OBE and ODF, as demonstrated in Figure 8.

Due to the varying inclination angles of the three specimens, the number of displacement cycles at final failure is inconsistent. Figure 9 illustrates the curve that represents the relationship between the equivalent viscous damping coefficient ${\xi }_{ep}$ and the number of displacement cycles $n$. The curve exhibits an overall upward trend following the cracking of the specimen, indicating its transition into the elastic-plastic stage. The energy consumption of all specimens gradually increases with the drift ratio $\delta$, and at the point of failure, the ${\xi }_{ep}$ for each specimen reaches 0.30. Notably, this value of ${\xi }_{ep}$ surpasses that of conventional reinforced concrete columns, which typically ranges from 0.1 to 0.2 [32]. This observation highlights the superior energy dissipation performance of SRCIC. Figure 10 presents the energy consumption $E_i$ for each displacement cycle throughout the loading process. The overall $E_i$-$n$ curve displays a step-like rising pattern. Prior to cracking, the $E_i$-$n$ curve remains relatively smooth, with energy consumption at a low level. Following cracking, the specimen promptly enters the elastic-plastic stage, resulting in a significant increase in energy consumption $E_i$. Even during the destruction phase, the energy consumption $E_i$ continues to exhibit robust growth, indicating that the specimen possesses strong energy consumption capacity throughout the entire loading process. Under a consistent drift ratio $\delta$, as the number of displacement cycles $n$ increases, the strength and stiffness of the specimen degrade, leading to a slight decrease in energy dissipation capacity, which is represented in a step-like manner. Furthermore, the $E_i$-$n$ curve for the SRCIC-18 specimen consistently remains higher than those of the other two specimens. This is attributed to the larger inclination angle, which enhances the peak load value in the north direction, thus increasing the area of the hysteresis loop.

Figure 11 illustrates the relationship between the cumulative energy consumption $E_{sum}$ of each specimen across displacement cycles and the number of displacement cycles $n$. The $E_{sum}$-$n$ curves for all specimens exhibit a similar developmental trend, characterized by exponential growth. Prior to cracking, the cumulative energy consumption $E_{sum}$ of each specimen increases gradually. However, once the elastic-plastic stage is reached, $E_{sum}$ rises sharply with an increase in the number of displacement cycles, and the rate of increase becomes significantly pronounced. Consistent with the behavior of the $E_i$-$n$ curve, the $E_{sum}$-$n$ curve for the SRCIC-18 specimen remains consistently higher than those of the other two specimens. It is important to note that SRCVC-0 has undergone 33 displacement cycles, whereas SRCIC-11 and SRCIC-18 have only experienced 28 displacement cycles. Consequently, upon final failure, the cumulative total energy consumption of SRCVC-0 was 1.69 and 1.34 times greater than that of SRCIC-11 and SRCIC-18, respectively. This indicates that the energy dissipation performance of vertical columns is superior to that of inclined columns. Nevertheless, the energy dissipation performance of inclined columns during each stage of the loading process is not inferior to that of vertical columns.

4. Finite Element Analysis

Considering the considerable time and labor expenses tied to experimental research, this study seeks to delve deeper into the effects of different design parameters on the seismic performance of SRCIC. To achieve this, the load–displacement response and failure mode of these columns were simulated numerically. A nonlinear analysis was executed employing the large-scale finite element analysis software ABAQUS Standard [33,34,35]. The detailed material and model parameters are outlined as follows:

4.1. Constitutive Model

A reasonable material constitutive model is essential for ensuring the reliability of numerical analysis results. The uniaxial stress–strain relationship curves for steel and rebars are represented using an ideal elastic-plastic constitutive relationship. ABAQUS plastic damage model is adopted for concrete, which is widely used in research [33,34]. The plastic damage model assumes that the failure mode of concrete is tensile cracking and crushing, and the concrete will continue to produce tensile and compressive damage after it enters plasticity. The stiffness of the specimen can be reduced by setting the tensile and compressive damage factors to simulate the degradation process of concrete under repeated loading, which is suitable for members under cyclic loading. Within the plastic damage model, the expansion angle and viscosity parameters for concrete are set at 30° and 0.005, respectively. The elastic modulus, $E_c$, is specified as 36,000 MPa, while the Poisson’s ratio, $\nu$, is 0.2. The constitutive relationship for concrete is derived from the uniaxial stress–strain relationship curve specified in GB50010-2010 [26].

The stress–strain relationship curve under uniaxial tension can be determined according to Formulas (10) and (11)

$$\sigma =\left\{\begin{array}{cc}\hfill (1.2-0.2x^5)·f_{t,r}·x,& \hspace{1em}x\le 1\hfill \\ \hfill {\displaystyle \frac{f_{t,r}·x}{{\alpha }_t·{\left(x-1\right)}^{1.7}+x}},& \hspace{1em}x>1\hfill \end{array}\right.$$

(10)

$$x={\displaystyle \frac{\epsilon }{{\epsilon }_{t,r}}}$$

(11)

The stress–strain relationship curve under uniaxial compression can be determined according to Formulas (12)–(14)

$$\sigma =\left\{\begin{array}{cc}\hfill {\displaystyle \frac{n·f_{c,r}·x}{n-1+x^n}},& \hspace{1em}x\le 1\hfill \\ \hfill {\displaystyle \frac{f_{c.r}·x}{{\alpha }_c·{\left(x-1\right)}^2+x}},& \hspace{1em}x>1\hfill \end{array}\right.$$

(12)

$$n={\displaystyle \frac{E_c·{\epsilon }_{c,r}}{E_c·{\epsilon }_{c,r}-f_{c,r}}}$$

(13)

$$x={\displaystyle \frac{\epsilon }{{\epsilon }_{c,r}}}$$

(14)

4.2. Establishment of Finite Element Model

Figure 12 illustrates the finite element model of the specimen. This model includes the concrete column body, integrated cross-section steel, and the steel skeleton. To ensure calculation accuracy, the embedded cross-shaped steel and concrete utilize the eight-node reduced integration three-dimensional solid element C3D8R, while the longitudinal bars and stirrups that constitute the steel skeleton employ the two-node linear three-dimensional truss element T3D2. The steel and steel skeleton are embedded within the concrete, without accounting for the bonding slip between the steel, steel skeleton, and concrete. Each element of the model features an average grid size of 50 mm, which facilitates good convergence and minimizes computational effort.

To simulate the boundary conditions for specimen loading, the upper portion of the specimen is permitted to rotate freely in the horizontal direction. To avoid concentrated forces from damaging the top of the specimen and to ensure the convergence of the calculation results, Reference Point 1 is coupled with the top of the specimen. A vertical concentrated force and a lateral displacement of specified amplitude are applied at Reference Point 1. During the test, the constraint effects of the screws and pressure beams on the bottom pedestal of the specimen rendered the displacement at the bottom negligible, resulting in a complete fixed constraint being applied to the bottom of the model column.

4.3. Finite Element Model Validation

As illustrated in Figure 6, the horizontal load-drift ratio curve derived from finite element analysis closely matches the outcomes observed experimentally. The model effectively captures the hysteretic performance of the specimen. Furthermore, the constitutive parameters for concrete and steel utilized in ABAQUS, along with the boundary conditions set, are appropriate for simulating the seismic performance of SRCIC subjected to low cyclic reciprocating loads. Additionally, Table 3 presents a comparison of the characteristic points for each specimen. The absolute differences in relative errors between the simulated and experimental values for the yield load and failure load range from 2.4% to 4.2% and 1.5% to 5.4%, respectively, indicating that the model effectively depicts the trend of lateral load variation for the specimen. However, the relative error between the simulated and experimental values of the average ductility coefficient, as shown in Table 3, is relatively large. This discrepancy arises because the test concrete possesses initial internal defects, while the concrete in the model is considered an ideal homogeneous material, resulting in an overestimation of the specimen’s initial stiffness. Consequently, the yield displacement is reduced. And the model’s neglect of bond slip between steel and concrete leads to a ductility coefficient that exceeds the test results.

Figure 13 illustrates the failure area and compression damage factor cloud diagram for SRCIC-11 and SRCIC-18 at a displacement ratio of 4.0%, as well as SRCVC-0 at a displacement ratio of 5.0%. This figure compares the crack and damage development observed in both the experimental tests and the numerical model. In the experimental results, the spalling area of the concrete protective layer was concentrated within 300 mm from the base of the specimen. In contrast, the numerical model exhibited a larger severely damaged area, extending up to 800 mm from the base of the specimen. However, the damage patterns of the concrete in both the north and south regions were consistent.

5. Numerical Investigation

Several factors influence the seismic performance of SRCIC, including inclination angle, steel ratio, reinforcement ratio, and stirrup ratio. An analysis comparing the test outcomes and simulation findings suggests that this finite element model effectively simulates the deformation capacity of SRCIC. Due to the large time and labor cost of experimental research, the finite element model can be used to analyze the influence of the above parameters on the seismic performance of SRCIC. The specific parameters selected for this analysis are as follows:

5.1. Inclination Angle

The test analysis results indicate that the column inclination angle significantly affects the failure mechanism and deformation capacity of SRCIC. Due to the test conditions, only specimens with inclination angles of 0°, 11° and 18° were produced. To further investigate the influence of additional inclination angles on the deformation capacity of SRCIC, specimens with angles of 3°, 6°, 9°, and 15° were included in the parameter analysis.

Figure 14a illustrates the skeleton curve at reference point 1 of the finite element model for various inclination angles. The trend of the curve indicates that as the inclination angle increases, the peak load in the north direction continues to rise, while the peak load in the south direction decreases. Concurrently, the asymmetry coefficient $\omega$ increases, highlighting a more pronounced asymmetry, which aligns with the results of the experimental analysis. Furthermore, as depicted in Figure 14b, the ductility coefficient for northward consistently increases, whereas the ductility coefficient for southward continues to decrease, exhibiting an approximately linear relationship with the inclination angle. This fitting formula can be employed to predict the ductility coefficient values of inclined columns at different inclination angles.

5.2. Steel Ratio

The steel sections of each test piece in the study were constructed from standard H-shaped steel. To ensure the appropriate thickness of the protective layer on the flange of the section steel and to maintain optimal joint performance between the section steel and concrete, the steel ratio in the specimen was kept relatively low. Typically, the steel ratio in steel reinforced concrete columns ranges from 4% to 15% [26]. During the parameter analysis, the steel ratio was varied by adjusting the thickness of the steel web and flange. This included five different steel ratios, such as 4.04%, 6.37%, 10.05%, 12.77% and 14.65%, among others.

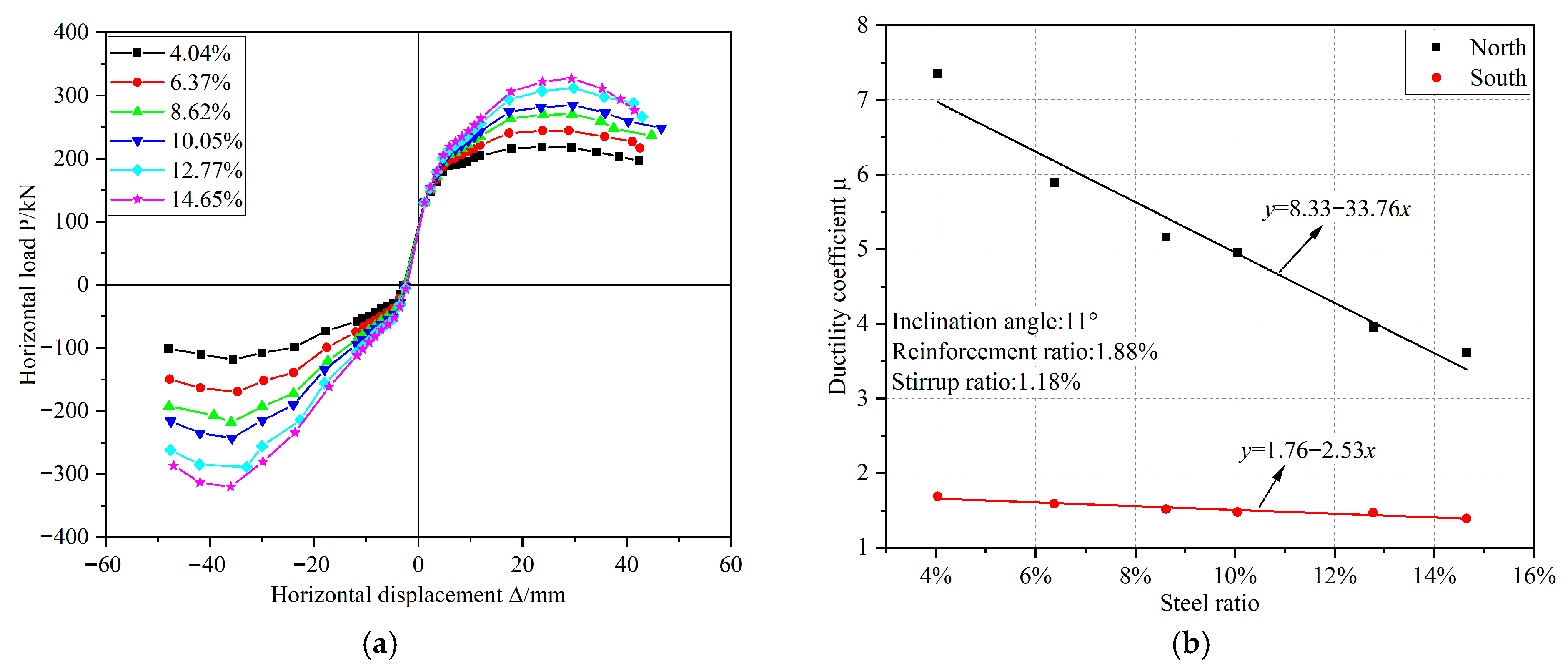
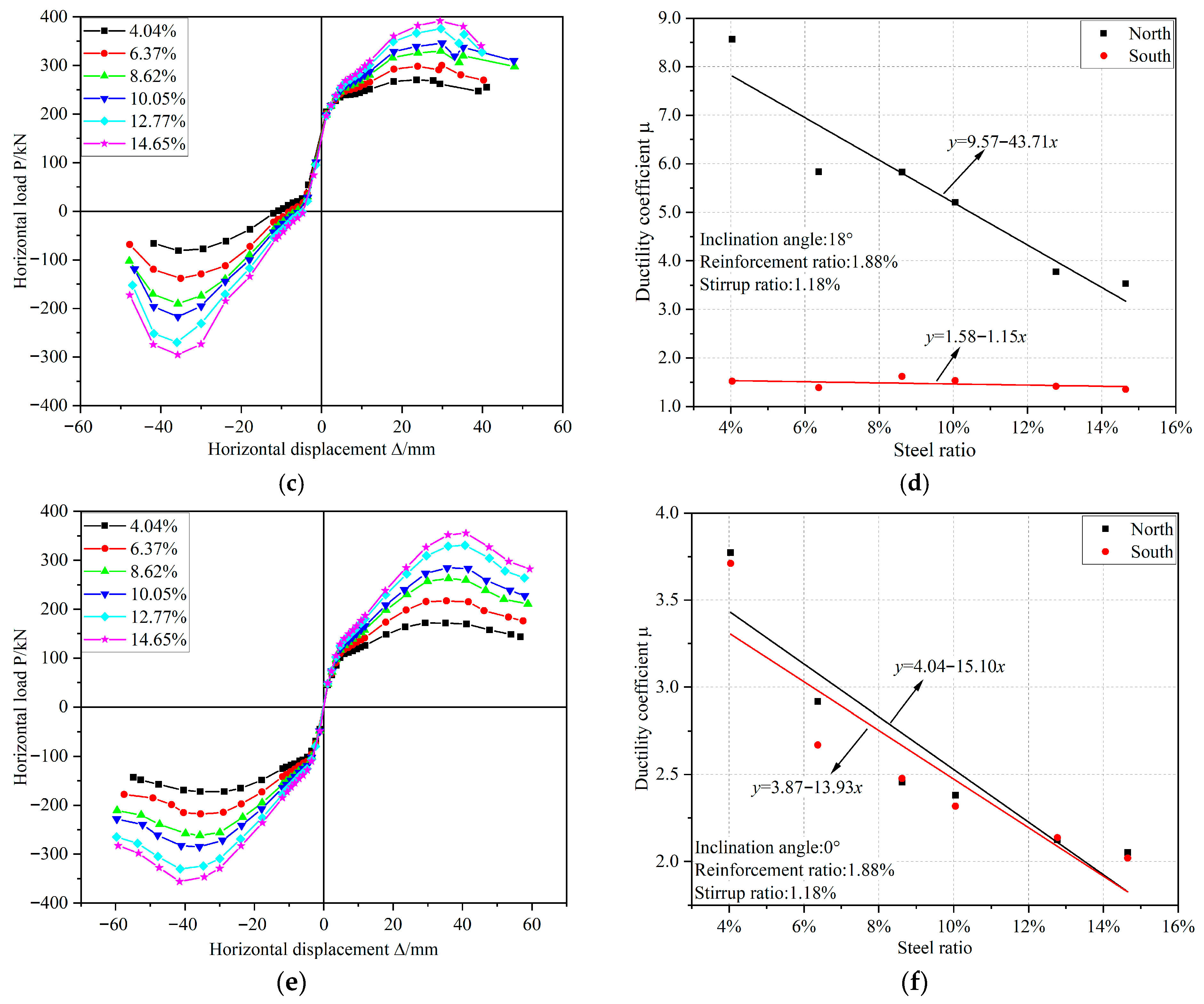
The skeleton curve for SRCIC-11, SRCIC-18, and SRCVC-0 at varying steel ratios, as illustrated in Figure 15, indicate that increasing the steel ratio significantly enhances the peak load capacity. However, it is observed that the slope of the descending portion of the skeleton curve becomes steeper. Moreover, the ductility coefficient exhibits an overall decreasing trend with increasing steel ratio. This phenomenon can be attributed to the higher steel ratio, which increases the specimen’s stiffness and reduces the yield displacement. Although the steel may not yield when the specimen fails, the concrete sustains considerable damage, leading to an inability to support the load. Consequently, the failure displacement does not improve significantly, resulting in a decrease in the ductility coefficient.

5.3. Reinforcement Ratio

The longitudinal reinforcement ratio of steel reinforced concrete column is typically required to be no less than 0.8% [26]. In the parameter analysis, the reinforcement ratio was varied by altering the number of longitudinal bars, resulting in three additional reinforcement ratios: 1.18%, 2.35%, and 3.53%.

As shown in Figure 16, the peak load increases with the reinforcement ratio. However, the ductility coefficient of SRCIC decreases slightly, while that of SRCVC increases slightly. The overall change in these coefficients is not significant, indicating that the reinforcement ratio affects the column primarily in terms of bearing capacity, with a lesser impact on deformation capacity.

5.4. Stirrup Ratio

The restraining effect of stirrups significantly influences the load-bearing capacity and ductility of SRCIC. In the parameter analysis, the stirrup ratio was modified by adjusting the stirrup spacing, resulting in five distinct stirrup ratios: 1.04%, 1.39%, 1.67%, 2.08%, and 2.78%. This variation reflects the impact of different stirrup ratios.

Figure 17 illustrates that the stirrup ratio can marginally enhance the peak bearing capacity of SRCIC and SRCVC. However, this improvement is limited, and the effect on the ductility coefficient is also minimal. This phenomenon can be attributed to the restricted contribution of stirrups to the bending bearing capacity, as the specimens in this test were specifically designed for bending and compression failures. Additionally, the cross-shaped steel in the column exerts a significant restraining effect on the concrete, thereby diminishing the effectiveness of the stirrups in restraining the concrete.

6. Conclusions

To investigate the seismic behavior of large inclination angle steel reinforced concrete columns, low-cycle repeated load tests were performed on two SRCICs and one SRCVC. Concurrently, a finite element model of SRCIC was developed in ABAQUS, followed by a range of numerical simulations to analyze the impact of inclination angle, steel ratio, reinforcement ratio, and stirrup ratio on the seismic performance of these columns. The key findings are summarized as follows:

(1)

The SRCIC exhibits a novel bending failure on the north side and a compression failure on the south side, influenced by the inclination angle and initial eccentricity, under the combined effects of lateral load P and vertical pressure N. Furthermore, the failure process of SRCIC occurs more rapidly than that of SRCVC. However, it still attains a drift ratio of 4.0% prior to failure, which significantly exceeds the specification limit. This observation indicates that SRCIC possesses commendable elastic-plastic deformation capabilities, making it suitable for widespread application in earthquake-prone regions.

(2)

The second-order effect of SRCIC is significant and exhibits asymmetry. Specifically, the second-order effect of northward has a greater impact, while the second-order effect of southward is less pronounced. This second-order effect will accelerate the failure process of the specimen. However, the inclination angle of the inclined column does not influence the lateral load-bearing capacity improvement coefficient $\alpha$ or the strength reduction coefficient of the specimen $\beta$.

(3)

The hysteresis curve of SRCIC exhibits pronounced asymmetry. The area of the hysteresis loop during northward loading is significantly larger than that during southward loading, and the degree of asymmetry increases with the inclination angle. Additionally, the ductility and energy consumption of SRCIC demonstrate a decreasing trend as the inclination angle increases.

(4)

The finite element model developed in this article effectively corroborates the experimental results. The maximum error between the yield load and the failure load is approximately 5%, while the maximum error in the ductility coefficient is around 16%. This model provides improved predictions of failure and damage in actual components. Furthermore, a linear relationship between the inclination angle and the ductility coefficient has been established through fitting, enabling accurate predictions of ductility coefficient values for inclined columns at various angles. Additionally, influence laws for the steel ratio, reinforcement ratio, and stirrup ratio of SRCIC on the skeleton curve and ductility coefficient are summarized, which will facilitate their promotion and application in real-world projects.

(5)

The study focuses on the seismic performance of inclined columns. In the future, we will deeply consider the soil structure interaction, and carry out the research on the damage and restoring force characteristics of inclined column structures from the two levels of component and overall structure.