Simulation and Analysis of the Constraint Effects of Multi-Cavity Double Steel Plate Composite Walls
Abstract
1. Introduction
- (1)
- An approach rooted in experimental foundations, augmented by semi-empirical mechanical derivations. A notable illustration is Mander’s work [24] on the confinement behavior in reinforced concrete columns. In this study, the confinement effect was compared to an equivalent stress, and a magnitude factor was derived for the compressive strength of reinforced concrete.
- (2)
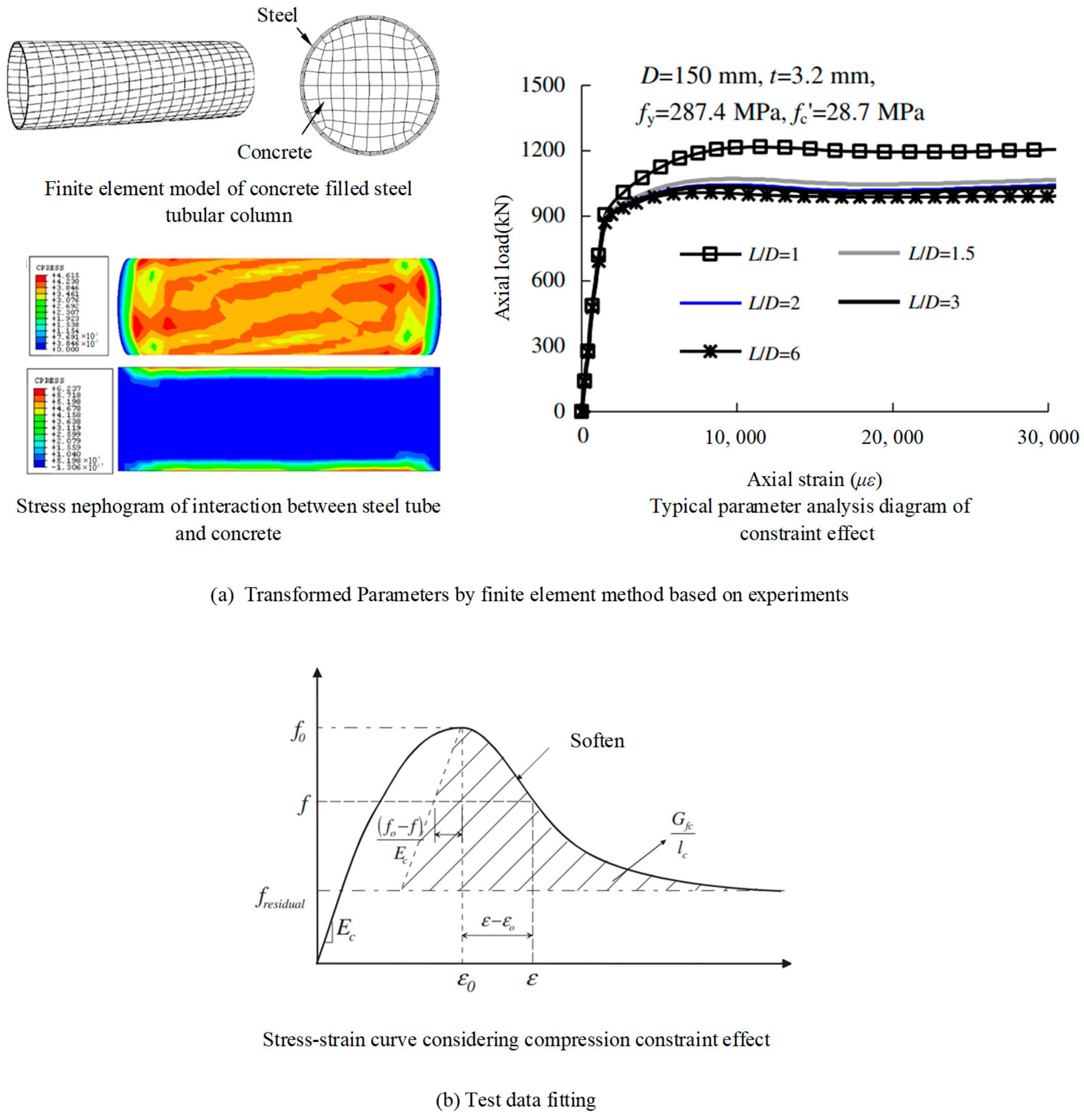
- A methodology that integrates experimental results with advanced finite element modelling. A prime example is the research conducted by Han et al. and Zhong et al. [25,26] on confinement effects in steel-reinforced concrete columns, depicted in Figure 3a. Their study delves into the stress–strain relationship, emphasizing the influence of confinement effect coefficients on the overall mechanical behavior.
- (3)
- A purely experimental data-fitting approach. Samani’s research [27] about concrete columns stands as a typical example. Leveraging statistical and regression techniques, they formulated a strain-stress model for concrete columns based on experimental data.
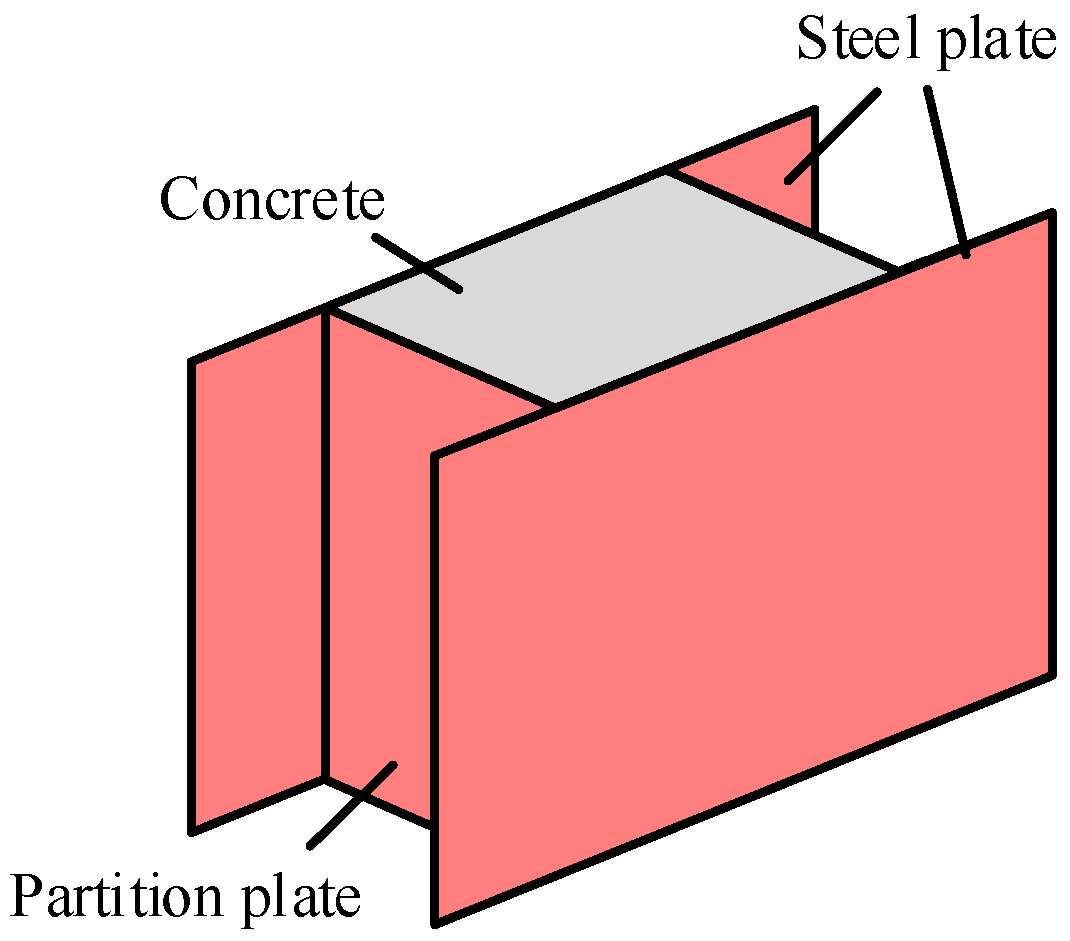
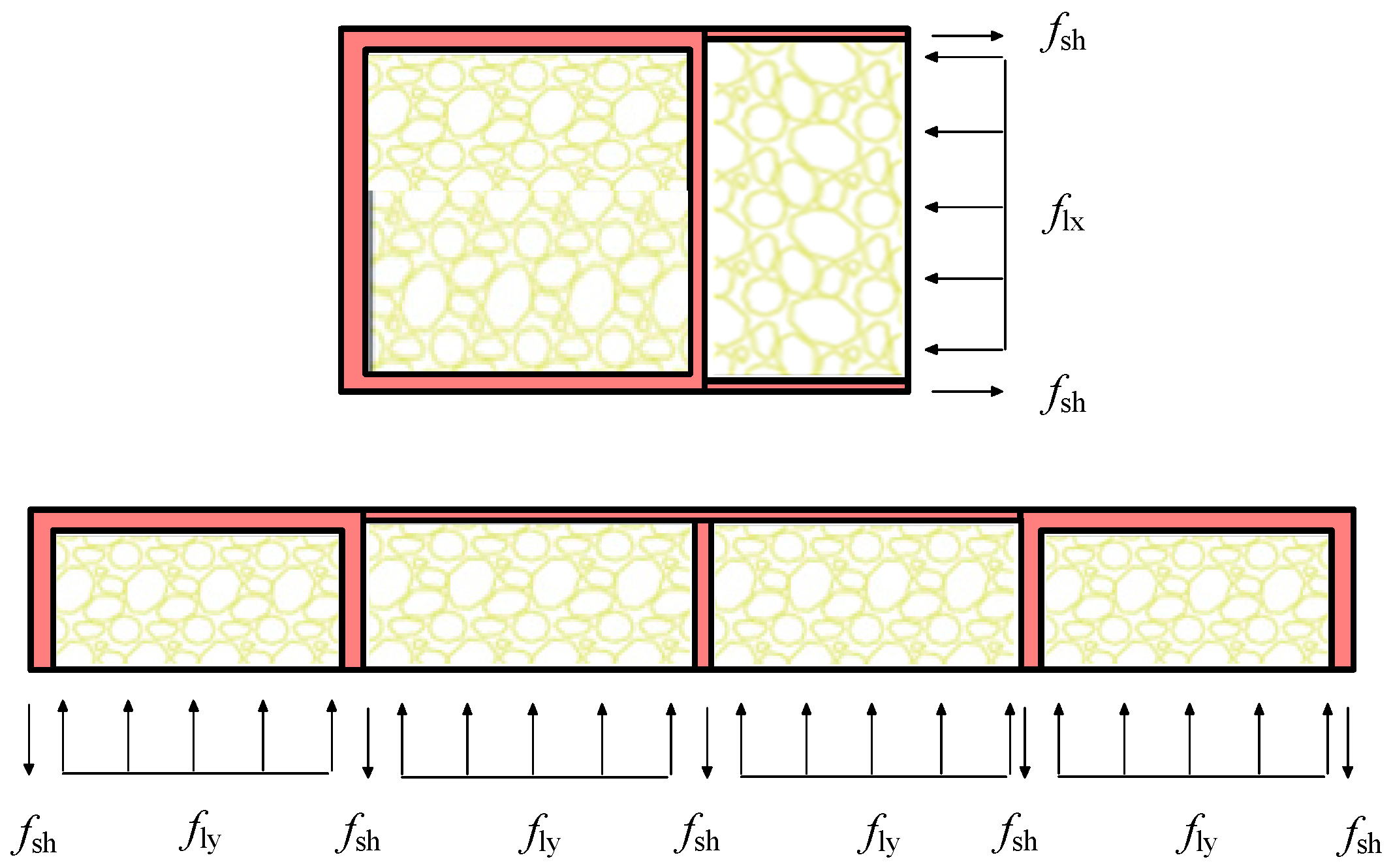
2. Theoretical Analysis of Constraint Mechanisms in MDSCCS
3. Three-Dimensional Finite Element Model of MDSCCS
3.1. Model Overview
3.1.1. Constitutive Model of Material
3.1.2. Interfacial Interactions
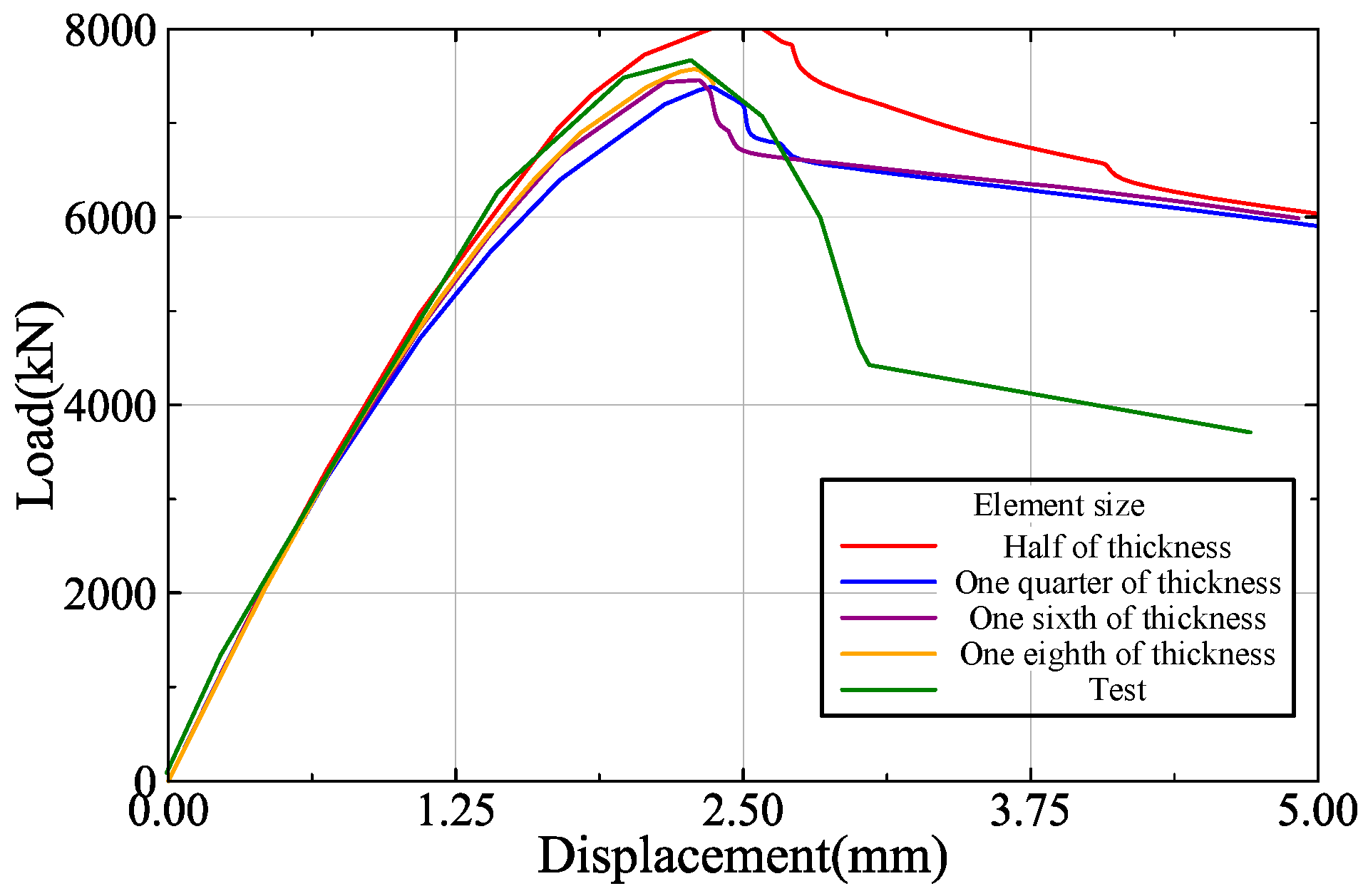
3.2. Finite Element Model Mesh Dimensional Assessment
3.3. Model Validation
4. Single-Parameter Influence Analysis of Constraint Effect of MDSCCS
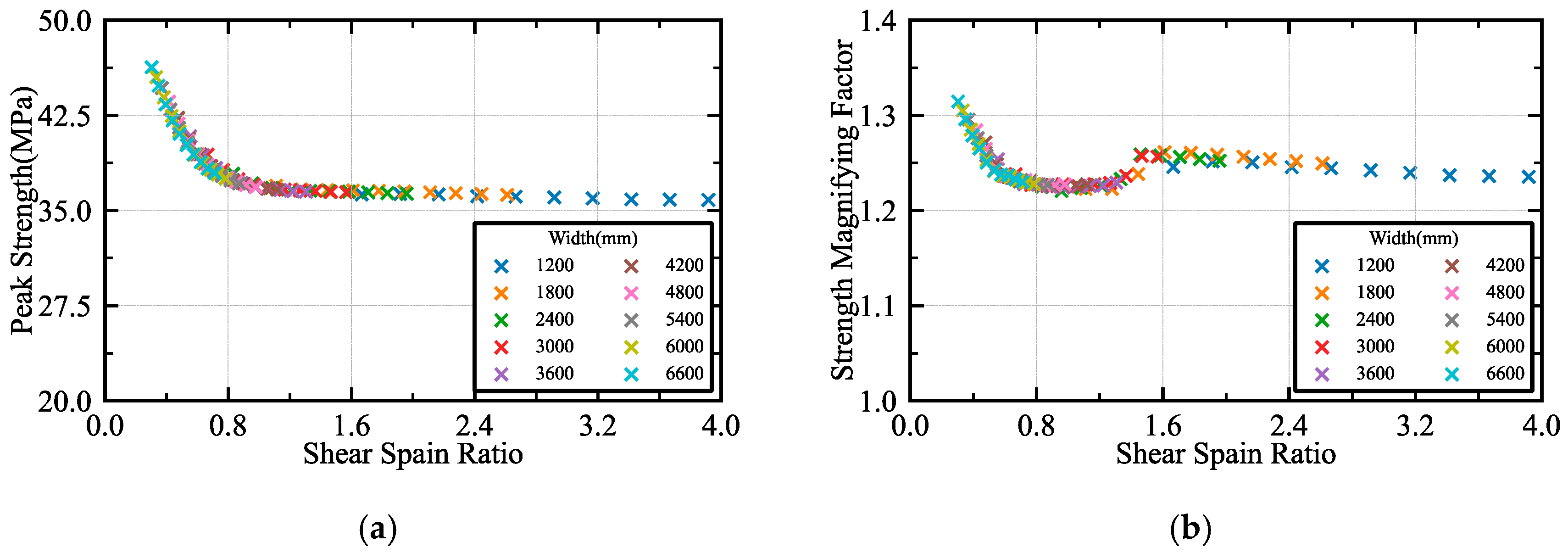
4.1. Parametric Analysis of Geometric Size
4.1.1. Height Effect
4.1.2. Width Effect
4.1.3. Thickness Effect
4.2. Parametric Analysis of Steel Thickness
4.3. Parametric Analysis of Steel Strength
4.4. Parametric Analysis of Concrete Strength
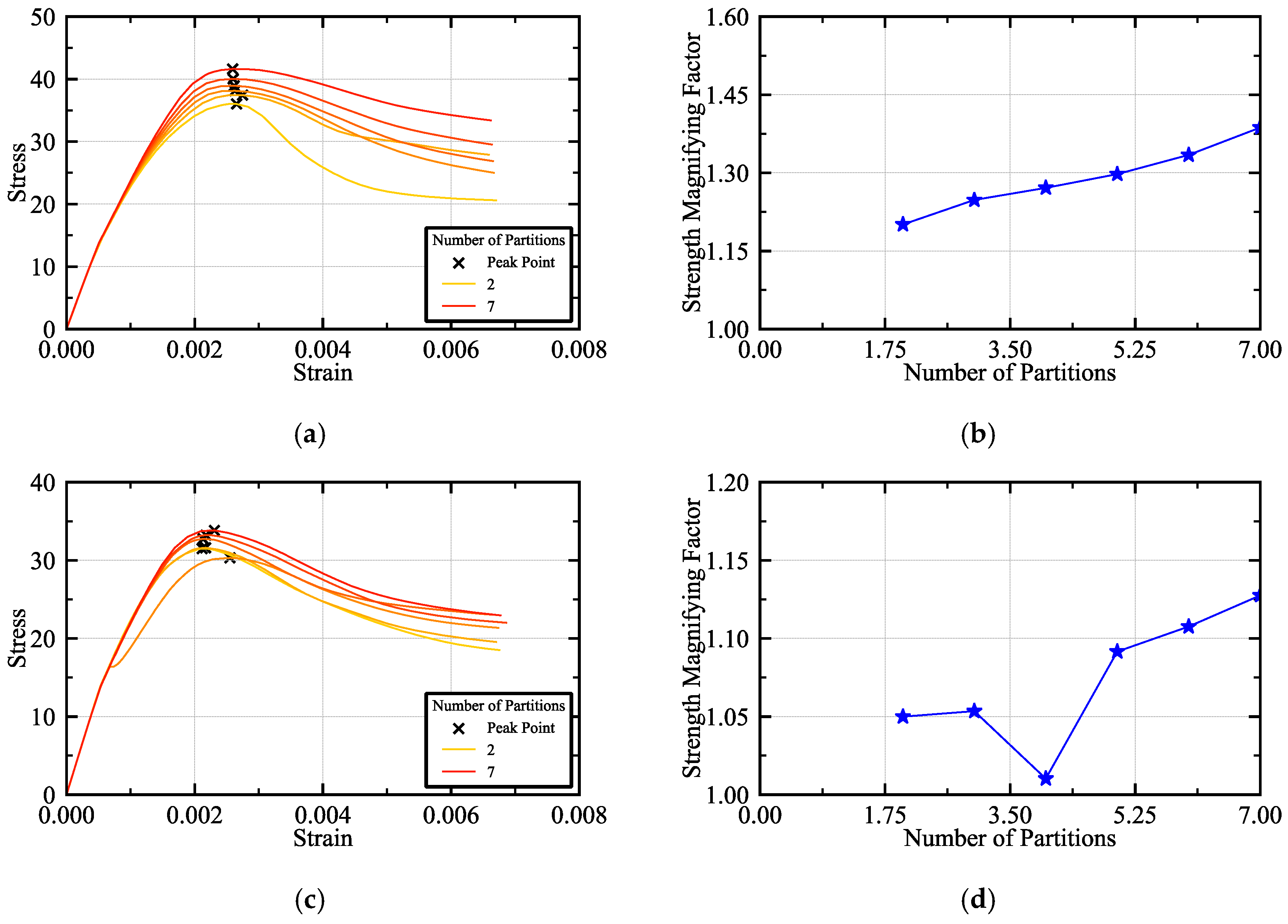
4.5. Parametric Analysis of Cavity Number
4.6. Summary of Single-Factor Analysis
5. Multiple Parametric Analysis of Constraint Effects in Multi-Cavity Double Steel Plate–Concrete Composite Structures
5.1. Dual-Parameter Analysis of Width and Height
5.2. Three-Parameter Analysis of Cavity Number, Partition Thickness, and Web Thickness
6. Research on Full-Parameter Batch Modelling of MDSCCS
6.1. Regression Analysis of Strength Enhancement Coefficient
6.2. Regression Analysis of Peak Strain and Gradient of the Descending Part
6.3. Constrained Constitutive of Concrete in MDSCCS
- (1)
- The concrete is monolithic and fully bonded to the steel plates; bond slip and partial interaction are not modeled.
- (2)
- The shear–span ratio must exceed 0.6, as validated in the simulations. Structures with low height-to-width ratios may require alternative formulations.
- (3)
- The cavity width should be equal to or greater than the wall thickness, since narrower configurations were excluded due to non-convergence or reduced confinement behavior.
- (4)
- The model is valid for uniaxial compression only; cyclic loading, multi-axial stress states, or time-dependent effects like creep are not included at this stage.
- (5)
- The diaphragm influence is excluded from the confinement factor to simplify computation, justified by the minimal effect demonstrated in Section 5.2.
7. Conclusions
- (1)
- The CDP-based shell–solid finite element model adeptly captures the comprehensive mechanical behavior of multi-cavity double steel plate composite structures, encompassing initial stiffness, peak stress, peak strain, and associated factors.
- (2)
- A comprehensive multi-parametric finite element batch analysis was conducted, introducing a parameter—the confinement factor—specifically tailored to quantify the extent of constraint in MDSCCS. This coefficient profoundly influences the peak stress, peak strain, and gradient of the descending part in confined concrete.
- (3)
- When the confinement factor ζ exceeds 2.0, the recommended descending slope of the stress–strain curve is approximately 0.15, and the ultimate strain increases proportionally with ζ. Moreover, the peak stress amplification factors in MDSCCS-1 and MDSCCS-2 show that typical confinement-enhanced strength coefficients are 1.23 and 1.06, respectively.
- (4)
- Using batch finite element modeling and statistical regression methodologies, a constitutive model for concrete under uniaxial compression was proposed, specifically designed for MDSCCS.
- (5)
- The confinement factor and stress–strain model developed herein may serve as a complementary tool or future supplement to existing design provisions, particularly for wind energy or offshore structures where MDSCCS applications are gaining traction.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Peng, X.K.; Liu, Z.C.; Jiang, D. A review of multiphase energy conversion in wind power generation. Renew. Sustain. Energy Rev. 2021, 147, 111172. [Google Scholar] [CrossRef]
- Zhang, R.; Shen, G.Q.P.; Ni, M.; Wong, J.K.W. An overview on the status quo of onshore and offshore wind power development and wind power enterprise localization in China. Int. J. Green Energy 2019, 16, 1646–1664. [Google Scholar] [CrossRef]
- Zhou, X.-H.; Wang, Y.-H.; Deng, R. Hybrid Wind Power Tower Based on Edge Stiffened Combined Shell. Patent CN109404224B, 18 June 2024. (In Chinese). [Google Scholar]
- Varma, A.H.; Malushte, S.R.; Sener, K.C.; Lai, Z. Steel-plate composite (SC) walls for safety related nuclear facilities: Design for in-plane forces and out-of-plane moments. Nucl. Eng. Des. 2014, 269, 240–249. [Google Scholar] [CrossRef]
- Seo, J.; Varma, A.H.; Sener, K.; Ayhan, D. Steelplate composite (SC) walls: In-plane shear behavior, database, and design. J. Constr. Steel Res. 2016, 119, 202–215. [Google Scholar] [CrossRef]
- Yan, J.-B.; Wang, X.-T.; Wang, T. Compressive Behaviour of Normal Weight Concrete Confined by the Steel Face Plates in SCS Sandwich Wall. Constr. Build. Mater. 2018, 171, 437–454. [Google Scholar] [CrossRef]
- Shen, K.; Wan, S.; Zhu, Y.; Lyu, D. A softened membrane model for single-box multi-cell composite box-girders with corrugated steel webs under pure torsion. Adv. Bridge Eng. 2022, 3, 2. [Google Scholar] [CrossRef]
- Kong, S.-Y.; Fan, J.-S.; Nie, X.; Ding, R.; Sun, Y.-L.; Chen, Y. Pullout behavior of lap splice connections between double-steel-plate composite walls and RC raft foundation in nuclear engineering. Eng. Struct. 2021, 230, 111720. [Google Scholar] [CrossRef]
- Deng, R.; Yang, J.-D.; Wang, Y.-H.; Li, Q.-Q.; Yu, Z.; Shen, Q.-W.; Yang, Y. Buckling and ultimate resistance of double-corrugated steel plates under in-plane shear load. Structures 2023, 53, 1267–1282. [Google Scholar] [CrossRef]
- Wang, B.-X.; Ding, R.; Fan, J.-S.; Cai, L.-J.; Feng, Z.-M.; Wang, C.-K. Shear performance of single steel-plate concrete composite beams with various transverse reinforcement configurations. Eng. Struct. 2022, 270, 114676. [Google Scholar] [CrossRef]
- Yang, Y.; Wu, B.; Xu, L.-Y.; Yao, Y.-P.; Zhang, D.; Zhao, C. Experimental study on the buckling behavior of double steel plate concrete composite slabs with stiffening ribs and tie plates. Eng. Struct. 2022, 255, 113895. [Google Scholar] [CrossRef]
- Ozaki, M.; Akita, S.; Osuga, H.; Nakayama, T.; Adachi, N. Study on Steel Plate Reinforced Concrete Panels Subjected to Cyclic In-Plane Shear. Nucl. Eng. Des. 2004, 228, 225–244. [Google Scholar] [CrossRef]
- Takeda, T.; Yamaguchi, T.; Nakayama, T.; Akiyama, K.; Kato, Y. Experimental study on shear characteristics of a concrete filled steel plate wall. In Transactions of 13th International Conference on Structural Mechanics in Reactor Technology (SMiRT 13); International Association for Structural Mechanics in Reactor Technology: Raleigh, NC, USA; pp. 21–26. Available online: https://repository.lib.ncsu.edu/server/api/core/bitstreams/291747bc-b889-40d9-ba63-d42131156838/content (accessed on 28 April 2025).
- Bu, F.-M. Studies on the Mechanical Performance of Composite Shear Wall with Double Steel Plates and Concrete Filled. Ph.D. Thesis, Tsinghua University, Beijing, China, 2011. (In Chinese). [Google Scholar]
- Nie, J.-G.; Ma, X.-W.; Tao, M.-X.; Fan, J.-S.; Bu, F.-M. Effective stiffness of composite shear wall with double plates and filled concrete. J. Constr. Steel Res. 2014, 99, 140–148. [Google Scholar] [CrossRef]
- Nie, X.; Wang, J.-J.; Tao, M.-X.; Fan, J.-S.; Bu, F.-M. Experimental study of flexural critical reinforced concrete filled composite plate shear walls. Eng. Struct. 2019, 197, 109439. [Google Scholar] [CrossRef]
- Wang, J.-J.; Nie, X.; Bu, F.-M.; Tao, M.-X.; Fan, J.-S. Experimental study and design method of shear-dominated composite plate shear walls. Eng. Struct. 2020, 215, 110656. [Google Scholar] [CrossRef]
- Guo, L.; Wang, Y.; Zhang, S. Experimental study of rectangular multi-partition steel-concrete composite shear walls. Thin-Walled Struct. 2018, 130, 577–592. [Google Scholar] [CrossRef]
- Wang, K. Study on Mechanism and Design Method of Multi-Cavity Composite Shear Wall With Double Steel Plates And Infilled Concrete. Ph.D. Thesis, Harbin Institute of Technology, Harbin, China, 2022. (In Chinese). [Google Scholar]
- Wang, K.; Zhang, W.; Chen, Y.; Ding, Y. Seismic Analysis and Design of Composite Shear Wall with Stiffened Steel Plate and Infilled Concrete. Materials 2021, 15, 182. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, K.; Chen, Y.; Ding, Y. Experimental Study on the Seismic Behaviour of Composite Shear Walls with Stiffened Steel Plates and Infilled Concrete. Thin-Walled Struct. 2019, 144, 106279. [Google Scholar] [CrossRef]
- Wang, Q. Experimental Study and Finite Element Analysis on Seismic Behavior of Multi-Cavity Steel Plate-Concrete Composite Shear Wall. Ph.D. Thesis, Harbin Institute of Technology, Harbin, China, 2017. (In Chinese). [Google Scholar]
- Zhang, X. Experimental and Theoretical Study on Seismic Behavior of Steel Tube Bundle Composite Shear Wall. Ph.D. Thesis, Tianjin University, Tianjin, China, 2016. (In Chinese). [Google Scholar]
- Mander, J.A.B.; Priestley, M.J.N. Theoretical Stress-Strain Model for Confined Concrete. J. Struct. Eng. 1988, 114, 1804–1826. [Google Scholar] [CrossRef]
- Han, L.-H.; Yao, G.-H.; Tao, Z. Performance of concrete-filled thin-walled steel tubes under pure torsion. Thin-Walled Struct. 2007, 45, 24–36. [Google Scholar] [CrossRef]
- Zhong, T.; Wang, Z.B.; Yu, Q. Finite element modelling of concrete-filled steel stub columns under axial compression. J. Constr. Steel Res. 2013, 89, 121–131. [Google Scholar]
- Samani, A.K.; Attard, M.M. A stress–strain model for uniaxial and confined concrete under compression. Eng. Struct. 2012, 41, 335–349. [Google Scholar] [CrossRef]
- Tao, M.-X.; Wang, Y.-L.; Ma, Z.-Y.; Zhao, J.-Z. Experimental database and analysis of in-plane seismic behaviour of double steel-plate composite walls for wind power tower. Thin-Walled Struct. 2024, 200, 111917. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, J.; Fan, J. Buckling behavior of double-skin composite walls: An experimental and modeling study. J. Constr. Steel Res. 2016, 121, 126–135. [Google Scholar] [CrossRef]
- Shi, J.; Guo, L.; Gao, S.; Li, Z. Buckling behavior of double skin composite walls under axial compressive load. Constr. Build. Mater. 2022, 321, 126345. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, X.; He, Q.; Yan, X. Experimental study on local stability of steel plate concrete composite wall under axial compression. J. Civ. Eng. 2016, 49, 62–68. (In Chinese) [Google Scholar]
- European Committee For Standardization. EN 1994-1-1 Eurocode 4: Design of Composite Steel and Concrete Structures-Part 1-1: General Rules and Rules for Buildings; European Committee For Standardization: Brussels, Belgium, 2004. [Google Scholar]
- Ministry of Housing and Urban Rural Development of the People’s Republic of China. JGJ 138-2016 Code for Design of Composite Structures; Ministry of Housing and Urban Rural Development of the People’s Republic of China: Beijing, China, 2016. (In Chinese) [Google Scholar]
- Hou, H.; Wang, W.; Wang, S. Nonlinear modeling methods for cyclic analysis of double-skin composite shear walls. Thin-Walled Struct. 2023, 187, 110737. [Google Scholar] [CrossRef]
- Attard, M.M.; Setunge, S. Stress-Strain Relationship of Confined and Unconfined Concrete. ACI Mater. J. 1996, 93, 432–442. [Google Scholar]
- Zhao, Y.; Li, Z.; Ma, H. Experimental and numerical studies on compressive behavior of steel–concrete–steel composite walls considering local buckling and post-buckling effect. Thin-Walled Struct. 2023, 182, 110278. [Google Scholar] [CrossRef]
- Han, L.; Tao, Z. Theoretical analysis and experimental study on the mechanical properties of concrete filled square steel tubular under axial compression. J. Civ. Eng. 2001, 2, 17–25. (In Chinese) [Google Scholar]


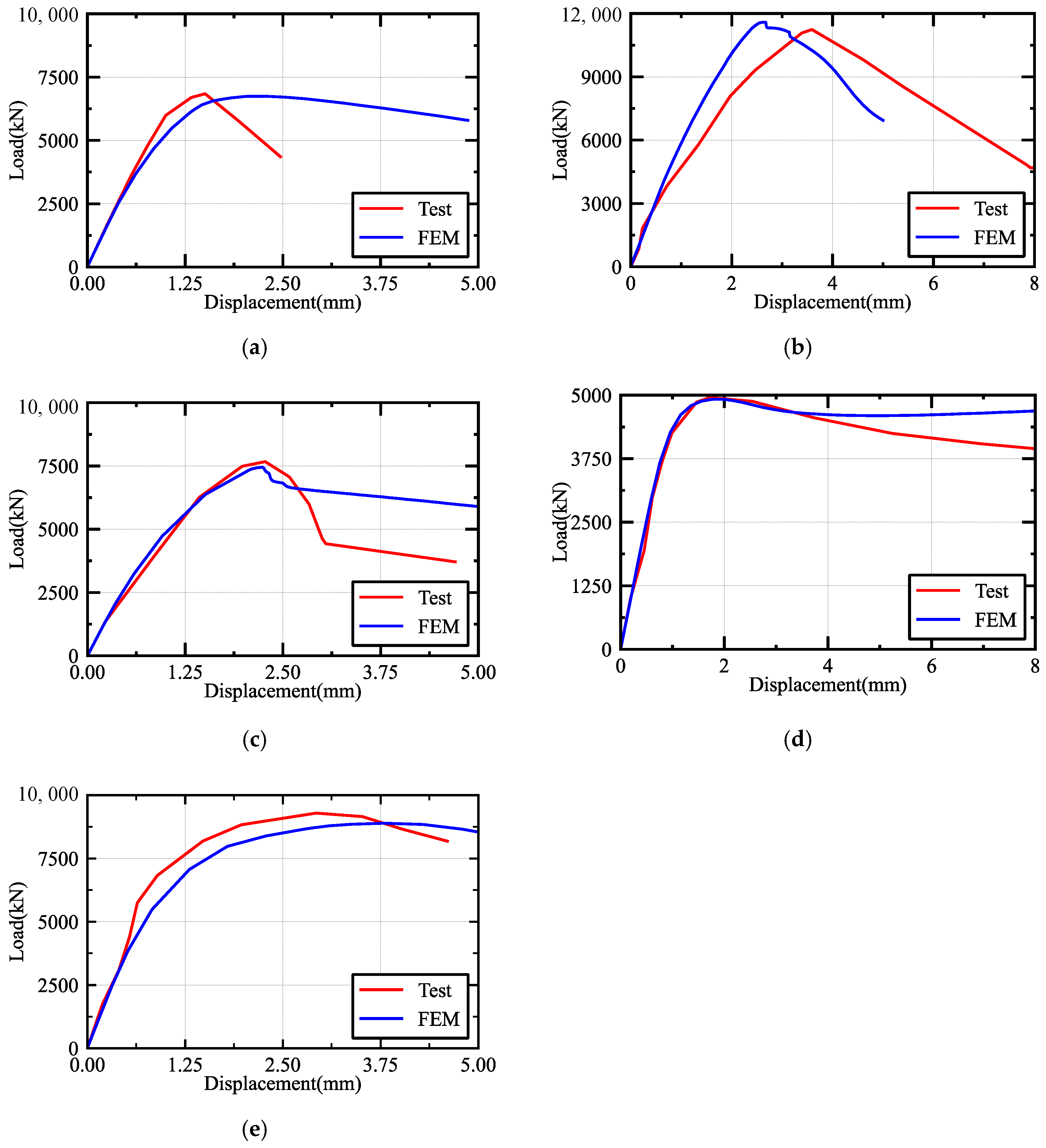





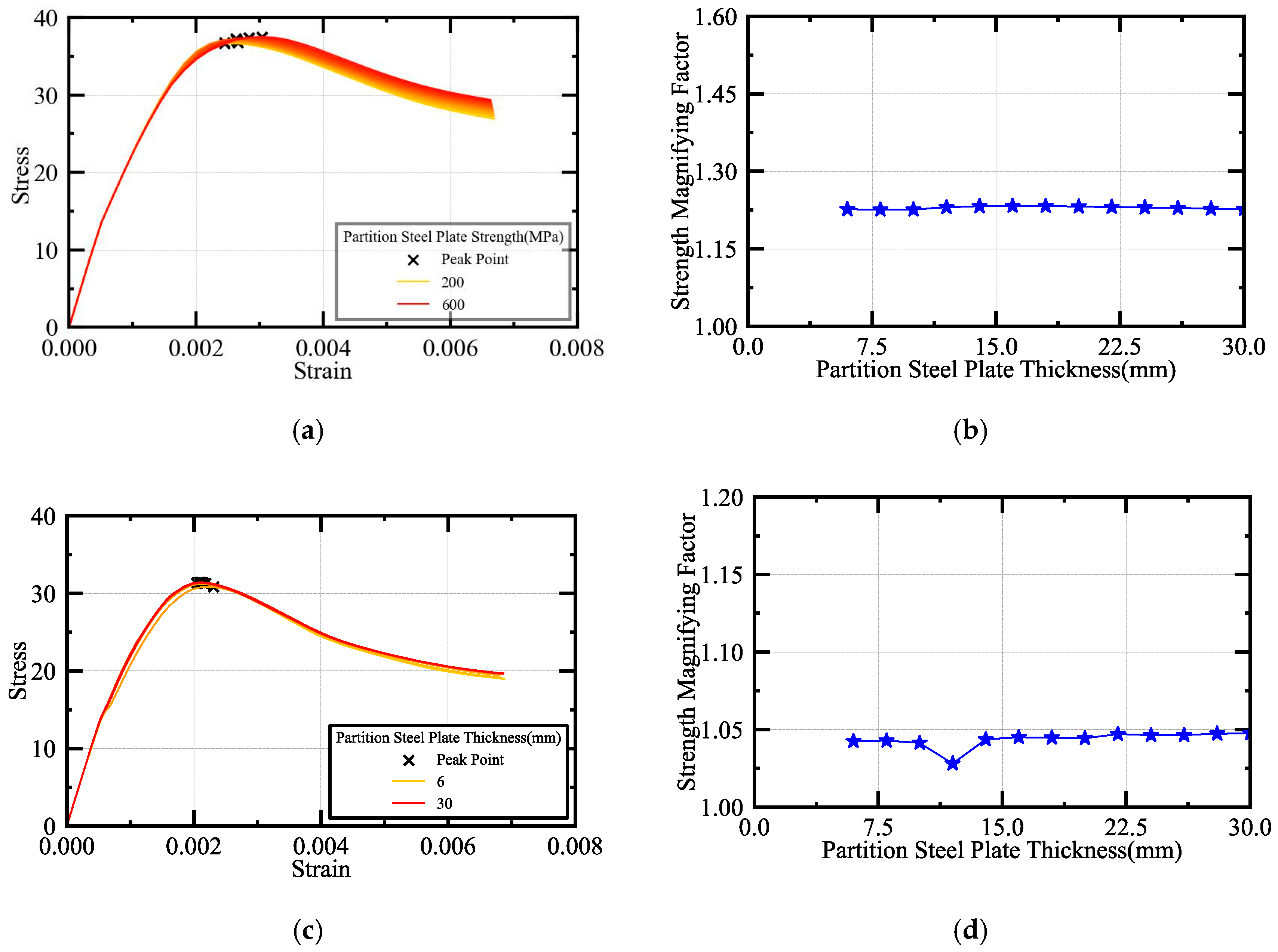
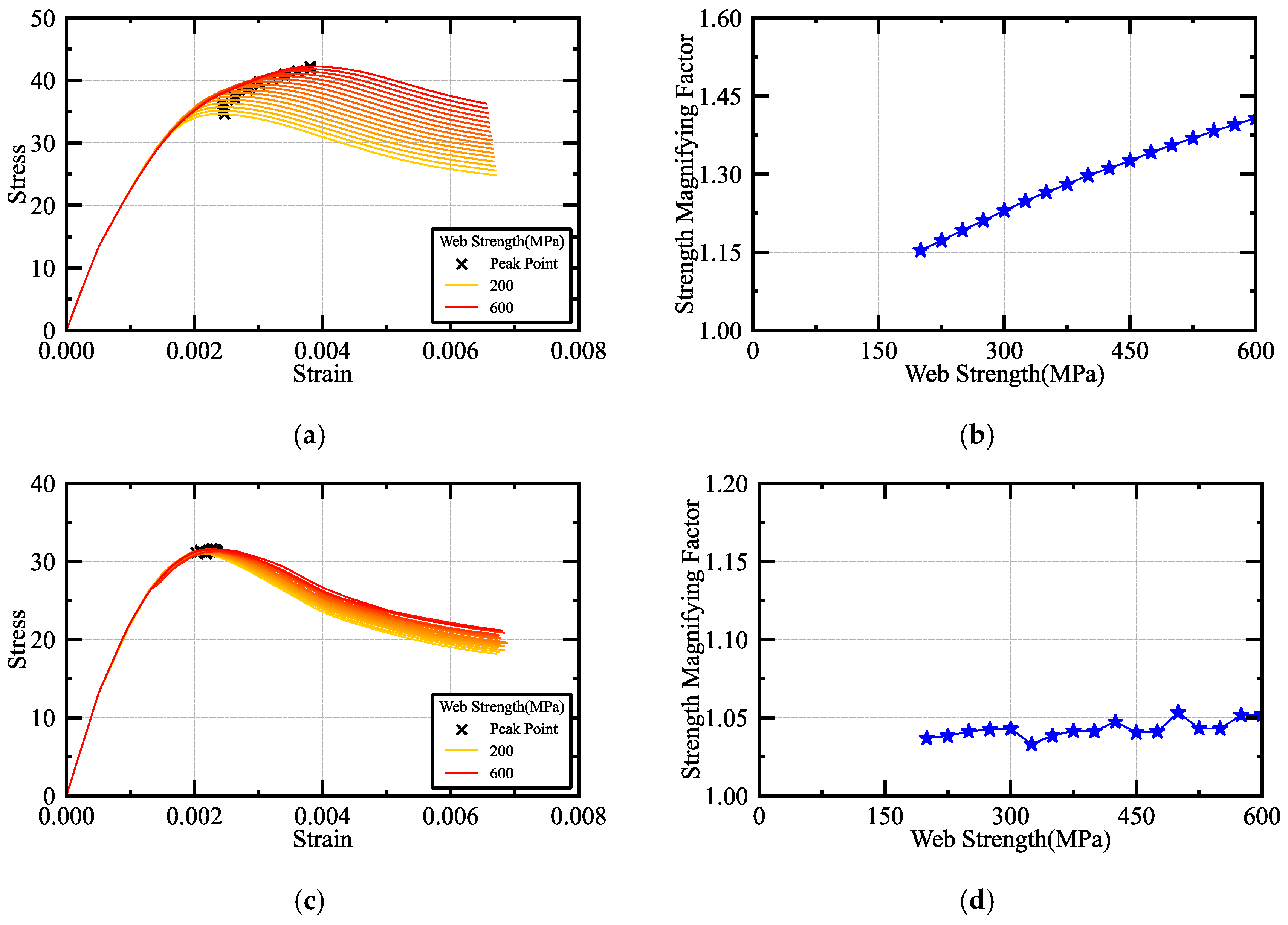

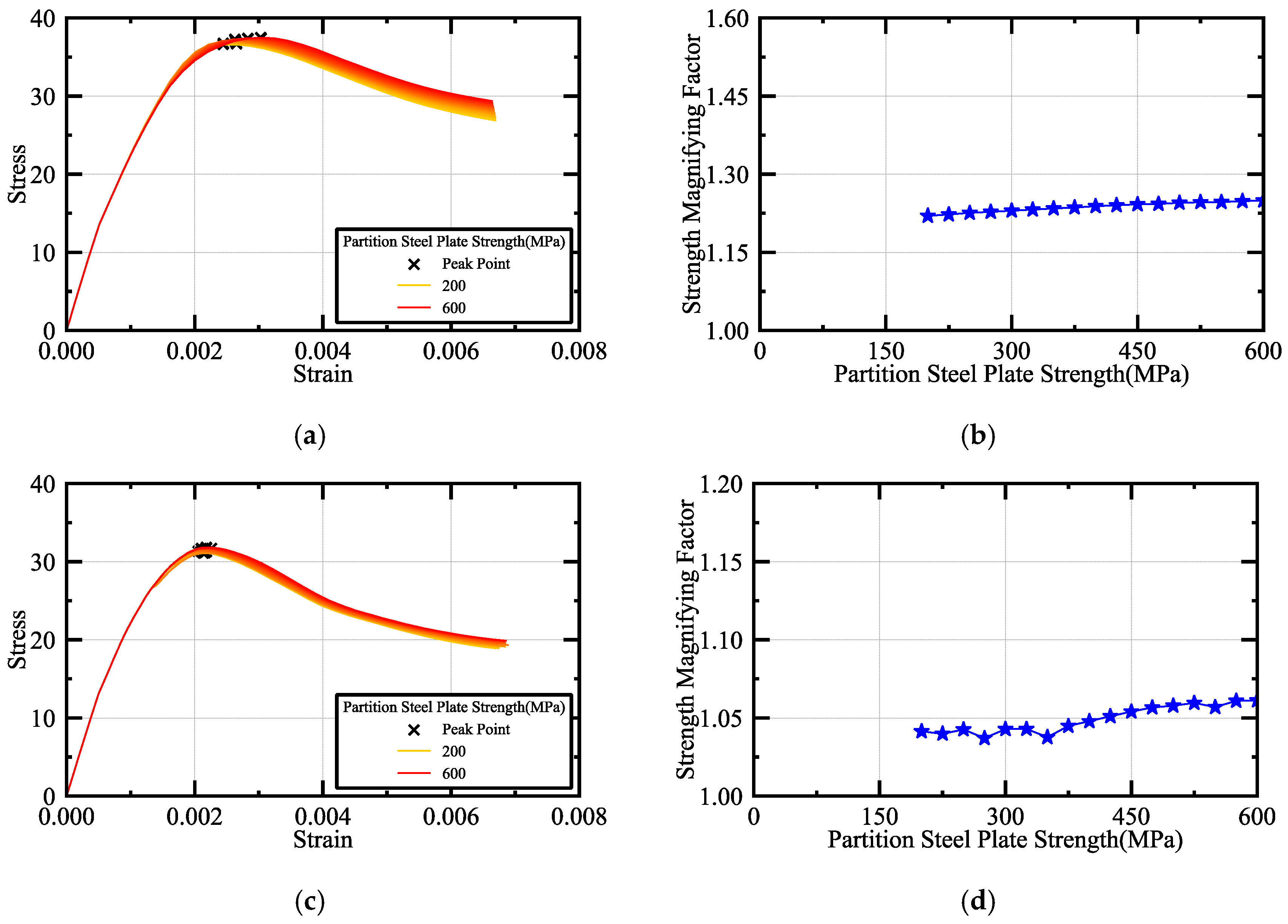





| MDSCCS-1 | MDSCCS-2 | |
|---|---|---|
| Height h | 3000 mm | 3000 mm |
| Thickness d | 500 mm | 600 mm |
| Width bc | 3000 mm | 3000 mm |
| Steel Thickness (tf = tw) | 20 mm | 10 mm |
| Concrete strength fc | 30 MPa | 30 MPa |
| Steel strength fy | 300 MPa | 300 MPa |
| Number of cavities | 5 | 4 |
| Thickness of the steel diaphragms | 8 mm | 8 mm |
| Fixed Parameters | Variable Parameters |
|---|---|
| Structural thickness: 500 mm | Structure width bc: {1500, 2500, 3500} (unit: mm) |
| Structural height: 3000 mm | steel plate thickness: {6, 11, 16, 21, 26} (unit: mm) |
| Height of the elastic loading beam: 150 mm | Cavity number: {2, 3, 4, 5, 6} |
| Height of the elastic foundation beam: 150 mm | Concrete strength fc: {20, 30, 40, 50, 60} (unit: MPa) |
| Steel strength: {200, 300, 400, 500, 600} (unit: MPa) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tao, M.; Wang, Y.; Zhao, J. Simulation and Analysis of the Constraint Effects of Multi-Cavity Double Steel Plate Composite Walls. Buildings 2025, 15, 1556. https://doi.org/10.3390/buildings15091556
Tao M, Wang Y, Zhao J. Simulation and Analysis of the Constraint Effects of Multi-Cavity Double Steel Plate Composite Walls. Buildings. 2025; 15(9):1556. https://doi.org/10.3390/buildings15091556
Chicago/Turabian StyleTao, Muxuan, Yulun Wang, and Jizhi Zhao. 2025. "Simulation and Analysis of the Constraint Effects of Multi-Cavity Double Steel Plate Composite Walls" Buildings 15, no. 9: 1556. https://doi.org/10.3390/buildings15091556
APA StyleTao, M., Wang, Y., & Zhao, J. (2025). Simulation and Analysis of the Constraint Effects of Multi-Cavity Double Steel Plate Composite Walls. Buildings, 15(9), 1556. https://doi.org/10.3390/buildings15091556







