Experimental Study of the Axial Tensile Properties of Basalt Fiber Textile–Reinforced Fine-Aggregate Concrete Thin Slab
Abstract
1. Introduction
2. Test Material
2.1. Basalt Fiber Mesh
2.2. PVA Fiber
2.3. Fine-Aggregate Concrete
3. Design and Preparation of Thin Slabs
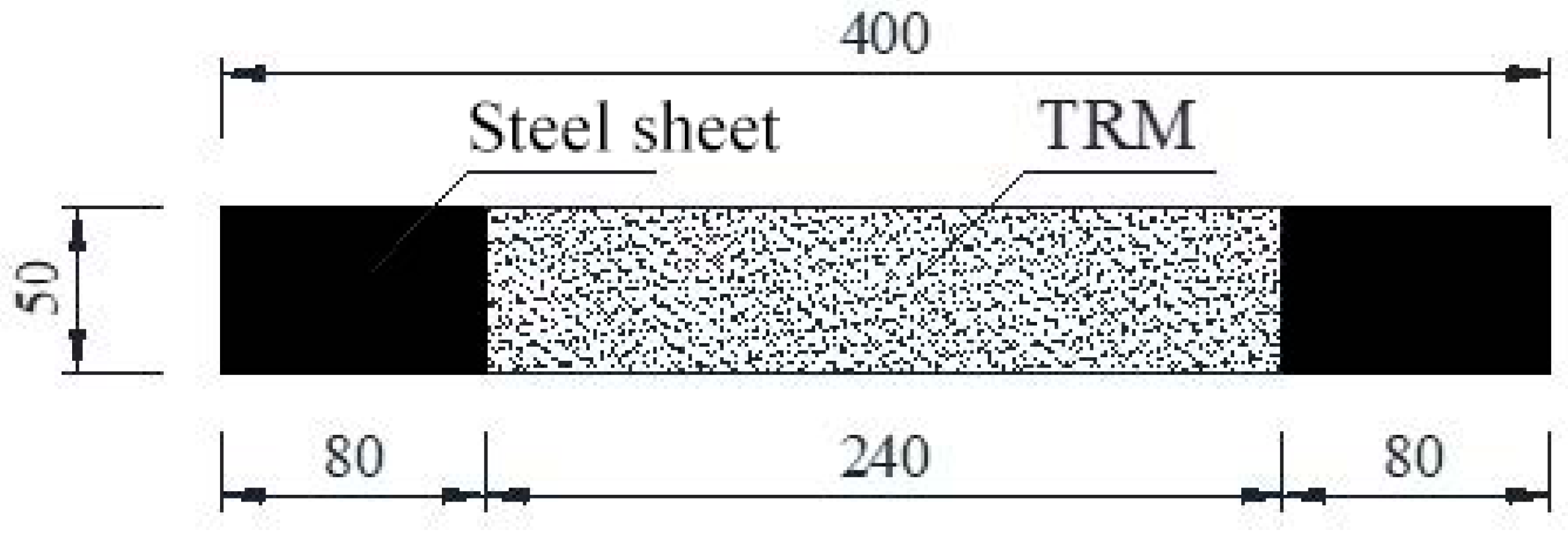
3.1. Design of Thin Slabs
3.2. Preparation of Thin Slabs
3.3. Test Conditions
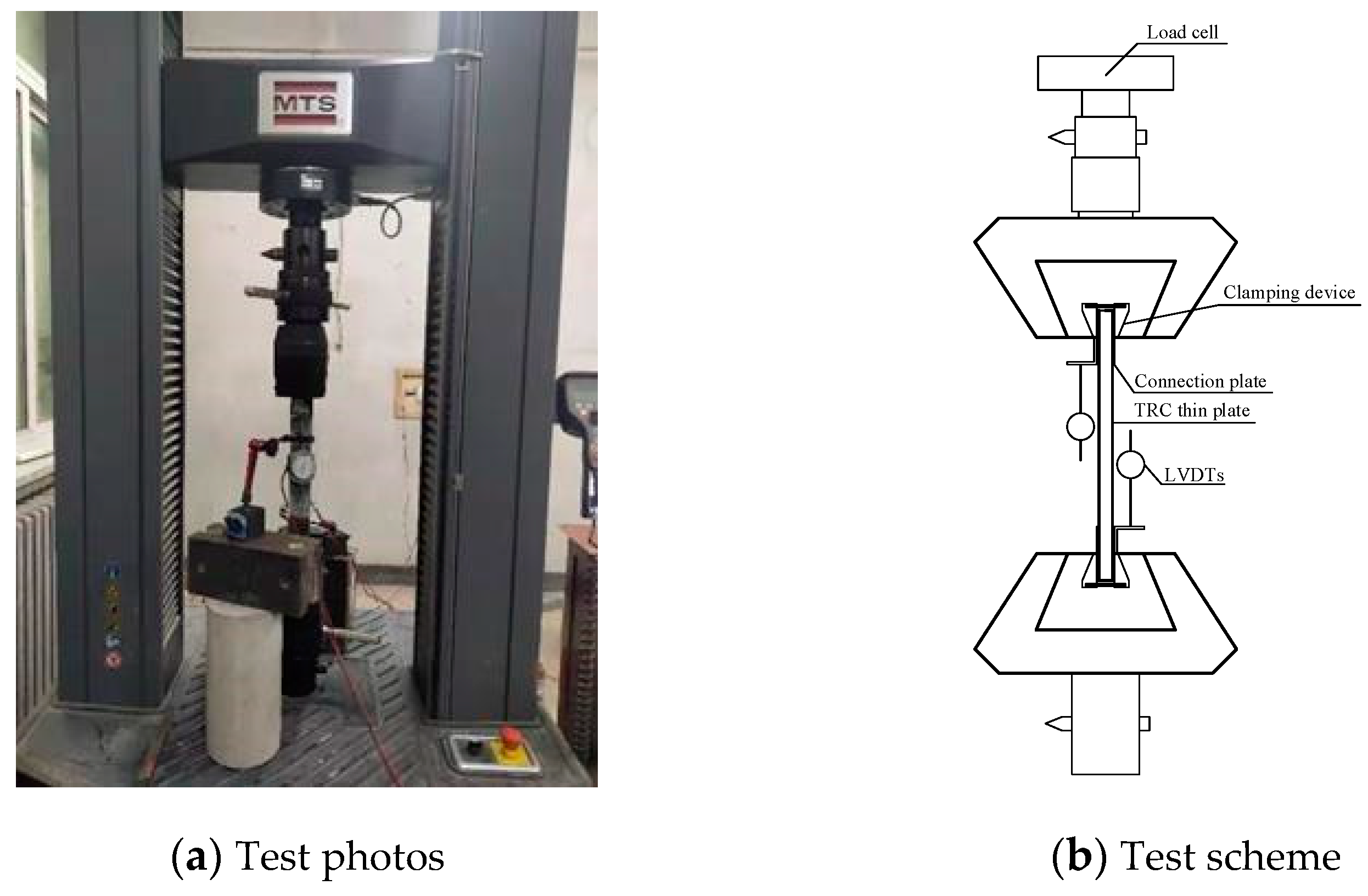
4. Test Method and Test Procedure
5. Test Results and Analysis
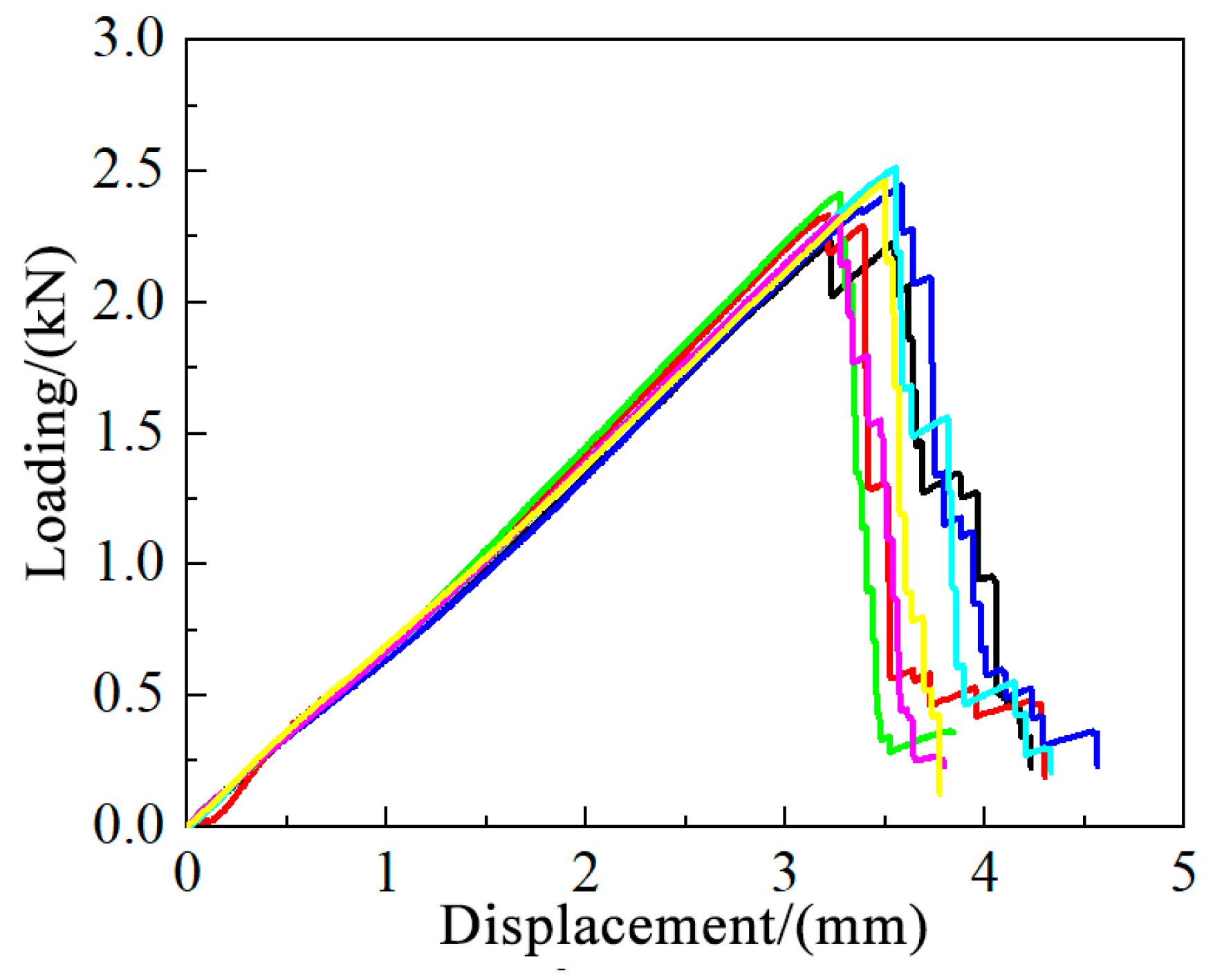
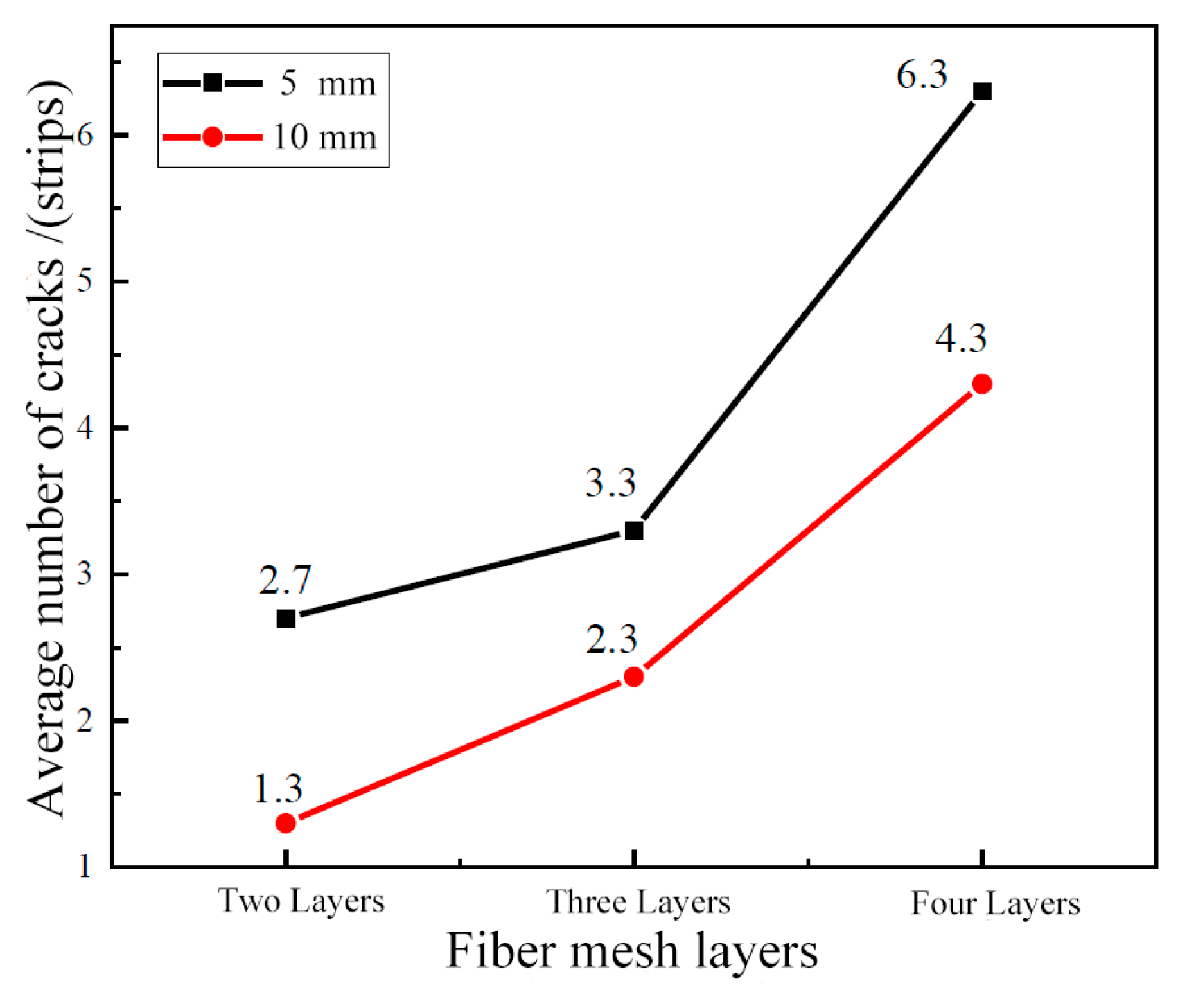
5.1. Test Phenomenon and Specimen Damage Mode
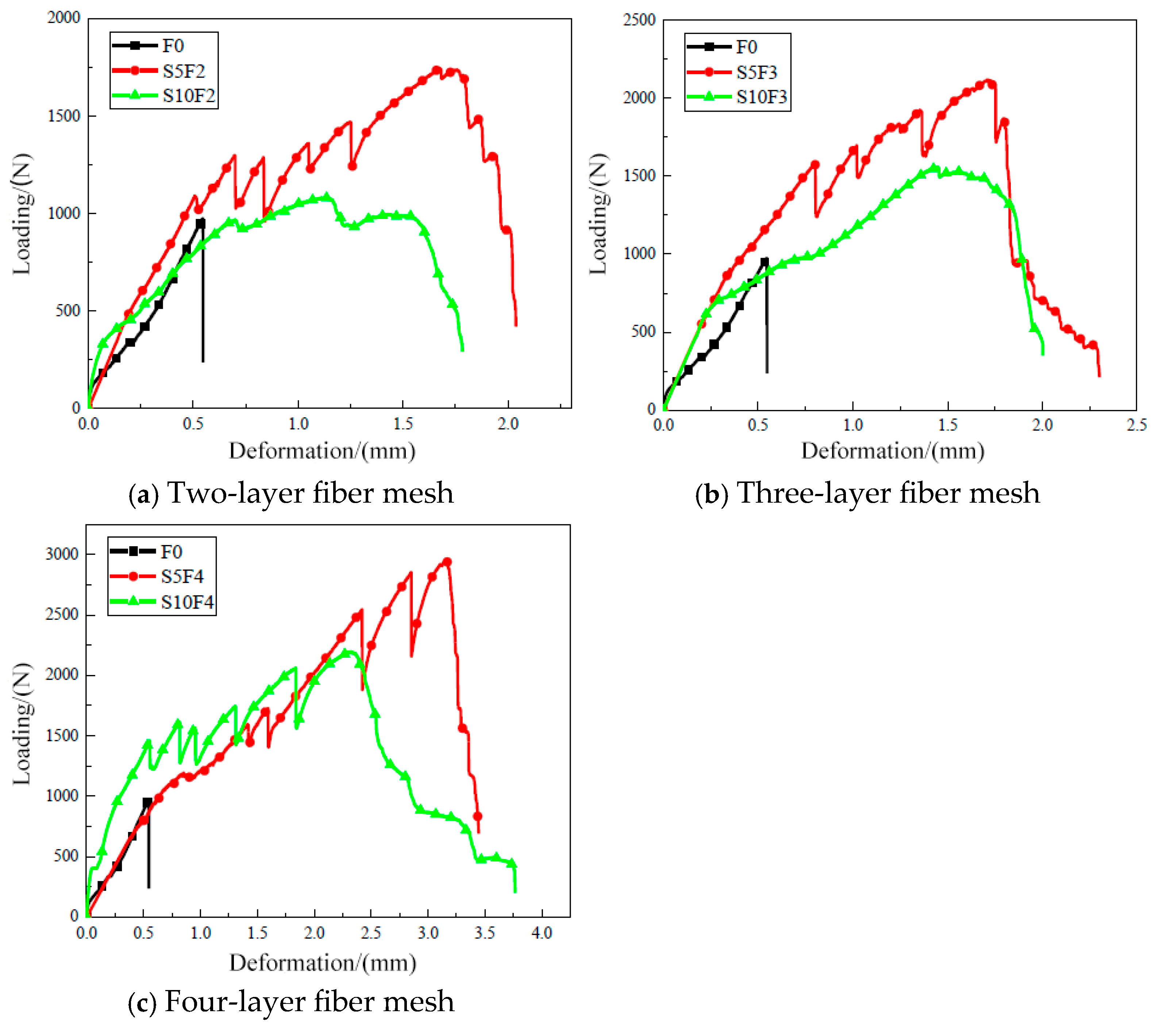
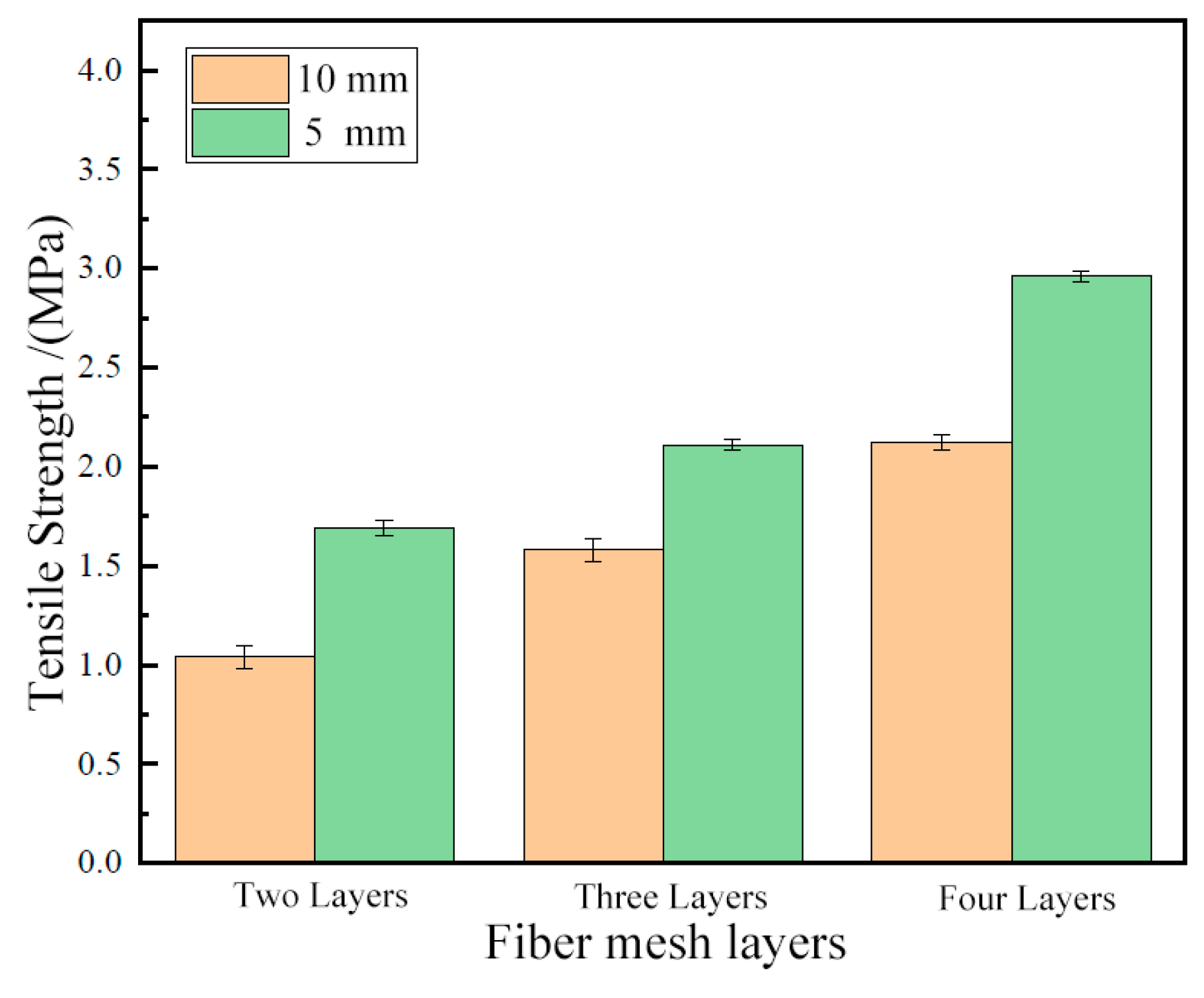
5.2. Effect of the Number of Fiber Mesh Layers on the Tensile Properties of BTRC Thin Slabs
5.3. Effect of Mesh Size on the Tensile Properties of BTRC Thin Slabs
6. Theoretical Analysis of Tensile Properties of TRC Thin Slabs
6.1. Elastic Modulus and Cracking Stress
6.2. Tensile Strength of TRC Thin Slabs
7. Conclusions
8. Discussion
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Symbols and Acronyms
| the theoretical cross-sectional area of a single fiber bundle, in mm2. | |
| the linear density of the fiber, in g/km. | |
| the volume density of the fiber, in g/cm3. | |
| the measured tensile strength of the fiber mesh strip, in MPa. | |
| the measured failure load from the test, in N. | |
| the number of fiber bundles within the width of the fiber mesh strip. | |
| the tensile elastic modulus of the fiber mesh strip. | |
| the load difference intercepted on the initial linear segment of the tensile stress–strain curve from the test, in N. | |
| the gauge length of the specimen, in mm. | |
| the elongation of the specimen’s gauge length relative to ∆P, in mm. | |
| the elongation rate at the failure of the specimen, in %. | |
| the mesh ratio of the specimen. | |
| the cross-sectional area of the fiber mesh in the TRC thin slab specimen in the direction of force, in mm2. | |
| the cross-sectional area of the TRC thin slab specimen, in mm2. | |
| the elastic modulus of the TRC tensile specimen before cracking, in GPa. | |
| the cracking stress of the TRC tensile specimen, in MPa. | |
| the elastic modulus of the matrix concrete, in GPa. | |
| the elastic modulus of the fiber mesh, in GPa. | |
| the tensile strength of the matrix concrete, in MPa. | |
| the tensile strength of the fiber mesh strip, in MPa. | |
| the failure load measured by the tensile test of the fiber woven mesh, in N. | |
| the cross-sectional area of the fiber woven mesh strip, mm2. | |
| the load-bearing capacity of the fiber mesh. | |
| related to the fiber mesh size; 0.6 (5 mm fiber mesh) or 0.5 (10 mm fiber mesh). | |
| BTRC | Basalt Fiber Textile–Reinforced Concrete. |
| TRC | Textile-Reinforced Concrete. |
| BTRM | Basalt Fiber Mesh–Reinforced Mortar. |
| BTRLM | Basalt Fiber Mesh–Reinforced Lime Mortar. |
| BFRCM | Basalt Fiber Mesh–Reinforced Cement Matrix. |
| BTRFAC | Basalt Textile–Reinforced Fine-Aggregate Concrete. |
References
- Wang, J.; Yu, D.; Zeng, C.; Ji, X.; Ye, L.; Zhou, P.; Zhao, S. Effect of Textile Layers and Hydroxypropyl Methylcellulose on Flexural Behavior of TRLC Thin Plates. Buildings 2024, 14, 924. [Google Scholar] [CrossRef]
- Yılmaz, M.C. Textile Types, Number of Layers and Wrapping Types Effect on Shear Strengthening of Reinforced Concrete Beams with Textile-Reinforced Mortar versus Carbon-Fiber-Reinforced Polymer. Buildings 2023, 13, 2744. [Google Scholar] [CrossRef]
- Hartig, J.; Häußler-Combe, U.; Schicktanz, K. Influence of Bond Properties on the Tensile Behaviour of Textile Reinforced Concrete. Cem. Concr. Compos. 2008, 30, 898–906. [Google Scholar] [CrossRef]
- Valeri, P.; Fernàndez Ruiz, M.; Muttoni, A. Tensile Response of Textile Reinforced Concrete. Constr. Build. Mater. 2020, 258, 119517. [Google Scholar] [CrossRef]
- Contamine, R.; Si Larbi, A.; Hamelin, P. Identifying the Contributing Mechanisms of Textile Reinforced Concrete (TRC) in the Case of Shear Repairing Damaged and Reinforced Concrete Beams. Eng. Struct. 2013, 46, 447–458. [Google Scholar] [CrossRef]
- Butler, M.; Mechtcherine, V.; Hempel, S. Experimental Investigations on the Durability of Fibre–Matrix Interfaces in Textile-Reinforced Concrete. Cem. Concr. Compos. 2009, 31, 221–231. [Google Scholar] [CrossRef]
- Kouris, L.A.S.; Triantafillou, T.C. State-of-the-Art on Strengthening of Masonry Structures with Textile Reinforced Mortar (TRM). Constr. Build. Mater. 2018, 188, 1221–1233. [Google Scholar] [CrossRef]
- Giese, A.C.H.; Giese, D.N.; Dutra, V.F.P.; Da Silva Filho, L.C.P. Flexural Behavior of Reinforced Concrete Beams Strengthened with Textile Reinforced Mortar. J. Build. Eng. 2021, 33, 101873. [Google Scholar] [CrossRef]
- Koutas, L.N.; Papakonstantinou, C.G. Flexural Strengthening of RC Beams with Textile-Reinforced Mortar Composites Focusing on the Influence of the Mortar Type. Eng. Struct. 2021, 246, 113060. [Google Scholar] [CrossRef]
- Signorini, C.; Sola, A.; Nobili, A. Hierarchical Composite Coating for Enhancing the Tensile Behaviour of Textile-Reinforced Mortar (TRM). Cem. Concr. Compos. 2023, 140, 105082. [Google Scholar] [CrossRef]
- Venigalla, S.G.; Nabilah, A.B.; Mohd Nasir, N.A.; Safiee, N.A.; Abd Aziz, F.N.A. Textile-Reinforced Concrete as a Structural Member: A Review. Buildings 2022, 12, 474. [Google Scholar] [CrossRef]
- Xie, W.; Sheng, J.; Yu, Z.; Li, Y.; Dou, G. Flexural Behavior of Corroded RC Beams Strengthened by Textile-Reinforced Concrete. Buildings 2023, 13, 2902. [Google Scholar] [CrossRef]
- Schladitz, F.; Frenzel, M.; Ehlig, D.; Curbach, M. Bending Load Capacity of Reinforced Concrete Slabs Strengthened with Textile Reinforced Concrete. Eng. Struct. 2012, 40, 317–326. [Google Scholar] [CrossRef]
- Du, Y.; Zhang, X.; Zhou, F.; Zhu, D.; Zhang, M.; Pan, W. Flexural Behavior of Basalt Textile-Reinforced Concrete. Constr. Build. Mater. 2018, 183, 7–21. [Google Scholar] [CrossRef]
- Halvaei, M.; Jamshidi, M.; Latifi, M.; Ejtemaei, M. Experimental Investigation and Modelling of Flexural Properties of Carbon Textile Reinforced Concrete. Constr. Build. Mater. 2020, 262, 120877. [Google Scholar] [CrossRef]
- Papanicolaou, C.G.; Triantafillou, T.C.; Papathanasiou, M.; Karlos, K. Textile Reinforced Mortar (TRM) versus FRP as Strengthening Material of URM Walls: Out-of-Plane Cyclic Loading. Mater. Struct. 2008, 41, 143–157. [Google Scholar] [CrossRef]
- Tetta, Z.C.; Koutas, L.N.; Bournas, D.A. Shear Strengthening of Full-Scale RC T-Beams Using Textile-Reinforced Mortar and Textile-Based Anchors. Compos. Part B Eng. 2016, 95, 225–239. [Google Scholar] [CrossRef]
- Guo, L.; Deng, M.; Chen, H.; Li, R.; Ma, X.; Zhang, Y. Experimental Study on Pre-Damaged RC Beams Shear-Strengthened with Textile-Reinforced Mortar (TRM). Eng. Struct. 2022, 256, 113956. [Google Scholar] [CrossRef]
- Koutas, L.N.; Bournas, D.A. Flexural Strengthening of Two-Way RC Slabs with Textile-Reinforced Mortar: Experimental Investigation and Design Equations. J. Compos. Constr. 2017, 21, 04016065. [Google Scholar] [CrossRef]
- Wan, C.; Wang, J.; Wang, S.; Ji, X.; Peng, Y.; Zhang, H. Tensile Behavior of Basalt Textile Reinforced Concrete: Effect of Test Setups and Textile Ratios. Materials 2022, 15, 8975. [Google Scholar] [CrossRef]
- Guo, S.; Ren, J.; Yang, T.; Rahman, M.Z.; Shi, C.; Zhu, D. Influences of Surface Treatment on the Mechanical Performances of Carbon and Basalt Textiles-Reinforced Concretes under Harsh Environments. Compos. Part B Eng. 2022, 246, 110195. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, X.; Liang, X.; Zhao, C.; Chen, Z.; Zhang, Y.; Zhou, J.; Wu, Z. Experimental Study and Theoretical Analysis on Tensile Properties of Concrete Reinforced with Different Polymer-Impregnated Basalt Textiles. J. Build. Eng. 2024, 87, 109003. [Google Scholar] [CrossRef]
- Pham, H.H.; Dinh, N.H.; Kim, S.-H.; Park, S.-H.; Choi, K.-K. Tensile Behavioral Characteristics of Lightweight Carbon Textile-Reinforced Cementitious Composites. J. Build. Eng. 2022, 57, 104848. [Google Scholar] [CrossRef]
- Ho, H.; Nguyen, H.C.; Dinh, H.T.; Ngo, D.Q.; Le, D.D. Experimental Study on the Tensile Strength Degradation of Curved Alkali Resistant Glass and Carbon Textile as Concrete Reinforcement under Complex Loading. Case Stud. Constr. Mater. 2023, 18, e01947. [Google Scholar] [CrossRef]
- Zhang, X.; Yin, R.; Chen, Y.; Lou, C. Experimental Study on the Axial Tensile Properties of Polypropylene Fiber Reinforced Concrete. Sci. Rep. 2023, 13, 16383. [Google Scholar] [CrossRef]
- Li, Z.; Jiang, Z.; Fang, Z.; Wang, Z.; Fang, Y. High-Temperature Axial Tensile Property and Fire Resisting Performance of CFRP Strand Cable. Constr. Build. Mater. 2024, 421, 135746. [Google Scholar] [CrossRef]
- Zhao, J.; Li, H.B. Experimental Determination of Dynamic Tensile Properties of a Granite. Int. J. Rock Mech. Min. Sci. 2000, 37, 861–866. [Google Scholar] [CrossRef]
- Qiu, Y.; Batchelor, S.D.; Jack, P.R.; McCord, M.G. Estimation of the Axial Tensile Modulus of a Particle-Reinforced Composite Fiber with Variable Radius. Compos. Sci. Technol. 2000, 60, 2731–2737. [Google Scholar] [CrossRef]
- Dong, Z.; Deng, M.; Zhang, C.; Zhang, Y.; Sun, H. Tensile Behavior of Glass Textile Reinforced Mortar (TRM) Added with Short PVA Fibers. Constr. Build. Mater. 2020, 260, 119897. [Google Scholar] [CrossRef]
- Suh, J.-I.; Park, S.-W.; Kim, K.-M. Tensile Behavior Assessment of Grid-Type CFRP Textile-Reinforced Mortar with Different Design Variables. Materials 2024, 17, 6049. [Google Scholar] [CrossRef]
- Ghannoum, M.; Shamoun, L.; Nasr, D.; Assaad, J.J.; Riahi, H.; Khatib, J. Efficiency of Stochastic Finite Element Random Fields and Variables to Predict Shear Strength of Fiber-Reinforced Concrete Beams Without Stirrups. Buildings 2025, 15, 721. [Google Scholar] [CrossRef]
- Assaad, J.J.; Khayat, K.H. Form Pressure Characteristics of Self-Consolidating Concrete Used in Repair. Cem. Concr. Compos. 2021, 122, 104118. [Google Scholar] [CrossRef]
- Shiping, Y.; Boxue, W.; Chenxue, Z.; Shuang, L. Bond Performance between Textile Reinforced Concrete (TRC) and Brick Masonry under Conventional Environment. Structures 2022, 36, 392–403. [Google Scholar] [CrossRef]
- Khalil, N.; Assaad, J.J. Bond Properties between Smooth Carbon Fibre-Reinforced Polymer Bars and Ultra-High Performance Concrete Modified with Polymeric Latexes and Fibres. Eur. J. Environ. Civ. Eng. 2022, 26, 6211–6228. [Google Scholar] [CrossRef]
- Jiang, J.; Jiang, C.; Li, B.; Feng, P. Bond Behavior of Basalt Textile Meshes in Ultra-High Ductility Cementitious Composites. Compos. Part B Eng. 2019, 174, 107022. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, X.; Liang, X.; Zhao, C.; Wu, Z. Experimental Study on the Durability of Polymer-Impregnated Basalt Textile Applied as Concrete Reinforcement. Polym. Compos. 2022, 43, 3498–3518. [Google Scholar] [CrossRef]
- Monaldo, E.; Nerilli, F.; Vairo, G. Basalt-Based Fiber-Reinforced Materials and Structural Applications in Civil Engineering. Compos. Struct. 2019, 214, 246–263. [Google Scholar] [CrossRef]
- Jagadeesh, P.; Rangappa, S.M.; Siengchin, S. Basalt Fibers: An Environmentally Acceptable and Sustainable Green Material for Polymer Composites. Constr. Build. Mater. 2024, 436, 136834. [Google Scholar] [CrossRef]
- Fang, L.; Zhou, Y.; Yi, D.; Yi, W. Experimental Study on Flexural Capacity of Corroded RC Slabs Reinforced with Basalt Fiber Textile. Appl. Sci. 2020, 11, 144. [Google Scholar] [CrossRef]
- Zhang, X.; He, W.; Zhang, Y.; Chen, C.; Wu, X. Tensile Behavior of Basalt-Fiber-Grid-Reinforced Mortar before and after Exposure to Elevated Temperature. Buildings 2022, 12, 2269. [Google Scholar] [CrossRef]
- Meriggi, P.; Caggegi, C.; Gabor, A.; De Felice, G. Shear-Compression Tests on Stone Masonry Walls Strengthened with Basalt Textile Reinforced Mortar (TRM). Constr. Build. Mater. 2022, 316, 125804. [Google Scholar] [CrossRef]
- Prasath, C.R.; Jayaguru, C.; Arunachelam, N. Cyclic Performance of Reinforced Concrete Columns Strengthened with Basalt-Fibre-Reinforced Cementitious Matrix (BFRCM). Buildings 2024, 14, 3496. [Google Scholar] [CrossRef]
- Zhu, D.; Mobasher, B.; Rajan, S.D. Dynamic Tensile Testing of Kevlar 49 Fabrics. J. Mater. Civ. Eng. 2011, 23, 230–239. [Google Scholar] [CrossRef]
- GB/T 3362-2005; Test Methods for Tensile Properties of Carbon Fiber Multifilament. China Building Industry Press: Beijing, China, 2017.
- Jabbour, R.; Assaad, J.J.; Hamad, B. Cost-to-Performance Assessment of Polyvinyl Alcohol Fibers in Concrete Structures. Mech. Adv. Mater. Struct. 2022, 29, 2973–2983. [Google Scholar] [CrossRef]
- Assaad, J.J. Development and Use of Polymer-Modified Cement for Adhesive and Repair Applications. Constr. Build. Mater. 2018, 163, 139–148. [Google Scholar] [CrossRef]
- Feng, S.; Xiao, H.; Geng, J. Bond Strength between Concrete Substrate and Repair Mortar: Effect of Fibre Stiffness and Substrate Surface Roughness. Cem. Concr. Compos. 2020, 114, 103746. [Google Scholar] [CrossRef]
- Contamine, R.; Si Larbi, A.; Hamelin, P. Contribution to Direct Tensile Testing of Textile Reinforced Concrete (TRC) Composites. Mater. Sci. Eng. A 2011, 528, 8589–8598. [Google Scholar] [CrossRef]
- JGJ/T 70-2009; Standard for Test Method of Basic Properties of Construction Mortar. China Building Industry Press: Beijing, China, 2009.
- Kong, K.; Mesticou, Z.; Michel, M.; Si Larbi, A.; Junes, A. Comparative Characterization of the Durability Behaviour of Textile-Reinforced Concrete (TRC) under Tension and Bending. Compos. Struct. 2017, 179, 107–123. [Google Scholar] [CrossRef]
- Mesticou, Z.; Bui, L.; Junes, A.; Si Larbi, A. Experimental Investigation of Tensile Fatigue Behaviour of Textile-Reinforced Concrete (TRC): Effect of Fatigue Load and Strain Rate. Compos. Struct. 2017, 160, 1136–1146. [Google Scholar] [CrossRef]
- Colombo, I.G.; Magri, A.; Zani, G.; Colombo, M.; Di Prisco, M. Erratum to: Textile Reinforced Concrete: Experimental Investigation on Design Parameters. Mater. Struct. 2013, 46, 1953–1971. [Google Scholar] [CrossRef]
- Larrinaga, P.; Chastre, C.; Biscaia, H.C.; San-José, J.T. Experimental and Numerical Modeling of Basalt Textile Reinforced Mortar Behavior under Uniaxial Tensile Stress. Mater. Des. 2014, 55, 66–74. [Google Scholar] [CrossRef]
- Baloch, W.L.; Siad, H.; Lachemi, M.; Sahmaran, M. A Review on the Durability of Concrete-to-Concrete Bond in Recent Rehabilitated Structures. J. Build. Eng. 2021, 44, 103315. [Google Scholar] [CrossRef]
- Zhang, X.; Du, M.; Fang, H.; Li, B.; Zhao, P.; Zhai, K.; Yao, X.; Du, X.; Shi, M.; Ma, D. Study on the Shear Strength and Damage Constitutive Model of the Contact Surface between PVA Fiber-Enhanced Cement Mortar and Concrete. Constr. Build. Mater. 2023, 400, 132571. [Google Scholar] [CrossRef]
- Li, L.; Cai, Z.; Yu, K.; Zhang, Y.X.; Ding, Y. Performance-Based Design of All-Grade Strain Hardening Cementitious Composites with Compressive Strengths from 40 MPa to 120 MPa. Cem. Concr. Compos. 2019, 97, 202–217. [Google Scholar] [CrossRef]
- Xu, S.L.; Yan, Z.Q. Mechanical Properties of Textile Reinforced Concrete Plate at Low Textile Ratios. Acta Mater. Compos. Sin. 2011, 28, 206–213. [Google Scholar] [CrossRef]
- Deng, Z.; Xu, J. Uniaxial tensile behavior of engineering cementitious composite reinforced with fiber textile grid and steel wire mesh. Mech. Adv. Mater. Struct. 2024, 32, 1853–1867. [Google Scholar] [CrossRef]










| Mesh Size | Tensile Strength (MPa) | Modulus of Elasticity (GPa) | Line Density (Tex) | Surface Density (g/m2) | Density (kg/m3) | Theoretical Thickness (mm) | Ultimate Tensile Strain (%) | |
|---|---|---|---|---|---|---|---|---|
| Warp | Weft | |||||||
| 5 mm × 5 mm | 2400 | 71 | 288 × 2 | 592 | 221 | 2.65 | 0.044 | 3.24 |
| 10 mm × 10 mm | 1700 | 72 | 289 × 2 | 605 | 104 | 2.65 | 0.044 | 3.15 |
| Fiber Name | Density (g/cm3) | Length (mm) | Diameter (mm) | Tensile Strength (MPa) | Modulus of Elasticity (GPa) |
|---|---|---|---|---|---|
| PVA | 1.29 | 6 | 0.039 | 1600 | 40 |
| P·O52.5R Cement | Water | Superplasticizer | Acrylic Emulsion | Sand | |
|---|---|---|---|---|---|
| 0–1 mm | 1–2 mm | ||||
| 640 | 292 | 1 | 100 | 940 | 260 |
| Specimen No. | Fiber Mesh Layers | Mesh Size (mm) | Number of Parallel Test Pieces |
|---|---|---|---|
| F0 | — | — | 3 |
| S5F2 | 2 | 5 | 3 |
| S5F3 | 3 | 5 | 3 |
| S5F4 | 4 | 5 | 3 |
| S10F2 | 2 | 10 | 3 |
| S10F3 | 3 | 10 | 3 |
| S10F4 | 4 | 10 | 3 |
| Specimen No. | Number of Cracks | Average Number of Cracks | Average Spacing of Cracks (cm) | ||
|---|---|---|---|---|---|
| Specimen 1 | Specimen 2 | Specimen 3 | |||
| S5F2 | 2 | 3 | 3 | 2.7 | 8.9 |
| S5F3 | 3 | 4 | 3 | 3.3 | 7.3 |
| S5F4 | 8 | 6 | 5 | 6.3 | 3.8 |
| S10F2 | 2 | 1 | 1 | 1.3 | 18.5 |
| S10F3 | 2 | 3 | 2 | 2.3 | 10.4 |
| S10F4 | 5 | 4 | 4 | 4.3 | 5.6 |
| Specimen No. | Peak Load (kN) | Average Peak Load (kN) | COV (%) | Tensile Strength (Peak Stress) (MPa) | COV/% | ||
|---|---|---|---|---|---|---|---|
| Specimen 1 | Specimen 2 | Specimen 3 | |||||
| F0 | 0.98 | 1.03 | 1.01 | 1.01 | 2.50 | 1.04 | 2.61 |
| S5F2 | 1.63 | 1.69 | 1.75 | 1.69 | 3.55 | 1.69 | 3.60 |
| S5F3 | 2.16 | 2.05 | 2.12 | 2.11 | 2.64 | 2.11 | 2.51 |
| S5F4 | 2.89 | 3.05 | 2.95 | 2.96 | 2.73 | 2.96 | 2.51 |
| S10F2 | 1.08 | 0.97 | 1.06 | 1.04 | 5.65 | 1.04 | 5.75 |
| S10F3 | 1.52 | 1.53 | 1.68 | 1.58 | 5.68 | 1.58 | 5.49 |
| S10F4 | 2.20 | 2.12 | 2.04 | 2.12 | 3.77 | 2.12 | 4.05 |
| Specimen No. | Average Deformation Peak Load (mm) | COV (%) | Average Limit Deformation (mm) | COV (%) | Peak Strain (με) | Extreme Tensile Strain (με) |
|---|---|---|---|---|---|---|
| F0 | 0.59 | 2.09 | 0.59 | 2.18 | 2458 | 2458 |
| S5F2 | 1.58 | 3.05 | 2.60 | 3.17 | 6583 | 10,833 |
| S5F3 | 1.70 | 1.56 | 2.32 | 1.85 | 7083 | 9667 |
| S5F4 | 3.03 | 0.76 | 3.54 | 1.32 | 12,611 | 14,750 |
| S10F2 | 1.09 | 5.30 | 1.80 | 6.18 | 4541 | 7500 |
| S10F3 | 1.57 | 4.90 | 2.04 | 5.56 | 6556 | 8500 |
| S10F4 | 2.35 | 2.78 | 3.76 | 3.64 | 9778 | 15,667 |
| Mesh Size | Mass per Unit Length (g/km) | Density (g/cm3) | Cross-Sectional Area of Fiber Bundle (mm2) | ||
|---|---|---|---|---|---|
| Warp | Weft | Warp | Weft | ||
| 5 mm × 5 mm | 288 | 592 | 2.65 | 0.1088 | 0.2234 |
| 10 mm × 10 mm | 289 | 605 | 0.1091 | 0.2283 | |
| Specimen No. | Mesh Ratio (%) | Tensile Strength (MPa) (Test Value) | Tensile Strength (MPa) (Theoretical Value) | Tested/Theoretical | Average Value of Tested/Theoretical |
|---|---|---|---|---|---|
| S5F2 | 0.22 | 1.69 | 1.70 | 1.07 | 1.14 |
| S5F3 | 0.32 | 2.11 | 2.54 | 1.29 | |
| S5F4 | 0.43 | 2.96 | 3.39 | 1.23 | |
| S10F2 | 0.11 | 1.04 | 0.88 | 1.08 | |
| S10F3 | 0.16 | 1.58 | 1.30 | 1.07 | |
| S10F4 | 0.22 | 2.12 | 1.77 | 1.07 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Deng, Z. Experimental Study of the Axial Tensile Properties of Basalt Fiber Textile–Reinforced Fine-Aggregate Concrete Thin Slab. Buildings 2025, 15, 1540. https://doi.org/10.3390/buildings15091540
Wang L, Deng Z. Experimental Study of the Axial Tensile Properties of Basalt Fiber Textile–Reinforced Fine-Aggregate Concrete Thin Slab. Buildings. 2025; 15(9):1540. https://doi.org/10.3390/buildings15091540
Chicago/Turabian StyleWang, Liyang, and Zongcai Deng. 2025. "Experimental Study of the Axial Tensile Properties of Basalt Fiber Textile–Reinforced Fine-Aggregate Concrete Thin Slab" Buildings 15, no. 9: 1540. https://doi.org/10.3390/buildings15091540
APA StyleWang, L., & Deng, Z. (2025). Experimental Study of the Axial Tensile Properties of Basalt Fiber Textile–Reinforced Fine-Aggregate Concrete Thin Slab. Buildings, 15(9), 1540. https://doi.org/10.3390/buildings15091540





