Lateral Force–Displacement Hysteretic Model for CFRP (Carbon Fiber-Reinforced Polymer)-Retrofitted Square RC Columns
Abstract
1. Introduction
2. Finite Element Analysis
2.1. Finite Element Model
2.1.1. Material Constitutive Models
2.1.2. Section and Element
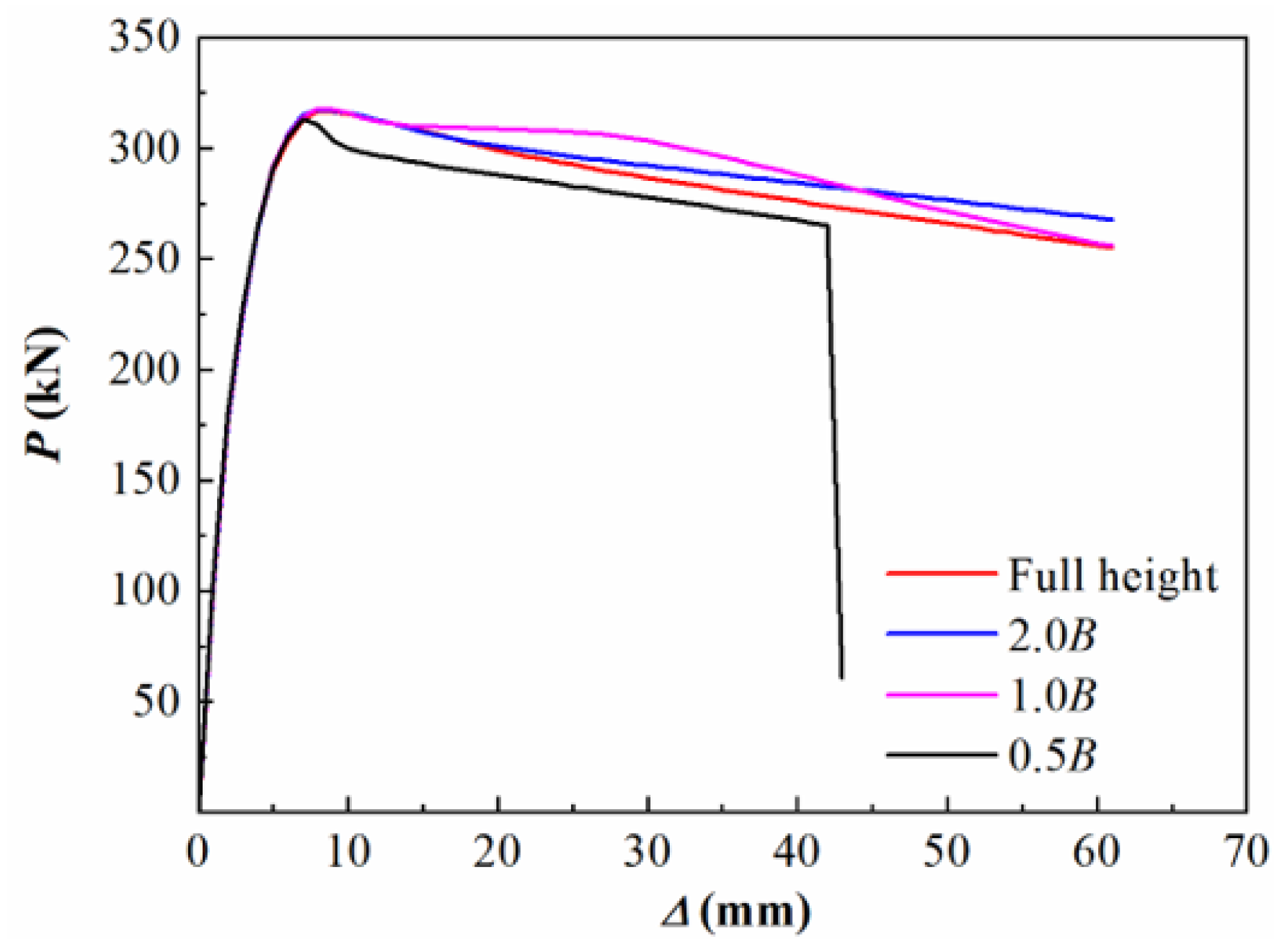
2.2. Verification of the FE Model
2.3. Parametric Analysis
3. Lateral Force–Displacement Hysteretic Model
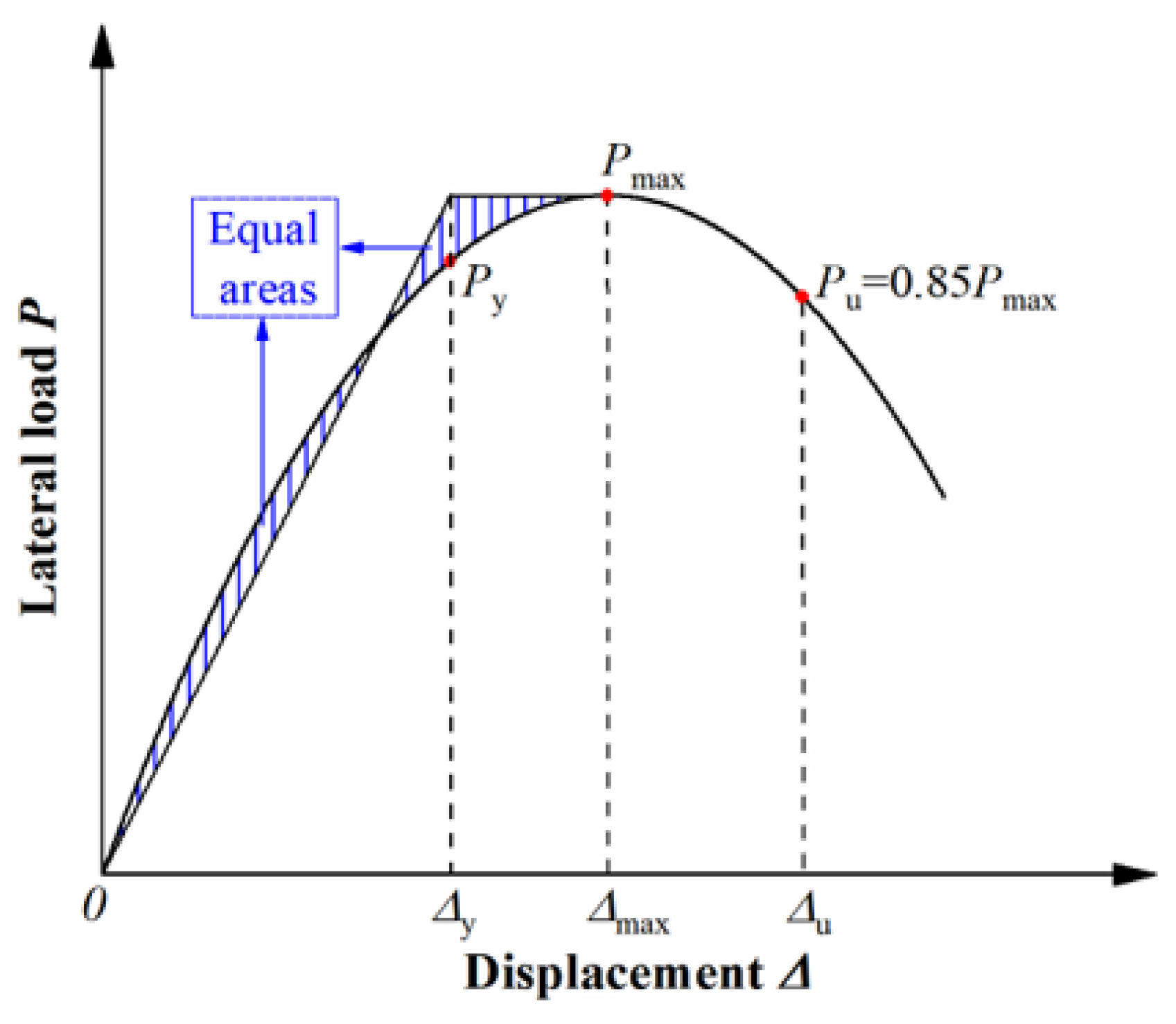
3.1. The Lateral Force–Displacement Skeleton Curve Model
3.2. Analysis of Characteristic Point
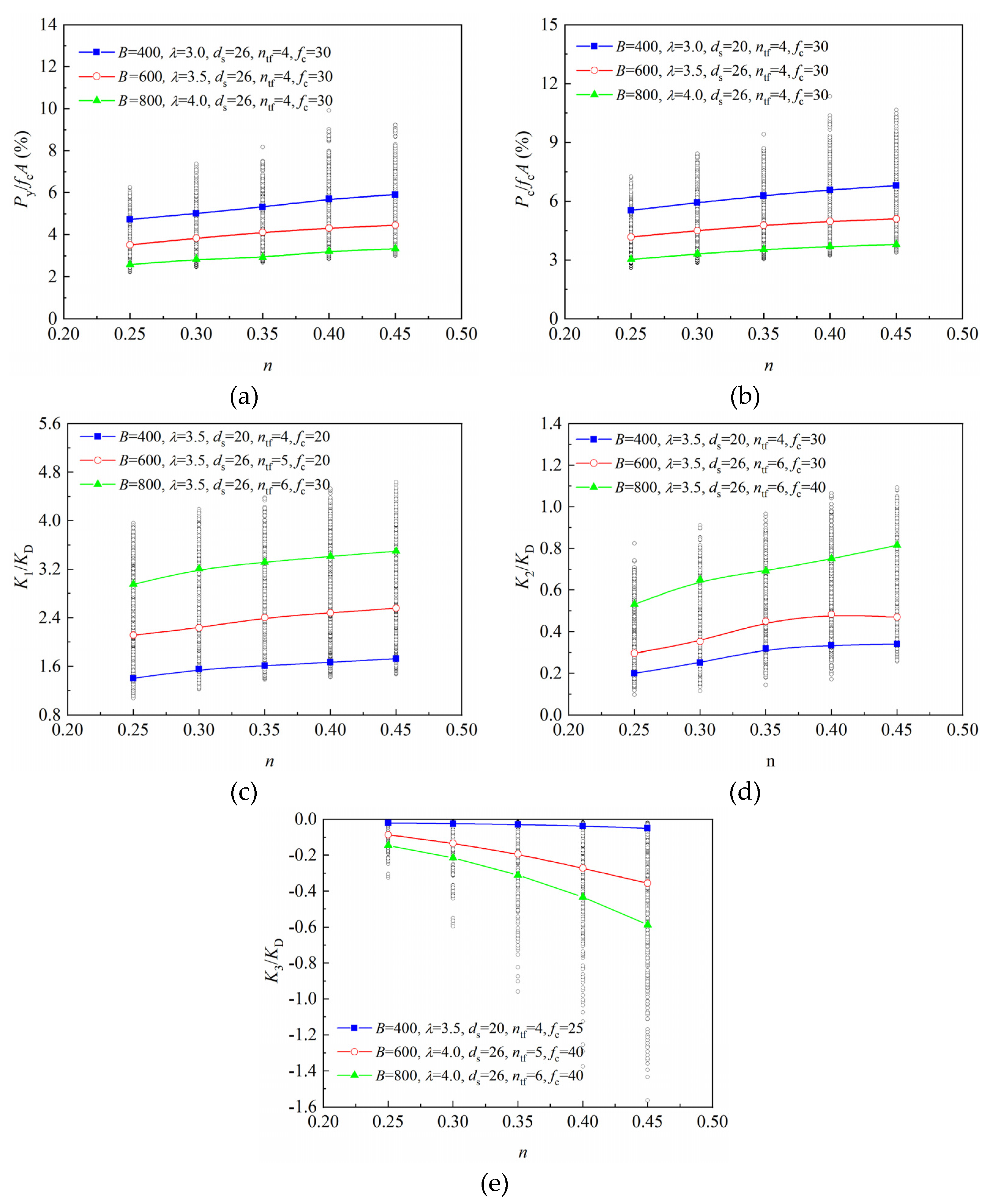
3.2.1. Influence of Axial Compression Ratio
- (1)
- The yield load of FRP-retrofitted square RC columns shows an overall linear increase with the increase in axial compression ratio;
- (2)
- The peak load of the columns tends to increase with the axial compression ratio, and it exhibits a good linear relationship with it;
- (3)
- The elastic stiffness K1 exhibits an approximately linear increase with the rise of the axial compression ratio;
- (4)
- The elastoplastic stiffness K2 demonstrates an overall linear or piecewise linear increase with the axial compression ratio;
- (5)
- The absolute values of the descent stiffness increase with the axial pressure ratio, indicating that the descent stage of the load–displacement curve becomes steeper and ductility decreases. While the descent stiffness exhibits a certain degree of nonlinearity with the axial compression ratio, it can be considered piecewise linear.
3.2.2. Influence of Shear/Span Ratio
- (1)
- There is a strong linear relationship between the shear/span ratio and the yield load, with the yield load decreasing linearly as the shear/span ratio increases;
- (2)
- The peak load capacity also tends to decrease with the increase in the shear/span ratio, and there is a good linear relationship between them;
- (3)
- The elastic stiffness K1 exhibits a clear linear increase with the shear/span ratio;
- (4)
- The elastoplastic stiffness K2 shows some nonlinearity with the shear/span ratio, but the overall trend can be approximated as being linear;
- (5)
- The descent stiffness K3 shows a more obvious linear decreasing trend with the increase in the shear/span ratio.
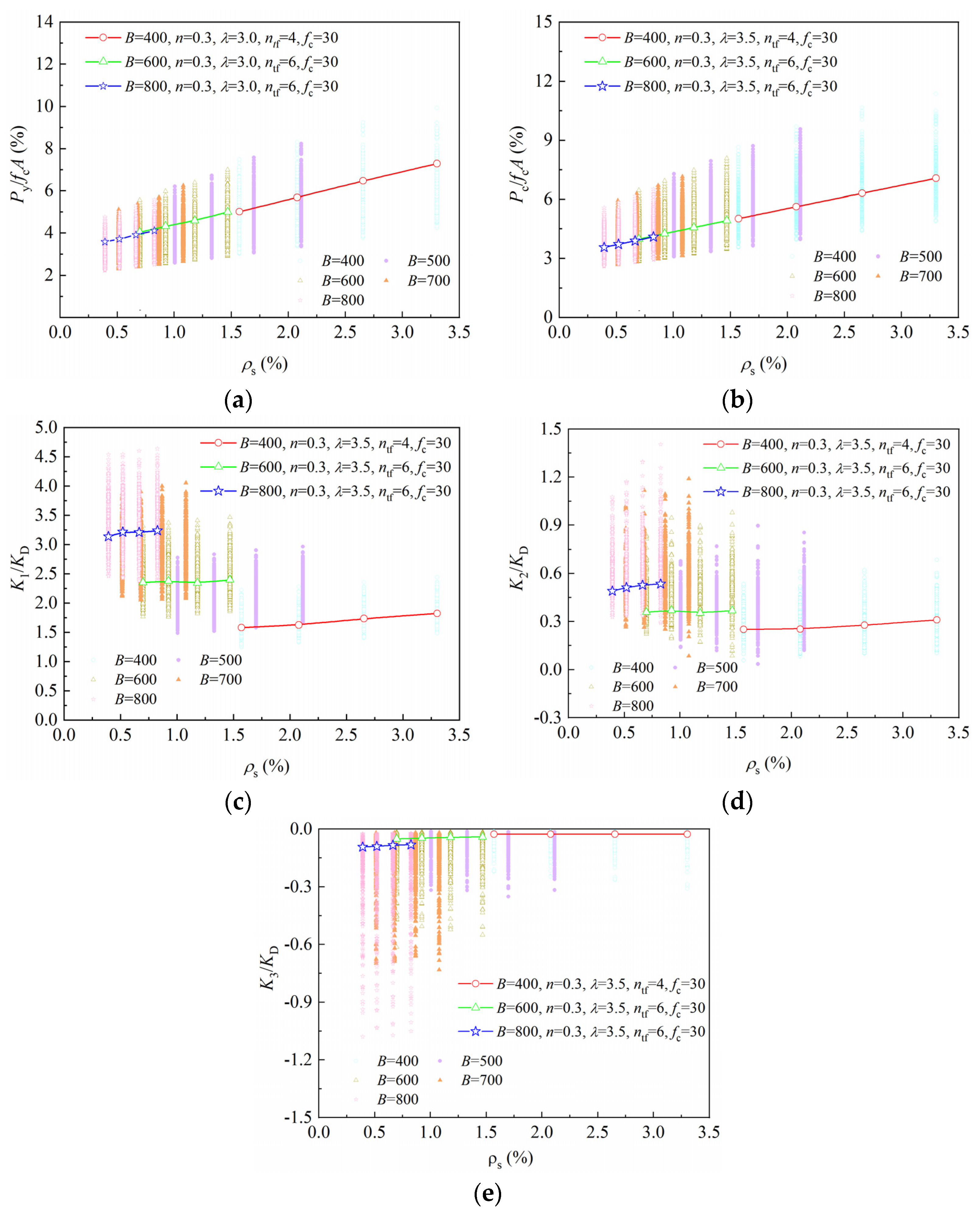
3.2.3. Influence of Steel Reinforcement Ratio
- (1)
- The yield load exhibits an overall linear increase with the reinforcement ratio. For columns with section sizes of 400 mm and 600 mm under identical conditions, the yield load increases linearly with the reinforcement ratio. When the reinforcement ratio is approximately equal (1.5%), the normalized yield load is also similar, indicating a continuous linear relationship between the reinforcement ratio and yield load, with minimal size effect on the normalized yield load. This is consistent with the test results provided in [17].
- (2)
- The influence of the reinforcement ratio on peak load is similar to yield load, with a linear relationship between peak load and the reinforcement ratio. For columns with section sizes of 400 mm and 600 mm under identical conditions, the peak load increases continuously and linearly with the reinforcement ratio.
- (3)
- For square RC columns with the same section size, the elastic stiffness increases linearly with the reinforcement ratio. When comparing columns with different section sizes (400 mm and 600 mm) but similar axial compression ratio, shear/span ratio, and confinement ratio, the normalized elastic stiffness differs when the reinforcement ratio is equal (1.5%). Larger cross-sectional sizes result in higher normalized elastic stiffness, indicating a significant size effect on normalized elastic stiffness. This differs from the influence of the reinforcement ratio on the yield and peak loads.
- (4)
- The elastoplastic stiffness also exhibits a linear relationship with the reinforcement ratio. When the reinforcement ratio reaches a certain level, this relationship approximates a horizontal line, indicating the minimal impact of the reinforcement ratio on elastoplastic stiffness at higher levels. A significant size effect on elastoplastic stiffness is also observed.
- (5)
- The descent stiffness shows an approximate horizontal linear relationship with the reinforcement ratio, indicating the minimal impact of reinforcement ratio variations on descent stiffness. However, the size effect also has a slight impact on descent stiffness.
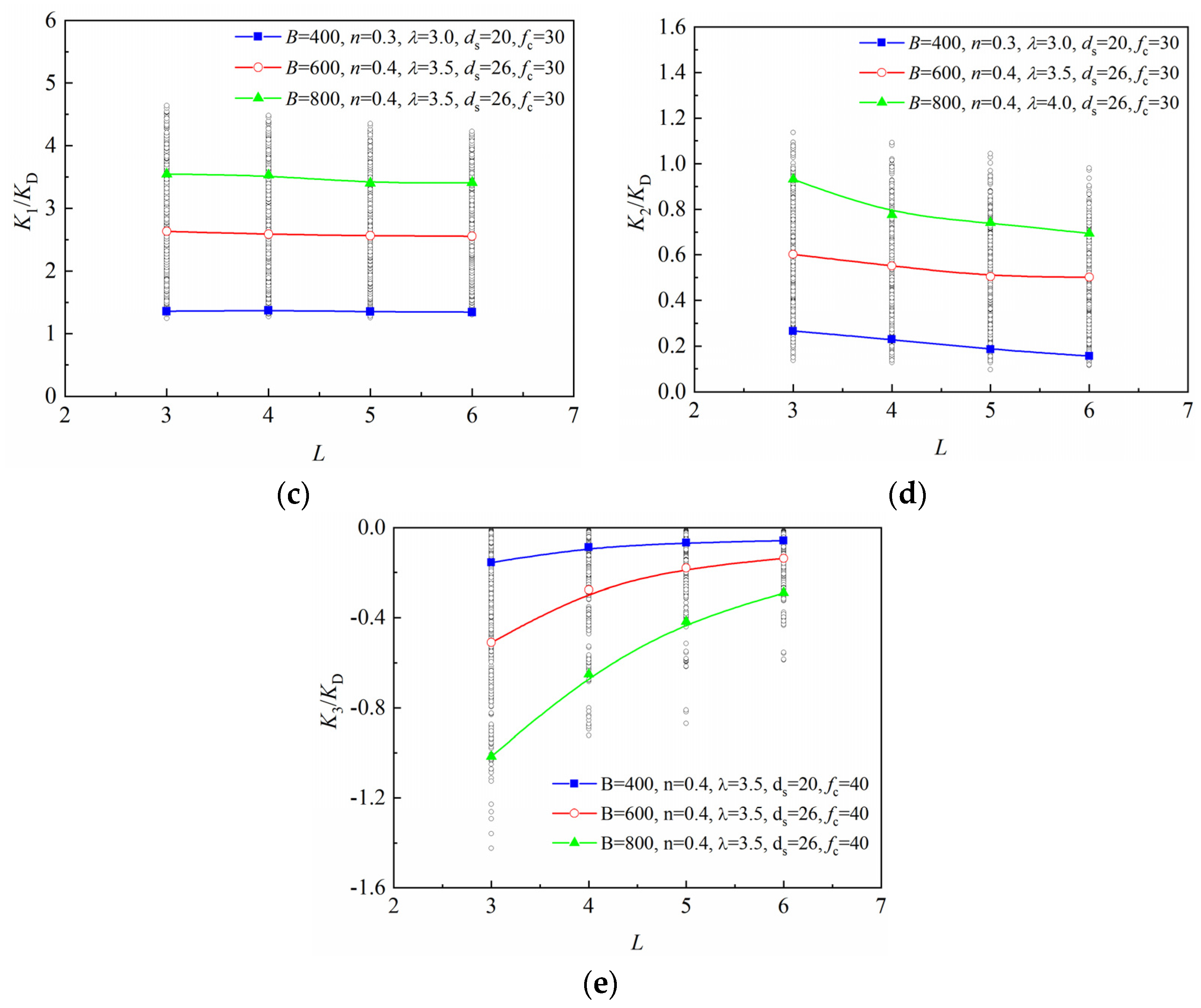
3.2.4. Influence of Number of Layers of FRP Wrap
- (1)
- The yield load exhibits a nearly horizontal linear relationship with the number of layers of FRP wrap. As the number of layers increases, the yield load of the retrofitted column increases slightly, indicating a minimal impact of FRP layers on yield load.
- (2)
- Similar to yield load, the peak load has a good linear relationship with the number of layers of FRP wrap. However, the impact is minimal, with peak load increasing slowly and linearly as the number of layers of FRP wrap increases.
- (3)
- The number of layers of FRP wrap has a minimal impact on elastic stiffness, similar to yield load. As the number of layers of FRP wrap increases, the normalized elastic stiffness of the retrofitted column remains nearly constant, indicating that FRP wrapping has minimal effect on elastic stiffness.
- (4)
- The elastoplastic stiffness of the retrofitted column decreases approximately linearly with an increase in the number of layers of FRP wrap. This indicates that more FRP layers result in a flatter elastoplastic stage of the load–displacement skeleton curve. Consequently, the peak displacement increases without significant changes in peak load, improving the ductility of columns.
- (5)
- The absolute value of the descent stiffness decreases nonlinearly with an increase in the number of layers of FRP wrap, following a quadratic nonlinear relationship by regression analysis. This trend suggests that with more FRP layers, the descent stage of the load–displacement skeleton curve becomes flatter, resulting in larger ultimate displacement and improved ductility. The nonlinear correlation indicates that beyond a certain number of layers of FRP wrap, the improvement in ductility becomes less significant with additional layers.
3.2.5. Influence of Concrete Strength
- (1)
- As concrete strength increases, the yield load of the retrofitted column generally decreases, exhibiting a slight nonlinear relationship. However, this nonlinearity is minimal and can be simplified to a linear or piecewise linear relationship.
- (2)
- Similar to the yield load, the peak load decreases in a slight nonlinearity as concrete strength increases. However, this relationship can generally be approximated by a linear or piecewise linear model.
- (3)
- The relationship between concrete strength and elastic stiffness is nearly linear. As concrete strength increases, the elastic stiffness shows a slight linear increase. However, the overall influence of concrete strength on elastic stiffness remains minimal.
- (4)
- The relationship between concrete strength and elastoplastic stiffness exhibits some nonlinearity, especially when the section size of a column is large and the number of layers of FRP wrap is low, resulting in weaker confinement. However, this relationship can be approximated by a piecewise linear correlation.
- (5)
- The absolute value of descent stiffness increases with concrete strength, indicating a decrease in column ductility. With other parameters constant and only concrete strength varying, descent stiffness shows a slight nonlinearity with concrete strength.
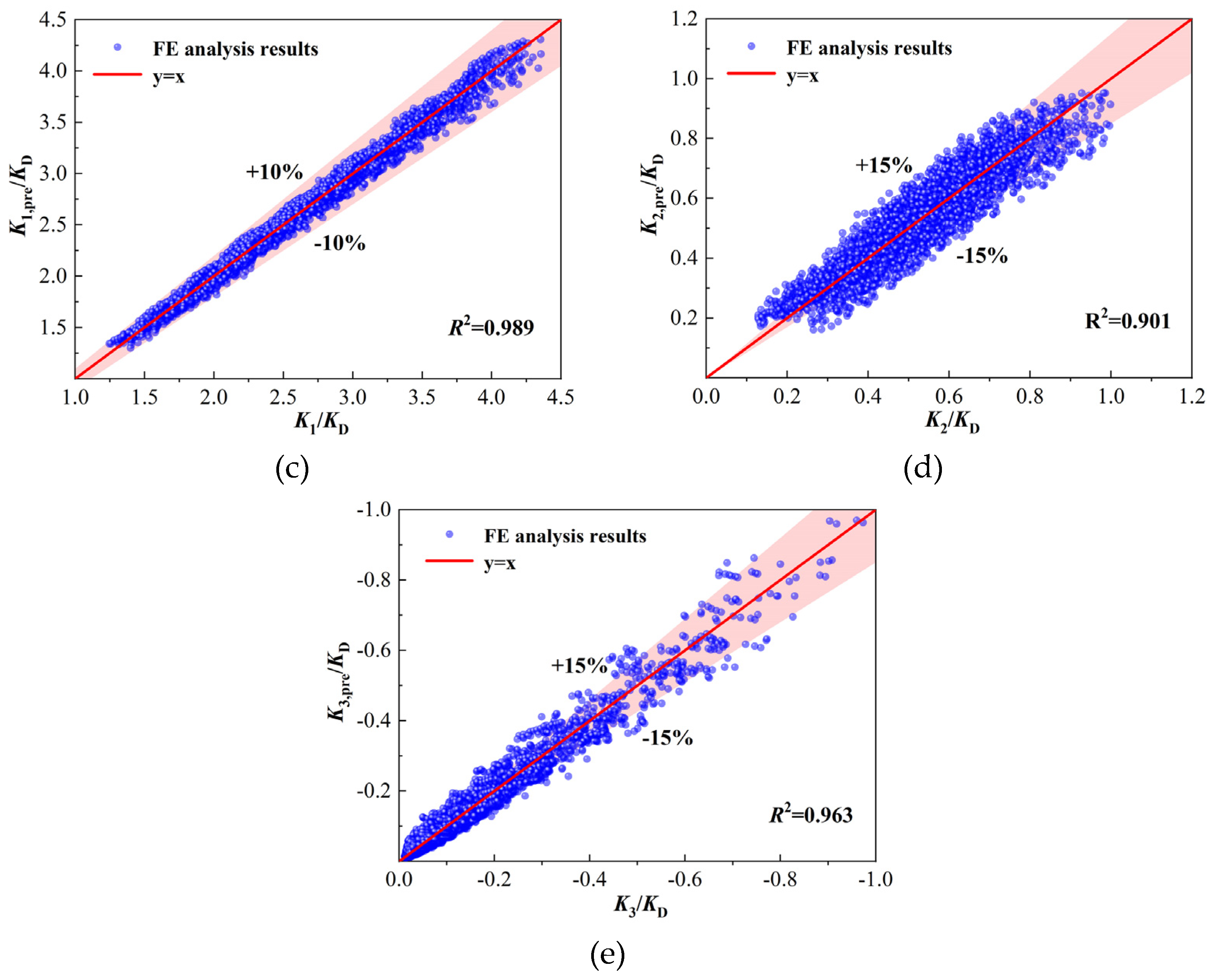
3.3. Calculation of Characteristic Point
3.3.1. Yield Load
3.3.2. Peak Load
3.3.3. Elastic Stiffness
3.3.4. Elastoplastic Stiffness
3.3.5. Descent Stiffness
3.4. Unloading/Reloading Hysteresis Rules
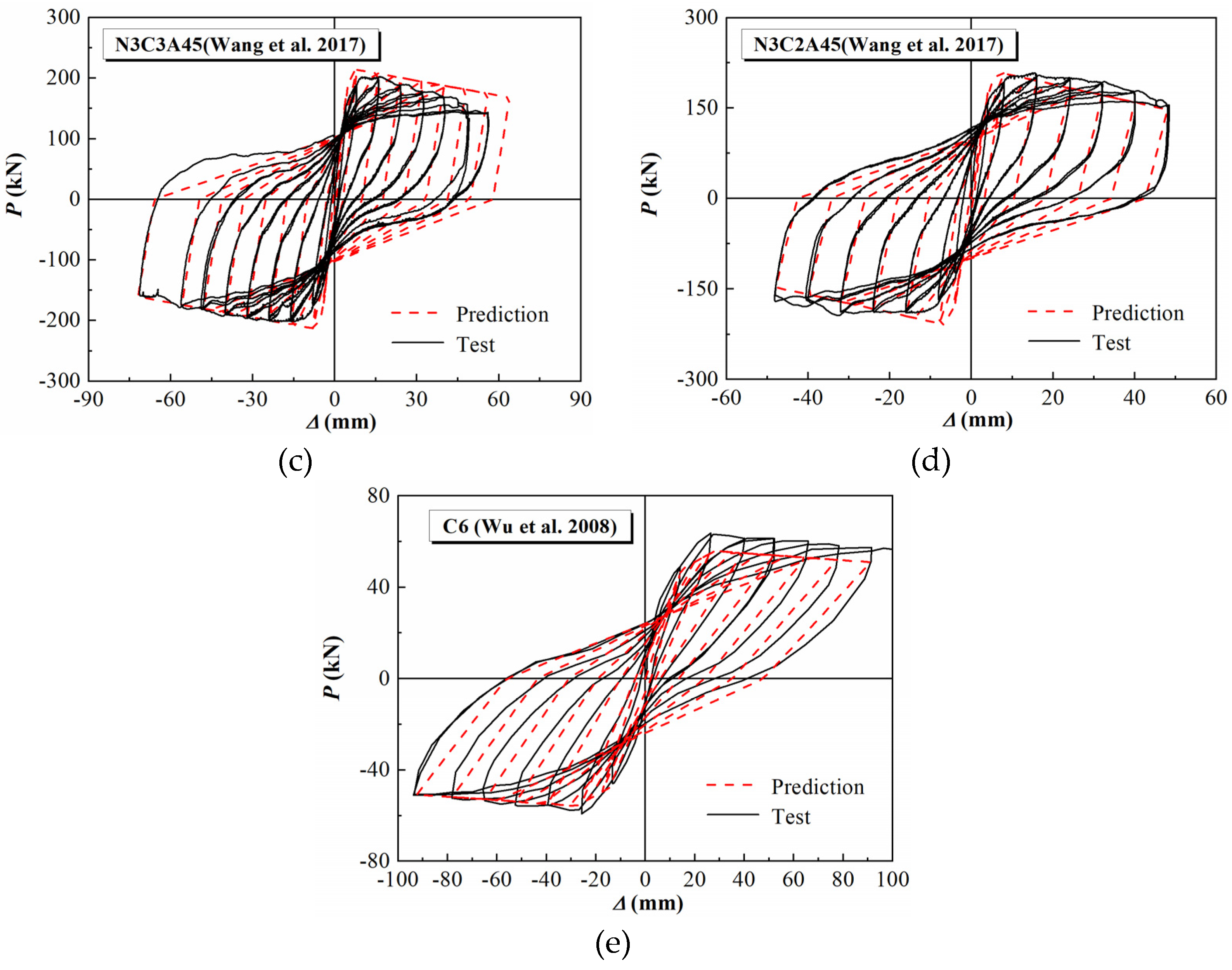
3.5. Validation of Lateral Force–Displacement Hysteretic Model
4. Conclusions
- (1)
- Based on the nonlinear beam–column element and a self-developed stress–strain model for FRP-confined concrete, the FE model for CFRP-retrofitted square RC columns was achieved using OpenSees software. The simulation results demonstrated good agreement with the test data, thereby validating the accuracy of the modeling method.
- (2)
- Parametric analysis was performed to investigate the effects of axial load ratio, shear/span ratio, reinforcement ratio, number of layers of FRP wrap, and concrete strength on the key characteristics of the force–displacement skeleton curve, including yield load, peak load, elastic stiffness, elastoplastic stiffness, and descent stiffness. The results show that, except for descent stiffness having a quadratic nonlinear relation with the number of FRP wrap layers, the other influencing parameters mainly have a linear relation with the parameters of the characteristic points of the skeleton curve.
- (3)
- The lateral load capacity of retrofitted columns increases with a higher axial load ratio and reinforcement ratio, while FRP confinement provides only a slight improvement. In contrast, increasing the shear/span ratio and concrete strength leads to a reduction in lateral load capacity.
- (4)
- The displacement of the retrofitted columns increases with the number of layers of FRP wrap but decreases with a higher axial load ratio, shear/span ratio, reinforcement ratio, and concrete strength, demonstrating that FRP confinement improves their ductility.
- (5)
- The trilinear load–displacement skeleton model was employed for CFRP-retrofitted square RC columns. Based on the regression analysis of the parameter analysis results, calculation models of yield load, peak load, elastic stiffness, elastoplastic stiffness, and descent stiffness for the skeleton model were developed.
- (6)
- A fixed-point directed hysteresis rule for FRP-retrofitted square RC columns was proposed, with both loading and unloading curves modeled as straight lines. By combining this hysteresis rule with the trilinear skeleton model, a load–displacement restoring force model for FRP-reinforced RC square columns was developed. This model’s predictions are in good overall agreement with test results, with all average load deviations falling within ±15%.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ali, O.; Abbas, A.; Khalil, E.; Madkour, H. Numerical investigation of FRP-confined short square RC columns. Constr. Build. Mater. 2021, 275, 122141. [Google Scholar] [CrossRef]
- Hao, M.; Chang, W.; Zheng, W. Hysteresis performance and restoring-force model of RC columns jacketed by octagonal and spiral stirrups. J. Build. Eng. 2024, 82, 108280. [Google Scholar] [CrossRef]
- Huang, Y.; Grünewald, S.; Schlangen, E.; Luković, M. Strengthening of concrete structures with ultra high performance fiber reinforced concrete (UHPFRC): A critical review. Constr. Build. Mater. 2022, 336, 127398. [Google Scholar] [CrossRef]
- Murugan, K.; Sengupta, A.K. Seismic performance of strengthened reinforced concrete columns. Structures 2020, 27, 487–505. [Google Scholar] [CrossRef]
- Parvin, A.; Brighton, D. FRP composites strengthening of concrete columns under various loading conditions. Polymers 2014, 6, 1040–1056. [Google Scholar] [CrossRef]
- Heydari, P.; Mostofinejad, D.; Mostafaei, H.; Ahmadi, H. Strengthening of deep RC coupling beams with FRP composites: A numerical study. Structures 2023, 51, 435–454. [Google Scholar] [CrossRef]
- Ali, O. Structural reliability of biaxial loaded short/slender-square FRP-confined RC columns. Constr. Build. Mater. 2017, 151, 370–382. [Google Scholar] [CrossRef]
- Chen, J.-F.; Smith, S.; Lam, L.; Teng, J.G. Behaviour and strength of FRP-strengthened RC structures: A state-of-the-art review. Proc. Inst. Civ. Eng.-Struct. Build. 2003, 156, 51–62. [Google Scholar] [CrossRef]
- Wu, Y.-F.; Wei, Y.-Y. Effect of cross-sectional aspect ratio on the strength of CFRP-confined rectangular concrete columns. Eng. Struct. 2010, 32, 32–45. [Google Scholar] [CrossRef]
- Xiao, Y. Applications of FRP composites in concrete columns. Adv. Struct. Eng. 2004, 7, 335–343. [Google Scholar] [CrossRef]
- Wang, W.; Sheikh, M.N.; Al-Baali, A.Q.; Hadi, M.N.S. Compressive behaviour of partially FRP confined concrete: Experimental observations and assessment of the stress-strain models. Constr. Build. Mater. 2018, 192, 785–797. [Google Scholar] [CrossRef]
- Harajli, M.H. Axial stress-strain relationship for FRP confined circular and rectangular concrete columns. Cem. Concr. Compos. 2006, 28, 938–948. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, D.; Smith, S.T.; Lu, D. CFRP-confined square RC columns. I: Experimental investigation. J. Compos. Constr. 2012, 16, 150–160. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, D.; Smith, S.T.; Lu, D. CFRP-confined square RC columns. II: Cyclic axial compression stress-strain model. J. Compos. Constr. 2012, 16, 161–170. [Google Scholar] [CrossRef]
- Memon, M.S.; Sheikh, S.A. Seismic resistance of square concrete columns retrofitted with glass fiber-reinforced polymer. Struct. J. 2005, 102, 774–783. [Google Scholar] [CrossRef]
- Ilki, A.; Demir, C.; Bedirhanoglu, I.; Kumbasar, N. Seismic retrofit of brittle and low strength RC columns using fiber reinforced polymer and cementitious composites. Adv. Struct. Eng. 2009, 12, 325–347. [Google Scholar] [CrossRef]
- Wang, D.; Huang, L.; Yu, T.; Wang, Z. Seismic performance of CFRP-retrofitted large-scale square RC columns with high axial compression ratios. J. Compos. Constr. 2017, 21, 04017031. [Google Scholar] [CrossRef]
- Peng, S.; Xiong, Z.; Zeng, X. A restoring force model for CFRP seismic-damaged RACFST columns: Theoretical, experimental, and simulation analysis. Structures 2022, 40, 273–283. [Google Scholar] [CrossRef]
- Lu, X.; Yin, X.; Jiang, H. Restoring force model for steel reinforced concrete columns with high steel ratio. Struct. Concr. 2013, 14, 415–422. [Google Scholar] [CrossRef]
- Shao, Y.; Aval, S.; Mirmiran, A. Fiber-element model for cyclic analysis of concrete-filled fiber reinforced polymer tubes. J. Struct. Eng. 2005, 131, 292–303. [Google Scholar] [CrossRef]
- Zhu, Z.; Ahmad, I.; Mirmiran, A. Fiber element modeling for seismic performance of bridge columns made of concrete-filled FRP tubes. Eng. Struct. 2006, 28, 2023–2035. [Google Scholar] [CrossRef]
- Mazzoni, S.; McKenna, F.; Scott, M.H.; Fenves, G.L. OpenSees Command Language Manual; Pacific Earthquake Engineering Research Centre, University of California: Berkeley, CA, USA, 2006. [Google Scholar]
- Samaan, M.; Mirmiran, A.; Shahawy, M. Model of concrete confined by fiber composites. J. Struct. Eng. 1998, 124, 1025–1031. [Google Scholar] [CrossRef]
- Liu, H.; He, M.; Luan, Y.; Guo, J.; Liu, L. A modified constitutive model for FRP confined concrete in circular sections and its implementation with OpenSees programming. J. Zhejiang Univ. Sci. A 2013, 14, 856–866. [Google Scholar] [CrossRef]
- Lam, L.; Teng, J.G. Design-oriented stress-strain model for FRP-confined concrete. Constr. Build. Mater. 2003, 17, 471–489. [Google Scholar] [CrossRef]
- Teng, J.G.; Jiang, T.; Lam, L.; Luo, Y.Z. Refinement of a design-oriented stress–strain model for FRP-confined concrete. J. Compos. Constr. 2009, 13, 269–278. [Google Scholar] [CrossRef]
- Teng, J.G.; Lam, L.; Lin, G.; Lu, J.Y.; Xiao, Q.G. Numerical simulation of FRP-jacketed RC columns subjected to cyclic and seismic loading. J. Compos. Constr. 2016, 20, 04015021. [Google Scholar] [CrossRef]
- Menegotto, M.; Pinto, P.E. Method of analysis for cyclically loaded reinforced concrete plane frames including changes in geometry and nonelastic behavior of elements under combined normal force and bending. In Proceedings of the IABSE Symposium on the Resistance and Ultimate Deformability of Structures Acted on by Well Defined Repeated Loads, Lisbon, Portugal, 13–14 September 1973; International Association for Bridge and Structural Engineering (IABSE): Zurich, Switzerland; pp. 15–22. [Google Scholar]
- Scott, B.D.; Park, R.; Priestley, M.J.N. Stress-strain behavior of concrete confined by overlapping hoops at low and high strain rates. ACI J. Proc. 1982, 79, 13–27. [Google Scholar] [CrossRef]
- Guo, Z.H.; Zhang, X.Q.; Zhang, D.C.; Wang, R.Q. Experimental investigation of the complete stress-strain curve of concrete. J. Build. Struct. 1982, 3, 1–12. (In Chinese) [Google Scholar]
- Yang, H.; Xu, H.; Wang, Z. Seismic responses analysis of RC frame based on fiber model considering bar slippage at column bottom section. J. Build. Struct. 2009, 30, 130–137. (In Chinese) [Google Scholar]
- Wang, D. Axial constitutive relationship and seismic performance of FRP confined column. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2008. [Google Scholar]
- Wu, Y.-F.; Liu, T.; Wang, L. Experimental investigation on seismic retrofitting of square RC columns by carbon FRP sheet confinement combined with transverse short glass FRP bars in bored holes. J. Compos. Constr. 2008, 12, 53–60. [Google Scholar] [CrossRef]
- Kunnath, S.K.; Reinhorn, A.M.; Park, Y.J. Analytical modeling of inelastic seismic response of R/C structures. J. Struct. Eng. 1990, 116, 996–1017. [Google Scholar] [CrossRef]
- Ozcan, O.; Binici, B.; Ozcebe, G. Improving seismic performance of deficient reinforced concrete columns using carbon fiber-reinforced polymers. Eng. Struct. 2008, 30, 1632–1646. [Google Scholar] [CrossRef]
- Cai, Z.; Wang, D.; Smith, S.T.; Wang, Z. Experimental investigation on the seismic performance of GFRP-wrapped thin-walled steel tube confined RC columns. Eng. Struct. 2016, 110, 269–280. [Google Scholar] [CrossRef]
- Dai, K.; Yu, X.; Jiang, Z.; Wang, D.; Qian, K. Hysteretic model for corroded reinforced concrete columns retrofitted with FRP. Constr. Build. Mater. 2023, 380, 131207. [Google Scholar] [CrossRef]
- Pessiki, S.; Harries, K.A.; Kestner, J.T.; Sause, R.; Ricles, J.M. Axial behavior of reinforced concrete columns confined with FRP jackets. J. Compos. Constr. 2001, 5, 237–245. [Google Scholar] [CrossRef]
- Wang, D.Y.; Wang, Z.Y.; Smith, S.T.; Yu, T. Size effect on axial stress-strain behavior of CFRP-confined square concrete columns. Constr. Build. Mater. 2016, 118, 116–126. [Google Scholar] [CrossRef]
- Du, Y.; Zhang, Y.; Chen, Z.; Dong, S.; Deng, X.; Qian, K. Seismic behavior of CFRP confined rectangular CFST columns using high-strength materials: Numerical analysis and restoring force model. Structures 2021, 34, 4237–4253. [Google Scholar] [CrossRef]
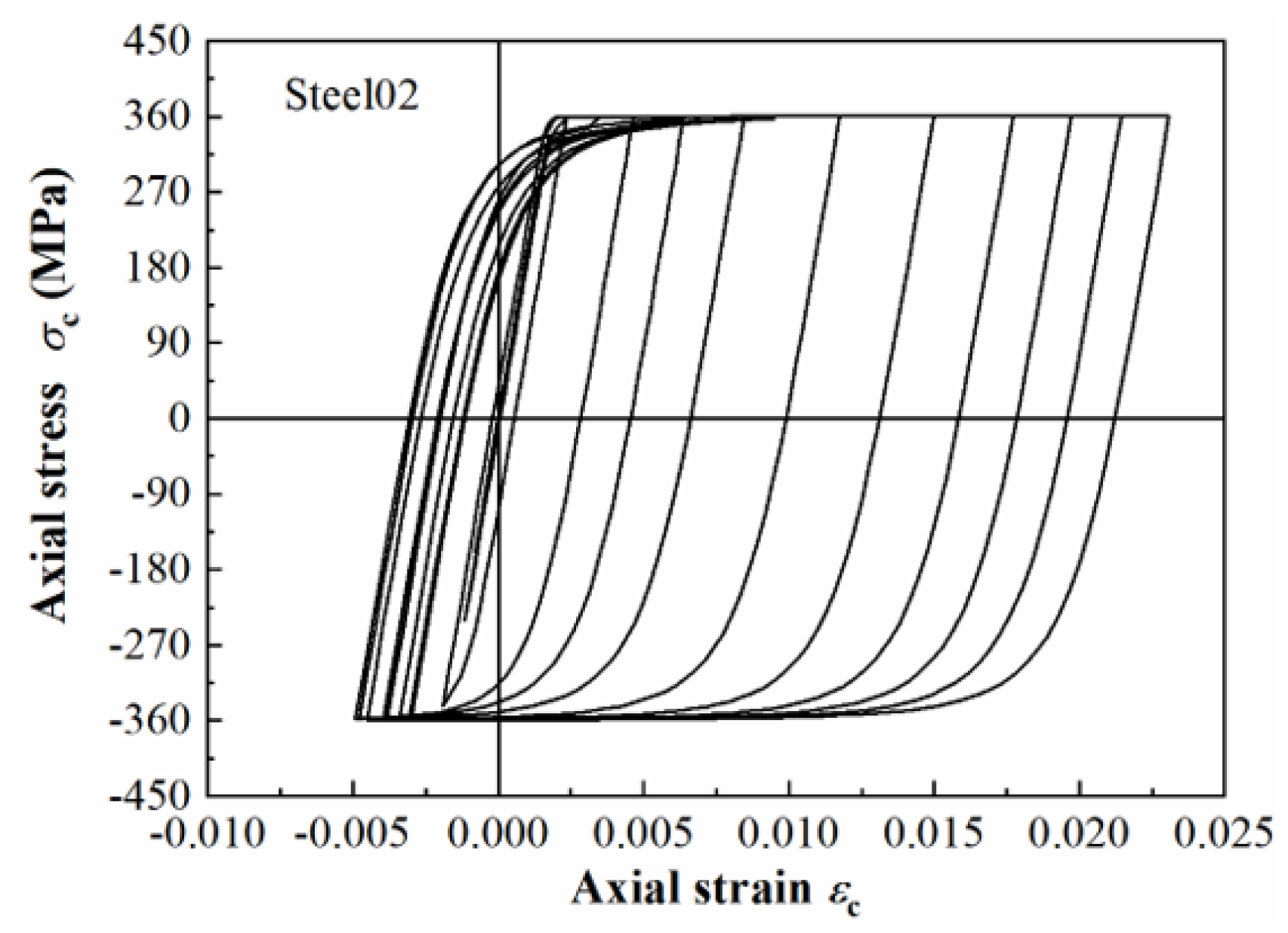
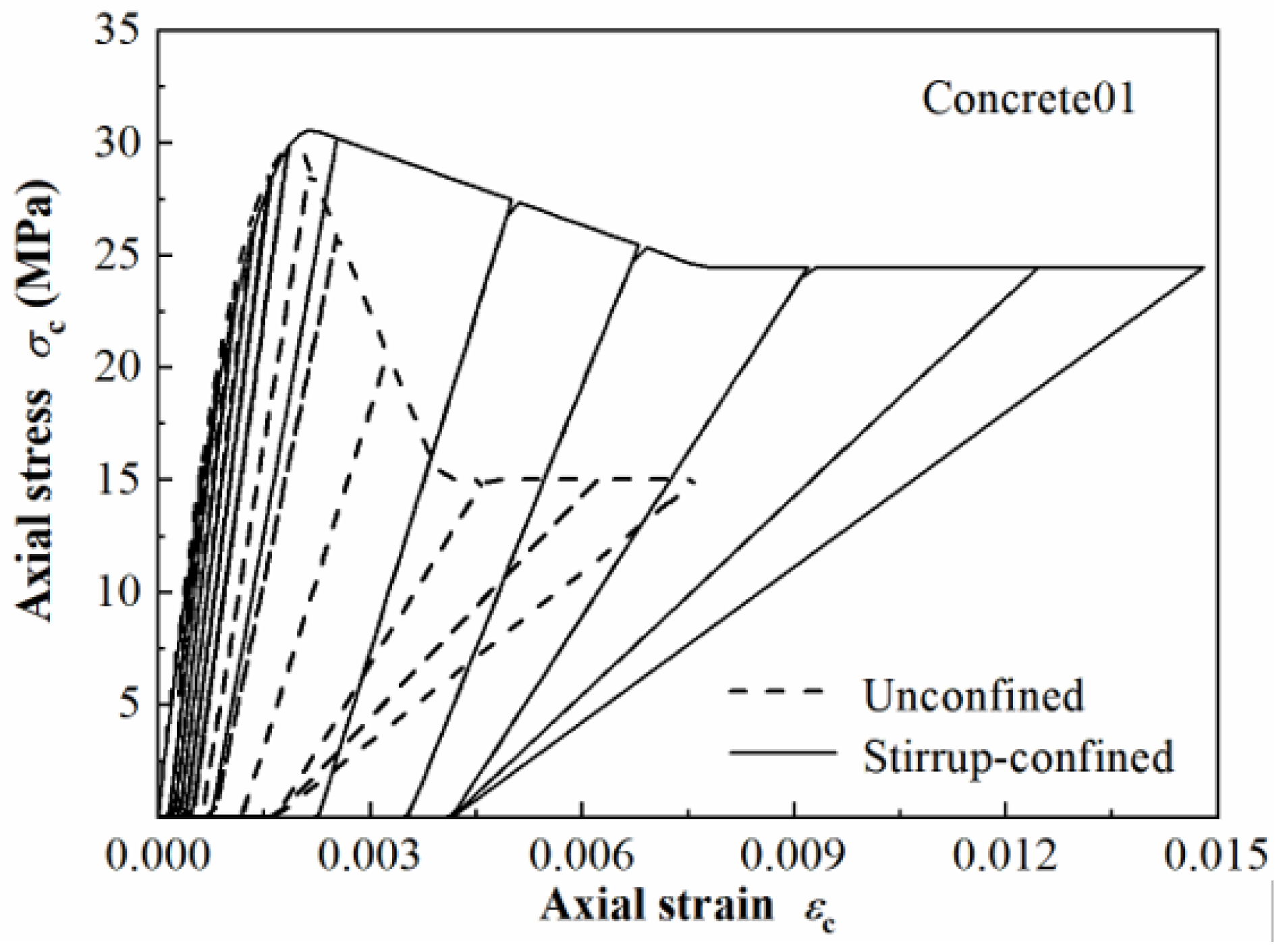
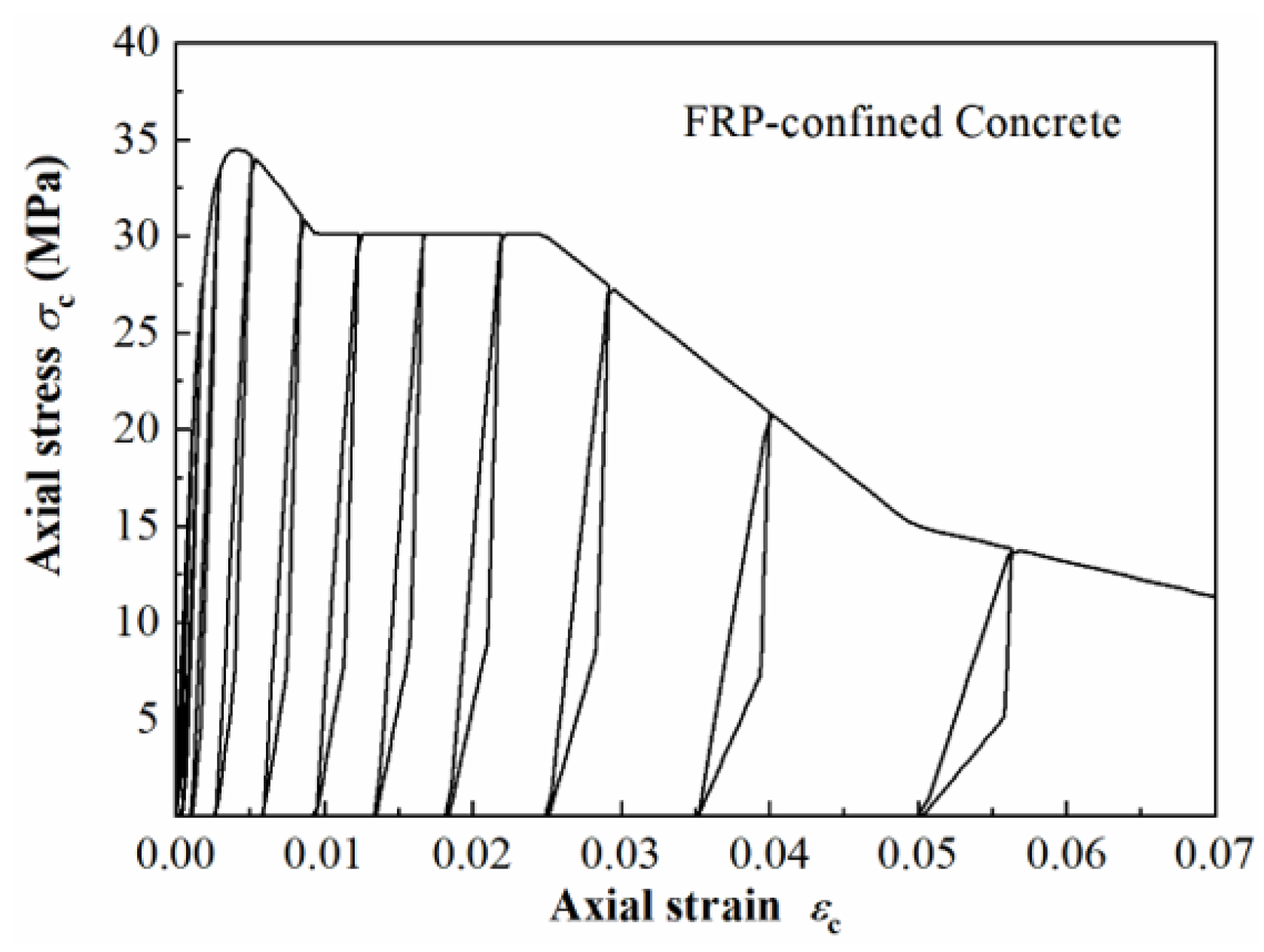
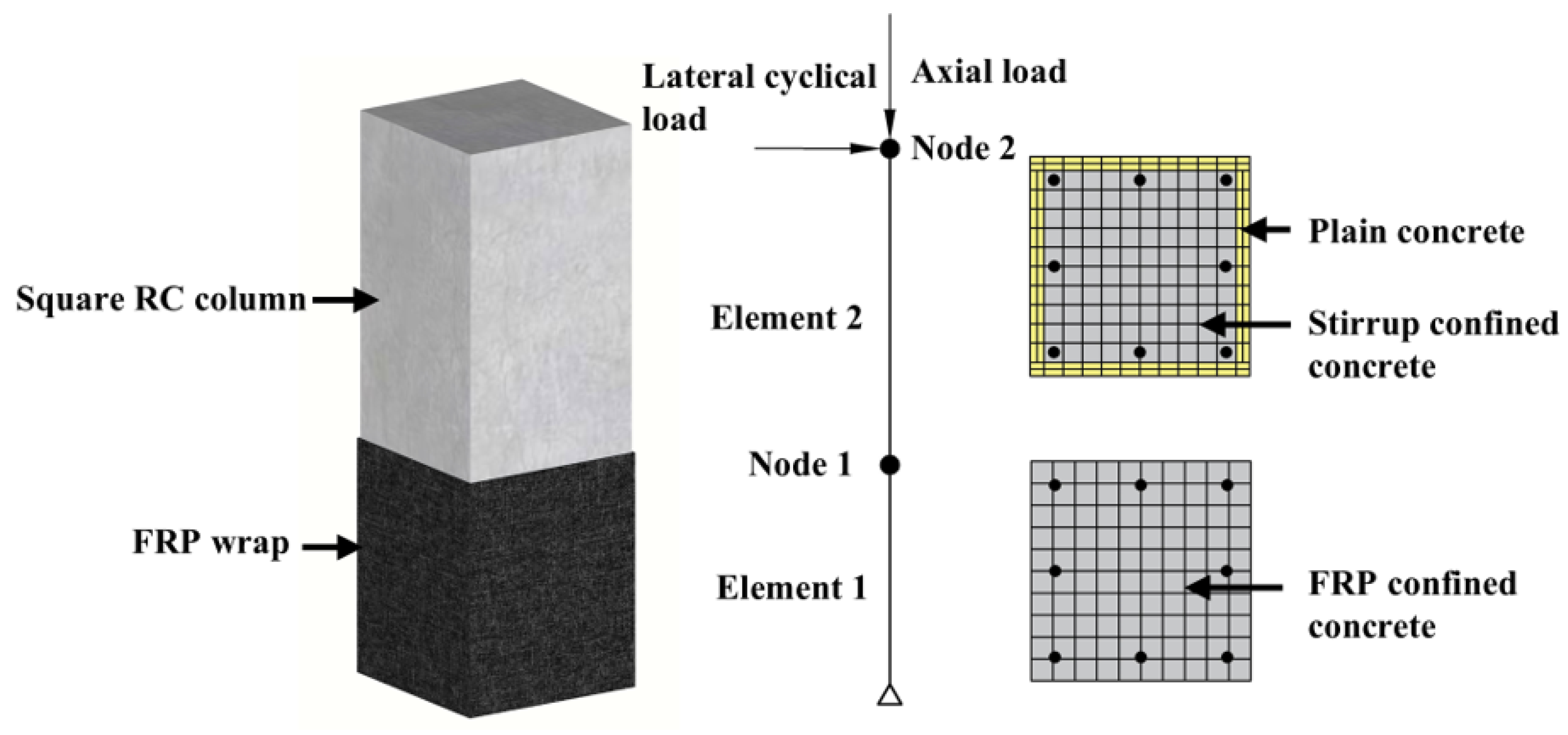








| Parameters | Strain-Hardening Ratio (b) | R0 | CR1 | CR2 |
|---|---|---|---|---|
| Parameter values | 0.0085 | 20 | 0.925 | 0.15 |
| Parameters | Equation |
|---|---|
| Peak point stress (fcc) | fcc = fc0 (1 + 0.5λt) |
| Peak point strain (εcc) | εcc = εc0 (1 + 2.5λt) |
| Ultimate point stress (fcu) | fcu = 0.8 fcc |
| Ultimate point stress (εcu) | εcu = 3.5 εcc |
| Parameters | Equation |
|---|---|
| Peak point stress (fcc) | fcc = fc0(1 + 0.35λf + 0.5λh + 0.85λl) |
| Peak point strain (εcc) | εcc = εc0(1 + 2.0λf + 2.5λh) |
| Ultimate point stress (fcu) | |
| Ultimate point stress (εcu) |
| Specimen Labels | Py,exp (kN) | Pc,exp (kN) | Py (kN) | Pc (kN) | Py/Py,exp | Pc/Pc,exp |
|---|---|---|---|---|---|---|
| S4C0A45 [32] | 292.4 | 346.9 | 263.9 | 307.65 | 0.90 | 0.89 |
| N4C3A45 [32] | 296.7 | 358.1 | 296.4 | 344.1 | 1.00 | 0.96 |
| N4C4A45 [32] | 333.8 | 383.9 | 305.1 | 353.95 | 0.91 | 0.92 |
| N3C2A45 [32] | 169.05 | 201.25 | 188.85 | 216.3 | 1.12 | 1.07 |
| N3C3A45 [32] | 172 | 202.1 | 197.1 | 225.25 | 1.15 | 1.11 |
| C6 [33] | 52 | 61.5 | 59.1 | 67.4 | 1.14 | 1.10 |
| Parameters | Parameter Variation |
|---|---|
| Section size B (mm) | 400, 500, 600, 700, 800 |
| Axial compression ratio n | 0.25, 0.3, 0.35, 0.4, 0.45 |
| Shear/span ratio λ | 3.0, 3.5, 4.0 |
| Layers of FRP wrap L | 3, 4, 5, 6 |
| Concrete strength (MPa) | 20, 25, 30, 35, 40 |
| Diameter of longitudinal bar (mm) | 20, 23, 26, 29 |
| Parameters | a0 | a1 | a2 | a3 | a4 | a5 | a6 | a7 | a8 | Comment |
|---|---|---|---|---|---|---|---|---|---|---|
| Py | −0.05 | 0.17 | 0.53 | 2.54 | 4.72 | 1.51 | - | - | - | - |
| Pc | −0.17 | 0.55 | 2.30 | 8.50 | 17.50 | 6.48 | - | - | - | - |
| K1 | 0.27 | 0.13 | 2.50 | 0.16 | 0.13 | −0.24 | 0.06 | −0.09 | - | - |
| K2 | 0.10 | −1.00 | 2.50 | 0.04 | 0.28 | −0.11 | 0.07 | −0.32 | - | n ≤ 0.35 |
| 0.15 | −0.10 | 0.45 | 0.32 | 0.53 | −0.57 | 0.39 | −1.17 | - | n > 0.35 | |
| K3 | −0.50 | 32.37 | −6.62 | 1.20 | −1.53 | −0.05 | 10.95 | −33.59 | −5.46 | - |
| Specimen Labels | Py,exp (kN) | Pc,exp (kN) | Py (kN) | Pc (kN) | Py/Py,exp | Pc/Pc,exp |
|---|---|---|---|---|---|---|
| N4C3A45 [32] | 296.7 | 358.1 | 318.1 | 348.8 | 1.07 | 0.97 |
| N4C4A45 [32] | 333.8 | 383.9 | 322.1 | 354.2 | 0.96 | 0.92 |
| N3C3A45 [32] | 172 | 202.1 | 194.4 | 213.9 | 1.13 | 1.06 |
| N3C2A45 [32] | 169.05 | 201.25 | 190.6 | 208.9 | 1.13 | 1.04 |
| C6 [33] | 52 | 61.5 | 47.88 | 55.85 | 0.92 | 0.91 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Zhang, M.; Zhou, F.; Wang, D. Lateral Force–Displacement Hysteretic Model for CFRP (Carbon Fiber-Reinforced Polymer)-Retrofitted Square RC Columns. Buildings 2025, 15, 1523. https://doi.org/10.3390/buildings15091523
Wang H, Zhang M, Zhou F, Wang D. Lateral Force–Displacement Hysteretic Model for CFRP (Carbon Fiber-Reinforced Polymer)-Retrofitted Square RC Columns. Buildings. 2025; 15(9):1523. https://doi.org/10.3390/buildings15091523
Chicago/Turabian StyleWang, Haoxiang, Mengjie Zhang, Fengjun Zhou, and Daiyu Wang. 2025. "Lateral Force–Displacement Hysteretic Model for CFRP (Carbon Fiber-Reinforced Polymer)-Retrofitted Square RC Columns" Buildings 15, no. 9: 1523. https://doi.org/10.3390/buildings15091523
APA StyleWang, H., Zhang, M., Zhou, F., & Wang, D. (2025). Lateral Force–Displacement Hysteretic Model for CFRP (Carbon Fiber-Reinforced Polymer)-Retrofitted Square RC Columns. Buildings, 15(9), 1523. https://doi.org/10.3390/buildings15091523






