Abstract
In practical engineering, uncertainties inevitably exist in the models and measurement data used for structures. Therefore, a statistical strategy related to damage detection methods become crucial. In this paper, a probabilistic statistical damage detection method for FG Euler–Bernoulli beam structures is proposed, extending the approach originally developed for isotropic materials. Our approach determines the probability of damage occurrence for each element, which aids in evaluating whether beam structures have been damaged. This evaluation is based on integrating the sensitivity of modal strain energy for each element with the perturbation method. To demonstrate the effectiveness and accuracy of the proposed method, several numerical examples are investigated. These examples include a simply supported FG Euler–Bernoulli beam subjected to both single and multiple element damages. The influence of gradient index, damage severity, boundary condition, and noise level on the accuracy of detection are also considered. The studies demonstrate that the probability of damage for each element remains relatively stable despite variations in the gradient indices. For the damaged elements, these probabilities approach 1, indicating that the proposed method effectively identifies damage in FG beams even when the gradient index varies. Additionally, as the level of damage increases, the accuracy of damage detection tends to improve. However, varying boundary conditions can substantially affect the outcomes of damage identification, potentially leading to inconsistencies in results. Furthermore, our proposed method demonstrates excellent resistance against noise levels of up to 5%. We also found that different boundary conditions have a great impact on the damage detection.
1. Introduction
Functionally graded materials (FGMs), which belong to a category of composite materials, were initially developed to meet the demands of thermal barrier materials [1]. Comprehensive reviews in terms of properties of FGMs can be observed from Naebe M. et al. [2] and Yu X. et al. [3] In contrast to conventional composites, FGMs exhibit a continuous gradient in microstructure and mechanical properties. This characteristic endows them with exceptional abilities to resist deformation and enhance toughness under extreme mechanical and thermal conditions [4]. Thus, functionally graded materials (FGMs) have garnered significant interest and undergone swift advancements over the past ten years. Currently, a variety of structural components produced using FGMs are employed in numerous fields, including aerospace, bioengineering, nuclear industries, and civil construction, among others [5,6]. As one of the most representative and fundamental structures of FGMs, a significant number of investigations have been performed on functionally graded (FG) Euler–Bernoulli beams under different conditions. The influence of material properties on the mechanical performances of FGMs have been investigated. For instance, the static and dynamic modeling of functionally graded Euler–Bernoulli microbeams, as investigated by Dinachandra, provides significant insights into their mechanical behavior [7], the mechanical characteristics of microstructure-dependent FG-MEE composite beams studied by Zhang et al. [8,9,10], the free vibration characteristics of the rectangle [11], tapered [12] Euler–Bernoulli functionally graded beams, or Timoshenko functionally graded beams [13]. The aforementioned theoretical research has significantly contributed to enhancing the understanding of the mechanical properties of functionally graded materials among researchers and practitioners.
Nevertheless, in practical engineering scenarios, FG Euler–Bernoulli beams might experience some degree of damage while being utilized [14]. Thus, improving the safety of functionally graded (FG) beams in practical applications requires critical research on damage identification, particularly when the damage is minimal [15]. Over the past few years, there has been growing interest in damage detection techniques that rely on vibration characteristics, as these are considered among the most efficient technologies available [16,17]. The primary concern is a dynamic characteristic index that exhibits sensitivity to the target structures both before and after the occurrence of damage [18,19]. Some dynamic parameters, such as frequencies, mode shapes or modal strain energy, are frequently employed in various analyses [20,21]. Especially, the modal identification of structures can be fully automated through ensemble learning, which offers even more advantages [22]. Among the aforementioned damage indexes, modal strain energy (MSE) has been widely adopted [23,24,25], due to their high sensitivity to damage and superior resistance to noise. Additionally, numerous researchers have shown that approaches based on MSE possess a strong capability to accurately identify the location or extent of damage. Seyedpoor [26] introduced a two-step approach for identifying structural damage, which utilizes a modal strain energy-based indicator and intelligent method. Subsequently, Alavinezhad [27] presented a new approach for identifying structural damage in offshore bridges based on this indicator. To further enhance the efficiency of damage detection, Yan et al. [28,29] proposed an effective approach utilizing element modal strain energy sensitivity (EMSES) for identifying structural damage in homogeneous materials. The findings indicate that this method provides a reliable means to determine both the location and severity of damage in beam-like structures. Further, to detect the damage of the beams whose material properties vary continuously along the axial direction, Lu [30] presented a finite element model updating method based on sensitivity. More recently, Yang [14] applied an EMSES method, originally used for detecting damage in isotropic materials, to identify damage in FG Euler–Bernoulli beams. The findings indicate that this approach exhibits exceptionally high performance.
In practical engineering, the models and measurement data used inevitably have different degrees of uncertainty. As a result, significant uncertainties may arise when detecting damage in functionally graded structures. These uncertainties can cause discrepancies between the identified damage and the actual damage, leading to missed detections and incorrect judgments. Thus, it is crucial to adopt a statistical approach to damage detection. It is well understood that statistical approaches are capable of efficiently handling uncertain issues. Currently, it has been applied to address damage detection issues in homogeneous beam structures [31]. In contrast to the deterministic damage detections means, this approach can effectively capture the uncertainties involved in damage detections. This enables a more thorough resolution of the issues affecting the damage detections outcomes, thereby enhancing the reliability of these results.
Despite the successful application of the statistical structural damage identification method for homogeneous materials, as far as we know, it still needs to be confirmed whether it is applicable to FG Euler–Bernoulli beams. On the other hand, it should be compared with the deterministic damage identification methods such as Yang’s [14]. Therefore, the study on this topic in necessary to be carried out. In this paper, a statistical structural damage detection method for FG Euler–Bernoulli beams based on element modal strain energy sensitivity and perturbation method is proposed. By considering the structural parameters (primarily stiffness parameters) as random variables, the perturbation method is employed to derive the mean and variance of the stiffness parameters for damaged structural elements. Subsequently, the probability distribution in terms of the variables for both damaged and healthy elements are obtained. Combined with the probability distribution of the stiffness parameters for the health elements, the structural damage probability can be determined. This provides a statistical method for uncertain problems to identify damages in FG Euler–Bernoulli beams which may not only reduce the adverse effects on damage identification outcomes but also improves the robustness and reliability of the results.
The structure of this paper is arranged as follows: Section 2 provides a detailed explanation of the statistical damage detection method for FG Euler–Bernoulli beams. Section 3 provides the numerical outcomes and examines how the gradient index, damage severity, noise level, and boundary conditions affect the results. The conclusion of the work is summarized in Section 4.
2. Statistical Damage Detection Method of FG Euler–Bernoulli Beams
2.1. Model of Functionally Graded Beam and the Assumptions of Model Shape Errors
In the process of finite element modeling, there will be model errors, which mainly include stiffness and mass parameter errors. For beam-like structures, the stiffness parameter always denotes the bending stiffness, while the mass parameter represents the weight per unit length of the beam. For an FG beam structure divided into an m element and n degrees of freedom, the stiffness () and mass matrix () before damage are expressed as stiffness parameters and mass parameters, respectively, as follows
where represents the element stiffness parameter of the th element in the FG beams, is bending stiffness (where I is moment of inertia), represents the unit quality parameter of the th element, namely the weight per unit beam length and the total count of elements is represented by n.
The global stiffness matrix and mass matrix of the structure after damage is represented as follows:
and are the element stiffness and mass parameter after damage. The modal shape and structural parameters (stiffness parameters and mass parameters) of the FG beam structure are assumed as random variables which obey mutually independent normal distribution. It can be expressed as follows:
where i represents the count of the vibration mode order, which is equivalent to the degrees of freedom. And j is the quantity of structural parameters that equals the number of structural elements.
2.2. Probability and Statistical Characteristics of Random Variables
Using the perturbation approach, Xia et al. [32] deduced the statistical characteristics of the stiffness parameters of isotropic beams and plates before and after damage. Combined with the isotropic Euler–Bernoulli beam damage equations [28], Yan et al. [31] derived the statistical characteristics (mean and variance) of the stiffness parameters of the isotropic Euler–Bernoulli beam before and after damage. On this basis, Yang et al. [14] successfully applied this method to the damage identification of FG beams. Furthermore, the mean and variance of the stiffness parameters of Euler–Bernoulli beams of FG materials before and after damage are derived in this work based on these methods. To aid the reader’s understanding, the equations of the statistical characteristics of Euler–Bernoulli beams for FG materials are presented in detail based on the isotropic ones [31].
According to the perturbation method, the damage equations [14], , is expanded as follows:
Substituting the above three formulas into , it shows the following:
According to Equation (5), the mean value of damage index is
It can be seen from Equation (7) that
Substituting Equation (11) into Equation (10), the mean result of βi is further written as follows:
The covariance matrix of the damage index can be derived as shown below:
In the above formula, the diagonal array is the variance of index βi for each element. The mean value and variance of element stiffness parameters for healthy and damaged are derived below. The relationship between index βi and stiffness parameters αi is defined as follows:
So the mean and variance value of stiffness parameters for every element before damage are as follows:
The average value of stiffness parameters for every element after damage can be obtained as follows:
The covariance matrix of stiffness parameters of each element after damage is as follows:
The values of each item in Equation (18) are as follows:
Substituting Equations (19)–(22) into (18), the covariance matrix for element stiffness after damage is obtained, and the diagonal of the covariance matrix is the variance of the element stiffness parameters after damage.
In order to solve Equation (18), it is necessary to know the solutions of and . Because random noise is independent of each other, only the value on the diagonal of is non-zero and equal to and the values of the other terms are 0.
The term can be calculated using , where and should be derived first.
According to the damage identification equations from Yang et al. [14], , then
Based on linear algebra, it has
Equation (23) can be further rewritten as
The above equation is the expression of . Then, can be obtained as
When
When
Once the term of and are obtained, the covariance matrix of the damage index can be calculated.
2.3. Probability and Statistics Method for Damage Identification
In the previous section, the expression for the mean value and variance of the element stiffness parameters for both healthy and damaged FG beam structures can be obtained. By comparing the change in the probability distribution of stiffness variable before and after damage, it can be determined whether the element is damaged. That is, if the probability distribution before and after the damage is almost unchanged, it can be considered that there is nearly no damage. However, if there is a large change, it can be considered damage exists and the probability of damage can be calculated at the same time. Yan et al. [31] and Xia et al. [32] introduced this method in detail, which is briefly introduced as follows.
It is assumed that the stiffness variable of the undamaged one adheres to a normal distribution, characterized by an average value of and a variance of . The probability density function is shown in Figure 1. Meanwhile, a confidence interval with a confidence level of is given, where is the lower limit of the confidence interval, which means that the probability of undamaged element stiffness parameter in interval is 95%. The expression is as follows:
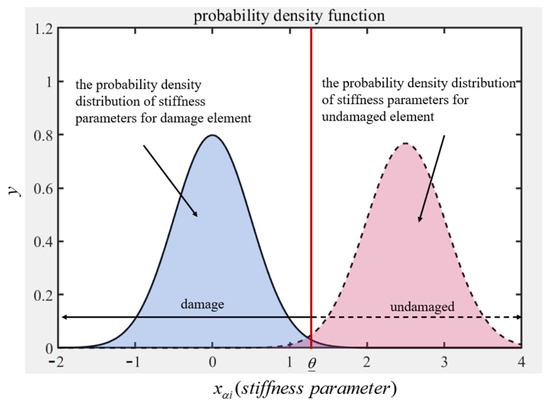
Figure 1.
The probability density function of element stiffness parameter.
Based on the probability and statistics, it has
Therefore, it can be obtained from the above formula that
assuming that the damage element stiffness parameters also follow the normal distribution with a mean value of and a variance of . If the probability density function is fd, the variability range of stiffness for both healthy and damaged components is and , respectively, the probability of damage can be calculated as
The above equation is the area of the shaded region in Figure 1. The value range of is 0 to 1. When tend to be 1, the possibility of structural damage becomes greater. While when tend to be 0, the possibility of structural damage maybe smaller. The aforementioned numerical simulations were conducted using Matlab R2023b.
3. Results and Discussion
A numerical example involving a simply supported beam is selected to verify the presented method which considers a variety of different damage conditions. The effects of gradient index k, damage severity, noise level and different boundary conditions on damage identification are also discussed in detail.
3.1. Description of Numerical Examples
As depicted in Figure 2, the dimensions of the FG Euler–Bernoulli simply supported beam are defined as follows: the length L is 6 m, the width b is 0.1 m, and the height h is 0.2 m. The substance located beneath the beam cross-section is steel with the elastic modulus El = 210 GPa and density equals ρl = 7800 kg/m3. The substance located at the upper part of the beam cross-section is aluminum oxide, the elastic modulus and density are Eu = 390 GPa and ρu = 3960 kg/m3. The materials are identical to those used by Alshorbagy A.E. et al. [11] to facilitate comparison and verification of the results. On the basis of plane beam element, the structure is divided into 10 elements leading to 11 nodes and 30 degrees of freedom.
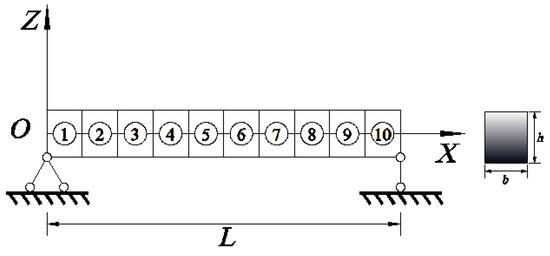
Figure 2.
A simply supported FG Euler–Bernoulli beam with ten elements.
3.2. Value of the Damaged Probability
The model error and the measurement error of vibration mode are assumed to be subjected to the normal distribution (the average value is 0, the noise level is 1%). The errors are independent of each other and the confidence level is . In order to verify the accuracy of the method in identifying damage in FG beam structure and for the purpose of comparison, the damage cases are the same as that of Yan et al. [31] shown in Table 1.

Table 1.
Cases of damage in FG simply supported Euler–Bernoulli beam.
The structural dynamic variable, including natural frequencies and mode shapes are obtained and the initial three mode shape for the three selected cases in Table 1 is displayed in Figure 3, respectively. As can be seen, the mode shapes are virtually identical in all scenarios.
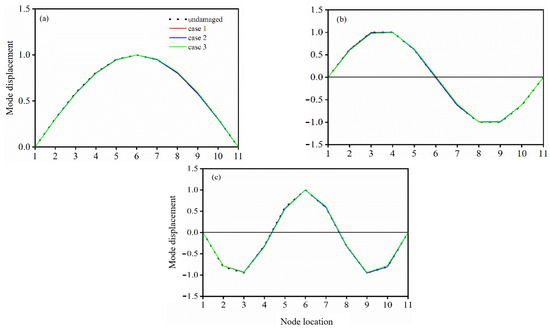
Figure 3.
(a) The first mode; (b) the second mode; (c) the third mode.
The probability density curve of the stiffness parameter for damage condition C1 in Table 1 before and after damage is shown in Figure 4. The forms of the probability density function curve of condition C2 and condition C3 are similar to that of condition C1.
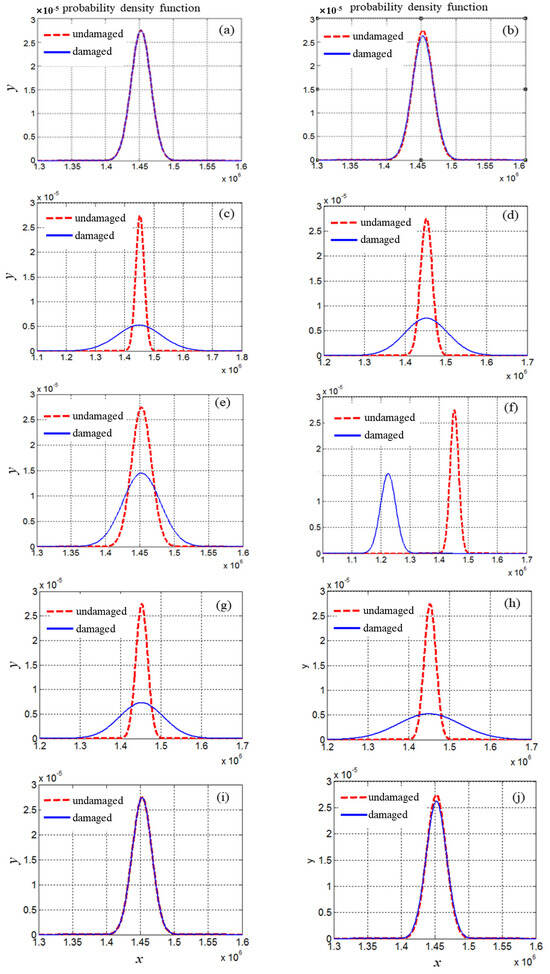
Figure 4.
Probability density function of elemental stiffness parameter before and after damage for C1: (a) element 1; (b) element 2; (c) element 3; (d) element 4; (e) element 5; (f) element 6; (g) element 7; (h) element 8; (i) element 9; (j) element 10.
It can be seen from Figure 4f that the curve of the probability density function of the stiffness parameters for the damaged element (element 6) deviates very distinctly before and after damage. However, if the undamaged elements are far from the damaged element, such as elements 1, 2, 9, and 10, the curves of probability density functions of them are almost coincident. Another noticeable phenomenon is that when healthy components are located near the damaged ones, such as elements 4, 5, 7, and 8, the resulting curves are also different but without any noticeable deviation. This suggests that the mean values of stiffness parameters remain similar before and after damage occurrence; however, the variance values exhibit significant differences when undamaged elements are in proximity to healthy elements. Changes in dispersion can significantly affect the calculated probability of damage. Now, utilizing the theory of statistical method for damage detection mentioned above, the probability of damage existence for each element damage under various damage conditions in Table 1 can be calculated and presented in Table 2.

Table 2.
Probability of damage in each element of the FG simply supported beam.
It can be seen from Table 2 that whether a single element is damaged (C1) or multiple elements are damaged (C2 and C3), results show that the probability of damage existence for damaged structure approaches 1. Compared with the damage element, the probability of damage existence for the healthy component is significantly small, especially for the ones near the support. This is because the damaged elements exert little influence on the probability density function curves of health components close to the supports (see Figure 4a, the curves are nearly the same), However, the presence of healthy elements near the damaged ones significantly affects the probability density function curves (see Figure 4c–e), resulting in a higher probability of damage. Therefore, the proposed probabilistic statistical method can be suitable when applied to FG Euler–Bernoulli beams.
3.3. Influence of Different Gradient Indexes on Probabilistic Damage Detection
The gradient parameters for the FG simply supported beam in the above example is k = 5. To examine the impact of the gradient indexes on damage identification results based on the probabilistic statistical method, only the gradient indexes which are set as 0, 1, 5, and 10 are changed. Other parameters are the same as those in the numerical example in 3.1. The cases of damage remain the same as those outlined in Table 1, and the results of damage detection are presented in Figure 5.
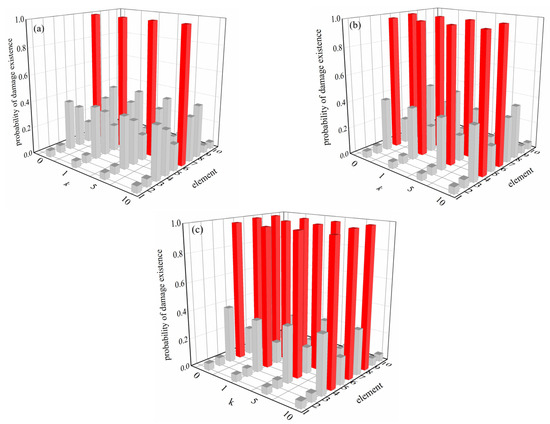
Figure 5.
Probability of damage existence of each element of FG simply supported beam when gradient indexes changes. (a) Damage condition C1, element 6 damaged, (b) damage condition C1, elements 4 and 6 damaged, (c) damage condition C3, elements 4, 6 and 8 damaged.
It can be seen from Figure 5 that when the gradient indexes vary from 0, 1, and 5 to 10, the probability of damage for each element remains relatively stable across the gradient indices. They are close to 1 for the damage elements in each damage condition; therefore, it can be implied that the proposed method is not influenced by the gradient index and is effective to detect damage in FG beam with changes in gradient index. For undamaged elements, the closer the support, the smaller the probability value. For example, the results of elements 1, 2, 9, and 10 are close to zero. However, it is worth mentioning that the elements remaining undamaged near the damaged ones, such as elements 3 and 7 in case 3, still have a maximum probability of damage existence of 0.4. Despite this, compared with the damaged elements they are still small, which may lead to some interference during the damage detection. If the error is large, it may cause misjudgment. This can be ascribed to the effect of supports, which results in the change in modal strain energy of elements near the supports being smaller compared to that of other elements located farther away [14].
3.4. Influence of Damage Severity on Probabilistic Damage Detection
To study the impact of changes in damage severity on damage detection, the severity levels of the damaged components are systematically modified while keeping other variables constant, which are set as 5%, 10%, 15%, 20%, and 25%, respectively. Other parameters are the same as those of numerical example 3.1. The damage conditions presented in Table 1 are utilized and the results of damage probability of each element are illustrated in Figure 6.
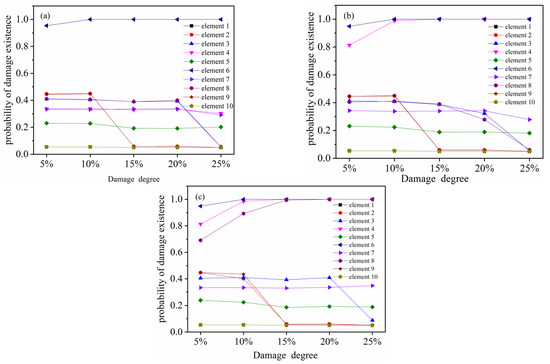
Figure 6.
Probability of damage existence in each case of an FG simply supported beam with an increasing of damage degree: (a) damage condition C1, element 6 damaged; (b) damage condition C2, element 4 and 6 damaged; (c) damage condition C3, element 4, 6 and 8 damaged.
As presented in Figure 6, regardless of whether the damage occurs in a single element or multiple elements, the results of the damaged elements progressively increase and eventually tend to one as the level of damage increases. And for most undamaged elements, the values decrease gradually and finally tend to 0.05. Only elements 5 and 7, which are very close to the damaged elements, show no obvious changes. Therefore, it can be assumed that the greater the extent of damage, the more precise the damage detection outcomes become.
3.5. Impact of Noise on Probabilistic Damage Detection Results
Since noise is unavoidable in practical engineering, it is essential to examine how noise affects the efficiency of damage detection. To investigate the influence of noise on damage identification outcomes, the noise levels for each case are set at 0.5%, 1%, 2%, 3%, 5%, and 10%, respectively. The other parameters remain unchanged. The results of the probability of damage existence for each case are shown in Figure 7.
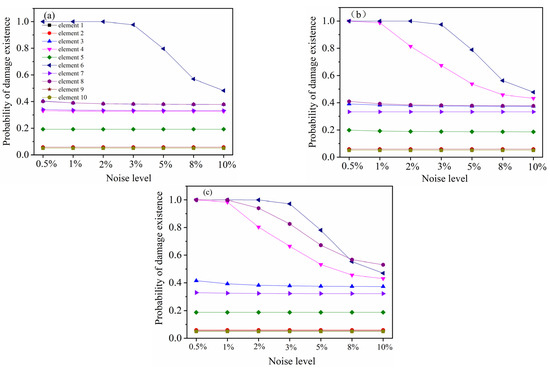
Figure 7.
Probability of damage existence of each case for FG simply supported beam with the increasing of noise levels: (a) damage condition C1, element 6 damaged; (b) damage condition C2, element 4 and 6 damaged; (c) damage condition C3, element 4, 6 and 8 damaged.
In Figure 7, the probability of damage existence is shown for different noise levels ranging from 0.5% to 5%. Our findings reveal that, irrespective of whether a single element is damaged or multiple elements are affected, as the noise level progressively increases, the results in the damaged elements gradually decreases. Conversely, the healthy elements tend to remain stable, with minimal or no variation. For example, the probability of damage existence in element 6 in case 1 is larger than 98% when noise levels vary from 0.5% to 3%, while the detection result decrease significantly with the value of 80%, when the noise levels are at 5%. It is worth noting that the damage can still be detected in this noisy situation. With the further increase in noise levels, the detection result is nearly the same as in the undamaged element. Therefore, this method could produce false positive results when the noise level is higher than 8%. However, in practical engineering applications, the noise level can be effectively reduced through various noise mitigation techniques, thereby demonstrating the method’s continued applicability and effectiveness.
3.6. Effect of Different Boundary Conditions on Probabilistic Damage Identification
To investigate the impact of boundary conditions on damage detection results and demonstrate the effectiveness of the proposed method for various FG beams, only the boundary condition is changed. The four types of the boundary condition models are shown in Figure 8 and the other parameters along with damage conditions remain unchanged. The results of the probability of damage existence for each case are shown in Figure 9.
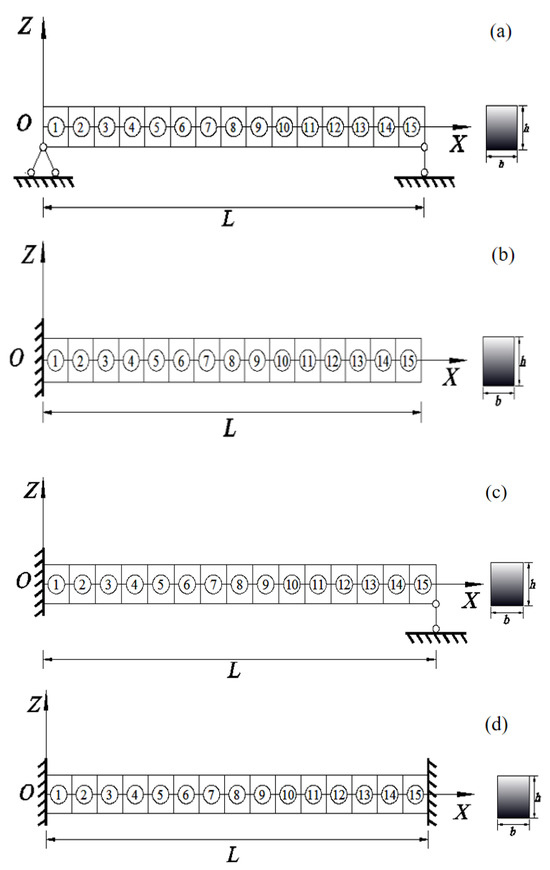
Figure 8.
The model of a functionally graded beam with different boundary conditions: (a) simply supported; (b) cantilever; (c) clamped–simply supported; (d) clamped–clamped supported.
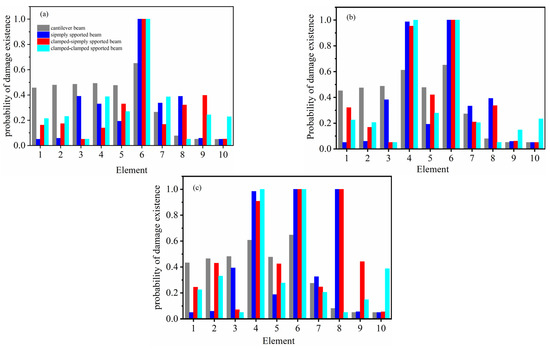
Figure 9.
Probability of damage existence in an FG beam when the boundary condition changes: (a) damage condition C1, element 6 damaged; (b) damage condition C2, element 4 and 6 damaged; (c) damage condition C3, element 4, 6 and 8 damaged.
As depicted in Figure 9, when the boundary conditions are different, the probability of damage of existence for each case is greatly affected. For the cantilever beam, whether for the one element (case 1) or multiple elements damaged (case 2), the damage identification results are not good. Specifically, the damage probability of the undamaged element on the clamped side is very close to that of the damaged element, which is prone to misjudgment. For example, the detection results of undamaged elements 1 to 5 are 46%, 48%, 49%, 49%, and 48%, respectively, which are very close to the damaged element 6 with a value of 65% in case 1. On the side of the cantilever end, both the damaged element and the undamaged element have a small probability of damage, so it is easy to make mistakes. This phenomenon may be attributed to the insensitivity of MSE changes at the cantilever end to the occurrence of damage.
For the simply supported beam, whether it is a single element damaged or multiple elements damaged, the damage identification effect is good. The results for the undamaged element at the boundary of both ends are very small. The probability of existence of damage to the undamaged element near the damaged element has an increasing trend, but it is still relatively small compared with the damaged element. For the beam with clamped-simply boundary conditions, the results of the damaged component are significant, thus allowing for the identification of the damaged element. However, the damage probability for the undamaged one at the left clamped end is higher compared to that of a simply supported beam. Additionally, the condition at the right simply supported end resembles that of a simply supported beam. For a beam with clamped–clamped boundary conditions, when one element (element 4) and two elements (elements 4 and 6) of the clamped beam at both ends are damaged, the damaged element can be identified. However, when three elements (elements 4, 6, and 8) are damaged, the probability of the damage of element 8 is very small and cannot be accurately identified. At the clamped ends on both the left and right sides, the damage result resembles that of the left clamped end of the simply clamped beam.
Generally, different boundary conditions have a great impact on the damage detection results. The clamped end and cantilever end have a prominent impact on the damage identification results, which makes the identification results unstable compared with the simply supported end. Therefore, the method presented in this paper can be improved to solve the adverse influence of clamped and cantilever boundary conditions in the future.
4. Conclusions
This paper presents a probabilistic statistical damage detection approach for FG Euler–Bernoulli beam structures, utilizing the sensitivity of element modal strain energy. The probability of damage existence, which can determine whether the beam structure is damaged or not, is calculated for each element. The influence of damage severity, boundary condition, and noise level on the detection effect are also considered. A numerical simply supported beam has confirmed this, and the conclusions can be presented as follows:
(1) The numerical outcomes confirm that the suggested approach provides an effective method for identifying damage occurrence in FG Euler–Bernoulli beams. Regardless of whether it involves damage to a single element or multiple elements, results show that the probability of damage existence for the damaged element tends to 1, while for undamaged elements the results are much smaller with the value of 0.05, especially for the elements near the support. It is worth mentioning that the undamaged elements close to the damaged ones may have a maximum probability of damage existence of 0.4. Even so, the value still much smaller than in the damaged elements. Thus, the proposed method, based on element modal strain energy sensitivity approach, is applicable to FG Euler–Bernoulli beams.
(2) As the severity of damage increases, the probability of damage existence in the damaged components gradually rises and eventually approaches a value of 1. In contrast, for the healthy one it slowly diminishes and ultimately converges to 0.05. As a result, it can be concluded that the greater the extent of damage, the more precise the outcomes of damage detection become.
(3) As the noise level continues to increase, the results of the damaged elements decrease gradually, while the healthy structures remain stable. When the noise level is higher than 8%, the proposed approach may produce false positive results, which can be attributed to measurement noise and modeling errors that render the changes in MSE less discernible. However, when the noise level is not higher than 5%, it can provide an effective way to detect damage locations.
(4) Different boundary conditions have a great impact on the damage identification. In contrast to the simply supported end, the clamped and cantilever ends have a prominent impact on the damage identification results, making the identification results unstable.
Author Contributions
Conceptualization, D.Y.; Methodology, D.Y., C.K., Z.H. and A.A.; Validation, S.C. and Z.H.; Investigation, D.Y., C.K., S.C. and Z.H.; Writing—original draft, C.K. and S.C.; Writing—review & editing, D.Y. and A.A.; Visualization, C.K., S.C. and Z.H.; Supervision, D.Y. and A.A.; Funding acquisition, D.Y. and A.A. All authors have read and agreed to the published version of the manuscript.
Funding
The research presented in this paper is funded by grants from the Science and Technology Research Project of Henan Province (222102320320, 242102521034, 242102321169). A. S. Ademiloye thanks the Royal Society for the International Exchange grant (IES\NSFC\223217).
Data Availability Statement
Underlying research materials related to this paper can be accessed by requesting them from the corresponding author.
Conflicts of Interest
The authors declared no potential conflicts of interest with respect to the research, authorship, and publication of this article.
References
- Kawasaki, A.; Watanabe, R. Concept and P/M fabrication of functionally gradient materials. Ceram. Int. 1997, 23, 73–83. [Google Scholar] [CrossRef]
- Naebe, M.; Shirvanimoghaddam, K. Functionally graded materials: A review of fabrication and properties. Appl. Mater. Today 2016, 5, 223–245. [Google Scholar] [CrossRef]
- Yu, X.; Zhou, J.; Liang, H.; Jiang, Z.; Wu, L. Mechanical metamaterials associated with stiffness, rigidity and compressibility: A brief review. Prog. Mater. Sci. 2018, 94, 114–173. [Google Scholar] [CrossRef]
- Gupta, A.; Talha, M. Recent development in modeling and analysis of functionally graded materials and structures. Prog. Aerosp. Sci. 2015, 79, 1–14. [Google Scholar] [CrossRef]
- Zhang, L.W.; Song, Z.G.; Qiao, P.Z.; Liew, K.M. Modeling of dynamic responses of CNT-reinforced composite cylindrical shells under impact loads. Comput. Methods Appl. Mech. Eng. 2017, 313, 889–903. [Google Scholar] [CrossRef]
- Salem, T.; Jiao, P.; Zaabar, I.; Li, X.; Zhu, R.; Lajnef, N. Functionally graded materials beams subjected to bilateral constraints: Structural instability and material topology. Int. J. Mech. Sci. 2021, 194, 106218. [Google Scholar] [CrossRef]
- Dinachandra, M.; Alankar, A. Static and dynamic modeling of functionally graded Euler-Bernoulli microbeams based on reformulated strain gradient elasticity theory using isogeometric analysis. Compos. Struct. 2022, 280, 114923. [Google Scholar] [CrossRef]
- Qu, Y.; Jin, F.; Zhang, G. Mechanically induced electric and magnetic fields in the bending and symmetric-shear deformations of a microstructure-dependent FG-MEE composite beam. Compos. Struct. 2021, 278, 114554. [Google Scholar] [CrossRef]
- Zhang, G.; Hao, Y.; Guo, Z.; Mi, C. A new model for thermal buckling of FG-MEE microbeams based on a non-classical third-order shear deformation beam theory. Mech. Solids 2024, 59, 1475–1495. [Google Scholar] [CrossRef]
- Hong, J.; Wang, S.; Zhang, G.; Mi, C. On the bending and vibration analysis of functionally graded magneto-electro-elastic Timoshenko microbeams. Crystals 2021, 11, 1206. [Google Scholar] [CrossRef]
- Alshorbagy, A.E.; Eltaher, M.A.; Mahmoud, F.F. Free vibration characteristics of a functionally graded beam by finite element method. Appl. Math. Model. 2011, 35, 412–425. [Google Scholar] [CrossRef]
- Shahba, A.; Rajasekaran, S. Free vibration and stability of tapered Euler–Bernoulli beams made of axially functionally graded materials. Appl. Math. Model. 2012, 36, 3094–3111. [Google Scholar] [CrossRef]
- Pradhan, K.K.; Chakraverty, S. Free vibration of Euler and Timoshenko functionally graded beams by Rayleigh–Ritz method. Compos. Part B Eng. 2013, 51, 175–184. [Google Scholar] [CrossRef]
- Yang, D.; Kang, C.; Hu, Z.; Ye, B.; Xiang, P. On the study of element modal strain energy sensitivity for damage detection of functionally graded beams. Compos. Struct. 2019, 224, 110989. [Google Scholar] [CrossRef]
- Zhu, L.F.; Ke, L.L.; Zhu, X.Q.; Xiang, Y.; Wang, Y.S. Crack identification of functionally graded beams using continuous wavelet transform. Compos. Struct. 2019, 210, 473–485. [Google Scholar] [CrossRef]
- Dang, V.H.; Vu, T.C.; Nguyen, B.D.; Nguyen, Q.H.; Nguyen, T.D. Structural damage detection framework based on graph convolutional network directly using vibration data. Structures 2022, 38, 40–51. [Google Scholar] [CrossRef]
- Hu, Z.M.; Wang, J.S.; Sun, Y.K.; Lin, K. The suppression of flow-induced vibrations for a single and two tandem-arrangement cylinders using three splitter plates. J. Mar. Sci. Eng. 2024, 12, 1487. [Google Scholar] [CrossRef]
- Ren, W.X.; Roeck, G.D. Structural damage identification using modal data. I: Simulation verification. J. Struct. Eng. 2002, 128, 87–95. [Google Scholar] [CrossRef]
- Ren, W.X.; Roeck, G.D. Structural damage identification using modal data. II, Test verification. J. Struct. Eng. 2002, 128, 96–104. [Google Scholar] [CrossRef]
- Avci, O.; Abdeljaber, O.; Kiranyaz, S.; Hussein, M.; Inman, D.J. A review of vibration-based damage detection in civil structures: From traditional methods to machine learning and deep learning applications. Mech. Syst. Signal Process. 2021, 147, 107077. [Google Scholar] [CrossRef]
- Pooya, S.M.H.; Massumi, A. A novel and efficient method for damage detection in beam-like structures solely based on damaged structure data and using mode shape curvature estimation. Appl. Math. Model. 2021, 91, 670–694. [Google Scholar] [CrossRef]
- Mostafaei, H.; Mostofinejad, D.; Ghamami, M.; Wu, C. Fully automated operational modal identification of regular and irregular buildings with ensemble learning. Structures 2023, 58, 105439. [Google Scholar] [CrossRef]
- Shi, Z.Y.; Law, S.S.; Zhang, L.M. Improved Damage Quantification from Elemental Modal Strain Energy Change. J. Eng. Mech. 2002, 128, 521–529. [Google Scholar] [CrossRef]
- Shi, Z.Y.; Law, S.S.; Zhang, L.M. Structural Damage Detection from Modal Strain Energy Change. J. Eng. Mech. 2000, 126, 1216–1223. [Google Scholar] [CrossRef]
- Pooya, S.M.H.; Massumi, A. A novel damage detection method in beam-like structures based on the relation between modal kinetic energy and modal strain energy and using only damaged structure data. J. Sound Vib. 2022, 530, 116943. [Google Scholar] [CrossRef]
- Seyedpoor, S.M. A two stage method for structural damage detection using a modal strain energy based index and particle swarm optimization. Int. J. Non-Linear Mech. 2012, 47, 1–8. [Google Scholar] [CrossRef]
- Alavinezhad, M.; Hassanabad, M.G.; Ketabdari, M.J.; Nekooei, M. Numerical and experimental structural damage detection in an offshore flare bridge using a proposed modal strain energy method. Ocean. Eng. 2022, 252, 111055. [Google Scholar] [CrossRef]
- Yan, W.J.; Ren, W.X. A direct algebraic method to calculate the sensitivity of element modal strain energy. Int. J. Numer. Methods Biomed. Eng. 2011, 27, 694–710. [Google Scholar] [CrossRef]
- Yan, W.J.; Huang, T.L.; Ren, W.X. Damage detection method based on element modal Strain energy sensitivity. Adv. Struct. Eng. 2010, 13, 1075–1088. [Google Scholar] [CrossRef]
- Lu, Z.R.; Lin, X.X.; Chen, Y.M.; Huang, M. Hybrid Sensitivity Matrix for Damage Identification in Axially Functionally Graded Beams. Appl. Math. Model. 2017, 41, 604–617. [Google Scholar] [CrossRef]
- Yan, W.J.; Ren, W.X.; Huang, T.L. Statistic structural damage detection based on the closed-form of element modal strain energy sensitivity. Mech. Syst. Signal Process. 2012, 28, 183–194. [Google Scholar] [CrossRef]
- Xia, Y.; Hao, H.; Brownjohn, J.M.W. Damage identification of structures with uncertain frequency and mode shape data. Earthq. Eng. Struct. Dyn. 2002, 31, 1053–1066. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).