Identification and Analysis of Earthquake Risks in Worn-Out Urban Fabrics Using the Intuitionistic Fuzzy Brainstorming (IFBS) Technique for Group Decision-Making
Abstract
1. Introduction
2. Literature Review
2.1. Decision-Making on Project Management Issues
2.2. Brainstorming Technique and Intuitionistic Fuzzy Sets
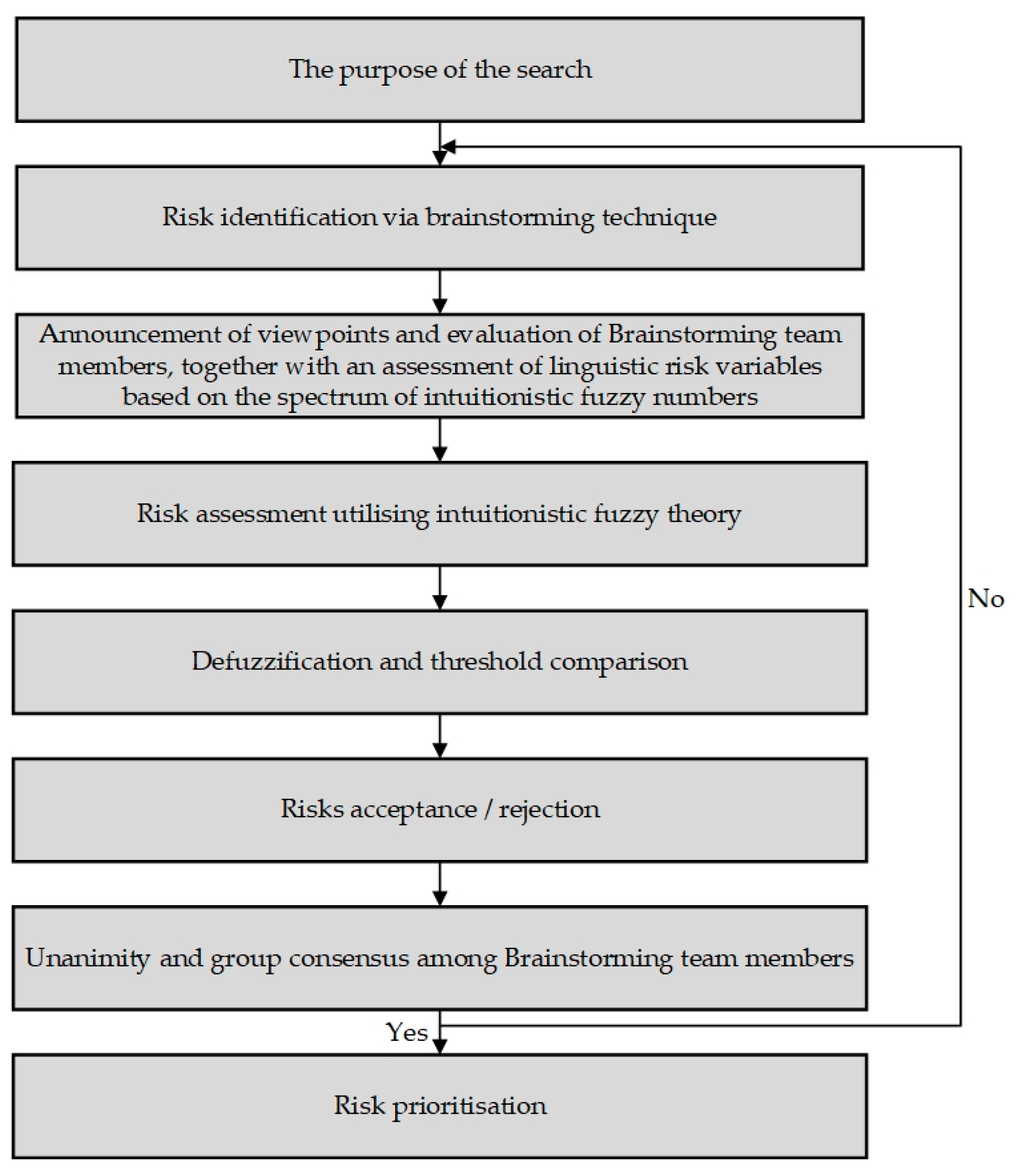
3. Research Methodology
3.1. Brainstorming Technique
- Presenting several ideas;
- No criticism of the ideas of others;
- Freedom in expression, participation, and proposing unreasonable or far-fetched ideas;
- Explaining, developing, and improving the existing ideas.
3.2. Fuzzy Set Theory and Intuitionistic Fuzzy Sets
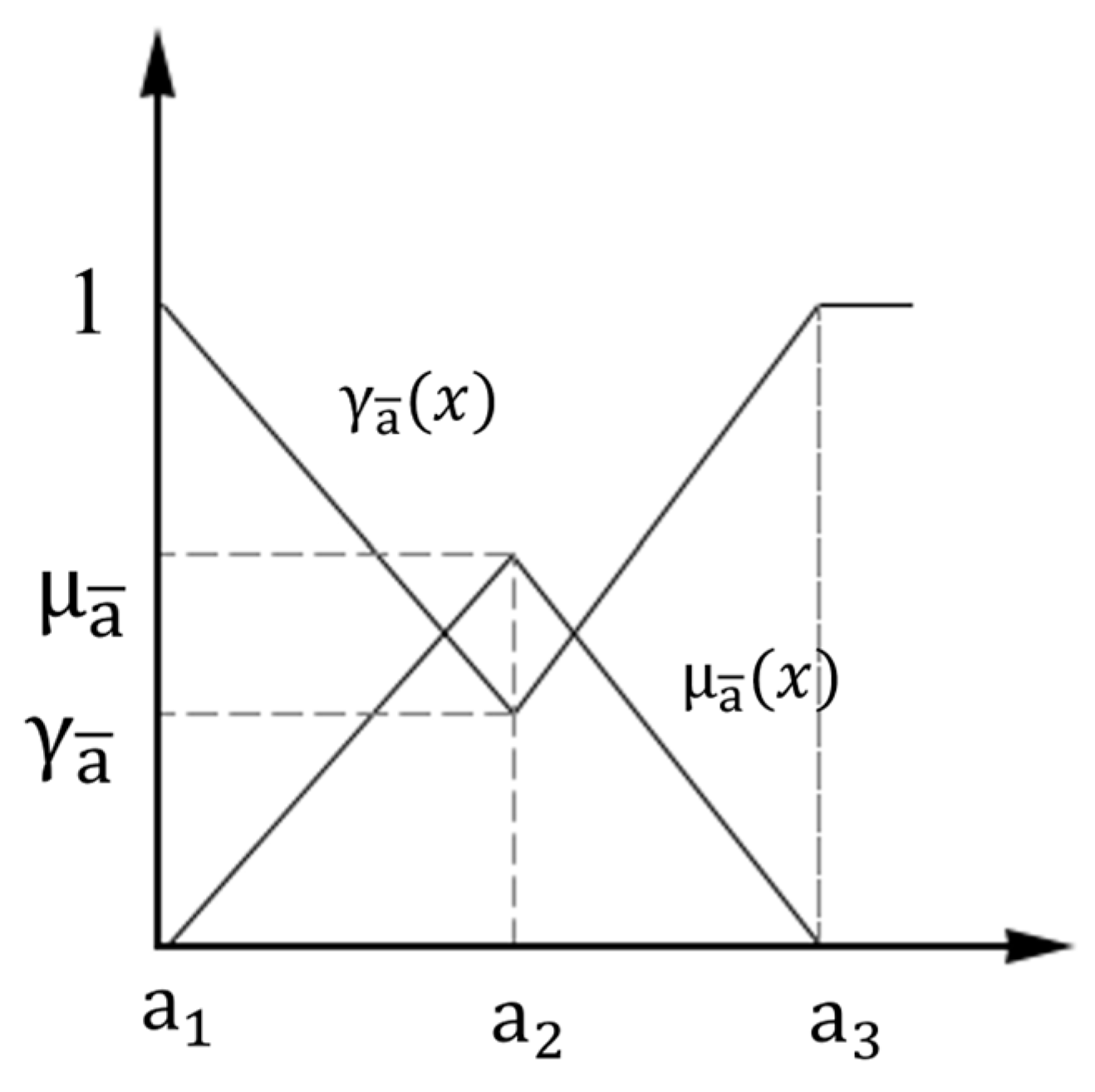
3.3. Intuitionistic Fuzzy Brainstorming (IFBS) Technique
Triangular Intuitionistic Fuzzy Numbers (TIFNs)
3.4. Intuitionistic Fuzzy Brainstorming (IFBS) Technique in Group Decisions to Select Options
4. Results
4.1. Identification of Earthquake Risks in Worn-Out Urban Fabrics Using the IFBS Technique
4.2. Comparison of the Results Between the IFBS Technique and the PMBOK-Based Qualitative Analysis Method
4.3. Research Limitations and Future Research Directions
- Reliance on expert opinions: The IFBS technique heavily depends on the subjective judgments of experts during brainstorming sessions, which can introduce biases and inconsistencies. Despite structured validation processes, such as iterative feedback loops, the variability in expert expertise and cognitive biases may affect the reliability of risk assessments, particularly in diverse urban contexts.
- Subjectivity in IFS function selection: The selection of membership and non-membership functions for TIFNs involves subjective expert judgment, which can compromise objectivity. Although the IFBS method employs standardized guidelines, the lack of fully objective criteria for function assignment remains a challenge.
- Information loss during defuzzification: The defuzzification process, which converts fuzzy numbers into crisp values, may lead to information loss, potentially reducing the precision of risk prioritization. While weighted aggregation techniques are used, the granularity of uncertainty representation may still be compromised.
- Expertise requirements for TIFNs conversion: Converting linguistic expressions into TIFNs requires specialized knowledge, limiting the method’s accessibility to non-specialists. Despite efforts to simplify this process with predefined scales, the technical complexity may restrict broader adoption.
- Computational complexity: The IFBS method’s computational demands increase with the number of criteria and experts, posing scalability challenges for large-scale urban risk assessments. This complexity can hinder practical implementation in resource-constrained settings.
- Context-specific application: This study focuses on worn-out urban fabrics in Iran, which may limit the generalizability of findings to other geographic or socio-economic contexts. Variations in urban infrastructure, cultural factors, and disaster preparedness levels may require methodological adaptations.
- Limited validation scope: The comparison between the IFBS method and PMBOK-based qualitative analysis is confined to a single case study, which may not fully validate the method’s superiority across diverse risk management scenarios. This study lacks broader empirical testing to confirm its robustness.
- Enhancing bias mitigation: Future research should explore advanced techniques to further reduce biases in expert opinions, such as integrating artificial intelligence (AI) algorithms to detect and correct cognitive biases during brainstorming sessions [21]. Developing automated validation tools could enhance objectivity in IFS function selection, building on Gavurova et al.’s [35] work on smart city risk models.
- Improving defuzzification techniques: Investigating novel defuzzification methods that minimize information loss, such as machine learning-based approaches, could improve the precision of risk prioritization [36]. Research could focus on adaptive defuzzification algorithms that retain the hesitancy parameter’s granularity, as suggested by Pu et al.’s [30] optimization models.
- Increasing accessibility for non-specialists: To broaden the IFBS method’s adoption, future studies should develop user-friendly interfaces and training modules that simplify TIFNs conversion for non-specialists. Collaborative frameworks, as proposed by Swaris et al. [29], could inform the design of inclusive decision-making platforms that empower diverse stakeholders.
- Optimizing computational efficiency: Research should focus on scalable algorithms to reduce the computational complexity of the IFBS method, particularly for large-scale urban risk assessments. Leveraging AI-driven optimization, as demonstrated by Xia et al. [36], could streamline calculations and enhance applicability in resource-constrained environments.
- Expanding contextual applicability: Future studies should test the IFBS method across diverse geographic and socio-economic contexts to validate its generalizability. Comparative studies in different urban settings, such as those with varying infrastructure resilience or disaster preparedness levels, could refine the method’s adaptability [26].
- Broader validation and comparative analysis: Conducting extensive empirical validations across multiple case studies and risk management scenarios would strengthen the IFBS method’s credibility. Future research could compare the IFBS method with other advanced decision-making frameworks, such as deep learning-based risk models, to establish its relative advantages [35].
- Integration with emerging technologies: Exploring the integration of the IFBS method with emerging technologies, such as GIS and real-time data analytics, could enhance its applicability in dynamic urban risk management. This could involve developing hybrid models that combine IFBS with predictive analytics for proactive disaster planning.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ataei, M. Multi-Criteria Decision Making; Shahroud University Technology: Shahrud, Iran, 2009. [Google Scholar]
- Chan, D.W.M.; Abdul Hadi Sadeq, D.; Mohammed Fadhil, A.; Cristofaro, M.; Sarvari, H. Barriers and solutions in adopting public–private partnerships in road transportation infrastructure projects for developing countries: Results of a Delphi survey in Iran. J. Facil. Manag. 2022; ahead-of-print. [Google Scholar] [CrossRef]
- Dabiri, M.; Oghabi, M.; Sarvari, H.; Sabeti, M.S.; Kashefi, H.; Chan, D.W. Assessing the post-earthquake temporary accommodation risk in Iran using Fuzzy Delphi Metheod. Open Constr. Build. Technol. J. 2021, 15, 93–105. [Google Scholar] [CrossRef]
- Rafieyan, A.; Sarvari, H.; Beer, M.; Chan, D.W. Determining the effective factors leading to incidence of human error accidents in industrial parks construction projects: Results of a fuzzy Delphi survey. Int. J. Constr. Manag. 2022, 24, 1–13. [Google Scholar] [CrossRef]
- Sadeghi, J.; Oghabi, M.; Sarvari, H.; Sabeti, M.S.; Kashefi, H.; Chan, D.W.; Lotfata, A. A hybrid risk assessment approach for assessing the earthquake risks in worn-out urban fabrics: A case study in Iran. Int. J. Disaster Resil. Built Environ. 2023, 14, 193–211. [Google Scholar] [CrossRef]
- Dhull, P.; Beniwal, R. Brainstorming technique—A step to creativity. Int. J. Res. Anal. Rev. 2018, 5, 550–555. [Google Scholar]
- Besant, H. The journey of brainstorming. J. Transform. Innov. 2016, 2, 1–7. [Google Scholar]
- Al-Samarraie, H.; Hurmuzan, S. A revive brainstorming techniques in higher education. Think. Ski. Creat. 2018, 27, 78–91. [Google Scholar] [CrossRef]
- Zadeh, L.A. Information and control. Fuzzy Sets 1965, 8, 338–353. [Google Scholar]
- Bustince, H.; Burillo, P. Vague sets are intuitionistic fuzzy sets. Fuzzy Sets Syst. 1996, 79, 403–405. [Google Scholar] [CrossRef]
- Atanassov, K.T. Intuitionistic fuzzy sets VII ITKR’s Session. Sofia 1983, 1, 983. [Google Scholar]
- Chen, L.; Pan, W. Review fuzzy multi-criteria decision-making in construction management using a network approach. Appl. Soft Comput. 2021, 102, 107103. [Google Scholar] [CrossRef]
- El Sayed, M.A.; Baky, I.A.; Singh, P. A modified TOPSIS approach for solving stochastic fuzzy multi-level multi-objective fractional decision making problem. Opsearch 2020, 57, 1374–1403. [Google Scholar] [CrossRef]
- El Sayed, M.A.; Baky, I.A. Multi-choice fractional stochastic multi-objective transportation problem. Soft Comput. 2023, 27, 11551–11567. [Google Scholar] [CrossRef]
- Najafi, E.; Karimi Kerdabadi, M. Flood risk evaluation and zoning using with AHP-fuzzy combined model with emphasis on urban safety (case study: Region 1 of Tehran Municipality). J. Geogr. Environ. Hazards 2020, 9, 43–60. [Google Scholar] [CrossRef]
- Nayeri, M.; Shieh, E.; Rezaei, M.; Saeidi Rezvani, N. Managing neighborhood resilience in earthquake encountered in urban exhausted tissues with FAHP method (Case study: Abdolabad, Tehran). Q. Geogr. Reg. Plan. 2018, 8, 21–38. [Google Scholar]
- Wang, X.; Zhao, T.; Chang, C.T. An integrated FAHP-MCGP approach to project selection and resource allocation in risk-based internal audit planning: A case study. Comput. Ind. Eng. 2021, 152, 107012. [Google Scholar] [CrossRef]
- Sarvari, H.; Rakhshanifar, M.; Tamošaitienė, J.; Chan, D.W.M.; Beer, M. A risk based approach to evaluating the impacts of Zayanderood drought on sustainable development indicators of riverside urban in Isfahan-Iran. Sustainability 2019, 11, 6797. [Google Scholar] [CrossRef]
- Tamosaitiene, J.; Sarvari, H.; Cristofaro, M.; Chan, D.W. Identifying and prioritizing the selection criteria of appropriate repair and maintenance methods for commercial buildings. Int. J. Strateg. Prop. Manag. 2021, 25, 413–431. [Google Scholar] [CrossRef]
- Dabiri, M.; Oghabi, M.; Sarvari, H.; Sabeti, M.S.; Kashefi, H.R. A combination risk-based approach to post-earthquake temporary accommodation site selection: A case study in Iran. Iran. J. Fuzzy Syst. 2020, 17, 54–74. [Google Scholar]
- Laurent, C.; Dinariyana, A.A.B.; Priyanta, D. Evaluation of Fuzzy Metheod to determine of failure compared with RBI analisis for pressure vessel in oil and gas company. IOP Conf. Ser. Earth Environ. Sci. 2020, 557, 012070. [Google Scholar] [CrossRef]
- Sadeghi, J.; Oghabi, M.; Sarvari, H.; Sabeti, M.S.; Kashefi, H.; Chan, D. Identification and prioritization of seismic risks in urban worn-out textures using fuzzy Delphi method. Environ. Eng. Manag. J. 2021, 20, 1035–1046. [Google Scholar]
- Kates, R.W. Major insights: A summary and recommendations. Reconstr. Follow. Disasters 1977, 261–293. [Google Scholar]
- Mohammadpour, S.; Zali, N.; Pourahmad, A. Analysis of seismic vulnerability factors in urban old texture with the approach of earthquake crisis management (case study: Sirus Neighborhood). Hum. Geogr. Res. Q. 2016, 48, 33–52. [Google Scholar]
- Salvati, A.; Monti, P.; Roura, H.C.; Cecere, C. Climatic performance of urban fabrics: Analysis tools for a Mediterranean urban context. Energy Build. 2019, 185, 162–179. [Google Scholar] [CrossRef]
- Sarvari, H.; Mehrabi, A.; Chan, D.W.; Cristofaro, M. Evaluating urban housing development patterns in developing countries: Case study of Worn-out Urban Fabrics in Iran. Sustain. Cities Soc. 2021, 70, 102941. [Google Scholar] [CrossRef]
- Kahraman, C. (Ed.) Fuzzy Multi-criteria Decision Making: Theory and Applications with Recent Developments; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2008; Volume 16. [Google Scholar]
- Huang, S.; Li, X.; Wang, Y. A new model of geo-environmental impact assessment of mining: A multiple-criteria assessment method integrating Fuzzy-AHP with fuzzy synthetic ranking. Environ. Earth Sci. 2012, 66, 275–284. [Google Scholar] [CrossRef]
- Swaris, N.; Halwatura, R.U.; Amaratunga, D. Policy coherence for resilience in Sri Lanka coherence of climate change adaptation (CCA) disaster risk reduction (DRR) and sustainable development goals (SDGs). Int. J. Disaster Resil. Built Environ. 2024, 15, 450–473. [Google Scholar] [CrossRef]
- Pu, J.; Mu, M.; Feng, J.; Zhong, X.; Li, H. A fast physics-based perturbation generator of machine learning weather model for efficient ensemble forecasts of tropical cyclone track. npj Clim. Atmos. Sci. 2025, 8, 128. [Google Scholar] [CrossRef]
- Tsai, C.H.; Chen, C.W. An earthquake disaster management mechanism based on risk assessment information for the tourism industry—A case study from the island of Taiwan. Tour. Manag. 2010, 31, 470–481. [Google Scholar] [CrossRef]
- PMI. A Guide to the Project Management Body of Knowledge, 6th ed.; Project Management Institute: Singapore, 2017; pp. 1–390. [Google Scholar]
- Dabiri, M.; Sarvari, H.; Chan, D.W.; Olawumi, T.O. Developing a hybrid risk assessment method for prioritizing the critical risks of temporary accommodation sites after destructive earthquakes. Habitat Int. 2022, 128, 102667. [Google Scholar] [CrossRef]
- Malibari, A.A.; Alotaibi, S.S.; Alshahrani, R.; Dhahbi, S.; Alabdan, R.; Al-wesabi, F.N.; Hilal, A.M. A novel metaheuristics with deep learning enabled intrusion detection system for secured smart environment. Sustain. Energy Technol. Assess. 2022, 52, 102312. [Google Scholar] [CrossRef]
- Gavurova, B.; Kelemen, M.; Polishchuk, V. Expert model of risk assessment for the selected components of smart city concept: From safe time to pandemics as COVID-19. Socio-Econ. Plan. Sci. 2022, 82, 101253. [Google Scholar] [CrossRef]
- Xia, H.; Sun, Z.; Wang, Y.; Zhang, J.Z.; Kamal, M.M.; Jasimuddin, S.M.; Islam, N. Emergency medical supplies scheduling during public health emergencies: Algorithm design based on AI techniques. Int. J. Prod. Res. 2025, 63, 628–650. [Google Scholar] [CrossRef]
- Nyimbili, P.H.; Erden, T.; Karaman, H. Integration of GIS, AHP and TOPSIS for earthquake hazard analysis. Nat. Hazards 2018, 92, 1523–1546. [Google Scholar] [CrossRef]
- Nazemfar, H.; Saredeh, A.; Eshgi, A.; Feizizadeh, B. Vulnerability evaluation of urban buildings to various earthquake intensities: A case study of the municipal zone 9 of Tehran. Hum. Ecol. Risk Assess. Int. J. 2019, 25, 455–474. [Google Scholar] [CrossRef]
- Liu, Y.; Li, Z.; Wei, B.; Li, X.; Fu, B. Seismic vulnerability assessment at urban scale using data mining and GIScience technology: Application to Urumqi (China). Geomat. Nat. Hazards Risk 2019, 10, 958–985. [Google Scholar] [CrossRef]
- Marinello, M. In Search of Better Brainstorming Through a Two Step Process. Master’s Thesis, Presented partial fulfilment of the requirements for the degree of Master of Science in Design. Arizona State University, Tempe, AZ, USA, 2013. [Google Scholar]
- Simone, M.R.; Mostert, N.M. How to facilitate a brainstorming session: The effect of idea generation techniques and of group brainstorm after individual brainstorm. Creat. Ind. J. 2018, 3, 263–277. [Google Scholar]
- Bozanic, D.; Pamucar, D.; Bojanic, D. Modification of the analytic hierarchy process (AHP) method using fuzzy logic: Fuzzy AHP approach as a support to the decision making process concerning engagement of the group for additional hindering. Serbian J. Manag. 2015, 10, 151–171. [Google Scholar] [CrossRef]
- Chakraborty, J.; Mukherjee, S.; Sahoo, L. Intuitionistic Fuzzy Multi-Index Multi-Criteria Decision-Making for Smart Phone Selection Using Similarity Measures in a Fuzzy Environment. J. Ind Intell. 2023, 1, 1–7. [Google Scholar] [CrossRef]
- Iqbal, Q.; Kalsoom, S. Advanced Logarithmic Aggregation Operators for Enhanced Decision-Making in Uncertain Environments. Int, J. Knowl. Innov Stud. 2024, 2, 57–69. [Google Scholar] [CrossRef]
- Faizi, S.; Salabun, W.; Rashid, T.; Zafar, S.; Watrobski, J. Intuitionistic fuzzy sets in multi-criteria group decision making problems using characteristic objects method. Symmetry 2020, 12, 1382–1397. [Google Scholar] [CrossRef]
- Bellman, R.E.; Zadeh, L.A. Decision-making in a fuzzy environment. Manag. Sci. 1970, 17, B-141. [Google Scholar] [CrossRef]
- Chen, S.J.; Hwang, C.L. Fuzzy multiple attribute decision making methods. In Fuzzy Multiple Attribute Decision Making; Springer: Berlin/Heidelberg, Germany, 1992; pp. 289–486. [Google Scholar]
- Das, S.; Kar, M.B.; Kar, S. Group multi-criteria decision making using intuitionistic multi-fuzzy sets. J. Uncertain. Anal. Appl. 2013, 1, 1–16. [Google Scholar] [CrossRef]
- Li, D.F. A ratio ranking method of triangular intuitionistic fuzzy numbers and its application to MADM problems. Comput. Math. Appl. 2010, 60, 1557–1570. [Google Scholar] [CrossRef]
- Sadeghi, J.; Sarvari, H.; Zangeneh, S.; Fatemi, A.; Edwards, D.J. An analysis of intuitionistic fuzzy sets in risk-based inspection: A case study of hydrogen crack damage in steel tanks under gas pressure. Clean. Eng. Technol. 2024, 23, 100855. [Google Scholar] [CrossRef]
- Chen, S.M.; Tan, J.M. Handling multi-criteria fuzzy decision-making problems based on vague set theory. Fuzzy Sets Syst. 1994, 67, 163–172. [Google Scholar] [CrossRef]
- Tan, C.; Chen, X. Intuitionistic fuzzy Choquet integral operator for multi-criteria decision making. Expert Syst. Appl. 2010, 37, 149–157. [Google Scholar] [CrossRef]
- Liu, H.W.; Wang, G.J. Multi-criteria decision-making methods based on intuitionistic fuzzy sets. Eur. J. Oper. Res. 2007, 179, 220–233. [Google Scholar] [CrossRef]
- Atanassov, K.; Pasi, G.; Yager, R. Intuitionistic fuzzy interpretations of multi-person multi-criteria decision making. In Proceedings of the First International IEEE Symposium on Intelligent Systems, Varna, Bulgaria, 10–12 September 2002; Volume 1, pp. 115–119. [Google Scholar]
- Osborn, A.F. Applied Imagination: Principles and Procedures of Creative Problem Solving; 3rd revised; Charles Scribner’s Sons: New York, NY, USA, 1963. [Google Scholar]
- Feinberg, M.; Nemeth, C. The “Rules” of Brainstorming: An Impediment to Creativity? Institute for Research on Labor and Employment (IRLE): Berkeley, CA, USA, 2008; No. 167-08. [Google Scholar]
- Sekhar, S.C.; Lidiya, K. Brainstorming. Management 2012, 2, 113–117. [Google Scholar] [CrossRef]
- Hosseini, D. Fuzzy logic, ambiguity and harvest paradox. Inst. Humanit. Cult. Stud. 2012, 1, 27–51. [Google Scholar]
- Pasha, E.; Farnoosh, R.; Fatemi, A. Fazzy entropy as cost funection image processing. In Proceedings of the 2nd IMT-GT Regional Conference on Mathematics, Statistics and Application, Penang, Malaysia, 13–15 June 2006; pp. 1–8. [Google Scholar]
- Atanasov, K.T. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Atanassov, K.T. More on intuitionistic fuzzy sets. Fuzzy Sets Syst. 1989, 33, 37–45. [Google Scholar] [CrossRef]
- Atanassov, K.T. New operations defined over the intuitionistic fuzzy sets. Fuzzy Sets Syst. 1994, 61, 137–142. [Google Scholar] [CrossRef]
- Cheng, C.H.; Lin, Y. Evaluating the best main battle tank using fuzzy decision theory with linguistic criteria evaluation. Eur. J. Oper. Res. 2002, 142, 174–186. [Google Scholar] [CrossRef]
- Habibi, A.; Jahantigh, F.F.; Sarafrazi, A. Fuzzy Delphi technique for forecasting and screening items. Asian J. Res. Bus. Econ. Manag. 2015, 5, 130–143. [Google Scholar] [CrossRef]
| Triangular Intuitionistic Fuzzy Numbers | Intuitionistic Fuzzy Number | Linguistic Expressions |
|---|---|---|
| (0, 0, 0.25; 0.05, 0.90) | 1 | Very unimportant (VUI) |
| (0, 0.25, 0.5; 0.35, 0.6) | 2 | Unimportant (UI) |
| (0.25, 0.5, 0.75; 0.5, 0.4) | 3 | Moderately important (MI) |
| (0.5, 0.75, 1; 0.75, 0.2) | 4 | Important (I) |
| (0.75, 1, 1; 0.9, 0.05) | 5 | Critical (VI) |
| # | Risk | Expert 1 | Expert 2 | Expert 3 | Expert 4 | Expert 5 |
|---|---|---|---|---|---|---|
| R1 | Vulnerability caused by the type of structure | MI | I | I | MI | VI |
| R2 | Vulnerability of infrastructure | UI | MI | VUI | I | MI |
| R3 | Vulnerability due to old buildings | I | VI | MI | VI | I |
| R4 | Lack of access to open space | VUI | MI | UI | MI | UI |
| R5 | Vulnerability caused by the quality of the building | MI | I | MI | VI | I |
| R6 | Building fire | I | UI | I | UI | MI |
| R7 | Obstruction of roads | VI | I | MI | VI | I |
| R8 | Explosion | VUI | MI | UI | VUI | UI |
| R9 | Vulnerability due to environmental and structural conditions | MI | UI | MI | I | MI |
| R10 | Vulnerability caused by non-compliance with construction material standards | I | MI | I | VI | I |
| R11 | Vulnerability caused by aftershocks | VI | I | MI | I | I |
| Risk | Expert 1 | Expert 2 | Expert 3 | Expert 4 | Expert 5 |
|---|---|---|---|---|---|
| R1 | (0.25, 0.5, 0.75; 0.5, 0.4) | (0.5, 0.75, 1; 0.75, 0.2) | (0.5, 0.75, 1; 0.75, 0.2) | (0.25, 0.5, 0.75; 0.5, 0.4) | (0.75, 1, 1; 0.9, 0.05) |
| R2 | (0, 0.25, 0.5; 0.35, 0.6) | (0.25, 0.5, 0.75; 0.5, 0.4) | (0, 0, 0.25; 0.05, 0.90) | (0.5, 0.75, 1; 0.75, 0.2) | (0.25, 0.5, 0.75; 0.5, 0.4) |
| R3 | (0.5, 0.75, 1; 0.75, 0.2) | (0.75, 1, 1; 0.9, 0.05) | (0.25, 0.5, 0.75; 0.5, 0.4) | (0.75, 1, 1; 0.9, 0.05) | (0.5, 0.75, 1; 0.75, 0.2) |
| R4 | (0, 0, 0.25; 0.05, 0.90) | (0.25, 0.5, 0.75; 0.5, 0.4) | (0, 0.25, 0.5; 0.35, 0.6) | (0.25, 0.5, 0.75; 0.5, 0.4) | (0, 0.25, 0.5; 0.35, 0.6) |
| R5 | (0.25, 0.5, 0.75; 0.5, 0.4) | (0.5, 0.75, 1; 0.75, 0.2) | (0.25, 0.5, 0.75; 0.5, 0.4) | (0.75, 1, 1; 0.9, 0.05) | (0.5, 0.75, 1; 0.75, 0.2) |
| R6 | (0.5, 0.75, 1; 0.75, 0.2) | (0, 0.25, 0.5; 0.35, 0.6) | (0.5, 0.75, 1; 0.75, 0.2) | (0, 0.25, 0.5; 0.35, 0.6) | (0.25, 0.5, 0.75; 0.5, 0.4) |
| R7 | (0.75, 1, 1; 0.9, 0.05) | (0.5, 0.75, 1; 0.75, 0.2) | (0.25, 0.5, 0.75; 0.5, 0.4) | (0.75, 1, 1; 0.9, 0.05) | (0.5, 0.75, 1; 0.75, 0.2) |
| R8 | (0, 0, 0.25; 0.05, 0.90) | (0.25, 0.5, 0.75; 0.5, 0.4) | (0, 0.25, 0.5; 0.35, 0.6) | (0, 0, 0.25; 0.05, 0.90) | (0, 0.25, 0.5; 0.35, 0.6) |
| R9 | (0.25, 0.5, 0.75; 0.5, 0.4) | (0, 0.25, 0.5; 0.35, 0.6) | (0.25, 0.5, 0.75; 0.5, 0.4) | (0.5, 0.75, 1; 0.75, 0.2) | (0.25, 0.5, 0.75; 0.5, 0.4) |
| R10 | (0.5, 0.75, 1; 0.75, 0.2) | (0.25, 0.5, 0.75; 0.5, 0.4) | (0.5, 0.75, 1; 0.75, 0.2) | (0.75, 1, 1; 0.9, 0.05) | (0.5, 0.75, 1; 0.75, 0.2) |
| R11 | (0.75, 1, 1; 0.9, 0.05) | (0.5, 0.75, 1; 0.75, 0.2) | (0.25, 0.5, 0.75; 0.5, 0.4) | (0.5, 0.75, 1; 0.75, 0.2) | (0.5, 0.75, 1; 0.75, 0.2) |
| Risk | a1 | a2 | a3 | |||
|---|---|---|---|---|---|---|
| R1 | 0.45 | 0.7 | 0.9 | 0.683 | 0.267 | 0.05 |
| R2 | 0.25 | 0.45 | 0.65 | 0.45 | 0.45 | 0.1 |
| R3 | 0.55 | 0.8 | 0.95 | 0.766 | 0.184 | 0.05 |
| R4 | 0.1 | 0.3 | 0.55 | 0.32 | 0.63 | 0.05 |
| R5 | 0.5 | 0.75 | 0.85 | 0.7 | 0.25 | 0.05 |
| R6 | 0.25 | 0.5 | 0.75 | 0.5 | 0.4 | 0.1 |
| R7 | 0.55 | 0.8 | 0.95 | 0.77 | 0.18 | 0.05 |
| R8 | 0.05 | 0.2 | 0.45 | 0.233 | 0.717 | 0.05 |
| R9 | 0.35 | 0.6 | 0.85 | 0.6 | 0.35 | 0.05 |
| R10 | 0.5 | 0.75 | 0.95 | 0.733 | 0.217 | 0.05 |
| R11 | 0.5 | 0.75 | 0.95 | 0.733 | 0.217 | 0.05 |
| Risk | L | U | Defuzzy | Result |
|---|---|---|---|---|
| R1 | 0.683 | 0.733 | 0.733 | Confirmation |
| R2 | 0.45 | 0.55 | 0.5 | Confirmation |
| R3 | 0.766 | 0.816 | 0.816 | Confirmation |
| R4 | 0.32 | 0.37 | 0.370 | Rejection |
| R5 | 0.7 | 0.75 | 0.750 | Confirmation |
| R6 | 0.5 | 0.6 | 0.550 | Confirmation |
| R7 | 0.77 | 0.82 | 0.820 | Confirmation |
| R8 | 0.233 | 0.283 | 0.283 | Rejection |
| R9 | 0.6 | 0.65 | 0.650 | Confirmation |
| R10 | 0.733 | 0.783 | 0.783 | Confirmation |
| R11 | 0.733 | 0.783 | 0.783 | Confirmation |
| Risk | Score of Linguistic Expression | Result of Qualitative Analysis | Selection/Confirmation or Rejection |
|---|---|---|---|
| R1 | 4 | I | Confirmation |
| R2 | 3 | MI | Confirmation |
| R3 | 4 | I | Confirmation |
| R4 | 2 | UI | Rejection |
| R5 | 4 | I | Confirmation |
| R6 | 3 | MI | Confirmation |
| R7 | 4 | I | Confirmation |
| R8 | 2 | UI | Rejection |
| R9 | 3 | MI | Confirmation |
| R10 | 4 | I | Confirmation |
| R11 | 4 | I | Confirmation |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sadeghi, J.; Sarvari, H.; Chan, D.W.M.; Edwards, D.J. Identification and Analysis of Earthquake Risks in Worn-Out Urban Fabrics Using the Intuitionistic Fuzzy Brainstorming (IFBS) Technique for Group Decision-Making. Buildings 2025, 15, 1520. https://doi.org/10.3390/buildings15091520
Sadeghi J, Sarvari H, Chan DWM, Edwards DJ. Identification and Analysis of Earthquake Risks in Worn-Out Urban Fabrics Using the Intuitionistic Fuzzy Brainstorming (IFBS) Technique for Group Decision-Making. Buildings. 2025; 15(9):1520. https://doi.org/10.3390/buildings15091520
Chicago/Turabian StyleSadeghi, Jalal, Hadi Sarvari, Daniel W. M. Chan, and David J. Edwards. 2025. "Identification and Analysis of Earthquake Risks in Worn-Out Urban Fabrics Using the Intuitionistic Fuzzy Brainstorming (IFBS) Technique for Group Decision-Making" Buildings 15, no. 9: 1520. https://doi.org/10.3390/buildings15091520
APA StyleSadeghi, J., Sarvari, H., Chan, D. W. M., & Edwards, D. J. (2025). Identification and Analysis of Earthquake Risks in Worn-Out Urban Fabrics Using the Intuitionistic Fuzzy Brainstorming (IFBS) Technique for Group Decision-Making. Buildings, 15(9), 1520. https://doi.org/10.3390/buildings15091520









