Rapid Damage Assessment and Bayesian-Based Debris Prediction for Building Clusters Against Earthquakes
Abstract
1. Introduction
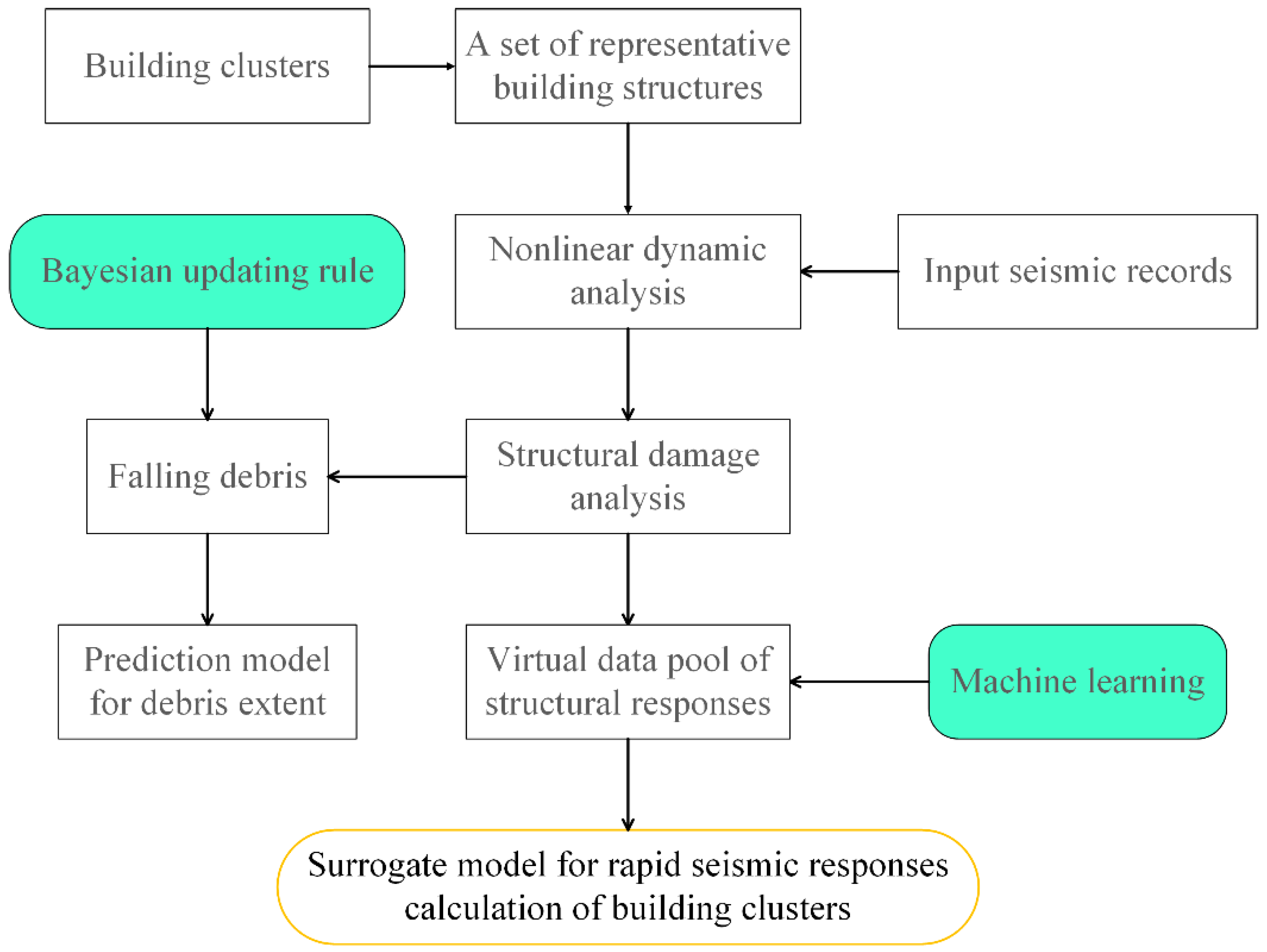
2. Framework for Developing the Surrogate Model for Rapid Seismic Responses Calculation of Building Clusters and Probabilistic Prediction Model of Debris Width
- (i)
- Using the nonlinear time-history analysis (NTHA) on the refined FE models of buildings on OpenSees platform to generate high-quality training data.
- (ii)
- A surrogate model is trained with the XGBOOST algorithm based on the data obtained by the NTHA method.
- (iii)
- The trained surrogate model is used to rapidly calculate the seismic-induced structural responses of building clusters replacing the NTHA.
3. The Surrogate Model and Debris Width Prediction Model for Multi-Story RC Frame Structures
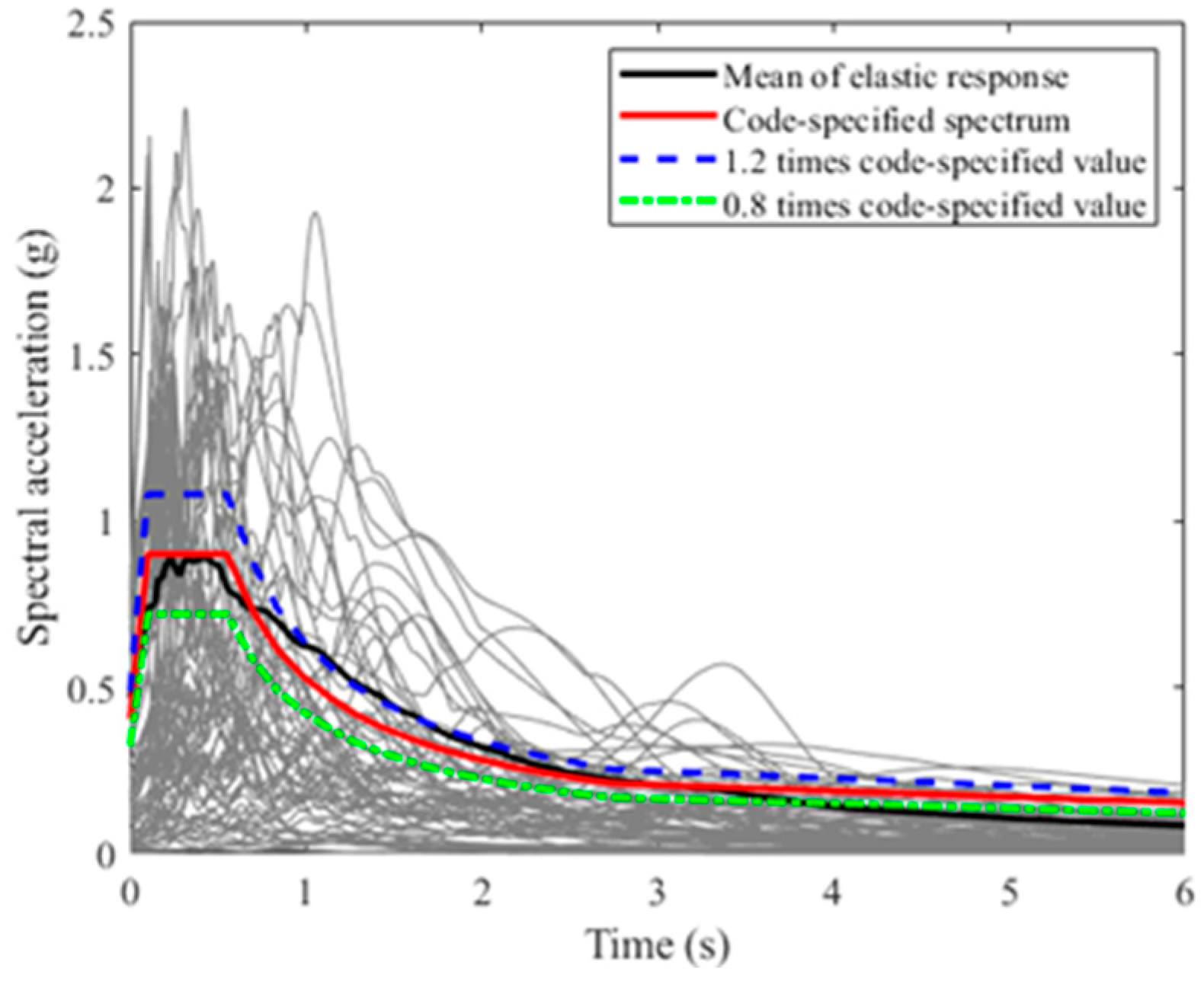
3.1. Input Seismic Ground Motion Records
3.2. Machine-Learning-Based Surrogate Model
3.3. Bayesian-Based Prediction Model of Debris Width
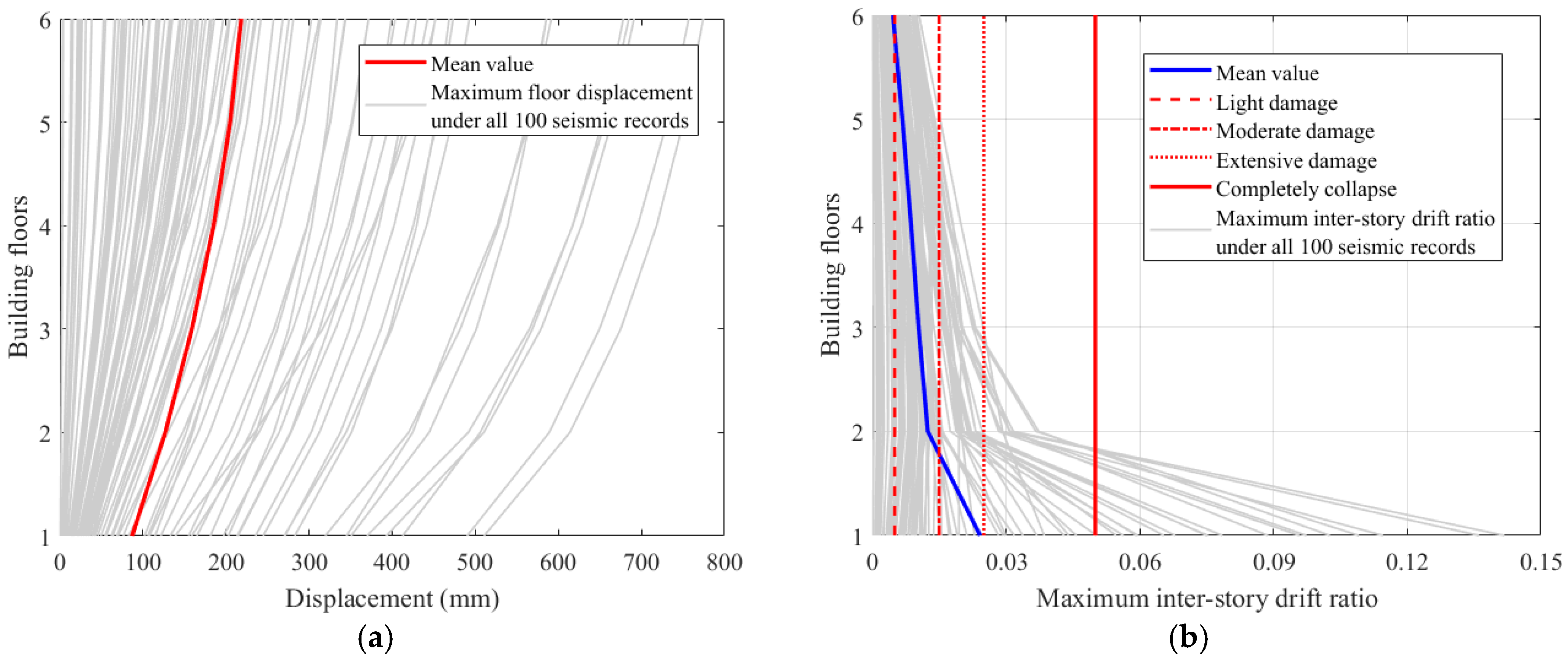
4. Seismic Damage Assessment for Building Clusters
5. Conclusions
- (1)
- The XGBoost-based surrogate model achieves exceptional accuracy in predicting structural responses (e.g., R2 > 0.99 for floor displacement and R2 = 0.989 for maximum inter-story drift ratio), reducing computational time by over 90% compared to traditional nonlinear time-history analyses. This surrogate model enables rapid damage assessment for large-scale building clusters, which is critical for real-time emergency decision making.
- (2)
- The Bayesian-updated model significantly reduces uncertainty in debris width prediction, narrowing the standard deviation of model error by 60%, from prior σ = 10.2 to posterior σ = 4.1. This probabilistic approach outperforms deterministic methods, providing 95% confidence intervals for debris blockage distances, which is essential for evacuation route planning.
- (3)
- Application to a campus building cluster under the Wenchuan earthquake event with PGA = 203.45 cm/s2 reveals severe damage (MIDR > 2.5%) in 35% of dormitory buildings, with debris blocking 45% of adjacent roads. These results highlight the utility of this presented framework in identifying high-risk zones and optimizing post-disaster rescue strategies.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Feng, K.; Li, Q.; Ellingwood, B.R. Post-earthquake modelling of transportation networks using an agent-based model. Struct. Infrastruct. Eng. 2020, 16, 1578–1592. [Google Scholar] [CrossRef]
- Byun, J.-E.; D’Ayala, D. Urban seismic resilience mapping: A transportation network in Istanbul, Turkey. Sci. Rep. 2022, 12, 8188. [Google Scholar] [CrossRef] [PubMed]
- Sediek Omar, A.; El-Tawil, S.; McCormick, J. Seismic Debris Field for Collapsed RC Moment Resisting Frame Buildings. J. Struct. Eng. 2021, 147, 04021045. [Google Scholar] [CrossRef]
- FEMA-P-58; Seismic Performance Assessment of Buildings, Methodology and Implementation. Federal Emergency Management Agency (FEMA): Washington, DC, USA, 2018.
- Zhang, B.; Xiong, F.; Lu, Y.; Ge, Q.; Liu, Y.; Mei, Z.; Ran, M. Regional seismic damage analysis considering soil–structure cluster interaction using lumped parameter models: A case study of Sichuan University Wangjiang Campus buildings. Bull. Earthq. Eng. 2021, 19, 4289–4310. [Google Scholar] [CrossRef]
- Xu, Z.; Wu, Y.; Lu, X.Z.; Jin, X.L. Photo-realistic visualization of seismic dynamic responses of urban building clusters based on oblique aerial photography. Adv. Eng. Inform. 2020, 43, 101025. [Google Scholar] [CrossRef]
- Hayashi, K.; Saito, T.; Horioka, T.; Sato, E. Implementation of real-time seismic diagnostic system on emergency management center buildings: System introduction and operational status on municipal government office buildings. J. Civ. Struct. Health Monit. 2019, 9, 529–541. [Google Scholar] [CrossRef]
- Morfidis, K.; Stefanidou, S.; Markogiannaki, O. A Rapid Seismic Damage Assessment (RASDA) Tool for RC Buildings Based on an Artificial Intelligence Algorithm. Appl. Sci. 2023, 13, 5100. [Google Scholar] [CrossRef]
- Kalakonas, P.; Silva, V. Seismic vulnerability modelling of building portfolios using artificial neural networks. Earthq. Eng. Struct. Dyn. 2022, 51, 310–327. [Google Scholar] [CrossRef]
- Chen, C.S. Seismic performance assessments of school buildings in Taiwan using artificial intelligence theories. Eng. Comput. 2020, 37, 3321–3343. [Google Scholar] [CrossRef]
- Ruggieri, S.; Liguori, F.S.; Leggieri, V.; Bilotta, A.; Madeo, A.; Casolo, S.; Uva, G. An archetype-based automated procedure to derive global-local seismic fragility of masonry building aggregates: META-FORMA-XL. Int. J. Disaster Risk Reduct. 2023, 95, 103903. [Google Scholar] [CrossRef]
- Stojadinovic, Z.; Kovacevic, M.; Marinkovic, D.; Stojadinovic, B. Rapid earthquake loss assessment based on machine learning and representative sampling. Earthq. Spectra 2022, 38, 152–177. [Google Scholar] [CrossRef]
- Zhang, C.; Wen, W.; Zhai, C.; Jia, J.; Zhou, B. Structural nonlinear seismic time-history response prediction of urban-scale reinforced concrete frames based on deep learning. Eng. Struct. 2024, 317, 118702. [Google Scholar] [CrossRef]
- Zhou, Y.; Meng, S.; Lou, Y.; Kong, Q. Physics-Informed Deep Learning-Based Real-Time Structural Response Prediction Method. Engineering 2024, 35, 140–157. [Google Scholar] [CrossRef]
- ASCE7-22; Minimum Design Loads and Associated Criteria for Buildings and Other Structures. American Society of Civil Engineers (ASCE): Reston, VA, USA, 2022.
- GB/T51327-2018; Standard for Urban Planning on Comprehensive Disaster Resistance and Prevention. China Architecture & Building Press: Beijing, China, 2018.
- Lu, X.; Yang, Z.; Chea, C.; Guan, H. Experimental study on earthquake-induced falling debris of exterior infill walls and its impact to pedestrian evacuation. Int. J. Disaster Risk Reduct. 2020, 43, 101372. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, N.; Wang, L.; Wang, Z.; Ma, D. A Study of Influence Distance and Road Safety Avoidance Distance from Postearthquake Building Debris Accumulation. Adv. Civ. Eng. 2020, 2020, 1–17. [Google Scholar] [CrossRef]
- Zhou, Y.; Chen, H.; Lin, X.; Chen, Z. Research on Emergency Evacuation Route Planning Method based on Building Groups Seismic Damage Simulation. J. Disaster Prev. Mitig. Eng. 2022, 42, 1174–1182. [Google Scholar]
- Zheng, X.-W.; Li, H.-N.; Shi, Z.-Q. Hybrid AI-Bayesian-based demand models and fragility estimates for tall buildings against multi-hazard of earthquakes and winds. Thin-Walled Struct. 2023, 187, 110749. [Google Scholar] [CrossRef]
- Zheng, X.-W.; Li, H.-N.; Gardoni, P. Hybrid Bayesian-Copula-based risk assessment for tall buildings subject to wind loads considering various uncertainties. Reliab. Eng. Syst. Saf. 2023, 233, 109100. [Google Scholar] [CrossRef]
- Zheng, X.-W.; Li, H.-N.; Lv, H.-L.; Huo, L.-S.; Zhang, Y.-Y. Bayesian-based seismic resilience assessment for high-rise buildings with the uncertainty in various variables. J. Build. Eng. 2022, 51, 104321. [Google Scholar] [CrossRef]
- Zheng, X.-W.; Li, H.-N.; Gardoni, P. Probabilistic seismic demand models and life-cycle fragility estimates for high-rise buildings. J. Struct. Eng. 2021, 147, 04021216. [Google Scholar] [CrossRef]
- Gardoni, P.; Der Kiureghian, A.; Mosalam, K.M. Probabilistic capacity models and fragility estimates for reinforced concrete columns based on experimental observations. J. Eng. Mech. 2002, 128, 1024–1038. [Google Scholar] [CrossRef]
- Berg, B.A.; Billoire, A. Markov Chain Monte Carlo Simulations; John Wiley & Sons, Inc.: New York, NY, USA, 2008. [Google Scholar]
- GB50011-2010; Code for Seismic Design of Buildings. China Architecture and Building Press: Beijing, China, 2016.
- Melchers, R.E. Structural Reliability Analysis and Prediction; John Wiley: New York, NY, USA, 1999. [Google Scholar]
- Barbato, M.; Gu, Q.; Conte, J.P. Probabilistic Pushover analysis of structural and soil-structure systems. J. Struct. Eng. 2010, 136, 1330–1341. [Google Scholar] [CrossRef]
- Porter, K.A.; Beck, J.L.; Shaikhutdinov, R.V.; Earthquake, P. Investigation of Sensitivity of Building Loss Estimates to Major Uncertain Variables for the Van Nuys Testbed; Pacific Earthquake Engineering Research Center: Berkeley, CA, USA, 2002. [Google Scholar]
- Wen, Y.K.; Kang, Y.J. Minimum building life-cycle cost design criteria. I: Methodology. J. Struct. Eng. 2001, 127, 330–337. [Google Scholar] [CrossRef]
- Sowmya, R.; Premkumar, M.; Jangir, P. Newton-Raphson-based optimizer: A new population-based metaheuristic algorithm for continuous optimization problems. Eng. Appl. Artif. Intell. 2024, 128, 107532. [Google Scholar] [CrossRef]
- He, Y.; Zhai, C.; Wen, W. Probabilistic prediction of post-earthquake rubble range for RC frame structures. Soil Dyn. Earthq. Eng. 2023, 171, 107927. [Google Scholar] [CrossRef]
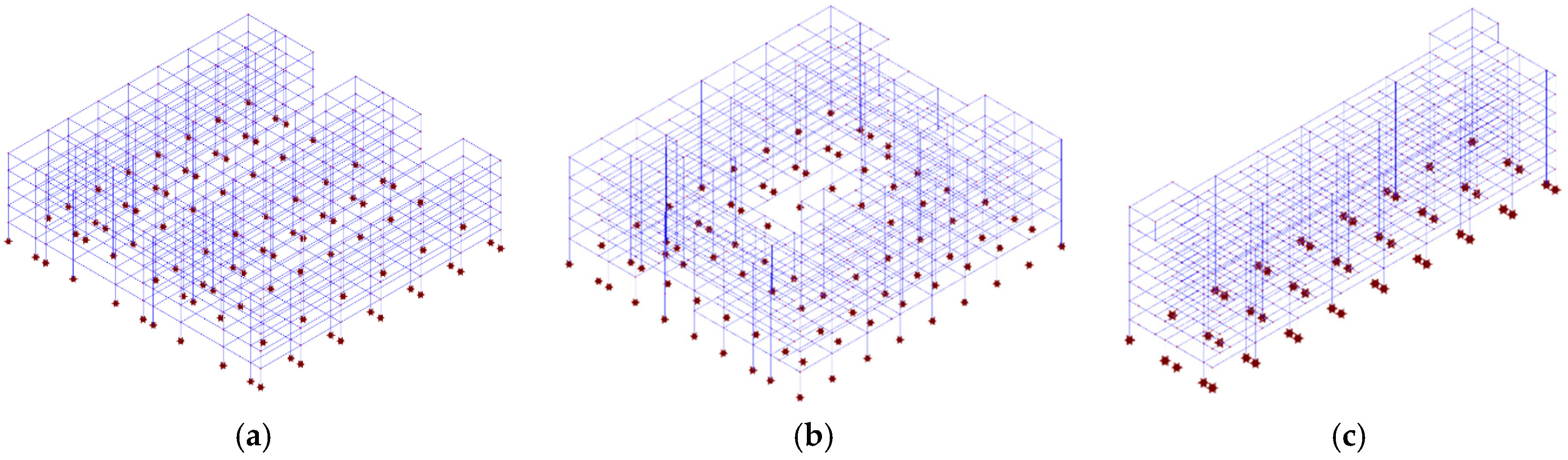
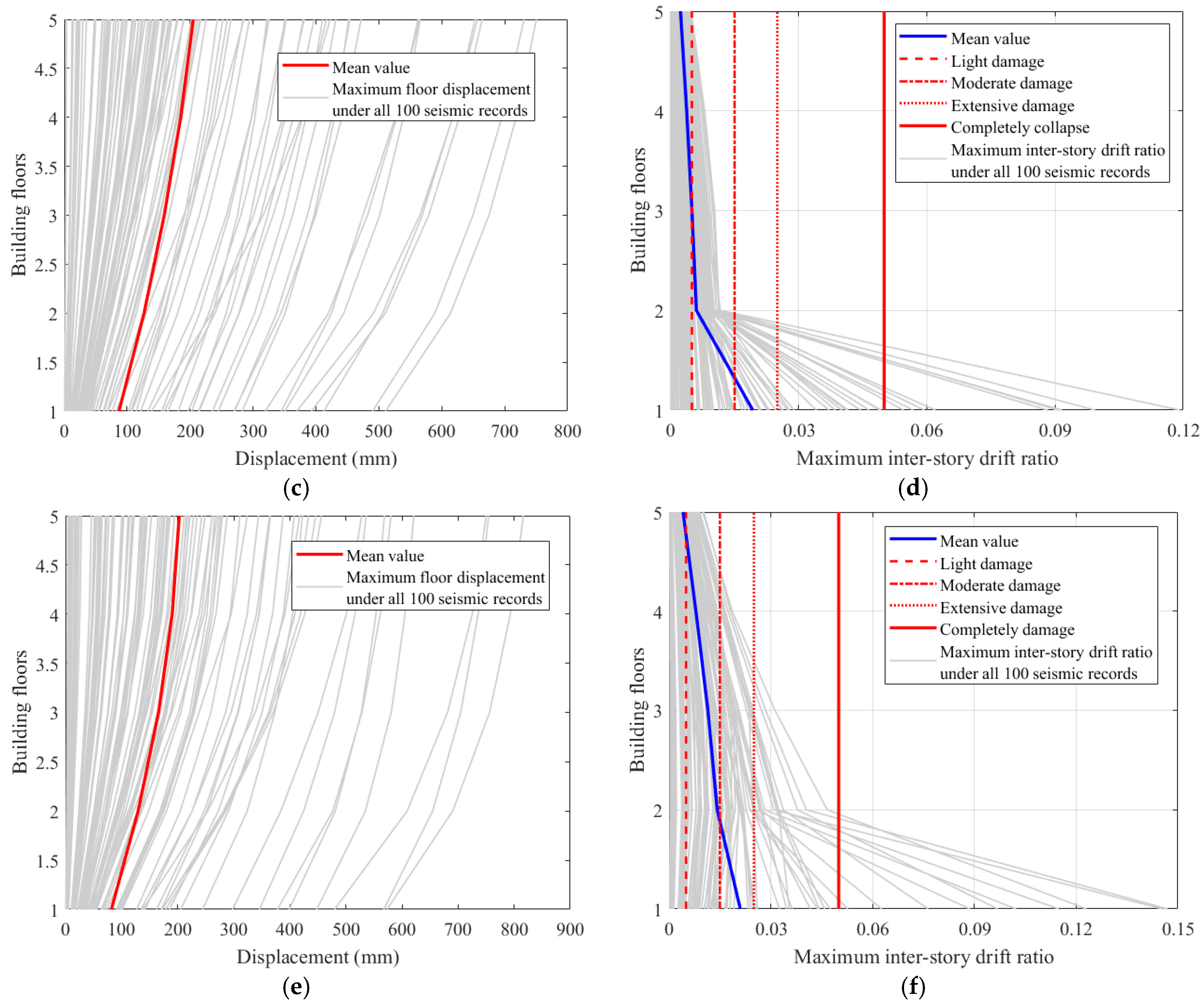

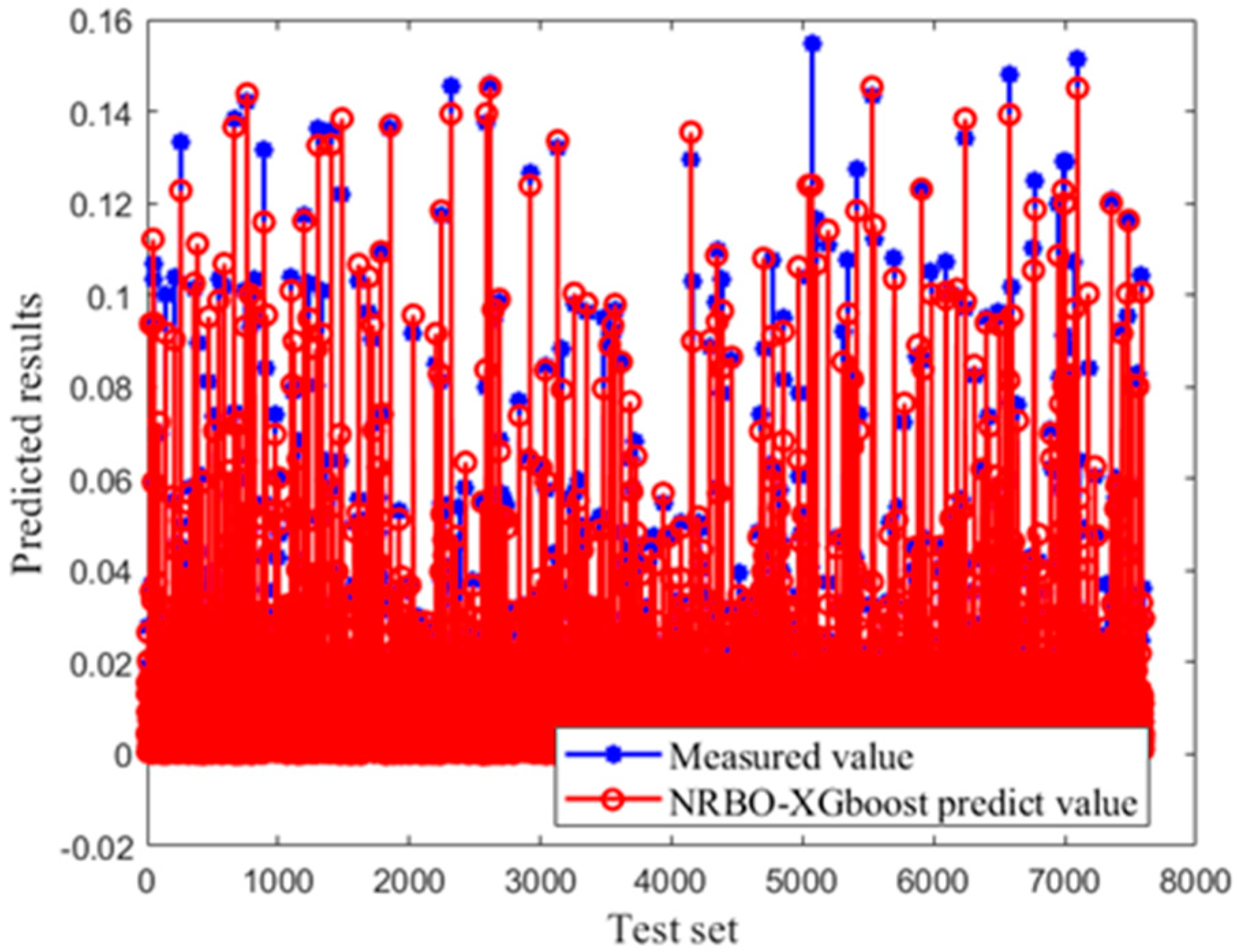
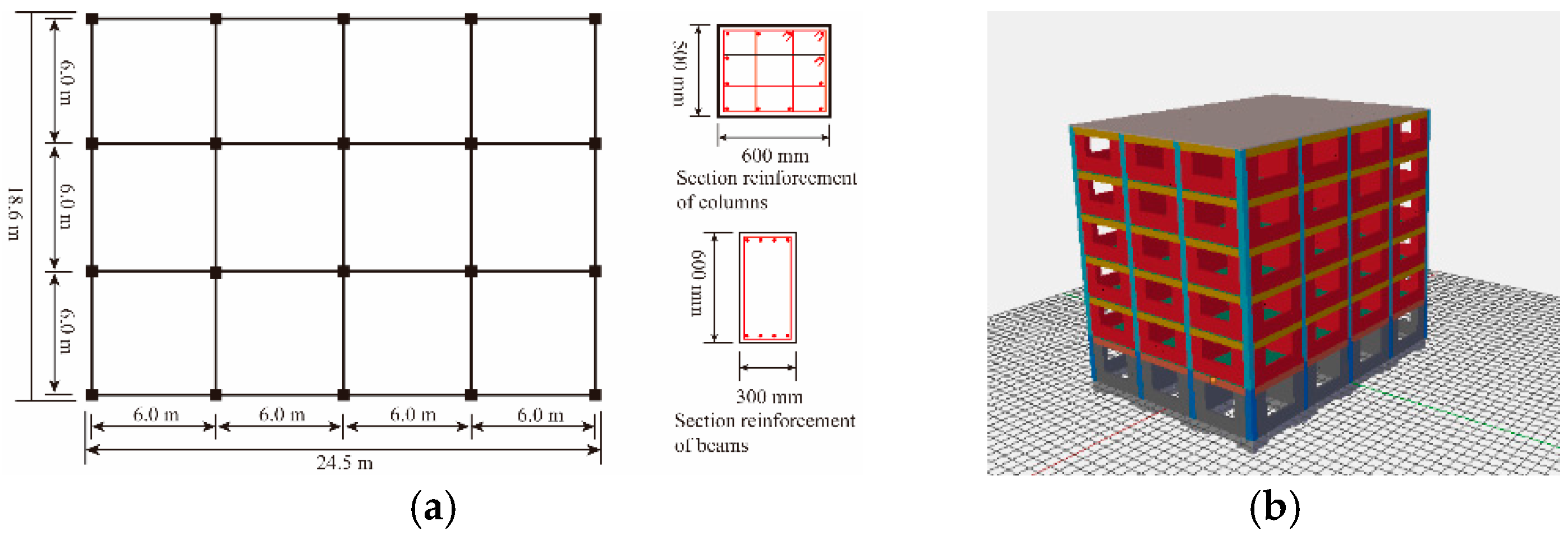
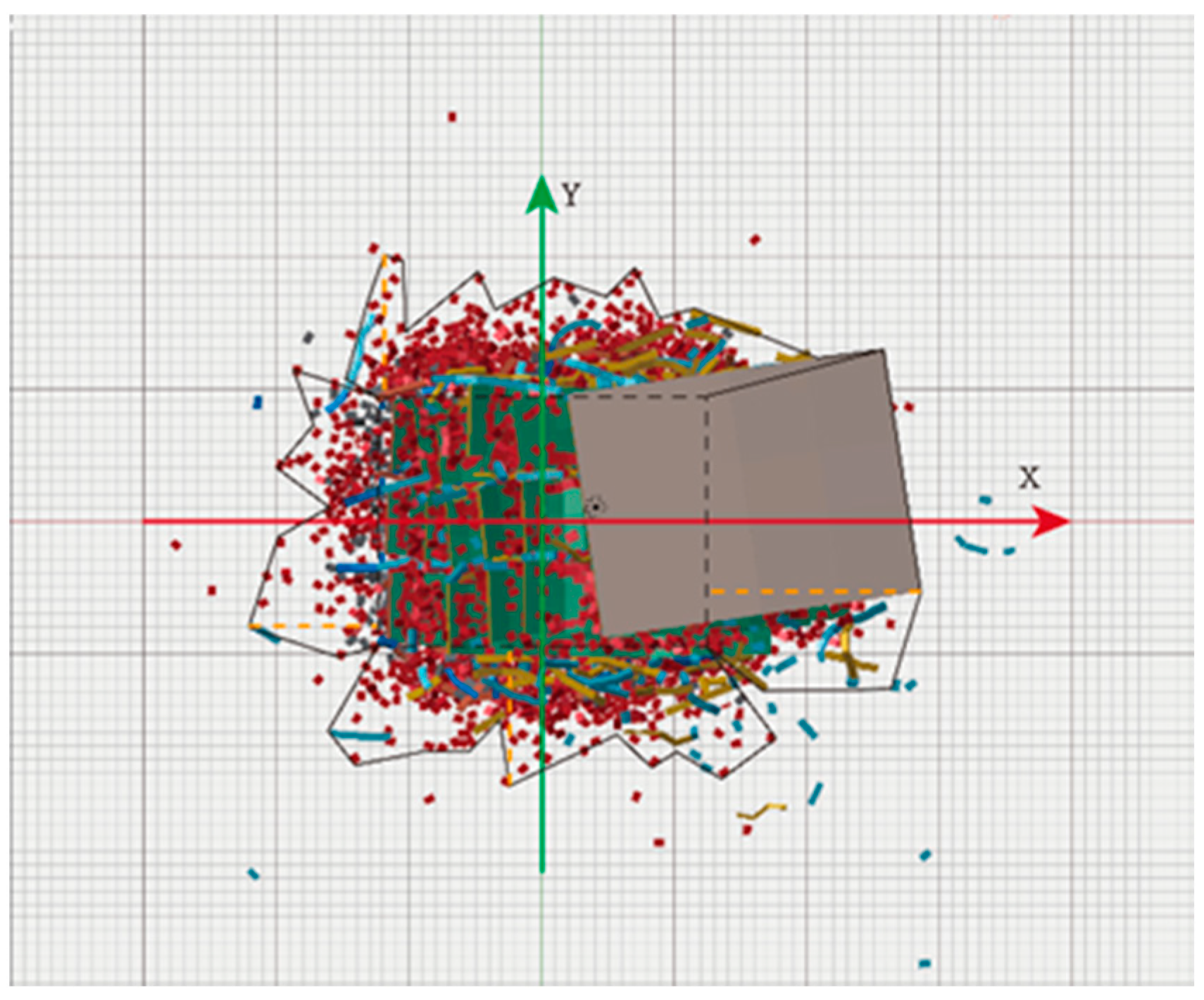
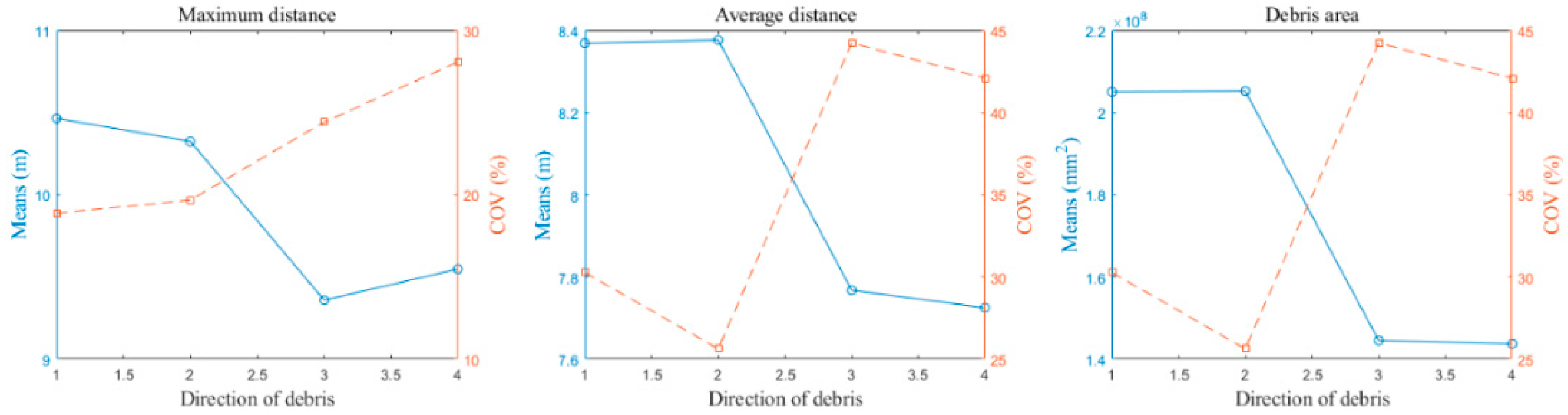


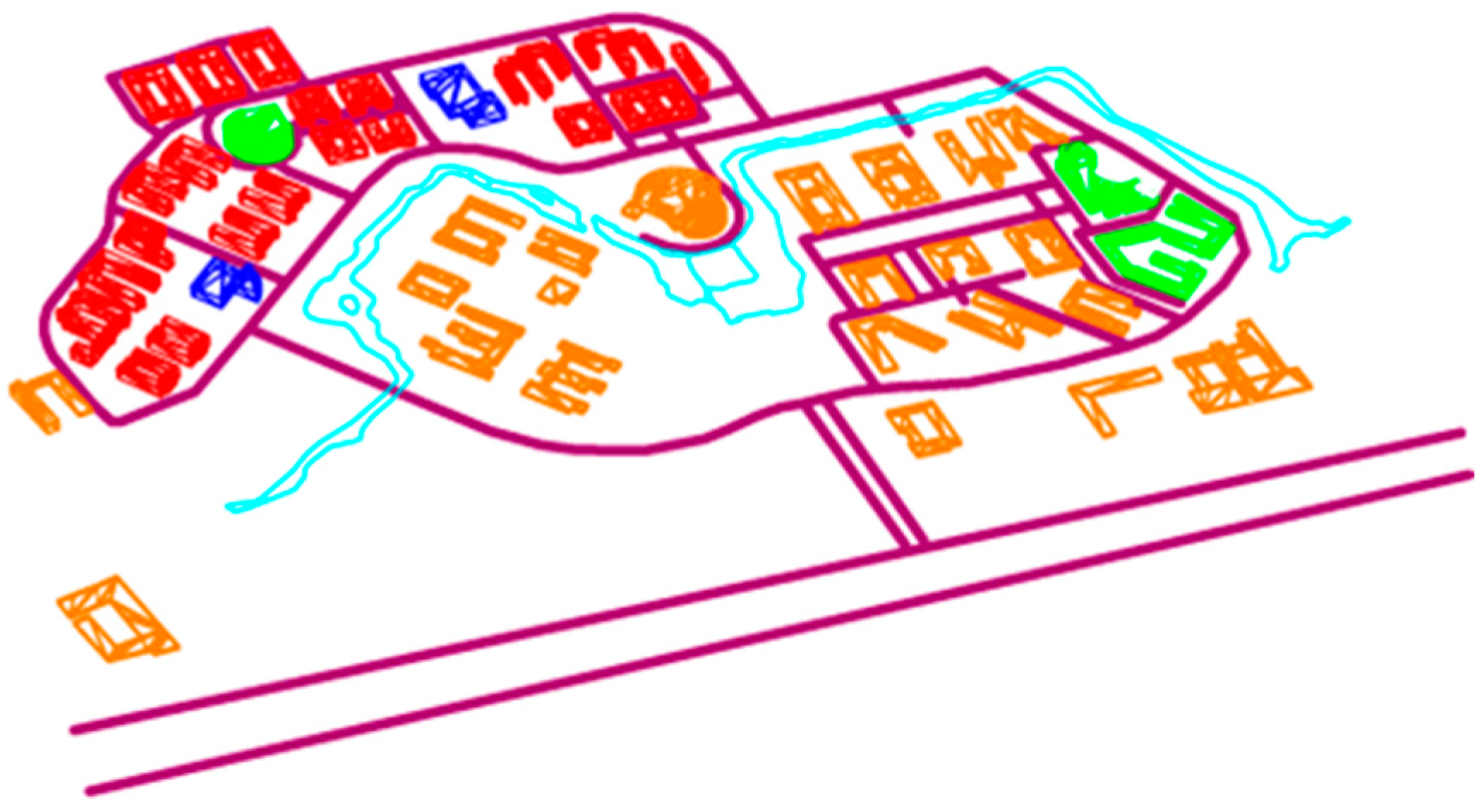
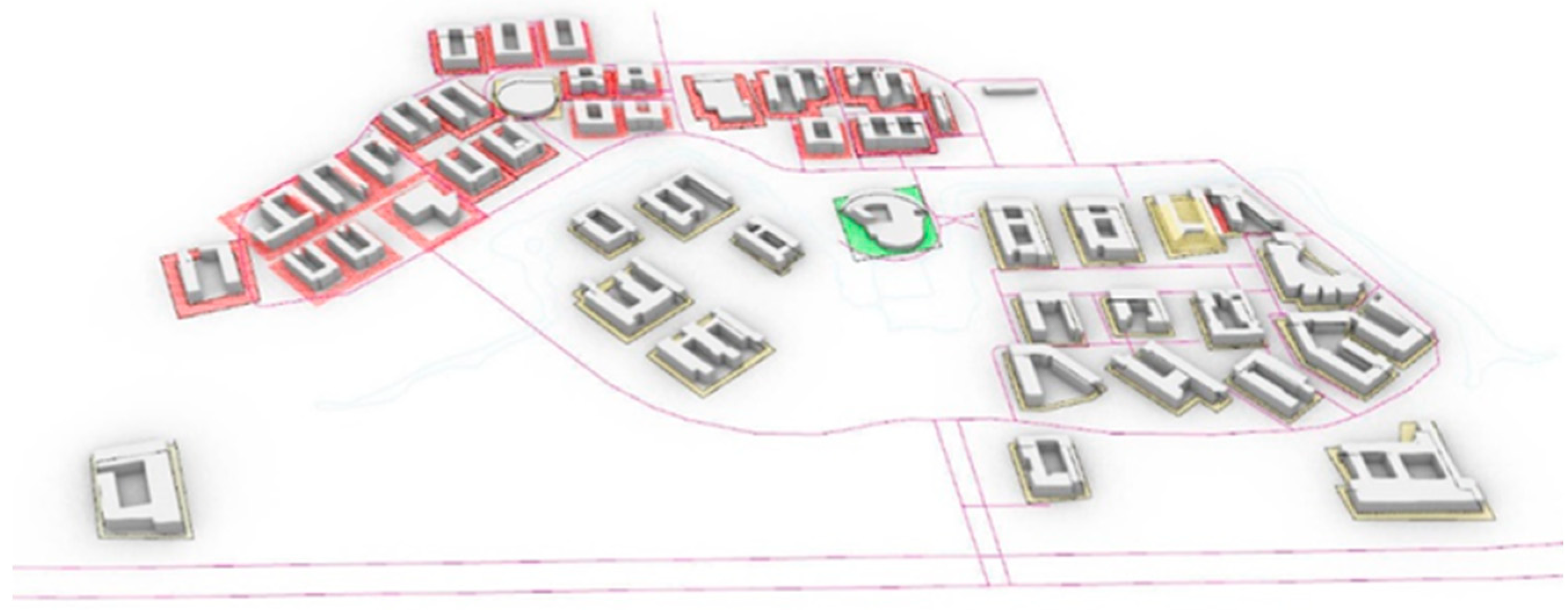
| Categories | Function | Height (m) | Section (mm) |
|---|---|---|---|
| Five floors structures | Teaching building | Ground floor: 3.9 Other floors: 3.6 Total height: 18.3 | Beams: 350 × 500 Reinforcement ratio: 2.285% Columns: 600 × 600 Reinforcement ratio: 1.111% |
| Five floors structures | Office building | Ground floor: 4.5 Other floors: 3.6 Total height: 18.9 | Beams: 600 × 800 Reinforcement ratio: 1.308%; Columns: 800 × 800 Reinforcement ratio: 0.981%; |
| Six floors structures | Dormitory building | Ground floor: 3.6, Other floors: 3.3 Total height: 23.4 | Beams: 400 × 600 Reinforcement ratio: 1.667%; Columns: 700 × 700 Reinforcement ratio: 0.816% |
| Natural Period of Vibration | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Te | 0.972 | 0.865 | 0.836 | 0.807 | 0.791 | 0.756 |
| To | 0.997 | 0.890 | 0.857 | 0.835 | 0.834 | 0.750 |
| ɛ | 2.54% | 2.90% | 2.48% | 3.39% | 5.49% | 4.50% |
| Parameter | Mean Value | COV/% | Probability Distribution | Upper Limit | Lower Limit | Source |
|---|---|---|---|---|---|---|
| fy (MPa) | 363.8 | 5 | Lognormal | 1.1 fy,mean | 0.9 fy,mean | Melchers [27] |
| αs (−) | 0.03 | 20 | Lognormal | 0.04 | 0.02 | Barbato et al. [28] |
| E (Mpa) | 201,000 | 3.3 | Lognormal | 214,266 | 187,734 | Barbato et al. [28] |
| ξ (−) | 0.05 | 40 | Normal | 1.4 ξmean | 0.6 ξmean | Porter et al. [29] |
| Eigenvalue Type | Parameter | Data Format |
|---|---|---|
| Earthquake | PGA, Δt, duration. | Numeric data |
| Uncertainty parameters | Damping ratio, modulus of elasticity, yield strength, post-yield stiffness ratio. | Numeric data |
| Architectural information | Use function. | Text data |
| X and Y direction natural period of vibration, maximum column spacing, span number, beam-column reinforcement ratio, floor height, number of building floors. | Numeric data |
| Output Characteristic | Set | MAE | MSE | RMSE | MAPE | R2 |
|---|---|---|---|---|---|---|
| Floor displacement | Training | 3.186 | 22.890 | 4.784 | 0.050 | 0.9990 |
| Testing | 5.048 | 65.998 | 8.124 | 0.072 | 0.9972 | |
| MIDR | Training | 3.252 × 10−4 | 3.727 × 10−7 | 6.105 × 10−4 | 0.054 | 0.9983 |
| Testing | 6.042 × 10−4 | 2.509 × 10−6 | 1.584 × 10−3 | 0.075 | 0.9890 |
| Parameters | Average Value | Standard Deviation | Correlation Coefficient Matrix | ||
|---|---|---|---|---|---|
| θ1 | θ2 | σ | |||
| θ1 | −8.226 | 4.198 | 1 | −0.98 | −0.01 |
| θ2 | 16.161 | 8.322 | −0.98 | 1 | 0.01 |
| σ | 4.116 | 0.289 | −0.01 | 0.01 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, X.; Hou, Y.; Cheng, J.; Xu, S.; Wang, W. Rapid Damage Assessment and Bayesian-Based Debris Prediction for Building Clusters Against Earthquakes. Buildings 2025, 15, 1481. https://doi.org/10.3390/buildings15091481
Zheng X, Hou Y, Cheng J, Xu S, Wang W. Rapid Damage Assessment and Bayesian-Based Debris Prediction for Building Clusters Against Earthquakes. Buildings. 2025; 15(9):1481. https://doi.org/10.3390/buildings15091481
Chicago/Turabian StyleZheng, Xiaowei, Yaozu Hou, Jie Cheng, Shuai Xu, and Wenming Wang. 2025. "Rapid Damage Assessment and Bayesian-Based Debris Prediction for Building Clusters Against Earthquakes" Buildings 15, no. 9: 1481. https://doi.org/10.3390/buildings15091481
APA StyleZheng, X., Hou, Y., Cheng, J., Xu, S., & Wang, W. (2025). Rapid Damage Assessment and Bayesian-Based Debris Prediction for Building Clusters Against Earthquakes. Buildings, 15(9), 1481. https://doi.org/10.3390/buildings15091481







