Abstract
Conventional analyses often simplify vertical loads as uniform radial loads while neglecting axial force effects in the buckling analyses of arches, leading to discrepancies between theoretical predictions and actual loading conditions. To address this issue, this research proposes a nonlinear analytical approach based on asymptotic methods, include the parameter perturbation method and the Wentzel–Kramers–Brillouin (WKB) method. The results show the following: (1) The parameter perturbation method is effective for the snap-buckling of a shallow arch, and the fifth-order solution is sufficiently accurate. (2) For shallow arches with a large modified slenderness ratio, the influence of the axial load component cannot be neglected. (3) Regardless of the rise-to-span ratio of the arch, the nonlinear bending moment is significantly larger than the linear bending moment. (4) In the anti-symmetric buckling analysis, the eigenvalue obtained using the second-order WKB method is smaller than that obtained using the third-order WKB method; therefore, the second-order solution can be used as the critical load. (5) For shallow arches with a small rise-to-span ratio, the critical load for anti-symmetric buckling closely matches the classical solution, and the results from arches subjected to a uniformly distributed radial load are reliable. For deep arches with a large rise-to-span ratio, the influence of the axial load component cannot be ignored.
1. Introduction
Arches are classified as shallow or deep based on the rise-to-span ratio, with a ratio of less than 0.2 typically considered shallow [1]. Under in-plane loading, shallow arches may exhibit either anti-symmetric bifurcation or snap-through buckling, while deep arches typically experience only anti-symmetric buckling [1,2,3,4,5,6]. Classical buckling theory is used to determine the elastic anti-symmetric buckling load of arches subjected to uniform radial loads, assuming linear pre-buckling behavior [5,6,7,8]. Analytical solutions for the arch stability problem can be obtained under specific load conditions, such as uniform radial and central concentrated loads; however, solutions are generally not available for other loading scenarios. In the analysis of arches subjected to uniform vertical loads, the vertical load is typically simplified to a uniform radial load [3,9], neglecting the influence of the axial load component. Y.-L. Pi et al. studied the nonlinear buckling behavior of circular shallow arches subjected to uniform radial loads and provided formulas for both snap-through instability and anti-symmetric buckling of the arches [2,3,4,5]. G. Tong et al. [1] investigated the anti-symmetric buckling of pin-ended circular arches subjected to uniform vertical and radial loads, considering the effects of transverse and shear stresses. The critical load of arches was obtained using the Galerkin method, though their study focused solely on deep arches. Eslami and Babaei [10,11,12] conducted a series of theoretical studies on the nonlinear snap-through buckling of shallow arches using the two-step perturbation method and the Galerkin method. Novel parametric studies have also been conducted to show the effects of nonlocal and length scale parameters, and the geometrical parameters of the shell. Y. Guo et al. [13] conducted experimental research on the in-plane stability and bearing capacity of pin-ended circular arches with I-beam cross-sections under combined compression and bending. They validated theoretical analysis results and proposed design formulas for the in-plane stability and bearing capacity of compressed circular arches. However, their study did not further investigate the differences between uniform vertical loads and uniform radial loads. Caporale et al. [14] illustrated the application of an original approach to the case of masonry arches to limit the analysis of structural models based upon the intersection properties of convex sets. Micaela et al. [15] investigated the nonlinear fracture of masonry arch structures under vertical loads using the Lattice Discrete Particle Model (LDPM) method and analyzed the size effect. Obviously, in the stability analysis of the arches subjected to vertical load, numerical methods such as the finite element method, Lattice Discrete Particle Model, and Galerkin method are conventionally employed. However, solutions obtained through purely numerical methods are often isolated and do not easily provide a systematic understanding of the physical phenomena. In contrast, solutions derived from asymptotic methods possess a clear analytical structure, providing semi-analytic solutions that are more advantageous for theoretical analysis. To investigate the stability of circular arches under uniform vertical loads, this study employs the asymptotic method, an approximate analytical technique for solving nonlinear structural problems [16,17]. The method of parameter perturbation is a classical approach in the large deflection and buckling analysis of plates [11,12], while the WKB method is widely used in the eigenvalue stability analysis of tubular and spherical shells and solid structures [18,19,20].
In this study, a specific analysis of the stability of a pin-ended circular arch subjected to a uniform vertical load was conducted. First, the nonlinear equilibrium equations of the arch were derived. Second, a nonlinear analysis of arches subjected to uniformly distributed radial and vertical loads was performed using the parameter perturbation method, and the results were compared with classical solutions. Third, the buckling equilibrium equations were established, and the asymptotic solution of the arch subjected to uniformly distributed vertical loads was obtained using the WKB method. The third-order and second-order solutions were compared along with the critical loads obtained using linear and nonlinear axial forces.
2. Nonlinear Equilibrium Equations
Figure 1 shows a pin-ended circular arch subjected to a uniformly distributed vertical load, with a radius of curvature R and a central angle of 2α.
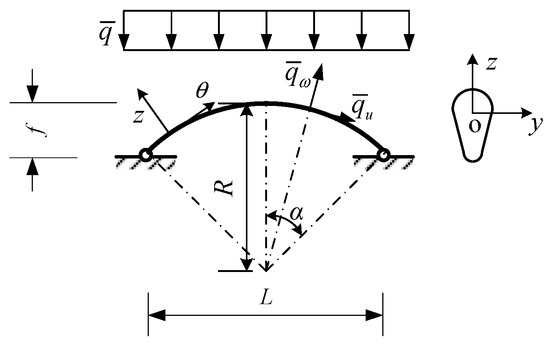
Figure 1.
Calculation mode of the arch.
The following strain–displacement relations for the arch are obtained [2]:
where ()’ = d()/dθ and and are the mid-axis axial and radial displacements, respectively. At equilibrium, the total virtual potential energy of the system is null, leading to the following form:
The axial force and bending moment are calculated as follows:
Nonlinear equilibrium equations and boundary conditions can be obtained through the application of the fundamental lemma of the calculus of variations:
The boundary conditions of the arch are obtained as follows:
To maintain generality, the following dimensionless quantities are defined:
where r represents the radius of gyration of the section. Based on Equations (3) and (6), the nonlinear equilibrium equations can then be revised as follows:
The boundary conditions are as follows:
3. Snap-Through Buckling of Shallow Arch
Equation (8) represents the nonlinear dimensionless equilibrium equation of the circular arch, which is difficult to solve analytically. Therefore, the parameter perturbation method is employed to solve it.
3.1. Solution Procedure
For the arch, the dimensionless deflection at the crown is undoubtedly a very small quantity (<<1). Therefore, the dimensionless vertical displacement at the crown is introduced as a small parameter, namely,
Expanding q, ω, and u in an ascending power series yields
Substituting Equation (10) into Equations (7) and (8), the perturbation equations and boundary conditions for each order can be obtained. Equation (11) presents the recurrence relations for the perturbation term:
The boundary conditions for each order are
Additionally, at θ = 0, the following conditions hold:
The first-order equations are linear, and their solutions can be easily obtained. By applying the boundary conditions and Equation (13), all the undetermined parameters and q1 in the solutions can be determined. Substituting the first-order solutions into the second-order equations and boundary conditions allows for the determination of the undetermined coefficients and q2 in the second-order solutions. Similarly, by substituting the first- and second-order solutions, the solution for the third-order equations can be obtained. This process can be continued to obtain solutions for any arbitrary n-th order. Finally, the dimensionless deformation–load relationship at the crown can be expressed in the following form:
Equation (14) can be further written in the following form:
where qp is the dimensionless classical critical load of the pin-ended circular arch subjected to a uniform radial load:
3.2. Circular Shallow Arches Subjected to Uniform Radial Load
To verify the effectiveness of the parameter perturbation method, the perturbation solutions for a circular shallow arch subjected to a uniform radial load were first calculated using Wolfram Mathematica at different orders. These results were then compared with the analytical solution [2]. The cross-section of the arch is a doubly symmetric I-beam section, H100 × 68 × 4.5 × 7.6, with the section parameters listed in Table 1.

Table 1.
Properties of the cross-section.
Figure 2 illustrates the relationship between and , where the modified slenderness is defined as
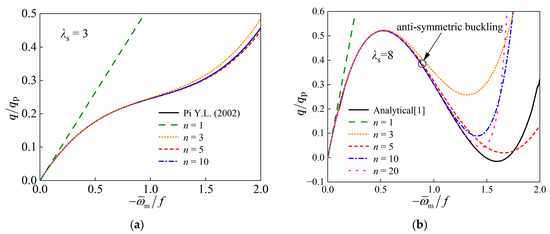
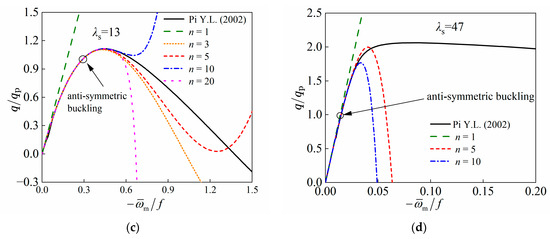
Figure 2.
Primary equilibrium paths for shallow arches with different modified slenderness values: (a) λs = 3; (b) λs = 8; (c) λs = 13; (d) λs = 47 [1].
Figure 2a,b shows that for a small λs, even with a large deformation of the arch, the perturbation solution remains in good agreement with the analytical solution. As the perturbation order increases, the perturbation solutions progressively approach the analytical solutions. In Figure 2a, the non-dimensional load–deformation curves do not exhibit the extreme point, indicating that the shallow arches will never experience snap-through buckling when λs = 3. When the perturbation order n = 3, the perturbation solution agrees reasonably well with the analytical solution, and by the time the perturbation order reaches n = 10, the solutions are almost identical. In the case of λs = 8, as shown in Figure 2b, the arch buckles in the snap-through mode first. The higher-order perturbation solutions (for n = 5, 10, 20) show good agreement before the occurrence of anti-symmetric buckling.
When λs is relatively large, as shown in Figure 2c, for λs = 13, snap-through buckling occurs after anti-symmetric buckling. The higher-order perturbation solutions provide a good approximation of the path following snap-through buckling.
When λs is very large, as shown in Figure 2d, for λs = 47, the critical load for anti-symmetric buckling of the arch is very small, significantly lower than the critical load at the extreme point. It can be observed that after the extreme point, the perturbation solution diverges completely from the analytical solution, and increasing the perturbation order does not improve the accuracy of the solution. However, the perturbation method still maintains high accuracy in calculating pre-buckling nonlinear deformations and does not require high perturbation orders; a fifth-order perturbation solution can effectively approximate the load–deformation curve.
The condition for the perturbation method to effectively approximate the true solution is that each subsequent term must be a small correction to the preceding one. For this problem, this implies that starting from the second term, the following condition must be met:
In Equation (18), δn and should be of the same order of magnitude. Table 2 shows the values of δn corresponding to the first 10 perturbation terms for different λs values. As λs increases, the magnitude of δn gradually decreases. The perturbation solution remains valid only when the relative deformation is within the same order of magnitude as δn, which is consistent with the trend shown in Figure 2, where the curve maintains high accuracy within the corresponding magnitude. When λs is further increased to 80, the perturbation solution remains valid within the order of 0.01. At this point, the corresponding value of for the classical buckling load is approximately 0.005. Clearly, the perturbation method is effective for pre-buckling calculations, and the fifth-order solution is sufficiently accurate.

Table 2.
δn with different λs values.
3.3. Circular Shallow Arches Subjected to Uniform Vertical Load
Based on the computational and analytical results of circular shallow arches under uniform radial loads, the perturbation method proves highly effective in calculating nonlinear pre-buckling deformations and snap-through buckling loads, with the fifth-order solution converging to an accurate result. Therefore, the fifth-order perturbation solution is applied to analyze the pre-buckling nonlinear deformations and snap-through buckling of shallow arches under uniform vertical loads using the same arch cross-section as in Section 3.1.
Figure 3 shows the non-dimensional load–displacement curves for circular shallow arches with the same λs under different rise-to-span ratios . Existing studies indicate that for circular shallow arches subjected to uniform radial loads, the rise-to-span ratio has a slight effect on the non-dimensional load–displacement relationship when λs is constant. However, for circular shallow arches under uniform vertical loads, the rise-to-span ratio clearly affects the non-dimensional load–displacement relationship.
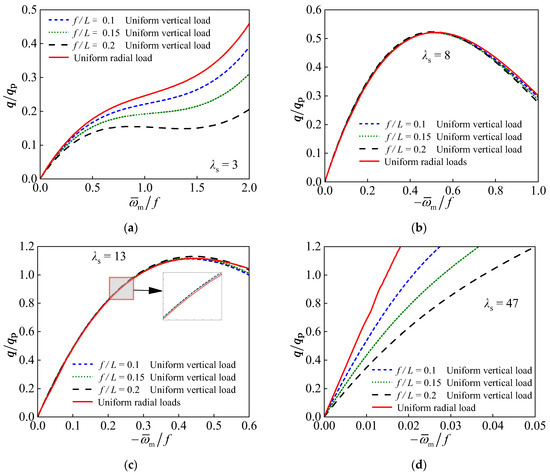
Figure 3.
Dimensionless load–displacement curves of arches under uniform vertical loads with different modified slenderness values: (a) λs = 3; (b) λs = 8; (c) λs = 13; (d) λs = 47.
Figure 3a shows that when λs = 3, the rise-to-span ratio has a prominent effect on the non-dimensional load–deformation curve before the relative deformation reaches 1. This is because when the slenderness ratio is low, the structure behaves more like a short column than a thin-walled beam, and the axial component has a significant influence. Therefore, the axial component significantly reduces the load-bearing capacity of the structure.
When λs = 8 and λs = 13, as the rise-to-span ratio increases, the critical load for snap-through buckling also increases, indicating enhanced bearing capacity of the arch, as shown in Figure 3b,c. The bearing capacity of shallow arches subjected to uniform vertical loads exceeds that of those subjected to uniform radial loads, suggesting that the axial load component contributes to improving the structural bearing capacity.
When λs = 47, the load-bearing behavior of shallow arches with different rise-to-span ratios varies significantly, as shown in Figure 3d. Circular shallow arches with a larger rise-to-span ratio exhibit a lower bearing capacity. Therefore, for shallow arches with a large modified slenderness ratio (λs), the influence of the axial load component cannot be neglected.
3.4. Internal Force Distribution of Arches Subjected to Uniform Vertical Load
Figure 4 shows the axial force distribution of the arch under a uniformly distributed vertical load. From Figure 4, it can be observed that as the rise-to-span ratio increases, the axial force distribution along the arch axis becomes more variable. The distribution patterns of the nonlinear and linear results are completely consistent, with the linear axial force being slightly smaller than the nonlinear result. In fact, the absolute difference between the nonlinear and linear axial forces is very small, with a discrepancy of about 1%.
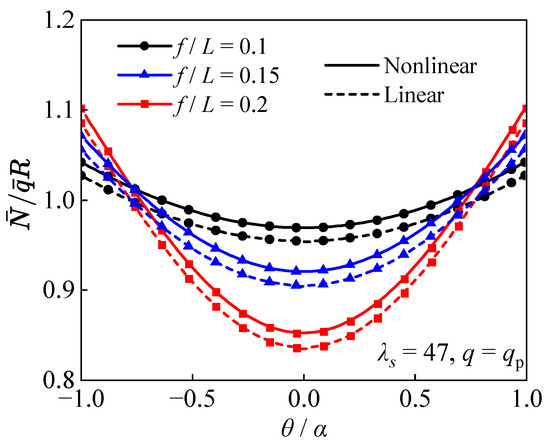
Figure 4.
The axial force distribution.
Figure 5 shows the bending moment distribution of the arch under a uniform vertical load, where represents the mid-span bending moment of a simply supported beam with the same span as the arch. Figure 5 shows that regardless of the rise-to-span ratio of the arch, the nonlinear bending moment is significantly larger than the linear bending moment. This highlights the importance of considering the nonlinear effects of bending moments in the analysis of shallow arches. In addition, compared to the simply supported beam with the same span, the bending moment of the arch is much smaller, further emphasizing the advantages of arch structures in load-bearing performance.
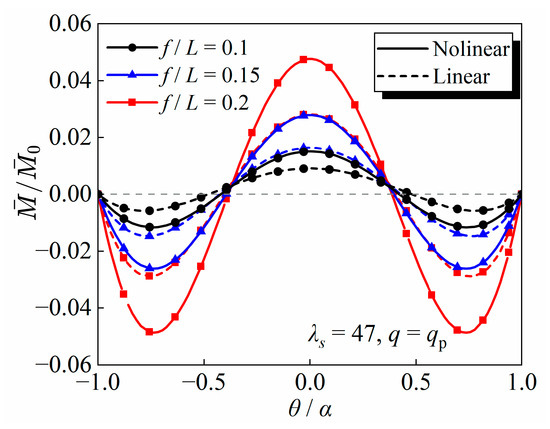
Figure 5.
The bending moment distribution.
4. Anti-Symmetric Bifurcation Buckling
4.1. Differential Equations for Buckling Analysis
According to the adjacent equilibrium criterion [2,3,4], the governing equilibrium equations of the bifurcation stage can be obtained. For this purpose, a pre-buckling state is considered with the pre-buckling displacement components and . The disturbed displacements and internal forces can then be expressed as
The equilibrium equations of the structure can be rewritten as
Since the structure is in a state of equilibrium before the disturbance, substituting Equation (4) into Equation (20) yields the differential equations for buckling analysis:
The following dimensionless quantities are defined:
The buckling equilibrium equations can be revised as follows:
Similarly, the dimensionless boundary conditions can be obtained:
The first equation in Equation (23) shows that the buckling axial force is constant. Therefore, by neglecting higher-order small terms, the buckling axial force can be written as [2]
For the anti-symmetric bifurcation buckling, the buckling radial displacement ωb is anti-symmetric, while the pre-buckling radial displacement ω is symmetric. Therefore, the term ωb + ω′ωb′ in Equation (25) is anti-symmetric. The boundary conditions also require that ub = 0 at θ = ± α. Therefore, the buckling axial force is zero. Alternatively, as pointed out by Eslami [6], the differential equations for buckling analysis must be homogeneous to ensure a nontrivial solution. The buckling equation can be written as
4.2. WKB Theory
Obviously, when the arch is subjected to uniform radial loads, the axial force before buckling remains constant, making Equation (26) a constant-coefficient differential equation with a closed-form solution. However, when the arch is subjected to loads with axial components, such as uniform vertical loads, Equation (26) becomes a variable-coefficient differential equation, making it difficult to obtain a closed-form solution. The WKB theory is a powerful tool for studying the eigenvalue problems of variable-coefficient differential equations, with the first two-order solutions, i.e., the physical optics approximation, offering high accuracy [16].
For an arch subjected to a uniform vertical load, the expression for is given by
As shown in Section 2, the pre-buckling axial force is negative across the entire span. The eigenvalue multiplicity of the differential equation remains constant within the domain, meaning that there are no turning points [21].
First, suppose that the solution to Equation (27) takes the following form:
where ξ is an undetermined parameter. Substituting Equation (28) into Equation (26) leads to Equation (29).
Applying the principle of dominant balance yields . Substituting into Equation (29) gives the dominant term as
Assume that Y(θ) ≠ 0, and let the i-th solution of S(θ) be denoted as S(i). Then,
S(θ) possesses a double root, which precludes the linear independence of first-order solutions. In cases involving repeated roots, the modified WKB method proposed by Fu (2002) is employed for the calculation [22]. We look for an asymptotic solution of the form
Substituting Equation (32) into Equation (29) leads to equations at each order of the WKB theory. From these equations, the expression for Y(θ) can be obtained. Similarly, denote the i-th solution of Y(θ) as Y(i). At order q3/2, we obtain
At order q, we obtain
At order q1/2, we obtain
Finally, the approximate solution for the pre-buckling radial displacement can be obtained from the above results:
Obviously, when the arch is subjected to a uniform radial load, Equation (36) degenerates into the solution for a shallow arch subjected to a uniform radial load. First, it can be obtained based on the symmetry of the boundary conditions:
Substituting Equations (36) and (37) into the boundary conditions at θ = α yields a matrix equation of the following form:
from which the characteristic equation is obtained as follows:
The modified WKB method transforms the eigenvalue problem of a differential equation with variable coefficients into a matrix eigenvalue problem. Figure 6 shows part of the images of the second- and third-order characteristic polynomials, and for anti-symmetric buckling, the flexural half-wave number is 2. From Figure 6, it can be seen that the third-order eigenvalues are all larger than the second-order eigenvalues, which is due to the fact that the third-order WKB method takes into account the axial component of the load more fully. From the construction of the WKB solution, the second-order WKB solution practically ignores the effect of the term in the buckling equation, which results in a small value of the critical load of the structure.

Figure 6.
Characteristic polynomial y(q).
Figure 7 illustrates the ratio of the critical load qcr to the classical critical load qp calculated using the WKB method under different rise-to-span ratio conditions. The figure also compares the computational results of the WKB solutions at various orders and highlights the differences in pre-buckling axial forces, depending on whether a nonlinear or linear axial force analysis is employed.
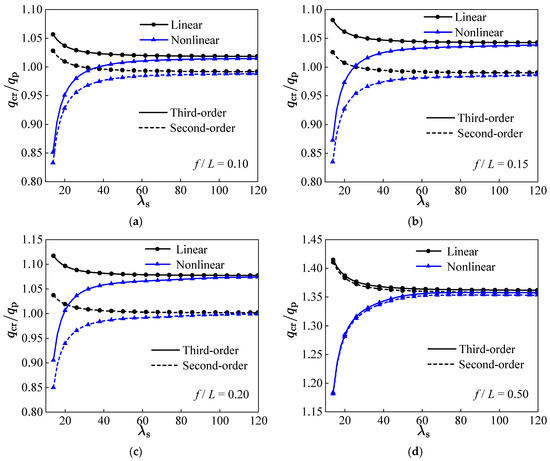
Figure 7.
qcr/qp with different rise-to-span ratios: (a) f/L = 0.1; (b) f/L = 0.15; (c) f/L = 0.12; (d) f/L = 0.5.
Figure 7 demonstrates the following:
- The larger the rise-to-span ratio, the larger the qcr/qp for the same modified slenderness λs, which is due to the effect of the axial component of the load. Obviously, the smaller the rise-to-span ratio of an arch subjected to a uniform vertical load, the closer the axial force distribution of the arch is to that of an arch subjected to a uniform radial load, and therefore the closer its critical load is to that of an arch subjected to a uniform radial load.
- The eigenvalue obtained using the second-order WKB method is smaller than that obtained using the third-order WKB method, consistent with the conclusions drawn from Figure 6 and their underlying reasons.
- The variation in qcr/qp with λs calculated using nonlinear axial force differs from that obtained with a linear axial force. When a linear axial force is used, the critical load decreases as λs increases, whereas with a nonlinear axial force, the critical load increases as λs increases. This difference arises because, for small values of λs, the nonlinear effects before buckling are significant, leading to lower critical loads when a nonlinear axial force is used. In contrast, the results based on a linear axial force are influenced solely by the axial component of the load, which results in higher critical loads compared to those under uniformly distributed radial loads. As λs becomes large, the difference between the critical loads calculated with nonlinear and linear axial forces diminishes.
The above analysis shows that for shallow arches with a small rise-to-span ratio, the critical load for anti-symmetric buckling closely matches the classical solution, and the results from arches subjected to a uniformly distributed radial load are reliable. For deep arches with a large rise-to-span ratio, the influence of the axial load component cannot be ignored. Since the eigenvalue obtained using the second-order WKB method is smaller than that obtained with the third-order WKB method, one can consider the second-order solution as an approximation in practical calculations. Therefore, the pre-buckling radial displacement can be simplified as follows:
4.3. WKB Results with Other Analytical Studies
To validate the WKB method, we performed comparative analyses with the numerical solutions obtained using the Galerkin method by Cheng [23]. A comparative analysis between the WKB solutions and numerical solutions under varying modified semi-span slenderness ratios λf = αR/r and central angles is presented in Table 3.

Table 3.
qcrR3/EI with different modified semi-span slenderness ratios.
The comparison shows that when the central angle α of the arch is small, the buckling load obtained using the WKB method is lower than that obtained using the Galerkin method, while when the central angle is large, it is higher than the buckling load from the Galerkin method. The reason for this difference lies in the fact that Cheng [23] did not neglect the transverse stresses of the arch in his analysis. Overall, when the arch is relatively shallow, the WKB method demonstrates effectiveness, indicating that the semi-analytical solution obtained using the WKB method can be used as the anti-symmetric buckling solution for shallow arches (α < 70°).
5. Conclusions
This research proposes a nonlinear analytical approach based on asymptotic methods, including the parameter perturbation method and the WKB method. The results show that
- The parameter perturbation method is effective for snap-buckling of shallow arches, and the fifth-order solution is sufficiently accurate. For shallow arches with a large modified slenderness ratio, the influence of the axial load component cannot be neglected.
- In the anti-symmetric buckling analysis, the eigenvalue obtained using the second-order WKB method is smaller than that obtained using the third-order WKB method; therefore, the second-order solution can be used as the critical load.
- The asymptotic solution for the buckling deformation of the two-hinged circular arch is provided. For shallow arches with a small rise-to-span ratio, the critical load for anti-symmetric buckling closely matches the classical solution. For deep arches with a large rise-to-span ratio, the influence of the axial load component cannot be ignored.
Author Contributions
Conceptualization, J.J. and M.S.; methodology, J.J.; software, J.J.; validation, J.J.; formal analysis, J.J.; investigation, M.S.; resources, M.S.; data curation, J.J.; writing—original draft preparation, J.J.; writing—review and editing, M.S.; visualization, J.J.; supervision, M.S.; project administration, J.J.; funding acquisition, M.S. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (grant number 51978564).
Data Availability Statement
The original contributions presented in the study are included in the article; further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Tong, G.; Pi, Y.L.; Bradford, M.A.; Tin-Loi, F. In-Plane Nonlinear Buckling Analysis of Deep Circular Arches Incorporating Transverse Stresses. J. Eng. Mech. 2008, 134, 362–373. [Google Scholar]
- Pi, Y.L.; Bradford, M.A.; Uy, B. In-Plane Stability of Arches. Int. J. Solids Struct. 2002, 39, 105–125. [Google Scholar]
- Pi, Y.L.; Trahair, N.S. In-Plane Buckling and Design of Steel Arches. J. Struct. Eng. 1999, 125, 1291–1298. [Google Scholar]
- Pi, Y.L.; Trahair, N.S. Nonlinear Buckling and Post-Buckling of Elastic Arches. Eng. Struct. 1998, 20, 571–579. [Google Scholar]
- Bradford, M.A.; Wang, T.; Pi, Y.L.; Gilbert, R.I. In-Plane Stability of Parabolic Arches with Horizontal Spring Supports. I: Theory. J. Constr. Steel Res. 2020, 164, 1057. [Google Scholar]
- Eslami, M.R. Buckling and Post-Buckling of Curved Beams and Rings. In Buckling and Postbuckling of Beams, Plates, and Shells; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Kang, Y.J.; Yoo, C.H. Thin-Walled Curved Beams. II: Analytical Solutions for Buckling of Arches. J. Eng. Mech. 1994, 120, 2102–2125. [Google Scholar] [CrossRef]
- Reddy, J.N. Theory and Analysis of Elastic Plates and Shells; CRC Press: Boca Raton, FL, USA, 2006. [Google Scholar]
- Hu, C.; Li, Z.; Hu, Q. On Non-Linear Behavior and Buckling of Arch-Beam Structures. Eng. Struct. 2021, 239, 112214. [Google Scholar] [CrossRef]
- Babaei, H.; Kiani, Y.; Eslami, M.R. Large amplitude free vibration analysis of shear deformable FGM shallow arches on nonlinear elastic foundation. Thin-Walled Struct. 2019, 144, 106237. [Google Scholar] [CrossRef]
- Babaei, H.; Eslami, M.R. On Nonlinear Vibration and Snap-Through Stability of Porous FG Curved Micro-Tubes Using Two-Step Perturbation Technique. Compos. Struct. 2020, 247, 112447. [Google Scholar]
- Babaei, H.; Eslami, M.R. On nonlinear vibration and snap-through buckling of long FG porous cylindrical panels using nonlocal strain gradient theory. Compos. Struct. 2021, 256, 113125. [Google Scholar]
- Guo, Y.; Lin, B.; Guo, Y. Theoretical and Experimental Studies of In-Plane Stability Design of Circular Arches Subjected to Axial Force and Moment. China Civ. Eng. J. 2011, 44, 8–15. (In Chinese) [Google Scholar]
- Caporale, A.; Luciano, R.; Rosati, L. Limit analysis of masonry arches with externally bonded FRP reinforcements. Comput. Methods Appl. Mech. Eng. 2006, 196, 247–260. [Google Scholar]
- Mercuri, M.; Pathirage, M.; Gregori, A.; Cusatis, G. Masonry vaulted structures under spreading supports: Analyses of fracturing behavior and size effect. J. Build. Eng. 2006, 45, 103396. [Google Scholar]
- Bender, C.M.; Orszag, S.A. Advanced Mathematical Methods for Scientists and Engineers I: Asymptotic Methods and Perturbation Theory; Springer: New York, NY, USA, 1999. [Google Scholar]
- Nayfeh, A.H. Introduction to Perturbation Techniques; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Jin, L.; Liu, Y.; Cai, Z. Asymptotic Solutions on the Circumferential Wrinkling of Growing Tubular Tissues. Int. J. Eng. Sci. 2018, 128, 31–43. [Google Scholar]
- Fu, Y. Some Asymptotic Results Concerning the Buckling of a Spherical Shell of Arbitrary Thickness. Int. J. Non-Linear Mech. 1998, 33, 1111–1122. [Google Scholar]
- Pour, M.S. WKB analysis of the buckling of a neo-Hookean cylindrical shell of arbitrary thickness subject to an external pressure. Int. J. Appl. Mech. 2010, 2, 857–870. [Google Scholar] [CrossRef]
- Wasow, W. Linear Turning Point Theory; Springer: New York, NY, USA, 1985. [Google Scholar]
- Fu, Y.; Pour, M.S. WKB Method with Repeated Roots and Its Application to the Buckling Analysis of an Everted Cylindrical Tube. SIAM J. Appl. Math. 2002, 65, 1856–1871. [Google Scholar]
- Cheng, P. In-Plane Nonlinear Theory and Elastic-Plastic Stability of Pined Circular Arches. Ph.D. Thesis, Zhejiang University, Hangzhou, China, 2005. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).