Shaking Table Test Research on Novel Frame Structures: A Review

Abstract

Frame structures are among the most widely used building forms. The advent of innovative materials, technologies, and structural configurations has led to the emergence of new frame structures. Therefore, it is necessary to understand the dynamic performance of these new frame structures under actual earthquakes. Shaking table tests of frame structures allow researchers to directly investigate their dynamic behavior. This study discusses scaling theories and seismic wave input methodologies adapted for shaking table tests. By analyzing data and conclusions from various experiments, this study details the performance of new frame structures under simulated seismic conditions, providing substantial empirical evidence for understanding their seismic performance. Based on the research, several rational recommendations are proposed to enhance the stability and safety of frame structures during seismic events. These recommendations, supported by both experimental and analytical results, offer practical guidance for design and engineering.

1. Introduction

Earthquakes have caused significant damage to buildings throughout the development of architecture. Therefore, structural engineers worldwide are dedicated to enhancing the seismic resilience of structures [1]. As a traditional and well-developed building form, frame structures are widely applied in construction engineering. The advent of innovative materials, technologies, and structural configurations has led to the diversification of frame structures. Extensive research and practical experience have demonstrated that frame structures, while offering simple forms and clear force transmission paths, exhibit reduced load-bearing capacities, lower stiffness, and large seismic responses. These factors present significant challenges to the seismic performance of frame structures under extreme earthquakes [2].

Earthquake-resistant frame structures began evolving in the early 20th century. As theoretical research has progressed and practical applications have expanded [3], the study of earthquake-resistant frame structures has evolved into a comprehensive scientific domain that plays a crucial role in guiding the seismic design of frame structure buildings. Experimental research is an integral component of structural seismic theory. It serves not only as a practical validation of theoretical research but also as a critical catalyst for theoretical advancements. Structural seismic resistance tests can generally be categorized into four methods: static, pseudo-static, pseudo-dynamic, and earthquake simulation shaking table tests. However, the majority of studies, influenced by varying experimental conditions and research objectives, have concentrated on the static seismic performance of individual components or isolated frames. Pseudo-static tests of individual components provide a clearer understanding of the local stress state and failure mechanisms within frame structures [4,5]. Nevertheless, the dynamic response of an entire frame structure to seismic excitation is inherently complex, involving intricate interactions among its multiple components and the dynamic characteristics of the whole structure. Hence, investigating the dynamic seismic performance of the entire frame structure is vital for enhancing its overall seismic resilience. The advent of earthquake simulation shaking table tests marked a milestone in developing structural seismic resistance. Shaking table tests can accurately replicate earthquake excitations by adjusting the structural dynamic parameters and input motions. Moreover, these tests can obtain the actual seismic response of an entire structure [6].

Shaking table tests offer the following irreplaceable advantages over pseudo-dynamic and static tests, providing a comprehensive assessment of structural performance under various seismic conditions:

(1) Shaking table tests can simulate earthquakes of different intensities and spectral characteristics, enabling multiple iterations to fully evaluate the responses of structures to diverse seismic events.

(2) Researchers can visually and quantitatively assess how structures react to seismic excitations of varying intensities, which is critical for understanding their seismic performance and identifying weak points.

(3) Shaking table tests also serve as a validation tool for seismic theories, allowing for the comparison of experimental results with theoretical predictions. This comparison can confirm the accuracy of test models and drive advancements in structural dynamic analysis.

(4) Shaking table tests can show the full progression of structural damage, from elasticity to plasticity and eventual failure, which is vital for studying seismic performance, failure mechanisms, and seismic mitigation strategies.

(5) Shaking table tests can reveal issues that arise during the construction of full-scale models, thereby enhancing the precision and reliability of the construction process.

The advantages of shaking table tests are presented in Figure 1.

In summary, shaking table tests can provide researchers with intuitive and precise experimental tools that significantly advance the field of structural seismic research. In shaking table tests for frame structures, a multitude of factors can influence the precision and reliability of test data. Among these factors, the choice of scaling theory, the accuracy of model construction, and the appropriateness of input ground motion data are particularly critical. Existing shaking table tests of frame structures have demonstrated that the variability in test conditions, objectives, and frame configurations results in substantial discrepancies in the design process of these tests. Shaking table tests for engineering structures are known for their high cost and complex design [7], making large-scale frame structure tests challenging. To enhance our understanding of shaking table tests for frame structures, this study analyzes and summarizes the scaling theories and earthquake wave selection criteria used, as well as the tests conducted on various frame structure configurations.

2. Scaling Theory for Frame Structures

The first shaking table was introduced in the 1960s at the University of California, Berkeley. Over the past decades, this technology has advanced significantly, with over a hundred operational and planned shaking tables worldwide. Despite improvements in scale and performance, simulating actual prototype structures in the laboratory remains difficult because of size limitations and equipment capacity. Moreover, full-scale prototype structures result in substantial waste of testing resources. Therefore, utilizing dimensional similarity principles for scaled testing of prototype structures is an effective method for reducing cost and complexity while maintaining accuracy [6].

Scaled tests fundamentally involve creating smaller models that behave similarly to full-scale structures under the same conditions, simplifying experiments and reducing costs. This approach relies on the principle of dimensional analysis, which means that similar physical phenomena can be effectively simulated while maintaining proportional relationships among physical quantities. Scaled tests are extensively employed to assess structural performance under seismic loading.

2.1. Calculation Methods for Similarity Relationships

The complexity of frame structures leads to numerous physical parameters, making it technically difficult to satisfy the principle of dimensional similarity. To accommodate specific testing needs and structural configurations, researchers have devised various approximation methods for calculating similarity relationships. By focusing on the minimization of less critical errors, these methodologies emphasize the precision of essential parameters, thereby achieving effective experimental results. The advantages and disadvantages of various similar methods are shown in Table 1. The commonly employed methods include the following:

(1) Analytical method [8]: By analyzing equations that describe physical phenomena, this method identifies similar terms and constants to determine similarity conditions. While rigorous in its theoretical foundation, this method is constrained by complex equations and a multitude of unknowns.

(2) Dimensional analysis method [6]: This method establishes similarity constants by examining the dimensions of physical quantities and identifying proportional relationships. It is highly useful in the preliminary analysis of physical phenomena and in the initial design of similar models.

(3) Extended dimensional analysis method [9]: By combining domain-specific knowledge with dimensional analysis, this method introduces new dimensional parameters by analyzing specific characteristics of physical phenomena, thereby enhancing the precision of their descriptions. Extended dimensional analysis offers high flexibility in establishing similarity relationships for complex physical phenomena.

Table 1. Methods for similarity relationships.

Methods for Similarity Relationships	Advantages	Disadvantages
Analytical method	The similarity accuracy of the model is the highest.	Complex equations and many unknowns
Dimensional analysis method	It ensures the similarity accuracy of the main parameters of the model and reduces the difficulty of analysis.	It cannot provide accurate results.
Extended dimensional analysis method	The accuracy of similarity is higher than the dimensional analysis method.	Its analysis is more difficult than dimensional analysis.

Table 1. Methods for similarity relationships.

Methods for Similarity Relationships	Advantages	Disadvantages
Analytical method	The similarity accuracy of the model is the highest.	Complex equations and many unknowns
Dimensional analysis method	It ensures the similarity accuracy of the main parameters of the model and reduces the difficulty of analysis.	It cannot provide accurate results.
Extended dimensional analysis method	The accuracy of similarity is higher than the dimensional analysis method.	Its analysis is more difficult than dimensional analysis.

2.2. Design Methods for Similarity Ratios

In the majority of dynamic tests on frame structures, researchers typically select appropriate methods for calculating similarity ratios based on test requirements and structural characteristics. They must also consider how the test conditions, material properties, and size effects influence the similarity relationships, ensuring the precision and reliability of the test results. Depending on the specific similarity theory, the scaled structure may exhibit varying characteristics; thus, the most suitable theory should be selected based on the objectives and conditions of the test.

The two predominant methods for similarity ratio design are the consistent similarity ratio proposed by Zhang [10] and the stress state-based consistent similarity ratio developed by Fu [11]. Both methods comprise three types of similarity ratio models: the full-mass, under-mass, and gravity-ignored [12] models. The research and analysis of these models revealed the following:

(1) The design methods for various similarity ratios are fundamentally identical, evolving from the principle of dimensional similarity, with minor differences based on their focus.

(2) In the full-mass model, both design methods consistently yield similar results for similarity ratios.

(3) When applying the under-mass similarity ratio, the stress state-based consistent similarity ratio method emphasizes the stress of structures under gravity. Employing this method for designing a gravity-ignored model would lead to erroneous results. In the under-mass model design, the acceleration similarity ratio is derived from the gravity stress similarity ratio. However, this gravity stress similarity ratio differs from the stress similarity ratio in the stress state-based consistent similarity ratio method, which results in the distortion of the horizontal stress. The vertical load stress of high-rise buildings has a great influence on the dynamic response of the structure. Hence, the stress state-based consistent similarity ratio method is more suitable for high-rise buildings or structures that are sensitive to vertical loads.

(4) The full-mass model offers the highest degree of similarity, with consistent results across design methods, allowing for the most accurate simulation. However, the substantial model weight demands excessive capabilities from test equipment, making it nearly unfeasible for some high-rise structures.

In addition to the primary similarity ratio design methods mentioned above, Huang et al. [13,14] introduced a graded similarity relationship design method based on consistent similarity principles, which accounts for the structural behavior in the nonlinear phase. After constructing five single-story reinforced concrete (RC) slab–column frame models and subjecting them to shaking table tests under three different conditions, they compared the results against tests of ungraded and graded similarity relationships. The results indicated that the graded similarity relationship could effectively mitigate errors in earthquake simulation tests. Cheng et al. [15] proposed a dynamic similarity design method based on the isomorphic yield strength coefficient criterion. They examined the dynamic similarity relationships for existing RC frame structures, considering parameters such as geometric dimensions, elastic modulus, mass, stiffness, time, acceleration, horizontal excitation, and moments. A 1:5 scale model of a five-story existing RC frame structure was designed using this method. Shaking table tests confirmed that the model, designed with equal yield strength coefficients, could effectively validate the structural seismic performance and actual earthquake damage patterns, providing insights into seismic retrofit designs. Lin et al. [16] proposed a fundamental similarity transformation principle between the elastic, gravity, and elastic force–gravity similarity laws and discussed their respective applicability. Chi and Lam [17] validated the efficacy of the elastic similarity principle and the elastic force-gravity similarity principle in shaking table tests on two differently scaled models. They used dimensional analysis to establish relationships among physical quantities and defined two pivotal constants related to mass and gravity similarity: the Cauchy and Froude values. The Cauchy number ensures that the ratio of inertial to elastic forces is preserved, governing material deformation under dynamic loads. The Froude number scales the influence of gravity, a factor critical for phenomena like overturning or sloshing. These criteria guide the design of our experiments to accurately replicate the prototype’s behavior.

In summary, a scale model of a prototype structure can conserve the experimental space and resources. Scaled experiments also enable the convenient adjustment of experimental parameters, facilitating investigations of structural performance under different seismic waves, structural types, and seismic resistance measures. However, scaled experiments have certain limitations. The scaling process requires careful consideration and the verification of the model’s similarity, as it involves transforming various physical quantities in terms of similarity. Scaled experimental results can be influenced by factors such as size effects, material property variations, and experimental conditions. In the process of shaking table tests, ideal similitude laws could not be fully satisfied in the damping ratio due to complex material properties. Therefore, a comprehensive consideration of these influencing factors is imperative to ensure the accuracy and reliability of shaking table experiments [18].

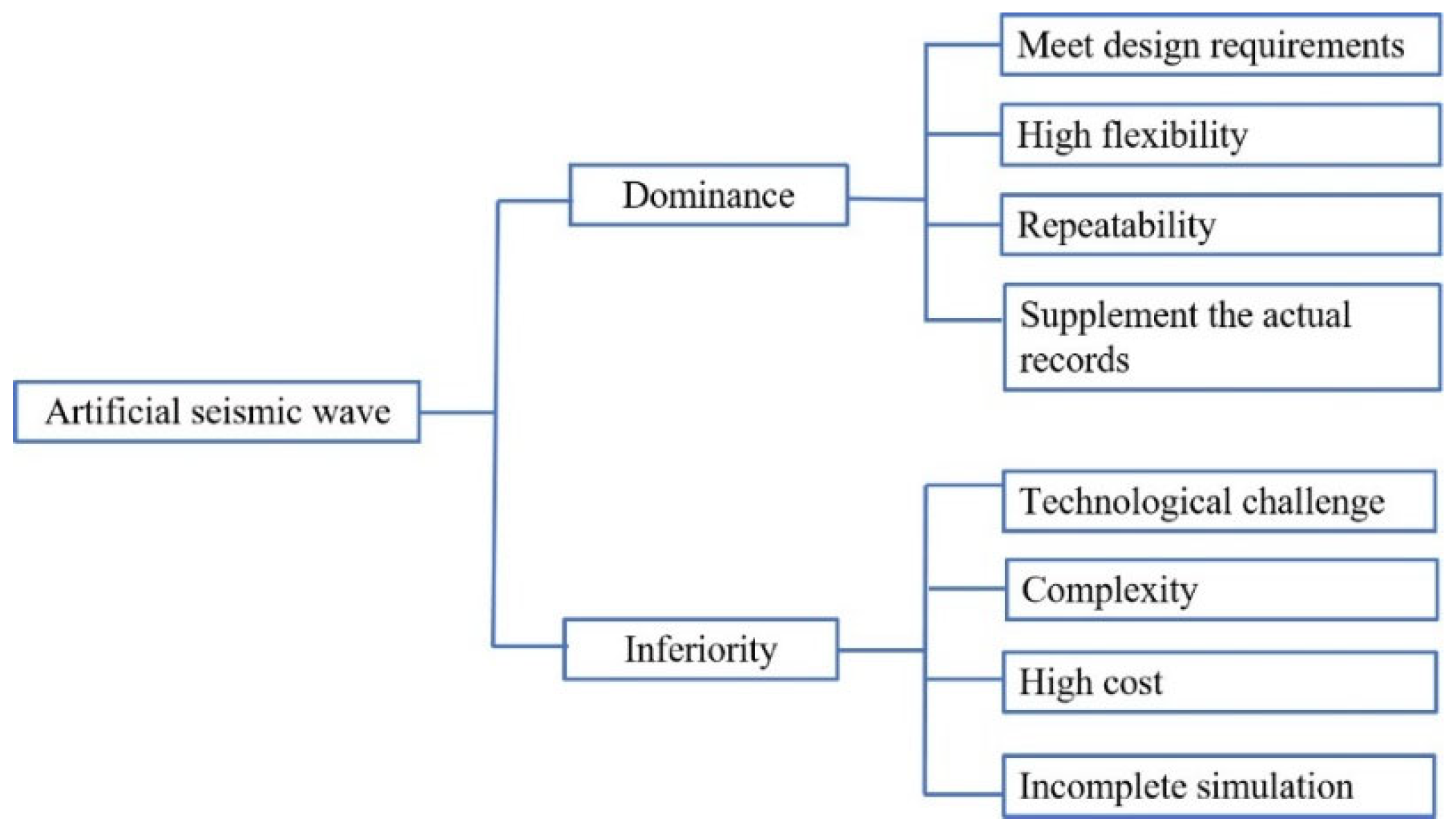
3. Selection of Seismic Excitation Inputs

Numerous studies have indicated that the choice of earthquake motion significantly influences the dynamic response of frame structures in shaking table tests. Some studies have investigated the effects of various earthquake motions on RC frames. The results showed that both horizontal and vertical components of ground motion led to alterations in the shear force and bending moment of the structure, affecting the overall stability [19,20]. In RC frames, the vertical motions may amplify axial forces in columns, leading to potential buckling or shear failure, especially in slender members. By comparing various earthquake motion inputs, additional studies have demonstrated the more pronounced effects of bidirectional seismic waves on structural deformation, highlighting the importance of considering multi-directional loads in seismic design [21,22]. It is evident that the selection of input motions is a critical aspect in shaking table tests of frame structures. Therefore, further investigating the selection criteria for seismic wave excitation is essential for enhancing the scientific basis and effectiveness of seismic design.

In shaking table tests of frame structures, the seismic excitation is primarily derived from real earthquake recordings and synthetic seismic waves. Real earthquake recordings are historical data obtained from strong-motion observations, encompassing parameters such as seismic wave acceleration, velocity, and displacement. When selecting earthquake recordings, factors such as event duration, peak ground acceleration (PGA), and frequency must be considered to ensure suitability for specific testing requirements. In contrast, synthetic seismic waves are created by adjusting parameters such as peak acceleration, spectral characteristics, and duration based on random vibration theory or specific algorithms to match the characteristics of ground motion, fulfilling the needs of various test scenarios. Synthetic seismic waves play a significant role in earthquake engineering and structural seismic analysis; however, they also present certain technical challenges and limitations. Therefore, in actual shaking table tests, researchers always used real earthquake recordings and synthetic earthquake recordings at the same time to ensure the accuracy of test results. It should be noted that the duration of the input seismic wave should be scaled before the test, while the peak acceleration only needs to be adjusted according to the test conditions. The advantages and disadvantages of using synthetic seismic waves in shaking table tests are shown in Figure 2.

When selecting seismic waves for shaking table tests of frame structures, various factors, including building site category, design earthquake grouping, and test objectives, should be considered. Researchers must select appropriate actual strong-motion records and synthetic seismic waves, adhering to specific selection protocols and considerations. This approach guarantees the accuracy and reliability of the test results. However, current studies often focus on a single type of frame and lack a comprehensive analysis of complex structures, limiting the applicability of their findings [23,24]. To address this issue, future studies should encompass a broader range of frame designs and material types to more thoroughly evaluate how seismic wave inputs affect frame structures. The process of selecting input seismic waves is illustrated in Figure 3.

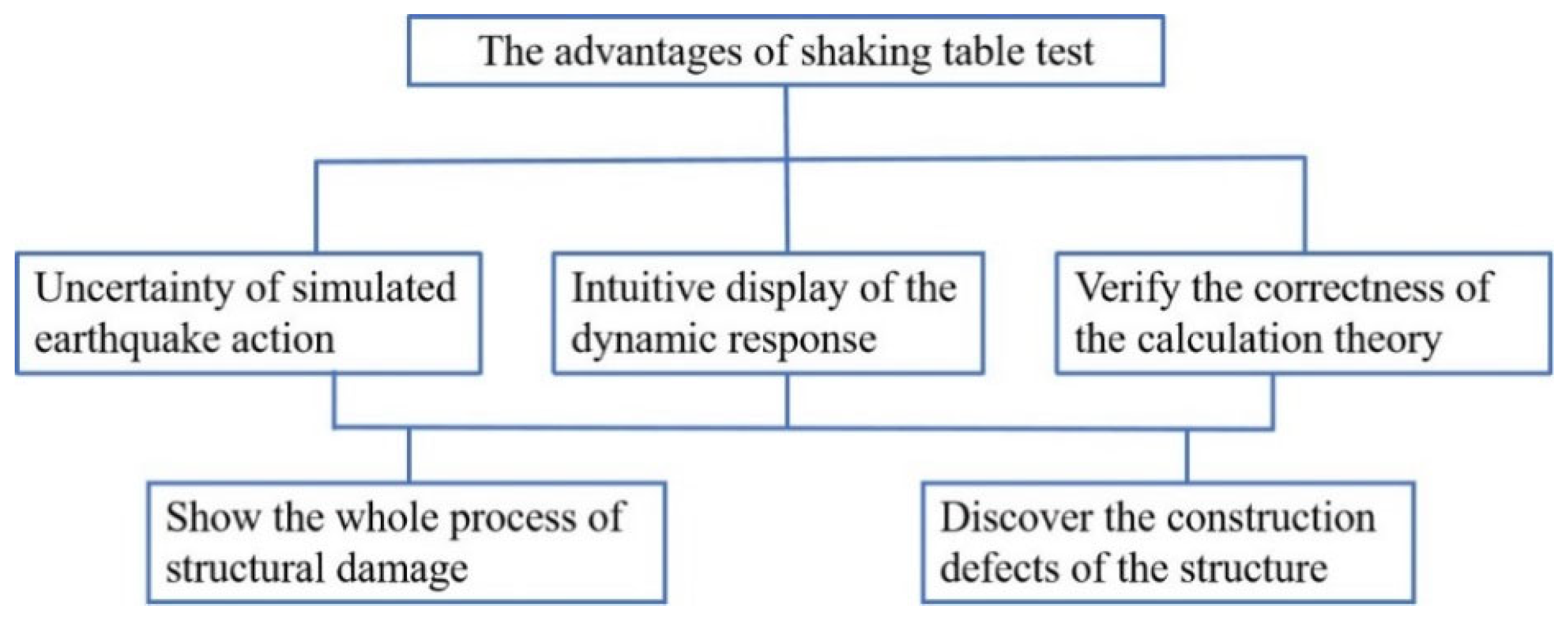
4. Shaking Table Tests of Novel Frame Structures

During shaking table tests, by selecting the correct scaling theory and appropriate seismic excitation based on experimental conditions, researchers can effectively investigate the dynamic responses, damage properties, collapse behavior, seismic hazard mitigation performance, and failure mechanisms of various frame structure configurations. The dynamic response of the structure was measured by acceleration sensors and displacement sensors. Studies focusing on the collapse behavior of frame structures have revealed that failure often initiates at beam–column joints, a vulnerable point particularly susceptible to damage during strong earthquakes [25,26]. Research on seismic control measures has demonstrated that well-designed controls can significantly reduce structural displacement and acceleration responses, thereby enhancing seismic performance [27,28]. This study reviews shaking table test research on novel frame structures, further analyzing their practical application in seismic performance studies and offering a reference for future tests. This review has great significance for the costly and complex field of frame structure shaking table tests, providing a scientific foundation for the seismic design and dynamic performance assessment of frame structures. In this review, the novel frame structure refers to a structural form that, based on traditional concrete frames and steel frames, incorporates new materials, technologies, and structural configurations to achieve greater diversity in frame structure types.

4.1. Shaking Table Tests of RC Frame Structures

RC frames are widely adopted in the construction of multi-story and high-rise buildings owing to their excellent ductility, structural strength, and simple construction technology. Benavent et al. [29] investigated the seismic response of scaled RC frames under low- and high-seismic intensities through shaking table tests, examining aspects such as displacement, strain, energy dissipation, and structural damage. The study further analyzed the torsional response in a series of uniaxial shaking table tests, which was attributed to the non-uniform yielding of structural components and uncertainties inherent in the construction process. Sun et al. [30] designed a 1:5 scale model of an existing concrete frame structure to simulate buildings that have been in service for many years and are characterized by low-seismic fortification levels and inadequate seismic resistance measures. Subsequently, a shaking table test was conducted on this scale model to investigate the cracking behavior of the masonry infill walls and main frame during low-intensity earthquakes, as well as the trend of dynamic characteristic changes due to frame cracking. Increasing the seismic intensity progressively damaged the frame, leading to reduced frequencies of high-order modes and modal shape amplitudes, indicating increased structural damage. Zhou et al. [31] performed a shaking table test on a 1:2.2 scale model of the lower two frames of an actual precast, prestressed concrete fully assembled frame structure project. The findings indicated that under rare earthquake conditions, no cracks occurred in the core area of the joint. The model maintained good integrity and exhibited satisfactory seismic performance, with a maximum natural frequency reduction of 21.89% and a maximum inter-story displacement angle of 1/122. Tang et al. [32] designed and tested a 1:8 scale model of a stilted RC frame structure and analyzed the structural damage phenomena of the test model. The damage to the stilted layer and second story of the stilted RC frame structure was significantly uneven. Severe damage was concentrated at the base of the second-story columns, with a decreasing degree of damage from the slope bottom column side to the slope top column side. These findings provide a scientific basis for the design and seismic evaluation of stilted RC frame structures in mountainous areas, considerably enhancing the safety of these constructions under seismic actions.

As new design philosophies emerge, the variety of RC frame structures has expanded. To ensure that these new structures meet seismic performance requirements, it is essential to investigate their actual seismic responses. Xiao et al. [33] introduced a new type of RC frame structure featuring folded steel bars and post-yield hardening columns and studied its seismic performance using shaking table tests, as displayed in Figure 4. The new frame structure effectively reduced inter-story displacement and residual displacement ratios compared to traditional frames, thereby demonstrating superior seismic performance and self-centering capabilities. Damage to the new frame initially occurred at the beam ends, intensifying with increasing earthquake intensity. The column ends remained largely undamaged, even under significant seismic actions. The failure mode of the frame exhibited a strong column and a weak beam form, which enhanced the repairability of the novel frame. Zhao et al. [34] designed and tested a 1:5 scale precast RC frame model that used simple bolted connections and compared it with a cast-in-place frame of equivalent stiffness. In contrast to the shear deformation pattern of the cast-in-place frame, the precast frame predominantly displayed a bending deformation pattern during an earthquake. The damage and inter-story displacement in the precast frame were more evenly distributed across floors, whereas the damage in the cast-in-place frame was concentrated on the first floor. Pang et al. [35] designed and constructed a 1:4 scale model of a four-story, two-bay, single-span frame for a fully precast RC floor with a distributed connection. The results of the shaking table tests showed that the fully precast RC floor performed satisfactorily throughout the loading process and effectively coordinated with the lateral force-resisting structures. The natural frequency of the test model decreased by 13.5% at 0.58 g. At the end of loading (2.0 g), the damping ratio increases to 0.038, which is 3.8 times the initial value (0.010). In the later stages of loading, the in-plane deformation of the floor became more pronounced, and the structure exhibited significant torsional responses.

Based on shaking table tests, researchers have discovered that incorporating infill walls into frame structures can significantly improve their seismic performance. Stavridis et al. [36] conducted a shaking table test on a 2:3 scale model of a three-story, two-bay RC frame structure with masonry infill walls, which is representative of typical Californian architecture from the 1920s. The structure remained elastic under seismic excitation below the median design criterion for the Los Angeles region. However, at the design-level excitation, cracking occurred in the infill walls. As the seismic intensity increased, these cracks progressively widened, leading to significant diagonal shear cracks in the RC columns. Even after sustaining severe damage, the structure retained 84% of its peak strength, with displacements reaching 1.03%. Benavent et al. [37] built a 2:5 scale model of a single-bay, single-story RC frame structure and induced moderate damage through successive shaking table tests. The retrofitted structure exhibited good seismic performance with no signs of catastrophic collapse, even at a displacement angle of approximately 5%. The inclusion of infill walls substantially increased the initial stiffness and lateral strength of the structure, which gradually degraded as damage accumulated. Zhao et al. [38] proposed a prefabricated straw-block infill wall frame structure to address the common problems of weak stories and stiffness discontinuities in conventional brick masonry infill wall frame structures during earthquakes. Seismic shaking table tests were conducted on two 1:3 scale models. The results showed that the prefabricated straw-block infill wall frame structure model exhibited plastic hinges at the beam ends with intact columns, indicating a strong column and a weak beam failure mode. The maximum inter-story displacement in the prefabricated straw-block infill wall frame structure model was distributed across the first and third floors.

Researchers have discovered that incorporating novel concrete materials can substantially affect the seismic performance of RC frames. Xiao et al. [39] performed shaking table tests on a six-story precast frame model constructed with recycled aggregate concrete (RAC). The structures possessed adequate load-bearing capacity and ductility under both moderate and severe seismic excitation. Hou et al. [40] conducted a shaking table test on a single-story, two-bay RC frame structure by utilizing piezoelectric smart aggregates to monitor structural damage and measure column end stress, reinforcement bar strain, structural acceleration, and displacement. Xu et al. [41] performed shaking table tests on two 1:3 scale models: a precast RC frame and a precast ECC/RC composite frame. The results indicated that utilizing ECC could significantly decrease damage to precast frames, and the precast ECC/RC composite frames demonstrated superior deformation capacity, energy dissipation, and slower stiffness degradation than the precast RC frames. When the PGA reached 0.411, 0.556, and 0.712 g, the inter-story drifts for the fourth, third, and second stories of the RC frame exceeded those of the ECC/RC composite frame, respectively, and their gaps increased with the PGA. Khan et al. [42] introduced crushed rubber concrete (CRC) and fabricated two 1:3 scale test models. The CRC frames exhibited diminished compressive strength and density yet increased fundamental frequency and damping ratio. Moreover, the seismic response acceleration and yield strength of these frames were 20.40% and 8.60% lower, respectively, than those of ordinary concrete frames. In addition to introducing innovative concrete materials, some researchers have engineered alternative composite materials and employed these advanced materials to strengthen existing RC frame structures externally. Wang et al. [43] used externally bonded carbon fiber-reinforced polymer (CFRP) composites to retrofit RC frame structures that did not meet the current seismic standards and assessed their seismic performance through shaking table tests on two scale models, as depicted in Figure 5. The test results indicated that CFRP retrofitting technology substantially improved the seismic performance of the substandard RC frames. The retrofitted frame specimen withstood a PGA of 1.0 g without significant damage.

Some researchers have investigated the collapse behavior of RC frames to further leverage the capabilities of shaking table tests. Li et al. [44] conducted shaking table tests on a 1:5 scale model of a three-story, single-span RC frame structure, revealing its collapse process under seismic loading, as illustrated in Figure 6. The frame transitioned from an elastic state to a highly nonlinear state, culminating in dynamic instability and eventual ground collapse. The collapse of the first, second, and third stories was attributed to the failure of plastic hinges in the columns. The analysis of the model’s dynamic characteristics, displacement, and acceleration response indicated that the frame had not yet collapsed when the maximum inter-story drift ratio and residual drift ratio reached 12.51% and 9.60%, respectively. Luo et al. [45] designed and tested a 1:5 scale model to investigate its complete collapse process and mechanisms under seismic loading. The model structure’s collapse process could be categorized into two phases: lateral incremental collapse and vertical continuous collapse. When the ground-floor inter-story drift angle reached 1/19, the test model was nearing collapse. During the collapse process, the ground-floor corner column first lost its vertical load-bearing capacity, initiating vertical collapse. Under the combined effects of gravity loads and input ground motion, the horizontal lateral displacement of the ground-floor columns continued to increase, causing the sequential failure of adjacent columns and the loss of their vertical load-bearing capacity. These studies provide valuable insights into the collapse behavior of RC frame structures in high-intensity seismic regions, providing experimental evidence to enhance their seismic performance and anti-collapse capabilities.

This study provides an analysis and synthesis of the dynamic responses, damage characteristics, collapse behavior, energy dissipation, and failure mechanisms of RC frame structures through shaking table tests. In terms of dynamic responses, shaking table tests allow for the direct observation and recording of displacement, acceleration, velocity, and other data under simulated earthquake conditions. For instance, the non-uniform yielding of frame structures and uncertainties inherent in construction significantly impact the torsional response, particularly during low-intensity earthquakes. In terms of dynamic characteristic damage, these tests directly reveal the damage evolution process of RC structures, from crack initiation to propagation and coalescence. As seismic intensity increases, structural damage accumulates, leading to reduced frequencies of higher-order modes and diminished modal shape amplitudes, indicating increased structural damage. Shaking table tests also elucidate the collapse process and failure mechanisms of RC frame structures under seismic loading, offering crucial insights into understanding their seismic performance and anti-collapse capabilities in high-intensity regions. Moreover, these tests verify the effectiveness of non-primary load-bearing components, such as infill walls, in improving the initial stiffness and lateral strength of frame structures. This study significantly enhances our understanding of the behavior of RC frame structures under seismic events and provides valuable data and insights for their design, evaluation, and strengthening. Future research should continue to explore innovative materials, technologies, and design methodologies to further optimize the seismic resilience and safety of these structures.

4.2. Shaking Table Tests of Steel Frame Structures

Compared to RC structures, steel frame structures exhibit superior ductility and toughness, offering better resistance to earthquakes. Therefore, some researchers have conducted studies on steel frame structures using shaking table tests to gain a deeper understanding of their seismic performance. Morita et al. [46] performed two damage detection tests on steel frame structures using shaking table tests. An increase in the seismic excitation amplitude led to a decrease in natural frequency, an increase in damping ratio, and a reduction in floor stiffness. These findings validated a damage assessment method based on micro-vibration observations and structural design principles, which was useful for assessing post-earthquake damage to buildings. Kim et al. [47] performed a shaking table test on a two-story unsupported steel frame structure to verify the accuracy of second-order inelastic dynamic analysis, as shown in Figure 7. The test results provided strain measurements across the elastic to plastic range, including the plastic–moment interaction curves and inter-story displacement–shear curves, which validate the effectiveness of second-order inelastic dynamic analysis. Saranik et al. [48] conducted a series of shaking table tests on a five-story steel frame and a large three-story steel frame equipped with a cement-based device. These tests focused on the inelastic behavior of steel frame structures under dynamic loads, particularly the progression of low-cycle fatigue (LCF) damage in frame connections and its impact on structural modal parameters. The results showed that increasing the earthquake’s amplitude led to decreased natural frequency, increased damping ratio, and reduced floor stiffness, consistent with cumulative damage effects. Based on the shaking table test findings, a fatigue damage-based hysteretic model was developed to simulate nonlinear behavior at connections, accounting for stiffness degradation due to the cumulative effects of LCF damage. Zhang et al. [49] conducted full-scale shaking table tests on a two-story model of an assembled light steel frame structure featuring L-shaped columns. As the PGA of the earthquake wave increased from 0.07 g to 0.9 g, the natural frequency and acceleration amplification factor gradually decreased, with the maximum inter-story displacement occurring on the first floor. The L-shaped truss columns remained in the elastic state at 0.2 g PGA, but at 0.4 g PGA, some truss joints cracked and entered the plastic state. At 0.62 g PGA, plastic deformation increased but the structure retained some load-bearing capacity. However, at 0.9 g PGA, the stiffness of the structure was seriously degraded. After experiencing gradual plastic deformation, the structure maintained a certain load-bearing capacity and exhibited good ductility, making it suitable for high-seismic fortification areas.

Owing to the advantageous characteristics of steel, a greater variety of connection forms in steel frame structures has been developed. Researchers have introduced innovative connection types and investigated their seismic performance through shaking table tests. Chung et al. [50] and Ji et al. [51] conducted a series of tests on a large-scale model representing high-rise steel structures using the E-Defense shaking table. The model incorporated two connection types prevalent in early high-rise construction in Japan during the 1970s: field-welded and shop-welded connections. The steel frame test model featured 24 beam–column connections that were subjected to repeated vibrations until failure. The field-welded connections failed at the bottom flange weld boundaries because of welding quality problems during on-site operations, even under relatively small cumulative rotations. However, the shop-welded connections endured multiple plastic rotations, demonstrating ductile failure after numerous cycles. Zhang et al. [52] investigated the seismic performance of a fully bolted prefabricated steel frame structure (ABPSFS) through shaking table tests on a 1:4 scale model, as shown in Figure 8. The test results indicated that the ABPSFS failure modes primarily included flange plate warping, washer slippage in bolted connections, and concrete slab cracking. As the PGA increased, the fundamental frequency and stiffness of the test model decreased, while the damping ratio increased. The splice layer became the weakest point of the frame, with a notable increase in its acceleration amplification factor. Cabaleiro et al. [53] assessed the stiffness variations between clamped and bolted joints in steel structures under dynamic external loads using shaking table tests. The frame structure with bolted connections exhibited a higher natural frequency than the clamped frame under the same dynamic load, indicating higher stiffness of bolted connections. The model maintained good integrity during the test, but its stiffness decreased. Li et al. [54] examined the effects of three steel connection types—common joint, reduced beam section joint (RJ), and cover plate joint (CPJ)—on the seismic performance of steel frame structures. Through shaking table tests, three different types of 1:2 scale steel frame models with different joints were tested. The seismic damage was primarily concentrated at the beam–column joints of the ground floor. By reinforcing beam ends and reducing flange sections, plastic hinge formation could be transferred, significantly improving the seismic capacity. As the seismic excitation increased, the seismic shear coefficients of the CPJ and RJ steel frames increased, and the structural capacity curve rose steadily, indicating excellent seismic performance and ductility. Reinforcing the lower flange can enhance the seismic performance of structures in engineering projects.

Diversified connection forms in steel frame structures allow for better adaptation to different architectural design needs. However, compared to concrete frame structures, steel frames exhibit lower inter-story stiffness, leading to greater inter-story displacement responses during seismic events. To enhance lateral displacement stiffness and seismic performance, some scholars have incorporated infill walls within steel frame structures. Yu et al. [55] performed shaking table tests and numerical analyses on a 1:12 scale model of a special centrally braced steel frame by using various ground motion acceleration records to simulate seismic excitation in high-intensity regions. During rare and extremely rare earthquakes, both the maximum inter-story displacement and the inter-story displacement angle demonstrated satisfactory seismic performance. Dong et al. [56] designed a 1:6.5 scale model of a structure featuring a three-story, three-bay, two-span steel frame with low-ductility herringbone central braces in the middle bay. Under a 0.2 g PGA earthquake, the bottom support of the structure failed, but the reserve system avoided the resonance period of the hard soil site earthquake wave, showing no obvious damage even after loading beyond 0.62 g PGA. The study indicated that well-designed reserve systems can enhance the seismic performance and anti-collapse capabilities of low-ductility centrally braced steel frame structures.

Incorporating bracing into steel frame structures significantly enhances their lateral stiffness. However, the complexity of the connections between the bracing and steel frame can impact the construction process. Consequently, some researchers have employed external wall panels to augment both the stiffness and damping properties of steel frame structures. Du et al. [57] proposed a prefabricated steel frame structure system incorporating autoclaved aerated concrete exterior wall panels. A two-story, full-scale steel frame structure model was subjected to seismic simulation tests to analyze the seismic responses under different seismic waves. The stiffness and damping ratio of the test model increased by 56% and 7.7%, respectively, compared to a steel structure without filled wall panels. At a PGA of 0.07 g, the maximum inter-story displacement angle was 1/429, with both wall panels and connection joints performing well. However, under a 0.4 g PGA earthquake, the frame’s stiffness was severely reduced, nearly equal to that of the bare frame. Rao et al. [58] integrated extruded cement-fiber wall panels into a steel frame structural system and investigated its dynamic characteristics and seismic performance via full-scale shaking table tests. Under a 7.5-degree earthquake (0.31 g), the steel frames remained elastic and exhibited good seismic performance. The wall panels and their joints also demonstrated robust seismic performance, with no cracks in the exterior parts, no structural adhesive detachment, and no abnormal phenomena such as bolt loosening in the connections. Zhang et al. [59] introduced an assembled steel frame structure featuring ribbed thin-walled panels. As the PGA increased, the thin-walled panels, which are the first line of defense against earthquakes, gradually cracked and deformed, leading to a gradual degradation of structural stiffness. In contrast, the steel frame damage remained minimal. The maximum inter-story displacement angles at the 8-degree frequent and rare earthquake intensities were 1/868 and 1/220, respectively. At 0.62 g PGA, the maximum inter-story displacement angle reached 1/71 without model collapse, indicating good seismic performance suitable for high-seismic fortification areas.

Shaking table tests provide further insights into the dynamic response and inelastic behavior of steel frame structures under seismic loading, demonstrating their potential and efficacy for seismic-resistant designs. Research indicates that the seismic performance and ductility of steel frame structures can be significantly enhanced through structural optimization, the implementation of innovative connection technologies, and the incorporation of bracing or infill wall devices. The dynamic response of steel frame structures to earthquakes is typically substantial, and shaking table tests can accurately capture this response. Damage in steel frame structures usually manifests as failures at connections and the buckling of members, which shaking table tests vividly illustrate. Steel frame structures often employ bracing or infill wall devices to enhance their seismic protection and damping capabilities. During extreme seismic actions, these devices act as the first line of defense, absorbing energy and sustaining damage before the main frame, effectively safeguarding the primary structure. Shaking table tests on steel frame structures offer valuable data and insights for their seismic design. These tests confirm that with proper design and reinforcement measures, the seismic performance of steel frame structures can be effectively improved, ensuring their safety and reliability under seismic loading. Future research should continue to investigate advanced technologies and structural systems to further enhance the seismic performance of steel frame structures.

4.3. Shaking Table Tests of Steel–Concrete Composite Frame Structures

The design philosophy behind steel–concrete composite frames aims to integrate the cost-effectiveness, fire resistance, and durability characteristics of RC structures with the rapid construction and convenient connection options offered by steel structures [60]. Research indicates that these composite frames exhibit favorable seismic performance and can satisfy the seismic design criteria for regions with high-seismic intensity [61]. However, the majority of current research focuses on the nodal level, and research on the seismic response of the overall structural system remains scarce. It should be noted that the current sensor configurations cannot easily capture interface behavior and bond–slip effects at steel–concrete interfaces in the overall frame shaking table test.

Some scholars have integrated steel sections typically used in steel frames with concrete to create steel–concrete composite frames that offer enhanced seismic performance. Xue et al. [62] performed shaking table tests on a 1:4 scale model of a three-bay, two-span, five-story steel–concrete composite special-shaped column spatial frame. Under strong seismic action, the steel–concrete special-shaped column frame exhibited a typical beam-hinge failure mechanism, fulfilling the seismic design principle of a strong column and weak beam. As the PGA increased, the cumulative damage of the test model gradually increased, and the natural frequency decreased. The hysteresis curve was full, indicating good energy-dissipation capacity. This suggests that the steel–concrete special-shaped column frame can satisfy the seismic fortification requirements of strong columns and weak beams and can resist collapse under strong earthquakes. Liu et al. [63] designed and fabricated a 1:4 scale model of a five-story, three-bay, two-span solid-web steel–concrete composite special-shaped column frame spatial structure. Through shaking table tests and numerical simulations, the researchers analyzed the distribution of floor displacement and inter-story displacement angles along the height of the structure, as well as the strain and moment–curvature hysteresis curves of the components.

Some researchers have harnessed the properties of steel tube concrete in frame structures, resulting in the development of innovative steel–concrete composite frames. Li et al. [64] introduced a novel prefabricated structural system that integrated the benefits of prefabricated construction with the performance of steel tube concrete columns and RC beams. To investigate the overall seismic performance of this novel system, the researchers designed and fabricated a 1:3 scale, six-story model and subjected it to seismic excitation of varying intensities. This structural system exhibited the desirable failure mode of strong steel tube concrete columns and weak RC beams. Beam failure occurred at the interface between the I-beam flange and RC beam section at a certain distance from the core area of the beam–column joint, ensuring the integrity of the core area of the joint. Zhang et al. [65] performed a full-scale shaking table test on a prefabricated square steel tube concrete–column frame structure. With increasing PGA, the natural frequency of the model decreased, while the damping ratio increased. The floor acceleration amplification coefficient ranged from 1.2 to 1.8 and showed a decreasing trend.

To harness the full potential of steel–concrete composite structures, some scholars have suggested employing various structural configurations across different floors and have explored their actual seismic performance through shaking table tests. Lu et al. [66] performed a shaking table test on a 12-story steel-RC (S/RC) hybrid structure to evaluate its performance under seismic excitation. The performance of the S/RC frame was assessed by comparing the test results with those of a standard 12-story RC frame structure. The results indicated that irregularities in the lateral stiffness distribution throughout the building height could lead to increased torsion at the connections between different structural components. This caused pronounced rigid deformation in the steel frame component of the S/RC structure, which exacerbated bending damage. Moreover, when the characteristic site period was close to the upper steel frame period, its acceleration response peaked. Zhao et al. [67] designed and constructed a 1:1 scale model of an innovative prefabricated light steel hybrid frame structure. The first floor was a steel frame, while the second floor was a steel–concrete hybrid structure. Under the action of a rare earthquake (0.9 g), the first two natural frequencies of the structure decreased slightly. This indicates that the structure’s stiffness changed minimally after the model test, and the components exhibited strong deformation capacity. The structure remained intact and could be reset well after loading, with no adverse phenomena such as local buckling or component damage.

In summary, steel–concrete composite structures combine the advantages of both RC and steel structures, offering diverse configurations and enhanced seismic resistance. The dynamic responses of these structures during seismic events tend to be more complex, necessitating a comprehensive assessment of the properties of both steel and concrete. The dynamic responses and failure mechanisms of steel–concrete composite structures under seismic loading differ from those of single-material structures, with damage and failure predominantly localized at joints and connections. Optimizing joint design and employing suitable connection techniques can significantly enhance the overall seismic performance of the structure. Research on shaking table tests of steel–concrete composite frames provides a scientific foundation for their application in seismically active regions, demonstrating the potential of these frames for improving the seismic performance of structures. Future studies should continue to focus on the overall performance of these structural systems, particularly their dynamic responses and collapse mechanisms under various seismic wave inputs. Additionally, research should explore the use of new materials and innovative designs to further enhance the seismic performance of steel–concrete composite frames. Steel–concrete composite structures often require the consideration of issues such as connection slippage and abrupt stiffness changes at the steel–concrete interface. Therefore, when designing shaking table tests for such structures, it is recommended to use fine aggregate concrete materials and apply the stiffness similarity principle to design the steel components of the structure.

4.4. Shaking Table Tests of External Dampers and Self-Centering Frame Structures

Because pure frame structural systems exhibit significant seismic responses during actual earthquakes and suffer from severe earthquake-induced disasters, some experts have incorporated external dampers into frame structures. By reviewing the shaking table test studies conducted on frame structures with external dampers, this study analyzes their dynamic response, impact of damage on dynamic characteristics, damping performance, and failure mechanisms under actual earthquake conditions.

Research has indicated that seismic isolation measures in frame structures typically employ devices to decouple the structure from earthquake excitation, thereby mitigating earthquake hazards. Zheng et al. [68] introduced a seismic isolation frame structure utilizing friction pendulums, which are common seismic isolation devices that separate foundations from superstructures, safeguarding them from seismic damage. A four-story frame structure and a seismic isolation structure were designed, and the shaking table test was conducted. The friction pendulum exhibited substantial seismic isolation capabilities, significantly reducing both floor displacement and acceleration by over 50%. This suggests that friction pendulum seismic isolation bearings can effectively shield the upper structure from earthquake excitation and reduce the overall structural impact. The friction pendulum seismic isolation bearing exhibited a plump hysteresis curve, indicative of its robust energy-dissipation capabilities. The friction pendulum showed almost no residual displacement after the test, and the sliding surface remained undamaged, further confirming the effectiveness and durability of friction pendulum seismic isolation bearings.

Seismic isolation measures can effectively mitigate structural responses to earthquakes; however, their complex designs hinder their widespread adoption. Consequently, seismic damping measures, which reduce structural responses by enhancing the energy-dissipation and damping capacities, have become the central focus of numerous researchers. Compared to traditional bracing, buckling-restrained braces provide a smaller increase in frame stiffness. Their core concept is to achieve seismic energy dissipation through plastic deformation of the brace core. Some scholars have employed buckling-restrained braces as external dampers in frame structures. Guerrero et al. [69] applied buckling restrained braces (BRBs) to precast RC models and evaluated their performance through shaking table tests. BRBs significantly increased the damping ratio and improved seismic performance, particularly under high-seismic intensity. BRBs also help delay and reduce stiffness degradation in RC models, which is crucial for short-period structures under low-frequency ground motion. Model 1 (without BRBs) started with 0.8% of the damping ratio and reached 5.8%, while Model 2 (with BRBs) started at 5.4% and reached 10.3%. The inter-story and lateral displacements of the model with BRBs were approximately half of those without BRBs.

In addition to the traditional bracing forms of dampers, some scholars have studied other forms of dampers. Xin et al. [70] investigated the seismic retrofit effectiveness and performance of viscous fluid dampers (VFDs) in large-space RC (LSRC) frames. Based on a completed test of a 1:6 scale, uncontrolled frame model, another shaking table test was conducted on a model with VFDs. The seismic damping model effectively controlled inter-story displacements, reducing the maximum inter-story displacement angle from 1/102 to 1/194 under rare earthquakes. The dampers performed well, with their force increasing as the seismic excitation intensified, reaching 88% of the designed limit. This demonstrates that adding VFDs to LSRC frames can significantly enhance seismic performance, particularly in reducing the maximum inter-story displacement angles. Yang et al. [71] examined a novel nonlinear vibration absorber, the nonlinear energy sink (NES), composed of a horizontal track and an additional mass that transfers energy by creating a horizontal nonlinear restoring excitation, thereby reducing the response of the primary structure. Theoretical analysis and shaking table experiments showed that NES dampers significantly reduced the response of damaged RC frames under seismic action and improved their seismic performance. After installing the NES, the top displacement and acceleration responses of the structure were considerably reduced. The NES demonstrated sufficient nonlinear displacement and energy-dissipation capacity under medium and strong earthquakes, with good damping effects.

Beyond directly enhancing structural damping and energy-dissipation capabilities, some scholars have emphasized that the post-earthquake recoverability of structures is essential for post-disaster reconstruction following earthquakes. Lu et al. [72] designed a self-centering RC frame and conducted shaking table tests on a 1:2 scale model. The model demonstrated its ability to withstand a PGA of up to 0.6 g with minor damage and effective self-centering capabilities, returning to its initial position with minimal residual deformation after seismic excitation. Cui et al. [73] proposed a three-axis self-centering RC frame structure in which post-tensioned strands passing through RC beams and columns provided self-centering capabilities. Rubber pads under the floor accommodated gap openings at beam–column joints, enabling smooth sliding between the RC beams and slabs, as presented in Figure 9. Slab sliding was measured directly using linear variable displacement transducers (LVDTs). Shaking table tests on a 1:2.5 scale model revealed that this self-centering RC frame structure exhibited ideal seismic performance with minimal damage, even under extreme earthquakes, and remained largely elastic with only a slight decrease in its natural frequency. The model demonstrated effective three-axis self-centering capabilities and minimal residual deformation. Li et al. [74] employed a shape memory alloy (SMA) and disk spring self-centering devices to retrofit existing frame structures, as displayed in Figure 10. Shaking table tests on the new structural test model and a comparison model without reinforcement showed that the unreinforced structure suffered severe damage and nearly collapsed after a PGA of 1.2 g, with some reinforcement bars at the bottom of the beams breaking and concrete at the beam ends and column feet being crushed. In contrast, the reinforced structure experienced significantly less damage after a PGA of 1.5 g, with only minor cracks and slightly crushed concrete at the column feet, as well as no noticeable damage to the self-centering devices. Compared to the unreinforced structure, the reinforced structure exhibited reductions of 86.7% in maximum inter-story displacement and 91.2% in residual deformation.

Some researchers have integrated external dampers and self-centering measures into frame structures and investigated their actual seismic responses through shaking table tests. Lu et al. [75] incorporated externally applied prestressing for enhancing structural lateral stiffness and displacement control strategies utilizing dampers within RC frames. Energy-dissipating dampers were installed between the structural stories to control the overall displacement and consume seismic energy. Shaking table tests on a 1:3 scale experimental model demonstrated that under rare earthquakes, the designed test model acceleration response was one-third to one-half of that of conventionally designed frames, whereas the displacement response met the preset requirements. The inter-story displacement angle under rare earthquakes was approximately 1/60, which is close to that of conventionally designed frames. Lu et al. [76] arranged energy-dissipating self-centering hinge joints (EDSC-HJs) in RC frame structures to achieve rapid restoration of post-earthquake functionality. They conducted shaking table tests on a 1:3 scale, three-story, two-span EDSC-HJ frame structure model. Under rare earthquakes, compared with conventionally designed frames, the acceleration seismic responses of the EDSC-HJ frame uncontrolled and controlled structures decreased by approximately 60–70% and 47–63%, respectively, with the displacement seismic response also meeting preset limit value requirements. The results show that EDSC-HJs are damage-resistant, easily repairable, and ductile. Self-centering capabilities enable structures to quickly restore functionality after an earthquake, thereby reducing the time and cost of post-disaster reconstruction. Besides the large-scaled test, the small-scaled shaking table test could also provide the dynamic performance of novel structures. Masnata et al. [77,78] investigates a hybrid passive vibration control strategy by combining a base-isolated (BI) structure with a sliding tuned liquid column damper (STLCD) to enhance seismic performance. The STLCD, featuring a U-shaped tank on rollers connected to the BI system via a spring–dashpot mechanism, offers improved tuning flexibility and damping compared to conventional TLCDs. Theoretical formulations derive optimal STLCD parameters under stochastic excitation, which were validated numerically and experimentally via small-scale shaking table tests. Results demonstrate that the BI-STLCD system reduces base displacements by up to 90%, outperforming TLCDs and matching TMD efficacy while leveraging cost-effective liquid mass. The study highlights STLCD’s potential as a versatile solution for seismic mitigation in BI structures.

In summary, incorporating external dampers and self-centering devices in frame structures can significantly mitigate the risks to structures during earthquakes. Shaking table tests allow for observing and recording the displacement and acceleration in seismic mitigation frame structures during earthquakes, thereby assessing their effectiveness. These tests can evaluate the operational performance of external dampers and self-centering devices, as well as their contributions to the overall seismic performance of the structures. Advancements in external dampers and self-centering technologies offer new avenues for the seismic design of frame structures. Future research on external dampers and self-centering frame structures should focus on their optimization and integration to ensure the high performance of structures during earthquakes and facilitate rapid post-disaster recovery. The continuous development and application of these technologies will considerably enhance the seismic resilience of building structures and minimize losses during earthquakes. The external damper has a higher similarity requirement for the damping ratio. Therefore, it is recommended to use the same material properties and full mass similarity in the shaking table test of such buildings.

5. Conclusions

Numerical shaking table tests for novel frames are proposed in this study. The main conclusions are as follows:

• The flexible form of frame structures makes it difficult to develop a unified test design method for shaking table tests. To accommodate specific test requirements and structural forms, a reasonable test design method must be selected from various similarity calculation methods and similarity rate design approaches. A highly flexible dimensional analysis method is suggested to determine the similarity relationships for the test. By disregarding less significant errors, the accuracy of critical parameter data can be ensured, leading to positive results in the testing process. Full-scale models provide the highest degree of similarity and can accurately simulate the dynamic characteristics of prototype structures under seismic action. Therefore, full-scale models are preferable when conditions allow for them. However, when conditions are constrained, particularly for high-rise buildings or structures sensitive to vertical loads, stress similarity should be prioritized. For low-rise frame structures, an equivalent density similarity design can be adopted to achieve a more precise simulation of the horizontal stress state.
• The input seismic waves should be selected from a seismic wave database that aligns with the site category and design seismic group specifications of the building location. This ensures that the selected seismic waves accurately reflect the actual conditions. Additionally, based on the specific objectives of the shaking table test, such as assessing seismic performance or evaluating seismic responses, additional appropriate seismic waves should be identified. By selecting suitable actual strong-motion earthquake records and artificially synthesized seismic waves, as well as adhering to specific selection procedures and considerations, the precision and effectiveness of the test results can be ensured.
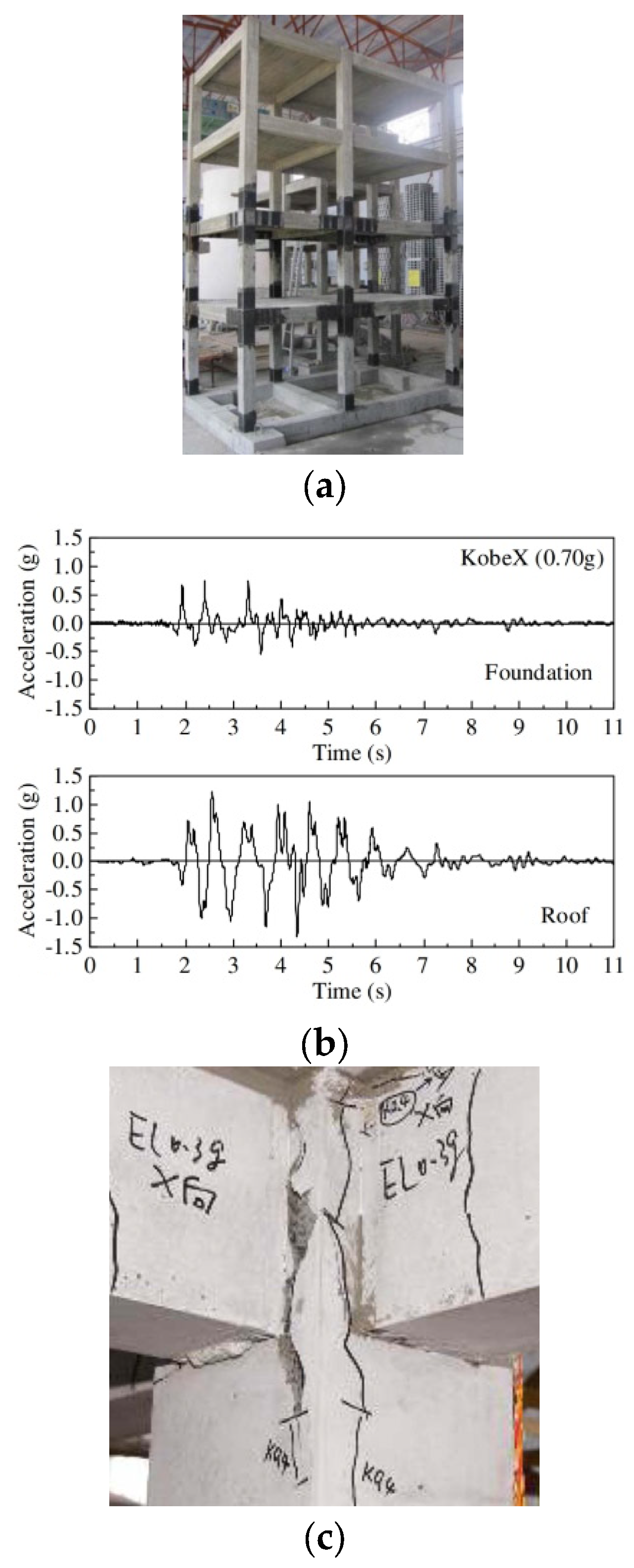
• Incorporating innovative materials, advanced reinforcement techniques, and sophisticated seismic protection measures can significantly enhance the seismic performance of RC frame structures under extreme earthquake conditions. These measures reduce structural damage and improve structural failure mechanisms. During low-intensity earthquakes, torsional effects can induce substantial damage to non-structural components. However, during high-intensity earthquakes, the impact of torsion on structural damage is minimal. As earthquake intensity increases, structural damage accumulates progressively, as evidenced by reductions in the higher-order vibration mode frequencies and modal shape amplitudes. Infill walls substantially augment the initial stiffness and lateral strength of RC frame structures. Nevertheless, as cumulative damage occurs, the stiffness of frame structures degrades. Infill walls can considerably enhance the safety of RC frame structures during major earthquakes. However, infill walls with openings are more susceptible to collapse than solid walls. Advanced concrete materials can significantly reduce structural damage, enhancing the structure’s deformability, energy-dissipation capabilities, and stiffness degradation rate.
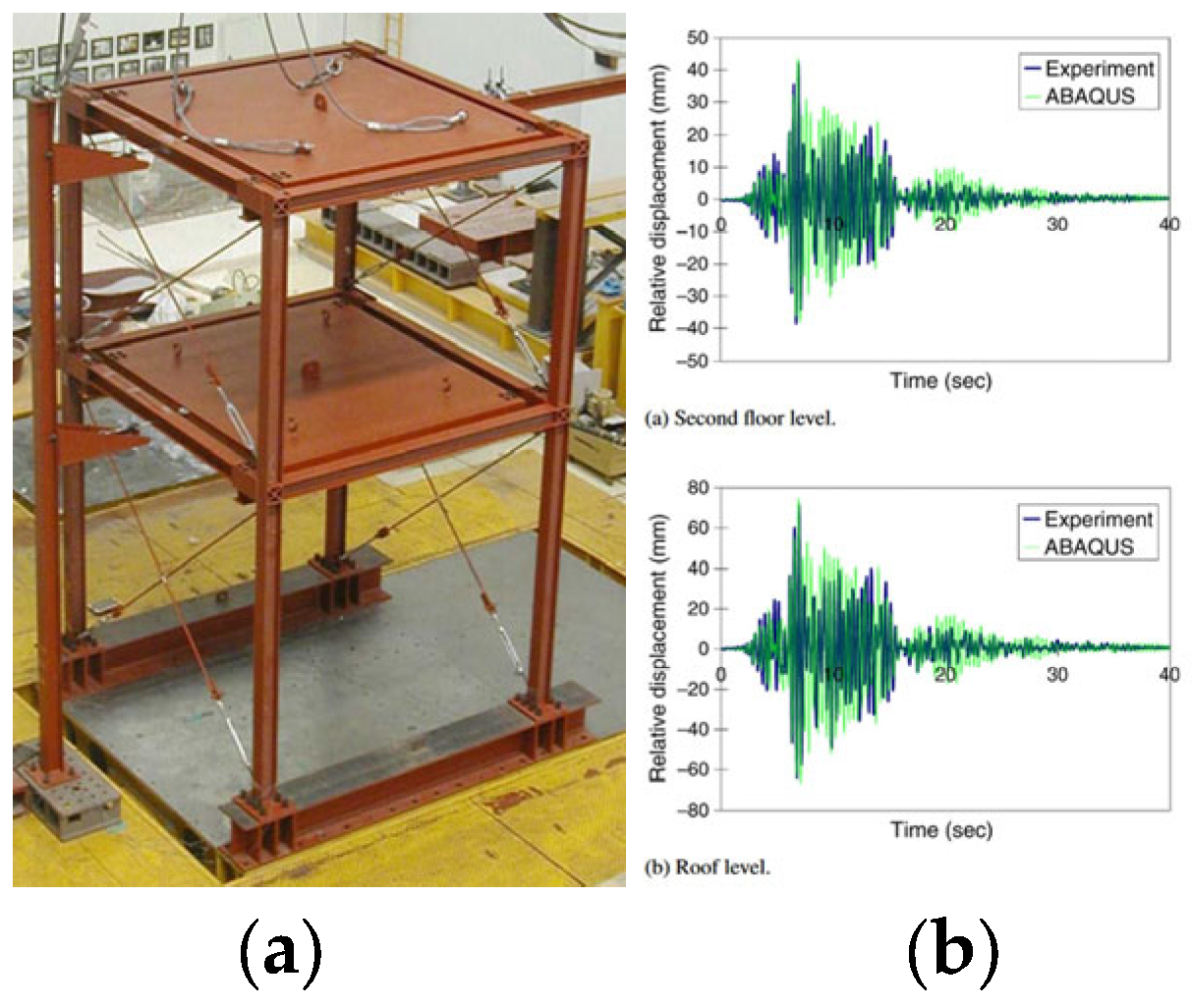
• Considering the inherent material properties of steel, steel frame structures typically exhibit significant dynamic responses during earthquakes. Despite experiencing plastic deformation, these structures maintain residual load-bearing capacity and demonstrate excellent ductility. In shaking table tests, damage to steel frame structures is often concentrated at connections. The configuration of connections considerably influences the seismic response of frame structures under actual earthquake conditions. Generally, steel connections outperform RC connections during earthquakes, and steel-connected frame structures demonstrate superior ductility. Integrating supplementary components, such as bracing and infill walls, can significantly augment the stiffness and damping characteristics of steel frame structures. These components reduce the seismic response, mitigate damage at connections, and act as a primary line of defense during extreme earthquakes. By sustaining damage before the main frame, they effectively protect the primary structure.
• Steel–concrete composite frame structures combine the distinctive attributes of both RC and steel structures, offering a diverse range of configurations with enhanced seismic resistance. The seismic performance of these composite structures is influenced by a multitude of factors, including the cross-sectional dimensions of steel and concrete components, as well as connection methodologies. These factors can be systematically evaluated through shaking table tests to assess their impacts on structural seismic performance. Composite structures incorporating steel sections and steel pipes with concrete typically exhibit a beam–hinge failure mechanism that aligns with the seismic design principle of strong columns and weak beams. Structural damage predominantly manifests as the initiation and propagation of concrete cracks within beams and columns; progressive yielding of flanges, webs, and longitudinal reinforcement at the beam ends of the steel sections; and bond–slip effects between the steel and concrete interfaces. As the structure transitions into the plastic stage, the base shear force initially increases rapidly and then gradually, forming complete hysteresis loops, indicative of a robust energy-dissipation capacity. In mixed-frame structures with varying structural configurations across different floors, the characteristic site period exerts the most significant influence on the peak acceleration response.
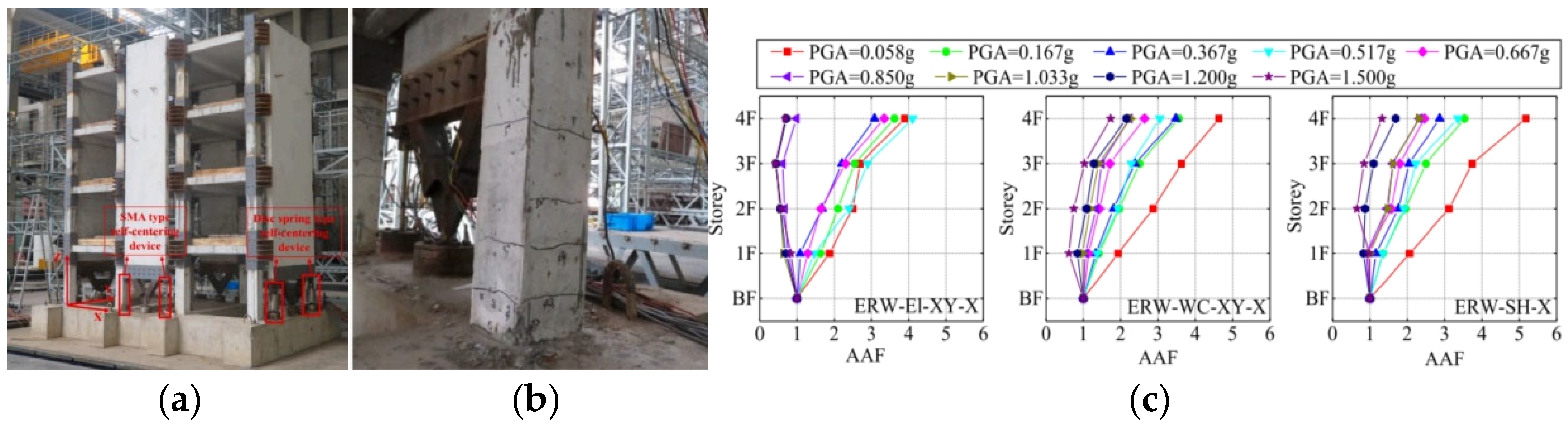
• The flexible design of external dampers can be more effectively integrated within frame structures to mitigate seismic risks. Among these dampers, seismic isolation dampers are particularly complex to design but are essential for protecting the upper structure and reducing seismic impact on the overall structure. In contrast, energy-dissipation dampers primarily protect the main structure by enhancing the energy-dissipation capacity of the frame, thereby reducing structural displacement and acceleration responses. Furthermore, under rare earthquakes, imparting a self-centering capability to frame structures is crucial for maintaining their integrity and functionality. This capability significantly diminishes post-seismic deformation and expedites rapid functionality restoration.